07-28-2023-1747 - draft (pharmacological classification system) (Draft)

 https://en.wikipedia.org/wiki/Category:Pharmacological_classification_systems

07-28-2023-1638 - Spectral theory and *-algebras (draft)

Functional analysis (topics – glossary)

v t e Spectral theory and *-algebras
Basic concepts	Involution/*-algebra Banach algebra B*-algebra C*-algebra Noncommutative topology Projection-valued measure Spectrum Spectrum of a C*-algebra Spectral radius Operator space
Main results	Gelfand–Mazur theorem Gelfand–Naimark theorem Gelfand representation Polar decomposition Singular value decomposition Spectral theorem Spectral theory of normal C*-algebras
Special Elements/Operators	Isospectral Normal operator Hermitian/Self-adjoint operator Unitary operator Unit
Spectrum	Krein–Rutman theorem Normal eigenvalue Spectrum of a C*-algebra Spectral radius Spectral asymmetry Spectral gap
Decomposition	Decomposition of a spectrum Continuous Point Residual Approximate point Compression Direct integral Discrete Spectral abscissa
Spectral Theorem	Borel functional calculus Min-max theorem Positive operator-valued measure Projection-valued measure Riesz projector Rigged Hilbert space Spectral theorem Spectral theory of compact operators Spectral theory of normal C*-algebras
Special algebras	Amenable Banach algebra With an Approximate identity Banach function algebra Disk algebra Nuclear C*-algebra Uniform algebra Von Neumann algebra Tomita–Takesaki theory
Finite-Dimensional	Alon–Boppana bound Bauer–Fike theorem Numerical range Schur–Horn theorem
Generalizations	Dirac spectrum Essential spectrum Pseudospectrum Structure space (Shilov boundary)
Miscellaneous	Abstract index group Banach algebra cohomology Cohen–Hewitt factorization theorem Extensions of symmetric operators Fredholm theory Limiting absorption principle Schröder–Bernstein theorems for operator algebras Sherman–Takeda theorem Unbounded operator
Examples	Wiener algebra
Applications	Almost Mathieu operator Corona theorem Hearing the shape of a drum (Dirichlet eigenvalue) Heat kernel Kuznetsov trace formula Lax pair Proto-value function Ramanujan graph Rayleigh–Faber–Krahn inequality Spectral geometry Spectral method Spectral theory of ordinary differential equations Sturm–Liouville theory Superstrong approximation Transfer operator Transform theory Weyl law Wiener–Khinchin theorem

Category:

• Spectral theory

 https://en.wikipedia.org/wiki/Spectral_radius

 

 

 

07-28-2023-1637 - spectral radius, spectral gap, spectrum of a matrix, etc.. draft

See also

• Spectral gap
• The Joint spectral radius is a generalization of the spectral radius to sets of matrices.
• Spectrum of a matrix
• Spectral abscissa

https://en.wikipedia.org/wiki/Spectral_radius

07-28-2023-1223 - DECOMPOSITION OF SPECTRUM (FUNCTIONAL ANALYSIS) (DRAFT)

The spectrum of a linear operator $T$ that operates on a Banach space $X$ is a fundamental concept of functional analysis. The spectrum consists of all scalars $\lambda$ such that the operator $T-\lambda$ does not have a bounded inverse on $X$. The spectrum has a standard decomposition into three parts:

• a point spectrum, consisting of the eigenvalues of $T$;
• a continuous spectrum, consisting of the scalars that are not eigenvalues but make the range of $T-\lambda$ a proper dense subset of the space;
• a residual spectrum, consisting of all other scalars in the spectrum.

This decomposition is relevant to the study of differential equations, and has applications to many branches of science and engineering. A well-known example from quantum mechanics is the explanation for the discrete spectral lines and the continuous band in the light emitted by excited atoms of hydrogen. 

https://en.wikipedia.org/wiki/Decomposition_of_spectrum_(functional_analysis)

07-28-2023-1222 - In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues.[1] More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by ρ(·). (DRAFT)

In mathematics, the spectral radius of a square matrix is the maximum of the absolute values of its eigenvalues.^[1] More generally, the spectral radius of a bounded linear operator is the supremum of the absolute values of the elements of its spectrum. The spectral radius is often denoted by ρ(·). 

https://en.wikipedia.org/wiki/Spectral_radius

07-28-2023-1210 - FASTER HARDWARE, LONG SHORT-TERM MEMORY, MULTI-LEVEL HIERARCHY, BACKPROPAGATION, FEATURE DETECTORS, LATENT VARIABLES, GENERATIVE MODEL, LOWER BOUND, DEEP BELIEF NETWORK, UNSUPERVISED LEARNING, SUPERVISED LEARNING VARIABLE TREND CURRICULUM INDOCTRINATION SCHEDULE, 1980, 1900, 1800 DUSTY BLUE, 1700 XLIF OR A BOMBER, 1600 WIFE OR N/A, -10000 HUMANS (HUMAN RECORD ONLY)(DRAFT)(VAR ENV)(DRAFT), <-10000 N/A, ETC.. DRAFT

Multi-level hierarchy

One is Jürgen Schmidhuber's multi-level hierarchy of networks (1992) pre-trained one level at a time through unsupervised learning, fine-tuned through backpropagation.^[10] Here each level learns a compressed representation of the observations that is fed to the next level.

Related approach

Similar ideas have been used in feed-forward neural networks for unsupervised pre-training to structure a neural network, making it first learn generally useful feature detectors. Then the network is trained further by supervised backpropagation to classify labeled data. The deep belief network model by Hinton et al. (2006) involves learning the distribution of a high level representation using successive layers of binary or real-valued latent variables. It uses a restricted Boltzmann machine to model each new layer of higher level features. Each new layer guarantees an increase on the lower-bound of the log likelihood of the data, thus improving the model, if trained properly. Once sufficiently many layers have been learned the deep architecture may be used as a generative model by reproducing the data when sampling down the model (an "ancestral pass") from the top level feature activations.^[11] Hinton reports that his models are effective feature extractors over high-dimensional, structured data.^[12]

Long short-term memory

Main article: Long short-term memory

Another technique particularly used for recurrent neural networks is the long short-term memory (LSTM) network of 1997 by Hochreiter & Schmidhuber.^[13] In 2009, deep multidimensional LSTM networks demonstrated the power of deep learning with many nonlinear layers, by winning three ICDAR 2009 competitions in connected handwriting recognition, without any prior knowledge about the three different languages to be learned.^[14][15] 

Faster hardware

Hardware advances have meant that from 1991 to 2015, computer power (especially as delivered by GPUs) has increased around a million-fold, making standard backpropagation feasible for networks several layers deeper than when the vanishing gradient problem was recognized. Schmidhuber notes that this "is basically what is winning many of the image recognition competitions now", but that it "does not really overcome the problem in a fundamental way"^[16] since the original models tackling the vanishing gradient problem by Hinton and others were trained in a Xeon processor, not GPUs.^[11]

https://en.wikipedia.org/wiki/Vanishing_gradient_problem

 

07-28-2023-1208 - VANISHING GRADIENT PROBLEM, EXPLODING GRADIENT PROBLEM, EXPLODING GRADIENT, ETC.. DRAFT

Part of a series on
Machine learning and data mining

Paradigms

Problems

Supervised learning (classification • regression)

Clustering

Dimensionality reduction

Structured prediction

Anomaly detection

Artificial neural network

Reinforcement learning

Learning with humans

Model diagnostics

Mathematical foundations

Machine-learning venues

Related articles

v t e

In machine learning, the vanishing gradient problem is encountered when training artificial neural networks with gradient-based learning methods and backpropagation. In such methods, during each iteration of training each of the neural networks weights receives an update proportional to the partial derivative of the error function with respect to the current weight.^[1] The problem is that in some cases, the gradient will be vanishingly small, effectively preventing the weight from changing its value.^[1] In the worst case, this may completely stop the neural network from further training.^[1] As one example of the problem cause, traditional activation functions such as the hyperbolic tangent function have gradients in the range (0,1], and backpropagation computes gradients by the chain rule. This has the effect of multiplying n of these small numbers to compute gradients of the early layers in an n-layer network, meaning that the gradient (error signal) decreases exponentially with n while the early layers train very slowly.

Back-propagation allowed researchers to train supervised deep artificial neural networks from scratch, initially with little success. Hochreiter's diplom thesis of 1991 formally identified the reason for this failure in the "vanishing gradient problem",^[2][3] which not only affects many-layered feedforward networks,^[4] but also recurrent networks.^[5] The latter are trained by unfolding them into very deep feedforward networks, where a new layer is created for each time step of an input sequence processed by the network. (The combination of unfolding and backpropagation is termed backpropagation through time.)

When activation functions are used whose derivatives can take on larger values, one risks encountering the related exploding gradient problem. 

https://en.wikipedia.org/wiki/Vanishing_gradient_problem

07-28-2023-1207 - Batch normalization (also known as batch norm) (DRAFT)

Batch normalization (also known as batch norm) is a method used to make training of artificial neural networks faster and more stable through normalization of the layers' inputs by re-centering and re-scaling. It was proposed by Sergey Ioffe and Christian Szegedy in 2015.^[1]

While the effect of batch normalization is evident, the reasons behind its effectiveness remain under discussion. It was believed that it can mitigate the problem of internal covariate shift, where parameter initialization and changes in the distribution of the inputs of each layer affect the learning rate of the network.^[1] Recently, some scholars have argued that batch normalization does not reduce internal covariate shift, but rather smooths the objective function, which in turn improves the performance.^[2] However, at initialization, batch normalization in fact induces severe gradient explosion in deep networks, which is only alleviated by skip connections in residual networks.^[3] Others maintain that batch normalization achieves length-direction decoupling, and thereby accelerates neural networks.^[4] 

https://en.wikipedia.org/wiki/Batch_normalization

07-28-2023-1206 - An echo state network (ESN)[1][2] (DRAFT)

The basic schema of an echo state network

An echo state network (ESN)^[1][2] is a type of reservoir computer that uses a recurrent neural network with a sparsely connected hidden layer (with typically 1% connectivity). The connectivity and weights of hidden neurons are fixed and randomly assigned. The weights of output neurons can be learned so that the network can produce or reproduce specific temporal patterns. The main interest of this network is that although its behaviour is non-linear, the only weights that are modified during training are for the synapses that connect the hidden neurons to output neurons. Thus, the error function is quadratic with respect to the parameter vector and can be differentiated easily to a linear system.

Alternatively, one may consider a nonparametric Bayesian formulation of the output layer, under which: (i) a prior distribution is imposed over the output weights; and (ii) the output weights are marginalized out in the context of prediction generation, given the training data. This idea has been demonstrated in^[3] by using Gaussian priors, whereby a Gaussian process model with ESN-driven kernel function is obtained. Such a solution was shown to outperform ESNs with trainable (finite) sets of weights in several benchmarks.

Some publicly available implementations of ESNs are: (i) aureservoir: an efficient C++ library for various kinds of echo state networks with python/numpy bindings; (ii) Matlab code: an efficient matlab for an echo state network; (iii) ReservoirComputing.jl: an efficient Julia-based implementation of various types of echo state networks; and (iv) pyESN: simple echo state networks in Python. 

https://en.wikipedia.org/wiki/Echo_state_network

07-28-2023-1205 - Deep learning speech synthesis uses Deep Neural Networks (DNN) (DRAFT)

Deep learning speech synthesis uses Deep Neural Networks (DNN) to produce artificial speech from text (text-to-speech) or spectrum (vocoder). The deep neural networks are trained using a large amount of recorded speech and, in the case of a text-to-speech system, the associated labels and/or input text.

Some DNN-based speech synthesizers are approaching the naturalness of the human voice. 

https://en.wikipedia.org/wiki/Deep_learning_speech_synthesis

07-28-2023-1204 - In mathematics and computer algebra, automatic differentiation (auto-differentiation, autodiff, or AD), also called algorithmic differentiation, computational differentiation,[1][2] is a set of techniques to evaluate the partial derivative of a function specified by a computer program. (DRAFT)

From Wikipedia, the free encyclopedia

In mathematics and computer algebra, automatic differentiation (auto-differentiation, autodiff, or AD), also called algorithmic differentiation, computational differentiation,^[1][2] is a set of techniques to evaluate the partial derivative of a function specified by a computer program.

Automatic differentiation exploits the fact that every computer calculation, no matter how complicated, executes a sequence of elementary arithmetic operations (addition, subtraction, multiplication, division, etc.) and elementary functions (exp, log, sin, cos, etc.). By applying the chain rule repeatedly to these operations, partial derivatives of arbitrary order can be computed automatically, accurately to working precision, and using at most a small constant factor of more arithmetic operations than the original program. 

https://en.wikipedia.org/wiki/Automatic_differentiation

Figure 1: How automatic differentiation relates to symbolic differentiation

Automatic differentiation is distinct from symbolic differentiation and numerical differentiation. Symbolic differentiation faces the difficulty of converting a computer program into a single mathematical expression and can lead to inefficient code. Numerical differentiation (the method of finite differences) can introduce round-off errors in the discretization process and cancellation. Both of these classical methods have problems with calculating higher derivatives, where complexity and errors increase. Finally, both of these classical methods are slow at computing partial derivatives of a function with respect to many inputs, as is needed for gradient-based optimization algorithms. Automatic differentiation solves all of these problems. 

https://en.wikipedia.org/wiki/Automatic_differentiation

Categories:

• Classification algorithms
• Neural network architectures

https://en.wikipedia.org/wiki/Multilayer_perceptron

 

Differentiable computing
General	Differentiable programming Information geometry Statistical manifold Automatic differentiation Neuromorphic engineering Pattern recognition Tensor calculus Computational learning theory Inductive bias
Concepts	Gradient descent SGD Clustering Regression Overfitting Hallucination Adversary Attention Convolution Loss functions Backpropagation Normalization (Batchnorm) Activation Softmax Sigmoid Rectifier Regularization Datasets Augmentation Diffusion Autoregression
Applications	Machine learning In-context learning Artificial neural network Deep learning Scientific computing Artificial Intelligence Language model Large language model
Hardware	IPU TPU VPU Memristor SpiNNaker
Software libraries	TensorFlow PyTorch Keras Theano JAX LangChain
Implementations	Audio–visual AlexNet WaveNet Human image synthesis HWR OCR Speech synthesis Speech recognition Facial recognition AlphaFold DALL-E Midjourney Stable Diffusion Verbal Word2vec Seq2seq BERT LaMDA Bard NMT Project Debater IBM Watson GPT-2 GPT-3 ChatGPT GPT-4 GPT-J Chinchilla AI PaLM BLOOM LLaMA Decisional AlphaGo AlphaZero Q-learning SARSA OpenAI Five Self-driving car MuZero Action selection Auto-GPT Robot control
People	Yoshua Bengio Alex Graves Ian Goodfellow Stephen Grossberg Demis Hassabis Geoffrey Hinton Yann LeCun Fei-Fei Li Andrew Ng Jürgen Schmidhuber David Silver
Organizations	Anthropic EleutherAI Google DeepMind Hugging Face OpenAI Meta AI Mila MIT CSAIL
Architectures	Neural Turing machine Differentiable neural computer Transformer Recurrent neural network (RNN) Long short-term memory (LSTM) Gated recurrent unit (GRU) Echo state network Multilayer perceptron (MLP) Convolutional neural network Residual network Autoencoder Variational autoencoder (VAE) Generative adversarial network (GAN) Graph neural network
Portals Computer programming Technology Categories Artificial neural networks Machine learning

07-28-2023-1202 - 1980 ML RECOG (OLD TECH), LAYERD MEMORY MAGNETICARY UNITS, ETC.. PERCEPTRONICS, ELECTRONIC, MAGNETRONICS, DARK MATTER, NUCLEAR, CONDENSED MATTER PHYSICS, NUCLEAR PHYSICS, ETC.. DRAFT

MLPs were a popular machine learning solution in the 1980s, finding applications in diverse fields such as speech recognition, image recognition, and machine translation software,^[23] but thereafter faced strong competition from much simpler (and related^[24]) support vector machines. Interest in backpropagation networks returned due to the successes of deep learning. 

https://en.wikipedia.org/wiki/Multilayer_perceptron

As late as 2021, a very simple NN architecture combining two deep MLPs with skip connections and layer normalizations was designed and called MLP-Mixer; its realizations featuring 19 to 431 millions of parameters were shown to be comparable to vision transformers of similar size on ImageNet and similar image classification tasks.^[22] 

https://en.wikipedia.org/wiki/Multilayer_perceptron

 

07-28-2023-1202 - Learning occurs in the perceptron by changing connection weights after each piece of data is processed, based on the amount of error in the output compared to the expected result. This is an example of supervised learning, and is carried out through backpropagation, a generalization of the least mean squares algorithm in the linear perceptron. (DRAFT)

Learning occurs in the perceptron by changing connection weights after each piece of data is processed, based on the amount of error in the output compared to the expected result. This is an example of supervised learning, and is carried out through backpropagation, a generalization of the least mean squares algorithm in the linear perceptron. 

https://en.wikipedia.org/wiki/Multilayer_perceptron

07-28-2023-1201 - In recent developments of deep learning the rectified linear unit (ReLU) is more frequently used as one of the possible ways to overcome the numerical problems related to the sigmoids. (DRAFT)

In recent developments of deep learning the rectified linear unit (ReLU) is more frequently used as one of the possible ways to overcome the numerical problems related to the sigmoids. 

https://en.wikipedia.org/wiki/Multilayer_perceptron

07-28-2023-1201 - A multilayer perceptron (MLP) (DRAFT)

From Wikipedia, the free encyclopedia

"MLP" is not to be confused with "NLP", which refers to natural language processing.

Part of a series on
Machine learning and data mining

Paradigms

Problems

Supervised learning (classification • regression)

Clustering

Dimensionality reduction

Structured prediction

Anomaly detection

Artificial neural network Autoencoder Cognitive computing Deep learning DeepDream Multilayer perceptron RNN LSTM GRU ESN reservoir computing Restricted Boltzmann machine GAN Diffusion model SOM Convolutional neural network U-Net Transformer Vision Spiking neural network Memtransistor Electrochemical RAM (ECRAM)

Reinforcement learning

Learning with humans

Model diagnostics

Mathematical foundations

Machine-learning venues

Related articles

v t e

A multilayer perceptron (MLP) is a fully connected class of feedforward artificial neural network (ANN). The term MLP is used ambiguously, sometimes loosely to mean any feedforward ANN, sometimes strictly to refer to networks composed of multiple layers of perceptrons (with threshold activation)^{[citation needed]}; see § Terminology. Multilayer perceptrons are sometimes colloquially referred to as "vanilla" neural networks, especially when they have a single hidden layer.^[1]

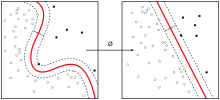
An MLP consists of at least three layers of nodes: an input layer, a hidden layer and an output layer. Except for the input nodes, each node is a neuron that uses a nonlinear activation function. MLP utilizes a chain rule^[2] based supervised learning technique called backpropagation or reverse mode of automatic differentiation for training.^{[3][4][5][6][7]} Its multiple layers and non-linear activation distinguish MLP from a linear perceptron. It can distinguish data that is not linearly separable.^[8] 

https://en.wikipedia.org/wiki/Multilayer_perceptron

07-28-2023-1200 - LATENT CLASS ANALYSIS DRAFT

• 
  
• 
  
• 
  
• 
  
• 
  
• 
  
• 
  
• 
  

• 
  
• 
  

From Wikipedia, the free encyclopedia

In statistics, a latent class model (LCM) relates a set of observed (usually discrete) multivariate variables to a set of latent variables. It is a type of latent variable model. It is called a latent class model because the latent variable is discrete. A class is characterized by a pattern of conditional probabilities that indicate the chance that variables take on certain values.

Latent class analysis (LCA) is a subset of structural equation modeling, used to find groups or subtypes of cases in multivariate categorical data. These subtypes are called "latent classes".^[1][2]

Confronted with a situation as follows, a researcher might choose to use LCA to understand the data: Imagine that symptoms a-d have been measured in a range of patients with diseases X, Y, and Z, and that disease X is associated with the presence of symptoms a, b, and c, disease Y with symptoms b, c, d, and disease Z with symptoms a, c and d.

The LCA will attempt to detect the presence of latent classes (the disease entities), creating patterns of association in the symptoms. As in factor analysis, the LCA can also be used to classify case according to their maximum likelihood class membership.^[1][3]

Because the criterion for solving the LCA is to achieve latent classes within which there is no longer any association of one symptom with another (because the class is the disease which causes their association), and the set of diseases a patient has (or class a case is a member of) causes the symptom association, the symptoms will be "conditionally independent", i.e., conditional on class membership, they are no longer related.^[1]

^{https://en.wikipedia.org/wiki/Latent_class_model}