Billy the Kid (1911 film)
| Billy the Kid | |
|---|---|
| Directed by | Laurence Trimble |
| Written by | Edward J. Montagne |
| Produced by | Vitagraph Company of America |
| Starring | Tefft Johnson Edith Storey |
| Distributed by | The General Film Company, Incorporated |
Release date |
|
Running time | One reel / 305 metres |
| Country | United States |
| Languages | Silent English intertitles |
Billy the Kid is a 1911 American silent Western film directed by Laurence Trimble for Vitagraph Studios. It is very loosely based on the life of Billy the Kid. It is believed to be a lost film.
Plot
The following is one of the only reviews of the 1911 short film from The Moving Picture World:[2]
The duties of the sheriff as performed by "Uncle Billy" were not a matter of pleasure. His son-in-law is a member of the posse; lie and "Uncle Billy" leave the house hurriedly to join their comrades in pursuit of the outlaws. Two hours later the son in-law is carried back to his home, the victim of the gang. A little daughter is born to the widow and left an orphan. "Uncle Billy" is anxious that the child should be a boy, but through the secrecy of the Spanish servant. "Uncle Billy" never knew that "Billy, the Kid." was a girl. The sheriff brought her up as a young cowboy, although he noticed there was a certain timidity in the "Kid" that was not at all becoming a boy. When "Billy, the Kid," is sixteen years of age, her grandfather sends her to a town school. Lee Curtis, the foreman of "Uncle Billy's" ranch, was the "Kid's" pal; they were very fond of each other, and it was hard for Lee to part with his young associate, when he accompanied her to the cross roads where they meet the stage. The stage is held up by the outlaws. The "Kid" is taken captive and held as a ransom; they send a note to "Uncle Billy" saying: "If he will grant them immunity, they will restore the 'Kid.'" When the sheriff gets this message, he is furious, and the Spanish servant who well knows that the "Kid" is a girl, is almost frantic with apprehension lest the "Kid's" captors discover this fact. She tells "Uncle Billy" why she has kept him in ignorance of the truth. Lee Curtis overhears the servant's statement, and with the sheriff, rushes out to get the posse in action. "Billy the Kid" has managed to escape from the outlaws and meets the sheriff and his posse. Her grandfather loses no time in getting her back home and into female attire. This time "Uncle Billy" Is going to send the "Kid" to a female seminary and he is going to take her there himself. She tells her grandfather she just wants to be "Billy the Kid" and have Lee for her life companion. "Uncle Billy" has nothing more to say, and it is not long before she changes her name to Mrs. Lee Curtis.
Cast
- Tefft Johnson as Lee Curtis
- Edith Storey as Billy the Kid
- Ralph Ince as Billy's Uncle
- Julia Swayne Gordon as Billy's Mother
- William R. Dunn
- Harry T. Morey
Production
- Directed by Laurence Trimble, this film was shot in a standard 35mm spherical 1.33:1 format.
- Edith Storey, who had played male characters prior in such films as Oliver Twist and A Florida Enchantment, portrays the "first 'cowgirl' film star" as Billy the Kid.[2]
Preservation status
This is presumed a lost film.
See also
References
- "When Billy the Kid Was Billie the Kid". October 9, 2014. Archived from the original on October 16, 2016. Retrieved July 6, 2017.
External links
- 1911 films
- 1911 Western (genre) films
- 1911 lost films
- American black-and-white films
- American silent short films
- Biographical films about Billy the Kid
- Films based on biographies
- Lost American films
- Lost Western (genre) films
- Silent American Western (genre) films
- Vitagraph Studios films
- Films directed by Laurence Trimble
- 1910s American films
https://en.wikipedia.org/wiki/Billy_the_Kid_(1911_film)
Category:1911 lost films
| This is a non-diffusing subcategory of Category:1911 films. It includes 1911 films that can also be found in the parent category, or in diffusing subcategories of the parent. |
Pages in category "1911 lost films"
The following 53 pages are in this category, out of 53 total. This list may not reflect recent changes.
A
B
C
F
L
https://en.wikipedia.org/wiki/Category:1911_lost_films
| The Vote That Counted | |
|---|---|
| Produced by | Thanhouser Company |
| Distributed by | Motion Picture Distributing and Sales Company |
Release date |
|
| Country | United States |
| Languages | Silent film English inter-titles |
The Vote That Counted is a 1911 American silent short drama film produced by the Thanhouser Company. The film focuses on a state senator who disappears from a train and detective Violet Gray investigates the case. Gray manages to find that he was kidnapped and that it was done because he opposed a powerful lobby. She manages to free the state senator in time for him to cast the deciding vote to defeat the lobby. The film was released on January 13, 1911, it was the second of four films in the "Violet Gray, Detective" series. The film received favorable reviews from Billboard and The New York Dramatic Mirror. The film is presumed lost.
Plot
The Moving Picture World synopsis states, "State Senator Jack Dare, one of the reform members of the legislature, starts to the state capitol to attend an important session of that body. That he took the midnight train from his home city is clearly proven, for his aged mother was a passenger on it, and besides the conductor and porter are certain that he retired for the night. In the morning, however, his berth is empty, although some of his garments are found there. The case puzzles the railroad officials and the police, and Violet Gray is given a chance to distinguish herself. She learns from the conductor and porter, who had happened to spend the night awake at opposite ends of the car, that the senator did not go by them. Consequently this leaves only the window as his means of egress, and she knows that he must have gone that way. Violet discovers that Dare is a hearty supporter of a bill that a powerful lobby is trying to defeat. The fight is so close that his is the deciding vote. Dare cannot be bribed, so his opponents spirited him away in a novel fashion. But the girl finds where he is hidden and brings him back, although he is much injured. He reaches his seat in time to cast the needed vote, and to astound and defeat the lobby."[1]
Cast and production
The only known credit in the cast is Julia M. Taylor as Violet Gray.[1] Film historian Q. David Bowers does not cite any scenario or directorial credits.[1] At this time the Thanhouser company operated out of their studio in New Rochelle, New York. In October 1910, an article in The Moving Picture World described the improvements to the studio as having permanently installed a lighting arrangement that was previously experimental in nature. The studio had amassed a collection of props for the productions and dressing rooms had been constructed for the actors. The studio had installed new equipment in the laboratories to improve the quality of the films.[2] By 1911, the Thanhouser company was recognized as one of leading Independent film makers, but Carl Laemmle's Independent Moving Picture Company (IMP) captured most of the publicity. Two production companies were maintained by the company, the first under Barry O'Neil and the second under Lucius J. Henderson and John Noble, an assistant director to Henderson. Though the company had at least two Bianchi cameras from Columbia Phonograph Company, it is believed that imported cameras were also used. The Bianchi cameras were unreliable and inferior to competitors, but it was believed to be a non-infringing camera, though with "rare fortune" it could shoot up to 200 feet of film before requiring repairs.[3]
Release and reception
The single reel drama, approximately 1,000 feet long, was released on January 13, 1911.[1] This would be billed as the second in the series following the successful Love And Law film. The two later releases would be The Norwood Necklace and The Court's Decree would conclude the "Violet Gray, Detective" series.[4] Apparently the film series made an impact because the Lubin Manufacturing Company released a film under the title Violet Dare, Detective in June 1913.[4] The film received a positive review from The Billboard for its interest plot, good acting and photography. The New York Dramatic Mirror found the film to be a good melodrama, but found fault in that a woman detective was used to resolve the case when the part would have had more dignity and realism if the case was resolved by a man.[1] The film would be shown in Pennsylvania and be advertised by theaters even a year after its release.[5][6]
References
- "New Photoplay". The Gettysburg Times (Gettysburg, Pennsylvania). February 8, 1912. p. 1. Retrieved May 28, 2015.
https://en.wikipedia.org/wiki/The_Vote_That_Counted
| Temperate season | |
|---|---|
 Forest covered in snow during winter | |
| Northern temperate zone | |
| Astronomical season | 22 December – 21 March |
| Meteorological season | 1 December – 28/29 February |
| Solar (Celtic) season | 1 November – 31 January |
| Southern temperate zone | |
| Astronomical season | 21 June – 23 September |
| Meteorological season | 1 June – 31 August |
| Solar (Celtic) season | 1 May – 31 July |
| Summer Spring Winter | |
| Part of a series on |
| Weather |
|---|
 |
|
|
|
|
|
|
|
|
|
|
|
|
Glossaries |
|
|
Winter is the coldest season of the year in polar and temperate climates. It occurs after autumn and before spring. The tilt of Earth's axis causes seasons; winter occurs when a hemisphere is oriented away from the Sun. Different cultures define different dates as the start of winter, and some use a definition based on weather.
When it is winter in the Northern Hemisphere, it is summer in the Southern Hemisphere, and vice versa. In many regions, winter brings snow and freezing temperatures. The moment of winter solstice is when the Sun's elevation with respect to the North or South Pole is at its most negative value; that is, the Sun is at its farthest below the horizon as measured from the pole. The day on which this occurs has the shortest day and the longest night, with day length increasing and night length decreasing as the season progresses after the solstice.
The earliest sunset and latest sunrise dates outside the polar regions differ from the date of the winter solstice and depend on latitude. They differ due to the variation in the solar day throughout the year caused by the Earth's elliptical orbit (see: earliest and latest sunrise and sunset).
Etymology
The English word winter comes from the Proto-Germanic noun *wintru-, whose origin is unclear. Several proposals exist, a commonly mentioned one connecting it to the Proto-Indo-European root *wed- 'water' or a nasal infix variant *wend-.[1]
Cause
The tilt of the Earth's axis relative to its orbital plane plays a large role in the formation of weather. The Earth is tilted at an angle of 23.44° to the plane of its orbit, causing different latitudes to directly face the Sun as the Earth moves through its orbit. This variation brings about seasons. When it is winter in the Northern Hemisphere, the Southern Hemisphere faces the Sun more directly and thus experiences warmer temperatures than the Northern Hemisphere. Conversely, winter in the Southern Hemisphere occurs when the Northern Hemisphere is tilted more toward the Sun. From the perspective of an observer on the Earth, the winter Sun has a lower maximum altitude in the sky than the summer Sun.
During winter in either hemisphere, the lower altitude of the Sun causes the sunlight to hit the Earth at an oblique angle. Thus a lower amount of solar radiation strikes the Earth per unit of surface area. Furthermore, the light must travel a longer distance through the atmosphere, allowing the atmosphere to dissipate more heat. Compared with these effects, the effect of the changes in the distance of the Earth from the Sun (due to the Earth's elliptical orbit) is negligible.
The manifestation of the meteorological winter (freezing temperatures) in the northerly snow–prone latitudes is highly variable depending on elevation, position versus marine winds and the amount of precipitation. For instance, within Canada (a country of cold winters), Winnipeg on the Great Plains, a long way from the ocean, has a January high of −11.3 °C (11.7 °F) and a low of −21.4 °C (−6.5 °F).[2]
In comparison, Vancouver on the west coast with a marine influence from moderating Pacific winds has a January low of 1.4 °C (34.5 °F) with days well above freezing at 6.9 °C (44.4 °F).[3] Both places are at 49°N latitude, and in the same western half of the continent. A similar but less extreme effect is found in Europe: in spite of their northerly latitude, the British Isles have not a single non-mountain weather station with a below-freezing mean January temperature.[4]
Meteorological reckoning
Meteorological reckoning is the method of measuring the winter season used by meteorologists based on "sensible weather patterns" for record keeping purposes,[5] so the start of meteorological winter varies with latitude.[6] Winter is often defined by meteorologists to be the three calendar months with the lowest average temperatures. This corresponds to the months of December, January and February in the Northern Hemisphere, and June, July and August in the Southern Hemisphere.
The coldest average temperatures of the season are typically experienced in January or February in the Northern Hemisphere and in June, July or August in the Southern Hemisphere. Nighttime predominates in the winter season, and in some regions winter has the highest rate of precipitation as well as prolonged dampness because of permanent snow cover or high precipitation rates coupled with low temperatures, precluding evaporation. Blizzards often develop and cause many transportation delays. Diamond dust, also known as ice needles or ice crystals, forms at temperatures approaching −40 °C (−40 °F) due to air with slightly higher moisture from above mixing with colder, surface-based air.[7] They are made of simple hexagonal ice crystals.[8]
The Swedish meteorological institute (SMHI) defines thermal winter as when the daily mean temperatures are below 0 °C (32 °F) for five consecutive days.[9] According to the SMHI, winter in Scandinavia is more pronounced when Atlantic low-pressure systems take more southerly and northerly routes, leaving the path open for high-pressure systems to come in and cold temperatures to occur. As a result, the coldest January on record in Stockholm, in 1987, was also the sunniest.[10][11]
Accumulations of snow and ice are commonly associated with winter in the Northern Hemisphere, due to the large land masses there. In the Southern Hemisphere, the more maritime climate and the relative lack of land south of 40°S makes the winters milder; thus, snow and ice are less common in inhabited regions of the Southern Hemisphere. In this region, snow occurs every year in elevated regions such as the Andes, the Great Dividing Range in Australia, and the mountains of New Zealand, and also occurs in the southerly Patagonia region of South Argentina. Snow occurs year-round in Antarctica.
Astronomical and other calendar-based reckoning
In the Northern Hemisphere, some authorities define the period of winter based on astronomical fixed points (i.e. based solely on the position of the Earth in its orbit around the Sun), regardless of weather conditions. In one version of this definition, winter begins at the winter solstice and ends at the March equinox.[12] These dates are somewhat later than those used to define the beginning and end of the meteorological winter – usually considered to span the entirety of December, January, and February in the Northern Hemisphere and June, July, and August in the Southern.[12][13]
Astronomically, the winter solstice, being the day of the year which has fewest hours of daylight, ought to be in the middle of the season,[14][15] but seasonal lag means that the coldest period normally follows the solstice by a few weeks. In some cultures, the season is regarded as beginning at the solstice and ending on the following equinox[16][17] – in the Northern Hemisphere, depending on the year, this corresponds to the period between 20, 21 or 22 December and 19, 20 or 21 March.[12]
In an old Norwegian tradition winter begins on 14 October and ends on the last day of February.[18]
In many countries in the Southern Hemisphere, including Australia,[19][20] New Zealand,[21] and South Africa, winter begins on 1 June and ends on 31 August.
In Celtic nations such as Ireland (using the Irish calendar) and in Scandinavia, the winter solstice is traditionally considered as midwinter, with the winter season beginning 1 November, on All Hallows, or Samhain. Winter ends and spring begins on Imbolc, or Candlemas, which is 1 or 2 February.[citation needed] In Chinese astronomy and other East Asian calendars, winter is taken to commence on or around 7 November, on Lìdōng, and end with the arrival of spring on 3 or 4 February, on Lìchūn.[22] Late Roman Republic scholar Marcus Terentius Varro defined winter as lasting from the fourth day before the Ides of November (10 November) to the eighth day before the Ides of Februarius (6 February).[23]
This system of seasons is based on the length of days exclusively. The three-month period of the shortest days and weakest solar radiation occurs during November, December and January in the Northern Hemisphere and May, June and July in the Southern Hemisphere.
Many mainland European countries tended to recognize Martinmas or St. Martin's Day (11 November), as the first calendar day of winter.[24] The day falls at the midpoint between the old Julian equinox and solstice dates. Also, Valentine's Day (14 February) is recognized by some countries as heralding the first rites of spring, such as flowers blooming.[25]
The three-month period associated with the coldest average temperatures typically begins somewhere in late November or early December in the Northern Hemisphere and lasts through late February or early March. This "thermological winter" is earlier than the solstice delimited definition, but later than the daylight (Celtic or Chinese) definition. Depending on seasonal lag, this period will vary between climatic regions.
Since by almost all definitions valid for the Northern Hemisphere, winter spans 31 December and 1 January, the season is split across years, just like summer in the Southern Hemisphere. Each calendar year includes parts of two winters. This causes ambiguity in associating a winter with a particular year, e.g. "Winter 2018". Solutions for this problem include naming both years, e.g. "Winter 18/19", or settling on the year the season starts in or on the year most of its days belong to, which is the later year for most definitions.
Ecological reckoning and activity
Ecological reckoning of winter differs from calendar-based by avoiding the use of fixed dates. It is one of six seasons recognized by most ecologists who customarily use the term hibernal for this period of the year (the other ecological seasons being prevernal, vernal, estival, serotinal, and autumnal).[26] The hibernal season coincides with the main period of biological dormancy each year whose dates vary according to local and regional climates in temperate zones of the Earth. The appearance of flowering plants like the crocus can mark the change from ecological winter to the prevernal season as early as late January in mild temperate climates.
To survive the harshness of winter, many animals have developed different behavioral and morphological adaptations for overwintering:
- Migration is a common effect of winter upon animals such as migratory birds. Some butterflies also migrate seasonally.
- Hibernation is a state of reduced metabolic activity during the winter. Some animals "sleep" during winter and only come out when the warm weather returns; e.g., gophers, frogs, snakes, and bats.
- Some animals store food for the winter and live on it instead of hibernating completely. This is the case for squirrels, beavers, skunks, badgers, and raccoons.
- Resistance is observed when an animal endures winter but changes in ways such as color and musculature. The color of the fur or plumage changes to white (in order to be confused with snow) and thus retains its cryptic coloration year-round. Examples are the rock ptarmigan, Arctic fox, weasel, white-tailed jackrabbit, and mountain hare.
- Some fur-coated mammals grow a heavier coat during the winter; this improves the heat-retention qualities of the fur. The coat is then shed following the winter season to allow better cooling. The heavier coat in winter made it a favorite season for trappers, who sought more profitable skins.
- Snow also affects the ways animals behave; many take advantage of the insulating properties of snow by burrowing in it. Mice and voles typically live under the snow layer.
Some annual plants never survive the winter. Other annual plants require winter cold to complete their life cycle; this is known as vernalization. As for perennials, many small ones profit from the insulating effects of snow by being buried in it. Larger plants, particularly deciduous trees, usually let their upper part go dormant, but their roots are still protected by the snow layer. Few plants bloom in the winter, one exception being the flowering plum, which flowers in time for Chinese New Year. The process by which plants become acclimated to cold weather is called hardening.
Examples
Exceptionally cold
- 1683–1684, "The Great Frost", when the Thames, hosting the River Thames frost fairs, was frozen all the way up to London Bridge and remained frozen for about two months. Ice was about 27 cm (11 in) thick in London and about 120 cm (47 in) thick in Somerset. The sea froze up to 2 miles (3.2 km) out around the coast of the southern North Sea, causing severe problems for shipping and preventing use of many harbours.
- 1739–1740, one of the most severe winters in the UK on record. The Thames remained frozen over for about 8 weeks. The Irish famine of 1740–1741 claimed the lives of at least 300,000 people.[27]
- 1816 was the Year Without a Summer in the Northern Hemisphere. The unusual coolness of the winter of 1815–1816 and of the following summer was primarily due to the eruption of Mount Tambora in Indonesia, in April 1815. There were secondary effects from an unknown eruption or eruptions around 1810, and several smaller eruptions around the world between 1812 and 1814. The cumulative effects were worldwide but were especially strong in the Eastern United States, Atlantic Canada, and Northern Europe. Frost formed in May in New England, killing many newly planted crops, and the summer never recovered. Snow fell in New York and Maine in June, and ice formed in lakes and rivers in July and August. In the UK, snow drifts remained on hills until late July, and the Thames froze in September. Agricultural crops failed and livestock died in much of the Northern Hemisphere, resulting in food shortages and the worst famine of the 19th century.
- 1887–1888, there were record cold temperatures in the Upper Midwest, heavy snowfalls worldwide, and amazing storms, including the Schoolhouse Blizzard of 1888 (in the Midwest in January), and the Great Blizzard of 1888 (in the Eastern US and Canada in March).
- In Europe, the winters of early 1947,[28] February 1956, 1962–1963, 1981–1982 and 2009–2010 were abnormally cold. The UK winter of 1946–1947 started out relatively normal, but became one of the snowiest UK winters to date, with nearly continuous snowfall from late January until March.
- In South America, the winter of 1975 was one of the strongest, with record snow occurring at 25°S in cities of low altitude, with the registration of −17 °C (1.4 °F) in some parts of southern Brazil.
- In the eastern United States and Canada, the winter of 2013–2014 and the second half of February 2015 were abnormally cold.
Historically significant
- 1310–1330, many severe winters and cold, wet summers in Europe – the first clear manifestation of the unpredictable weather of the Little Ice Age that lasted for several centuries (from about 1300 to 1900). The persistently cold, wet weather caused great hardship, was primarily responsible for the Great Famine of 1315–1317, and strongly contributed to the weakened immunity and malnutrition leading up to the Black Death (1348–1350).
- 1600–1602, extremely cold winters in Switzerland and Baltic region after eruption of Huaynaputina in Peru in 1600.
- 1607–1608, in North America, ice persisted on Lake Superior until June. Londoners held their first frost fair on the frozen-over River Thames.
- 1622, in Turkey, the Golden Horn and southern section of Bosphorus froze over.
- 1690s, extremely cold, snowy, severe winters. Ice surrounded Iceland for miles in every direction.
- 1779–1780, Scotland's coldest winter on record, and ice surrounded Iceland in every direction (like in the 1690s). In the United States, a record five-week cold spell bottomed out at −20 °F (−29 °C) at Hartford, Connecticut, and −16 °F (−27 °C) in New York City. Hudson River and New York's harbor froze over.
- 1783–1786, the Thames partially froze, and snow remained on the ground for months. In February 1784, the North Carolina was frozen in Chesapeake Bay.
- 1794–1795, severe winter, with the coldest January in the UK and lowest temperature ever recorded in London: −21 °C (−6 °F) on 25 January. The cold began on Christmas Eve and lasted until late March, with a few temporary warm-ups. The Severn and Thames froze, and frost fairs started up again. The French army tried to invade the Netherlands over its frozen rivers, while the Dutch fleet was stuck in its harbor. The winter had easterlies (from Siberia) as its dominant feature.
- 1813–1814, severe cold, last freeze-over of Thames, and last frost fair. (Removal of old London Bridge and changes to river's banks made freeze-overs less likely.)
- 1883–1888, colder temperatures worldwide, including an unbroken string of abnormally cold and brutal winters in the Upper Midwest, related to the explosion of Krakatoa in August 1883. There was snow recorded in the UK as early as October and as late as July during this time period.
- 1976–1977, one of the coldest winters in the US in decades.
- 1985, Arctic outbreak in US resulting from shift in polar vortex, with many cold temperature records broken.
- 2002–2003 was an unusually cold winter in the Northern and Eastern US.
- 2010–2011, persistent bitter cold in the entire eastern half of the US from December onward, with few or no mid-winter warm-ups, and with cool conditions continuing into spring. La Niña and negative Arctic oscillation were strong factors. Heavy and persistent precipitation contributed to almost constant snow cover in the Northeastern US which finally receded in early May.
- 2011 was one of the coldest on record in New Zealand with sea level snow falling in Wellington in July for the first time in 35 years and a much heavier snowstorm for 3 days in a row in August.
Effect on humans
Humans are sensitive to winter cold, which compromises the body's ability to maintain both core and surface heat of the body.[29] Slipping on icy surfaces is a common cause of winter injury.[30] Other cold injuries include:[31]
- Hypothermia – Shivering, leading to uncoordinated movements and death.
- Frostbite – Freezing of skin, leading to loss of feeling and damaged tissue.
- Trench foot – Numbness, leading to damaged tissue and gangrene.
- Chilblains – Capillary damage in digits can lead to more severe cold injuries.
Rates of influenza, COVID-19 and other respiratory diseases also increase during the winter.[32][33]
Mythology
In Persian culture, the winter solstice is called Yaldā (meaning: birth) and it has been celebrated for thousands of years. It is referred to as the eve of the birth of Mithra, who symbolised light, goodness and strength on earth.
In Greek mythology, Hades kidnapped Persephone to be his wife. Zeus ordered Hades to return her to Demeter, the goddess of the Earth and her mother. Hades tricked Persephone into eating the food of the dead, so Zeus decreed that she spend six months with Demeter and six months with Hades. During the time her daughter is with Hades, Demeter became depressed and caused winter.
In Welsh mythology, Gwyn ap Nudd abducted a maiden named Creiddylad. On May Day, her lover, Gwythr ap Greidawl, fought Gwyn to win her back. The battle between them represented the contest between summer and winter.
See also
References
On St. Martin's day (11 November) winter begins, summer takes its end, harvest is completed. ...This text is one of many that preserves vestiges of the ancient Indo-European system of two seasons, winter and summer.
- "Why cold winter weather makes it harder for the body to fight respiratory infections". Science. 15 December 2020. Retrieved 24 April 2022.
Further reading
- Rosenthal, Norman E. (1998). Winter Blues. New York: The Guilford Press. ISBN 1-57230-395-6.
External links
 Media related to Winter (category) at Wikimedia Commons
Media related to Winter (category) at Wikimedia Commons Quotations related to Winter at Wikiquote
Quotations related to Winter at Wikiquote Cold weather travel guide from Wikivoyage
Cold weather travel guide from Wikivoyage The dictionary definition of winter at Wiktionary
The dictionary definition of winter at Wiktionary
https://en.wikipedia.org/wiki/Winter
https://en.wikipedia.org/wiki/Post_hoc_ergo_propter_hoc
See also
- Apophenia – Tendency to perceive connections between unrelated things
- Affirming the consequent – Type of fallacious argument (logical fallacy)
- Association fallacy – Informal inductive fallacy
- Cargo cult – New religious movement
- Causal inference – Branch of statistics concerned with inferring causal relationships between variables
- Coincidence – Concurrence of events with no connection
- Confirmation bias – Bias confirming existing attitudes
- Correlation does not imply causation – Refutation of a logical fallacy
- Jumping to conclusions – Psychological term
- Magical thinking – Belief in the connection of unrelated events
- Superstition – Belief or behavior that is considered irrational or supernatural
- Surrogate endpoint
https://en.wikipedia.org/wiki/Post_hoc_ergo_propter_hoc
https://en.wikipedia.org/wiki/Questionable_cause
https://en.wikipedia.org/wiki/Informal_fallacy
A simple example is "The rooster crows immediately before sunrise; therefore the rooster causes the sun to rise."[3]
https://en.wikipedia.org/wiki/Post_hoc_ergo_propter_hoc
A false dilemma, also referred to as false dichotomy or false binary, is an informal fallacy based on a premise that erroneously limits what options are available. The source of the fallacy lies not in an invalid form of inference but in a false premise. This premise has the form of a disjunctive claim: it asserts that one among a number of alternatives must be true. This disjunction is problematic because it oversimplifies the choice by excluding viable alternatives, presenting the viewer with only two absolute choices when in fact, there could be many.
https://en.wikipedia.org/wiki/False_dilemma
https://en.wikipedia.org/wiki/Destructive_dilemma
https://en.wikipedia.org/wiki/Defeasible_reasoning
https://en.wikipedia.org/wiki/Disjunctive_syllogism
https://en.wikipedia.org/wiki/Double_negative
https://en.wikipedia.org/wiki/Morphology_(linguistics)
https://en.wikipedia.org/wiki/Morphological_typology
https://en.wikipedia.org/wiki/Monarchy
https://en.wikipedia.org/wiki/no-contendre
https://en.wikipedia.org/wiki/Rule_of_inference
https://en.wikipedia.org/wiki/Biconditional_introduction
https://en.wikipedia.org/wiki/Propositional_calculus
https://en.wikipedia.org/wiki/Undecidable_problem
https://en.wikipedia.org/wiki/Paradox
https://en.wikipedia.org/wiki/Markov_chain_central_limit_theorem
https://en.wikipedia.org/wiki/Asymptotic_distribution#Central_limit_theorem
https://en.wikipedia.org/wiki/Limiting_density_of_discrete_points
https://en.wikipedia.org/wiki/Central_limit_theorem?wprov=srpw1_0
https://en.wikipedia.org/wiki/Independent_and_identically_distributed_random_variables
https://en.wikipedia.org/wiki/Cumulative_distribution_functions
https://en.wikipedia.org/wiki/Right-continuous
https://en.wikipedia.org/wiki/Semi-continuity
https://en.wikipedia.org/wiki/Hemicontinuity
https://en.wikipedia.org/wiki/Transfinite_number
https://en.wikipedia.org/wiki/Cardinal_number
https://en.wikipedia.org/wiki/Bijection
https://en.wikipedia.org/wiki/Surjective_function
https://en.wikipedia.org/wiki/Codomain
https://en.wikipedia.org/wiki/Image_(mathematics)
https://en.wikipedia.org/wiki/Binary_relation#Operations
https://en.wikipedia.org/wiki/Duality_(order_theory)
https://en.wikipedia.org/wiki/If_and_only_if
https://en.wikipedia.org/wiki/Necessity_and_sufficiency#Simultaneous_necessity_and_sufficiency
https://en.wikipedia.org/wiki/Extension_(semantics)
https://en.wikipedia.org/wiki/Extension_(predicate_logic)
https://en.wikipedia.org/wiki/Function_(mathematics)
https://en.wikipedia.org/wiki/Calculus
https://en.wikipedia.org/wiki/Limit_of_a_function#(%CE%B5,_%CE%B4)-definition_of_limit
https://en.wikipedia.org/wiki/Arity
In logic, mathematics, and computer science, arity (/ˈærɪti/ (![]() listen)) is the number of arguments or operands taken by a function, operation or relation. In mathematics, arity may also be called rank,[1][2] but this word can have many other meanings. In logic and philosophy, arity may also be called adicity and degree.[3][4] In linguistics, it is usually named valency.[5]
listen)) is the number of arguments or operands taken by a function, operation or relation. In mathematics, arity may also be called rank,[1][2] but this word can have many other meanings. In logic and philosophy, arity may also be called adicity and degree.[3][4] In linguistics, it is usually named valency.[5]
https://en.wikipedia.org/wiki/Arity
https://en.wikipedia.org/wiki/Hexadecimal
https://en.wikipedia.org/wiki/Hex_file
https://en.wikipedia.org/wiki/Intel_HEX#MT
https://en.wikipedia.org/wiki/Programmable_ROM
https://en.wikipedia.org/wiki/Punched_tape
https://en.wikipedia.org/wiki/Teleprinter
https://en.wikipedia.org/wiki/Telex
https://en.wikipedia.org/wiki/Digital_signal
https://en.wikipedia.org/wiki/Mark_and_space
https://en.wikipedia.org/wiki/Modem
https://en.wikipedia.org/wiki/Subcarrier
https://en.wikipedia.org/wiki/Radio_broadcasting
https://en.wikipedia.org/wiki/Simulcast
https://en.wikipedia.org/wiki/Mass_media
Simulcast (a portmanteau of simultaneous broadcast) is the broadcasting of programmes/programs or events across more than one resolution, bitrate or medium, or more than one service on the same medium, at exactly the same time (that is, simultaneously). For example, Absolute Radio is simulcast on both AM and on satellite radio.[1][2] Likewise, the BBC's Prom concerts were formerly simulcast on both BBC Radio 3 and BBC Television. Another application is the transmission of the original-language soundtrack of movies or TV series over local or Internet radio, with the television broadcast having been dubbed into a local language.
https://en.wikipedia.org/wiki/Simulcast
https://en.wikipedia.org/wiki/Frequency-shift_keying#Audio_FSK
Speeds
Modems are frequently classified by the maximum amount of data they can send in a given unit of time, usually expressed in bits per second (symbol bit/s, sometimes abbreviated "bps") or rarely in bytes per second (symbol B/s). Modern broadband modem speeds are typically expressed in megabits per second (Mbit/s).
Historically, modems were often classified by their symbol rate, measured in baud. The baud unit denotes symbols per second, or the number of times per second the modem sends a new signal. For example, the ITU V.21 standard used audio frequency-shift keying with two possible frequencies, corresponding to two distinct symbols (or one bit per symbol), to carry 300 bits per second using 300 baud. By contrast, the original ITU V.22 standard, which could transmit and receive four distinct symbols (two bits per symbol), transmitted 1,200 bits by sending 600 symbols per second (600 baud) using phase-shift keying.
https://en.wikipedia.org/wiki/Modem
https://en.wikipedia.org/wiki/Modem
Overall history
Modems grew out of the need to connect teleprinters over ordinary phone lines instead of the more expensive leased lines which had previously been used for current loop–based teleprinters and automated telegraphs. The earliest devices that satisfy the definition of a modem may be the multiplexers used by news wire services in the 1920s.[1]
In 1941, the Allies developed a voice encryption system called SIGSALY which used a vocoder to digitize speech, then encrypted the speech with one-time pad and encoded the digital data as tones using frequency shift keying. This was also a digital modulation technique, making this an early modem.[2]
Commercial modems largely did not become available until the late 1950s, when the rapid development of computer technology created demand for a method of connecting computers together over long distances, resulting in the Bell Company and then other businesses producing an increasing number of computer modems for use over both switched and leased telephone lines.
Later developments would produce modems that operated over cable television lines, power lines, and various radio technologies, as well as modems that achieved much higher speeds over telephone lines.
https://en.wikipedia.org/wiki/Modem
In electrical signalling an analog current loop is used where a device must be monitored or controlled remotely over a pair of conductors. Only one current level can be present at any time.
A major application of current loops is the industry de facto standard 4–20 mA current loop for process control applications, where they are extensively used to carry signals from process instrumentation to PID controllers, SCADA systems, and programmable logic controllers (PLCs). They are also used to transmit controller outputs to the modulating field devices such as control valves. These loops have the advantages of simplicity and noise immunity, and have a large international user and equipment supplier base. Some 4–20 mA field devices can be powered by the current loop itself, removing the need for separate power supplies, and the "smart" HART protocol uses the loop for communications between field devices and controllers. Various automation protocols may replace analog current loops, but 4–20 mA is still a principal industrial standard.
https://en.wikipedia.org/wiki/Current_loop
A control valve is a valve used to control fluid flow by varying the size of the flow passage as directed by a signal from a controller.[1] This enables the direct control of flow rate and the consequential control of process quantities such as pressure, temperature, and liquid level.
In automatic control terminology, a control valve is termed a "final control element".
https://en.wikipedia.org/wiki/Control_valve
The opening or closing of automatic control valves is usually done by electrical, hydraulic or pneumatic actuators. Normally with a modulating valve, which can be set to any position between fully open and fully closed, valve positioners are used to ensure the valve attains the desired degree of opening.[2]
Air-actuated valves are commonly used because of their simplicity, as they only require a compressed air supply, whereas electrically operated valves require additional cabling and switch gear, and hydraulically actuated valves required high pressure supply and return lines for the hydraulic fluid.
The pneumatic control signals are traditionally based on a pressure range of 3–15 psi (0.2–1.0 bar), or more commonly now, an electrical signal of 4-20mA for industry, or 0–10 V for HVAC systems. Electrical control now often includes a "Smart" communication signal superimposed on the 4–20 mA control current, such that the health and verification of the valve position can be signalled back to the controller. The HART, Fieldbus Foundation, and Profibus are the most common protocols.
An automatic control valve consists of three main parts in which each part exist in several types and designs:
- Valve actuator – which moves the valve's modulating element, such as ball or butterfly.
- Valve positioner – which ensures the valve has reached the desired degree of opening. This overcomes the problems of friction and wear.
- Valve body – in which the modulating element, a plug, globe, ball or butterfly, is contained.
Control action
Taking the example of an air-operated valve, there are two control actions possible:
- "Air or current to open" – The flow restriction decreases with increased control signal value.
- "Air or current to close" – The flow restriction increases with increased control signal value.
There can also be failure to safety modes:
- "Air or control signal failure to close" – On failure of compressed air to the actuator, the valve closes under spring pressure or by backup power.
- "Air or control signal failure to open" – On failure of compressed air to actuator, the valve opens under spring pressure or by backup power.
The modes of failure operation are requirements of the failure to safety process control specification of the plant. In the case of cooling water it may be to fail open, and the case of delivering a chemical it may be to fail closed.
Valve positioners
The fundamental function of a positioner is to deliver pressurized air to the valve actuator, such that the position of the valve stem or shaft corresponds to the set point from the control system. Positioners are typically used when a valve requires throttling action. A positioner requires position feedback from the valve stem or shaft and delivers pneumatic pressure to the actuator to open and close the valve. The positioner must be mounted on or near the control valve assembly. There are three main categories of positioners, depending on the type of control signal, the diagnostic capability, and the communication protocol: pneumatic, analog, and digital.[3]
Pneumatic positioners
Processing units may use pneumatic pressure signaling as the control set point to the control valves. Pressure is typically modulated between 20.7 and 103 kPa (3 to 15 psig) to move the valve from 0 to 100% position. In a common pneumatic positioner, the position of the valve stem or shaft is compared with the position of a bellows that receives the pneumatic control signal. When the input signal increases, the bellows expands and moves a beam. The beam pivots about an input axis, which moves a flapper closer to the nozzle. The nozzle pressure increases, which increases the output pressure to the actuator through a pneumatic amplifier relay. The increased output pressure to the actuator causes the valve stem to move.
Stem movement is fed back to the beam by means of a cam. As the cam rotates, the beam pivots about the feedback axis to move the flapper slightly away from the nozzle. The nozzle pressure decreases and reduces the output pressure to the actuator. Stem movement continues, backing the flapper away from the nozzle until equilibrium is reached. When the input signal decreases, the bellows contracts (aided by an internal range spring) and the beam pivots about the input axis to move the flapper away from the nozzle. Nozzle decreases and the relay permits the release of diaphragm casing pressure to the atmosphere, which allows the actuator stem to move upward.
Through the cam, stem movement is fed back to the beam to reposition the flapper closer to the nozzle. When equilibrium conditions are obtained, stem movement stops and the flapper is positioned to prevent any further decrease in actuator pressure.[3]
Analog positioners
The second type of positioner is an analog I/P positioner. Most modern processing units use a 4 to 20 mA DC signal to modulate the control valves. This introduces electronics into the positioner design and requires that the positioner convert the electronic current signal into a pneumatic pressure signal (current-to-pneumatic or I/P). In a typical analog I/P positioner, the converter receives a DC input signal and provides a proportional pneumatic output signal through a nozzle/flapper arrangement. The pneumatic output signal provides the input signal to the pneumatic positioner. Otherwise, the design is the same as the pneumatic positioner[3]
Digital positioners
While pneumatic positioners and analog I/P positioners provide basic valve position control, digital valve controllers add another dimension to positioner capabilities. This type of positioner is a microprocessor-based instrument. The microprocessor enables diagnostics and two-way communication to simplify setup and troubleshooting.
In a typical digital valve controller, the control signal is read by the microprocessor, processed by a digital algorithm, and converted into a drive current signal to the I/P converter. The microprocessor performs the position control algorithm rather than a mechanical beam, cam, and flapper assembly. As the control signal increases, the drive signal to the I/P converter increases, increasing the output pressure from the I/P converter. This pressure is routed to a pneumatic amplifier relay and provides two output pressures to the actuator. With increasing control signal, one output pressure always increases and the other output pressure decreases
Double-acting actuators use both outputs, whereas single-acting actuators use only one output. The changing output pressure causes the actuator stem or shaft to move. Valve position is fed back to the microprocessor. The stem continues to move until the correct position is attained. At this point, the microprocessor stabilizes the drive signal to the I/P converter until equilibrium is obtained.
In addition to the function of controlling the position of the valve, a digital valve controller has two additional capabilities: diagnostics and two-way digital communication.[3]
Widely used communication protocols include HART, FOUNDATION fieldbus, and PROFIBUS.
Advantages of placing a smart positioner on a control valve:
- Automatic calibration and configuration of positioner.
- Real time diagnostics.
- Reduced cost of loop commissioning, including installation and calibration.
- Use of diagnostics to maintain loop performance levels.
- Improved process control accuracy that reduces process variability.
Types of control valve
Control valves are classified by attributes and features.
Based on the pressure drop profile
- High recovery valve: These valves typically regain most of static pressure drop from the inlet to vena contracta at the outlet. They are characterised by a lower recovery coefficient. Examples: butterfly valve, ball valve, plug valve, gate valve
- Low recovery valve: These valves typically regain little of the static pressure drop from the inlet to vena contracta at the outlet. They are characterised by a higher recovery coefficient. Examples: globe valve, angle valve
Based on the movement profile of the controlling element
- Sliding stem: The valve stem / plug moves in a linear, or straight line motion. Examples: Globe valve,[4] angle valve, wedge type gate valve
- Rotary valve: The valve disc rotates. Examples: Butterfly valve, ball valve
Based on the functionality
- Control valve: Controls flow parameters proportional to an input signal received from the central control system. Examples: Globe valve, angle valve, ball valve
- Shut-off / On-off valve: These valves are either completely open or closed. Examples: Gate valve, ball valve, globe valve, angle valve, pinch valve, diaphragm valve
- Check valve: Allows flow only in a single direction
- Steam conditioning valve: Regulates the pressure and temperature of inlet media to required parameters at outlet. Examples: Turbine bypass valve, process steam letdown station
- Spring-loaded safety valve: Closed by the force of a spring, which retracts to open when the inlet pressure is equal to the spring force
Based on the actuating medium
- Manual valve: Actuated by hand wheel
- Pneumatic valve: Actuated using a compressible medium like air, hydrocarbon, or nitrogen, with a spring diaphragm, piston cylinder or piston-spring type actuator
- Hydraulic valve: Actuated by a non-compressible medium such as water or oil
- Electric valve: Actuated by an electric motor
A wide variety of valve types and control operation exist. However, there are two main forms of action, the sliding stem and the rotary.
The most common and versatile types of control valves are sliding-stem globe, V-notch ball, butterfly and angle types. Their popularity derives from rugged construction and the many options available that make them suitable for a variety of process applications.[5] Control valve bodies may be categorized as below:[3]
List of common types of control valve
- Sliding stem
- Globe valve – Flow control device
- Angle body valve
- Angle seat piston valve
- Axial Flow valve
- Rotary
- Butterfly valve – Flow control device
- Ball valve – Flow control device
- Other
- Pinch valve – PINCH VALVES ARE PRESSURE CONTROLLED SHUT-OFF VALVES FOR APPLICATIONS IN INDUSTRIAL AUTOMATION
- Diaphragm valve – Flow control device
See also
- Check valve – Flow control device
- Control engineering – Engineering discipline that deals with control systems
- Control system – System that manages the behavior of other systems
- Distributed control system – Computerized control systems with distributed decision-making
- Fieldbus Foundation
- Flow control valve – Valve that regulates the flow or pressure of a fluid
- Highway Addressable Remote Transducer Protocol, also known as HART Protocol – hybrid analog+digital industrial automation protocol; can communicate over legacy 4–20 mA analog instrumentation current loops, sharing the pair of wires used by the analog only host systems
- Instrumentation – Measuring instruments which monitor and control a process
- PID controller – Control loop feedback mechanism
- Process control – Discipline that uses industrial control to achieve a production level of consistency
- Profibus – Communications protocol
- SCADA, also known as Supervisory control and data acquisition system – Control system architecture for supervision of machines and processes
References
External links
- Process Instrumentation (Lecture 8): Control valves Article from a University of South Australia website.
- Control Valve Sizing Calculator Control Valve Sizing Calculator to determine Cv for a valve.
https://en.wikipedia.org/wiki/Control_valve
Denying the antecedent, sometimes also called inverse error or fallacy of the inverse, is a formal fallacy of inferring the inverse from the original statement. It is committed by reasoning in the form:[1]
- If P, then Q.
- Therefore, if not P, then not Q.
which may also be phrased as
(P implies Q)
(therefore, not-P implies not-Q)[1]
Arguments of this form are invalid. Informally, this means that arguments of this form do not give good reason to establish their conclusions, even if their premises are true. In this example, a valid conclusion would be: ~P or Q.
The name denying the antecedent derives from the premise "not P", which denies the "if" clause of the conditional premise.
One way to demonstrate the invalidity of this argument form is with an example that has true premises but an obviously false conclusion. For example:
- If you are a ski instructor, then you have a job.
- You are not a ski instructor.
- Therefore, you have no job.[1]
That argument is intentionally bad, but arguments of the same form can sometimes seem superficially convincing, as in the following example offered by Alan Turing in the article "Computing Machinery and Intelligence":
If each man had a definite set of rules of conduct by which he regulated his life he would be no better than a machine. But there are no such rules, so men cannot be machines.[2]
However, men could still be machines that do not follow a definite set of rules. Thus, this argument (as Turing intends) is invalid.
It is possible that an argument that denies the antecedent could be valid if the argument instantiates some other valid form. For example, if the claims P and Q express the same proposition, then the argument would be trivially valid, as it would beg the question. In everyday discourse, however, such cases are rare, typically only occurring when the "if-then" premise is actually an "if and only if" claim (i.e., a biconditional/equality). The following argument is not valid, but would be if the first premise was "If I can veto Congress, then I am the US President." This claim is now modus tollens, and thus valid.
- If I am President of the United States, then I can veto Congress.
- I am not President.
- Therefore, I cannot veto Congress.
See also
References
- Turing, Alan (October 1950), "Computing Machinery and Intelligence", Mind, LIX (236): 433–460, doi:10.1093/mind/LIX.236.433, ISSN 0026-4423
External links
https://en.wikipedia.org/wiki/Denying_the_antecedent
In propositional logic, affirming the consequent, sometimes called converse error, fallacy of the converse, or confusion of necessity and sufficiency, is a formal fallacy of taking a true conditional statement (e.g., "if the lamp were broken, then the room would be dark"), and invalidly inferring its converse ("the room is dark, so the lamp must be broken"), even though that statement may not be true. This arises when the consequent ("the room would be dark") has other possible antecedents (for example, "the lamp is in working order, but is switched off" or "there is no lamp in the room").
Converse errors are common in everyday thinking and communication and can result from, among other causes, communication issues, misconceptions about logic, and failure to consider other causes.
The opposite statement, denying the consequent, is called modus tollens and is a valid form of argument.[1]
Formal description
Affirming the consequent is the action of taking a true statement 




Affirming the consequent can also result from overgeneralizing the experience of many statements having true converses. If P and Q are "equivalent" statements, i.e. 



Of the possible forms of "mixed hypothetical syllogisms," two are valid and two are invalid. Affirming the antecedent (modus ponens) and denying the consequent (modus tollens) are valid. Affirming the consequent and denying the antecedent are invalid(see table).[6]
Additional examples
Example 1
One way to demonstrate the invalidity of this argument form is with a counterexample with true premises but an obviously false conclusion. For example:
- If someone lives in San Diego, then they live in California.
- Joe lives in California.
- Therefore, Joe lives in San Diego.
There are many places to live in California other than San Diego; however, one can affirm with certainty that "if someone does not live in California" (non-Q), then "this person does not live in San Diego" (non-P). This is the contrapositive of the first statement, and it must be true if and only if the original statement is true.
Example 2
Here is another useful, obviously fallacious example.
- If an animal is a dog, then it has four legs.
- My cat has four legs.
- Therefore, my cat is a dog.
Here, it is immediately intuitive that any number of other antecedents ("If an animal is a deer...", "If an animal is an elephant...", "If an animal is a moose...", etc.) can give rise to the consequent ("then it has four legs"), and that it is preposterous to suppose that having four legs must imply that the animal is a dog and nothing else. This is useful as a teaching example since most people can immediately recognize that the conclusion reached must be wrong (intuitively, a cat cannot be a dog), and that the method by which it was reached must therefore be fallacious.
Example 3
Arguments of the same form can sometimes seem superficially convincing, as in the following example:
- If Brian had been thrown off the top of the Eiffel Tower, then he would be dead.
- Brian is dead.
- Therefore, Brian was thrown off the top of the Eiffel Tower.
Being thrown off the top of the Eiffel Tower is not the only cause of death, since there exist numerous different causes of death.
Example 4
In Catch-22,[7] the chaplain is interrogated for supposedly being "Washington Irving"/"Irving Washington", who has been blocking out large portions of soldiers' letters home. The colonel has found such a letter, but with the Chaplain's name signed.
- "You can read, though, can't you?" the colonel persevered sarcastically. "The author signed his name."
- "That's my name there."
- "Then you wrote it. Q.E.D."
P in this case is 'The chaplain signs his own name', and Q 'The chaplain's name is written'. The chaplain's name may be written, but he did not necessarily write it, as the colonel falsely concludes.[7]
Example 5
When teaching the scientific method, the following example is used to illustrate why, via the fallacy of affirming the consequent, no scientific theory is ever proven true but rather simply failed to be falsified.
- If this theory is correct, we will observe X.
- We observe X.
- Therefore, this theory is correct.
Concluding or assuming that a theory is true because of a prediction it makes being observed is invalid. This is one of the challenges of applying the scientific method though rarely is it brought up in academic contexts as it is unlikely to be of consequence to the results of the study. Much more common is questioning the validity of the theory, the validity of expected the theory to have predicted the observation, and/or the validity of the observation itself.
See also
References
- Heller, Joseph (1994). Catch-22. Vintage. pp. 438, 8. ISBN 0-09-947731-9.
https://en.wikipedia.org/wiki/Affirming_the_consequent
Appeal to consequences, also known as argumentum ad consequentiam (Latin for "argument to the consequence"), is an argument that concludes a hypothesis (typically a belief) to be either true or false based on whether the premise leads to desirable or undesirable consequences.[1] This is based on an appeal to emotion and is a type of informal fallacy, since the desirability of a premise's consequence does not make the premise true. Moreover, in categorizing consequences as either desirable or undesirable, such arguments inherently contain subjective points of view.
In logic, appeal to consequences refers only to arguments that assert a conclusion's truth value (true or false) without regard to the formal preservation of the truth from the premises; appeal to consequences does not refer to arguments that address a premise's consequential desirability (good or bad, or right or wrong) instead of its truth value. Therefore, an argument based on appeal to consequences is valid in long-term decision making (which discusses possibilities that do not exist yet in the present) and abstract ethics, and in fact such arguments are the cornerstones of many moral theories, particularly related to consequentialism. Appeal to consequences also should not be confused with argumentum ad baculum, which is the bringing up of 'artificial' consequences (i.e. punishments) to argue that an action is wrong.
https://en.wikipedia.org/wiki/Appeal_to_consequences
Ad hominem (Latin for 'to the person'), short for argumentum ad hominem, is a term that refers to several types of arguments, most of which are fallacious. Typically this term refers to a rhetorical strategy where the speaker attacks the character, motive, or some other attribute of the person making an argument rather than attacking the substance of the argument itself. This avoids genuine debate by creating a diversion to some irrelevant but often highly charged issue. The most common form of this fallacy is "A makes a claim x, B asserts that A holds a property that is unwelcome, and hence B concludes that argument x is wrong".
The valid types of ad hominem arguments are generally only encountered in specialized philosophical usage. These typically refer to the dialectical strategy of using the target's own beliefs and arguments against them, while not agreeing with the validity of those beliefs and arguments. Ad hominem arguments were first studied in ancient Greece; John Locke revived the examination of ad hominem arguments in the 17th century. Many contemporary politicians routinely use ad hominem attacks, which can be encapsulated to a derogatory nickname for a political opponent.
https://en.wikipedia.org/wiki/Ad_hominem
Wishful thinking is the formation of beliefs based on what might be pleasing to imagine, rather than on evidence, rationality, or reality. It is a product of resolving conflicts between belief and desire.[1] Methodologies to examine wishful thinking are diverse. Various disciplines and schools of thought examine related mechanisms such as neural circuitry, human cognition and emotion, types of bias, procrastination, motivation, optimism, attention and environment. This concept has been examined as a fallacy. It is related to the concept of wishful seeing.
https://en.wikipedia.org/wiki/Wishful_thinking
The fallacy of the undistributed middle (Latin: non distributio medii) is a formal fallacy that is committed when the middle term in a categorical syllogism is not distributed in either the minor premise or the major premise. It is thus a syllogistic fallacy.
https://en.wikipedia.org/wiki/Fallacy_of_the_undistributed_middle
| Type | |
|---|---|
| Field | |
| Statement |  implies implies  . .  is true. Therefore is true. Therefore  must also be true. must also be true. |
| Symbolic statement |  |
In propositional logic, modus ponens (/ˈmoʊdəs ˈpoʊnɛnz/; MP), also known as modus ponendo ponens (Latin for "method of putting by placing"),[1] implication elimination, or affirming the antecedent,[2] is a deductive argument form and rule of inference.[3] It can be summarized as "P implies Q. P is true. Therefore Q must also be true."
Modus ponens is closely related to another valid form of argument, modus tollens. Both have apparently similar but invalid forms such as affirming the consequent, denying the antecedent, and evidence of absence. Constructive dilemma is the disjunctive version of modus ponens. Hypothetical syllogism is closely related to modus ponens and sometimes thought of as "double modus ponens."
The history of modus ponens goes back to antiquity.[4] The first to explicitly describe the argument form modus ponens was Theophrastus.[5] It, along with modus tollens, is one of the standard patterns of inference that can be applied to derive chains of conclusions that lead to the desired goal.
https://en.wikipedia.org/wiki/Modus_ponens
| Type | |
|---|---|
| Field | |
| Statement |  implies implies  . .  is false. Therefore is false. Therefore  must also be false. must also be false. |
| Symbolic statement |   [1] [1] |
In propositional logic, modus tollens (/ˈmoʊdəs ˈtɒlɛnz/) (MT), also known as modus tollendo tollens (Latin for "method of removing by taking away")[2] and denying the consequent,[3] is a deductive argument form and a rule of inference. Modus tollens takes the form of "If P, then Q. Not Q. Therefore, not P." It is an application of the general truth that if a statement is true, then so is its contrapositive. The form shows that inference from P implies Q to the negation of Q implies the negation of P is a valid argument.
The history of the inference rule modus tollens goes back to antiquity.[4] The first to explicitly describe the argument form modus tollens was Theophrastus.[5]
Modus tollens is closely related to modus ponens. There are two similar, but invalid, forms of argument: affirming the consequent and denying the antecedent. See also contraposition and proof by contrapositive.
https://en.wikipedia.org/wiki/Modus_tollens
In logic and mathematics, contraposition refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as proof by contraposition. The contrapositive of a statement has its antecedent and consequent inverted and flipped.
Conditional statement 


If P, Then Q. — If not Q, Then not P. "If it is raining, then I wear my coat" — "If I don't wear my coat, then it isn't raining."
The law of contraposition says that a conditional statement is true if, and only if, its contrapositive is true.[2]
The contrapositive (
- Inversion (the inverse),
- "If it is not raining, then I don't wear my coat." Unlike the contrapositive, the inverse's truth value is not at all dependent on whether or not the original proposition was true, as evidenced here.
- Conversion (the converse),
- "If I wear my coat, then it is raining." The converse is actually the contrapositive of the inverse, and so always has the same truth value as the inverse (which as stated earlier does not always share the same truth value as that of the original proposition).
- Negation (the logical complement),
- "It is not the case that if it is raining then I wear my coat.", or equivalently, "Sometimes, when it is raining, I don't wear my coat. " If the negation is true, then the original proposition (and by extension the contrapositive) is false.
Note that if 




https://en.wikipedia.org/wiki/Contraposition
Evidence of absence is evidence of any kind that suggests something is missing or that it does not exist. What counts as evidence of absence has been a subject of debate between scientists and philosophers. It is often distinguished from absence of evidence.
Overview
Evidence of absence and absence of evidence are similar but distinct concepts. This distinction is captured in the aphorism "Absence of evidence is not evidence of absence." This antimetabole is often attributed to Martin Rees or Carl Sagan, but a version appeared as early as 1888 in a writing by William Wright.[1] In Sagan's words, the expression is a critique of the "impatience with ambiguity" exhibited by appeals to ignorance.[2] Despite what the expression may seem to imply, a lack of evidence can be informative. For example, when testing a new drug, if no harmful effects are observed then this suggests that the drug is safe.[3] This is because, if the drug were harmful, evidence of that fact can be expected to turn up during testing. The expectation of evidence makes its absence significant.[4]
As the previous example shows, the difference between evidence that something is absent (e.g., an observation that suggests there were no dragons here today) and simple absence of evidence (e.g., no careful research has been done) can be nuanced. Indeed, scientists will often debate whether an experiment's result should be considered evidence of absence, or if it remains absence of evidence. The debate regards whether the experiment would have detected the phenomenon of interest if it were there.[5]
The argument from ignorance for "absence of evidence" is not necessarily fallacious, for example, that a potentially life-saving new drug poses no long-term health risk unless proved otherwise. On the other hand, were such an argument to rely imprudently on the lack of research to promote its conclusion, it would be considered an informal fallacy whereas the former can be a persuasive way to shift the burden of proof in an argument or debate.[6]
Science
In carefully designed scientific experiments, even null results can be evidence of absence.[7] For instance, a hypothesis may be falsified if a vital predicted observation is not found empirically. At this point, the underlying hypothesis may be rejected or revised and sometimes, additional ad hoc explanations may even be warranted. Whether the scientific community will accept a null result as evidence of absence depends on many factors, including the detection power of the applied methods, the confidence of the inference, as well as confirmation bias within the community.
Law
In many legal systems, a lack of evidence for a defendant's guilt is sufficient for acquittal. This is because of the presumption of innocence and the belief that it is worse to convict an innocent person than to let a guilty one go free.[3]
On the other hand, the absence of evidence in the defendant's favor (e.g. an alibi) can make their guilt seem more likely. A jury can be persuaded to convict because of "evidentiary lacunae", or a lack of evidence they expect to hear.[8]
Proving a negative
This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (October 2021) (Learn how and when to remove this template message) |
A negative claim is a colloquialism for an affirmative claim that asserts the non-existence or exclusion of something.[9] Proofs of negative claims are common in mathematics. Such claims include Euclid's theorem that there is no largest prime number, and Arrow's impossibility theorem.[citation needed] There can be multiple claims within a debate, nevertheless, whoever makes a claim usually carries the burden of proof regardless of positive or negative content in the claim.[citation needed]
A negative claim may or may not exist as a counterpoint to a previous claim. A proof of impossibility or an evidence of absence argument are typical methods to fulfill the burden of proof for a negative claim.[9][10]
Philosopher Steven Hales argues that typically one can logically be as confident with the negation of an affirmation. Hales says that if one's standards of certainty leads them to say "there is never 'proof' of non-existence", then they must also say that "there is never 'proof' of existence either". Hales argues that there are many cases where we may be able to prove something does not exist with as much certainty as proving something does exist.[9]: 109–112 A similar position is taken by philosopher Stephen Law who highlights that rather than focusing on the existence of "proof", a better question would be whether there is any reasonable doubt for existence or non-existence.[11]
See also
References
Appeal to ignorance—the claim that whatever has not been proved false must be true, and vice versa (e.g., There is no compelling evidence that UFOs are not visiting the Earth; therefore UFOs exist—and there is intelligent life elsewhere in the Universe. Or: There may be seventy kazillion other worlds, but not one is known to have the moral advancement of the Earth, so we're still central to the Universe.) This impatience with ambiguity can be criticized in the phrase: absence of evidence is not evidence of absence.
[Advocates] of the presumption of atheism... insist that it is precisely the absence of evidence for theism that justifies their claim that God does not exist. The problem with such a position is captured neatly by the aphorism, beloved of forensic scientists, that "absence of evidence is not evidence of absence." The absence of evidence is evidence of absence only in case in which, were the postulated entity to exist, we should expect to have more evidence of its existence than we do.
- "You Can Prove a Negative | Psychology Today". www.psychologytoday.com. Retrieved 2022-11-28.
In classical logic, a hypothetical syllogism is a valid argument form, a syllogism with a conditional statement for one or both of its premises.
An example in English:
- If I do not wake up, then I cannot go to work.
- If I cannot go to work, then I will not get paid.
- Therefore, if I do not wake up, then I will not get paid.
The term originated with Theophrastus.[2]
A pure hypothetical syllogism is a syllogism in which both premises and conclusions are conditionals. The antecedent of one premise must match the consequent of the other for the conditional to be valid. Consequently, conditionals contain remained antecedent as antecedent and remained consequent as consequent.
- If p, then q.
- If q, then r.
- ∴ If p, then r.
A mixed hypothetical syllogism consists of one conditional statement and one statement that expresses either affirmation or denial with either the antecedent or consequence of that conditional. Therefore, such a mixed hypothetical syllogism has four possible forms, of which two are valid, while the other two are invalid(See Table). The first way to get a valid conclusion is to affirm the antecedent. A valid hypothetical syllogism either denies the consequent (modus tollens) or affirms the antecedent (modus ponens).[1]
https://en.wikipedia.org/wiki/Hypothetical_syllogism
Confusion of the inverse, also called the conditional probability fallacy or the inverse fallacy, is a logical fallacy whereupon a conditional probability is equated with its inverse; that is, given two events A and B, the probability of A happening given that B has happened is assumed to be about the same as the probability of B given A, when there is actually no evidence for this assumption.[1][2] More formally, P(A|B) is assumed to be approximately equal to P(B|A).
https://en.wikipedia.org/wiki/Confusion_of_the_inverse
| Part of a series on |
| Bayesian statistics |
|---|
| Posterior = Likelihood × Prior ÷ Evidence |
| Background |
| Model building |
| Posterior approximation |
| Estimators |
| Evidence approximation |
| Model evaluation |
A prior probability distribution of an uncertain quantity, often simply called the prior, is its assumed probability distribution before some evidence is taken into account. For example, the prior could be the probability distribution representing the relative proportions of voters who will vote for a particular politician in a future election. The unknown quantity may be a parameter of the model or a latent variable rather than an observable variable.
https://en.wikipedia.org/wiki/Prior_probability
https://en.wikipedia.org/wiki/Conditional_probability
Abductive reasoning (also called abduction,[1] abductive inference,[1] or retroduction[2]) is a form of logical inference that seeks the simplest and most likely conclusion from a set of observations. It was formulated and advanced by American philosopher Charles Sanders Peirce beginning in the last third of the 19th century.
Abductive reasoning, unlike deductive reasoning, yields a plausible conclusion but does not definitively verify it. Abductive conclusions do not eliminate uncertainty or doubt, which is expressed in retreat terms such as "best available" or "most likely". One can understand abductive reasoning as inference to the best explanation,[3] although not all usages of the terms abduction and inference to the best explanation are equivalent.[4][5]
In the 1990s, as computing power grew, the fields of law,[6] computer science, and artificial intelligence research[7] spurred renewed interest in the subject of abduction.[8] Diagnostic expert systems frequently employ abduction.[9]
https://en.wikipedia.org/wiki/Abductive_reasoning
Backward chaining (or backward reasoning) is an inference method described colloquially as working backward from the goal. It is used in automated theorem provers, inference engines, proof assistants, and other artificial intelligence applications.[1]
In game theory, researchers apply it to (simpler) subgames to find a solution to the game, in a process called backward induction. In chess, it is called retrograde analysis, and it is used to generate table bases for chess endgames for computer chess.
Backward chaining is implemented in logic programming by SLD resolution. Both rules are based on the modus ponens inference rule. It is one of the two most commonly used methods of reasoning with inference rules and logical implications – the other is forward chaining. Backward chaining systems usually employ a depth-first search strategy, e.g. Prolog.[2]
https://en.wikipedia.org/wiki/Backward_chaining
In chess and other similar games, the endgame (or end game or ending) is the stage of the game when few pieces are left on the board.
The line between middlegame and endgame is often not clear, and may occur gradually or with the quick exchange of a few pairs of pieces. The endgame, however, tends to have different characteristics from the middlegame, and the players have correspondingly different strategic concerns. In particular, pawns become more important as endgames often revolve around attempting to promote a pawn by advancing it to the eighth rank. The king, which normally should stay hidden during the game[1] should become active in the endgame, as it can help escort pawns to the promotion square, attack enemy pawns, protect other pieces, and restrict the movement of the enemy king.
All chess positions with up to seven pieces on the board have been solved,[2] that is, the outcome (win, loss, or draw) of best play by both sides is known, and textbooks and reference works teach the best play. Most endgames are not solved, and textbooks teach useful strategies and tactics for them. The body of chess theory devoted to endgames is known as endgame theory. Compared to chess opening theory, which changes frequently, giving way to middlegame positions that fall in and out of popularity, endgame theory is less subject to change.
Many endgame studies have been composed, endgame positions which are solved by finding a win for White when there is no obvious way to win, or a draw when it seems White must lose. In some compositions, the starting position would be unlikely to occur in an actual game; but if the starting position is not so exotic, the composition is sometimes incorporated into endgame theory.
Chess players classify endgames according to the type of pieces that remain.
https://en.wikipedia.org/wiki/Chess_endgame
In game theory, a subgame is any part (a subset) of a game that meets the following criteria (the following terms allude to a game described in extensive form):[1]
- It has a single initial node that is the only member of that node's information set (i.e. the initial node is in a singleton information set).
- If a node is contained in the subgame then so are all of its successors.
- If a node in a particular information set is in the subgame then all members of that information set belong to the subgame.
It is a notion used in the solution concept of subgame perfect Nash equilibrium, a refinement of the Nash equilibrium that eliminates non-credible threats.
The key feature of a subgame is that it, when seen in isolation, constitutes a game in its own right. When the initial node of a subgame is reached in a larger game, players can concentrate only on that subgame; they can ignore the history of the rest of the game (provided they know what subgame they are playing). This is the intuition behind the definition given above of a subgame. It must contain an initial node that is a singleton information set since this is a requirement of a game. Otherwise, it would be unclear where the player with first move should start at the beginning of a game (but see nature's choice). Even if it is clear in the context of the larger game which node of a non-singleton information set has been reached, players could not ignore the history of the larger game once they reached the initial node of a subgame if subgames cut across information sets. Furthermore, a subgame can be treated as a game in its own right, but it must reflect the strategies available to players in the larger game of which it is a subset. This is the reasoning behind 2 and 3 of the definition. All the strategies (or subsets of strategies) available to a player at a node in a game must be available to that player in the subgame the initial node of which is that node.
https://en.wikipedia.org/wiki/Subgame
Backward induction is the process of reasoning backwards in time, from the end of a problem or situation, to determine a sequence of optimal actions. It proceeds by examining the last point at which a decision is to be made and then identifying what action would be most optimal at that moment. Using this information, one can then determine what to do at the second-to-last time of decision. This process continues backwards until one has determined the best action for every possible situation (i.e. for every possible information set) at every point in time. Backward induction was first used in 1875 by Arthur Cayley, who uncovered the method while trying to solve the infamous Secretary problem.[1]
In the mathematical optimization method of dynamic programming, backward induction is one of the main methods for solving the Bellman equation.[2][3] In game theory, backward induction is a method used to compute subgame perfect equilibria in sequential games.[4] The only difference is that optimization involves just one decision maker, who chooses what to do at each point of time, whereas game theory analyzes how the decisions of several players interact. That is, by anticipating what the last player will do in each situation, it is possible to determine what the second-to-last player will do, and so on. In the related fields of automated planning and scheduling and automated theorem proving, the method is called backward search or backward chaining. In chess it is called retrograde analysis.
Backward induction has been used to solve games as long as the field of game theory has existed. John von Neumann and Oskar Morgenstern suggested solving zero-sum, two-person games by backward induction in their Theory of Games and Economic Behavior (1944), the book which established game theory as a field of study.[5][6]
https://en.wikipedia.org/wiki/Backward_induction
In the field of artificial intelligence, an inference engine is a component of the system that applies logical rules to the knowledge base to deduce new information. The first inference engines were components of expert systems. The typical expert system consisted of a knowledge base and an inference engine. The knowledge base stored facts about the world. The inference engine applies logical rules to the knowledge base and deduced new knowledge. This process would iterate as each new fact in the knowledge base could trigger additional rules in the inference engine. Inference engines work primarily in one of two modes either special rule or facts: forward chaining and backward chaining. Forward chaining starts with the known facts and asserts new facts. Backward chaining starts with goals, and works backward to determine what facts must be asserted so that the goals can be achieved.[1]
https://en.wikipedia.org/wiki/Inference_engine
In chess problems, retrograde analysis is a technique employed to determine which moves were played leading up to a given position. While this technique is rarely needed for solving ordinary chess problems, there is a whole subgenre of chess problems in which it is an important part; such problems are known as retros.
Retros may ask, for example, for a mate in two, but the main puzzle is in explaining the history of the position. This may be important to determine, for example, if castling is disallowed or an en passant capture is possible. Other problems may ask specific questions relating to the history of the position, such as, "Is the bishop on c1 promoted?". This is essentially a matter of logical reasoning, with high appeal for puzzle enthusiasts.
Sometimes it is necessary to determine if a particular position is legal, with "legal" meaning that it could be reached by a series of legal moves, no matter how illogical. Another important branch of retrograde analysis problems is proof game problems.
https://en.wikipedia.org/wiki/Retrograde_analysis
Forward chaining (or forward reasoning) is one of the two main methods of reasoning when using an inference engine and can be described logically as repeated application of modus ponens. Forward chaining is a popular implementation strategy for expert systems, business and production rule systems. The opposite of forward chaining is backward chaining.
Forward chaining starts with the available data and uses inference rules to extract more data (from an end user, for example) until a goal is reached. An inference engine using forward chaining searches the inference rules until it finds one where the antecedent (If clause) is known to be true. When such a rule is found, the engine can conclude, or infer, the consequent (Then clause), resulting in the addition of new information to its data.[1]
Inference engines will iterate through this process until a goal is reached.
https://en.wikipedia.org/wiki/Forward_chaining
The set cover problem is a classical question in combinatorics, computer science, operations research, and complexity theory. It is one of Karp's 21 NP-complete problems shown to be NP-complete in 1972.
Given a set of elements {1, 2, …, n} (called the universe) and a collection S of m sets whose union equals the universe, the set cover problem is to identify the smallest sub-collection of S whose union equals the universe. For example, consider the universe U = {1, 2, 3, 4, 5} and the collection of sets S = { {1, 2, 3}, {2, 4}, {3, 4}, {4, 5} }. Clearly the union of S is U. However, we can cover all of the elements with the following, smaller number of sets: { {1, 2, 3}, {4, 5} }.
More formally, given a universe 








The decision version of set covering is NP-complete, and the optimization/search version of set cover is NP-hard.[1] It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms.[2] If each set is assigned a cost, it becomes a weighted set cover problem.
https://en.wikipedia.org/wiki/Set_cover_problem
Proof theory is a major branch[1] of mathematical logic and theoretical computer science that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as lists, boxed lists, or trees, which are constructed according to the axioms and rules of inference of the logical system. Consequently, proof theory is syntactic in nature, in contrast to model theory, which is semantic in nature.
Some of the major areas of proof theory include structural proof theory, ordinal analysis, provability logic, reverse mathematics, proof mining, automated theorem proving, and proof complexity. Much research also focuses on applications in computer science, linguistics, and philosophy.
https://en.wikipedia.org/wiki/Proof_theory
Gödel's incompleteness theorems are two theorems of mathematical logic that are concerned with the limits of provability in formal axiomatic theories. These results, published by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The theorems are widely, but not universally, interpreted as showing that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible.
The first incompleteness theorem states that no consistent system of axioms whose theorems can be listed by an effective procedure (i.e., an algorithm) is capable of proving all truths about the arithmetic of natural numbers. For any such consistent formal system, there will always be statements about natural numbers that are true, but that are unprovable within the system. The second incompleteness theorem, an extension of the first, shows that the system cannot demonstrate its own consistency.
Employing a diagonal argument, Gödel's incompleteness theorems were the first of several closely related theorems on the limitations of formal systems. They were followed by Tarski's undefinability theorem on the formal undefinability of truth, Church's proof that Hilbert's Entscheidungsproblem is unsolvable, and Turing's theorem that there is no algorithm to solve the halting problem.
https://en.wikipedia.org/wiki/G%C3%B6del%27s_incompleteness_theorems
Reverse mathematics is a program in mathematical logic that seeks to determine which axioms are required to prove theorems of mathematics. Its defining method can briefly be described as "going backwards from the theorems to the axioms", in contrast to the ordinary mathematical practice of deriving theorems from axioms. It can be conceptualized as sculpting out necessary conditions from sufficient ones.
The reverse mathematics program was foreshadowed by results in set theory such as the classical theorem that the axiom of choice and Zorn's lemma are equivalent over ZF set theory. The goal of reverse mathematics, however, is to study possible axioms of ordinary theorems of mathematics rather than possible axioms for set theory.
Reverse mathematics is usually carried out using subsystems of second-order arithmetic,[1] where many of its definitions and methods are inspired by previous work in constructive analysis and proof theory. The use of second-order arithmetic also allows many techniques from recursion theory to be employed; many results in reverse mathematics have corresponding results in computable analysis. In higher-order reverse mathematics, the focus is on subsystems of higher-order arithmetic, and the associated richer language.[clarification needed]
The program was founded by Harvey Friedman (1975, 1976)[2] and brought forward by Steve Simpson. A standard reference for the subject is Simpson (2009), while an introduction for non-specialists is Stillwell (2018). An introduction to higher-order reverse mathematics, and also the founding paper, is Kohlenbach (2005).
https://en.wikipedia.org/wiki/Reverse_mathematics
Provability logic is a modal logic, in which the box (or "necessity") operator is interpreted as 'it is provable that'. The point is to capture the notion of a proof predicate of a reasonably rich formal theory, such as Peano arithmetic.
https://en.wikipedia.org/wiki/Provability_logic
https://en.wikipedia.org/wiki/Well-founded_relation
In mathematical logic, a tautology (from Greek: ταυτολογία) is a formula or assertion that is true in every possible interpretation. An example is "x=y or x≠y". Similarly, "either the ball is green, or the ball is not green" is always true, regardless of the colour of the ball.
https://en.wikipedia.org/wiki/Tautology_(logic)
In philosophy and logic, contingency is the status of propositions that are neither true under every possible valuation (i.e. tautologies) nor false under every possible valuation (i.e. contradictions). A contingent proposition is neither necessarily true nor necessarily false.
https://en.wikipedia.org/wiki/Contingency_(philosophy)
Propositions that are contingent may be so because they contain logical connectives which, along with the truth value of any of its atomic parts, determine the truth value of the proposition. This is to say that the truth value of the proposition is contingent upon the truth values of the sentences which comprise it. Contingent propositions depend on the facts, whereas analytic propositions are true without regard to any facts about which they speak.
Along with contingent propositions, there are at least three other classes of propositions, some of which overlap:
- Tautological propositions, which must be true, no matter what the circumstances are or could be (example: "It is the case that the sky is blue or it is not the case that the sky is blue.").
- Contradictions which must necessarily be untrue, no matter what the circumstances are or could be (example: "It's raining and it's not raining.").
- Possible propositions, which are true or could have been true given certain circumstances (examples: x + y = 4 which is true with some values of x and y, but false with others; Or there are only three planets which may be true since we may be talking about a different world which itself could be real or hypothetical. The same is true for There are more than three planets ). Every necessarily true proposition, and every contingent proposition, is also a possible proposition.
https://en.wikipedia.org/wiki/Contingency_(philosophy)
The formal fallacy of affirming a disjunct also known as the fallacy of the alternative disjunct or a false exclusionary disjunct occurs when a deductive argument takes the following logical form:[1]
- A or B
- A
- Therefore, not B
Or in logical operators:
¬
Where 
The fallacy lies in concluding that one disjunct must be false because the other disjunct is true; in fact they may both be true because "or" is defined inclusively rather than exclusively. It is a fallacy of equivocation between the operations OR and XOR.
Affirming the disjunct should not be confused with the valid argument known as the disjunctive syllogism.
https://en.wikipedia.org/wiki/Affirming_a_disjunct
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).[1]
It is symbolized by the prefix operator J[2] and by the infix operators XOR (/ˌɛks ˈɔːr/, /ˌɛks ˈɔː/, /ˈksɔːr/ or /ˈksɔː/), EOR, EXOR, ⊻, ⩒, ⩛, ⊕, 
It gains the name "exclusive or" because the meaning of "or" is ambiguous when both operands are true; the exclusive or operator excludes that case. This is sometimes thought of as "one or the other but not both". This could be written as "A or B, but not, A and B".
Since it is associative, it may be considered to be an n-ary operator which is true if and only if an odd number of arguments are true. That is, a XOR b XOR ... may be treated as XOR(a,b,...).
https://en.wikipedia.org/wiki/Exclusive_or
In logic and mathematics, the logical biconditional, sometimes known as the material biconditional, is the logical connective (


Semantically, the only case where a logical biconditional is different from a material conditional is the case where the hypothesis is false but the conclusion is true. In this case, the result is true for the conditional, but false for the biconditional.[1]
In the conceptual interpretation, P = Q means "All P's are Q's and all Q's are P's". In other words, the sets P and Q coincide: they are identical. However, this does not mean that P and Q need to have the same meaning (e.g., P could be "equiangular trilateral" and Q could be "equilateral triangle"). When phrased as a sentence, the antecedent is the subject and the consequent is the predicate of a universal affirmative proposition (e.g., in the phrase "all men are mortal", "men" is the subject and "mortal" is the predicate).
In the propositional interpretation, 
A common way of demonstrating a biconditional of the form 




When both members of the biconditional are propositions, it can be separated into two conditionals, of which one is called a theorem and the other its reciprocal.[citation needed] Thus whenever a theorem and its reciprocal are true, we have a biconditional. A simple theorem gives rise to an implication, whose antecedent is the hypothesis and whose consequent is the thesis of the theorem.
It is often said that the hypothesis is the sufficient condition of the thesis, and that the thesis is the necessary condition of the hypothesis. That is, it is sufficient that the hypothesis be true for the thesis to be true, while it is necessary that the thesis be true if the hypothesis were true. When a theorem and its reciprocal are true, its hypothesis is said to be the necessary and sufficient condition of the thesis. That is, the hypothesis is both the cause and the consequence of the thesis at the same time.
https://en.wikipedia.org/wiki/Logical_biconditional
| EQ, XNOR | |
|---|---|
 | |
| Definition |  |
| Truth table |  |
| Logic gate | |
| Normal forms | |
| Disjunctive |  |
| Conjunctive |  |
| Zhegalkin polynomial |  |
| Post's lattices | |
| 0-preserving | no |
| 1-preserving | yes |
| Monotone | no |
| Affine | yes |
Logical equality is a logical operator that corresponds to equality in Boolean algebra and to the logical biconditional in propositional calculus. It gives the functional value true if both functional arguments have the same logical value, and false if they are different.
It is customary practice in various applications, if not always technically precise, to indicate the operation of logical equality on the logical operands x and y by any of the following forms:
Some logicians, however, draw a firm distinction between a functional form, like those in the left column, which they interpret as an application of a function to a pair of arguments — and thus a mere indication that the value of the compound expression depends on the values of the component expressions — and an equational form, like those in the right column, which they interpret as an assertion that the arguments have equal values, in other words, that the functional value of the compound expression is true.
In mathematics, the plus sign "+" almost invariably indicates an operation that satisfies the axioms assigned to addition in the type of algebraic structure that is known as a field. For boolean algebra, this means that the logical operation signified by "+" is not the same as the inclusive disjunction signified by "∨" but is actually equivalent to the logical inequality operator signified by "≠", or what amounts to the same thing, the exclusive disjunction signified by "XOR" or "⊕". Naturally, these variations in usage have caused some failures to communicate between mathematicians and switching engineers over the years. At any rate, one has the following array of corresponding forms for the symbols associated with logical inequality:
This explains why "EQ" is often called "XNOR" in the combinational logic of circuit engineers, since it is the negation of the XOR operation; "NXOR" is a less commonly used alternative.[1] Another rationalization of the admittedly circuitous name "XNOR" is that one begins with the "both false" operator NOR and then adds the eXception "or both true".
Definition
Logical equality is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if both operands are false or both operands are true.
The truth table of p EQ q (also written as p = q, p ↔ q, Epq, p ≡ q, or p == q) is as follows:
Logical equality p q p = q 0 0 1 0 1 0 1 0 0 1 1 1
https://en.wikipedia.org/wiki/Logical_equality

meant as shorthand for


The Venn diagram directly below,
and line (ABC ) in this matrix
represent the same operation.
https://en.wikipedia.org/wiki/Logical_biconditional
| Algebraic structure → Ring theory Ring theory |
|---|
 |
|
|
Basic concepts |
|
|
|
|
In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.
| Algebraic structures |
|---|
|
|
Group-like |
|
|
|
|
Lattice-like |
|
|
Module-like |
|
|
Algebra-like |
Formally, a ring is an abelian group whose operation is called addition, with a second binary operation called multiplication that is associative, is distributive over the addition operation, and has a multiplicative identity element. (Some authors use the term "rng" with a missing "i" to refer to the more general structure that omits this last requirement; see § Notes on the definition.)
Whether a ring is commutative (that is, whether the order in which two elements are multiplied might change the result) has profound implications on its behavior. Commutative algebra, the theory of commutative rings, is a major branch of ring theory. Its development has been greatly influenced by problems and ideas of algebraic number theory and algebraic geometry. The simplest commutative rings are those that admit division by non-zero elements; such rings are called fields.
Examples of commutative rings include the set of integers with their standard addition and multiplication, the set of polynomials with their addition and multiplication, the coordinate ring of an affine algebraic variety, and the ring of integers of a number field. Examples of noncommutative rings include the ring of n × n real square matrices with n ≥ 2, group rings in representation theory, operator algebras in functional analysis, rings of differential operators, and cohomology rings in topology.
The conceptualization of rings spanned the 1870s to the 1920s, with key contributions by Dedekind, Hilbert, Fraenkel, and Noether. Rings were first formalized as a generalization of Dedekind domains that occur in number theory, and of polynomial rings and rings of invariants that occur in algebraic geometry and invariant theory. They later proved useful in other branches of mathematics such as geometry and analysis.
https://en.wikipedia.org/wiki/Ring_(mathematics)
Definition
A ring is a set R equipped with two binary operations[a] + (addition) and ⋅ (multiplication) satisfying the following three sets of axioms, called the ring axioms[1][2][3]
- R is an abelian group under addition, meaning that:
- (a + b) + c = a + (b + c) for all a, b, c in R (that is, + is associative).
- a + b = b + a for all a, b in R (that is, + is commutative).
- There is an element 0 in R such that a + 0 = a for all a in R (that is, 0 is the additive identity).
- For each a in R there exists −a in R such that a + (−a) = 0 (that is, −a is the additive inverse of a).
- R is a monoid under multiplication, meaning that:
- (a · b) · c = a · (b · c) for all a, b, c in R (that is, ⋅ is associative).
- There is an element 1 in R such that a · 1 = a and 1 · a = a for all a in R (that is, 1 is the multiplicative identity). [b]
- Multiplication is distributive with respect to addition, meaning that:
- a · (b + c) = (a · b) + (a · c) for all a, b, c in R (left distributivity).
- (b + c) · a = (b · a) + (c · a) for all a, b, c in R (right distributivity).
Notes on the definition
In the terminology of this article, a ring is defined to have a multiplicative identity, while a structure with the same axiomatic definition but without the requirement for a multiplicative identity is instead called a rng (IPA: /rʊŋ/). For example, the set of even integers with the usual + and ⋅ is a rng, but not a ring. As explained in § History below, many authors apply the term "ring" without requiring a multiplicative identity.
The multiplication symbol ⋅ is usually omitted; for example, xy means x · y.
Although ring addition is commutative, ring multiplication is not required to be commutative: ab need not necessarily equal ba. Rings that also satisfy commutativity for multiplication (such as the ring of integers) are called commutative rings. Books on commutative algebra or algebraic geometry often adopt the convention that ring means commutative ring, to simplify terminology.
In a ring, multiplicative inverses are not required to exist. A nonzero commutative ring in which every nonzero element has a multiplicative inverse is called a field.
The additive group of a ring is the underlying set equipped with only the operation of addition. Although the definition requires that the additive group be abelian, this can be inferred from the other ring axioms.[4] The proof makes use of the "1", and does not work in a rng. (For a rng, omitting the axiom of commutativity of addition leaves it inferable from the remaining rng assumptions only for elements that are products: ab + cd = cd + ab.)
Although most modern authors use the term "ring" as defined here, there are a few who use the term to refer to more general structures in which there is no requirement for multiplication to be associative.[5] For these authors, every algebra is a "ring".
Illustration
The most familiar example of a ring is the set of all integers 
The axioms of a ring were elaborated as a generalization of familiar properties of addition and multiplication of integers.
Some properties
Some basic properties of a ring follow immediately from the axioms:
- The additive identity is unique.
- The additive inverse of each element is unique.
- The multiplicative identity is unique.
- For any element x in a ring R, one has x0 = 0 = 0x (zero is an absorbing element with respect to multiplication) and (–1)x = –x.
- If 0 = 1 in a ring R (or more generally, 0 is a unit element), then R has only one element, and is called the zero ring.
- If a ring R contains the zero ring as a subring, then R itself is the zero ring.[6]
- The binomial formula holds for any x and y satisfying xy = yx.
Example: Integers modulo 4
Equip the set 
- The sum
in
is the remainder when the integer x + y is divided by 4 (as x + y is always smaller than 8, this remainder is either x + y or x + y − 4). For example,
and
- The product
in
is the remainder when the integer xy is divided by 4. For example,
and
Then 







Example: 2-by-2 matrices
The set of 2-by-2 square matrices with entries in a field F is[7][8][9][10]
With the operations of matrix addition and matrix multiplication, 





More generally, for any ring R, commutative or not, and any nonnegative integer n, the square matrices of dimension n with entries in R form a ring: see Matrix ring.
History
Dedekind
The study of rings originated from the theory of polynomial rings and the theory of algebraic integers.[11] In 1871, Richard Dedekind defined the concept of the ring of integers of a number field.[12] In this context, he introduced the terms "ideal" (inspired by Ernst Kummer's notion of ideal number) and "module" and studied their properties. Dedekind did not use the term "ring" and did not define the concept of a ring in a general setting.
Hilbert
The term "Zahlring" (number ring) was coined by David Hilbert in 1892 and published in 1897.[13]
In 19th century German, the word "Ring" could mean "association", which
is still used today in English in a limited sense (for example, spy
ring),[14]
so if that were the etymology then it would be similar to the way
"group" entered mathematics by being a non-technical word for
"collection of related things". According to Harvey Cohn, Hilbert used
the term for a ring that had the property of "circling directly back" to
an element of itself (in the sense of an equivalence).[15]
Specifically, in a ring of algebraic integers, all high powers of an
algebraic integer can be written as an integral combination of a fixed
set of lower powers, and thus the powers "cycle back". For instance, if 
and so on; in general, an is going to be an integral linear combination of 1, a, and a2.
Fraenkel and Noether
The first axiomatic definition of a ring was given by Adolf Fraenkel in 1915,[16][17] but his axioms were stricter than those in the modern definition. For instance, he required every non-zero-divisor to have a multiplicative inverse.[18] In 1921, Emmy Noether gave a modern axiomatic definition of commutative rings (with and without 1) and developed the foundations of commutative ring theory in her paper Idealtheorie in Ringbereichen.[19]
Multiplicative identity and the term "ring"
Fraenkel's axioms for a "ring" included that of a multiplicative identity,[20] whereas Noether's did not.[19]
Most or all books on algebra[21][22] up to around 1960 followed Noether's convention of not requiring a 1 for a "ring". Starting in the 1960s, it became increasingly common to see books including the existence of 1 in the definition of "ring", especially in advanced books by notable authors such as Artin,[23] Atiyah and MacDonald,[24] Bourbaki,[25] Eisenbud,[26] and Lang.[3] There are also books published as late as 2022 that use the term without the requirement for a 1.[27][28][29][30]
Gardner and Wiegandt assert that, when dealing with several objects in the category of rings (as opposed to working with a fixed ring), if one requires all rings to have a 1, then some consequences include the lack of existence of infinite direct sums of rings, and that proper direct summands of rings are not subrings. They conclude that "in many, maybe most, branches of ring theory the requirement of the existence of a unity element is not sensible, and therefore unacceptable."[31] Poonen makes the counterargument that the natural notion for rings is the direct product rather than the direct sum. He further argues that rings without a multiplicative identity are not totally associative (the product of any finite sequence of ring elements, including the empty sequence, is well-defined, independent of the order of operations) and writes "the natural extension of associativity demands that rings should contain an empty product, so it is natural to require rings to have a 1".[32]
Authors who follow either convention for the use of the term "ring" may use one of the following terms to refer to objects satisfying the other convention:
- to include a requirement for a multiplicative identity: "unital ring", "unitary ring", "unit ring", "ring with unity", "ring with identity", "ring with a unit",[33] or "ring with 1".[34]
- to omit a requirement for a multiplicative identity: "rng"[35] or "pseudo-ring",[36] although the latter may be confusing because it also has other meanings.
Basic examples
Commutative rings
- The prototypical example is the ring of integers with the two operations of addition and multiplication.
- The rational, real and complex numbers are commutative rings of a type called fields.
- A unital associative algebra over a commutative ring R is itself a ring as well as an R-module. Some examples:
- The algebra R[X] of polynomials with coefficients in R.
- The algebra
of formal power series with coefficients in R.
- The set of all continuous real-valued functions defined on the real line forms a commutative
-algebra. The operations are pointwise addition and multiplication of functions.
- Let X be a set, and let R be a ring. Then the set of all functions from X to R forms a ring, which is commutative if R is commutative.
- The ring of quadratic integers, the integral closure of
in a quadratic extension of
It is a subring of the ring of all algebraic integers.
- The ring of profinite integers
the (infinite) product of the rings of p-adic integers
over all prime numbers p.
- The Hecke ring, the ring generated by Hecke operators.
- If S is a set, then the power set of S becomes a ring if we define addition to be the symmetric difference of sets and multiplication to be intersection. This is an example of a Boolean ring.
Noncommutative rings
- For any ring R and any natural number n, the set of all square n-by-n matrices with entries from R, forms a ring with matrix addition and matrix multiplication as operations. For n = 1, this matrix ring is isomorphic to R itself. For n > 1 (and R not the zero ring), this matrix ring is noncommutative.
- If G is an abelian group, then the endomorphisms of G form a ring, the endomorphism ring End(G) of G. The operations in this ring are addition and composition of endomorphisms. More generally, if V is a left module over a ring R, then the set of all R-linear maps forms a ring, also called the endomorphism ring and denoted by EndR(V).
- The endomorphism ring of an elliptic curve. It is a commutative ring if the elliptic curve is defined over a field of characteristic zero.
- If G is a group and R is a ring, the group ring of G over R is a free module over R having G as basis. Multiplication is defined by the rules that the elements of G commute with the elements of R and multiply together as they do in the group G.
- The ring of differential operators (depending on the context). In fact, many rings that appear in analysis are noncommutative. For example, most Banach algebras are noncommutative.
Non-rings
- The set of natural numbers
with the usual operations is not a ring, since
is not even a group (not all the elements are invertible with respect to addition – for instance, there is no natural number which can be added to 3 to get 0 as a result). There is a natural way to enlarge it to a ring, by including negative numbers to produce the ring of integers
The natural numbers (including 0) form an algebraic structure known as a semiring (which has all of the axioms of a ring excluding that of an additive inverse).
- Let R
be the set of all continuous functions on the real line that vanish
outside a bounded interval that depends on the function, with addition
as usual but with multiplication defined as convolution: Then R is a rng, but not a ring: the Dirac delta function has the property of a multiplicative identity, but it is not a function and hence is not an element of R.
Basic concepts
Products and powers
For each nonnegative integer n, given a sequence 

As a special case, one can define nonnegative integer powers of an element a of a ring: a0 = 1 and an = an−1a for n ≥ 1. Then am+n = aman for all m, n ≥ 0.
Elements in a ring
A left zero divisor of a ring R is an element a in the ring such that there exists a nonzero element b of R such that ab = 0.[c] A right zero divisor is defined similarly.
A nilpotent element is an element a such that an = 0 for some n > 0. One example of a nilpotent element is a nilpotent matrix. A nilpotent element in a nonzero ring is necessarily a zero divisor.
An idempotent 
A unit is an element a having a multiplicative inverse; in this case the inverse is unique, and is denoted by a–1. The set of units of a ring is a group under ring multiplication; this group is denoted by R× or R* or U(R). For example, if R is the ring of all square matrices of size n over a field, then R× consists of the set of all invertible matrices of size n, and is called the general linear group.
Subring
A subset S of R is called a subring if any one of the following equivalent conditions holds:
- the addition and multiplication of R restrict to give operations S × S → S making S a ring with the same multiplicative identity as R.
- 1 ∈ S; and for all x, y in S, the elements xy, x + y, and −x are in S.
- S can be equipped with operations making it a ring such that the inclusion map S → R is a ring homomorphism.
For example, the ring 
![{\displaystyle \mathbb {Z} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a538d203a057d4c604f799c28e9a7be410fdcac)




An intersection of subrings is a subring. Given a subset E of R, the smallest subring of R containing E is the intersection of all subrings of R containing E, and it is called the subring generated by E.
For a ring R, the smallest subring of R is called the characteristic subring of R. It can be generated through addition of copies of 1 and −1. It is possible that n · 1 = 1 + 1 + ... + 1 (n times) can be zero. If n is the smallest positive integer such that this occurs, then n is called the characteristic of R. In some rings, n · 1 is never zero for any positive integer n, and those rings are said to have characteristic zero.
Given a ring R, let Z(R) denote the set of all elements x in R such that x commutes with every element in R: xy = yx for any y in R. Then Z(R) is a subring of R, called the center of R. More generally, given a subset X of R, let S be the set of all elements in R that commute with every element in X. Then S is a subring of R, called the centralizer (or commutant) of X. The center is the centralizer of the entire ring R. Elements or subsets of the center are said to be central in R; they (each individually) generate a subring of the center.
Ideal
Let R be a ring. A left ideal of R is a nonempty subset I of R such that for any x, y in I and r in R, the elements x + y and rx are in I. If R I denotes the R-span of I, that is, the set of finite sums
then I is a left ideal if 

If x is in R, then Rx and xR are left ideals and right ideals, respectively; they are called the principal left ideals and right ideals generated by x. The principal ideal RxR is written as (x). For example, the set of all positive and negative multiples of 2 along with 0 form an ideal of the integers, and this ideal is generated by the integer 2. In fact, every ideal of the ring of integers is principal.
Like a group, a ring is said to be simple if it is nonzero and it has no proper nonzero two-sided ideals. A commutative simple ring is precisely a field.
Rings are often studied with special conditions set upon their ideals. For example, a ring in which there is no strictly increasing infinite chain of left ideals is called a left Noetherian ring. A ring in which there is no strictly decreasing infinite chain of left ideals is called a left Artinian ring. It is a somewhat surprising fact that a left Artinian ring is left Noetherian (the Hopkins–Levitzki theorem). The integers, however, form a Noetherian ring which is not Artinian.
For commutative rings, the ideals generalize the classical notion
of divisibility and decomposition of an integer into prime numbers in
algebra. A proper ideal P of R is called a prime ideal if for any elements 







Homomorphism
A homomorphism from a ring (R, +, ⋅) to a ring (S, ‡, ∗) is a function f from R to S that preserves the ring operations; namely, such that, for all a, b in R the following identities hold:
If one is working with rngs, then the third condition is dropped.
A ring homomorphism f is said to be an isomorphism if there exists an inverse homomorphism to f (that is, a ring homomorphism that is an inverse function). Any bijective ring homomorphism is a ring isomorphism. Two rings R, S are said to be isomorphic if there is an isomorphism between them and in that case one writes 
Examples:
- The function that maps each integer x to its remainder modulo 4 (a number in { 0, 1, 2, 3 }) is a homomorphism from the ring
to the quotient ring
("quotient ring" is defined below).
- If u is a unit element in a ring R, then
is a ring homomorphism, called an inner automorphism of R.
- Let R be a commutative ring of prime characteristic p. Then
is a ring endomorphism of R called the Frobenius homomorphism.
- The Galois group of a field extension L/K is the set of all automorphisms of L whose restrictions to n are the identity.
- For any ring R, there are a unique ring homomorphism
and a unique ring homomorphism R → 0.
- An epimorphism (that is, right-cancelable morphism) of rings need not be surjective. For example, the unique map
is an epimorphism.
- An algebra homomorphism from a k-algebra to the endomorphism algebra of a vector space over k is called a representation of the algebra.
Given a ring homomorphism f : R → S, the set of all elements mapped to 0 by f is called the kernel of f. The kernel is a two-sided ideal of R. The image of f, on the other hand, is not always an ideal, but it is always a subring of S.
To give a ring homomorphism from a commutative ring R to a ring A with image contained in the center of A is the same as to give a structure of an algebra over R to A (which in particular gives a structure of an A-module).
Quotient ring
The notion of quotient ring is analogous to the notion of a quotient group. Given a ring (R, +, ⋅ ) and a two-sided ideal I of (R, +, ⋅ ), view I as subgroup of (R, +); then the quotient ring R/I is the set of cosets of I together with the operations
for all a, b in R. The ring R/I is also called a factor ring.
As with a quotient group, there is a canonical homomorphism p : R → R/I, given by 
- If f : R → S is a ring homomorphism such that f(I) = 0, then there is a unique homomorphism
such that
For any ring homomorphism f : R → S, invoking the universal property with I = ker f produces a homomorphism 
Module
The concept of a module over a ring generalizes the concept of a vector space (over a field) by generalizing from multiplication of vectors with elements of a field (scalar multiplication) to multiplication with elements of a ring. More precisely, given a ring R, an R-module M is an abelian group equipped with an operation R × M → M (associating an element of M to every pair of an element of R and an element of M) that satisfies certain axioms. This operation is commonly denoted by juxtaposition and called multiplication. The axioms of modules are the following: for all a, b in R and all x, y in M,
- M is an abelian group under addition.
When the ring is noncommutative these axioms define left modules; right modules are defined similarly by writing xa instead of ax. This is not only a change of notation, as the last axiom of right modules (that is x(ab) = (xa)b) becomes (ab)x = b(ax), if left multiplication (by ring elements) is used for a right module.
Basic examples of modules are ideals, including the ring itself.
Although similarly defined, the theory of modules is much more complicated than that of vector space, mainly, because, unlike vector spaces, modules are not characterized (up to an isomorphism) by a single invariant (the dimension of a vector space). In particular, not all modules have a basis.
The axioms of modules imply that (−1)x = −x, where the first minus denotes the additive inverse in the ring and the second minus the additive inverse in the module. Using this and denoting repeated addition by a multiplication by a positive integer allows identifying abelian groups with modules over the ring of integers.
Any ring homomorphism induces a structure of a module: if f : R → S is a ring homomorphism, then S is a left module over R by the multiplication: rs = f(r)s. If R is commutative or if f(R) is contained in the center of S, the ring S is called a R-algebra. In particular, every ring is an algebra over the integers.
Constructions
Direct product
Let R and S be rings. Then the product R × S can be equipped with the following natural ring structure:
for all r1, r2 in R and s1, s2 in S. The ring R × S with the above operations of addition and multiplication and the multiplicative identity (1, 1) is called the direct product of R with S. The same construction also works for an arbitrary family of rings: if Ri are rings indexed by a set I, then 
Let R be a commutative ring and 


A "finite" direct product may also be viewed as a direct sum of ideals.[37] Namely, let 






 one has that ei are central idempotents and eiej = 0, i ≠ j
(orthogonal). Again, one can reverse the construction. Namely, if one
is given a partition of 1 in orthogonal central idempotents, then let
one has that ei are central idempotents and eiej = 0, i ≠ j
(orthogonal). Again, one can reverse the construction. Namely, if one
is given a partition of 1 in orthogonal central idempotents, then let  which are two-sided ideals. If each ei is not a sum of orthogonal central idempotents,[d] then their direct sum is isomorphic to R.
which are two-sided ideals. If each ei is not a sum of orthogonal central idempotents,[d] then their direct sum is isomorphic to R.
An important application of an infinite direct product is the construction of a projective limit of rings (see below). Another application is a restricted product of a family of rings (cf. adele ring).
Polynomial ring
Given a symbol t (called a variable) and a commutative ring R, the set of polynomials
forms a commutative ring with the usual addition and multiplication, containing R as a subring. It is called the polynomial ring over R. More generally, the set ![{\displaystyle R\left[t_{1},\ldots ,t_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4cf3e812fcb5095239260dbc2ba56ceae257e5)

![{\displaystyle R\left[t_{i}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e9b4f740e9cf30c4b29d9510608e04a28906ec6)
If R is an integral domain, then R[t] is also an integral domain; its field of fractions is the field of rational functions. If R is a Noetherian ring, then R[t] is a Noetherian ring. If R is a unique factorization domain, then R[t] is a unique factorization domain. Finally, R is a field if and only if R[t] is a principal ideal domain.
Let 
(that is, the substitution). If S = R[t] and x = t, then f(t) = f. Because of this, the polynomial f is often also denoted by f(t). The image of the map 
Example: ![{\displaystyle k\left[t^{2},t^{3}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e4541532126a442f0b3099109c17c60a30b0bb5)
In other words, it is the subalgebra of k[t] generated by t2 and t3.
Example: let f be a polynomial in one variable, that is, an element in a polynomial ring R. Then f(x + h) is an element in R[h] and f(x + h) – f(x) is divisible by h in that ring. The result of substituting zero to h in (f(x + h) – f(x)) / h is f' (x), the derivative of f at x.
The substitution is a special case of the universal property of a
polynomial ring. The property states: given a ring homomorphism 
![{\overline {\phi }}:R[t]\to S](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9727858171f165d5705e60857e97068df5611bd)


To give an example, let S be the ring of all functions from R to itself; the addition and the multiplication are those of functions. Let x be the identity function. Each r in R defines a constant function, giving rise to the homomorphism R → S. The universal property says that this map extends uniquely to
(t maps to x) where 
Given a non-constant monic polynomial f in R[t], there exists a ring S containing R such that f is a product of linear factors in S[t].[39]
Let k be an algebraically closed field. The Hilbert's Nullstellensatz (theorem of zeros) states that there is a natural one-to-one correspondence between the set of all prime ideals in ![{\displaystyle k\left[t_{1},\ldots ,t_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/627d900f3df1fb1ea626778cc817791536cad857)
There are some other related constructions. A formal power series ring ![R[\![t]\!]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b0ed61bc4efa03186f6fadccd730eb17bc9e0c5)
together with multiplication and addition that mimic those for convergent series. It contains R[t] as a subring. A formal power series ring does not have the universal property of a polynomial ring; a series may not converge after a substitution. The important advantage of a formal power series ring over a polynomial ring is that it is local (in fact, complete).
Matrix ring and endomorphism ring
Let R be a ring (not necessarily commutative). The set of all square matrices of size n with entries in R forms a ring with the entry-wise addition and the usual matrix multiplication. It is called the matrix ring and is denoted by Mn(R). Given a right R-module U, the set of all R-linear maps from U to itself forms a ring with addition that is of function and multiplication that is of composition of functions; it is called the endomorphism ring of U and is denoted by EndR(U).
As in linear algebra, a matrix ring may be canonically interpreted as an endomorphism ring: 

Any ring homomorphism R → S induces Mn(R) → Mn(S).[40]
Schur's lemma says that if U is a simple right R-module, then EndR(U) is a division ring.[41] If 

The Artin–Wedderburn theorem states any semisimple ring (cf. below) is of this form.
A ring R and the matrix ring Mn(R) over it are Morita equivalent: the category of right modules of R is equivalent to the category of right modules over Mn(R).[40] In particular, two-sided ideals in R correspond in one-to-one to two-sided ideals in Mn(R).
Limits and colimits of rings
Let Ri be a sequence of rings such that Ri is a subring of Ri + 1 for all i. Then the union (or filtered colimit) of Ri is the ring 
Examples of colimits:
- A polynomial ring in infinitely many variables:
- The algebraic closure of finite fields of the same characteristic
- The field of formal Laurent series over a field k:
(it is the field of fractions of the formal power series ring
)
- The function field of an algebraic variety over a field k is
where the limit runs over all the coordinate rings k[U] of nonempty open subsets U (more succinctly it is the stalk of the structure sheaf at the generic point.)
Any commutative ring is the colimit of finitely generated subrings.
A projective limit (or a filtered limit) of rings is defined as follows. Suppose we're given a family of rings Ri, i running over positive integers, say, and ring homomorphisms Rj → Ri, j ≥ i such that Ri → Ri are all the identities and Rk → Rj → Ri is Rk → Ri whenever k ≥ j ≥ i. Then 

For an example of a projective limit, see § Completion.
Localization
The localization generalizes the construction of the field of fractions of an integral domain to an arbitrary ring and modules. Given a (not necessarily commutative) ring R and a subset S of R, there exists a ring ![R[S^{-1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc8e9aca12e1c82bcb76786e721b503057d121bb)
![{\displaystyle R\to R\left[S^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ff24251e09611253a5e59710f41fef5e9ea8295)
![{\displaystyle R\left[S^{-1}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc5da3880f2a84e3c59d744d4a6a70c91648127f)
![{\displaystyle R\left[S^{-1}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477d928832e71936d39c6e196a1ec4c7f9c5f003)
![{\displaystyle R\left[S^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a2fa5e7650f1b84116f5dd0986162ed090cafea)
![{\displaystyle R\left[f^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/866a1856d4f363ae6d4d2f3818ff980b72442c51)

![{\displaystyle R\left[f^{-1}\right]=R[t]/(tf-1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/751001e38a83d034e0cf683b63cf45ac724151ad)
The localization is frequently applied to a commutative ring R with respect to the complement of a prime ideal (or a union of prime ideals) in R. In that case 

![{\displaystyle R\left[S^{-1}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477d928832e71936d39c6e196a1ec4c7f9c5f003)






If M is a left R-module, then the localization of M with respect to S is given by a change of rings ![{\displaystyle M\left[S^{-1}\right]=R\left[S^{-1}\right]\otimes _{R}M.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/182e09cf0feec2967d8337e197459da4d0084bde)
The most important properties of localization are the following: when R is a commutative ring and S a multiplicatively closed subset
is a bijection between the set of all prime ideals in R disjoint from S and the set of all prime ideals in
[44]
f running over elements in S with partial ordering given by divisibility.[45]
- The localization is exact: is exact over
whenever
is exact over R.
- Conversely, if
is exact for any maximal ideal
then
is exact.
- A remark: localization is no help in proving a global existence. One instance of this is that if two modules are isomorphic at all prime ideals, it does not follow that they are isomorphic. (One way to explain this is that the localization allows one to view a module as a sheaf over prime ideals and a sheaf is inherently a local notion.)
In category theory, a localization of a category amounts to making some morphisms isomorphisms. An element in a commutative ring R may be thought of as an endomorphism of any R-module. Thus, categorically, a localization of R with respect to a subset S of R is a functor from the category of R-modules to itself that sends elements of S viewed as endomorphisms to automorphisms and is universal with respect to this property. (Of course, R then maps to ![{\displaystyle R\left[S^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a2fa5e7650f1b84116f5dd0986162ed090cafea)
![{\displaystyle R\left[S^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a2fa5e7650f1b84116f5dd0986162ed090cafea)
Completion
Let R be a commutative ring, and let I be an ideal of R.
The completion of R at I is the projective limit 


The basic example is the completion of 
















Similarly, the formal power series ring R[{[t]}] is the completion of R[t] at (t) (see also Hensel's lemma)
A complete ring has much simpler structure than a commutative ring. This owns to the Cohen structure theorem, which says, roughly, that a complete local ring tends to look like a formal power series ring or a quotient of it. On the other hand, the interaction between the integral closure and completion has been among the most important aspects that distinguish modern commutative ring theory from the classical one developed by the likes of Noether. Pathological examples found by Nagata led to the reexamination of the roles of Noetherian rings and motivated, among other things, the definition of excellent ring.
Rings with generators and relations
The most general way to construct a ring is by specifying generators and relations. Let F be a free ring (that is, free algebra over the integers) with the set X of symbols, that is, F consists of polynomials with integral coefficients in noncommuting variables that are elements of X. A free ring satisfies the universal property: any function from the set X to a ring R factors through F so that F → R is the unique ring homomorphism. Just as in the group case, every ring can be represented as a quotient of a free ring.[47]
Now, we can impose relations among symbols in X by taking a quotient. Explicitly, if E is a subset of F, then the quotient ring of F by the ideal generated by E is called the ring with generators X and relations E. If we used a ring, say, A as a base ring instead of 

In the category-theoretic terms, the formation 
Let A, B be algebras over a commutative ring R. Then the tensor product of R-modules 

Special kinds of rings
Domains
A nonzero ring with no nonzero zero-divisors is called a domain. A commutative domain is called an integral domain. The most important integral domains are principal ideal domains, PIDs for short, and fields. A principal ideal domain is an integral domain in which every ideal is principal. An important class of integral domains that contain a PID is a unique factorization domain (UFD), an integral domain in which every nonunit element is a product of prime elements (an element is prime if it generates a prime ideal.) The fundamental question in algebraic number theory is on the extent to which the ring of (generalized) integers in a number field, where an "ideal" admits prime factorization, fails to be a PID.
Among theorems concerning a PID, the most important one is the structure theorem for finitely generated modules over a principal ideal domain. The theorem may be illustrated by the following application to linear algebra.[48] Let V be a finite-dimensional vector space over a field k and f : V → V a linear map with minimal polynomial q. Then, since k[t] is a unique factorization domain, q factors into powers of distinct irreducible polynomials (that is, prime elements):

Letting 
![{\displaystyle k[t]/\left(p_{i}^{k_{j}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20d1f6688eda0ad0b9ab06a59cc999e376b2b3fa)

In algebraic geometry, UFDs arise because of smoothness. More precisely, a point in a variety (over a perfect field) is smooth if the local ring at the point is a regular local ring. A regular local ring is a UFD.[49]
The following is a chain of class inclusions that describes the relationship between rings, domains and fields:
- rngs ⊃ rings ⊃ commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ GCD domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ algebraically closed fields
Division ring
A division ring is a ring such that every non-zero element is a unit. A commutative division ring is a field. A prominent example of a division ring that is not a field is the ring of quaternions. Any centralizer in a division ring is also a division ring. In particular, the center of a division ring is a field. It turned out that every finite domain (in particular finite division ring) is a field; in particular commutative (the Wedderburn's little theorem).
Every module over a division ring is a free module (has a basis); consequently, much of linear algebra can be carried out over a division ring instead of a field.
The study of conjugacy classes figures prominently in the classical theory of division rings; see, for example, the Cartan–Brauer–Hua theorem.
A cyclic algebra, introduced by L. E. Dickson, is a generalization of a quaternion algebra.
Semisimple rings
A semisimple module is a direct sum of simple modules. A semisimple ring is a ring that is semisimple as a left module (or right module) over itself.
Examples
- A division ring is semisimple (and simple).
- For any division ring D and positive integer n, the matrix ring Mn(D) is semisimple (and simple).
- For a field k and finite group G, the group ring kG is semisimple if and only if the characteristic of k does not divide the order of G (Maschke's theorem).
- Clifford algebras are semisimple.
The Weyl algebra over a field is a simple ring, but it is not semisimple. The same holds for a ring of differential operators in many variables.
Properties
Any module over a semisimple ring is semisimple. (Proof: A free module over a semisimple ring is semisimple and any module is a quotient of a free module.)
For a ring R, the following are equivalent:
- R is semisimple.
- R is artinian and semiprimitive.
- R is a finite direct product
where each ni is a positive integer, and each Di is a division ring (Artin–Wedderburn theorem).
Semisimplicity is closely related to separability. A unital associative algebra A over a field k is said to be separable if the base extension 
Central simple algebra and Brauer group
For a field k, a k-algebra is central if its center is k and is simple if it is a simple ring. Since the center of a simple k-algebra is a field, any simple k-algebra is a central simple algebra over its center. In this section, a central simple algebra is assumed to have finite dimension. Also, we mostly fix the base field; thus, an algebra refers to a k-algebra. The matrix ring of size n over a ring R will be denoted by Rn.
The Skolem–Noether theorem states any automorphism of a central simple algebra is inner.
Two central simple algebras A and B are said to be similar if there are integers n and m such that 

![{\displaystyle [A][B]=\left[A\otimes _{k}B\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9181c4c9330a227ae8d9ffaabb33c18ed73459d6)
For example, Br(k) is trivial if k is a finite field or an algebraically closed field (more generally quasi-algebraically closed field; cf. Tsen's theorem). 


Now, if F is a field extension of k, then the base extension 


Azumaya algebras generalize the notion of central simple algebras to a commutative local ring.
Valuation ring
If K is a field, a valuation v is a group homomorphism from the multiplicative group K∗ to a totally ordered abelian group G such that, for any f, g in K with f + g nonzero, v(f + g) ≥ min{v(f), v(g)}. The valuation ring of v is the subring of K consisting of zero and all nonzero f such that v(f) ≥ 0.
Examples:
- The field of formal Laurent series
over a field k comes with the valuation v such that v(f) is the least degree of a nonzero term in f; the valuation ring of v is the formal power series ring
- More generally, given a field k and a totally ordered abelian group G, let
be the set of all functions from G to k whose supports (the sets of points at which the functions are nonzero) are well ordered. It is a field with the multiplication given by convolution:
It also comes with the valuation v such that v(f) is the least element in the support of f. The subring consisting of elements with finite support is called the group ring of G (which makes sense even if G is not commutative). If G is the ring of integers, then we recover the previous example (by identifying f with the series whose n-th coefficient is f(n).)
Rings with extra structure
A ring may be viewed as an abelian group (by using the addition operation), with extra structure: namely, ring multiplication. In the same way, there are other mathematical objects which may be considered as rings with extra structure. For example:
- An associative algebra is a ring that is also a vector space over a field n such that the scalar multiplication is compatible with the ring multiplication. For instance, the set of n-by-n matrices over the real field
has dimension n2 as a real vector space.
- A ring R is a topological ring if its set of elements R is given a topology which makes the addition map (
) and the multiplication map
to be both continuous as maps between topological spaces (where X × X inherits the product topology or any other product in the category). For example, n-by-n matrices over the real numbers could be given either the Euclidean topology, or the Zariski topology, and in either case one would obtain a topological ring.
- A λ-ring is a commutative ring R together with operations λn: R → R that are like n-th exterior powers:
- For example,
is a λ-ring with
the binomial coefficients. The notion plays a central rule in the algebraic approach to the Riemann–Roch theorem.
- A totally ordered ring is a ring with a total ordering that is compatible with ring operations.
Some examples of the ubiquity of rings
Many different kinds of mathematical objects can be fruitfully analyzed in terms of some associated ring.
Cohomology ring of a topological space
To any topological space X one can associate its integral cohomology ring
a graded ring. There are also homology groups 
The ring structure in cohomology provides the foundation for characteristic classes of fiber bundles, intersection theory on manifolds and algebraic varieties, Schubert calculus and much more.
Burnside ring of a group
To any group is associated its Burnside ring which uses a ring to describe the various ways the group can act on a finite set. The Burnside ring's additive group is the free abelian group whose basis are the transitive actions of the group and whose addition is the disjoint union of the action. Expressing an action in terms of the basis is decomposing an action into its transitive constituents. The multiplication is easily expressed in terms of the representation ring: the multiplication in the Burnside ring is formed by writing the tensor product of two permutation modules as a permutation module. The ring structure allows a formal way of subtracting one action from another. Since the Burnside ring is contained as a finite index subring of the representation ring, one can pass easily from one to the other by extending the coefficients from integers to the rational numbers.
Representation ring of a group ring
To any group ring or Hopf algebra is associated its representation ring or "Green ring". The representation ring's additive group is the free abelian group whose basis are the indecomposable modules and whose addition corresponds to the direct sum. Expressing a module in terms of the basis is finding an indecomposable decomposition of the module. The multiplication is the tensor product. When the algebra is semisimple, the representation ring is just the character ring from character theory, which is more or less the Grothendieck group given a ring structure.
Function field of an irreducible algebraic variety
To any irreducible algebraic variety is associated its function field. The points of an algebraic variety correspond to valuation rings contained in the function field and containing the coordinate ring. The study of algebraic geometry makes heavy use of commutative algebra to study geometric concepts in terms of ring-theoretic properties. Birational geometry studies maps between the subrings of the function field.
Face ring of a simplicial complex
Every simplicial complex has an associated face ring, also called its Stanley–Reisner ring. This ring reflects many of the combinatorial properties of the simplicial complex, so it is of particular interest in algebraic combinatorics. In particular, the algebraic geometry of the Stanley–Reisner ring was used to characterize the numbers of faces in each dimension of simplicial polytopes.
Category-theoretic description
Every ring can be thought of as a monoid in Ab, the category of abelian groups (thought of as a monoidal category under the tensor product of 
Let (A, +) be an abelian group and let End(A) be its endomorphism ring (see above). Note that, essentially, End(A) is the set of all morphisms of A, where if f is in End(A), and g is in End(A), the following rules may be used to compute f + g and f ⋅ g:
where + as in f(x) + g(x) is addition in A, and function composition is denoted from right to left. Therefore, associated to any abelian group, is a ring. Conversely, given any ring, (R, +, ⋅ ), (R, +) is an abelian group. Furthermore, for every r in R, right (or left) multiplication by r gives rise to a morphism of (R, +), by right (or left) distributivity. Let A = (R, +). Consider those endomorphisms of A, that "factor through" right (or left) multiplication of R. In other words, let EndR(A) be the set of all morphisms m of A, having the property that m(r ⋅ x) = r ⋅ m(x). It was seen that every r in R gives rise to a morphism of A: right multiplication by r. It is in fact true that this association of any element of R, to a morphism of A, as a function from R to EndR(A), is an isomorphism of rings. In this sense, therefore, any ring can be viewed as the endomorphism ring of some abelian X-group (by X-group, it is meant a group with X being its set of operators).[52] In essence, the most general form of a ring, is the endomorphism group of some abelian X-group.
Any ring can be seen as a preadditive category with a single object. It is therefore natural to consider arbitrary preadditive categories to be generalizations of rings. And indeed, many definitions and theorems originally given for rings can be translated to this more general context. Additive functors between preadditive categories generalize the concept of ring homomorphism, and ideals in additive categories can be defined as sets of morphisms closed under addition and under composition with arbitrary morphisms.
Generalization
Algebraists have defined structures more general than rings by weakening or dropping some of ring axioms.
Rng
A rng is the same as a ring, except that the existence of a multiplicative identity is not assumed.[53]
Nonassociative ring
A nonassociative ring is an algebraic structure that satisfies all of the ring axioms except the associative property and the existence of a multiplicative identity. A notable example is a Lie algebra. There exists some structure theory for such algebras that generalizes the analogous results for Lie algebras and associative algebras.[citation needed]
Semiring
A semiring (sometimes rig) is obtained by weakening the assumption that (R, +) is an abelian group to the assumption that (R, +) is a commutative monoid, and adding the axiom that 0 ⋅ a = a ⋅ 0 = 0 for all a in R (since it no longer follows from the other axioms).
Examples:
- the non-negative integers
with ordinary addition and multiplication;
- the tropical semiring.
Other ring-like objects
Ring object in a category
Let C be a category with finite products. Let pt denote a terminal object of C (an empty product). A ring object in C is an object R equipped with morphisms 






Ring scheme
In algebraic geometry, a ring scheme over a base scheme S is a ring object in the category of S-schemes. One example is the ring scheme Wn over 
Ring spectrum
In algebraic topology, a ring spectrum is a spectrum X together with a multiplication 
See also
Special types of rings:
Notes
- Such a central idempotent is called centrally primitive.
Citations
- Serre, p. 44.
References
General references
- Artin, Michael (2018). Algebra (2nd ed.). Pearson.
- Atiyah, Michael; Macdonald, Ian G. (1969). Introduction to commutative algebra. Addison–Wesley.
- Bourbaki, N. (1964). Algèbre commutative. Hermann.
- Bourbaki, N. (1989). Algebra I, Chapters 1–3. Springer.
- Cohn, Paul Moritz (2003), Basic algebra: groups, rings, and fields, Springer, ISBN 978-1-85233-587-8.
- Eisenbud, David (1995). Commutative algebra with a view toward algebraic geometry. Springer.
- Gallian, Joseph A. (2006). Contemporary Abstract Algebra, Sixth Edition. Houghton Mifflin. ISBN 9780618514717.
- Gardner, J.W.; Wiegandt, R. (2003). Radical Theory of Rings. Chapman & Hall/CRC Pure and Applied Mathematics. ISBN 0824750330.
- Herstein, I. N. (1994) [reprint of the 1968 original]. Noncommutative rings. Carus Mathematical Monographs. Vol. 15. With an afterword by Lance W. Small. Mathematical Association of America. ISBN 0-88385-015-X.
- Hungerford, Thomas W. (1997). Abstract Algebra: an Introduction, Second Edition. Brooks/Cole. ISBN 9780030105593.
- Jacobson, Nathan (2009). Basic algebra. Vol. 1 (2nd ed.). Dover. ISBN 978-0-486-47189-1.
- Jacobson, Nathan (1964). "Structure of rings". American Mathematical Society Colloquium Publications (Revised ed.). 37.
- Jacobson, Nathan (1943). "The Theory of Rings". American Mathematical Society Mathematical Surveys. I.
- Kaplansky, Irving (1974), Commutative rings (Revised ed.), University of Chicago Press, ISBN 0-226-42454-5, MR 0345945.
- Lam, Tsit Yuen (2001). A first course in noncommutative rings. Graduate Texts in Mathematics. Vol. 131 (2nd ed.). Springer. ISBN 0-387-95183-0.
- Lam, Tsit Yuen (2003). Exercises in classical ring theory. Problem Books in Mathematics (2nd ed.). Springer. ISBN 0-387-00500-5.
- Lam, Tsit Yuen (1999). Lectures on modules and rings. Graduate Texts in Mathematics. Vol. 189. Springer. ISBN 0-387-98428-3.
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556, Zbl 0984.00001.
- Matsumura, Hideyuki (1989). Commutative Ring Theory. Cambridge Studies in Advanced Mathematics (2nd ed.). Cambridge University Press. ISBN 978-0-521-36764-6.
- Milne, J. "A primer of commutative algebra".
- Rotman, Joseph (1998), Galois Theory (2nd ed.), Springer, ISBN 0-387-98541-7.
- van der Waerden, Bartel Leendert (1930), Moderne Algebra. Teil I, Die Grundlehren der mathematischen Wissenschaften, vol. 33, Springer, ISBN 978-3-540-56799-8, MR 0009016.
- Warner, Seth (1965). Modern Algebra. Dover. ISBN 9780486663418.
- Wilder, Raymond Louis (1965). Introduction to Foundations of Mathematics. Wiley.
- Zariski, Oscar; Samuel, Pierre (1958). Commutative Algebra. Vol. 1. Van Nostrand.
Special references
- Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Commutative Noetherian and Krull rings, Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155615-7
- Balcerzyk, Stanisław; Józefiak, Tadeusz (1989), Dimension, multiplicity and homological methods, Mathematics and its Applications, Chichester: Ellis Horwood Ltd., ISBN 978-0-13-155623-2
- Ballieu, R. (1947). "Anneaux finis; systèmes hypercomplexes de rang trois sur un corps commutatif". Ann. Soc. Sci. Bruxelles. I (61): 222–227.
- Berrick, A. J.; Keating, M. E. (2000). An Introduction to Rings and Modules with K-Theory in View. Cambridge University Press.
- Cohn, Paul Moritz (1995), Skew Fields: Theory of General Division Rings, Encyclopedia of Mathematics and its Applications, vol. 57, Cambridge University Press, ISBN 9780521432177
- Eisenbud, David (1995), Commutative algebra. With a view toward algebraic geometry., Graduate Texts in Mathematics, vol. 150, Springer, ISBN 978-0-387-94268-1, MR 1322960
- Gilmer, R.; Mott, J. (1973). "Associative Rings of Order". Proc. Japan Acad. 49: 795–799. doi:10.3792/pja/1195519146.
- Harris, J. W.; Stocker, H. (1998). Handbook of Mathematics and Computational Science. Springer.
- Isaacs, I. M. (1994). Algebra: A Graduate Course. AMS. ISBN 978-0-8218-4799-2.
- Jacobson, Nathan (1945), "Structure theory of algebraic algebras of bounded degree", Annals of Mathematics, Annals of Mathematics, 46 (4): 695–707, doi:10.2307/1969205, ISSN 0003-486X, JSTOR 1969205
- Knuth, D. E. (1998). The Art of Computer Programming. Vol. 2: Seminumerical Algorithms (3rd ed.). Addison–Wesley.
- Korn, G. A.; Korn, T. M. (2000). Mathematical Handbook for Scientists and Engineers. Dover. ISBN 9780486411477.
- Milne, J. "Class field theory".
- Nagata, Masayoshi (1962) [1975 reprint], Local rings, Interscience Tracts in Pure and Applied Mathematics, vol. 13, Interscience Publishers, ISBN 978-0-88275-228-0, MR 0155856
- Pierce, Richard S. (1982). Associative algebras. Graduate Texts in Mathematics. Vol. 88. Springer. ISBN 0-387-90693-2.
- Poonen, Bjorn (2018), Why all rings should have a 1 (PDF), arXiv:1404.0135, archived (PDF) from the original on 2015-04-24
- Serre, Jean-Pierre (1979), Local fields, Graduate Texts in Mathematics, vol. 67, Springer
- Springer, Tonny A. (1977), Invariant theory, Lecture Notes in Mathematics, vol. 585, Springer, ISBN 9783540373704
- Weibel, Charles. "The K-book: An introduction to algebraic K-theory".
- Zariski, Oscar; Samuel, Pierre (1975). Commutative algebra. Graduate Texts in Mathematics. Vol. 28–29. Springer. ISBN 0-387-90089-6.
Primary sources
- Fraenkel, A. (1915). "Über die Teiler der Null und die Zerlegung von Ringen". J. Reine Angew. Math. 1915 (145): 139–176. doi:10.1515/crll.1915.145.139. S2CID 118962421.
- Hilbert, David (1897). "Die Theorie der algebraischen Zahlkörper". Jahresbericht der Deutschen Mathematiker-Vereinigung. 4.
- Noether, Emmy (1921). "Idealtheorie in Ringbereichen". Math. Annalen. 83 (1–2): 24–66. doi:10.1007/bf01464225. S2CID 121594471.
Historical references
- History of ring theory at the MacTutor Archive
- Garrett Birkhoff and Saunders Mac Lane (1996) A Survey of Modern Algebra, 5th ed. New York: Macmillan.
- Bronshtein, I. N. and Semendyayev, K. A. (2004) Handbook of Mathematics, 4th ed. New York: Springer-Verlag ISBN 3-540-43491-7.
- Faith, Carl (1999) Rings and things and a fine array of twentieth century associative algebra. Mathematical Surveys and Monographs, 65. American Mathematical Society ISBN 0-8218-0993-8.
- Itô, K. editor (1986) "Rings." §368 in Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 2. Cambridge, MA: MIT Press.
- Israel Kleiner (1996) "The Genesis of the Abstract Ring Concept", American Mathematical Monthly 103: 417–424 doi:10.2307/2974935
- Kleiner, I. (1998) "From numbers to rings: the early history of ring theory", Elemente der Mathematik 53: 18–35.
- B. L. van der Waerden (1985) A History of Algebra, Springer-Verlag,
https://en.wikipedia.org/wiki/Ring_(mathematics)
In linguistic semantics, a downward entailing (DE) propositional operator is one that constrains the meaning of an expression to a lower number or degree than would be possible without the expression. For example, "not," "nobody," "few people," "at most two boys." Conversely, an upward-entailing operator constrains the meaning of an expression to a higher number or degree, for example "more than one." A context that is neither downward nor upward entailing is non-monotone[citation needed], such as "exactly five."
A downward-entailing operator reverses the relation of semantic strength among expressions. An expression like "run fast" is semantically stronger than the expression "run" since "John ran fast" entails "John ran," but not conversely. But a downward-entailing context reverses this strength; for example, the proposition "At most two boys ran" entails that "At most two boys ran fast" but not the other way around.
An upward-entailing operator preserves the relation of semantic strength among a set of expressions; for example "more than three ran fast" entails "more than three ran" but not the other way around.
Ladusaw (1980) proposed that downward entailment is the property that licenses polarity items. Indeed, "Nobody saw anything" is downward entailing and admits the negative polarity item anything, while *"I saw anything" is unacceptable (the upward-entailing context does not license such a polarity item). This approach explains many but not all typical cases of polarity item sensitivity. Subsequent attempts to describe the behavior of polarity items rely on a broader notion of nonveridicality.
https://en.wikipedia.org/wiki/Downward_entailing
In linguistics, a polarity item is a lexical item that is associated with affirmation or negation. An affirmation is a positive polarity item, abbreviated PPI or AFF. A negation is a negative polarity item, abbreviated NPI or NEG.
The linguistic environment in which a polarity item appears is a licensing context. In the simplest case, an affirmative statement provides a licensing context for a PPI, while negation provides a licensing context for an NPI. However, there are many complications, and not all polarity items of a particular type have the same licensing contexts.
https://en.wikipedia.org/wiki/Polarity_item
Because standard English does not have negative concord, that is, double negatives are not used to intensify each other, the language makes frequent use of certain NPIs that correspond in meaning to negative items, and can be used in the environment of another negative. For example, anywhere is an NPI corresponding to the negative nowhere, as used in the following sentences:
- I was going nowhere. (the negative nowhere is used when not preceded by another negative)
- I was not going anywhere. (the NPI anywhere is used in the environment of the preceding negative not)
Note that double-negative constructions like I was not going nowhere take on an opposing meaning in formal usage, but that this is not necessarily the case in colloquial contexts and in various lects, which parallels other languages which have negative concord. Anywhere, like most of the other NPIs listed below, is also used in other senses where it is not an NPI, as in I would go anywhere with you.
- nobody/no one – anybody/anyone
- nothing – anything
- no/none – any
- never – ever
- nowhere – anywhere
- no longer/no more – any longer/any more
See also English grammar § Negation, and Affirmation and negation § Multiple negation.
https://en.wikipedia.org/wiki/Polarity_item
In linguistics, veridicality (from Latin "truthfully said") is a semantic or grammatical assertion of the truth of an utterance.
https://en.wikipedia.org/wiki/Veridicality
In linguistics, veridicality (from Latin "truthfully said") is a semantic or grammatical assertion of the truth of an utterance.
Definition
Merriam-Webster defines "veridical" as truthful, veracious and non illusory. It stems from the Latin "veridicus", composed of Latin verus, meaning "true", and dicere, which means "to say". For example, the statement "Paul saw a snake" asserts the truthfulness of the claim, while "Paul did see a snake" is an even stronger assertion.
The formal definition of veridicality views the context as a propositional operator (Giannakidou 1998).
- A propositional operator F is veridical iff Fp entails p, that is, Fp → p; otherwise F is nonveridical.
- Additionally, a nonveridical operator F is antiveridical iff Fp entails not p, that is, Fp → ¬p.
For temporal and aspectual operators, the definition of veridicality is somewhat more complex:
- For operators relative to instants of time: Let F be a temporal or aspectual operator, and t an instant of time.
- F is veridical iff for Fp to be true at time t, p must be true at a (contextually relevant) time t′ ≤ t; otherwise F is nonveridical.
- A nonveridical operator F is antiveridical iff for Fp to be true at time t, ¬p must be true at a (contextually relevant) time t′ ≤ t.
- For operators relative to intervals of time: Let F be a temporal or aspectual operator, and t an interval of time.
- F is veridical iff for Fp to be true of t, p must be true of all (contextually relevant) t′ ⊆ t; otherwise F is nonveridical.
- A nonveridical operator F is antiveridical iff for Fp to be true of t, ¬p must be true of all (contextually relevant) t′ ⊆ t.
Nonveridical operators
Negation is veridical, though of opposite polarity, sometimes called antiveridical: "Paul didn't see a snake" asserts that the statement "Paul saw a snake" is false. In English, non-indicative moods or irrealis moods are frequently used in a nonveridical sense: "Paul may have seen a snake" and "Paul would have seen a snake" do not assert that Paul actually saw a snake and the second implies that he did not. "Paul would indeed have seen a snake" is veridical, and some languages have separate veridical conditional moods for such cases.[citation needed]
Nonveridicality has been proposed to be behind the licensing of polarity items such as the English words any and ever, as an alternative to the influential downward entailment theory (see below) proposed by Ladusaw (1980). Anastasia Giannakidou (1998) argued that various polarity phenomena observed in language are manifestations of the dependency of polarity items to the (non)veridicality of the context of appearance. The (non)veridical dependency may be positive (licensing), or negative (anti-licensing), and arises from the sensitivity semantics of polarity items. Across languages, different polarity items may show sensitivity to veridicality, anti-veridicality, or non-veridicality.
Nonveridical operators typically license the use of polarity items, which in veridical contexts normally is ungrammatical:
- * Mary saw any students. (The context is veridical.)
- Mary didn't see any students. (The context is nonveridical.)
Downward entailment
All downward entailing contexts are nonveridical. Because of this, theories based on nonveridicality can be seen as extending those based on downward entailment, allowing more cases of polarity item licensing to be explained.
Downward entailment predicts that polarity items will be licensed in the scope of negation, downward entailing quantifiers like few N, at most n N, no N, and the restriction of every:
- No students saw anything.
- Mary didn't see anything.
- Few children saw anything.
- Every student who saw anything should report to the police.
Non-monotone quantifiers
Quantifiers like exactly three students, nobody but John, and almost nobody are non-monotone (and thus not downward entailing) but nevertheless admit any:
- % Exactly three students saw anything.
- Nobody but Mary saw anything.
- Almost nobody saw anything.
Hardly and barely
Hardly and barely allow for any despite not being downward entailing.
- Mary hardly talked to anybody. (Does not entail "Mary hardly talked to her mother".)
- Mary barely studied anything. (Does not entail "Mary barely studied linguistics".)
Questions
Polarity items are quite frequent in questions, although questions are not monotone.
- Did you see anything?
Although questions biased towards the negative answer, such as "Do you [even] give a damn about any books?" (tag questions based on negative sentences exhibit even more such bias), can sometimes be seen as downward entailing, this approach cannot account for the general case, such as the above example where the context is perfectly neutral. Neither can it explain why negative questions, which naturally tend to be biased, don't license negative polarity items.
In semantics which treats a question as the set of its true answers, the denotation of a polar question contains two possible answers:
- [[Did you see Mary?]] = { you saw Mary ∨ you didn't see Mary }
Because disjunction p ∨ q entails neither p nor q, the context is nonveridical, which explains the admittance of any.[further explanation needed]
Future
Polarity items appear in future sentences.
- Mary will buy any bottle of wine.
- The children will leave as soon as they discover anything.
According to the formal definition of veridicality for temporal operators, future is nonveridical: that "John will buy a bottle of Merlot" is true now does not entail that "John buys a bottle of Merlot" is true at any instant up to and including now. On the other hand, past is veridical: that "John bought a bottle of Merlot" is true now entails that there is an instant preceding now at which "John buys a bottle of Merlot" is true.
Habitual aspect
Likewise, nonveridicality of the habitual aspect licenses polarity items.
- He usually reads any book very carefully.
The habitual aspect is nonveridical because e.g., that "He is usually cheerful" is true over some interval of time does not entail that "He is cheerful" is true over every subinterval of that. This is in contrast to e.g., the progressive aspect, which is veridical and prohibits negative polarity items.
Generic sentences
Non-monotone generic sentences accept polarity items.
- Any cat hunts mice.
Modal verbs
Modal verbs create generally good environments for polarity items:
- Mary may talk to anybody.
- Any minors must be accompanied by their parents.
- The committee can give the job to any candidate.
Such contexts are nonveridical despite being non-monotone and sometimes even upward entailing ("Mary must tango" entails "Mary must dance").
Imperatives
Imperatives are roughly parallel to modal verbs and intensional contexts in general.
- Take any apple. (cf. "You may/must take any apple", "I want you to take any apple".)
Protasis of conditionals
Protasis of conditionals is one of the most common environments for polarity items.
- If you sleep with anybody, I'll kill you.
Directive intensional verbs
Polarity items are licensed with directive propositional attitudes but not with epistemic ones.
- Mary would like to invite any student.
- Mary asked us to invite any student.
- * Mary believes that we invited any student.
- * Mary dreamt that we invited any student.
References
- Giannakidou, Anastasia (1998). Polarity Sensitivity as (Non)Veridical Dependency. John Benjamins Publishing Company. ISBN 9789027227447.
- Giannakidou, Anastasia (2002). "Licensing and Sensitivity in Polarity Items: From Downward Entailment to Nonveridicality" (PDF format; Adobe Acrobat required). In Andronis, Maria; Pycha, Anne; Yoshimura, Keiko (eds.). CLS 38: Papers from the 38th Annual Meeting of the Chicago Linguistic Society, Parasession on Polarity and Negation. Retrieved December 15, 2011.
- Ladusaw, William (1980). Polarity Sensitivity as Inherent Scope Relations. Garland, NY.
https://en.wikipedia.org/wiki/Veridicality
A faultless disagreement is a disagreement when Party A states that P is true, while Party B states that non-P is true, and neither party is at fault. Disagreements of this kind may arise in areas of evaluative discourse, such as aesthetics, justification of beliefs or moral values, etc. A representative example is that John says Paris is more interesting than Rome, while Bob claims Rome is more interesting than Paris. Furthermore, in the case of a faultless disagreement, it is possible that if any party gives up their claim, there will be no improvement in the position of any of them.[1]
Within the framework of formal logic it is impossible that both P and not-P are true, and it was attempted to justify faultless disagreements within the framework of relativism of the Truth,[2] Max Kölbel and Sven Rosenkranz present arguments to the point that genuine faultless disagreements are impossible.[1][2] However, defenses of faultless disagreement, and of alethic relativism more generally, continue to be made by critics of formal logic as it is currently constructed.[3]
https://en.wikipedia.org/wiki/Faultless_disagreement
In linguistics and philosophy, the denotation of an expression is its literal meaning. For instance, the English word "warm" denotes the property of being warm. Denotation is contrasted with other aspects of meaning including connotation. For instance, the word "warm" may evoke calmness or cosiness, but these associations are not part of the word's denotation. Similarly, an expression's denotation is separate from pragmatic inferences it may trigger. For instance, describing something as "warm" often implicates that it is not hot, but this is once again not part of the word's denotation.
Denotation plays a major role in several fields. Within philosophy of language, denotation is studied as an important aspect of meaning. In mathematics and computer science, assignments of denotations are assigned to expressions are a crucial step in defining interpreted formal languages. The main task of formal semantics is to reverse engineer the computational system which assigns denotations to expressions of natural languages.
https://en.wikipedia.org/wiki/Denotation
In semantics, mathematical logic and related disciplines, the principle of compositionality is the principle that the meaning of a complex expression is determined by the meanings of its constituent expressions and the rules used to combine them. This principle is also called Frege's principle, because Gottlob Frege is widely credited for the first modern formulation of it. The principle was never explicitly stated by Frege,[1] and it was arguably already assumed by George Boole[2] decades before Frege's work.
The principle of compositionality is highly debated in linguistics, and among its most challenging problems there are the issues of contextuality, the non-compositionality of idiomatic expressions, and the non-compositionality of quotations.[3]
https://en.wikipedia.org/wiki/Principle_of_compositionality
In formal semantics, a generalized quantifier (GQ) is an expression that denotes a set of sets. This is the standard semantics assigned to quantified noun phrases. For example, the generalized quantifier every boy denotes the set of sets of which every boy is a member:

This treatment of quantifiers has been essential in achieving a compositional semantics for sentences containing quantifiers.[1][2]
https://en.wikipedia.org/wiki/Generalized_quantifier
In any of several fields of study that treat the use of signs — for example, in linguistics, logic, mathematics, semantics, semiotics, and philosophy of language — the extension of a concept, idea, or sign consists of the things to which it applies, in contrast with its comprehension or intension, which consists very roughly of the ideas, properties, or corresponding signs that are implied or suggested by the concept in question.
In philosophical semantics or the philosophy of language, the 'extension' of a concept or expression is the set of things it extends to, or applies to, if it is the sort of concept or expression that a single object by itself can satisfy. Concepts and expressions of this sort are monadic or "one-place" concepts and expressions.
So the extension of the word "dog" is the set of all (past, present and future) dogs in the world: the set includes Fido, Rover, Lassie, Rex, and so on. The extension of the phrase "Wikipedia reader" includes each person who has ever read Wikipedia, including you.
The extension of a whole statement, as opposed to a word or phrase, is defined (since Gottlob Frege's "On Sense and Reference") as its truth value. So the extension of "Lassie is famous" is the logical value 'true', since Lassie is famous.
Some concepts and expressions are such that they don't apply to objects individually, but rather serve to relate objects to objects. For example, the words "before" and "after" do not apply to objects individually—it makes no sense to say "Jim is before" or "Jim is after"—but to one thing in relation to another, as in "The wedding is before the reception" and "The reception is after the wedding". Such "relational" or "polyadic" ("many-place") concepts and expressions have, for their extension, the set of all sequences of objects that satisfy the concept or expression in question. So the extension of "before" is the set of all (ordered) pairs of objects such that the first one is before the second one.
https://en.wikipedia.org/wiki/Extension_(semantics)
Logical consequence (also entailment) is a fundamental concept in logic which describes the relationship between statements that hold true when one statement logically follows from one or more statements. A valid logical argument is one in which the conclusion is entailed by the premises, because the conclusion is the consequence of the premises. The philosophical analysis of logical consequence involves the questions: In what sense does a conclusion follow from its premises? and What does it mean for a conclusion to be a consequence of premises?[1] All of philosophical logic is meant to provide accounts of the nature of logical consequence and the nature of logical truth.[2]
Logical consequence is necessary and formal, by way of examples that explain with formal proof and models of interpretation.[1] A sentence is said to be a logical consequence of a set of sentences, for a given language, if and only if, using only logic (i.e., without regard to any personal interpretations of the sentences) the sentence must be true if every sentence in the set is true.[3]
Logicians make precise accounts of logical consequence regarding a given language 


https://en.wikipedia.org/wiki/Logical_consequence
In any of several fields of study that treat the use of signs — for example, in linguistics, logic, mathematics, semantics, semiotics, and philosophy of language — an intension is any property or quality connoted by a word, phrase, or another symbol.[1] In the case of a word, the word's definition often implies an intension. For instance, the intensions of the word plant include properties such as "being composed of cellulose (not always true)", "alive", and "organism", among others. A comprehension is the collection of all such intensions.
Overview
The meaning of a word can be thought of as the bond between the idea the word means and the physical form of the word. Swiss linguist Ferdinand de Saussure (1857–1913) contrasts three concepts:
- the signifier – the "sound image" or the string of letters on a page that one recognizes as the form of a sign
- the signified – the meaning, the concept or idea that a sign expresses or evokes
- the referent – the actual thing or set of things a sign refers to. See Dyadic signs and Reference (semantics).
Without intension of some sort, a word has no meaning.[2] For instance, the terms rantans or brillig have no intension and hence no meaning. Such terms may be suggestive, but a term can be suggestive without being meaningful. For instance, ran tan is an archaic onomatopoeia for chaotic noise or din and may suggest to English speakers a din or meaningless noise, and brillig though made up by Lewis Carroll may be suggestive of 'brilliant' or 'frigid'. Such terms, it may be argued, are always intensional since they connote the property 'meaningless term', but this is only an apparent paradox and does not constitute a counterexample to the claim that without intension a word has no meaning. Part of its intension is that it has no extension. Intension is analogous to the signified in the Saussurean system, extension to the referent.
In philosophical arguments about dualism versus monism, it is noted that thoughts have intensionality and physical objects do not (S. E. Palmer, 1999), but rather have extension in space and time.
Statement forms
A statement-form is simply a form obtained by putting blanks into a sentence where one or more expressions with extensions occur—for instance, "The quick brown ___ jumped over the lazy ___'s back." An instance of the form is a statement obtained by filling the blanks in.
Intensional statement form
An intensional statement-form is a statement-form with at least one instance such that substituting co-extensive expressions into it does not always preserve logical value. An intensional statement is a statement that is an instance of an intensional statement-form. Here co-extensive expressions are expressions with the same extension.[citation needed]
That is, a statement-form is intensional if it has, as one of its instances, a statement for which there are two co-extensive expressions (in the relevant language) such that one of them occurs in the statement, and if the other one is put in its place (uniformly, so that it replaces the former expression wherever it occurs in the statement), the result is a (different) statement with a different logical value. An intensional statement, then, is an instance of such a form; it has the same form as a statement in which substitution of co-extensive terms fails to preserve logical value.
Examples
- Everyone who has read Huckleberry Finn knows that Mark Twain wrote it.
- It is possible that Aristotle did not tutor Alexander the Great.
- Aristotle was pleased that he had a sister.
To see that these are intensional, make the following substitutions: (1) "Mark Twain" → "The author of 'Corn-pone Opinions'"; (2) "Aristotle" → "the tutor of Alexander the Great"; (3) can be seen to be intensional given "had a sister" → "had a sibling whose body was capable of producing egg cells."
The intensional statements above feature expressions like "knows", "possible", and "pleased". Such expressions always, or nearly always, produce intensional statements when added (in some intelligible manner) to an extensional statement, and thus they (or more complex expressions like "It is possible that") are sometimes called intensional operators. A large class of intensional statements, but by no means all, can be spotted from the fact that they contain intensional operators.
Extensional statement form
An extensional statement is a non-intensional statement. Substitution of co-extensive expressions into it always preserves logical value. A language is intensional if it contains intensional statements, and extensional otherwise. All natural languages are intensional.[3] The only extensional languages are artificially constructed languages used in mathematical logic or for other special purposes and small fragments of natural languages.
Examples
- Mark Twain wrote Huckleberry Finn.
- Aristotle had a sister.
Note that if "Samuel Clemens" is put into (1) in place of "Mark Twain", the result is as true as the original statement. It should be clear that no matter what is put for "Mark Twain", so long as it is a singular term picking out the same man, the statement remains true. Likewise, we can put in place of the predicate any other predicate belonging to Mark Twain and only to Mark Twain, without changing the logical value. For (2), likewise, consider the following substitutions: "Aristotle" → "The tutor of Alexander the Great"; "Aristotle" → "The author of the 'Prior Analytics'"; "had a sister" → "had a sibling whose body was capable of producing egg cells"; "had a sister" → "had a parent who had a female child".
See also
- Description logic
- Connotation
- Extension (predicate logic)
- Extensionality
- Intensional definition
- Intensional logic
- Montague grammar
- Temperature paradox
- Set-builder notation
Notes
- Carnap, Rudolf (April 1955). "Meaning and synonymy in natural languages". Philosophical Studies. 6 (3): 33–47. doi:10.1007/BF02330951. ISSN 0031-8116. S2CID 170508331.
References
- Ferdinand de Saussure, Course in General Linguistics. Open Court Classics, July 1986. ISBN 0-8126-9023-0
- S. E. Palmer, Vision Science: From Photons to Phenomenology, 1999. MIT Press, ISBN 0-2621-6183-4
External links
https://en.wikipedia.org/wiki/Intension
In the branch of linguistics known as pragmatics, a presupposition (or PSP) is an implicit assumption about the world or background belief relating to an utterance whose truth is taken for granted in discourse. Examples of presuppositions include:
- Jane no longer writes fiction.
- Presupposition: Jane once wrote fiction.
- Have you stopped eating meat?
- Presupposition: you had once eaten meat.
- Have you talked to Hans?
- Presupposition: Hans exists.
A presupposition must be mutually known or assumed by the speaker and addressee for the utterance to be considered appropriate in context. It will generally remain a necessary assumption whether the utterance is placed in the form of an assertion, denial, or question, and can be associated with a specific lexical item or grammatical feature (presupposition trigger) in the utterance.
Crucially, negation of an expression does not change its presuppositions: I want to do it again and I don't want to do it again both presuppose that the subject has done it already one or more times; My wife is pregnant and My wife is not pregnant both presuppose that the subject has a wife. In this respect, presupposition is distinguished from entailment and implicature. For example, The president was assassinated entails that The president is dead, but if the expression is negated, the entailment is not necessarily true.
https://en.wikipedia.org/wiki/Presupposition
A reference is a relationship between objects in which one object designates, or acts as a means by which to connect to or link to, another object. The first object in this relation is said to refer to the second object. It is called a name for the second object. The second object, the one to which the first object refers, is called the referent of the first object. A name is usually a phrase or expression, or some other symbolic representation. Its referent may be anything – a material object, a person, an event, an activity, or an abstract concept.
References can take on many forms, including: a thought, a sensory perception that is audible (onomatopoeia), visual (text), olfactory, or tactile, emotional state, relationship with other,[1] spacetime coordinate, symbolic or alpha-numeric, a physical object or an energy projection. In some cases, methods are used that intentionally hide the reference from some observers, as in cryptography.[citation needed]
Reference feature in many spheres of human activity and knowledge, and the term adopts shades of meaning particular to the contexts in which it is used. Some of them are described in the sections below.
https://en.wikipedia.org/wiki/Reference
In formal semantics, the scope of a semantic operator is the semantic object to which it applies. For instance, in the sentence "Paulina doesn't drink beer but she does drink wine," the proposition that Paulina drinks beer occurs within the scope of negation, but the proposition that Paulina drinks wine does not. Scope can be thought of as the semantic order of operations.
One of the major concerns of research in formal semantics is the relationship between operators' syntactic positions and their semantic scope. This relationship is not transparent, since the scope of an operator need not directly correspond to its surface position and a single surface form can be semantically ambiguous between different scope construals. Some theories of scope posit a level of syntactic structure called logical form, in which an item's syntactic position corresponds to its semantic scope. Others theories compute scope relations in the semantics itself, using formal tools such as type shifters, monads, and continuations.
https://en.wikipedia.org/wiki/Scope_(formal_semantics)
| Part of a series on |
| Linguistics |
|---|
|
|
General linguistics |
|
|
Applied linguistics |
|
|
Theoretical frameworks |
|
|
Topics |
|
|
In linguistics, the syntax–semantics interface is the interaction between syntax and semantics. Its study encompasses phenomena that pertain to both syntax and semantics, with the goal of explaining correlations between form and meaning.[1] Specific topics include scope,[2][3] binding,[2] and lexical semantic properties such as verbal aspect and nominal individuation,[4][5][6][7][8] semantic macroroles,[8] and unaccusativity.[4]
The interface is conceived of very differently in formalist and functionalist approaches. While functionalists tend to look into semantics and pragmatics for explanations of syntactic phenomena, formalists try to limit such explanations within syntax itself.[9] It is sometimes referred to as the morphosyntax–semantics interface or the syntax-lexical semantics interface.[3]
https://en.wikipedia.org/wiki/Syntax%E2%80%93semantics_interface
In semiotics, linguistics, anthropology, and philosophy of language, indexicality is the phenomenon of a sign pointing to (or indexing) some element in the context in which it occurs. A sign that signifies indexically is called an index or, in philosophy, an indexical.
The modern concept originates in the semiotic theory of Charles Sanders Peirce, in which indexicality is one of the three fundamental sign modalities by which a sign relates to its referent (the others being iconicity and symbolism).[1] Peirce's concept has been adopted and extended by several twentieth-century academic traditions, including those of linguistic pragmatics,[2]: 55–57 linguistic anthropology,[3] and Anglo-American philosophy of language.[4]
Words and expressions in language often derive some part of their referential meaning from indexicality. For example, I indexically refers to the entity that is speaking; now indexically refers to a time frame including the moment at which the word is spoken; and here indexically refers to a locational frame including the place where the word is spoken. Linguistic expressions that refer indexically are known as deictics, which thus form a particular subclass of indexical signs, though there is some terminological variation among scholarly traditions.
Linguistic signs may also derive nonreferential meaning from indexicality, for example when features of a speaker's register indexically signal their social class. Nonlinguistic signs may also display indexicality: for example, a pointing index finger may index (without referring to) some object in the direction of the line implied by the orientation of the finger, and smoke may index the presence of a fire.
In linguistics and philosophy of language, the study of indexicality tends to focus specifically on deixis, while in semiotics and anthropology equal attention is generally given to nonreferential indexicality, including altogether nonlinguistic indexicality.
https://en.wikipedia.org/wiki/Indexicality
In linguistics, binding is the phenomenon in which anaphoric elements such as pronouns are grammatically associated with their antecedents.[citation needed] For instance in the English sentence "Mary saw herself", the anaphor "herself" is bound by its antecedent "Mary". Binding can be licensed or blocked in certain contexts or syntactic configurations, e.g. the pronoun "her" cannot be bound by "Mary" in the English sentence "Mary saw her". While all languages have binding, restrictions on it vary even among closely related languages. Binding has been a major area of research in syntax and semantics since the 1970s, and was a major for the government and binding theory paradigm.
https://en.wikipedia.org/wiki/Binding_(linguistics)
In linguistics, anaphora (/əˈnæfərə/) is the use of an expression whose interpretation depends upon another expression in context (its antecedent or postcedent). In a narrower sense, anaphora is the use of an expression that depends specifically upon an antecedent expression and thus is contrasted with cataphora, which is the use of an expression that depends upon a postcedent expression. The anaphoric (referring) term is called an anaphor. For example, in the sentence Sally arrived, but nobody saw her, the pronoun her is an anaphor, referring back to the antecedent Sally. In the sentence Before her arrival, nobody saw Sally, the pronoun her refers forward to the postcedent Sally, so her is now a cataphor (and an anaphor in the broader, but not the narrower, sense). Usually, an anaphoric expression is a pro-form or some other kind of deictic (contextually dependent) expression.[1] Both anaphora and cataphora are species of endophora, referring to something mentioned elsewhere in a dialog or text.
Anaphora is an important concept for different reasons and on different levels: first, anaphora indicates how discourse is constructed and maintained; second, anaphora binds different syntactical elements together at the level of the sentence; third, anaphora presents a challenge to natural language processing in computational linguistics, since the identification of the reference can be difficult; and fourth, anaphora partially reveals how language is understood and processed, which is relevant to fields of linguistics interested in cognitive psychology.[2]
https://en.wikipedia.org/wiki/Anaphora_(linguistics)
Antecedent-contained deletion (ACD), also called antecedent-contained ellipsis, is a phenomenon whereby an elided verb phrase appears to be contained within its own antecedent. For instance, in the sentence "I read every book that you did", the verb phrase in the main clause appears to license ellipsis inside the relative clause which modifies its object. ACD is a classic puzzle for theories of the syntax-semantics interface, since it threatens to introduce an infinite regress. It is commonly taken as motivation for syntactic transformations such as quantifier raising, though some approaches explain it using semantic composition rules or by adoption more flexible notions of what it means to be a syntactic unit.
https://en.wikipedia.org/wiki/Antecedent-contained_deletion
| OR | |
|---|---|
 | |
| Definition |  |
| Truth table |  |
| Logic gate | |
| Normal forms | |
| Disjunctive |  |
| Conjunctive |  |
| Zhegalkin polynomial |  |
| Post's lattices | |
| 0-preserving | yes |
| 1-preserving | yes |
| Monotone | yes |
| Affine | no |

In logic, disjunction is a logical connective typically notated as 



In classical logic, disjunction is given a truth functional semantics according to which a formula 


https://en.wikipedia.org/wiki/Logical_disjunction
De se is Latin for "of oneself" and, in philosophy, it is a phrase used to delineate what some consider a category of ascription distinct from "de dicto and de re". Such ascriptions are found with propositional attitudes, mental states held by an agent toward a proposition. Such de se ascriptions occur when an agent holds a mental state towards a proposition about themselves, knowing that this proposition is about themselves.
https://en.wikipedia.org/wiki/De_se
In formal semantics a responsive predicate is an embedding predicate which can take either a declarative or an interrogative complement. For instance, the English verb know is responsive as shown by the following examples.[1][2][3]
- Bill knows whether Mary left.
- Bill knows that Mary left.
Responsives are contrasted with rogatives such as wonder which can only take an interrogative complement and anti-rogatives such as believe which can only take a declarative complement.
- Bill wonders whether Mary left.
- *Bill wonders that Mary left.
- *Bill believes whether Mary left.
- Bill wonders that Mary left.
Some analyses have derived these distinctions from type compatibility while others explain them in terms of particular properties of the embedding verbs and their complements.
https://en.wikipedia.org/wiki/Responsive_predicate
Deontic modality (abbreviated DEO) is a linguistic modality that indicates how the world ought to be[1] according to certain norms, expectations, speaker desires, etc. In other words, a deontic expression indicates that the state of the world (where 'world' is loosely defined here in terms of the surrounding circumstances) does not meet some standard or ideal, whether that standard be social (such as laws), personal (desires), etc. The sentence containing the deontic modal generally indicates some action that would change the world so that it becomes closer to the standard or ideal.
This category includes the following subcategories:[2]
- Commissive modality (the speaker's commitment to do something, like a promise or threat; alethic logic or temporal logic would apply):[3] "I shall help you."
- Directive modality (commands, requests, etc.; deontic logic would apply): "Come!", "Let's go!", "You've got to taste this curry!"
- Volitive modality (wishes, desires, etc.; boulomaic logic would apply): "If only I were rich!"
A related type of modality is dynamic modality, which indicates a subject's internal capabilities or willingness as opposed to external factors such as permission or orders given.[4]
https://en.wikipedia.org/wiki/Deontic_modality
In pragmatics, scalar implicature, or quantity implicature,[1] is an implicature that attributes an implicit meaning beyond the explicit or literal meaning of an utterance, and which suggests that the utterer had a reason for not using a more informative or stronger term on the same scale. The choice of the weaker characterization suggests that, as far as the speaker knows, none of the stronger characterizations in the scale holds. This is commonly seen in the use of 'some' to suggest the meaning 'not all', even though 'some' is logically consistent with 'all'.[2] If Bill says 'I have some of my money in cash', this utterance suggests to a hearer (though the sentence uttered does not logically imply it) that Bill does not have all his money in cash.
https://en.wikipedia.org/wiki/Scalar_implicature
Logophoricity is a phenomenon of binding relation that may employ a morphologically different set of anaphoric forms, in the context where the referent is an entity whose speech, thoughts, or feelings are being reported.[1] This entity may or may not be distant from the discourse, but the referent must reside in a clause external to the one in which the logophor resides. The specially-formed anaphors that are morphologically distinct from the typical pronouns of a language are known as logophoric pronouns, originally coined by the linguist Claude Hagège.[2] The linguistic importance of logophoricity is its capability to do away with ambiguity as to who is being referred to.[1][3] A crucial element of logophoricity is the logophoric context, defined as the environment where use of logophoric pronouns is possible.[4] Several syntactic and semantic accounts have been suggested. While some languages may not be purely logophoric (meaning they do not have logophoric pronouns in their lexicon), logophoric context may still be found in those languages; in those cases, it is common to find that in the place where logophoric pronouns would typically occur, non-clause-bounded reflexive pronouns (or long-distance reflexives) appear instead.[1][2]
https://en.wikipedia.org/wiki/Logophoricity
An opaque context or referentially opaque context is a linguistic context in which it is not always possible to substitute "co-referential" expressions (expressions referring to the same object) without altering the truth of sentences.[1] The expressions involved are usually grammatically singular terms. So, substitution of co-referential expressions into an opaque context does not always preserve truth. For example, "Lois believes x is a hero" is an opaque context because "Lois believes Superman is a hero" is true while "Lois believes Clark Kent is a hero" is false, even though 'Superman' and 'Clark Kent' are co-referential expressions.
https://en.wikipedia.org/wiki/Opaque_context
Quantificational variability effect (QVE) is the intuitive equivalence of certain sentences with quantificational adverbs (Q-adverbs) and sentences without these, but with quantificational determiner phrases (DP) in argument position instead.
- 1. (a) A cat is usually smart. (Q-adverb)
- 1. (b) Most cats are smart. (DP)
- 2. (a) A dog is always smart. (Q-adverb)
- 2. (b) All dogs are smart. (DP)[1]
Analysis of QVE is widely cited as entering the literature with David Lewis' "Adverbs of Quantification" (1975), where he proposes QVE as a solution to Peter Geach's donkey sentence (1962). Terminology, and comprehensive analysis, is normally attributed to Stephen Berman's "Situation-Based Semantics for Adverbs of Quantification" (1987).
https://en.wikipedia.org/wiki/Quantificational_variability_effect
In formal semantics, existential closure is an operation which introduces existential quantification. It was first posited by Irene Heim in her 1982 dissertation, as part of her analysis of indefinites. In her formulation, existential closure is a form of unselective binding which binds any number of variables of any semantic type.[1][2] In alternative semantics and related frameworks, the term is often applied to a closely related operation which existentially quantifies over a set of propositional alternatives.[3][4]
https://en.wikipedia.org/wiki/Existential_closure
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation (symbol) that specifies places in an expression where substitution may take place and is not a parameter of this or any container expression. Some older books use the terms real variable and apparent variable for free variable and bound variable, respectively. The idea is related to a placeholder (a symbol that will later be replaced by some value), or a wildcard character that stands for an unspecified symbol.
https://en.wikipedia.org/wiki/Free_variables_and_bound_variables
Lambda lifting is a meta-process that restructures a computer program so that functions are defined independently of each other in a global scope. An individual "lift" transforms a local function into a global function. It is a two step process, consisting of;
- Eliminating free variables in the function by adding parameters.
- Moving functions from a restricted scope to broader or global scope.
The term "lambda lifting" was first introduced by Thomas Johnsson around 1982 and was historically considered as a mechanism for implementing functional programming languages. It is used in conjunction with other techniques in some modern compilers.
https://en.wikipedia.org/wiki/Lambda_lifting
In computer programming and software design, code refactoring is the process of restructuring existing computer code—changing the factoring—without changing its external behavior. Refactoring is intended to improve the design, structure, and/or implementation of the software (its non-functional attributes), while preserving its functionality. Potential advantages of refactoring may include improved code readability and reduced complexity; these can improve the source code's maintainability and create a simpler, cleaner, or more expressive internal architecture or object model to improve extensibility. Another potential goal for refactoring is improved performance; software engineers face an ongoing challenge to write programs that perform faster or use less memory.
Typically, refactoring applies a series of standardized basic micro-refactorings, each of which is (usually) a tiny change in a computer program's source code that either preserves the behavior of the software, or at least does not modify its conformance to functional requirements. Many development environments provide automated support for performing the mechanical aspects of these basic refactorings. If done well, code refactoring may help software developers discover and fix hidden or dormant bugs or vulnerabilities in the system by simplifying the underlying logic and eliminating unnecessary levels of complexity. If done poorly, it may fail the requirement that external functionality not be changed, and may thus introduce new bugs.
By continuously improving the design of code, we make it easier and easier to work with. This is in sharp contrast to what typically happens: little refactoring and a great deal of attention paid to expediently add new features. If you get into the hygienic habit of refactoring continuously, you'll find that it is easier to extend and maintain code.
— Joshua Kerievsky, Refactoring to Patterns[1]
https://en.wikipedia.org/wiki/Code_refactoring
Extensibility is a software engineering and systems design principle that provides for future growth. Extensibility is a measure of the ability to extend a system and the level of effort required to implement the extension. Extensions can be through the addition of new functionality or through modification of existing functionality. The principle provides for enhancements without impairing existing system functions.
An extensible system is one whose internal structure and dataflow are minimally or not affected by new or modified functionality, for example recompiling or changing the original source code might be unnecessary when changing a system’s behavior, either by the creator or other programmers.[1] Because software systems are long lived and will be modified for new features and added functionalities demanded by users, extensibility enables developers to expand or add to the software’s capabilities and facilitates systematic reuse. Some of its approaches include facilities for allowing users’ own program routines to be inserted and the abilities to define new data types as well as to define new formatting markup tags.[2]
https://en.wikipedia.org/wiki/Extensibility
Intensional versus extensional equality
Another difficulty for the interpretation of lambda calculus as a deductive system is the representation of values as lambda terms, which represent functions. The untyped lambda calculus is implemented by performing reductions on a lambda term, until the term is in normal form. The intensional interpretation[6] [7] of equality is that the reduction of a lambda term to normal form is the value of the lambda term.
This interpretation considers the identity of a lambda expression to be its structure. Two lambda terms are equal if they are alpha convertible.
The extensional definition of function equality is that two functions are equal if they perform the same mapping;
One way to describe this is that extensional equality describes equality of functions, where as intensional equality describes equality of function implementations.
The extensional definition of equality is not equivalent to the intensional definition. This can be seen in the example below. This inequivalence is created by considering lambda terms as values. In typed lambda calculus this problem is circumvented, because built-in types may be added to carry values that are in a canonical form and have both extensional and intensional equality.
Example
In arithmetic, the distributive law implies that 
So the distributive law says that the two functions,
are equal, as functions on Church numerals. (Here we encounter a technical weakness of the untyped lambda calculus: there is no way to restrict the domain of a function to the Church numerals. In the following argument we will ignore this difficulty, by pretending that "all" lambda expressions are Church numerals.) The distributive law should apply if the Church numerals provided a satisfactory implementation of numbers.
The two terms beta reduce to similar expressions. Still they are not alpha convertible, or even eta convertible (the latter follows because both terms are already in eta-long form). So according to the intensional definition of equality, the expressions are not equal. But if the two functions are applied to the same Church numerals they produce the same result, by the distributive law; thus they are extensionally equal.
This is a significant problem, as it means that the intensional value of a lambda-term may change under extensionally valid transformations. A solution to this problem is to introduce an omega-rule,
- If, for all lambda-expressions t we have
, then
.
In our situation, "all lambda-expressions" means "all Church
numerals", so this is an omega-rule in the standard sense as well. Note
that the omega-rule implies the eta-rule, since 
https://en.wikipedia.org/wiki/Deductive_lambda_calculus#Intensional_versus_extensional_equality
Lambda dropping in lambda calculus
Lambda dropping[4] is making the scope of functions smaller and using the context from the reduced scope to reduce the number of parameters to functions. Reducing the number of parameters makes functions easier to comprehend.
In the Lambda lifting section, a meta function for first lifting and then converting the resulting lambda expression into recursive equation was described. The Lambda Drop meta function performs the reverse by first converting recursive equations to lambda abstractions, and then dropping the resulting lambda expression, into the smallest scope which covers all references to the lambda abstraction.
Lambda dropping is performed in two steps,
Lambda drop
A Lambda drop is applied to an expression which is part of a program. Dropping is controlled by a set of expressions from which the drop will be excluded.
where,
- L is the lambda abstraction to be dropped.
- P is the program
- X is a set of expressions to be excluded from dropping.
Lambda drop transformation
The lambda drop transformation sinks all abstractions in an expression. Sinking is excluded from expressions in a set of expressions,
where,
- L is the expression to be transformed.
- X is a set of sub expressions to be excluded from the dropping.
sink-tran sinks each abstraction, starting from the innermost,
Abstraction sinking
Sinking is moving a lambda abstraction inwards as far as possible such that it is still outside all references to the variable.
Application - 4 cases.
Abstraction. Use renaming to insure that the variable names are all distinct.
Variable - 2 cases.
Sink test excludes expressions from dropping,
Example
| Example of sinking |
|---|
Parameter dropping
Parameter dropping is optimizing a function for its position in the function. Lambda lifting added parameters that were necessary so that a function can be moved out of its context. In dropping, this process is reversed, and extra parameters that contain variables that are free may be removed.
Dropping a parameter is removing an unnecessary parameter from a function, where the actual parameter being passed in is always the same expression. The free variables of the expression must also be free where the function is defined. In this case the parameter that is dropped is replaced by the expression in the body of the function definition. This makes the parameter unnecessary.
For example, consider,
In this example the actual parameter for the formal parameter o is always p. As p is a free variable in the whole expression, the parameter may be dropped. The actual parameter for the formal parameter y is always n. However n is bound in a lambda abstraction. So this parameter may not be dropped.
The result of dropping the parameter is,
For the main example,
The definition of drop-params-tran is,
where,
Build parameter lists
For each abstraction that defines a function, build the information required to make decisions on dropping names. This information describes each parameter; the parameter name, the expression for the actual value, and an indication that all the expressions have the same value.
For example, in,
the parameters to the function g are,
| Formal Parameter | All Same Value | Actual parameter expression |
|---|---|---|
| x | false | _ |
| o | true | p |
| y | true | n |
Each abstraction is renamed with a unique name, and the parameter list is associated with the name of the abstraction. For example, g there is parameter list.
build-param-lists builds all the lists for an expression, by traversing the expression. It has four parameters;
- The lambda expression being analyzed.
- The table parameter lists for names.
- The table of values for parameters.
- The returned parameter list, which is used internally by the
Abstraction - A lambda expression of the form 
Locate the name and start building the parameter list for the name, filling in the formal parameter names. Also receive any actual parameter list from the body of the expression, and return it as the actual parameter list from this expression
Variable - A call to a function.
For a function name or parameter start populating actual parameter list by outputting the parameter list for this name.
Application - An application (function call) is processed to extract actual parameter details.
Retrieve the parameter lists for the expression, and the parameter. Retrieve a parameter record from the parameter list from the expression, and check that the current parameter value matches this parameter. Record the value for the parameter name for use later in checking.
The above logic is quite subtle in the way that it works. The same value indicator is never set to true. It is only set to false if all the values cannot be matched. The value is retrieved by using S to build a set of the Boolean values allowed for S. If true is a member then all the values for this parameter are equal, and the parameter may be dropped.
Similarly, def uses set theory to query if a variable has been given a value;
Let - Let expression.
And - For use in "let".
Examples
For example, building the parameter lists for,
gives,
and the parameter o is dropped to give,
Build parameter list for 
|
|---|
Another example is,
Here x is equal to f. The parameter list mapping is,
and the parameter x is dropped to give,
Build parameter list for 
|
|---|
Drop parameters
Use the information obtained by Build parameter lists to drop actual parameters that are no longer required. drop-params has the parameters,
- The lambda expression in which the parameters are to be dropped.
- The mapping of variable names to parameter lists (built in Build parameter lists).
- The set of variables free in the lambda expression.
- The returned parameter list. A parameter used internally in the algorithm.
Abstraction
where,
where,
Variable
For a function name or parameter start populating actual parameter list by outputting the parameter list for this name.
Application - An application (function call) is processed to extract
Let - Let expression.
And - For use in "let".
| Drop parameters from applications |
|---|
Drop formal parameters
drop-formal removes formal parameters, based on the contents of the drop lists. Its parameters are,
- The drop list,
- The function definition (lambda abstraction).
- The free variables from the function definition.
drop-formal is defined as,
Which can be explained as,
- If all the actual parameters have the same value, and all the free variables of that value are available for definition of the function then drop the parameter, and replace the old parameter with its value.
- else do not drop the parameter.
- else return the body of the function.
| Condition |
|---|
| Expression |
|---|
Example
Starting with the function definition of the Y-combinator,
| Transformation | Expression |
|---|---|
|
|

|
| abstract * 4 | 
|
| lambda-abstract-tran | 
|
| sink-tran | 
|
| sink-tran | 
|
| drop-param | 
|
| beta-redex | 
|
Which gives back the Y combinator,
See also
- Let expression
- Fixed-point combinator
- Lambda calculus
- Deductive lambda calculus
- Supercombinator
- Curry's paradox
References
- Danvy, Olivier; Schultz, Ulrik P. (October 2000). "Lambda-Dropping: Transforming Recursive Equations into Programs with Block Structure" (PDF). Theoretical Computer Science. 248 (1–2): 243–287. CiteSeerX 10.1.1.16.3943. doi:10.1016/S0304-3975(00)00054-2. BRICS-RS-99-27.
External links
- Explanation on Stack Overflow, with a JavaScript example
- Slonneger, Ken; Kurtz, Barry. "5. Some discussion of let expressions" (PDF). Programming Language Foundations. University of Iowa.
https://en.wikipedia.org/wiki/Lambda_lifting#Lambda_dropping_in_lambda_calculus
Deductive lambda calculus considers what happens when lambda terms are regarded as mathematical expressions. One interpretation of the untyped lambda calculus is as a programming language where evaluation proceeds by performing reductions on an expression until it is in normal form. In this interpretation, if the expression never reduces to normal form then the program never terminates, and the value is undefined. Considered as a mathematical deductive system, each reduction would not alter the value of the expression. The expression would equal the reduction of the expression.
https://en.wikipedia.org/wiki/Deductive_lambda_calculus
Alternative semantics (or Hamblin semantics) is a framework in formal semantics and logic. In alternative semantics, expressions denote alternative sets, understood as sets of objects of the same semantic type.
For instance, while the word "Lena" might denote Lena herself in a
classical semantics, it would denote the singleton set containing Lena
in alternative semantics. The framework was introduced by Charles Leonard Hamblin in 1973 as a way of extending Montague grammar to provide an analysis for questions. In this framework, a question denotes the set of its possible answers. Thus, if 




https://en.wikipedia.org/wiki/Alternative_semantics
Free choice is a phenomenon in natural language where a linguistic disjunction appears to receive a logical conjunctive interpretation when it interacts with a modal operator. For example, the following English sentences can be interpreted to mean that the addressee can watch a movie AND that they can also play video games, depending on their preference:[1]
- You can watch a movie OR play video games.
- You can watch a movie OR you can play video games.
Free choice inferences are a major topic of research in formal semantics and philosophical logic because they are not valid in classical systems of modal logic. If they were valid, then the semantics of natural language would validate the Free Choice Principle.
- Free Choice Principle:
This symbolic logic formula above is not valid in classical modal logic: Adding this principle as an axiom to standard modal logics would allow one to conclude 



Free choice inferences are most widely studied for deontic modals, but also arise with other flavors of modality as well as imperatives, conditionals, and other kinds of operators.[1][8][9][4] Indefinite noun phrases give rise to a similar inference which is also referred to as "free choice" though researchers disagree as to whether it forms a natural class with disjunctive free choice.[9][10]
https://en.wikipedia.org/wiki/Free_choice_inference
In formal semantics and philosophical logic, simplification of disjunctive antecedents (SDA) is the phenomenon whereby a disjunction in the antecedent of a conditional appears to distribute over the conditional as a whole. This inference is shown schematically below:[1][2]
This inference has been argued to be valid on the basis of sentence pairs such as that below, since Sentence 1 seems to imply Sentence 2.[1][2]
- If Yde or Dani had come to the party, it would have been fun.
- If Yde had come to the party, it would be been fun and if Dani had come to the party, it would have been fun.
The SDA inference was first discussed as a potential problem for the similarity analysis of counterfactuals. In these approaches, a counterfactual 











In more intuitive terms, imagine that Yde missed the most recent party because he happened to get a flat tire while Dani missed it because she hates parties and is also deceased. In all of the closest worlds where either Yde or Dani comes to the party, it will be Yde and not Dani who attends. If Yde is a fun person to have at parties, this will mean that Sentence 1 above is predicted to be true on the similarity approach. However, if Dani tends to have the opposite effect on parties she attends, then Sentence 2 is predicted false, in violation of SDA.[3][1][2]
SDA has been analyzed in a variety of ways. One is to derive it as a semantic entailment by positing a non-classical treatment of disjunction such as that of alternative semantics or inquisitive semantics.[4][5][6][1][2] Another approach also derives it as a semantic entailment, but does so by adopting an alternative denotation for conditionals such as the strict conditional or any of the options made available in situation semantics.[1][2] Finally, some researchers have suggested that it can be analyzed as a pragmatic implicature derived on the basis of classical disjunction and a standard semantics for conditionals.[7][1][2] SDA is sometimes considered an embedded instance of the free choice inference.[8]
https://en.wikipedia.org/wiki/Simplification_of_disjunctive_antecedents
In situation theory, situation semantics (pioneered by Jon Barwise and John Perry in the early 1980s)[1] attempts to provide a solid theoretical foundation for reasoning about common-sense and real world situations, typically in the context of theoretical linguistics, theoretical philosophy, or applied natural language processing,
https://en.wikipedia.org/wiki/Situation_semantics
Variably strict conditional
In the variably strict approach, the semantics of a conditional A > B is given by some function on the relative closeness of worlds where A is true and B is true, on the one hand, and worlds where A is true but B is not, on the other.
On Lewis's account, A > C is (a) vacuously true if and only if there are no worlds where A is true (for example, if A is logically or metaphysically impossible); (b) non-vacuously true if and only if, among the worlds where A is true, some worlds where C is true are closer to the actual world than any world where C is not true; or (c) false otherwise. Although in Lewis's Counterfactuals it was unclear what he meant by 'closeness', in later writings, Lewis made it clear that he did not intend the metric of 'closeness' to be simply our ordinary notion of overall similarity.
Example:
- If he had eaten more at breakfast, he would not have been hungry at 11 am.
On Lewis's account, the truth of this statement consists in the fact that, among possible worlds where he ate more for breakfast, there is at least one world where he is not hungry at 11 am and which is closer to our world than any world where he ate more for breakfast but is still hungry at 11 am.
Stalnaker's account differs from Lewis's most notably in his acceptance of the limit and uniqueness assumptions. The uniqueness assumption is the thesis that, for any antecedent A, among the possible worlds where A is true, there is a single (unique) one that is closest to the actual world. The limit assumption is the thesis that, for a given antecedent A, if there is a chain of possible worlds where A is true, each closer to the actual world than its predecessor, then the chain has a limit: a possible world where A is true that is closer to the actual worlds than all worlds in the chain. (The uniqueness assumption entails the limit assumption, but the limit assumption does not entail the uniqueness assumption.) On Stalnaker's account, A > C is non-vacuously true if and only if, at the closest world where A is true, C is true. So, the above example is true just in case at the single, closest world where he ate more breakfast, he does not feel hungry at 11 am. Although it is controversial, Lewis rejected the limit assumption (and therefore the uniqueness assumption) because it rules out the possibility that there might be worlds that get closer and closer to the actual world without limit. For example, there might be an infinite series of worlds, each with a coffee cup a smaller fraction of an inch to the left of its actual position, but none of which is uniquely the closest. (See Lewis 1973: 20.)
One consequence of Stalnaker's acceptance of the uniqueness assumption is that, if the law of excluded middle is true, then all instances of the formula (A > C) ∨ (A > ¬C) are true. The law of excluded middle is the thesis that for all propositions p, p ∨ ¬p is true. If the uniqueness assumption is true, then for every antecedent A, there is a uniquely closest world where A is true. If the law of excluded middle is true, any consequent C is either true or false at that world where A is true. So for every counterfactual A > C, either A > C or A > ¬C is true. This is called conditional excluded middle (CEM). Example:
- (1) If the fair coin had been flipped, it would have landed heads.
- (2) If the fair coin had been flipped, it would have landed tails (i.e. not heads).
On Stalnaker's analysis, there is a closest world where the fair coin mentioned in (1) and (2) is flipped and at that world either it lands heads or it lands tails. So either (1) is true and (2) is false or (1) is false and (2) true. On Lewis's analysis, however, both (1) and (2) are false, for the worlds where the fair coin lands heads are no more or less close than the worlds where they land tails. For Lewis, "If the coin had been flipped, it would have landed heads or tails" is true, but this does not entail that "If the coin had been flipped, it would have landed heads, or: If the coin had been flipped it would have landed tails."
Other accounts
Causal models
This section needs expansion. You can help by adding to it. (September 2020) |
The causal models framework analyzes counterfactuals in terms of systems of structural equations. In a system of equations, each variable is assigned a value that is an explicit function of other variables in the system. Given such a model, the sentence "Y would be y had X been x" (formally, X = x > Y = y ) is defined as the assertion: If we replace the equation currently determining X with a constant X = x, and solve the set of equations for variable Y, the solution obtained will be Y = y. This definition has been shown to be compatible with the axioms of possible world semantics and forms the basis for causal inference in the natural and social sciences, since each structural equation in those domains corresponds to a familiar causal mechanism that can be meaningfully reasoned about by investigators. This approach was developed by Judea Pearl (2000) as a means of encoding fine-grained intuitions about causal relations which are difficult to capture in other proposed systems.[23]
Belief revision
This section needs expansion. You can help by adding to it. (September 2020) |
In the belief revision framework, counterfactuals are treated using a formal implementation of the Ramsey test. In these systems, a counterfactual A > B holds if and only if the addition of A to the current body of knowledge has B as a consequence. This condition relates counterfactual conditionals to belief revision, as the evaluation of A > B can be done by first revising the current knowledge with A and then checking whether B is true in what results. Revising is easy when A is consistent with the current beliefs, but can be hard otherwise. Every semantics for belief revision can be used for evaluating conditional statements. Conversely, every method for evaluating conditionals can be seen as a way for performing revision.
Ginsberg
Ginsberg (1986) has proposed a semantics for conditionals which assumes that the current beliefs form a set of propositional formulae, considering the maximal sets of these formulae that are consistent with A, and adding A to each. The rationale is that each of these maximal sets represents a possible state of belief in which A is true that is as similar as possible to the original one. The conditional statement A > B therefore holds if and only if B is true in all such sets.[24]
The grammar of counterfactuality
Languages use different strategies for expressing counterfactuality. Some have a dedicated counterfactual morphemes, while others recruit morphemes which otherwise express tense, aspect, mood, or a combination thereof. Since the early 2000s, linguists, philosophers of language, and philosophical logicians have intensely studied the nature of this grammatical marking, and it continues to be an active area of study.
Fake tense
Description
In many languages, counterfactuality is marked by past tense morphology.[25] Since these uses of the past tense do not convey their typical temporal meaning, they are called fake past or fake tense.[26][27][28] English is one language which uses fake past to mark counterfactuality, as shown in the following minimal pair.[29] In the indicative example, the bolded words are present tense forms. In the counterfactual example, both words take their past tense form. This use of the past tense cannot have its ordinary temporal meaning, since it can be used with the adverb "tomorrow" without creating a contradiction.[25][26][27][28]
- Indicative: If Natalia leaves tomorrow, she will arrive on time.
- Counterfactual: If Natalia left tomorrow, she would arrive on time.
Modern Hebrew is another language where counterfactuality is marked with a fake past morpheme:[30]
'If Dani had been home tomorrow, we would’ve visited him.'im Dani haya ba-bayit maχa ɾ hayinu mevakRim oto if Dani be.pst.3sm in-home tomorrow be.pst.1pl visit.ptc.pl he.acc
Palestinian Arabic is another:[30]
'If he had been home tomorrow, we would’ve visited him.'iza kaan fi l-bet bukra kunna zurna-a if be.pst.3sm in the-house tomorrow be.pst.1pl visit.pst.pfv.1pl-him
Fake past is extremely prevalent cross-linguistically, either on its own or in combination with other morphemes. Moreover, theoretical linguists and philosophers of language have argued that other languages' strategies for marking counterfactuality are actually realizations of fake tense along with other morphemes. For this reason, fake tense has often been treated as the locus of the counterfactual meaning itself.[26][31]
Formal analyses
In formal semantics and philosophical logic, fake past is regarded as a puzzle, since it is not obvious why so many unrelated languages would repurpose a tense morpheme to mark counterfactuality. Proposed solutions to this puzzle divide into two camps: past as modal and past as past. These approaches differ in whether or not they take the past tense's core meaning to be about time.[32][33]
In the past as modal approach, the denotation of the past tense is not fundamentally about time. Rather, it is an underspecified skeleton which can apply either to modal or temporal content.[26][32][34] For instance, the particular past as modal proposal of Iatridou (2000), the past tense's core meaning is what's shown schematically below:
- The topic x is not the contextually-provided x
Depending on how this denotation composes, x can be a time interval or a possible world. When x is a time, the past tense will convey that the sentence is talking about non-current times, i.e. the past. When x is a world, it will convey that the sentence is talking about a potentially non-actual possibility. The latter is what allows for a counterfactual meaning.
The past as past approach treats the past tense as having an inherently temporal denotation. On this approach, so-called fake tense isn't actually fake. It differs from "real" tense only in how it takes scope, i.e. which component of the sentence's meaning is shifted to an earlier time. When a sentence has "real" past marking, it discusses something that happened at an earlier time; when a sentence has so-called fake past marking, it discusses possibilities that were accessible at an earlier time but may no longer be.[35][36][37]
Fake aspect
Fake aspect often accompanies fake tense in languages that mark aspect. In some languages (e.g. Modern Greek, Zulu, and the Romance languages) this fake aspect is imperfective. In other languages (e.g. Palestinian Arabic) it is perfective. However, in other languages including Russian and Polish, counterfactuals can have either perfective or imperfective aspect.[31]
Fake imperfective aspect is demonstrated by the two Modern Greek sentences below. These examples form a minimal pair, since they are identical except that the first uses past imperfective marking where the second uses past perfective marking. As a result of this morphological difference, the first has a counterfactual meaning, while the second does not.[26]
'If he took this syrup, he would get better'An eperne afto to sirpoi θa γinotan kala if take.PST.IMPV this syrup FUT become.PST.IMPV well
'If he took this syrup, he must be better'An ipχe afto to sirpoi θa eγine kala if take.PST.PFV this syrup FUT become.PST.PFV well
This imperfective marking has been argued to be fake on the grounds that it is compatible with completive adverbials such as "in one month":[26]
'If you built this house in a month, you would be able to sell it before the summer.'An eχtizes to spiti (mesa) se ena mina θa prolavenes na to pulisis prin to kalokeri if build.IMPV the house in one month FUT have-time-enough.IMPV to it sell before the summer
In ordinary non-conditional sentences, such adverbials are compatible with perfective aspect but not with imperfective aspect:[26]
'She built this house in one month'Eχtise afto to spiti (mesa) se ena mina build.PFV this house in one month
'She was building this house in one month'*Eχtize afto to spiti (mesa) se ena mina build.IMPV this house in one month
Psychology
People engage in counterfactual thinking frequently. Experimental evidence indicates that people's thoughts about counterfactual conditionals differ in important ways from their thoughts about indicative conditionals.
Comprehension
Participants in experiments were asked to read sentences, including counterfactual conditionals, e.g., ‘If Mark had left home early, he would have caught the train’. Afterwards, they were asked to identify which sentences they had been shown. They often mistakenly believed they had been shown sentences corresponding to the presupposed facts, e.g., ‘Mark did not leave home early’ and ‘Mark did not catch the train’.[38] In other experiments, participants were asked to read short stories that contained counterfactual conditionals, e.g., ‘If there had been roses in the flower shop then there would have been lilies’. Later in the story, they read sentences corresponding to the presupposed facts, e.g., ‘there were no roses and there were no lilies’. The counterfactual conditional primed them to read the sentence corresponding to the presupposed facts very rapidly; no such priming effect occurred for indicative conditionals.[39] They spent different amounts of time 'updating' a story that contains a counterfactual conditional compared to one that contains factual information[40] and focused on different parts of counterfactual conditionals.[41]
Reasoning
Experiments have compared the inferences people make from counterfactual conditionals and indicative conditionals. Given a counterfactual conditional, e.g., 'If there had been a circle on the blackboard then there would have been a triangle', and the subsequent information 'in fact there was no triangle', participants make the modus tollens inference 'there was no circle' more often than they do from an indicative conditional.[42] Given the counterfactual conditional and the subsequent information 'in fact there was a circle', participants make the modus ponens inference as often as they do from an indicative conditional.
Psychological accounts
Byrne argues that people construct mental representations that encompass two possibilities when they understand, and reason from, a counterfactual conditional, e.g., 'if Oswald had not shot Kennedy, then someone else would have'. They envisage the conjecture 'Oswald did not shoot Kennedy and someone else did' and they also think about the presupposed facts 'Oswald did shoot Kennedy and someone else did not'.[43] According to the mental model theory of reasoning, they construct mental models of the alternative possibilities.[44]
See also
https://en.wikipedia.org/wiki/Counterfactual_conditional#Variably_strict_conditional
In natural languages, an indicative conditional is a conditional sentence such as "If Leona is at home, she isn't in Paris", whose grammatical form restricts it to discussing what could be true. Indicatives are typically defined in opposition to counterfactual conditionals, which have extra grammatical marking which allows them to discuss eventualities which are no longer possible.
Indicatives are a major topic of research in philosophy of language, philosophical logic, and linguistics. Open questions include which logical operation indicatives denote, how such denotations could be composed from their grammatical form, and the implications of those denotations for areas including metaphysics, psychology of reasoning, and philosophy of mathematics.
https://en.wikipedia.org/wiki/Indicative_conditional
Frame semantics is a theory of linguistic meaning developed by Charles J. Fillmore[1] that extends his earlier case grammar. It relates linguistic semantics to encyclopedic knowledge. The basic idea is that one cannot understand the meaning of a single word without access to all the essential knowledge that relates to that word. For example, one would not be able to understand the word "sell" without knowing anything about the situation of commercial transfer, which also involves, among other things, a seller, a buyer, goods, money, the relation between the money and the goods, the relations between the seller and the goods and the money, the relation between the buyer and the goods and the money and so on. Thus, a word activates, or evokes, a frame of semantic knowledge relating to the specific concept to which it refers (or highlights, in frame semantic terminology).
The idea of the encyclopedic organisation of knowledge itself is old and was discussed by Age of Enlightenment philosophers such as Denis Diderot[2] and Giambattista Vico.[3] Fillmore and other evolutionary and cognitive linguists like John Haiman and Adele Goldberg, however, make an argument against generative grammar and truth-conditional semantics. As is elementary for Lakoffian–Langackerian Cognitive Linguistics, it is claimed that knowledge of language is no different from other types of knowledge; therefore there is no grammar in the traditional sense, and language is not an independent cognitive function.[4] Instead, the spreading and survival of linguistic units is directly comparable to that of other types of units of cultural evolution, like in memetics and other cultural replicator theories.[5][6][7]
https://en.wikipedia.org/wiki/Frame_semantics_(linguistics)
Use in cognitive linguistics and construction grammar
The theory applies the notion of a semantic frame also used in artificial intelligence, which is a collection of facts that specify "characteristic features, attributes, and functions of a denotatum, and its characteristic interactions with things necessarily or typically associated with it."[8] A semantic frame can also be defined as a coherent structure of related concepts that are related such that without knowledge of all of them, one does not have complete knowledge of any one; they are in that sense types of gestalt. Frames are based on recurring experiences, therefore the commercial transaction frame is based on recurring experiences of commercial transactions.
Words not only highlight individual concepts, but also specify a certain perspective from which the frame is viewed. For example "sell" views the situation from the perspective of the seller and "buy" from the perspective of the buyer. This, according to Fillmore, explains the observed asymmetries in many lexical relations.
While originally only being applied to lexemes, frame semantics has now been expanded to grammatical constructions and other larger and more complex linguistic units and has more or less been integrated into construction grammar as the main semantic principle. Semantic frames are also becoming used in information modeling, for example in Gellish, especially in the form of 'definition models' and 'knowledge models'.
Frame semantics has much in common with the semantic principle of profiling from Ronald W. Langacker's cognitive grammar.[9]
The concept of frames has been several times considered in philosophy and psycholinguistics, namely supported by Lawrence W. Barsalou,[10] and more recently by Sebastian Löbner.[11] They are viewed as a cognitive representation of the real world. From a computational linguistics viewpoint, there are semantic models of a sentence. This approach going further than just the lexical aspect is especially studied in SFB 991 in Düsseldorf.
Applications
Google originally started a frame semantic parser project that aims parse the information on Wikipedia and transfer it into Wikidata by coming up with relevant relations using artificial intelligence.[12]
See also
- Conceptual space
- Figurative system of human knowledge
- FrameNet
- Formal semantics (natural language)
- Frame language
- Metaphorical framing
- Prototype theory
- Universal Darwinism
https://en.wikipedia.org/wiki/Frame_semantics_(linguistics)
In logic, a strict conditional (symbol: 

https://en.wikipedia.org/wiki/Strict_conditional
The paradoxes of material implication are a group of true formulae involving material conditionals
whose translations into natural language are intuitively false when the
conditional is translated as "if ... then ...". A material conditional
formula 


https://en.wikipedia.org/wiki/Paradoxes_of_material_implication
In classical logic, intuitionistic logic and similar logical systems, the principle of explosion (Latin: ex falso [sequitur] quodlibet, 'from falsehood, anything [follows]'; or ex contradictione [sequitur] quodlibet, 'from contradiction, anything [follows]'), or the principle of Pseudo-Scotus (falsely attributed to Duns Scotus), is the law according to which any statement can be proven from a contradiction.[1] That is, once a contradiction has been asserted, any proposition (including their negations) can be inferred from it; this is known as deductive explosion.[2][3]
The proof of this principle was first given by 12th-century French philosopher William of Soissons.[4] Due to the principle of explosion, the existence of a contradiction (inconsistency) in a formal axiomatic system is disastrous; since any statement can be proven, it trivializes the concepts of truth and falsity.[5] Around the turn of the 20th century, the discovery of contradictions such as Russell's paradox at the foundations of mathematics thus threatened the entire structure of mathematics. Mathematicians such as Gottlob Frege, Ernst Zermelo, Abraham Fraenkel, and Thoralf Skolem put much effort into revising set theory to eliminate these contradictions, resulting in the modern Zermelo–Fraenkel set theory.
As a demonstration of the principle, consider two contradictory statements—"All lemons are yellow" and "Not all lemons are yellow"—and suppose that both are true. If that is the case, anything can be proven, e.g., the assertion that "unicorns exist", by using the following argument:
- We know that "Not all lemons are yellow", as it has been assumed to be true.
- We know that "All lemons are yellow", as it has been assumed to be true.
- Therefore, the two-part statement "All lemons are yellow or unicorns exist" must also be true, since the first part "All lemons are yellow" of the two-part statement is true (as this has been assumed).
- However, since we know that "Not all lemons are yellow" (as this has been assumed), the first part is false, and hence the second part must be true to ensure the two-part statement to be true, i.e., unicorns exist.
In a different solution to these problems, a few mathematicians have devised alternative theories of logic called paraconsistent logics, which eliminate the principle of explosion.[5] These allow some contradictory statements to be proven without affecting other proofs.
https://en.wikipedia.org/wiki/Principle_of_explosion
Logical consequence (also entailment) is a fundamental concept in logic which describes the relationship between statements that hold true when one statement logically follows from one or more statements. A valid logical argument is one in which the conclusion is entailed by the premises, because the conclusion is the consequence of the premises. The philosophical analysis of logical consequence involves the questions: In what sense does a conclusion follow from its premises? and What does it mean for a conclusion to be a consequence of premises?[1] All of philosophical logic is meant to provide accounts of the nature of logical consequence and the nature of logical truth.[2]
Logical consequence is necessary and formal, by way of examples that explain with formal proof and models of interpretation.[1] A sentence is said to be a logical consequence of a set of sentences, for a given language, if and only if, using only logic (i.e., without regard to any personal interpretations of the sentences) the sentence must be true if every sentence in the set is true.[3]
Logicians make precise accounts of logical consequence regarding a given language 


https://en.wikipedia.org/wiki/Logical_consequence
In linguistics, the autonomy of syntax is the assumption that syntax is arbitrary and self-contained with respect to meaning, semantics, pragmatics, discourse function, and other factors external to language.[1] The autonomy of syntax is advocated by linguistic formalists, and in particular by generative linguistics, whose approaches have hence been called autonomist linguistics.
The autonomy of syntax is at the center of the debates between formalist and functionalist linguistics,[1][2][3] and since the 1980s research has been conducted on the syntax–semantics interface within functionalist approaches, aimed at finding instances of semantically determined syntactic structures, to disprove the formalist argument of the autonomy of syntax.[4]
The principle of iconicity is contrasted, for some scenarios, with that of the autonomy of syntax. The weaker version of the argument for the autonomy of syntax (or that for the autonomy of grammar), includes only for the principle of arbitrariness, while the stronger version includes the claim of self-containedness.[1] The principle of arbitrariedness of syntax is actually accepted by most functionalist linguist, and the real dispute between functionalist and generativists is on the claim of self-containedness of grammar or syntax.[5]
https://en.wikipedia.org/wiki/Autonomy_of_syntax
In computer science, a continuation is an abstract representation of the control state of a computer program. A continuation implements (reifies) the program control state, i.e. the continuation is a data structure that represents the computational process at a given point in the process's execution; the created data structure can be accessed by the programming language, instead of being hidden in the runtime environment. Continuations are useful for encoding other control mechanisms in programming languages such as exceptions, generators, coroutines, and so on.
The "current continuation" or "continuation of the computation step" is the continuation that, from the perspective of running code, would be derived from the current point in a program's execution. The term continuations can also be used to refer to first-class continuations, which are constructs that give a programming language the ability to save the execution state at any point and return to that point at a later point in the program, possibly multiple times.
https://en.wikipedia.org/wiki/Continuation
In formal semantics and philosophy of language, a meaning postulate is a way of stipulating a relationship between the meanings of two or more words. They were introduced by Rudolf Carnap as a way of approaching the analytic/synthetic distinction.[1] Subsequently, Richard Montague made heavy use of meaning postulates in the development of Montague grammar,[2] and they have features prominently in formal semantics following in Montague's footsteps.[3]
https://en.wikipedia.org/wiki/Meaning_postulate
In formal semantics, a predicate is quantized if it being true of an entity requires that it is not true of any proper subparts of that entity. For example, if something is an "apple", then no proper subpart of that thing is an "apple". If something is "water", then many of its subparts will also be "water". Hence, the predicate "apple" is quantized, while "water" is not.[1][2]
Formally, a quantization predicate QUA can be defined as follows, where 





Quantization was first proposed by Manfred Krifka as part of his mereological approach to the semantics of nominals. It has since been applied to other phenomena such as telicity.
https://en.wikipedia.org/wiki/Quantization_(linguistics)
| Grammatical features |
|---|
|
|
Related to nouns |
|
|
Related to verbs |
|
|
General features |
|
|
Syntax relationships |
|
|
Semantics |
|
|
Phenomena |
In linguistics, a mass noun, uncountable noun, non-count noun, uncount noun, or just uncountable, is a noun with the syntactic property that any quantity of it is treated as an undifferentiated unit, rather than as something with discrete elements. Non-count nouns are distinguished from count nouns.
Given that different languages have different grammatical features, the actual test for which nouns are mass nouns may vary between languages. In English, mass nouns are characterized by the impossibility of being directly modified by a numeral without specifying a unit of measurement and by the impossibility of being combined with an indefinite article (a or an). Thus, the mass noun "water" is quantified as "20 litres of water" while the count noun "chair" is quantified as "20 chairs". However, both mass and count nouns can be quantified in relative terms without unit specification (e.g., "so much water", "so many chairs").
Mass nouns have no concept of singular and plural, although in English they take singular verb forms. However, many mass nouns in English can be converted to count nouns, which can then be used in the plural to denote (for instance) more than one instance or variety of a certain sort of entity – for example, "Many cleaning agents today are technically not soaps [i.e. types of soap], but detergents," or "I drank about three beers [i.e. bottles or glasses of beer]".
Some nouns can be used indifferently as mass or count nouns, e.g., three cabbages or three heads of cabbage; three ropes or three lengths of rope. Some have different senses as mass and count nouns: paper is a mass noun as a material (three reams of paper, one sheet of paper), but a count noun as a unit of writing ("the students passed in their papers").
https://en.wikipedia.org/wiki/Mass_noun
Inferential role semantics (also conceptual role semantics, functional role semantics, procedural semantics, semantic inferentialism) is an approach to the theory of meaning that identifies the meaning of an expression with its relationship to other expressions (typically its inferential relations with other expressions), in contradistinction to denotationalism, according to which denotations are the primary sort of meaning.[1]
In linguistics, deixis (/ˈdaɪksɪs/, /ˈdeɪksɪs/)[1] is the use of general words and phrases to refer to a specific time, place, or person in context, e.g., the words tomorrow, there, and they. Words are deictic if their semantic meaning is fixed but their denoted meaning varies depending on time and/or place. Words or phrases that require contextual information to be fully understood—for example, English pronouns—are deictic. Deixis is closely related to anaphora. Although this article deals primarily with deixis in spoken language, the concept is sometimes applied to written language, gestures, and communication media as well. In linguistic anthropology, deixis is treated as a particular subclass of the more general semiotic phenomenon of indexicality, a sign "pointing to" some aspect of its context of occurrence.
Although this article draws examples primarily from English, deixis is believed to be a feature (to some degree) of all natural languages.[2] The term's origin is Ancient Greek: δεῖξις, romanized: deixis, lit. 'display, demonstration, or reference', the meaning point of reference in contemporary linguistics having been taken over from Chrysippus.[3][clarification needed]
https://en.wikipedia.org/wiki/Deixis
Truth-conditional semantics is an approach to semantics of natural language that sees meaning (or at least the meaning of assertions) as being the same as, or reducible to, their truth conditions. This approach to semantics is principally associated with Donald Davidson, and attempts to carry out for the semantics of natural language what Tarski's semantic theory of truth achieves for the semantics of logic.[1]
Truth-conditional theories of semantics attempt to define the meaning of a given proposition by explaining when the sentence is true. So, for example, because 'snow is white' is true if and only if snow is white, the meaning of 'snow is white' is snow is white.
https://en.wikipedia.org/wiki/Truth-conditional_semantics
Inquisitive semantics is a framework in logic and natural language semantics. In inquisitive semantics, the semantic content of a sentence captures both the information that the sentence conveys and the issue that it raises. The framework provides a foundation for the linguistic analysis of statements and questions.[1][2] It was originally developed by Ivano Ciardelli, Jeroen Groenendijk, Salvador Mascarenhas, and Floris Roelofsen.[3][4][5][6][7]
https://en.wikipedia.org/wiki/Inquisitive_semantics
Upper closure and lower closure
Given an element 






 , denoted by
, denoted by 
 or
or  is defined by
is defined by

The sets 








In this way, 

The upper and lower closures, when viewed as functions from the power set of 
https://en.wikipedia.org/wiki/Upper_set#Downward_closure
Relative pseudocomplement
A relative pseudocomplement of a with respect to b is a maximal element c such that a∧c≤b. This binary operation is denoted a→b. A lattice with the pseudocomplement for each two elements is called implicative lattice, or Brouwerian lattice. In general, an implicative lattice may not have a minimal element. If such a minimal element exists, then each pseudocomplement a* could be defined using relative pseudocomplement as a → 0.[4]
https://en.wikipedia.org/wiki/Pseudocomplement#Relative_pseudocomplement
In topology and related areas of mathematics, a subset A of a topological space X is said to be dense in X if every point of X either belongs to A or else is arbitrarily "close" to a member of A — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it (see Diophantine approximation).
Formally, 




The density of a topological space 

In topology and related areas of mathematics, a subset A of a topological space X is said to be dense in X if every point of X either belongs to A or else is arbitrarily "close" to a member of A — for instance, the rational numbers are a dense subset of the real numbers because every real number either is a rational number or has a rational number arbitrarily close to it (see Diophantine approximation).
Formally, 




The density of a topological space 

Definition
A subset 


- The smallest closed subset of
containing
is
itself.
- The closure of
in
is equal to
That is,
- The interior of the complement of
is empty. That is,
- Every point in
either belongs to
or is a limit point of
- For every
every neighborhood
of
intersects
that is,
intersects every non-empty open subset of
and if 

- For every
every basic neighborhood
of
intersects
intersects every non-empty
Density in metric spaces
An alternative definition of dense set in the case of metric spaces is the following. When the topology of 






Then 


If 



Examples
The real numbers with the usual topology have the rational numbers as a countable dense subset which shows that the cardinality of a dense subset of a topological space may be strictly smaller than the cardinality of the space itself. The irrational numbers are another dense subset which shows that a topological space may have several disjoint dense subsets (in particular, two dense subsets may be each other's complements), and they need not even be of the same cardinality. Perhaps even more surprisingly, both the rationals and the irrationals have empty interiors, showing that dense sets need not contain any non-empty open set. The intersection of two dense open subsets of a topological space is again dense and open.[proof 1] The empty set is a dense subset of itself. But every dense subset of a non-empty space must also be non-empty.
By the Weierstrass approximation theorem, any given complex-valued continuous function defined on a closed interval ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![C[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c1625217aad8c105c50c975599e45192b2bfbec)
![[a, b],](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842)
Every metric space is dense in its completion.
Properties
Every topological space is a dense subset of itself. For a set 

Denseness is transitive: Given three subsets 









The image of a dense subset under a surjective continuous function is again dense. The density of a topological space (the least of the cardinalities of its dense subsets) is a topological invariant.
A topological space with a connected dense subset is necessarily connected itself.
Continuous functions into Hausdorff spaces are determined by their values on dense subsets: if two continuous functions 



For metric spaces there are universal spaces, into which all spaces of given density can be embedded: a metric space of density 
![{\displaystyle C\left([0,1]^{\alpha },\mathbb {R} \right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/809452f4d7ae5513ace8ea8b9f7045218657f271)

Related notions
A point 








A subset 








A topological space with a countable dense subset is called separable. A topological space is a Baire space if and only if the intersection of countably many dense open sets is always dense. A topological space is called resolvable if it is the union of two disjoint dense subsets. More generally, a topological space is called κ-resolvable for a cardinal κ if it contains κ pairwise disjoint dense sets.
An embedding of a topological space 

A linear operator between topological vector spaces 



A topological space 

If 



One can then show that 


See also
- Blumberg theorem – Any real function on R adhttps://en.wikipedia.org/wiki/Dense_setmits a continuous restriction on a dense subset of R
- Dense order – Partial order where for every two distinct elements have another element between them
- Dense (lattice theory)
References
- Kleiber, Martin; Pervin, William J. (1969). "A generalized Banach-Mazur theorem". Bull. Austral. Math. Soc. 1 (2): 169–173. doi:10.1017/S0004972700041411.
proofs
- Suppose that
and
are dense open subset of a topological space
If
then the conclusion that the open set
is dense in
is immediate, so assume otherwise. Let
is a non-empty open subset of
so it remains to show that
is also not empty. Because
is dense in
and
is a non-empty open subset of
their intersection
is not empty. Similarly, because
is a non-empty open subset of
and
is dense in
their intersection
is not empty.
General references
- Nicolas Bourbaki (1989) [1971]. General Topology, Chapters 1–4. Elements of Mathematics. Springer-Verlag. ISBN 3-540-64241-2.
- Bourbaki, Nicolas (1989) [1966]. General Topology: Chapters 1–4 [Topologie Générale]. Éléments de mathématique. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC 18588129.
- Dixmier, Jacques (1984). General Topology. Undergraduate Texts in Mathematics. Translated by Berberian, S. K. New York: Springer-Verlag. ISBN 978-0-387-90972-1. OCLC 10277303.
- Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
- Steen, Lynn Arthur; Seebach, J. Arthur Jr. (1995) [1978], Counterexamples in Topology (Dover reprint of 1978 ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-486-68735-3, MR 0507446
- Willard, Stephen (2004) [1970]. General Topology. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.
https://en.wikipedia.org/wiki/Dense_set
https://en.wikipedia.org/wiki/Diophantine_approximation
https://en.wikipedia.org/wiki/Glossary_of_artificial_intelligence
A
- abductive logic programming (ALP)
- A high-level knowledge-representation framework that can be used to solve problems declaratively based on abductive reasoning. It extends normal logic programming by allowing some predicates to be incompletely defined, declared as abducible predicates.
- abductive reasoning
- A form of logical inference which starts with an observation or set of observations then seeks to find the simplest and most likely explanation. This process, unlike deductive reasoning, yields a plausible conclusion but does not positively verify it.[1] abductive inference,[1] or retroduction[2]
- abstract data type
- A mathematical model for data types, where a data type is defined by its behavior (semantics) from the point of view of a user of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations.
- abstraction
- The process of removing physical, spatial, or temporal details[3] or attributes in the study of objects or systems in order to more closely attend to other details of interest[4]
- accelerating change
- A perceived increase in the rate of technological change throughout history, which may suggest faster and more profound change in the future and may or may not be accompanied by equally profound social and cultural change.
- action language
- A language for specifying state transition systems, and is commonly used to create formal models of the effects of actions on the world.[5] Action languages are commonly used in the artificial intelligence and robotics domains, where they describe how actions affect the states of systems over time, and may be used for automated planning.
- action model learning
- An area of machine learning concerned with creation and modification of software agent's knowledge about effects and preconditions of the actions that can be executed within its environment. This knowledge is usually represented in logic-based action description language and used as the input for automated planners.
- action selection
- A way of characterizing the most basic problem of intelligent systems: what to do next. In artificial intelligence and computational cognitive science, "the action selection problem" is typically associated with intelligent agents and animats—artificial systems that exhibit complex behaviour in an agent environment.
- activation function
- In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs.
- adaptive algorithm
- An algorithm that changes its behavior at the time it is run, based on a priori defined reward mechanism or criterion.
- adaptive neuro fuzzy inference system (ANFIS)
- A kind of artificial neural network that is based on Takagi–Sugeno fuzzy inference system. The technique was developed in the early 1990s.[6][7] Since it integrates both neural networks and fuzzy logic principles, it has potential to capture the benefits of both in a single framework. Its inference system corresponds to a set of fuzzy IF–THEN rules that have learning capability to approximate nonlinear functions.[8] Hence, ANFIS is considered to be a universal estimator.[9] For using the ANFIS in a more efficient and optimal way, one can use the best parameters obtained by genetic algorithm.[10][11]
- admissible heuristic
- In computer science, specifically in algorithms related to pathfinding, a heuristic function is said to be admissible if it never overestimates the cost of reaching the goal, i.e. the cost it estimates to reach the goal is not higher than the lowest possible cost from the current point in the path.[12]
- affective computing
- The study and development of systems and devices that can recognize, interpret, process, and simulate human affects. Affective computing is an interdisciplinary field spanning computer science, psychology, and cognitive science.[13][14]
- agent architecture
- A blueprint for software agents and intelligent control systems, depicting the arrangement of components. The architectures implemented by intelligent agents are referred to as cognitive architectures.[15]
- AI accelerator
- A class of microprocessor[16] or computer system[17] designed as hardware acceleration for artificial intelligence applications, especially artificial neural networks, machine vision, and machine learning.
- AI-complete
- In the field of artificial intelligence, the most difficult problems are informally known as AI-complete or AI-hard, implying that the difficulty of these computational problems is equivalent to that of solving the central artificial intelligence problem—making computers as intelligent as people, or strong AI.[18] To call a problem AI-complete reflects an attitude that it would not be solved by a simple specific algorithm.
- algorithm
- An unambiguous specification of how to solve a class of problems. Algorithms can perform calculation, data processing, and automated reasoning tasks.
- algorithmic efficiency
- A property of an algorithm which relates to the number of computational resources used by the algorithm. An algorithm must be analyzed to determine its resource usage, and the efficiency of an algorithm can be measured based on usage of different resources. Algorithmic efficiency can be thought of as analogous to engineering productivity for a repeating or continuous process.
- algorithmic probability
- In algorithmic information theory, algorithmic probability, also known as Solomonoff probability, is a mathematical method of assigning a prior probability to a given observation. It was invented by Ray Solomonoff in the 1960s.[19]
- AlphaGo
- A computer program that plays the board game Go.[20] It was developed by Alphabet Inc.'s Google DeepMind in London. AlphaGo has several versions including AlphaGo Zero, AlphaGo Master, AlphaGo Lee, etc.[21] In October 2015, AlphaGo became the first computer Go program to beat a human professional Go player without handicaps on a full-sized 19×19 board.[22][23]
- ambient intelligence (AmI)
- Electronic environments that are sensitive and responsive to the presence of people.
- analysis of algorithms
- The determination of the computational complexity of algorithms, that is the amount of time, storage and/or other resources necessary to execute them. Usually, this involves determining a function that relates the length of an algorithm's input to the number of steps it takes (its time complexity) or the number of storage locations it uses (its space complexity).
- analytics
- The discovery, interpretation, and communication of meaningful patterns in data.
- answer set programming (ASP)
- A form of declarative programming oriented towards difficult (primarily NP-hard) search problems. It is based on the stable model (answer set) semantics of logic programming. In ASP, search problems are reduced to computing stable models, and answer set solvers—programs for generating stable models—are used to perform search.
- anytime algorithm
- An algorithm that can return a valid solution to a problem even if it is interrupted before it ends.
- application programming interface (API)
- A set of subroutine definitions, communication protocols, and tools for building software. In general terms, it is a set of clearly defined methods of communication among various components. A good API makes it easier to develop a computer program by providing all the building blocks, which are then put together by the programmer. An API may be for a web-based system, operating system, database system, computer hardware, or software library.
- approximate string matching
- The technique of finding strings that match a pattern approximately (rather than exactly). The problem of approximate string matching is typically divided into two sub-problems: finding approximate substring matches inside a given string and finding dictionary strings that match the pattern approximately.
- approximation error
- The discrepancy between an exact value and some approximation to it.
- argumentation framework
- A way to deal with contentious information and draw conclusions from it. In an abstract argumentation framework,[24] entry-level information is a set of abstract arguments that, for instance, represent data or a proposition. Conflicts between arguments are represented by a binary relation on the set of arguments. In concrete terms, you represent an argumentation framework with a directed graph such that the nodes are the arguments, and the arrows represent the attack relation. There exist some extensions of the Dung's framework, like the logic-based argumentation frameworks[25] or the value-based argumentation frameworks.[26]
- artificial general intelligence (AGI)
- artificial immune system (AIS)
- A class of computationally intelligent, rule-based machine learning systems inspired by the principles and processes of the vertebrate immune system. The algorithms are typically modeled after the immune system's characteristics of learning and memory for use in problem-solving.
- artificial intelligence (AI)
- Any intelligence demonstrated by machines, in contrast to the natural intelligence displayed by humans and other animals. In computer science, AI research is defined as the study of "intelligent agents": any device that perceives its environment and takes actions that maximize its chance of successfully achieving its goals.[27] Colloquially, the term "artificial intelligence" is applied when a machine mimics "cognitive" functions that humans associate with other human minds, such as "learning" and "problem solving".[28]
- Artificial Intelligence Markup Language
- An XML dialect for creating natural language software agents.
- artificial neural network (ANN)
- Any computing system vaguely inspired by the biological neural networks that constitute animal brains.
- Association for the Advancement of Artificial Intelligence (AAAI)
- An international, nonprofit, scientific society devoted to promote research in, and responsible use of, artificial intelligence. AAAI also aims to increase public understanding of artificial intelligence (AI), improve the teaching and training of AI practitioners, and provide guidance for research planners and funders concerning the importance and potential of current AI developments and future directions.[29]
- asymptotic computational complexity
- In computational complexity theory, asymptotic computational complexity is the usage of asymptotic analysis for the estimation of computational complexity of algorithms and computational problems, commonly associated with the usage of the big O notation.
- attributional calculus
- A logic and representation system defined by Ryszard S. Michalski. It combines elements of predicate logic, propositional calculus, and multi-valued logic. Attributional calculus provides a formal language for natural induction, an inductive learning process whose results are in forms natural to people.
- augmented reality (AR)
- An interactive experience of a real-world environment where the objects that reside in the real-world are "augmented" by computer-generated perceptual information, sometimes across multiple sensory modalities, including visual, auditory, haptic, somatosensory, and olfactory.[30]
- automata theory
- The study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science and discrete mathematics (a subject of study in both mathematics and computer science).
- automated machine learning (AutoML)
- A field of machine learning which aims to automatically configure a machine learning system to maximize its performance (e.g, classification accuracy).
- automated planning and scheduling
- A branch of artificial intelligence that concerns the realization of strategies or action sequences, typically for execution by intelligent agents, autonomous robots and unmanned vehicles. Unlike classical control and classification problems, the solutions are complex and must be discovered and optimized in multidimensional space. Planning is also related to decision theory.[31]
- automated reasoning
- An area of computer science and mathematical logic dedicated to understanding different aspects of reasoning. The study of automated reasoning helps produce computer programs that allow computers to reason completely, or nearly completely, automatically. Although automated reasoning is considered a sub-field of artificial intelligence, it also has connections with theoretical computer science, and even philosophy.
- autonomic computing (AC)
- The self-managing characteristics of distributed computing resources, adapting to unpredictable changes while hiding intrinsic complexity to operators and users. Initiated by IBM in 2001, this initiative ultimately aimed to develop computer systems capable of self-management, to overcome the rapidly growing complexity of computing systems management, and to reduce the barrier that complexity poses to further growth.[32]
- autonomous car
- A vehicle that is capable of sensing its environment and moving with little or no human input.[33][34][35]
- autonomous robot
- A robot that performs behaviors or tasks with a high degree of autonomy. Autonomous robotics is usually considered to be a subfield of artificial intelligence, robotics, and information engineering.[36]
Also abduction.
Also adaptive network-based fuzzy inference system.
Also artificial emotional intelligence or emotion AI.
Also fuzzy string searching.
Also argumentation system.
Also machine intelligence.
Also connectionist system.
Also simply AI planning.
Also self-driving car, robot car, and driverless car.
B
- backpropagation
- A method used in artificial neural networks to calculate a gradient that is needed in the calculation of the weights to be used in the network.[37] Backpropagation is shorthand for "the backward propagation of errors", since an error is computed at the output and distributed backwards throughout the network's layers. It is commonly used to train deep neural networks,[38] a term referring to neural networks with more than one hidden layer.[39]
- backpropagation through time (BPTT)
- A gradient-based technique for training certain types of recurrent neural networks. It can be used to train Elman networks. The algorithm was independently derived by numerous researchers[40][41][42]
- backward chaining
- An inference method described colloquially as working backward from the goal. It is used in automated theorem provers, inference engines, proof assistants, and other artificial intelligence applications.[43]
- bag-of-words model
- A simplifying representation used in natural language processing and information retrieval (IR). In this model, a text (such as a sentence or a document) is represented as the bag (multiset) of its words, disregarding grammar and even word order but keeping multiplicity. The bag-of-words model has also been used for computer vision.[44] The bag-of-words model is commonly used in methods of document classification where the (frequency of) occurrence of each word is used as a feature for training a classifier.[45]
- bag-of-words model in computer vision
- In computer vision, the bag-of-words model (BoW model) can be applied to image classification, by treating image features as words. In document classification, a bag of words is a sparse vector of occurrence counts of words; that is, a sparse histogram over the vocabulary. In computer vision, a bag of visual words is a vector of occurrence counts of a vocabulary of local image features.
- batch normalization
- A technique for improving the performance and stability of artificial neural networks. It is a technique to provide any layer in a neural network with inputs that are zero mean/unit variance.[46] Batch normalization was introduced in a 2015 paper.[47][48] It is used to normalize the input layer by adjusting and scaling the activations.[49]
- Bayesian programming
- A formalism and a methodology for having a technique to specify probabilistic models and solve problems when less than the necessary information is available.
- bees algorithm
- A population-based search algorithm which was developed by Pham, Ghanbarzadeh and et al. in 2005.[50] It mimics the food foraging behaviour of honey bee colonies. In its basic version the algorithm performs a kind of neighbourhood search combined with global search, and can be used for both combinatorial optimization and continuous optimization. The only condition for the application of the bees algorithm is that some measure of distance between the solutions is defined. The effectiveness and specific abilities of the bees algorithm have been proven in a number of studies.[51][52][53][54]
- behavior informatics (BI)
- The informatics of behaviors so as to obtain behavior intelligence and behavior insights.[55]
- behavior tree (BT)
- A mathematical model of plan execution used in computer science, robotics, control systems and video games. They describe switchings between a finite set of tasks in a modular fashion. Their strength comes from their ability to create very complex tasks composed of simple tasks, without worrying how the simple tasks are implemented. BTs present some similarities to hierarchical state machines with the key difference that the main building block of a behavior is a task rather than a state. Its ease of human understanding make BTs less error-prone and very popular in the game developer community. BTs have shown to generalize several other control architectures.[56][57]
- belief-desire-intention software model (BDI)
- A software model developed for programming intelligent agents. Superficially characterized by the implementation of an agent's beliefs, desires and intentions, it actually uses these concepts to solve a particular problem in agent programming. In essence, it provides a mechanism for separating the activity of selecting a plan (from a plan library or an external planner application) from the execution of currently active plans. Consequently, BDI agents are able to balance the time spent on deliberating about plans (choosing what to do) and executing those plans (doing it). A third activity, creating the plans in the first place (planning), is not within the scope of the model, and is left to the system designer and programmer.
- bias–variance tradeoff
- In statistics and machine learning, the bias–variance tradeoff is the property of a set of predictive models whereby models with a lower bias in parameter estimation have a higher variance of the parameter estimates across samples, and vice versa.
- big data
- A term used to refer to data sets that are too large or complex for traditional data-processing application software to adequately deal with. Data with many cases (rows) offer greater statistical power, while data with higher complexity (more attributes or columns) may lead to a higher false discovery rate.[58]
- Big O notation
- A mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. It is a member of a family of notations invented by Paul Bachmann,[59] Edmund Landau,[60] and others, collectively called Bachmann–Landau notation or asymptotic notation.
- binary tree
- A tree data structure in which each node has at most two children, which are referred to as the left child and the right child. A recursive definition using just set theory notions is that a (non-empty) binary tree is a tuple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set.[61] Some authors allow the binary tree to be the empty set as well.[62]
- blackboard system
- An artificial intelligence approach based on the blackboard architectural model,[63][64][65][66] where a common knowledge base, the "blackboard", is iteratively updated by a diverse group of specialist knowledge sources, starting with a problem specification and ending with a solution. Each knowledge source updates the blackboard with a partial solution when its internal constraints match the blackboard state. In this way, the specialists work together to solve the problem.
- Boltzmann machine
- A type of stochastic recurrent neural network and Markov random field.[67] Boltzmann machines can be seen as the stochastic, generative counterpart of Hopfield networks.
- Boolean satisfiability problem
- The problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.
- brain technology
- A technology that employs the latest findings in neuroscience. The term was first introduced by the Artificial Intelligence Laboratory in Zurich, Switzerland, in the context of the ROBOY project.[68] Brain Technology can be employed in robots,[69] know-how management systems[70] and any other application with self-learning capabilities. In particular, Brain Technology applications allow the visualization of the underlying learning architecture often coined as "know-how maps".
- branching factor
- In computing, tree data structures, and game theory, the number of children at each node, the outdegree. If this value is not uniform, an average branching factor can be calculated.
- brute-force search
- A very general problem-solving technique and algorithmic paradigm that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's statement.
Also backward reasoning.
Also stochastic Hopfield network with hidden units.
Also propositional satisfiability problem; abbreviated SATISFIABILITY or SAT.
Also self-learning know-how system.
Also exhaustive search or generate and test.
C
- capsule neural network (CapsNet)
- A machine learning system that is a type of artificial neural network (ANN) that can be used to better model hierarchical relationships. The approach is an attempt to more closely mimic biological neural organization.[71]
- case-based reasoning (CBR)
- Broadly construed, the process of solving new problems based on the solutions of similar past problems.
- chatbot
- A computer program or an artificial intelligence which conducts a conversation via auditory or textual methods.[72]
- cloud robotics
- A field of robotics that attempts to invoke cloud technologies such as cloud computing, cloud storage, and other Internet technologies centred on the benefits of converged infrastructure and shared services for robotics. When connected to the cloud, robots can benefit from the powerful computation, storage, and communication resources of modern data center in the cloud, which can process and share information from various robots or agent (other machines, smart objects, humans, etc.). Humans can also delegate tasks to robots remotely through networks. Cloud computing technologies enable robot systems to be endowed with powerful capability whilst reducing costs through cloud technologies. Thus, it is possible to build lightweight, low cost, smarter robots have intelligent "brain" in the cloud. The "brain" consists of data center, knowledge base, task planners, deep learning, information processing, environment models, communication support, etc.[73][74][75][76]
- cluster analysis
- The task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of exploratory data mining, and a common technique for statistical data analysis, used in many fields, including machine learning, pattern recognition, image analysis, information retrieval, bioinformatics, data compression, and computer graphics.
- Cobweb
- An incremental system for hierarchical conceptual clustering. COBWEB was invented by Professor Douglas H. Fisher, currently at Vanderbilt University.[77][78] COBWEB incrementally organizes observations into a classification tree. Each node in a classification tree represents a class (concept) and is labeled by a probabilistic concept that summarizes the attribute-value distributions of objects classified under the node. This classification tree can be used to predict missing attributes or the class of a new object.[79]
- cognitive architecture
- The Institute of Creative Technologies defines cognitive architecture as: "hypothesis about the fixed structures that provide a mind, whether in natural or artificial systems, and how they work together – in conjunction with knowledge and skills embodied within the architecture – to yield intelligent behavior in a diversity of complex environments."[80]
- cognitive computing
- In general, the term cognitive computing has been used to refer to new hardware and/or software that mimics the functioning of the human brain[81][82][83][84][85][86] and helps to improve human decision-making.[87][88] In this sense, CC is a new type of computing with the goal of more accurate models of how the human brain/mind senses, reasons, and responds to stimulus.
- cognitive science
- The interdisciplinary scientific study of the mind and its processes.[89]
- combinatorial optimization
- In Operations Research, applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects.[90]
- committee machine
- A type of artificial neural network using a divide and conquer strategy in which the responses of multiple neural networks (experts) are combined into a single response.[91] The combined response of the committee machine is supposed to be superior to those of its constituent experts. Compare ensembles of classifiers.
- commonsense knowledge
- In artificial intelligence research, commonsense knowledge consists of facts about the everyday world, such as "Lemons are sour", that all humans are expected to know. The first AI program to address common sense knowledge was Advice Taker in 1959 by John McCarthy.[92]
- commonsense reasoning
- A branch of artificial intelligence concerned with simulating the human ability to make presumptions about the type and essence of ordinary situations they encounter every day.[93]
- computational chemistry
- A branch of chemistry that uses computer simulation to assist in solving chemical problems.
- computational complexity theory
- Focuses on classifying computational problems according to their inherent difficulty, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.
- computational creativity
- A multidisciplinary endeavour that includes the fields of artificial intelligence, cognitive psychology, philosophy, and the arts.
- computational cybernetics
- The integration of cybernetics and computational intelligence techniques.
- computational humor
- A branch of computational linguistics and artificial intelligence which uses computers in humor research.[94]
- computational intelligence (CI)
- Usually refers to the ability of a computer to learn a specific task from data or experimental observation.
- computational learning theory
- In computer science, computational learning theory (or just learning theory) is a subfield of artificial intelligence devoted to studying the design and analysis of machine learning algorithms.[95]
- computational linguistics
- An interdisciplinary field concerned with the statistical or rule-based modeling of natural language from a computational perspective, as well as the study of appropriate computational approaches to linguistic questions.
- computational mathematics
- The mathematical research in areas of science where computing plays an essential role.
- computational neuroscience
- A branch of neuroscience which employs mathematical models, theoretical analysis and abstractions of the brain to understand the principles that govern the development, structure, physiology, and cognitive abilities of the nervous system.[96][97][98][99]
- computational number theory
- The study of algorithms for performing number theoretic computations.
- computational problem
- In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might be able to solve.
- computational statistics
- The interface between statistics and computer science.
- computer-automated design (CAutoD)
- Design automation usually refers to electronic design automation, or Design Automation which is a Product Configurator. Extending Computer-Aided Design (CAD), automated design and computer-automated design[100][101][102] are concerned with a broader range of applications, such as automotive engineering, civil engineering,[103][104][105][106] composite material design, control engineering,[107] dynamic system identification and optimization,[108] financial systems, industrial equipment, mechatronic systems, steel construction,[109] structural optimisation,[110] and the invention of novel systems. More recently, traditional CAD simulation is seen to be transformed to CAutoD by biologically inspired machine learning,[111] including heuristic search techniques such as evolutionary computation,[112][113] and swarm intelligence algorithms.[114]
- computer audition (CA)
- See machine listening.
- computer science
- The theory, experimentation, and engineering that form the basis for the design and use of computers. It involves the study of algorithms that process, store, and communicate digital information. A computer scientist specializes in the theory of computation and the design of computational systems.[115]
- computer vision
- An interdisciplinary scientific field that deals with how computers can be made to gain high-level understanding from digital images or videos. From the perspective of engineering, it seeks to automate tasks that the human visual system can do.[116][117][118]
- concept drift
- In predictive analytics and machine learning, the concept drift means that the statistical properties of the target variable, which the model is trying to predict, change over time in unforeseen ways. This causes problems because the predictions become less accurate as time passes.
- connectionism
- An approach in the fields of cognitive science, that hopes to explain mental phenomena using artificial neural networks.[119]
- consistent heuristic
- In the study of path-finding problems in artificial intelligence, a heuristic function is said to be consistent, or monotone, if its estimate is always less than or equal to the estimated distance from any neighboring vertex to the goal, plus the cost of reaching that neighbor.
- constrained conditional model (CCM)
- A machine learning and inference framework that augments the learning of conditional (probabilistic or discriminative) models with declarative constraints.
- constraint logic programming
- A form of constraint programming, in which logic programming is extended to include concepts from constraint satisfaction.
A constraint logic program is a logic program that contains constraints
in the body of clauses. An example of a clause including a constraint
is
A(X,Y) :- X+Y>0, B(X), C(Y). In this clause,X+Y>0is a constraint;A(X,Y),B(X), andC(Y)are literals as in regular logic programming. This clause states one condition under which the statementA(X,Y)holds:X+Yis greater than zero and bothB(X)andC(Y)are true. - constraint programming
- A programming paradigm wherein relations between variables are stated in the form of constraints. Constraints differ from the common primitives of imperative programming languages in that they do not specify a step or sequence of steps to execute, but rather the properties of a solution to be found.
- constructed language
- A language whose phonology, grammar, and vocabulary are consciously devised, instead of having developed naturally. Constructed languages may also be referred to as artificial, planned, or invented languages.[120]
- control theory
- In control systems engineering is a subfield of mathematics that deals with the control of continuously operating dynamical systems in engineered processes and machines. The objective is to develop a control model for controlling such systems using a control action in an optimum manner without delay or overshoot and ensuring control stability.
- convolutional neural network
- In deep learning, a convolutional neural network (CNN, or ConvNet) is a class of deep neural networks, most commonly applied to analyzing visual imagery. CNNs use a variation of multilayer perceptrons designed to require minimal preprocessing.[121] They are also known as shift invariant or space invariant artificial neural networks (SIANN), based on their shared-weights architecture and translation invariance characteristics.[122][123]
- crossover
- In genetic algorithms and evolutionary computation, a genetic operator used to combine the genetic information of two parents to generate new offspring. It is one way to stochastically generate new solutions from an existing population, and analogous to the crossover that happens during sexual reproduction in biological organisms. Solutions can also be generated by cloning an existing solution, which is analogous to asexual reproduction. Newly generated solutions are typically mutated before being added to the population.
Also smartbot, talkbot, chatterbot, bot, IM bot, interactive agent, conversational interface, or artificial conversational entity.
Also clustering.
Also artificial creativity, mechanical creativity, creative computing, or creative computation.
Also theoretical neuroscience or mathematical neuroscience.
Also algorithmic number theory.
Also statistical computing.
Also conlang.
Also recombination.
D
- Darkforest
- A computer go program developed by Facebook, based on deep learning techniques using a convolutional neural network. Its updated version Darkfores2 combines the techniques of its predecessor with Monte Carlo tree search.[124][125] The MCTS effectively takes tree search methods commonly seen in computer chess programs and randomizes them.[126] With the update, the system is known as Darkfmcts3.[127]
- Dartmouth workshop
- The Dartmouth Summer Research Project on Artificial Intelligence was the name of a 1956 summer workshop now considered by many[128][129] (though not all[130]) to be the seminal event for artificial intelligence as a field.
- data augmentation
- Data augmentation in data analysis are techniques used to increase the amount of data. It helps reduce overfitting when training a machine learning.
- data fusion
- The process of integrating multiple data sources to produce more consistent, accurate, and useful information than that provided by any individual data source.[131]
- data integration
- The process of combining data residing in different sources and providing users with a unified view of them.[132] This process becomes significant in a variety of situations, which include both commercial (such as when two similar companies need to merge their databases) and scientific (combining research results from different bioinformatics repositories, for example) domains. Data integration appears with increasing frequency as the volume (that is, big data) and the need to share existing data explodes.[133] It has become the focus of extensive theoretical work, and numerous open problems remain unsolved.
- data mining
- The process of discovering patterns in large data sets involving methods at the intersection of machine learning, statistics, and database systems.
- data science
- An interdisciplinary field that uses scientific methods, processes, algorithms and systems to extract knowledge and insights from data in various forms, both structured and unstructured,[134][135] similar to data mining. Data science is a "concept to unify statistics, data analysis, machine learning and their related methods" in order to "understand and analyze actual phenomena" with data.[136] It employs techniques and theories drawn from many fields within the context of mathematics, statistics, information science, and computer science.
- data set
- A collection of data. Most commonly a data set corresponds to the contents of a single database table, or a single statistical data matrix, where every column of the table represents a particular variable, and each row corresponds to a given member of the data set in question. The data set lists values for each of the variables, such as height and weight of an object, for each member of the data set. Each value is known as a datum. The data set may comprise data for one or more members, corresponding to the number of rows.
- data warehouse (DW or DWH)
- A system used for reporting and data analysis.[137] DWs are central repositories of integrated data from one or more disparate sources. They store current and historical data in one single place[138]
- Datalog
- A declarative logic programming language that syntactically is a subset of Prolog. It is often used as a query language for deductive databases. In recent years, Datalog has found new application in data integration, information extraction, networking, program analysis, security, and cloud computing.[139]
- decision boundary
- In the case of backpropagation-based artificial neural networks or perceptrons, the type of decision boundary that the network can learn is determined by the number of hidden layers the network has. If it has no hidden layers, then it can only learn linear problems. If it has one hidden layer, then it can learn any continuous function on compact subsets of Rn as shown by the Universal approximation theorem, thus it can have an arbitrary decision boundary.
- decision support system (DSS)
- Aan information system that supports business or organizational decision-making activities. DSSs serve the management, operations and planning levels of an organization (usually mid and higher management) and help people make decisions about problems that may be rapidly changing and not easily specified in advance—i.e. unstructured and semi-structured decision problems. Decision support systems can be either fully computerized or human-powered, or a combination of both.
- decision theory
- The study of the reasoning underlying an agent's choices.[140] Decision theory can be broken into two branches: normative decision theory, which gives advice on how to make the best decisions given a set of uncertain beliefs and a set of values, and descriptive decision theory which analyzes how existing, possibly irrational agents actually make decisions.
- decision tree learning
- Uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves). It is one of the predictive modeling approaches used in statistics, data mining and machine learning.
- declarative programming
- A programming paradigm—a style of building the structure and elements of computer programs—that expresses the logic of a computation without describing its control flow.[141]
- deductive classifier
- A type of artificial intelligence inference engine. It takes as input a set of declarations in a frame language about a domain such as medical research or molecular biology. For example, the names of classes, sub-classes, properties, and restrictions on allowable values.
- Deep Blue
- was a chess-playing computer developed by IBM. It is known for being the first computer chess-playing system to win both a chess game and a chess match against a reigning world champion under regular time controls.
- deep learning
- Part of a broader family of machine learning methods based on learning data representations, as opposed to task-specific algorithms. Learning can be supervised, semi-supervised, or unsupervised.[142][143][144]
- DeepMind Technologies
- A British artificial intelligence company founded in September 2010, currently owned by Alphabet Inc. The company is based in London, with research centres in Canada,[145] France,[146] and the United States. Acquired by Google in 2014, the company has created a neural network that learns how to play video games in a fashion similar to that of humans,[147] as well as a neural Turing machine,[148] or a neural network that may be able to access an external memory like a conventional Turing machine, resulting in a computer that mimics the short-term memory of the human brain.[149][150] The company made headlines in 2016 after its AlphaGo program beat human professional Go player Lee Sedol, the world champion, in a five-game match, which was the subject of a documentary film.[151] A more general program, AlphaZero, beat the most powerful programs playing Go, chess, and shogi (Japanese chess) after a few days of play against itself using reinforcement learning.[152]
- default logic
- A non-monotonic logic proposed by Raymond Reiter to formalize reasoning with default assumptions.
- description logic (DL)
- A family of formal knowledge representation languages. Many DLs are more expressive than propositional logic but less expressive than first-order logic. In contrast to the latter, the core reasoning problems for DLs are (usually) decidable, and efficient decision procedures have been designed and implemented for these problems. There are general, spatial, temporal, spatiotemporal, and fuzzy descriptions logics, and each description logic features a different balance between DL expressivity and reasoning complexity by supporting different sets of mathematical constructors.[153]
- developmental robotics (DevRob)
- A scientific field which aims at studying the developmental mechanisms, architectures, and constraints that allow lifelong and open-ended learning of new skills and new knowledge in embodied machines.
- diagnosis
- Concerned with the development of algorithms and techniques that are able to determine whether the behaviour of a system is correct. If the system is not functioning correctly, the algorithm should be able to determine, as accurately as possible, which part of the system is failing, and which kind of fault it is facing. The computation is based on observations, which provide information on the current behaviour.
- dialogue system
- A computer system intended to converse with a human with a coherent structure. Dialogue systems have employed text, speech, graphics, haptics, gestures, and other modes for communication on both the input and output channel.
- dimensionality reduction
- The process of reducing the number of random variables under consideration[154] by obtaining a set of principal variables. It can be divided into feature selection and feature extraction.[155]
- discrete system
- Any system with a countable number of states. Discrete systems may be contrasted with continuous systems, which may also be called analog systems. A final discrete system is often modeled with a directed graph and is analyzed for correctness and complexity according to computational theory. Because discrete systems have a countable number of states, they may be described in precise mathematical models. A computer is a finite state machine that may be viewed as a discrete system. Because computers are often used to model not only other discrete systems but continuous systems as well, methods have been developed to represent real-world continuous systems as discrete systems. One such method involves sampling a continuous signal at discrete time intervals.
- distributed artificial intelligence (DAI)
- A subfield of artificial intelligence research dedicated to the development of distributed solutions for problems. DAI is closely related to and a predecessor of the field of multi-agent systems.[156]
- dynamic epistemic logic (DEL)
- A logical framework dealing with knowledge and information change. Typically, DEL focuses on situations involving multiple agents and studies how their knowledge changes when events occur.
Also dataset.
Also enterprise data warehouse (EDW).
Also theory of choice.
Also deep structured learning or hierarchical learning.
Also epigenetic robotics.
Also conversational agent (CA).
Also dimension reduction.
Also decentralized artificial intelligence.
E
- eager learning
- A learning method in which the system tries to construct a general, input-independent target function during training of the system, as opposed to lazy learning, where generalization beyond the training data is delayed until a query is made to the system.[157]
- Ebert test
- A test which gauges whether a computer-based synthesized voice[158][159] can tell a joke with sufficient skill to cause people to laugh.[160] It was proposed by film critic Roger Ebert at the 2011 TED conference as a challenge to software developers to have a computerized voice master the inflections, delivery, timing, and intonations of a speaking human.[158] The test is similar to the Turing test proposed by Alan Turing in 1950 as a way to gauge a computer's ability to exhibit intelligent behavior by generating performance indistinguishable from a human being.[161]
- echo state network (ESN)
- A recurrent neural network with a sparsely connected hidden layer (with typically 1% connectivity). The connectivity and weights of hidden neurons are fixed and randomly assigned. The weights of output neurons can be learned so that the network can (re)produce specific temporal patterns. The main interest of this network is that although its behaviour is non-linear, the only weights that are modified during training are for the synapses that connect the hidden neurons to output neurons. Thus, the error function is quadratic with respect to the parameter vector and can be differentiated easily to a linear system.[162][163]
- embodied agent
- An intelligent agent that interacts with the environment through a physical body within that environment. Agents that are represented graphically with a body, for example a human or a cartoon animal, are also called embodied agents, although they have only virtual, not physical, embodiment.[164]
- embodied cognitive science
- An interdisciplinary field of research, the aim of which is to explain the mechanisms underlying intelligent behavior. It comprises three main methodologies: 1) the modeling of psychological and biological systems in a holistic manner that considers the mind and body as a single entity, 2) the formation of a common set of general principles of intelligent behavior, and 3) the experimental use of robotic agents in controlled environments.
- error-driven learning
- A sub-area of machine learning concerned with how an agent ought to take actions in an environment so as to minimize some error feedback. It is a type of reinforcement learning.
- ensemble averaging
- In machine learning, particularly in the creation of artificial neural networks, ensemble averaging is the process of creating multiple models and combining them to produce a desired output, as opposed to creating just one model.
- ethics of artificial intelligence
- The part of the ethics of technology specific to artificial intelligence.
- evolutionary algorithm (EA)
- A subset of evolutionary computation,[165] a generic population-based metaheuristic optimization algorithm. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions (see also loss function). Evolution of the population then takes place after the repeated application of the above operators.
- evolutionary computation
- A family of algorithms for global optimization inspired by biological evolution, and the subfield of artificial intelligence and soft computing studying these algorithms. In technical terms, they are a family of population-based trial and error problem solvers with a metaheuristic or stochastic optimization character.
- evolving classification function (ECF)
- Evolving classifier functions or evolving classifiers are used for classifying and clustering in the field of machine learning and artificial intelligence, typically employed for data stream mining tasks in dynamic and changing environments.
- existential risk
- The hypothesis that substantial progress in artificial general intelligence (AGI) could someday result in human extinction or some other unrecoverable global catastrophe.[166][167][168]
- expert system
- A computer system that emulates the decision-making ability of a human expert.[169] Expert systems are designed to solve complex problems by reasoning through bodies of knowledge, represented mainly as if–then rules rather than through conventional procedural code.[170]
Also interface agent.
F
- fast-and-frugal trees
- A type of classification tree. Fast-and-frugal trees can be used as decision-making tools which operate as lexicographic classifiers, and, if required, associate an action (decision) to each class or category.[171]
- feature extraction
- In machine learning, pattern recognition, and image processing, feature extraction starts from an initial set of measured data and builds derived values (features) intended to be informative and non-redundant, facilitating the subsequent learning and generalization steps, and in some cases leading to better human interpretations.
- feature learning
- In machine learning, feature learning or representation learning[142] is a set of techniques that allows a system to automatically discover the representations needed for feature detection or classification from raw data. This replaces manual feature engineering and allows a machine to both learn the features and use them to perform a specific task.
- feature selection
- In machine learning and statistics, feature selection, also known as variable selection, attribute selection or variable subset selection, is the process of selecting a subset of relevant features (variables, predictors) for use in model construction.
- federated learning
- A type of machine learning that allows for training on multiple devices with decentralized data, thus helping preserve the privacy of individual users and their data.
- first-order logic
- A collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects and allows the use of sentences that contain variables, so that rather than propositions such as Socrates is a man one can have expressions in the form "there exists X such that X is Socrates and X is a man" and there exists is a quantifier while X is a variable.[172] This distinguishes it from propositional logic, which does not use quantifiers or relations.[173]
- fluent
- A condition that can change over time. In logical approaches to reasoning about actions, fluents can be represented in first-order logic by predicates having an argument that depends on time.
- formal language
- A set of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules.
- forward chaining
- One of the two main methods of reasoning when using an inference engine and can be described logically as repeated application of modus ponens. Forward chaining is a popular implementation strategy for expert systems, businesses and production rule systems. The opposite of forward chaining is backward chaining. Forward chaining starts with the available data and uses inference rules to extract more data (from an end user, for example) until a goal is reached. An inference engine using forward chaining searches the inference rules until it finds one where the antecedent (If clause) is known to be true. When such a rule is found, the engine can conclude, or infer, the consequent (Then clause), resulting in the addition of new information to its data.[174]
- frame
- An artificial intelligence data structure used to divide knowledge into substructures by representing "stereotyped situations". Frames are the primary data structure used in artificial intelligence frame language.
- frame language
- A technology used for knowledge representation in artificial intelligence. Frames are stored as ontologies of sets and subsets of the frame concepts. They are similar to class hierarchies in object-oriented languages although their fundamental design goals are different. Frames are focused on explicit and intuitive representation of knowledge whereas objects focus on encapsulation and information hiding. Frames originated in AI research and objects primarily in software engineering. However, in practice the techniques and capabilities of frame and object-oriented languages overlap significantly.
- frame problem
- The problem of finding adequate collections of axioms for a viable description of a robot environment.[175]
- friendly artificial intelligence
- A hypothetical artificial general intelligence (AGI) that would have a positive effect on humanity. It is a part of the ethics of artificial intelligence and is closely related to machine ethics. While machine ethics is concerned with how an artificially intelligent agent should behave, friendly artificial intelligence research is focused on how to practically bring about this behaviour and ensuring it is adequately constrained.
- futures studies
- The study of postulating possible, probable, and preferable futures and the worldviews and myths that underlie them.[176]
- fuzzy control system
- A control system based on fuzzy logic—a mathematical system that analyzes analog input values in terms of logical variables that take on continuous values between 0 and 1, in contrast to classical or digital logic, which operates on discrete values of either 1 or 0 (true or false, respectively).[177][178]
- fuzzy logic
- A simple form for the many-valued logic, in which the truth values of variables may have any degree of "Truthfulness" that can be represented by any real number in the range between 0 (as in Completely False) and 1 (as in Completely True) inclusive. Consequently, It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. In contrast to Boolean logic, where the truth values of variables may have the integer values 0 or 1 only.
- fuzzy rule
- A rule used within fuzzy logic systems to infer an output based on input variables.
- fuzzy set
- In classical set theory, the membership of elements in a set is assessed in binary terms according to a bivalent condition — an element either belongs or does not belong to the set. By contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set; this is described with the aid of a membership function valued in the real unit interval [0, 1]. Fuzzy sets generalize classical sets, since the indicator functions (aka characteristic functions) of classical sets are special cases of the membership functions of fuzzy sets, if the latter only take values 0 or 1.[179] In fuzzy set theory, classical bivalent sets are usually called crisp sets. The fuzzy set theory can be used in a wide range of domains in which information is incomplete or imprecise, such as bioinformatics.[180]
Also known as first-order predicate calculus and predicate logic.
Also forward reasoning.
Also friendly AI or FAI.
G
- game theory
- The study of mathematical models of strategic interaction between rational decision-makers.[181]
- general game playing (GGP)
- General game playing is the design of artificial intelligence programs to be able to run and play more than one game successfully.[182][183][184]
- generative adversarial network (GAN)
- A class of machine learning systems. Two neural networks contest with each other in a zero-sum game framework.
- genetic algorithm (GA)
- A metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover and selection.[185]
- genetic operator
- An operator used in genetic algorithms to guide the algorithm towards a solution to a given problem. There are three main types of operators (mutation, crossover and selection), which must work in conjunction with one another in order for the algorithm to be successful.
- glowworm swarm optimization
- A swarm intelligence optimization algorithm based on the behaviour of glowworms (also known as fireflies or lightning bugs).
- graph (abstract data type)
- In computer science, a graph is an abstract data type that is meant to implement the undirected graph and directed graph concepts from mathematics; specifically, the field of graph theory.
- graph (discrete mathematics)
- In mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices (also called nodes or points) and each of the related pairs of vertices is called an edge (also called an arc or line).[186]
- graph database (GDB)
- A database that uses graph structures for semantic queries with nodes, edges, and properties to represent and store data. A key concept of the system is the graph (or edge or relationship), which directly relates data items in the store a collection of nodes of data and edges representing the relationships between the nodes. The relationships allow data in the store to be linked together directly, and in many cases retrieved with one operation. Graph databases hold the relationships between data as a priority. Querying relationships within a graph database is fast because they are perpetually stored within the database itself. Relationships can be intuitively visualized using graph databases, making it useful for heavily inter-connected data.[187][188]
- graph theory
- The study of graphs, which are mathematical structures used to model pairwise relations between objects.
- graph traversal
- The process of visiting (checking and/or updating) each vertex in a graph. Such traversals are classified by the order in which the vertices are visited. Tree traversal is a special case of graph traversal.
Also graph search.
H
- halting problem
- heuristic
- A technique designed for solving a problem more quickly when classic methods are too slow, or for finding an approximate solution when classic methods fail to find any exact solution. This is achieved by trading optimality, completeness, accuracy, or precision for speed. In a way, it can be considered a shortcut. A heuristic function, also called simply a heuristic, is a function that ranks alternatives in search algorithms at each branching step based on available information to decide which branch to follow. For example, it may approximate the exact solution.[189]
- hidden layer
- An internal layer of neurons in an artificial neural network, not dedicated to input or output.
- hidden unit
- A neuron in a hidden layer in an artificial neural network.
- hyper-heuristic
- A heuristic search method that seeks to automate the process of selecting, combining, generating, or adapting several simpler heuristics (or components of such heuristics) to efficiently solve computational search problems, often by the incorporation of machine learning techniques. One of the motivations for studying hyper-heuristics is to build systems which can handle classes of problems rather than solving just one problem.[190][191][192]
I
- IEEE Computational Intelligence Society
- A professional society of the Institute of Electrical and Electronics Engineers (IEEE) focussing on "the theory, design, application, and development of biologically and linguistically motivated computational paradigms emphasizing neural networks, connectionist systems, genetic algorithms, evolutionary programming, fuzzy systems, and hybrid intelligent systems in which these paradigms are contained".[193]
- incremental learning
- A method of machine learning, in which input data is continuously used to extend the existing model's knowledge i.e. to further train the model. It represents a dynamic technique of supervised learning and unsupervised learning that can be applied when training data becomes available gradually over time or its size is out of system memory limits. Algorithms that can facilitate incremental learning are known as incremental machine learning algorithms.
- inference engine
- A component of the system that applies logical rules to the knowledge base to deduce new information.
- information integration (II)
- The merging of information from heterogeneous sources with differing conceptual, contextual and typographical representations. It is used in data mining and consolidation of data from unstructured or semi-structured resources. Typically, information integration refers to textual representations of knowledge but is sometimes applied to rich-media content. Information fusion, which is a related term, involves the combination of information into a new set of information towards reducing redundancy and uncertainty.[131]
- Information Processing Language (IPL)
- A programming language that includes features intended to help with programs that perform simple problem solving actions such as lists, dynamic memory allocation, data types, recursion, functions as arguments, generators, and cooperative multitasking. IPL invented the concept of list processing, albeit in an assembly-language style.
- intelligence amplification (IA)
- The effective use of information technology in augmenting human intelligence.
- intelligence explosion
- A possible outcome of humanity building artificial general intelligence (AGI). AGI would be capable of recursive self-improvement leading to rapid emergence of ASI (artificial superintelligence), the limits of which are unknown, at the time of the technological singularity.
- intelligent agent (IA)
- An autonomous entity which acts, directing its activity towards achieving goals (i.e. it is an agent), upon an environment using observation through sensors and consequent actuators (i.e. it is intelligent). Intelligent agents may also learn or use knowledge to achieve their goals. They may be very simple or very complex.
- intelligent control
- A class of control techniques that use various artificial intelligence computing approaches like neural networks, Bayesian probability, fuzzy logic, machine learning, reinforcement learning, evolutionary computation and genetic algorithms.[194]
- intelligent personal assistant
- A software agent that can perform tasks or services for an individual based on verbal commands. Sometimes the term "chatbot" is used to refer to virtual assistants generally or specifically accessed by online chat (or in some cases online chat programs that are exclusively for entertainment purposes). Some virtual assistants are able to interpret human speech and respond via synthesized voices. Users can ask their assistants questions, control home automation devices and media playback via voice, and manage other basic tasks such as email, to-do lists, and calendars with verbal commands.[195]
- interpretation
- An assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation. The general study of interpretations of formal languages is called formal semantics.
- intrinsic motivation
- An intelligent agent is intrinsically motivated to act if the information content alone, of the experience resulting from the action, is the motivating factor. Information content in this context is measured in the information theory sense as quantifying uncertainty. A typical intrinsic motivation is to search for unusual (surprising) situations, in contrast to a typical extrinsic motivation such as the search for food. Intrinsically motivated artificial agents display behaviours akin to exploration and curiosity.[196]
- issue tree
- A graphical breakdown of a question that dissects it into its different components vertically and that progresses into details as it reads to the right.[197]: 47 Issue trees are useful in problem solving to identify the root causes of a problem as well as to identify its potential solutions. They also provide a reference point to see how each piece fits into the whole picture of a problem.[198]
Also cognitive augmentation, machine augmented intelligence, and enhanced intelligence.
Also virtual assistant or personal digital assistant.
Also logic tree.
J
- junction tree algorithm
- A method used in machine learning to extract marginalization in general graphs. In essence, it entails performing belief propagation on a modified graph called a junction tree. The graph is called a tree because it branches into different sections of data; nodes of variables are the branches.[199]
Also Clique Tree.
K
- kernel method
- In machine learning, kernel methods are a class of algorithms for pattern analysis, whose best known member is the support vector machine (SVM). The general task of pattern analysis is to find and study general types of relations (for example clusters, rankings, principal components, correlations, classifications) in datasets.
- KL-ONE
- A well-known knowledge representation system in the tradition of semantic networks and frames; that is, it is a frame language. The system is an attempt to overcome semantic indistinctness in semantic network representations and to explicitly represent conceptual information as a structured inheritance network.[200][201][202]
- knowledge acquisition
- The process used to define the rules and ontologies required for a knowledge-based system. The phrase was first used in conjunction with expert systems to describe the initial tasks associated with developing an expert system, namely finding and interviewing domain experts and capturing their knowledge via rules, objects, and frame-based ontologies.
- knowledge-based system (KBS)
- A computer program that reasons and uses a knowledge base to solve complex problems. The term is broad and refers to many different kinds of systems. The one common theme that unites all knowledge based systems is an attempt to represent knowledge explicitly and a reasoning system that allows it to derive new knowledge. Thus, a knowledge-based system has two distinguishing features: a knowledge base and an inference engine.
- knowledge engineering (KE)
- All technical, scientific, and social aspects involved in building, maintaining, and using knowledge-based systems.
- knowledge extraction
- The creation of knowledge from structured (relational databases, XML) and unstructured (text, documents, images) sources. The resulting knowledge needs to be in a machine-readable and machine-interpretable format and must represent knowledge in a manner that facilitates inferencing. Although it is methodically similar to information extraction (NLP) and ETL (data warehouse), the main criterion is that the extraction result goes beyond the creation of structured information or the transformation into a relational schema. It requires either the reuse of existing formal knowledge (reusing identifiers or ontologies) or the generation of a schema based on the source data.
- knowledge Interchange Format (KIF)
- A computer language designed to enable systems to share and re-use information from knowledge-based systems. KIF is similar to frame languages such as KL-ONE and LOOM but unlike such language its primary role is not intended as a framework for the expression or use of knowledge but rather for the interchange of knowledge between systems. The designers of KIF likened it to PostScript. PostScript was not designed primarily as a language to store and manipulate documents but rather as an interchange format for systems and devices to share documents. In the same way KIF is meant to facilitate sharing of knowledge across different systems that use different languages, formalisms, platforms, etc.
- knowledge representation and reasoning (KR² or KR&R)
- The field of artificial intelligence dedicated to representing information about the world in a form that a computer system can utilize to solve complex tasks such as diagnosing a medical condition or having a dialog in a natural language. Knowledge representation incorporates findings from psychology[203] about how humans solve problems and represent knowledge in order to design formalisms that will make complex systems easier to design and build. Knowledge representation and reasoning also incorporates findings from logic to automate various kinds of reasoning, such as the application of rules or the relations of sets and subsets.[204] Examples of knowledge representation formalisms include semantic nets, systems architecture, frames, rules, and ontologies. Examples of automated reasoning engines include inference engines, theorem provers, and classifiers.
L
- lazy learning
- In machine learning, lazy learning is a learning method in which generalization of the training data is, in theory, delayed until a query is made to the system, as opposed to in eager learning, where the system tries to generalize the training data before receiving queries.
- Lisp (programming language) (LISP)
- A family of programming languages with a long history and a distinctive, fully parenthesized prefix notation.[205]
- logic programming
- A type of programming paradigm which is largely based on formal logic. Any program written in a logic programming language is a set of sentences in logical form, expressing facts and rules about some problem domain. Major logic programming language families include Prolog, answer set programming (ASP), and Datalog.
- long short-term memory (LSTM)
- An artificial recurrent neural network architecture[206] used in the field of deep learning. Unlike standard feedforward neural networks, LSTM has feedback connections that make it a "general purpose computer" (that is, it can compute anything that a Turing machine can).[207] It can not only process single data points (such as images), but also entire sequences of data (such as speech or video).
M
- machine vision (MV)
- The technology and methods used to provide imaging-based automatic inspection and analysis for such applications as automatic inspection, process control, and robot guidance, usually in industry. Machine vision is a term encompassing a large number of technologies, software and hardware products, integrated systems, actions, methods and expertise. Machine vision as a systems engineering discipline can be considered distinct from computer vision, a form of computer science. It attempts to integrate existing technologies in new ways and apply them to solve real world problems. The term is the prevalent one for these functions in industrial automation environments but is also used for these functions in other environments such as security and vehicle guidance.
- Markov chain
- A stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event.[208][209][210]
- Markov decision process (MDP)
- A discrete time stochastic control process. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying optimization problems solved via dynamic programming and reinforcement learning.
- mathematical optimization
- In mathematics, computer science, and operations research, the selection of a best element (with regard to some criterion) from some set of available alternatives.[211]
- machine learning (ML)
- The scientific study of algorithms and statistical models that computer systems use in order to perform a specific task effectively without using explicit instructions, relying on patterns and inference instead.
- machine listening
- A general field of study of algorithms and systems for audio understanding by machine.[212][213]
- machine perception
- The capability of a computer system to interpret data in a manner that is similar to the way humans use their senses to relate to the world around them.[214][215][216]
- mechanism design
- A field in economics and game theory that takes an engineering approach to designing economic mechanisms or incentives, toward desired objectives, in strategic settings, where players act rationally. Because it starts at the end of the game, then goes backwards, it is also called reverse game theory. It has broad applications, from economics and politics (markets, auctions, voting procedures) to networked-systems (internet interdomain routing, sponsored search auctions).
- mechatronics
- A multidisciplinary branch of engineering that focuses on the engineering of both electrical and mechanical systems, and also includes a combination of robotics, electronics, computer, telecommunications, systems, control, and product engineering.[217][218]
- metabolic network reconstruction and simulation
- Allows for an in-depth insight into the molecular mechanisms of a particular organism. In particular, these models correlate the genome with molecular physiology.[219]
- metaheuristic
- In computer science and mathematical optimization, a metaheuristic is a higher-level procedure or heuristic designed to find, generate, or select a heuristic (partial search algorithm) that may provide a sufficiently good solution to an optimization problem, especially with incomplete or imperfect information or limited computation capacity.[220][221] Metaheuristics sample a set of solutions which is too large to be completely sampled.
- model checking
- In computer science, model checking or property checking is, for a given model of a system, exhaustively and automatically checking whether this model meets a given specification. Typically, one has hardware or software systems in mind, whereas the specification contains safety requirements such as the absence of deadlocks and similar critical states that can cause the system to crash. Model checking is a technique for automatically verifying correctness properties of finite-state systems.
- modus ponens
- In propositional logic, modus ponens is a rule of inference.[222] It can be summarized as "P implies Q and P is asserted to be true, therefore Q must be true."
- modus tollens
- In propositional logic, modus tollens is a valid argument form and a rule of inference. It is an application of the general truth that if a statement is true, then so is its contrapositive. The inference rule modus tollens asserts that the inference from P implies Q to the negation of Q implies the negation of P is valid.
- Monte Carlo tree search
- In computer science, Monte Carlo tree search (MCTS) is a heuristic search algorithm for some kinds of decision processes.
- multi-agent system (MAS)
- A computerized system composed of multiple interacting intelligent agents. Multi-agent systems can solve problems that are difficult or impossible for an individual agent or a monolithic system to solve. Intelligence may include methodic, functional, procedural approaches, algorithmic search or reinforcement learning.
- multi-swarm optimization
- A variant of particle swarm optimization (PSO) based on the use of multiple sub-swarms instead of one (standard) swarm. The general approach in multi-swarm optimization is that each sub-swarm focuses on a specific region while a specific diversification method decides where and when to launch the sub-swarms. The multi-swarm framework is especially fitted for the optimization on multi-modal problems, where multiple (local) optima exist.
- mutation
- A genetic operator used to maintain genetic diversity from one generation of a population of genetic algorithm chromosomes to the next. It is analogous to biological mutation. Mutation alters one or more gene values in a chromosome from its initial state. In mutation, the solution may change entirely from the previous solution. Hence GA can come to a better solution by using mutation. Mutation occurs during evolution according to a user-definable mutation probability. This probability should be set low. If it is set too high, the search will turn into a primitive random search.
- Mycin
- An early backward chaining expert system that used artificial intelligence to identify bacteria causing severe infections, such as bacteremia and meningitis, and to recommend antibiotics, with the dosage adjusted for patient's body weight – the name derived from the antibiotics themselves, as many antibiotics have the suffix "-mycin". The MYCIN system was also used for the diagnosis of blood clotting diseases.
Also mathematical programming.
Also computer audition (CA).
Also mechatronic engineering.
Also self-organized system.
N
- naive Bayes classifier
- In machine learning, naive Bayes classifiers are a family of simple probabilistic classifiers based on applying Bayes' theorem with strong (naive) independence assumptions between the features.
- naive semantics
- An approach used in computer science for representing basic knowledge about a specific domain, and has been used in applications such as the representation of the meaning of natural language sentences in artificial intelligence applications. In a general setting the term has been used to refer to the use of a limited store of generally understood knowledge about a specific domain in the world, and has been applied to fields such as the knowledge based design of data schemas.[223]
- name binding
- In programming languages, name binding is the association of entities (data and/or code) with identifiers.[224] An identifier bound to an object is said to reference that object. Machine languages
have no built-in notion of identifiers, but name-object bindings as a
service and notation for the programmer is implemented by programming
languages. Binding is intimately connected with scoping, as scope determines which names bind to which objects – at which locations in the program code (lexically) and in which one of the possible execution paths (temporally). Use of an identifier
idin a context that establishes a binding foridis called a binding (or defining) occurrence. In all other occurrences (e.g., in expressions, assignments, and subprogram calls), an identifier stands for what it is bound to; such occurrences are called applied occurrences. - named-entity recognition (NER)
- A subtask of information extraction that seeks to locate and classify named entity mentions in unstructured text into pre-defined categories such as the person names, organizations, locations, medical codes, time expressions, quantities, monetary values, percentages, etc.
- named graph
- A key concept of Semantic Web architecture in which a set of Resource Description Framework statements (a graph) are identified using a URI,[225] allowing descriptions to be made of that set of statements such as context, provenance information or other such metadata. Named graphs are a simple extension of the RDF data model[226] through which graphs can be created but the model lacks an effective means of distinguishing between them once published on the Web at large.
- natural language generation (NLG)
- A software process that transforms structured data into plain-English content. It can be used to produce long-form content for organizations to automate custom reports, as well as produce custom content for a web or mobile application. It can also be used to generate short blurbs of text in interactive conversations (a chatbot) which might even be read out loud by a text-to-speech system.
- natural language processing (NLP)
- A subfield of computer science, information engineering, and artificial intelligence concerned with the interactions between computers and human (natural) languages, in particular how to program computers to process and analyze large amounts of natural language data.
- natural language programming
- An ontology-assisted way of programming in terms of natural-language sentences, e.g. English.[227]
- network motif
- All networks, including biological networks, social networks, technological networks (e.g., computer networks and electrical circuits) and more, can be represented as graphs, which include a wide variety of subgraphs. One important local property of networks are so-called network motifs, which are defined as recurrent and statistically significant sub-graphs or patterns.
- neural machine translation (NMT)
- An approach to machine translation that uses a large artificial neural network to predict the likelihood of a sequence of words, typically modeling entire sentences in a single integrated model.
- neural Turing machine (NTM)
- A recurrent neural network model. NTMs combine the fuzzy pattern matching capabilities of neural networks with the algorithmic power of programmable computers. An NTM has a neural network controller coupled to external memory resources, which it interacts with through attentional mechanisms. The memory interactions are differentiable end-to-end, making it possible to optimize them using gradient descent.[228] An NTM with a long short-term memory (LSTM) network controller can infer simple algorithms such as copying, sorting, and associative recall from examples alone.[229]
- neuro-fuzzy
- Combinations of artificial neural networks and fuzzy logic.
- neurocybernetics
- A direct communication pathway between an enhanced or wired brain and an external device. BCI differs from neuromodulation in that it allows for bidirectional information flow. BCIs are often directed at researching, mapping, assisting, augmenting, or repairing human cognitive or sensory-motor functions.[230]
- neuromorphic engineering
- A concept describing the use of very-large-scale integration (VLSI) systems containing electronic analog circuits to mimic neuro-biological architectures present in the nervous system.[231] In recent times, the term neuromorphic has been used to describe analog, digital, mixed-mode analog/digital VLSI, and software systems that implement models of neural systems (for perception, motor control, or multisensory integration). The implementation of neuromorphic computing on the hardware level can be realized by oxide-based memristors,[232] spintronic memories,[233] threshold switches, and transistors.[234][235][236][237]
- node
- A basic unit of a data structure, such as a linked list or tree data structure. Nodes contain data and also may link to other nodes. Links between nodes are often implemented by pointers.
- nondeterministic algorithm
- An algorithm that, even for the same input, can exhibit different behaviors on different runs, as opposed to a deterministic algorithm.
- nouvelle AI
- Nouvelle AI differs from classical AI by aiming to produce robots with intelligence levels similar to insects. Researchers believe that intelligence can emerge organically from simple behaviors as these intelligences interacted with the "real world", instead of using the constructed worlds which symbolic AIs typically needed to have programmed into them.[238]
- NP
- In computational complexity theory, NP (nondeterministic polynomial time) is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time.[239][Note 1]
- NP-completeness
- In computational complexity theory, a problem is NP-complete when it can be solved by a restricted class of brute force search algorithms and it can be used to simulate any other problem with a similar algorithm. More precisely, each input to the problem should be associated with a set of solutions of polynomial length, whose validity can be tested quickly (in polynomial time[240]), such that the output for any input is "yes" if the solution set is non-empty and "no" if it is empty.
- NP-hardness
- In computational complexity theory, the defining property of a class of problems that are, informally, "at least as hard as the hardest problems in NP". A simple example of an NP-hard problem is the subset sum problem.
Also entity identification, entity chunking, and entity extraction.
Also brain–computer interface (BCI), neural-control interface (NCI), mind-machine interface (MMI), direct neural interface (DNI), or brain–machine interface (BMI).
Also neuromorphic computing.
Also non-deterministic polynomial-time hardness.
O
- Occam's razor
- The problem-solving principle that states that when presented with competing hypotheses that make the same predictions, one should select the solution with the fewest assumptions;[241] the principle is not meant to filter out hypotheses that make different predictions. The idea is attributed to the English Franciscan friar William of Ockham (c. 1287–1347), a scholastic philosopher and theologian.
- offline learning
- online machine learning
- A method of machine learning in which data becomes available in a sequential order and is used to update the best predictor for future data at each step, as opposed to batch learning techniques which generate the best predictor by learning on the entire training data set at once. Online learning is a common technique used in areas of machine learning where it is computationally infeasible to train over the entire dataset, requiring the need of out-of-core algorithms. It is also used in situations where it is necessary for the algorithm to dynamically adapt to new patterns in the data, or when the data itself is generated as a function of time.
- ontology learning
- The automatic or semi-automatic creation of ontologies, including extracting the corresponding domain's terms and the relationships between the concepts that these terms represent from a corpus of natural language text, and encoding them with an ontology language for easy retrieval.
- OpenAI
- The for-profit corporation OpenAI LP, whose parent organization is the non-profit organization OpenAI Inc[242] that conducts research in the field of artificial intelligence (AI) with the stated aim to promote and develop friendly AI in such a way as to benefit humanity as a whole.
- OpenCog
- A project that aims to build an open-source artificial intelligence framework. OpenCog Prime is an architecture for robot and virtual embodied cognition that defines a set of interacting components designed to give rise to human-equivalent artificial general intelligence (AGI) as an emergent phenomenon of the whole system.[243]
- Open Mind Common Sense
- An artificial intelligence project based at the Massachusetts Institute of Technology (MIT) Media Lab whose goal is to build and utilize a large commonsense knowledge base from the contributions of many thousands of people across the Web.
- open-source software (OSS)
- A type of computer software in which source code is released under a license in which the copyright holder grants users the rights to study, change, and distribute the software to anyone and for any purpose.[244] Open-source software may be developed in a collaborative public manner. Open-source software is a prominent example of open collaboration.[245]
Also Ockham's razor or Ocham's razor.
Also ontology extraction, ontology generation, or ontology acquisition.
P
- partial order reduction
- A technique for reducing the size of the state-space to be searched by a model checking or automated planning and scheduling algorithm. It exploits the commutativity of concurrently executed transitions, which result in the same state when executed in different orders.
- partially observable Markov decision process (POMDP)
- A generalization of a Markov decision process (MDP). A POMDP models an agent decision process in which it is assumed that the system dynamics are determined by an MDP, but the agent cannot directly observe the underlying state. Instead, it must maintain a probability distribution over the set of possible states, based on a set of observations and observation probabilities, and the underlying MDP.
- particle swarm optimization (PSO)
- A computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formulae over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.
- pathfinding
- The plotting, by a computer application, of the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra's algorithm for finding a shortest path on a weighted graph.
- pattern recognition
- Concerned with the automatic discovery of regularities in data through the use of computer algorithms and with the use of these regularities to take actions such as classifying the data into different categories.[246]
- predicate logic
- A collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects and allows the use of sentences that contain variables, so that rather than propositions such as Socrates is a man one can have expressions in the form "there exists x such that x is Socrates and x is a man" and there exists is a quantifier while x is a variable.[172] This distinguishes it from propositional logic, which does not use quantifiers or relations;[247] in this sense, propositional logic is the foundation of first-order logic.
- predictive analytics
- A variety of statistical techniques from data mining, predictive modelling, and machine learning, that analyze current and historical facts to make predictions about future or otherwise unknown events.[248][249]
- principal component analysis (PCA)
- A statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables (entities each of which takes on various numerical values) into a set of values of linearly uncorrelated variables called principal components. This transformation is defined in such a way that the first principal component has the largest possible variance (that is, accounts for as much of the variability in the data as possible), and each succeeding component, in turn, has the highest variance possible under the constraint that it is orthogonal to the preceding components. The resulting vectors (each being a linear combination of the variables and containing n observations) are an uncorrelated orthogonal basis set. PCA is sensitive to the relative scaling of the original variables.
- principle of rationality
- A principle coined by Karl R. Popper in his Harvard Lecture of 1963, and published in his book Myth of Framework.[250] It is related to what he called the 'logic of the situation' in an Economica article of 1944/1945, published later in his book The Poverty of Historicism.[251] According to Popper's rationality principle, agents act in the most adequate way according to the objective situation. It is an idealized conception of human behavior which he used to drive his model of situational analysis.
- probabilistic programming (PP)
- A programming paradigm in which probabilistic models are specified and inference for these models is performed automatically.[252] It represents an attempt to unify probabilistic modeling and traditional general-purpose programming in order to make the former easier and more widely applicable.[253][254] It can be used to create systems that help make decisions in the face of uncertainty. Programming languages used for probabilistic programming are referred to as "Probabilistic programming languages" (PPLs).
- production system
- programming language
- A formal language, which comprises a set of instructions that produce various kinds of output. Programming languages are used in computer programming to implement algorithms.
- Prolog
- A logic programming language associated with artificial intelligence and computational linguistics.[255][256][257] Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is intended primarily as a declarative programming language: the program logic is expressed in terms of relations, represented as facts and rules. A computation is initiated by running a query over these relations.[258]
- propositional calculus
- A branch of logic which deals with propositions (which can be true or false) and argument flow. Compound propositions are formed by connecting propositions by logical connectives. The propositions without logical connectives are called atomic propositions. Unlike first-order logic, propositional logic does not deal with non-logical objects, predicates about them, or quantifiers. However, all the machinery of propositional logic is included in first-order logic and higher-order logics. In this sense, propositional logic is the foundation of first-order logic and higher-order logic.
- Python
- An interpreted, high-level, general-purpose programming language created by Guido van Rossum and first released in 1991. Python's design philosophy emphasizes code readability with its notable use of significant whitespace. Its language constructs and object-oriented approach aim to help programmers write clear, logical code for small and large-scale projects.[259]
Also pathing.
Also first-order logic, predicate logic, and first-order predicate calculus.
Also rationality principle.
Also propositional logic, statement logic, sentential calculus, sentential logic, and zeroth-order logic.
Q
- qualification problem
- In philosophy and artificial intelligence (especially knowledge-based systems), the qualification problem is concerned with the impossibility of listing all of the preconditions required for a real-world action to have its intended effect.[260][261] It might be posed as how to deal with the things that prevent me from achieving my intended result. It is strongly connected to, and opposite the ramification side of, the frame problem.[260]
- quantifier
- In logic, quantification specifies the quantity of specimens in the domain of discourse that satisfy an open formula. The two most common quantifiers mean "for all" and "there exists". For example, in arithmetic, quantifiers allow one to say that the natural numbers go on forever, by writing that for all n (where n is a natural number), there is another number (say, the successor of n) which is one bigger than n.
- quantum computing
- The use of quantum-mechanical phenomena such as superposition and entanglement to perform computation. A quantum computer is used to perform such computation, which can be implemented theoretically or physically.[262]: I-5
- query language
- Query languages or data query languages (DQLs) are computer languages used to make queries in databases and information systems. Broadly, query languages can be classified according to whether they are database query languages or information retrieval query languages. The difference is that a database query language attempts to give factual answers to factual questions, while an information retrieval query language attempts to find documents containing information that is relevant to an area of inquiry.
R
- R programming language
- A programming language and free software environment for statistical computing and graphics supported by the R Foundation for Statistical Computing.[263] The R language is widely used among statisticians and data miners for developing statistical software[264] and data analysis.[265]
- radial basis function network
- In the field of mathematical modeling, a radial basis function network is an artificial neural network that uses radial basis functions as activation functions. The output of the network is a linear combination of radial basis functions of the inputs and neuron parameters. Radial basis function networks have many uses, including function approximation, time series prediction, classification, and system control. They were first formulated in a 1988 paper by Broomhead and Lowe, both researchers at the Royal Signals and Radar Establishment.[266][267][268]
- random forest
- An ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time and outputting the class that is the mode of the classes (classification) or mean prediction (regression) of the individual trees.[269][270] Random decision forests correct for decision trees' habit of overfitting to their training set.[271]
- reasoning system
- In information technology a reasoning system is a software system that generates conclusions from available knowledge using logical techniques such as deduction and induction. Reasoning systems play an important role in the implementation of artificial intelligence and knowledge-based systems.
- recurrent neural network (RNN)
- A class of artificial neural networks where connections between nodes form a directed graph along a temporal sequence. This allows it to exhibit temporal dynamic behavior. Unlike feedforward neural networks, RNNs can use their internal state (memory) to process sequences of inputs. This makes them applicable to tasks such as unsegmented, connected handwriting recognition[272] or speech recognition.[273][274]
- region connection calculus
- reinforcement learning (RL)
- An area of machine learning concerned with how software agents ought to take actions in an environment so as to maximize some notion of cumulative reward. Reinforcement learning is one of three basic machine learning paradigms, alongside supervised learning and unsupervised learning. It differs from supervised learning in that labelled input/output pairs need not be presented, and sub-optimal actions need not be explicitly corrected. Instead the focus is finding a balance between exploration (of uncharted territory) and exploitation (of current knowledge).[275]
- reservoir computing
- A framework for computation that may be viewed as an extension of neural networks.[276] Typically an input signal is fed into a fixed (random) dynamical system called a reservoir and the dynamics of the reservoir map the input to a higher dimension. Then a simple readout mechanism is trained to read the state of the reservoir and map it to the desired output. The main benefit is that training is performed only at the readout stage and the reservoir is fixed. Liquid-state machines[277] and echo state networks[278] are two major types of reservoir computing.[279]
- Resource Description Framework (RDF)
- A family of World Wide Web Consortium (W3C) specifications[280] originally designed as a metadata data model. It has come to be used as a general method for conceptual description or modeling of information that is implemented in web resources, using a variety of syntax notations and data serialization formats. It is also used in knowledge management applications.
- restricted Boltzmann machine (RBM)
- A generative stochastic artificial neural network that can learn a probability distribution over its set of inputs.
- Rete algorithm
- A pattern matching algorithm for implementing rule-based systems. The algorithm was developed to efficiently apply many rules or patterns to many objects, or facts, in a knowledge base. It is used to determine which of the system's rules should fire based on its data store, its facts.
- robotics
- An interdisciplinary branch of science and engineering that includes mechanical engineering, electronic engineering, information engineering, computer science, and others. Robotics deals with the design, construction, operation, and use of robots, as well as computer systems for their control, sensory feedback, and information processing.
- rule-based system
- In computer science, a rule-based system is used to store and manipulate knowledge to interpret information in a useful way. It is often used in artificial intelligence applications and research. Normally, the term rule-based system is applied to systems involving human-crafted or curated rule sets. Rule-based systems constructed using automatic rule inference, such as rule-based machine learning, are normally excluded from this system type.
Also random decision forest.
S
- satisfiability
- In mathematical logic, satisfiability and validity are elementary concepts of semantics. A formula is satisfiable if it is possible to find an interpretation (model) that makes the formula true.[281] A formula is valid if all interpretations make the formula true. The opposites of these concepts are unsatisfiability and invalidity, that is, a formula is unsatisfiable if none of the interpretations make the formula true, and invalid if some such interpretation makes the formula false. These four concepts are related to each other in a manner exactly analogous to Aristotle's square of opposition.
- search algorithm
- Any algorithm which solves the search problem, namely, to retrieve information stored within some data structure, or calculated in the search space of a problem domain, either with discrete or continuous values.
- selection
- The stage of a genetic algorithm in which individual genomes are chosen from a population for later breeding (using the crossover operator).
- self-management
- The process by which computer systems manage their own operation without human intervention.
- semantic network
- A knowledge base that represents semantic relations between concepts in a network. This is often used as a form of knowledge representation. It is a directed or undirected graph consisting of vertices, which represent concepts, and edges, which represent semantic relations between concepts,[282] mapping or connecting semantic fields.
- semantic reasoner
- A piece of software able to infer logical consequences from a set of asserted facts or axioms. The notion of a semantic reasoner generalizes that of an inference engine, by providing a richer set of mechanisms to work with. The inference rules are commonly specified by means of an ontology language, and often a description logic language. Many reasoners use first-order predicate logic to perform reasoning; inference commonly proceeds by forward chaining and backward chaining.
- semantic query
- Allows for queries and analytics of associative and contextual nature. Semantic queries enable the retrieval of both explicitly and implicitly derived information based on syntactic, semantic and structural information contained in data. They are designed to deliver precise results (possibly the distinctive selection of one single piece of information) or to answer more fuzzy and wide-open questions through pattern matching and digital reasoning.
- semantics
- In programming language theory, semantics is the field concerned with the rigorous mathematical study of the meaning of programming languages. It does so by evaluating the meaning of syntactically valid strings defined by a specific programming language, showing the computation involved. In such a case that the evaluation would be of syntactically invalid strings, the result would be non-computation. Semantics describes the processes a computer follows when executing a program in that specific language. This can be shown by describing the relationship between the input and output of a program, or an explanation of how the program will be executed on a certain platform, hence creating a model of computation.
- sensor fusion
- The combining of sensory data or data derived from disparate sources such that the resulting information has less uncertainty than would be possible when these sources were used individually.
- separation logic
- An extension of Hoare logic, a way of reasoning about programs. The assertion language of separation logic is a special case of the logic of bunched implications (BI).[283]
- similarity learning
- An area of supervised machine learning in artificial intelligence. It is closely related to regression and classification, but the goal is to learn from a similarity function that measures how similar or related two objects are. It has applications in ranking, in recommendation systems, visual identity tracking, face verification, and speaker verification.
- simulated annealing (SA)
- A probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem.
- situated approach
- In artificial intelligence research, the situated approach builds agents that are designed to behave effectively successfully in their environment. This requires designing AI "from the bottom-up" by focussing on the basic perceptual and motor skills required to survive. The situated approach gives a much lower priority to abstract reasoning or problem-solving skills.
- situation calculus
- A logic formalism designed for representing and reasoning about dynamical domains.
- Selective Linear Definite clause resolution
- The basic inference rule used in logic programming. It is a refinement of resolution, which is both sound and refutation complete for Horn clauses.
- software
- A collection of data or computer instructions that tell the computer how to work. This is in contrast to physical hardware, from which the system is built and actually performs the work. In computer science and software engineering, computer software is all information processed by computer systems, programs and data. Computer software includes computer programs, libraries and related non-executable data, such as online documentation or digital media.
- software engineering
- The application of engineering to the development of software in a systematic method.[284][285][286]
- spatial-temporal reasoning
- An area of artificial intelligence which draws from the fields of computer science, cognitive science, and cognitive psychology. The theoretic goal—on the cognitive side—involves representing and reasoning spatial-temporal knowledge in mind. The applied goal—on the computing side—involves developing high-level control systems of automata for navigating and understanding time and space.
- SPARQL
- An RDF query language—that is, a semantic query language for databases—able to retrieve and manipulate data stored in Resource Description Framework (RDF) format.[287][288]
- speech recognition
- An interdisciplinary subfield of computational linguistics that develops methodologies and technologies that enables the recognition and translation of spoken language into text by computers. It is also known as automatic speech recognition (ASR), computer speech recognition or speech to text (STT). It incorporates knowledge and research in the linguistics, computer science, and electrical engineering fields.
- spiking neural network (SNN)
- An artificial neural network that more closely mimics a natural neural network.[289] In addition to neuronal and synaptic state, SNNs incorporate the concept of time into their Operating Model.
- state
- In information technology and computer science, a program is described as stateful if it is designed to remember preceding events or user interactions;[290] the remembered information is called the state of the system.
- statistical classification
- In machine learning and statistics, classification is the problem of identifying to which of a set of categories (sub-populations) a new observation belongs, on the basis of a training set of data containing observations (or instances) whose category membership is known. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagnosis to a given patient based on observed characteristics of the patient (sex, blood pressure, presence or absence of certain symptoms, etc.). Classification is an example of pattern recognition.
- statistical relational learning (SRL)
- A subdiscipline of artificial intelligence and machine learning that is concerned with domain models that exhibit both uncertainty (which can be dealt with using statistical methods) and complex, relational structure.[291][292] Note that SRL is sometimes called Relational Machine Learning (RML) in the literature. Typically, the knowledge representation formalisms developed in SRL use (a subset of) first-order logic to describe relational properties of a domain in a general manner (universal quantification) and draw upon probabilistic graphical models (such as Bayesian networks or Markov networks) to model the uncertainty; some also build upon the methods of inductive logic programming.
- stochastic optimization (SO)
- Any optimization method that generates and uses random variables. For stochastic problems, the random variables appear in the formulation of the optimization problem itself, which involves random objective functions or random constraints. Stochastic optimization methods also include methods with random iterates. Some stochastic optimization methods use random iterates to solve stochastic problems, combining both meanings of stochastic optimization.[293] Stochastic optimization methods generalize deterministic methods for deterministic problems.
- stochastic semantic analysis
- An approach used in computer science as a semantic component of natural language understanding. Stochastic models generally use the definition of segments of words as basic semantic units for the semantic models, and in some cases involve a two layered approach.[294]
- Stanford Research Institute Problem Solver (STRIPS)
- subject-matter expert
- superintelligence
- A hypothetical agent that possesses intelligence far surpassing that of the brightest and most gifted human minds. Superintelligence may also refer to a property of problem-solving systems (e.g., superintelligent language translators or engineering assistants) whether or not these high-level intellectual competencies are embodied in agents that act within the physical world. A superintelligence may or may not be created by an intelligence explosion and be associated with a technological singularity.
- supervised learning
- The machine learning task of learning a function that maps an input to an output based on example input-output pairs.[295] It infers a function from labeled training data consisting of a set of training examples.[296] In supervised learning, each example is a pair consisting of an input object (typically a vector) and a desired output value (also called the supervisory signal). A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. An optimal scenario will allow for the algorithm to correctly determine the class labels for unseen instances. This requires the learning algorithm to generalize from the training data to unseen situations in a "reasonable" way (see inductive bias).
- support-vector machines
- In machine learning, support-vector machines (SVMs, also support-vector networks[297]) are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis.
- swarm intelligence (SI)
- The collective behavior of decentralized, self-organized systems, either natural or artificial. The expression was introduced in the context of cellular robotic systems.[298]
- symbolic artificial intelligence
- The term for the collection of all methods in artificial intelligence research that are based on high-level "symbolic" (human-readable) representations of problems, logic, and search.
- synthetic intelligence (SI)
- An alternative term for artificial intelligence which emphasizes that the intelligence of machines need not be an imitation or in any way artificial; it can be a genuine form of intelligence.[299][300]
- systems neuroscience
- A subdiscipline of neuroscience and systems biology that studies the structure and function of neural circuits and systems. It is an umbrella term, encompassing a number of areas of study concerned with how nerve cells behave when connected together to form neural pathways, neural circuits, and larger brain networks.
Also frame network.
Also reasoning engine, rules engine, or simply reasoner.
Also simply SLD resolution.
T
- technological singularity
- A hypothetical point in the future when technological growth becomes uncontrollable and irreversible, resulting in unfathomable changes to human civilization.[301][302][303]
- temporal difference learning
- A class of model-free reinforcement learning methods which learn by bootstrapping from the current estimate of the value function. These methods sample from the environment, like Monte Carlo methods, and perform updates based on current estimates, like dynamic programming methods.[304]
- tensor network theory
- A theory of brain function (particularly that of the cerebellum) that provides a mathematical model of the transformation of sensory space-time coordinates into motor coordinates and vice versa by cerebellar neuronal networks. The theory was developed as a geometrization of brain function (especially of the central nervous system) using tensors.[305][306]
- TensorFlow
- A free and open-source software library for dataflow and differentiable programming across a range of tasks. It is a symbolic math library, and is also used for machine learning applications such as neural networks.[307]
- theoretical computer science (TCS)
- A subset of general computer science and mathematics that focuses on more mathematical topics of computing and includes the theory of computation.
- theory of computation
- In theoretical computer science and mathematics, the theory of computation is the branch that deals with how efficiently problems can be solved on a model of computation, using an algorithm. The field is divided into three major branches: automata theory and languages, computability theory, and computational complexity theory, which are linked by the question: "What are the fundamental capabilities and limitations of computers?".[308]
- Thompson sampling
- A heuristic for choosing actions that addresses the exploration-exploitation dilemma in the multi-armed bandit problem. It consists in choosing the action that maximizes the expected reward with respect to a randomly drawn belief.[309][310]
- time complexity
- The computational complexity that describes the amount of time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to differ by at most a constant factor.
- transhumanism
- An international philosophical movement that advocates for the transformation of the human condition by developing and making widely available sophisticated technologies to greatly enhance human intellect and physiology.[311][312]
- transition system
- In theoretical computer science, a transition system is a concept used in the study of computation. It is used to describe the potential behavior of discrete systems. It consists of states and transitions between states, which may be labeled with labels chosen from a set; the same label may appear on more than one transition. If the label set is a singleton, the system is essentially unlabeled, and a simpler definition that omits the labels is possible.
- tree traversal
- A form of graph traversal and refers to the process of visiting (checking and/or updating) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited.
- true quantified Boolean formula
- In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified (or bound), using either existential or universal quantifiers, at the beginning of the sentence. Such a formula is equivalent to either true or false (since there are no free variables). If such a formula evaluates to true, then that formula is in the language TQBF. It is also known as QSAT (Quantified SAT).
- Turing machine
- Turing test
- A test of a machine's ability to exhibit intelligent behaviour equivalent to, or indistinguishable from, that of a human, developed by Alan Turing in 1950. Turing proposed that a human evaluator would judge natural language conversations between a human and a machine designed to generate human-like responses. The evaluator would be aware that one of the two partners in conversation is a machine, and all participants would be separated from one another. The conversation would be limited to a text-only channel such as a computer keyboard and screen so the result would not depend on the machine's ability to render words as speech.[313] If the evaluator cannot reliably tell the machine from the human, the machine is said to have passed the test. The test results do not depend on the machine's ability to give correct answers to questions, only how closely its answers resemble those a human would give.
- type system
- In programming languages, a set of rules that assigns a property called type to the various constructs of a computer program, such as variables, expressions, functions, or modules.[314] These types formalize and enforce the otherwise implicit categories the programmer uses for algebraic data types, data structures, or other components (e.g. "string", "array of float", "function returning boolean"). The main purpose of a type system is to reduce possibilities for bugs in computer programs[315] by defining interfaces between different parts of a computer program, and then checking that the parts have been connected in a consistent way. This checking can happen statically (at compile time), dynamically (at run time), or as a combination of static and dynamic checking. Type systems have other purposes as well, such as expressing business rules, enabling certain compiler optimizations, allowing for multiple dispatch, providing a form of documentation, etc.
Also simply the singularity.
Abbreviated H+ or h+.
Also tree search.
U
- unsupervised learning
- A type of self-organized Hebbian learning that helps find previously unknown patterns in data set without pre-existing labels. It is also known as self-organization and allows modeling probability densities of given inputs.[316] It is one of the main three categories of machine learning, along with supervised and reinforcement learning. Semi-supervised learning has also been described and is a hybridization of supervised and unsupervised techniques.
V
- vision processing unit (VPU)
- A type of microprocessor designed to accelerate machine vision tasks.[317][318]Value-alignment complete – Analogous to an AI-complete problem, a value-alignment complete problem is a problem where the AI control problem needs to be fully solved to solve it.[citation needed]
W
- Watson
- A question-answering computer system capable of answering questions posed in natural language,[319] developed in IBM's DeepQA project by a research team led by principal investigator David Ferrucci.[320] Watson was named after IBM's first CEO, industrialist Thomas J. Watson.[321][322]
- weak AI
- Artificial intelligence that is focused on one narrow task.[323][324][325]
- World Wide Web Consortium (W3C)
- The main international standards organization for the World Wide Web (abbreviated WWW or W3).
Also narrow AI.
See also
References
- Poole, Mackworth & Goebel 1998, p. 1, which provides the version that is used in this article. Note that they use the term "computational intelligence" as a synonym for artificial intelligence.
- Russell & Norvig (2003) (who prefer the term "rational agent") and write "The whole-agent view is now widely accepted in the field" (Russell & Norvig 2003, p. 55).
- Nilsson 1998
- Legg & Hutter 2007.
With the help of his wife, two colleagues and the Alex-equipped MacBook that he uses to generate his computerized voice, famed film critic Roger Ebert delivered the final talk at the TED conference on Friday in Long Beach, California....
Now perhaps, there is the Ebert Test, a way to see if a synthesized voice can deliver humor with the timing to make an audience laugh.... He proposed the Ebert Test as a way to gauge the humanness of a synthesized voice.
Meanwhile, the technology that enables Ebert to "speak" continues to see improvements – for example, adding more realistic inflection for question marks and exclamation points. In a test of that, which Ebert called the "Ebert test" for computerized voices,
He calls it the "Ebert Test," after Turing's AI standard...
A graph is an object consisting of two sets called its vertex set and its edge set.
R is also the name of a popular programming language used by a growing number of data analysts inside corporations and academia. It is becoming their lingua franca...
R is also the name of a popular programming language used by a growing number of data analysts inside corporations and academia. It is becoming their lingua franca...
central areas of the theory of computation: automata, computability, and complexity. (Page 1)
- TechCrunch discusses AI App building regarding Narrow AI. Published 16 Oct 2015. Retrieved 17 Oct 2015. https://techcrunch.com/2015/10/15/machine-learning-its-the-hard-problems-that-are-valuable/
Works cited
- Abran, Alain; Moore, James W.; Bourque, Pierre; Dupuis, Robert; Tripp, Leonard L. (2004). Guide to the Software Engineering Body of Knowledge. IEEE. ISBN 978-0-7695-2330-9.
- Cardelli, Luca (2004). "Type systems" (PDF). In Allen B. Tucker (ed.). CRC Handbook of Computer Science and Engineering (2nd ed.). CRC Press. ISBN 978-1584883609.
- Haugeland, John (1985). Artificial Intelligence: The Very Idea. Cambridge, Mass.: MIT Press. ISBN 978-0-262-08153-5.
- Legg, Shane; Hutter, Marcus (15 June 2007). "A Collection of Definitions of Intelligence". arXiv:0706.3639 [cs.AI].
- Mitchell, Melanie (1996). An Introduction to Genetic Algorithms. Cambridge, MA: MIT Press. ISBN 9780585030944.
- Nilsson, Nils (1998). Artificial Intelligence: A New Synthesis. Morgan Kaufmann. ISBN 978-1-55860-467-4. Archived from the original on 26 July 2020. Retrieved 18 November 2019.
- Pierce, Benjamin C. (2002). Types and Programming Languages. MIT Press. ISBN 978-0-262-16209-8.
- Poole, David; Mackworth, Alan; Goebel, Randy (1998). Computational Intelligence: A Logical Approach. New York: Oxford University Press. ISBN 978-0-19-510270-3. Archived from the original on 26 July 2020. Retrieved 22 August 2020.
- Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, ISBN 0-13-790395-2
- Turing, Alan (October 1950), "Computing Machinery and Intelligence", Mind, LIX (236): 433–460, doi:10.1093/mind/LIX.236.433, ISSN 0026-4423
Notes
- polynomial time refers to how quickly the number of operations needed by an algorithm, relative to the size of the problem, grows. It is therefore a measure of efficiency of an algorithm.









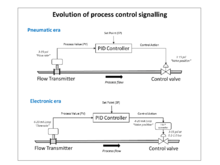
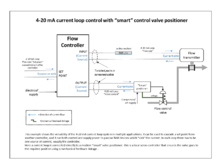

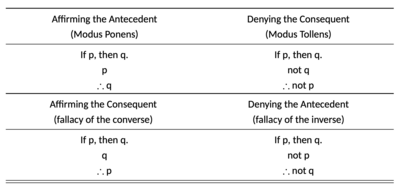





















![R[t]=\left\{a_{n}t^{n}+a_{n-1}t^{n-1}+\dots +a_{1}t+a_{0}\mid n\geq 0,a_{j}\in R\right\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eebb362f161716c1bcb50a5656fbfbc21532a5d)
![R[t]\to S,\quad f\mapsto f(x)](https://wikimedia.org/api/rest_v1/media/math/render/svg/0226daa10f64386e959d3aadf12fb73e82b45082)
![{\displaystyle k[x,y]\to k[t],\,f\mapsto f\left(t^{2},t^{3}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70de42b23023914ef0b1a1e71bcff1fdc76af67b)
![R[t]\to S,\quad f\mapsto {\overline {f}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15eb76de81b0c53d2b82343a721fc4d0cc6f6e29)



![R[t_{1},t_{2},\cdots ]=\varinjlim R[t_{1},t_{2},\cdots ,t_{m}].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c562ae4e64063e5aedc587c8442c596aed80eb0)

![{\displaystyle 0\to M'\left[S^{-1}\right]\to M\left[S^{-1}\right]\to M''\left[S^{-1}\right]\to 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/645fb810cb3b83f73d5257efcb9871cde5ddd25a)








![\operatorname {lambda-drop-op}[L,P,X]=P[L:=\operatorname {drop-params-tran}[\operatorname {sink-test}[L,X]]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/27de3976b9b43faf9c172323272b713186d81dc6)
![\operatorname {lambda-drop-tran}[L,X]=\operatorname {drop-params-tran}[\operatorname {sink-tran}[\operatorname {de-let}[L,X]]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a9af29cdb89755330111813a37d101b105d0d93)
![{\displaystyle {\begin{cases}\operatorname {sink-tran} [(\lambda N.B)\ Y,X]=\operatorname {sink-test} [(\lambda N.\operatorname {sink-tran} [B])\ \operatorname {sink-tran} [Y],X]\\\operatorname {sink-tran} [\lambda N.B,X]=\lambda N.\operatorname {sink-tran} [B,X]\\\operatorname {sink-tran} [M\ N,X]=\operatorname {sink-tran} [M,X]\ \operatorname {sink-tran} [M,X]\\\operatorname {sink-tran} [V,X]=V\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97513c2fecfb9eacba686eff9b7e945795632429)
![{\displaystyle {\begin{cases}E\not \in \operatorname {FV} [G]\land E\not \in \operatorname {FV} [H]\to \operatorname {sink} [(\lambda E.G\ H)\ Y,X]=G\ H\\E\not \in \operatorname {FV} [G]\land E\in \operatorname {FV} [H]\to \operatorname {sink} [(\lambda E.G\ H)\ Y,X]=\operatorname {sink-test} [G\ \operatorname {sink-test} [(\lambda E.H)\ Y,X]]\\E\in \operatorname {FV} [G]\land E\not \in \operatorname {FV} [H]\to \operatorname {sink} [(\lambda E.G\ H)\ Y,X]=(\operatorname {sink-test} [(\lambda E.G)\ Y,X])\ H\\E\in \operatorname {FV} [G]\land E\in \operatorname {FV} [H]\to \operatorname {sink} [(\lambda E.G\ H)\ Y,X]=(\lambda E.G\ H)\ Y\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2049873e2315208fad245e5e430fcc185d786e5)
![V\neq W\to \operatorname {sink}[(\lambda V.\lambda W.E)\ Y,X]=\lambda W.\operatorname {sink-test}[(\lambda V.E)\ Y,X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/04db7c9bce9b7cc6f9392aedb8f74ec20322a386)
![E\neq V\to \operatorname {sink}[(\lambda E.V)\ Y,X]=V](https://wikimedia.org/api/rest_v1/media/math/render/svg/c514513bf5cefbd8c7f3e57ef82453c3d320caa5)
![E=V\to \operatorname {sink}[(\lambda E.V)\ Y,X]=Y](https://wikimedia.org/api/rest_v1/media/math/render/svg/a393d1e4583899566ee0e11224e5d5c9e9bf92e5)
![L\in X\to \operatorname {sink-test}[L,X]=L](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2ed0d8d66482f29a5dbf8f2a0e72f99e6ad102b)
![L\not \in X\to \operatorname {sink-test}[L,X]=\operatorname {sink}[L,X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/008bb1f25d290d88c5079ef9abb796bb6307faa0)


![\operatorname {drop-params-tran}[\lambda f.(\lambda p.(p\ f)\ (p\ f))\ (\lambda f.\lambda x.f\ (x\ x))]](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa67127ffd3481a55d52b254ead36bdd5bf2d8a2)

![\operatorname {drop-params-tran}[L]\equiv (\operatorname {drop-params}[L,D,FV[L],[]])](https://wikimedia.org/api/rest_v1/media/math/render/svg/7159e7b56a1b8f5bd9bb6b77d2d30d7b507467b8)
![\operatorname {build-param-list}[L,D,V,\_]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7705cccf60d29665a881caf7680895ba27b39afa)
![D[g]=[[x,\operatorname {false},\_],[o,\_,p],[y,\_,n]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0a09568d8c330802df4aa1853b329e3c7f36173)
![{\displaystyle {\begin{cases}\operatorname {build-param-lists} [(\lambda N.S)\ L,D,V,R]\equiv \operatorname {build-param-lists} [S,D,V,R]\land \operatorname {build-list} [L,D,V,D[N]]\\\operatorname {build-param-lists} [\lambda N.S,D,V,R]\equiv \operatorname {build-param-lists} [S,D,V,R]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe3fca310614795b43de1fcb0113e22885dd7aae)
![{\displaystyle {\begin{cases}\operatorname {build-list} [\lambda P.B,D,V,[X,\_,\_]::L]\equiv \operatorname {build-list} [B,D,V,L]\\\operatorname {build-list} [B,D,V,[]]\equiv \operatorname {build-param-lists} [B,D,V,\_]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a8d939f9d1309cfafc0ae13a9ecc5fee8aeb4eb)
![\operatorname {build-param-lists}[N,D,V,D[N]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/b23041cdcb8a8157801202a20ee90032721144af)
![{\displaystyle \operatorname {build-param-lists} [E\ P,D,V,R]\equiv \operatorname {build-param-lists} [E,D,V,T]\land \operatorname {build-param-lists} [P,D,V,K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ada884dd8d7c6fef85f5aaa7f34dec35c65b1e1)
![{\displaystyle \land T=[F,S,A]::R\land (S\implies (\operatorname {equate} [A,P]\land V[F]=A))\land D[F]=K}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9db5ac4c7e6d52eda80d5f35ce7c20de390f32ab)
![{\displaystyle {\begin{cases}\operatorname {equate} [A,N]\equiv A=N\lor (\operatorname {def} [V[N]]\land A=V[N])&{\text{if }}N{\text{ is a variable.}}\\\operatorname {equate} [A,E]\equiv A=E&{\text{otherwise.}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/362ae7798b92be1ea6ce821106ecb06a88806aa5)
![\operatorname {ask}[S]\equiv S\in \{X:X=S\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2182d11819218934dde6797fb27fae7e90765a89)
![\operatorname {def}[F]\equiv |\{X:X=F\}|](https://wikimedia.org/api/rest_v1/media/math/render/svg/435272b0981b4a5a8349725b4108adf7ba9fd13f)
![{\displaystyle \operatorname {build-param-list} [\operatorname {let} V:E\operatorname {in} L,D,V,\_]\equiv \operatorname {build-param-list} [E,D,V,\_]\land \operatorname {build-param-list} [L,D,V,\_]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0df3ab20a70b95844dd32192ccd7460f9032c79)
![{\displaystyle \operatorname {build-param-lists} [E\land F,D,V,\_]\equiv \operatorname {build-param-lists} [E,D,V,\_]\land \operatorname {build-param-lists} [F,D,V,\_]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/027b8521db6a82f697e9b6c3d90c8fda5a5d5011)
![D[g]=[[x,\operatorname {false},\_],[o,\operatorname {true},p],[y,\operatorname {true},n]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/27f5c0b372250a852802c2279113b4617c5b0b34)

![D[p]=[[q,\_,p],[x,\_,f]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da991103c8d1a0ecdda1808fdfe8c50855bb402)

![\operatorname {drop-params}[(\lambda N.S)\ L,D,V,R]\equiv (\lambda N.\operatorname {drop-params}[S,D,F,R])\ \operatorname {drop-formal}[D[N],L,F]](https://wikimedia.org/api/rest_v1/media/math/render/svg/99aba550f80eeb0680206c6d210784af5086f33a)
![F=FV[(\lambda N.S)\ L]](https://wikimedia.org/api/rest_v1/media/math/render/svg/823a8c75779698f7e8d3bb31433d87ffe41e7f29)
![\operatorname {drop-params}[\lambda N.S,D,V,R]\equiv (\lambda N.\operatorname {drop-params}[S,D,F,R])](https://wikimedia.org/api/rest_v1/media/math/render/svg/e323ea82ded175bec1079f368d89a8c1c5faace9)
![F=FV[\lambda N.S]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd6fc1c379ca519dac82d228b2174aff1c42f8a6)
![\operatorname {drop-params}[N,D,V,D[N]]\equiv N](https://wikimedia.org/api/rest_v1/media/math/render/svg/69aee36ec7d514017ed0614d3220339f024f5a04)
![{\displaystyle (\operatorname {def} [F]\land \operatorname {ask} [S]\land FV[A]\subset V)\to \operatorname {drop-params} [E\ P,D,V,R]\equiv \operatorname {drop-params} [E,D,V,[F,S,A]::R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c6dec4e775ccfd57eb9cc96ec7c39261e6c1e9)
![{\displaystyle \neg (\operatorname {def} [F]\land \operatorname {ask} [S]\land FV[A]\subset V)\to \operatorname {drop-params} [E\ P,D,V,R]\equiv \operatorname {drop-params} [E,D,V,[F,S,A]::R]\ \operatorname {drop-params} [P,D,V,\_]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6820b50410d5cd2dac84a803212b9ab4be839b5)
![\operatorname {drop-params}[\operatorname {let}V:E\operatorname {in}L]\equiv \operatorname {let}V:\operatorname {drop-params}[E,D,FV[E],[]]\operatorname {in}\operatorname {drop-params}[L,D,FV[L],[]]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e317339f316247242bd7581321e7596cb54ce7bf)
![{\displaystyle \operatorname {drop-params} [E\land F,D,V,\_]\equiv \operatorname {drop-params} [E,D,V,\_]\land \operatorname {drop-params} [F,D,V,\_]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e363abba3dd6d7dc20ba91036a9dd6a88145165f)
![{\displaystyle (\operatorname {ask} [S]\land FV[A]\subset V)\to \operatorname {drop-formal} [[F,S,A]::Z,\lambda F.Y,V]\equiv \operatorname {drop-formal} [[F,S,A]::Z,Y[F:=A],L]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a6c960f47a989fd6137a31cef8c44d56d69f3b0)
![{\displaystyle \neg (\operatorname {ask} [S]\land FV[A]\subset V)\to \operatorname {drop-formal} [[F,S,A]::Z,\lambda F.Y,V]\equiv \lambda F.\operatorname {drop-formal} [[F,S,A]::Z,Y,V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94cdd9a6017b3540edf73ca993c1adf3a517ce78)
![\operatorname {drop-formal}[Z,Y,V]\equiv Y](https://wikimedia.org/api/rest_v1/media/math/render/svg/854482d904bbd4418f04a70213ea6dcac7b58174)









