The Einstein–Podolsky–Rosen paradox (EPR paradox) is a thought experiment proposed by physicists Albert Einstein, Boris Podolsky and Nathan Rosen (EPR), with which they argued that the description of physical reality provided by quantum mechanics was incomplete.[1] In a 1935 paper titled "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?", they argued for the existence of "elements of reality" that were not part of quantum theory, and speculated that it should be possible to construct a theory containing them. Resolutions of the paradox have important implications for the interpretation of quantum mechanics.
The thought experiment involves a pair of particles prepared in an entangled state (note that this terminology was invented only later). Einstein, Podolsky, and Rosen pointed out that, in this state, if the position of the first particle were measured, the result of measuring the position of the second particle could be predicted. If instead the momentum of the first particle were measured, then the result of measuring the momentum of the second particle could be predicted. They argued that no action taken on the first particle could instantaneously affect the other, since this would involve information being transmitted faster than light, which is forbidden by the theory of relativity. They invoked a principle, later known as the "EPR criterion of reality", positing that, "If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of reality corresponding to that quantity". From this, they inferred that the second particle must have a definite value of position and of momentum prior to either being measured. This contradicted the view associated with Niels Bohr and Werner Heisenberg, according to which a quantum particle does not have a definite value of a property like momentum until the measurement takes place.
Locality has several different meanings in physics. EPR describe the principle of locality as asserting that physical processes occurring at one place should have no immediate effect on the elements of reality at another location. At first sight, this appears to be a reasonable assumption to make, as it seems to be a consequence of special relativity, which states that energy can never be transmitted faster than the speed of light without violating causality;[20]: 427–428 [30] however, it turns out that the usual rules for combining quantum mechanical and classical descriptions violate EPR's principle of locality without violating special relativity or causality.[20]: 427–428 [30] Causality is preserved because there is no way for Alice to transmit messages (i.e., information) to Bob by manipulating her measurement axis. Whichever axis she uses, she has a 50% probability of obtaining "+" and 50% probability of obtaining "−", completely at random; according to quantum mechanics, it is fundamentally impossible for her to influence what result she gets. Furthermore, Bob is only able to perform his measurement once: there is a fundamental property of quantum mechanics, the no-cloning theorem, which makes it impossible for him to make an arbitrary number of copies of the electron he receives, perform a spin measurement on each, and look at the statistical distribution of the results. Therefore, in the one measurement he is allowed to make, there is a 50% probability of getting "+" and 50% of getting "−", regardless of whether or not his axis is aligned with Alice's.
As a summary, the results of the EPR thought experiment do not contradict the predictions of special relativity. Neither the EPR paradox nor any quantum experiment demonstrates that superluminal signaling is possible; however, the principle of locality appeals powerfully to physical intuition, and Einstein, Podolsky and Rosen were unwilling to abandon it. Einstein derided the quantum mechanical predictions as "spooky action at a distance".[b] The conclusion they drew was that quantum mechanics is not a complete theory.[32]
See also[edit]
Bohr-Einstein debates: The argument of EPR
CHSH Bell test
Coherence
Correlation does not imply causation
ER=EPR
GHZ experiment
Measurement problem
Philosophy of information
Philosophy of physics
Popper's experiment
Superdeterminism
Quantum entanglement
Quantum information
Quantum pseudo-telepathy
Quantum teleportation
Quantum Zeno effect
Synchronicity
Ward's probability amplitude
https://en.wikipedia.org/wiki/EPR_paradox#Paradox
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation.[1][2][3] It is a statement that, despite apparently valid reasoning from true premises, leads to a seemingly self-contradictory or a logically unacceptable conclusion.[4][5]A paradox usually involves contradictory-yet-interrelated elements that exist simultaneously and persist over time.[6][7][8]
In logic, many paradoxes exist that are known to be invalid arguments, yet are nevertheless valuable in promoting critical thinking,[9] while other paradoxes have revealed errors in definitions that were assumed to be rigorous, and have caused axioms of mathematics and logic to be re-examined.[1] One example is Russell's paradox, which questions whether a "list of all lists that do not contain themselves" would include itself, and showed that attempts to found set theory on the identification of sets with properties or predicates were flawed.[10][11] Others, such as Curry's paradox, cannot be easily resolved by making foundational changes in a logical system.[12]
Examples outside logic include the ship of Theseus from philosophy, a paradox that questions whether a ship repaired over time by replacing each and all of its wooden parts, one at a time, would remain the same ship.[13] Paradoxes can also take the form of images or other media. For example, M.C. Escher featured perspective-based paradoxes in many of his drawings, with walls that are regarded as floors from other points of view, and staircases that appear to climb endlessly.[14]
In common usage, the word "paradox" often refers to statements that are ironic or unexpected, such as "the paradox that standing is more tiring than walking".[15]
Common themes in paradoxes include self-reference, infinite regress, circular definitions, and confusion or equivocation between different levels of abstraction.
Patrick Hughes outlines three laws of the paradox:[16]
- Self-reference
- An example is the statement "This statement is false", a form of the liar paradox. The statement is referring to itself. Another example of self-reference is the question of whether the barber shaves himself in the barber paradox. Yet another example involves the question "Is the answer to this question 'No'?"
- Contradiction
- "This statement is false"; the statement cannot be false and true at the same time. Another example of contradiction is if a man talking to a genie wishes that wishes couldn't come true. This contradicts itself because if the genie grants his wish, he did not grant his wish, and if he refuses to grant his wish, then he did indeed grant his wish, therefore making it impossible either to grant or not grant his wish without leading to a contradiction.
- Vicious circularity, or infinite regress
- "This statement is false"; if the statement is true, then the statement is false, thereby making the statement true. Another example of vicious circularity is the following group of statements:
- "The following sentence is true."
- "The previous sentence is false."
Other paradoxes involve false statements and half-truths ("impossible is not in my vocabulary") or rely on a hasty assumption. (A father and his son are in a car crash; the father is killed and the boy is rushed to the hospital. The doctor says, "I can't operate on this boy. He's my son." There is no paradox if the boy's mother is a surgeon.)
Paradoxes that are not based on a hidden error generally occur at the fringes of context or language, and require extending the context or language in order to lose their paradoxical quality. Paradoxes that arise from apparently intelligible uses of language are often of interest to logicians and philosophers. "This sentence is false" is an example of the well-known liar paradox: it is a sentence that cannot be consistently interpreted as either true or false, because if it is known to be false, then it can be inferred that it must be true, and if it is known to be true, then it can be inferred that it must be false. Russell's paradox, which shows that the notion of the set of all those sets that do not contain themselves leads to a contradiction, was instrumental in the development of modern logic and set theory.[10]
Thought-experiments can also yield interesting paradoxes. The grandfather paradox, for example, would arise if a time-traveler were to kill his own grandfather before his mother or father had been conceived, thereby preventing his own birth.[17] This is a specific example of the more general observation of the butterfly effect, or that a time-traveller's interaction with the past—however slight—would entail making changes that would, in turn, change the future in which the time-travel was yet to occur, and would thus change the circumstances of the time-travel itself.
Often a seemingly paradoxical conclusion arises from an inconsistent or inherently contradictory definition of the initial premise. In the case of that apparent paradox of a time-traveler killing his own grandfather, it is the inconsistency of defining the past to which he returns as being somehow different from the one that leads up to the future from which he begins his trip, but also insisting that he must have come to that past from the same future as the one that it leads up to.
Quine's classification[edit]
W. V. O. Quine (1962) distinguished between three classes of paradoxes:[18][19]
According to Quine's classification of paradoxes:
- A veridical paradox produces a result that appears absurd, but is demonstrated to be true nonetheless. The paradox of Frederic's birthday in The Pirates of Penzance establishes the surprising fact that a twenty-one-year-old would have had only five birthdays had he been born on a leap day. Likewise, Arrow's impossibility theorem demonstrates difficulties in mapping voting results to the will of the people. Monty Hall paradox (or equivalently Three Prisoners problem) demonstrates that a decision that has an intuitive fifty–fifty chance is in fact heavily biased towards making a decision that, given the intuitive conclusion, the player would be unlikely to make. In 20th-century science, Hilbert's paradox of the Grand Hotel, Schrödinger's cat, Wigner's friend or Ugly duckling theorem are famously vivid examples of a theory being taken to a logical but paradoxical end.
- A falsidical paradox establishes a result that not only appears false but actually is false, due to a fallacy in the demonstration. The various invalid mathematical proofs (e.g., that 1 = 2) are classic examples of this, often relying on a hidden division by zero. Another example is the inductive form of the horse paradox, which falsely generalises from true specific statements. Zeno's paradoxes are 'falsidical', concluding, for example, that a flying arrow never reaches its target or that a speedy runner cannot catch up to a tortoise with a small head-start. Therefore, falsidical paradoxes can be classified as fallacious arguments.
- A paradox that is in neither class may be an antinomy, which reaches a self-contradictory result by properly applying accepted ways of reasoning. For example, the Grelling–Nelson paradox points out genuine problems in our understanding of the ideas of truth and description.
A fourth kind, which may be alternatively interpreted as a special case of the third kind, has sometimes been described since Quine's work:
- A paradox that is both true and false at the same time and in the same sense is called a dialetheia. In Western logics, it is often assumed, following Aristotle, that no dialetheia exist, but they are sometimes accepted in Eastern traditions (e.g. in the Mohists,[20] the Gongsun Longzi,[21] and in Zen[22]) and in paraconsistent logics. It would be mere equivocation or a matter of degree, for example, to both affirm and deny that "John is here" when John is halfway through the door, but it is self-contradictory simultaneously to affirm and deny the event.
Ramsey's classification[edit]
Frank Ramsey drew a distinction between logical paradoxes and semantical paradoxes, with Russell’s paradox belonging to the former category, and Liar's paradox and Grelling’s paradoxes to the latter.[23] Ramsey introduced the by-now standard distinction between logical and semantical contradictions. While logical contradictions involve mathematical or logical terms, like class, number, and hence show that our logic or mathematics is problematic, semantical contradictions involve, besides purely logical terms, notions like “thought”, “language”, “symbolism”, which, according to Ramsey, are empirical (not formal) terms. Hence these contradictions are due to faulty ideas about thought or language and they properly belong to “epistemology”(semantics). [24]
In philosophy[edit]
A taste for paradox is central to the philosophies of Laozi, Zeno of Elea, Zhuangzi, Heraclitus, Bhartrhari, Meister Eckhart, Hegel, Kierkegaard, Nietzsche, and G.K. Chesterton, among many others. Søren Kierkegaard, for example, writes in the Philosophical Fragments that:
In medicine[edit]
A paradoxical reaction to a drug is the opposite of what one would expect, such as becoming agitated by a sedative or sedated by a stimulant. Some are common and are used regularly in medicine, such as the use of stimulants such as Adderall and Ritalin in the treatment of attention deficit hyperactivity disorder (also known as ADHD), while others are rare and can be dangerous as they are not expected, such as severe agitation from a benzodiazepine.[26]
In the smoker's paradox, cigarette smoking, despite its proven harms, has a surprising inverse correlation with the epidemiological incidence of certain diseases.
See also[edit]
- Animalia Paradoxa – Mythical, magical or otherwise suspect animals mentioned in Systema Naturae
- Antinomy – Real or apparent mutual incompatibility of two laws
- Aporia – State of puzzlement or expression of doubt, in philosophy and rhetoric
- Contradiction – Logical incompatibility between two or more propositions
- Dilemma – Problem requiring a choice between equally undesirable alternatives
- Ethical dilemma
- Eubulides – Ancient Greek philosopher known for paradoxes
- Fallacy – Argument that uses faulty reasoning
- Formal fallacy – Faulty deductive reasoning due to a logical flaw
- Four-valued logic – Any logic with four truth values
- Impossible object – Type of optical illusion
- Category:Mathematical paradoxes
- List of paradoxes – Wikipedia list article
- Mu (negative) – Buddhist term, "not" or "without" or "un-" (negative prefix)
- Oxymoron – figure of speech that entails an ostensible self-contradiction to illustrate a rhetorical point or to reveal a paradox
- Paradox of tolerance – Logical paradox in decision-making theory
- Paradox of value
- Paradoxes of material implication
- Plato's beard – Example of a paradoxical argument
- Revision theory
- Self-refuting ideas
- Syntactic ambiguity – Sentences with structures permitting multiple possible interpretations
- Temporal paradox – Theoretical paradox resulting from time travel
- Twin paradox – Thought experiment in special relativity
- Zeno's paradoxes – Set of philosophical problems
Paradoxes
Philosophical
Analysis Buridan's bridge Dream argument Epicurean Fiction Fitch's knowability Free will Goodman's Hedonism Liberal Meno's Mere addition Moore's Newcomb's Nihilism Omnipotence Preface Rule-following White horse Zeno's
Logical
Self-reference
Barber Berry Bhartrhari's Burali-Forti Court Crocodile Curry's Epimenides Free choice paradox Grelling–Nelson Kleene–Rosser Liar Card No-no Pinocchio Quine's Yablo's Opposite Day Richard's Russell's Socratic Hilbert's Hotel
Vagueness
Theseus' ship List of examples Sorites
Others
Temperature paradox Barbershop Catch-22 Drinker Entailment Lottery Plato's beard Raven Ross's Unexpected hanging "What the Tortoise Said to Achilles" Heat death paradox Olbers' paradox
Economic
Allais Antitrust Arrow information Bertrand Braess's Competition Income and fertility Downs–Thomson Easterlin Edgeworth Ellsberg European Gibson's Giffen good Icarus Jevons Leontief Lerner Lucas Mandeville's Mayfield's Metzler Plenty Productivity Prosperity Scitovsky Service recovery St. Petersburg Thrift Toil Tullock Value
Decision theory
Abilene Apportionment Alabama New states Population Arrow's Buridan's ass Chainstore Condorcet's Decision-making Downs Ellsberg Fenno's Fredkin's Green Hedgehog's Inventor's Kavka's toxin puzzle Morton's fork Navigation Newcomb's Parrondo's Prevention Prisoner's dilemma Tolerance Willpower
List-Class article List Category Category
hidevte
Logic
Outline History
Fields
Computer science Formal semantics (natural language) Inference Philosophy of logic Proof Semantics of logic Syntax
Logics
Classical Informal Critical thinking Reason Mathematical Non-classical Philosophical
Theories
Argumentation Metalogic Metamathematics Set
Foundations
Abduction Analytic and synthetic propositions Contradiction Paradox Antinomy Deduction Deductive closure Definition Description Entailment Linguistic Form Induction Logical truth Name Necessity and sufficiency Premise Probability Reference Statement Substitution Truth Validity
Lists
topics
Mathematical logic Boolean algebra Set theory
other
Logicians Rules of inference Paradoxes Fallacies Logic symbols
Socrates.png Philosophy portal Category WikiProject (talk) changes
show
Authority control Edit this at Wikidata
Categories: ParadoxesConcepts in epistemologyConcepts in logicConcepts in metaphysicsCritical thinkingPhilosophical logicThought
https://en.wikipedia.org/wiki/Paradox
A temporal paradox, time paradox, or time travel paradox is a paradox, an apparent contradiction, or logical contradiction associated with the idea of time and time travel. In physics, temporal paradoxes fall into two broad groups: consistency paradoxes exemplified by the grandfather paradox; and causal loops.[1] Other paradoxes associated with time travel are a variation of the Fermi paradox and paradoxes of free will that stem from causal loops such as Newcomb's paradox.[2]
https://en.wikipedia.org/wiki/Temporal_paradox
The grandfather paradox is a paradox of time travel in which inconsistencies emerge through changing the past.[1] The name comes from the paradox's description: a person travels to the past and kills their own grandfather before the conception of their father or mother, which prevents the time traveller's existence.[2] Despite its title, the grandfather paradox does not exclusively regard the contradiction of killing one's own grandfather to prevent one's birth. Rather, the paradox regards any action that alters the past,[3] since there is a contradiction whenever the past becomes different from the way it was.[4]
https://en.wikipedia.org/wiki/Grandfather_paradox
A causal loop is a theoretical proposition in which, by means of either retrocausality or time travel, a sequence of events (actions, information, objects, people)[1][2] is among the causes of another event, which is in turn among the causes of the first-mentioned event.[3][4] Such causally looped events then exist in spacetime, but their origin cannot be determined.[1][2] A hypothetical example of a causality loop is given of a billiard ball striking its past self: the billiard ball moves in a path towards a time machine, and the future self of the billiard ball emerges from the time machine before its past self enters it, giving its past self a glancing blow, altering the past ball's path and causing it to enter the time machine at an angle that would cause its future self to strike its past self the very glancing blow that altered its path. In this sequence of events, the change in the ball's path is its own cause, which might appear paradoxical.[5]
https://en.wikipedia.org/wiki/Causal_loop#Terminology_in_physics,_philosophy,_and_fiction
A thought experiment is a hypothetical situation in which a hypothesis, theory,[1] or principle is laid out for the purpose of thinking through its consequences.
https://en.wikipedia.org/wiki/Thought_experiment
Syntactic ambiguity, also called structural ambiguity,[1] amphiboly or amphibology, is a situation where a sentence may be interpreted in more than one way due to ambiguous sentence structure.
Syntactic ambiguity arises not from the range of meanings of single words, but from the relationship between the words and clauses of a sentence, and the sentence structure underlying the word order therein. In other words, a sentence is syntactically ambiguous when a reader or listener can reasonably interpret one sentence as having more than one possible structure.
In legal disputes, courts may be asked to interpret the meaning of syntactic ambiguities in statutes or contracts. In some instances, arguments asserting highly unlikely interpretations have been deemed frivolous.[citation needed] A set of possible parse trees for an ambiguous sentence is called a parse forest.[2][3] The process of resolving syntactic ambiguity is called syntactic disambiguation.[4]
Kantian[edit]
Immanuel Kant employs the term "amphiboly" in a sense of his own, as he has done in the case of other philosophical words. He denotes by it a confusion of the notions of the pure understanding with the perceptions of experience, and a consequent ascription to the latter of what belongs only to the former.[18]
Formal semantics (natural language)
Central concepts
Compositionality Denotation Entailment Extension Generalized quantifier Intension Logical form Presupposition Proposition Reference Scope Speech act Syntax–semantics interface Truth conditions
Topics
Areas
Anaphora Ambiguity Binding Conditionals Definiteness Disjunction Evidentiality Focus Indexicality Lexical semantics Modality Negation Propositional attitudes Tense–aspect–mood Quantification Vagueness
Phenomena
Antecedent-contained deletion Cataphora Coercion Conservativity Counterfactuals Cumulativity De dicto and de re De se Deontic modality Discourse relations Donkey anaphora Epistemic modality Faultless disagreement Free choice inferences Givenness Crossover effects Hurford disjunction Inalienable possession Intersective modification Logophoricity Mirativity Modal subordination Negative polarity items Opaque contexts Performatives Privative adjectives Quantificational variability effect Responsive predicate Rising declaratives Scalar implicature Sloppy identity Subsective modification Telicity Temperature paradox Veridicality
Formalism
Formal systems
Alternative semantics Categorial grammar Combinatory categorial grammar Discourse representation theory Dynamic semantics Generative grammar Glue semantics Inquisitive semantics Intensional logic Lambda calculus Mereology Montague grammar Segmented discourse representation theory Situation semantics Supervaluationism Type theory TTR
Concepts
Autonomy of syntax Context set Continuation Conversational scoreboard Existential closure Function application Meaning postulate Monads Possible world Quantifier raising Quantization Question under discussion Squiggle operator Type shifter Universal grinder
See also
Cognitive semantics Computational semantics Distributional semantics Formal grammar Inferentialism Linguistics wars Philosophy of language Pragmatics Semantics of logic
Categories: AmbiguitySyntaxSemantics
https://en.wikipedia.org/wiki/Syntactic_ambiguity
The major unsolved problems[1] in physics are either problematic with regard to theoretically considered scientific data, meaning that existing analysis and theory seem incapable of explaining certain observed phenomenon or experimental results, or problematic with regard to experimental design, meaning that there is a difficulty in creating an experiment to test a proposed theory or investigate a phenomenon in greater detail.
There are still some questions beyond the Standard Model of physics, such as the strong CP problem, neutrino mass, matter–antimatter asymmetry, and the nature of dark matter and dark energy.[2][3] Another problem lies within the mathematical frameworkof the Standard Model itself—the Standard Model is inconsistent with that of general relativity, to the point that one or both theories break down under certain conditions (for example within known spacetime singularities like the Big Bang and the centres of black holes beyond the event horizon).
https://en.wikipedia.org/wiki/List_of_unsolved_problems_in_physics
In physics, hidden-variable theories are proposals to provide explanations of quantum mechanical phenomena through the introduction of unobservable hypothetical entities. The existence of fundamental indeterminacy for some measurements is assumed as part of the mathematical formulation of quantum mechanics; moreover, bounds for indeterminacy can be expressed in a quantitative form by the Heisenberg uncertainty principle. Most hidden-variable theories are attempts at a deterministic description of quantum mechanics, to avoid quantum indeterminacy, but at the expense of requiring the existence of nonlocal interactions.
Albert Einstein objected to the fundamentally probabilistic nature of quantum mechanics,[1]and famously declared "I am convinced God does not play dice".[2][3] Einstein, Podolsky, and Rosen argued that quantum mechanics is an incomplete description of reality.[4][5] Bell's theorem would later suggest that local hidden variables (a way for finding a complete description of reality) of certain types are impossible. A famous non-local theory is the De Broglie–Bohm theory.
https://en.wikipedia.org/wiki/List_of_unsolved_problems_in_physics
An unobservable (also called impalpable) is an entity whose existence, nature, properties, qualities or relations are not directly observable by humans. In philosophy of science, typical examples of "unobservables" are the force of gravity, causation and beliefsor desires.[1]: 7 [2] The distinction between observable and unobservable plays a central role in Immanuel Kant's distinction between noumena and phenomena as well as in John Locke's distinction between primary and secondary qualities. The theory that unobservables posited by scientific theories exist is referred to as scientific realism. It contrasts with instrumentalism, which asserts that we should withhold ontological commitments to unobservables even though it is useful for scientific theories to refer to them. There is considerable disagreement about which objects should be classified as unobservable, for example, whether bacteria studied using microscopes or positrons studied using cloud chambers count as unobservable. Different notions of unobservability have been formulated corresponding to different types of obstacles to their observation.
Metaphysics
Metaphysicians
Parmenides Plato Aristotle Plotinus Duns Scotus Thomas Aquinas Francisco Suárez Nicolas Malebranche René Descartes John Locke David Hume Thomas Reid Immanuel Kant Isaac Newton Arthur Schopenhauer Baruch Spinoza Georg W. F. Hegel George Berkeley Gottfried Wilhelm Leibniz Christian Wolff Bernard Bolzano Hermann Lotze Henri Bergson Friedrich Nietzsche Charles Sanders Peirce Joseph Maréchal Ludwig Wittgenstein Martin Heidegger Alfred N. Whitehead Bertrand Russell G. E. Moore Jean-Paul Sartre Gilbert Ryle Hilary Putnam P. F. Strawson R. G. Collingwood Rudolf Carnap Saul Kripke W. V. O. Quine G. E. M. Anscombe Donald Davidson Michael Dummett D. M. Armstrong David Lewis Alvin Plantinga Héctor-Neri Castañeda Peter van Inwagen Derek Parfit Alexius Meinong Ernst Mally Edward N. Zalta more ...
Theories
Abstract object theory Action theory Anti-realism Determinism Dualism Enactivism Essentialism Existentialism Free will Idealism Libertarianism Liberty Materialism Meaning of life Monism Naturalism Nihilism Phenomenalism Realism Physicalism Platonic idealism Relativism Scientific realism Solipsism Subjectivism Substance theory Truthmaker theory Type theory
Concepts
Abstract object Anima mundi Being Category of being Causality Causal closure Choice Cogito, ergo sum Concept Embodied cognition Essence Existence Experience Hypostatic abstraction Idea Identity Information Insight Intelligence Intention Linguistic modality Matter Meaning Memetics Mental representation Mind Motion Nature Necessity Notion Object Pattern Perception Physical object Principle Property Qualia Quality Reality Relation Soul Subject Substantial form Thought Time Truth Type–token distinction Universal Unobservable Value more ...
Related topics
Axiology Cosmology Epistemology Feminist metaphysics Interpretations of quantum mechanics Mereology Meta- Ontology Philosophy of mind Philosophy of psychology Philosophy of self Philosophy of space and time Teleology
Category Category Socrates.png Philosophy portal
Categories: Concepts in metaphysicsConcepts in epistemology
https://en.wikipedia.org/wiki/Unobservable
Observer, Observable Universe, Empiricism, Causality, Mechanical Physics, etc..
https://en.wikipedia.org/wiki/Observable_universe
https://en.wikipedia.org/wiki/Observer_effect_(physics)
https://en.wikipedia.org/wiki/Observer_(quantum_physics)
Epistemology (/ɪˌpɪstɪˈmɒlədʒi/ (![]() listen); from Greek ἐπιστήμη, epistēmē 'knowledge', and -logy) is the branch of philosophy concerned with knowledge. Epistemologists study the nature, origin, and scope of knowledge, epistemic justification, the rationalityof belief, and various related issues. Epistemology is considered a major subfield of philosophy, along with other major subfields such as ethics, logic, and metaphysics.[1]
listen); from Greek ἐπιστήμη, epistēmē 'knowledge', and -logy) is the branch of philosophy concerned with knowledge. Epistemologists study the nature, origin, and scope of knowledge, epistemic justification, the rationalityof belief, and various related issues. Epistemology is considered a major subfield of philosophy, along with other major subfields such as ethics, logic, and metaphysics.[1]
Debates in epistemology are generally clustered around four core areas:[2][3][4]
- The philosophical analysis of the nature of knowledge and the conditions required for a belief to constitute knowledge, such as truth and justification
- Potential sources of knowledge and justified belief, such as perception, reason, memory, and testimony
- The structure of a body of knowledge or justified belief, including whether all justified beliefs must be derived from justified foundational beliefs or whether justification requires only a coherent set of beliefs
- Philosophical skepticism, which questions the possibility of knowledge, and related problems, such as whether skepticism poses a threat to our ordinary knowledge claims and whether it is possible to refute skeptical arguments
In these debates and others, epistemology aims to answer questions such as "What do we know?", "What does it mean to say that we know something?", "What makes justified beliefs justified?", and "How do we know that we know?".[1][2][5][6][7]
Part of a series on
Epistemology
Category Index Outline
Core concepts
Belief Justification Knowledge Truth
Distinctions
A priori vs. A posteriori Analytic vs. synthetic
Schools of thought
Empiricism Naturalism Pragmatism Rationalism Relativism Skepticism
Topics and views
Certainty Coherentism Contextualism Dogmatism Experience Fallibilism Foundationalism Induction Infallibilism Infinitism Perspectivism Rationality Reason Solipsism
https://en.wikipedia.org/wiki/Epistemology
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities[1] asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, x, and momentum, p, can be predicted from initial conditions.
Such variable pairs are known as complementary variables or canonically conjugate variables; and, depending on interpretation, the uncertainty principle limits to what extent such conjugate properties maintain their approximate meaning, as the mathematical framework of quantum physics does not support the notion of simultaneously well-defined conjugate properties expressed by a single value. The uncertainty principle implies that it is in general not possible to predict the value of a quantity with arbitrary certainty, even if all initial conditions are specified.
Introduced first in 1927 by the German physicist Werner Heisenberg, the uncertainty principle states that the more precisely the position of some particle is determined, the less precisely its momentum can be predicted from initial conditions, and vice versa.[2] The formal inequality relating the standard deviation of position σx and the standard deviation of momentum σp was derived by Earle Hesse Kennard[3] later that year and by Hermann Weyl[4] in 1928:
where ħ is the reduced Planck constant, h/(2π).
Historically, the uncertainty principle has been confused[5][6] with a related effect in physics, called the observer effect, which notes that measurements of certain systems cannot be made without affecting the system, that is, without changing something in a system. Heisenberg utilized such an observer effect at the quantum level (see below) as a physical "explanation" of quantum uncertainty.[7] It has since become clearer, however, that the uncertainty principle is inherent in the properties of all wave-like systems,[8] and that it arises in quantum mechanics simply due to the matter wave nature of all quantum objects. Thus, the uncertainty principle actually states a fundamental property of quantum systems and is not a statement about the observational success of current technology.[9] It must be emphasized that measurement does not mean only a process in which a physicist-observer takes part, but rather any interaction between classical and quantum objects regardless of any observer.[10][note 1][note 2]
Since the uncertainty principle is such a basic result in quantum mechanics, typical experiments in quantum mechanics routinely observe aspects of it. Certain experiments, however, may deliberately test a particular form of the uncertainty principle as part of their main research program. These include, for example, tests of number–phase uncertainty relations in superconducting[12] or quantum optics[13] systems. Applications dependent on the uncertainty principle for their operation include extremely low-noise technology such as that required in gravitational wave interferometers.[14]
https://en.wikipedia.org/wiki/Uncertainty_principle
In physics, the principle of locality states that an object is directly influenced only by its immediate surroundings. A theory that includes the principle of locality is said to be a "local theory". This is an alternative to the older concept of instantaneous "action at a distance". Locality evolved out of the field theories of classical physics. The concept is that for an action at one point to have an influence at another point, something in the space between those points such as a field must mediate the action. To exert an influence, something, such as a wave or particle, must travel through the space between the two points, carrying the influence.
The special theory of relativity limits the speed at which all such influences can travel to the speed of light, . Therefore, the principle of locality implies that an event at one point cannot cause a simultaneous result at another point. An event at point cannot cause a result at point in a time less than , where is the distance between the points and is the speed of light in a vacuum.
In 1935 Albert Einstein, Boris Podolsky and Nathan Rosen in their EPR paradox theorised that quantum mechanics might not be a local theory, because a measurement made on one of a pair of separated but entangled particles causes a simultaneous effect, the collapse of the wave function, in the remote particle (i.e. an effect exceeding the speed of light). But because of the probabilistic nature of wave function collapse, this violation of locality cannot be used to transmit information faster than light. In 1964 John Stewart Bell formulated the "Bell inequality", which, if violated in actual experiments, implies that quantum mechanics violates either local causality or statistical independence, another principle. The second principle is commonly referred to as free will.
Experimental tests of the Bell inequality, beginning with Alain Aspect's 1982 experiments, show that quantum mechanics seems to violate the inequality, so it must violate either locality or statistical independence. However, critics have noted these experiments contained "loopholes", which prevented a definitive answer to this question. This might be partially resolved: in 2015 Dr Ronald Hanson at Delft University performed what has been called the first loophole-free experiment.[1] On the other hand, some loopholes might persist, and may continue to persist to the point of being difficult to test.[2]
https://en.wikipedia.org/wiki/Principle_of_locality
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty.[note 1][1][2] The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%).
These concepts have been given an axiomatic mathematical formalization in probability theory, which is used widely in areas of study such as statistics, mathematics, science, finance, gambling, artificial intelligence, machine learning, computer science, game theory, and philosophy to, for example, draw inferences about the expected frequency of events. Probability theory is also used to describe the underlying mechanics and regularities of complex systems.[3]
https://en.wikipedia.org/wiki/Probability
In common parlance, randomness is the apparent or actual lack of pattern or predictability in events.[1][2] A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual random events are, by definition, unpredictable, but if the probability distribution is known, the frequency of different outcomes over repeated events (or "trials") is predictable.[3][note 1] For example, when throwing two dice, the outcome of any particular roll is unpredictable, but a sum of 7 will tend to occur twice as often as 4. In this view, randomness is not haphazardness; it is a measure of uncertainty of an outcome. Randomness applies to concepts of chance, probability, and information entropy.
The fields of mathematics, probability, and statistics use formal definitions of randomness. In statistics, a random variable is an assignment of a numerical value to each possible outcome of an event space. This association facilitates the identification and the calculation of probabilities of the events. Random variables can appear in random sequences. A random process is a sequence of random variables whose outcomes do not follow a deterministic pattern, but follow an evolution described by probability distributions. These and other constructs are extremely useful in probability theory and the various applications of randomness.
Randomness is most often used in statistics to signify well-defined statistical properties. Monte Carlo methods, which rely on random input (such as from random number generators or pseudorandom number generators), are important techniques in science, particularly in the field of computational science.[4] By analogy, quasi-Monte Carlo methods use quasi-random number generators.
Random selection, when narrowly associated with a simple random sample, is a method of selecting items (often called units) from a population where the probability of choosing a specific item is the proportion of those items in the population. For example, with a bowl containing just 10 red marbles and 90 blue marbles, a random selection mechanism would choose a red marble with probability 1/10. Note that a random selection mechanism that selected 10 marbles from this bowl would not necessarily result in 1 red and 9 blue. In situations where a population consists of items that are distinguishable, a random selection mechanism requires equal probabilities for any item to be chosen. That is, if the selection process is such that each member of a population, say research subjects, has the same probability of being chosen, then we can say the selection process is random.[2]
According to Ramsey theory, pure randomness is impossible, especially for large structures. Mathematician Theodore Motzkin suggested that "while disorder is more probable in general, complete disorder is impossible".[5] Misunderstanding this can lead to numerous conspiracy theories.[6] Cristian S. Calude stated that "given the impossibility of true randomness, the effort is directed towards studying degrees of randomness".[7] It can be proven that there is infinite hierarchy (in terms of quality or strength) of forms of randomness.[7]
https://en.wikipedia.org/wiki/Randomness
Stochastic (from Greek στόχος (stókhos) 'aim, guess'[1]) refers to the property of being well described by a random probability distribution.[1] Although stochasticity and randomness are distinct in that the former refers to a modeling approach and the latter refers to phenomena themselves, these two terms are often used synonymously. Furthermore, in probability theory, the formal concept of a stochastic process is also referred to as a random process.[2][3][4][5][6]
Stochasticity is used in many different fields, including the natural sciences such as biology,[7] chemistry,[8] ecology,[9]neuroscience,[10] and physics,[11] as well as technology and engineering fields such as image processing, signal processing,[12]information theory,[13] computer science,[14] cryptography,[15] and telecommunications.[16] It is also used in finance, due to seemingly random changes in financial markets[17][18][19] as well as in medicine, linguistics, music, media, colour theory, botany, manufacturing, and geomorphology. Stochastic modeling is also used in social science.
https://en.wikipedia.org/wiki/Stochastic
Perception (from the Latin perceptio, meaning gathering or receiving) is the organization, identification, and interpretation of sensory information in order to represent and understand the presented information or environment.[2]
https://en.wikipedia.org/wiki/Perception
Sensation refers to the processing of senses by the sensory system; see also sensation (psychology). Sensation & perception are not to be confused. Strictly speaking sensation is when the info reaches the CNS. E.g.you see a red, spherical object. Perceptions is when you compare it with previously seen objects and you realise it is an apple.
https://en.wikipedia.org/wiki/Sensation
Cognition (/kɒɡˈnɪʃ(ə)n/ (![]() listen)) refers to "the mental action or process of acquiring knowledge and understanding through thought, experience, and the senses".[2]
listen)) refers to "the mental action or process of acquiring knowledge and understanding through thought, experience, and the senses".[2]
https://en.wikipedia.org/wiki/Cognition
Analysis is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it.[1] The technique has been applied in the study of mathematics and logic since before Aristotle (384–322 B.C.), though analysis as a formal concept is a relatively recent development.[2]
https://en.wikipedia.org/wiki/Analysis
Reason is the capacity of consciously applying logic to seek truth and draw conclusions from new or existing information.[1][2] It is closely associated with such characteristically human activities as philosophy, science, language, mathematics, and art, and is normally considered to be a distinguishing ability possessed by humans.[3]Reason is sometimes referred to as rationality.[4]
https://en.wikipedia.org/wiki/Reason
Rationality is the quality or state of being rational – that is, being based on or agreeable to reason.[1][2] Rationality implies the conformity of one's beliefs with one's reasons to believe, and of one's actions with one's reasons for action. "Rationality" has different specialized meanings in philosophy,[3] economics, sociology, psychology, evolutionary biology, game theory and political science.
https://en.wikipedia.org/wiki/Rationality
Reality is the sum or aggregate of all that is real or existent within a system, as opposed to that which is only imaginary. The term is also used to refer to the ontological status of things, indicating their existence.[1] In physical terms, reality is the totality of a system, known and unknown.[2] Philosophical questions about the nature of reality or existence or being are considered under the rubric of ontology, which is a major branch of metaphysics in the Western philosophical tradition. Ontological questions also feature in diverse branches of philosophy, including the philosophy of science, philosophy of religion, philosophy of mathematics, and philosophical logic. These include questions about whether only physical objects are real (i.e., Physicalism), whether reality is fundamentally immaterial (e.g., Idealism), whether hypothetical unobservable entities posited by scientific theories exist, whether God exists, whether numbers and other abstract objects exist, and whether possible worlds exist.
https://en.wikipedia.org/wiki/Reality
In mathematics, a real number is a value of a continuous quantity that can represent a distance along a line(or alternatively, a quantity that can be represented as an infinite decimal expansion). The adjective real in this context was introduced in the 17th century by René Descartes, who distinguished between real and imaginary roots of polynomials. The real numbers include all the rational numbers, such as the integer −5 and the fraction 4/3, and all the irrational numbers, such as √2 (1.41421356..., the square root of 2, an irrational algebraic number). Included within the irrationals are the real transcendental numbers, such as π(3.14159265...).[1] In addition to measuring distance, real numbers can be used to measure quantities such as time, mass, energy, velocity, and many more. The set of real numbers is denoted using the symbol R or [2][3] and is sometimes called "the reals".[4]
https://en.wikipedia.org/wiki/Real_number
Existence is the ability of an entity to interact with physical or mental reality. In philosophy, it refers to the ontological property[1] of being.[2]
Etymology[edit]
The term existence comes from Old French existence, from Medieval Latin existentia/exsistentia.[3]
Context in philosophy[edit]
Materialism holds that the only things that exist are matter and energy, that all things are composed of material, that all actions require energy, and that all phenomena (including consciousness) are the result of the interaction of matter. Dialectical materialismdoes not make a distinction between being and existence, and defines it as the objective reality of various forms of matter.[2]
Idealism holds that the only things that exist are thoughts and ideas, while the material world is secondary.[4][5] In idealism, existence is sometimes contrasted with transcendence, the ability to go beyond the limits of existence.[2] As a form of epistemological idealism, rationalism interprets existence as cognizable and rational, that all things are composed of strings of reasoning, requiring an associated idea of the thing, and all phenomena (including consciousness) are the result of an understanding of the imprint from the noumenal world in which lies beyond the thing-in-itself.
In scholasticism, existence of a thing is not derived from its essence but is determined by the creative volition of God, the dichotomy of existence and essence demonstrates that the dualism of the created universe is only resolvable through God.[2] Empiricismrecognizes existence of singular facts, which are not derivable and which are observable through empirical experience.
The exact definition of existence is one of the most important and fundamental topics of ontology, the philosophical study of the nature of being, existence, or reality in general, as well as of the basic categories of being and their relations. Traditionally listed as a part of the major branch of philosophy known as metaphysics, ontology deals with questions concerning what things or entities exist or can be said to exist, and how such things or entities can be grouped, related within a hierarchy, and subdivided according to similarities and differences.
Anti-realism is the view of idealists who are skeptics about the physical world, maintaining either: (1) that nothing exists outside the mind, or (2) that we would have no access to a mind-independent reality even if it may exist. Realists, in contrast, hold that perceptions or sense data are caused by mind-independent objects. An "anti-realist" who denies that other minds exist (i. e., a solipsist) is different from an "anti-realist" who claims that there is no fact of the matter as to whether or not there are unobservable other minds (i. e., a logical behaviorist).
See also[edit]
- Cogito ergo sum
- Conservation law (physics)
- Existence precedes essence
- Existence theorem
- Existential quantification
- Existentialism
- Human condition
- Religious views on the self
- Solipsism
- Three marks of existence
- Universal quantification
https://en.wikipedia.org/wiki/Existence
In philosophy, potentiality and actuality[1] are a pair of closely connected principles which Aristotle used to analyze motion, causality, ethics, and physiology in his Physics, Metaphysics, Nicomachean Ethics and De Anima.[2]
The concept of potentiality, in this context, generally refers to any "possibility" that a thing can be said to have. Aristotle did not consider all possibilities the same, and emphasized the importance of those that become real of their own accord when conditions are right and nothing stops them.[3] Actuality, in contrast to potentiality, is the motion, change or activity that represents an exercise or fulfillment of a possibility, when a possibility becomes real in the fullest sense.[4]
These concepts, in modified forms, remained very important into the Middle Ages, influencing the development of medieval theologyin several ways. In modern times the dichotomy has gradually lost importance, as understandings of nature and deity have changed. However the terminology has also been adapted to new uses, as is most obvious in words like energy and dynamic. These were words first used in modern physics by the German scientist and philosopher, Gottfried Wilhelm Leibniz. Another more recent example is the highly controversial biological concept of an "entelechy".
Entelecheia in modern philosophy and biology[edit]
As discussed above, terms derived from dunamis and energeia have become parts of modern scientific vocabulary with a very different meaning from Aristotle's. The original meanings are not used by modern philosophers unless they are commenting on classical or medieval philosophy. In contrast, entelecheia, in the form of entelechy is a word used much less in technical senses in recent times.
As mentioned above, the concept had occupied a central position in the metaphysics of Leibniz, and is closely related to his monadin the sense that each sentient entity contains its own entire universe within it. But Leibniz' use of this concept influenced more than just the development of the vocabulary of modern physics. Leibniz was also one of the main inspirations for the important movement in philosophy known as German Idealism, and within this movement and schools influenced by it entelechy may denote a force propelling one to self-fulfillment.
In the biological vitalism of Hans Driesch, living things develop by entelechy, a common purposive and organising field. Leading vitalists like Driesch argued that many of the basic problems of biology cannot be solved by a philosophy in which the organism is simply considered a machine.[52] Vitalism and its concepts like entelechy have since been discarded as without value for scientific practice by the overwhelming majority of professional biologists.
However, in philosophy aspects and applications of the concept of entelechy have been explored by scientifically interested philosophers and philosophically inclined scientists alike. One example was the American critic and philosopher Kenneth Burke(1897–1993) whose concept of the "terministic screens" illustrates his thought on the subject. Most prominent was perhaps the German quantum physicist Werner Heisenberg. He looked to the notions of potentiality and actuality in order to better understand the relationship of quantum theory to the world.[53]
Prof Denis Noble argues that, just as teleological causation is necessary to the social sciences, a specific teleological causation in biology, expressing functional purpose, should be restored and that it is already implicit in neo-Darwinism (e.g. "selfish gene"). Teleological analysis proves parsimonious when the level of analysis is appropriate to the complexity of the required 'level' of explanation (e.g. whole body or organ rather than cell mechanism).[54]
See also[edit]
Actual infinity
Actus purus
Alexander of Aphrodisias
Essence–Energies distinction
First cause
Henosis
Hylomorphism
Hypokeimenon
Hypostasis (philosophy and religion)
Sumbebekos
Theosis
Unmoved movers
https://en.wikipedia.org/wiki/Potentiality_and_actuality
In scholastic philosophy, actus purus (English: "pure actuality," "pure act") is the absolute perfection of God.
https://en.wikipedia.org/wiki/Actus_purus
Scholasticism was a medieval school of philosophy that employed a critical method of philosophical analysis predicated upon a Latin Catholic theistic curriculum which dominated teaching in the medieval universities in Europe from about 1100 to 1700. It originated within the Christian monastic schools that were the basis of the earliest European universities.[1] The rise of scholasticism was closely associated with these schools that flourished in Italy, France, Spain and England.[2]
https://en.wikipedia.org/wiki/Scholasticism
In the philosophy of mathematics, the abstraction of actual infinity involves the acceptance (if the axiom of infinity is included) of infinite entities as given, actual and completed objects. These might include the set of natural numbers, extended real numbers, transfinite numbers, or even an infinite sequence of rational numbers.[1] Actual infinity is to be contrasted with potential infinity, in which a non-terminating process (such as "add 1 to the previous number") produces a sequence with no last element, and where each individual result is finite and is achieved in a finite number of steps. As a result, potential infinity is often formalized using the concept of limit.[2]
https://en.wikipedia.org/wiki/Actual_infinity
In axiomatic set theory and the branches of mathematics and philosophy that use it, the axiom of infinity is one of the axioms of Zermelo–Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural numbers. It was first published by Ernst Zermelo as part of his set theory in 1908.[1]
https://en.wikipedia.org/wiki/Axiom_of_infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo–Fraenkel set theory. It says that sets having the same elements are the same set.
https://en.wikipedia.org/wiki/Axiom_of_extensionality
In many popular versions of axiomatic set theory, the axiom schema of specification, also known as the axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension is an axiom schema. Essentially, it says that any definable subclass of a set is a set.
Some mathematicians call it the axiom schema of comprehension, although others use that term for unrestrictedcomprehension, discussed below.
Because restricting comprehension avoided Russell's paradox, several mathematicians including Zermelo, Fraenkel, and Gödelconsidered it the most important axiom of set theory.[1]
https://en.wikipedia.org/wiki/Axiom_schema_of_specification
The word schema comes from the Greek word σχῆμα (skhēma), which means shape, or more generally, plan. The plural is σχήματα (skhēmata). In English, both schemas and schemata are used as plural forms.
https://en.wikipedia.org/wiki/Schema
In mathematical logic, an axiom schema (plural: axiom schemata or axiom schemas) generalizes the notion of axiom.
https://en.wikipedia.org/wiki/Axiom_schema
In psychology and cognitive science, a schema (plural schemata or schemas) describes a pattern of thought or behavior that organizes categories of information and the relationships among them.[1][2] It can also be described as a mental structure of preconceived ideas, a framework representing some aspect of the world, or a system of organizing and perceiving new information.[3] Schemata influence attention and the absorption of new knowledge: people are more likely to notice things that fit into their schema, while re-interpreting contradictions to the schema as exceptions or distorting them to fit. Schemata have a tendency to remain unchanged, even in the face of contradictory information.[4] Schemata can help in understanding the world and the rapidly changing environment.[5] People can organize new perceptions into schemata quickly as most situations do not require complex thought when using schema, since automatic thought is all that is required.[5]
People use schemata to organize current knowledge and provide a framework for future understanding. Examples of schemata include academic rubrics, social schemas, stereotypes, social roles, scripts, worldviews, and archetypes. In Piaget's theory of development, children construct a series of schemata, based on the interactions they experience, to help them understand the world.[6]
https://en.wikipedia.org/wiki/Schema_(psychology)
In Kantian philosophy, a transcendental schema (plural: schemata; from Greek: σχῆμα, "form, shape, figure") is the procedural rule by which a category or pure, non-empirical concept is associated with a sense impression. A private, subjective intuition is thereby discursively thought to be a representation of an external object. Transcendental schemata are supposedly produced by the imagination in relation to time.
https://en.wikipedia.org/wiki/Schema_(Kant)
In philosophy, philosophy of physics deals with conceptual and interpretational issues in modern physics, many of which overlap with research done by certain kinds of theoretical physicists. Philosophy of physics can be broadly lumped into three areas:
- interpretations of quantum mechanics: mainly concerning issues with how to formulate an adequate response to the measurement problem and understand what the theory says about reality
- the nature of space and time: Are space and time substances, or purely relational? Is simultaneity conventional or only relative? Is temporal asymmetry purely reducible to thermodynamic asymmetry?
- inter-theoretic relations: the relationship between various physical theories, such as thermodynamics and statistical mechanics. This overlaps with the issue of scientific reduction.
The philosophy of information (PI) is a branch of philosophy that studies topics relevant to information processing, representational system and consciousness, computer science, information science and information technology.
It includes:
- the critical investigation of the conceptual nature and basic principles of information, including its dynamics, utilisation and sciences
- the elaboration and application of information-theoretic and computational methodologies to philosophical problems.[1]
In quantum mechanics, the measurement problem considers how, or whether, wave function collapse occurs. The inability to observe such a collapse directly has given rise to different interpretations of quantum mechanics and poses a key set of questions that each interpretation must answer.
The wave function in quantum mechanics evolves deterministically according to the Schrödinger equation as a linear superposition of different states. However, actual measurements always find the physical system in a definite state. Any future evolution of the wave function is based on the state the system was discovered to be in when the measurement was made, meaning that the measurement "did something" to the system that is not obviously a consequence of Schrödinger evolution. The measurement problem is describing what that "something" is, how a superposition of many possible values becomes a single measured value.
To express matters differently (paraphrasing Steven Weinberg),[1][2] the Schrödinger wave equation determines the wave function at any later time. If observers and their measuring apparatus are themselves described by a deterministic wave function, why can we not predict precise results for measurements, but only probabilities? As a general question: How can one establish a correspondence between quantum reality and classical reality?[3]
https://en.wikipedia.org/wiki/Measurement_problem
Subcategories
This category has the following 3 subcategories, out of 3 total.
Pages in category "Physical paradoxes"
The following 44 pages are in this category, out of 44 total. This list may not reflect recent changes (learn more).
Categories: Paradoxes Philosophy of physics Thought experiments in physics
https://en.wikipedia.org/wiki/Category:Physical_paradoxes
https://en.wikipedia.org/wiki/EPR_paradox#Paradox
Formulated in 1862 by Lord Kelvin, Hermann von Helmholtz and William John Macquorn Rankine,[1] the heat death paradox, also known as Clausius's paradox and thermodynamic paradox,[2] is a reductio ad absurdum argument that uses thermodynamics to show the impossibility of an infinitely old universe.
This paradox is directed at the then-mainstream strand of belief in a classical view of a sempiternal universe whereby its matter is postulated as everlasting and having always been recognisably the universe. Clausius's paradox is one of paradigm. It was necessary to amend the fundamental cosmic ideas meaning change of the paradigm. The paradox was solved when the paradigm was changed.
The paradox was based upon the rigid mechanical point of view of the second law of thermodynamics postulated by Rudolf Clausiusaccording to which heat can only be transferred from a warmer to a colder object. It notes: if the universe were eternal, as claimed classically, it should already be cold and isotropic (its objects the same temperature).[3]
Any hot object transfers heat to its cooler surroundings, until everything is at the same temperature. For two objects at the same temperature as much heat flows from one body as flows from the other, and the net effect is no change. If the universe were infinitely old, there must have been enough time for the stars to cool and warm their surroundings. Everywhere should therefore be at the same temperature and there should either be no stars, or everything should be as hot as stars.
Since there are stars and colder objects the universe is not in thermal equilibrium so it cannot be infinitely old.
The paradox does not arise in Big Bang nor modern steady state cosmology. In the former the universe is too young to have reached equilibrium; in the latter including the more nuanced quasi-steady state theory sufficient hydrogen is posited to have been replenished or regenerated continuously to allow constant average density. Star population depletion and reduction in temperature is slowed by the formation or coalescing of great stars which between certain masses and certain temperatures form supernovae remnant nebulae—such reincarnation postpones the heat death as does expansion of the universe.
See also[edit]
https://en.wikipedia.org/wiki/Heat_death_paradox
Vertical pressure variation is the variation in pressure as a function of elevation. Depending on the fluid in question and the context being referred to, it may also vary significantly in dimensions perpendicular to elevation as well, and these variations have relevance in the context of pressure gradient force and its effects. However, the vertical variation is especially significant, as it results from the pull of gravity on the fluid; namely, for the same given fluid, a decrease in elevation within it corresponds to a taller column of fluid weighing down on that point.
Hydrostatic paradox[edit]
| Wikimedia Commons has media related to Hydrostatic paradox. |
The barometric formula depends only on the height of the fluid chamber, and not on its width or length. Given a large enough height, any pressure may be attained. This feature of hydrostatics has been called the hydrostatic paradox. As expressed by W. H. Besant,[2]
- Any quantity of liquid, however small, may be made to support any weight, however large.
The Dutch scientist Simon Stevin was the first to explain the paradox mathematically.[3] In 1916 Richard Glazebrook mentioned the hydrostatic paradox as he described an arrangement he attributed to Pascal: a heavy weight W rests on a board with area A resting on a fluid bladder connected to a vertical tube with cross-sectional area α. Pouring water of weight w down the tube will eventually raise the heavy weight. Balance of forces leads to the equation
Glazebrook says, "By making the area of the board considerable and that of the tube small, a large weight W can be supported by a small weight w of water. This fact is sometimes described as the hydrostatic paradox."[4]
Demonstrations of the hydrostatic paradox are used in teaching the phenomenon.[5][6]
https://en.wikipedia.org/wiki/Vertical_pressure_variation#Hydrostatic_paradox
A gravitational singularity, spacetime singularity or simply singularity is a location in spacetime where the density and gravitational field of a celestial body is predicted to become infinite by general relativity in a way that does not depend on the coordinate system. The quantities used to measure gravitational field strength are the scalar invariant curvatures of spacetime, which includes a measure of the density of matter. Since such quantities become infinite at the singularity point, the laws of normal spacetime break down.[1][2]
https://en.wikipedia.org/wiki/Gravitational_singularity
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.[1] As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions (i.e., leptons and quarks), and force fields, whose quanta are bosons (e.g., photons and gluons). All these fields have zero-point energy.[2] These fluctuating zero-point fields lead to a kind of reintroduction of an aether in physics[1][3] since some systems can detect the existence of this energy. However, this aether cannot be thought of as a physical medium if it is to be Lorentz invariant such that there is no contradiction with Einstein's theory of special relativity.[1]
https://en.wikipedia.org/wiki/Zero-point_energy
The quantum vacuum state or simply quantum vacuum refers to the quantum state with the lowest possible energy.
Quantum vacuum may also refer to:
- Quantum chromodynamic vacuum (QCD vacuum), a non-perturbative vacuum
- Quantum electrodynamic vacuum (QED vacuum), a field-theoretic vacuum
- Quantum vacuum (ground state), the state of lowest energy of a quantum system
- Quantum vacuum collapse, a hypothetical vacuum metastability event
- Quantum vacuum expectation value, an operator's average, expected value in a quantum vacuum
- Quantum vacuum energy, an underlying background energy that exists in space throughout the entire Universe
- The Quantum Vacuum, a physics textbook by Peter W. Milonni
See also[edit]
https://en.wikipedia.org/wiki/Quantum_vacuum_(disambiguation)
In astronomy, the Zero Point in a photometric system is defined as the magnitude of an object that produces 1 count per second on the detector.[1] The zero point is used to calibrate a system to the standard magnitude system, as the flux detected from stars will vary from detector to detector.[2] Traditionally, Vega is used as the calibration star for the zero point magnitude in specific pass bands (U, B, and V), although often, an average of multiple stars is used for higher accuracy.[3] It is not often practical to find Vega in the sky to calibrate the detector, so for general purposes, any star may be used in the sky that has a known apparent magnitude.[4]
https://en.wikipedia.org/wiki/Zero_Point_(photometry)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space.
In physical problems, the choice of origin is often arbitrary, meaning any choice of origin will ultimately give the same answer. This allows one to pick an origin point that makes the mathematics as simple as possible, often by taking advantage of some kind of geometric symmetry.
https://en.wikipedia.org/wiki/Origin_(mathematics)
ee also[edit]
- Zero-point energy, the minimum energy a quantum mechanical system may have
- Zero-point field, a synonym for the vacuum state in quantum field theory
- Hofstadter zero-point, a special point associated with every plane triangle
- Point of origin (disambiguation)
- Triple zero (disambiguation)
- Point Zero (disambiguation)
https://en.wikipedia.org/wiki/Zero_point
MissingNo. (Japanese: けつばん[1], Hepburn: Ketsuban), short for "Missing Number" and sometimes spelled without the period, is an unofficial Pokémon species found in the video games Pokémon Red and Blue. Due to the programming of certain in-game events, players can encounter MissingNo. via a glitch.
https://en.wikipedia.org/wiki/MissingNo.
In triangle geometry, a Hofstadter point is a special point associated with every plane triangle. In fact there are several Hofstadter points associated with a triangle. All of them are triangle centers. Two of them, the Hofstadter zero-point and Hofstadter one-point, are particularly interesting.[1] They are two transcendental triangle centers. Hofstadter zero-point is the center designated as X(360) and the Hofstafter one-point is the center denoted as X(359) in Clark Kimberling's Encyclopedia of Triangle Centers. The Hofstadter zero-point was discovered by Douglas Hofstadter in 1992.[1]
https://en.wikipedia.org/wiki/Hofstadter_points
In quantum field theory, the quantum vacuum state (also called the quantum vacuum or vacuum state) is the quantum state with the lowest possible energy. Generally, it contains no physical particles. the word Zero-point field is sometimes used as a synonym for the vacuum state of an quantized field which is completely individual.
According to present-day understanding of what is called the vacuum state or the quantum vacuum, it is "by no means a simple empty space".[1][2] According to quantum mechanics, the vacuum state is not truly empty but instead contains fleeting electromagnetic waves and particles that pop into and out of the quantum field.[3][4][5]
The QED vacuum of quantum electrodynamics (or QED) was the first vacuum of quantum field theory to be developed. QED originated in the 1930s, and in the late 1940s and early 1950s it was reformulated by Feynman, Tomonaga and Schwinger, who jointly received the Nobel prize for this work in 1965.[6] Today the electromagnetic interactions and the weak interactions are unified (at very high energies only) in the theory of the electroweak interaction.
The Standard Model is a generalization of the QED work to include all the known elementary particles and their interactions (except gravity). Quantum chromodynamics(or QCD) is the portion of the Standard Model that deals with strong interactions, and QCD vacuum is the vacuum of quantum chromodynamics. It is the object of study in the Large Hadron Collider and the Relativistic Heavy Ion Collider, and is related to the so-called vacuum structure of strong interactions.[7]
https://en.wikipedia.org/wiki/Quantum_vacuum_state
In philosophical epistemology, there are two types of coherentism: the coherence theory of truth;[1] and the coherence theory of justification[2] (also known as epistemic coherentism).[3]
Coherent truth is divided between an anthropological approach, which applies only to localized networks ('true within a given sample of a population, given our understanding of the population'), and an approach that is judged on the basis of universals, such as categorical sets. The anthropological approach belongs more properly to the correspondence theory of truth, while the universal theories are a small development within analytic philosophy.
The coherentist theory of justification, which may be interpreted as relating to either theory of coherent truth, characterizes epistemic justification as a property of a belief only if that belief is a member of a coherent set. What distinguishes coherentism from other theories of justification is that the set is the primary bearer of justification.[4]
As an epistemological theory, coherentism opposes dogmatic foundationalism and also infinitism through its insistence on definitions. It also attempts to offer a solution to the regress argument that plagues correspondence theory. In an epistemological sense, it is a theory about how belief can be proof-theoretically justified.
Coherentism is a view about the structure and system of knowledge, or else justified belief. The coherentist's thesis is normally formulated in terms of a denial of its contrary, such as dogmatic foundationalism, which lacks a proof-theoretical framework, or correspondence theory, which lacks universalism. Counterfactualism, through a vocabulary developed by David K. Lewis and his many worlds theory[5]although popular with philosophers, has had the effect of creating wide disbelief of universals amongst academics. Many difficulties lie in between hypothetical coherence and its effective actualization. Coherentism claims, at a minimum, that not all knowledge and justified belief rest ultimately on a foundation of noninferential knowledge or justified belief. To defend this view, they may argue that conjunctions (and) are more specific, and thus in some way more defensible, than disjunctions (or).
After responding to foundationalism, coherentists normally characterize their view positively by replacing the foundationalism metaphor of a building as a model for the structure of knowledge with different metaphors, such as the metaphor that models our knowledge on a ship at sea whose seaworthiness must be ensured by repairs to any part in need of it. This metaphor fulfills the purpose of explaining the problem of incoherence, which was first raised in mathematics. Coherentists typically hold that justification is solely a function of some relationship between beliefs, none of which are privileged beliefs in the way maintained by dogmatic foundationalists. In this way universal truths are in closer reach. Different varieties of coherentism are individuated by the specific relationship between a system of knowledge and justified belief, which can be interpreted in terms of predicate logic, or ideally, proof theory.[6]
https://en.wikipedia.org/wiki/Coherentism
In epistemology, the coherence theory of truth regards truth as coherence within some specified set of sentences, propositions or beliefs. The model is contrasted with the correspondence theory of truth.
A positive tenet is the idea that truth is a property of whole systems of propositions and can be ascribed to individual propositions only derivatively according to their coherence with the whole. While modern coherence theorists hold that there are many possible systems to which the determination of truth may be based upon coherence, others, particularly those with strong religious beliefs, hold that the truth only applies to a single absolute system. In general, truth requires a proper fit of elements within the whole system. Very often, though, coherence is taken to imply something more than simple formal coherence. For example, the coherence of the underlying set of concepts is considered to be a critical factor in judging validity. In other words, the set of base concepts in a universe of discourse must form an intelligible paradigm before many theorists consider that the coherence theory of truth is applicable.[citation needed]
https://en.wikipedia.org/wiki/Coherence_theory_of_truth
Justification (also called epistemic justification) is a concept in epistemology used to describe beliefs that one has good reason for holding.[1] Epistemologists are concerned with various epistemic features of belief, which include the ideas of warrant(a proper justification for holding a belief), knowledge, rationality, and probability, among others. Loosely speaking, justification is the reason that someone holds a rationally admissible belief (although the term is also sometimes applied to other propositional attitudes such as doubt).
Debates surrounding epistemic justification often involve the structure of justification, including whether there are foundational justified beliefs or whether mere coherence is sufficient for a system of beliefs to qualify as justified. Another major subject of debate is the sources of justification, which might include perceptual experience (the evidence of the senses), reason, and authoritative testimony, among others.
https://en.wikipedia.org/wiki/Justification_(epistemology)
Proof theory is a major branch[1] of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed according to the axioms and rules of inference of the logical system. As such, proof theory is syntactic in nature, in contrast to model theory, which is semantic in nature.
Some of the major areas of proof theory include structural proof theory, ordinal analysis, provability logic, reverse mathematics, proof mining, automated theorem proving, and proof complexity. Much research also focuses on applications in computer science, linguistics, and philosophy.
https://en.wikipedia.org/wiki/Proof_theory
Foundationalism concerns philosophical theories of knowledge resting upon justified belief, or some secure foundation of certainty such as a conclusion inferred from a basis of sound premises.[1] The main rival of the foundationalist theory of justification is the coherence theory of justification, whereby a body of knowledge, not requiring a secure foundation, can be established by the interlocking strength of its components, like a puzzle solved without prior certainty that each small region was solved correctly.[1]
https://en.wikipedia.org/wiki/Foundationalism
Infinitism is the view that knowledge may be justified by an infinite chain of reasons. It belongs to epistemology, the branch of philosophy that considers the possibility, nature, and means of knowledge.
https://en.wikipedia.org/wiki/Infinitism
In epistemology, the regress argument is the argument that any proposition requires a justification. However, any justification itself requires support. This means that any proposition whatsoever can be endlessly (infinitely) questioned, resulting in infinite regress. It is a problem in epistemology and in any general situation where a statement has to be justified.[1][2][3]
The argument is also known as diallelus[4] (Latin) or diallelon, from Greek di allelon"through or by means of one another" and as the epistemic regress problem. It is an element of the Münchhausen trilemma.[5]
https://en.wikipedia.org/wiki/Regress_argument
In metaphysics and philosophy of language, the correspondence theory of truth states that the truth or falsity of a statement is determined only by how it relates to the world and whether it accurately describes (i.e., corresponds with) that world.[1]
Correspondence theories claim that true beliefs and true statements correspond to the actual state of affairs. This type of theory attempts to posit a relationship between thoughts or statements on one hand, and things or facts on the other.
https://en.wikipedia.org/wiki/Correspondence_theory_of_truth
Analytic philosophy is a branch and tradition of philosophy using analysis which is popular in the Western World and particularly the Anglosphere, which began around the turn of the 20th century in the contemporary era in the United Kingdom, United States, Canada, Australia, New Zealand and Scandinavia and continues today. Writing in 2003, John Searle claimed that "the best philosophy departments in the United States are dominated by analytic philosophy."[1]
Central figures in this historical development of analytic philosophy are Gottlob Frege, Bertrand Russell, G. E. Moore, and Ludwig Wittgenstein. Other important figures in its history include the logical positivists (particularly Rudolf Carnap), W. V. O. Quine, Saul Kripke, and Karl Popper.
Analytic philosophy is characterized by an emphasis on language, known as the linguistic turn, and for its clarity and rigor in arguments, making use of formal logic and mathematics, and, to a lesser degree, the natural sciences.[2][3][4] It also takes things piecemeal, in "an attempt to focus philosophical reflection on smaller problems that lead to answers to bigger questions."[5][6]
Analytic philosophy is often understood in contrast to other philosophical traditions, most notably continental philosophies such as existentialism, phenomenology, and Hegelianism.[7]
https://en.wikipedia.org/wiki/Analytic_philosophy
A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may be scientific, belong to a non-scientific discipline, or no discipline at all. Depending on the context, a theory's assertions might, for example, include generalized explanations of how nature works. The word has its roots in ancient Greek, but in modern use it has taken on several related meanings.
In modern science, the term "theory" refers to scientific theories, a well-confirmed type of explanation of nature, made in a way consistent with scientific method, and fulfilling the criteria required by modern science. Such theories are described in such a way that scientific tests should be able to provide empirical support for it, or empirical contradiction ("falsify") of it. Scientific theories are the most reliable, rigorous, and comprehensive form of scientific knowledge,[1] in contrast to more common uses of the word "theory" that imply that something is unproven or speculative (which in formal terms is better characterized by the word hypothesis).[2]Scientific theories are distinguished from hypotheses, which are individual empirically testable conjectures, and from scientific laws, which are descriptive accounts of the way nature behaves under certain conditions.
Theories guide the enterprise of finding facts rather than of reaching goals, and are neutral concerning alternatives among values.[3]: 131 A theory can be a body of knowledge, which may or may not be associated with particular explanatory models. To theorize is to develop this body of knowledge.[4]: 46
The word theory or "in theory" is sometimes used erroneously by people to explain something which they individually did not experience or test before.[5] In those instances, semantically, it is being substituted for another concept, a hypothesis. Instead of using the word "hypothetically", it is replaced by a phrase: "in theory". In some instances the theory's credibility could be contested by calling it "just a theory" (implying that the idea has not even been tested).[6] Hence, that word "theory" is very often contrasted to "practice" (from Greek praxis, πρᾶξις) a Greek term for doing, which is opposed to theory.[6] A "classical example" of the distinction between "theoretical" and "practical" uses the discipline of medicine: medical theory involves trying to understand the causes and nature of health and sickness, while the practical side of medicine is trying to make people healthy. These two things are related but can be independent, because it is possible to research health and sickness without curing specific patients, and it is possible to cure a patient without knowing how the cure worked.[a]
https://en.wikipedia.org/wiki/Theory
A scientific theory is an explanation of an aspect of the natural world and universe that has been repeatedly tested and verified in accordance with the scientific method, using accepted protocols of observation, measurement, and evaluation of results. Where possible, theories are tested under controlled conditions in an experiment.[1][2] In circumstances not amenable to experimental testing, theories are evaluated through principles of abductive reasoning. Established scientific theories have withstood rigorous scrutiny and embody scientific knowledge.[3]
A scientific theory differs from a scientific fact or scientific law in that a theory explains "why" or "how": a fact is a simple, basic observation, whereas a law is a statement (often a mathematical equation) about a relationship between facts. For example, Newton’s Law of Gravity is a mathematical equation that can be used to predict the attraction between bodies, but it is not a theory to explain how gravity works.[4] Stephen Jay Gould wrote that "...facts and theories are different things, not rungs in a hierarchy of increasing certainty. Facts are the world's data. Theories are structures of ideas that explain and interpret facts."[5]
The meaning of the term scientific theory (often contracted to theory for brevity) as used in the disciplines of science is significantly different from the common vernacular usage of theory.[6][note 1] In everyday speech, theory can imply an explanation that represents an unsubstantiated and speculative guess,[6] whereas in science it describes an explanation that has been tested and is widely accepted as valid.[citation needed]
The strength of a scientific theory is related to the diversity of phenomena it can explain and its simplicity. As additional scientific evidence is gathered, a scientific theory may be modified and ultimately rejected if it cannot be made to fit the new findings; in such circumstances, a more accurate theory is then required. Some theories are so well-established that they are unlikely ever to be fundamentally changed (for example, scientific theories such as evolution, heliocentric theory, cell theory, theory of plate tectonics, germ theory of disease, etc.). In certain cases, a scientific theory or scientific law that fails to fit all data can still be useful (due to its simplicity) as an approximation under specific conditions. An example is Newton's laws of motion, which are a highly accurate approximation to special relativity at velocities that are small relative to the speed of light.[citation needed]
Scientific theories are testable and make falsifiable predictions.[7] They describe the causes of a particular natural phenomenon and are used to explain and predict aspects of the physical universe or specific areas of inquiry (for example, electricity, chemistry, and astronomy). As with other forms of scientific knowledge, scientific theories are both deductive and inductive,[8] aiming for predictiveand explanatory power. Scientists use theories to further scientific knowledge, as well as to facilitate advances in technology or medicine.
https://en.wikipedia.org/wiki/Scientific_theory
Epistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with applications in many fields, including philosophy, theoretical computer science, artificial intelligence, economics and linguistics. While philosophers since Aristotle have discussed modal logic, and Medieval philosophers such as Avicenna, Ockham, and Duns Scotus developed many of their observations, it was C. I. Lewis who created the first symbolic and systematic approach to the topic, in 1912. It continued to mature as a field, reaching its modern form in 1963 with the work of Kripke.
https://en.wikipedia.org/wiki/Epistemic_modal_logic
In mathematics, a homogeneous binary relation R on a set X is reflexive if it relates every element of X to itself.[1][2]
An example of a reflexive relation is the relation "is equal to" on the set of real numbers, since every real number is equal to itself. A reflexive relation is said to have the reflexive property or is said to possess reflexivity. Along with symmetry and transitivity, reflexivity is one of three properties defining equivalence relations.
https://en.wikipedia.org/wiki/Reflexive_relation
Logical atomism is a philosophical view that originated in the early 20th century with the development of analytic philosophy. Its principal exponent was the British philosopher Bertrand Russell. It is also widely held that the early works[a] of his Austrian-born pupil and colleague, Ludwig Wittgenstein, defend a version of logical atomism. Some philosophers in the Vienna Circle were also influenced by logical atomism (particularly Rudolf Carnap, who was deeply sympathetic to some of its philosophical aims, especially in his earlier works).[1] Gustav Bergmann also developed a form of logical atomism that focused on an ideal phenomenalisticlanguage, particularly in his discussions of J.O. Urmson's work on analysis.[2]
https://en.wikipedia.org/wiki/Logical_atomism
In Philosophy, logical holism is the belief that the world operates in such a way that no part can be known without the whole being known first.
Theoretical holism is a theory in philosophy of science, that a theory of science can only be understood in its entirety, introduced by Pierre Duhem. Different total theories of science are understood by making them commensurable allowing statements in one theory to be converted to sentences in another.[1]: II Richard Rorty argued that when two theories are incompatible a process of hermeneutics is necessary.[1]: II
Practical holism is a concept in the work of Martin Heidegger than posits it not possible to produce a complete understanding of one's own experience of reality because your mode of existence is embedded in cultural practices, the constraints of the task that you are doing.[1]: III
Bertrand Russell concluded that "Hegel's dialectical logical holism should be dismissed in favour of the new logic of propositional analysis."[2] and introduced a form of logical atomism.[3]
https://en.wikipedia.org/wiki/Logical_holism
The doctrine of internal relations is the philosophical doctrine that all relations are internal to their bearers, in the sense that they are essential to them and the bearers would not be what they are without them. It was a term used in British philosophy around in the early 1900s.[1][2]
https://en.wikipedia.org/wiki/Doctrine_of_internal_relations
An a priori probability is a probability that is derived purely by deductive reasoning.[1] One way of deriving a priori probabilities is the principle of indifference, which has the character of saying that, if there are N mutually exclusive and collectively exhaustiveevents and if they are equally likely, then the probability of a given event occurring is 1/N. Similarly the probability of one of a given collection of K events is K / N.
One disadvantage of defining probabilities in the above way is that it applies only to finite collections of events.
In Bayesian inference, "uninformative priors" or "objective priors" are particular choices of a priori probabilities.[2] Note that "prior probability" is a broader concept.
Similar to the distinction in philosophy between a priori and a posteriori, in Bayesian inference a priori denotes general knowledge about the data distribution before making an inference, while a posteriori denotes knowledge that incorporates the results of making an inference.[3]
https://en.wikipedia.org/wiki/A_priori_probability
An uninformative prior or diffuse prior expresses vague or general information about a variable. The term "uninformative prior" is somewhat of a misnomer. Such a prior might also be called a not very informative prior, or an objective prior, i.e. one that's not subjectively elicited.
Uninformative priors can express "objective" information such as "the variable is positive" or "the variable is less than some limit". The simplest and oldest rule for determining a non-informative prior is the principle of indifference, which assigns equal probabilities to all possibilities. In parameter estimation problems, the use of an uninformative prior typically yields results which are not too different from conventional statistical analysis, as the likelihood function often yields more information than the uninformative prior.
Some attempts have been made at finding a priori probabilities, i.e. probability distributions in some sense logically required by the nature of one's state of uncertainty; these are a subject of philosophical controversy, with Bayesians being roughly divided into two schools: "objective Bayesians", who believe such priors exist in many useful situations, and "subjective Bayesians" who believe that in practice priors usually represent subjective judgements of opinion that cannot be rigorously justified (Williamson 2010). Perhaps the strongest arguments for objective Bayesianism were given by Edwin T. Jaynes, based mainly on the consequences of symmetries and on the principle of maximum entropy.
https://en.wikipedia.org/wiki/Prior_probability#Uninformative_priors
In Roman mythology, Veritas (Classical Latin: [ˈweː.rɪ.t̪aːs]), meaning truth, is the goddess of truth, a daughter of Saturn (called Cronus by the Greeks, the Titan of Time, perhaps first by Plutarch), and the mother of Virtus. She is also sometimes considered the daughter of Jupiter (called Zeus by the Greeks),[1] or a creation of Prometheus.[2][3] The elusive goddess is said to have hidden in the bottom of a holy well.[4] She is depicted both as a virgin dressed in white and as the "naked truth" (nuda veritas) holding a hand mirror.[5][6][7]
Veritas is also the name given to the Roman virtue of truthfulness, which was considered one of the main virtues any good Roman should possess. The Greek goddess of truth is Aletheia (Ancient Greek: Ἀλήθεια). The German philosopher Martin Heidegger argues that the truth represented by aletheia (which essentially means "unconcealment") is different from that represented by veritas, which is linked to a Roman understanding of rightness and finally to a Nietzschean sense of justice and a will to power.[8]
In Western culture, the word may also serve as a motto.
Goddess of truth | |
 Veritas depicted on the monument to Pope Alexander VII |
https://en.wikipedia.org/wiki/Veritas
Saturn (Latin: Sāturnus [saːˈturnus]) was a god in ancient Roman religion, and a character in Roman mythology. He was described as a god of generation, dissolution, plenty, wealth, agriculture, periodic renewal and liberation. Saturn's mythological reign was depicted as a Golden Age of plenty and peace. After the Roman conquest of Greece, he was conflated with the Greek Titan Cronus. Saturn's consort was his sister Ops, with whom he fathered Jupiter, Neptune, Pluto, Juno, Ceres and Vesta.
Saturn was especially celebrated during the festival of Saturnalia each December, perhaps the most famous of the Roman festivals, a time of feasting, role reversals, free speech, gift-giving and revelry. The Temple of Saturn in the Roman Forum housed the state treasury and archives (aerarium) of the Roman Republic and the early Roman Empire. The planet Saturn and the day of the week Saturday are both named after and were associated with him.
https://en.wikipedia.org/wiki/Saturn_(mythology)
In ancient Roman religion, Ops or Opis (Latin: "Plenty") was a fertility deity and earth goddess of Sabine origin.
https://en.wikipedia.org/wiki/Ops
Via et veritas et vita (Classical Latin: [ˈwɪ.a ɛt ˈweːrɪtaːs ɛt ˈwiːta], Ecclesiastical Latin: [ˈvi.a et ˈveritas et ˈvita]) is a Latin phrase meaning "the way and the truth and the life". The words are taken from Vulgate version of John 14:6, and were spoken by Jesus Christ in reference to himself.
These words, and sometimes the asyndetic variant via veritas vita, have been used as the motto of various educational institutions and governments.
https://en.wikipedia.org/wiki/Via_et_veritas_et_vita
Asyndeton (UK: /æˈsɪndɪtən, ə-/, US: /əˈsɪndətɒn, ˌeɪ-/;[1][2] from the Greek: ἀσύνδετον, "unconnected", sometimes called asyndetism) is a literary scheme in which one or several conjunctions are deliberately omitted from a series of related clauses.[3][4]Examples include veni, vidi, vici and its English translation "I came, I saw, I conquered". Its use can have the effect of speeding up the rhythm of a passage and making a single idea more memorable. Asyndeton may be contrasted with syndeton (syndetic coordination) and polysyndeton, which describe the use of one or multiple coordinating conjunctions, respectively.
More generally, in grammar, an asyndetic coordination is a type of coordination in which no coordinating conjunction is present between the conjuncts.[5]
Quickly, resolutely, he strode into the bank.
No coordinator is present here, but the conjoins are still coordinated.
https://en.wikipedia.org/wiki/Asyndeton
In Bayesian statistical inference, a prior probability distribution, often simply called the prior, of an uncertain quantity is the probability distribution that would express one's beliefs about this quantity before some evidence is taken into account. For example, the prior could be the probability distribution representing the relative proportions of voters who will vote for a particular politician in a future election. The unknown quantity may be a parameter of the model or a latent variable rather than an observable variable.
Bayes' theorem calculates the renormalized pointwise product of the prior and the likelihood function, to produce the posterior probability distribution, which is the conditional distribution of the uncertain quantity given the data.
Similarly, the prior probability of a random event or an uncertain proposition is the unconditional probability that is assigned before any relevant evidence is taken into account.
https://en.wikipedia.org/wiki/Prior_probability
Argument–deduction–proof distinctions originated with logic itself.[1] Naturally, the terminology evolved.
An argument, more fully a premise–conclusion argument, is a two-part system composed of premises and conclusion. An argument is valid if and only if its conclusion is a consequence of its premises. Every premise set has infinitely many consequences each giving rise to a valid argument. Some consequences are obviously so, but most are not: most are hidden consequences. Most valid arguments are not yet known to be valid. To determine validity in non-obvious cases deductive reasoning is required. There is no deductive reasoning in an argument per se; such must come from the outside.
Every argument's conclusion is a premise of other arguments. The word constituent may be used for either a premise or conclusion. In the context of this article and in most classical contexts, all candidates for consideration as argument constituents fall under the category of truth-bearer: propositions, statements, sentences, judgments, etc.
https://en.wikipedia.org/wiki/Argument–deduction–proof_distinctions
Deductive reasoning, also deductive logic, is the process of reasoning from one or more statements (premises) to reach a logical conclusion.[1]
Deductive reasoning goes in the same direction as that of the conditionals, and links premises with conclusions. If all premises are true, the terms are clear, and the rules of deductive logic are followed, then the conclusion reached is necessarily true.
Deductive reasoning ("top-down logic") contrasts with inductive reasoning ("bottom-up logic"): in deductive reasoning, a conclusion is reached reductively by applying general rules which hold over the entirety of a closed domain of discourse, narrowing the range under consideration until only the conclusion(s) remains. In deductive reasoning there is no uncertainty.[2] In inductive reasoning, the conclusion is reached by generalizing or extrapolating from specific cases to general rules resulting in a conclusion that has epistemic uncertainty.[2]
The inductive reasoning is not the same as induction used in mathematical proofs – mathematical induction is actually a form of deductive reasoning.
Deductive reasoning differs from abductive reasoning by the direction of the reasoning relative to the conditionals. The idea of "deduction" popularized in Sherlock Holmes stories is technically abduction, rather than deductive reasoning. Deductive reasoninggoes in the same direction as that of the conditionals, whereas abductive reasoning goes in the direction contrary to that of the conditionals.
https://en.wikipedia.org/wiki/Deductive_reasoning
Abductive reasoning (also called abduction,[1] abductive inference,[1] or retroduction[2]) is a form of logical inference formulated and advanced by American philosopher Charles Sanders Peircebeginning in the last third of the 19th century. It starts with an observation or set of observations and then seeks the simplest and most likely conclusion from the observations. This process, unlike deductive reasoning, yields a plausible conclusion but does not positively verify it. Abductive conclusions are thus qualified as having a remnant of uncertainty or doubt, which is expressed in retreat terms such as "best available" or "most likely". One can understand abductive reasoning as inference to the best explanation,[3] although not all usages of the terms abduction and inference to the best explanation are exactly equivalent.[4][5]
In the 1990s, as computing power grew, the fields of law,[6] computer science, and artificial intelligenceresearch[7] spurred renewed interest in the subject of abduction.[8] Diagnostic expert systemsfrequently employ abduction.[9]
https://en.wikipedia.org/wiki/Abductive_reasoning
The closed-world assumption (CWA), in a formal system of logic used for knowledge representation, is the presumption that a statement that is true is also known to be true. Therefore, conversely, what is not currently known to be true, is false. The same name also refers to a logical formalization of this assumption by Raymond Reiter.[1] The opposite of the closed-world assumption is the open-world assumption (OWA), stating that lack of knowledge does not imply falsity. Decisions on CWA vs. OWA determine the understanding of the actual semantics of a conceptual expression with the same notations of concepts. A successful formalization of natural language semantics usually cannot avoid an explicit revelation of whether the implicit logical backgrounds are based on CWA or OWA.
Negation as failure is related to the closed-world assumption, as it amounts to believing false every predicate that cannot be proved to be true.
https://en.wikipedia.org/wiki/Closed-world_assumption
Negation as failure (NAF, for short) is a non-monotonic inference rule in logic programming, used to derive (i.e. that is assumed not to hold) from failure to derive . Note that can be different from the statement of the logical negation of , depending on the completeness of the inference algorithm and thus also on the formal logic system.
Negation as failure has been an important feature of logic programming since the earliest days of both Planner and Prolog. In Prolog, it is usually implemented using Prolog's extralogical constructs.
More generally, this kind of negation is known as weak negation,[1][2] in contrast with the strong (i.e. explicit, provable) negation.
https://en.wikipedia.org/wiki/Negation_as_failure
A non-monotonic logic is a formal logic whose conclusion relation is not monotonic. In other words, non-monotonic logics are devised to capture and represent defeasible inferences (cf. defeasible reasoning), i.e., a kind of inference in which reasoners draw tentative conclusions, enabling reasoners to retract their conclusion(s) based on further evidence.[1] Most studied formal logics have a monotonic entailment relation, meaning that adding a formula to a theory never produces a pruning of its set of conclusions. Intuitively, monotonicity indicates that learning a new piece of knowledge cannot reduce the set of what is known. A monotonic logic cannot handle various reasoning tasks such as reasoning by default (conclusions may be derived only because of lack of evidence of the contrary), abductive reasoning (conclusions are only deduced as most likely explanations), some important approaches to reasoning about knowledge (the ignorance of a conclusion must be retracted when the conclusion becomes known), and similarly, belief revision (new knowledge may contradict old beliefs).
https://en.wikipedia.org/wiki/Non-monotonic_logic
Monotonicity of entailment is a property of many logical systems that states that the hypotheses of any derived fact may be freely extended with additional assumptions. In sequent calculi this property can be captured by an inference rule called weakening, or sometimes thinning, and in such systems one may say that entailment is monotone if and only if the rule is admissible. Logical systems with this property are occasionally called monotonic logics in order to differentiate them from non-monotonic logics.
https://en.wikipedia.org/wiki/Monotonicity_of_entailment
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rulesclosely related to the "natural" way of reasoning. This contrasts with Hilbert-style systems, which instead use axioms as much as possible to express the logical laws of deductive reasoning.
Motivation[edit]
Natural deduction grew out of a context of dissatisfaction with the axiomatizations of deductive reasoning common to the systems of Hilbert, Frege, and Russell (see, e.g., Hilbert system). Such axiomatizations were most famously used by Russell and Whitehead in their mathematical treatise Principia Mathematica. Spurred on by a series of seminars in Poland in 1926 by Łukasiewicz that advocated a more natural treatment of logic, Jaśkowski made the earliest attempts at defining a more natural deduction, first in 1929 using a diagrammatic notation, and later updating his proposal in a sequence of papers in 1934 and 1935.[1] His proposals led to different notations such as Fitch-style calculus (or Fitch's diagrams) or Suppes' method for which Lemmon gave a variant called system L.
Natural deduction in its modern form was independently proposed by the German mathematician Gerhard Gentzen in 1934, in a dissertation delivered to the faculty of mathematical sciences of the University of Göttingen.[2] The term natural deduction (or rather, its German equivalent natürliches Schließen) was coined in that paper:
Gentzen was motivated by a desire to establish the consistency of number theory. He was unable to prove the main result required for the consistency result, the cut elimination theorem—the Hauptsatz—directly for natural deduction. For this reason he introduced his alternative system, the sequent calculus, for which he proved the Hauptsatz both for classical and intuitionistic logic. In a series of seminars in 1961 and 1962 Prawitz gave a comprehensive summary of natural deduction calculi, and transported much of Gentzen's work with sequent calculi into the natural deduction framework. His 1965 monograph Natural deduction: a proof-theoretical study[4] was to become a reference work on natural deduction, and included applications for modal and second-order logic.
In natural deduction, a proposition is deduced from a collection of premises by applying inference rules repeatedly. The system presented in this article is a minor variation of Gentzen's or Prawitz's formulation, but with a closer adherence to Martin-Löf's description of logical judgments and connectives.[5]
Judgments and propositions[edit]
A judgment is something that is knowable, that is, an object of knowledge. It is evident if one in fact knows it.[6] Thus "it is raining" is a judgment, which is evident for the one who knows that it is actually raining; in this case one may readily find evidence for the judgment by looking outside the window or stepping out of the house. In mathematical logic however, evidence is often not as directly observable, but rather deduced from more basic evident judgments. The process of deduction is what constitutes a proof; in other words, a judgment is evident if one has a proof for it.
The most important judgments in logic are of the form "A is true". The letter A stands for any expression representing a proposition; the truth judgments thus require a more primitive judgment: "A is a proposition". Many other judgments have been studied; for example, "A is false" (see classical logic), "A is true at time t" (see temporal logic), "A is necessarily true" or "A is possibly true" (see modal logic), "the program M has type τ" (see programming languages and type theory), "A is achievable from the available resources" (see linear logic), and many others. To start with, we shall concern ourselves with the simplest two judgments "A is a proposition" and "A is true", abbreviated as "A prop" and "A true" respectively.
The judgment "A prop" defines the structure of valid proofs of A, which in turn defines the structure of propositions. For this reason, the inference rules for this judgment are sometimes known as formation rules. To illustrate, if we have two propositions A and B (that is, the judgments "A prop" and "B prop" are evident), then we form the compound proposition A and B, written symbolically as "". We can write this in the form of an inference rule:
where the parentheses are omitted to make the inference rule more succinct:
This inference rule is schematic: A and B can be instantiated with any expression. The general form of an inference rule is:
where each is a judgment and the inference rule is named "name". The judgments above the line are known as premises, and those below the line are conclusions. Other common logical propositions are disjunction (), negation (), implication (), and the logical constants truth () and falsehood (). Their formation rules are below.
Introduction and elimination[edit]
Now we discuss the "A true" judgment. Inference rules that introduce a logical connective in the conclusion are known as introduction rules. To introduce conjunctions, i.e., to conclude "A and B true" for propositions A and B, one requires evidence for "Atrue" and "B true". As an inference rule:
It must be understood that in such rules the objects are propositions. That is, the above rule is really an abbreviation for:
This can also be written:
In this form, the first premise can be satisfied by the formation rule, giving the first two premises of the previous form. In this article we shall elide the "prop" judgments where they are understood. In the nullary case, one can derive truth from no premises.
If the truth of a proposition can be established in more than one way, the corresponding connective has multiple introduction rules.
Note that in the nullary case, i.e., for falsehood, there are no introduction rules. Thus one can never infer falsehood from simpler judgments.
Dual to introduction rules are elimination rules to describe how to deconstruct information about a compound proposition into information about its constituents. Thus, from "A ∧ B true", we can conclude "A true" and "B true":
As an example of the use of inference rules, consider commutativity of conjunction. If A ∧ B is true, then B ∧ A is true; this derivation can be drawn by composing inference rules in such a fashion that premises of a lower inference match the conclusion of the next higher inference.
The inference figures we have seen so far are not sufficient to state the rules of implication introduction or disjunction elimination; for these, we need a more general notion of hypothetical derivation.
Hypothetical derivations[edit]
A pervasive operation in mathematical logic is reasoning from assumptions. For example, consider the following derivation:
This derivation does not establish the truth of B as such; rather, it establishes the following fact:
- If A ∧ (B ∧ C) is true then B is true.
In logic, one says "assuming A ∧ (B ∧ C) is true, we show that B is true"; in other words, the judgment "B true" depends on the assumed judgment "A ∧ (B ∧ C) true". This is a hypothetical derivation, which we write as follows:
The interpretation is: "B true is derivable from A ∧ (B ∧ C) true". Of course, in this specific example we actually know the derivation of "B true" from "A ∧ (B ∧ C) true", but in general we may not a priori know the derivation. The general form of a hypothetical derivation is:
Each hypothetical derivation has a collection of antecedent derivations (the Di) written on the top line, and a succedent judgment (J) written on the bottom line. Each of the premises may itself be a hypothetical derivation. (For simplicity, we treat a judgment as a premise-less derivation.)
The notion of hypothetical judgment is internalised as the connective of implication. The introduction and elimination rules are as follows.
In the introduction rule, the antecedent named u is discharged in the conclusion. This is a mechanism for delimiting the scope of the hypothesis: its sole reason for existence is to establish "B true"; it cannot be used for any other purpose, and in particular, it cannot be used below the introduction. As an example, consider the derivation of "A ⊃ (B ⊃ (A ∧ B)) true":
This full derivation has no unsatisfied premises; however, sub-derivations are hypothetical. For instance, the derivation of "B ⊃ (A ∧ B) true" is hypothetical with antecedent "A true" (named u).
With hypothetical derivations, we can now write the elimination rule for disjunction:
In words, if A ∨ B is true, and we can derive "C true" both from "A true" and from "B true", then C is indeed true. Note that this rule does not commit to either "A true" or "B true". In the zero-ary case, i.e. for falsehood, we obtain the following elimination rule:
This is read as: if falsehood is true, then any proposition C is true.
Negation is similar to implication.
The introduction rule discharges both the name of the hypothesis u, and the succedent p, i.e., the proposition p must not occur in the conclusion A. Since these rules are schematic, the interpretation of the introduction rule is: if from "A true" we can derive for every proposition p that "p true", then A must be false, i.e., "not A true". For the elimination, if both A and not A are shown to be true, then there is a contradiction, in which case every proposition C is true. Because the rules for implication and negation are so similar, it should be fairly easy to see that not A and A ⊃ ⊥ are equivalent, i.e., each is derivable from the other.
Consistency, completeness, and normal forms[edit]
A theory is said to be consistent if falsehood is not provable (from no assumptions) and is complete if every theorem or its negation is provable using the inference rules of the logic. These are statements about the entire logic, and are usually tied to some notion of a model. However, there are local notions of consistency and completeness that are purely syntactic checks on the inference rules, and require no appeals to models. The first of these is local consistency, also known as local reducibility, which says that any derivation containing an introduction of a connective followed immediately by its elimination can be turned into an equivalent derivation without this detour. It is a check on the strength of elimination rules: they must not be so strong that they include knowledge not already contained in their premises. As an example, consider conjunctions.
| ⇒ |
Dually, local completeness says that the elimination rules are strong enough to decompose a connective into the forms suitable for its introduction rule. Again for conjunctions:
| ⇒ |
These notions correspond exactly to β-reduction (beta reduction) and η-conversion (eta conversion) in the lambda calculus, using the Curry–Howard isomorphism. By local completeness, we see that every derivation can be converted to an equivalent derivation where the principal connective is introduced. In fact, if the entire derivation obeys this ordering of eliminations followed by introductions, then it is said to be normal. In a normal derivation all eliminations happen above introductions. In most logics, every derivation has an equivalent normal derivation, called a normal form. The existence of normal forms is generally hard to prove using natural deduction alone, though such accounts do exist in the literature, most notably by Dag Prawitz in 1961.[7] It is much easier to show this indirectly by means of a cut-free sequent calculus presentation.
First and higher-order extensions[edit]
The logic of the earlier section is an example of a single-sorted logic, i.e., a logic with a single kind of object: propositions. Many extensions of this simple framework have been proposed; in this section we will extend it with a second sort of individuals or terms. More precisely, we will add a new kind of judgment, "t is a term" (or "t term") where t is schematic. We shall fix a countable set V of variables, another countable set F of function symbols, and construct terms with the following formation rules:
and
For propositions, we consider a third countable set P of predicates, and define atomic predicates over terms with the following formation rule:
The first two rules of formation provide a definition of a term that is effectively the same as that defined in term algebra and model theory, although the focus of those fields of study is quite different from natural deduction. The third rule of formation effectively defines an atomic formula, as in first-order logic, and again in model theory.
To these are added a pair of formation rules, defining the notation for quantified propositions; one for universal (∀) and existential (∃) quantification:
The universal quantifier has the introduction and elimination rules:
The existential quantifier has the introduction and elimination rules:
In these rules, the notation [t/x] A stands for the substitution of t for every (visible) instance of x in A, avoiding capture.[8] As before the superscripts on the name stand for the components that are discharged: the term a cannot occur in the conclusion of ∀I (such terms are known as eigenvariables or parameters), and the hypotheses named u and v in ∃E are localised to the second premise in a hypothetical derivation. Although the propositional logic of earlier sections was decidable, adding the quantifiers makes the logic undecidable.
So far, the quantified extensions are first-order: they distinguish propositions from the kinds of objects quantified over. Higher-order logic takes a different approach and has only a single sort of propositions. The quantifiers have as the domain of quantification the very same sort of propositions, as reflected in the formation rules:
A discussion of the introduction and elimination forms for higher-order logic is beyond the scope of this article. It is possible to be in-between first-order and higher-order logics. For example, second-order logic has two kinds of propositions, one kind quantifying over terms, and the second kind quantifying over propositions of the first kind.
Different presentations of natural deduction[edit]
Tree-like presentations[edit]
Gentzen's discharging annotations used to internalise hypothetical judgments can be avoided by representing proofs as a tree of sequents Γ ⊢A instead of a tree of A true judgments.
Sequential presentations[edit]
Jaśkowski's representations of natural deduction led to different notations such as Fitch-style calculus (or Fitch's diagrams) or Suppes' method, of which Lemmon gave a variant called system L. Such presentation systems, which are more accurately described as tabular, include the following.
- 1940: In a textbook, Quine[9] indicated antecedent dependencies by line numbers in square brackets, anticipating Suppes' 1957 line-number notation.
- 1950: In a textbook, Quine (1982, pp. 241–255) demonstrated a method of using one or more asterisks to the left of each line of proof to indicate dependencies. This is equivalent to Kleene's vertical bars. (It is not totally clear if Quine's asterisk notation appeared in the original 1950 edition or was added in a later edition.)
- 1957: An introduction to practical logic theorem proving in a textbook by Suppes (1999, pp. 25–150). This indicated dependencies (i.e. antecedent propositions) by line numbers at the left of each line.
- 1963: Stoll (1979, pp. 183–190, 215–219) uses sets of line numbers to indicate antecedent dependencies of the lines of sequential logical arguments based on natural deduction inference rules.
- 1965: The entire textbook by Lemmon (1965) is an introduction to logic proofs using a method based on that of Suppes.
- 1967: In a textbook, Kleene (2002, pp. 50–58, 128–130) briefly demonstrated two kinds of practical logic proofs, one system using explicit quotations of antecedent propositions on the left of each line, the other system using vertical bar-lines on the left to indicate dependencies.[10]
Proofs and type theory[edit]
The presentation of natural deduction so far has concentrated on the nature of propositions without giving a formal definition of a proof. To formalise the notion of proof, we alter the presentation of hypothetical derivations slightly. We label the antecedents with proof variables (from some countable set V of variables), and decorate the succedent with the actual proof. The antecedents or hypotheses are separated from the succedent by means of a turnstile (⊢). This modification sometimes goes under the name of localised hypotheses. The following diagram summarises the change.
| ⇒ |
The collection of hypotheses will be written as Γ when their exact composition is not relevant. To make proofs explicit, we move from the proof-less judgment "A true" to a judgment: "π is a proof of (A true)", which is written symbolically as "π : A true". Following the standard approach, proofs are specified with their own formation rules for the judgment "π proof". The simplest possible proof is the use of a labelled hypothesis; in this case the evidence is the label itself.
For brevity, we shall leave off the judgmental label true in the rest of this article, i.e., write "Γ ⊢ π : A". Let us re-examine some of the connectives with explicit proofs. For conjunction, we look at the introduction rule ∧I to discover the form of proofs of conjunction: they must be a pair of proofs of the two conjuncts. Thus:
The elimination rules ∧E1 and ∧E2 select either the left or the right conjunct; thus the proofs are a pair of projections—first (fst) and second (snd).
For implication, the introduction form localises or binds the hypothesis, written using a λ; this corresponds to the discharged label. In the rule, "Γ, u:A" stands for the collection of hypotheses Γ, together with the additional hypothesis u.
With proofs available explicitly, one can manipulate and reason about proofs. The key operation on proofs is the substitution of one proof for an assumption used in another proof. This is commonly known as a substitution theorem, and can be proved by inductionon the depth (or structure) of the second judgment.
- Substitution theorem
- If Γ ⊢ π1 : A and Γ, u:A ⊢ π2 : B, then Γ ⊢ [π1/u] π2 : B.
So far the judgment "Γ ⊢ π : A" has had a purely logical interpretation. In type theory, the logical view is exchanged for a more computational view of objects. Propositions in the logical interpretation are now viewed as types, and proofs as programs in the lambda calculus. Thus the interpretation of "π : A" is "the program π has type A". The logical connectives are also given a different reading: conjunction is viewed as product (×), implication as the function arrow (→), etc. The differences are only cosmetic, however. Type theory has a natural deduction presentation in terms of formation, introduction and elimination rules; in fact, the reader can easily reconstruct what is known as simple type theory from the previous sections.
The difference between logic and type theory is primarily a shift of focus from the types (propositions) to the programs (proofs). Type theory is chiefly interested in the convertibility or reducibility of programs. For every type, there are canonical programs of that type which are irreducible; these are known as canonical forms or values. If every program can be reduced to a canonical form, then the type theory is said to be normalising (or weakly normalising). If the canonical form is unique, then the theory is said to be strongly normalising. Normalisability is a rare feature of most non-trivial type theories, which is a big departure from the logical world. (Recall that almost every logical derivation has an equivalent normal derivation.) To sketch the reason: in type theories that admit recursive definitions, it is possible to write programs that never reduce to a value; such looping programs can generally be given any type. In particular, the looping program has type ⊥, although there is no logical proof of "⊥ true". For this reason, the propositions as types; proofs as programs paradigm only works in one direction, if at all: interpreting a type theory as a logic generally gives an inconsistent logic.
Example: Dependent Type Theory[edit]
Like logic, type theory has many extensions and variants, including first-order and higher-order versions. One branch, known as dependent type theory, is used in a number of computer-assisted proof systems. Dependent type theory allows quantifiers to range over programs themselves. These quantified types are written as Π and Σ instead of ∀ and ∃, and have the following formation rules:
These types are generalisations of the arrow and product types, respectively, as witnessed by their introduction and elimination rules.
Dependent type theory in full generality is very powerful: it is able to express almost any conceivable property of programs directly in the types of the program. This generality comes at a steep price — either typechecking is undecidable (extensional type theory), or extensional reasoning is more difficult (intensional type theory). For this reason, some dependent type theories do not allow quantification over arbitrary programs, but rather restrict to programs of a given decidable index domain, for example integers, strings, or linear programs.
Since dependent type theories allow types to depend on programs, a natural question to ask is whether it is possible for programs to depend on types, or any other combination. There are many kinds of answers to such questions. A popular approach in type theory is to allow programs to be quantified over types, also known as parametric polymorphism; of this there are two main kinds: if types and programs are kept separate, then one obtains a somewhat more well-behaved system called predicative polymorphism; if the distinction between program and type is blurred, one obtains the type-theoretic analogue of higher-order logic, also known as impredicative polymorphism. Various combinations of dependency and polymorphism have been considered in the literature, the most famous being the lambda cube of Henk Barendregt.
The intersection of logic and type theory is a vast and active research area. New logics are usually formalised in a general type theoretic setting, known as a logical framework. Popular modern logical frameworks such as the calculus of constructions and LFare based on higher-order dependent type theory, with various trade-offs in terms of decidability and expressive power. These logical frameworks are themselves always specified as natural deduction systems, which is a testament to the versatility of the natural deduction approach.
Classical and modal logics[edit]
For simplicity, the logics presented so far have been intuitionistic. Classical logic extends intuitionistic logic with an additional axiomor principle of excluded middle:
- For any proposition p, the proposition p ∨ ¬p is true.
This statement is not obviously either an introduction or an elimination; indeed, it involves two distinct connectives. Gentzen's original treatment of excluded middle prescribed one of the following three (equivalent) formulations, which were already present in analogous forms in the systems of Hilbert and Heyting:
(XM3 is merely XM2 expressed in terms of E.) This treatment of excluded middle, in addition to being objectionable from a purist's standpoint, introduces additional complications in the definition of normal forms.
A comparatively more satisfactory treatment of classical natural deduction in terms of introduction and elimination rules alone was first proposed by Parigot in 1992 in the form of a classical lambda calculus called λμ. The key insight of his approach was to replace a truth-centric judgment A true with a more classical notion, reminiscent of the sequent calculus: in localised form, instead of Γ ⊢ A, he used Γ ⊢ Δ, with Δ a collection of propositions similar to Γ. Γ was treated as a conjunction, and Δ as a disjunction. This structure is essentially lifted directly from classical sequent calculi, but the innovation in λμ was to give a computational meaning to classical natural deduction proofs in terms of a callcc or a throw/catch mechanism seen in LISP and its descendants. (See also: first class control.)
Another important extension was for modal and other logics that need more than just the basic judgment of truth. These were first described, for the alethic modal logics S4 and S5, in a natural deduction style by Prawitz in 1965,[4] and have since accumulated a large body of related work. To give a simple example, the modal logic S4 requires one new judgment, "A valid", that is categorical with respect to truth:
- If "A true" under no assumptions of the form "B true", then "A valid".
This categorical judgment is internalised as a unary connective ◻A (read "necessarily A") with the following introduction and elimination rules:
Note that the premise "A valid" has no defining rules; instead, the categorical definition of validity is used in its place. This mode becomes clearer in the localised form when the hypotheses are explicit. We write "Ω;Γ ⊢ A true" where Γ contains the true hypotheses as before, and Ω contains valid hypotheses. On the right there is just a single judgment "A true"; validity is not needed here since "Ω ⊢ A valid" is by definition the same as "Ω;⋅ ⊢ A true". The introduction and elimination forms are then:
The modal hypotheses have their own version of the hypothesis rule and substitution theorem.
- Modal substitution theorem
- If Ω;⋅ ⊢ π1 : A true and Ω, u: (A valid) ; Γ ⊢ π2 : C true, then Ω;Γ ⊢ [π1/u] π2 : C true.
This framework of separating judgments into distinct collections of hypotheses, also known as multi-zoned or polyadic contexts, is very powerful and extensible; it has been applied for many different modal logics, and also for linear and other substructural logics, to give a few examples. However, relatively few systems of modal logic can be formalised directly in natural deduction. To give proof-theoretic characterisations of these systems, extensions such as labelling or systems of deep inference.
The addition of labels to formulae permits much finer control of the conditions under which rules apply, allowing the more flexible techniques of analytic tableaux to be applied, as has been done in the case of labelled deduction. Labels also allow the naming of worlds in Kripke semantics; Simpson (1993) presents an influential technique for converting frame conditions of modal logics in Kripke semantics into inference rules in a natural deduction formalisation of hybrid logic. Stouppa (2004) surveys the application of many proof theories, such as Avron and Pottinger's hypersequents and Belnap's display logic to such modal logics as S5 and B.
Comparison with other foundational approaches[edit]
Sequent calculus[edit]
The sequent calculus is the chief alternative to natural deduction as a foundation of mathematical logic. In natural deduction the flow of information is bi-directional: elimination rules flow information downwards by deconstruction, and introduction rules flow information upwards by assembly. Thus, a natural deduction proof does not have a purely bottom-up or top-down reading, making it unsuitable for automation in proof search. To address this fact, Gentzen in 1935 proposed his sequent calculus, though he initially intended it as a technical device for clarifying the consistency of predicate logic. Kleene, in his seminal 1952 book Introduction to Metamathematics, gave the first formulation of the sequent calculus in the modern style.[11]
In the sequent calculus all inference rules have a purely bottom-up reading. Inference rules can apply to elements on both sides of the turnstile. (To differentiate from natural deduction, this article uses a double arrow ⇒ instead of the right tack ⊢ for sequents.) The introduction rules of natural deduction are viewed as right rules in the sequent calculus, and are structurally very similar. The elimination rules on the other hand turn into left rules in the sequent calculus. To give an example, consider disjunction; the right rules are familiar:
On the left:
Recall the ∨E rule of natural deduction in localised form:
The proposition A ∨ B, which is the succedent of a premise in ∨E, turns into a hypothesis of the conclusion in the left rule ∨L. Thus, left rules can be seen as a sort of inverted elimination rule. This observation can be illustrated as follows:
| natural deduction | sequent calculus | |
|---|---|---|
| ⇒ |
In the sequent calculus, the left and right rules are performed in lock-step until one reaches the initial sequent, which corresponds to the meeting point of elimination and introduction rules in natural deduction. These initial rules are superficially similar to the hypothesis rule of natural deduction, but in the sequent calculus they describe a transposition or a handshake of a left and a right proposition:
The correspondence between the sequent calculus and natural deduction is a pair of soundness and completeness theorems, which are both provable by means of an inductive argument.
- Soundness of ⇒ wrt. ⊢
- If Γ ⇒ A, then Γ ⊢ A.
- Completeness of ⇒ wrt. ⊢
- If Γ ⊢ A, then Γ ⇒ A.
It is clear by these theorems that the sequent calculus does not change the notion of truth, because the same collection of propositions remain true. Thus, one can use the same proof objects as before in sequent calculus derivations. As an example, consider the conjunctions. The right rule is virtually identical to the introduction rule
| sequent calculus | natural deduction | |
|---|---|---|
The left rule, however, performs some additional substitutions that are not performed in the corresponding elimination rules.
| sequent calculus | natural deduction | |
|---|---|---|
The kinds of proofs generated in the sequent calculus are therefore rather different from those of natural deduction. The sequent calculus produces proofs in what is known as the β-normal η-long form, which corresponds to a canonical representation of the normal form of the natural deduction proof. If one attempts to describe these proofs using natural deduction itself, one obtains what is called the intercalation calculus (first described by John Byrnes), which can be used to formally define the notion of a normal formfor natural deduction.
The substitution theorem of natural deduction takes the form of a structural rule or structural theorem known as cut in the sequent calculus.
- Cut (substitution)
- If Γ ⇒ π1 : A and Γ, u:A ⇒ π2 : C, then Γ ⇒ [π1/u] π2 : C.
In most well behaved logics, cut is unnecessary as an inference rule, though it remains provable as a meta-theorem; the superfluousness of the cut rule is usually presented as a computational process, known as cut elimination. This has an interesting application for natural deduction; usually it is extremely tedious to prove certain properties directly in natural deduction because of an unbounded number of cases. For example, consider showing that a given proposition is not provable in natural deduction. A simple inductive argument fails because of rules like ∨E or E which can introduce arbitrary propositions. However, we know that the sequent calculus is complete with respect to natural deduction, so it is enough to show this unprovability in the sequent calculus. Now, if cut is not available as an inference rule, then all sequent rules either introduce a connective on the right or the left, so the depth of a sequent derivation is fully bounded by the connectives in the final conclusion. Thus, showing unprovability is much easier, because there are only a finite number of cases to consider, and each case is composed entirely of sub-propositions of the conclusion. A simple instance of this is the global consistency theorem: "⋅ ⊢ ⊥ true" is not provable. In the sequent calculus version, this is manifestly true because there is no rule that can have "⋅ ⇒ ⊥" as a conclusion! Proof theorists often prefer to work on cut-free sequent calculus formulations because of such properties.
See also[edit]
- Mathematical logic
- Sequent calculus
- Gerhard Gentzen
- System L (tabular natural deduction)
- Argument map, the general term for tree-like logic notation
Notes[edit]
- ^ Jaśkowski 1934.
- ^ Gentzen 1934, Gentzen 1935.
- ^ Gentzen 1934, p. 176.
- ^ a b Prawitz 1965, Prawitz 2006.
- ^ Martin-Löf 1996.
- ^ This is due to Bolzano, as cited by Martin-Löf 1996, p. 15.
- ^ See also his book Prawitz 1965, Prawitz 2006.
- ^ See the article on lambda calculus for more detail about the concept of substitution.
- ^ Quine (1981). See particularly pages 91–93 for Quine's line-number notation for antecedent dependencies.
- ^ A particular advantage of Kleene's tabular natural deduction systems is that he proves the validity of the inference rules for both propositional calculus and predicate calculus. See Kleene 2002, pp. 44–45, 118–119.
- ^ Kleene 2009, pp. 440–516. See also Kleene 1980.
References[edit]
- Barker-Plummer, Dave; Barwise, Jon; Etchemendy, John (2011). Language Proof and Logic (2nd ed.). CSLI Publications. ISBN 978-1575866321.
- Gallier, Jean (2005). "Constructive Logics. Part I: A Tutorial on Proof Systems and Typed λ-Calculi". Retrieved 12 June 2014.
- Gentzen, Gerhard Karl Erich (1934). "Untersuchungen über das logische Schließen. I". Mathematische Zeitschrift. 39 (2): 176–210. doi:10.1007/BF01201353. S2CID 121546341. (English translation Investigations into Logical Deduction in M. E. Szabo. The Collected Works of Gerhard Gentzen. North-Holland Publishing Company, 1969.)
- Gentzen, Gerhard Karl Erich (1935). "Untersuchungen über das logische Schließen. II". Mathematische Zeitschrift. 39 (3): 405–431. doi:10.1007/bf01201363. S2CID 186239837.
- Girard, Jean-Yves (1990). Proofs and Types. Cambridge Tracts in Theoretical Computer Science. Cambridge University Press, Cambridge, England. Archived from the original on 2016-07-04. Retrieved 2006-04-20. Translated and with appendices by Paul Taylor and Yves Lafont.
- Jaśkowski, Stanisław (1934). On the rules of suppositions in formal logic. Reprinted in Polish logic 1920–39, ed. Storrs McCall.
- Kleene, Stephen Cole (1980) [1952]. Introduction to metamathematics (Eleventh ed.). North-Holland. ISBN 978-0-7204-2103-3.
- Kleene, Stephen Cole (2009) [1952]. Introduction to metamathematics. Ishi Press International. ISBN 978-0-923891-57-2.
- Kleene, Stephen Cole (2002) [1967]. Mathematical logic. Mineola, New York: Dover Publications. ISBN 978-0-486-42533-7.
- Lemmon, Edward John (1965). Beginning logic. Thomas Nelson. ISBN 978-0-17-712040-4.
- Martin-Löf, Per (1996). "On the meanings of the logical constants and the justifications of the logical laws" (PDF). Nordic Journal of Philosophical Logic. 1 (1): 11–60. Lecture notes to a short course at Università degli Studi di Siena, April 1983.
- Pfenning, Frank; Davies, Rowan (2001). "A judgmental reconstruction of modal logic" (PDF). Mathematical Structures in Computer Science. 11 (4): 511–540. CiteSeerX 10.1.1.43.1611. doi:10.1017/S0960129501003322. S2CID 16467268.
- Prawitz, Dag (1965). Natural deduction: A proof-theoretical study. Acta Universitatis Stockholmiensis, Stockholm studies in philosophy 3. Stockholm, Göteborg, Uppsala: Almqvist & Wicksell.
- Prawitz, Dag (2006) [1965]. Natural deduction: A proof-theoretical study. Mineola, New York: Dover Publications. ISBN 978-0-486-44655-4.
- Quine, Willard Van Orman (1981) [1940]. Mathematical logic (Revised ed.). Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-55451-1.
- Quine, Willard Van Orman (1982) [1950]. Methods of logic (Fourth ed.). Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-57176-1.
- Simpson, Alex (1993). The proof theory and semantics of intuitionistic modal logic (PDF). University of Edinburgh. PhD thesis.
- Stoll, Robert Roth (1979) [1963]. Set Theory and Logic. Mineola, New York: Dover Publications. ISBN 978-0-486-63829-4.
- Stouppa, Phiniki (2004). The Design of Modal Proof Theories: The Case of S5. University of Dresden. CiteSeerX 10.1.1.140.1858. MSc thesis.
- Suppes, Patrick Colonel (1999) [1957]. Introduction to logic. Mineola, New York: Dover Publications. ISBN 978-0-486-40687-9.
External links[edit]
- Laboreo, Daniel Clemente, "Introduction to natural deduction."
- Domino On Acid. Natural deduction visualized as a game of dominoes.
- Pelletier, Jeff, "A History of Natural Deduction and Elementary Logic Textbooks."
- Levy, Michel, A Propositional Prover.
https://en.wikipedia.org/wiki/Natural_deduction
METHODS OF PROOF
Subcategories
This category has only the following subcategory.
M
Mathematical induction (1 C, 8 P)
Pages in category "Methods of proof"
The following 11 pages are in this category, out of 11 total. This list may not reflect recent changes (learn more).
A
Analytic proof
Axiomatic system
C
Conditional proof
Counterexample
M
Method of analytic tableaux
N
Natural deduction
P
Proof by contradiction
Proof by contrapositive
Proof by exhaustion
Proof of impossibility
R
RecycleUnits
https://en.wikipedia.org/wiki/Category:Methods_of_proof
In mathematics, an analytic proof is a proof of a theorem in analysis that only makes use of methods from analysis, and which does not predominantly make use of algebraic or geometrical methods. The term was first used by Bernard Bolzano, who first provided a non-analytic proof of his intermediate value theorem and then, several years later provided a proof of the theorem which was free from intuitions concerning lines crossing each other at a point, and so he felt happy calling it analytic (Bolzano 1817).
Bolzano's philosophical work encouraged a more abstract reading of when a demonstration could be regarded as analytic, where a proof is analytic if it does not go beyond its subject matter (Sebastik 2007). In proof theory, an analytic proof has come to mean a proof whose structure is simple in a special way, due to conditions on the kind of inferences that ensure none of them go beyond what is contained in the assumptions and what is demonstrated.
Structural proof theory[edit]
In proof theory, the notion of analytic proof provides the fundamental concept that brings out the similarities between a number of essentially distinct proof calculi, so defining the subfield of structural proof theory. There is no uncontroversial general definition of analytic proof, but for several proof calculi there is an accepted notion. For example:
- In Gerhard Gentzen's natural deduction calculus the analytic proofs are those in normal form; that is, no formula occurrence is both the principal premise of an elimination rule and the conclusion of an introduction rule;
- In Gentzen's sequent calculus the analytic proofs are those that do not use the cut rule.
However, it is possible to extend the inference rules of both calculi so that there are proofs that satisfy the condition but are not analytic. For example, a particularly tricky example of this is the analytic cut rule, used widely in the tableau method, which is a special case of the cut rule where the cut formula is a subformula of side formulae of the cut rule: a proof that contains an analytic cut is by virtue of that rule not analytic.
Furthermore, structural proof theories that are not analogous to Gentzen's theories have other notions of analytic proof. For example, the calculus of structures organises its inference rules into pairs, called the up fragment and the down fragment, and an analytic proof is one that only contains the down fragment.
See also[edit]
References[edit]
- Bernard Bolzano (1817). Purely analytic proof of the theorem that between any two values which give results of opposite sign, there lies at least one real root of the equation. In Abhandlungen der koniglichen bohmischen Gesellschaft der WissenschaftenVol. V, pp.225-48.
- Pfenning (1984). Analytic and Non-analytic Proofs. In Proc. 7th International Conference on Automated Deduction.
- Sebastik (2007). Bolzano's Logic. Entry in the Stanford Encyclopedia of Philosophy.
https://en.wikipedia.org/wiki/Analytic_proof
Proof by exhaustion, also known as proof by cases, proof by case analysis, complete induction or the brute force method, is a method of mathematical proof in which the statement to be proved is split into a finite number of cases or sets of equivalent cases, and where each type of case is checked to see if the proposition in question holds.[1] This is a method of direct proof. A proof by exhaustion typically contains two stages:
- A proof that the set of cases is exhaustive; i.e., that each instance of the statement to be proved matches the conditions of (at least) one of the cases.
- A proof of each of the cases.
The prevalence of digital computers has greatly increased the convenience of using the method of exhaustion (e.g., the first computer-assisted proof of four color theorem in 1976), though such approaches can also be challenged on the basis of mathematical elegance.[2] Expert systems can be used to arrive at answers to many of the questions posed to them. In theory, the proof by exhaustion method can be used whenever the number of cases is finite. However, because most mathematical sets are infinite, this method is rarely used to derive general mathematical results.[3]
In the Curry–Howard isomorphism, proof by exhaustion and case analysis are related to ML-style pattern matching.[citation needed]
https://en.wikipedia.org/wiki/Proof_by_exhaustion
Inductive reasoning is a method of reasoning in which a body of observations is synthesized to come up with a general principle.[1]Inductive reasoning is distinct from deductive reasoning. If the premises are correct, the conclusion of a deductive argument is certain; in contrast, the truth of the conclusion of an inductive argument is probable, based upon the evidence given.[2]
https://en.wikipedia.org/wiki/Inductive_reasoning#Enumerative_induction
A conditional proof is a proof that takes the form of asserting a conditional, and proving that the antecedent of the conditional necessarily leads to the consequent.
https://en.wikipedia.org/wiki/Conditional_proof
In mathematics and logic, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A theory is a consistent, relatively-self-contained body of knowledge which usually contains an axiomatic system and all its derived theorems.[1] An axiomatic system that is completely described is a special kind of formal system. A formal theory is an axiomatic system (usually formulated within model theory) that describes a set of sentences that is closed under logical implication.[2] A formal proof is a complete rendition of a mathematical proof within a formal system.
https://en.wikipedia.org/wiki/Axiomatic_system
In proof theory, the semantic tableau (/tæˈbloʊ, ˈtæbloʊ/; plural: tableaux, also called truth tree) is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic. An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics (Girle 2000).
https://en.wikipedia.org/wiki/Method_of_analytic_tableaux
In mathematics, a proof of impossibility, also known as negative proof, proof of an impossibility theorem, or negative result is a proof demonstrating that a particular problem cannot be solved as described in the claim, or that a particular set of problems cannot be solved in general.[1] Proofs of impossibility often put decades or centuries of work attempting to find a solution to rest. To prove that something is impossible is usually much harder than the opposite task, as it is often necessary to develop a theory.[2]Impossibility theorems are usually expressible as negative existential propositions, or universal propositions in logic (see universal quantification for more).
Perhaps one of the oldest proofs of impossibility is that of the irrationality of square root of 2, which shows that it is impossible to express the square root of 2 as a ratio of integers. Another famous proof of impossibility was the 1882 proof of Ferdinand von Lindemann, showing that the ancient problem of squaring the circle cannot be solved,[3] because the number π is transcendental(i.e., non-algebraic) and only a subset of the algebraic numbers can be constructed by compass and straightedge. Two other classical problems—trisecting the general angle and doubling the cube—were also proved impossible in the 19th century.
A problem arising in the 16th century was that of creating a general formula using radicals expressing the solution of any polynomial equation of fixed degree k, where k ≥ 5. In the 1820s, the Abel–Ruffini theorem (also known as Abel's impossibility theorem) showed this to be impossible,[4] using concepts such as solvable groups from Galois theory—a new subfield of abstract algebra.
Among the most important proofs of impossibility of the 20th century were those related to undecidability, which showed that there are problems that cannot be solved in general by any algorithm at all, with the most famous one being the halting problem. Other similarly-related findings are those of the Gödel's incompleteness theorems, which uncovers some fundamental limitations in the provability of formal systems.[5]
In computational complexity theory, techniques like relativization (see oracle machine) provide "weak" proofs of impossibility excluding certain proof techniques. Other techniques, such as proofs of completeness for a complexity class, provide evidence for the difficulty of problems, by showing them to be just as hard to solve as other known problems that have proved intractable.
https://en.wikipedia.org/wiki/Proof_of_impossibility
In mathematics, a proof by infinite descent, also known as Fermat's method of descent, is a particular kind of proof by contradictionused to show that a statement cannot possibly hold for any number, by showing that if the statement were to hold for a number, then the same would be true for a smaller number, leading to an infinite descent and ultimately a contradiction.[1][2] It is a method which relies on the well-ordering principle, and is often used to show that a given equation, such as a Diophantine equation, has no solutions.[3][4]
Typically, one shows that if a solution to a problem existed, which in some sense was related to one or more natural numbers, it would necessarily imply that a second solution existed, which was related to one or more 'smaller' natural numbers. This in turn would imply a third solution related to smaller natural numbers, implying a fourth solution, therefore a fifth solution, and so on. However, there cannot be an infinity of ever-smaller natural numbers, and therefore by mathematical induction, the original premise—that any solution exists— is incorrect: its correctness produces a contradiction.
An alternative way to express this is to assume one or more solutions or examples exists, from which a smallest solution or example—a minimal counterexample—can then be inferred. Once there, one would try to prove that if a smallest solution exists, then it must imply the existence of a smaller solution (in some sense), which again proves that the existence of any solution would lead to a contradiction.
The earliest uses of the method of infinite descent appear in Euclid's Elements.[3] A typical example is Proposition 31 of Book 7, in which Euclid proves that every composite integer is divided (in Euclid's terminology "measured") by some prime number.[2]
The method was much later developed by Fermat, who coined the term and often used it for Diophantine equations.[4][5] Two typical examples are showing the non-solvability of the Diophantine equation r2 + s4 = t4 and proving Fermat's theorem on sums of two squares, which states that an odd prime p can be expressed as a sum of two squares when p ≡ 1 (mod 4) (see proof). In this way Fermat was able to show the non-existence of solutions in many cases of Diophantine equations of classical interest (for example, the problem of four perfect squares in arithmetic progression).
In some cases, to the modern eye, his "method of infinite descent" is an exploitation of the inversion of the doubling function for rational points on an elliptic curve E. The context is of a hypothetical non-trivial rational point on E. Doubling a point on E roughly doubles the length of the numbers required to write it (as number of digits), so that a "halving" a point gives a rational with smaller terms. Since the terms are positive, they cannot decrease forever.
https://en.wikipedia.org/wiki/Proof_by_infinite_descent
In mathematics, a minimal counterexample is the smallest example which falsifies a claim, and a proof by minimal counterexample is a method of proof which combines the use of a minimal counterexample with the ideas of proof by induction and proof by contradiction.[1][2][3] More specifically, in trying to prove a proposition P, one first assumes by contradiction that it is false, and that therefore there must be at least one counterexample. With respect to some idea of size (which may need to be chosen carefully), one then concludes that there is such a counterexample C that is minimal. In regard to the argument, C is generally something quite hypothetical (since the truth of P excludes the possibility of C), but it may be possible to argue that if C existed, then it would have some definite properties which, after applying some reasoning similar to that in an inductive proof, would lead to a contradiction, thereby showing that the proposition P is indeed true.[4]
If the form of the contradiction is that we can derive a further counterexample D, that is smaller than C in the sense of the working hypothesis of minimality, then this technique is traditionally called proof by infinite descent.[1] In which case, there may be multiple and more complex ways to structure the argument of the proof.
The assumption that if there is a counterexample, there is a minimal counterexample, is based on a well-ordering of some kind. The usual ordering on the natural numbers is clearly possible, by the most usual formulation of mathematical induction; but the scope of the method can include well-ordered induction of any kind.
https://en.wikipedia.org/wiki/Minimal_counterexample
Number theory[edit]
In the number theory of the twentieth century, the infinite descent method was taken up again, and pushed to a point where it connected with the main thrust of algebraic number theory and the study of L-functions. The structural result of Mordell, that the rational points on an elliptic curve E form a finitely-generated abelian group, used an infinite descent argument based on E/2E in Fermat's style.
To extend this to the case of an abelian variety A, André Weil had to make more explicit the way of quantifying the size of a solution, by means of a height function – a concept that became foundational. To show that A(Q)/2A(Q) is finite, which is certainly a necessary condition for the finite generation of the group A(Q) of rational points of A, one must do calculations in what later was recognised as Galois cohomology. In this way, abstractly-defined cohomology groups in the theory become identified with descentsin the tradition of Fermat. The Mordell–Weil theorem was at the start of what later became a very extensive theory.
Irrationality of √2[edit]
The proof that the square root of 2 (√2) is irrational (i.e. cannot be expressed as a fraction of two whole numbers) was discovered by the ancient Greeks, and is perhaps the earliest known example of a proof by infinite descent. Pythagoreans discovered that the diagonal of a square is incommensurable with its side, or in modern language, that the square root of two is irrational. Little is known with certainty about the time or circumstances of this discovery, but the name of Hippasus of Metapontum is often mentioned. For a while, the Pythagoreans treated as an official secret the discovery that the square root of two is irrational, and, according to legend, Hippasus was murdered for divulging it.[6][7][8] The square root of two is occasionally called "Pythagoras' number" or "Pythagoras' Constant", for example Conway & Guy (1996).[9]
The ancient Greeks, not having algebra, worked out a geometric proof by infinite descent (John Horton Conway presented another geometric proof by infinite descent that may be more accessible[10]). The following is an algebraic proof along similar lines:
Suppose that √2 were rational. Then it could be written as
for two natural numbers, p and q. Then squaring would give
so 2 must divide p2. Because 2 is a prime number, it must also divide p, by Euclid's lemma. So p = 2r, for some integer r.
But then,
which shows that 2 must divide q as well. So q = 2s for some integer s.
This gives
- .
Therefore, if √2 could be written as a rational number, then it could always be written as a rational number with smaller parts, which itself could be written with yet-smaller parts, ad infinitum. But this is impossible in the set of natural numbers. Since √2 is a real number, which can be either rational or irrational, the only option left is for √2 to be irrational.[11]
(Alternatively, this proves that if √2 were rational, no "smallest" representation as a fraction could exist, as any attempt to find a "smallest" representation p/q would imply that a smaller one existed, which is a similar contradiction.)
https://en.wikipedia.org/wiki/Proof_by_infinite_descent
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."[1][note 1] Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers).
Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, for example, as approximated by the latter (Diophantine approximation).
The older term for number theory is arithmetic. By the early twentieth century, it had been superseded by "number theory".[note 2] (The word "arithmetic" is used by the general public to mean "elementary calculations"; it has also acquired other meanings in mathematical logic, as in Peano arithmetic, and computer science, as in floating point arithmetic.) The use of the term arithmetic for number theory regained some ground in the second half of the 20th century, arguably in part due to French influence.[note 3] In particular, arithmetical is commonly preferred as an adjective to number-theoretic.
https://en.wikipedia.org/wiki/Number_theory
In mathematics, an L-function is a meromorphic function on the complex plane, associated to one out of several categories of mathematical objects. An L-series is a Dirichlet series, usually convergent on a half-plane, that may give rise to an L-function via analytic continuation. The Riemann zeta function is an example of an L-function, and one important conjecture involving L-functions is the Riemann hypothesis and its generalization.
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases still out of reach of proof, are set out in a systematic way. Because of the Euler product formula there is a deep connection between L-functions and the theory of prime numbers.
https://en.wikipedia.org/wiki/L-function
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these L-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case (not the number field case).
Global L-functions can be associated to elliptic curves, number fields (in which case they are called Dedekind zeta-functions), Maass forms, and Dirichlet characters (in which case they are called Dirichlet L-functions). When the Riemann hypothesis is formulated for Dedekind zeta-functions, it is known as the extended Riemann hypothesis (ERH) and when it is formulated for Dirichlet L-functions, it is known as the generalized Riemann hypothesis (GRH). These two statements will be discussed in more detail below. (Many mathematicians use the label generalized Riemann hypothesis to cover the extension of the Riemann hypothesis to all global L-functions, not just the special case of Dirichlet L-functions.)
https://en.wikipedia.org/wiki/Generalized_Riemann_hypothesis
In analytic number theory and related branches of mathematics, a complex-valued arithmetic function is a Dirichlet character of modulus (where is a positive integer) if for all integers and :[1]
- 1) i.e. is completely multiplicative.
- 2)
- 3) ; i.e. is periodic with period .
The simplest possible character, called the principal character, usually denoted , (see Notation below) exists for all moduli:[2]
Dirichlet introduced these functions in his 1837 paper on primes in arithmetic progressions.[3][4]
https://en.wikipedia.org/wiki/Dirichlet_character
Generalized Riemann hypothesis (GRH)[edit]
The generalized Riemann hypothesis (for Dirichlet L-functions) was probably formulated for the first time by Adolf Piltz in 1884.[1]Like the original Riemann hypothesis, it has far reaching consequences about the distribution of prime numbers.
The formal statement of the hypothesis follows. A Dirichlet character is a completely multiplicative arithmetic function χ such that there exists a positive integer k with χ(n + k) = χ(n) for all n and χ(n) = 0 whenever gcd(n, k) > 1. If such a character is given, we define the corresponding Dirichlet L-function by
for every complex number s such that Re s > 1. By analytic continuation, this function can be extended to a meromorphic function(only when is primitive) defined on the whole complex plane. The generalized Riemann hypothesis asserts that, for every Dirichlet character χ and every complex number s with L(χ, s) = 0, if s is not a negative real number, then the real part of s is 1/2.
The case χ(n) = 1 for all n yields the ordinary Riemann hypothesis.
Extended Riemann hypothesis (ERH)[edit]
Suppose K is a number field (a finite-dimensional field extension of the rationals Q) with ring of integers OK (this ring is the integral closure of the integers Z in K). If a is an ideal of OK, other than the zero ideal, we denote its norm by Na. The Dedekind zeta-function of K is then defined by
for every complex number s with real part > 1. The sum extends over all non-zero ideals a of OK.
The Dedekind zeta-function satisfies a functional equation and can be extended by analytic continuation to the whole complex plane. The resulting function encodes important information about the number field K. The extended Riemann hypothesis asserts that for every number field K and every complex number s with ζK(s) = 0: if the real part of s is between 0 and 1, then it is in fact 1/2.
The ordinary Riemann hypothesis follows from the extended one if one takes the number field to be Q, with ring of integers Z.
The ERH implies an effective version[6] of the Chebotarev density theorem: if L/K is a finite Galois extension with Galois group G, and C a union of conjugacy classes of G, the number of unramified primes of K of norm below x with Frobenius conjugacy class in Cis
where the constant implied in the big-O notation is absolute, n is the degree of L over Q, and Δ its discriminant.
See also[edit]
https://en.wikipedia.org/wiki/Generalized_Riemann_hypothesis
The Artin conjecture[edit]
The Artin conjecture on Artin L-functions states that the Artin L-function of a non-trivial irreducible representation ρ is analytic in the whole complex plane.[1]
This is known for one-dimensional representations, the L-functions being then associated to Hecke characters — and in particular for Dirichlet L-functions.[1] More generally Artin showed that the Artin conjecture is true for all representations induced from 1-dimensional representations. If the Galois group is supersolvable or more generally monomial, then all representations are of this form so the Artin conjecture holds.
André Weil proved the Artin conjecture in the case of function fields.
Two-dimensional representations are classified by the nature of the image subgroup: it may be cyclic, dihedral, tetrahedral, octahedral, or icosahedral. The Artin conjecture for the cyclic or dihedral case follows easily from Erich Hecke's work. Langlands used the base change lifting to prove the tetrahedral case, and Jerrold Tunnell extended his work to cover the octahedral case; Andrew Wiles used these cases in his proof of the Taniyama–Shimura conjecture. Richard Taylor and others have made some progress on the (non-solvable) icosahedral case; this is an active area of research. The Artin conjecture for odd, irreducible, two-dimensional representations follows from the proof of Serre's modularity conjecture, regardless of projective image subgroup.
Brauer's theorem on induced characters implies that all Artin L-functions are products of positive and negative integral powers of Hecke L-functions, and are therefore meromorphic in the whole complex plane.
Langlands (1970) pointed out that the Artin conjecture follows from strong enough results from the Langlands philosophy, relating to the L-functions associated to automorphic representations for GL(n) for all . More precisely, the Langlands conjectures associate an automorphic representation of the adelic group GLn(AQ) to every n-dimensional irreducible representation of the Galois group, which is a cuspidal representation if the Galois representation is irreducible, such that the Artin L-function of the Galois representation is the same as the automorphic L-function of the automorphic representation. The Artin conjecture then follows immediately from the known fact that the L-functions of cuspidal automorphic representations are holomorphic. This was one of the major motivations for Langlands' work.
https://en.wikipedia.org/wiki/Artin_L-function#The_Artin_conjecture
In mathematics, a group is supersolvable (or supersoluble) if it has an invariant normal series where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability.
https://en.wikipedia.org/wiki/Supersolvable_group
In group theory, a branch of abstract algebra, a cyclic group or monogenous group is a group that is generated by a single element.[1] That is, it is a set of invertible elements with a single associative binary operation, and it contains an element g such that every other element of the group may be obtained by repeatedly applying the group operation to g or its inverse. Each element can be written as a power of g in multiplicative notation, or as a multiple of g in additive notation. This element g is called a generator of the group.[1]
Every infinite cyclic group is isomorphic to the additive group of Z, the integers. Every finite cyclic group of order n is isomorphic to the additive group of Z/nZ, the integers modulo n. Every cyclic group is an abelian group (meaning that its group operation is commutative), and every finitely generated abelian group is a direct product of cyclic groups.
Every cyclic group of prime order is a simple group, which cannot be broken down into smaller groups. In the classification of finite simple groups, one of the three infinite classes consists of the cyclic groups of prime order. The cyclic groups of prime order are thus among the building blocks from which all groups can be built.
https://en.wikipedia.org/wiki/Cyclic_group
In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminates in the trivial subgroup.
https://en.wikipedia.org/wiki/Solvable_group
Tuesday, September 14, 2021
09-14-2021-0302 - Ferredoxins redox iron
Ferredoxins (from Latin ferrum: iron + redox, often abbreviated "fd") are iron–sulfur proteins that mediate electron transfer in a range of metabolic reactions. The term "ferredoxin" was coined by D.C. Wharton of the DuPont Co. and applied to the "iron protein" first purified in 1962 by Mortenson, Valentine, and Carnahan from the anaerobic bacterium Clostridium pasteurianum.[1][2]
Another redox protein, isolated from spinach chloroplasts, was termed "chloroplast ferredoxin".[3] The chloroplast ferredoxin is involved in both cyclic and non-cyclic photophosphorylation reactions of photosynthesis. In non-cyclic photophosphorylation, ferredoxin is the last electron acceptor thus reducing the enzyme NADP+ reductase. It accepts electrons produced from sunlight-excited chlorophyll and transfers them to the enzyme ferredoxin: NADP+ oxidoreductase EC 1.18.1.2.
Ferredoxins are small proteins containing iron and sulfur atoms organized as iron–sulfur clusters. These biological "capacitors" can accept or discharge electrons, with the effect of a change in the oxidation state of the iron atoms between +2 and +3. In this way, ferredoxin acts as an electron transfer agent in biological redox reactions.
Other bioinorganic electron transport systems include rubredoxins, cytochromes, blue copper proteins, and the structurally related Rieske proteins.
Ferredoxins can be classified according to the nature of their iron–sulfur clusters and by sequence similarity.
https://en.wikipedia.org/wiki/Ferredoxin
Friday, September 17, 2021
09-17-2021-0056 - Phantom Energy
Phantom energy is a hypothetical form of dark energy satisfying the equation of state with . It possesses negative kinetic energy, and predicts expansion of the universe in excess of that predicted by a cosmological constant, which leads to a Big Rip. The idea of phantom energy is often dismissed, as it would suggest that the vacuum is unstable with negative mass particles bursting into existence.[1] The concept is hence tied to emerging theories of a continuously-created negative mass dark fluid, in which the cosmological constant can vary as a function of time.[2][3]
Big Rip mechanism[edit]
The existence of phantom energy could cause the expansion of the universe to accelerate so quickly that a scenario known as the Big Rip, a possible end to the universe, occurs. The expansion of the universe reaches an infinite degree in finite time, causing expansion to accelerate without bounds. This acceleration necessarily passes the speed of light (since it involves expansion of the universe itself, not particles moving within it), causing more and more objects to leave our observable universe faster than its expansion, as light and information emitted from distant stars and other cosmic sources cannot "catch up" with the expansion. As the observable universe expands, objects will be unable to interact with each other via fundamental forces, and eventually, the expansion will prevent any action of forces between any particles, even within atoms, "ripping apart" the universe, making distances between individual particles infinite.
One application of phantom energy in 2007 was to a cyclic model of the universe, which reverses its expansion extremely shortly before the would-be Big Rip.[4]
See also[edit]
References[edit]
- ^ Carroll, Sean (September 14, 2004). "Vacuum stability". Preposterous Universe Blog. Retrieved February 1, 2019.; however, note that the preceding source also contains a link to another blog post on the same blog (a post dated one day earlier!) that also discusses (a lot) the topic of "", etc.; therefore, [feel free to] "see also": Carroll, Sean (September 13, 2004). "Phantom Energy". "Preposterous Universe" [blog]. Archived from the original on October 28, 2014. Retrieved November 2, 2020.
- ^ Farnes, J. S. (2018). "A Unifying Theory of Dark Energy and Dark Matter: Negative Masses and Matter Creation within a Modified ΛCDM Framework". Astronomy and Astrophysics. 620: A92. arXiv:1712.07962. Bibcode:2018A&A...620A..92F. doi:10.1051/0004-6361/201832898. S2CID 53600834.
- ^ Farnes, Jamie (December 17, 2018). "Bizarre 'Dark Fluid' with Negative Mass Could Dominate the Universe".
- ^ Lauris Baum and Paul Frampton (2007). "Turnaround In Cyclic Cosmology". Phys. Rev. Lett. 98 (7): 071301. arXiv:hep-th/0610213. Bibcode:2007PhRvL..98g1301B. doi:10.1103/PhysRevLett.98.071301. PMID 17359014. S2CID 17698158.
Further reading[edit]
- Robert R. Caldwell et al.: Phantom Energy and Cosmic Doomsday
https://en.wikipedia.org/wiki/Phantom_energy
https://en.wikipedia.org/wiki/Sfermion#Sleptons
https://en.wikipedia.org/wiki/Introduction_to_eigenstates
https://en.wikipedia.org/wiki/Spacetime_symmetries
https://en.wikipedia.org/wiki/Soliton
https://en.wikipedia.org/wiki/Replica_trick
https://en.wikipedia.org/wiki/Universe
https://www.livescience.com/strange-theories-about-the-universe.html
https://www.vox.com/2015/6/29/8847863/holographic-principle-universe-theory-physics
https://en.wikipedia.org/wiki/Holographic_principle
The holographic principle is a tenet of string theories and a supposed property of quantum gravity that states that the description of a volume of space can be thought of as encoded on a lower-dimensional boundary to the region—such as a light-likeboundary like a gravitational horizon. First proposed by Gerard 't Hooft, it was given a precise string-theory interpretation by Leonard Susskind,[1] who combined his ideas with previous ones of 't Hooft and Charles Thorn.[1][2] As pointed out by Raphael Bousso,[3] Thorn observed in 1978 that string theory admits a lower-dimensional description in which gravity emerges from it in what would now be called a holographic way. The prime example of holography is the AdS/CFT correspondence.
The holographic principle was inspired by black hole thermodynamics, which conjectures that the maximal entropy in any region scales with the radius squared, and not cubed as might be expected. In the case of a black hole, the insight was that the informational content of all the objects that have fallen into the hole might be entirely contained in surface fluctuations of the event horizon. The holographic principle resolves the black hole information paradox within the framework of string theory.[4]However, there exist classical solutions to the Einstein equations that allow values of the entropy larger than those allowed by an area law, hence in principle larger than those of a black hole. These are the so-called "Wheeler's bags of gold". The existence of such solutions conflicts with the holographic interpretation, and their effects in a quantum theory of gravity including the holographic principle are not fully understood yet.[5]
https://en.wikipedia.org/wiki/Holographic_principle
In physics, black hole thermodynamics[1] is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black-hole event horizons. As the study of the statistical mechanics of black-body radiation led to the development of the theory of quantum mechanics, the effort to understand the statistical mechanics of black holes has had a deep impact upon the understanding of quantum gravity, leading to the formulation of the holographic principle.[2]
https://en.wikipedia.org/wiki/Black_hole_thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, radiation, and physical properties of matter. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopicconstituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology.
https://en.wikipedia.org/wiki/Thermodynamics
Chemical thermodynamics is the study of the interrelation of heat and work with chemical reactions or with physical changes of state within the confines of the laws of thermodynamics. Chemical thermodynamics involves not only laboratory measurements of various thermodynamic properties, but also the application of mathematical methods to the study of chemical questions and the spontaneity of processes.
The structure of chemical thermodynamics is based on the first two laws of thermodynamics. Starting from the first and second laws of thermodynamics, four equations called the "fundamental equations of Gibbs" can be derived. From these four, a multitude of equations, relating the thermodynamic properties of the thermodynamic system can be derived using relatively simple mathematics. This outlines the mathematical framework of chemical thermodynamics.[1]
https://en.wikipedia.org/wiki/Chemical_thermodynamics
An object with relatively high entropy is microscopically random, like a hot gas. A known configuration of classical fields has zero entropy: there is nothing random about electric and magnetic fields, or gravitational waves. Since black holes are exact solutions of Einstein's equations, they were thought not to have any entropy either.
But Jacob Bekenstein noted that this leads to a violation of the second law of thermodynamics. If one throws a hot gas with entropy into a black hole, once it crosses the event horizon, the entropy would disappear. The random properties of the gas would no longer be seen once the black hole had absorbed the gas and settled down. One way of salvaging the second law is if black holes are in fact random objects with an entropy that increases by an amount greater than the entropy of the consumed gas.
Bekenstein assumed that black holes are maximum entropy objects—that they have more entropy than anything else in the same volume. In a sphere of radius R, the entropy in a relativistic gas increases as the energy increases. The only known limit is gravitational; when there is too much energy the gas collapses into a black hole. Bekenstein used this to put an upper bound on the entropy in a region of space, and the bound was proportional to the area of the region. He concluded that the black hole entropy is directly proportional to the area of the event horizon.[9] Gravitational time dilation causes time, from the perspective of a remote observer, to stop at the event horizon. Due to the natural limit on maximum speed of motion, this prevents falling objects from crossing the event horizon no matter how close they get to it. Since any change in quantum state requires time to flow, all objects and their quantum information state stay imprinted on the event horizon. Bekenstein concluded that from the perspective of any remote observer, the black hole entropy is directly proportional to the area of the event horizon.
Stephen Hawking had shown earlier that the total horizon area of a collection of black holes always increases with time. The horizon is a boundary defined by light-like geodesics; it is those light rays that are just barely unable to escape. If neighboring geodesics start moving toward each other they eventually collide, at which point their extension is inside the black hole. So the geodesics are always moving apart, and the number of geodesics which generate the boundary, the area of the horizon, always increases. Hawking's result was called the second law of black hole thermodynamics, by analogy with the law of entropy increase, but at first, he did not take the analogy too seriously.
Hawking knew that if the horizon area were an actual entropy, black holes would have to radiate. When heat is added to a thermal system, the change in entropy is the increase in mass-energy divided by temperature:
(Here the term δM c2 is substituted for the thermal energy added to the system, generally by non-integrable random processes, in contrast to dS, which is a function of a few "state variables" only, i.e. in conventional thermodynamics only of the Kelvin temperature T and a few additional state variables as, e.g., the pressure.)
If black holes have a finite entropy, they should also have a finite temperature. In particular, they would come to equilibrium with a thermal gas of photons. This means that black holes would not only absorb photons, but they would also have to emit them in the right amount to maintain detailed balance.
Time-independent solutions to field equations do not emit radiation, because a time-independent background conserves energy. Based on this principle, Hawking set out to show that black holes do not radiate. But, to his surprise, a careful analysis convinced him that they do, and in just the right way to come to equilibrium with a gas at a finite temperature. Hawking's calculation fixed the constant of proportionality at 1/4; the entropy of a black hole is one quarter its horizon area in Planck units.[10]
The entropy is proportional to the logarithm of the number of microstates, the ways a system can be configured microscopically while leaving the macroscopic description unchanged. Black hole entropy is deeply puzzling – it says that the logarithm of the number of states of a black hole is proportional to the area of the horizon, not the volume in the interior.[11]
Later, Raphael Bousso came up with a covariant version of the bound based upon null sheets.[12]
Black hole information paradox[edit]
Hawking's calculation suggested that the radiation which black holes emit is not related in any way to the matter that they absorb. The outgoing light rays start exactly at the edge of the black hole and spend a long time near the horizon, while the infalling matter only reaches the horizon much later. The infalling and outgoing mass/energy interact only when they cross. It is implausible that the outgoing state would be completely determined by some tiny residual scattering.[citation needed]
Hawking interpreted this to mean that when black holes absorb some photons in a pure state described by a wave function, they re-emit new photons in a thermal mixed state described by a density matrix. This would mean that quantum mechanics would have to be modified because, in quantum mechanics, states which are superpositions with probability amplitudes never become states which are probabilistic mixtures of different possibilities.[note 1]
Troubled by this paradox, Gerard 't Hooft analyzed the emission of Hawking radiation in more detail.[13][self-published source?] He noted that when Hawking radiation escapes, there is a way in which incoming particles can modify the outgoing particles. Their gravitational field would deform the horizon of the black hole, and the deformed horizon could produce different outgoing particles than the undeformed horizon. When a particle falls into a black hole, it is boosted relative to an outside observer, and its gravitational field assumes a universal form. 't Hooft showed that this field makes a logarithmic tent-pole shaped bump on the horizon of a black hole, and like a shadow, the bump is an alternative description of the particle's location and mass. For a four-dimensional spherical uncharged black hole, the deformation of the horizon is similar to the type of deformation which describes the emission and absorption of particles on a string-theory world sheet. Since the deformations on the surface are the only imprint of the incoming particle, and since these deformations would have to completely determine the outgoing particles, 't Hooft believed that the correct description of the black hole would be by some form of string theory.
This idea was made more precise by Leonard Susskind, who had also been developing holography, largely independently. Susskind argued that the oscillation of the horizon of a black hole is a complete description[note 2] of both the infalling and outgoing matter, because the world-sheet theory of string theory was just such a holographic description. While short strings have zero entropy, he could identify long highly excited string states with ordinary black holes. This was a deep advance because it revealed that strings have a classical interpretation in terms of black holes.
This work showed that the black hole information paradox is resolved when quantum gravity is described in an unusual string-theoretic way assuming the string-theoretical description is complete, unambiguous and non-redundant.[15] The space-time in quantum gravity would emerge as an effective description of the theory of oscillations of a lower-dimensional black-hole horizon, and suggest that any black hole with appropriate properties, not just strings, would serve as a basis for a description of string theory.
In 1995, Susskind, along with collaborators Tom Banks, Willy Fischler, and Stephen Shenker, presented a formulation of the new M-theory using a holographic description in terms of charged point black holes, the D0 branes of type IIA string theory. The matrix theory they proposed was first suggested as a description of two branes in 11-dimensional supergravity by Bernard de Wit, Jens Hoppe, and Hermann Nicolai. The later authors reinterpreted the same matrix models as a description of the dynamics of point black holes in particular limits. Holography allowed them to conclude that the dynamics of these black holes give a complete non-perturbative formulation of M-theory. In 1997, Juan Maldacena gave the first holographic descriptions of a higher-dimensional object, the 3+1-dimensional type IIB membrane, which resolved a long-standing problem of finding a string description which describes a gauge theory. These developments simultaneously explained how string theory is related to some forms of supersymmetric quantum field theories.
Information content is defined as the logarithm of the reciprocal of the probability that a system is in a specific microstate, and the information entropy of a system is the expected value of the system's information content. This definition of entropy is equivalent to the standard Gibbs entropy used in classical physics. Applying this definition to a physical system leads to the conclusion that, for a given energy in a given volume, there is an upper limit to the density of information (the Bekenstein bound) about the whereabouts of all the particles which compose matter in that volume. In particular, a given volume has an upper limit of information it can contain, at which it will collapse into a black hole.
This suggests that matter itself cannot be subdivided infinitely many times and there must be an ultimate level of fundamental particles. As the degrees of freedom of a particle are the product of all the degrees of freedom of its sub-particles, were a particle to have infinite subdivisions into lower-level particles, the degrees of freedom of the original particle would be infinite, violating the maximal limit of entropy density. The holographic principle thus implies that the subdivisions must stop at some level.
The most rigorous realization of the holographic principle is the AdS/CFT correspondence by Juan Maldacena. However, J.D. Brown and Marc Henneaux had rigorously proved already in 1986, that the asymptotic symmetry of 2+1 dimensional gravity gives rise to a Virasoro algebra, whose corresponding quantum theory is a 2-dimensional conformal field theory.[16]
See also[edit]
https://en.wikipedia.org/wiki/Holographic_principle
In geometry, a geodesic (/ˌdʒiːəˈdɛsɪk, ˌdʒiːoʊ-, -ˈdiː-, -zɪk/[1][2]) is commonly a curve representing in some sense the shortest[a] path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a "straight line" to a more general setting.
The noun geodesic[b] and the adjective geodetic[c] come from geodesy, the science of measuring the size and shape of Earth, while many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.
In a Riemannian manifold or submanifold, geodesics are characterised by the property of having vanishing geodesic curvature. More generally, in the presence of an affine connection, a geodesic is defined to be a curve whose tangent vectors remain parallel if they are transported along it. Applying this to the Levi-Civita connection of a Riemannian metric recovers the previous notion.
Geodesics are of particular importance in general relativity. Timelike geodesics in general relativity describe the motion of free fallingtest particles.
https://en.wikipedia.org/wiki/Geodesic
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations. In contrast, the macrostate of a system refers to its macroscopic properties, such as its temperature, pressure, volume and density.[1] Treatments on statistical mechanics[2][3] define a macrostate as follows: a particular set of values of energy, the number of particles, and the volume of an isolated thermodynamic system is said to specify a particular macrostate of it. In this description, microstates appear as different possible ways the system can achieve a particular macrostate.
https://en.wikipedia.org/wiki/Microstate_(statistical_mechanics)
Entropic gravity, also known as emergent gravity, is a theory in modern physics that describes gravity as an entropic force—a force with macro-scale homogeneity but which is subject to quantum-level disorder—and not a fundamental interaction. The theory, based on string theory, black hole physics, and quantum information theory, describes gravity as an emergent phenomenon that springs from the quantum entanglement of small bits of spacetimeinformation. As such, entropic gravity is said to abide by the second law of thermodynamicsunder which the entropy of a physical system tends to increase over time.
The theory has been controversial within the physics community but has sparked research and experiments to test its validity.
https://en.wikipedia.org/wiki/Entropic_gravity
Implicate order and explicate order are ontological concepts for quantum theory coined by theoretical physicist David Bohmduring the early 1980s. They are used to describe two different frameworks for understanding the same phenomenon or aspect of reality. In particular, the concepts were developed in order to explain the bizarre behavior of subatomic particles which quantum physics struggles to explain.
In Bohm's Wholeness and the Implicate Order, he used these notions to describe how the appearance of such phenomena might appear differently, or might be characterized by, varying principal factors, depending on contexts such as scales.[1] The implicate (also referred to as the "enfolded") order is seen as a deeper and more fundamental order of reality. In contrast, the explicate or "unfolded" order includes the abstractions that humans normally perceive. As he wrote:
- In the enfolded [or implicate] order, space and time are no longer the dominant factors determining the relationships of dependence or independence of different elements. Rather, an entirely different sort of basic connection of elements is possible, from which our ordinary notions of space and time, along with those of separately existent material particles, are abstracted as forms derived from the deeper order. These ordinary notions in fact appear in what is called the "explicate" or "unfolded" order, which is a special and distinguished form contained within the general totality of all the implicate orders (Bohm 1980, p. xv).
https://en.wikipedia.org/wiki/Implicate_and_explicate_order
https://en.wikipedia.org/wiki/Cosmological_principle
- Ordinary (baryonic) matter (4.9%)
- Dark matter (26.8%)
- Dark energy (68.3%)[6]
https://en.wikipedia.org/wiki/Observable_universe
https://en.wikipedia.org/wiki/Observable_universe
https://en.wikipedia.org/wiki/Inflation_(cosmology)
https://en.wikipedia.org/wiki/Lambda-CDM_model
https://en.wikipedia.org/wiki/Observable_universe
https://en.wikipedia.org/wiki/Dark_matter
https://en.wikipedia.org/wiki/Dark_energy
https://en.wikipedia.org/wiki/Dark_fluid
https://en.wikipedia.org/wiki/Dark_flow
https://en.wikipedia.org/wiki/Anisotropy
https://en.wikipedia.org/wiki/Great_Attractor
https://en.wikipedia.org/wiki/Virgocentric_flow
https://en.wikipedia.org/wiki/Category:Exotic_matter
https://en.wikipedia.org/wiki/Strangelet
https://en.wikipedia.org/wiki/Quark–gluon_plasma
https://en.wikipedia.org/wiki/Strange_matter
https://en.wikipedia.org/wiki/Rydberg_polaron
https://en.wikipedia.org/wiki/Spinor_condensate
https://en.wikipedia.org/wiki/Hypernucleus
https://en.wikipedia.org/wiki/Hyperon
https://en.wikipedia.org/wiki/Hypertriton
https://en.wikipedia.org/wiki/Macroscopic_quantum_phenomena
https://en.wikipedia.org/wiki/Negative_mass
https://en.wikipedia.org/wiki/Wormhole
https://en.wikipedia.org/wiki/Space-division_multiple_access
https://en.wikipedia.org/wiki/Weak_interaction
https://en.wikipedia.org/wiki/Mirror_Universe
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Circular_symmetry
https://en.wikipedia.org/wiki/White_dwarf
https://en.wikipedia.org/wiki/Negative_mass
Neutronium and the periodic table[edit]
The term "neutronium" was coined in 1926 by Andreas von Antropoff for a conjectured form of matter made up of neutrons with no protons or electrons, which he placed as the chemical element of atomic number zero at the head of his new version of the periodic table.[6] It was subsequently placed in the middle of several spiral representations of the periodic system for classifying the chemical elements, such as those of Charles Janet (1928), E. I. Emerson (1944), and John D. Clark (1950).
Although the term is not used in the scientific literature either for a condensed form of matter, or as an element, there have been reports that, besides the free neutron, there may exist two bound forms of neutrons without protons.[7] If neutronium were considered to be an element, then these neutron clusters could be considered to be the isotopes of that element. However, these reports have not been further substantiated.
- Mononeutron: An isolated neutron undergoes beta decay with a mean lifetime of approximately 15 minutes (half-life of approximately 10 minutes), becoming a proton (the nucleus of hydrogen), an electron and an antineutrino.
- Dineutron: The dineutron, containing two neutrons, was unambiguously observed in 2012 in the decay of beryllium-16.[8][9] It is not a bound particle, but had been proposed as an extremely short-lived resonance state produced by nuclear reactions involving tritium. It has been suggested to have a transitory existence in nuclear reactions produced by helions (helium 3 nuclei, completely ionised) that result in the formation of a proton and a nucleus having the same atomic number as the target nucleus but a mass number two units greater. The dineutron hypothesis had been used in nuclear reactions with exotic nuclei for a long time.[10] Several applications of the dineutron in nuclear reactions can be found in review papers.[11] Its existence has been proven to be relevant for nuclear structure of exotic nuclei.[12] A system made up of only two neutrons is not bound, though the attraction between them is very nearly enough to make them so.[13] This has some consequences on nucleosynthesis and the abundance of the chemical elements.[11][14]
- Trineutron: A trineutron state consisting of three bound neutrons has not been detected, and is not expected to exist[citation needed]even for a short time.
- Tetraneutron: A tetraneutron is a hypothetical particle consisting of four bound neutrons. Reports of its existence have not been replicated.[15]
- Pentaneutron: Calculations indicate that the hypothetical pentaneutron state, consisting of a cluster of five neutrons, would not be bound.[16]
Although not called "neutronium", the National Nuclear Data Center's Nuclear Wallet Cards lists as its first "isotope" an "element" with the symbol n and atomic number Z = 0 and mass number A = 1. This isotope is described as decaying to element H with a half life of 10.24±0.2 min.[17]
Properties[edit]
Neutron matter is equivalent to a chemical element with atomic number 0, which is to say that it is equivalent to a species of atoms having no protons in their atomic nuclei. It is extremely radioactive; its only legitimate equivalent isotope, the free neutron, has a half-life of 10 minutes, which is approximately half that of the most stable known isotope of francium. Neutron matter decays quickly into hydrogen. Neutron matter has no electronic structure on account of its total lack of electrons. As an equivalent element, however, it could be classified as a noble gas.
Bulk neutron matter has never been viewed. It is assumed that neutron matter would appear as a chemically inert gas, if enough could be collected together to be viewed as a bulk gas or liquid, because of the general appearance of the elements in the noble gas column of the periodic table.
While this lifetime is long enough to permit the study of neutronium's chemical properties, there are serious practical problems. Having no charge or electrons, neutronium would not interact strongly with ordinary low-energy photons (visible light) and would feel no electrostatic forces, so it would diffuse into the walls of most containers made of ordinary matter. Certain materials are able to resist diffusion or absorption of ultracold neutrons due to nuclear-quantum effects, specifically reflection caused by the strong interaction. At ambient temperature and in the presence of other elements, thermal neutrons readily undergo neutron capture to form heavier (and often radioactive) isotopes of that element.
Neutron matter at standard pressure and temperature is predicted by the ideal gas law to be less dense than even hydrogen, with a density of only 0.045 kg/m3 (roughly 27 times less dense than air and half as dense as hydrogen gas). Neutron matter is expected to remain gaseous down to absolute zero at normal pressures, as the zero-point energy of the system is too high to allow condensation. However, neutron matter should in theory form a degenerate gaseous superfluid at these temperatures, composed of transient neutron-pairs called dineutrons. Under extremely low pressure, this low temperature, gaseous superfluid should exhibit quantum coherence producing a Bose–Einstein condensate. At higher temperatures, neutron matter will only condense with sufficient pressure, and solidify with even greater pressure. Such pressures exist in neutron stars, where the extreme pressure causes the neutron matter to become degenerate. However, in the presence of atomic matter compressed to the state of electron degeneracy, β− decay may be inhibited due to the Pauli exclusion principle, thus making free neutrons stable. Also, elevated pressures should make neutrons degenerate themselves.
Compared to ordinary elements, neutronium should be more compressible due to the absence of electrically charged protons and electrons. This makes neutronium more energetically favorable than (positive-Z) atomic nuclei and leads to their conversion to (degenerate) neutronium through electron capture, a process that is believed to occur in stellar cores in the final seconds of the lifetime of massive stars, where it is facilitated by cooling via
ν
e emission. As a result, degenerate neutronium can have a density of 4×1017 kg/m3[citation needed], roughly 14 orders of magnitude denser than the densest known ordinary substances. It was theorized that extreme pressures of order 100 MeV/fm3 might deform the neutrons into a cubic symmetry, allowing tighter packing of neutrons,[18] or cause a strange matter formation.
See also[edit]
https://en.wikipedia.org/wiki/Neutronium
The pressuron is a hypothetical scalar particle which couples to both gravity and matter theorised in 2013.[1] Although originally postulated without self-interaction potential, the pressuron is also a dark energy candidate when it has such a potential.[2]
Decoupling mechanism[edit]
If one considers a pressure-free perfect fluid (also known as a "dust"), the effective material Lagrangian becomes ,[6] where is the mass of the ith particle, its position, and the Dirac delta function, while at the same time the trace of the stress-energy tensor reduces to . Thus, there is an exact cancellation of the pressuron material source term , and hence the pressuron effectively decouples from pressure-free matter fields.
In other words, the specific coupling between the scalar field and the material fields in the Lagrangian leads to a decoupling between the scalar field and the matter fields in the limit that the matter field is exerting zero pressure.
https://en.wikipedia.org/wiki/Pressuron
Vertical pressure variation is the variation in pressure as a function of elevation. Depending on the fluid in question and the context being referred to, it may also vary significantly in dimensions perpendicular to elevation as well, and these variations have relevance in the context of pressure gradient force and its effects. However, the vertical variation is especially significant, as it results from the pull of gravity on the fluid; namely, for the same given fluid, a decrease in elevation within it corresponds to a taller column of fluid weighing down on that point.
Hydrostatic paradox[edit]
| Wikimedia Commons has media related to Hydrostatic paradox. |
The barometric formula depends only on the height of the fluid chamber, and not on its width or length. Given a large enough height, any pressure may be attained. This feature of hydrostatics has been called the hydrostatic paradox. As expressed by W. H. Besant,[2]
- Any quantity of liquid, however small, may be made to support any weight, however large.
The Dutch scientist Simon Stevin was the first to explain the paradox mathematically.[3] In 1916 Richard Glazebrook mentioned the hydrostatic paradox as he described an arrangement he attributed to Pascal: a heavy weight W rests on a board with area A resting on a fluid bladder connected to a vertical tube with cross-sectional area α. Pouring water of weight w down the tube will eventually raise the heavy weight. Balance of forces leads to the equation
Glazebrook says, "By making the area of the board considerable and that of the tube small, a large weight W can be supported by a small weight w of water. This fact is sometimes described as the hydrostatic paradox."[4]
Demonstrations of the hydrostatic paradox are used in teaching the phenomenon.[5][6]
https://en.wikipedia.org/wiki/Vertical_pressure_variation#Hydrostatic_paradox
A gravitational singularity, spacetime singularity or simply singularity is a location in spacetime where the density and gravitational field of a celestial body is predicted to become infinite by general relativity in a way that does not depend on the coordinate system. The quantities used to measure gravitational field strength are the scalar invariant curvatures of spacetime, which includes a measure of the density of matter. Since such quantities become infinite at the singularity point, the laws of normal spacetime break down.[1][2]
https://en.wikipedia.org/wiki/Gravitational_singularity
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.[1] As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions (i.e., leptons and quarks), and force fields, whose quanta are bosons (e.g., photons and gluons). All these fields have zero-point energy.[2] These fluctuating zero-point fields lead to a kind of reintroduction of an aether in physics[1][3] since some systems can detect the existence of this energy. However, this aether cannot be thought of as a physical medium if it is to be Lorentz invariant such that there is no contradiction with Einstein's theory of special relativity.[1]
https://en.wikipedia.org/wiki/Zero-point_energy
The quantum vacuum state or simply quantum vacuum refers to the quantum state with the lowest possible energy.
Quantum vacuum may also refer to:
- Quantum chromodynamic vacuum (QCD vacuum), a non-perturbative vacuum
- Quantum electrodynamic vacuum (QED vacuum), a field-theoretic vacuum
- Quantum vacuum (ground state), the state of lowest energy of a quantum system
- Quantum vacuum collapse, a hypothetical vacuum metastability event
- Quantum vacuum expectation value, an operator's average, expected value in a quantum vacuum
- Quantum vacuum energy, an underlying background energy that exists in space throughout the entire Universe
- The Quantum Vacuum, a physics textbook by Peter W. Milonni
See also[edit]
https://en.wikipedia.org/wiki/Quantum_vacuum_(disambiguation)
In astronomy, the Zero Point in a photometric system is defined as the magnitude of an object that produces 1 count per second on the detector.[1] The zero point is used to calibrate a system to the standard magnitude system, as the flux detected from stars will vary from detector to detector.[2] Traditionally, Vega is used as the calibration star for the zero point magnitude in specific pass bands (U, B, and V), although often, an average of multiple stars is used for higher accuracy.[3] It is not often practical to find Vega in the sky to calibrate the detector, so for general purposes, any star may be used in the sky that has a known apparent magnitude.[4]
https://en.wikipedia.org/wiki/Zero_Point_(photometry)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space.
In physical problems, the choice of origin is often arbitrary, meaning any choice of origin will ultimately give the same answer. This allows one to pick an origin point that makes the mathematics as simple as possible, often by taking advantage of some kind of geometric symmetry.
https://en.wikipedia.org/wiki/Origin_(mathematics)
H2 diatom zero dipole moment
https://en.wikipedia.org/wiki/Perfect_fluid
https://en.wikipedia.org/wiki/Dirac_delta_function
In mathematics, a function is said to vanish at infinity if its values approach 0 as the input grows without bounds. There are two different ways to define this with one definition applying to functions defined on normed vector spaces and the other applying to functions defined on locally compact spaces. Aside from this difference, both of these notions correspond to the intuitive notion of adding a point at infinity, and requiring the values of the function to get arbitrarily close to zero as one approaches it. This definition can be formalized in many cases by adding an (actual) point at infinity.
https://en.wikipedia.org/wiki/Vanish_at_infinity#Rapidly_decreasing
Infinite divisibility arises in different ways in philosophy, physics, economics, order theory (a branch of mathematics), and probability theory (also a branch of mathematics). One may speak of infinite divisibility, or the lack thereof, of matter, space, time, money, or abstract mathematical objects such as the continuum.
https://en.wikipedia.org/wiki/Infinite_divisibility
https://en.wikipedia.org/wiki/Kronecker_delta
https://en.wikipedia.org/wiki/Characteristic_function_(probability_theory)
https://en.wikipedia.org/wiki/Moment-generating_function
https://en.wikipedia.org/wiki/Scale_factor_(cosmology)#Dark_energy-dominated_era
https://en.wikipedia.org/wiki/Neutrino
https://en.wikipedia.org/wiki/Photon
Chronology[edit]
Radiation-dominated era[edit]
After Inflation, and until about 47,000 years after the Big Bang, the dynamics of the early universe were set by radiation (referring generally to the constituents of the universe which moved relativistically, principally photons and neutrinos).[9]
For a radiation-dominated universe the evolution of the scale factor in the Friedmann–Lemaître–Robertson–Walker metric is obtained solving the Friedmann equations:
Matter-dominated era[edit]
Between about 47,000 years and 9.8 billion years after the Big Bang,[11] the energy density of matter exceeded both the energy density of radiation and the vacuum energy density.[12]
When the early universe was about 47,000 years old (redshift 3600), mass–energy density surpassed the radiation energy, although the universe remained optically thick to radiation until the universe was about 378,000 years old (redshift 1100). This second moment in time (close to the time of recombination), at which the photons which compose the cosmic microwave background radiation were last scattered, is often mistaken[neutrality is disputed] as marking the end of the radiation era.
For a matter-dominated universe the evolution of the scale factor in the Friedmann–Lemaître–Robertson–Walker metric is easily obtained solving the Friedmann equations:
Dark-energy-dominated era[edit]
In physical cosmology, the dark-energy-dominated era is proposed as the last of the three phases of the known universe, the other two being the matter-dominated era and the radiation-dominated era. The dark-energy-dominated era began after the matter-dominated era, i.e. when the Universe was about 9.8 billion years old.[13] In the era of cosmic inflation, the Hubble parameter is also thought to be constant, so the expansion law of the dark-energy-dominated era also holds for the inflationary prequel of the big bang.
The cosmological constant is given the symbol Λ, and, considered as a source term in the Einstein field equation, can be viewed as equivalent to a "mass" of empty space, or dark energy. Since this increases with the volume of the universe, the expansion pressure is effectively constant, independent of the scale of the universe, while the other terms decrease with time. Thus, as the density of other forms of matter – dust and radiation – drops to very low concentrations, the cosmological constant (or "dark energy") term will eventually dominate the energy density of the Universe. Recent measurements of the change in Hubble constant with time, based on observations of distant supernovae, show this acceleration in expansion rate,[14] indicating the presence of such dark energy.
For a dark-energy-dominated universe, the evolution of the scale factor in the Friedmann–Lemaître–Robertson–Walker metric is easily obtained solving the Friedmann equations:
Here, the coefficient in the exponential, the Hubble constant, is
This exponential dependence on time makes the spacetime geometry identical to the de Sitter universe, and only holds for a positive sign of the cosmological constant, which is the case according to the currently accepted value of the cosmological constant, Λ, that is approximately 2 · 10−35 s−2. The current density of the observable universe is of the order of 9.44 · 10−27 kg m−3 and the age of the universe is of the order of 13.8 billion years, or 4.358 · 1017 s. The Hubble constant, , is ≈70.88 km s−1 Mpc−1 (The Hubble time is 13.79 billion years).
See also[edit]
https://en.wikipedia.org/wiki/Scale_factor_(cosmology)#Dark_energy-dominated_era
https://en.wikipedia.org/wiki/Category:Subatomic_particles_with_spin_0
https://en.wikipedia.org/wiki/Sgoldstino
https://en.wikipedia.org/wiki/Spontaneous_symmetry_breaking
https://en.wikipedia.org/wiki/Supersymmetry_breaking
https://en.wikipedia.org/wiki/Hierarchy_problem
https://en.wikipedia.org/wiki/Supersymmetry_breaking_scale
https://en.wikipedia.org/wiki/Phantom_energy
https://en.wikipedia.org/wiki/Quintessence_(physics)
https://en.wikipedia.org/wiki/Aether_(classical_element)
https://en.wikipedia.org/wiki/Mirror
https://en.wikipedia.org/wiki/Grid
https://en.wikipedia.org/wiki/Dust
If one considers a pressure-free perfect fluid (also known as a "dust")
https://en.wikipedia.org/wiki/Pressuron
In particle physics, preons are point particles, conceived of as sub-components of quarks and leptons.[1]
https://en.wikipedia.org/wiki/Preon
Baryon problem: In particle physics, a hyperon is any baryon containing one or more strange quarks, but no charm, bottom, or top quark.[1] This form of matter may exist in a stable form within the core of some neutron stars.[2]
https://en.wikipedia.org/wiki/Hyperon
https://en.wikipedia.org/wiki/Hyperion_(Titan)
A pentaquark is a human-made subatomic particle, consisting of four quarks and one antiquark bound together; they are not known to occur naturally, or exist outside of experiments specifically carried out to create them.
https://en.wikipedia.org/wiki/Pentaquark
A gluon (/ˈɡluːɒn/) is an elementary particle that acts as the exchange particle (or gauge boson) for the strong force between quarks. It is analogous to the exchange of photons in the electromagnetic force between two charged particles.[6] In layman's terms, they "glue" quarks together, forming hadrons such as protons and neutrons.
https://en.wikipedia.org/wiki/Gluon
https://en.wikipedia.org/wiki/Quantum_chromodynamics
https://en.wikipedia.org/wiki/Lagrangian_(field_theory)
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Diffeomorphism
https://en.wikipedia.org/wiki/Gauge_theory_gravity
https://en.wikipedia.org/wiki/Lanczos_tensor
Continuum theories[edit]
The two gauge theories mentioned above, continuum electrodynamics and general relativity, are continuum field theories. The techniques of calculation in a continuum theory implicitly assume that:
- given a completely fixed choice of gauge, the boundary conditions of an individual configuration are completely described
- given a completely fixed gauge and a complete set of boundary conditions, the least action determines a unique mathematical configuration and therefore a unique physical situation consistent with these bounds
- fixing the gauge introduces no anomalies in the calculation, due either to gauge dependence in describing partial information about boundary conditions or to incompleteness of the theory.
Determination of the likelihood of possible measurement outcomes proceed by:
- establishing a probability distribution over all physical situations determined by boundary conditions consistent with the setup information
- establishing a probability distribution of measurement outcomes for each possible physical situation
- convolving these two probability distributions to get a distribution of possible measurement outcomes consistent with the setup information
These assumptions have enough validity across a wide range of energy scales and experimental conditions to allow these theories to make accurate predictions about almost all of the phenomena encountered in daily life: light, heat, and electricity, eclipses, spaceflight, etc. They fail only at the smallest and largest scales due to omissions in the theories themselves, and when the mathematical techniques themselves break down, most notably in the case of turbulence and other chaotic phenomena.
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Continuum_mechanics
https://en.wikipedia.org/wiki/Convolution
https://en.wikipedia.org/wiki/Stationary-action_principle
https://en.wikipedia.org/wiki/Action_(physics)
https://en.wikipedia.org/wiki/Gauge_fixing
https://en.wikipedia.org/wiki/Anomaly_(physics)#Anomaly_cancellation
https://en.wikipedia.org/wiki/Perturbation_theory_(quantum_mechanics)
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Faddeev–Popov_ghost
https://en.wikipedia.org/wiki/Low-dimensional_topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
History[edit]
A number of advances starting in the 1960s had the effect of emphasising low dimensions in topology. The solution by Stephen Smale, in 1961, of the Poincaré conjecture in five or more dimensions made dimensions three and four seem the hardest; and indeed they required new methods, while the freedom of higher dimensions meant that questions could be reduced to computational methods available in surgery theory. Thurston's geometrization conjecture, formulated in the late 1970s, offered a framework that suggested geometry and topology were closely intertwined in low dimensions, and Thurston's proof of geometrization for Haken manifolds utilized a variety of tools from previously only weakly linked areas of mathematics. Vaughan Jones' discovery of the Jones polynomial in the early 1980s not only led knot theory in new directions but gave rise to still mysterious connections between low-dimensional topology and mathematical physics. In 2002, Grigori Perelman announced a proof of the three-dimensional Poincaré conjecture, using Richard S. Hamilton's Ricci flow, an idea belonging to the field of geometric analysis.
Overall, this progress has led to better integration of the field into the rest of mathematics.
Two dimensions[edit]
A surface is a two-dimensional, topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3—for example, the surface of a ball. On the other hand, there are surfaces, such as the Klein bottle, that cannot be embedded in three-dimensional Euclidean space without introducing singularities or self-intersections.
Classification of surfaces[edit]
The classification theorem of closed surfaces states that any connected closed surface is homeomorphic to some member of one of these three families:
- the sphere;
- the connected sum of g tori, for ;
- the connected sum of k real projective planes, for .
The surfaces in the first two families are orientable. It is convenient to combine the two families by regarding the sphere as the connected sum of 0 tori. The number g of tori involved is called the genus of the surface. The sphere and the torus have Euler characteristics 2 and 0, respectively, and in general the Euler characteristic of the connected sum of g tori is 2 − 2g.
The surfaces in the third family are nonorientable. The Euler characteristic of the real projective plane is 1, and in general the Euler characteristic of the connected sum of k of them is 2 − k.
Teichmüller space[edit]
In mathematics, the Teichmüller space TX of a (real) topological surface X, is a space that parameterizes complex structures on Xup to the action of homeomorphisms that are isotopic to the identity homeomorphism. Each point in TX may be regarded as an isomorphism class of 'marked' Riemann surfaces where a 'marking' is an isotopy class of homeomorphisms from X to X. The Teichmüller space is the universal covering orbifold of the (Riemann) moduli space.
Teichmüller space has a canonical complex manifold structure and a wealth of natural metrics. The underlying topological space of Teichmüller space was studied by Fricke, and the Teichmüller metric on it was introduced by Oswald Teichmüller (1940).[1]
Uniformization theorem[edit]
In mathematics, the uniformization theorem says that every simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature. This classifies Riemannian surfaces as elliptic (positively curved—rather, admitting a constant positively curved metric), parabolic (flat), and hyperbolic (negatively curved) according to their universal cover.
The uniformization theorem is a generalization of the Riemann mapping theorem from proper simply connected open subsets of the plane to arbitrary simply connected Riemann surfaces.
Three dimensions[edit]
A topological space X is a 3-manifold if every point in X has a neighbourhood that is homeomorphic to Euclidean 3-space.
The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.
Phenomena in three dimensions can be strikingly different from phenomena in other dimensions, and so there is a prevalence of very specialized techniques that do not generalize to dimensions greater than three. This special role has led to the discovery of close connections to a diversity of other fields, such as knot theory, geometric group theory, hyperbolic geometry, number theory, Teichmüller theory, topological quantum field theory, gauge theory, Floer homology, and partial differential equations. 3-manifold theory is considered a part of low-dimensional topology or geometric topology.
Knot and braid theory[edit]
Knot theory is the study of mathematical knots. While inspired by knots that appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3 (since we're using topology, a circle isn't bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
Knot complements are frequently-studied 3-manifolds. The knot complement of a tame knot K is the three-dimensional space surrounding the knot. To make this precise, suppose that K is a knot in a three-manifold M (most often, M is the 3-sphere). Let N be a tubular neighborhood of K; so N is a solid torus. The knot complement is then the complement of N,
A related topic is braid theory. Braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a second on the twisted strings'. Such groups may be described by explicit presentations, as was shown by Emil Artin (1947).[2] For an elementary treatment along these lines, see the article on braid groups. Braid groups may also be given a deeper mathematical interpretation: as the fundamental group of certain configuration spaces.
Hyperbolic 3-manifolds[edit]
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously. See also Kleinian model.
Its thick-thin decomposition has a thin part consisting of tubular neighborhoods of closed geodesics and/or ends that are the product of a Euclidean surface and the closed half-ray. The manifold is of finite volume if and only if its thick part is compact. In this case, the ends are of the form torus cross the closed half-ray and are called cusps. Knot complements are the most commonly studied cusped manifolds.
Poincaré conjecture and geometrization[edit]
Thurston's geometrization conjecture states that certain three-dimensional topological spaces each have a unique geometric structure that can be associated with them. It is an analogue of the uniformization theorem for two-dimensional surfaces, which states that every simply-connected Riemann surface can be given one of three geometries (Euclidean, spherical, or hyperbolic). In three dimensions, it is not always possible to assign a single geometry to a whole topological space. Instead, the geometrization conjecture states that every closed 3-manifold can be decomposed in a canonical way into pieces that each have one of eight types of geometric structure. The conjecture was proposed by William Thurston (1982), and implies several other conjectures, such as the Poincaré conjecture and Thurston's elliptization conjecture.[3]
Four dimensions[edit]
A 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different. There exist some topological 4-manifolds that admit no smooth structure and even if there exists a smooth structure it need not be unique (i.e. there are smooth 4-manifolds that are homeomorphic but not diffeomorphic).
4-manifolds are of importance in physics because, in General Relativity, spacetime is modeled as a pseudo-Riemannian 4-manifold.
Exotic R4[edit]
An exotic R4 is a differentiable manifold that is homeomorphic but not diffeomorphic to the Euclidean space R4. The first examples were found in the early 1980s by Michael Freedman, by using the contrast between Freedman's theorems about topological 4-manifolds, and Simon Donaldson's theorems about smooth 4-manifolds.[4] There is a continuum of non-diffeomorphic differentiable structures of R4, as was shown first by Clifford Taubes.[5]
Prior to this construction, non-diffeomorphic smooth structures on spheres—exotic spheres—were already known to exist, although the question of the existence of such structures for the particular case of the 4-sphere remained open (and still remains open as of 2018). For any positive integer n other than 4, there are no exotic smooth structures on Rn; in other words, if n ≠ 4 then any smooth manifold homeomorphic to Rn is diffeomorphic to Rn.[6]
Other special phenomena in four dimensions[edit]
There are several fundamental theorems about manifolds that can be proved by low-dimensional methods in dimensions at most 3, and by completely different high-dimensional methods in dimension at least 5, but which are false in four dimensions. Here are some examples:
- In dimensions other than 4, the Kirby–Siebenmann invariant provides the obstruction to the existence of a PL structure; in other words a compact topological manifold has a PL structure if and only if its Kirby–Siebenmann invariant in H4(M,Z/2Z) vanishes. In dimension 3 and lower, every topological manifold admits an essentially unique PL structure. In dimension 4 there are many examples with vanishing Kirby–Siebenmann invariant but no PL structure.
- In any dimension other than 4, a compact topological manifold has only a finite number of essentially distinct PL or smooth structures. In dimension 4, compact manifolds can have a countable infinite number of non-diffeomorphic smooth structures.
- Four is the only dimension n for which Rn can have an exotic smooth structure. R4 has an uncountable number of exotic smooth structures; see exotic R4.
- The solution to the smooth Poincaré conjecture is known in all dimensions other than 4 (it is usually false in dimensions at least 7; see exotic sphere). The Poincaré conjecture for PL manifolds has been proved for all dimensions other than 4, but it is not known whether it is true in 4 dimensions (it is equivalent to the smooth Poincaré conjecture in 4 dimensions).
- The smooth h-cobordism theorem holds for cobordisms provided that neither the cobordism nor its boundary has dimension 4. It can fail if the boundary of the cobordism has dimension 4 (as shown by Donaldson). If the cobordism has dimension 4, then it is unknown whether the h-cobordism theorem holds.
- A topological manifold of dimension not equal to 4 has a handlebody decomposition. Manifolds of dimension 4 have a handlebody decomposition if and only if they are smoothable.
- There are compact 4-dimensional topological manifolds that are not homeomorphic to any simplicial complex. In dimension at least 5 the existence of topological manifolds not homeomorphic to a simplicial complex was an open problem. In 2013, Ciprian Manolescu posted a preprint on the ArXiv showing that there are manifolds in each dimension greater than or equal to 5, that are not homeomorphic to a simplicial complex.
A few typical theorems that distinguish low-dimensional topology[edit]
There are several theorems that in effect state that many of the most basic tools used to study high-dimensional manifolds do not apply to low-dimensional manifolds, such as:
Steenrod's theorem states that an orientable 3-manifold has a trivial tangent bundle. Stated another way, the only characteristic class of a 3-manifold is the obstruction to orientability.
Any closed 3-manifold is the boundary of a 4-manifold. This theorem is due independently to several people: it follows from the Dehn–Lickorish theorem via a Heegaard splitting of the 3-manifold. It also follows from René Thom's computation of the cobordismring of closed manifolds.
The existence of exotic smooth structures on R4. This was originally observed by Michael Freedman, based on the work of Simon Donaldson and Andrew Casson. It has since been elaborated by Freedman, Robert Gompf, Clifford Taubes and Laurence Taylor to show there exists a continuum of non-diffeomorphic smooth structures on R4. Meanwhile, Rn is known to have exactly one smooth structure up to diffeomorphism provided n ≠ 4.
See also[edit]
https://en.wikipedia.org/wiki/Low-dimensional_topology
Results[edit]
The goal of the experiment was to measure the rate at which time passes in a higher gravitational potential, so to test this the maser in the probe was compared to a similar maser that remained on Earth.[citation needed] Before the two clock rates could be compared, the Doppler shift was subtracted from the clock rate measured by the maser that was sent into space, to correct for the relative motion between the observers on Earth and the motion of the probe. The two clock rates were then compared and further compared against the theoretical predictions of how the two clock rates should differ. The stability of the maser permitted measurement of changes in the rate of the maser of 1 part in 1014 for a 100-second measurement.
The experiment was thus able to test the equivalence principle. Gravity Probe A confirmed the prediction that deeper in the gravity well time flows slower,[7] and the observed effects matched the predicted effects to an accuracy of about 70 parts per million.
https://en.wikipedia.org/wiki/Gravity_Probe_A
https://en.wikipedia.org/wiki/Hydrogen_maser
https://en.wikipedia.org/wiki/Low-dimensional_topology
https://en.wikipedia.org/wiki/Category:Atomic_clocks
https://en.wikipedia.org/wiki/Dark_matter
https://en.wikipedia.org/wiki/Thermodynamics
https://en.wikipedia.org/wiki/Energy
https://en.wikipedia.org/wiki/Space_rock
https://en.wikipedia.org/wiki/Oldest_dated_rocks
https://en.wikipedia.org/wiki/Radiation
https://en.wikipedia.org/wiki/Black_hole
https://en.wikipedia.org/wiki/Magnum_opus_(alchemy)
https://en.wikipedia.org/wiki/Dimensional_transmutation
https://en.wikipedia.org/wiki/Nuclear_transmutation
https://en.wikipedia.org/wiki/Nuclear_reaction
https://en.wikipedia.org/wiki/Nuclear_fission
https://en.wikipedia.org/wiki/Fusion
https://en.wikipedia.org/wiki/Atmosphere
https://en.wikipedia.org/wiki/Hertz
https://en.wikipedia.org/wiki/Terahertz_radiation
https://en.wikipedia.org/wiki/Terahertz_gap
https://en.wikipedia.org/wiki/T-ray_(disambiguation)
https://en.wikipedia.org/wiki/Higgs_mechanism
https://en.wikipedia.org/wiki/Gauge_boson
https://en.wikipedia.org/wiki/W_and_Z_bosons
The
Z0
boson is electrically neutral and is its own antiparticle.
https://en.wikipedia.org/wiki/W_and_Z_bosons
https://en.wikipedia.org/wiki/Elementary_particle
https://en.wikipedia.org/wiki/Antimatter
https://en.wikipedia.org/wiki/List_of_particles#Composite_particles
https://en.wikipedia.org/wiki/Force_carrier
Pressuron
https://en.wikipedia.org/wiki/Static_forces_and_virtual-particle_exchange
https://en.wikipedia.org/wiki/Virtual_particle
https://en.wikipedia.org/wiki/Casimir_effect
https://en.wikipedia.org/wiki/Scattering_theory
https://en.wikipedia.org/wiki/Pion
https://en.wikipedia.org/wiki/Path_integral_formulation
https://en.wikipedia.org/wiki/Nucleon
https://en.wikipedia.org/wiki/Static_forces_and_virtual-particle_exchange#The_Coulomb_potential_in_a_vacuum
https://en.wikipedia.org/wiki/Static_forces_and_virtual-particle_exchange#Electrostatics
https://en.wikipedia.org/wiki/Static_forces_and_virtual-particle_exchange#The_Yukawa_potential:_The_force_between_two_nucleons_in_an_atomic_nucleus
https://en.wikipedia.org/wiki/Holon_(physics)
https://en.wikipedia.org/wiki/Orbiton
https://en.wikipedia.org/wiki/Quasiparticle
https://en.wikipedia.org/wiki/Spinon
Spinons are one of three quasiparticles, along with holons and orbitons, that electrons in solids are able to split into during the process of spin–charge separation, when extremely tightly confined at temperatures close to absolute zero.[1] The electron can always be theoretically considered as a bound state of the three, with the spinon carrying the spin of the electron, the orbitoncarrying the orbital location and the holon carrying the charge, but in certain conditions they can behave as independent quasiparticles.
The term spinon is frequently used in discussions of experimental facts within the framework of both quantum spin liquid and strongly correlated quantum spin liquid.[2]
Electrons, being of like charge, repel each other. As a result, in order to move past each other in an extremely crowded environment, they are forced to modify their behavior. Research published in July 2009 by the University of Cambridge and the University of Birmingham in England showed that electrons could jump from the surface of the metal onto a closely located quantum wire by quantum tunneling, and upon doing so, will separate into two quasiparticles, named spinons and holons by the researchers.[3]
The orbiton was predicted theoretically by van den Brink, Khomskii and Sawatzky in 1997-1998.[4][5] Its experimental observation as a separate quasiparticle was reported in paper sent to publishers in September 2011.[6][7] The research states that by firing a beam of X-ray photons at a single electron in a one-dimensional sample of strontium cuprate, this will excite the electron to a higher orbital, causing the beam to lose a fraction of its energy in the process. In doing so, the electron will be separated into a spinon and an orbiton. This can be traced by observing the energy and momentum of the X-rays before and after the collision.
See also[edit]
https://en.wikipedia.org/wiki/Spinon
https://en.wikipedia.org/wiki/Superpartner
https://en.wikipedia.org/wiki/Gaugino
https://en.wikipedia.org/wiki/Gluino
https://en.wikipedia.org/wiki/Stop_squark
https://en.wikipedia.org/wiki/R-parity
A scalar boson is a boson whose spin equals zero.[1] Boson means that the particle's wavefunction is symmetric under particle exchange and therefore follows Bose–Einstein statistics. The spin-statistics theorem implies that all bosons have an integer-valued spin;[2] the scalar fixes this value to zero.
The name scalar boson arises from quantum field theory, which demands that fields of spin-zero particles transform like a scalar under Lorentz transformation (i.e. are Lorentz invariant).
A pseudoscalar boson is a scalar boson that has odd parity, whereas "regular" scalar bosons have even parity.[3]
https://en.wikipedia.org/wiki/Scalar_boson
In particle physics, a stop squark, symbol
t͂
, is the superpartner of the top quark as predicted by supersymmetry (SUSY). It is a sfermion, which means it is a spin-0 boson (scalar boson). While the top quark is the heaviest known quark, the stop squark is actually often the lightest squark in many supersymmetry models.[1]
https://en.wikipedia.org/wiki/Stop_squark
Spinons are one of three quasiparticles, along with holons and orbitons, that electrons in solids are able to split into during the process of spin–charge separation, when extremely tightly confined at temperatures close to absolute zero.[1] T
https://en.wikipedia.org/wiki/Spinon
In particle physics, the chargino is a hypothetical particle which refers to the mass eigenstates of a charged superpartner, i.e. any new electrically charged fermion (with spin 1/2) predicted by supersymmetry.[1][2] They are linear combinations of the charged wino and charged higgsinos. There are two charginos that are fermions and are electrically charged, which are typically labeled
C͂±
1 (the lightest) and
C͂±
2 (the heaviest), although sometimes and are also used to refer to charginos, when is used to refer to neutralinos. The heavier chargino can decay through the neutral Z boson to the lighter chargino. Both can decay through a charged W boson to a neutralino:
C͂±
2 →
C͂±
1 +
Z0
C͂±
2 →
N͂0
2 +
W±
C͂±
1 →
N͂0
1 +
W±
See also[edit]
In condensed matter physics, spin–charge separation is an unusual behavior of electrons in some materials in which they 'split' into three independent particles, the spinon, the orbiton and the holon (or chargon). The electron can always be theoretically considered as a bound state of the three, with the spinon carrying the spin of the electron, the orbiton carrying the orbital degree of freedom and the chargon carrying the charge, but in certain conditions they can behave as independent quasiparticles.
The theory of spin–charge separation originates with the work of Sin-Itiro Tomonaga who developed an approximate method for treating one-dimensional interacting quantum systems in 1950.[1] This was then developed by Joaquin Mazdak Luttinger in 1963 with an exactly solvable model which demonstrated spin–charge separation.[2] In 1981 F. Duncan M. Haldane generalized Luttinger's model to the Tomonaga–Luttinger liquid concept[3] whereby the physics of Luttinger's model was shown theoretically to be a general feature of all one-dimensional metallic systems. Although Haldane treated spinless fermions, the extension to spin-½fermions and associated spin–charge separation was so clear that the promised follow-up paper did not appear.
Spin–charge separation is one of the most unusual manifestations of the concept of quasiparticles. This property is counterintuitive, because neither the spinon, with zero charge and spin half, nor the chargon, with charge minus one and zero spin, can be constructed as combinations of the electrons, holes, phonons and photons that are the constituents of the system. It is an example of fractionalization, the phenomenon in which the quantum numbers of the quasiparticles are not multiples of those of the elementary particles, but fractions.[citation needed]
The same theoretical ideas have been applied in the framework of ultracold atoms. In a two-component Bose gas in 1D, strong interactions can produce a maximal form of spin–charge separation.[4]
This property is counterintuitive, because neither the spinon, with zero charge and spin half, nor the chargon, with charge minus one and zero spin, can be constructed as combinations of the electrons, holes, phonons and photons that are the constituents of the system. It is an example of fractionalization, the phenomenon in which the quantum numbers of the quasiparticles are not multiples of those of the elementary particles, but fractions.[citation needed]
Building on physicist F. Duncan M. Haldane's 1981 theory, experts from the Universities of Cambridge and Birmingham proved experimentally in 2009 that a mass of electrons artificially confined in a small space together will split into spinons and holons due to the intensity of their mutual repulsion (from having the same charge).[5][6] A team of researchers working at the Advanced Light Source (ALS) of the U.S. Department of Energy’s Lawrence Berkeley National Laboratory observed the peak spectral structures of spin–charge separation three years prior.[7]
References[edit]
- ^ Tomonaga, S.-i. (1950). "Remarks on Bloch's method of sound waves applied to many-fermion problems". Progress of Theoretical Physics. 5 (4): 544. Bibcode:1950PThPh...5..544T. doi:10.1143/ptp/5.4.544.
- ^ Luttinger, J. M. (1963). "An Exactly Soluble Model of a Many‐Fermion System". Journal of Mathematical Physics. 4 (9): 1154. Bibcode:1963JMP.....4.1154L. doi:10.1063/1.1704046.
- ^ Haldane, F. D. M. (1981). "'Luttinger liquid theory' of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas". Journal of Physics C: Solid State Physics. 14 (19): 2585. Bibcode:1981JPhC...14.2585H. doi:10.1088/0022-3719/14/19/010.
- ^ "Spin-charge separation optical lattices". Optical-lattice.com. Retrieved 2016-07-11.
- ^ "UK | England | Physicists 'make electrons split'". BBC News. 2009-08-28. Retrieved 2016-07-11.
- ^ Discovery About Behavior Of Building Block Of Nature Could Lead To Computer Revolution. Science Daily (July 31, 2009)
- ^ Yarris, Lynn (2006-07-13). "First Direct Observations of Spinons and Holons". Lbl.gov. Retrieved 2016-07-11.
External links[edit]
- Observation of Spin-Charge Separation in One-Dimensional SrCuO2
- Distinct spinon and holon dispersions in photoemission spectral functions from one-dimensional SrCuO2 : Abstract
https://en.wikipedia.org/wiki/Spin–charge_separation
Ultracold atoms are atoms that are maintained at temperatures close to 0 kelvin (absolute zero), typically below several tens of microkelvin (µK). At these temperatures the atom's quantum-mechanical properties become important.
To reach such low temperatures, a combination of several techniques typically has to be used.[1] First, atoms are usually trapped and pre-cooled via laser cooling in a magneto-optical trap. To reach the lowest possible temperature, further cooling is performed using evaporative cooling in a magnetic or optical trap. Several Nobel prizes in physics are related to the development of the techniques to manipulate quantum properties of individual atoms (e.g. 1995-1997, 2001, 2005, 2012, 2017).
Experiments with ultracold atoms study a variety of phenomena, including quantum phase transitions, Bose–Einstein condensation (BEC), bosonic superfluidity, quantum magnetism, many-body spin dynamics, Efimov states, Bardeen–Cooper–Schrieffer (BCS) superfluidity and the BEC–BCS crossover.[2] Some of these research directions utilize ultracold atom systems as quantum simulators to study the physics of other systems, including the unitary Fermi gas and the Ising and Hubbard models.[3] Ultracold atoms could also be used for realization of quantum computers.[4]
https://en.wikipedia.org/wiki/Ultracold_atom
https://en.wikipedia.org/wiki/Nitrogen-vacancy_center
https://en.wikipedia.org/wiki/Kane_quantum_computer
https://en.wikipedia.org/wiki/Toric_code
https://en.wikipedia.org/wiki/Quantum_logic_gate
https://en.wikipedia.org/wiki/Stop_squark
https://en.wikipedia.org/wiki/Scalar_boson
https://en.wikipedia.org/wiki/Spin–charge_separation
Pionium is an exotic atom consisting of one
π+
and one
π−
meson. It can be created, for instance, by interaction of a proton beam accelerated by a particle accelerator and a target nucleus. Pionium has a short lifetime, predicted by chiral perturbation theory to be 2.89×10−15 s. It decays mainly into two
π0
mesons, and to a smaller extent into two photons.
https://en.wikipedia.org/wiki/Pionium
A mesonic molecule is a set of two or more mesons bound together by the strong force.[1][2] Unlike baryonic molecules, which form the nuclei of all elements in nature save hydrogen-1, a mesonic molecule has yet to be definitively observed.[3] The X(3872)discovered in 2003 and the Z(4430) discovered in 2007 by the Belle experiment are the best candidates for such an observation.
https://en.wikipedia.org/wiki/Mesonic_molecule
https://en.wikipedia.org/wiki/X(3872)
https://en.wikipedia.org/wiki/Dark_photon
Preons come in four varieties, plus, anti-plus, zero and anti-zero. W bosons have 6 preons and quarks have only 3.
https://en.wikipedia.org/wiki/Preon
https://en.wikipedia.org/wiki/X_and_Y_bosons
https://en.wikipedia.org/wiki/XYZ_particle
https://en.wikipedia.org/wiki/Grand_Unified_Theory
https://en.wikipedia.org/wiki/Elementary_particle
https://en.wikipedia.org/wiki/Chargino
https://en.wikipedia.org/wiki/Delta_baryon
https://en.wikipedia.org/wiki/Phi_meson
https://en.wikipedia.org/wiki/Quarkonium
https://en.wikipedia.org/wiki/Hexaquark
https://en.wikipedia.org/wiki/Pomeron
https://en.wikipedia.org/wiki/Exciton
https://en.wikipedia.org/wiki/Davydov_soliton
https://en.wikipedia.org/wiki/Magnon
https://en.wikipedia.org/wiki/Plasmaron
https://en.wikipedia.org/wiki/Trion_(physics)
https://en.wikipedia.org/wiki/List_of_mesons
https://en.wikipedia.org/wiki/Eightfold_way_(physics)
https://en.wikipedia.org/wiki/Polariton
Plane waves in vacuum[edit]
Plane waves in vacuum are the simplest case of wave propagation: no geometric constraint, no interaction with a transmitting medium.
Electromagnetic waves in a vacuum[edit]
For electromagnetic waves in vacuum, the angular frequency is proportional to the wavenumber:
This is a linear dispersion relation. In this case, the phase velocity and the group velocity are the same:
they are given by c, the speed of light in vacuum, a frequency-independent constant.
De Broglie dispersion relations[edit]
Total energy, momentum, and mass of particles are connected through the relativistic dispersion relation[1] established by Paul Dirac:
which in the ultrarelativistic limit is
and in the nonrelativistic limit is
where is the invariant mass. In the nonrelativistic limit, is a constant, and is the familiar kinetic energy expressed in terms of the momentum .
The transition from ultrarelativistic to nonrelativistic behaviour shows up as a slope change from p to p2 as shown in the log–log dispersion plot of E vs. p.
Elementary particles, atomic nuclei, atoms, and even molecules behave in some contexts as matter waves. According to the de Broglie relations, their kinetic energy E can be expressed as a frequency ω, and their momentum p as a wavenumber k, using the reduced Planck constant ħ:
Accordingly, angular frequency and wavenumber are connected through a dispersion relation, which in the nonrelativistic limit reads
showAnimation: phase and group velocity of electrons
https://en.wikipedia.org/wiki/Dispersion_relation
https://en.wikipedia.org/wiki/Dispersion_(optics)
https://en.wikipedia.org/wiki/Dissipative_system
See also[edit]
- Conservation equation
- Complex system
- Non-equilibrium thermodynamics
- Extremal principles in non-equilibrium thermodynamics
- Autowave
- Self-organization
- Information metabolism
- Autocatalytic reactions and order creation
- Dynamical system
- Autopoiesis
- Relational order theories
- Loschmidt's paradox
- Viable system theory
https://en.wikipedia.org/wiki/Decoupling
https://en.wikipedia.org/wiki/Decoupling_(cosmology)
https://en.wikipedia.org/wiki/Decoupling_(meteorology)
https://en.wikipedia.org/wiki/Uncoupling_(neuropsychopharmacology)
https://en.wikipedia.org/wiki/Nuclear_magnetic_resonance_decoupling
https://en.wikipedia.org/wiki/Decoupling_(probability)
https://en.wikipedia.org/wiki/Decoupling_(electronics)
https://en.wikipedia.org/wiki/Decoupling_capacitor
https://en.wikipedia.org/wiki/Railway_coupling
https://en.wikipedia.org/wiki/Quantum_decoherence
https://en.wikipedia.org/wiki/Quantum_depolarizing_channel
https://en.wikipedia.org/wiki/Quantum_state#Mixed_states
https://en.wikipedia.org/wiki/Quantum_depolarizing_channel
https://en.wikipedia.org/wiki/Quantum_channel
https://en.wikipedia.org/wiki/Quantum_operation
https://en.wikipedia.org/wiki/Bloch_sphere
The ΛCDM (Lambda cold dark matter) or Lambda-CDM model is a parameterizationof the Big Bang cosmological model in which the universe contains three major components: first, a cosmological constant denoted by Lambda (Greek Λ) associated with dark energy; second, the postulated cold dark matter (abbreviated CDM); and third, ordinary matter. It is frequently referred to as the standard model of Big Bang cosmology because it is the simplest model that provides a reasonably good account of the following properties of the cosmos:
- the existence and structure of the cosmic microwave background
- the large-scale structure in the distribution of galaxies
- the observed abundances of hydrogen (including deuterium), helium, and lithium
- the accelerating expansion of the universe observed in the light from distant galaxies and supernovae
https://en.wikipedia.org/wiki/Zero_element#Additive_identities
https://en.wikipedia.org/wiki/Absorbing_element
https://en.wikipedia.org/wiki/Measure_(mathematics)
- The zero module, containing only the identity (a zero object in the category of modules over a ring)
Properties[edit]
Pointwise operations inherit such properties as associativity, commutativity and distributivity from corresponding operations on the codomain. If is some algebraic structure, the set of all functions to the carrier set of can be turned into an algebraic structure of the same type in an analogous way.
https://en.wikipedia.org/wiki/Pointwise
Pointwise relations[edit]
In order theory it is common to define a pointwise partial order on functions. With A, B posets, the set of functions A → B can be ordered by f ≤ g if and only if (∀x ∈ A) f(x) ≤ g(x). Pointwise orders also inherit some properties of the underlying posets. For instance if A and B are continuous lattices, then so is the set of functions A → B with pointwise order.[1] Using the pointwise order on functions one can concisely define other important notions, for instance:[2]
- A closure operator c on a poset P is a monotone and idempotent self-map on P (i.e. a projection operator) with the additional property that idA ≤ c, where id is the identity function.
- Similarly, a projection operator k is called a kernel operator if and only if k ≤ idA.
An example of an infinitary pointwise relation is pointwise convergence of functions—a sequence of functions
with
converges pointwise to a function if for each in
https://en.wikipedia.org/wiki/Pointwise
https://en.wikipedia.org/wiki/Category:Mathematical_terminology
https://en.wikipedia.org/wiki/Glossary_of_order_theory#P
https://en.wikipedia.org/wiki/Partially_ordered_set
https://en.wikipedia.org/wiki/Monotonic_function
https://en.wikipedia.org/wiki/Idempotence
https://en.wikipedia.org/wiki/Identity_function
https://en.wikipedia.org/wiki/Closure_operator#Closure_operators_on_partially_ordered_sets
https://en.wikipedia.org/wiki/Lattice_(order)#Continuity_and_algebraicity
https://en.wikipedia.org/wiki/Finitary
https://en.wikipedia.org/wiki/Pointwise_convergence
https://en.wikipedia.org/wiki/Semiring
https://en.wikipedia.org/wiki/Zero_element#Additive_identities
Multivalued functions[edit]
Many functions do not have a unique inverse. For instance, while squaring a number gives a unique value, there are two possible square roots of a positive number. The square root is multivalued. One value can be chosen by convention as the principal value; in the case of the square root the non-negative value is the principal value, but there is no guarantee that the square root given as the principal value of the square of a number will be equal to the original number (e.g. the principal square root of the square of −2 is 2). This remains true for nth roots.
Positive and negative roots[edit]
Care must be taken when taking the square root of both sides of an equality. Failing to do so results in a "proof" of[9] 5 = 4.
Proof:
- Start from
- Write this as
- Rewrite as
- Add 814 on both sides:
- These are perfect squares:
- Take the square root of both sides:
- Add 92 on both sides:
- Q.E.D.
The fallacy is in the second to last line, where the square root of both sides is taken: a2 = b2 only implies a = b if a and b have the same sign, which is not the case here. In this case, it implies that a = –b, so the equation should read
which, by adding 92 on both sides, correctly reduces to 5 = 5.
Another example illustrating the danger of taking the square root of both sides of an equation involves the following fundamental identity[10]
which holds as a consequence of the Pythagorean theorem. Then, by taking a square root,
Evaluating this when x = π , we get that
or
which is incorrect.
The error in each of these examples fundamentally lies in the fact that any equation of the form
where , has two solutions:
and it is essential to check which of these solutions is relevant to the problem at hand.[11] In the above fallacy, the square root that allowed the second equation to be deduced from the first is valid only when cos x is positive. In particular, when x is set to π, the second equation is rendered invalid.
Square roots of negative numbers[edit]
Invalid proofs utilizing powers and roots are often of the following kind:
The fallacy is that the rule is generally valid only if at least one of and is non-negative (when dealing with real numbers), which is not the case here.[12]
Alternatively, imaginary roots are obfuscated in the following:
The error here lies in the third equality, as the rule only holds for positive real a and real b,c.
Complex exponents[edit]
When a number is raised to a complex power, the result is not uniquely defined (see Failure of power and logarithm identities). If this property is not recognized, then errors such as the following can result:
The error here is that the rule of multiplying exponents as when going to the third line does not apply unmodified with complex exponents, even if when putting both sides to the power i only the principal value is chosen. When treated as multivalued functions, both sides produce the same set of values, being {e2πn | n ∈ ℤ}.
https://en.wikipedia.org/wiki/Mathematical_fallacy
https://en.wikipedia.org/wiki/Negative_mass
Traversable wormholes[edit]
The Casimir effect shows that quantum field theory allows the energy density in certain regions of space to be negative relative to the ordinary matter vacuum energy, and it has been shown theoretically that quantum field theory allows states where energy can be arbitrarily negative at a given point.[26] Many physicists, such as Stephen Hawking,[27] Kip Thorne,[28] and others,[29][30][31]argued that such effects might make it possible to stabilize a traversable wormhole.[32][33] The only known natural process that is theoretically predicted to form a wormhole in the context of general relativity and quantum mechanics was put forth by Leonard Susskind in his ER=EPR conjecture. The quantum foam hypothesis is sometimes used to suggest that tiny wormholes might appear and disappear spontaneously at the Planck scale,[34]: 494–496 [35] and stable versions of such wormholes have been suggested as dark matter candidates.[36][37] It has also been proposed that, if a tiny wormhole held open by a negative mass cosmic string had appeared around the time of the Big Bang, it could have been inflated to macroscopic size by cosmic inflation.[38]
Lorentzian traversable wormholes would allow travel in both directions from one part of the universe to another part of that same universe very quickly or would allow travel from one universe to another. The possibility of traversable wormholes in general relativity was first demonstrated in a 1973 paper by Homer Ellis[39] and independently in a 1973 paper by K. A. Bronnikov.[40] Ellis analyzed the topology and the geodesics of the Ellis drainhole, showing it to be geodesically complete, horizonless, singularity-free, and fully traversable in both directions. The drainhole is a solution manifold of Einstein's field equations for a vacuum spacetime, modified by inclusion of a scalar field minimally coupled to the Ricci tensor with antiorthodox polarity (negative instead of positive). (Ellis specifically rejected referring to the scalar field as 'exotic' because of the antiorthodox coupling, finding arguments for doing so unpersuasive.) The solution depends on two parameters: m, which fixes the strength of its gravitational field, and n, which determines the curvature of its spatial cross sections. When m is set equal to 0, the drainhole's gravitational field vanishes. What is left is the Ellis wormhole, a nongravitating, purely geometric, traversable wormhole.
Kip Thorne and his graduate student Mike Morris, unaware of the 1973 papers by Ellis and Bronnikov, manufactured, and in 1988 published, a duplicate of the Ellis wormhole for use as a tool for teaching general relativity.[41] For this reason, the type of traversable wormhole they proposed, held open by a spherical shell of exotic matter, was from 1988 to 2015 referred to in the literature as a Morris–Thorne wormhole.
Later, other types of traversable wormholes were discovered as allowable solutions to the equations of general relativity, including a variety analyzed in a 1989 paper by Matt Visser, in which a path through the wormhole can be made where the traversing path does not pass through a region of exotic matter. However, in the pure Gauss–Bonnet gravity (a modification to general relativity involving extra spatial dimensions which is sometimes studied in the context of brane cosmology) exotic matter is not needed in order for wormholes to exist—they can exist even with no matter.[42] A type held open by negative mass cosmic strings was put forth by Visser in collaboration with Cramer et al.,[38] in which it was proposed that such wormholes could have been naturally created in the early universe.
Wormholes connect two points in spacetime, which means that they would in principle allow travel in time, as well as in space. In 1988, Morris, Thorne and Yurtsever worked out how to convert a wormhole traversing space into one traversing time by accelerating one of its two mouths.[28] However, according to general relativity, it would not be possible to use a wormhole to travel back to a time earlier than when the wormhole was first converted into a time "machine". Until this time it could not have been noticed or have been used.[34]: 504
https://en.wikipedia.org/wiki/Wormhole#Traversable_wormholes
Thus the drainhole is 'traversable' by test particles in both directions. The same holds for photons.
A complete catalog of geodesics of the drainhole can be found in the Ellis paper.[1]
Absence of horizons and singularities; geodesical completeness[edit]
For a metric of the general form of the drainhole metric, with as the velocity field of a flowing ether, the coordinate velocities of radial null geodesics are found to be for light waves traveling against the ether flow, and for light waves traveling with the flow. Wherever , so that , light waves struggling against the ether flow can gain ground. On the other hand, at places where upstream light waves can at best hold their own (if ), or otherwise be swept downstream to wherever the ether is going (if ). (This situation is described in jest by: "People in light canoes should avoid ethereal rapids."[1])
The latter situation is seen in the Schwarzschild metric, where , which is at the Schwarzschild event horizon where , and less than inside the horizon where .
By contrast, in the drainhole and , for every value of , so nowhere is there a horizon on one side of which light waves struggling against the ether flow cannot gain ground.
Because
- and are defined on the whole real line, and
- is bounded away from by ), and
- is bounded away from (by ),
the drainhole metric encompasses neither a 'coordinate singularity' where nor a 'geometric singularity' where , not even asymptotic ones. For the same reasons, every geodesic with an unbound orbit, and with some additional argument every geodesic with a bound orbit, has an affine parametrization whose parameter extends from to . The drainhole manifold is, therefore, geodesically complete.
The order-zero graph, , is the unique graph having no vertices (hence its order is zero). It follows that also has no edges. Thus the null graph is a regular graph of degree zero. Some authors exclude from consideration as a graph (either by definition, or more simply as a matter of convenience). Whether including as a valid graph is useful depends on context. On the positive side, follows naturally from the usual set-theoretic definitions of a graph (it is the ordered pair (V, E) for which the vertex and edge sets, V and E, are both empty), in proofs it serves as a natural base case for mathematical induction, and similarly, in recursively defined data structures is useful for defining the base case for recursion (by treating the null tree as the child of missing edges in any non-null binary tree, every non-null binary tree has exactly two children). On the negative side, including as a graph requires that many well-defined formulas for graph properties include exceptions for it (for example, either "counting all strongly connected components of a graph" becomes "counting all non-null strongly connected components of a graph", or the definition of connected graphs has to be modified not to include K0). To avoid the need for such exceptions, it is often assumed in literature that the term graph implies "graph with at least one vertex" unless context suggests otherwise.[1][2]
In category theory, the order-zero graph is, according to some definitions of "category of graphs," the initial object in the category.
does fulfill (vacuously) most of the same basic graph properties as does (the graph with one vertex and no edges). As some examples, is of size zero, it is equal to its complement graph , a forest, and a planar graph. It may be considered undirected, directed, or even both; when considered as directed, it is a directed acyclic graph. And it is both a complete graph and an edgeless graph. However, definitions for each of these graph properties will vary depending on whether context allows for .
Edgeless graph[edit]
| Edgeless graph (empty graph, null graph) | |
|---|---|
| Vertices | n |
| Edges | 0 |
| Radius | 0 |
| Diameter | 0 |
| Girth | |
| Automorphisms | n! |
| Chromatic number | 1 |
| Chromatic index | 0 |
| Genus | 0 |
| Properties | Integral Symmetric |
| Notation | |
| Table of graphs and parameters | |
For each natural number n, the edgeless graph (or empty graph) of order n is the graph with n vertices and zero edges. An edgeless graph is occasionally referred to as a null graph in contexts where the order-zero graph is not permitted.[1][2]
It is a 0-regular graph. The notation arises from the fact that the n-vertex edgeless graph is the complement of the complete graph .
See also[edit]
List of forbidden characterizations for graphs and hypergraphs[edit]
| Family | Obstructions | Relation | Reference |
|---|---|---|---|
| Forests | loops, pairs of parallel edges, and cycles of all lengths | subgraph | Definition |
| a loop (for multigraphs) or a triangle K3 (for simple graphs) | graph minor | Definition | |
| Claw-free graphs | star K1,3 | induced subgraph | Definition |
| Comparability graphs | induced subgraph | ||
| Triangle-free graphs | triangle K3 | induced subgraph | Definition |
| Planar graphs | K5 and K3,3 | homeomorphic subgraph | Kuratowski's theorem |
| K5 and K3,3 | graph minor | Wagner's theorem | |
| Outerplanar graphs | K4 and K2,3 | graph minor | Diestel (2000),[1]p. 107 |
| Outer 1-planar graphs | six forbidden minors | graph minor | Auer et al. (2013)[2] |
| Graphs of fixed genus | a finite obstruction set | graph minor | Diestel (2000),[1]p. 275 |
| Apex graphs | a finite obstruction set | graph minor | [3] |
| Linklessly embeddable graphs | The Petersen family | graph minor | [4] |
| Bipartite graphs | odd cycles | subgraph | [5] |
| Chordal graphs | cycles of length 4 or more | induced subgraph | [6] |
| Perfect graphs | cycles of odd length 5 or more or their complements | induced subgraph | [7] |
| Line graph of graphs | nine forbidden subgraphs (listed here) | induced subgraph | [8] |
| Graph unions of cactus graphs | the four-vertex diamond graph formed by removing an edge from the complete graph K4 | graph minor | [9] |
| Ladder graphs | K2,3 and its dual graph | homeomorphic subgraph | [10] |
| Split graphs | induced subgraph | [11] | |
| 2-connected series–parallel(treewidth ≤ 2, branchwidth ≤ 2) | K4 | graph minor | Diestel (2000),[1]p. 327 |
| Treewidth ≤ 3 | K5, octahedron, pentagonal prism, Wagner graph | graph minor | [12] |
| Branchwidth ≤ 3 | K5, octahedron, cube, Wagner graph | graph minor | [13] |
| Complement-reducible graphs (cographs) | 4-vertex path P4 | induced subgraph | [14] |
| Trivially perfect graphs | 4-vertex path P4 and 4-vertex cycle C4 | induced subgraph | [15] |
| Threshold graphs | 4-vertex path P4, 4-vertex cycle C4, and complement of C4 | induced subgraph | [15] |
| Line graph of 3-uniform linear hypergraphs | a finite list of forbidden induced subgraphs with minimum degree at least 19 | induced subgraph | [16] |
| Line graph of k-uniform linear hypergraphs, k > 3 | a finite list of forbidden induced subgraphs with minimum edge degree at least 2k2 − 3k + 1 | induced subgraph | [17][18] |
| Graphs ΔY-reducible to a single vertex | a finite list of at least 68 billion distinct (1,2,3)-clique sums | graph minor | [19] |
| General theorems | |||
| A family defined by an induced-hereditary property | a, possibly non-finite, obstruction set | induced subgraph | |
| A family defined by a minor-hereditary property | a finite obstruction set | graph minor | Robertson–Seymour theorem |
See also[edit]
https://en.wikipedia.org/wiki/Forbidden_graph_characterizationAdditive identities[edit]
An additive identity is the identity element in an additive group. It corresponds to the element 0 such that for all x in the group, 0 + x = x + 0 = x. Some examples of additive identity include:
- The zero vector under vector addition: the vector of length 0 and whose components are all 0. Often denoted as or .[1][2][3]
- The zero function or zero map defined by z(x) = 0, under pointwise addition (f + g)(x) = f(x) + g(x)
- The empty set under set union
- An empty sum or empty coproduct
- An initial object in a category (an empty coproduct, and so an identity under coproducts)
Absorbing elements[edit]
An absorbing element in a multiplicative semigroup or semiring generalises the property 0 ⋅ x = 0. Examples include:
- The empty set, which is an absorbing element under Cartesian product of sets, since { } × S = { }
- The zero function or zero map defined by z(x) = 0 under pointwise multiplication (f ⋅ g)(x) = f(x) ⋅ g(x)
Many absorbing elements are also additive identities, including the empty set and the zero function. Another important example is the distinguished element 0 in a field or ring, which is both the additive identity and the multiplicative absorbing element, and whose principal ideal is the smallest ideal.
Zero objects[edit]
A zero object in a category is both an initial and terminal object (and so an identity under both coproducts and products). For example, the trivial structure (containing only the identity) is a zero object in categories where morphisms must map identities to identities. Specific examples include:
- The trivial group, containing only the identity (a zero object in the category of groups)
- The zero module, containing only the identity (a zero object in the category of modules over a ring)
Zero morphisms[edit]
A zero morphism in a category is a generalised absorbing element under function composition: any morphism composed with a zero morphism gives a zero morphism. Specifically, if 0XY : X → Y is the zero morphism among morphisms from X to Y, and f : A → X and g : Y → B are arbitrary morphisms, then g ∘ 0XY = 0XB and 0XY ∘ f = 0AY.
If a category has a zero object 0, then there are canonical morphisms X → 0 and 0 → Y, and composing them gives a zero morphism 0XY : X → Y. In the category of groups, for example, zero morphisms are morphisms which always return group identities, thus generalising the function z(x) = 0.
Least elements[edit]
A least element in a partially ordered set or lattice may sometimes be called a zero element, and written either as 0 or ⊥.
Zero module[edit]
In mathematics, the zero module is the module consisting of only the additive identity for the module's addition function. In the integers, this identity is zero, which gives the name zero module. That the zero module is in fact a module is simple to show; it is closed under addition and multiplication trivially.
Zero ideal[edit]
In mathematics, the zero ideal in a ring is the ideal consisting of only the additive identity (or zero element). The fact that this is an ideal follows directly from the definition.
Zero matrix[edit]
In mathematics, particularly linear algebra, a zero matrix is a matrix with all its entries being zero. It is alternately denoted by the symbol .[1] Some examples of zero matrices are
The set of m × n matrices with entries in a ring K forms a module . The zero matrix in is the matrix with all entries equal to , where is the additive identity in K.
The zero matrix is the additive identity in . That is, for all :
There is exactly one zero matrix of any given size m × n (with entries from a given ring), so when the context is clear, one often refers to the zero matrix. In general, the zero element of a ring is unique, and typically denoted as 0 without any subscript to indicate the parent ring. Hence the examples above represent zero matrices over any ring.
The zero matrix also represents the linear transformation which sends all vectors to the zero vector.
Zero tensor[edit]
In mathematics, the zero tensor is a tensor, of any order, all of whose components are zero. The zero tensor of order 1 is sometimes known as the zero vector.
Taking a tensor product of any tensor with any zero tensor results in another zero tensor. Adding the zero tensor is equivalent to the identity operation.
See also[edit]
- Null semigroup
- Zero divisor
- Zero object
- Zero of a function
- Zero — non-mathematical uses
https://en.wikipedia.org/wiki/Exotic_sphere
https://en.wikipedia.org/wiki/Surface_(topology)#Classification_of_closed_surfaces
https://en.wikipedia.org/wiki/Continuous_function#Continuous_functions_between_topological_spaces
In mathematics, a directed set (or a directed preorder or a filtered set) is a nonempty set together with a reflexive and transitive binary relation (that is, a preorder), with the additional property that every pair of elements has an upper bound.[1] In other words, for any and in there must exist in with and A directed set's preorder is called a direction.
The notion defined above is sometimes called an upward directed set. A downward directed set is defined analogously,[2]meaning that every pair of elements is bounded below.[3] Some authors (and this article) assume that a directed set is directed upward, unless otherwise stated. Be aware that other authors call a set directed if and only if it is directed both upward and downward.[4]
Directed sets are a generalization of nonempty totally ordered sets. That is, all totally ordered sets are directed sets (contrast partially ordered sets, which need not be directed). Join semilattices (which are partially ordered sets) are directed sets as well, but not conversely. Likewise, lattices are directed sets both upward and downward.
In topology, directed sets are used to define nets, which generalize sequences and unite the various notions of limit used in analysis. Directed sets also give rise to direct limits in abstract algebra and (more generally) category theory.
Binary relations are used in many branches of mathematics to model a wide variety of concepts. These include, among others:
- the "is greater than", "is equal to", and "divides" relations in arithmetic;
- the "is congruent to" relation in geometry;
- the "is adjacent to" relation in graph theory;
- the "is orthogonal to" relation in linear algebra.
A function may be defined as a special kind of binary relation.[3] Binary relations are also heavily used in computer science.
A binary relation over sets X and Y is an element of the power set of Since the latter set is ordered by inclusion (⊆), each relation has a place in the lattice of subsets of A binary relation is either a homogeneous relation or a heterogeneous relation depending on whether X = Y or not.
https://en.wikipedia.org/wiki/Binary_relation
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.[1] As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions (i.e., leptons and quarks), and force fields, whose quanta are bosons (e.g., photons and gluons). All these fields have zero-point energy.[2] These fluctuating zero-point fields lead to a kind of reintroduction of an aether in physics[1][3] since some systems can detect the existence of this energy. However, this aether cannot be thought of as a physical medium if it is to be Lorentz invariant such that there is no contradiction with Einstein's theory of special relativity.[1]
Physics currently lacks a full theoretical model for understanding zero-point energy; in particular, the discrepancy between theorized and observed vacuum energy is a source of major contention.[4]
In metals, anisotropic elasticity behavior is present in all single crystals with three independent coefficients for cubic crystals, for example. For face centered cubic materials such as Nickel and Copper, the stiffness is highest along the <111> direction, normal to the close packed planes, and smallest parallel to <100>. Tungsten is so nearly isotropic at room temperature that it can be considered to have only two stiffness coefficients; Aluminum is another metal that is nearly isotropic.
For an isotropic material,
,
where is the shear modulus, is the Young's modulus, and is the material's Poisson's ratio. Therefore, for cubic materials, we can think of anisotropy, , as the ratio between the empirically determined shear modulus for the cubic material and its (isotropic) equivalent:
The latter expression is known as the Zener ratio, , where refers to Elastic constants in Voigt (vector-matrix) notation. For an isotropic material, the ratio is one.
Fiber-reinforced or layered composite materials exhibit anisotropic mechanical properties, due to orientation of the reinforcement material. In many fiber-reinforced composites like carbon fiber or glass fiber based composites, the weave of the material (e.g. unidirectional or plain weave) can determine the extent of the anisotropy of the bulk material.[9] The tunability of orientation of the fibers, allows for application-based designs of composite materials, depending on the direction of stresses applied onto the material.
Amorphous materials such as glass and polymers are typically isotropic. Due to the highly randomized orientation of macromolecules in polymeric materials, polymers are in general described as isotropic. However, polymers can be engineered to have directionally dependent properties through processing techniques or introduction of anisotropy-inducing elements. Researchers have built composite materials with aligned fibers and voids to generate anisotropic hydrogels, in order to mimic hierarchically ordered biological soft matter.[10] 3D printing, especially Fused Deposition Modeling, can introduce anisotropy into printed parts. This is due to the fact that FDM is designed to extrude and print layers of thermoplastic materials.[11] This creates materials that are strong when tensile stress is applied in parallel to the layers and weak when the material is perpendicular to the layers.
https://en.wikipedia.org/wiki/Anisotropy
https://en.wikipedia.org/wiki/Brownian_motion
https://en.wikipedia.org/wiki/Transverse_isotropy
https://en.wikipedia.org/wiki/Single_crystal
https://en.wikipedia.org/wiki/Kyropoulos_method
https://en.wikipedia.org/wiki/Transport_phenomena
https://en.wikipedia.org/wiki/Thermodynamics
Narrow escape[edit]
The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology which has the following formulation: a Brownian particle (ion, molecule, or protein) is confined to a bounded domain (a compartment or a cell) by a reflecting boundary, except for a small window through which it can escape. The narrow escape problem is that of calculating the mean escape time. This time diverges as the window shrinks, thus rendering the calculation a singular perturbation problem.
See also[edit]
- Brownian bridge: a Brownian motion that is required to "bridge" specified values at specified times
- Brownian covariance
- Brownian dynamics
- Brownian motion of sol particles
- Brownian motor
- Brownian noise (Martin Gardner proposed this name for sound generated with random intervals. It is a pun on Brownian motion and white noise.)
- Brownian ratchet
- Brownian surface
- Brownian tree
- Brownian web
- Rotational Brownian motion
- Clinamen
- Complex system
- Continuity equation
- Diffusion equation
- Geometric Brownian motion
- Itō diffusion: a generalisation of Brownian motion
- Langevin equation
- Lévy arcsine law
- Local time (mathematics)
- Many-body problem
- Marangoni effect
- Nanoparticle tracking analysis
- Narrow escape problem
- Osmosis
- Random walk
- Schramm–Loewner evolution
- Single particle tracking
- Statistical mechanics
- Surface diffusion: a type of constrained Brownian motion.
- Thermal equilibrium
- Thermodynamic equilibrium
- Tyndall effect: physical chemistry phenomenon where particles are involved; used to differentiate between the different types of mixtures.
- Ultramicroscope
https://en.wikipedia.org/wiki/Brownian_motion#Narrow_escape
The narrow escape problem[1][2] is a ubiquitous problem in biology, biophysics and cellular biology.
The mathematical formulation is the following: a Brownian particle (ion, molecule, or protein) is confined to a bounded domain (a compartment or a cell) by a reflecting boundary, except for a small window through which it can escape. The narrow escape problem is that of calculating the mean escape time. This time diverges as the window shrinks, thus rendering the calculation a singular perturbation problem.[3][4][5][6][7][8][9]
When escape is even more stringent due to severe geometrical restrictions at the place of escape, the narrow escape problem becomes the dire strait problem.[10][11]
The narrow escape problem was proposed in the context of biology and biophysics by D. Holcman and Z. Schuss,[12] and later on with A.Singer and led to the narrow escape theory in applied mathematics and computational biology.[13][14][15]
https://en.wikipedia.org/wiki/Narrow_escape_problem
https://en.wikipedia.org/wiki/Central_limit_theorem
https://en.wikipedia.org/wiki/Fluctuating_asymmetry
https://en.wikipedia.org/wiki/Vacuum
https://en.wikipedia.org/wiki/Pressure
https://en.wikipedia.org/wiki/Pressure_measurement#Gauge
https://en.wikipedia.org/wiki/Atmospheric_pressure
https://en.wikipedia.org/wiki/Pressure#Surface_pressure_and_surface_tension
https://en.wikipedia.org/wiki/Critical_point_(thermodynamics)
https://en.wikipedia.org/wiki/Internal_pressure
https://en.wikipedia.org/wiki/Dynamic_pressure
https://en.wikipedia.org/wiki/Electron_degeneracy_pressure
https://en.wikipedia.org/wiki/Partial_pressure
https://en.wikipedia.org/wiki/Static_pressure
https://en.wikipedia.org/wiki/Pitot-static_system#Static_pressure
https://en.wikipedia.org/wiki/Vertical_pressure_variation
https://en.wikipedia.org/wiki/Density
https://en.wikipedia.org/wiki/Vacuum
https://en.wikipedia.org/wiki/Borexino
https://en.wikipedia.org/wiki/Background_radiation
https://en.wikipedia.org/wiki/Category:Atmospheric_thermodynamics
https://en.wikipedia.org/wiki/Category:Underwater_diving_physics
https://en.wikipedia.org/wiki/Category:Fluid_mechanics







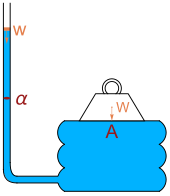






































![{\displaystyle {\begin{matrix}{\cfrac {}{a{\hbox{ term}}}}{\hbox{ u}}\\\vdots \\{\cfrac {[a/x]A{\hbox{ true}}}{\forall x.A{\hbox{ true}}}}\;\forall _{I^{u,a}}\end{matrix}}\qquad \qquad {\frac {\forall x.A{\hbox{ true}}\qquad t{\hbox{ term}}}{[t/x]A{\hbox{ true}}}}\;\forall _{E}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb528166c4cacfdcbcd8479b3b992af7ad9026e4)
![{\displaystyle {\frac {[t/x]A{\hbox{ true}}}{\exists x.A{\hbox{ true}}}}\;\exists _{I}\qquad \qquad {\cfrac {{\begin{matrix}\\\\\\\\\exists x.A{\hbox{ true}}\\\end{matrix}}\qquad {\begin{matrix}{\cfrac {}{a{\hbox{ term}}}}{\hbox{ u}}\qquad {\cfrac {}{[a/x]A{\hbox{ true}}}}{\hbox{ v}}\\\vdots \\C{\hbox{ true}}\\\end{matrix}}}{C{\hbox{ true}}}}\exists _{E^{a,u,v}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a79e883a892e5535870bc62b6815908a4a3afd3)















































































 is non-negative (when dealing with real numbers), which is not the case here.
is non-negative (when dealing with real numbers), which is not the case here.

















![{\displaystyle \textstyle f(\rho )=-\left[f^{2}(\rho )\right]^{1/2}>-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67429ac8033219ec8bf5efebf480b42e9fd7c22)



































![{\displaystyle G=E/[2(1+\nu )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/090fc763b44b04a7440fbbc42f812c2315e34b7d)




![{\displaystyle a_{r}={\frac {G}{E/[2(1+\nu )]}}={\frac {2(1+\nu )G}{E}}\equiv {\frac {2C_{44}}{C_{11}-C_{12}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f41d6821eb2a7288d1421770c47c1ff4ae80191)
