Bunsen detected previously unknown new blue spectral emission lines in samples of mineral water from Dürkheim.
https://en.wikipedia.org/wiki/Robert_Bunsen
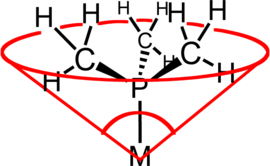
Cadet's fuming liquid was a red-brown oily liquid prepared in 1760 by the French chemist Louis Claude Cadet de Gassicourt (1731-1799) by the reaction of potassium acetate with arsenic trioxide.[1] It consisted mostly of dicacodyl (((CH3)2As)2) and cacodyl oxide (((CH3)2As)2O). The reaction for forming the oxide was something like:
- 4 KCH3COO + As2O3 → ((CH3)2As)2O + 2 K2CO3 + 2 CO2
These were the first organometallic substances prepared; as such, Cadet has been regarded as the father of organometallic chemistry.[2]
This liquid develops white fumes when exposed to air, resulting in a pale flame producing carbon dioxide, water, and arsenic trioxide. It has a nauseating and very disagreeable garlic-like odor.
Around 1840, Robert Bunsen did much work on characterizing the compounds in the liquid and its derivatives. His research was important in the development of radical theory.
https://en.wikipedia.org/wiki/Cadet%27s_fuming_liquid
Gustav Robert Kirchhoff (German: [ˈkɪʁçhɔf]; 12 March 1824 – 17 October 1887) was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects.[1][2]
He coined the term black-body radiation in 1862. Several different sets of concepts are named "Kirchhoff's laws" after him, concerning such diverse subjects as black-body radiation and spectroscopy, electrical circuits, and thermochemistry. The Bunsen–Kirchhoff Award for spectroscopy is named after him and his colleague, Robert Bunsen.
Gustav Kirchhoff | |
|---|---|
 | |
| Born | Gustav Robert Kirchhoff 12 March 1824 |
| Died | 17 October 1887 (aged 63) |
| Nationality | Prussian (1824–1871) German (1871–1887) |
| Alma mater | University of Königsberg |
| Known for | Kirchhoff's circuit laws Kirchhoff's law of thermal radiation Kirchhoff's laws of spectroscopy Kirchhoff's law of thermochemistry |
| Awards | Rumford medal (1862) Davy Medal (1877) Matteucci Medal (1877) Janssen Medal (1887) |
| Scientific career | |
| Fields | Physics Chemistry |
| Institutions | University of Berlin University of Breslau University of Heidelberg |
| Doctoral advisor | Franz Ernst Neumann[citation needed] |
| Notable students | Loránd Eötvös Edward Nichols Gabriel Lippmann[citation needed] Dmitri Ivanovich Mendeleev Max Planck Jules Piccard Max Noether Heike Kamerlingh Onnes Ernst Schröder |
https://en.wikipedia.org/wiki/Gustav_Kirchhoff
Jonas Ferdinand Gabriel Lippmann[2] (16 August 1845 – 13 July 1921) was a Franco-Luxembourgish physicist and inventor, and Nobel laureate in physics for his method of reproducing colours photographically based on the phenomenon of interference.[3]
Gabriel Lippmann | |
|---|---|
 | |
| Born | Jonas Ferdinand Gabriel Lippmann 16 August 1845 Bonnevoie/Bouneweg, Luxembourg (since 1921 part of Luxembourg City) |
| Died | 13 July 1921 (aged 75) SS France, Atlantic Ocean |
| Nationality | France |
| Alma mater | École Normale Supérieure |
| Known for | Lippmann colour photography Integral 3-D photography Lippmann electrometer |
| Awards | Nobel Prize for Physics(1908) |
| Scientific career | |
| Fields | Physics |
| Institutions | Sorbonne |
| Doctoral advisor | Gustav Kirchhoff |
| Other academic advisors | Hermann von Helmholtz[1] |
| Doctoral students | Marie Curie |
Career[edit]
Lippmann made several important contributions to various branches of physics over the years.
The capillary electrometer[edit]
One of Lippmann's early discoveries was the relationship between electrical and capillary phenomena which allowed him to develop a sensitive capillary electrometer, subsequently known as the Lippmann electrometer which was used in the first ECG machine. In a paper delivered to the Philosophical Society of Glasgow on 17 January 1883, John G. M'Kendrick described the apparatus as follows:
- Lippmann's electrometer consists of a tube of ordinary glass, 1 metre long and 7 millimetres in diameter, open at both ends, and kept in the vertical position by a stout support. The lower end is drawn into a capillary point, until the diameter of the capillary is .005 of a millimetre. The tube is filled with mercury, and the capillary point is immersed in dilute sulphuric acid (1 to 6 of water in volume), and in the bottom of the vessel containing the acid there is a little more mercury. A platinum wire is put into connection with the mercury in each tube, and, finally, arrangements are made by which the capillary point can be seen with a microscope magnifying 250 diameters. Such an instrument is very sensitive; and Lippmann states that it is possible to determine a difference of potential so small as that of one 10,080th of a Daniell. It is thus a very delicate means of observing and (as it can be graduated by a compensation-method) of measuring minute electromotive forces.[9][10]
Lippmann's PhD thesis, presented to the Sorbonne on 24 July 1875, was on electrocapillarity.[11]
Piezoelectricity[edit]
In 1881, Lippmann predicted the converse piezoelectric effect.[12]
Colour photography[edit]
Above all, Lippmann is remembered as the inventor of a method for reproducing colours by photography, based on the interference phenomenon, which earned him the Nobel Prize in Physics for 1908.[7]
In 1886, Lippmann's interest turned to a method of fixing the colours of the solar spectrum on a photographic plate. On 2 February 1891, he announced to the Academy of Sciences: "I have succeeded in obtaining the image of the spectrum with its colours on a photographic plate whereby the image remains fixed and can remain in daylight without deterioration." By April 1892, he was able to report that he had succeeded in producing colour images of a stained glass window, a group of flags, a bowl of oranges topped by a red poppy and a multicoloured parrot. He presented his theory of colour photography using the interference method in two papers to the Academy, one in 1894, the other in 1906.[5]
The interference phenomenon in optics occurs as a result of the wave propagation of light. When light of a given wavelength is reflected back upon itself by a mirror, standing waves are generated, much as the ripples resulting from a stone dropped into still water create standing waves when reflected back by a surface such as the wall of a pool. In the case of ordinary incoherent light, the standing waves are distinct only within a microscopically thin volume of space next to the reflecting surface.
Lippmann made use of this phenomenon by projecting an image onto a special photographic plate capable of recording detail smaller than the wavelengths of visible light. The light passed through the supporting glass sheet into a very thin and nearly transparent photographic emulsion containing sub microscopically small silver halide grains. A temporary mirror of liquid mercury in intimate contact reflected the light back through the emulsion, creating standing waves whose nodes had little effect while their antinodes created a latent image. After development, the result was a structure of laminae, distinct parallel layers composed of submicroscopic metallic silver grains, which was a permanent record of the standing waves. In each part of the image, the spacing of the laminae corresponded to the half-wavelengths of the light photographed.
The finished plate was illuminated from the front at a nearly perpendicular angle, using daylight or another source of white light containing the full range of wavelengths in the visible spectrum. At each point on the plate, light of approximately the same wavelength as the light which had generated the laminae was strongly reflected back toward the viewer. Light of other wavelengths which was not absorbed or scattered by the silver grains simply passed through the emulsion, usually to be absorbed by a black anti-reflection coating applied to the back of the plate after it had been developed. The wavelengths, and therefore the colours, of the light which had formed the original image were thus reconstituted and a full-colour image was seen.[13][14][15]
In practice, the Lippmann process was not easy to use. Extremely fine-grained high-resolution photographic emulsions are inherently much less light-sensitive than ordinary emulsions, so long exposure times were required. With a lens of large aperture and a very brightly sunlit subject, a camera exposure of less than one minute was sometimes possible, but exposures measured in minutes were typical. Pure spectral colours reproduced brilliantly, but the ill-defined broad bands of wavelengths reflected by real-world objects could be problematic. The process did not produce colour prints on paper and it proved impossible to make a good duplicate of a Lippmann colour photograph by rephotographing it, so each image was unique. A very shallow-angled prism was usually cemented to the front of the finished plate to deflect unwanted surface reflections, and this made plates of any substantial size impractical. The lighting and viewing arrangement required to see the colours to best effect precluded casual use. Although the special plates and a plate holder with a built-in mercury reservoir were commercially available for a few years circa 1900, even expert users found consistent good results elusive and the process never graduated from being a scientifically elegant laboratory curiosity. It did, however, stimulate interest in the further development of colour photography.[15]
Lippmann's process foreshadowed laser holography, which is also based on recording standing waves in a photographic medium. Denisyuk reflection holograms, often referred to as Lippmann-Bragg holograms, have similar laminar structures that preferentially reflect certain wavelengths. In the case of actual multiple-wavelength colour holograms of this type, the colour information is recorded and reproduced just as in the Lippmann process, except that the highly coherent laser light passing through the recording medium and reflected back from the subject generates the required distinct standing waves throughout a relatively large volume of space, eliminating the need for reflection to occur immediately adjacent to the recording medium. Unlike Lippmann colour photography, however, the lasers, the subject and the recording medium must all be kept stable to within one quarter of a wavelength during the exposure in order for the standing waves to be recorded adequately or at all.
Integral photography[edit]
In 1908, Lippmann introduced what he called "integral photography", in which a plane array of closely spaced, small, spherical lenses is used to photograph a scene, recording images of the scene as it appears from many slightly different horizontal and vertical locations. When the resulting images are rectified and viewed through a similar array of lenses, a single integrated image, composed of small portions of all the images, is seen by each eye. The position of the eye determines which parts of the small images it sees. The effect is that the visual geometry of the original scene is reconstructed, so that the limits of the array seem to be the edges of a window through which the scene appears life-size and in three dimensions, realistically exhibiting parallax and perspective shift with any change in the position of the observer.[16] This principle of using numerous lenses or imaging apertures to record what was later termed a light field underlies the evolving technology of light-field cameras and microscopes.
When Lippmann presented the theoretical foundations of his "integral photography" in March 1908, it was impossible to accompany them with concrete results. At the time, the materials necessary for producing a lenticular screen with the proper optical qualities were lacking. In the 1920s, promising trials were made by Eugène Estanave, using glass Stanhope lenses, and by Louis Lumière, using celluloid.[17] Lippmann's integral photography was the foundation of research on 3D and animated lenticular imagery and also on color lenticular processes.
Measurement of time[edit]
In 1895, Lippmann evolved a method of eliminating the personal equation in measurements of time, using photographic registration, and he studied the eradication of irregularities of pendulum clocks, devising a method of comparing the times of oscillation of two pendulums of nearly equal period.[4]
The coelostat[edit]
Lippmann also invented the coelostat, an astronomical tool that compensated for the Earth's rotation and allowed a region of the sky to be photographed without apparent movement.[4]
https://en.wikipedia.org/wiki/Gabriel_Lippmann
Baron Loránd Eötvös de Vásárosnamény (or Loránd Eötvös, pronounced [ˈloraːnd ˈøtvøʃ], Hungarian: vásárosnaményi báró Eötvös Loránd Ágoston; 27 July 1848 – 8 April 1919), also called Baron Roland von Eötvös in English literature,[2] was a Hungarian physicist. He is remembered today largely for his work on gravitation and surface tension, and the invention of the torsion pendulum.
In addition to Eötvös Loránd University[3] and the Eötvös Loránd Institute of Geophysics in Hungary, the Eötvös crater on the Moon,[4] the asteroid 12301 Eötvösand the mineral lorándite also bear his name.
Loránd Eötvös | |
|---|---|
 Eötvös in 1912 | |
| Born | 27 July 1848 |
| Died | 8 April 1919 (aged 70) |
| Nationality | Hungarian |
| Alma mater | University of Heidelberg |
| Known for | Eötvös experiment Eötvös rule Eötvös pendulum |
| Spouse(s) | Gizella Horvát |
| Children | Jolán Rolanda Ilona |
| Parent(s) | József Eötvös Agnes Rosty de Barkócz |
| Scientific career | |
| Fields | Physics |
| Institutions | University of Budapest |
| Doctoral advisor | Hermann Helmholtz[1] |
Life[edit]
Born in 1848, the year of the Hungarian revolution, Eötvös was the son of the Baron József Eötvös de Vásárosnamény (1813–1871), a well-known poet, writer, and liberal politician, who was cabinet minister at the time, and played an important part in 19th century Hungarian intellectual and political life. His mother was the Hungarian noble lady Agnes Rosty de Barkócz (1825–1913), member of the illustrious noble family Rosty de Barkócz that originally hailed from the Vas county, and through this, he descended from the ancient medieval Hungarian noble Perneszy family, which died out in the 18th century. Loránd's uncle was Pál Rosty de Barkócz (1830–1874) was a Hungarian nobleman, photographer, explorer, who visited Texas, New Mexico, Mexico, Cuba and Venezuela between 1857 and 1859.
Loránd Eötvös first studied law, but soon switched to physics and went abroad to study in Heidelberg and Königsberg. After earning his doctorate, he became a university professor in Budapest and played a leading part in Hungarian science for almost half a century. He gained international recognition first by his innovative work on capillarity, then by his refined experimental methods and extensive field studies in gravity.
Eötvös is remembered today for his experimental work on gravity, in particular his study of the equivalence of gravitational and inertial mass (the so-called weak equivalence principle) and his study of the gravitational gradient on the Earth's surface. The weak equivalence principle plays a prominent role in relativity theoryand the Eötvös experiment was cited by Albert Einstein in his 1916 paper The Foundation of the General Theory of Relativity. Measurements of the gravitational gradient are important in applied geophysics, such as the location of petroleum deposits. The CGS unit for gravitational gradient is named the eotvos in his honor.
From 1886 until his death, Loránd Eötvös researched and taught in the University of Budapest, which in 1950 was renamed after him (Eötvös Loránd University).
Eötvös is buried in the Kerepesi Cemetery in Budapest, Hungary.[5]
Torsion balance[edit]
A variation of the earlier invention, the torsion balance, the Eötvös pendulum, designed by Hungarian Baron Loránd Eötvös, is a sensitive instrument for measuring the density of underlying rock strata. The device measures not only the direction of force of gravity, but the change in the force of gravity's extent in the horizontal plane. It determines the distribution of masses in the Earth's crust. The Eötvös torsion balance, an important instrument of geodesy and geophysics throughout the whole world, studies the Earth's physical properties. It is used for mine exploration, and also in the search for minerals, such as oil, coal and ores. The Eötvös pendulum was never patented, but after the demonstration of its accuracy and numerous visits to Hungary from abroad, several instruments were exported worldwide, and the richest oilfields in the United States were discovered by using it. The Eötvös pendulum was used to prove the equivalence of the inertial mass and the gravitational mass accurately, as a response to the offer of a prize. This equivalence was used later by Albert Einstein in setting out the theory of general relativity.
This is how Eötvös describes his balance:
One of Eötvös' assistants who later became a noted scientist was Radó von Kövesligethy.
Honors[edit]
To honor Eötvös, a postage stamp was issued by Hungary on 1 July 1932.[6] Another stamp was issued on 27 July 1948 to commemorate the centenary of the birth of the physicist.[7] Hungary issued a postage stamp on 31 January 1991.[8]
See also[edit]
- Eotvos, a unit of gravitational gradient
- Eötvös effect, a concept in geodesy
- Eötvös number, a concept in fluid dynamics
- Eötvös rule for predicting surface tension dependent on temperature
- List of geophysicists
- Lorándite, a mineral named after Loránd Eötvös
References[edit]
- ^ Physics Tree – Hermann von Helmholtz Family Tree
- ^ L. Bod, E. Fishbach, G. Marx, and Maria Náray-Ziegler: One hundred years of the Eötvös experiment, – Acta Physica Hungarica 69/3-4 (1991) 335–355
- ^ Brief History of ELTE, Eötvös Loránd University, archived from the original on 7 May 2016, retrieved 7 May 2016
- ^ Pickover, Clifford (2008), Archimedes to Hawking: Laws of Science and the Great Minds Behind Them, Oxford University Press, p. 383, ISBN 9780199792689.
- ^ See this site for a photograph of his gravesite.
- ^ colnect.com/en/stamps/stamp/141647-Baron_Loránd_Eötvös_1848-1919_physicist-Personalities-Hungary.
- ^ colnect.com/en/stamps/stamp/179845-Baron_Lóránd_Eötvös_1848-1919_physicist-Lóránd_Eötvös-Hungary
- ^ colnect.com/en/stamps/stamp/181792-Lóránd_Eötvös-People-Hungary
Further reading[edit]
- Antall, J. (1971), "The Pest School of Medicine and the health policy of the Centralists. On the centenary of the death of József Eötvös", Orvosi Hetilap (published 9 May 1971), 112 (19), pp. 1083–9, PMID 4932574
https://en.wikipedia.org/wiki/Loránd_Eötvös
The eotvos is a unit of acceleration divided by distance that was used in conjunction with the older centimetre–gram–second system of units (cgs). The eotvos is defined as 10−9 galileos per centimetre. The symbol of the eotvos unit is E.[1][2]
In SI units or in cgs units, 1 eotvos = 10−9 second−2.[3]
The gravitational gradient of the Earth, that is, the change in the gravitational acceleration vector from one point on the Earth's surface to another, is customarily measured in units of eotvos. The Earth's gravity gradient is dominated by the component due to Earth's near-spherical shape, which results in a vertical tensile gravity gradient of 3,080 E (an elevation increase of 1 m gives a decrease of gravity of about 0.3 mGal), and horizontal compressive gravity gradients of one half that, or 1,540 E. Earth's rotation perturbs this in a direction-dependent manner by about 5 E. Gravity gradient anomalies in mountainous areas can be as large as several hundred eotvos.
The eotvos unit is named for the physicist Loránd Eötvös, who made pioneering studies of the gradient of the Earth's gravitational field.[4]
| eotvos | |
|---|---|
| Unit system | Non-SI metric unit |
| Unit of | Linear acceleration density |
| Symbol | E |
| Named after | Loránd Eötvös |
| Derivation | 10−9 Gal/cm |
| Conversions | |
| 1 E in ... | ... is equal to ... |
| CGS base units | 10−9 s−2 |
| SI base units | 10−9 s−2 |
https://en.wikipedia.org/wiki/Eotvos_(unit)
Gravity gradiometry is the study and measurement of variations (anomalies) in the Earth's gravitational field. The gravity gradient is the spatial rate of change of gravitational acceleration. As acceleration is a vector quantity, with magnitude and three-dimensional direction, the full gravity gradient is a 3x3 tensor.
Gravity gradiometry is used by oil and mineral prospectors to measure the density of the subsurface, effectively by measuring the rate of change of gravitational acceleration due to underlying rock properties. From this information it is possible to build a picture of subsurface anomalies which can then be used to more accurately target oil, gas and mineral deposits. It is also used to image water column density, when locating submerged objects, or determining water depth (bathymetry). Physical scientists use gravimeters to determine the exact size and shape of the earth and they contribute to the gravity compensations applied to inertial navigation systems.
https://en.wikipedia.org/wiki/Gravity_gradiometry
Friedrich Wilhelm Karl Ernst Schröder (25 November 1841 in Mannheim, Baden, Germany – 16 June 1902 in Karlsruhe, Germany) was a Germanmathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic, by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce. He is best known for his monumental Vorlesungen über die Algebra der Logik (Lectures on the Algebra of Logic, 1890–1905), in three volumes, which prepared the way for the emergence of mathematical logic as a separate discipline in the twentieth century by systematizing the various systems of formal logic of the day.
Ernst Schröder | |
|---|---|
 Ernst Schröder | |
| Born | 25 November 1841 |
| Died | 16 June 1902 (aged 60) |
| Nationality | German |
| Scientific career | |
| Fields | Mathematics |
https://en.wikipedia.org/wiki/Ernst_Schröder
Heike Kamerlingh Onnes (21 September 1853 – 21 February 1926) was a Dutch physicist and Nobel laureate. He exploited the Hampson–Linde cycle to investigate how materials behave when cooled to nearly absolute zero and later to liquefy helium for the first time, in 1908. He also discovered superconductivity in 1911.[1][2][3]
Heike Kamerlingh Onnes | |
|---|---|
 | |
| Born | Heike Kamerlingh Onnes 21 September 1853 Groningen, Netherlands |
| Died | 21 February 1926 (aged 72) Leiden, Netherlands |
| Nationality | Netherlands |
| Alma mater | Heidelberg University University of Groningen |
| Known for | Liquid helium Onnes-effect Superconductivity Virial equation of state Coining the term “enthalpy” Kamerlingh Onnes Award |
| Awards | Matteucci Medal (1910) Rumford Medal (1912) Nobel Prize in Physics (1913) Franklin Medal (1915) |
| Scientific career | |
| Fields | Physics |
| Institutions | University of Leiden Delft Polytechnic |
| Doctoral advisor | Rudolf Adriaan Mees |
| Other academic advisors | Robert Bunsen Gustav Kirchhoff Johannes Bosscha |
| Doctoral students | Jacob Clay Wander de Haas Gilles Holst Johannes Kuenen Pieter Zeeman |
| Influences | Johannes Diderik van der Waals |
| Influenced | Willem Hendrik Keesom Cryogenics |
University of Leiden[edit]
From 1882 to 1923 Kamerlingh Onnes served as professor of experimental physics at the University of Leiden. In 1904 he founded a very large cryogenicslaboratory and invited other researchers to the location, which made him highly regarded in the scientific community. The laboratory is known now as Kamerlingh Onnes Laboratory.[4] Only one year after his appointment as professor he became member of the Royal Netherlands Academy of Arts and Sciences.[5]
Liquefaction of helium[edit]
On 10 July 1908, he was the first to liquefy helium, using several precooling stages and the Hampson–Linde cycle based on the Joule–Thomson effect. This way he lowered the temperature to the boiling point of helium (−269 °C, 4.2 K). By reducing the pressure of the liquid helium he achieved a temperature near 1.5 K. These were the coldest temperatures achieved on earth at the time. The equipment employed is at the Museum Boerhaave in Leiden.[4]
Superconductivity[edit]
In 1911 Kamerlingh Onnes measured the electrical conductivity of pure metals (mercury, and later tin and lead) at very low temperatures. Some scientists, such as William Thomson (Lord Kelvin), believed that electrons flowing through a conductor would come to a complete halt or, in other words, metal resistivity would become infinitely large at absolute zero. Others, including Kamerlingh Onnes, felt that a conductor's electrical resistance would steadily decrease and drop to nil. Augustus Matthiessen said that when the temperature decreases, the metal conductivity usually improves or in other words, the electrical resistivity usually decreases with a decrease of temperature.[6][7]
On 8 April 1911, Kamerlingh Onnes found that at 4.2 K the resistance in a solid mercury wire immersed in liquid helium suddenly vanished. He immediately realized the significance of the discovery (as became clear when his notebook was deciphered a century later).[8] He reported that "Mercury has passed into a new state, which on account of its extraordinary electrical properties may be called the superconductive state". He published more articles about the phenomenon, initially referring to it as "supraconductivity" and, only later adopting the term "superconductivity".
Kamerlingh Onnes received widespread recognition for his work, including the 1913 Nobel Prize in Physics for (in the words of the committee) "his investigations on the properties of matter at low temperatures which led, inter alia, to the production of liquid helium".
https://en.wikipedia.org/wiki/Heike_Kamerlingh_Onnes
https://en.wikipedia.org/wiki/Superfluidity
https://en.wikipedia.org/wiki/Superfluid_helium-4
https://en.wikipedia.org/wiki/Hydrogen_fuel
https://en.wikipedia.org/wiki/Vapor-compression_refrigeration
https://en.wikipedia.org/wiki/Lossless_compression
https://en.wikipedia.org/wiki/Infinite_divisibility
https://en.wikipedia.org/wiki/Shear_force
https://en.wikipedia.org/wiki/Compression_(physics)
https://en.wikipedia.org/wiki/Tension_(physics)
https://en.wikipedia.org/wiki/Trapped_ion_quantum_computer
https://en.wikipedia.org/wiki/Quantum_computing
https://en.wikipedia.org/wiki/Coupling_(physics)
https://en.wikipedia.org/wiki/Oscillation
https://en.wikipedia.org/wiki/Hooke%27s_law
https://en.wikipedia.org/wiki/Christiaan_Huygens
https://en.wikipedia.org/wiki/Aromatic_ring_current
https://en.wikipedia.org/wiki/Magnetic_susceptibility
https://en.wikipedia.org/wiki/Ferromagnetism
https://en.wikipedia.org/wiki/scalar
https://en.wikipedia.org/wiki/surface
https://en.wikipedia.org/wiki/tension
https://en.wikipedia.org/wiki/tensor
https://en.wikipedia.org/wiki/dimension
https://en.wikipedia.org/wiki/plane
https://en.wikipedia.org/wiki/vertical
https://en.wikipedia.org/wiki/pressure
https://en.wikipedia.org/wiki/acceleration
https://en.wikipedia.org/wiki/angular
https://en.wikipedia.org/wiki/dihedral_angle
https://en.wikipedia.org/wiki/Ferromagnetic_resonance
https://en.wikipedia.org/wiki/Eddy_current
https://en.wikipedia.org/wiki/Antiferromagnetism#antiferromagnetic_materials
https://en.wikipedia.org/wiki/Geometrical_frustration
https://en.wikipedia.org/wiki/Saturation_(magnetic)
https://en.wikipedia.org/wiki/Coercivity
https://en.wikipedia.org/wiki/Tensor
https://en.wikipedia.org/wiki/Superconductivity
https://en.wikipedia.org/wiki/Gaussian_units
https://en.wikipedia.org/wiki/Electric_susceptibility
https://en.wikipedia.org/wiki/Magnetic_field
https://en.wikipedia.org/wiki/Permeability_(electromagnetism)#Relative_permeability_and_magnetic_susceptibility
https://en.wikipedia.org/wiki/Dimensionless_quantity
https://en.wikipedia.org/wiki/Superconductivity
https://en.wikipedia.org/wiki/Kinetic_theory_of_gases
https://en.wikipedia.org/wiki/Permeability_(electromagnetism)#Relative_permeability_and_magnetic_susceptibility
https://en.wikipedia.org/wiki/Magnetic_susceptibility
https://en.wikipedia.org/wiki/Cyclophane
https://en.wikipedia.org/wiki/Proton_nuclear_magnetic_resonance
https://en.wikipedia.org/wiki/Non-coordinating_anion
https://en.wikipedia.org/wiki/Tetrakis(3,5-bis(trifluoromethyl)phenyl)borate
https://en.wikipedia.org/wiki/Faraday_effect
https://en.wikipedia.org/wiki/Axial_chirality
Karl Johann Freudenberg ForMemRS[1] (29 January 1886 Weinheim, Baden – 3 April 1983 Weinheim) was a German chemist who did early seminal work on the absolute configurations to carbohydrates, terpenes, and steroids, and on the structure of cellulose (first correct formula published, 1928) and other polysaccharides, and on the nature, structure, and biosynthesis of lignin. The Research Institute for the Chemistry of Wood and Polysaccharides at the University of Heidelberg was created for him in the mid to late 1930s, and he led this until 1969.[2]
Life[edit]
Freudenberg studied at Bonn University in 1904, and the University of Berlin from 1907 to 1910, where he studied with Emil Fischer. In July 1910, he married Doris Nieden; they had five children.[3] His grandfather Carl Johann Freudenberg was a tanner and businessman, who in 1849, with Heinrich Christian Heintze, founded Freudenberg Group.
Freudenberg was a professor at University of Freiburg in 1921, at Heidelberg University in 1922, at Karlsruhe University from 1926 to 1956, and director of the Research Institute at the University of Heidelberg, noted above, from 1936 to 1969.[4]
Works[edit]
- Chemie der natürlichen Gerbstoffe (1920) [studies on tannins and their relations to catechins]
- Stereochemie (1933)
- Tannin, Cellulose, Lignin (1933)
https://en.wikipedia.org/wiki/Karl_Freudenberg
https://en.wikipedia.org/wiki/Karl_Freudenberg
https://en.wikipedia.org/wiki/Christiaan_Huygens
https://en.wikipedia.org/wiki/CRC_Handbook_of_Chemistry_and_Physics
Johannes Diderik van der Waals (Dutch pronunciation: [joːˈɦɑnəz ˈdidərɪk fɑn dər ˈʋaːls] (![]() listen)[note 1]; 23 November 1837 – 8 March 1923) was a Dutch theoretical physicist and thermodynamicist famous for his pioneering work on the equation of state for gases and liquids. Van der Waals started his career as a school teacher. He became the first physics professor of the University of Amsterdam when in 1877 the old Athenaeum was upgraded to Municipal University. Van der Waals won the 1910 Nobel Prize in physics for his work on the equation of state for gases and liquids.[1]
listen)[note 1]; 23 November 1837 – 8 March 1923) was a Dutch theoretical physicist and thermodynamicist famous for his pioneering work on the equation of state for gases and liquids. Van der Waals started his career as a school teacher. He became the first physics professor of the University of Amsterdam when in 1877 the old Athenaeum was upgraded to Municipal University. Van der Waals won the 1910 Nobel Prize in physics for his work on the equation of state for gases and liquids.[1]
His name is primarily associated with the Van der Waals equation of state that describes the behavior of gases and their condensation to the liquid phase. His name is also associated with Van der Waals forces (forces between stable molecules),[2] with Van der Waals molecules (small molecular clusters bound by Van der Waals forces), and with Van der Waals radii (sizes of molecules). As James Clerk Maxwell said, "there can be no doubt that the name of Van der Waals will soon be among the foremost in molecular science."[3]
In his 1873 thesis, Van der Waals noted the non-ideality of real gases and attributed it to the existence of intermolecular interactions. He introduced the first equation of state derived by the assumption of a finite volume occupied by the constituent molecules.[4] Spearheaded by Ernst Mach and Wilhelm Ostwald, a strong philosophical current that denied the existence of molecules arose towards the end of the 19th century. The molecular existence was considered unproven and the molecular hypothesis unnecessary. At the time Van der Waals's thesis was written (1873), the molecular structure of fluids had not been accepted by most physicists, and liquid and vapor were often considered as chemically distinct. But Van der Waals's work affirmed the reality of molecules and allowed an assessment of their size and attractive strength. His new formula revolutionized the study of equations of state. By comparing his equation of state with experimental data, Van der Waals was able to obtain estimates for the actual size of molecules and the strength of their mutual attraction.[5]
The effect of Van der Waals's work on molecular physics in the 20th century was direct and fundamental.[6] By introducing parameters characterizing molecular size and attraction in constructing his equation of state, Van der Waals set the tone for modern molecular science. That molecular aspects such as size, shape, attraction, and multipolar interactions should form the basis for mathematical formulations of the thermodynamic and transport properties of fluids is presently considered an axiom.[7] With the help of the Van der Waals's equation of state, the critical-point parameters of gases could be accurately predicted from thermodynamic measurements made at much higher temperatures. Nitrogen, oxygen, hydrogen, and helium subsequently succumbed to liquefaction. Heike Kamerlingh Onnes was significantly influenced by the pioneering work of Van der Waals. In 1908, Onnes became the first to make liquid helium; this led directly to his 1911 discovery of superconductivity.[8]
https://en.wikipedia.org/wiki/Johannes_Diderik_van_der_Waals
Max Noether (24 September 1844 – 13 December 1921) was a German mathematician who worked on algebraic geometry and the theory of algebraic functions. He has been called "one of the finest mathematicians of the nineteenth century".[1] He was the father of Emmy Noether.
https://en.wikipedia.org/wiki/Max_Noether
Jules Piccard, also known as Julius Piccard (20 September 1840, in Lausanne – 11 April 1933, in Lausanne) was a Swiss chemist. He was the father of twins Auguste Piccard (1884–1962) and Jean Felix Piccard (1884–1963), both renowned balloonists.
He studied chemistry at the University of Heidelberg as a student of Robert Bunsen, receiving his doctorate in 1862. Shortly afterwards, he obtained his habilitation at the polytechnical institute in Zürich. From 1869 to 1903 he was a professor of chemistry at the University of Basel.[1][2]
He made contributions in the field of food chemistry and in his research of cantharidin, dinitrocresol, chrysin and resorcinol.[2][3] He is also known for his studies involving the atomic weight of rubidium.[4]
https://en.wikipedia.org/wiki/Jules_Piccard
Justus Freiherr von Liebig[2] (12 May 1803 – 18 April 1873)[3] was a German scientist who made major contributions to agricultural and biological chemistry, and is considered one of the principal founders of organic chemistry.[4] As a professor at the University of Giessen, he devised the modern laboratory-oriented teaching method, and for such innovations, he is regarded as one of the greatest chemistry teachers of all time.[5] He has been described as the "father of the fertilizerindustry" for his emphasis on nitrogen and trace minerals as essential plant nutrients, and his formulation of the law of the minimum, which described how plant growth relied on the scarcest nutrient resource, rather than the total amount of resources available.[6] He also developed a manufacturing process for beef extracts,[7] and with his consent a company, called Liebig Extract of Meat Company, was founded to exploit the concept; it later introduced the Oxo brand beef bouillon cube. He popularized an earlier invention for condensing vapors, which came to be known as the Liebig condenser.[8]
https://en.wikipedia.org/wiki/Justus_von_Liebig
Eilhard Mitscherlich (German pronunciation: [ˈaɪ̯lhaʁt ˈmɪtʃɐlɪç];[1][2] 7 January 1794 – 28 August 1863) was a German chemist, who is perhaps best remembered today for his discovery of the phenomenon of crystallographic isomorphism in 1819.
https://en.wikipedia.org/wiki/Eilhard_Mitscherlich
Friedlieb Ferdinand Runge (8 February 1794 – 25 March 1867) was a German analytical chemist. Runge identified the mydriatic (pupil dilating) effects of belladonna (deadly nightshade) extract, identified caffeine, and discovered the first coal tar dye (aniline blue).
https://en.wikipedia.org/wiki/Friedlieb_Ferdinand_Runge
Johann Friedrich Ludwig Hausmann (22 February 1782, Hannover – 26 December 1859, Göttingen) was a German mineralogist.[1]
https://en.wikipedia.org/wiki/Johann_Friedrich_Ludwig_Hausmann
Johann Carl Friedrich Gauss (/ɡaʊs/; German: Gauß [kaʁl ˈfʁiːdʁɪç ˈɡaʊs] (![]() listen);[1][2] Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science.[3] Sometimes referred to as the Princeps mathematicorum[4] (Latin for '"the foremost of mathematicians"') and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and is ranked among history's most influential mathematicians.[5]
listen);[1][2] Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science.[3] Sometimes referred to as the Princeps mathematicorum[4] (Latin for '"the foremost of mathematicians"') and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and is ranked among history's most influential mathematicians.[5]
https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss
Planar chirality, also known as 2D chirality, is the special case of chirality for two dimensions.
Most fundamentally, planar chirality is a mathematical term, finding use in chemistry, physics and related physical sciences, for example, in astronomy, optics and metamaterials. Recent occurrences in latter two fields are dominated by microwave and terahertz applications as well as micro- and nanostructured planar interfaces for infrared and visible light.
https://en.wikipedia.org/wiki/Planar_chirality#Planar_chirality_in_chemistry
A cyclophane is a hydrocarbon consisting of an aromatic unit (typically a benzene ring) and an aliphatic chain that forms a bridge between two non-adjacent positions of the aromatic ring. More complex derivatives with multiple aromatic units and bridges forming cagelike structures are also known. Cyclophanes are well-studied in organic chemistry because they adopt unusual chemical conformations due to build-up of strain.
Basic cyclophane types are [n]metacyclophanes (I) in scheme 1, [n]paracyclophanes (II) and [n.n']cyclophanes (III). The prefixes meta and paracorrespond to the usual arene substitution patterns and n refers to the number of carbon atoms making up the bridge.
Structure[edit]
Paracyclophanes adopt the boat conformation normally observed in cyclohexanes but are still able to retain aromaticity. The smaller the value of n the larger the deviation from aromatic planarity. In '[6]paracyclophane' which is one of the smallest, yet stable, cyclophanes X-ray crystallography shows that the aromatic bridgehead carbon atom makes an angle of 20.5° with the plane. The benzyl carbons deviate by another 20.2°. The carbon-to-carbon bond length alternation has increased from 0 for benzene to 39 pm.[1][2]
In organic reactions [6]cyclophane tends to react as a diene derivative and not as an arene. With bromine it gives 1,4-addition and with chlorine the 1,2-addition product forms.
Yet the proton NMR spectrum displays the aromatic protons and their usual deshielded positions around 7.2 ppm and the central methylene protons in the aliphatic bridge are even severely shielded to a position of around - 0.5 ppm, that is, even shielded compared to the internal reference tetramethylsilane. With respect to the diamagnetic ring current criterion for aromaticity this cyclophane is still aromatic.
One particular research field in cyclophanes involves probing just how close atoms can get above the center of an aromatic nucleus.[3] In so-called in-cyclophanes with part of the molecule forced to point inwards one of the closest hydrogen to arene distances experimentally determined is just 168 picometers (pm).
A non-bonding nitrogen to arene distance of 244 pm is recorded for a pyridinophane and in the unusual superphane the two benzene rings are separated by a mere 262 pm. Other representative of this group are in-methylcyclophanes,[4] in-ketocyclophanes[5] and in,in-Bis(hydrosilane).[6]
Synthetic methods[edit]
[6]paracyclophane can be synthesized[7][8] in the laboratory by a Bamford-Stevens reaction with spiro ketone 1 in scheme 3 rearranging in a pyrolysis reaction through the carbene intermediate 4. The cyclophane can be photochemically converted to the Dewar benzene 6 and back again by application of heat. A separate route to the Dewar form is by a cationic silver perchlorate induced rearrangement reaction of the bicyclopropenyl compound 7.
Metaparacyclophanes constitute another class of cyclophans like the [14][14]metaparacyclophane[9] in scheme 4[10] featuring a in-situ Ramberg-Bäcklund Reaction converting the sulfone 3 to the alkene 4.
Naturally occurring cyclophanes[edit]
Despite carrying strain, the cyclophane motif does exist in nature. One example of a metacyclophane is cavicularin.
Haouamine A is a paracyclophane found in a certain species of tunicate. Because of its potential application as an anticancer drug it is also available from total synthesis via an alkyne - pyrone Diels-Alder reaction in the crucial step with expulsion of carbon dioxide (scheme 5).[11]
In this compound the deviation from planarity is 13° for the benzene ring and 17° for the bridgehead carbons.[12] An alternative cyclophane formation strategy in scheme 6[13] was developed based on aromatization of the ring well after the formation of the bridge.
Two additional types of cyclophanes were discovered in nature when they were isolated from two species of cyanobacteria from the family Nostocacae.[14] These two classes of cyclophanes are both [7,7] paracyclophanes and were named after the species from which they were extracted: cylindrocyclophanes from Cylindrospermum lichenforme and nostocyclophanes from Nostoc linckia.
[n.n]Paracyclophanes[edit]
A well exploited member of the [n.n]paracyclophane family is [2.2]paracyclophane.[15][16] One method for its preparation is by a 1,6-Hofmann elimination:[17]
The [2.2]paracyclophane-1,9-diene has been applied in ROMP to a poly(p-phenylene vinylene) with alternating cis-alkene and trans-alkene bonds using Grubbs' second generation catalyst:[18]
The driving force for ring-opening and polymerization is strain relief. The reaction is believed to be a living polymerization due to the lack of competing reactions.
Because the two benzene rings are in close proximity this cyclophane type also serves as guinea pig for photochemical dimerization reactions as illustrated by this example:[19]
The product formed has an octahedrane skeleton. When the amine group is replaced by a methylene group no reaction takes place: the dimerization requires through-bond overlap between the aromatic pi electrons and the sigma electrons in the C-N bond in the reactants LUMO.
Cycloparaphenylenes[edit]
[n]Cycloparaphenylenes ([n]CPPs) consist of cyclic all-para-linked phenyl groups.[20] This compound class is of some interest as potential building block for nanotubes. Members have been reported with 18, 12, 10, 9, 8, 7, 6 and 5 phenylenes. These molecules are unique in that they contain no aliphatic linker group that places strain on the aromatic unit. Instead the entire molecule is a strained aromatic unit.
Phanes[edit]
Generalization of cyclophanes led to the concept of phanes in the IUPAC nomenclature.
The systematic phane nomenclature name for e.g. [14]metacyclophane is 1(1,3)-benzenacyclopentadecaphane;
and [2.2']paracyclophane (or [2.2]paracyclophane) is 1,4(1,4)-dibenzenacyclohexaphane.
References
https://en.wikipedia.org/wiki/Cyclophane
An aromatic ring current is an effect observed in aromatic molecules such as benzene and naphthalene. If a magnetic field is directed perpendicular to the plane of the aromatic system, a ring current is induced in the delocalized π electrons of the aromatic ring.[1] This is a direct consequence of Ampère's law; since the electrons involved are free to circulate, rather than being localized in bonds as they would be in most non-aromatic molecules, they respond much more strongly to the magnetic field.
The ring current creates its own magnetic field. Outside the ring, this field is in the same direction as the externally applied magnetic field; inside the ring, the field counteracts the externally applied field. As a result, the net magnetic field outside the ring is greater than the externally applied field alone, and is less inside the ring.
Aromatic ring currents are relevant to NMR spectroscopy, as they dramatically influence the chemical shifts of 1H nuclei in aromatic molecules.[2] The effect helps distinguish these nuclear environments and is therefore of great use in molecular structure determination. In benzene, the ring protons experience deshieldingbecause the induced magnetic field has the same direction outside the ring as the external field and their chemical shift is 7.3 ppm compared to 5.6 for the vinylicproton in cyclohexene. In contrast any proton inside the aromatic ring experiences shielding because both fields are in opposite direction. This effect can be observed in cyclooctadecanonaene ([18]annulene) with 6 inner protons at −3 ppm.
The situation is reversed in antiaromatic compounds. In the dianion of [18]annulene the inner protons are strongly deshielded at 20.8 ppm and 29.5 ppm with the outer protons significantly shielded (with respect to the reference) at −1.1 ppm. Hence a diamagnetic ring current or diatropic ring current is associated with aromaticity whereas a paratropic ring current signals antiaromaticity.
A similar effect is observed in three-dimensional fullerenes; in this case it is called a sphere current.[3]
https://en.wikipedia.org/wiki/Aromatic_ring_current
Proton nuclear magnetic resonance (proton NMR, hydrogen-1 NMR, or 1H NMR) is the application of nuclear magnetic resonancein NMR spectroscopy with respect to hydrogen-1 nuclei within the molecules of a substance, in order to determine the structure of its molecules.[1] In samples where natural hydrogen (H) is used, practically all the hydrogen consists of the isotope 1H (hydrogen-1; i.e. having a proton for a nucleus).
Simple NMR spectra are recorded in solution, and solvent protons must not be allowed to interfere. Deuterated (deuterium = 2H, often symbolized as D) solvents especially for use in NMR are preferred, e.g. deuterated water, D2O, deuterated acetone, (CD3)2CO, deuterated methanol, CD3OD, deuterated dimethyl sulfoxide, (CD3)2SO, and deuterated chloroform, CDCl3. However, a solvent without hydrogen, such as carbon tetrachloride, CCl4 or carbon disulfide, CS2, may also be used.
Historically, deuterated solvents were supplied with a small amount (typically 0.1%) of tetramethylsilane (TMS) as an internal standardfor calibrating the chemical shifts of each analyte proton. TMS is a tetrahedral molecule, with all protons being chemically equivalent, giving one single signal, used to define a chemical shift = 0 ppm. [2] It is volatile, making sample recovery easy as well. Modern spectrometers are able to reference spectra based on the residual proton in the solvent (e.g. the CHCl3, 0.01% in 99.99% CDCl3). Deuterated solvents are now commonly supplied without TMS.
Deuterated solvents permit the use of deuterium frequency-field lock (also known as deuterium lock or field lock) to offset the effect of the natural drift of the NMR's magnetic field . In order to provide deuterium lock, the NMR constantly monitors the deuterium signal resonance frequency from the solvent and makes changes to the to keep the resonance frequency constant.[3] Additionally, the deuterium signal may be used to accurately define 0 ppm as the resonant frequency of the lock solvent and the difference between the lock solvent and 0 ppm (TMS) are well known.
Proton NMR spectra of most organic compounds are characterized by chemical shifts in the range +14 to -4 ppm and by spin-spin coupling between protons. The integration curve for each proton reflects the abundance of the individual protons.
Simple molecules have simple spectra. The spectrum of ethyl chloride consists of a triplet at 1.5 ppm and a quartet at 3.5 ppm in a 3:2 ratio. The spectrum of benzene consists of a single peak at 7.2 ppm due to the diamagnetic ring current.
Together with carbon-13 NMR, proton NMR is a powerful tool for molecular structure characterization.
https://en.wikipedia.org/wiki/Proton_nuclear_magnetic_resonance
Pyrones or pyranones are a class of heterocyclic chemical compounds. They contain an unsaturated six-membered ring containing one oxygen atom and a ketone functional group.[1]There are two isomers denoted as 2-pyrone and 4-pyrone. The 2-pyrone (or α-pyrone) structure is found in nature as part of the coumarin ring system. 4-Pyrone (or γ-pyrone) is found in some natural chemical compounds such as chromone, maltol and kojic acid.
See also[edit]
- Furanone, which has one fewer carbon atom in the ring.
A nanostructure is a structure of intermediate size between microscopic and molecular structures. Nanostructural detail is microstructure at nanoscale.
In describing nanostructures, it is necessary to differentiate between the number of dimensions in the volume of an object which are on the nanoscale. Nanotextured surfaces have one dimension on the nanoscale, i.e., only the thickness of the surface of an object is between 0.1 and 100 nm. Nanotubes have two dimensions on the nanoscale, i.e., the diameter of the tube is between 0.1 and 100 nm; its length can be far more. Finally, spherical nanoparticles have three dimensions on the nanoscale, i.e., the particle is between 0.1 and 100 nm in each spatial dimension. The terms nanoparticles and ultrafine particles (UFP) are often used synonymously although UFP can reach into the micrometre range. The term nanostructure is often used when referring to magnetic technology.
Nanoscale structure in biology is often called ultrastructure.
Properties of nanoscale objects and ensembles of these objects are widely studied in physics.[2]
List of nanostructures[edit]
- Gradient multilayer nanofilm (GML nanofilm)
- Icosahedral twins
- Nanocages
- Magnetic nanochains
- Nanocomposite
- Nanofabrics
- Nanofiber
- Nanoflower
- Nanofoam
- Nanohole
- Nanomesh
- Box-shaped
- Nanoparticle
- Nanopillar
- Nanopin film
- Nanoplatelet
- Nanoribbon
- Nanoring
- Nanorod
- Nanosheet
- Nanoshell
- Nanotip
- Nanowire
- Nanostructured film
- Self-assembled
- Quantum dot
- Quantum heterostructure
- Sculptured thin film
- Nano WaterCube
https://en.wikipedia.org/wiki/Nanostructure
Phanes are abstractions of highly complex organic molecules introduced for simplification of the naming of these highly complex molecules.
Systematic nomenclature of organic chemistry consists of building a name for the structure of an organic compound by a collection of names of its composite parts but describing also its relative positions within the structure. Naming information is summarised by IUPAC:[1][2][3]
Whilst the cyclophane name describes only a limited number of sub-structures of benzene rings interconnected by individual atoms or chains, 'phane' is a class name which includes others, hence heterocyclic rings as well. Therefore, the various cyclophanes are perfectly good for the general class of phanes as well keeping in mind that the cyclic structures in phanes could have much greater diversity.
References[edit]
- ^ International Union of Pure and Applied Chemistry - Recommendations on Organic & Biochemical Nomenclature, Symbols & Terminology etc. http://www.chem.qmul.ac.uk/iupac/ World Wide Web material prepared by G. P. Moss, Department of Chemistry, Queen Mary University of London, Mile End Road, London, E1 4NS, UKg.p.moss@qmul.ac.uk
- ^ International Union of Pure and Applied Chemistry - Organic Chemistry Division - Commission on nomenclature of organic chemistry http://www.chem.qmul.ac.uk/iupac/phane/ Archived 2006-07-03 at the Wayback Machine Phane Nomenclature Part I: Phane Parent Names IUPAC Recommendations 1998 Prepared for publication by W. H. Powell 1436 Havencrest Ct, Columbus, OH 43220-3841, USA
- ^ Phane Nomenclature Part II: Modification of the Degree of Hydrogenation and Substitution Derivatives of Phane Parent Hydrides
https://en.wikipedia.org/wiki/Phanes_(organic_chemistry)
https://en.wikipedia.org/wiki/Charles_Blagden
https://en.wikipedia.org/wiki/Antoine_Lavoisier
https://en.wikipedia.org/wiki/Category:Independent_scientists
https://en.wikipedia.org/wiki/Category:Executed_scientists
https://en.wikipedia.org/wiki/Rose_Center_for_Earth_and_Space
https://en.wikipedia.org/wiki/Nazis_at_the_Center_of_the_Earth
https://en.wikipedia.org/wiki/Earth%27s_inner_core
https://en.wikipedia.org/wiki/Geographical_centre_of_Earth
https://en.wikipedia.org/wiki/Equirectangular_projection
https://en.wikipedia.org/wiki/Earth
Spontaneous; Center; Symmetry
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by a: Ta(p) = p + a.
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation. Discrete translational symmetry is invariant under discrete translation.
Analogously an operator A on functions is said to be translationally invariant with respect to a translation operator if the result after applying A doesn't change if the argument function is translated. More precisely it must hold that
Laws of physics are translationally invariant under a spatial translation if they do not distinguish different points in space. According to Noether's theorem, space translational symmetry of a physical system is equivalent to the momentum conservation law.
Translational symmetry of an object means that a particular translation does not change the object. For a given object, the translations for which this applies form a group, the symmetry group of the object, or, if the object has more kinds of symmetry, a subgroup of the symmetry group.
https://en.wikipedia.org/wiki/Translational_symmetry
Many powerful theories in physics are described by Lagrangians that are invariant under some symmetry transformation groups.
Gauge theories are important as the successful field theories explaining the dynamics of elementary particles. Quantum electrodynamics is an abelian gauge theory with the symmetry group U(1) and has one gauge field, the electromagnetic four-potential, with the photon being the gauge boson. The Standard Model is a non-abelian gauge theory with the symmetry group U(1) × SU(2) × SU(3) and has a total of twelve gauge bosons: the photon, three weak bosons and eight gluons.
Gauge theories are also important in explaining gravitation in the theory of general relativity. Its case is somewhat unusual in that the gauge field is a tensor, the Lanczos tensor. Theories of quantum gravity, beginning with gauge gravitation theory, also postulate the existence of a gauge boson known as the graviton. Gauge symmetries can be viewed as analogues of the principle of general covariance of general relativity in which the coordinate system can be chosen freely under arbitrary diffeomorphisms of spacetime. Both gauge invariance and diffeomorphism invariance reflect a redundancy in the description of the system. An alternative theory of gravitation, gauge theory gravity, replaces the principle of general covariance with a true gauge principle with new gauge fields.
Historically, these ideas were first stated in the context of classical electromagnetism and later in general relativity. However, the modern importance of gauge symmetries appeared first in the relativistic quantum mechanics of electrons – quantum electrodynamics, elaborated on below. Today, gauge theories are useful in condensed matter, nuclear and high energy physicsamong other subfields.
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Mathematical_formulation_of_the_Standard_Model
https://en.wikipedia.org/wiki/Higgs_mechanism
Gluon radiation
rotation symmetry
electroweak in baryon v. electroweak in exotics v. scale
memory time on chip (signal infinite w/ maintainenance by human)
gravity graviton pressure material surface range tensor step scale friction air intermo intramo force attractiorepulsio channel vaccume space mater void vortex differential gradient
integral net force
slip sppoints topology turbulence (oxygen electron slip point; scale of hydrogen and proton; protonium)
symmetry spontaneous symmetry center spinor
atomic subatomic; baryoinic v. dark matter; tension torque torsion axial plane vertical pressuron preon dust particle syst large expanding particle nuclear
voltage pressure non ideal force v mass and charge hydroelectric thermodynamics
levels time supersymmetry charge mass transitivity
supramolecular chemistry nuclear neutron mirror multilayer particle space division multiplexing hyperfine quantum computing ion scale quantum interace eigenstate
skew asymmetry spiral
molecular gyroscope flyweel maglev linear induction motor rotation energy no activation energy with non covalent bond quantum energy nuclear hydrogen trihydrogencation universe dark matter universe baryonic matter chains hydroelectric nuclear fusion fission transmutation molecular inversion bond rotation energy
phase change water hydrogen microwave matrix glycerine cellulose point particle or particle space division multiplexing cascade change time space quantum ion quantum ion computing oscillation frequency measure hydrogen emission spectra
bunsen Lippmann (physics, 1908)
https://www.nobelprize.org/prizes/physics/1908/summary/
In a supersymmetric theory the equations for force and the equations for matter are identical. In theoretical and mathematical physics, any theory with this property has the principle of supersymmetry (SUSY). Dozens of supersymmetric theories exist.[1]Supersymmetry is a spacetime symmetry between two basic classes of particles: bosons, which have an integer-valued spin and follow Bose–Einstein statistics, and fermions, which have a half-integer-valued spin and follow Fermi-Dirac statistics.[2][3] In supersymmetry, each particle from one class would have an associated particle in the other, known as its superpartner, the spin of which differs by a half-integer. For example, if the electron exists in a supersymmetric theory, then there would be a particle called a "selectron" (superpartner electron), a bosonic partner of the electron. In the simplest supersymmetry theories, with perfectly "unbroken" supersymmetry, each pair of superpartners would share the same mass and internal quantum numbers besides spin. More complex supersymmetry theories have a spontaneously broken symmetry, allowing superpartners to differ in mass.[4][5][6]
Supersymmetry has various applications to different areas of physics, such as quantum mechanics, statistical mechanics, quantum field theory, condensed matter physics, nuclear physics, optics, stochastic dynamics, particle physics, astrophysics, quantum gravity, string theory, and cosmology. Supersymmetry has also been applied outside of physics, such as in finance. In particle physics, a supersymmetric extension of the Standard Model is a possible candidate for physics beyond the Standard Model, and in cosmology, supersymmetry could explain the issue of cosmological inflation.
In quantum field theory, supersymmetry is motivated by solutions to several theoretical problems, for generally providing many desirable mathematical properties, and for ensuring sensible behavior at high energies. Supersymmetric quantum field theory is often much easier to analyze, as many more problems become mathematically tractable. When supersymmetry is imposed as a local symmetry, Einstein's theory of general relativity is included automatically, and the result is said to be a theory of supergravity. Another theoretically appealing property of supersymmetry is that it offers the only "loophole" to the Coleman–Mandula theorem, which prohibits spacetime and internal symmetries from being combined in any nontrivial way, for quantum field theories with very general assumptions. The Haag–Łopuszański–Sohnius theorem demonstrates that supersymmetry is the only way spacetime and internal symmetries can be combined consistently.[7]
https://en.wikipedia.org/wiki/Supersymmetry
In a supersymmetric theory the equations for force and the equations for matter are identical. In theoretical and mathematical physics, any theory with this property has the principle of supersymmetry (SUSY). Dozens of supersymmetric theories exist.[1]Supersymmetry is a spacetime symmetry between two basic classes of particles: bosons, which have an integer-valued spin and follow Bose–Einstein statistics, and fermions, which have a half-integer-valued spin and follow Fermi-Dirac statistics.[2][3] In supersymmetry, each particle from one class would have an associated particle in the other, known as its superpartner, the spin of which differs by a half-integer. For example, if the electron exists in a supersymmetric theory, then there would be a particle called a "selectron" (superpartner electron), a bosonic partner of the electron. In the simplest supersymmetry theories, with perfectly "unbroken" supersymmetry, each pair of superpartners would share the same mass and internal quantum numbers besides spin. More complex supersymmetry theories have a spontaneously broken symmetry, allowing superpartners to differ in mass.[4][5][6]
Supersymmetry has various applications to different areas of physics, such as quantum mechanics, statistical mechanics, quantum field theory, condensed matter physics, nuclear physics, optics, stochastic dynamics, particle physics, astrophysics, quantum gravity, string theory, and cosmology. Supersymmetry has also been applied outside of physics, such as in finance. In particle physics, a supersymmetric extension of the Standard Model is a possible candidate for physics beyond the Standard Model, and in cosmology, supersymmetry could explain the issue of cosmological inflation.
In quantum field theory, supersymmetry is motivated by solutions to several theoretical problems, for generally providing many desirable mathematical properties, and for ensuring sensible behavior at high energies. Supersymmetric quantum field theory is often much easier to analyze, as many more problems become mathematically tractable. When supersymmetry is imposed as a local symmetry, Einstein's theory of general relativity is included automatically, and the result is said to be a theory of supergravity. Another theoretically appealing property of supersymmetry is that it offers the only "loophole" to the Coleman–Mandula theorem, which prohibits spacetime and internal symmetries from being combined in any nontrivial way, for quantum field theories with very general assumptions. The Haag–Łopuszański–Sohnius theorem demonstrates that supersymmetry is the only way spacetime and internal symmetries can be combined consistently.[7]
Supersymmetric quantum mechanics[edit]
Main article: Supersymmetric quantum mechanics
Supersymmetric quantum mechanics adds the SUSY superalgebra to quantum mechanics as opposed to quantum field theory. Supersymmetric quantum mechanics often becomes relevant when studying the dynamics of supersymmetric solitons, and due to the simplified nature of having fields which are only functions of time (rather than space-time), a great deal of progress has been made in this subject and it is now studied in its own right.
SUSY quantum mechanics involves pairs of Hamiltonians which share a particular mathematical relationship, which are called partner Hamiltonians. (The potential energy terms which occur in the Hamiltonians are then known as partner potentials.) An introductory theorem shows that for every eigenstate of one Hamiltonian, its partner Hamiltonian has a corresponding eigenstate with the same energy. This fact can be exploited to deduce many properties of the eigenstate spectrum. It is analogous to the original description of SUSY, which referred to bosons and fermions. We can imagine a "bosonic Hamiltonian", whose eigenstates are the various bosons of our theory. The SUSY partner of this Hamiltonian would be "fermionic", and its eigenstates would be the theory's fermions. Each boson would have a fermionic partner of equal energy.
In finance[edit]
In 2021, supersymmetric quantum mechanics was applied to option pricing and the analysis of markets in finance,[19] and to financial networks.[20]
Supersymmetry in condensed matter physics[edit]
SUSY concepts have provided useful extensions to the WKB approximation. Additionally, SUSY has been applied to disorder averaged systems both quantum and non-quantum (through statistical mechanics), the Fokker–Planck equation being an example of a non-quantum theory. The 'supersymmetry' in all these systems arises from the fact that one is modelling one particle and as such the 'statistics' do not matter. The use of the supersymmetry method provides a mathematical rigorous alternative to the replica trick, but only in non-interacting systems, which attempts to address the so-called 'problem of the denominator' under disorder averaging. For more on the applications of supersymmetry in condensed matter physics see Efetov (1997).[21]
In 2021, a group of researchers showed that, in theory, {\displaystyle N=(0,1)} SUSY could be realised at the edge of a Moore-Read quantum Hall state.[22] However, to date, no experiments have been done yet to realise it at an edge of a Moore-Read state.
Supersymmetry in optics[edit]
In 2013, integrated optics was found[23] to provide a fertile ground on which certain ramifications of SUSY can be explored in readily-accessible laboratory settings. Making use of the analogous mathematical structure of the quantum-mechanical Schrödinger equation and the wave equation governing the evolution of light in one-dimensional settings, one may interpret the refractive indexdistribution of a structure as a potential landscape in which optical wave packets propagate. In this manner, a new class of functional optical structures with possible applications in phase matching, mode conversion[24] and space-division multiplexing becomes possible. SUSY transformations have been also proposed as a way to address inverse scattering problems in optics and as a one-dimensional transformation optics.[25]
Supersymmetry in dynamical systems[edit]
Main article: Supersymmetric theory of stochastic dynamics
All stochastic (partial) differential equations, the models for all types of continuous time dynamical systems, possess topological supersymmetry.[26][27] In the operator representation of stochastic evolution, the topological supersymmetry is the exterior derivativewhich is commutative with the stochastic evolution operator defined as the stochastically averaged pullback induced on differential forms by SDE-defined diffeomorphisms of the phase space. The topological sector of the so-emerging supersymmetric theory of stochastic dynamics can be recognized as the Witten-type topological field theory.
The meaning of the topological supersymmetry in dynamical systems is the preservation of the phase space continuity—infinitely close points will remain close during continuous time evolution even in the presence of noise. When the topological supersymmetry is broken spontaneously, this property is violated in the limit of the infinitely long temporal evolution and the model can be said to exhibit (the stochastic generalization of) the butterfly effect. From a more general perspective, spontaneous breakdown of the topological supersymmetry is the theoretical essence of the ubiquitous dynamical phenomenon variously known as chaos, turbulence, self-organized criticality etc. The Goldstone theorem explains the associated emergence of the long-range dynamical behavior that manifests itself as 1/f noise, butterfly effect, and the scale-free statistics of sudden (instantonic) processes, such as earthquakes, neuroavalanches, and solar flares, known as the Zipf's law and the Richter scale.
https://en.wikipedia.org/wiki/Supersymmetry
https://en.wikipedia.org/wiki/Refractive_index
https://en.wikipedia.org/wiki/Topology
https://en.wikipedia.org/wiki/Symmetry
https://en.wikipedia.org/wiki/Equilateral_Triangle
https://en.wikipedia.org/wiki/Perception_Sensation_Cognition
https://en.wikipedia.org/wiki/Goldstone_boson
https://en.wikipedia.org/wiki/Space-division_multiple_access
https://en.wikipedia.org/wiki/Richter_magnitude_scale
https://en.wikipedia.org/wiki/Zipf%27s_law
https://en.wikipedia.org/wiki/Butterfly_effect
https://en.wikipedia.org/wiki/Topological_quantum_field_theory
https://en.wikipedia.org/wiki/Supersymmetric_theory_of_stochastic_dynamics
https://en.wikipedia.org/wiki/Quantum_Hall_effect
https://en.wikipedia.org/wiki/Quantum_state#Pure_states
https://en.wikipedia.org/wiki/WKB_approximation
https://en.wikipedia.org/wiki/Lambda-CDM_model
https://en.wikipedia.org/wiki/Hyperfine_structure
https://en.wikipedia.org/wiki/Electron_paramagnetic_resonance#Hyperfine_coupling
https://en.wikipedia.org/wiki/Hyperfinite_type_II_factor
https://en.wikipedia.org/wiki/Hypertext_Transfer_Protocol
Friday, September 17, 2021
09-17-2021-0229 - Space-division multiple access (SDMA)
Thermodynamics[edit]
Supramolecular chemistry deals with subtle interactions, and consequently control over the processes involved can require great precision. In particular, non-covalent bonds have low energies and often no activation energy for formation. As demonstrated by the Arrhenius equation, this means that, unlike in covalent bond-forming chemistry, the rate of bond formation is not increased at higher temperatures. In fact, chemical equilibrium equations show that the low bond energy results in a shift towards the breaking of supramolecular complexes at higher temperatures.
However, low temperatures can also be problematic to supramolecular processes. Supramolecular chemistry can require molecules to distort into thermodynamically disfavored conformations (e.g. during the "slipping" synthesis of rotaxanes), and may include some covalent chemistry that goes along with the supramolecular. In addition, the dynamic nature of supramolecular chemistry is utilized in many systems (e.g. molecular mechanics), and cooling the system would slow these processes.
Saturday, August 14, 2021
08-13-2021-2226 - Time Reversal Symmetry
T-symmetry or time reversal symmetry is the theoretical symmetry of physical laws under the transformation of time reversal,
Since the second law of thermodynamics states that entropy increases as time flows toward the future, in general, the macroscopic universe does not show symmetry under time reversal. In other words, time is said to be non-symmetric, or asymmetric, except for special equilibrium states when the second law of thermodynamics predicts the time symmetry to hold. However, quantum noninvasive measurements are predicted to violate time symmetry even in equilibrium,[1] contrary to their classical counterparts, although this has not yet been experimentally confirmed.
Time asymmetries generally are caused by one of three categories:
- intrinsic to the dynamic physical law (e.g., for the weak force)
- due to the initial conditions of the universe (e.g., for the second law of thermodynamics)
- due to measurements (e.g., for the noninvasive measurements)
https://en.wikipedia.org/wiki/Molecular_recognition

Phthalocyanine (H
2Pc) is a large, aromatic, macrocyclic, organic compound with the formula (C
8H
4N
2)
4H
2 and is of theoretical or specialized interest in chemical dyes and photoelectricity.
It is composed of four isoindole units[a] linked by a ring of nitrogen atoms. (C
8H
4N
2)
4H
2= H
2Pc has a two-dimensional geometry and a ring system consisting of 18 π-electrons. The extensive delocalization of the π-electrons affords the molecule useful properties, lending itself to applications in dyes and pigments. Metal complexesderived from Pc2−
, the conjugate base of H
2Pc, are valuable in catalysis, organic solar cells, and photodynamic therapy.
https://en.wikipedia.org/wiki/Electrochemistry
https://en.wikipedia.org/wiki/Sarcosine
https://en.wikipedia.org/wiki/Hydrazone
The electron transfer is fast because the redox process induces little structural change.

Redox properties[edit]
Viologens, in their dicationic form, typically undergo two one-electron reductions. The first reduction affords the deeply colored radical cation:[2]
- [V]2+ + e− [V]+
The radical cations are blue for 4,4'-viologens and green for 2,2'-derivatives. The second reduction yields a yellow quinoidcompounds:
- [V]+ + e− [V]0
The electron transfer is fast because the redox process induces little structural change.
[edit]
Diquat is an isomer of viologens, being derived from 2,2'-bipyridine (instead of the 4,4'-isomer). It also is a potent herbicide that functions by disrupting electron-transfer.
Extended viologens have been developed based on conjugated oligomers such as based on aryl, ethylene, and thiophene units are inserted between the pyridine units.[7] The bipolaron di-octyl bis(4-pyridyl)biphenyl viologen 2 in scheme 2 can be reduced by sodium amalgam in DMF to the neutral viologen 3.
The resonance structures of the quinoid 3a and the biradical 3b contribute equally to the hybrid structure. The driving force for the contributing 3b is the restoration of aromaticity with the biphenyl unit. It has been established using X-ray crystallography that the molecule is, in effect, coplanar with slight nitrogen pyramidalization, and that the central carbon bonds are longer (144 pm) than what would be expected for a double bond (136 pm). Further research shows that the diradical exists as a mixture of triplets and singlets, although an ESR signal is absent. In this sense, the molecule resembles Tschischibabin's hydrocarbon, discovered during 1907. It also shares with this molecule a blue color in solution, and a metallic-green color as crystals.
Compound 3 is a very strong reducing agent, with a redox potential of −1.48 V.
Sodium amalgam, commonly denoted Na(Hg), is an alloy of mercury and sodium. The term amalgam is used for alloys, intermetallic compounds, and solutions (both solid solutions and liquid solutions) involving mercury as a major component. Sodium amalgams are often used in reactions as strong reducing agents with better handling properties compared to solid sodium. They are less dangerously reactive toward water and in fact are often used as an aqueous suspension.
Sodium amalgam was used as a reagent as early as 1862.[1] A synthesis method was described by J. Alfred Wanklyn in 1866.[2]
Uses[edit]
Sodium amalgam has been used in organic chemistry as a powerful reducing agent, which is safer to handle than sodium itself. It is used in Emde degradation, and also for reduction of aromatic ketones to hydrols.[9]
A sodium amalgam is used in the design of the high pressure sodium lamp providing sodium to produce the proper color, and mercury to tailor the electrical characteristics of the lamp.
Mercury cell electrolysis[edit]
Sodium amalgam is a by-product of chlorine manufactured by mercury cell electrolysis. In this cell, brine (concentrated sodium chloride solution) is electrolysed between a liquid mercury cathode and a titanium or graphite anode. Chlorine is formed at the anode, while sodium formed at the cathode dissolves into the mercury, making sodium amalgam. Normally this sodium amalgam is drawn off and reacted with water in a "decomposer cell" to produce hydrogen gas, concentrated sodium hydroxide solution, and mercury to be recycled through the process. In principle, all the mercury should be completely recycled, but inevitably a small portion goes missing. Because of concerns about this mercury escaping into the environment, the mercury cell process is generally being replaced by plants which use a less toxic cathode.
https://en.wikipedia.org/wiki/Sodium_amalgam
https://en.wikipedia.org/wiki/Emde_degradation
https://en.wikipedia.org/wiki/Bipolaron
A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933[1] and Solomon Pekar in 1946[2] to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. For comparison of the models proposed in these papers see M. I. Dykman and E. I. Rashba, The roots of polaron theory, Physics Today 68, 10 (2015). This lowers the electron mobility and increases the electron's effective mass.
https://en.wikipedia.org/wiki/Polaron
In organic chemistry, the Menshutkin reaction converts a tertiary amine into a quaternary ammonium salt by reaction with an alkyl halide. Similar reactions occur when tertiary phosphines are treated with alkyl halides.
https://en.wikipedia.org/wiki/Menshutkin_reaction
A coupling reaction in organic chemistry is a general term for a variety of reactions where two fragments are joined together with the aid of a metal catalyst. In one important reaction type, a main group organometallic compound of the type R-M (R = organic fragment, M = main group center) reacts with an organic halide of the type R'-X with formation of a new carbon-carbon bond in the product R-R'. The most common type of coupling reaction is the cross coupling reaction.[1][2][3]
Richard F. Heck, Ei-ichi Negishi, and Akira Suzuki were awarded the 2010 Nobel Prize in Chemistry for developing palladium-catalyzed cross coupling reactions.[4][5]
Broadly speaking, two types of coupling reactions are recognized:
- Heterocouplings combine two different partners, such as in the Heck reaction of an alkene (RC=CH) and an alkyl halide (R'-X) to give a substituted alkene. Heterocouplings are called cross-couplings.
- Homocouplings couple two identical partners, as in the Glaser coupling of two acetylides (RC≡CH) to form a dialkyne (RC≡C-C≡CR).
Mechanism of action[edit]
Viologens with 2,2'-, 4,4'-, or 2,4'-bipyridylium are highly toxic because these bipyridyl molecules readily form stable free radicals.[8]The delocalization of charge, which allows for the molecule to stay as a free radical and these structures can be easily stabilized because the nitrogens can be readily hydrogenated. When in the body, these viologens interfere with electron transport chain, often causing cell death.[8][9] These molecules act as redox cycling agents and are able to transfer their electron to molecular oxygen.[10][9] Once the electron has been transferred to the molecular oxygen, it forms a superoxide radical that causes disproportionation, simultaneous reduction and oxidation.
https://en.wikipedia.org/wiki/Viologen
https://en.wikipedia.org/wiki/Thiophene
https://en.wikipedia.org/wiki/Disproportionation
https://en.wikipedia.org/wiki/Superoxide
https://en.wikipedia.org/wiki/Electron_transport_chain
https://en.wikipedia.org/wiki/Delocalized_electron
https://en.wikipedia.org/wiki/Radical_(chemistry)
https://en.wikipedia.org/wiki/Trigonal_planar_molecular_geometry
https://en.wikipedia.org/wiki/Aromaticity
https://en.wikipedia.org/wiki/Coplanarity
https://en.wikipedia.org/wiki/Line_(geometry)
https://en.wikipedia.org/wiki/Skew_lines
https://en.wikipedia.org/wiki/Line–line_intersection
https://en.wikipedia.org/wiki/Parallel_(geometry)
https://en.wikipedia.org/wiki/Distance_geometry
https://en.wikipedia.org/wiki/Empty_set
https://en.wikipedia.org/wiki/Non-Kekulé_molecule
https://en.wikipedia.org/wiki/Resonance_(chemistry)
https://en.wikipedia.org/wiki/Aryl
https://en.wikipedia.org/wiki/Ethylene
https://en.wikipedia.org/wiki/Oligomer
https://en.wikipedia.org/wiki/Conjugated_system
https://en.wikipedia.org/wiki/Pyridine
https://en.wikipedia.org/wiki/Sodium_amalgam
https://en.wikipedia.org/wiki/Viologen
https://en.wikipedia.org/wiki/Reduction_potential
https://en.wikipedia.org/wiki/Reducing_agent
https://en.wikipedia.org/wiki/Aromaticity
These reactive free radicals can cause oxidative stress, which leads to cell death and one example of this is lipid peroxidation. When in a cellular system, the superoxide radicals react with unsaturated lipids, which contain a reactive hydrogen, and produce lipid hydroperoxides.[10] These lipid hydroperoxides then decompose into lipid free radicals, and causes a chain reaction of lipid peroxidation, damaging the cellular macromolecules and eventually causing cell death. The superoxide radicals have also been found to deplete NADPH, alter other redox reactions that naturally occur in the organism, and interfere with how iron is stored and released in the body.[9]
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "viologens". doi:10.1351/goldbook.V06624
https://en.wikipedia.org/wiki/Viologen
https://en.wikipedia.org/wiki/Oxidative_stress
https://en.wikipedia.org/wiki/Lipid_peroxidation
https://en.wikipedia.org/wiki/Sharon_Petersen_subject_sample-group(2020)
https://en.wikipedia.org/wiki/Indium_tin_oxide
https://en.wikipedia.org/wiki/Titanium_dioxide
https://en.wikipedia.org/wiki/Category:Superoxide_generating_substances
https://en.wikipedia.org/wiki/Antimycin_A
https://en.wikipedia.org/wiki/NADPH_oxidase
https://en.wikipedia.org/wiki/Xanthine_oxidase
https://en.wikipedia.org/wiki/Category:Bipyridines
https://en.wikipedia.org/wiki/Phanquinone
https://en.wikipedia.org/wiki/Monomethylhydrazine
https://en.wikipedia.org/wiki/Dinitrogen_tetroxide
https://en.wikipedia.org/wiki/Liquid-propellant_rocket
Electrostatic[edit]
If the acceleration is caused mainly by the Coulomb force (i.e. application of a static electric field in the direction of the acceleration) the device is considered electrostatic. The types of electrostatic drives and their propellants:
- Gridded ion thruster – using positive ions as the propellant, accelerated by an electrically charged grid
- NASA Solar Technology Application Readiness (NSTAR) – positive ions accelerated using high-voltage electrodes
- HiPEP – using positive ions as the propellant, created using microwaves
- Radiofrequency ion thruster – generalization of HiPEP
- Hall-effect thruster, including its subtypes Stationary Plasma Thruster (SPT) and Thruster with Anode Layer (TAL) – use the Hall effect to orient electrons to create positive ions for propellant
- Colloid ion thruster- electrostatic acceleration of droplets of liquid salt as the propellant
- Field emission electric propulsion - using electrodes to accelerate ionized liquid metal as a propellant
- Nano-particle field extraction thruster - using charged cylindrical carbon nanotubes as propellant
Electrothermal[edit]
These are engines that use electromagnetic fields to generate a plasma which is used as the propellant. They use a nozzle to direct the energized propellant. The nozzle itself may be composed simply of a magnetic field. Low molecular weight gases (e.g. hydrogen, helium, ammonia) are preferred propellants for this kind of system.[6]
- Resistojet - using a usually inert compressed propellant that is energized by simple resistive heating
- Arcjet - uses (usually) hydrazine or ammonia as a propellant which is energized with an electrical arc
- Microwave - a type of Radiofrequency ion thruster
- Variable specific impulse magnetoplasma rocket (VASIMR) - using microwave-generated plasma as the propellant and magnetic field to direct its expulsion
Electromagnetic[edit]
Electromagnetic thrusters use ions as the propellant, which are accelerted by the Lorentz force or by magnetic fields, either of which is generated by electicity:
- Electrodeless plasma thruster - a complex system that uses cold plasma as a propellant that is accelerated by ponderomotive force
- Magnetoplasmadynamic thruster - propellants include xenon, neon, argon, hydrogen, hydrazine, or lithium; expelled using the Lorentz force
- Pulsed inductive thruster - because this reacitve engine uses a radial magnetic field, it acts on both positive and negative particles and so it may use a wide range of gases as a propellant including water, hydrazine, ammonia, argon, xenon and many others
- Pulsed plasma thruster - uses a Teflon plasma as a propellant, which is created by an electrical arc and expelled using the Lorantz force
- Helicon Double Layer Thruster - a plasma propellant is generated and excited from a gas using a helicon induced by high frequency band radiowaves which form a magnetic nozzle in a cylinder
Nuclear[edit]
Nuclear reactions may be used to produce the energy for the expulsion of the propellants. Many types of nuclear reactors have been used/proposed to produce electricity for electrical propulsion as outlined above. Nuclear pulse propulsion uses a series of nuclear explosions to create large amounts of energy to expel the products of the nuclear reaction as the propellant. Nuclear thermal rocketsuse the heat of a nuclear reaction to heat a propellant. Usually the propellant is hydrogen because the force is a function of the energy irrespective of the mass of the propellant, so the lightest propellant (hydrogen) produces the greatest specific impulse.
Photonic[edit]
A photonic reactive engine uses photons as the propellant and their discrete relativistic energy to produce thrust.
See also[edit]
In extreme examples, in spacetimes with suitably high-curvature metrics, the light cone can be tilted beyond 45 degrees. That means there are potential "future" positions, from the object's frame of reference, that are spacelike separated to observers in an external rest frame. From this outside viewpoint, the object can move instantaneously through space. In these situations the object would have to move, since its present spatial location would not be in its own future light cone. Additionally, with enough of a tilt, there are event locations that lie in the "past" as seen from the outside. With a suitable movement of what appears to it its own space axis, the object appears to travel through time as seen externally.
A closed timelike curve can be created if a series of such light cones are set up so as to loop back on themselves, so it would be possible for an object to move around this loop and return to the same place and time that it started. An object in such an orbit would repeatedly return to the same point in spacetime if it stays in free fall. Returning to the original spacetime location would be only one possibility; the object's future light cone would include spacetime points both forwards and backwards in time, and so it should be possible for the object to engage in time travel under these conditions.
General relativity[edit]
CTCs appear in locally unobjectionable exact solutions to the Einstein field equation of general relativity, including some of the most important solutions. These include:
- the Misner space (which is Minkowski space orbifolded by a discrete boost)
- the Kerr vacuum (which models a rotating uncharged black hole)
- the interior of a rotating BTZ black hole
- the van Stockum dust (which models a cylindrically symmetric configuration of dust)
- the Gödel lambdadust (which models a dust with a carefully chosen cosmological constant term)
- the Tipler cylinder (a cylindrically symmetric metric with CTCs)
- Bonnor-Steadman solutions describing laboratory situations such as two spinning balls
- J. Richard Gott has proposed a mechanism for creating CTCs using cosmic strings.
Some of these examples are, like the Tipler cylinder, rather artificial, but the exterior part of the Kerr solution is thought to be in some sense generic, so it is rather unnerving to learn that its interior contains CTCs. Most physicists feel that CTCs in such solutions are artifacts.[citation needed]
No CTC can be continuously deformed as a CTC to a point (that is, a CTC and a point are not timelike homotopic), as the manifold would not be causally well behaved at that point. The topological feature which prevents the CTC from being deformed to a point is known as a timelike topological feature.
Contractible versus noncontractible[edit]
There are two classes of CTCs. We have CTCs contractible to a point (if we no longer insist it has to be future-directed timelike everywhere), and we have CTCs which are not contractible. For the latter, we can always go to the universal covering space, and reestablish causality. For the former, such a procedure is not possible. No closed timelike curve is contractible to a point by a timelike homotopy among timelike curves, as that point would not be causally well behaved.[3]
Cauchy horizon[edit]
The chronology violating set is the set of points through which CTCs pass. The boundary of this set is the Cauchy horizon. The Cauchy horizon is generated by closed null geodesics. Associated with each closed null geodesic is a redshift factor describing the rescaling of the rate of change of the affine parameter around a loop. Because of this redshift factor, the affine parameter terminates at a finite value after infinitely many revolutions because the geometric series converges.
See also[edit]
Time[edit]
A temporal dimension, or time dimension, is a dimension of time. Time is often referred to as the "fourth dimension" for this reason, but that is not to imply that it is a spatial dimension. A temporal dimension is one way to measure physical change. It is perceived differently from the three spatial dimensions in that there is only one of it, and that we cannot move freely in time but subjectively move in one direction.
The equations used in physics to model reality do not treat time in the same way that humans commonly perceive it. The equations of classical mechanics are symmetric with respect to time, and equations of quantum mechanics are typically symmetric if both time and other quantities (such as charge and parity) are reversed. In these models, the perception of time flowing in one direction is an artifact of the laws of thermodynamics (we perceive time as flowing in the direction of increasing entropy).
The best-known treatment of time as a dimension is Poincaré and Einstein's special relativity (and extended to general relativity), which treats perceived space and time as components of a four-dimensional manifold, known as spacetime, and in the special, flat case as Minkowski space. Time is different from other spatial dimensions as time is operates in all spacial dimensions. Time operates in the first, second and third as well as theoretical spacial dimensions such as a fourth spatial dimension. Time is not however present in a single point of absolute infinite singularity as defined as a geometric point, as an infinitely small point can have no change and therefore no time. Just as when an object moves through positions in space, it also moves through positions in time. In this sense the force moving any object to change is time.[9][10][11][12]
https://en.wikipedia.org/wiki/Dimension
https://en.wikipedia.org/wiki/Gravitational_wave
https://en.wikipedia.org/wiki/Time_translation_symmetry
https://en.wikipedia.org/wiki/Thermal_time_hypothesis
https://en.wikipedia.org/wiki/Thermodynamics
https://en.wikipedia.org/wiki/Loop_quantum_gravity
https://en.wikipedia.org/wiki/Causal_dynamical_triangulation
https://en.wikipedia.org/wiki/Spin_foam
https://en.wikipedia.org/wiki/Superfluid_vacuum_theory
https://en.wikipedia.org/wiki/Dark_radiation
https://en.wikipedia.org/wiki/T-symmetry
https://en.wikipedia.org/wiki/Fourth,_fifth,_and_sixth_derivatives_of_position
https://en.wikipedia.org/wiki/Relaxation_(physics)
https://en.wikipedia.org/wiki/Baryonic_dark_matter
https://en.wikipedia.org/wiki/Antimatter
https://en.wikipedia.org/wiki/Negative_mass
https://en.wikipedia.org/wiki/Energy_condition
https://en.wikipedia.org/wiki/Space
https://en.wikipedia.org/wiki/Stress–energy_tensor
https://en.wikipedia.org/wiki/Self-interacting_dark_matter
https://en.wikipedia.org/wiki/Scalar_field_dark_matter
https://en.wikipedia.org/wiki/Minimal_Supersymmetric_Standard_Model
https://en.wikipedia.org/wiki/Neutralino
https://en.wikipedia.org/wiki/Fuzzy_cold_dark_matter
https://en.wikipedia.org/wiki/Cosmic_microwave_background
https://en.wikipedia.org/wiki/Superfluidity
https://en.wikipedia.org/wiki/Supercritical_fluid
https://en.wikipedia.org/wiki/Supercritical_flow
https://en.wikipedia.org/wiki/Sonic_black_hole
https://en.wikipedia.org/wiki/Optical_black_hole
https://en.wikipedia.org/wiki/Analog_models_of_gravity
https://en.wikipedia.org/wiki/Transformation_optics
https://en.wikipedia.org/wiki/Black_hole
https://en.wikipedia.org/wiki/Cold_dark_matter
https://en.wikipedia.org/wiki/Primordial_black_hole
https://en.wikipedia.org/wiki/Neutrino_oscillation
https://en.wikipedia.org/wiki/Rotating_black_hole
https://en.wikipedia.org/wiki/Spin-flip
https://en.wikipedia.org/wiki/Black_hole_bomb
https://en.wikipedia.org/wiki/Neutron_reflector
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Photofission
In physics, mirror matter, also called shadow matter or Alice matter, is a hypothetical counterpart to ordinary matter.[1]
Modern physics deals with three basic types of spatial symmetry: reflection, rotation, and translation. The known elementary particles respect rotation and translation symmetry but do not respect mirror reflection symmetry (also called P-symmetry or parity). Of the four fundamental interactions—electromagnetism, the strong interaction, the weak interaction, and gravity—only the weak interaction breaks parity.
Parity violation in weak interactions was first postulated by Tsung Dao Lee and Chen Ning Yang[2] in 1956 as a solution to the τ-θ puzzle. They suggested a number of experiments to test if the weak interaction is invariant under parity. These experiments were performed half a year later and they confirmed that the weak interactions of the known particles violate parity.[3][4][5]
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Neutron_supermirror
https://en.wikipedia.org/wiki/Neutron_flux
https://en.wikipedia.org/wiki/Plane_mirror
https://en.wikipedia.org/wiki/Mirror_nuclei
https://en.wikipedia.org/wiki/Interacting_boson_model
https://en.wikipedia.org/wiki/Nuclear_binding_energy
https://en.wikipedia.org/wiki/Valley_of_stability
https://en.wikipedia.org/wiki/Neutron–proton_ratio
https://en.wikipedia.org/wiki/Isotope#Variation_in_properties_between_isotopes
https://en.wikipedia.org/wiki/Neutron_emission
https://en.wikipedia.org/wiki/Decay_chain
https://en.wikipedia.org/wiki/Bateman_equation
https://en.wikipedia.org/wiki/Island_of_stability
https://en.wikipedia.org/wiki/Photofission
https://en.wikipedia.org/wiki/List_of_equations_in_nuclear_and_particle_physics
https://en.wikipedia.org/wiki/Secular_equilibrium
https://en.wikipedia.org/wiki/Transient_equilibrium
https://en.wikipedia.org/wiki/Scalar_(physics)
In physics and relativity, time dilation is the difference in the elapsed time as measured by two clocks. It is either due to a relative velocity between them (special relativistic "kinetic" time dilation) or to a difference in gravitational potential between their locations (general relativistic gravitational time dilation). When unspecified, "time dilation" usually refers to the effect due to velocity.
After compensating for varying signal delays due to the changing distance between an observer and a moving clock (i.e. Doppler effect), the observer will measure the moving clock as ticking slower than a clock that is at rest in the observer's own reference frame. In addition, a clock that is close to a massive body (and which therefore is at lower gravitational potential) will record less elapsed time than a clock situated further from the said massive body (and which is at a higher gravitational potential).
These predictions of the theory of relativity have been repeatedly confirmed by experiment, and they are of practical concern, for instance in the operation of satellite navigation systems such as GPS and Galileo.[1] Time dilation has also been the subject of science fiction works.
https://en.wikipedia.org/wiki/Time_dilation
The axion (/ˈæksiɒn/) is a hypothetical elementary particle postulated by the Peccei–Quinn theory in 1977 to resolve the strong CP problem in quantum chromodynamics (QCD). If axions exist and have low mass within a specific range, they are of interest as a possible component of cold dark matter.
https://en.wikipedia.org/wiki/Axion
Because dark matter has not yet been observed directly, if it exists, it must barely interact with ordinary baryonic matter and radiation, except through gravity. Most dark matter is thought to be non-baryonic in nature; it may be composed of some as-yet undiscovered subatomic particles.[b] The primary candidate for dark matter is some new kind of elementary particle that has not yet been discovered, in particular, weakly interacting massive particles(WIMPs).[14]Many experiments to directly detect and study dark matter particles are being actively undertaken, but none have yet succeeded.[15] Dark matter is classified as "cold", "warm", or "hot" according to its velocity (more precisely, its free streaming length). Current models favor a cold dark matterscenario, in which structures emerge by gradual accumulation of particles.
https://en.wikipedia.org/wiki/Dark_matter
Forward used the properties of negative-mass matter to create the concept of diametric drive, a design for spacecraft propulsion using negative mass that requires no energy input and no reaction mass to achieve arbitrarily high acceleration.
Forward also coined a term, "nullification", to describe what happens when ordinary matter and negative matter meet: they are expected to be able to cancel out or nullify each other's existence. An interaction between equal quantities of positive mass matter (hence of positive energy E = mc2) and negative mass matter (of negative energy −E = −mc2) would release no energy, but because the only configuration of such particles that has zero momentum (both particles moving with the same velocity in the same direction) does not produce a collision, such interactions would leave a surplus of momentum.
https://en.wikipedia.org/wiki/Negative_mass
https://en.wikipedia.org/wiki/Antimatter
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Effective_mass_(spring–mass_system)
https://en.wikipedia.org/wiki/Lambda-CDM_model
https://en.wikipedia.org/wiki/Negative_mass
https://en.wikipedia.org/wiki/Linear_induction_accelerator
https://en.wikipedia.org/wiki/Angular_acceleration
https://en.wikipedia.org/wiki/0
https://en.wikipedia.org/wiki/Magnetic_scalar_potential
https://en.wikipedia.org/wiki/Accelerator_physics
https://en.wikipedia.org/wiki/Pyrolytic_carbon
https://en.wikipedia.org/wiki/Bismuth
https://en.wikipedia.org/wiki/Hyperloop
https://en.wikipedia.org/wiki/Electrodynamic_suspension#Levitation_melting
https://en.wikipedia.org/wiki/Aerodynamic_levitation
https://en.wikipedia.org/wiki/Electrostatic_levitation
Magnetic levitation
https://en.wikipedia.org/wiki/Launch_loop
https://en.wikipedia.org/wiki/Synchronous_motor
https://en.wikipedia.org/wiki/Linear_stage
https://en.wikipedia.org/wiki/Skew-symmetric_matrix
Supramolecular chemistry
09-18-2021-0806 - Spiro compounds
https://en.wikipedia.org/wiki/Compressible_flow
https://en.wikipedia.org/wiki/Shear_rate
https://en.wikipedia.org/wiki/Hyperfine_structure
https://en.wikipedia.org/wiki/Void_(astronomy)
https://en.wikipedia.org/wiki/Quintessence_(physics)
https://en.wikipedia.org/wiki/Scalar_field
https://en.wikipedia.org/wiki/Symmetric_matrix
https://en.wikipedia.org/wiki/Quadrupole
https://en.wikipedia.org/wiki/Vector_field
https://en.wikipedia.org/wiki/Preon
https://en.wikipedia.org/wiki/Pressuron
https://en.wikipedia.org/wiki/Spinor
Saturday, September 18, 2021
09-18-2021-0754 - ferrite core Magnetic-core memoryhttps://en.wikipedia.org/wiki/Ferrite_core
https://en.wikipedia.org/wiki/Magnetic-core_memory
https://en.wikipedia.org/wiki/Prussian_blue
https://en.wikipedia.org/wiki/Sodium_ferrocyanide
Qubit in ion-trap quantum computing[edit]
The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.[16]
See also[edit]
Dynamic nuclear polarisation
Electron paramagnetic resonance
https://en.wikipedia.org/wiki/Hyperfine_structure
Saturday, September 18, 2021
09-18-2021-0818 - Ligand Cone Angle Tolman Cone Angle ligand cone angle Tolman cone angle tolman cone angle
Asymmetric cases[edit]
The concept of cone angle is most easily visualized with symmetrical ligands, e.g. PR3. But the approach has been refined to include less symmetrical ligands of the type PRR′R″ as well as diphosphines. In such asymmetric cases, the substituent angles' half angles, θi2, are averaged and then doubled to find the total cone angle, θ. In the case of diphosphines, the θi2 of the backbone is approximated as half the chelate bite angle, assuming a bite angle of 74°, 85°, and 90° for diphosphines with methylene, ethylene, and propylene backbones, respectively. The Manz cone angle is often easier to compute than the Tolman cone angle:[4]
| Ligand | Angle (°) |
|---|---|
| PH3 | 87[1] |
| PF3 | 104[1] |
| P(OCH3)3 | 107[1] |
| dmpe | 107 |
| depe | 115 |
| P(CH3)3 | 118[1] |
| dppm | 121 |
| dppe | 125 |
| dppp | 127 |
| P(CH2CH3)3 | 132[1] |
| dcpe | 142 |
| P(C6H5)3 | 145[1] |
| P(cyclo-C6H11)3 | 179[1] |
| P(t-Bu)3 | 182[1] |
| P(C6F5)3 | 184[1] |
| P(C6H4-2-CH3)3 | 194[1] |
| P(2,4,6-Me3C6H2)3 | 212 |
Variations[edit]
The Tolman cone angle method assumes empirical bond data and defines the perimeter as the maximum possible circumscription of an idealized free-spinning substituent. The metal-ligand bond length in the Tolman model was determined empirically from crystal structures of tetrahedral nickel complexes. In contrast, the solid-angle concept derives both bond length and the perimeter from empirical solid state crystal structures.[5][6] There are advantages to each system.
If the geometry of a ligand is known, either through crystallography or computations, an exact cone angle (θ) can be calculated.[7][8][9] No assumptions about the geometry are made, unlike the Tolman method.
Application[edit]
The concept of cone angle is of practical importance in homogeneous catalysis because the size of the ligand affects the reactivity of the attached metal center. In an[10] example, the selectivity of hydroformylation catalysts is strongly influenced by the size of the coligands. Despite being monovalent, some phosphines are large enough to occupy more than half of the coordination sphere of a metal center.
See also[edit]
- Bite angle
- Steric effects (versus electronic effects)
- Tolman electronic parameter
Time dilation caused by a relative velocity[edit]
Special relativity indicates that, for an observer in an inertial frame of reference, a clock that is moving relative to them will be measured to tick slower than a clock that is at rest in their frame of reference. This case is sometimes called special relativistic time dilation. The faster the relative velocity, the greater the time dilation between one another, with time slowing to a stop as one approaches the speed of light (299,792,458 m/s).
Theoretically, time dilation would make it possible for passengers in a fast-moving vehicle to advance further into the future in a short period of their own time. For sufficiently high speeds, the effect is dramatic. For example, one year of travel might correspond to ten years on Earth. Indeed, a constant 1 gacceleration would permit humans to travel through the entire known Universe in one human lifetime.[9]
With current technology severely limiting the velocity of space travel, however, the differences experienced in practice are minuscule: after 6 months on the International Space Station (ISS), orbiting Earth at a speed of about 7,700 m/s, an astronaut would have aged about 0.005 seconds less than those on Earth.[10] The cosmonauts Sergei Krikalev and Sergei Avdeyev both experienced time dilation of about 20 milliseconds compared to time that passed on Earth.[11][12]
https://en.wikipedia.org/wiki/Time_dilation#Velocity_time_dilation
In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.
In mathematics, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.[1]
Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body.https://en.wikipedia.org/wiki/Gravitational_potential
Astrophysical applications[edit]
Gravitational lensing[edit]
The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing.[108]Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an Einstein ring, or partial rings called arcs.[109] The earliest example was discovered in 1979;[110] since then, more than a hundred gravitational lenses have been observed.[111] Even if the multiple images are too close to each other to be resolved, the effect can still be measured, e.g., as an overall brightening of the target object; a number of such "microlensing events" have been observed.[112]
Gravitational lensing has developed into a tool of observational astronomy. It is used to detect the presence and distribution of dark matter, provide a "natural telescope" for observing distant galaxies, and to obtain an independent estimate of the Hubble constant. Statistical evaluations of lensing data provide valuable insight into the structural evolution of galaxies.[113]
https://en.wikipedia.org/wiki/General_relativity#Light_deflection_and_gravitational_time_delay
https://en.wikipedia.org/wiki/Wormhole#Traversable_wormholes
https://en.wikipedia.org/wiki/Tipler_cylinder
https://en.wikipedia.org/wiki/Category:Lorentzian_manifolds
https://en.wikipedia.org/wiki/Supramolecular_chemistry
https://en.wikipedia.org/wiki/Molecular_self-assembly
https://en.wikipedia.org/wiki/Supersymmetry
https://en.wikipedia.org/wiki/Spacetime_symmetries
https://en.wikipedia.org/wiki/Symmetry_(physics)
https://en.wikipedia.org/wiki/Rotation
https://en.wikipedia.org/wiki/Reflection_(physics)
https://en.wikipedia.org/wiki/General_covariance
https://en.wikipedia.org/wiki/Cosmological_principle
https://en.wikipedia.org/wiki/Accretion_(astrophysics)
https://en.wikipedia.org/wiki/Astrophysical_jet#Relativistic_jet
https://en.wikipedia.org/wiki/Physical_cosmology
https://en.wikipedia.org/wiki/Thermal_radiation
https://en.wikipedia.org/wiki/Closed_timelike_curve#Contractible_versus_noncontractible
https://en.wikipedia.org/wiki/Supersymmetry
https://en.wikipedia.org/wiki/Spherically_symmetric_spacetime
https://en.wikipedia.org/wiki/Gravitational_potential
https://en.wikipedia.org/wiki/Gravitational_lens
https://en.wikipedia.org/wiki/Time_dilation#Velocity_time_dilation
https://en.wikipedia.org/wiki/Gravitational_redshift
https://en.wikipedia.org/wiki/Vector_field
https://en.wikipedia.org/wiki/Local_diffeomorphism
https://en.wikipedia.org/wiki/Killing_vector_field
https://en.wikipedia.org/wiki/Homothetic_vector_field
https://en.wikipedia.org/wiki/Affine_vector_field
https://en.wikipedia.org/wiki/Conformal_Killing_vector_field
https://en.wikipedia.org/wiki/Curvature_collineation
https://en.wikipedia.org/wiki/Matter_collineation
https://en.wikipedia.org/wiki/Static_spacetime
https://en.wikipedia.org/wiki/Field_(physics)
https://en.wikipedia.org/wiki/Symmetry_in_quantum_mechanics
https://en.wikipedia.org/wiki/Spontaneous_symmetry_breaking
https://en.wikipedia.org/wiki/Light_cone
https://en.wikipedia.org/wiki/Vacuum_solution_(general_relativity)
https://en.wikipedia.org/wiki/Equations_of_motion
https://en.wikipedia.org/wiki/Dimension
The Gödel metric is an exact solution of the Einstein field equations in which the stress–energy tensor contains two terms, the first representing the matter density of a homogeneous distribution of swirling dust particles (dust solution), and the second associated with a nonzero cosmological constant (see lambdavacuum solution). It is also known as the Gödel solution or Gödel universe.
This solution has many unusual properties—in particular, the existence of closed timelike curves that would allow time travel in a universe described by the solution. Its definition is somewhat artificial in that the value of the cosmological constant must be carefully chosen to match the density of the dust grains, but this spacetime is an important pedagogical example.
The solution was found in 1949 by Kurt Gödel.[1]
https://en.wikipedia.org/wiki/Gödel_metric
https://en.wikipedia.org/wiki/Closed_timelike_curve
https://en.wikipedia.org/wiki/Ionic_liquid
https://en.wikipedia.org/wiki/Colloid_thruster
https://en.wikipedia.org/wiki/Field-emission_electric_propulsion
https://en.wikipedia.org/wiki/Carbon_nanotube
https://en.wikipedia.org/wiki/Nano-particle_field_extraction_thruster
https://en.wikipedia.org/wiki/Propellant#Liquid_propellant
https://en.wikipedia.org/wiki/Cucurbituril
https://en.wikipedia.org/wiki/Singularity_(mathematics)
https://en.wikipedia.org/wiki/Henri_Poincaré
https://en.wikipedia.org/wiki/Tensor
https://en.wikipedia.org/wiki/Light_cone
https://en.wikipedia.org/wiki/Topology
https://en.wikipedia.org/wiki/Light
https://en.wikipedia.org/wiki/Pressure
https://en.wikipedia.org/wiki/Magnetic_force
https://en.wikipedia.org/wiki/Plane
https://en.wikipedia.org/wiki/Vertical
https://en.wikipedia.org/wiki/Pressure
https://en.wikipedia.org/wiki/Magnetic_force
https://en.wikipedia.org/wiki/Loop_(topology)
https://en.wikipedia.org/wiki/Free_loop
https://en.wikipedia.org/wiki/Loop_space
https://en.wikipedia.org/wiki/Pendulum
https://en.wikipedia.org/wiki/Spring
https://en.wikipedia.org/wiki/String
https://en.wikipedia.org/wiki/Observable_universe
https://en.wikipedia.org/wiki/Ball_(mathematics)
Saturday, September 18, 2021
09-18-2021-1152 - Gravitational time dilation (two disparities on a plane; two size disparate spheres on a plane; two weight disparate or size disparate on a warped plane)
https://en.wikipedia.org/wiki/Gravitational_time_dilation
https://en.wikipedia.org/wiki/Gravitational_lens
Saturday, September 18, 2021
09-18-2021-1712 - Pressure Measurement (Absolute, gauge and differential pressures — zero reference)
Pressure measurement is the analysis of an applied force by a fluid (liquid or gas) on a surface. Pressure is typically measured in units of force per unit of surface area. Many techniques have been developed for the measurement of pressure and vacuum. Instruments used to measure and display pressure in an integral unit are called pressure meters or pressure gauges or vacuum gauges. A manometer is a good example, as it uses the surface area and weight of a column of liquid to both measure and indicate pressure. Likewise the widely used Bourdon gauge is a mechanical device, which both measures and indicates and is probably the best known type of gauge.
A vacuum gauge is a pressure gauge used to measure pressures lower than the ambient atmospheric pressure, which is set as the zero point, in negative values (e.g.: −15 psig or −760 mmHg equals total vacuum). Most gauges measure pressure relative to atmospheric pressure as the zero point, so this form of reading is simply referred to as "gauge pressure". However, anything greater than total vacuum is technically a form of pressure. For very accurate readings, especially at very low pressures, a gauge that uses total vacuum as the zero point may be used, giving pressure readings in an absolute scale.
Other methods of pressure measurement involve sensors that can transmit the pressure reading to a remote indicator or control system (telemetry).
Absolute, gauge and differential pressures — zero reference[edit]
Everyday pressure measurements, such as for vehicle tire pressure, are usually made relative to ambient air pressure. In other cases measurements are made relative to a vacuum or to some other specific reference. When distinguishing between these zero references, the following terms are used:
Absolute pressure is zero-referenced against a perfect vacuum, using an absolute scale, so it is equal to gauge pressure plus atmospheric pressure.
Gauge pressure is zero-referenced against ambient air pressure, so it is equal to absolute pressure minus atmospheric pressure. Negative signs are usually omitted.[citation needed] To distinguish a negative pressure, the value may be appended with the word "vacuum" or the gauge may be labeled a "vacuum gauge". These are further divided into two subcategories: high and low vacuum (and sometimes ultra-high vacuum). The applicable pressure ranges of many of the techniques used to measure vacuums overlap. Hence, by combining several different types of gauge, it is possible to measure system pressure continuously from 10 mbar down to 10−11 mbar.
Differential pressure is the difference in pressure between two points.
The zero reference in use is usually implied by context, and these words are added only when clarification is needed. Tire pressureand blood pressure are gauge pressures by convention, while atmospheric pressures, deep vacuum pressures, and altimeter pressuresmust be absolute.
For most working fluids where a fluid exists in a closed system, gauge pressure measurement prevails. Pressure instruments connected to the system will indicate pressures relative to the current atmospheric pressure. The situation changes when extreme vacuum pressures are measured, then absolute pressures are typically used instead.
Differential pressures are commonly used in industrial process systems. Differential pressure gauges have two inlet ports, each connected to one of the volumes whose pressure is to be monitored. In effect, such a gauge performs the mathematical operation of subtraction through mechanical means, obviating the need for an operator or control system to watch two separate gauges and determine the difference in readings.
Moderate vacuum pressure readings can be ambiguous without the proper context, as they may represent absolute pressure or gauge pressure without a negative sign. Thus a vacuum of 26 inHg gauge is equivalent to an absolute pressure of 4 inHg, calculated as 30 inHg (typical atmospheric pressure) − 26 inHg (gauge pressure).
Atmospheric pressure is typically about 100 kPa at sea level, but is variable with altitude and weather. If the absolute pressure of a fluid stays constant, the gauge pressure of the same fluid will vary as atmospheric pressure changes. For example, when a car drives up a mountain, the (gauge) tire pressure goes up because atmospheric pressure goes down. The absolute pressure in the tire is essentially unchanged.
Using atmospheric pressure as reference is usually signified by a "g" for gauge after the pressure unit, e.g. 70 psig, which means that the pressure measured is the total pressure minus atmospheric pressure. There are two types of gauge reference pressure: vented gauge (vg) and sealed gauge (sg).
A vented-gauge pressure transmitter, for example, allows the outside air pressure to be exposed to the negative side of the pressure-sensing diaphragm, through a vented cable or a hole on the side of the device, so that it always measures the pressure referred to ambient barometric pressure. Thus a vented-gauge reference pressure sensor should always read zero pressure when the process pressure connection is held open to the air.
A sealed gauge reference is very similar, except that atmospheric pressure is sealed on the negative side of the diaphragm. This is usually adopted on high pressure ranges, such as hydraulics, where atmospheric pressure changes will have a negligible effect on the accuracy of the reading, so venting is not necessary. This also allows some manufacturers to provide secondary pressure containment as an extra precaution for pressure equipment safety if the burst pressure of the primary pressure sensing diaphragm is exceeded.
There is another way of creating a sealed gauge reference, and this is to seal a high vacuum on the reverse side of the sensing diaphragm. Then the output signal is offset, so the pressure sensor reads close to zero when measuring atmospheric pressure.
A sealed gauge reference pressure transducer will never read exactly zero because atmospheric pressure is always changing and the reference in this case is fixed at 1 bar.
To produce an absolute pressure sensor, the manufacturer seals a high vacuum behind the sensing diaphragm. If the process-pressure connection of an absolute-pressure transmitter is open to the air, it will read the actual barometric pressure.
https://en.wikipedia.org/wiki/Pressure_measurement#Gauge
A vacuum gauge is a pressure gauge used to measure pressures lower than the ambient atmospheric pressure, which is set as the zero point, in negative values (e.g.: −15 psig or −760 mmHg equals total vacuum). Most gauges measure pressure relative to atmospheric pressure as the zero point, so this form of reading is simply referred to as "gauge pressure". However, anything greater than total vacuum is technically a form of pressure. For very accurate readings, especially at very low pressures, a gauge that uses total vacuum as the zero point may be used, giving pressure readings in an absolute scale.
Other methods of pressure measurement involve sensors that can transmit the pressure reading to a remote indicator or control system (telemetry).
Absolute, gauge and differential pressures — zero reference[edit]
Everyday pressure measurements, such as for vehicle tire pressure, are usually made relative to ambient air pressure. In other cases measurements are made relative to a vacuum or to some other specific reference. When distinguishing between these zero references, the following terms are used:
Absolute pressure is zero-referenced against a perfect vacuum, using an absolute scale, so it is equal to gauge pressure plus atmospheric pressure.
Gauge pressure is zero-referenced against ambient air pressure, so it is equal to absolute pressure minus atmospheric pressure. Negative signs are usually omitted.[citation needed] To distinguish a negative pressure, the value may be appended with the word "vacuum" or the gauge may be labeled a "vacuum gauge". These are further divided into two subcategories: high and low vacuum (and sometimes ultra-high vacuum). The applicable pressure ranges of many of the techniques used to measure vacuums overlap. Hence, by combining several different types of gauge, it is possible to measure system pressure continuously from 10 mbar down to 10−11 mbar.
Differential pressure is the difference in pressure between two points.
The zero reference in use is usually implied by context, and these words are added only when clarification is needed. Tire pressureand blood pressure are gauge pressures by convention, while atmospheric pressures, deep vacuum pressures, and altimeter pressuresmust be absolute.
For most working fluids where a fluid exists in a closed system, gauge pressure measurement prevails. Pressure instruments connected to the system will indicate pressures relative to the current atmospheric pressure. The situation changes when extreme vacuum pressures are measured, then absolute pressures are typically used instead.
Differential pressures are commonly used in industrial process systems. Differential pressure gauges have two inlet ports, each connected to one of the volumes whose pressure is to be monitored. In effect, such a gauge performs the mathematical operation of subtraction through mechanical means, obviating the need for an operator or control system to watch two separate gauges and determine the difference in readings.
Moderate vacuum pressure readings can be ambiguous without the proper context, as they may represent absolute pressure or gauge pressure without a negative sign. Thus a vacuum of 26 inHg gauge is equivalent to an absolute pressure of 4 inHg, calculated as 30 inHg (typical atmospheric pressure) − 26 inHg (gauge pressure).
Atmospheric pressure is typically about 100 kPa at sea level, but is variable with altitude and weather. If the absolute pressure of a fluid stays constant, the gauge pressure of the same fluid will vary as atmospheric pressure changes. For example, when a car drives up a mountain, the (gauge) tire pressure goes up because atmospheric pressure goes down. The absolute pressure in the tire is essentially unchanged.
Using atmospheric pressure as reference is usually signified by a "g" for gauge after the pressure unit, e.g. 70 psig, which means that the pressure measured is the total pressure minus atmospheric pressure. There are two types of gauge reference pressure: vented gauge (vg) and sealed gauge (sg).
A vented-gauge pressure transmitter, for example, allows the outside air pressure to be exposed to the negative side of the pressure-sensing diaphragm, through a vented cable or a hole on the side of the device, so that it always measures the pressure referred to ambient barometric pressure. Thus a vented-gauge reference pressure sensor should always read zero pressure when the process pressure connection is held open to the air.
A sealed gauge reference is very similar, except that atmospheric pressure is sealed on the negative side of the diaphragm. This is usually adopted on high pressure ranges, such as hydraulics, where atmospheric pressure changes will have a negligible effect on the accuracy of the reading, so venting is not necessary. This also allows some manufacturers to provide secondary pressure containment as an extra precaution for pressure equipment safety if the burst pressure of the primary pressure sensing diaphragm is exceeded.
There is another way of creating a sealed gauge reference, and this is to seal a high vacuum on the reverse side of the sensing diaphragm. Then the output signal is offset, so the pressure sensor reads close to zero when measuring atmospheric pressure.
A sealed gauge reference pressure transducer will never read exactly zero because atmospheric pressure is always changing and the reference in this case is fixed at 1 bar.
To produce an absolute pressure sensor, the manufacturer seals a high vacuum behind the sensing diaphragm. If the process-pressure connection of an absolute-pressure transmitter is open to the air, it will read the actual barometric pressure.
https://en.wikipedia.org/wiki/Pressure_measurement#Gauge
Saturday, September 18, 2021
09-18-2021-1015 - Linear Stage Translation Stage motion system single axis
A linear stage or translation stage is a component of a precise motion system used to restrict an object to a single axis of motion. The term linear slide is often used interchangeably with "linear stage", though technically "linear slide" refers to a linear motion bearing, which is only a component of a linear stage. All linear stages consist of a platform and a base, joined by some form of guide or linear bearing in such a way that the platform is restricted to linear motion with respect to the base. In common usage, the term linear stage may or may not also include the mechanism by which the position of the platform is controlled relative to the base.
https://en.wikipedia.org/wiki/Linear_stage
A linear stage or translation stage is a component of a precise motion system used to restrict an object to a single axis of motion. The term linear slide is often used interchangeably with "linear stage", though technically "linear slide" refers to a linear motion bearing, which is only a component of a linear stage. All linear stages consist of a platform and a base, joined by some form of guide or linear bearing in such a way that the platform is restricted to linear motion with respect to the base. In common usage, the term linear stage may or may not also include the mechanism by which the position of the platform is controlled relative to the base.
https://en.wikipedia.org/wiki/Linear_stage
External links[edit]
https://en.wikipedia.org/wiki/Differential_(mathematics)
Saturday, September 18, 2021
09-18-2021-1226 - scalar field dark matter
In astrophysics and cosmology scalar field dark matter is a classical, minimally coupled, scalar field postulated to account for the inferred dark matter.[2]
In astrophysics and cosmology scalar field dark matter is a classical, minimally coupled, scalar field postulated to account for the inferred dark matter.[2]
Background[edit]
The universe may be accelerating, fueled perhaps by a cosmological constant or some other field possessing long range ‘repulsive’ effects. A model must predict the correct form for the large scale clustering spectrum,[3] account for cosmic microwave background anisotropies on large and intermediate angular scales, and provide agreement with the luminosity distance relation obtained from observations of high redshift supernovae. The modeled evolution of the universe includes a large amount of unknown matter and energy in order to agree with such observations. This energy density has two components: cold dark matter and dark energy. Each contributes to the theory of the origination of galaxies and the expansion of the universe. The universe must have a critical density, a density not explained by baryonic matter (ordinary matter) alone.
The universe may be accelerating, fueled perhaps by a cosmological constant or some other field possessing long range ‘repulsive’ effects. A model must predict the correct form for the large scale clustering spectrum,[3] account for cosmic microwave background anisotropies on large and intermediate angular scales, and provide agreement with the luminosity distance relation obtained from observations of high redshift supernovae. The modeled evolution of the universe includes a large amount of unknown matter and energy in order to agree with such observations. This energy density has two components: cold dark matter and dark energy. Each contributes to the theory of the origination of galaxies and the expansion of the universe. The universe must have a critical density, a density not explained by baryonic matter (ordinary matter) alone.
Scalar field[edit]
The dark matter can be modeled as a scalar field using two fitted parameters, mass and self-interaction.[4][5] In this picture the dark matter consists of an ultralight particle with a mass of ~10−22 eV when there is no self-interaction.[6][7][8] If there is a self-interaction a wider mass range is allowed.[9] The uncertainty in position of a particle is larger than its Compton wavelength (a particle with mass 10−22 eV has a Compton wavelength of 1.3 light years), and for some reasonable estimates of particle mass and density of dark matter there is no point talking about the individual particles’ positions and momenta. Ultra-light dark matter would be more like a wave than a particle, and the galactic halos are giant systems of condensed bose liquid, possibly superfluid. The dark matter can be described as a Bose–Einstein condensate of the ultralight quanta of the field[10] and as boson stars.[9] The enormous Compton wavelength of these particles prevents structure formation on small, subgalactic scales, which is a major problem in traditional cold dark matter models. The collapse of initial over-densities is studied in the references.[11][12][13][14]
This dark matter model is also known as BEC dark matter or wave dark matter. Fuzzy dark matter and ultra-light axion are examples of scalar field dark matter.
The dark matter can be modeled as a scalar field using two fitted parameters, mass and self-interaction.[4][5] In this picture the dark matter consists of an ultralight particle with a mass of ~10−22 eV when there is no self-interaction.[6][7][8] If there is a self-interaction a wider mass range is allowed.[9] The uncertainty in position of a particle is larger than its Compton wavelength (a particle with mass 10−22 eV has a Compton wavelength of 1.3 light years), and for some reasonable estimates of particle mass and density of dark matter there is no point talking about the individual particles’ positions and momenta. Ultra-light dark matter would be more like a wave than a particle, and the galactic halos are giant systems of condensed bose liquid, possibly superfluid. The dark matter can be described as a Bose–Einstein condensate of the ultralight quanta of the field[10] and as boson stars.[9] The enormous Compton wavelength of these particles prevents structure formation on small, subgalactic scales, which is a major problem in traditional cold dark matter models. The collapse of initial over-densities is studied in the references.[11][12][13][14]
This dark matter model is also known as BEC dark matter or wave dark matter. Fuzzy dark matter and ultra-light axion are examples of scalar field dark matter.
See also[edit]
- Weakly interacting massive particles – Hypothetical particles that are thought to constitute dark matter
- Minimal Supersymmetric Standard Model
- Neutralino – Neutral mass eigenstate formed from superpartners of gauge and Higgs bosons
- Axion – Hypothetical elementary particle
- Dark matter halo – A theoretical component of a galaxy that envelops the galactic disc and extends well beyond the edge of the visible galaxy
- Light dark matter – Dark matter weakly interacting massive particles candidates with masses less than 1 GeV
- Hot dark matter – A theoretical form of dark matter which consists of particles that travel with ultrarelativistic velocities
- Warm dark matter – Hypothesized form of dark matter
- Fuzzy cold dark matter – Hypothetical form of cold dark matter proposed to solve the cuspy halo problem
Pie chart showing the fractions of energy in the universe contributed by different sources. Ordinary matter is divided into luminous matter (the stars and luminous gases and 0.005% radiation) and nonluminous matter (intergalactic gas and about 0.1% neutrinos and 0.04% supermassive black holes). Ordinary matter is uncommon. Modeled after Ostriker and Steinhardt.[1] For more information, see NASA.https://en.wikipedia.org/wiki/Scalar_field_dark_matter
- Weakly interacting massive particles – Hypothetical particles that are thought to constitute dark matter
- Minimal Supersymmetric Standard Model
- Neutralino – Neutral mass eigenstate formed from superpartners of gauge and Higgs bosons
- Axion – Hypothetical elementary particle
- Dark matter halo – A theoretical component of a galaxy that envelops the galactic disc and extends well beyond the edge of the visible galaxy
- Light dark matter – Dark matter weakly interacting massive particles candidates with masses less than 1 GeV
- Hot dark matter – A theoretical form of dark matter which consists of particles that travel with ultrarelativistic velocities
- Warm dark matter – Hypothesized form of dark matter
- Fuzzy cold dark matter – Hypothetical form of cold dark matter proposed to solve the cuspy halo problem
https://en.wikipedia.org/wiki/Scalar_field_dark_matter
Saturday, September 18, 2021
09-18-2021-1710 - Degree of Freedom is an Independent Physical Parameter in the Formal Description of the state of a physical system.
In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space.
The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic, where the state at one instant uniquely determines its past and future position and velocity as a function of time, such a system has six degrees of freedom.[citation needed] If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the other hand, a system with an extended object that can rotate or vibrate can have more than six degrees of freedom.
In classical mechanics, the state of a point particle at any given time is often described with position and velocity coordinates in the Lagrangian formalism, or with position and momentum coordinates in the Hamiltonian formalism.
In statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system.[1] The specification of all microstates of a system is a point in the system's phase space.
In the 3D ideal chain model in chemistry, two angles are necessary to describe the orientation of each monomer.
It is often useful to specify quadratic degrees of freedom. These are degrees of freedom that contribute in a quadratic function to the energy of the system.
Depending on what one is counting, there are several different ways that degrees of freedom can be defined, each with a different value.[2]
https://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry)
In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space.
The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic, where the state at one instant uniquely determines its past and future position and velocity as a function of time, such a system has six degrees of freedom.[citation needed] If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the other hand, a system with an extended object that can rotate or vibrate can have more than six degrees of freedom.
In classical mechanics, the state of a point particle at any given time is often described with position and velocity coordinates in the Lagrangian formalism, or with position and momentum coordinates in the Hamiltonian formalism.
In statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system.[1] The specification of all microstates of a system is a point in the system's phase space.
In the 3D ideal chain model in chemistry, two angles are necessary to describe the orientation of each monomer.
It is often useful to specify quadratic degrees of freedom. These are degrees of freedom that contribute in a quadratic function to the energy of the system.
Depending on what one is counting, there are several different ways that degrees of freedom can be defined, each with a different value.[2]
https://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry)
Saturday, September 18, 2021
09-18-2021-1708 - alternating current oscillating particle or wave perturbed γ-γ angular correlation heterodyne gyroscope
Alternating current (AC) is an electric current which periodically reverses direction and changes its magnitude continuously with time in contrast to direct current(DC) which flows only in one direction. Alternating current is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans and electric lamps into a wall socket. A common source of DC power is a battery cell in a flashlight. The abbreviations AC and DC are often used to mean simply alternating and direct, as when they modify current or voltage.[1][2]
The usual waveform of alternating current in most electric power circuits is a sine wave, whose positive half-period corresponds with positive direction of the current and vice versa. In certain applications, like guitar amplifiers, different waveforms are used, such as triangular waves or square waves. Audio and radiosignals carried on electrical wires are also examples of alternating current. These types of alternating current carry information such as sound (audio) or images (video) sometimes carried by modulation of an AC carrier signal. These currents typically alternate at higher frequencies than those used in power transmission.
https://en.wikipedia.org/wiki/Alternating_current
The perturbed γ-γ angular correlation, PAC for short or PAC-Spectroscopy, is a method of nuclear solid-state physics with which magnetic and electric fields in crystal structures can be measured. In doing so, electrical field gradients and the Larmor frequency in magnetic fields as well as dynamic effects are determined. With this very sensitive method, which requires only about 10-1000 billion atoms of a radioactive isotope per measurement, material properties in the local structure, phase transitions, magnetism and diffusion can be investigated. The PAC method is related to nuclear magnetic resonance and the Mössbauer effect, but shows no signal attenuation at very high temperatures. Today only the time-differential perturbed angular correlation (TDPAC) is used.
https://en.wikipedia.org/wiki/Perturbed_angular_correlation
rotation translation vibration
https://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry)
Alternating current (AC) is an electric current which periodically reverses direction and changes its magnitude continuously with time in contrast to direct current(DC) which flows only in one direction. Alternating current is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans and electric lamps into a wall socket. A common source of DC power is a battery cell in a flashlight. The abbreviations AC and DC are often used to mean simply alternating and direct, as when they modify current or voltage.[1][2]
The usual waveform of alternating current in most electric power circuits is a sine wave, whose positive half-period corresponds with positive direction of the current and vice versa. In certain applications, like guitar amplifiers, different waveforms are used, such as triangular waves or square waves. Audio and radiosignals carried on electrical wires are also examples of alternating current. These types of alternating current carry information such as sound (audio) or images (video) sometimes carried by modulation of an AC carrier signal. These currents typically alternate at higher frequencies than those used in power transmission.
https://en.wikipedia.org/wiki/Alternating_current
The perturbed γ-γ angular correlation, PAC for short or PAC-Spectroscopy, is a method of nuclear solid-state physics with which magnetic and electric fields in crystal structures can be measured. In doing so, electrical field gradients and the Larmor frequency in magnetic fields as well as dynamic effects are determined. With this very sensitive method, which requires only about 10-1000 billion atoms of a radioactive isotope per measurement, material properties in the local structure, phase transitions, magnetism and diffusion can be investigated. The PAC method is related to nuclear magnetic resonance and the Mössbauer effect, but shows no signal attenuation at very high temperatures. Today only the time-differential perturbed angular correlation (TDPAC) is used.
https://en.wikipedia.org/wiki/Perturbed_angular_correlation
rotation translation vibration
https://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry)
Saturday, September 18, 2021
09-18-2021-1315 - Absolute, gauge and differential pressures — zero reference
Saturday, September 18, 2021
09-18-2021-1243 - mirror nuclei
In physics, mirror nuclei are a pair of isotopes of two different elements where the number of protons of isotope one (Z1) equals the number of neutrons of isotope two (N2) and the number of protons of isotope two (Z2) equals the number of neutrons in isotope one (N1); in short: Z1 = N2 and Z2 = N1. This implies that the mass numbers of the isotopes are the same: N1 + Z1 = N2 + Z2.
Examples of mirror nuclei:
Isotope 1 Z1 N1 Isotope 2 Z2 N2 3H 1 2 3He 2 1 14C 6 8 14O 8 6 15N 7 8 15O 8 7 24Na 11 13 24Al 13 11
Pairs of mirror nuclei have the same spin and parity. If we constrain to odd number of nucleons (A=Z+N) then we find mirror nuclei that differ from one another by exchanging a proton by a neutron. Interesting to observe is their binding energy which is mainly due to the strong interaction and also due to Coulomb interaction. Since the strong interaction is invariant to protons and neutrons one can expect these mirror nuclei to have very similar binding energies.[1][2]
In 2020 Strontium-73 and bromine-73 were found to not behave as expected.[3]
In physics, mirror nuclei are a pair of isotopes of two different elements where the number of protons of isotope one (Z1) equals the number of neutrons of isotope two (N2) and the number of protons of isotope two (Z2) equals the number of neutrons in isotope one (N1); in short: Z1 = N2 and Z2 = N1. This implies that the mass numbers of the isotopes are the same: N1 + Z1 = N2 + Z2.
Examples of mirror nuclei:
| Isotope 1 | Z1 | N1 | Isotope 2 | Z2 | N2 |
|---|---|---|---|---|---|
| 3H | 1 | 2 | 3He | 2 | 1 |
| 14C | 6 | 8 | 14O | 8 | 6 |
| 15N | 7 | 8 | 15O | 8 | 7 |
| 24Na | 11 | 13 | 24Al | 13 | 11 |
Pairs of mirror nuclei have the same spin and parity. If we constrain to odd number of nucleons (A=Z+N) then we find mirror nuclei that differ from one another by exchanging a proton by a neutron. Interesting to observe is their binding energy which is mainly due to the strong interaction and also due to Coulomb interaction. Since the strong interaction is invariant to protons and neutrons one can expect these mirror nuclei to have very similar binding energies.[1][2]
In 2020 Strontium-73 and bromine-73 were found to not behave as expected.[3]
References[edit]
- ^ Cottle, P. D. (2002-04-12). "Excitations in the Mirror Nuclei 32Ar and 32Si". Physical Review Letters. 88 (17): 172502. Bibcode:2002PhRvL..88q2502C. doi:10.1103/PhysRevLett.88.172502. PMID 12005747. Retrieved 2018-01-08.
- ^ Kamat, Sharmila (2002-04-23). "Focus: Gazing into a Nuclear Mirror". Physics. American Physical Society. Retrieved 2016-04-11.
- ^ Discovery by UMass Lowell-led team challenges nuclear theory
https://en.wikipedia.org/wiki/Mirror_nuclei
- ^ Cottle, P. D. (2002-04-12). "Excitations in the Mirror Nuclei 32Ar and 32Si". Physical Review Letters. 88 (17): 172502. Bibcode:2002PhRvL..88q2502C. doi:10.1103/PhysRevLett.88.172502. PMID 12005747. Retrieved 2018-01-08.
- ^ Kamat, Sharmila (2002-04-23). "Focus: Gazing into a Nuclear Mirror". Physics. American Physical Society. Retrieved 2016-04-11.
- ^ Discovery by UMass Lowell-led team challenges nuclear theory
Saturday, September 18, 2021
09-18-2021-0944 - Maxwell stress tensor Poynting vector
The Maxwell stress tensor (named after James Clerk Maxwell) is a symmetric second-order tensor used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
In the relativistic formulation of electromagnetism, the Maxwell's tensor appears as a part of the electromagnetic stress–energy tensor which is the electromagnetic component of the total stress–energy tensor. The latter describes the density and flux of energy and momentum in spacetime.
https://en.wikipedia.org/wiki/Maxwell_stress_tensor
In physics, the Poynting vector represents the directional energy flux (the energy transfer per unit area per unit time) of an electromagnetic field. The SI unit of the Poynting vector is the watt per square metre (W/m2). It is named after its discoverer John Henry Poynting who first derived it in 1884.[1]: 132 Oliver Heaviside also discovered it independently in the more general form that recognises the freedom of adding the curl of an arbitrary vector field to the definition.[2] The Poynting vector is used throughout electromagnetics in conjunction with Poynting's theorem, the continuity equation expressing conservation of electromagnetic energy, to calculate the power flow in electric and magnetic fields.
https://en.wikipedia.org/wiki/Poynting_vector
Electrostatics is a branch of physics that studies electric charges at rest (static electricity).
Since classical physics, it has been known that some materials, such as amber, attract lightweight particles after rubbing. The Greek word for amber, or electron, was thus the source of the word 'electricity'. Electrostatic phenomena arise from the forces that electric charges exert on each other. Such forces are described by Coulomb's law. Even though electrostatically induced forces seem to be rather weak, some electrostatic forces such as the one between an electron and a proton, that together make up a hydrogen atom, is about 36 orders of magnitude stronger than the gravitational force acting between them.
There are many examples of electrostatic phenomena, from those as simple as the attraction of plastic wrap to one's hand after it is removed from a package, to the apparently spontaneous explosion of grain silos, the damage of electronic components during manufacturing, and photocopier & laser printer operation. Electrostatics involves the buildup of charge on the surface of objects due to contact with other surfaces. Although charge exchange happens whenever any two surfaces contact and separate, the effects of charge exchange are usually noticed only when at least one of the surfaces has a high resistance to electrical flow, because the charges that transfer are trapped there for a long enough time for their effects to be observed. These charges then remain on the object until they either bleed off to ground, or are quickly neutralized by a discharge. The familiar phenomenon of a static "shock" is caused by the neutralization of charge built up in the body from contact with insulated surfaces.
https://en.wikipedia.org/wiki/Electrostatics
A gyroscope (from Ancient Greek γῦρος gûros, "circle" and σκοπέω skopéō, "to look") is a device used for measuring or maintaining orientation and angular velocity.[1][2] It is a spinning wheel or disc in which the axis of rotation (spin axis) is free to assume any orientation by itself. When rotating, the orientation of this axis is unaffected by tilting or rotation of the mounting, according to the conservation of angular momentum.
Gyroscopes based on other operating principles also exist, such as the microchip-packaged MEMS gyroscopes found in electronic devices (sometimes called gyrometers), solid-state ring lasers, fibre optic gyroscopes, and the extremely sensitive quantum gyroscope.[3]
Applications of gyroscopes include inertial navigation systems, such as in the Hubble Telescope, or inside the steel hull of a submerged submarine. Due to their precision, gyroscopes are also used in gyrotheodolites to maintain direction in tunnel mining.[4] Gyroscopes can be used to construct gyrocompasses, which complement or replace magnetic compasses (in ships, aircraft and spacecraft, vehicles in general), to assist in stability (bicycles, motorcycles, and ships) or be used as part of an inertial guidance system.
MEMS gyroscopes are popular in some consumer electronics, such as smartphones.
https://en.wikipedia.org/wiki/Gyroscope
A control moment gyroscope (CMG) is an attitude control device generally used in spacecraft attitude control systems. A CMG consists of a spinning rotor and one or more motorized gimbals that tilt the rotor’s angular momentum. As the rotor tilts, the changing angular momentum causes a gyroscopic torque that rotates the spacecraft.[1][2]
https://en.wikipedia.org/wiki/Control_moment_gyroscope
https://en.wikipedia.org/wiki/Accumulator_(energy)
https://en.wikipedia.org/wiki/Escape_velocity
https://en.wikipedia.org/wiki/Aircraft_catapult#Steam_catapult
https://en.wikipedia.org/wiki/Linear_stage
https://en.wikipedia.org/wiki/Category:Magnetic_propulsion_devices
https://en.wikipedia.org/wiki/Magnetostatics
Aerodynamics, from Greek ἀήρ aero (air) + δυναμική (dynamics), is the study of motion of air, particularly when affected by a solid object, such as an airplane wing. It is a sub-field of fluid dynamics and gas dynamics, and many aspects of aerodynamics theory are common to these fields. The term aerodynamics is often used synonymously with gas dynamics, the difference being that "gas dynamics" applies to the study of the motion of all gases, and is not limited to air. The formal study of aerodynamics began in the modern sense in the eighteenth century, although observations of fundamental concepts such as aerodynamic drag were recorded much earlier. Most of the early efforts in aerodynamics were directed toward achieving heavier-than-air flight, which was first demonstrated by Otto Lilienthal in 1891.[1] Since then, the use of aerodynamics through mathematical analysis, empirical approximations, wind tunnel experimentation, and computer simulations has formed a rational basis for the development of heavier-than-air flight and a number of other technologies. Recent work in aerodynamics has focused on issues related to compressible flow, turbulence, and boundary layers and has become increasingly computational in nature.
https://en.wikipedia.org/wiki/Aerodynamics
Compressible flow (or gas dynamics) is the branch of fluid mechanics that deals with flows having significant changes in fluid density. While all flows are compressible, flows are usually treated as being incompressible when the Mach number (the ratio of the speed of the flow to the speed of sound) is smaller than 0.3 (since the density change due to velocity is about 5% in that case).[1]The study of compressible flow is relevant to high-speed aircraft, jet engines, rocket motors, high-speed entry into a planetary atmosphere, gas pipelines, commercial applications such as abrasive blasting, and many other fields.
The Maxwell stress tensor (named after James Clerk Maxwell) is a symmetric second-order tensor used in classical electromagnetism to represent the interaction between electromagnetic forces and mechanical momentum. In simple situations, such as a point charge moving freely in a homogeneous magnetic field, it is easy to calculate the forces on the charge from the Lorentz force law. When the situation becomes more complicated, this ordinary procedure can become impractically difficult, with equations spanning multiple lines. It is therefore convenient to collect many of these terms in the Maxwell stress tensor, and to use tensor arithmetic to find the answer to the problem at hand.
In the relativistic formulation of electromagnetism, the Maxwell's tensor appears as a part of the electromagnetic stress–energy tensor which is the electromagnetic component of the total stress–energy tensor. The latter describes the density and flux of energy and momentum in spacetime.
https://en.wikipedia.org/wiki/Maxwell_stress_tensor
In physics, the Poynting vector represents the directional energy flux (the energy transfer per unit area per unit time) of an electromagnetic field. The SI unit of the Poynting vector is the watt per square metre (W/m2). It is named after its discoverer John Henry Poynting who first derived it in 1884.[1]: 132 Oliver Heaviside also discovered it independently in the more general form that recognises the freedom of adding the curl of an arbitrary vector field to the definition.[2] The Poynting vector is used throughout electromagnetics in conjunction with Poynting's theorem, the continuity equation expressing conservation of electromagnetic energy, to calculate the power flow in electric and magnetic fields.
https://en.wikipedia.org/wiki/Poynting_vector
Electrostatics is a branch of physics that studies electric charges at rest (static electricity).
Since classical physics, it has been known that some materials, such as amber, attract lightweight particles after rubbing. The Greek word for amber, or electron, was thus the source of the word 'electricity'. Electrostatic phenomena arise from the forces that electric charges exert on each other. Such forces are described by Coulomb's law. Even though electrostatically induced forces seem to be rather weak, some electrostatic forces such as the one between an electron and a proton, that together make up a hydrogen atom, is about 36 orders of magnitude stronger than the gravitational force acting between them.
There are many examples of electrostatic phenomena, from those as simple as the attraction of plastic wrap to one's hand after it is removed from a package, to the apparently spontaneous explosion of grain silos, the damage of electronic components during manufacturing, and photocopier & laser printer operation. Electrostatics involves the buildup of charge on the surface of objects due to contact with other surfaces. Although charge exchange happens whenever any two surfaces contact and separate, the effects of charge exchange are usually noticed only when at least one of the surfaces has a high resistance to electrical flow, because the charges that transfer are trapped there for a long enough time for their effects to be observed. These charges then remain on the object until they either bleed off to ground, or are quickly neutralized by a discharge. The familiar phenomenon of a static "shock" is caused by the neutralization of charge built up in the body from contact with insulated surfaces.
https://en.wikipedia.org/wiki/Electrostatics
A gyroscope (from Ancient Greek γῦρος gûros, "circle" and σκοπέω skopéō, "to look") is a device used for measuring or maintaining orientation and angular velocity.[1][2] It is a spinning wheel or disc in which the axis of rotation (spin axis) is free to assume any orientation by itself. When rotating, the orientation of this axis is unaffected by tilting or rotation of the mounting, according to the conservation of angular momentum.
Gyroscopes based on other operating principles also exist, such as the microchip-packaged MEMS gyroscopes found in electronic devices (sometimes called gyrometers), solid-state ring lasers, fibre optic gyroscopes, and the extremely sensitive quantum gyroscope.[3]
Applications of gyroscopes include inertial navigation systems, such as in the Hubble Telescope, or inside the steel hull of a submerged submarine. Due to their precision, gyroscopes are also used in gyrotheodolites to maintain direction in tunnel mining.[4] Gyroscopes can be used to construct gyrocompasses, which complement or replace magnetic compasses (in ships, aircraft and spacecraft, vehicles in general), to assist in stability (bicycles, motorcycles, and ships) or be used as part of an inertial guidance system.
MEMS gyroscopes are popular in some consumer electronics, such as smartphones.
https://en.wikipedia.org/wiki/Gyroscope
A control moment gyroscope (CMG) is an attitude control device generally used in spacecraft attitude control systems. A CMG consists of a spinning rotor and one or more motorized gimbals that tilt the rotor’s angular momentum. As the rotor tilts, the changing angular momentum causes a gyroscopic torque that rotates the spacecraft.[1][2]
https://en.wikipedia.org/wiki/Control_moment_gyroscope
https://en.wikipedia.org/wiki/Accumulator_(energy)
https://en.wikipedia.org/wiki/Escape_velocity
https://en.wikipedia.org/wiki/Aircraft_catapult#Steam_catapult
https://en.wikipedia.org/wiki/Linear_stage
https://en.wikipedia.org/wiki/Category:Magnetic_propulsion_devices
https://en.wikipedia.org/wiki/Magnetostatics
Aerodynamics, from Greek ἀήρ aero (air) + δυναμική (dynamics), is the study of motion of air, particularly when affected by a solid object, such as an airplane wing. It is a sub-field of fluid dynamics and gas dynamics, and many aspects of aerodynamics theory are common to these fields. The term aerodynamics is often used synonymously with gas dynamics, the difference being that "gas dynamics" applies to the study of the motion of all gases, and is not limited to air. The formal study of aerodynamics began in the modern sense in the eighteenth century, although observations of fundamental concepts such as aerodynamic drag were recorded much earlier. Most of the early efforts in aerodynamics were directed toward achieving heavier-than-air flight, which was first demonstrated by Otto Lilienthal in 1891.[1] Since then, the use of aerodynamics through mathematical analysis, empirical approximations, wind tunnel experimentation, and computer simulations has formed a rational basis for the development of heavier-than-air flight and a number of other technologies. Recent work in aerodynamics has focused on issues related to compressible flow, turbulence, and boundary layers and has become increasingly computational in nature.
https://en.wikipedia.org/wiki/Aerodynamics
Compressible flow (or gas dynamics) is the branch of fluid mechanics that deals with flows having significant changes in fluid density. While all flows are compressible, flows are usually treated as being incompressible when the Mach number (the ratio of the speed of the flow to the speed of sound) is smaller than 0.3 (since the density change due to velocity is about 5% in that case).[1]The study of compressible flow is relevant to high-speed aircraft, jet engines, rocket motors, high-speed entry into a planetary atmosphere, gas pipelines, commercial applications such as abrasive blasting, and many other fields.
Irregular reflection[edit]
An irregular reflection is much like the case described above, with the caveat that δ is larger than the maximum allowable turning angle. Thus a detached shock is formed and a more complicated reflection occurs.
An irregular reflection is much like the case described above, with the caveat that δ is larger than the maximum allowable turning angle. Thus a detached shock is formed and a more complicated reflection occurs.
Supersonic wind tunnels[edit]
Supersonic wind tunnels are used for testing and research in supersonic flows, approximately over the Mach number range of 1.2 to 5. The operating principle behind the wind tunnel is that a large pressure difference is maintained upstream to downstream, driving the flow.
https://en.wikipedia.org/wiki/Compressible_flow
https://en.wikipedia.org/wiki/Eötvös_number
https://en.wikipedia.org/wiki/Thermodynamics
Above. landing baryonic zone
https://en.wikipedia.org/wiki/Graetz_number
https://en.wikipedia.org/wiki/Görtler_vortices
https://en.wikipedia.org/wiki/Dean_number
https://en.wikipedia.org/wiki/Dukhin_number
https://en.wikipedia.org/wiki/Ohnesorge_number
https://en.wikipedia.org/wiki/Archimedes_number
https://en.wikipedia.org/wiki/Cauchy_number
https://en.wikipedia.org/wiki/Péclet_number
https://en.wikipedia.org/wiki/Damköhler_numbers
https://en.wikipedia.org/wiki/Biot_number
https://en.wikipedia.org/wiki/Prandtl_number
https://en.wikipedia.org/wiki/Stanton_number
https://en.wikipedia.org/wiki/Laplace_number
https://en.wikipedia.org/wiki/Ursell_number
https://en.wikipedia.org/wiki/Weissenberg_number
https://en.wikipedia.org/wiki/Viscoelasticity
https://en.wikipedia.org/wiki/Shear_rate
https://en.wikipedia.org/wiki/Category:Continuum_mechanics
https://en.wikipedia.org/wiki/Category:Temporal_rates
https://en.wikipedia.org/wiki/Linear_induction_motor
https://en.wikipedia.org/wiki/Category:Electric_and_magnetic_fields_in_matter
https://en.wikipedia.org/wiki/Demagnetizing_field
https://en.wikipedia.org/wiki/Micromagnetics
https://en.wikipedia.org/wiki/Domain_wall_(magnetism)
https://en.wikipedia.org/wiki/Magnetocrystalline_anisotropy
https://en.wikipedia.org/wiki/Spin–orbit_interaction
https://en.wikipedia.org/wiki/Hyperfine_structure
https://en.wikipedia.org/wiki/Electrostriction
https://en.wikipedia.org/wiki/Tensor
https://en.wikipedia.org/wiki/Relaxor_ferroelectric
https://en.wikipedia.org/wiki/Magnetostriction
https://en.wikipedia.org/wiki/Torque
https://en.wikipedia.org/wiki/Electric_field_gradient
https://en.wikipedia.org/wiki/Magnetization
https://en.wikipedia.org/wiki/Spin_(physics)
https://en.wikipedia.org/wiki/Point_particle
https://en.wikipedia.org/wiki/Rigid_body
https://en.wikipedia.org/wiki/Energy
https://en.wikipedia.org/wiki/Void_(astronomy)
https://en.wikipedia.org/wiki/Equation_of_state_(cosmology)
https://en.wikipedia.org/wiki/Quintessence_(physics)
https://en.wikipedia.org/wiki/Scalar_field
https://en.wikipedia.org/wiki/Symmetric_matrix
https://en.wikipedia.org/wiki/Quadrupole
https://en.wikipedia.org/wiki/Vector_field
Supersonic wind tunnels are used for testing and research in supersonic flows, approximately over the Mach number range of 1.2 to 5. The operating principle behind the wind tunnel is that a large pressure difference is maintained upstream to downstream, driving the flow.
https://en.wikipedia.org/wiki/Compressible_flow
https://en.wikipedia.org/wiki/Eötvös_number
https://en.wikipedia.org/wiki/Thermodynamics
Above. landing baryonic zone
https://en.wikipedia.org/wiki/Graetz_number
https://en.wikipedia.org/wiki/Görtler_vortices
https://en.wikipedia.org/wiki/Dean_number
https://en.wikipedia.org/wiki/Dukhin_number
https://en.wikipedia.org/wiki/Ohnesorge_number
https://en.wikipedia.org/wiki/Archimedes_number
https://en.wikipedia.org/wiki/Cauchy_number
https://en.wikipedia.org/wiki/Péclet_number
https://en.wikipedia.org/wiki/Damköhler_numbers
https://en.wikipedia.org/wiki/Biot_number
https://en.wikipedia.org/wiki/Prandtl_number
https://en.wikipedia.org/wiki/Stanton_number
https://en.wikipedia.org/wiki/Laplace_number
https://en.wikipedia.org/wiki/Ursell_number
https://en.wikipedia.org/wiki/Weissenberg_number
https://en.wikipedia.org/wiki/Viscoelasticity
https://en.wikipedia.org/wiki/Shear_rate
https://en.wikipedia.org/wiki/Category:Continuum_mechanics
https://en.wikipedia.org/wiki/Category:Temporal_rates
https://en.wikipedia.org/wiki/Linear_induction_motor
https://en.wikipedia.org/wiki/Category:Electric_and_magnetic_fields_in_matter
https://en.wikipedia.org/wiki/Demagnetizing_field
https://en.wikipedia.org/wiki/Micromagnetics
https://en.wikipedia.org/wiki/Domain_wall_(magnetism)
https://en.wikipedia.org/wiki/Magnetocrystalline_anisotropy
https://en.wikipedia.org/wiki/Spin–orbit_interaction
https://en.wikipedia.org/wiki/Hyperfine_structure
https://en.wikipedia.org/wiki/Electrostriction
https://en.wikipedia.org/wiki/Tensor
https://en.wikipedia.org/wiki/Relaxor_ferroelectric
https://en.wikipedia.org/wiki/Magnetostriction
https://en.wikipedia.org/wiki/Torque
https://en.wikipedia.org/wiki/Electric_field_gradient
https://en.wikipedia.org/wiki/Magnetization
https://en.wikipedia.org/wiki/Spin_(physics)
https://en.wikipedia.org/wiki/Point_particle
https://en.wikipedia.org/wiki/Rigid_body
https://en.wikipedia.org/wiki/Energy
https://en.wikipedia.org/wiki/Void_(astronomy)
https://en.wikipedia.org/wiki/Equation_of_state_(cosmology)
https://en.wikipedia.org/wiki/Quintessence_(physics)
https://en.wikipedia.org/wiki/Scalar_field
https://en.wikipedia.org/wiki/Symmetric_matrix
https://en.wikipedia.org/wiki/Quadrupole
https://en.wikipedia.org/wiki/Vector_field
Small molecule hyperfine structure[edit]
A typical simple example of the hyperfine structure due to the interactions discussed above is in the rotational transitions of hydrogen cyanide (1H12C14N) in its ground vibrational state. Here, the electric quadrupole interaction is due to the 14N-nucleus, the hyperfine nuclear spin-spin splitting is from the magnetic coupling between nitrogen, 14N (IN = 1), and hydrogen, 1H (IH = 1⁄2), and a hydrogen spin-rotation interaction due to the 1H-nucleus. These contributing interactions to the hyperfine structure in the molecule are listed here in descending order of influence. Sub-doppler techniques have been used to discern the hyperfine structure in HCN rotational transitions.[11]
The dipole selection rules for HCN hyperfine structure transitions are , , where J is the rotational quantum number and F is the total rotational quantum number inclusive of nuclear spin (), respectively. The lowest transition () splits into a hyperfine triplet. Using the selection rules, the hyperfine pattern of transition and higher dipole transitions is in the form of a hyperfine sextet. However, one of these components () carries only 0.6% of the rotational transition intensity in the case of . This contribution drops for increasing J. So, from upwards the hyperfine pattern consists of three very closely spaced stronger hyperfine components (, ) together with two widely spaced components; one on the low frequency side and one on the high frequency side relative to the central hyperfine triplet. Each of these outliers carry ~ (J is the upper rotational quantum number of the allowed dipole transition) the intensity of the entire transition. For consecutively higher-J transitions, there are small but significant changes in the relative intensities and positions of each individual hyperfine component.[12]
A typical simple example of the hyperfine structure due to the interactions discussed above is in the rotational transitions of hydrogen cyanide (1H12C14N) in its ground vibrational state. Here, the electric quadrupole interaction is due to the 14N-nucleus, the hyperfine nuclear spin-spin splitting is from the magnetic coupling between nitrogen, 14N (IN = 1), and hydrogen, 1H (IH = 1⁄2), and a hydrogen spin-rotation interaction due to the 1H-nucleus. These contributing interactions to the hyperfine structure in the molecule are listed here in descending order of influence. Sub-doppler techniques have been used to discern the hyperfine structure in HCN rotational transitions.[11]
The dipole selection rules for HCN hyperfine structure transitions are , , where J is the rotational quantum number and F is the total rotational quantum number inclusive of nuclear spin (), respectively. The lowest transition () splits into a hyperfine triplet. Using the selection rules, the hyperfine pattern of transition and higher dipole transitions is in the form of a hyperfine sextet. However, one of these components () carries only 0.6% of the rotational transition intensity in the case of . This contribution drops for increasing J. So, from upwards the hyperfine pattern consists of three very closely spaced stronger hyperfine components (, ) together with two widely spaced components; one on the low frequency side and one on the high frequency side relative to the central hyperfine triplet. Each of these outliers carry ~ (J is the upper rotational quantum number of the allowed dipole transition) the intensity of the entire transition. For consecutively higher-J transitions, there are small but significant changes in the relative intensities and positions of each individual hyperfine component.[12]
Measurements[edit]
Hyperfine interactions can be measured, among other ways, in atomic and molecular spectra and in electron paramagnetic resonance spectra of free radicals and transition-metal ions.
Hyperfine interactions can be measured, among other ways, in atomic and molecular spectra and in electron paramagnetic resonance spectra of free radicals and transition-metal ions.
Applications[edit]
Astrophysics[edit]
As the hyperfine splitting is very small, the transition frequencies are usually not located in the optical, but are in the range of radio- or microwave (also called sub-millimeter) frequencies.
Hyperfine structure gives the 21 cm line observed in H I regions in interstellar medium.
Carl Sagan and Frank Drake considered the hyperfine transition of hydrogen to be a sufficiently universal phenomenon so as to be used as a base unit of time and length on the Pioneer plaque and later Voyager Golden Record.
In submillimeter astronomy, heterodyne receivers are widely used in detecting electromagnetic signals from celestial objects such as star-forming core or young stellar objects. The separations among neighboring components in a hyperfine spectrum of an observed rotational transition are usually small enough to fit within the receiver's IF band. Since the optical depth varies with frequency, strength ratios among the hyperfine components differ from that of their intrinsic (or optically thin) intensities (these are so-called hyperfine anomalies, often observed in the rotational transitions of HCN[12]). Thus, a more accurate determination of the optical depth is possible. From this we can derive the object's physical parameters.[13]
As the hyperfine splitting is very small, the transition frequencies are usually not located in the optical, but are in the range of radio- or microwave (also called sub-millimeter) frequencies.
Hyperfine structure gives the 21 cm line observed in H I regions in interstellar medium.
Carl Sagan and Frank Drake considered the hyperfine transition of hydrogen to be a sufficiently universal phenomenon so as to be used as a base unit of time and length on the Pioneer plaque and later Voyager Golden Record.
In submillimeter astronomy, heterodyne receivers are widely used in detecting electromagnetic signals from celestial objects such as star-forming core or young stellar objects. The separations among neighboring components in a hyperfine spectrum of an observed rotational transition are usually small enough to fit within the receiver's IF band. Since the optical depth varies with frequency, strength ratios among the hyperfine components differ from that of their intrinsic (or optically thin) intensities (these are so-called hyperfine anomalies, often observed in the rotational transitions of HCN[12]). Thus, a more accurate determination of the optical depth is possible. From this we can derive the object's physical parameters.[13]
Nuclear spectroscopy[edit]
In nuclear spectroscopy methods, the nucleus is used to probe the local structure in materials. The methods mainly base on hyperfine interactions with the surrounding atoms and ions. Important methods are nuclear magnetic resonance, Mössbauer spectroscopy, and perturbed angular correlation.
In nuclear spectroscopy methods, the nucleus is used to probe the local structure in materials. The methods mainly base on hyperfine interactions with the surrounding atoms and ions. Important methods are nuclear magnetic resonance, Mössbauer spectroscopy, and perturbed angular correlation.
Nuclear technology[edit]
The atomic vapor laser isotope separation (AVLIS) process uses the hyperfine splitting between optical transitions in uranium-235 and uranium-238 to selectively photo-ionize only the uranium-235 atoms and then separate the ionized particles from the non-ionized ones. Precisely tuned dye lasers are used as the sources of the necessary exact wavelength radiation.
The atomic vapor laser isotope separation (AVLIS) process uses the hyperfine splitting between optical transitions in uranium-235 and uranium-238 to selectively photo-ionize only the uranium-235 atoms and then separate the ionized particles from the non-ionized ones. Precisely tuned dye lasers are used as the sources of the necessary exact wavelength radiation.
Use in defining the SI second and meter[edit]
The hyperfine structure transition can be used to make a microwave notch filter with very high stability, repeatability and Q factor, which can thus be used as a basis for very precise atomic clocks. The term transition frequency denotes the frequency of radiation corresponding to the transition between the two hyperfine levels of the atom, and is equal to f = ΔE/h, where ΔE is difference in energy between the levels and h is the Planck constant. Typically, the transition frequency of a particular isotope of caesium or rubidium atoms is used as a basis for these clocks.
Due to the accuracy of hyperfine structure transition-based atomic clocks, they are now used as the basis for the definition of the second. One second is now defined to be exactly 9192631770cycles of the hyperfine structure transition frequency of caesium-133 atoms.
On October 21, 1983, the 17th CGPM defined the metre as the length of the path travelled by light in a vacuum during a time interval of 1299,792,458 of a second.[14][15]
The hyperfine structure transition can be used to make a microwave notch filter with very high stability, repeatability and Q factor, which can thus be used as a basis for very precise atomic clocks. The term transition frequency denotes the frequency of radiation corresponding to the transition between the two hyperfine levels of the atom, and is equal to f = ΔE/h, where ΔE is difference in energy between the levels and h is the Planck constant. Typically, the transition frequency of a particular isotope of caesium or rubidium atoms is used as a basis for these clocks.
Due to the accuracy of hyperfine structure transition-based atomic clocks, they are now used as the basis for the definition of the second. One second is now defined to be exactly 9192631770cycles of the hyperfine structure transition frequency of caesium-133 atoms.
On October 21, 1983, the 17th CGPM defined the metre as the length of the path travelled by light in a vacuum during a time interval of 1299,792,458 of a second.[14][15]
Precision tests of quantum electrodynamics[edit]
The hyperfine splitting in hydrogen and in muonium have been used to measure the value of the fine structure constant α. Comparison with measurements of α in other physical systems provides a stringent test of QED.
The hyperfine splitting in hydrogen and in muonium have been used to measure the value of the fine structure constant α. Comparison with measurements of α in other physical systems provides a stringent test of QED.
Qubit in ion-trap quantum computing[edit]
The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.[16]
The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.[16]
See also[edit]
https://en.wikipedia.org/wiki/Hyperfine_structure
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion[1][2] while a true scalar does not.
Any scalar product between a pseudovector and an ordinary vector is a pseudoscalar. The prototypical example of a pseudoscalar is the scalar triple product, which can be written as the scalar product between one of the vectors in the triple product and the cross product between the two other vectors, where the latter is a pseudovector. A pseudoscalar, when multiplied by an ordinary vector, becomes a pseudovector (axial vector); a similar construction creates the pseudotensor.
Mathematically, a pseudoscalar is an element of the top exterior power of a vector space, or the top power of a Clifford algebra; see pseudoscalar (Clifford algebra). More generally, it is an element of the canonical bundle of a differentiable manifold.
https://en.wikipedia.org/wiki/Hyperfine_structure
In linear algebra, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion[1][2] while a true scalar does not.
Any scalar product between a pseudovector and an ordinary vector is a pseudoscalar. The prototypical example of a pseudoscalar is the scalar triple product, which can be written as the scalar product between one of the vectors in the triple product and the cross product between the two other vectors, where the latter is a pseudovector. A pseudoscalar, when multiplied by an ordinary vector, becomes a pseudovector (axial vector); a similar construction creates the pseudotensor.
Mathematically, a pseudoscalar is an element of the top exterior power of a vector space, or the top power of a Clifford algebra; see pseudoscalar (Clifford algebra). More generally, it is an element of the canonical bundle of a differentiable manifold.
In physics[edit]
In physics, a pseudoscalar denotes a physical quantity analogous to a scalar. Both are physical quantities which assume a single value which is invariant under proper rotations. However, under the parity transformation, pseudoscalars flip their signs while scalars do not. As reflections through a plane are the combination of a rotation with the parity transformation, pseudoscalars also change signs under reflections.
https://en.wikipedia.org/wiki/Pseudoscalar
In geometry and physics, spinors /spɪnər/ are elements of a complex vector space that can be associated with Euclidean space.[b] Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation.[c] However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms).
It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geometry by Élie Cartan in 1913.[1][d] In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.[e]
Spinors are characterized by the specific way in which they behave under rotations. They change in different ways depending not just on the overall final rotation, but the details of how that rotation was achieved (by a continuous path in the rotation group). There are two topologically distinguishable classes (homotopy classes) of paths through rotations that result in the same overall rotation, as illustrated by the belt trick puzzle. These two inequivalent classes yield spinor transformations of opposite sign. The spin group is the group of all rotations keeping track of the class.[f] It doubly covers the rotation group, since each rotation can be obtained in two inequivalent ways as the endpoint of a path. The space of spinors by definition is equipped with a (complex) linear representation of the spin group, meaning that elements of the spin group act as linear transformations on the space of spinors, in a way that genuinely depends on the homotopy class.[g] In mathematical terms, spinors are described by a double-valued projective representation of the rotation group SO(3).
Although spinors can be defined purely as elements of a representation space of the spin group (or its Lie algebra of infinitesimal rotations), they are typically defined as elements of a vector space that carries a linear representation of the Clifford algebra. The Clifford algebra is an associative algebra that can be constructed from Euclidean space and its inner product in a basis-independent way. Both the spin group and its Lie algebra are embedded inside the Clifford algebra in a natural way, and in applications the Clifford algebra is often the easiest to work with.[h] A Clifford space operates on a spinor space, and the elements of a spinor space are spinors.[3] After choosing an orthonormal basis of Euclidean space, a representation of the Clifford algebra is generated by gamma matrices, matrices that satisfy a set of canonical anti-commutation relations. The spinors are the column vectors on which these matrices act. In three Euclidean dimensions, for instance, the Pauli spin matrices are a set of gamma matrices,[i] and the two-component complex column vectors on which these matrices act are spinors. However, the particular matrix representation of the Clifford algebra, hence what precisely constitutes a "column vector" (or spinor), involves the choice of basis and gamma matrices in an essential way. As a representation of the spin group, this realization of spinors as (complex[j]) column vectors will either be irreducible if the dimension is odd, or it will decompose into a pair of so-called "half-spin" or Weyl representations if the dimension is even.[k]
https://en.wikipedia.org/wiki/Spinor
In topology, a branch of mathematics, the loop space ΩX of a pointed topological space X is the space of (based) loops in X, i.e. continuous pointed maps from the pointed circle S1 to X, equipped with the compact-open topology. Two loops can be multiplied by concatenation. With this operation, the loop space is an A∞-space. That is, the multiplication is homotopy-coherently associative.
The set of path components of ΩX, i.e. the set of based-homotopy equivalence classes of based loops in X, is a group, the fundamental group π1(X).
The iterated loop spaces of X are formed by applying Ω a number of times.
There is an analogous construction for topological spaces without basepoint. The free loop space of a topological space X is the space of maps from the circle S1 to X with the compact-open topology. The free loop space of X is often denoted by .
As a functor, the free loop space construction is right adjoint to cartesian product with the circle, while the loop space construction is right adjoint to the reduced suspension. This adjunction accounts for much of the importance of loop spaces in stable homotopy theory. (A related phenomenon in computer science is currying, where the cartesian product is adjoint to the hom functor.) Informally this is referred to as Eckmann–Hilton duality.
https://en.wikipedia.org/wiki/Loop_space
https://en.wikipedia.org/wiki/Hom_functor
https://en.wikipedia.org/wiki/Suspension_(topology)#Reduced_suspension
In special and general relativity, a light cone is the path that a flash of light, emanating from a single event (localized to a single point in space and a single moment in time) and traveling in all directions, would take through spacetime.
Light cone in 2D space plus a time dimension.https://en.wikipedia.org/wiki/Light_cone
https://en.wikipedia.org/wiki/Hypercone
https://en.wikipedia.org/wiki/Hermann_Minkowski
Plane horizontal
verticle pressuron
preon point particle
JND threshold excission
light cone
not detectable not obs comp
Riddle
https://en.wikipedia.org/wiki/Supersymmetry
https://en.wikipedia.org/wiki/Refractive_index
https://en.wikipedia.org/wiki/Topology
https://en.wikipedia.org/wiki/Symmetry
https://en.wikipedia.org/wiki/Equilateral_Triangle
https://en.wikipedia.org/wiki/Perception_Sensation_Cognition
https://en.wikipedia.org/wiki/Light_cone
https://en.wikipedia.org/wiki/White_dwarf
https://en.wikipedia.org/wiki/Nuclear_fusion
https://en.wikipedia.org/wiki/Nuclear_transmutation
https://en.wikipedia.org/wiki/Hydrogen
https://en.wikipedia.org/wiki/Helium-4
https://en.wikipedia.org/wiki/Helium_dimer
https://en.wikipedia.org/wiki/Helium–neon_laser
https://en.wikipedia.org/wiki/Infrared
https://en.wikipedia.org/wiki/Microwave
https://en.wikipedia.org/wiki/Terahertz_radiation
https://en.wikipedia.org/wiki/Fusor_(astronomy)
https://en.wikipedia.org/wiki/Fusor
https://en.wikipedia.org/wiki/Hydrogen_maser
https://en.wikipedia.org/wiki/Stellar_core
https://en.wikipedia.org/wiki/Isotopes_of_hydrogen
https://en.wikipedia.org/wiki/F-type_main-sequence_star
https://en.wikipedia.org/wiki/Red-giant_branch
https://en.wikipedia.org/wiki/Schönberg–Chandrasekhar_limit
https://en.wikipedia.org/wiki/Tritium
https://en.wikipedia.org/wiki/Neutron_source
https://en.wikipedia.org/wiki/TRAPPIST-1f
https://en.wikipedia.org/wiki/Suspension_(topology)#Reduced_suspension
https://en.wikipedia.org/wiki/Pointed_space#Category_of_pointed_spaces
https://en.wikipedia.org/wiki/Baryon#Baryonic_matter
https://en.wikipedia.org/wiki/Symmetry_breaking
https://en.wikipedia.org/wiki/X_and_Y_bosons
https://en.wikipedia.org/wiki/Mirror
https://en.wikipedia.org/wiki/Preon
https://en.wikipedia.org/wiki/Pressuron
https://en.wikipedia.org/wiki/Vertical_pressure_variation
https://en.wikipedia.org/wiki/Pressure-gradient_force
https://en.wikipedia.org/wiki/Pressure_cooker
https://en.wikipedia.org/wiki/Hydrostatic_equilibrium
https://en.wikipedia.org/wiki/List_of_gravitationally_rounded_objects_of_the_Solar_System
https://en.wikipedia.org/wiki/Galactic_Center
https://en.wikipedia.org/wiki/Barycenter
https://en.wikipedia.org/wiki/Plane_axial_one_dimension
https://en.wikipedia.org/wiki/Two-body_problem
https://en.wikipedia.org/wiki/Point_particle
https://en.wikipedia.org/wiki/Acid–base_reaction
https://en.wikipedia.org/wiki/Metal
https://en.wikipedia.org/wiki/Hydrogen
https://en.wikipedia.org/wiki/Oxygen
https://en.wikipedia.org/wiki/Hydrogenation
https://en.wikipedia.org/wiki/Hantzsch_pyridine_synthesis
https://en.wikipedia.org/wiki/Water_gas
https://en.wikipedia.org/wiki/Hydrothermal_synthesis
https://en.wikipedia.org/wiki/Strecker_amino_acid_synthesis
https://en.wikipedia.org/wiki/Dehydration_reaction
https://en.wikipedia.org/wiki/Kiliani–Fischer_synthesis
https://en.wikipedia.org/wiki/Polyester
https://en.wikipedia.org/wiki/Liquid-crystal_polymer
https://en.wikipedia.org/wiki/Ultimate_tensile_strength
https://en.wikipedia.org/wiki/Yield_(engineering)
https://en.wikipedia.org/wiki/Sensory_threshold
https://en.wikipedia.org/wiki/Threshold
https://en.wikipedia.org/wiki/Absolute_threshold
https://en.wikipedia.org/wiki/Reference_range#cutoff
https://en.wikipedia.org/wiki/Transparency_(data_compression)
https://en.wikipedia.org/wiki/Threshold_energy
https://en.wikipedia.org/wiki/Threshold_voltage
https://en.wikipedia.org/wiki/Comparator_applications
https://en.wikipedia.org/wiki/Threshold_cryptosystem
https://en.wikipedia.org/wiki/Percolation_threshold
https://en.wikipedia.org/wiki/Threshold_graph
https://en.wikipedia.org/wiki/Polygyny_threshold_model
https://en.wikipedia.org/wiki/Threshold_model
https://en.wikipedia.org/wiki/Critical_value
https://en.wikipedia.org/wiki/Displaced_threshold
https://en.wikipedia.org/wiki/Electoral_threshold
https://en.wikipedia.org/wiki/Poverty_thresholds_(United_States_Census_Bureau)
https://en.wikipedia.org/wiki/Poverty_in_the_United_States#Poverty_income_guidelines
https://en.wikipedia.org/wiki/Prison
https://en.wikipedia.org/wiki/State_(polity)
https://en.wikipedia.org/wiki/Hydrogen_bondhttps://en.wikipedia.org/wiki/Carcerandhttps://en.wikipedia.org/wiki/Prisonhttps://en.wikipedia.org/wiki/Oligomer
https://en.wikipedia.org/wiki/Grigory_Mairanovsky
https://en.wikipedia.org/wiki/Antoine_Lavoisier
https://en.wikipedia.org/wiki/Divine_right_of_kings
In stereochemistry, a torsion angle is defined as a particular example of a dihedral angle, describing the geometric relation of two parts of a molecule joined by a chemical bond.[5][6] Every set of three not-colinear atoms of a molecule defines a half-plane. As explained above, when two such half-planes intersect (i.e., a set of four consecutively-bonded atoms), the angle between them is a dihedral angle. Dihedral angles are used to specify the molecular conformation.[7] Stereochemical arrangements corresponding to angles between 0° and ±90° are called syn (s), those corresponding to angles between ±90° and 180° anti (a). Similarly, arrangements corresponding to angles between 30° and 150° or between −30° and −150° are called clinal (c) and those between 0° and ±30° or ±150° and 180° are called periplanar (p).
The two types of terms can be combined so as to define four ranges of angle; 0° to ±30° synperiplanar (sp); 30° to 90° and −30° to −90° synclinal (sc); 90° to 150° and −90° to −150° anticlinal (ac); ±150° to 180° antiperiplanar (ap). The synperiplanar conformation is also known as the syn- or cis-conformation; antiperiplanar as anti or trans; and synclinal as gauche or skew.
For example, with n-butane two planes can be specified in terms of the two central carbon atoms and either of the methyl carbon atoms. The syn-conformation shown above, with a dihedral angle of 60° is less stable than the anti-conformation with a dihedral angle of 180°.
For macromolecular usage the symbols T, C, G+, G−, A+ and A− are recommended (ap, sp, +sc, −sc, +ac and −ac respectively).
https://en.wikipedia.org/wiki/Dihedral_angle#In_stereochemistry
Saturday, September 18, 2021
09-18-2021-1248 - Rotation as possible energy source
Rotation as possible energy source [edit]
Because of the enormous amount of energy needed to launch a relativistic jet, some jets are possibly powered by spinning black holes. However, the frequency of high-energy astrophysical sources with jets suggest combinations of different mechanisms indirectly identified with the energy within the associated accretion disk and X-ray emissions from the generating source. Two early theories have been used to explain how energy can be transferred from a black hole into an astrophysical jet:
Blandford–Znajek process.[14] This theory explains the extraction of energy from magnetic fields around an accretion disk, which are dragged and twisted by the spin of the black hole. Relativistic material is then feasibly launched by the tightening of the field lines.
Penrose mechanism.[15] Here energy is extracted from a rotating black hole by frame dragging, which was later theoretically proven to be able to extract relativistic particle energy and momentum,[16] and subsequently shown to be a possible mechanism for jet formation.[17] This effect may also be explained in terms of gravitoelectromagnetism.
https://en.wikipedia.org/wiki/Astrophysical_jet#Relativistic_jet
In physics, a pseudoscalar denotes a physical quantity analogous to a scalar. Both are physical quantities which assume a single value which is invariant under proper rotations. However, under the parity transformation, pseudoscalars flip their signs while scalars do not. As reflections through a plane are the combination of a rotation with the parity transformation, pseudoscalars also change signs under reflections.
https://en.wikipedia.org/wiki/Pseudoscalar
In geometry and physics, spinors /spɪnər/ are elements of a complex vector space that can be associated with Euclidean space.[b] Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation.[c] However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms).
It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geometry by Élie Cartan in 1913.[1][d] In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.[e]
Spinors are characterized by the specific way in which they behave under rotations. They change in different ways depending not just on the overall final rotation, but the details of how that rotation was achieved (by a continuous path in the rotation group). There are two topologically distinguishable classes (homotopy classes) of paths through rotations that result in the same overall rotation, as illustrated by the belt trick puzzle. These two inequivalent classes yield spinor transformations of opposite sign. The spin group is the group of all rotations keeping track of the class.[f] It doubly covers the rotation group, since each rotation can be obtained in two inequivalent ways as the endpoint of a path. The space of spinors by definition is equipped with a (complex) linear representation of the spin group, meaning that elements of the spin group act as linear transformations on the space of spinors, in a way that genuinely depends on the homotopy class.[g] In mathematical terms, spinors are described by a double-valued projective representation of the rotation group SO(3).
Although spinors can be defined purely as elements of a representation space of the spin group (or its Lie algebra of infinitesimal rotations), they are typically defined as elements of a vector space that carries a linear representation of the Clifford algebra. The Clifford algebra is an associative algebra that can be constructed from Euclidean space and its inner product in a basis-independent way. Both the spin group and its Lie algebra are embedded inside the Clifford algebra in a natural way, and in applications the Clifford algebra is often the easiest to work with.[h] A Clifford space operates on a spinor space, and the elements of a spinor space are spinors.[3] After choosing an orthonormal basis of Euclidean space, a representation of the Clifford algebra is generated by gamma matrices, matrices that satisfy a set of canonical anti-commutation relations. The spinors are the column vectors on which these matrices act. In three Euclidean dimensions, for instance, the Pauli spin matrices are a set of gamma matrices,[i] and the two-component complex column vectors on which these matrices act are spinors. However, the particular matrix representation of the Clifford algebra, hence what precisely constitutes a "column vector" (or spinor), involves the choice of basis and gamma matrices in an essential way. As a representation of the spin group, this realization of spinors as (complex[j]) column vectors will either be irreducible if the dimension is odd, or it will decompose into a pair of so-called "half-spin" or Weyl representations if the dimension is even.[k]
https://en.wikipedia.org/wiki/Spinor
In topology, a branch of mathematics, the loop space ΩX of a pointed topological space X is the space of (based) loops in X, i.e. continuous pointed maps from the pointed circle S1 to X, equipped with the compact-open topology. Two loops can be multiplied by concatenation. With this operation, the loop space is an A∞-space. That is, the multiplication is homotopy-coherently associative.
The set of path components of ΩX, i.e. the set of based-homotopy equivalence classes of based loops in X, is a group, the fundamental group π1(X).
The iterated loop spaces of X are formed by applying Ω a number of times.
There is an analogous construction for topological spaces without basepoint. The free loop space of a topological space X is the space of maps from the circle S1 to X with the compact-open topology. The free loop space of X is often denoted by .
As a functor, the free loop space construction is right adjoint to cartesian product with the circle, while the loop space construction is right adjoint to the reduced suspension. This adjunction accounts for much of the importance of loop spaces in stable homotopy theory. (A related phenomenon in computer science is currying, where the cartesian product is adjoint to the hom functor.) Informally this is referred to as Eckmann–Hilton duality.
https://en.wikipedia.org/wiki/Loop_space
https://en.wikipedia.org/wiki/Hom_functor
https://en.wikipedia.org/wiki/Suspension_(topology)#Reduced_suspension
In special and general relativity, a light cone is the path that a flash of light, emanating from a single event (localized to a single point in space and a single moment in time) and traveling in all directions, would take through spacetime.
https://en.wikipedia.org/wiki/Light_cone
https://en.wikipedia.org/wiki/Hypercone
https://en.wikipedia.org/wiki/Hermann_Minkowski
Plane horizontal
verticle pressuron
preon point particle
JND threshold excission
light cone
not detectable not obs comp
Riddle
https://en.wikipedia.org/wiki/Supersymmetry
https://en.wikipedia.org/wiki/Refractive_index
https://en.wikipedia.org/wiki/Topology
https://en.wikipedia.org/wiki/Symmetry
https://en.wikipedia.org/wiki/Equilateral_Triangle
https://en.wikipedia.org/wiki/Perception_Sensation_Cognition
https://en.wikipedia.org/wiki/Light_cone
https://en.wikipedia.org/wiki/White_dwarf
https://en.wikipedia.org/wiki/Nuclear_fusion
https://en.wikipedia.org/wiki/Nuclear_transmutation
https://en.wikipedia.org/wiki/Hydrogen
https://en.wikipedia.org/wiki/Helium-4
https://en.wikipedia.org/wiki/Helium_dimer
https://en.wikipedia.org/wiki/Helium–neon_laser
https://en.wikipedia.org/wiki/Infrared
https://en.wikipedia.org/wiki/Microwave
https://en.wikipedia.org/wiki/Terahertz_radiation
https://en.wikipedia.org/wiki/Fusor_(astronomy)
https://en.wikipedia.org/wiki/Fusor
https://en.wikipedia.org/wiki/Hydrogen_maser
https://en.wikipedia.org/wiki/Stellar_core
https://en.wikipedia.org/wiki/Isotopes_of_hydrogen
https://en.wikipedia.org/wiki/F-type_main-sequence_star
https://en.wikipedia.org/wiki/Red-giant_branch
https://en.wikipedia.org/wiki/Schönberg–Chandrasekhar_limit
https://en.wikipedia.org/wiki/Tritium
https://en.wikipedia.org/wiki/Neutron_source
https://en.wikipedia.org/wiki/TRAPPIST-1f
https://en.wikipedia.org/wiki/Suspension_(topology)#Reduced_suspension
https://en.wikipedia.org/wiki/Pointed_space#Category_of_pointed_spaces
https://en.wikipedia.org/wiki/Baryon#Baryonic_matter
https://en.wikipedia.org/wiki/Symmetry_breaking
https://en.wikipedia.org/wiki/X_and_Y_bosons
https://en.wikipedia.org/wiki/Mirror
https://en.wikipedia.org/wiki/Preon
https://en.wikipedia.org/wiki/Pressuron
https://en.wikipedia.org/wiki/Vertical_pressure_variation
https://en.wikipedia.org/wiki/Pressure-gradient_force
https://en.wikipedia.org/wiki/Pressure_cooker
https://en.wikipedia.org/wiki/Hydrostatic_equilibrium
https://en.wikipedia.org/wiki/List_of_gravitationally_rounded_objects_of_the_Solar_System
https://en.wikipedia.org/wiki/Galactic_Center
https://en.wikipedia.org/wiki/Barycenter
https://en.wikipedia.org/wiki/Plane_axial_one_dimension
https://en.wikipedia.org/wiki/Two-body_problem
https://en.wikipedia.org/wiki/Point_particle
https://en.wikipedia.org/wiki/Acid–base_reaction
https://en.wikipedia.org/wiki/Metal
https://en.wikipedia.org/wiki/Hydrogen
https://en.wikipedia.org/wiki/Oxygen
https://en.wikipedia.org/wiki/Hydrogenation
https://en.wikipedia.org/wiki/Hantzsch_pyridine_synthesis
https://en.wikipedia.org/wiki/Water_gas
https://en.wikipedia.org/wiki/Hydrothermal_synthesis
https://en.wikipedia.org/wiki/Strecker_amino_acid_synthesis
https://en.wikipedia.org/wiki/Dehydration_reaction
https://en.wikipedia.org/wiki/Kiliani–Fischer_synthesis
https://en.wikipedia.org/wiki/Polyester
https://en.wikipedia.org/wiki/Liquid-crystal_polymer
https://en.wikipedia.org/wiki/Ultimate_tensile_strength
https://en.wikipedia.org/wiki/Yield_(engineering)
https://en.wikipedia.org/wiki/Sensory_threshold
https://en.wikipedia.org/wiki/Threshold
https://en.wikipedia.org/wiki/Absolute_threshold
https://en.wikipedia.org/wiki/Reference_range#cutoff
https://en.wikipedia.org/wiki/Transparency_(data_compression)
https://en.wikipedia.org/wiki/Threshold_energy
https://en.wikipedia.org/wiki/Threshold_voltage
https://en.wikipedia.org/wiki/Comparator_applications
https://en.wikipedia.org/wiki/Threshold_cryptosystem
https://en.wikipedia.org/wiki/Percolation_threshold
https://en.wikipedia.org/wiki/Threshold_graph
https://en.wikipedia.org/wiki/Polygyny_threshold_model
https://en.wikipedia.org/wiki/Threshold_model
https://en.wikipedia.org/wiki/Critical_value
https://en.wikipedia.org/wiki/Displaced_threshold
https://en.wikipedia.org/wiki/Electoral_threshold
https://en.wikipedia.org/wiki/Poverty_thresholds_(United_States_Census_Bureau)
https://en.wikipedia.org/wiki/Poverty_in_the_United_States#Poverty_income_guidelines
https://en.wikipedia.org/wiki/Prison
https://en.wikipedia.org/wiki/State_(polity)
https://en.wikipedia.org/wiki/Divine_right_of_kings
In stereochemistry, a torsion angle is defined as a particular example of a dihedral angle, describing the geometric relation of two parts of a molecule joined by a chemical bond.[5][6] Every set of three not-colinear atoms of a molecule defines a half-plane. As explained above, when two such half-planes intersect (i.e., a set of four consecutively-bonded atoms), the angle between them is a dihedral angle. Dihedral angles are used to specify the molecular conformation.[7] Stereochemical arrangements corresponding to angles between 0° and ±90° are called syn (s), those corresponding to angles between ±90° and 180° anti (a). Similarly, arrangements corresponding to angles between 30° and 150° or between −30° and −150° are called clinal (c) and those between 0° and ±30° or ±150° and 180° are called periplanar (p).
The two types of terms can be combined so as to define four ranges of angle; 0° to ±30° synperiplanar (sp); 30° to 90° and −30° to −90° synclinal (sc); 90° to 150° and −90° to −150° anticlinal (ac); ±150° to 180° antiperiplanar (ap). The synperiplanar conformation is also known as the syn- or cis-conformation; antiperiplanar as anti or trans; and synclinal as gauche or skew.
For example, with n-butane two planes can be specified in terms of the two central carbon atoms and either of the methyl carbon atoms. The syn-conformation shown above, with a dihedral angle of 60° is less stable than the anti-conformation with a dihedral angle of 180°.
For macromolecular usage the symbols T, C, G+, G−, A+ and A− are recommended (ap, sp, +sc, −sc, +ac and −ac respectively).
https://en.wikipedia.org/wiki/Dihedral_angle#In_stereochemistry
Saturday, September 18, 2021
09-18-2021-1248 - Rotation as possible energy source
Rotation as possible energy source [edit]
Because of the enormous amount of energy needed to launch a relativistic jet, some jets are possibly powered by spinning black holes. However, the frequency of high-energy astrophysical sources with jets suggest combinations of different mechanisms indirectly identified with the energy within the associated accretion disk and X-ray emissions from the generating source. Two early theories have been used to explain how energy can be transferred from a black hole into an astrophysical jet:
Blandford–Znajek process.[14] This theory explains the extraction of energy from magnetic fields around an accretion disk, which are dragged and twisted by the spin of the black hole. Relativistic material is then feasibly launched by the tightening of the field lines.
Penrose mechanism.[15] Here energy is extracted from a rotating black hole by frame dragging, which was later theoretically proven to be able to extract relativistic particle energy and momentum,[16] and subsequently shown to be a possible mechanism for jet formation.[17] This effect may also be explained in terms of gravitoelectromagnetism.
https://en.wikipedia.org/wiki/Astrophysical_jet#Relativistic_jet
Saturday, September 18, 2021
09-18-2021-0909 - In a single-sided version, the magnetic field can create repulsion forces that push the conductor away from the stator, levitating it and carrying it along the direction of the moving magnetic field.
The history of linear electric motors can be traced back at least as far as the 1840s to the work of Charles Wheatstone at King's College in London,[3] but Wheatstone's model was too inefficient to be practical. A feasible linear induction motor is described in US patent 782312 (1905; inventor Alfred Zehden of Frankfurt-am-Main), and is for driving trains or lifts. German engineer Hermann Kemper built a working model in 1935.[4] In the late 1940s, professor Eric Laithwaite of Imperial College in London developed the first full-size working model.
In a single-sided version, the magnetic field can create repulsion forces that push the conductor away from the stator, levitating it and carrying it along the direction of the moving magnetic field. Laithwaite called the later versions a magnetic river. These versions of the linear induction motor use a principle called transverse flux where two opposite poles are placed side by side. This permits very long poles to be used, and thus permits high speed and efficiency.[5]
https://en.wikipedia.org/wiki/Linear_induction_motor
The history of linear electric motors can be traced back at least as far as the 1840s to the work of Charles Wheatstone at King's College in London,[3] but Wheatstone's model was too inefficient to be practical. A feasible linear induction motor is described in US patent 782312 (1905; inventor Alfred Zehden of Frankfurt-am-Main), and is for driving trains or lifts. German engineer Hermann Kemper built a working model in 1935.[4] In the late 1940s, professor Eric Laithwaite of Imperial College in London developed the first full-size working model.
In a single-sided version, the magnetic field can create repulsion forces that push the conductor away from the stator, levitating it and carrying it along the direction of the moving magnetic field. Laithwaite called the later versions a magnetic river. These versions of the linear induction motor use a principle called transverse flux where two opposite poles are placed side by side. This permits very long poles to be used, and thus permits high speed and efficiency.[5]
https://en.wikipedia.org/wiki/Linear_induction_motor
Qubit in ion-trap quantum computing[edit]
The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.[16]
The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.[16]
See also[edit]
https://en.wikipedia.org/wiki/Hyperfine_structure
https://en.wikipedia.org/wiki/Hyperfine_structure
Saturday, September 18, 2021
09-18-2021-1708 - alternating current oscillating particle or wave perturbed γ-γ angular correlation heterodyne gyroscope
Saturday, September 18, 2021
09-18-2021-1315 - Absolute, gauge and differential pressures — zero reference
Saturday, September 18, 2021
09-18-2021-0944 - Maxwell stress tensor Poynting vector
Sunday, September 19, 2021
09-19-2021-0918 - Oxy-fuel welding (commonly called oxyacetylene welding, oxy welding, or gas welding in the United States) and oxy-fuel cutting
https://en.wikipedia.org/wiki/Henry_Grey,_1st_Duke_of_Kent 1702
https://en.wikipedia.org/wiki/Henry_Cavendish 1731
https://en.wikipedia.org/wiki/Torbern_Bergman 1735
https://en.wikipedia.org/wiki/Antoine_Lavoisier 1743
https://en.wikipedia.org/wiki/Thomas_Charles_Hope 1766
https://en.wikipedia.org/wiki/Hydrogen_fuel
https://en.wikipedia.org/wiki/Pierre-Simon_Laplace - French 1749
https://en.wikipedia.org/wiki/Alessandro_Volta - Italy 1745
https://en.wikipedia.org/wiki/William_Herschel - German 1738
https://en.wikipedia.org/wiki/Isaac_Newton 1643
https://en.wikipedia.org/wiki/Pendulum
https://en.wikipedia.org/wiki/Harmonic_oscillator
https://en.wikipedia.org/wiki/Christiaan_Huygens 1629
https://en.wikipedia.org/wiki/Hooke%27s_law
https://en.wikipedia.org/wiki/Robert_Hooke 1635
A point particle (ideal particle[1] or point-like particle, often spelled pointlike particle) is an idealization of particles heavily used in physics.[2] Its defining feature is that it lacks spatial extension; being dimensionless, it does not take up space.[3] A point particle is an appropriate representation of any object whenever its size, shape, and structure are irrelevant in a given context. For example, from far enough away, any finite-size object will look and behave as a point-like object. A point particle can also be referred in the case of a moving body in terms of physics.
In the theory of gravity, physicists often discuss a point mass, meaning a point particle with a nonzero mass and no other properties or structure. Likewise, in electromagnetism, physicists discuss a point charge, a point particle with a nonzero charge.[4]
Sometimes, due to specific combinations of properties, extended objects behave as point-like even in their immediate vicinity. For example, spherical objects interacting in 3-dimensional space whose interactions are described by the inverse square law behave in such a way as if all their matter were concentrated in their centers of mass.[citation needed] In Newtonian gravitation and classical electromagnetism, for example, the respective fields outside a spherical object are identical to those of a point particle of equal charge/mass located at the center of the sphere.[5][6]
In quantum mechanics, the concept of a point particle is complicated by the Heisenberg uncertainty principle, because even an elementary particle, with no internal structure, occupies a nonzero volume. For example, the atomic orbit of an electron in the hydrogen atom occupies a volume of ~10−30 m3. There is nevertheless a distinction between elementary particles such as electronsor quarks, which have no known internal structure, versus composite particles such as protons, which do have internal structure: A proton is made of three quarks.
Elementary particles are sometimes called "point particles", but this is in a different sense than discussed above.
https://en.wikipedia.org/wiki/Henry_Grey,_1st_Duke_of_Kent 1702
https://en.wikipedia.org/wiki/Henry_Cavendish 1731
https://en.wikipedia.org/wiki/Torbern_Bergman 1735
https://en.wikipedia.org/wiki/Antoine_Lavoisier 1743
https://en.wikipedia.org/wiki/Thomas_Charles_Hope 1766
https://en.wikipedia.org/wiki/Hydrogen_fuel
https://en.wikipedia.org/wiki/Pierre-Simon_Laplace - French 1749
https://en.wikipedia.org/wiki/Alessandro_Volta - Italy 1745
https://en.wikipedia.org/wiki/William_Herschel - German 1738
https://en.wikipedia.org/wiki/Isaac_Newton 1643
https://en.wikipedia.org/wiki/Pendulum
https://en.wikipedia.org/wiki/Harmonic_oscillator
https://en.wikipedia.org/wiki/Christiaan_Huygens 1629
https://en.wikipedia.org/wiki/Hooke%27s_law
https://en.wikipedia.org/wiki/Robert_Hooke 1635
A point particle (ideal particle[1] or point-like particle, often spelled pointlike particle) is an idealization of particles heavily used in physics.[2] Its defining feature is that it lacks spatial extension; being dimensionless, it does not take up space.[3] A point particle is an appropriate representation of any object whenever its size, shape, and structure are irrelevant in a given context. For example, from far enough away, any finite-size object will look and behave as a point-like object. A point particle can also be referred in the case of a moving body in terms of physics.
In the theory of gravity, physicists often discuss a point mass, meaning a point particle with a nonzero mass and no other properties or structure. Likewise, in electromagnetism, physicists discuss a point charge, a point particle with a nonzero charge.[4]
Sometimes, due to specific combinations of properties, extended objects behave as point-like even in their immediate vicinity. For example, spherical objects interacting in 3-dimensional space whose interactions are described by the inverse square law behave in such a way as if all their matter were concentrated in their centers of mass.[citation needed] In Newtonian gravitation and classical electromagnetism, for example, the respective fields outside a spherical object are identical to those of a point particle of equal charge/mass located at the center of the sphere.[5][6]
In quantum mechanics, the concept of a point particle is complicated by the Heisenberg uncertainty principle, because even an elementary particle, with no internal structure, occupies a nonzero volume. For example, the atomic orbit of an electron in the hydrogen atom occupies a volume of ~10−30 m3. There is nevertheless a distinction between elementary particles such as electronsor quarks, which have no known internal structure, versus composite particles such as protons, which do have internal structure: A proton is made of three quarks.
Elementary particles are sometimes called "point particles", but this is in a different sense than discussed above.
Contents
Property concentrated at a single point[edit]
When a point particle has an additive property, such as mass or charge, concentrated at a single point in space, this can be represented by a Dirac delta function.
When a point particle has an additive property, such as mass or charge, concentrated at a single point in space, this can be represented by a Dirac delta function.
Physical point mass[edit]
Point mass (pointlike mass) is the concept, for example in classical physics, of a physical object (typically matter) that has nonzero mass, and yet explicitly and specifically is (or is being thought of or modeled as) infinitesimal (infinitely small) in its volume or linear dimensions.
Point mass (pointlike mass) is the concept, for example in classical physics, of a physical object (typically matter) that has nonzero mass, and yet explicitly and specifically is (or is being thought of or modeled as) infinitesimal (infinitely small) in its volume or linear dimensions.
Application[edit]
A common use for point mass lies in the analysis of the gravitational fields. When analyzing the gravitational forces in a system, it becomes impossible to account for every unit of massindividually. However, a spherically symmetric body affects external objects gravitationally as if all of its mass were concentrated at its center.
A common use for point mass lies in the analysis of the gravitational fields. When analyzing the gravitational forces in a system, it becomes impossible to account for every unit of massindividually. However, a spherically symmetric body affects external objects gravitationally as if all of its mass were concentrated at its center.
Probability point mass[edit]
A point mass in probability and statistics does not refer to mass in the sense of physics, but rather refers to a finite nonzero probability that is concentrated at a point in the probability mass distribution, where there is a discontinuous segment in a probability density function. To calculate such a point mass, an integration is carried out over the entire range of the random variable, on the probability density of the continuous part. After equating this integral to 1, the point mass can be found by further calculation.
A point mass in probability and statistics does not refer to mass in the sense of physics, but rather refers to a finite nonzero probability that is concentrated at a point in the probability mass distribution, where there is a discontinuous segment in a probability density function. To calculate such a point mass, an integration is carried out over the entire range of the random variable, on the probability density of the continuous part. After equating this integral to 1, the point mass can be found by further calculation.
Point charge[edit]
A point charge is an idealized model of a particle which has an electric charge. A point charge is an electric charge at a mathematical point with no dimensions.
The fundamental equation of electrostatics is Coulomb's law, which describes the electric force between two point charges. The electric field associated with a classical point charge increases to infinity as the distance from the point charge decreases towards zero making energy (thus mass) of point charge infinite.
Earnshaw's theorem states that a collection of point charges cannot be maintained in an equilibrium configuration solely by the electrostatic interaction of the charges.
A point charge is an idealized model of a particle which has an electric charge. A point charge is an electric charge at a mathematical point with no dimensions.
The fundamental equation of electrostatics is Coulomb's law, which describes the electric force between two point charges. The electric field associated with a classical point charge increases to infinity as the distance from the point charge decreases towards zero making energy (thus mass) of point charge infinite.
Earnshaw's theorem states that a collection of point charges cannot be maintained in an equilibrium configuration solely by the electrostatic interaction of the charges.
In quantum mechanics[edit]
In quantum mechanics, there is a distinction between an elementary particle (also called "point particle") and a composite particle. An elementary particle, such as an electron, quark, or photon, is a particle with no known internal structure. Whereas a composite particle, such as a proton or neutron, has an internal structure (see figure). However, neither elementary nor composite particles are spatially localized, because of the Heisenberg uncertainty principle. The particle wavepacketalways occupies a nonzero volume. For example, see atomic orbital: The electron is an elementary particle, but its quantum states form three-dimensional patterns.
Nevertheless, there is good reason that an elementary particle is often called a point particle. Even if an elementary particle has a delocalized wavepacket, the wavepacket can be represented as a quantum superposition of quantum states wherein the particle is exactly localized. Moreover, the interactions of the particle can be represented as a superposition of interactions of individual states which are localized. This is not true for a composite particle, which can never be represented as a superposition of exactly-localized quantum states. It is in this sense that physicists can discuss the intrinsic "size" of a particle: The size of its internal structure, not the size of its wavepacket. The "size" of an elementary particle, in this sense, is exactly zero.
For example, for the electron, experimental evidence shows that the size of an electron is less than 10−18 m.[7] This is consistent with the expected value of exactly zero. (This should not be confused with the classical electron radius, which, despite the name, is unrelated to the actual size of an electron.)
In quantum mechanics, there is a distinction between an elementary particle (also called "point particle") and a composite particle. An elementary particle, such as an electron, quark, or photon, is a particle with no known internal structure. Whereas a composite particle, such as a proton or neutron, has an internal structure (see figure). However, neither elementary nor composite particles are spatially localized, because of the Heisenberg uncertainty principle. The particle wavepacketalways occupies a nonzero volume. For example, see atomic orbital: The electron is an elementary particle, but its quantum states form three-dimensional patterns.
Nevertheless, there is good reason that an elementary particle is often called a point particle. Even if an elementary particle has a delocalized wavepacket, the wavepacket can be represented as a quantum superposition of quantum states wherein the particle is exactly localized. Moreover, the interactions of the particle can be represented as a superposition of interactions of individual states which are localized. This is not true for a composite particle, which can never be represented as a superposition of exactly-localized quantum states. It is in this sense that physicists can discuss the intrinsic "size" of a particle: The size of its internal structure, not the size of its wavepacket. The "size" of an elementary particle, in this sense, is exactly zero.
For example, for the electron, experimental evidence shows that the size of an electron is less than 10−18 m.[7] This is consistent with the expected value of exactly zero. (This should not be confused with the classical electron radius, which, despite the name, is unrelated to the actual size of an electron.)
See also[edit]
- Test particle
- Elementary particle
- Brane
- Charge (physics) (general concept, not limited to electric charge)
- Standard Model of particle physics
- Wave–particle duality
- Test particle
- Elementary particle
- Brane
- Charge (physics) (general concept, not limited to electric charge)
- Standard Model of particle physics
- Wave–particle duality
Notes and references
https://en.wikipedia.org/wiki/Point_particle
https://en.wikipedia.org/wiki/Two-body_problem
https://en.wikipedia.org/wiki/Warped_plane
https://en.wikipedia.org/wiki/N-body_problem
https://en.wikipedia.org/wiki/Mass_ratio
https://en.wikipedia.org/wiki/Mass_ratio
https://en.wikipedia.org/wiki/Escape_velocity
https://en.wikipedia.org/wiki/Vis-viva_equation
https://en.wikipedia.org/wiki/Perturbation_(astronomy)
https://en.wikipedia.org/wiki/Mass_ratio
https://en.wikipedia.org/wiki/Lyapunov_stability
https://en.wikipedia.org/wiki/Propellant_mass_fraction
https://en.wikipedia.org/wiki/Oberth_effect
https://en.wikipedia.org/wiki/Category:Astrodynamics
https://en.wikipedia.org/wiki/Propellant
https://en.wikipedia.org/wiki/Line_segment
https://en.wikipedia.org/wiki/String
https://en.wikipedia.org/wiki/Chord_(geometry)
https://en.wikipedia.org/wiki/Loop
https://en.wikipedia.org/wiki/Spring
https://en.wikipedia.org/wiki/Spiral
https://en.wikipedia.org/wiki/Angular_acceleration
https://en.wikipedia.org/wiki/Period
https://en.wikipedia.org/wiki/Pendulum
https://en.wikipedia.org/wiki/Linear_energy_transfer
https://en.wikipedia.org/wiki/Longest_path_problem
https://en.wikipedia.org/wiki/Linear_motor
https://en.wikipedia.org/wiki/Bipartite_graph
https://en.wikipedia.org/wiki/Eulerian_path
https://en.wikipedia.org/wiki/Phonograph
https://en.wikipedia.org/wiki/Linear_induction_motor
https://en.wikipedia.org/wiki/Electrostatics
https://en.wikipedia.org/wiki/Point_particle
https://en.wikipedia.org/wiki/Two-body_problem
https://en.wikipedia.org/wiki/Warped_plane
https://en.wikipedia.org/wiki/N-body_problem
https://en.wikipedia.org/wiki/Mass_ratio
https://en.wikipedia.org/wiki/Mass_ratio
https://en.wikipedia.org/wiki/Escape_velocity
https://en.wikipedia.org/wiki/Vis-viva_equation
https://en.wikipedia.org/wiki/Perturbation_(astronomy)
https://en.wikipedia.org/wiki/Mass_ratio
https://en.wikipedia.org/wiki/Lyapunov_stability
https://en.wikipedia.org/wiki/Propellant_mass_fraction
https://en.wikipedia.org/wiki/Oberth_effect
https://en.wikipedia.org/wiki/Category:Astrodynamics
https://en.wikipedia.org/wiki/Propellant
https://en.wikipedia.org/wiki/Line_segment
https://en.wikipedia.org/wiki/String
https://en.wikipedia.org/wiki/Chord_(geometry)
https://en.wikipedia.org/wiki/Loop
https://en.wikipedia.org/wiki/Spring
https://en.wikipedia.org/wiki/Spiral
https://en.wikipedia.org/wiki/Angular_acceleration
https://en.wikipedia.org/wiki/Period
https://en.wikipedia.org/wiki/Pendulum
https://en.wikipedia.org/wiki/Linear_energy_transfer
https://en.wikipedia.org/wiki/Longest_path_problem
https://en.wikipedia.org/wiki/Linear_motor
https://en.wikipedia.org/wiki/Bipartite_graph
https://en.wikipedia.org/wiki/Eulerian_path
https://en.wikipedia.org/wiki/Phonograph
https://en.wikipedia.org/wiki/Linear_induction_motor
https://en.wikipedia.org/wiki/Electrostatics





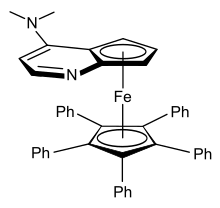
![Scheme 2. [6]paracyclophanes](https://upload.wikimedia.org/wikipedia/commons/thumb/d/d9/-6-cyclophanes.png/300px--6-cyclophanes.png)

![Scheme 3. [6]paracyclophane synthesis](https://upload.wikimedia.org/wikipedia/commons/thumb/3/31/-6-cyclophaneSynthesis.png/500px--6-cyclophaneSynthesis.png)
![Scheme 4. [14][14]metaparacyclophane](https://upload.wikimedia.org/wikipedia/commons/thumb/9/93/Metaparacyclophane.png/600px-Metaparacyclophane.png)