Nikiya Anton Bettey 2021: 09/18/21

Saturday, September 18, 2021

09-18-2021-1715 - 3383/4-5,6

09-18-2021-1714 - Differential (mathematics)

In mathematics, differential refers to infinitesimal differences or to the derivatives of functions.^[1] The term is used in various branches of mathematics such as calculus, differential geometry, algebraic geometry and algebraic topology.

Basic notions[edit]

In calculus, the differential represents a change in the linearization of a function.
- The total differential is its generalization for functions of multiple variables.
In traditional approaches to calculus, the differentials (e.g. dx, dy, dt, etc.) are interpreted as infinitesimals. There are several methods of defining infinitesimals rigorously, but it is sufficient to say that an infinitesimal number is smaller in absolute value than any positive real number, just as an infinitely large number is larger than any real number.
The differential is another name for the Jacobian matrix of partial derivatives of a function from Rⁿ to R^m (especially when this matrix is viewed as a linear map).
More generally, the differential or pushforward refers to the derivative of a map between smooth manifolds and the pushforward operations it defines. The differential is also used to define the dual concept of pullback.
Stochastic calculus provides a notion of stochastic differential and an associated calculus for stochastic processes.
The integrator in a Stieltjes integral is represented as the differential of a function. Formally, the differential appearing under the integral behaves exactly as a differential: thus, the integration by substitution and integration by parts formulae for Stieltjes integral correspond, respectively, to the chain rule and product rule for the differential.

Differential geometry[edit]

The notion of a differential motivates several concepts in differential geometry (and differential topology).

The differential (Pushforward) of a map between manifolds.
Differential forms provide a framework which accommodates multiplication and differentiation of differentials.
The exterior derivative is a notion of differentiation of differential forms which generalizes the differential of a function (which is a differential 1-form).
Pullback is, in particular, a geometric name for the chain rule for composing a map between manifolds with a differential form on the target manifold.
Covariant derivatives or differentials provide a general notion for differentiating of vector fields and tensor fields on a manifold, or, more generally, sections of a vector bundle: see Connection (vector bundle). This ultimately leads to the general concept of a connection.

Algebraic geometry[edit]

Differentials are also important in algebraic geometry, and there are several important notions.

Abelian differentials usually mean differential one-forms on an algebraic curve or Riemann surface.
Quadratic differentials (which behave like "squares" of abelian differentials) are also important in the theory of Riemann surfaces.
Kähler differentials provide a general notion of differential in algebraic geometry.

Other meanings[edit]

The term differential has also been adopted in homological algebra and algebraic topology, because of the role the exterior derivative plays in de Rham cohomology: in a cochain complex $(C_{\bullet },d_{\bullet })$ , the maps (or coboundary operators) d_i are often called differentials. Dually, the boundary operators in a chain complex are sometimes called codifferentials.

The properties of the differential also motivate the algebraic notions of a derivation and a differential algebra.

References[edit]

^ "differential - Definition of differential in US English by Oxford Dictionaries". Oxford Dictionaries - English. Retrieved 13 April 2018.

External links[edit]

Weisstein, Eric W. "Differentials". MathWorld.

https://en.wikipedia.org/wiki/Differential_(mathematics)

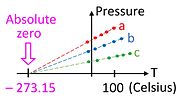
09-18-2021-1712 - Pressure Measurement (Absolute, gauge and differential pressures — zero reference)

Pressure measurement is the analysis of an applied force by a fluid (liquid or gas) on a surface. Pressure is typically measured in units of force per unit of surface area. Many techniques have been developed for the measurement of pressure and vacuum. Instruments used to measure and display pressure in an integral unit are called pressure meters or pressure gauges or vacuum gauges. A manometer is a good example, as it uses the surface area and weight of a column of liquid to both measure and indicate pressure. Likewise the widely used Bourdon gauge is a mechanical device, which both measures and indicates and is probably the best known type of gauge.

A vacuum gauge is a pressure gauge used to measure pressures lower than the ambient atmospheric pressure, which is set as the zero point, in negative values (e.g.: −15 psig or −760 mmHg equals total vacuum). Most gauges measure pressure relative to atmospheric pressure as the zero point, so this form of reading is simply referred to as "gauge pressure". However, anything greater than total vacuum is technically a form of pressure. For very accurate readings, especially at very low pressures, a gauge that uses total vacuum as the zero point may be used, giving pressure readings in an absolute scale.

Other methods of pressure measurement involve sensors that can transmit the pressure reading to a remote indicator or control system (telemetry).

Absolute, gauge and differential pressures — zero reference[edit]

Everyday pressure measurements, such as for vehicle tire pressure, are usually made relative to ambient air pressure. In other cases measurements are made relative to a vacuum or to some other specific reference. When distinguishing between these zero references, the following terms are used:
Absolute pressure is zero-referenced against a perfect vacuum, using an absolute scale, so it is equal to gauge pressure plus atmospheric pressure.
Gauge pressure is zero-referenced against ambient air pressure, so it is equal to absolute pressure minus atmospheric pressure. Negative signs are usually omitted.[citation needed] To distinguish a negative pressure, the value may be appended with the word "vacuum" or the gauge may be labeled a "vacuum gauge". These are further divided into two subcategories: high and low vacuum (and sometimes ultra-high vacuum). The applicable pressure ranges of many of the techniques used to measure vacuums overlap. Hence, by combining several different types of gauge, it is possible to measure system pressure continuously from 10 mbar down to 10−11 mbar.
Differential pressure is the difference in pressure between two points.

The zero reference in use is usually implied by context, and these words are added only when clarification is needed. Tire pressureand blood pressure are gauge pressures by convention, while atmospheric pressures, deep vacuum pressures, and altimeter pressuresmust be absolute.

For most working fluids where a fluid exists in a closed system, gauge pressure measurement prevails. Pressure instruments connected to the system will indicate pressures relative to the current atmospheric pressure. The situation changes when extreme vacuum pressures are measured, then absolute pressures are typically used instead.

Differential pressures are commonly used in industrial process systems. Differential pressure gauges have two inlet ports, each connected to one of the volumes whose pressure is to be monitored. In effect, such a gauge performs the mathematical operation of subtraction through mechanical means, obviating the need for an operator or control system to watch two separate gauges and determine the difference in readings.

Moderate vacuum pressure readings can be ambiguous without the proper context, as they may represent absolute pressure or gauge pressure without a negative sign. Thus a vacuum of 26 inHg gauge is equivalent to an absolute pressure of 4 inHg, calculated as 30 inHg (typical atmospheric pressure) − 26 inHg (gauge pressure).

Atmospheric pressure is typically about 100 kPa at sea level, but is variable with altitude and weather. If the absolute pressure of a fluid stays constant, the gauge pressure of the same fluid will vary as atmospheric pressure changes. For example, when a car drives up a mountain, the (gauge) tire pressure goes up because atmospheric pressure goes down. The absolute pressure in the tire is essentially unchanged.

Using atmospheric pressure as reference is usually signified by a "g" for gauge after the pressure unit, e.g. 70 psig, which means that the pressure measured is the total pressure minus atmospheric pressure. There are two types of gauge reference pressure: vented gauge (vg) and sealed gauge (sg).

A vented-gauge pressure transmitter, for example, allows the outside air pressure to be exposed to the negative side of the pressure-sensing diaphragm, through a vented cable or a hole on the side of the device, so that it always measures the pressure referred to ambient barometric pressure. Thus a vented-gauge reference pressure sensor should always read zero pressure when the process pressure connection is held open to the air.

A sealed gauge reference is very similar, except that atmospheric pressure is sealed on the negative side of the diaphragm. This is usually adopted on high pressure ranges, such as hydraulics, where atmospheric pressure changes will have a negligible effect on the accuracy of the reading, so venting is not necessary. This also allows some manufacturers to provide secondary pressure containment as an extra precaution for pressure equipment safety if the burst pressure of the primary pressure sensing diaphragm is exceeded.

There is another way of creating a sealed gauge reference, and this is to seal a high vacuum on the reverse side of the sensing diaphragm. Then the output signal is offset, so the pressure sensor reads close to zero when measuring atmospheric pressure.

A sealed gauge reference pressure transducer will never read exactly zero because atmospheric pressure is always changing and the reference in this case is fixed at 1 bar.

To produce an absolute pressure sensor, the manufacturer seals a high vacuum behind the sensing diaphragm. If the process-pressure connection of an absolute-pressure transmitter is open to the air, it will read the actual barometric pressure.

https://en.wikipedia.org/wiki/Pressure_measurement#Gauge

09-18-2021-1710 - Degree of Freedom is an Independent Physical Parameter in the Formal Description of the state of a physical system.

In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space.

The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic, where the state at one instant uniquely determines its past and future position and velocity as a function of time, such a system has six degrees of freedom.^{[citation needed]} If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the other hand, a system with an extended object that can rotate or vibrate can have more than six degrees of freedom.

In classical mechanics, the state of a point particle at any given time is often described with position and velocity coordinates in the Lagrangian formalism, or with position and momentum coordinates in the Hamiltonian formalism.

In statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system.^[1] The specification of all microstates of a system is a point in the system's phase space.

In the 3D ideal chain model in chemistry, two angles are necessary to describe the orientation of each monomer.

It is often useful to specify quadratic degrees of freedom. These are degrees of freedom that contribute in a quadratic function to the energy of the system.

Depending on what one is counting, there are several different ways that degrees of freedom can be defined, each with a different value.^[2]

https://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry)

09-18-2021-1708 - alternating current oscillating particle or wave perturbed γ-γ angular correlation heterodyne gyroscope

Alternating current (AC) is an electric current which periodically reverses direction and changes its magnitude continuously with time in contrast to direct current(DC) which flows only in one direction. Alternating current is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans and electric lamps into a wall socket. A common source of DC power is a battery cell in a flashlight. The abbreviations AC and DC are often used to mean simply alternating and direct, as when they modify current or voltage.^[1]^[2]

The usual waveform of alternating current in most electric power circuits is a sine wave, whose positive half-period corresponds with positive direction of the current and vice versa. In certain applications, like guitar amplifiers, different waveforms are used, such as triangular waves or square waves. Audio and radiosignals carried on electrical wires are also examples of alternating current. These types of alternating current carry information such as sound (audio) or images (video) sometimes carried by modulation of an AC carrier signal. These currents typically alternate at higher frequencies than those used in power transmission.

https://en.wikipedia.org/wiki/Alternating_current

The perturbed γ-γ angular correlation, PAC for short or PAC-Spectroscopy, is a method of nuclear solid-state physics with which magnetic and electric fields in crystal structures can be measured. In doing so, electrical field gradients and the Larmor frequency in magnetic fields as well as dynamic effects are determined. With this very sensitive method, which requires only about 10-1000 billion atoms of a radioactive isotope per measurement, material properties in the local structure, phase transitions, magnetism and diffusion can be investigated. The PAC method is related to nuclear magnetic resonance and the Mössbauer effect, but shows no signal attenuation at very high temperatures. Today only the time-differential perturbed angular correlation (TDPAC) is used.

https://en.wikipedia.org/wiki/Perturbed_angular_correlation

rotation translation vibration

https://en.wikipedia.org/wiki/Degrees_of_freedom_(physics_and_chemistry)

09-18-2021-1315 - Absolute, gauge and differential pressures — zero reference

For some substances, such as carbon and arsenic, sublimation is much easier than evaporation from the melt, because the pressure of their triple point is very high, and it is difficult to obtain them as liquids.

The pressure referred to is the partial pressure of the substance, not the total (e.g. atmospheric) pressure of the entire system. So, all solids that possess an appreciable vapour pressure at a certain temperature usually can sublime in air (e.g. water ice just below 0 °C).

The term sublimation refers to a physical change of state (imp. indep chemical/element or standard mixture non reactive ; nested systems in testing) and is not used to describe the transformation of a solid to a gas in a chemical reaction.

https://en.wikipedia.org/wiki/Sublimation_(phase_transition)

In a mixture of gases, each constituent gas has a partial pressure which is the notional pressure of that constituent gas if it alone occupied the entire volume of the original mixture at the same temperature.[1] The total pressure of an ideal gas mixture is the sum of the partial pressures of the gases in the mixture (Dalton's Law).
The partial pressure of a gas is a measure of thermodynamic activity of the gas's molecules.
Gases dissolve, diffuse, and react according to their partial pressures, and not according to their concentrations in gas mixtures or liquids.
https://en.wikipedia.org/wiki/Partial_pressure

Pressure (symbol: p or P) is the force applied perpendicular to the surface of an object per unit area over which that force is distributed.: 445 [1] Gauge pressure(also spelled gage pressure)[a] is the pressure relative to the ambient pressure.

Various units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the SI unit of pressure, the pascal (Pa), for example, is one newton per square metre (N/m2); similarly, the pound-force per square inch (psi) is the traditional unit of pressure in the imperial and U.S. customary systems. Pressure may also be expressed in terms of standard atmospheric pressure; the atmosphere (atm) is equal to this pressure, and the torr is defined as 1⁄760 of this. Manometric units such as the centimetre of water, millimetre of mercury, and inch of mercury are used to express pressures in terms of the height of column of a particular fluid in a manometer.

Pressure is the amount of force applied at right angles to the surface of an object per unit area. The symbol for it is "p" or P.^[2] The IUPAC recommendation for pressure is a lower-case p.^[3] However, upper-case P is widely used. The usage of P vs p depends upon the field in which one is working, on the nearby presence of other symbols for quantities such as power and momentum, and on writing style.

Formula

Mathematically:

p={\frac {F}{A}},

^[4]

where:

p

is the pressure,

F

is the magnitude of the normal force,

A

is the area of the surface on contact.

Pressure is a scalar quantity. It relates the vector area element (a vector normal to the surface) with the normal force acting on it. The pressure is the scalar proportionality constant that relates the two normal vectors:

d\mathbf {F} _{n}=-p\,d\mathbf {A} =-p\,\mathbf {n} \,dA.

The minus sign comes from the fact that the force is considered towards the surface element, while the normal vector points outward. The equation has meaning in that, for any surface S in contact with the fluid, the total force exerted by the fluid on that surface is the surface integral over S of the right-hand side of the above equation.

It is incorrect (although rather usual) to say "the pressure is directed in such or such direction". The pressure, as a scalar, has no direction. The force given by the previous relationship to the quantity has a direction, but the pressure does not. If we change the orientation of the surface element, the direction of the normal force changes accordingly, but the pressure remains the same.

Pressure is distributed to solid boundaries or across arbitrary sections of fluid normal to these boundaries or sections at every point. It is a fundamental parameter in thermodynamics, and it is conjugate to volume.

https://en.wikipedia.org/wiki/Pressure

https://en.wikipedia.org/wiki/Proportionality_(mathematics)#Direct_proportionality

https://en.wikipedia.org/wiki/Scalar_(physics)

https://en.wikipedia.org/wiki/Normal_force

https://en.wikipedia.org/wiki/Scalar_(mathematics)

https://en.wikipedia.org/wiki/Euclidean_vector

https://en.wikipedia.org/wiki/Magnitude_(mathematics)

https://en.wikipedia.org/wiki/Vector_area

https://en.wikipedia.org/wiki/Volume_(thermodynamics)

Absolute, gauge and differential pressures — zero reference[edit]

Everyday pressure measurements, such as for vehicle tire pressure, are usually made relative to ambient air pressure. In other cases measurements are made relative to a vacuum or to some other specific reference. When distinguishing between these zero references, the following terms are used:
Absolute pressure is zero-referenced against a perfect vacuum, using an absolute scale, so it is equal to gauge pressure plus atmospheric pressure.
Gauge pressure is zero-referenced against ambient air pressure, so it is equal to absolute pressure minus atmospheric pressure. Negative signs are usually omitted.[citation needed] To distinguish a negative pressure, the value may be appended with the word "vacuum" or the gauge may be labeled a "vacuum gauge". These are further divided into two subcategories: high and low vacuum (and sometimes ultra-high vacuum). The applicable pressure ranges of many of the techniques used to measure vacuums overlap. Hence, by combining several different types of gauge, it is possible to measure system pressure continuously from 10 mbar down to 10−11 mbar.
Differential pressure is the difference in pressure between two points.

The zero reference in use is usually implied by context, and these words are added only when clarification is needed. Tire pressure and blood pressure are gauge pressures by convention, while atmospheric pressures, deep vacuum pressures, and altimeter pressures must be absolute.

For most working fluids where a fluid exists in a closed system, gauge pressure measurement prevails. Pressure instruments connected to the system will indicate pressures relative to the current atmospheric pressure. The situation changes when extreme vacuum pressures are measured, then absolute pressures are typically used instead.

Differential pressures are commonly used in industrial process systems. Differential pressure gauges have two inlet ports, each connected to one of the volumes whose pressure is to be monitored. In effect, such a gauge performs the mathematical operation of subtraction through mechanical means, obviating the need for an operator or control system to watch two separate gauges and determine the difference in readings.

Moderate vacuum pressure readings can be ambiguous without the proper context, as they may represent absolute pressure or gauge pressure without a negative sign. Thus a vacuum of 26 inHg gauge is equivalent to an absolute pressure of 4 inHg, calculated as 30 inHg (typical atmospheric pressure) − 26 inHg (gauge pressure).

Atmospheric pressure is typically about 100 kPa at sea level, but is variable with altitude and weather. If the absolute pressure of a fluid stays constant, the gauge pressure of the same fluid will vary as atmospheric pressure changes. For example, when a car drives up a mountain, the (gauge) tire pressure goes up because atmospheric pressure goes down. The absolute pressure in the tire is essentially unchanged.

Using atmospheric pressure as reference is usually signified by a "g" for gauge after the pressure unit, e.g. 70 psig, which means that the pressure measured is the total pressure minus atmospheric pressure. There are two types of gauge reference pressure: vented gauge (vg) and sealed gauge (sg).

A vented-gauge pressure transmitter, for example, allows the outside air pressure to be exposed to the negative side of the pressure-sensing diaphragm, through a vented cable or a hole on the side of the device, so that it always measures the pressure referred to ambient barometric pressure. Thus a vented-gauge reference pressure sensor should always read zero pressure when the process pressure connection is held open to the air.

A sealed gauge reference is very similar, except that atmospheric pressure is sealed on the negative side of the diaphragm. This is usually adopted on high pressure ranges, such as hydraulics, where atmospheric pressure changes will have a negligible effect on the accuracy of the reading, so venting is not necessary. This also allows some manufacturers to provide secondary pressure containment as an extra precaution for pressure equipment safety if the burst pressure of the primary pressure sensing diaphragm is exceeded.

There is another way of creating a sealed gauge reference, and this is to seal a high vacuum on the reverse side of the sensing diaphragm. Then the output signal is offset, so the pressure sensor reads close to zero when measuring atmospheric pressure.

A sealed gauge reference pressure transducer will never read exactly zero because atmospheric pressure is always changing and the reference in this case is fixed at 1 bar.

To produce an absolute pressure sensor, the manufacturer seals a high vacuum behind the sensing diaphragm. If the process-pressure connection of an absolute-pressure transmitter is open to the air, it will read the actual barometric pressure.

https://en.wikipedia.org/wiki/Pressure_measurement#Gauge

Atmospheric pressure, also known as barometric pressure (after the barometer), is the pressure within the atmosphere of Earth. The standard atmosphere (symbol: atm) is a unit of pressure defined as 101,325 Pa (1,013.25 hPa; 1,013.25 mbar), which is equivalent to 760 mm Hg, 29.9212 inches Hg, or 14.696 psi.^[1] The atm unit is roughly equivalent to the mean sea-level atmospheric pressure on Earth; that is, the Earth's atmospheric pressure at sea level is approximately 1 atm.

In most circumstances, atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point. As elevation increases, there is less overlying atmospheric mass, so that atmospheric pressure decreases with increasing elevation. Because the atmosphere is thin relative to the Earth's radius—especially the dense atmospheric layer at low altitudes—the Earth's gravitational acceleration as a function of altitude can be approximated as constant and contributes little to this fall off. Pressure measures force per unit area, with SI units of pascals (1 pascal = 1 newton per square metre, 1 N/m²). On average, a column of air with a cross-sectional area of 1 square centimetre (cm²), measured from mean (average) sea level to the top of Earth's atmosphere, has a mass of about 1.03 kilogram and exerts a force or "weight" of about 10.1 newtons, resulting in a pressure of 10.1 N/cm² or 101 kN/m² (101 kilopascals, kPa). A column of air with a cross-sectional area of 1 in² would have a weight of about 14.7 lb_f, resulting in a pressure of 14.7 lb_f/in².

https://en.wikipedia.org/wiki/Atmospheric_pressure

Standard temperature and pressure (STP) are standard sets of conditions for experimental measurements to be established to allow comparisons to be made between different sets of data. The most used standards are those of the International Union of Pure and Applied Chemistry (IUPAC) and the National Institute of Standards and Technology (NIST), although these are not universally accepted standards. Other organizations have established a variety of alternative definitions for their standard reference conditions.

In chemistry, IUPAC changed the definition of standard temperature and pressure in 1982:^[1]^[2]

Until 1982, STP was defined as a temperature of 273.15 K (0 °C, 32 °F) and an absolute pressure of exactly 1 atm (101.325 kPa).
Since 1982, STP is defined as a temperature of 273.15 K (0 °C, 32 °F) and an absolute pressure of exactly 10⁵ Pa (100 kPa, 1 bar).

STP should not be confused with the standard state commonly used in thermodynamic evaluations of the Gibbs energy of a reaction.

NIST uses a temperature of 20 °C (293.15 K, 68 °F) and an absolute pressure of 1 atm (14.696 psi, 101.325 kPa). This standard is also called normal temperature and pressure (abbreviated as NTP). These stated values of STP used by NIST have not been verified and require a source. However, values cited in Modern Thermodynamics with Statistical Mechanics by Carl S. Helrich and A Guide to the NIST Chemistry WebBook by Peter J.^[vague] Linstrom suggest a common STP in use by NIST for thermodynamic experiments is 298.15 K (25°C, 77°F) and 1 bar (14.5038 psi, 100 kPa).^[3]^[4]

The International Standard Metric Conditions for natural gas and similar fluids are 288.15 K (15.00 °C; 59.00 °F) and 101.325 kPa.^[5]

In industry and commerce, standard conditions for temperature and pressure are often necessary to define the standard reference conditions to express the volumes of gases and liquids and related quantities such as the rate of volumetric flow (the volumes of gases vary significantly with temperature and pressure): standard cubic meters per second (Sm³/s), and normal cubic meters per second (Nm³/s).

However, many technical publications (books, journals, advertisements for equipment and machinery) simply state "standard conditions" without specifying them; often substituting the term with older "normal conditions", or "NC". In special cases this can lead to confusion and errors. Good practice always incorporates the reference conditions of temperature and pressure. If not stated, some room environment conditions are supposed, close to 1 atm pressure, 293 K (20 °C), and 0% humidity.

https://en.wikipedia.org/wiki/Standard_conditions_for_temperature_and_pressure

In chemistry, the standard state of a material (pure substance, mixture or solution) is a reference point used to calculate its properties under different conditions. A superscript circle is used to designate a thermodynamic quantity in the standard state, such as change in enthalpy (ΔH°), change in entropy (ΔS°), or change in Gibbs free energy (ΔG°).^[1]^[2] (See discussion about typesetting below.)

In principle, the choice of standard state is arbitrary, although the International Union of Pure and Applied Chemistry (IUPAC) recommends a conventional set of standard states for general use.^[3] IUPAC recommends using a standard pressure p^⦵ = 10⁵ Pa.^[4] Strictly speaking, temperature is not part of the definition of a standard state. For example, as discussed below, the standard state of a gas is conventionally chosen to be unit pressure (usually in bar) ideal gas, regardless of the temperature. However, most tables of thermodynamic quantities are compiled at specific temperatures, most commonly 298.15 K (25.00 °C; 77.00 °F) or, somewhat less commonly, 273.15 K (0.00 °C; 32.00 °F).^[5]

The standard state should not be confused with standard temperature and pressure (STP) for gases,^[6] nor with the standard solutions used in analytical chemistry.^[7] STP is commonly used for calculations involving gases that approximate an ideal gas, whereas standard state conditions are used for thermodynamic calculations.^[5]

For a given material or substance, the standard state is the reference state for the material's thermodynamic state properties such as enthalpy, entropy, Gibbs free energy, and for many other material standards. The standard enthalpy change of formation for an element in its standard state is zero, and this convention allows a wide range of other thermodynamic quantities to be calculated and tabulated. The standard state of a substance does not have to exist in nature: for example, it is possible to calculate values for steam at 298.15 K and 10⁵ Pa, although steam does not exist (as a gas) under these conditions. The advantage of this practice is that tables of thermodynamic properties prepared in this way are self-consistent.

Conventional standard states[edit]

Many standard states are non-physical states, often referred to as "hypothetical states". Nevertheless, their thermodynamic properties are well-defined, usually by an extrapolation from some limiting condition, such as zero pressure or zero concentration, to a specified condition (usually unit concentration or pressure) using an ideal extrapolating function, such as ideal solution or ideal gas behavior, or by empirical measurements.
Gases[edit]

The standard state for a gas is the hypothetical state it would have as a pure substance obeying the ideal gas equation at standard pressure (105 Pa, or 1 bar). No real gas has perfectly ideal behavior, but this definition of the standard state allows corrections for non-ideality to be made consistently for all the different gases.
Liquids and solids[edit]

The standard state for liquids and solids is simply the state of the pure substance subjected to a total pressure of 105 Pa. For most elements, the reference point of ΔHf⦵ = 0 is defined for the most stable allotrope of the element, such as graphite in the case of carbon, and the β-phase (white tin) in the case of tin. An exception is white phosphorus, the most common allotrope of phosphorus, which is defined as the standard state despite the fact that it is only metastable.[8]
Solutes[edit]

For a substance in solution (solute), the standard state is usually chosen as the hypothetical state it would have at the standard state molality or amount concentration but exhibiting infinite-dilution behavior (where there are no solute-solute interactions, but solute-solvent interactions are present). The reason for this unusual definition is that the behavior of a solute at the limit of infinite dilution is described by equations which are very similar to the equations for ideal gases. Hence taking infinite-dilution behavior to be the standard state allows corrections for non-ideality to be made consistently for all the different solutes. The standard state molality is 1 mol kg−1, while the standard state molarity is 1 mol dm−3.

Other choices are possible. For example, the use of a standard state concentration of mol L−1 for the hydrogen ion in a real, aqueous solution is common in the field of biochemistry.[9][10] In other application areas such as electrochemistry, the standard state is sometimes chosen as the actual state of the real solution at a standard concentration (often 1 mol dm−3).[11] The activity coefficients will not transfer from convention to convention and so it is very important to know and understand what conventions were used in the construction of tables of standard thermodynamic properties before using them to describe solutions.
Adsorbates[edit]

For molecules adsorbed on surfaces there have been various conventions proposed based on hypothetical standard states. For adsorption that occurs on specific sites (Langmuir adsorption) the most common standard state is a relative coverage of θ°=0.5, as this choice results in a cancellation of the configurational entropy term and is also consistent with neglecting to include the standard state (which is a common error).[12] The advantage of using θ°=0.5 is that the configurational term cancels and the entropy extracted from thermodynamic analyses is thus reflective of intra-molecular changes between the bulk phase (such as gas or liquid) and the adsorbed state. There may be benefit to tabulating values based on both a relative coverage based standard state and in additional column an absolute coverage based standard state. For 2D gas states, the complication of discrete states does not arise and an absolute density base standard state has been proposed, similar for the 3D gas phase.[12]
Typesetting[edit]

At the time of development in the nineteenth century, the superscript Plimsoll symbol (⦵) was adopted to indicate the non-zero nature of the standard state.[13] IUPAC recommends in the 3rd edition of Quantities, Units and Symbols in Physical Chemistry a symbol which seems to be a degree sign (°) as a substitute for the plimsoll mark. In the very same publication the plimsoll mark appears to be constructed by combining a horizontal stroke with a degree sign.[14] A range of similar symbols are used in the literature: a stroked lowercase letter O (o),[15] a superscript zero (0)[16] or a circle with a horizontal bar either where the bar extends beyond the boundaries of the circle (U+29B5 ⦵ CIRCLE WITH HORIZONTAL BAR) or is enclosed by the circle, dividing the circle in half (U+2296 ⊖ CIRCLED MINUS).[17][18] When compared to the plimsoll symbol used on vessels, the horizontal bar should extend beyond the boundaries of the circle; care should be taken not to confuse the symbol with the Greek letter theta (uppercase Θ or ϴ, lowercase θ ).

The use of a degree symbol (°) or superscript zero () has come into widespread use in general, inorganic, and physical chemistry textbooks in recent years, as suggested by Mills (vide supra).[19][20][21]
See also[edit]
Standard conditions for temperature and pressure
Standard molar entropy
References[edit]
International Union of Pure and Applied Chemistry (1982). "Notation for states and processes, significance of the word standard in chemical thermodynamics, and remarks on commonly tabulated forms of thermodynamic functions" (PDF). Pure Appl. Chem. 54 (6): 1239–50. doi:10.1351/pac198254061239.
IUPAC–IUB–IUPAB Interunion Commission of Biothermodynamics (1976). "Recommendations for measurement and presentation of biochemical equilibrium data" (PDF). J. Biol. Chem. 251 (22): 6879–85.

https://en.wikipedia.org/wiki/Standard_state

In chemistry, the standard molar entropy is the entropy content of one mole of pure substance at a standard state of pressure and any temperature of interest. These are often (but not necessarily) chosen to be the standard temperature and pressure.

The standard molar entropy at pressure = $P^0$ is usually given the symbol $S°$ , and has units of joules per mole kelvin (J⋅mol⁻¹⋅K⁻¹). Unlike standard enthalpies of formation, the value of $S°$ is absolute. That is, an element in its standard state has a definite, nonzero value of $S$ at room temperature. The entropy of a pure crystalline structure can be 0 J⋅mol⁻¹⋅K⁻¹ only at 0 K, according to the third law of thermodynamics. However, this assumes that the material forms a 'perfect crystal' without any residual entropy. This can be due to crystallographic defects, dislocations, and/or incomplete rotational quenching within the solid, as originally pointed out by Linus Pauling.^[1]) These contributions to the entropy are always present, because crystals always grow at a finite rate and at temperature. However, the residual entropy is often quite negligible and can be accounted for when it occurs using statistical mechanics.

Thermodynamics[edit]

If a mole of a solid substance is a perfectly ordered solid at 0 K, then if the solid warmed by its surroundings to 298.15 K without melting, its absolute molar entropy would be the sum of a series of $N$ stepwise and reversible entropy changes. The limit of this sum as $N\rightarrow \infty$ becomes an integral:

S^{\circ }=\sum _{k=1}^{N}\Delta S_{k}=\sum _{k=1}^{N}{\frac {dQ_{k}}{T}}\rightarrow \int _{0}^{T_{2}}{\frac {dS}{dT}}dT=\int _{0}^{T_{2}}{\frac {C_{p_{k}}}{T}}dT

In this example, $T_{2}=298.15K$ and $C_{p_{k}}$ is the molar heat capacity at a constant pressure of the substance in the reversible process $k$ . The molar heat capacity is not constant during the experiment because it changes depending on the (increasing) temperature of the substance. Therefore, a table of values for ${\frac {C_{p_{k}}}{T}}$ is required to find the total molar entropy. The quantity ${\frac {dQ_{k}}{T}}$ represents the ratio of a very small exchange of heat energy to the temperature $T$ . The total molar entropy is the sum of many small changes in molar entropy, where each small change can be considered a reversible process.

Chemistry[edit]

The standard molar entropy of a gas at STP includes contributions from:^[2]

The heat capacity of one mole of the solid from 0 K to the melting point (including heat absorbed in any changes between different crystal structures).
The latent heat of fusion of the solid.
The heat capacity of the liquid from the melting point to the boiling point.
The latent heat of vaporization of the liquid.
The heat capacity of the gas from the boiling point to room temperature.

Changes in entropy are associated with phase transitions and chemical reactions. Chemical equations make use of the standard molar entropy of reactants and products to find the standard entropy of reaction:^[3]

{\Delta S^{\circ }}_{rxn}=S_{products}^{\circ }-S_{reactants}^{\circ }

The standard entropy of reaction helps determine whether the reaction will take place spontaneously. According to the second law of thermodynamics, a spontaneous reaction always results in an increase in total entropy of the system and its surroundings:

(\Delta S_{total}=\Delta S_{system}+\Delta S_{surroundings})>0

Molar entropy is not same for all gases. Under identical conditions, it is greater for a heavier gas.

Introduction[edit]

A description of any thermodynamic system employs the four laws of thermodynamics that form an axiomatic basis. The first law specifies that energy can be transferred between physical systems as heat, as work, and with transfer of matter.^[12] The second law defines the existence of a quantity called entropy, that describes the direction, thermodynamically, that a system can evolve and quantifies the state of order of a system and that can be used to quantify the useful work that can be extracted from the system.^[13]

In thermodynamics, interactions between large ensembles of objects are studied and categorized. Central to this are the concepts of the thermodynamic system and its surroundings. A system is composed of particles, whose average motions define its properties, and those properties are in turn related to one another through equations of state. Properties can be combined to express internal energy and thermodynamic potentials, which are useful for determining conditions for equilibrium and spontaneous processes.

With these tools, thermodynamics can be used to describe how systems respond to changes in their environment. This can be applied to a wide variety of topics in science and engineering, such as engines, phase transitions, chemical reactions, transport phenomena, and even black holes. The results of thermodynamics are essential for other fields of physics and for chemistry, chemical engineering, corrosion engineering, aerospace engineering, mechanical engineering, cell biology, biomedical engineering, materials science, and economics, to name a few.^[14]^[15]

This article is focused mainly on classical thermodynamics which primarily studies systems in thermodynamic equilibrium. Non-equilibrium thermodynamics is often treated as an extension of the classical treatment, but statistical mechanics has brought many advances to that field.

The history of thermodynamics as a scientific discipline generally begins with Otto von Guericke who, in 1650, built and designed the world's first vacuum pump and demonstrated a vacuum using his Magdeburg hemispheres. Guericke was driven to make a vacuum in order to disprove Aristotle's long-held supposition that 'nature abhors a vacuum'. Shortly after Guericke, the Anglo-Irish physicist and chemist Robert Boyle had learned of Guericke's designs and, in 1656, in coordination with English scientist Robert Hooke, built an air pump.^[17] Using this pump, Boyle and Hooke noticed a correlation between pressure, temperature, and volume. In time, Boyle's Law was formulated, which states that pressure and volume are inversely proportional. Then, in 1679, based on these concepts, an associate of Boyle's named Denis Papin built a steam digester, which was a closed vessel with a tightly fitting lid that confined steam until a high pressure was generated.

Later designs implemented a steam release valve that kept the machine from exploding. By watching the valve rhythmically move up and down, Papin conceived of the idea of a piston and a cylinder engine. He did not, however, follow through with his design. Nevertheless, in 1697, based on Papin's designs, engineer Thomas Savery built the first engine, followed by Thomas Newcomen in 1712. Although these early engines were crude and inefficient, they attracted the attention of the leading scientists of the time.

https://en.wikipedia.org/wiki/Thermodynamics

The laws of thermodynamics define a group of physical quantities, such as temperature, energy, and entropy, that characterize thermodynamic systems in thermodynamic equilibrium. The laws also use various parameters for thermodynamic processes, such as thermodynamic work and heat, and establish relationships between them. They state empirical facts that form a basis of precluding the possibility of certain phenomena, such as perpetual motion. In addition to their use in thermodynamics, they are important fundamental laws of physics in general, and are applicable in other natural sciences.

Traditionally, thermodynamics has recognized three fundamental laws, simply named by an ordinal identification, the first law, the second law, and the third law.^[1]^[2]^[3] A more fundamental statement was later labelled as the zeroth law, after the first three laws had been established.

The zeroth law of thermodynamics defines thermal equilibrium and forms a basis for the definition of temperature: If two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.

The first law of thermodynamics states that, when energy passes into or out of a system (as work, heat, or matter), the system's internal energy changes in accord with the law of conservation of energy.

The second law of thermodynamics states that in a natural thermodynamic process, the sum of the entropies of the interacting thermodynamic systems never decreases. Another form of the statement is that heat does not spontaneously pass from a colder body to a warmer body.

The third law of thermodynamics states that a system's entropy approaches a constant value as the temperature approaches absolute zero. With the exception of non-crystalline solids (glasses) the entropy of a system at absolute zero is typically close to zero.^[2]

The first and second law prohibit two kinds of perpetual motion machines, respectively: the perpetual motion machine of the first kind which produces work with no energy input, and the perpetual motion machine of the second kind which spontaneously converts thermal energy into mechanical work.

https://en.wikipedia.org/wiki/Laws_of_thermodynamics

In thermodynamics, the internal energy of a system is expressed in terms of pairs of conjugate variables such as temperature and entropy or pressure and volume. In fact, all thermodynamic potentials are expressed in terms of conjugate pairs. The product of two quantities that are conjugate has units of energy or sometimes power.

For a mechanical system, a small increment of energy is the product of a force times a small displacement. A similar situation exists in thermodynamics. An increment in the energy of a thermodynamic system can be expressed as the sum of the products of certain generalized "forces" that, when unbalanced, cause certain generalized "displacements", and the product of the two is the energy transferred as a result. These forces and their associated displacements are called conjugate variables. The thermodynamic force is always an intensive variable and the displacement is always an extensive variable, yielding an extensive energy transfer. The intensive (force) variable is the derivative of the internal energy with respect to the extensive (displacement) variable, while all other extensive variables are held constant.

The thermodynamic square can be used as a tool to recall and derive some of the thermodynamic potentials based on conjugate variables.

In the above description, the product of two conjugate variables yields an energy. In other words, the conjugate pairs are conjugate with respect to energy. In general, conjugate pairs can be defined with respect to any thermodynamic state function. Conjugate pairs with respect to entropy are often used, in which the product of the conjugate pairs yields an entropy. Such conjugate pairs are particularly useful in the analysis of irreversible processes, as exemplified in the derivation of the Onsager reciprocal relations.

https://en.wikipedia.org/wiki/Conjugate_variables_(thermodynamics)

The thermodynamic square (also known as the thermodynamic wheel, Guggenheim scheme or Born square) is a mnemonic diagram attributed to Max Born and used to help determine thermodynamic relations. Born presented the thermodynamic square in a 1929 lecture.^[1] The symmetry of thermodynamics appears in a paper by F.O. Koenig.^[2] The corners represent common conjugate variables while the sides represent thermodynamic potentials. The placement and relation among the variables serves as a key to recall the relations they constitute.

A mnemonic used by students to remember the Maxwell relations (in thermodynamics) is "Good Physicists Have Studied Under Very Fine Teachers", which helps them remember the order of the variables in the square, in clockwise direction. Another mnemonic used here is "Valid Facts and Theoretical Understanding Generate Solutions to Hard Problems", which gives the letter in the normal left-to-right writing direction. Both times A has to be identified with F, another common symbol for Helmholtz' Free Energy. To prevent the need for this switch the following mnemonic is also widely used:"Good Physicists Have Studied Under Very Ambitious Teachers"; another one is Good Physicists Have SUVAT, in reference to the equations of motion. One other useful variation of the mnemonic when the symbol E is used for internal energy instead of U is the following: "Some Hard Problems Go To Finish Very Easy".^[3]

The thermodynamic square with potentials highlighted in red.

https://en.wikipedia.org/wiki/Thermodynamic_square

The atmosphere of Earth, commonly known as air, is the layer of gases retained by Earth's gravity that surrounds the planet and forms its planetary atmosphere. The atmosphere of Earth protects life on Earth by creating pressure allowing for liquid water to exist on the Earth's surface, absorbing ultraviolet solar radiation, warming the surface through heat retention (greenhouse effect), and reducing temperature extremes between day and night (the diurnal temperature variation).

By mole fraction (i.e., by number of molecules), dry air contains 78.08% nitrogen, 20.95% oxygen, 0.93% argon, 0.04% carbon dioxide, and small amounts of other gases.^[8] Air also contains a variable amount of water vapor, on average around 1% at sea level, and 0.4% over the entire atmosphere. Air composition, temperature, and atmospheric pressure vary with altitude. Within the atmosphere, air suitable for use in photosynthesis by terrestrial plants and breathing of terrestrial animals is found only in Earth's troposphere.^{[citation needed]}

Earth's early atmosphere consisted of gases in the solar nebula, primarily hydrogen. The atmosphere changed significantly over time, affected by many factors such as volcanism, life, and weathering. Recently, human activity has also contributed to atmospheric changes, such as global warming, ozone depletion and acid deposition.

The atmosphere has a mass of about 5.15×10¹⁸ kg,^[9] three quarters of which is within about 11 km (6.8 mi; 36,000 ft) of the surface. The atmosphere becomes thinner with increasing altitude, with no definite boundary between the atmosphere and outer space. The Kármán line, at 100 km (62 mi) or 1.57% of Earth's radius, is often used as the border between the atmosphere and outer space. Atmospheric effects become noticeable during atmospheric reentry of spacecraft at an altitude of around 120 km (75 mi). Several layers can be distinguished in the atmosphere, based on characteristics such as temperature and composition.

The study of Earth's atmosphere and its processes is called atmospheric science (aerology), and includes multiple subfields, such as climatology and atmospheric physics. Early pioneers in the field include Léon Teisserenc de Bort and Richard Assmann.^[10] The study of historic atmosphere is called paleoclimatology.

https://en.wikipedia.org/wiki/Atmosphere_of_Earth

In astrophysics, accretion is the accumulation of particles into a massive object by gravitationally attracting more matter, typically gaseous matter, in an accretion disk.^[1]^[2] Most astronomical objects, such as galaxies, stars, and planets, are formed by accretion processes.

https://en.wikipedia.org/wiki/Accretion_(astrophysics)

Nuclear transmutation is the conversion of one chemical element or an isotope into another chemical element.^[1] Nuclear transmutation occurs in any process where the number of protons or neutrons in the nucleus of an atom is changed.

A transmutation can be achieved either by nuclear reactions (in which an outside particle reacts with a nucleus) or by radioactive decay, where no outside cause is needed.

Natural transmutation by stellar nucleosynthesis in the past created most of the heavier chemical elements in the known existing universe, and continues to take place to this day, creating the vast majority of the most common elements in the universe, including helium, oxygen and carbon. Most stars carry out transmutation through fusion reactions involving hydrogen and helium, while much larger stars are also capable of fusing heavier elements up to iron late in their evolution.

Elements heavier than iron, such as gold or lead, are created through elemental transmutations that can only naturally occur in supernovae. As stars begin to fuse heavier elements, substantially less energy is released from each fusion reaction. This continues until it reaches iron which is produced by an endothermic reaction consuming energy. No heavier element can be produced in such conditions.

One type of natural transmutation observable in the present occurs when certain radioactive elements present in nature spontaneously decay by a process that causes transmutation, such as alpha or beta decay. An example is the natural decay of potassium-40 to argon-40, which forms most of the argon in the air. Also on Earth, natural transmutations from the different mechanisms of natural nuclear reactions occur, due to cosmic ray bombardment of elements (for example, to form carbon-14), and also occasionally from natural neutron bombardment (for example, see natural nuclear fission reactor).

Artificial transmutation may occur in machinery that has enough energy to cause changes in the nuclear structure of the elements. Such machines include particle accelerators and tokamak reactors. Conventional fission power reactors also cause artificial transmutation, not from the power of the machine, but by exposing elements to neutrons produced by fission from an artificially produced nuclear chain reaction. For instance, when a uranium atom is bombarded with slow neutrons, fission takes place. This releases, on average, 3 neutrons and a large amount of energy. The released neutrons then cause fission of other uranium atoms, until all of the available uranium is exhausted. This is called a chain reaction.

Artificial nuclear transmutation has been considered as a possible mechanism for reducing the volume and hazard of radioactive waste.^[2]

https://en.wikipedia.org/wiki/Nuclear_transmutation

Stellar nucleosynthesis is the creation (nucleosynthesis) of chemical elements by nuclear fusion reactions within stars. Stellar nucleosynthesis has occurred since the original creation of hydrogen, helium and lithium during the Big Bang. As a predictive theory, it yields accurate estimates of the observed abundances of the elements. It explains why the observed abundances of elements change over time and why some elements and their isotopes are much more abundant than others. The theory was initially proposed by Fred Hoyle in 1946,^[1] who later refined it in 1954.^[2] Further advances were made, especially to nucleosynthesis by neutron capture of the elements heavier than iron, by Margaret and Geoffrey Burbidge, William Alfred Fowler and Hoyle in their famous 1957 B²FH paper,^[3] which became one of the most heavily cited papers in astrophysics history.

Stars evolve because of changes in their composition (the abundance of their constituent elements) over their lifespans, first by burning hydrogen(main sequence star), then helium (horizontal branch star), and progressively burning higher elements. However, this does not by itself significantly alter the abundances of elements in the universe as the elements are contained within the star. Later in its life, a low-mass star will slowly eject its atmosphere via stellar wind, forming a planetary nebula, while a higher–mass star will eject mass via a sudden catastrophic event called a supernova. The term supernova nucleosynthesis is used to describe the creation of elements during the explosion of a massive star or white dwarf.

The advanced sequence of burning fuels is driven by gravitational collapse and its associated heating, resulting in the subsequent burning of carbon, oxygen and silicon. However, most of the nucleosynthesis in the mass range A = 28–56 (from silicon to nickel) is actually caused by the upper layers of the star collapsing onto the core, creating a compressional shock wave rebounding outward. The shock front briefly raises temperatures by roughly 50%, thereby causing furious burning for about a second. This final burning in massive stars, called explosive nucleosynthesis or supernova nucleosynthesis, is the final epoch of stellar nucleosynthesis.

A stimulus to the development of the theory of nucleosynthesis was the discovery of variations in the abundances of elements found in the universe. The need for a physical description was already inspired by the relative abundances of the chemical elements in the solar system. Those abundances, when plotted on a graph as a function of the atomic number of the element, have a jagged sawtooth shape that varies by factors of tens of millions (see history of nucleosynthesis theory).^[4] This suggested a natural process that is not random. A second stimulus to understanding the processes of stellar nucleosynthesis occurred during the 20th century, when it was realized that the energy released from nuclear fusion reactions accounted for the longevity of the Sun as a source of heat and light.^[5]

https://en.wikipedia.org/wiki/Stellar_nucleosynthesis

In 1980, he transmuted several thousand atoms of bismuth into gold at the Lawrence Berkeley Laboratory. His experimental technique, using nuclear physics, was able to remove protons and neutrons from the bismuth atoms. Seaborg's technique would have been far too expensive to enable routine manufacturing of gold, but his work was close to the mythical Philosopher's Stone.^[45]^[46]

https://en.wikipedia.org/wiki/Glenn_T._Seaborg#Return_to_California

In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag). This is the steady gain in speed caused exclusively by the force of gravitational attraction. At a fixed point on the Earth's surface, all bodies accelerate in vacuum at the same rate, regardless of the masses or compositions of the bodies;^[1] the measurement and analysis of these rates is known as gravimetry.

At different points on Earth's surface, the free fall acceleration ranges from 9.764 m/s² to 9.834 m/s²^[2] depending on altitude, latitude, and longitude. A conventional standard value is defined exactly as 9.80665 m/s² (approximately 32.17405 ft/s²). Locations of significant variation from this value are known as gravity anomalies. This does not take into account other effects, such as buoyancy or drag.

https://en.wikipedia.org/wiki/Gravitational_acceleration

In the thermodynamics of equilibrium, a state function, function of state, or point function is a function defined for a system relating several state variables or state quantities that depends only on the current equilibrium thermodynamic state of the system^[1] (e.g. gas, liquid, solid, crystal, or emulsion), not the path which the system took to reach its present state. A state function describes the equilibrium state of a system, thus also describing the type of system. For example, a state function could describe an atom or molecule in a gaseous, liquid, or solid form; a heterogeneous or homogeneous mixture; and the amounts of energy required to create such systems or change them into a different equilibrium state.

Heat, enthalpy, and entropy are examples of state quantities because they quantitatively describe an equilibrium state of a thermodynamic system, regardless of how the system arrived in that state. In contrast, mechanical work and heat are process quantities or path functions because their values depend on the specific "transition" (or "path") between two equilibrium states. Heat (in certain discrete amounts) can describe a state function such as enthalpy, but in general, does not truly describe the system unless it is defined as the state function of a certain system, and thus enthalpy is described by an amount of heat. This can also apply to entropy when heat is compared to temperature. The description breaks down for quantities exhibiting hysteresis.^[2]

https://en.wikipedia.org/wiki/State_function

Statics is the branch of mechanics that is concerned with the analysis of (force and torque, or "moment") acting on physical systems that do not experience an acceleration (a=0), but rather, are in static equilibrium with their environment. The application of Newton's second law to a system gives:

{\textbf {F}}=m{\textbf {a}}\,.

Where bold font indicates a vector that has magnitude and direction. ${\textbf {F}}$ is the total of the forces acting on the system, $m$ is the mass of the system and ${\textbf {a}}$ is the acceleration of the system. The summation of forces will give the direction and the magnitude of the acceleration and will be inversely proportional to the mass. The assumption of static equilibrium of ${\textbf {a}}$ = 0 leads to:

{\textbf {F}}=0\,.

The summation of forces, one of which might be unknown, allows that unknown to be found. So when in static equilibrium, the acceleration of the system is zero and the system is either at rest, or its center of mass moves at constant velocity. Likewise the application of the assumption of zero acceleration to the summation of moments acting on the system leads to:

{\textbf {M}}=I\alpha =0\,.

Here, ${\textbf {M}}$ is the summation of all moments acting on the system, $I$ is the moment of inertia of the mass and $\alpha$ = 0 the angular acceleration of the system, which when assumed to be zero leads to:

{\textbf {M}}=0\,.

The summation of moments, one of which might be unknown, allows that unknown to be found. These two equations together, can be applied to solve for as many as two loads (forces and moments) acting on the system.

From Newton's first law, this implies that the net force and net torque on every part of the system is zero. The net forces equaling zero is known as the first condition for equilibrium, and the net torque equaling zero is known as the second condition for equilibrium. See statically indeterminate.

https://en.wikipedia.org/wiki/Statics

https://en.wikipedia.org/wiki/Component

https://en.wikipedia.org/wiki/Exergy_efficiency

https://en.wikipedia.org/wiki/Absolute_zero

https://en.wikipedia.org/wiki/Absolute_zero#Thermodynamics_near_absolute_zero

https://en.wikipedia.org/wiki/Adiabatic_process

https://en.wikipedia.org/wiki/Environment_(systems)

https://en.wikipedia.org/wiki/Thermodynamic_system

https://en.wikipedia.org/wiki/Steam-electric_power_station

https://en.wikipedia.org/wiki/Enthalpy–entropy_chart

https://en.wikipedia.org/wiki/Deposition_(phase_transition)

https://en.wikipedia.org/wiki/Sublimation_(phase_transition)

https://en.wikipedia.org/wiki/Endothermic_process

https://en.wikipedia.org/wiki/Exothermic_process

https://en.wikipedia.org/wiki/Enthalpy

https://en.wikipedia.org/wiki/Bond_energy

https://en.wikipedia.org/wiki/Thermal_energy

https://en.wikipedia.org/wiki/Potential_energy

https://en.wikipedia.org/wiki/Kinetic_energy

https://en.wikipedia.org/wiki/Molecule

https://en.wikipedia.org/wiki/Heat

https://en.wikipedia.org/wiki/Energy

https://en.wikipedia.org/wiki/Work_(thermodynamics)

https://en.wikipedia.org/wiki/State_function

https://en.wikipedia.org/wiki/Process_function

https://en.wikipedia.org/wiki/List_of_thermodynamic_properties

https://en.wikipedia.org/wiki/Partial_pressure

https://en.wikipedia.org/wiki/Equilibrium_constant

https://en.wikipedia.org/wiki/Determination_of_equilibrium_constants

https://en.wikipedia.org/wiki/State_of_matter

https://en.wikipedia.org/wiki/Physical_property

https://en.wikipedia.org/wiki/Phase_transition

https://en.wikipedia.org/wiki/Sublimation_(phase_transition)

https://en.wikipedia.org/wiki/Physical_change

https://en.wikipedia.org/wiki/Enthalpy_of_fusion

https://en.wikipedia.org/wiki/Specific_heat_capacity

https://en.wikipedia.org/wiki/Chemistry

https://en.wikipedia.org/wiki/Thermodynamics

https://en.wikipedia.org/wiki/Category:Equilibrium_chemistry

https://en.wikipedia.org/wiki/Non-equilibrium_thermodynamics

https://en.wikipedia.org/wiki/Equilibrium_thermodynamics

https://en.wikipedia.org/wiki/Thermodynamic_system

https://en.wikipedia.org/wiki/Environment_(systems)

https://en.wikipedia.org/wiki/Intensive_and_extensive_properties

https://en.wikipedia.org/wiki/Fundamental_thermodynamic_relation

https://en.wikipedia.org/wiki/Energy_system

https://en.wikipedia.org/wiki/Chemical_potential

https://en.wikipedia.org/wiki/Stochastic

https://en.wikipedia.org/wiki/Entropy_(energy_dispersal)

https://en.wikipedia.org/wiki/Thermodynamic_equilibrium

https://en.wikipedia.org/wiki/Thermodynamic_operation

https://en.wikipedia.org/wiki/Thermodynamic_process

https://en.wikipedia.org/wiki/Thermodynamic_cycle

https://en.wikipedia.org/wiki/First_law_of_thermodynamics_(fluid_mechanics)

https://en.wikipedia.org/wiki/Combustion_chemical_vapor_deposition

https://en.wikipedia.org/wiki/Atomic_layer_deposition

https://en.wikipedia.org/wiki/Plasma-enhanced_chemical_vapor_deposition

https://en.wikipedia.org/wiki/Deposition_(phase_transition)

https://en.wikipedia.org/wiki/Laws_of_thermodynamics

https://en.wikipedia.org/wiki/Thermodynamic_system

https://en.wikipedia.org/wiki/Material_properties_(thermodynamics)

https://en.wikipedia.org/wiki/List_of_thermodynamic_properties

https://en.wikipedia.org/wiki/Thermodynamic_state

https://en.wikipedia.org/wiki/Thermodynamic_diagrams

https://en.wikipedia.org/wiki/Entropy

https://en.wikipedia.org/wiki/SI_base_unit

https://en.wikipedia.org/wiki/Thermodynamic_instruments

https://en.wikipedia.org/wiki/State_function

https://en.wikipedia.org/wiki/State_space

https://en.wikipedia.org/wiki/Monatomic_gas

https://en.wikipedia.org/wiki/State_postulate

https://en.wikipedia.org/wiki/Process_function

A thermodynamic instrument is any device which facilitates the quantitative measurement of thermodynamic systems. In order for a thermodynamic parameter to be truly defined, a technique for its measurement must be specified. For example, the ultimate definition of temperature is "what a thermometer reads". The question follows – what is a thermometer?

There are two types of thermodynamic instruments, the meter and the reservoir. A thermodynamic meter is any device which measures any parameter of a thermodynamic system. A thermodynamic reservoir is a system which is so large that it does not appreciably alter its state parameters when brought into contact with the test system.

Thermodynamic meters[edit]

A meter is a thermodynamic system which displays some aspect of its thermodynamic state to the observer. The nature of its contact with the system it is measuring can be controlled, and it is sufficiently small that it does not appreciably affect the state of the system being measured. The theoretical thermometer described below is just such a meter.

In some cases, the thermodynamic parameter is actually defined in terms of an idealized measuring instrument. For example, the zeroth law of thermodynamics states that if two bodies are in thermal equilibrium with a third body, they are also in thermal equilibrium with each other. This principle, as noted by James Maxwell in 1872, asserts that it is possible to measure temperature. An idealized thermometer is a sample of an ideal gas at constant pressure. From the ideal gas law, the volume of such a sample can be used as an indicator of temperature; in this manner it defines temperature. Although pressure is defined mechanically, a pressure-measuring device called a barometer may also be constructed from a sample of an ideal gas held at a constant temperature. A calorimeter is a device which is used to measure and define the internal energy of a system.

Some common thermodynamic meters are:

Thermometer - a device which measures temperature as described above
Barometer - a device which measures pressure. An ideal gas barometer may be constructed by mechanically connecting an ideal gas to the system being measured, while thermally insulating it. The volume will then measure pressure, by the ideal gas equation P=NkT/V .
Calorimeter - a device which measures the heat energy added to a system. A simple calorimeter is simply a thermometer connected to a thermally isolated system.

Thermodynamic reservoirs[edit]

A reservoir is a thermodynamic system which controls the state of a system, usually by "imposing" itself upon the system being controlled. This means that the nature of its contact with the system can be controlled. A reservoir is so large that its thermodynamic state is not appreciably affected by the state of the system being controlled. The term "atmospheric pressure" in the below description of a theoretical thermometer is essentially a "pressure reservoir" which imposes atmospheric pressure upon the thermometer.

Some common reservoirs are:

Pressure reservoir - by far the most common pressure reservoir is the Earth's atmosphere.
Temperature reservoir - A large quantity of water at its triple point forms an effective temperature reservoir.

Theory[edit]

Let's assume that we understand mechanics well enough to understand and measure volume, area, mass, and force. These may be combined to understand the concept of pressure, which is force per unit area and density, which is mass per unit volume. It has been experimentally determined that, at low enough pressures and densities, all gases behave as ideal gases. The behavior of an ideal gas is given by the ideal gas law:

PV=NkT\,

where P is pressure, V is volume, N is the number of particles (total mass divided by mass per particle), k is Boltzmann's constant, and T is temperature. In fact, this equation is more than a phenomenological equation, it gives an operational, or experimental, definition of temperature. A thermometer is a tool that measures temperature - a primitive thermometer would simply be a small container of an ideal gas, that was allowed to expand against atmospheric pressure. If we bring it into thermal contact with the system whose temperature we wish to measure, wait until it equilibrates, and then measure the volume of the thermometer, we will be able to calculate the temperature of the system in question via T=PV/Nk. Hopefully, the thermometer will be small enough that it does not appreciably alter the temperature of the system it is measuring, and also that the atmospheric pressure is not affected by the expansion of the thermometer.

The ideal gas thermometer can be defined more precisely by saying it is a system containing an ideal gas, which is thermally connected to the system it is measuring, while being dynamically and materially insulated from it. It is simultaneously dynamically connected to an external pressure reservoir, from which it is materially and thermally insulated. Other thermometers (e.g. mercury thermometers, which display the volume of mercury to the observer) may now be constructed, and calibrated against the ideal gas thermometer.

https://en.wikipedia.org/wiki/Thermodynamic_instruments

A gas thermometer is a thermometer that measures temperature by the variation in volume or pressure of a gas.^[1]

Two variants of a gas thermometer

Volume Thermometer[edit]

This thermometer functions by Charles's Law. Charles's Law states that when the temperature of a gas increases, so does the volume. ^[2]

Using Charles's Law, the temperature can be measured by knowing the volume of gas at a certain temperature by using the formula, written below. Translating it to the correct levels of the device that is holding the gas. This works on the same principle as mercury thermometers.

V\propto T\,

{\frac {V}{T}}=k

$V$ is the volume,

$T$ is the thermodynamic temperature,

$k$ is the constant for the system.

$k$ is not a fixed constant across all systems and therefore needs to be found experimentally for a given system through testing with known temperature values.

Pressure Thermometer and Absolute Zero

The constant volume gas thermometer plays a crucial role in understanding how absolute zero could be discovered long before the advent of cryogenics. Consider a graph of pressure versus temperature made not far from standard conditions (well above absolute zero) for three different samples of any ideal gas (a, b, c). To the extent that the gas is ideal, the pressure depends linearly on temperature, and the extrapolation to zero pressure occurs at absolute zero.^[3] Note that data could have been collected with three different amounts of the same gas, which would have rendered this experiment easy to do in the eighteenth century.

Plots of pressure vs temperature for three different gas samples extrapolate to absolute zero.

https://en.wikipedia.org/wiki/Gas_thermometer

https://en.wikipedia.org/wiki/Category:Thermometers

https://en.wikipedia.org/wiki/Category:Gases

https://en.wikipedia.org/wiki/Temperature

https://en.wikipedia.org/wiki/Pressure

https://en.wikipedia.org/wiki/Volume

https://en.wikipedia.org/wiki/International_System_of_Units

https://en.wikipedia.org/wiki/Periodic_table

https://en.wikipedia.org/wiki/Algebra

https://en.wikipedia.org/wiki/Trigonometry

https://en.wikipedia.org/wiki/Geometry

https://en.wikipedia.org/wiki/Calculus

https://en.wikipedia.org/wiki/Integral

https://en.wikipedia.org/wiki/Vector_calculus

https://en.wikipedia.org/wiki/Arithmetic

https://en.wikipedia.org/wiki/Algebraic_expression

https://en.wikipedia.org/wiki/Quadratic_equation

https://en.wikipedia.org/wiki/Order_of_operations

https://en.wikipedia.org/wiki/Algebraic_function

https://en.wikipedia.org/wiki/Elementary_algebra

https://en.wikipedia.org/wiki/Category:Elementary_mathematics

https://en.wikipedia.org/wiki/Logarithm

https://en.wikipedia.org/wiki/Trigonometric_functions

https://en.wikipedia.org/wiki/Exponentiation

https://en.wikipedia.org/wiki/Fundamental_theorem_of_arithmetic

https://en.wikipedia.org/wiki/Arithmetic#Arithmetic_operations

https://en.wikipedia.org/wiki/Glossary_of_mathematical_symbols

https://en.wikipedia.org/wiki/List_of_mathematical_constants

https://en.wikipedia.org/wiki/Operator_(mathematics)

https://en.wikipedia.org/wiki/Operation_(mathematics)

https://en.wikipedia.org/wiki/Boyle%27s_law

https://en.wikipedia.org/wiki/Ideal_gas_law#Combined_gas_law

https://en.wikipedia.org/wiki/Avogadro%27s_law

https://en.wikipedia.org/wiki/Ideal_gas_law

https://en.wikipedia.org/wiki/Ideal_gas_law#Combined_gas_law

https://en.wikipedia.org/wiki/Conservative_vector_field

https://en.wikipedia.org/wiki/State_variable

https://en.wikipedia.org/wiki/Equation_of_state

https://en.wikipedia.org/wiki/Nonholonomic_system

https://en.wikipedia.org/wiki/Category:Continuum_mechanics

https://en.wikipedia.org/wiki/Category:Fluid_dynamics

https://en.wikipedia.org/wiki/Category:Units_of_flow

https://en.wikipedia.org/wiki/Category:Transport_phenomena

https://en.wikipedia.org/wiki/Category:Fluid_mechanics

https://en.wikipedia.org/wiki/Solid_mechanics

https://en.wikipedia.org/wiki/Compression_(physics)

https://en.wikipedia.org/wiki/Configurational_mechanics

https://en.wikipedia.org/wiki/Materials_with_memory

https://en.wikipedia.org/wiki/Rheology

https://en.wikipedia.org/wiki/Glass

https://en.wikipedia.org/wiki/Magnetic_hysteresis

https://en.wikipedia.org/wiki/Deformation_(physics)

https://en.wikipedia.org/wiki/Ferrofluid

https://en.wikipedia.org/wiki/Enstrophy

https://en.wikipedia.org/wiki/Eigenstrain

https://en.wikipedia.org/wiki/Eckert_number

https://en.wikipedia.org/wiki/Category:Classical_mechanics

https://en.wikipedia.org/wiki/Polynomial_(hyperelastic_model)

https://en.wikipedia.org/wiki/Variational_asymptotic_method

https://en.wikipedia.org/wiki/Stress_resultants

https://en.wikipedia.org/wiki/Yield_surface

https://en.wikipedia.org/wiki/Vorticity

https://en.wikipedia.org/wiki/Torsion_constant

https://en.wikipedia.org/wiki/Thixotropy

https://en.wikipedia.org/wiki/Wave_action_(continuum_mechanics)

https://en.wikipedia.org/wiki/Collapsible_flow

https://en.wikipedia.org/wiki/Mesophase

https://en.wikipedia.org/wiki/Single_domain_(magnetic)

https://en.wikipedia.org/wiki/Thermal_fluctuations

https://en.wikipedia.org/wiki/Spheroid#Prolate_spheroids

https://en.wikipedia.org/wiki/Ellipsoid#Dynamical_properties

https://en.wikipedia.org/wiki/Multivariate_normal_distribution

https://en.wikipedia.org/wiki/Stable_distribution#A_generalized_central_limit_theorem

https://en.wikipedia.org/wiki/Dirac_delta_function

https://en.wikipedia.org/wiki/Ensemble_(fluid_mechanics)

https://en.wikipedia.org/wiki/Algebra_over_a_field

https://en.wikipedia.org/wiki/Change_of_rings#Extension_of_scalars

https://en.wikipedia.org/wiki/Complexification

https://en.wikipedia.org/wiki/Functor

https://en.wikipedia.org/wiki/Morphism#Definition

https://en.wikipedia.org/wiki/Function_composition

https://en.wikipedia.org/wiki/Measurable_function

https://en.wikipedia.org/wiki/Function_space

https://en.wikipedia.org/wiki/Mathematical_analysis#Measure_theory

https://en.wikipedia.org/wiki/Probability_space

https://en.wikipedia.org/wiki/Dimension_(vector_space)

https://en.wikipedia.org/wiki/Morphism

https://en.wikipedia.org/wiki/Real_analysis

https://en.wikipedia.org/wiki/Function_(mathematics)

https://en.wikipedia.org/wiki/Algorithm

https://en.wikipedia.org/wiki/Collapsible_flow

https://en.wikipedia.org/wiki/International_Bureau_of_Weights_and_Measures

https://en.wikipedia.org/wiki/Specific_heat_capacity

https://en.wikipedia.org/wiki/Table_of_specific_heat_capacities

https://en.wikipedia.org/wiki/Molar_heat_capacity

https://en.wikipedia.org/wiki/Amount_of_substance

https://en.wikipedia.org/wiki/Avogadro_constant

History[edit]

Origin of the concept[edit]

Jean Perrin in 1926

The Avogadro constant is named after the Italian scientist Amedeo Avogadro (1776–1856), who, in 1811, first proposed that the volume of a gas (at a given pressure and temperature) is proportional to the number of atoms or molecules regardless of the nature of the gas.^[16]

The name Avogadro's number was coined in 1909 by the physicist Jean Perrin, who defined it as the number of molecules in exactly 32 grams of oxygen.^[7] The goal of this definition was to make the mass of a mole of a substance, in grams, be numerically equal to the mass of one molecule relative to the mass of the hydrogen atom; which, because of the law of definite proportions, was the natural unit of atomic mass, and was assumed to be 1/16 of the atomic mass of oxygen.

First measurements[edit]

Josef Loschmidt

The value of Avogadro's number (not yet known by that name) was first obtained indirectly by Josef Loschmidt in 1865, by estimating the number of particles in a given volume of gas.^[14] This value, the number density n₀ of particles in an ideal gas, is now called the Loschmidt constant in his honor, and is related to the Avogadro constant, N_A, by

n_{0}={\frac {p_{0}N_{\rm {A}}}{R\,T_{0}}},

where p₀ is the pressure, R is the gas constant, and T₀ is the absolute temperature. Because of this work, the symbol L is sometimes used for the Avogadro constant,^[17] and, in German literature, that name may be used for both constants, distinguished only by the units of measurement.^[18] (However, N_A should not be confused with the entirely different Loschmidt constant in English-language literature.)

Perrin himself determined Avogadro's number by several different experimental methods. He was awarded the 1926 Nobel Prize in Physics, largely for this work.^[19]

The electric charge per mole of electrons is a constant called the Faraday constant and has been known since 1834, when Michael Faraday published his works on electrolysis. In 1910, Robert Millikan obtained the first measurement of the charge on an electron. Dividing the charge on a mole of electrons by the charge on a single electron provided a more accurate estimate of the Avogadro number.^[20]

SI definition of 1971[edit]

In 1971 the International Bureau of Weights and Measures (BIPM) decided to regard the amount of substance as an independent dimension of measurement, with the mole as its base unit in the International System of Units (SI).^[17] Specifically, the mole was defined as an amount of a substance that contains as many elementary entities as there are atoms in 0.012 kilograms of carbon-12.

By this definition, the common rule of thumb that "one gram of matter contains N₀ nucleons" was exact for carbon-12, but slightly inexact for other elements and isotopes. On the other hand, one mole of any substance contained exactly as many molecules as one mole of any other substance.

As a consequence of this definition, in the SI system the Avogadro constant N_A had the dimensionality of reciprocal of amount of substance rather than of a pure number, and had the approximate value 6.02×10²³ with units of mol⁻¹.^[17] By this definition, the value of N_A inherently had to be determined experimentally.

The BIPM also named N_A the "Avogadro constant", but the term "Avogadro number" continued to be used especially in introductory works.^[21]

SI redefinition of 2019[edit]

In 2017, the BIPM decided to change the definitions of mole and amount of substance.^[22]^[4] The mole was redefined as being the amount of substance containing exactly 6.02214076×10²³ elementary entities. One consequence of this change is that the mass of a mole of ¹²C atoms is no longer exactly 0.012 kg. On the other hand, the dalton (a.k.a. universal atomic mass unit) remains unchanged as 1/12 of the mass of ¹²C.^[23]^[24] Thus, the molar mass constant is no longer exactly 1 g/mol, although the difference (4.5×10⁻¹⁰ in relative terms, as of March 2019) is insignificant for practical purposes.^[4]^[1]

Connection to other constants[edit]

The Avogadro constant, N_A is related to other physical constants and properties.

It relates the molar gas constant R and the Boltzmann constant k_B, which in the SI (since 20 May 2019) is defined to be exactly 1.380649×10⁻²³ J/K:^[4]
$R=k_{\text{B}}N_{\text{A}}$ = 8.31446261815324 J⋅K⁻¹⋅mol⁻¹
It relates the Faraday constant F and the elementary charge e, which in the SI (since 20 May 2019) is defined as exactly 1.602176634×10⁻¹⁹ coulombs:^[4]
$F=eN_{\text{A}}$ = 96485.3321233100184 C/mol
It relates the molar mass constant, M_u and the atomic mass constant m_u, currently 1.66053906660(50)×10⁻²⁷ kg:^[25]
$M_{\text{u}}=m_{\text{u}}N_{\text{A}}$ = 0.99999999965(30)×10⁻³ kg⋅mol⁻¹^[26]

https://en.wikipedia.org/wiki/Avogadro_constant

https://en.wikipedia.org/wiki/Thermodynamic_temperature

https://en.wikipedia.org/wiki/Pressure

https://en.wikipedia.org/wiki/Particle_number

https://en.wikipedia.org/wiki/Gas_constant

A thermodynamic temperature reading of zero denotes the point at which the fundamental physical property that imbues matter with a temperature, transferable kinetic energy due to atomic motion, begins. In science, thermodynamic temperature is measured on the Kelvin scale and the unit of measure is the kelvin (unit symbol: K). For comparison, a temperature of 295 K is a comfortable one, equal to 21.85 °C and 71.33 °F.

At the zero point of thermodynamic temperature, absolute zero, the particle constituents of matter have minimal motion and can become no colder.^[1]^[2] Absolute zero, which is a temperature of zero kelvin (0 K), is precisely equal to −273.15 °C and −459.67 °F. Matter at absolute zero has no remaining transferable average kinetic energy and the only remaining particle motion is due to an ever-pervasive quantum mechanical phenomenon called zero-point energy.^[3]

https://en.wikipedia.org/wiki/Thermodynamic_temperature

Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.^[1] As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions (i.e., leptons and quarks), and force fields, whose quanta are bosons (e.g., photons and gluons). All these fields have zero-point energy.^[2] These fluctuating zero-point fields lead to a kind of reintroduction of an aether in physics^[1]^[3] since some systems can detect the existence of this energy. However, this aether cannot be thought of as a physical medium if it is to be Lorentz invariant such that there is no contradiction with Einstein's theory of special relativity.^[1]

Physics currently lacks a full theoretical model for understanding zero-point energy; in particular, the discrepancy between theorized and observed vacuum energy is a source of major contention.^[4] Physicists Richard Feynman and John Wheeler calculated the zero-point radiation of the vacuum to be an order of magnitude greater than nuclear energy, with a single light bulb containing enough energy to boil all the world's oceans.^[5] Yet according to Einstein's theory of general relativity, any such energy would gravitate and the experimental evidence from both the expansion of the universe, dark energy and the Casimir effect shows any such energy to be exceptionally weak. A popular proposal that attempts to address this issue is to say that the fermion field has a negative zero-point energy, while the boson field has positive zero-point energy and thus these energies somehow cancel each other out.^[6]^[7] This idea would be true if supersymmetry were an exact symmetry of nature; however, the LHC at CERN has so far found no evidence to support it. Moreover, it is known that if supersymmetry is valid at all, it is at most a broken symmetry, only true at very high energies, and no one has been able to show a theory where zero-point cancellations occur in the low energy universe we observe today.^[7] This discrepancy is known as the cosmological constant problem and it is one of the greatest unsolved mysteries in physics. Many physicists believe that "the vacuum holds the key to a full understanding of nature".^[8]

https://en.wikipedia.org/wiki/Zero-point_energy

In astronomy, the Zero Point in a photometric system is defined as the magnitude of an object that produces 1 count per second on the detector.^[1] The zero point is used to calibrate a system to the standard magnitude system, as the flux detected from stars will vary from detector to detector.^[2] Traditionally, Vega is used as the calibration star for the zero point magnitude in specific pass bands (U, B, and V), although often, an average of multiple stars is used for higher accuracy.^[3] It is not often practical to find Vega in the sky to calibrate the detector, so for general purposes, any star may be used in the sky that has a known apparent magnitude.^[4]

https://en.wikipedia.org/wiki/Zero_Point_(photometry)

The quantum vacuum state or simply quantum vacuum refers to the quantum state with the lowest possible energy.

Quantum vacuum may also refer to:

Quantum chromodynamic vacuum (QCD vacuum), a non-perturbative vacuum
Quantum electrodynamic vacuum (QED vacuum), a field-theoretic vacuum
Quantum vacuum (ground state), the state of lowest energy of a quantum system
- Quantum vacuum collapse, a hypothetical vacuum metastability event
- Quantum vacuum expectation value, an operator's average, expected value in a quantum vacuum
Quantum vacuum energy, an underlying background energy that exists in space throughout the entire Universe
The Quantum Vacuum, a physics textbook by Peter W. Milonni

Chemical Engineering[edit]

Chemical engineering unit operations consist of five classes:

Fluid flow processes, including fluids transportation, filtration, and solids fluidization.
Heat transfer processes, including evaporation and heat exchange.
Mass transfer processes, including gas absorption, distillation, extraction, adsorption, and drying.
Thermodynamic processes, including gas liquefaction, and refrigeration.
Mechanical processes, including solids transportation, crushing and pulverization, and screening and sieving.

Chemical engineering unit operations also fall in the following categories which involve elements from more than one class:

Combination (mixing)
Separation (distillation, crystallization)
Reaction (chemical reaction)

Furthermore, there are some unit operations which combine even these categories, such as reactive distillation and stirred tank reactors. A "pure" unit operation is a physical transport process, while a mixed chemical/physical process requires modeling both the physical transport, such as diffusion, and the chemical reaction. This is usually necessary for designing catalytic reactions, and is considered a separate discipline, termed chemical reaction engineering.

Chemical engineering unit operations and chemical engineering unit processing form the main principles of all kinds of chemical industries and are the foundation of designs of chemical plants, factories, and equipment used.

https://en.wikipedia.org/wiki/Unit_operation

In physics, transport phenomena are all irreversible processes of statistical nature stemming from the random continuous motion of molecules, mostly observed in fluids. Every aspect of transport phenomena is grounded in two primary concepts : the conservation laws, and the constitutive equations. The conservation laws, which in the context of transport phenomena are formulated as continuity equations, describe how the quantity being studied must be conserved. The constitutive equations describe how the quantity in question responds to various stimuli via transport. Prominent examples include Fourier's law of heat conduction and the Navier–Stokes equations, which describe, respectively, the response of heat flux to temperature gradients and the relationship between fluid flux and the forces applied to the fluid. These equations also demonstrate the deep connection between transport phenomena and thermodynamics, a connection that explains why transport phenomena are irreversible. Almost all of these physical phenomena ultimately involve systems seeking their lowest energy state in keeping with the principle of minimum energy. As they approach this state, they tend to achieve true thermodynamic equilibrium, at which point there are no longer any driving forces in the system and transport ceases. The various aspects of such equilibrium are directly connected to a specific transport: heat transfer is the system's attempt to achieve thermal equilibrium with its environment, just as mass and momentum transport move the system towards chemical and mechanical equilibrium.

Examples of transport processes include heat conduction (energy transfer), fluid flow (momentum transfer), molecular diffusion (mass transfer), radiation and electric charge transfer in semiconductors.^[3]^[4]^[5]^[6]

Transport phenomena have wide application. For example, in solid state physics, the motion and interaction of electrons, holes and phonons are studied under "transport phenomena". Another example is in biomedical engineering, where some transport phenomena of interest are thermoregulation, perfusion, and microfluidics. In chemical engineering, transport phenomena are studied in reactor design, analysis of molecular or diffusive transport mechanisms, and metallurgy.

The transport of mass, energy, and momentum can be affected by the presence of external sources:

An odor dissipates more slowly (and may intensify) when the source of the odor remains present.
The rate of cooling of a solid that is conducting heat depends on whether a heat source is applied.
The gravitational force acting on a rain drop counteracts the resistance or drag imparted by the surrounding air.

Diffusion[edit]There are some notable similarities in equations for momentum, energy, and mass transfer[7] which can all be transported by diffusion, as illustrated by the following examples:
Mass: the spreading and dissipation of odors in air is an example of mass diffusion.
Energy: the conduction of heat in a solid material is an example of heat diffusion.
Momentum: the drag experienced by a rain drop as it falls in the atmosphere is an example of momentum diffusion (the rain drop loses momentum to the surrounding air through viscous stresses and decelerates).
The molecular transfer equations of Newton's law for fluid momentum, Fourier's law for heat, and Fick's law for mass are very similar. One can convert from one transport coefficient to another in order to compare all three different transport phenomena.[8]
Comparison of diffusion phenomenaTransported quantityPhysical phenomenonEquation
MomentumViscosity
(Newtonian fluid)
EnergyHeat conduction
(Fourier's law)
MassMolecular diffusion
(Fick's law)
(Definitions of these formulas are given below).
A great deal of effort has been devoted in the literature to developing analogies among these three transport processes for turbulent transfer so as to allow prediction of one from any of the others. The Reynolds analogy assumes that the turbulent diffusivities are all equal and that the molecular diffusivities of momentum (μ/ρ) and mass (DAB) are negligible compared to the turbulent diffusivities. When liquids are present and/or drag is present, the analogy is not valid. Other analogies, such as von Karman's and Prandtl's, usually result in poor relations.
The most successful and most widely used analogy is the Chilton and Colburn J-factor analogy.[9] This analogy is based on experimental data for gases and liquids in both the laminar and turbulent regimes. Although it is based on experimental data, it can be shown to satisfy the exact solution derived from laminar flow over a flat plate. All of this information is used to predict transfer of mass.
Onsager reciprocal relations[edit]Main article: Onsager reciprocal relations
In fluid systems described in terms of temperature, matter density, and pressure, it is known that temperature differences lead to heat flows from the warmer to the colder parts of the system; similarly, pressure differences will lead to matter flow from high-pressure to low-pressure regions (a "reciprocal relation"). What is remarkable is the observation that, when both pressure and temperature vary, temperature differences at constant pressure can cause matter flow (as in convection) and pressure differences at constant temperature can cause heat flow. Perhaps surprisingly, the heat flow per unit of pressure difference and the density (matter) flow per unit of temperature difference are equal.
This equality was shown to be necessary by Lars Onsager using statistical mechanics as a consequence of the time reversibility of microscopic dynamics. The theory developed by Onsager is much more general than this example and capable of treating more than two thermodynamic forces at once.[10]
Momentum transfer[edit]In momentum transfer, the fluid is treated as a continuous distribution of matter. The study of momentum transfer, or fluid mechanics can be divided into two branches: fluid statics (fluids at rest), and fluid dynamics (fluids in motion). When a fluid is flowing in the x-direction parallel to a solid surface, the fluid has x-directed momentum, and its concentration is υxρ. By random diffusion of molecules there is an exchange of molecules in the z-direction. Hence the x-directed momentum has been transferred in the z-direction from the faster- to the slower-moving layer. The equation for momentum transfer is Newton's law of viscosity written as follows:
where τzx is the flux of x-directed momentum in the z-direction, ν is μ/ρ, the momentum diffusivity, z is the distance of transport or diffusion, ρ is the density, and μ is the dynamic viscosity. Newton's law of viscosity is the simplest relationship between the flux of momentum and the velocity gradient.
Mass transfer[edit]When a system contains two or more components whose concentration vary from point to point, there is a natural tendency for mass to be transferred, minimizing any concentration difference within the system. Mass Transfer in a system is governed by Fick's First Law: 'Diffusion flux from higher concentration to lower concentration is proportional to the gradient of the concentration of the substance and the diffusivity of the substance in the medium.' Mass transfer can take place due to different driving forces. Some of them are:[11]
Mass can be transferred by the action of a pressure gradient (pressure diffusion)
Forced diffusion occurs because of the action of some external force
Diffusion can be caused by temperature gradients (thermal diffusion)
Diffusion can be caused by differences in chemical potential
This can be compared to Fick's Law of Diffusion, for a species A in a binary mixture consisting of A and B:
where D is the diffusivity constant.
Energy transfer[edit]All processes in engineering involve the transfer of energy. Some examples are the heating and cooling of process streams, phase changes, distillations, etc. The basic principle is the first law of thermodynamics which is expressed as follows for a static system:
The net flux of energy through a system equals the conductivity times the rate of change of temperature with respect to position.
For other systems that involve either turbulent flow, complex geometries or difficult boundary conditions another equation would be easier to use:
where A is the surface area, : is the temperature driving force, Q is the heat flow per unit time, and h is the heat transfer coefficient.
Within heat transfer, two types of convection can occur:
Forced convection can occur in both laminar and turbulent flow. In the situation of laminar flow in circular tubes, several dimensionless numbers are used such as Nusselt number, Reynolds number, and Prandtl number. The commonly used equation is .
Natural or free convection is a function of Grashof and Prandtl numbers. The complexities of free convection heat transfer make it necessary to mainly use empirical relations from experimental data.[11]
Heat transfer is analyzed in packed beds, nuclear reactors and heat exchangers.
Applications[edit]Pollution[edit]The study of transport processes is relevant for understanding the release and distribution of pollutants into the environment. In particular, accurate modeling can inform mitigation strategies. Examples include the control of surface water pollution from urban runoff, and policies intended to reduce the copper content of vehicle brake pads in the U.S.[12][13]
See also[edit]Constitutive equation
Continuity equation
Wave propagation
Pulse
Action potential
Bioheat transfer

Comparison of diffusion phenomena
Transported quantity	Physical phenomenon	Equation
Momentum	Viscosity (Newtonian fluid)	$\tau =-\nu {\frac {\partial \rho \upsilon }{\partial x}}$
Energy	Heat conduction (Fourier's law)	${\frac {q}{A}}=-k{\frac {dT}{dx}}$
Mass	Molecular diffusion (Fick's law)	$J=-D{\frac {\partial C}{\partial x}}$

https://en.wikipedia.org/wiki/Transport_phenomena

https://en.wikipedia.org/wiki/Statistical_mechanics

https://en.wikipedia.org/wiki/Reversible_process_(thermodynamics)

https://en.wikipedia.org/wiki/Trihydrogen_cation

https://en.wikipedia.org/wiki/Hydride

https://en.wikipedia.org/wiki/Positronium_hydride

https://en.wikipedia.org/wiki/Exotic_atom#exotic_molecules

https://en.wikipedia.org/wiki/Isotopologue

https://en.wikipedia.org/wiki/Ionosphere

https://en.wikipedia.org/wiki/Triatomic_molecule

https://en.wikipedia.org/wiki/Three-center_two-electron_bond

https://en.wikipedia.org/wiki/Polyhedral_skeletal_electron_pair_theory

https://en.wikipedia.org/wiki/Isotopomers

https://en.wikipedia.org/wiki/Pseudohalogen

https://en.wikipedia.org/wiki/Nuclear_transmutation

https://en.wikipedia.org/wiki/Dark_matter

https://en.wikipedia.org/wiki/Lambda-CDM_model

https://en.wikipedia.org/wiki/Dark_energy

https://en.wikipedia.org/wiki/Dark_fluid

https://en.wikipedia.org/wiki/Cosmic_microwave_background

https://en.wikipedia.org/wiki/Cosmic_neutrino_background

https://en.wikipedia.org/wiki/Annihilation

https://en.wikipedia.org/wiki/Nuclear_fission

https://en.wikipedia.org/wiki/Exponential_decay

https://en.wikipedia.org/wiki/Weak_interaction

https://en.wikipedia.org/wiki/Vacuum

https://en.wikipedia.org/wiki/Mirror_matter

https://en.wikipedia.org/wiki/Fusion_power#Magnetic_Mirror

https://en.wikipedia.org/wiki/Fictitious_force

Outer space is an even higher-quality vacuum, with the equivalent of just a few hydrogen atoms per cubic meter on average in intergalactic space.^[5]

https://en.wikipedia.org/wiki/Vacuum

https://en.wikipedia.org/wiki/Magnetohydrodynamics

Nuclides with even numbers of both have a total spin of zero and are therefore NMR-inactive.

https://en.wikipedia.org/wiki/Nuclear_magnetic_resonance

https://en.wikipedia.org/wiki/Degaussing

https://en.wikipedia.org/wiki/Ferromagnetism

https://en.wikipedia.org/wiki/Magnetic_field

https://en.wikipedia.org/wiki/Nuclear_magnetic_resonance

https://en.wikipedia.org/wiki/Angular_momentum

https://en.wikipedia.org/wiki/Nuclide

https://en.wikipedia.org/wiki/Larmor_precession

https://en.wikipedia.org/wiki/Magnetic_coupling

https://en.wikipedia.org/wiki/Magnetic_hysteresis

https://en.wikipedia.org/wiki/Magnetic_flux

https://en.wikipedia.org/wiki/Magnetized_target_fusion

https://en.wikipedia.org/wiki/Heat_exchanger

https://en.wikipedia.org/wiki/Drag_(physics)

https://en.wikipedia.org/wiki/Electrodynamic_suspension

https://en.wikipedia.org/wiki/Magnetic_levitation

https://en.wikipedia.org/wiki/Lenz%27s_law

https://en.wikipedia.org/wiki/Ampère%27s_force_law

https://en.wikipedia.org/wiki/Earnshaw%27s_theorem#Proofs_for_magnetic_dipoles

https://en.wikipedia.org/wiki/Gyroscope

https://en.wikipedia.org/wiki/Linear_induction_motor

https://en.wikipedia.org/wiki/Pyrolytic_carbon

https://en.wikipedia.org/wiki/Bismuth

https://en.wikipedia.org/wiki/Vacuum_permeability

https://en.wikipedia.org/wiki/Electrostatic_levitation

https://en.wikipedia.org/wiki/Magnetic_levitation

https://en.wikipedia.org/wiki/Magnetic_pressure

https://en.wikipedia.org/wiki/Dipole_magnet

https://en.wikipedia.org/wiki/Permeability_(electromagnetism)

https://en.wikipedia.org/wiki/Nonlinear_optics

https://en.wikipedia.org/wiki/Heat_exchanger
https://en.wikipedia.org/wiki/Drag_(physics)
https://en.wikipedia.org/wiki/Electrodynamic_suspension
https://en.wikipedia.org/wiki/Magnetic_levitation
https://en.wikipedia.org/wiki/Field-reversed_configuration
https://en.wikipedia.org/wiki/Superconductivity

https://en.wikipedia.org/wiki/Diol_cyclization
cyclicization ringulants
https://en.wikipedia.org/wiki/Magnetic_dipole–dipole_interaction
https://en.wikipedia.org/wiki/J-coupling
https://en.wikipedia.org/wiki/Electron_electric_dipole_moment
https://en.wikipedia.org/wiki/Zero-point_energy
https://en.wikipedia.org/wiki/Van_der_Waals_force
https://en.wikipedia.org/wiki/Zero_field_splitting
https://en.wikipedia.org/wiki/Quadrupole
https://en.wikipedia.org/wiki/Quadrupole#Gravitational_quadrupole
https://en.wikipedia.org/wiki/Trace_(linear_algebra)
https://en.wikipedia.org/wiki/Overtone_band

https://en.wikipedia.org/wiki/Lockheed_Martin_Compact_Fusion_Reactor
https://en.wikipedia.org/wiki/Deuterium–tritium_fusion
https://en.wikipedia.org/wiki/Magnetized_target_fusion

https://en.wikipedia.org/wiki/Magnetic_levitation
https://en.wikipedia.org/wiki/Dimensionless_quantity
https://en.wikipedia.org/wiki/Linear_stability

https://en.wikipedia.org/wiki/Heat_exchanger
https://en.wikipedia.org/wiki/Field-reversed_configuration
https://en.wikipedia.org/wiki/Superconductivity
https://en.wikipedia.org/wiki/Magneto-inertial_fusion

https://en.wikipedia.org/wiki/Neutronium
https://en.wikipedia.org/wiki/Preon

https://en.wikipedia.org/wiki/Meson_bomb

https://en.wikipedia.org/wiki/Pressuron
https://en.wikipedia.org/wiki/Vertical_pressure_variation

https://en.wikipedia.org/wiki/Zero-point_energy

https://en.wikipedia.org/wiki/Quantum_vacuum_(disambiguation)

https://en.wikipedia.org/wiki/Muon-catalyzed_fusion

https://en.wikipedia.org/wiki/Energy_amplifier

https://en.wikipedia.org/wiki/Triple-alpha_process

https://en.wikipedia.org/wiki/Silicon-burning_process

https://en.wikipedia.org/wiki/R-process

https://en.wikipedia.org/wiki/Carbon-burning_process

https://en.wikipedia.org/wiki/CNO_cycle

https://en.wikipedia.org/wiki/Pion

https://en.wikipedia.org/wiki/Proton–proton_chain

https://en.wikipedia.org/wiki/Helium_flash

https://en.wikipedia.org/wiki/Lithium_burning

https://en.wikipedia.org/wiki/Neon-burning_process

https://en.wikipedia.org/wiki/Photodisintegration

https://en.wikipedia.org/wiki/Alpha_particle

https://en.wikipedia.org/wiki/Oxygen-burning_process

https://en.wikipedia.org/wiki/Levitated_dipole

https://en.wikipedia.org/wiki/Magnetic_confinement_fusion

https://en.wikipedia.org/wiki/Magnetic_field

https://en.wikipedia.org/wiki/Fusion_power

https://en.wikipedia.org/wiki/Magnetic_confinement_fusion

https://en.wikipedia.org/wiki/Muon-catalyzed_fusion

https://en.wikipedia.org/wiki/Plasma_(physics)

https://en.wikipedia.org/wiki/Tokamak

https://en.wikipedia.org/wiki/Magnetic_mirror

https://en.wikipedia.org/wiki/Pinch_(plasma_physics)

https://en.wikipedia.org/wiki/Stellarator

https://en.wikipedia.org/wiki/Reversed_field_pinch

https://en.wikipedia.org/wiki/Gas_torus

https://en.wikipedia.org/wiki/Magnetosphere

https://en.wikipedia.org/wiki/List_of_plasma_physics_articles

https://en.wikipedia.org/wiki/Category:Astrophysics

https://en.wikipedia.org/wiki/Magnetized_Liner_Inertial_Fusion

Magnetized Liner Inertial Fusion (MagLIF) is an emerging method of producing controlled nuclear fusion. It is part of the broad category of inertial fusion energy (IFE) systems, which drives the inward movement of fusion fuel, thereby compressing it to reach densities and temperatures where fusion reactions occur. Previous IFE experiments used laser drivers to reach these conditions, whereas MagLIF uses a combination of lasers for heating and Z-pinch for compression. A variety of theoretical considerations suggest such a system will reach the required conditions for fusion with a machine of significantly less complexity than the pure-laser approach. There are currently at least two facilities testing feasibility of the MagLIF concept, the Z-machine at Sandia Labs in the US and Primary Test Stand (PTS) located in Mianyang, China.^[1]

Description[edit]

MagLIF is a method of generating energy by using a 100 nanosecond pulse of electricity to create an intense Z-pinch magnetic field that inwardly crushes a fuel filled cylindrical metal liner (a hohlraum) through which the electric pulse runs. Just before the cylinder implodes, a laser is used to preheat fusion fuel (such as deuterium-tritium) that is held within the cylinder and contained by a magnetic field. Sandia National Labs is currently exploring the potential for this method to generate energy by utilizing the Z machine.

MagLIF has characteristics of both Inertial confinement fusion (due to the usage of a laser and pulsed compression) and magnetic confinement (due to the utilization of a powerful magnetic field to inhibit thermal conduction and contain the plasma). In results published in 2012, a LASNEX based computer simulation of a 70 megaampere facility showed the prospect of a spectacular energy return of 1000 times the expended energy. A 60 MA facility would produce a 100x yield. The currently available facility at Sandia, Z machine, is capable of 27 MA and may be capable of producing slightly more than breakeven energy while helping to validate the computer simulations.^[2] The Z-machine conducted MagLIF experiments in November 2013 with a view towards breakeven experiments using D-T fuel in 2018.^[3]

Sandia Labs planned to proceed to ignition experiments after establishing the following:^[4]

That the liner will not break apart too quickly under the intense energy. This has been apparently confirmed by recent experiments. This hurdle was the biggest concern regarding MagLIF following its initial proposal.
That laser preheating is able to correctly heat the fuel — to be confirmed by experiments starting in December 2012.
That magnetic fields generated by a pair of coils above and below the hohlraum can serve to trap the preheated fusion fuel and importantly inhibit thermal conduction without causing the target to buckle prematurely. — to be confirmed by experiments starting in December 2012.

Following these experiments, an integrated test started in November 2013. The test yielded about 10¹⁰ high-energy neutrons.

As of November 2013, the facility at Sandia labs had the following capabilities:^[3]^[5]

10 tesla magnetic field
2 kJ laser
16 MA
D-D fuel

In 2014, the test yielded up to 2×10¹² D-D neutrons under the following conditions:^[6]

10 tesla magnetic field
2.5 kJ laser
19 MA
D-D fuel

Experiments aiming for energy breakeven with D-T fuel were expected to occur in 2018.^[7]
To achieve scientific breakeven, the facility is going through a 5-year upgrade to:

30 teslas
8 kJ laser
27 MA
D-T fuel handling^[3]

In 2019, after encountering significant problems related to mixing of imploding foil with fuel and helical instability of plasma,^[8] the tests yielded up to 3.2×10¹² neutrons under the following conditions:^[9]

1.2 kJ laser
18 MA

In 2020, "the burn-averaged ion temperature doubled to 3.1 keV and the primary deuterium-deuterium neutron yield increased by more than an order of magnitude to 1.1 × 10^13 (2 kJ deuterium-tritium equivalent) through a simultaneous increase in the applied magnetic field (from 10.4 to 15.9 T), laser preheat energy (from 0.46 to 1.2 kJ), and current coupling (from 16 to 20 MA). " ^[10]

Nucleosynthesis

Stellar nucleosynthesis Big Bang nucleosynthesis Supernova nucleosynthesis Cosmic ray spallation
Related topics
Astrophysics Nuclear fusion R-process S-process Nuclear fission
v t e

fuel	T [keV]	<σv>/T² [m³/s/keV²]
2 1D -3 1T	13.6	1.24×10⁻²⁴
2 1D -2 1D	15	1.28×10⁻²⁶
2 1D -3 2He	58	2.24×10⁻²⁶
p⁺-6 3Li	66	1.46×10⁻²⁷
p⁺-11 5B	123	3.01×10⁻²⁷

fuel	Z	E_fus [MeV]	E_ch [MeV]	neutronicity
2 1D -3 1T	1	17.6	3.5	0.80
2 1D -2 1D	1	12.5	4.2	0.66
2 1D -3 2He	2	18.3	18.3	≈0.05
p⁺-11 5B	5	8.7	8.7	≈0.001

fuel	<σv>/T²	penalty/bonus	inverse reactivity	Lawson criterion	power density (W/m³/kPa²)	inverse ratio of power density
2 1D -3 1T	1.24×10⁻²⁴	1	1	1	34	1
2 1D -2 1D	1.28×10⁻²⁶	2	48	30	0.5	68
2 1D -3 2He	2.24×10⁻²⁶	2/3	83	16	0.43	80
p⁺-6 3Li	1.46×10⁻²⁷	1/2	1700		0.005	6800
p⁺-11 5B	3.01×10⁻²⁷	1/3	1240	500	0.014	2500

fuel	T_i (keV)	P_fusion/P_{Bremsstrahlung}
2 1D -3 1T	50	140
2 1D -2 1D	500	2.9
2 1D -3 2He	100	5.3
3 2He -3 2He	1000	0.72
p⁺-6 3Li	800	0.21
p⁺-11 5B	300	0.57

Mathematical description of cross section[edit]

Fusion under classical physics[edit]

In a classical picture, nuclei can be understood as hard spheres that repel each other through the Coulomb force but fuse once the two spheres come close enough for contact. Estimating the radius of an atomic nuclei as about one femtometer, the energy needed for fusion of two hydrogen is:

$E_{\text{thresh}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {Z_{1}Z_{2}}{r}}{\xrightarrow {\text{2 protons}}}{\frac {1}{4\pi \epsilon _{0}}}{\frac {e^{2}}{1{\text{ fm}}}}\approx 1.4{\text{ MeV}}$

This would imply that for the core of the sun, which has a Boltzmann distribution with a temperature of around 1.4 keV, the probability hydrogen would reach the threshold is $10^{-290}$ , that is, fusion would never occur. However, fusion in the sun does occur due to quantum mechanics.

Parameterization of cross section[edit]

The probability that fusion occurs is greatly increased compared to the classical picture, thanks to the smearing of the effective radius as the DeBroglie wavelength as well as quantum tunnelling through the potential barrier. To determine the rate of fusion reactions, the value of most interest is the cross section, which describes the probability that particles will fuse by giving a characteristic area of interaction. An estimation of the fusion cross-sectional area is often broken into three pieces:

\sigma \approx \sigma _{geometry}\times T\times R

Where $\sigma _{geometry}$ is the geometric cross section, $T$ is the barrier transparency and $R$ is the reaction characteristics of the reaction.

$\sigma _{geometry}$ is of the order of the square of the de-Broglie wavelength $\sigma _{geometry}\approx \lambda ^{2}={\bigg (}{\frac {\hbar }{m_{r}v}}{\bigg )}^{2}\propto {\frac {1}{\epsilon }}$ where $m_{r}$ is the reduced mass of the system and $\epsilon$ is the center of mass energy of the system.

$T$ can be approximated by the Gamow transparency, which has the form: $T\approx e^{-{\sqrt {\epsilon _{G}/\epsilon }}}$ where $\epsilon _{G}=(\pi \alpha Z_{1}Z_{2})^{2}\times 2m_{r}c^{2}$ is the Gamow factor and comes from estimating the quantum tunneling probability through the potential barrier.

$R$ contains all the nuclear physics of the specific reaction and takes very different values depending on the nature of the interaction. However, for most reactions, the variation of $R(\epsilon )$ is small compared to the variation from the Gamow factor and so is approximated by a function called the Astrophysical S-factor, $S(\epsilon )$ , which is weakly varying in energy. Putting these dependencies together, one approximation for the fusion cross section as a function of energy takes the form:

\sigma (\epsilon )\approx {\frac {S(\epsilon )}{\epsilon }}e^{-{\sqrt {\epsilon _{G}/\epsilon }}}

More detailed forms of the cross-section can be derived through nuclear physics-based models and R-matrix theory.

https://en.wikipedia.org/wiki/Nuclear_fusion#Criteria_and_candidates_for_terrestrial_reactions

In mathematics, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.^[1]
Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body.
https://en.wikipedia.org/wiki/Gravitational_potential

The axion (/ˈæksiɒn/) is a hypothetical elementary particle postulated by the Peccei–Quinn theory in 1977 to resolve the strong CP problem in quantum chromodynamics (QCD). If axions exist and have low mass within a specific range, they are of interest as a possible component of cold dark matter.

https://en.wikipedia.org/wiki/Axion

Because dark matter has not yet been observed directly, if it exists, it must barely interact with ordinary baryonic matter and radiation, except through gravity. Most dark matter is thought to be non-baryonic in nature; it may be composed of some as-yet undiscovered subatomic particles.[b] The primary candidate for dark matter is some new kind of elementary particle that has not yet been discovered, in particular, weakly interacting massive particles(WIMPs).[14] Many experiments to directly detect and study dark matter particles are being actively undertaken, but none have yet succeeded.[15] Dark matter is classified as "cold", "warm", or "hot" according to its velocity (more precisely, its free streaming length). Current models favor a cold dark matterscenario, in which structures emerge by gradual accumulation of particles.

https://en.wikipedia.org/wiki/Dark_matter

Small molecule hyperfine structure[edit]

A typical simple example of the hyperfine structure due to the interactions discussed above is in the rotational transitions of hydrogen cyanide (¹H¹²C¹⁴N) in its ground vibrational state. Here, the electric quadrupole interaction is due to the ¹⁴N-nucleus, the hyperfine nuclear spin-spin splitting is from the magnetic coupling between nitrogen, ¹⁴N (I_N = 1), and hydrogen, ¹H (I_H = 1⁄2), and a hydrogen spin-rotation interaction due to the ¹H-nucleus. These contributing interactions to the hyperfine structure in the molecule are listed here in descending order of influence. Sub-doppler techniques have been used to discern the hyperfine structure in HCN rotational transitions.^[11]
The dipole selection rules for HCN hyperfine structure transitions are $\Delta J=1$ , $\Delta F=\{0,\pm 1\}$ , where $J$ is the rotational quantum number and $F$ is the total rotational quantum number inclusive of nuclear spin ( $F=J+I_{\text{N}}$ ), respectively. The lowest transition ( $J=1\rightarrow 0$ ) splits into a hyperfine triplet. Using the selection rules, the hyperfine pattern of $J=2\rightarrow 1$ transition and higher dipole transitions is in the form of a hyperfine sextet. However, one of these components ( $\Delta F=-1$ ) carries only 0.6% of the rotational transition intensity in the case of $J=2\rightarrow 1$ . This contribution drops for increasing J. So, from $J=2\rightarrow 1$ upwards the hyperfine pattern consists of three very closely spaced stronger hyperfine components ( $\Delta J=1$ , $\Delta F=1$ ) together with two widely spaced components; one on the low frequency side and one on the high frequency side relative to the central hyperfine triplet. Each of these outliers carry ~ ${\tfrac {1}{2}}J^{2}$ ( $J$ is the upper rotational quantum number of the allowed dipole transition) the intensity of the entire transition. For consecutively higher- $J$ transitions, there are small but significant changes in the relative intensities and positions of each individual hyperfine component.^[12]

Measurements[edit]

Hyperfine interactions can be measured, among other ways, in atomic and molecular spectra and in electron paramagnetic resonance spectra of free radicals and transition-metal ions.

Applications[edit]

Astrophysics[edit]

The hyperfine transition as depicted on the Pioneer plaque
As the hyperfine splitting is very small, the transition frequencies are usually not located in the optical, but are in the range of radio- or microwave (also called sub-millimeter) frequencies.
Hyperfine structure gives the 21 cm line observed in H I regions in interstellar medium.
Carl Sagan and Frank Drake considered the hyperfine transition of hydrogen to be a sufficiently universal phenomenon so as to be used as a base unit of time and length on the Pioneer plaque and later Voyager Golden Record.
In submillimeter astronomy, heterodyne receivers are widely used in detecting electromagnetic signals from celestial objects such as star-forming core or young stellar objects. The separations among neighboring components in a hyperfine spectrum of an observed rotational transition are usually small enough to fit within the receiver's IF band. Since the optical depth varies with frequency, strength ratios among the hyperfine components differ from that of their intrinsic (or optically thin) intensities (these are so-called hyperfine anomalies, often observed in the rotational transitions of HCN^[12]). Thus, a more accurate determination of the optical depth is possible. From this we can derive the object's physical parameters.^[13]

Nuclear spectroscopy[edit]

In nuclear spectroscopy methods, the nucleus is used to probe the local structure in materials. The methods mainly base on hyperfine interactions with the surrounding atoms and ions. Important methods are nuclear magnetic resonance, Mössbauer spectroscopy, and perturbed angular correlation.

Nuclear technology[edit]

The atomic vapor laser isotope separation (AVLIS) process uses the hyperfine splitting between optical transitions in uranium-235 and uranium-238 to selectively photo-ionize only the uranium-235 atoms and then separate the ionized particles from the non-ionized ones. Precisely tuned dye lasers are used as the sources of the necessary exact wavelength radiation.

Use in defining the SI second and meter[edit]

The hyperfine structure transition can be used to make a microwave notch filter with very high stability, repeatability and Q factor, which can thus be used as a basis for very precise atomic clocks. The term transition frequency denotes the frequency of radiation corresponding to the transition between the two hyperfine levels of the atom, and is equal to $f = Δ E / h$ , where $Δ E$ is difference in energy between the levels and $h$ is the Planck constant. Typically, the transition frequency of a particular isotope of caesium or rubidium atoms is used as a basis for these clocks.
Due to the accuracy of hyperfine structure transition-based atomic clocks, they are now used as the basis for the definition of the second. One second is now defined to be exactly 9192631770cycles of the hyperfine structure transition frequency of caesium-133 atoms.
On October 21, 1983, the 17th CGPM defined the metre as the length of the path travelled by light in a vacuum during a time interval of 1/299,792,458 of a second.^[14]^[15]

Precision tests of quantum electrodynamics[edit]

The hyperfine splitting in hydrogen and in muonium have been used to measure the value of the fine structure constant α. Comparison with measurements of α in other physical systems provides a stringent test of QED.

Qubit in ion-trap quantum computing[edit]

The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.^[16]

In physics[edit]

In physics, a pseudoscalar denotes a physical quantity analogous to a scalar. Both are physical quantities which assume a single value which is invariant under proper rotations. However, under the parity transformation, pseudoscalars flip their signs while scalars do not. As reflections through a plane are the combination of a rotation with the parity transformation, pseudoscalars also change signs under reflections.

https://en.wikipedia.org/wiki/Pseudoscalar

In geometry and physics, spinors /spɪnər/ are elements of a complex vector space that can be associated with Euclidean space.^[b] Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation.^[c] However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms).
It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geometry by Élie Cartan in 1913.^[1]^[d] In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.^[e]
Spinors are characterized by the specific way in which they behave under rotations. They change in different ways depending not just on the overall final rotation, but the details of how that rotation was achieved (by a continuous path in the rotation group). There are two topologically distinguishable classes (homotopy classes) of paths through rotations that result in the same overall rotation, as illustrated by the belt trick puzzle. These two inequivalent classes yield spinor transformations of opposite sign. The spin group is the group of all rotations keeping track of the class.^[f] It doubly covers the rotation group, since each rotation can be obtained in two inequivalent ways as the endpoint of a path. The space of spinors by definition is equipped with a (complex) linear representation of the spin group, meaning that elements of the spin group act as linear transformations on the space of spinors, in a way that genuinely depends on the homotopy class.^[g] In mathematical terms, spinors are described by a double-valued projective representation of the rotation group SO(3).
Although spinors can be defined purely as elements of a representation space of the spin group (or its Lie algebra of infinitesimal rotations), they are typically defined as elements of a vector space that carries a linear representation of the Clifford algebra. The Clifford algebra is an associative algebra that can be constructed from Euclidean space and its inner product in a basis-independent way. Both the spin group and its Lie algebra are embedded inside the Clifford algebra in a natural way, and in applications the Clifford algebra is often the easiest to work with.^[h] A Clifford space operates on a spinor space, and the elements of a spinor space are spinors.^[3] After choosing an orthonormal basis of Euclidean space, a representation of the Clifford algebra is generated by gamma matrices, matrices that satisfy a set of canonical anti-commutation relations. The spinors are the column vectors on which these matrices act. In three Euclidean dimensions, for instance, the Pauli spin matrices are a set of gamma matrices,^[i] and the two-component complex column vectors on which these matrices act are spinors. However, the particular matrix representation of the Clifford algebra, hence what precisely constitutes a "column vector" (or spinor), involves the choice of basis and gamma matrices in an essential way. As a representation of the spin group, this realization of spinors as (complex^[j]) column vectors will either be irreducible if the dimension is odd, or it will decompose into a pair of so-called "half-spin" or Weyl representations if the dimension is even.^[k]
https://en.wikipedia.org/wiki/Spinor
https://en.wikipedia.org/wiki/S-factor

Parameterization of cross section[edit]

The probability that fusion occurs is greatly increased compared to the classical picture, thanks to the smearing of the effective radius as the DeBroglie wavelength as well as quantum tunnelling through the potential barrier. To determine the rate of fusion reactions, the value of most interest is the cross section, which describes the probability that particles will fuse by giving a characteristic area of interaction. An estimation of the fusion cross-sectional area is often broken into three pieces:
$\sigma \approx \sigma _{geometry}\times T\times R$
Where $\sigma _{geometry}$ is the geometric cross section, $T$ is the barrier transparency and $R$ is the reaction characteristics of the reaction.
$\sigma _{geometry}$ is of the order of the square of the de-Broglie wavelength $\sigma _{geometry}\approx \lambda ^{2}={\bigg (}{\frac {\hbar }{m_{r}v}}{\bigg )}^{2}\propto {\frac {1}{\epsilon }}$ where $m_{r}$ is the reduced mass of the system and $\epsilon$ is the center of mass energy of the system.
$T$ can be approximated by the Gamow transparency, which has the form: $T\approx e^{-{\sqrt {\epsilon _{G}/\epsilon }}}$ where $\epsilon _{G}=(\pi \alpha Z_{1}Z_{2})^{2}\times 2m_{r}c^{2}$ is the Gamow factor and comes from estimating the quantum tunneling probability through the potential barrier.
$R$ contains all the nuclear physics of the specific reaction and takes very different values depending on the nature of the interaction. However, for most reactions, the variation of $R(\epsilon )$ is small compared to the variation from the Gamow factor and so is approximated by a function called the Astrophysical S-factor, $S(\epsilon )$ , which is weakly varying in energy. Putting these dependencies together, one approximation for the fusion cross section as a function of energy takes the form:
$\sigma (\epsilon )\approx {\frac {S(\epsilon )}{\epsilon }}e^{-{\sqrt {\epsilon _{G}/\epsilon }}}$
More detailed forms of the cross-section can be derived through nuclear physics-based models and R-matrix theory.

Formulas of fusion cross sections[edit]

The Naval Research Lab's plasma physics formulary^[36] gives the total cross section in barns as a function of the energy (in keV) of the incident particle towards a target ion at rest fit by the formula:
$\sigma ^{NRL}(\epsilon )={\frac {A_{5}+{\big (}(A_{4}-A_{3}\epsilon )^{2}+1{\big )}^{-1}A_{2}}{\epsilon (e^{A_{1}\epsilon ^{-1/2}}-1)}}$ with the following coefficient values:
NRL Formulary Cross Section Coefficients
DT(1) DD(2i) DD(2ii) DHe³(3) TT(4) The³(6)
A1 45.95 46.097 47.88 89.27 38.39 123.1
A2 50200 372 482 25900 448 11250
A3 1.368e-2 4.36e-4 3.08e-4 3.98e-3 1.02e-3 0
A4 1.076 1.22 1.177 1.297 2.09 0
A5 409 0 0 647 0 0
Bosch-Hale^[37] also reports a R-matrix calculated cross sections fitting observation data with Padé rational approximating coefficients. With energy in units of keV and cross sections in units of millibarn, the factor has the form:
$S^{\text{Bosch-Hale}}(\epsilon )={\frac {A_{1}+\epsilon {\bigg (}A_{2}+\epsilon {\big (}A_{3}+\epsilon (A_{4}+\epsilon A_{5}){\big )}{\bigg )}}{1+\epsilon {\bigg (}B_{1}+\epsilon {\big (}B_{2}+\epsilon (B_{3}+\epsilon B_{4}){\big )}{\bigg )}}}$ , with the coefficient values:
Bosch-Hale coefficients for the fusion cross section
DT(1) DD(2ii) DHe³(3) THe⁴
$\epsilon _{G}$ 31.3970 68.7508 31.3970 34.3827
A1 5.5576e4 5.7501e6 5.3701e4 6.927e4
A2 2.1054e2 2.5226e3 3.3027e2 7.454e8
A3 -3.2638e-2 4.5566e1 -1.2706e-1 2.050e6
A4 1.4987e-6 0 2.9327e-5 5.2002e4
A5 1.8181e-10 0 -2.5151e-9 0
B1 0 -3.1995e-3 0 6.38e1
B2 0 -8.5530e-6 0 -9.95e-1
B3 0 5.9014e-8 0 6.981e-5
B4 0 0 0 1.728e-4
Applicable Energy Range [keV] 0.5-5000 0.3-900 0.5-4900 0.5-550
$(\Delta S)_{\text{max}}\%$ 2.0 2.2 2.5 1.9
where $\sigma ^{\text{Bosch-Hale}}(\epsilon )={\frac {S^{\text{Bosch-Hale}}(\epsilon )}{\epsilon \exp(\epsilon _{G}/{\sqrt {\epsilon }})}}$
$https://en.wikipedia.org/wiki/Nuclear_fusion#Criteria_and_candidates_for_terrestrial_reactions$
Obtaining the correct abundance of dark matter today via thermal production requires a self-annihilation cross section of $\langle \sigma v\rangle \simeq 3\times 10^{-26}\mathrm {cm} ^{3}\;\mathrm {s} ^{-1}$ , which is roughly what is expected for a new particle in the 100 GeV mass range that interacts via the electroweak force.
WIMP-like particles are predicted by R-parity-conserving supersymmetry, a popular type of extension to the Standard Model of particle physics, although none of the large number of new particles in supersymmetry have been observed.^[6] WIMP-like particles are also predicted by universal extra dimension and little Higgs theories.
Model parity candidate
SUSY R-parity lightest supersymmetric particle (LSP)
UED KK-parity lightest Kaluza-Klein particle (LKP)
little Higgs T-parity lightest T-odd particle (LTP)
The main theoretical characteristics of a WIMP are:
Interactions only through the weak nuclear force and gravity, or possibly other interactions with cross-sections no higher than the weak scale;^[7]
Large mass compared to standard particles (WIMPs with sub-GeV masses may be considered to be light dark matter).
Because of their lack of electromagnetic interaction with normal matter, WIMPs would be invisible through normal electromagnetic observations. Because of their large mass, they would be relatively slow moving and therefore "cold".^[8] Their relatively low velocities would be insufficient to overcome the mutual gravitational attraction, and as a result, WIMPs would tend to clump together.^[9] WIMPs are considered one of the main candidates for cold dark matter, the others being massive compact halo objects (MACHOs) and axions. (These names were deliberately chosen for contrast, with MACHOs named later than WIMPs.^[10]) Also, in contrast to MACHOs, there are no known stable particles within the Standard Model of particle physics that have all the properties of WIMPs. The particles that have little interaction with normal matter, such as neutrinos, are all very light, and hence would be fast moving, or "hot".
https://en.wikipedia.org/wiki/Weakly_interacting_massive_particles
https://en.wikipedia.org/wiki/Preon
https://en.wikipedia.org/wiki/Pressuron
https://en.wikipedia.org/wiki/Spinor

NRL Formulary Cross Section Coefficients
	DT(1)	DD(2i)	DD(2ii)	DHe³(3)	TT(4)	The³(6)
A1	45.95	46.097	47.88	89.27	38.39	123.1
A2	50200	372	482	25900	448	11250
A3	1.368e-2	4.36e-4	3.08e-4	3.98e-3	1.02e-3	0
A4	1.076	1.22	1.177	1.297	2.09	0
A5	409	0	0	647	0	0

Bosch-Hale coefficients for the fusion cross section
	DT(1)	DD(2ii)	DHe³(3)	THe⁴
$\epsilon _{G}$	31.3970	68.7508	31.3970	34.3827
A1	5.5576e4	5.7501e6	5.3701e4	6.927e4
A2	2.1054e2	2.5226e3	3.3027e2	7.454e8
A3	-3.2638e-2	4.5566e1	-1.2706e-1	2.050e6
A4	1.4987e-6	0	2.9327e-5	5.2002e4
A5	1.8181e-10	0	-2.5151e-9	0
B1	0	-3.1995e-3	0	6.38e1
B2	0	-8.5530e-6	0	-9.95e-1
B3	0	5.9014e-8	0	6.981e-5
B4	0	0	0	1.728e-4
Applicable Energy Range [keV]	0.5-5000	0.3-900	0.5-4900	0.5-550
$(\Delta S)_{\text{max}}\%$	2.0	2.2	2.5	1.9

Model	parity	candidate
SUSY	R-parity	lightest supersymmetric particle (LSP)
UED	KK-parity	lightest Kaluza-Klein particle (LKP)
little Higgs	T-parity	lightest T-odd particle (LTP)

Hyperfine Structure

Qubit in ion-trap quantum computing[edit]

The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.^[16]

Multipole magnets[edit]

Quadrupole electromagnet from the storage ring of the Australian Synchrotronserves much the same purpose as the sextupole magnets.
Modern systems often use multipole magnets, such as quadrupole and sextupole magnets, to focus the beam down, as magnets give a more powerful deflection effect than earlier electrostatic systems at high beam kinetic energies. The multipole magnets refocus the beam after each deflection section, as deflection sections have a defocusing effect that can be countered with a convergent magnet 'lens'.
This can be shown schematically as a sequence of divergent and convergent lenses. The quadrupoles are often laid out in what are called FODO patterns (where F focusses vertically and defocusses horizontally, and D focusses horizontally and defocusses vertically and O is a space or deflection magnet). Following the beam particles in their trajectories through the focusing arrangement, an oscillating pattern would be seen.

Mathematical modeling[edit]

The action upon a set of charged particles by a set of linear magnets (i.e. only dipoles, quadrupoles and the field-free drift regions between them) can be expressed as matrices which can be multiplied together to give their net effect, using ray transfer matrix analysis.^[7] Higher-order terms such as sextupoles, octupoles etc. may be treated by a variety of methods, depending on the phenomena of interest.

Aerodynamic levitation as a scientific tool[edit]

These systems allow spherical samples to be levitated by passing gas up through a diverging conical nozzle. Combining this with >200W continuous CO₂laser heating allows sample temperatures in excess of 3000 degrees Celsius to be achieved.
When heating materials to these extremely high temperatures levitation in general provides two key advantages over traditional furnaces. First, contamination that would otherwise occur from a solid container is eliminated. Second, the sample can be undercooled, i.e. cooled below its normal freezing temperature without actually freezing.

Undercooling of liquid samples[edit]

Undercooling, or supercooling, is the cooling of a liquid below its equilibrium freezing temperature while it remains a liquid. This can occur wherever crystal nucleation is suppressed. In levitated samples, heterogeneous nucleation is suppressed due to lack of contact with a solid surface. Levitation techniques typically allow samples to be cooled several hundred degrees Celsius below their equilibrium freezing temperatures.

Glass produced by aerodynamic levitation[edit]

Since crystal nucleation is suppressed by levitation, and since it is not limited by sample conductivity (unlike electromagnetic levitation), aerodynamic levitation can be used to make glassy materials, from high temperature melts that cannot be made by standard methods. Several silica-free, aluminium oxide based glasses have been made.^[2]^[3]^[4]

Physical property measurements[edit]

In the last few years a range of in situ measurement techniques have also been developed. The following measurements can be made with varying precision:
electrical conductivity, viscosity,^[5] density, surface tension,^[6] specific heat capacity,
In situ aerodynamic levitation has also been combined with:
X-ray synchrotron radiation, neutron scattering, NMR spectroscopy

Saturday, September 18, 2021

09-18-2021-0747 - Levitron

Levitron is a brand of levitating toys and gifts in science and educational markets marketed by Creative Gifts Inc. and Fascination Toys & Gifts.^[1]The Levitron top device is a commercial toy under this brand that displays the phenomenon known as spin-stabilized magnetic levitation. This method, with moving permanent magnets, is quite distinct from other versions which use changing electromagnetic fields, levitating various items such as a rotating world globe, model space shuttle or VW Beetle, and picture frame.^[2] 750,000 units of the top were sold from 1994 through 1999.^[1]
https://en.wikipedia.org/wiki/Levitron

Saturday, September 18, 2021

09-18-2021-0414 - Psuedoforce Notes Drafting

Saturday, September 18, 2021

09-18-2021-0813 - azide-alkyne Huisgen cycloaddition

Silver catalysis[edit]

Recently, the discovery of a general Ag(I)-catalyzed azide–alkyne cycloaddition reaction (Ag-AAC) leading to 1,4-triazoles is reported. Mechanistic features are similar to the generally accepted mechanism of the copper(I)-catalyzed process. Silver(I)-salts alone are not sufficient to promote the cycloaddition. However the ligated Ag(I) source has proven to be exceptional for AgAAC reaction.^[24]^[25] Curiously, pre-formed silver acetylides do not react with azides; however, silver acetylides do react with azides under catalysis with copper(I).^[26]
https://en.wikipedia.org/wiki/Azide-alkyne_Huisgen_cycloaddition

Saturday, September 18, 2021

09-18-2021-0818 - Thiol-yne reaction

https://en.wikipedia.org/wiki/Thiol-yne_reaction

Saturday, September 18, 2021

09-18-2021-0919 - Maglev

https://en.wikipedia.org/wiki/Linear_induction_motor
A linear induction motor (LIM) is an alternating current (AC), asynchronous linear motor that works by the same general principles as other induction motorsbut is typically designed to directly produce motion in a straight line. Characteristically, linear induction motors have a finite primary or secondary length, which generates end-effects, whereas a conventional induction motor is arranged in an endless loop.^[1]
Despite their name, not all linear induction motors produce linear motion; some linear induction motors are employed for generating rotations of large diameters where the use of a continuous primary would be very expensive.
As with rotary motors, linear motors frequently run on a three-phase power supply and can support very high speeds. However, there are end-effects that reduce the motor's force, and it is often not possible to fit a gearbox to trade off force and speed. Linear induction motors are thus frequently less energy efficient than normal rotary motors for any given required force output.
LIMs, unlike their rotary counterparts, can give a levitation effect. They are therefore often used where contactless force is required, where low maintenance is desirable, or where the duty cycle is low. Their practical uses include magnetic levitation, linear propulsion, and linear actuators. They have also been used for pumping liquid metals.^[2]
https://en.wikipedia.org/wiki/Linear_induction_motor
https://en.wikipedia.org/wiki/Linear_motor

https://en.wikipedia.org/wiki/Regenerative_brake
https://en.wikipedia.org/wiki/Vactrain
https://en.wikipedia.org/wiki/Linear_motor
https://en.wikipedia.org/wiki/Atmospheric_railway
https://en.wikipedia.org/wiki/StarTram
https://en.wikipedia.org/wiki/Category:Magnetic_propulsion_devices
https://en.wikipedia.org/wiki/Category:Electrodynamics
https://en.wikipedia.org/wiki/Halbach_array

https://en.wikipedia.org/wiki/Earnshaw%27s_theorem
https://en.wikipedia.org/wiki/Drag_(physics)
https://en.wikipedia.org/wiki/Linear_stage

https://en.wikipedia.org/wiki/Electromagnetic_Aircraft_Launch_System
https://en.wikipedia.org/wiki/Aircraft_catapult#Steam_catapult
https://en.wikipedia.org/wiki/Spacecraft_propulsion

https://en.wikipedia.org/wiki/Escape_velocity

https://en.wikipedia.org/wiki/Electric_generator
https://en.wikipedia.org/wiki/Flywheel
https://en.wikipedia.org/wiki/Spindle_(textiles)
https://en.wikipedia.org/wiki/Flywheel_energy_storage

https://en.wikipedia.org/wiki/Rotational_energy
https://en.wikipedia.org/wiki/Rotational_speed

https://en.wikipedia.org/wiki/Inductor
https://en.wikipedia.org/wiki/Accumulator_(energy)
https://en.wikipedia.org/wiki/Reciprocating_engine
https://en.wikipedia.org/wiki/Reaction_wheel

https://en.wikipedia.org/wiki/Gyroscope
https://en.wikipedia.org/wiki/Homopolar_generator

https://en.wikipedia.org/wiki/Electrolysis
https://en.wikipedia.org/wiki/Angular_momentum
https://en.wikipedia.org/wiki/Spectrum_(functional_analysis)#Point_spectrum
https://en.wikipedia.org/wiki/Synchrotron

https://en.wikipedia.org/wiki/Coilgun
https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss

https://en.wikipedia.org/wiki/Self-interacting_dark_matter
https://en.wikipedia.org/wiki/Scalar_field_dark_matter
https://en.wikipedia.org/wiki/Minimal_Supersymmetric_Standard_Model
https://en.wikipedia.org/wiki/Neutralino
https://en.wikipedia.org/wiki/Fuzzy_cold_dark_matter
https://en.wikipedia.org/wiki/Cosmic_microwave_background
https://en.wikipedia.org/wiki/Superfluidity
https://en.wikipedia.org/wiki/Supercritical_fluid
https://en.wikipedia.org/wiki/Supercritical_flow
https://en.wikipedia.org/wiki/Sonic_black_hole
https://en.wikipedia.org/wiki/Optical_black_hole
https://en.wikipedia.org/wiki/Analog_models_of_gravity
https://en.wikipedia.org/wiki/Transformation_optics
https://en.wikipedia.org/wiki/Black_hole
https://en.wikipedia.org/wiki/Cold_dark_matter
https://en.wikipedia.org/wiki/Primordial_black_hole
https://en.wikipedia.org/wiki/Neutrino_oscillation
https://en.wikipedia.org/wiki/Rotating_black_hole
https://en.wikipedia.org/wiki/Spin-flip
https://en.wikipedia.org/wiki/Black_hole_bomb
https://en.wikipedia.org/wiki/Neutron_reflector
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Photofission

Inertial confinement[edit]

Inertial confinement is the use of rapid implosion to heat and confine plasma. A shell surrounding the fuel is imploded using a direct laser blast (direct drive), a secondary x-ray blast (indirect drive), or heavy beams. The fuel must be compressed to about 30 times solid density with energetic beams. Direct drive can in principle be efficient, but insufficient uniformity has prevented success.^[65]^:19-20 Indirect drive uses beams to heat a shell, driving the shell to radiate x-rays, which then implode the pellet. The beams are commonly laser beams, but ion and electron beams have been investigated.^[65]^:182-193

Electrostatic confinement[edit]

Electrostatic confinement fusion devices use electrostatic fields. The best known is the fusor. This device has a cathode inside an anode wire cage. Positive ions fly towards the negative inner cage, and are heated by the electric field in the process. If they miss the inner cage they can collide and fuse. Ions typically hit the cathode, however, creating prohibitory high conduction losses. Fusion rates in fusors are low because of competing physical effects, such as energy loss in the form of light radiation.^[66] Designs have been proposed to avoid the problems associated with the cage, by generating the field using a non-neutral cloud. These include a plasma oscillating device,^[67] a magnetically-shielded-grid,^[68] a penning trap, the polywell,^[69] and the F1 cathode driver concept.^[70]
https://en.wikipedia.org/wiki/Fusion_power#Magnetic_Mirror

Heating[edit]

Main articles: Radio-Frequency Heating, Magnetic reconnection, Inertial electrostatic confinement, and Neutral beam injection
Electrostatic heating: an electric field can do work on charged ions or electrons, heating them.^[43]
Neutral beam injection: hydrogen is ionized and accelerated by an electric field to form a charged beam that is shone through a source of neutral hydrogen gas towards the plasma which itself is ionized and contained by a magnetic field. Some of the intermediate hydrogen gas is accelerated towards the plasma by collisions with the charged beam while remaining neutral: this neutral beam is thus unaffected by the magnetic field and so reaches the plasma. Once inside the plasma the neutral beam transmits energy to the plasma by collisions which ionize it and allow it to be contained by the magnetic field, thereby both heating and refueling the reactor in one operation. The remainder of the charged beam is diverted by magnetic fields onto cooled beam dumps.^[44]
Radio frequency heating: a radio wave causes the plasma to oscillate (i.e., microwave oven). This is also known as electron cyclotron resonance heating or dielectric heating.^[45]
Magnetic reconnection: when plasma gets dense, its electromagnetic properties can change, which can lead to magnetic reconnection. Reconnection helps fusion because it instantly dumps energy into a plasma, heating it quickly. Up to 45% of the magnetic field energy can heat the ions.^[46]^[47]
Magnetic oscillations: varying electrical currents can be supplied to magnetic coils that heat plasma confined within a magnetic wall.^[48]
Antiproton annihilation: antiprotons injected into a mass of fusion fuel can induce thermonuclear reactions. This possibility as a method of spacecraft propulsion, known as antimatter-catalyzed nuclear pulse propulsion, was investigated at Pennsylvania State University in connection with the proposed AIMStar project.^{[citation needed]}
https://en.wikipedia.org/wiki/Fusion_power

Alternating current (AC) is an electric current which periodically reverses direction and changes its magnitude continuously with time in contrast to direct current(DC) which flows only in one direction. Alternating current is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans and electric lamps into a wall socket. A common source of DC power is a battery cell in a flashlight. The abbreviations AC and DC are often used to mean simply alternating and direct, as when they modify current or voltage.^[1]^[2]
The usual waveform of alternating current in most electric power circuits is a sine wave, whose positive half-period corresponds with positive direction of the current and vice versa. In certain applications, like guitar amplifiers, different waveforms are used, such as triangular waves or square waves. Audio and radiosignals carried on electrical wires are also examples of alternating current. These types of alternating current carry information such as sound (audio) or images (video) sometimes carried by modulation of an AC carrier signal. These currents typically alternate at higher frequencies than those used in power transmission.
https://en.wikipedia.org/wiki/Alternating_current

The perturbed γ-γ angular correlation, PAC for short or PAC-Spectroscopy, is a method of nuclear solid-state physics with which magnetic and electric fields in crystal structures can be measured. In doing so, electrical field gradients and the Larmor frequency in magnetic fields as well as dynamic effects are determined. With this very sensitive method, which requires only about 10-1000 billion atoms of a radioactive isotope per measurement, material properties in the local structure, phase transitions, magnetism and diffusion can be investigated. The PAC method is related to nuclear magnetic resonance and the Mössbauer effect, but shows no signal attenuation at very high temperatures. Today only the time-differential perturbed angular correlation (TDPAC) is used.
https://en.wikipedia.org/wiki/Perturbed_angular_correlation

https://en.wikipedia.org/wiki/Analog
https://en.wikipedia.org/wiki/Superheterodyne_receiver
https://en.wikipedia.org/wiki/Gyroscope
https://en.wikipedia.org/wiki/Accumulator_(energy)
https://en.wikipedia.org/wiki/Nuclear_fusion#Criteria_and_candidates_for_terrestrial_reactions
https://www.osti.gov/servlets/purl/5545055
https://www.science.gov/topicpages/a/accelerated+beam+experiments
https://www.mdpi.com/1996-1073/3/5/1014/htm

n⁰	+	6 3Li	→	3 1T	+	4 2He + 4.784 MeV
n⁰	+	7 3Li	→	3 1T	+	4 2He + n⁰ – 2.467 MeV

Blog Archive

Saturday, September 18, 2021

09-18-2021-1715 - 3383/4-5,6

09-18-2021-1714 - Differential (mathematics)

Basic notions[edit]

Differential geometry[edit]

Algebraic geometry[edit]

Other meanings[edit]

References[edit]

External links[edit]

09-18-2021-1712 - Pressure Measurement (Absolute, gauge and differential pressures — zero reference)

09-18-2021-1710 - Degree of Freedom is an Independent Physical Parameter in the Formal Description of the state of a physical system.

09-18-2021-1708 - alternating current oscillating particle or wave perturbed γ-γ angular correlation heterodyne gyroscope

09-18-2021-1315 - Absolute, gauge and differential pressures — zero reference

Thermodynamics[edit]

Chemistry[edit]

See also[edit]

Introduction[edit]

Thermodynamic meters[edit]

Thermodynamic reservoirs[edit]

Theory[edit]

Volume Thermometer[edit]

Pressure Thermometer and Absolute Zero

History[edit]

Origin of the concept[edit]

First measurements[edit]

SI definition of 1971[edit]

SI redefinition of 2019[edit]

Connection to other constants[edit]

See also[edit]

Formation[edit]

Formation of monatomic ions[edit]

Hyperfine Structure

Qubit in ion-trap quantum computing[edit]

See also[edit]

Plasma behavior[edit]

Magnetic confinement[edit]

Magnetic Mirror[edit]

Magnetic Loops[edit]

Inertial confinement[edit]

Electrostatic confinement[edit]

Chemical Engineering[edit]

Diffusion[edit]

Onsager reciprocal relations[edit]

Momentum transfer[edit]

Mass transfer[edit]

Energy transfer[edit]

Applications[edit]

Pollution[edit]

See also[edit]

Description[edit]

See also[edit]

Other principles[edit]

Neutronicity, confinement requirement, and power density[edit]

Bremsstrahlung losses in quasineutral, isotropic plasmas[edit]

Mathematical description of cross section[edit]

Fusion under classical physics[edit]

Parameterization of cross section[edit]

Small molecule hyperfine structure[edit]

Measurements[edit]

Hyperfine interactions can be measured, among other ways, in atomic and molecular spectra and in electron paramagnetic resonance spectra of free radicals and transition-metal ions.

Applications[edit]

Astrophysics[edit]

Nuclear spectroscopy[edit]

In nuclear spectroscopy methods, the nucleus is used to probe the local structure in materials. The methods mainly base on hyperfine interactions with the surrounding atoms and ions. Important methods are nuclear magnetic resonance, Mössbauer spectroscopy, and perturbed angular correlation.

Nuclear technology[edit]

Use in defining the SI second and meter[edit]

Precision tests of quantum electrodynamics[edit]

The hyperfine splitting in hydrogen and in muonium have been used to measure the value of the fine structure constant α. Comparison with measurements of α in other physical systems provides a stringent test of QED.

Qubit in ion-trap quantum computing[edit]

See also[edit]

In physics[edit]

Parameterization of cross section[edit]

Formulas of fusion cross sections[edit]

Hyperfine Structure

Qubit in ion-trap quantum computing[edit]

See also[edit]

Dynamic nuclear polarisationElectron paramagnetic resonancehttps://en.wikipedia.org/wiki/Hyperfine_structure

Multipole magnets[edit]

Mathematical modeling[edit]

Dynamic nuclear polarisation
Electron paramagnetic resonance
https://en.wikipedia.org/wiki/Hyperfine_structure