Magnetic inductance
Circuit equivalence between a magnetic inductance and an electric capacitance.
In the context of the gyrator-capacitor model of a magnetic circuit, magnetic inductance  (SI unit: F) is the analogy to inductance in an electrical circuit.
(SI unit: F) is the analogy to inductance in an electrical circuit.
For phasor analysis the magnetic inductive reactance is:

where:
In the complex form it is a positive imaginary number:

The magnetic potential energy sustained by magnetic inductance
varies with the frequency of oscillations in electric fields. The
average power in a given period is equal to zero. Due to its dependence
on frequency, magnetic inductance is mainly observable in magnetic
circuits which operate at VHF and/or UHF frequencies.[citation needed]
The notion of magnetic inductance is employed in analysis and
computation of circuit behavior in the gyrator–capacitor model in a way
analogous to inductance in electrical circuits.
A magnetic inductor can represent an electrical capacitor.[4]: 43
A shunt capacitance in the electrical circuit, such as intra-winding
capacitance can be represented as a series inductance in the magnetic
circuit.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
The gyrator–capacitor model[1] - sometimes also the capacitor-permeance model[2] - is a lumped-element model for magnetic circuits, that can be used in place of the more common resistance–reluctance model. The model makes permeance elements analogous to electrical capacitance (see magnetic capacitance section) rather than electrical resistance (see magnetic reluctance). Windings are represented as gyrators, interfacing between the electrical circuit and the magnetic model.
The primary advantage of the gyrator–capacitor model compared to
the magnetic reluctance model is that the model preserves the correct
values of energy flow, storage and dissipation.[3][4] The gyrator–capacitor model is an example of a group of analogies
that preserve energy flow across energy domains by making power
conjugate pairs of variables in the various domains analogous. It fills
the same role as the impedance analogy for the mechanical domain.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
Category:Magnetic circuits
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Magnetic_circuits
Category:Electrical analogies
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Electrical_analogies
Magnetic induction
From Wikipedia, the free encyclopedia
Magnetic induction may refer to:
Category:
https://en.wikipedia.org/wiki/Magnetic_induction
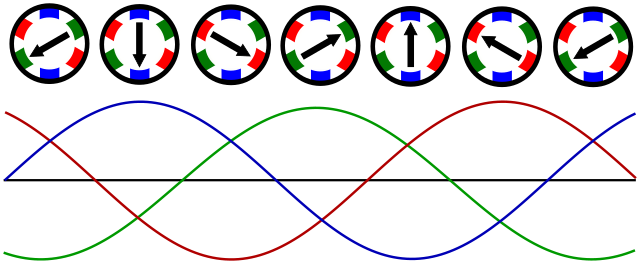
https://en.wikipedia.org/wiki/Synchronization_(alternating_current)
https://en.wikipedia.org/wiki/Category:AC_power
https://en.wikipedia.org/wiki/Category:Three-phase_AC_power
https://en.wikipedia.org/wiki/Symmetrical_components
https://en.wikipedia.org/wiki/Linearly_independent
https://en.wikipedia.org/wiki/Root_mean_square#Voltage
https://en.wikipedia.org/wiki/Droop_speed_control
https://en.wikipedia.org/wiki/Beat_(acoustics)
https://en.wikipedia.org/wiki/Interference_(wave_propagation)
In AC electrical power systems, a synchroscope is a device that indicates the degree to which two systems (generators or power networks) are synchronized with each other.[1]
For two electrical systems to be synchronized, both systems must operate at the same frequency, and the phase angle between the systems must be zero (and two polyphase systems must have the same phase sequence).
Synchroscopes measure and display the frequency difference and phase
angle between two power systems. Only when these two quantities are zero
is it safe to connect the two systems together. Connecting two
unsynchronized AC power systems together is likely to cause high
currents to flow, which will severely damage any equipment not protected
by fuses or circuit breakers.

This synchroscope was used to synchronize a factory's power plant with the utility's power grid.
https://en.wikipedia.org/wiki/Synchroscope
https://en.wikipedia.org/wiki/Three-phase_electric_power#Phase_sequence
https://en.wikipedia.org/wiki/Relay
https://en.wikipedia.org/wiki/Circuit_breaker
https://en.wikipedia.org/wiki/Deformed_power
https://en.wikipedia.org/wiki/Leading_and_lagging_current
A rotary phase converter, abbreviated RPC, is an electrical machine that converts power from one polyphase system to another, converting through rotary motion. Typically, single-phase electric power is used to produce three-phase electric power locally to run three-phase loads in premises where only single-phase is available.

A simple homemade phase converter
https://en.wikipedia.org/wiki/Rotary_phase_converter
In communication theory, time-varying phasors are used for analyzing narrow-band signals, whose signal bandwidths in the frequency domain are considerably smaller than the carrier frequency.[1][2] Time-varying phasors are mostly used for analysis of frequency domain of band-pass systems.[2][1] The method uses classical impulse response.[1]
In electrical power system, phasors are used for transient analysis of the power system keeping the quasi-stationary conditions.[1][3][4] They were introduced to facilitate the computation and analysis of power systems in stationary operation.[3] Time-varying phasors are used in dynamic analysis of a large power system.[1][5] The phasor representation of sinusoidal voltages and currents is generalized to arbitrary waveforms.[2] This mathematical transformation eliminates the 60 Hertz (Hz) carrier which is the only time-varying element in the stationary case.[3]
The longer usage of time-varying phasors in large power systems since
1920s have created many misconceptions. One of the misuses suggest that quasi-stationary
models are always accurate, but only when the system dynamics are slow
as compared to nominal system frequency which is usually 60 Hz.[4]
The concern to study time-varying phasors is raised to understand
in-depth the fast amplitude and phase variations of emerging electrical
power generator technologies.[4] This is because current and voltage signals of latest machines may have harmonic components and they can damage the entire transmission system which is coupled with the machine.[3][4]
However, if we employ quasi-static model, we can accurately model AC
signals by using time-varying phasors as opposed to traditional
quasi-static model which supports constant voltage and current signals
throughout the network.[5]
https://en.wikipedia.org/wiki/Time-varying_phasor
Single-phase generator (also known as single-phase alternator) is an alternating current electrical generator that produces a single, continuously alternating voltage. Single-phase generators can be used to generate power in single-phase electric power systems. However, polyphase generators are generally used to deliver power in three-phase distribution
system and the current is converted to single-phase near the
single-phase loads instead. Therefore, single-phase generators are found
in applications that are most often used when the loads being driven
are relatively light,[1] and not connected to a three-phase distribution, for instance, portable engine-generators. Larger single-phase generators are also used in special applications such as single-phase traction power for railway electrification systems.[2]

Elementary generator is an example of single-phase generators with two poles
https://en.wikipedia.org/wiki/Single-phase_generator
Polyphase coils are electromagnetic coils connected together in a polyphase system such as a generator or motor. In modern systems, the number of phases is usually three or a multiple of three. Each phase carries a sinusoidal alternating current whose phase
is delayed relative to one of its neighbours and advanced relative to
its other neighbour. The phase currents are separated in time evenly
within each period of the alternating current. For example, in a
three-phase system, the phases are separated from each other by
one-third of the period.
Coil construction
Like all coils used in electrical machinery, polyphase coils (made from insulated conducting wire) are wound around ferromagnetic armatures with radial projections and maximum core-surface exposure to the magnetic field.
The windings are physically separated around the circumference of an electrical machine. The result of such an arrangement is a rotating magnetic field that is used to convert electrical power to rotary mechanical work, or vice versa.
https://en.wikipedia.org/wiki/Polyphase_coil
https://en.wikipedia.org/wiki/Category:AC_power
A Scott-T transformer (also called a Scott connection) is a type of circuit used to produce two-phase electric power (2 φ, 90 degree phase rotation)[1] from a three-phase
(3 φ, 120 degree phase rotation) source, or vice versa. The Scott
connection evenly distributes a balanced load between the phases of the
source. The Scott three-phase transformer was invented by a Westinghouse engineer Charles F. Scott in the late 1890s to bypass Thomas Edison's more expensive rotary converter and thereby permit two-phase generator plants to drive three-phase motors.[2]
https://en.wikipedia.org/wiki/Scott-T_transformer
History
The first locomotive with a phase converter (only for demonstration purposes)
The Kandó phase converter (1933)
The "Kandó" locomotive, the first locomotive using a phase converter system
At the beginning of the 20th century, there were two main principles of electric railway traction current systems:
- DC system
- 16⅔ Hz single phase system
These systems used series-wound traction motors. All of them needed a separated supply system or converters to take power from the standard 50 Hz electric network.
https://en.wikipedia.org/wiki/Rotary_phase_converter
Unbalanced loads
Two-phase
motors draw constant power, just as three-phase motors do, so a
balanced two-phase load is converted to a balanced three-phase load.
However if a two-phase load is not balanced (more power drawn from one
phase than the other), no arrangement of transformers (including the
Scott-T transformers) can restore balance: Unbalanced current on the
two-phase side causes unbalanced current on the three-phase side. Since
the typical two-phase load was a motor, the current in the two phases
was presumed inherently equal during the Scott-T development.
In modern times people have tried to revive the Scott connection as a way to power single-phase electric railways
from three-phase Utility supplies. This will not result in balanced
current on the three-phase of being equal. The instantaneous
difference in loading on the two sections will be seen as an imbalance
in the three-phase supply; there is no way to smooth it out with
transformers.[4]
https://en.wikipedia.org/wiki/Scott-T_transformer
Back to back arrangement
Scott Connection 3 φ to 3 φ
The Scott-T transformer connection may also be used in a back-to-back
T-to-T arrangement for a three-phase to three-phase connection. This is
a cost-saving in the lower-power transformers due to the two-coil T
connected to a secondary two-coil T instead of the traditional
three-coil primary to three-coil secondary transformer. In this
arrangement the X0 neutral tap is part way up on the secondary teaser
transformer (see right). The voltage stability of this T-to-T
arrangement as compared to the traditional three-coil primary to
three-coil secondary transformer is questioned, as the "per unit"
impedance of the two windings (primary and secondary, respectively) are not the same in a T-to-T configuration, whereas the three windings (primary and secondary, respectively) are the same in a three transformer configuration, if the three transformers are identical.
Three-phase to three-phase (also called "T-connected")
distribution transformers are seeing increasing applications. The
primary must be delta-connected (Δ), but the secondary may be either delta or "wye"-connected (Y),
at the customer's option, with X0 providing the neutral for the "wye"
case. Taps for either case are usually provided. The customary maximum
capacity of such a distribution transformer is 333 kVA (a third of a
megawatt at unity power factor).[citation needed]
https://en.wikipedia.org/wiki/Scott-T_transformer
An induction regulator is an alternating current electrical machine, somewhat similar to an induction motor, which can provide a continuously variable output voltage.
The induction regulator was an early device used to control the voltage
of electric networks. Since the 1930s it has been replaced in
distribution network applications by the tap transformer. Its usage is now mostly confined to electrical laboratories, electrochemical processes and arc welding. With minor variations, its setup can be used as a phase-shifting power transformer.
https://en.wikipedia.org/wiki/Induction_regulator
Magnet wire or enameled wire is a copper (Cu) or aluminium (Al) wire coated with a very thin layer of insulation. It is used in the construction of transformers, inductors, motors, generators,
speakers, hard disk head actuators, electromagnets, electric guitar pickups and other applications that require tight coils of insulated wire.
The wire itself is most often fully annealed,
electrolytically refined copper. Aluminium magnet wire is sometimes
used for large transformers and motors. The insulation is typically made
of tough polymer film materials rather than vitreous enamel, as the name might suggest.
https://en.wikipedia.org/wiki/Magnet_wire
In electronics, a center tap (CT) is a contact made to a point halfway along a winding of a transformer or inductor, or along the element of a resistor or a potentiometer.
Taps are sometimes used on inductors for the coupling of signals,
and may not necessarily be at the half-way point, but rather, closer to
one end. A common application of this is in the Hartley oscillator. Inductors with taps also permit the transformation of the amplitude of alternating current (AC) voltages for the purpose of power conversion, in which case, they are referred to as autotransformers, since there is only one winding. An example of an autotransformer is an automobile ignition coil.
Potentiometer tapping provides one or more connections along the
device's element, along with the usual connections at each of the two
ends of the element, and the slider connection. Potentiometer taps allow
for circuit functions that would otherwise not be available with the
usual construction of just the two end connections and one slider
connection.
https://en.wikipedia.org/wiki/Center_tap
A relief valve or pressure relief valve (PRV) is a type of safety valve used to control or limit the pressure
in a system; excessive pressure might otherwise build up and create a
process upset, instrument or equipment failure, explosion, or fire.
https://en.wikipedia.org/wiki/Relief_valve
The open-circuit test, or no-load test, is one of the methods used in electrical engineering to determine the no-load impedance in the excitation branch of a transformer.
The no load is represented by the open circuit, which is represented on
the right side of the figure as the "hole" or incomplete part of the
circuit.
https://en.wikipedia.org/wiki/Open-circuit_test
Electrical insulation papers are paper types that are used as electrical insulation in many applications due to pure cellulose having outstanding electrical properties. Cellulose is a good insulator and is also polar,[clarification needed] having a dielectric constant significantly greater than one.[1]
Electrical paper products are classified by their thickness, with tissue
considered papers less than 1.5 mils (0.0381 mm) thickness, and board considered more than 20 mils (0.508 mm) thickness.[2]
https://en.wikipedia.org/wiki/Electrical_insulation_paper
A balun (from "balanced to unbalanced", originally, but now dated from "balancing unit")[1] is an electrical device that allows balanced and unbalanced lines to be interfaced without disturbing the impedance arrangement of either line.[2] A balun can take many forms and may include devices that also transform impedances but need not do so. Sometimes, in the case of transformer baluns, they use magnetic coupling but need not do so. Common-mode chokes are also used as baluns and work by eliminating, rather than rejecting, common mode signals.
https://en.wikipedia.org/wiki/Balun
In electrical engineering, the method of symmetrical components simplifies analysis of unbalanced three-phase power systems under both normal and abnormal conditions. The basic idea is that an asymmetrical set of N phasors can be expressed as a linear combination of N symmetrical sets of phasors by means of a complex linear transformation.[1] Fortescue's theorem (symmetrical components) is based on superposition principle,[2] so it is applicable to linear power systems only, or to linear approximations of non-linear power systems.
In the most common case of three-phase systems, the resulting "symmetrical" components are referred to as direct (or positive), inverse (or negative) and zero (or homopolar).
The analysis of power system is much simpler in the domain of
symmetrical components, because the resulting equations are mutually linearly independent if the circuit itself is balanced.[citation needed]
https://en.wikipedia.org/wiki/Symmetrical_components
A solid-state transformer (SST), power electronic transformer (PET), or electronic power transformer is actually an AC-to-AC converter, a type of electric power converter that replaces a conventional transformer used in AC electric power distribution. It is more complex than a conventional transformer operating at utility frequency,
but it can be smaller and more efficient than a conventional
transformer because it operates at high frequency. The main types are
"true" AC-to-AC converter (with no DC stages) and AC-to-DC-to-DC-to-AC
converter (in which an active rectifier supplies power to a DC-to-DC converter, which supplies power to a power inverter).
A solid-state transformer usually contains a transformer, inside the
AC-to-AC converter or DC-to-DC converter, which provides electrical
isolation and carries the full power. This transformer is smaller due to
smaller DC-DC inverting stages between transformer coils, which
consequently mean smaller transformer coils required to step up or step
down voltages. A solid-state transformer can actively regulate voltage
and current. Some can convert single-phase power to three-phase power
and vice versa. Variations can input or output DC power to reduce the number of conversions, for greater end-to-end efficiency. A Modular Solid-state transformer consists of several high-frequency transformers[1] and is similar to a Multi-level converter.
As a complex electronic circuit, it must be designed to withstand
lightning and other surges. Solid-state transformer is an emerging
technology.
https://en.wikipedia.org/wiki/Solid-state_transformer
A grounding transformer or earthing transformer is a type of auxiliary transformer used in three-phase electric power systems to provide a ground path to either an ungrounded wye or a delta-connected system.[1][2] Grounding transformers are part of an earthing system of the network. They let three-phase (delta connected) systems accommodate phase-to-neutral loads by providing a return path for current to a neutral.
Grounding transformers are typically used to:
- Provide a relatively low-impedance path to ground, thereby maintaining the system neutral at or near ground potential.[3]
- Limit the magnitude of transient overvoltages when restriking ground faults occur.
- Provide a source of ground fault current during line-to-ground faults.
- Permit the connection of phase-to-neutral loads when desired.[2]
Earthing transformer with a zig-zag
Grounding transformers most commonly incorporate a single winding transformer with a zigzag winding configuration, but may also be created with a wye-delta winding transformer.[2][4] Neutral grounding transformers are very common on generators in power plants and wind farms.[2]
Neutral grounding transformers are sometimes applied on high-voltage
(sub-transmission) systems, such as at 33 kV, where the circuit would
otherwise not have a ground; for example, if a system is fed by a
delta-connected transformer. The grounding point of the transformer may
be connected through a resistor or arc suppression coil to limit the
fault current on the system in the event of a line-to-ground fault. [5]
https://en.wikipedia.org/wiki/Grounding_transformer
An autotransformer is an electrical transformer with only one winding. The "auto" (Greek for "self") prefix refers to the single coil acting alone, not to any kind of automatic mechanism. In an autotransformer, portions of the same winding act as both the primary winding and secondary winding
sides of the transformer. In contrast, an ordinary transformer has
separate primary and secondary windings which have no metallic
conducting path between them.
The autotransformer winding has at least three taps
where electrical connections are made. Since part of the winding does
"double duty", autotransformers have the advantages of often being
smaller, lighter, and cheaper than typical dual-winding transformers,
but the disadvantage of not providing electrical isolation between primary and secondary circuits. Other advantages of autotransformers include lower leakage reactance, lower losses, lower excitation current, and increased VA rating for a given size and mass.[1]
An example of an application of an autotransformer is one style
of traveler's voltage converter, that allows 230-volt devices to be used
on 120-volt supply circuits, or the reverse. An autotransformer with
multiple taps may be applied to adjust the voltage at the end of a long
distribution circuit to correct for excess voltage drop; when
automatically controlled, this is one example of a voltage regulator.

Single-phase tapped autotransformer with an output voltage range of 40%–115% of input
https://en.wikipedia.org/wiki/Autotransformer
See also
https://en.wikipedia.org/wiki/Autotransformer
A zigzag transformer is a special-purpose transformer with a zigzag or "interconnected star" winding connection, such that each output is the vector sum of two (2) phases offset by 120°.[1] It is used as a grounding transformer, creating a missing neutral connection from an ungrounded 3-phase system to permit the grounding of that neutral to an earth reference point; to perform harmonic mitigation, as they can suppress triplet (3rd, 9th, 15th, 21st, etc.) harmonic currents;[2] to supply 3-phase power as an autotransformer (serving as the primary and secondary with no isolated circuits);[3] and to supply non-standard, phase-shifted, 3-phase power.[1]
9-winding zigzag transformer
Nine-winding, three-phase transformers typically have three primaries
and six identical secondary windings, which can be used in zigzag
winding connection as pictured.[1] As with the conventional delta or wye winding configuration three-phase
transformer, a standard, stand-alone transformer containing only six
windings on three cores can also be used in zigzag winding connection,
such transformer sometimes being referred to as a zigzag bank.[1]
In all cases, six or nine winding, the first coil on each zigzag
winding core is connected contrariwise to the second coil on the next
core. The second coils are then all tied together to form the neutral,
and the phases are connected to the primary coils. Each phase,
therefore, couples with each other phase, and the voltages cancel out.
As such, there would be negligible current through the neutral point,
which can be tied to ground.[4]
Each of the three "limbs" are split into two sections. The two
halves of each limb have an equal number of turns and are wound in
opposite directions. With the neutral grounded, during a phase-to-ground
short fault, a third of the current returns to the fault current, and
the remainder must go through two of the three phases when used to
derive a grounding point from a delta source.[5]
If one or more phases fault to earth, the voltage applied to each
phase of the transformer is no longer in balance; fluxes in the
windings no longer oppose. (Using symmetrical components, this is Ia0 = Ib0 = Ic0.)
Zero-sequence (earth fault) current exists between the transformer’s
neutral to the faulting phase. The purpose of a zigzag transformer in
this application is to provide a return path for earth faults on
delta-connected systems. With negligible current in the neutral under
normal conditions, an undersized (unable to carry a continuous fault
load) transformer may be used only as short-time rating is required,
provided the defective load will be automatically disconnected in a
fault condition. The transformer's impedance should not be too low for
desired maximum fault current. Impedance can be added after the
secondaries are summed to limit maximum fault currents (the 3Io path).[6]
A combination of Y (wye or star), delta, and zigzag windings may be used to achieve a vector phase shift.
For example, an electrical network may have a transmission network of
110 kV/33 kV star/star transformers, with 33 kV/11 kV delta/star for the
high voltage distribution network. If a transformation is required
directly between the 110 kV/11 kV network an option is to use a 110
kV/11 kV star/delta transformer. The problem is that the 11 kV delta no
longer has an earth reference point. Installing a zigzag transformer
near the secondary side of the 110 kV/11 kV transformer provides the
required earth reference point.[7]
https://en.wikipedia.org/wiki/Zigzag_transformer
Railway electrification systems using alternating current (AC) at 25 kilovolts (kV) are used worldwide, especially for high-speed rail. It is usually supplied at the standard utility frequency (typically 50 or 60 Hz), which simplifies traction substations. The development of 25 kV AC electrification is closely connected with that of successfully using utility frequency.
This electrification is ideal for railways that cover long distances or carry heavy traffic. After some experimentation before World War II in Hungary and in the Black Forest in Germany, it came into widespread use in the 1950s.
One of the reasons why it was not introduced earlier was the lack
of suitable small and lightweight control and rectification equipment
before the development of solid-state rectifiers
and related technology. Another reason was the increased clearance
distances required where it ran under bridges and in tunnels, which
would have required major civil engineering in order to provide the increased clearance to live parts.
Railways using older, lower-capacity direct current systems have introduced or are introducing 25 kV AC instead of 3 kV DC/1.5 kV DC for their new high-speed lines.
https://en.wikipedia.org/wiki/25_kV_AC_railway_electrification
In electronics, impedance matching is the practice of designing or adjusting the input impedance or output impedance of an electrical device for a desired value. Often, the desired value is selected to maximize power transfer or minimize signal reflection.
For example, impedance matching typically is used to improve power
transfer from a radio transmitter via the interconnecting transmission
line to the antenna. Signals on a transmission line will be transmitted without reflections if the transmission line is terminated with a matching impedance.
Techniques of impedance matching include transformers, adjustable networks of lumped resistance, capacitance and inductance,
or properly proportioned transmission lines. Practical
impedance-matching devices will generally provide best results over a
specified frequency band.
The concept of impedance matching is widespread in electrical engineering, but is relevant in other applications in which a form of energy, not necessarily electrical, is transferred between a source and a load, such as in acoustics or optics.

Source and
load impedance circuit
https://en.wikipedia.org/wiki/Impedance_matching
In electronics, electrical termination is the practice of ending a transmission line with a device that matches the characteristic impedance of the line. Termination prevents signals from reflecting off the end of the transmission line. Reflections at the ends of unterminated transmission lines cause distortion, which can produce ambiguous digital signal levels and misoperation of digital systems. Reflections in analog signal systems cause such effects as video ghosting, or power loss in radio transmitter transmission lines.
https://en.wikipedia.org/wiki/Electrical_termination
In telecommunications, signal reflection occurs when a signal is transmitted along a transmission medium, such as a copper cable or an optical fiber.
Some of the signal power may be reflected back to its origin rather
than being carried all the way along the cable to the far end. This
happens because imperfections in the cable cause impedance
mismatches and non-linear changes in the cable characteristics. These
abrupt changes in characteristics cause some of the transmitted signal
to be reflected. In radio frequency (RF) practice this is often measured in a dimensionless ratio known as voltage standing wave ratio (VSWR) with a VSWR bridge. The ratio of energy bounced back depends on the impedance mismatch. Mathematically, it is defined using the reflection coefficient.
Because the principles are the same, this concept is perhaps
easiest to understand when considering an optical fiber. Imperfections
in the glass create mirrors that reflect the light back along the fiber.
Impedance discontinuities cause attenuation, attenuation distortion, standing waves, ringing and other effects because a portion of a transmitted signal will be reflected back to the transmitting device rather than continuing to the receiver, much like an echo.
This effect is compounded if multiple discontinuities cause additional
portions of the remaining signal to be reflected back to the
transmitter. This is a fundamental problem with the daisy chain method of connecting electronic components.
When a returning reflection strikes another discontinuity, some
of the signal rebounds in the original signal direction, creating
multiple echo effects. These forward echoes
strike the receiver at different intervals making it difficult for the
receiver to accurately detect data values on the signal. The effects can
resemble those of jitter.
Because damage to the cable can cause reflections, an instrument called an electrical time-domain reflectometer (ETDR; for electrical cables) or an optical time-domain reflectometer
(OTDR; for optical cables) can be used to locate the damaged part of a
cable. These instruments work by sending a short pulsed signal into the
cable and measuring how long the reflection takes to return. If only
reflection magnitudes are desired, however, and exact fault locations
are not required, VSWR bridges perform a similar but lesser function for
RF cables.
The combination of the effects of signal attenuation and impedance discontinuities on a communications link is called insertion loss. Proper network operation depends on constant characteristic impedance in all cables and connectors, with no impedance discontinuities in the entire cable system. When a sufficient degree of impedance matching is not practical, echo suppressors or echo cancellers, or both, can sometimes reduce the problems.
The Bergeron diagram method, valid for both linear and non-linear models, evaluates the reflection's effects in an electric line.
See also
https://en.wikipedia.org/wiki/Signal_reflection
https://en.wikipedia.org/wiki/Optics
An induction motor or asynchronous motor is an AC electric motor in which the electric current in the rotor needed to produce torque is obtained by electromagnetic induction from the magnetic field of the stator winding.[1] An induction motor can therefore be made without electrical connections to the rotor.[a] An induction motor's rotor can be either wound type or squirrel-cage type.
Three-phase squirrel-cage induction motors are widely used as industrial drives because they are self-starting, reliable, and economical. Single-phase induction motors are used extensively for smaller loads, such as garbage disposals
and stationary power tools. Although traditionally only used for
one-speed service, single- and three-phase induction motors are
increasingly being installed in variable-speed applications using variable-frequency drives (VFD). VFDs offer especially important energy savings
opportunities for existing and prospective induction motors in
applications like fans, pumps and compressors that have a variable load.
https://en.wikipedia.org/wiki/Induction_motor
In telecommunications and electrical engineering in general, an unbalanced line is a pair of conductors intended to carry electrical signals, which have unequal impedances along their lengths and to ground and other circuits. Examples of unbalanced lines are coaxial cable or the historic earth return system invented for the telegraph, but rarely used today. Unbalanced lines are to be contrasted with balanced lines, such as twin-lead or twisted pair
which use two identical conductors to maintain impedance balance
throughout the line. Balanced and unbalanced lines can be interfaced
using a device called a balun.
The chief advantage of the unbalanced line format is cost
efficiency. Multiple unbalanced lines can be provided in the same cable
with one conductor per line plus a single common return conductor,
typically the cable shielding. Likewise, multiple microstrip circuits can all use the same ground plane
for the return path. This compares well with balanced cabling which
requires two conductors for each line, nearly twice as many. Another
benefit of unbalanced lines is that they do not require more expensive,
balanced driver and receiver circuits to operate correctly.
Unbalanced lines are sometimes confused with single-ended signalling,
but these are entirely separate concepts. The former is a cabling
scheme while the latter is a signalling scheme. However, single-ended
signalling is commonly sent over unbalanced lines. Unbalanced lines are
not to be confused with single-wire transmission lines which do not use a return path at all.
General description
Any
line that has a different impedance of the return path may be
considered an unbalanced line. However, unbalanced lines usually
consist of a conductor that is considered the signal line and another
conductor that is grounded, or is ground itself. The ground conductor often takes the form of a ground plane or the screen of a cable.
The ground conductor may be, and often is, common to multiple
independent circuits. For this reason the ground conductor may be
referred to as common.
Telegraph lines
The earliest use of unbalanced transmission lines was for electric telegraph
communications. These consisted of single wires strung between poles.
The return path for the current was originally provided by a separate
conductor. Some early telegraph systems, such as Schilling's experimental needle telegraph (1832) and the Cooke & Wheatstone five-needle telegraph (1837) used by British railways required multiple code wires. Essentially, they were parallel bus
coding. In these systems the cost of the return conductor was not so
significant (one conductor in seven for Schilling's earliest needle
telegraph[1] and one conductor in six for the Cooke and Wheatstone telegraph[2])
but the number of coding conductors was progressively reduced with
improved systems. Soon only one coding wire was required with the data
being transmitted serially. Important examples of these single-wire systems were the Morse telegraph (1837) and the Cooke & Wheatstone single-needle telegraph
(1843). In such systems the cost of a return conductor was fully 50
percent of the cable costs. It was discovered that a return conductor
could be replaced with a return path through the Earth using grounding spikes. Using earth return was a significant cost saving and rapidly became the norm.
Underground telegraph cables into large buildings or between
stations often needed to carry multiple independent telegraph lines.
These cables took the form of multiple insulated conductors enclosed by a
metal screen and overall protective jacket. In such cables the screen
can be used as the return conductor. Undersea telegraph cables were
usually a single conductor protected by steel-wire armour, effectively a coaxial cable. The first transatlantic cable of this kind was completed in 1866.
Early telephone
lines (telephone invented 1876) used the same transmission line scheme
as telegraph of unbalanced single wires. However, telephone
communication started to suffer after the widespread introduction of
electrical power lines. Telephone transmission started to use balanced lines to combat this problem and the modern norm for telephone presentation is the balanced twisted pair cable.
Coaxial lines
A coaxial line
(coax) has a central signal conductor surrounded by a cylindrical
shielding conductor. The shield conductor is normally grounded. The
coaxial format was developed during World War II for use in radar.
It was originally constructed from rigid copper pipes, but the usual
form today is a flexible cable with a braided screen. The advantages of
coax are a theoretically perfect electrostatic screen
and highly predictable transmission parameters. The latter is a result
of the fixed geometry of the format which leads to a precision not
found with loose wires. Open wire systems are also affected by nearby
objects altering the field pattern around the conductor. Coax does not
suffer from this since the field is entirely contained within the cable
due to the surrounding screen.
Coaxial lines are the norm for connections between radio
transmitters and their antennae, for interconnection of electronic
equipment where high frequency or above is involved, and were formerly widely used for forming local area networks before twisted pair became popular for this purpose.
Triaxial cable
(triax) is a variant of coax with a second shield conductor surrounding
the first with a layer of insulation in between. As well as providing
additional shielding, the outer conductors can be used for other
purposes such as providing power to equipment or control signals. Triax is widely used for the connection of cameras in television studios.
Planar technologies
Microstrip parallel-coupled transmission lines. The design forms a
band-pass filterPlanar format transmission lines are flat conductors manufactured by a
number of techniques on to a substrate. They are nearly always an
unbalanced format. At the low transmission speeds of early telegraph it was only necessary to consider transmission line theory for a circuit design when the transmission was over many miles. Similarly, the audio frequencies
used by telephones are relatively low and transmission line theory only
becomes significant for distances of at least between buildings.
However, at the higher radio frequencies and microwave frequencies transmission line considerations can become important inside a device, just a matter of centimetres. At the very high data rates handled by modern computer processors, transmission line considerations can even be important inside an individual integrated circuit.
Planar technologies were developed for these kinds of small size
applications and are not very appropriate for long distance
transmissions.
- Stripline
Stripline
is a flat conductor with a ground plane both above and below the
conductor. The variant of stripline where the space between the two
ground planes is completely filled with a dielectric material is sometimes known as triplate. Stripline can be manufactured by etching the transmission line pattern on to a printed circuit board.
The bottom of this board is left completely covered in copper and
forms the bottom ground plane. A second board is clamped on top of the
first. This second board has no pattern on the bottom and plain copper
on the top to form the top ground plane. A sheet of copper foil may be
wrapped around the two boards to electrically bond the two ground planes
firmly together. On the other hand, stripline for high power
applications such as radar will more likely be made as solid metal
strips with periodic dielectric supports, essentially air dielectric.
- Microstrip
Microstrip
is similar to stripline but is open above the conductor. There is no
dielectric or ground plane above the transmission line, there is only
dielectric and a ground plane below the line. Microstrip is a popular
format, especially in domestic products, because microstrip components
can be made using the established manufacturing techniques of printed
circuit boards. Designers are thus able to mix discrete component
circuits with microstrip components. Furthermore, since the board has
to be made anyway, the microstrip components have no additional
manufacturing cost. For applications where performance is more
important than cost a ceramic substrate might be used instead of a
printed circuit. Microstrip has another small advantage over stripline;
the line widths are wider in microstrip for the same impedance
and thus manufacturing tolerances and minimum width are less critical
on high-impedance lines. A drawback of microstrip is that the mode of
transmission is not entirely transverse.
Strictly speaking, standard transmission line analysis does not apply
because other modes are present, but it can be a usable approximation.
- Integrated circuits
Connections within integrated circuits are normally planar so planar
transmission lines are a natural choice where these are needed. The
need for transmission lines is most frequently found in microwave integrated circuits
(MICs). There are a great many materials and techniques used to make
MICs, and transmission lines can be formed in any of these technologies.
Planar transmission lines are used for far more than merely
connecting components or units together. They can themselves be used as
components and units. Any transmission line format can be used in this
way, but for the planar formats it is often their primary purpose.
Typical circuit blocks implemented by transmission lines include filters, directions couplers and power splitters, and impedance matching.
At microwave frequencies discrete components need to be impractically
small and a transmission line solution is the only viable one. On the
other hand, at low frequencies such as audio applications, transmission
line devices need to be impractically large.
Power transmission
Electric power distribution is normally in the form of balanced
three-phase transmission. However, in some remote locations where a
relatively small amount of power is required, a single-wire earth return system may be used.
References
Huurdeman, p. 54
Bibliography
- Huurdeman, Anton A., The Worldwide History of Telecommunications, John Wiley & Sons, 2003 ISBN 0471205052.
- Curran, J.E.; Jeanes, R.; Sewell, H, "A Technology of Thin-Film Hybrid Microwave Circuits", IEEE Transactions on Parts, Hybrids, and Packaging, vol. 12, iss. 4, December 1976.
https://en.wikipedia.org/wiki/Unbalanced_line
A motor soft starter is a device used with AC electrical motors to temporarily reduce the load and torque in the powertrain and electric current surge of the motor during start-up. This reduces the mechanical stress on the motor and shaft, as well as the electrodynamic stresses on the attached power cables and electrical distribution network, extending the lifespan of the system.[1]: 150
It can consist of mechanical or electrical devices, or a combination of both. Mechanical soft starters include clutches and several types of couplings using a fluid, magnetic forces, or steel shot to transmit torque, similar to other forms of torque limiter. Electrical soft starters can be any control system that reduces the torque by temporarily reducing the voltage or current input, or a device that temporarily alters how the motor is connected in the electric circuit.

Compact soft starter for a 3 phase machine, 15kW/10HP
https://en.wikipedia.org/wiki/Motor_soft_starter
A torque limiter is an automatic device that protects
mechanical equipment, or its work, from damage by mechanical overload. A
torque limiter may limit the torque by slipping (as in a friction plate slip-clutch), or uncouple the load entirely (as in a shear pin). The action of a torque limiter is especially useful to limit any damage due to crash stops and jams.
Torque limiters may be packaged as a shaft coupling or as a hub for sprocket or sheave. A torque limiting device is also known as an overload clutch.
https://en.wikipedia.org/wiki/Torque_limiter
Inverter drives (VFDs)
The popularity of the Variable-frequency drive
(VFD) has increased in the last decade, especially in the home-shop
market. This is because of their relative low cost and ability to
generate three-phase output from single phase input. A VFD converts AC
power to DC and then converts it back to AC through a transistor bridge, a technology that is somewhat analogous to that of a switch-mode power supply.
As the VFD generates its AC output from the DC bus, it is possible to
power a three-phase motor from a single-phase source. Nevertheless,
commercial-grade VFDs are produced that require three-phase input, as
there are some efficiency gains to be had with such an arrangement.
A typical VFD functions by rapidly switching transistors on and
off to "chop" the voltage on the DC bus through what is known as pulse-width modulation
(PWM). Proper use of PWM will result in an AC output whose voltage and
frequency can be varied over a fairly wide range. As an induction motor's
rotational speed is proportional to input frequency, a change in the
VFD's output frequency will cause the motor to change speed. Voltage is
also changed in a way that results in the motor producing a relatively
constant torque over the useful speed range.
The output of a quality VFD is an approximation of a sine wave, with some high frequency harmonic content.
Harmonic content will elevate motor temperature and may produce some
whistling or whining noise that could be objectionable. The effects of
unwanted harmonics can be mitigated by the use of reactive output filtering,
which is incorporated into better quality VFDs. Reactive filtration
impedes the high frequency harmonic content but has little effect on the
fundamental frequency that determines motor speed. The result is an output to the motor that is closer to an ideal sine wave.
In the past, VFDs that have a capacity greater than 3 hp (2.2 kW)
were costly, thus making the rotary phase converter (RPC) an attractive
alternative. However, modern VFDs have dropped considerably in cost,
making them more affordable than comparable RPCs. Also working in the
VFD's favor is its more compact size relative to its electrical
capacity. A plus is many VFDs can produce a "soft start" effect (in
which power is gradually applied to the motor), which reduces the amount
of current that must be delivered at machine start-up.
Use of a VFD may result in motor damage if the motor is not rated
for such an application. This is primarily because most induction
motors are forced-air cooled by a fan or blower driven by the motor
itself. Operating such a motor at a lower-than-normal speed will
substantially reduce the cooling airflow, increasing the likelihood of
overheating and winding damage or failure, especially while operating at
full load. A manufacturer may void the warranty on a motor powered by a
VFD unless the motor is "inverter-rated." As VFDs are the most popular
method of powering motors in new commercial installations, most
three-phase motors sold today are, in fact, inverter-rated.
See also
https://en.wikipedia.org/wiki/Rotary_phase_converter
A shear pin is a mechanical detail designed to allow a specific
outcome to occur once a predetermined force is applied. It can either
function as a safeguard designed to break to protect other parts, or as a
conditional operator that will not allow a mechanical device to operate
until the correct force is applied.
https://en.wikipedia.org/wiki/Shear_pin
Magnetic levitation (maglev) or magnetic suspension is a method by which an object is suspended with no support other than magnetic fields. Magnetic force is used to counteract the effects of the gravitational force and any other forces.
The two primary issues involved in magnetic levitation are lifting forces: providing an upward force sufficient to counteract gravity, and stability: ensuring that the system does not spontaneously slide or flip into a configuration where the lift is neutralized.
Magnetic levitation is used for maglev trains, contactless melting, magnetic bearings, and for product display purposes.
https://en.wikipedia.org/wiki/Magnetic_levitation
In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current (such as electromagnets), permanent magnets, elementary particles (such as electrons), various molecules, and many astronomical objects (such as many planets, some moons, stars, etc).
More precisely, the term magnetic moment normally refers to a system's magnetic dipole moment, the component of the magnetic moment that can be represented by an equivalent magnetic dipole:
a magnetic north and south pole separated by a very small distance. The
magnetic dipole component is sufficient for small enough magnets or for
large enough distances. Higher-order terms (such as the magnetic quadrupole moment) may be needed in addition to the dipole moment for extended objects.
The magnetic dipole moment of an object is readily defined in
terms of the torque that the object experiences in a given magnetic
field. The same applied magnetic field creates larger torques on objects
with larger magnetic moments. The strength (and direction) of this
torque depends not only on the magnitude of the magnetic moment but also
on its orientation relative to the direction of the magnetic field. The
magnetic moment may be considered, therefore, to be a vector. The direction of the magnetic moment points from the south to north pole of the magnet (inside the magnet).
https://en.wikipedia.org/wiki/Magnetic_moment
An electric motor is an electrical machine that converts electrical energy into mechanical energy. Most electric motors operate through the interaction between the motor's magnetic field and electric current in a wire winding to generate force in the form of torque applied on the motor's shaft. An electric generator
is mechanically identical to an electric motor, but operates with a
reversed flow of power, converting mechanical energy into electrical
energy.
Electric motors can be powered by direct current (DC) sources, such as from batteries, or rectifiers, or by alternating current (AC) sources, such as a power grid, inverters or electrical generators.
Electric motors may be classified by considerations such as power
source type, construction, application and type of motion output. They
can be powered by AC or DC, be brushed or brushless, single-phase, two-phase, or three-phase, axial or radial flux, and may be air-cooled or liquid-cooled.
Standardized motors provide convenient mechanical power for
industrial use. The largest are used for ship propulsion, pipeline
compression and pumped-storage applications with output exceeding 100 megawatts.
Applications include industrial fans, blowers and pumps, machine
tools, household appliances, power tools, vehicles, and disk drives.
Small motors may be found in electric watches. In certain applications,
such as in regenerative braking with traction motors, electric motors can be used in reverse as generators to recover energy that might otherwise be lost as heat and friction.
Electric motors produce linear or rotary force (torque)
intended to propel some external mechanism, such as a fan or an
elevator. An electric motor is generally designed for continuous
rotation, or for linear movement over a significant distance compared to
its size. Magnetic solenoids are also transducers that convert electrical power to mechanical motion, but can produce motion over only a limited distance.
https://en.wikipedia.org/wiki/Electric_motor
In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
https://en.wikipedia.org/wiki/Dynamo_theory
Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circular birefringence and circular dichroism are the manifestations of optical activity. Optical activity occurs only in chiral materials, those lacking microscopic mirror symmetry. Unlike other sources of birefringence which alter a beam's state of polarization, optical activity can be observed in fluids. This can include gases or solutions of chiral molecules such as sugars, molecules with helical secondary structure such as some proteins, and also chiral liquid crystals. It can also be observed in chiral solids such as certain crystals with a rotation between adjacent crystal planes (such as quartz) or metamaterials.
When looking at the source of light, the rotation of the plane of polarization may be either to the right (dextrorotatory or dextrorotary — d-rotary, represented by (+), clockwise), or to the left (levorotatory or levorotary — l-rotary, represented by (−), counter-clockwise) depending on which stereoisomer is dominant. For instance, sucrose and camphor are d-rotary whereas cholesterol is l-rotary.
For a given substance, the angle by which the polarization of light of a
specified wavelength is rotated is proportional to the path length
through the material and (for a solution) proportional to its
concentration.
Optical activity is measured using a polarized source and polarimeter. This is a tool particularly used in the sugar industry to measure the sugar concentration of syrup, and generally in chemistry to measure the concentration or enantiomeric ratio of chiral molecules in solution. Modulation of a liquid crystal's optical activity, viewed between two sheet polarizers, is the principle of operation of liquid-crystal displays (used in most modern televisions and computer monitors).
Forms
Dextrorotation and laevorotation (also spelled levorotation)[1][2][3] are terms used in chemistry and physics to describe the optical rotation of plane-polarized light. From the point of view of the observer, dextrorotation refers to clockwise or right-handed rotation, and laevorotation refers to counterclockwise or left-handed rotation.[4][5]
A chemical compound that causes dextrorotation is called dextrorotatory or dextrorotary, while a compound that causes laevorotation is called laevorotatory or laevorotary.[6] Compounds with these properties consist of chiral molecules and are said to have optical activity. If a chiral molecule is dextrorotary, its enantiomer
(geometric mirror image) will be laevorotary, and vice versa.
Enantiomers rotate plane-polarized light the same number of degrees, but
in opposite directions.
Chirality prefixes
A compound may be labeled as dextrorotary by using the "(+)-" or "d-" prefix. Likewise, a laevorotary compound may be labeled using the "(−)-" or "l-" prefix. The lowercase "d-" and "l-" prefixes are obsolete, and are distinct from the SMALL CAPS "D-" and "L-" prefixes. The "D-" and "L-" prefixes are used to specify the enantiomer of chiral organic compounds in biochemistry and are based on the compound's absolute configuration relative to (+)-glyceraldehyde, which is the D-form
by definition. The prefix used to indicate absolute configuration is
not directly related to the (+) or (−) prefix used to indicate optical
rotation in the same molecule. For example, nine of the nineteen L-amino acids naturally occurring in proteins are, despite the L- prefix, actually dextrorotary (at a wavelength of 589 nm), and D-fructose is sometimes called "laevulose" because it is laevorotary.
The D- and L- prefixes describe the molecule as a whole, as do the (+) and (−) prefixes for optical rotation. In contrast, the (R)- and (S)- prefixes from the Cahn–Ingold–Prelog priority rules characterize the absolute configuration of each specific chiral stereocenter
with the molecule, rather than a property of the molecule as a whole. A
molecule having exactly one chiral stereocenter (usually an asymmetric carbon atom) can be labeled (R) or (S), but a molecule having multiple stereocenters needs more than one label. For example, the essential amino acid L-threonine contains two chiral stereocenters and is written (2S,3S)-threonine. There is no strict relationship between the R/S, the D/L, and (+)/(−) designations, although some correlations exist. For example, of the naturally occurring amino acids, all are L, and most are (S). For some molecules the (R)-enantiomer
is the dextrorotary (+) enantiomer, and in other cases it is the
laevorotary (−) enantiomer. The relationship must be determined on a
case-by-case basis with experimental measurements or detailed computer
modeling.[7]
History
The two asymmetric crystal forms, dextrorotatory and levorotatory, of
tartaric acid.
Sucrose solution concentration measuring experiment, demonstrating optical rotation.
The rotation of the orientation of linearly polarized light was first observed in 1811 in quartz by French physicist François Arago.[8] In 1820, the English astronomer Sir John F.W. Herschel
discovered that different individual quartz crystals, whose crystalline
structures are mirror images of each other (see illustration), rotate
linear polarization by equal amounts but in opposite directions.[9] Jean Baptiste Biot also observed the rotation of the axis of polarization in certain liquids[10] and vapors of organic substances such as turpentine.[11] In 1822, Augustin-Jean Fresnel found that optical rotation could be explained as a species of birefringence:
whereas previously known cases of birefringence were due to the
different speeds of light polarized in two perpendicular planes, optical
rotation was due to the different speeds of right-hand and left-hand
circularly polarized light.[12] Simple polarimeters have been used since this time to measure the concentrations of simple sugars, such as glucose, in solution. In fact one name for D-glucose (the biological isomer), is dextrose, referring to the fact that it causes linearly polarized light to rotate to the right or dexter side. In a similar manner, levulose, more commonly known as fructose, causes the plane of polarization to rotate to the left. Fructose is even more strongly levorotatory than glucose is dextrorotatory. Invert sugar syrup, commercially formed by the hydrolysis of sucrose
syrup to a mixture of the component simple sugars, fructose, and
glucose, gets its name from the fact that the conversion causes the
direction of rotation to "invert" from right to left.
In 1849, Louis Pasteur resolved a problem concerning the nature of tartaric acid.[13] A solution of this compound derived from living things (to be specific, wine lees) rotates the plane of polarization of light passing through it, but tartaric acid derived by chemical synthesis
has no such effect, even though its reactions are identical and its
elemental composition is the same. Pasteur noticed that the crystals
come in two asymmetric forms that are mirror images of one another.
Sorting the crystals by hand gave two forms of the compound: Solutions
of one form rotate polarized light clockwise, while the other form
rotate light counterclockwise. An equal mix of the two has no
polarizing effect on light. Pasteur deduced that the molecule in
question is asymmetric and could exist in two different forms that
resemble one another as would left- and right-hand gloves, and that the
organic form of the compound consists of purely the one type.
In 1874, Jacobus Henricus van 't Hoff[14] and Joseph Achille Le Bel[15]
independently proposed that this phenomenon of optical activity in
carbon compounds could be explained by assuming that the 4 saturated
chemical bonds between carbon atoms and their neighbors are directed
towards the corners of a regular tetrahedron. If the 4 neighbors are all
different, then there are two possible orderings of the neighbors
around the tetrahedron, which will be mirror images of each other. This
led to a better understanding of the three-dimensional nature of
molecules.
In 1945, Charles William Bunn[16]
predicted optical activity of achiral structures, if the wave's
propagation direction and the achiral structure form an experimental
arrangement that is different from its mirror image. Such optical
activity due to extrinsic chirality was observed in the 1960s in liquid crystals.[17][18]
In 1950, Sergey Vavilov[19]
predicted optical activity that depends on the intensity of light and
the effect of nonlinear optical activity was observed in 1979 in lithium iodate crystals.[20]
Optical activity is normally observed for transmitted light.
However, in 1988, M. P. Silverman discovered that polarization rotation
can also occur for light reflected from chiral substances.[21]
Shortly after, it was observed that chiral media can also reflect
left-handed and right-handed circularly polarized waves with different
efficiencies.[22]
These phenomena of specular circular birefringence and specular
circular dichroism are jointly known as specular optical activity.
Specular optical activity is very weak in natural materials.
In 1898 Jagadish Chandra Bose described the ability of twisted artificial structures to rotate the polarization of microwaves.[23] Since the early 21st century, the development of artificial materials has led to the prediction[24] and realization[25][26]
of chiral metamaterials with optical activity exceeding that of natural
media by orders of magnitude in the optical part of the spectrum.
Extrinsic chirality associated with oblique illumination of metasurfaces
lacking two-fold rotational symmetry has been observed to lead to large
linear optical activity in transmission[27] and reflection,[28] as well as nonlinear optical activity exceeding that of lithium iodate by 30 million times.[29]
Theory
Optical
activity occurs due to molecules dissolved in a fluid or due to the
fluid itself only if the molecules are one of two (or more) stereoisomers; this is known as an enantiomer. The structure of such a molecule is such that it is not identical to its mirror image
(which would be that of a different stereoisomer, or the "opposite
enantiomer"). In mathematics, this property is also known as chirality. For instance, a metal rod is not chiral, since its appearance in a mirror is not distinct from itself. However a screw or light bulb base (or any sort of helix) is
chiral; an ordinary right-handed screw thread, viewed in a mirror,
would appear as a left-handed screw (very uncommon) which could not
possibly screw into an ordinary (right-handed) nut. A human viewed in a
mirror would have their heart on the right side, clear evidence of
chirality, whereas the mirror reflection of a doll might well be
indistinguishable from the doll itself.
In order to display optical activity, a fluid must contain only
one, or a preponderance of one, stereoisomer. If two enantiomers are
present in equal proportions then their effects cancel out and no
optical activity is observed; this is termed a racemic mixture. But when there is an enantiomeric excess,
more of one enantiomer than the other, the cancellation is incomplete
and optical activity is observed. Many naturally occurring molecules are
present as only one enantiomer (such as many sugars). Chiral molecules
produced within the fields of organic chemistry or inorganic chemistry are racemic unless a chiral reagent was employed in the same reaction.
At the fundamental level, polarization rotation in an optically
active medium is caused by circular birefringence, and can best be
understood in that way. Whereas linear birefringence in a crystal involves a small difference in the phase velocity
of light of two different linear polarizations, circular birefringence
implies a small difference in the velocities between right and
left-handed circular polarizations.[12]
Think of one enantiomer in a solution as a large number of little
helices (or screws), all right-handed, but in random orientations.
Birefringence of this sort is possible even in a fluid because the
handedness of the helices is not dependent on their orientation: even
when the direction of one helix is reversed, it still appears right
handed. And circularly polarized light itself is chiral: as the wave
proceeds in one direction the electric (and magnetic) fields composing
it are rotating clockwise (or counterclockwise for the opposite circular
polarization), tracing out a right (or left) handed screw pattern in
space. In addition to the bulk refractive index which substantially lowers the phase velocity of light in any dielectric (transparent) material compared to the speed of light (in vacuum), there is an additional interaction between the chirality of the wave and the chirality of the molecules.
Where their chiralities are the same, there will be a small additional
effect on the wave's velocity, but the opposite circular polarization
will experience an opposite small effect as its chirality is opposite
that of the molecules.
Unlike linear birefringence, however, natural optical rotation
(in the absence of a magnetic field) cannot be explained in terms of a
local material permittivity
tensor (i.e., a charge response that only depends on the local electric
field vector), as symmetry considerations forbid this. Rather, circular
birefringence only appears when considering nonlocality of the material
response, a phenomenon known as spatial dispersion.[30]
Nonlocality means that electric fields in one location of the material
drive currents in another location of the material. Light travels at a
finite speed, and even though it is much faster than the electrons, it
makes a difference whether the charge response naturally wants to travel
along with the electromagnetic wavefront, or opposite to it. Spatial
dispersion means that light travelling in different directions
(different wavevectors) sees a slightly different permittivity tensor.
Natural optical rotation requires a special material, but it also relies
on the fact that the wavevector of light is nonzero, and a nonzero
wavevector bypasses the symmetry restrictions on the local
(zero-wavevector) response. However, there is still reversal symmetry,
which is why the direction of natural optical rotation must be
'reversed' when the direction of the light is reversed, in contrast to
magnetic Faraday rotation.
All optical phenomena have some nonlocality/wavevector influence but it
is usually negligible; natural optical rotation, rather uniquely,
absolutely requires it.[30]
The phase velocity of light in a medium is commonly expressed using the index of refraction n,
defined as the speed of light (in free space) divided by its speed in
the medium. The difference in the refractive indices between the two
circular polarizations quantifies the strength of the circular
birefringence (polarization rotation),
 .
.
While  is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
The familiar rotation of the axis of linear polarization relies on the understanding that a linearly polarized wave can as well be described as the superposition
(addition) of a left and right circularly polarized wave in equal
proportion. The phase difference between these two waves is dependent on
the orientation of the linear polarization which we'll call  , and their electric fields have a relative phase difference of
, and their electric fields have a relative phase difference of  which then add to produce linear polarization:
which then add to produce linear polarization:

where  is the electric field of the net wave, while
is the electric field of the net wave, while  and
and  are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write
are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write  and
and  in terms of their x and y components as follows:
in terms of their x and y components as follows:


where  and
and  are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by
are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by  and then the actual electric field at any instant is given by the real part of that product.
and then the actual electric field at any instant is given by the real part of that product.
Substituting these expressions for  and
and  into the equation for
into the equation for  we obtain:
we obtain:



The last equation shows that the resulting vector has the x and y components in phase and oriented exactly in the  direction, as we had intended, justifying the representation of any linearly polarized state at angle
direction, as we had intended, justifying the representation of any linearly polarized state at angle  as the superposition of right and left circularly polarized components with a relative phase difference of
as the superposition of right and left circularly polarized components with a relative phase difference of  .
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of
.
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of  . Let us call
. Let us call  the result of passing the original wave linearly polarized at angle
the result of passing the original wave linearly polarized at angle  through this medium. This will apply additional phase factors of
through this medium. This will apply additional phase factors of  and
and  to the right and left circularly polarized components of
to the right and left circularly polarized components of  :
:

Using similar math as above we find:

thus describing a wave linearly polarized at angle  , thus rotated by
, thus rotated by  relative to the incoming wave:
relative to the incoming wave: 
We defined above the difference in the refractive indices for right and left circularly polarized waves of  . Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of
. Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of  (as we used above) given by:
(as we used above) given by:
 ,
,
where  is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by
is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by  as we have shown.
as we have shown.
In general, the refractive index depends on wavelength (see dispersion) and the differential refractive index  will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
So we find that the degree of rotation depends on the color of the light (the yellow sodium D line near 589 nm wavelength is commonly used for measurements), and is directly proportional to the path length  through the substance and the amount of circular birefringence of the material
through the substance and the amount of circular birefringence of the material  which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
Although optical activity is normally thought of as a property of fluids, particularly aqueous solutions, it has also been observed in crystals such as quartz (SiO2). Although quartz has a substantial linear birefringence, that effect is cancelled when propagation is along the optic axis.
In that case, rotation of the plane of polarization is observed due to
the relative rotation between crystal planes, thus making the crystal
formally chiral as we have defined it above. The rotation of the crystal
planes can be right or left-handed, again producing opposite optical
activities. On the other hand, amorphous forms of silica such as fused quartz,
like a racemic mixture of chiral molecules, has no net optical activity
since one or the other crystal structure does not dominate the
substance's internal molecular structure.
Applications
For a pure substance in solution, if the color and path length are fixed and the specific rotation is known, the observed rotation can be used to calculate the concentration. This usage makes a polarimeter a tool of great importance to those trading in or using sugar syrups in bulk.
Comparison to the Faraday effect
Rotation of light's plane of polarization may also occur through the Faraday effect which involves a static magnetic field.
However, this is a distinct phenomenon that is not classified as
"optical activity." Optical activity is reciprocal, i.e. it is the same
for opposite directions of wave propagation through an optically active
medium, for example clockwise polarization rotation from the point of
view of an observer. In case of optically active isotropic media, the
rotation is the same for any direction of wave propagation. In contrast,
the Faraday effect is non-reciprocal, i.e opposite directions of wave
propagation through a Faraday medium will result in clockwise and
anti-clockwise polarization rotation from the point of view of an
observer. Faraday rotation depends on the propagation direction relative
to that of the applied magnetic field. All compounds can exhibit
polarization rotation in the presence of an applied magnetic field,
provided that (a component of) the magnetic field is oriented in the
direction of light propagation. The Faraday effect is one of the first
discoveries of the relationship between light and electromagnetic
effects.
See also
References
The first word component dextro- comes from the Latin word dexter, meaning "right" (as opposed to left). Laevo- or levo- comes from the Latin laevus, meaning "left side".
The equivalent French terms are dextrogyre and levogyre. These are used infrequently in English.
Sebti; Hamilton, eds. (2001). Farnesyltransferase inhibitors in cancer therapy. p. 126. ISBN 9780896036291. Retrieved 2015-10-18.
LibreTexts Chemistry – Polarimetry
"Determination of optical rotation and specific rotation" (PDF). The International Pharmacopoeia. World Health Organization. 2017. ISBN 9789241550031. Archived (PDF) from the original on 2022-10-09.
Solomons, T.W. Graham; Fryhle, Graig B. (2004). Organic Chemistry (8th ed.). Hoboken: John Wiley & Sons, Inc.
See, for example,Stephens,
P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J.; Bortolini, O.;
Besse, P. (2003). "Determination of absolute configuration using
calculation of optical rotation". Chirality. 15: S57–64. doi:10.1002/chir.10270. PMID 12884375.
Arago (1811) "Mémoire
sur une modification remarquable qu'éprouvent les rayons lumineux dans
leur passage à travers certains corps diaphanes et sur quelques autres
nouveaux phénomènes d'optique" (Memoir on a remarkable modification
that light rays experience during their passage through certain
translucent substances and on some other new optical phenomena), Mémoires de la classe des sciences mathématiques et physiques de l'Institut Impérial de France, 1st part : 93–134.
Herschel, J.F.W. (1820) "On
the rotation impressed by plates of rock crystal on the planes of
polarization of the rays of light, as connected with certain
peculiarities in its crystallization," Transactions of the Cambridge Philosophical Society, 1 : 43–51.
Biot, J. B. (1815) "Phenomene de polarisation successive, observés dans des fluides homogenes" (Phenomenon of successive polarization, observed in homogeneous fluids), Bulletin des Sciences, par la Société Philomatique de Paris, 190–192.
Biot
(1818 & 1819) "Extrait d'un mémoire sur les rotations que certaines
substances impriment aux axes de polarisation des rayons lumineux"
(Extract from a memoir on the [optical] rotations that certain
substances impress on the axes of polarization of light rays), Annales de Chimie et de Physique, 2nd series, 9 : 372-389 ; 10 : 63-81 ; for Biot's experiments with turpentine vapor (vapeur d'essence de térébenthine), see pp. 72-81.
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); especially §13.
Pasteur, L. (1850) "Recherches sur les propriétés spécifiques des deux acides qui composent l'acide racémique" (Researches on the specific properties of the two acids that compose the racemic acid), Annales de chimie et de physique, 3rd series, 28 : 56–99 ; see also appendix, pp. 99–117.
van 't Hoff, J.H. (1874) "Sur les formules de structure dans l'espace" (On structural formulas in space), Archives Néerlandaises des Sciences Exactes et Naturelles, 9 : 445–454.
Le Bel, J.-A. (1874) "Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions" (On the relations that exist between the atomic formulas of organic substances and the rotatory power of their solutions), Bulletin de la Société Chimique de Paris, 22 : 337–347.
Bunn, C. W. (1945). Chemical Crystallography. New York: Oxford University Press. p. 88.
R. Williams (1968). "Optical Rotatory Effect in the Nematic Liquid Phase of p-Azoxyanisole". Physical Review Letters. 21 (6): 342. Bibcode:1968PhRvL..21..342W. doi:10.1103/PhysRevLett.21.342.
R. Williams (1969). "Optical-rotary power and linear electro-optic effect in nematic liquid crystals of p-azoxyanisole". Journal of Chemical Physics. 50 (3): 1324. Bibcode:1969JChPh..50.1324W. doi:10.1063/1.1671194.
Vavilov, S. I. (1950). Mikrostruktura Sveta (Microstructure of Light). Moscow: USSR Academy of Sciences Publishing.
Akhmanov,
S. A.; Zhdanov, B. V.; Zheludev, N. I.; Kovrigin, A. I.; Kuznetsov, V.
I. (1979). "Nonlinear optical activity in crystals". JETP Letters. 29: 264.
Silverman,
M.; Ritchie, N.; Cushman, G.; Fisher, B. (1988). "Experimental
configurations using optical phase modulation to measure chiral
asymmetries in light specularly reflected from a naturally gyrotropic
medium". Journal of the Optical Society of America A. 5 (11): 1852. Bibcode:1988JOSAA...5.1852S. doi:10.1364/JOSAA.5.001852.
Silverman, M.; Badoz, J.; Briat, B. (1992). "Chiral reflection from a naturally optically active medium". Optics Letters. 17 (12): 886. Bibcode:1992OptL...17..886S. doi:10.1364/OL.17.000886. PMID 19794663.
Bose, Jagadis Chunder (1898). "On the Rotation of Plane of Polarisation of Electric Waves by a Twisted Structure". Proceedings of the Royal Society. 63 (389–400): 146–152. doi:10.1098/rspl.1898.0019. JSTOR 115973. S2CID 89292757.
Svirko, Y.; Zheludev, N. I.; Osipov, M. (2001). "Layered chiral metallic microstructures with inductive coupling". Applied Physics Letters. 78 (4): 498. Bibcode:2001ApPhL..78..498S. doi:10.1063/1.1342210.
Kuwata-Gonokami,
M.; Saito, N.; Ino, Y.; Kauranen, M.; Jefimovs, K.; Vallius, T.;
Turunen, J.; Svirko, Y. (2005). "Giant Optical Activity in
Quasi-Two-Dimensional Planar Nanostructures". Physical Review Letters. 95 (22): 227401. Bibcode:2005PhRvL..95v7401K. doi:10.1103/PhysRevLett.95.227401. PMID 16384264.
Plum,
E.; Fedotov, V. A.; Schwanecke, A. S.; Zheludev, N. I.; Chen, Y.
(2007). "Giant optical gyrotropy due to electromagnetic coupling". Applied Physics Letters. 90 (22): 223113. Bibcode:2007ApPhL..90v3113P. doi:10.1063/1.2745203.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2008). "Optical activity in extrinsically chiral metamaterial" (PDF). Applied Physics Letters. 93 (19): 191911. arXiv:0807.0523. Bibcode:2008ApPhL..93s1911P. doi:10.1063/1.3021082. S2CID 117891131.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2016). "Specular optical activity of achiral metasurfaces" (PDF). Applied Physics Letters. 108 (14): 141905. Bibcode:2016ApPhL.108n1905P. doi:10.1063/1.4944775. hdl:10220/40854.
Ren, M.; Plum, E.; Xu, J.; Zheludev, N. I. (2012). "Giant nonlinear optical activity in a plasmonic metamaterial". Nature Communications. 3: 833. Bibcode:2012NatCo...3..833R. doi:10.1038/ncomms1805. PMID 22588295.
L.D. Landau; E.M. Lifshitz; L.P. Pitaevskii (1984). Electrodynamics of Continuous Media. Vol. 8 (2nd ed.). Butterworth-Heinemann. pp. 362–365. ISBN 978-0-7506-2634-7.
Plum, E.; Zhou, J.; Dong, J.; Fedotov, V. A.; Koschny, T.; Soukoulis, C. M.; Zheludev, N. I. (2009). "Metamaterial with negative index due to chirality" (PDF). Physical Review B. 79 (3): 035407. Bibcode:2009PhRvB..79c5407P. doi:10.1103/PhysRevB.79.035407. S2CID 119259753.
Further reading
- Eugene Hecht, Optics, 3rd Ed., Addison-Wesley, 1998, ISBN 0-201-30425-2
- Akhlesh Lakhtakia, Beltrami Fields in Chiral Media, World Scientific, Singapore, 1994
- A step by step tutorial on Optical Rotation
- Morrison. Robert. T, and Boyd. Robert. N, "Organic Chemistry (6th ed)". Prentice-Hall Inc (1992).

Operating principle of a
polarimeter
for measuring optical rotation. 1. Light source 2. Unpolarized light
3. Linear polarizer 4. Linearly polarized light 5. Sample tube
containing molecules under study 6. Optical rotation due to molecules 7.
Rotatable linear analyzer 8. Detector
https://en.wikipedia.org/wiki/Optical_rotation
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave.
In electrodynamics, the strength and direction of an electric
field is defined by its electric field vector. In the case of a
circularly polarized wave, the tip of the electric field vector,
at a given point in space, relates to the phase of the light as it
travels through time and space. At any instant of time, the electric
field vector of the wave indicates a point on a helix
oriented along the direction of propagation. A circularly polarized
wave can rotate in one of two possible senses: clockwise or right-handed circular polarization (RHCP) in which the electric field vector rotates in a right-hand sense with respect to the direction of propagation, and counter-clockwise or left-handed circular polarization (LHCP) in which the vector rotates in a left-hand sense.
Circular polarization is a limiting case of elliptical polarization. The other special case is the easier-to-understand linear polarization. All three terms were coined by Augustin-Jean Fresnel, in a memoir read to the French Academy of Sciences on 9 December 1822.[1][2] Fresnel had first described the case of circular polarization, without yet naming it, in 1821.[3]
The phenomenon of polarization arises as a consequence of the fact that light behaves as a two-dimensional transverse wave.
Circular polarization occurs when the two orthogonal electric
field component vectors are of equal magnitude and are out of phase by
exactly 90°, or one-quarter wavelength.
Characteristics
Right-handed/clockwise
circularly polarized light displayed with and without the use of
components. This would be considered left-handed/counterclockwise
circularly polarized if defined from the point of view of the source
rather than the receiver
In a circularly polarized electromagnetic wave, the individual
electric field vectors, as well as their combined vector, have a
constant magnitude, and with changing phase angle. Given that this is a plane wave,
each vector represents the magnitude and direction of the electric
field for an entire plane that is perpendicular to the optical axis.
Specifically, given that this is a circularly polarized plane wave,
these vectors indicate that the electric field, from plane to plane,
has a constant strength while its direction steadily rotates. Refer to these two images[dead link]
in the plane wave article to better appreciate this dynamic. This light
is considered to be right-hand, clockwise circularly polarized if
viewed by the receiver. Since this is an electromagnetic wave, each electric field vector has a corresponding, but not illustrated, magnetic field vector that is at a right angle to the electric field vector and proportional in magnitude to it. As a result, the magnetic field vectors would trace out a second helix if displayed.
Circular polarization is often encountered in the field of optics
and, in this section, the electromagnetic wave will be simply referred
to as light.
The nature of circular polarization and its relationship to other
polarizations is often understood by thinking of the electric field as
being divided into two components
that are perpendicular to each other. The vertical component and its
corresponding plane are illustrated in blue, while the horizontal
component and its corresponding plane are illustrated in green. Notice
that the rightward (relative to the direction of travel) horizontal
component leads the vertical component by one quarter of a wavelength, a 90° phase difference. It is this quadrature phase relationship that creates the helix
and causes the points of maximum magnitude of the vertical component to
correspond with the points of zero magnitude of the horizontal
component, and vice versa. The result of this alignment are select
vectors, corresponding to the helix, which exactly match the maxima of
the vertical and horizontal components.
To appreciate how this quadrature phase
shift corresponds to an electric field that rotates while maintaining a
constant magnitude, imagine a dot traveling clockwise in a circle.
Consider how the vertical and horizontal displacements of the dot, relative to the center of the circle, vary sinusoidally
in time and are out of phase by one quarter of a cycle. The
displacements are said to be out of phase by one quarter of a cycle
because the horizontal maximum displacement (toward the left) is reached
one quarter of a cycle before the vertical maximum displacement is
reached. Now referring again to the illustration, imagine the center of
the circle just described, traveling along the axis from the front to
the back. The circling dot will trace out a helix with the displacement
toward our viewing left, leading the vertical displacement. Just as the
horizontal and vertical displacements of the rotating dot are out of
phase by one quarter of a cycle in time, the magnitude of the horizontal
and vertical components of the electric field are out of phase by one
quarter of a wavelength.
Left-handed/counterclockwise
circularly polarized light displayed with and without the use of
components. This would be considered right-handed/clockwise circularly
polarized if defined from the point of view of the source rather than
the receiver.
The next pair of illustrations is that of left-handed,
counterclockwise circularly polarized light when viewed by the receiver.
Because it is left-handed, the rightward (relative to the direction of
travel) horizontal component is now lagging the vertical component by one quarter of a wavelength, rather than leading it.
Reversal of handedness
Waveplate
To convert circularly polarized light to the other handedness, one can use a half-waveplate.
A half-waveplate shifts a given linear component of light one half of a
wavelength relative to its orthogonal linear component.
Reflection
The
handedness of polarized light is reversed reflected off a surface at
normal incidence. Upon such reflection, the rotation of the plane of polarization of the reflected light is identical to that of the incident field. However, with propagation now in the opposite
direction, the same rotation direction that would be described as
"right-handed" for the incident beam, is "left-handed" for propagation
in the reverse direction, and vice versa. Aside from the reversal of
handedness, the ellipticity of polarization is also preserved (except in
cases of reflection by a birefringent surface).
Note that this principle only holds strictly for light reflected
at normal incidence. For instance, right circularly polarized light
reflected from a dielectric surface at grazing incidence (an angle
beyond the Brewster angle)
will still emerge as right-handed, but elliptically, polarized. Light
reflected by a metal at non-normal incidence will generally have its
ellipticity changed as well. Such situations may be solved by
decomposing the incident circular (or other) polarization into
components of linear polarization parallel and perpendicular to the plane of incidence, commonly denoted p and s respectively. The reflected components in the p and s linear polarizations are found by applying the Fresnel coefficients
of reflection, which are generally different for those two linear
polarizations. Only in the special case of normal incidence, where there
is no distinction between p and s, are the Fresnel coefficients for the two components identical, leading to the above property.
A
3-slide series of pictures taken with and without a pair of MasterImage
3D circularly polarized movie glasses of some dead European rose
chafers (Cetonia aurata) whose shiny green color comes from
left-polarized light. Note that, without glasses, both the beetles and
their images have shiny color. The right-polarizer removes the color of
the beetles but leaves the color of the images. The left-polarizer does
the opposite, showing reversal of handedness of the reflected light.
Conversion to and from linear polarization
Circularly polarized light can be converted into linearly polarized light by passing it through a quarter-waveplate.
Passing linearly polarized light through a quarter-waveplate with its
axes at 45° to its polarization axis will convert it to circular
polarization. In fact, this is the most common way of producing circular
polarization in practice. Note that passing linearly polarized light
through a quarter-waveplate at an angle other than 45° will generally produce elliptical polarization.
Handedness conventions
A
right-handed/clockwise circularly polarized wave as defined from the
point of view of the source. It would be considered
left-handed/anti-clockwise circularly polarized if defined from the
point of view of the receiver.
A
left-handed/anti-clockwise circularly polarized wave as defined from
the point of view of the source. It would be considered
right-handed/clockwise circularly polarized if defined from the point of
view of the receiver.
Circular polarization may be referred to as right-handed or
left-handed, and clockwise or anti-clockwise, depending on the direction
in which the electric field vector rotates. Unfortunately, two opposing
historical conventions exist.
From the point of view of the source
Using
this convention, polarization is defined from the point of view of the
source. When using this convention, left- or right-handedness is
determined by pointing one's left or right thumb away from the source, in the same
direction that the wave is propagating, and matching the curling of
one's fingers to the direction of the temporal rotation of the field at a
given point in space. When determining if the wave is clockwise or
anti-clockwise circularly polarized, one again takes the point of view
of the source, and while looking away from the source and in the same direction of the wave's propagation, one observes the direction of the field's spatial rotation.
Using this convention, the electric field vector of a left-handed circularly polarized wave is as follows:

As a specific example, refer to the circularly polarized wave in
the first animation. Using this convention, that wave is defined as
right-handed because when one points one's right thumb in the same
direction of the wave's propagation, the fingers of that hand curl in
the same direction of the field's temporal rotation. It is considered
clockwise circularly polarized because, from the point of view of the
source, looking in the same direction of the wave's propagation, the
field rotates in the clockwise direction. The second animation is that
of left-handed or anti-clockwise light, using this same convention.
This convention is in conformity with the Institute of Electrical and Electronics Engineers (IEEE) standard and, as a result, it is generally used in the engineering community.[4][5][6]
Quantum physicists also use this convention of handedness because
it is consistent with their convention of handedness for a particle's
spin.[7]
Radio astronomers also use this convention in accordance with an International Astronomical Union (IAU) resolution made in 1973.[8]
From the point of view of the receiver
In
this alternative convention, polarization is defined from the point of
view of the receiver. Using this convention, left- or right-handedness
is determined by pointing one's left or right thumb toward the source, against the direction of propagation, and then matching the curling of one's fingers to the spatial rotation of the field.
When using this convention, in contrast to the other convention,
the defined handedness of the wave matches the handedness of the screw
type nature of the field in space. Specifically, if one freezes a
right-handed wave in time, when one curls the fingers of one's right
hand around the helix, the thumb will point in the direction of
progression for the helix, given the sense of rotation. Note that, in
the context of the nature of all screws and helices, it does not matter
in which direction you point your thumb when determining its handedness.
When determining if the wave is clockwise or anti-clockwise
circularly polarized, one again takes the point of view of the receiver
and, while looking toward the source, against the direction of propagation, one observes the direction of the field's temporal rotation.
Just as in the other convention, right-handedness corresponds to a
clockwise rotation, and left-handedness corresponds to an
anti-clockwise rotation.
Many optics textbooks use this second convention.[9][10] It is also used by SPIE[11] as well as the International Union of Pure and Applied Chemistry (IUPAC).[12]
Uses of the two conventions
As
stated earlier, there is significant confusion with regards to these
two conventions. As a general rule, the engineering, quantum physics,
and radio astronomy communities use the first convention, in which the
wave is observed from the point of view of the source.[5][7][8]
In many physics textbooks dealing with optics, the second convention is
used, in which the light is observed from the point of view of the
receiver.[7][9]
To avoid confusion, it is good practice to specify "as defined
from the point of view of the source" or "as defined from the point of
view of the receiver" when discussing polarization matters.
The archive of the US Federal Standard 1037C proposes two contradictory conventions of handedness.[13]
FM radio
The term "circular polarization" is often used erroneously to describe mixed polarity signals[citation needed] used mostly in FM radio
(87.5 to 108.0 MHz in the USA), in which a vertical and a horizontal
component are propagated simultaneously by a single or a combined array.
This has the effect of producing greater penetration into buildings and
difficult reception areas than a signal with just one plane of
polarization. This would be an instance in which the polarization would
more appropriately be called random polarization because the
polarization at a receiver, although constant, will vary depending on
the direction from the transmitter and other factors in the transmitting
antenna design. See Stokes parameters.
The term "FM radio" above refers to FM broadcasting, not two-way radio (more properly called land mobile radio), which uses vertical polarization almost exclusively.
Dichroism
Circular dichroism (CD) is the differential absorption of left- and right-handed circularly polarized light. Circular dichroism is the basis of a form of spectroscopy that can be used to determine the optical isomerism and secondary structure of molecules.
In general, this phenomenon will be exhibited in absorption bands of any optically active molecule. As a consequence, circular dichroism is exhibited by most biological molecules, because of the dextrorotary (e.g., some sugars) and levorotary (e.g., some amino acids) molecules they contain. Noteworthy as well is that a secondary structure will also impart a distinct CD to its respective molecules. Therefore, the alpha helix, beta sheet and random coil regions of proteins and the double helix of nucleic acids have CD spectral signatures representative of their structures.
Also, under the right conditions, even non-chiral molecules will exhibit magnetic circular dichroism — that is, circular dichroism induced by a magnetic field.
Luminescence
Circularly polarized luminescence (CPL) can occur when either a luminophore or an ensemble of luminophores is chiral. The extent to which emissions are polarized is quantified in the same way it is for circular dichroism, in terms of the dissymmetry factor, also sometimes referred to as the anisotropy factor. This value is given by:

where  corresponds to the quantum yield of left-handed circularly polarized light, and
corresponds to the quantum yield of left-handed circularly polarized light, and  to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
Mathematical description
The classical sinusoidal plane wave solution of the electromagnetic wave equation for the electric and magnetic fields is:
![{\displaystyle {\begin{aligned}\mathbf {E} (\mathbf {r} ,t)&=\left|\,\mathbf {E} \,\right|\mathrm {Re} \left\{\mathbf {Q} \left|\psi \right\rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\\\mathbf {B} (\mathbf {r} ,t)&={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72e6f4e48ffd9eabf206d7664ee54e2e2ba2780c)
where k is the wavenumber;

is the angular frequency of the wave; ![\mathbf{Q} = \left [ \hat{ \mathbf{x}}, \hat{\mathbf{y}} \right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c6f209c9644cf3ab69fd75e6d696bb9278c0c12) is an orthogonal
is an orthogonal  matrix whose columns span the transverse x-y plane; and
matrix whose columns span the transverse x-y plane; and  is the speed of light.
is the speed of light.
Here,

is the amplitude of the field, and

is the normalized Jones vector in the x-y plane.
If  is rotated by
is rotated by  radians with respect to
radians with respect to  and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:
and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:

where the plus sign indicates left circular polarization, and the
minus sign indicates right circular polarization. In the case of
circular polarization, the electric field vector of constant magnitude
rotates in the x-y plane.
If basis vectors are defined such that:

and:

then the polarization state can be written in the "R-L basis" as:

where:

and:

Antennas
A number of different types of antenna elements can be used to
produce circularly polarized (or nearly so) radiation; following
Balanis,[14] one can use dipole elements:
"... two crossed dipoles provide the two orthogonal field
components.... If the two dipoles are identical, the field intensity of
each along zenith ... would be of the same intensity. Also, if the two
dipoles were fed with a 90° degree time-phase difference (phase
quadrature), the polarization along zenith would be circular.... One way
to obtain the 90° time-phase difference between the two orthogonal
field components, radiated respectively by the two dipoles, is by
feeding one of the two dipoles with a transmission line which is 1/4
wavelength longer or shorter than that of the other," p.80;
or helical elements:
"To achieve circular polarization [in axial or end-fire mode] ... the circumference C of the helix must be ... with C/wavelength = 1 near optimum, and the spacing about S = wavelength/4," p.571;
or patch elements:
"... circular and elliptical polarizations can be
obtained using various feed arrangements or slight modifications made to
the elements.... Circular polarization can be obtained if two
orthogonal modes are excited with a 90° time-phase difference between
them. This can be accomplished by adjusting the physical dimensions of
the patch.... For a square patch element, the easiest way to excite
ideally circular polarization is to feed the element at two adjacent
edges.... The quadrature phase difference is obtained by feeding the
element with a 90° power divider," p.859.
In quantum mechanics
In the quantum mechanical view, light is composed of photons. Polarization is a manifestation of the spin angular momentum of light.
More specifically, in quantum mechanics, the direction of spin of a
photon is tied to the handedness of the circularly polarized light, and
the spin of a beam of photons is similar to the spin of a beam of
particles, such as electrons.[15]
In nature
The
rose chafer's external surface reflects almost exclusively left-circularly polarized light.
Only a few mechanisms in nature are known to systematically produce circularly polarized light. In 1911, Albert Abraham Michelson discovered that light reflected from the golden scarab beetle Chrysina resplendens is preferentially left-polarized. Since then, circular polarization has been measured in several other scarab beetles such as Chrysina gloriosa,[16] as well as some crustaceans such as the mantis shrimp. In these cases, the underlying mechanism is the molecular-level helicity of the chitinous cuticle.[17]
The bioluminescence of the larvae of fireflies is also circularly polarized, as reported in 1980 for the species Photuris lucicrescens and Photuris versicolor.
For fireflies, it is more difficult to find a microscopic explanation
for the polarization, because the left and right lanterns of the larvae
were found to emit polarized light of opposite senses. The authors
suggest that the light begins with a linear polarization due to inhomogeneities inside aligned photocytes, and it picks up circular polarization while passing through linearly birefringent tissue.[18]
Water-air interfaces provide another source of circular
polarization. Sunlight that gets scattered back up towards the surface
is linearly polarized. If this light is then totally internally reflected back down, its vertical component undergoes a phase shift. To an underwater observer looking up, the faint light outside Snell's window therefore is (partially) circularly polarized.[19]
Weaker sources of circular polarization in nature include multiple scattering by linear polarizers[dubious – discuss], as in the circular polarization of starlight, and selective absorption by circularly dichroic media.
Radio emission from stars and pulsars can be strongly circularly polarized[citation needed].
Two species of mantis shrimp have been reported to be able to detect circular polarized light.[20][21]
See also
References
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); §§9–10.
Académie des Sciences, Procès-verbaux des séances de l'Académie tenues depuis la fondation de l'Institut jusqu'au mois d'août 1835, vol. 7 (for 1820–23), Hendaye, Basses Pyrénées: Imprimerie de l'Observatoire d'Abbadia, 1916, p. 401.
A. Fresnel, "Note sur le calcul des teintes que la polarisation développe dans les lames cristallisées" et seq., Annales de Chimie et de Physique,
Ser. 2, vol. 17, pp. 102–11 (May 1821), 167–96 (June 1821), 312–15
("Postscript", July 1821); reprinted (with added section nos.) in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 609–48; translated as "On the calculation of the
tints that polarization develops in crystalline plates,
& postscript", Zenodo: 4058004 (Creative Commons), 2021; author's footnote to §16.
IEEE
Std 149-1979 (R2008), "IEEE Standard Test Procedures for Antennas".
Reaffirmed December 10, 2008, Approved December 15, 1977, IEEE-SA
Standards Board. Approved October 9, 2003, American National Standards
Institute. ISBN 0-471-08032-2. doi:10.1109/IEEESTD.1979.120310,
sec. 11.1, p. 61."the sense of polarization, or handedness ... is
called right handed (left handed) if the direction of rotation is
clockwise (anti-clockwise) for an observer looking in the direction of
propagation"
Electromagnetic
Waves & Antennas – S. J. Orfanidis: Footnote p.45, "most
engineering texts use the IEEE convention and most physics texts, the
opposite convention."
Electromagnetic
Waves & Antennas – S. J. Orfanidis Pg 44 "Curl the fingers of your
left and right hands into a fist and point both thumbs towards the direction of propagation"
Lectures
on Physics Feynman (Vol. 1, ch.33-1) "If the end of the electric
vector, when we look at it as the light comes straight toward us, goes
around in an anti-clockwise direction, we call it right-hand circular
polarization. ... Our convention for labeling left-hand and right-hand
circular polarization is consistent with that which is used today for
all the other particles in physics which exhibit polarization (e.g.,
electrons). However, in some books on optics the opposite conventions
are used, so one must be careful."
IAU
General Assembly Meeting, 1973, Commission 40 (Radio
Astronomy/Radioastronomie), 8. POLARIZATION DEFINITIONS -- "A working
Group chaired by Westerhout was convened to discuss the definition of
polarization brightness temperatures used in the description of
polarized extended objects and the galactic
background. The following resolution was adopted by Commissions 25 and
40: 'RESOLVED, that the frame of reference for the Stokes parameters is
that of Right Ascension and Declination with the position angle of
electric-vector maximum, q, starting from North and increasing through
East. Elliptical polarization is defined in conformity with the
definitions of the Institute of Electrical and Electronics Engineers
(IEEE Standard 211, 1969). This means that the polarization of incoming
radiation, for which the position angle, q, of the electric vector,
measured at a fixed point in space, increases with time, is described as
right-handed and positive.'"
Polarization
in Spectral Lines. 2004 E. Landi Degl'innocenti, M Landolfi Section 1.2
"When ... the tip of the electric field vector rotates clockwise for an
observer facing the radiation source, ... (it will be considered)...
positive (or righthanded) circular polarization, Our convention ...
agrees with those proposed in the classical textbooks on polarized light
by Shurcliff (1952) and by Clarke and Grainger (1971). The same
convention is also used, although with some few exceptions, by optical
astronomers working in the field of polarimetry. Many radio astronomers,
on the other hand, use the opposite convention. [1]
HANDBOOK
OPTICS Volume I,Devices, Measurements and Properties,Michael Bass Page
272 Footnote: "Right-circularly polarized light is defined as a
clockwise rotation of the electric vector when the observer is looking against the direction the wave is traveling."
"The Polarization Ellipse". spie.org. Retrieved 13 April 2018.
S. E. Braslavsky (1 January 2009). "Glossary of terms used in photochemistry, 3rd edition (IUPAC Recommendations 2006)" (PDF). Pure and Applied Chemistry. 79 (3): 293–465. doi:10.1351/pac200779030293. S2CID 96601716. Archived (PDF) from the original on 2022-10-09.
In
one location it is stated..."Note 1. ... In general, the figure, i.e.,
polarization, is elliptical and is traced in a clockwise or
anti-clockwise sense, as viewed in the direction of propagation. ...
Rotation of the electric vector in a clockwise sense is designated
right-hand polarization, and rotation in an anti-clockwise sense is
designated left-hand polarization. "[2] Archived 2011-05-14 at the Wayback Machine
In another location it is stated... "Note 4: Circular polarization may
be referred to as "right-hand" or "left-hand", depending on whether the
helix describes the thread of a right-hand or left-hand screw,
respectively". [3] Archived 2011-06-06 at the Wayback Machine
Balanis, Constantine A. "Antenna Theory – Analysis and Design", 2005, 3rd Edition, John Wiley & Sons.
Introduction
to Quantum Theory 2ED David Park Sec 2.2 Pg32 "... the polarization of a
beam of light is exactly the same kind of thing as the spin of a beam
of electrons, the differences of terminology reflecting only the
accidents of the historical order of discovery."
Srinivasarao, Mohan; Park, Jung Ok; Crne, Matija; Sharma, Vivek (July 24, 2009). "Structural Origin of Circularly Polarized Iridescence in Jeweled Beetles". Science. 325 (5939): 449–451. Bibcode:2009Sci...325..449S. doi:10.1126/science.1172051. PMID 19628862. S2CID 206519071 – via science.sciencemag.org.
Hegedüs, Ramón; Győző Szélb; Gábor Horváth (September 2006). "Imaging polarimetry of the circularly polarizing cuticle of scarab beetles (Coleoptera: Rutelidae, Cetoniidae)". Vision Research. 46 (17): 2786–2797. doi:10.1016/j.visres.2006.02.007. PMID 16564066. S2CID 14974820.
Wynberg, Hans; Meijer, E.W.; Hummelen, J.C.; Dekkers, H.P.J.M.; Schippers, P.H.; Carlson, A.D. (7 August 1980). "Circular polarization observed in bioluminescence" (PDF). Nature. 286 (5773): 641–642. Bibcode:1980Natur.286..641W. doi:10.1038/286641a0. S2CID 4324467. Archived from the original (PDF) on 24 July 2011.
Horváth, Gábor; Dezsö Varjú (2003). Polarized Light in Animal Vision: Polarization Patterns in Nature. Springer. pp. 100–103. ISBN 978-3-540-40457-6.
Tsyr-Huei
Chiou; Sonja Kleinlogel; Tom Cronin; Roy Caldwell; Birte Loeffler;
Afsheen Siddiqi; Alan Goldizen; Justin Marshall (2008). "Circular polarization vision in a stomatopod crustacean". Current Biology. 18 (6): 429–34. doi:10.1016/j.cub.2008.02.066. PMID 18356053. S2CID 6925705.
Further reading
External links
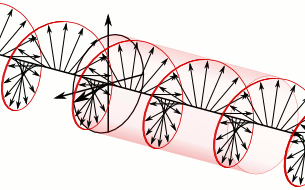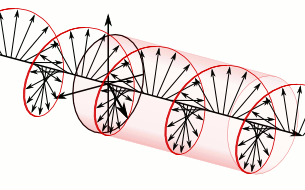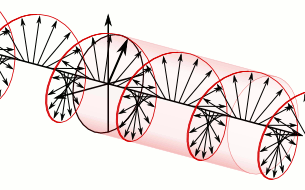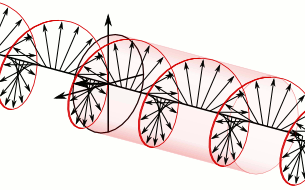
The
electric field
vectors of a traveling circularly polarized electromagnetic wave. This
wave is right-circularly-polarized, since the direction of rotation of
the vector is related by the
right-hand rule to the direction the wave is moving; or left-circularly-polarized according to alternative convention.
https://en.wikipedia.org/wiki/Circular_polarization
A stellar magnetic field is a magnetic field generated by the motion of conductive plasma inside a star. This motion is created through convection, which is a form of energy transport involving the physical movement of material. A localized magnetic field
exerts a force on the plasma, effectively increasing the pressure
without a comparable gain in density. As a result, the magnetized region
rises relative to the remainder of the plasma, until it reaches the
star's photosphere. This creates starspots on the surface, and the related phenomenon of coronal loops.[1]
https://en.wikipedia.org/wiki/Stellar_magnetic_field
In solar physics, a coronal loop is a well-defined arch-like structure in the Sun's atmosphere made up of relatively dense plasma confined and isolated from the surrounding medium by magnetic flux tubes. Coronal loops begin and end at two footpoints on the photosphere and project into the transition region and lower corona. They typically form and dissipate over periods of seconds to days[1] and may span anywhere from 1 to 1,000 megametres (621 to 621,000 mi) in length.[2]
Coronal loops are often associated with the strong magnetic fields located within active regions and sunspots. The number of coronal loops varies with the 11 year solar cycle.
https://en.wikipedia.org/wiki/Coronal_loop
The photosphere is a star's outer shell from which light is radiated.
The term itself is derived from Ancient Greek roots, φῶς, φωτός/phos, photos meaning "light" and σφαῖρα/sphaira meaning "sphere", in reference to it being a spherical surface that is perceived to emit light.[citation needed] It extends into a star's surface until the plasma becomes opaque, equivalent to an optical depth of approximately 2⁄3,[1] or equivalently, a depth from which 50% of light will escape without being scattered.
A photosphere is the deepest region of a luminous object, usually a star, that is transparent to photons of certain wavelengths.
https://en.wikipedia.org/wiki/Photosphere
In physics, the magnetomotive force (mmf)  is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:
is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:

where
Φ is the magnetic flux and

is the
reluctance of the circuit. It can be seen that the magnetomotive force plays a role in this equation analogous to the voltage
V in
Ohm's law:
V = IR, since it is the cause of magnetic flux in a magnetic circuit:
[2]
 where N is the number of turns in the coil and I is the electric current through the circuit.
where N is the number of turns in the coil and I is the electric current through the circuit. where Φ is the magnetic flux and
where Φ is the magnetic flux and  is the magnetic reluctance
is the magnetic reluctance where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
https://en.wikipedia.org/wiki/Magnetomotive_force
In physics, mainly quantum mechanics and particle physics, a spin magnetic moment is the magnetic moment caused by the spin of elementary particles. For example, the electron is an elementary spin-1/2 fermion. Quantum electrodynamics gives the most accurate prediction of the anomalous magnetic moment of the electron.
In general, a magnetic moment can be defined in terms of an electric current and the area enclosed by the current loop.
Since angular momentum corresponds to rotational motion, the magnetic
moment can be related to the orbital angular momentum of the charge carriers in the constituting current. However, in magnetic materials, the atomic and molecular dipoles have magnetic moments not just because of their quantized orbital angular momentum, but also due to the spin of elementary particles constituting them.[a][b]
"Spin" is a non-classical property of elementary particles, since classically the "spin angular momentum" of a material object is really just the total orbital angular momenta of the object's constituents about the rotation axis. Elementary particles are conceived as point objects with no axis around which to "spin" (see wave–particle duality).
https://en.wikipedia.org/wiki/Spin_magnetic_moment
Coercivity, also called the magnetic coercivity, coercive field or coercive force, is a measure of the ability of a ferromagnetic material to withstand an external magnetic field without becoming demagnetized. Coercivity is usually measured in oersted or ampere/meter units and is denoted HC.
An analogous property in electrical engineering and materials science, electric coercivity, is the ability of a ferroelectric material to withstand an external electric field without becoming depolarized.
Ferromagnetic materials with high coercivity are called magnetically hard, and are used to make permanent magnets. Materials with low coercivity are said to be magnetically soft. The latter are used in transformer and inductor cores, recording heads, microwave devices, and magnetic shielding.
https://en.wikipedia.org/wiki/Coercivity
Magnetic shielding
Equipment sometimes requires isolation from external magnetic fields.[8]
For static or slowly varying magnetic fields (below about 100 kHz) the
Faraday shielding described above is ineffective. In these cases
shields made of high magnetic permeability metal alloys can be used, such as sheets of permalloy and mu-metal[9][10] or with nanocrystalline grain structure ferromagnetic metal coatings.[11]
These materials do not block the magnetic field, as with electric
shielding, but rather draw the field into themselves, providing a path
for the magnetic field lines
around the shielded volume. The best shape for magnetic shields is
thus a closed container surrounding the shielded volume. The
effectiveness of this type of shielding depends on the material's
permeability, which generally drops off at both very low magnetic field
strengths and high field strengths where the material becomes saturated.
Therefore, to achieve low residual fields, magnetic shields often
consist of several enclosures, one inside the other, each of which
successively reduces the field inside it. Entry holes within shielding
surfaces may degrade their performance significantly.
Because of the above limitations of passive shielding, an
alternative used with static or low-frequency fields is active
shielding, in which a field created by electromagnets cancels the ambient field within a volume.[12] Solenoids and Helmholtz coils
are types of coils that can be used for this purpose, as well as more
complex wire patterns designed using methods adapted from those used in
coil design for magnetic resonance imaging. Active shields may also be designed accounting for the electromagnetic coupling with passive shields,[13][14][15][16][17] referred to as hybrid shielding,[18]
so that there is broadband shielding from the passive shield and
additional cancellation of specific components using the active system.
Additionally, superconducting materials can expel magnetic fields via the Meissner effect.
https://en.wikipedia.org/wiki/Electromagnetic_shielding#Magnetic_shielding
First time-dependent rotation
Consider another (non-inertial) observer (the 2-O) located at the center of the Earth but rotating about the NS-axis by  We establish coordinates attached to this observer as
We establish coordinates attached to this observer as

so that the unit

versor

is mapped to the point

.
For the 2-O neither the Earth nor the barycenter of the gyroscope is
moving. The rotation of 2-O relative to 1-O is performed with angular
velocity

. We suppose that the

axis denotes points with zero longitude (the prime, or Greenwich, meridian).
Second and third fixed rotations
We now rotate about the  axis, so that the
axis, so that the  -axis has the longitude of the barycenter. In this case we have
-axis has the longitude of the barycenter. In this case we have

With the next rotation (about the axis  of an angle
of an angle  , the co-latitude) we bring the
, the co-latitude) we bring the  axis along the local zenith (
axis along the local zenith ( -axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)
-axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)

so that the  versor
versor  is mapped to the point
is mapped to the point 
Constant translation
We
now choose another coordinate basis whose origin is located at the
barycenter of the gyroscope. This can be performed by the following
translation along the zenith axis

so that the origin of the new system,  is located at the point
is located at the point  and
and  is the radius of the Earth. Now the
is the radius of the Earth. Now the  -axis points towards the south direction.
-axis points towards the south direction.
Fourth time-dependent rotation
Now we rotate about the zenith  -axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find
-axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find

The axis of symmetry of the gyrocompass is now along the  -axis.
-axis.
Last time-dependent rotation
The last rotation is a rotation on the axis of symmetry of the gyroscope as in

Dynamics of the system
Since
the height of the gyroscope's barycenter does not change (and the
origin of the coordinate system is located at this same point), its gravitational potential energy is constant. Therefore its Lagrangian  corresponds to its kinetic energy
corresponds to its kinetic energy  only. We have
only. We have

where

is the mass of the gyroscope, and

is the squared inertial speed of the origin of the coordinates of the
final coordinate system (i.e. the center of mass). This constant term
does not affect the dynamics of the gyroscope and it can be neglected.
On the other hand, the tensor of inertia is given by

and

Therefore we find
![{\displaystyle {\begin{aligned}{\mathcal {L}}&={\frac {1}{2}}\left[I_{1}\omega _{1}^{2}+I_{2}\left(\omega _{2}^{2}+\omega _{3}^{2}\right)\right]\\&={\frac {1}{2}}I_{1}\left({\dot {\psi }}-\Omega \sin \delta \cos \alpha \right)^{2}+{\frac {1}{2}}I_{2}\left\{\left[{\dot {\alpha }}\sin \psi +\Omega (\sin \delta \sin \alpha \cos \psi +\cos \delta \sin \psi )\right]^{2}+\left[{\dot {\alpha }}\cos \psi +\Omega (-\sin \delta \sin \alpha \sin \psi +\cos \delta \cos \psi )\right]^{2}\right\}\\&={\frac {1}{2}}I_{1}\left({\dot {\psi }}-\Omega \sin \delta \cos \alpha \right)^{2}+{\frac {1}{2}}I_{2}\left\{{\dot {\alpha }}^{2}+\Omega ^{2}\left(\cos ^{2}\delta +\sin ^{2}\alpha \sin ^{2}\delta \right)+2{\dot {\alpha }}\Omega \cos \delta \right\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99ea7fb4d7a5a7959dd44adbf50a88c24e3c5f8c)
The Lagrangian can be rewritten as

where

is the part of the Lagrangian responsible for the dynamics of the system. Then, since

, we find

Since the angular momentum  of the gyrocompass is given by
of the gyrocompass is given by  we see that the constant
we see that the constant  is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable
is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable  as
as

or

Particular case: the poles
At the poles we find  and the equations of motion become
and the equations of motion become

This simple solution implies that the gyroscope is uniformly
rotating with constant angular velocity in both the vertical and
symmetrical axis.
The general and physically relevant case
Let us suppose now that  and that
and that  ,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find
,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find

Consider the case that

and, further, we allow for fast gyro-rotations, that is

Therefore, for fast spinning rotations,  implies
implies  In this case, the equations of motion further simplify to
In this case, the equations of motion further simplify to

Therefore we find small oscillations about the north-south line, as  ,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by
,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by

which corresponds to a period for the oscillations given by

Therefore  is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required
is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required  ,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the
,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the  -axis, the axis of symmetry. As a side result, on measuring
-axis, the axis of symmetry. As a side result, on measuring  (and knowing
(and knowing  ), one can deduce the local co-latitude
), one can deduce the local co-latitude 
See also
Notes
- Although
the effect is not visible in the specific case when the gyroscope's
axis is precisely parallel to the Earth's rotational axis.
References
Gade, Kenneth (2016). "The Seven Ways to Find Heading" (PDF). The Journal of Navigation. Cambridge University Press. 69 (5): 955–970. doi:10.1017/S0373463316000096. S2CID 53587934.
Elliott-Laboratories (2003). The Anschutz Gyro-Compass and Gyroscope Engineering. pp. 7–24. ISBN 978-1-929148-12-7. Archived from the original on 2017-03-04.
Time Inc. (Mar 15, 1943). "The gyroscope pilots ships & planes". Life. pp. 80–83. Archived from the original on 2017-02-27.
Galison, Peter (1987). How experiments end. pp. 34–37. ISBN 978-0-226-27915-2. Archived from the original on 2012-03-02.
"Archived copy" (PDF). Archived (PDF) from the original on 2015-06-29. Retrieved 2012-02-19. Standard 22
Anschütz Gyro Compass [sic] System: Gyro Compass [sic] Technology [sic] for over than [sic] 100 years
Chambers of Commerce and Industry in Schleswig-Holstein Archived 2017-02-22 at the Wayback Machine Retrieved on February 22, 2017.
Gyrocompass, Auxiliary Gyrocompass, and Dead Reckoning Analyzing Indicator and Tracer Systems Archived 2013-06-01 at the Wayback Machine, San Francisco Maritime National Park Association.
The Invention of Precision Navigational Instruments for Air and Sea Navigation Archived 2011-07-18 at the Wayback Machine, Weems & Plath.
Collinson, R. P. G. (2003), Introduction to avionics systems, Springer, p. 293, ISBN 978-1-4020-7278-9, archived from the original on 2014-07-07
NASA NASA Callback: Heading for Trouble Archived 2011-07-16 at the Wayback Machine, NASA Callback Safety Bulletin website, December 2005, No. 305. Retrieved August 29, 2010.
Bowditch, Nathaniel. American Practical Navigator Archived 2017-03-07 at the Wayback Machine, Paradise Cay Publications, 2002, pp.93-94, ISBN 978-0-939837-54-0.
Gyrocompass: Steaming Error Archived 2008-12-22 at the Wayback Machine, Navis. Accessed 15 December 2008.
- Seamanship Techniques:Shipboard and Marine Operations, D. J. House, Butterworth-Heinemann, 2004, p. 341
Bibliography
External links
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
This article is about devices used on ships. For the type of gyroscope used to determine aircraft heading, see
Heading indicator.
Cutaway of an Anschütz gyrocompass
A gyrocompass is a type of non-magnetic compass which is based on a fast-spinning disc and the rotation of the Earth (or another planetary body if used elsewhere in the universe) to find geographical direction automatically. The use of a gyrocompass is one of the seven fundamental ways to determine the heading of a vehicle.[1] A gyroscope is an essential component of a gyrocompass, but they are different devices; a gyrocompass is built to use the effect of gyroscopic precession, which is a distinctive aspect of the general gyroscopic effect.[2][3] Gyrocompasses are widely used for navigation on ships, because they have two significant advantages over magnetic compasses:[3]
Aircraft commonly use gyroscopic instruments (but not a gyrocompass) for navigation and altitude monitoring; for details, see Flight instruments and Gyroscopic autopilot.
History
The first, not yet practical,[4] form of gyrocompass was patented in 1885 by Marinus Gerardus van den Bos.[4] A usable gyrocompass was invented in 1906 in Germany by Hermann Anschütz-Kaempfe, and after successful tests in 1908 became widely used in the German Imperial Navy.[2][4][5] Anschütz-Kaempfe founded the company Anschütz & Co. in Kiel, to mass produce gyrocompasses; the company is today Raytheon Anschütz GmbH.[6]
The gyrocompass was an important invention for nautical navigation
because it allowed accurate determination of a vessel’s location at all
times regardless of the vessel’s motion, the weather and the amount of
steel used in the construction of the ship.[7]
In the United States, Elmer Ambrose Sperry produced a workable gyrocompass system (1908: U.S. Patent 1,242,065), and founded the Sperry Gyroscope Company. The unit was adopted by the U.S. Navy (1911[3]),
and played a major role in World War I. The Navy also began using
Sperry's "Metal Mike": the first gyroscope-guided autopilot steering
system. In the following decades, these and other Sperry devices were
adopted by steamships such as the RMS Queen Mary, airplanes, and the warships of World War II. After his death in 1930, the Navy named the USS Sperry after him.
Meanwhile, in 1913, C. Plath (a Hamburg, Germany-based
manufacturer of navigational equipment including sextants and magnetic
compasses) developed the first gyrocompass to be installed on a
commercial vessel. C. Plath sold many gyrocompasses to the Weems’
School for Navigation in Annapolis, MD, and soon the founders of each
organization formed an alliance and became Weems & Plath.[8]
The 1889 Dumoulin-Krebs gyroscope
Before the success of the gyrocompass, several attempts had been made in Europe to use a gyroscope instead. By 1880, William Thomson (Lord Kelvin) tried to propose a gyrostat to the British Navy. In 1889, Arthur Krebs adapted an electric motor to the Dumoulin-Froment marine gyroscope, for the French Navy. That gave the Gymnote submarine the ability to keep a straight line while underwater for several hours, and it allowed her to force a naval block in 1890.
In 1923 Max Schuler published his paper containing his observation that if a gyrocompass possessed Schuler tuning
such that it had an oscillation period of 84.4 minutes (which is the
orbital period of a notional satellite orbiting around the Earth at sea
level), then it could be rendered insensitive to lateral motion and
maintain directional stability.[9]
Operation
A gyroscope, not to be confused with a gyrocompass, is a spinning wheel mounted on a set of gimbals so that its axis is free to orient itself in any way.[3] When it is spun up to speed with its axis pointing in some direction, due to the law of conservation of angular momentum, such a wheel will normally maintain its original orientation to a fixed point in outer space
(not to a fixed point on Earth). Since the Earth rotates, it appears to
a stationary observer on Earth that a gyroscope's axis is completing a
full rotation once every 24 hours.[note 1] Such a rotating gyroscope is used for navigation in some cases, for example on aircraft, where it is known as heading indicator
or directional gyro, but cannot ordinarily be used for long-term marine
navigation. The crucial additional ingredient needed to turn a
gyroscope into a gyrocompass, so it would automatically position to true
north,[2][3] is some mechanism that results in an application of torque whenever the compass's axis is not pointing north.
One method uses friction to apply the needed torque:[7]
the gyroscope in a gyrocompass is not completely free to reorient
itself; if for instance a device connected to the axis is immersed in a
viscous fluid, then that fluid will resist reorientation of the axis.
This friction force caused by the fluid results in a torque acting on the axis, causing the axis to turn in a direction orthogonal to the torque (that is, to precess) along a line of longitude.
Once the axis points toward the celestial pole, it will appear to be
stationary and won't experience any more frictional forces. This is
because true north (or true south) is the only direction for which the
gyroscope can remain on the surface of the earth and not be required to
change. This axis orientation is considered to be a point of minimum potential energy.
Another, more practical, method is to use weights to force the
axis of the compass to remain horizontal (perpendicular to the direction
of the center of the Earth), but otherwise allow it to rotate freely
within the horizontal plane.[2][3]
In this case, gravity will apply a torque forcing the compass's axis
toward true north. Because the weights will confine the compass's axis
to be horizontal with respect to the Earth's surface, the axis can never
align with the Earth's axis (except on the Equator) and must realign
itself as the Earth rotates. But with respect to the Earth's surface,
the compass will appear to be stationary and pointing along the Earth's
surface toward the true North Pole.
Since the gyrocompass's north-seeking function depends on the rotation around the axis of the Earth that causes torque-induced gyroscopic precession,
it will not orient itself correctly to true north if it is moved very
fast in an east to west direction, thus negating the Earth's rotation.
However, aircraft commonly use heading indicators or directional gyros,
which are not gyrocompasses and do not align themselves to north via
precession, but are periodically aligned manually to magnetic north.[10][11]
Errors
A gyrocompass is subject to certain errors. These include steaming error, where rapid changes in course, speed and latitude cause deviation before the gyro can adjust itself.[12] On most modern ships the GPS or other navigational aids feed data to the gyrocompass allowing a small computer to apply a correction.
Alternatively a design based on a strapdown architecture (including a triad of fibre optic gyroscopes, ring laser gyroscopes or hemispherical resonator gyroscopes
and a triad of accelerometers) will eliminate these errors, as they do
not depend upon mechanical parts to determinate rate of rotation.[13]
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
A rotating magnetic field is the resultant magnetic field produced by a system of coils symmetrically placed and supplied with polyphase currents.[1]
A rotating magnetic field can be produced by a poly-phase (two or more
phases) current or by a single phase current provided that, in the
latter case, two field windings are supplied and are so designed that
the two resulting magnetic fields generated thereby are out of phase.[2]
Rotating magnetic fields are often utilized for electromechanical applications, such as induction motors, electric generators and induction regulators.
History
In 1824, the French physicist François Arago formulated the existence of rotating magnetic fields using a rotating copper disk and a needle, termed “Arago's rotations.” English experimenters Charles Babbage and John Herschel found they could induce rotation in Arago's copper disk by spinning a horseshoe magnet under it, with English scientist Michael Faraday later attributing the effect to electromagnetic induction.[3] In 1879, English physicist Walter Baily
replaced the horseshoe magnets with four electromagnets and, by
manually turning switches on and off, demonstrated a primitive induction
motor.[4][5][6][7][8]
The idea of a rotating magnetic field in an AC motor was explored by the Italian physicist and electrical engineer Galileo Ferraris and the Serbian-American inventor and electrical engineer Nikola Tesla.[9] Ferraris wrote about researching the concept and built a working model in 1885.[10]
Tesla attempted several (unsuccessful) designs and working models
through the early 1880s before building a working prototype in 1887[11][12][13]
According to Ferraris principle of rotating magnetic field, Friedrich
August Haselwander developed the first AC 3 phase generator in 1887.[14] In 1888, Ferraris published his research in a paper to the Royal Academy of Sciences in Turin and Tesla obtained a United States patent (U.S. Patent 0,381,968)
for his design. Based on the Haselwander generator, Mikhail
Dolivo-Dobrovolsky will develop a three-phase generator and motor for
the world's first three-phase power plant built in 1891 in Frankfurt,
Germany.[15]
Description
The rotating magnetic field is the key principle in the operation of induction machines. The induction motor consists of a stator and rotor.
In the stator a group of fixed windings are so arranged that a two
phase current, for example, produces a magnetic field which rotates at
an angular velocity determined by the frequency of the alternating current. The rotor or armature consists of coils wound in slots, which are short circuited and in which the changing flux
generated by the field poles induce a current. The flux generated by
the armature current reacts upon the field poles and the armature is set
in rotation in a definite direction.[2]
Rotating fields.
As the direction of the current through the windings changes, the
polarity of the windings changes as well. Since there are two windings
acting in conjunction with each other, the polarity of the main field
will depend upon the polarity of each winding. The arrow or vector below
each diagram indicates the direction of the magnetic field in each
case.
[16] A symmetric rotating magnetic field can be produced with as few as two polar wound coils driven at 90-degree phasing. However, three sets of coils are nearly always used, because it is compatible with a symmetric three-phase AC sine current system. The three coils are driven with each set 120 degrees in phase from the others. For the purpose of this example, the magnetic field is taken to be the linear function of the coil's current.
The result of adding three 120-degree phased sine waves on the axis of the motor is a single rotating vector that always remains constant in magnitude.[17]
The rotor has a constant magnetic field. The north pole of the rotor
will move toward the south pole of the magnetic field of the stator, and
vice versa. This magnetomechanical attraction creates a force that will drive the rotor to follow the rotating magnetic field in a synchronous manner.
Rotating three-phase magnetic field, as indicated by the rotating black arrow
A permanent magnet
in such a field will rotate so as to maintain its alignment with the
external field. This effect was utilized in early alternating-current
electric motors. A rotating magnetic field can be constructed using two
orthogonal coils with a 90-degree phase difference in their alternating
currents. However, in practice, such a system would be supplied through
a three-wire arrangement with unequal currents. This inequality would
cause serious problems in the standardization of the conductor size. In
order to overcome this, three-phase systems are used in which the three
currents are equal in magnitude and have a 120-degree phase difference.
Three similar coils having mutual geometrical angles of 120 degrees will
create the rotating magnetic field in this case. The ability of the
three-phase system to create the rotating field utilized in electric
motors is one of the main reasons why three-phase systems dominate the
world’s electric power-supply systems.
Rotating magnetic fields are also used in induction motors.
Because magnets degrade with time, induction motors use short-circuited
rotors (instead of a magnet), which follow the rotating magnetic field
of a multicoiled stator. In these motors, the short-circuited turns of
the rotor develop eddy currents in the rotating field of the stator, which in turn move the rotor by Lorentz force.
These types of motors are not usually synchronous, but instead
necessarily involve a degree of 'slip' in order that the current may be
produced due to the relative movement of the field and the rotor.
See also
References
Graham, Frank Duncan (1921). Audels Engineers and Mechanics Guide. New York: THEO. AUDEL & CO. p. 594.
The Wireless Age. Vol. 6. New York: Macroni Pub. Corp'n. October 1918. pp. 18–19.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 52–54. ISBN 978-1400846559.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. p. 55. ISBN 978-1400846559.
Babbage, C.; Herschel, J. F. W. (Jan 1825). "Account
of the Repetition of M. Arago's Experiments on the Magnetism Manifested
by Various Substances during the Act of Rotation". Philosophical Transactions of the Royal Society. 115: 467–496. Bibcode:1825RSPT..115..467B. doi:10.1098/rstl.1825.0023. Retrieved 2 December 2012.
Thompson, Silvanus Phillips (1895). Polyphase Electric Currents and Alternate-Current Motors (1st ed.). London: E. & F.N. Spon. p. 261. Retrieved 2 December 2012.
Baily, Walter (June 28, 1879). "A Mode of producing Arago's Rotation". Philosophical Magazine. Taylor & Francis. 3 (1): 115–120. Bibcode:1879PPSL....3..115B. doi:10.1088/1478-7814/3/1/318.
Vučković, Vladan (November 2006). "Interpretation of a Discovery" (PDF). The Serbian Journal of Electrical Engineers. 3 (2). Retrieved 10 February 2013.
Hughes, Thomas Parke (1983). Networks of power: electrification in Western society, 1880-1930. Baltimore: Johns Hopkins University Press. p. 117.
Encyclopedia Americana: Meyer to Nauvoo. Vol. 12. Danbury, Connecticut: Scholastic Library Pub. 2006. p. 558.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 63–68. ISBN 978-1400846559.
Debunking the Tesla Myth
O'Neill, John. Prodigal Genius: The Life of Nikola Tesla. pp. 55–58.
https://ieeexplore.ieee.org/document/4401482?arnumber=4401482 H. Hooshyar; M. Savaghebi; A. Vahedi: Synchronous generator - Past, present and future
AC Power History and Timeline
United States, Bureau of Naval Personnel (1945). Advanced Work In Aircraft Electricity. Washington: U.S. Govt. Print. Off. pp. 149–150.
 This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
Further reading
- C Mackechnie Jarvis (1970). "Nikola Tesla and the induction motor". Phys Educ. 5 (5): 280–7. Bibcode:1970PhyEd...5..280M. doi:10.1088/0031-9120/5/5/306. S2CID 250845406.
- Owen, E.L. (October 1988). "The induction motor's historical past". IEEE Potentials. 7 (3): 27–30. doi:10.1109/45.9969. S2CID 19271710.
- Beckhard, Arthur J., "Electrical genius Nikola Tesla". New York,
Messner, 1959. LCCN 59007009 /L/AC/r85 (ed. 192 p.; 22 cm.; biography
with notes on the inventions of the rotating magnetic field motors for
alternating current.)
- Kline, R. (1987). "Science and Engineering Theory in the Invention and Development of the Induction Motor, 1880–1900". Technology and Culture. 28 (2): 283–313. doi:10.2307/3105568. JSTOR 3105568.
- Cēbers, A. (December 13, 2002). "Dynamics of an elongated magnetic droplet in a rotating field". Phys. Rev. E. 66 (6): 061402. Bibcode:2002PhRvE..66f1402C. doi:10.1103/PhysRevE.66.061402. PMID 12513280.
- Cēbers, A. & I. Javaitis (2004). "Dynamics of a flexible magnetic chain in a rotating magnetic field". Phys. Rev. E. 69 (2): 021404. Bibcode:2004PhRvE..69b1404C. doi:10.1103/PhysRevE.69.021404. PMID 14995441.
- Cēbers, A. & M. Ozols (2006). "Dynamics of an active magnetic particle in a rotating magnetic field". Phys. Rev. E. 73 (2): 021505. Bibcode:2006PhRvE..73b1505C. doi:10.1103/PhysRevE.73.021505. PMID 16605340.
- Tao Song; et al. (June 2004). "Rotating permanent magnetic fields exposure system for in vitro study". IEEE Transactions on Applied Superconductivity. 14 (2): 1643–6. Bibcode:2004ITAS...14.1643S. doi:10.1109/TASC.2004.831024.
- Labzovskii, L.N., A.O. Mitrushchenkov, and A.I. Frenkel, "Parity Nonconserving Current in Conductors of Electricity". 6 July 1987. (ed., Shows that the continuous current arises under the influence of the rotating magnetic field.)
- Naval Electrical Engineering Training Series, Module 05 -
Introduction to Generators and Motors, Chapter 4 Alternating Current
Motors, Rotating magnetic fields (ed. different copy of the NEETS book is available, Add-free version)
- Rotating Magnetic Field, eng.ox.ac.uk
- Tesla's Autobiography, III. My Later Endeavors; The Discovery of the Rotating Magnetic Field
- Nikola Tesla and the electro-magnetic motor, Inventor of the Week Archive.
- Galileo Ferraris: the rotating magnetic field
- Single Phase Induction Motors
- H.Y. Guo, A.L. Hoffman, D. Lotz, S.J. Tobin, W.A. Reass, L.S. Schrank and G.A. Wurden, The Rotating Magnetic Field Oscillator System for Current Drive in the Translation, Confinement and Sustainment Experiment, March 22, 2001.
- Putko, V. F., and V. S. Sobolev, Effect of a rotating magnetic field on the characteristics of a direct-current plasma generator.
External links
Patents
|
|---|
Career and
inventions | | |
|---|
| Writings | |
|---|
| Other | |
|---|
| Related | |
|---|
https://en.wikipedia.org/wiki/Rotating_magnetic_field
Earth's rotation or Earth's spin is the rotation of planet Earth around its own axis, as well as changes in the orientation of the rotation axis in space. Earth rotates eastward, in prograde motion. As viewed from the northern polar star Polaris, Earth turns counterclockwise.
https://en.wikipedia.org/wiki/Earth%27s_rotation
Magnetic hysteresis occurs when an external magnetic field is applied to a ferromagnet such as iron and the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. This is the effect that provides the element of memory in a hard disk drive.
https://en.wikipedia.org/wiki/Magnetic_hysteresis
Magnetic reluctance, or magnetic resistance, is a concept used in the analysis of magnetic circuits. It is defined as the ratio of magnetomotive force (mmf) to magnetic flux. It represents the opposition to magnetic flux, and depends on the geometry and composition of an object.
Magnetic reluctance in a magnetic circuit is analogous to electrical resistance in an electrical circuit in that resistance is a measure of the opposition to the electric current. The definition of magnetic reluctance is analogous to Ohm's law
in this respect. However, magnetic flux passing through a reluctance
does not give rise to dissipation of heat as it does for current through
a resistance. Thus, the analogy cannot be used for modelling energy
flow in systems where energy crosses between the magnetic and electrical
domains. An alternative analogy to the reluctance model which does
correctly represent energy flows is the gyrator–capacitor model.
Magnetic reluctance is a scalar extensive quantity. The unit for magnetic reluctance is inverse henry, H−1.
https://en.wikipedia.org/wiki/Magnetic_reluctance
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model
https://en.wikipedia.org/wiki/Lumped-element_model
The lumped-element model (also called lumped-parameter model, or lumped-component model) simplifies the description of the behaviour of spatially distributed physical systems, such as electrical circuits, into a topology
consisting of discrete entities that approximate the behaviour of the
distributed system under certain assumptions. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc. This may be contrasted to distributed parameter systems or models in which the behaviour is distributed spatially and cannot be considered as localized into discrete entities.
Mathematically speaking, the simplification reduces the state space of the system to a finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters.
https://en.wikipedia.org/wiki/Lumped-element_model
https://en.wikipedia.org/wiki/Utility_frequency#Load-frequency_control
Steam turbine governing is the procedure of controlling the flow rate of steam to a steam turbine
so as to maintain its speed of rotation as constant. The variation in
load during the operation of a steam turbine can have a significant
impact on its performance. In a practical situation the load frequently
varies from the designed or economic load and thus there always exists a
considerable deviation from the desired performance of the turbine.[1]
The primary objective in the steam turbine operation is to maintain a
constant speed of rotation irrespective of the varying load. This can
be achieved by means of governing in a steam turbine. There are many types of governors.
https://en.wikipedia.org/wiki/Steam_turbine_governing
A virtual power plant (VPP) is a cloud-based distributed power plant that aggregates the capacities of heterogeneous distributed energy resources
(DER) for the purposes of enhancing power generation, trading or
selling power on the electricity market, and demand side options for
load reduction.[1]
DER assets in a VPP can include photovoltaic solar, energy
storage, electric vehicle chargers, and demand-responsive devices (such
as water heaters, thermostats, and appliances) with examples of virtual
power plants existing in the United States, Europe, and Australia.
https://en.wikipedia.org/wiki/Virtual_power_plant
Power generation
A virtual power plant is a system that integrates several types of power sources to give a reliable overall power supply.[2]
The sources often form a cluster of different types of dispatchable and
non-dispatchable, controllable or flexible load (CL or FL) distributed generation (DG) systems that are controlled by a central authority and can include microCHPs, natural gas-fired reciprocating engines, small-scale wind power plants (WPP), photovoltaics (PV), run-of-river hydroelectricity plants, small hydro, biomass, backup generators, and energy storage systems (ESS).
This system has benefits such as the ability to deliver peak load electricity or load-following power
generation on short notice. Such a VPP can replace a conventional power
plant while providing higher efficiency and more flexibility, which
allows the system to react better to load fluctuations. The drawback is a
higher complexity of the system, which requires complicated
optimization, control, and secure communications.[3] An interactive simulation on the website of the VPP operator Next Kraftwerke illustrates how the technology works.[4]
According to a 2012 report by Pike Research, VPP capacity would,
from 2011 to 2017, increase by 65%, from 55.6 gigawatts (GW) to 91.7 GW
worldwide, generating from $5.3 billion to $6.5 billion in worldwide
revenue in 2017.[5]
In a more aggressive forecast scenario, the clean-tech market
intelligence firm forecasts that global VPP revenues could reach as high
as $12.7 billion during the same period.[6]
"Virtual power plants represent an 'Internet of Energy'",
said senior analyst Peter Asmus of Pike Research. "These systems tap
existing grid networks to tailor electricity supply and demand services
for a customer. VPPs maximize value for both the end user and the
distribution utility using a sophisticated set of software-based
systems. They are dynamic, deliver value in real time, and can react
quickly to changing customer load conditions."
Ancillary services
Virtual power plants can also be used to provide ancillary services to grid operators in order to help maintain grid stability. Ancillary services include frequency regulation, load following, and providing operating reserve.
These services are primarily used to maintain the instantaneous balance
of electrical supply and demand. Power plants providing ancillary
services must respond to signals from grid operators to increase or
decrease load on the order of seconds to minutes in response to varying
levels of consumer demand.
Since ancillary services are typically provided by controllable
fossil-fuel generators, future carbon-free electrical grids that contain
high percentages of solar and wind must rely on other forms of
controllable power generation or consumption. One of the most well-known
examples of this is Vehicle to Grid
technology. In this case, distributed electrical vehicles connected to
the grid can be controlled together to act as a single virtual power
plant. By selectively controlling the rate at which each individual
vehicle charges, the grid sees a net injection or consumption of energy
as if a large scale battery was providing this service.
Similarly, flexible demand in the form of heat pumps or air conditioners has also been explored to provide ancillary services to the grid.[7]
As long as indoor thermal comfort is maintained, an aggregation of
distributed heat pumps can be selectively turned off and on in order to
vary their aggregate power consumption and follow an ancillary service
signal. Again, the effect on the grid is the same as if a large scale
power plant was providing the service.
Since they operate in parallel, virtual power plants can have the
advantage of higher ramp rates than thermal generators, which is
especially important in grids that experience a duck curve
and have high ramping requirements in the morning and evening. However,
the distributed nature generates communication and latency issues,
which could be problematic for providing fast services like frequency
regulation.
Energy trading
A
virtual power plant is also a cloud-based central or distributed
control center that takes advantage of information and communication
technologies (ICTs) and Internet of things (IoT) devices to aggregate the capacities of heterogeneous Distributed Energy Resources (DERs) to form "a coalition of heterogeneous DERs" for the purpose of energy trading on the wholesale electricity markets or providing ancillary services for system operators on behalf of non-eligible individual DERs.[8][9][10][11][12]
A VPP acts as an intermediary between DERs and the wholesale
electricity market and trades energy on behalf of DER owners who by
themselves are unable to participate in that market.[11]
The VPP behaves as a conventional dispatchable power plant from the
point of view of other market participants, although it is indeed a
cluster of many diverse DERs. Also, in the competitive electricity
markets, a virtual power plant acts as an arbitrageur between diverse
energy trading floors (i.e., bilateral and PPA contracts, forward and
futures markets, and the pool).[8][9][10][12]
So far, for risk management purposes, five different risk-hedging
strategies (i.e., IGDT, RO, CVaR, FSD, and SSD) have been applied to
the decision-making problems of VPPs in the research articles to measure
the level of conservatism of VPPs' decisions in diverse energy trading
floors (e.g., day-ahead electricity market, derivatives exchange market,
and bilateral contracts):
- IGDT : Information Gap Decision Theory[8]
- RO : Robust optimization[9]
- CVaR : Conditional Value at Risk[10]
- FSD : First-order Stochastic Dominance[11]
- SSD : Second-order Stochastic Dominance[12][13]
United States
Energy markets are those commodity markets that deal specifically with the trade and supply of energy.[14]
In the United States, virtual power plants not only deal with the
supply side, but also help manage demand, and ensure reliability of grid
functions through demand response (DR) and other load-shifting approaches, in real time.[15]
An often-reported energy crisis in America[16]
has opened the door for government-subsidized companies to enter an
arena that has only been available to utilities and multinational
billion-dollar companies until now. With the deregulation of markets
around the United States, the wholesale market pricing became the
exclusive domain of large retail suppliers; however local and federal
legislation along with large end-users are beginning to recognize the
advantages of wholesale activities.[17]
Texas is in the stage of developing pilot VPP projects to evaluate the impact on service and reliability.[18]
They have had several meetings of their ADER (Aggregated Distributed
Energy Resources) task force to develop the criteria for pilot projects
to operate.[19]
In California there are two electrical markets: private retail
and wholesale. California Senate Bill 2X—which passed the California
legislature on March 30, 2011—mandates 33% renewables by 2020 without
mandating any particular method to reach that goal.[20] PG&E pays VPP providers $2/kWh during peak times.[21][22]
As of August/September 2022, SunRun VPP inputs 80 MW at peak times,[23] and Tesla VPP inputs 68 MW.[24][25]
Europe
The Institute for Solar Energy Supply Technology of the University of Kassel in Germany pilot-tested a combined power plant that linked solar, wind, biogas, and pumped-storage hydroelectricity to provide load-following power around the clock, completely from renewable sources.[26]
Virtual power station operators are also commonly referred to as aggregators.
To test the effects of micro combined heat and power on a smart grid, 45 natural gas SOFC units (each generating 1.5 kW) from Republiq Power (Ceramic Fuel Cells) will be placed in 2013 on Ameland to function as a virtual power plant.[27]
An example of a real-world virtual power plant can be found on the Scottish Inner Hebrides island of Eigg.[28]
Next Kraftwerke from Cologne, Germany operates a virtual power
plant in seven European countries providing peak-load operation, power
trading and grid balancing services. The company aggregates distributed
energy resources from biogas, solar and wind as well as large-scale
power consumers.[29]
Distribution network operator, UK Power Networks,
and Powervault, a battery manufacturer and power aggregator, created
London's first virtual power plant in 2018, installing a trial fleet of
battery systems on over 40 homes across the London Borough of Barnet,
providing a combined capacity of 0.32 MWh.[30] This scheme was further expanded through a second contract in St Helier, London in 2020.[31]
In September 2019, SMS plc entered the virtual power plant sector
in the United Kingdom following the acquisition of Irish energy tech
start-up, Solo Energy.[32]
In October 2020, Tesla launched its Tesla Energy Plan in the UK in partnership with Octopus Energy,
allowing households to join its UK Tesla Virtual Power Plant. Homes
under the scheme are powered with 100% renewable energy from either
solar panels on the roof or from Octopus Energy.[33]
Australia
Commencing
in August 2020, Tesla will install a 5 kW rooftop solar system and 13.5
kWh Powerwall battery at each Housing SA premises, at no upfront cost
to the tenant. As South Australia's largest virtual power plant, the
battery and solar systems can be centrally managed, collectively
delivering 20 MW of generation capacity and 54 MWh of energy storage.[34]
In August 2016, AGL Energy announced a 5 MW virtual-power-plant scheme for Adelaide, Australia. The company will supply battery and photovoltaic systems from Sunverge Energy, of San Francisco, to 1000 households and businesses. The systems will cost consumers AUD $3500 and are expected to recoup the expense in savings in 7 years under current distribution network tariffs. The scheme is worth AUD $20 million and is being billed as the largest in the world.[35]
See also
References
Zurborg, Aaron (2010). "Unlocking Customer Value: the Virtual Power Plant" (PDF). Energy.gov. Retrieved 15 January 2023.
Feasibility, beneficiality, and institutional compatibility of a micro-CHP virtual power plant in the Netherlands
Smart Grid - The New and Improved Power Grid: A Survey; IEEE Communications Surveys and Tutorials 2011; X. Fang, S. Misra, G. Xue, and D. Yang; doi:10.1109/SURV.2011.101911.00087.
"Manage the Virtual Power and prevent a blackout!". Next Kraftwerke. Retrieved 2 December 2019.
"Revenue from Virtual Power Plants Will Reach $5.3 Billion by 2017, Forecasts Pike Research" (Press release). Navigant Consulting. 18 April 2012. Retrieved 20 November 2017 – via Business Wire.
"Virtual-Power-Plant
Market Capacity Expected To Double By 2015 - Apr 16, 2011 -
renewgridmag.com - Transmission - Technical Articles - Index - Library -
GENI - Global Energy Network Institute". Global Energy Network Institute. 2011-04-16. Retrieved 2022-01-05.
Lee,
Zachary E.; Sun, Qingxuan; Ma, Zhao; Wang, Jiangfeng; MacDonald, Jason
S.; Zhang, K. Max (Feb 2020). "Providing Grid Services With Heat Pumps: A
Review". Journal of Engineering for Sustainable Buildings and Cities. 1 (1). doi:10.1115/1.4045819. S2CID 213898377.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2015). "Decision
Making Tool for Virtual Power Plants Considering Midterm Bilateral
Contracts". 3rd Iranian Regional CIRED Conference and Exhibition on
Electricity Distribution, at Niroo Research Institute (NRI), Tehran,
Iran. 3 (3): 1–6. doi:10.13140/2.1.5086.4969.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (October 2015). "The design
of a risk-hedging tool for virtual power plants via robust optimization
approach". Applied Energy. 155: 766–777. doi:10.1016/j.apenergy.2015.06.059.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (May 2016). "A medium-term
coalition-forming model of heterogeneous DERs for a commercial virtual
power plant". Applied Energy. 169: 663–681. doi:10.1016/j.apenergy.2016.02.058.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2017). "Risk-based
medium-term trading strategy for a virtual power plant with first-order
stochastic dominance constraints". IET Generation, Transmission & Distribution. 11 (2): 520–529. doi:10.1049/iet-gtd.2016.1072. S2CID 114478127.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (April 2016). "Modeling the
cooperation between neighboring VPPs: Cross-regional bilateral
transactions". 2016 Iranian Conference on Renewable Energy & Distributed Generation (ICREDG). 11: 520–529. doi:10.1109/ICREDG.2016.7875909. ISBN 978-1-5090-0857-5. S2CID 16453458.
Shabanzadeh,
Morteza; Sheikh-El-Eslami, Mohammad-Kazem; Haghifam, Mahmoud-Reza
(2017). "An interactive cooperation model for neighboring virtual power
plants". Applied Energy. 200: 273–289. doi:10.1016/j.apenergy.2017.05.066. S2CID 157309706.
JEAN-PHILIPPE TAILLON, CFA (2021-10-14). "Introduction to the World of Electricity Trading". Investopedia. Retrieved 2022-01-04.
Aaron Zurborg (2010). "Unlocking Customer Value: The Virtual Power Plant". WorldPower 2010: 1–5.
"Energy Crisis (1970s) - HISTORY". history.com. 2018-08-21. Retrieved 2022-01-04.
"Electricity Deregulation". PennStation Extension. 2010-06-15. Retrieved 2022-01-05.
https://interchange.puc.texas.gov/Documents/51603_66_1221955.PDF
"Admin Monitor - Texas - Public Utility Commission of Texas".
PATRICK MCGREEVY (2011-04-13). "Gov. Brown signs law requiring 33% of energy be renewable by 2020 - Los Angeles Times". Los Angeles Times. Retrieved 2021-01-05.
"PG&E, Tesla virtual power plant delivers 16.5 MW to California grid amid calls for energy conservation". Utility Dive. 23 August 2022.
"Admin Monitor - Texas - Public Utility Commission of Texas".
Colthorpe, Andy (8 September 2022). "California's fleet of battery storage working to avert energy crisis". Energy Storage News.
Lambert, Fred (2022-09-02). "Tesla virtual power plant is rocketing up, reaches 50 MW". Electrek. Retrieved 2022-09-08.
"Tesla's Virtual Power Plant Tracker". Lastbulb. Retrieved 2022-09-08.
"The Combined Power Plant: the first stage in providing 100% power from renewable energy". SolarServer. January 2008. Retrieved 2008-10-10.
"Bijlage persbericht 010/MK – Verleende subsidies – 3. Methaanbrandstoffen op Ameland" [Press release 010/MK appendix – Granted subsidies – 3. Methane fuels on Ameland] (PDF). Wadden Fund (Press release) (in Dutch). 2013. Archived from the original (PDF) on 1 November 2013. Retrieved 21 November 2017.
BBC Radio 4. Costing the Earth- Electric Island
"Next Kraftwerk Reimagines & Redefines The Electrical Grid With Virtual Power Plants". Clean Technica. October 2016. Retrieved 2019-03-13.
"Electricity network plan to launch London's first virtual power station". UK Power Networks. 22 June 2018. Retrieved 15 October 2021.
"London pioneers first 'virtual power station'". GOV.UK. 6 March 2020. Retrieved 1 July 2021.
Grundy, Alice (27 March 2020). "Smart Metering Systems reveals Solo Energy acquisition as it enters VPP market". Current News. Retrieved 1 July 2021.
Lempriere, Molly (27 October 2020). "Tesla Energy Plan launched inviting homes to become part of Virtual Power Plant". Current News. Retrieved 1 July 2021.
"Social housing added to the Tesla virtual power plant - ARENAWIRE". Australian Renewable Energy Agency. Retrieved 2021-01-06.
External links
|
|---|
| Concepts | | |
|---|
| Sources | |
|---|
| Generation | |
|---|
| |
|---|
| Failure modes | |
|---|
Protective
devices | |
|---|
Economics
and policies | |
|---|
Statistics and
production | |
|---|
|
https://en.wikipedia.org/wiki/Virtual_power_plant
lectrical busbar systems[1] (sometimes simply referred to as busbar systems) are a modular approach to electrical wiring,
where instead of a standard cable wiring to every single electrical
device, the electrical devices are mounted onto an adapter which is
directly fitted to a current carrying busbar. This modular approach is used in distribution boards, automation panels and other kinds of installation in an electrical enclosure.[2]
Busbar systems are subject to safety standards for design and installation along with electrical enclosure according to IEC 61439-1 and vary between countries and regions.[3]
https://en.wikipedia.org/wiki/Electrical_busbar_system
A black start is the process of restoring an electric power station or a part of an electric grid to operation without relying on the external electric power transmission network to recover from a total or partial shutdown.[1]
Power to restart a generating station may come from an on-site
standby generator. Alternatively, where a large amount of power is
required, a tie-line to another generating plant may be used to start
the facility. Once the main generating units are running, the electrical
transmission network can be re-connected and electrical loads restored.
Black-start power may be ensured by an agreement where a
particular energy supplier is paid to make black start power available
when required. Not all generating plants are suitable for providing
black-start power to a network.
https://en.wikipedia.org/wiki/Black_start
A rolling blackout, also referred to as rota or rotational load shedding, rota disconnection, feeder rotation, or a rotating outage, is an intentionally engineered electrical power shutdown in which electricity delivery
is stopped for non-overlapping periods of time over different parts of
the distribution region. Rolling blackouts are a last-resort measure
used by an electric utility company to avoid a total blackout of the power system.
Rolling blackouts are a measure of demand response
if the demand for electricity exceeds the power supply capability of
the network. Rolling blackouts may be localised to a specific part of
the electricity network, or they may be more widespread and affect
entire countries and continents. Rolling blackouts generally result from
two causes: insufficient generation capacity or inadequate transmission infrastructure to deliver power to where it is needed.
Rolling blackouts are also used as a response strategy to cope with reduced output beyond reserve capacity from power stations taken offline unexpectedly.
https://en.wikipedia.org/wiki/Rolling_blackout
Magnetic inductance
Circuit equivalence between a magnetic inductance and an electric capacitance.
In the context of the gyrator-capacitor model of a magnetic circuit, magnetic inductance  (SI unit: F) is the analogy to inductance in an electrical circuit.
(SI unit: F) is the analogy to inductance in an electrical circuit.
For phasor analysis the magnetic inductive reactance is:
where:
In the complex form it is a positive imaginary number:
The magnetic potential energy sustained by magnetic inductance
varies with the frequency of oscillations in electric fields. The
average power in a given period is equal to zero. Due to its dependence
on frequency, magnetic inductance is mainly observable in magnetic
circuits which operate at VHF and/or UHF frequencies.[citation needed]
The notion of magnetic inductance is employed in analysis and
computation of circuit behavior in the gyrator–capacitor model in a way
analogous to inductance in electrical circuits.
A magnetic inductor can represent an electrical capacitor.[4]: 43
A shunt capacitance in the electrical circuit, such as intra-winding
capacitance can be represented as a series inductance in the magnetic
circuit.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
The gyrator–capacitor model[1] - sometimes also the capacitor-permeance model[2] - is a lumped-element model for magnetic circuits, that can be used in place of the more common resistance–reluctance model. The model makes permeance elements analogous to electrical capacitance (see magnetic capacitance section) rather than electrical resistance (see magnetic reluctance). Windings are represented as gyrators, interfacing between the electrical circuit and the magnetic model.
The primary advantage of the gyrator–capacitor model compared to
the magnetic reluctance model is that the model preserves the correct
values of energy flow, storage and dissipation.[3][4] The gyrator–capacitor model is an example of a group of analogies
that preserve energy flow across energy domains by making power
conjugate pairs of variables in the various domains analogous. It fills
the same role as the impedance analogy for the mechanical domain.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
Category:Magnetic circuits
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Magnetic_circuits
Category:Electrical analogies
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Electrical_analogies
Magnetic induction
From Wikipedia, the free encyclopedia
Magnetic induction may refer to:
Category:
https://en.wikipedia.org/wiki/Magnetic_induction
https://en.wikipedia.org/wiki/Synchronization_(alternating_current)
https://en.wikipedia.org/wiki/Category:AC_power
https://en.wikipedia.org/wiki/Category:Three-phase_AC_power
https://en.wikipedia.org/wiki/Symmetrical_components
https://en.wikipedia.org/wiki/Linearly_independent
https://en.wikipedia.org/wiki/Root_mean_square#Voltage
https://en.wikipedia.org/wiki/Droop_speed_control
https://en.wikipedia.org/wiki/Beat_(acoustics)
https://en.wikipedia.org/wiki/Interference_(wave_propagation)
In AC electrical power systems, a synchroscope is a device that indicates the degree to which two systems (generators or power networks) are synchronized with each other.[1]
For two electrical systems to be synchronized, both systems must operate at the same frequency, and the phase angle between the systems must be zero (and two polyphase systems must have the same phase sequence).
Synchroscopes measure and display the frequency difference and phase
angle between two power systems. Only when these two quantities are zero
is it safe to connect the two systems together. Connecting two
unsynchronized AC power systems together is likely to cause high
currents to flow, which will severely damage any equipment not protected
by fuses or circuit breakers.

This synchroscope was used to synchronize a factory's power plant with the utility's power grid.
https://en.wikipedia.org/wiki/Synchroscope
https://en.wikipedia.org/wiki/Three-phase_electric_power#Phase_sequence
https://en.wikipedia.org/wiki/Relay
https://en.wikipedia.org/wiki/Circuit_breaker
https://en.wikipedia.org/wiki/Deformed_power
https://en.wikipedia.org/wiki/Leading_and_lagging_current
A rotary phase converter, abbreviated RPC, is an electrical machine that converts power from one polyphase system to another, converting through rotary motion. Typically, single-phase electric power is used to produce three-phase electric power locally to run three-phase loads in premises where only single-phase is available.

A simple homemade phase converter
https://en.wikipedia.org/wiki/Rotary_phase_converter
In communication theory, time-varying phasors are used for analyzing narrow-band signals, whose signal bandwidths in the frequency domain are considerably smaller than the carrier frequency.[1][2] Time-varying phasors are mostly used for analysis of frequency domain of band-pass systems.[2][1] The method uses classical impulse response.[1]
In electrical power system, phasors are used for transient analysis of the power system keeping the quasi-stationary conditions.[1][3][4] They were introduced to facilitate the computation and analysis of power systems in stationary operation.[3] Time-varying phasors are used in dynamic analysis of a large power system.[1][5] The phasor representation of sinusoidal voltages and currents is generalized to arbitrary waveforms.[2] This mathematical transformation eliminates the 60 Hertz (Hz) carrier which is the only time-varying element in the stationary case.[3]
The longer usage of time-varying phasors in large power systems since
1920s have created many misconceptions. One of the misuses suggest that quasi-stationary
models are always accurate, but only when the system dynamics are slow
as compared to nominal system frequency which is usually 60 Hz.[4]
The concern to study time-varying phasors is raised to understand
in-depth the fast amplitude and phase variations of emerging electrical
power generator technologies.[4] This is because current and voltage signals of latest machines may have harmonic components and they can damage the entire transmission system which is coupled with the machine.[3][4]
However, if we employ quasi-static model, we can accurately model AC
signals by using time-varying phasors as opposed to traditional
quasi-static model which supports constant voltage and current signals
throughout the network.[5]
https://en.wikipedia.org/wiki/Time-varying_phasor
Single-phase generator (also known as single-phase alternator) is an alternating current electrical generator that produces a single, continuously alternating voltage. Single-phase generators can be used to generate power in single-phase electric power systems. However, polyphase generators are generally used to deliver power in three-phase distribution
system and the current is converted to single-phase near the
single-phase loads instead. Therefore, single-phase generators are found
in applications that are most often used when the loads being driven
are relatively light,[1] and not connected to a three-phase distribution, for instance, portable engine-generators. Larger single-phase generators are also used in special applications such as single-phase traction power for railway electrification systems.[2]

Elementary generator is an example of single-phase generators with two poles
https://en.wikipedia.org/wiki/Single-phase_generator
Polyphase coils are electromagnetic coils connected together in a polyphase system such as a generator or motor. In modern systems, the number of phases is usually three or a multiple of three. Each phase carries a sinusoidal alternating current whose phase
is delayed relative to one of its neighbours and advanced relative to
its other neighbour. The phase currents are separated in time evenly
within each period of the alternating current. For example, in a
three-phase system, the phases are separated from each other by
one-third of the period.
Coil construction
Like all coils used in electrical machinery, polyphase coils (made from insulated conducting wire) are wound around ferromagnetic armatures with radial projections and maximum core-surface exposure to the magnetic field.
The windings are physically separated around the circumference of an electrical machine. The result of such an arrangement is a rotating magnetic field that is used to convert electrical power to rotary mechanical work, or vice versa.
https://en.wikipedia.org/wiki/Polyphase_coil
https://en.wikipedia.org/wiki/Category:AC_power
A Scott-T transformer (also called a Scott connection) is a type of circuit used to produce two-phase electric power (2 φ, 90 degree phase rotation)[1] from a three-phase
(3 φ, 120 degree phase rotation) source, or vice versa. The Scott
connection evenly distributes a balanced load between the phases of the
source. The Scott three-phase transformer was invented by a Westinghouse engineer Charles F. Scott in the late 1890s to bypass Thomas Edison's more expensive rotary converter and thereby permit two-phase generator plants to drive three-phase motors.[2]
https://en.wikipedia.org/wiki/Scott-T_transformer
History
The first locomotive with a phase converter (only for demonstration purposes)
The Kandó phase converter (1933)
The "Kandó" locomotive, the first locomotive using a phase converter system
At the beginning of the 20th century, there were two main principles of electric railway traction current systems:
- DC system
- 16⅔ Hz single phase system
These systems used series-wound traction motors. All of them needed a separated supply system or converters to take power from the standard 50 Hz electric network.
https://en.wikipedia.org/wiki/Rotary_phase_converter
Unbalanced loads
Two-phase
motors draw constant power, just as three-phase motors do, so a
balanced two-phase load is converted to a balanced three-phase load.
However if a two-phase load is not balanced (more power drawn from one
phase than the other), no arrangement of transformers (including the
Scott-T transformers) can restore balance: Unbalanced current on the
two-phase side causes unbalanced current on the three-phase side. Since
the typical two-phase load was a motor, the current in the two phases
was presumed inherently equal during the Scott-T development.
In modern times people have tried to revive the Scott connection as a way to power single-phase electric railways
from three-phase Utility supplies. This will not result in balanced
current on the three-phase of being equal. The instantaneous
difference in loading on the two sections will be seen as an imbalance
in the three-phase supply; there is no way to smooth it out with
transformers.[4]
https://en.wikipedia.org/wiki/Scott-T_transformer
Back to back arrangement
Scott Connection 3 φ to 3 φ
The Scott-T transformer connection may also be used in a back-to-back
T-to-T arrangement for a three-phase to three-phase connection. This is
a cost-saving in the lower-power transformers due to the two-coil T
connected to a secondary two-coil T instead of the traditional
three-coil primary to three-coil secondary transformer. In this
arrangement the X0 neutral tap is part way up on the secondary teaser
transformer (see right). The voltage stability of this T-to-T
arrangement as compared to the traditional three-coil primary to
three-coil secondary transformer is questioned, as the "per unit"
impedance of the two windings (primary and secondary, respectively) are not the same in a T-to-T configuration, whereas the three windings (primary and secondary, respectively) are the same in a three transformer configuration, if the three transformers are identical.
Three-phase to three-phase (also called "T-connected")
distribution transformers are seeing increasing applications. The
primary must be delta-connected (Δ), but the secondary may be either delta or "wye"-connected (Y),
at the customer's option, with X0 providing the neutral for the "wye"
case. Taps for either case are usually provided. The customary maximum
capacity of such a distribution transformer is 333 kVA (a third of a
megawatt at unity power factor).[citation needed]
https://en.wikipedia.org/wiki/Scott-T_transformer
An induction regulator is an alternating current electrical machine, somewhat similar to an induction motor, which can provide a continuously variable output voltage.
The induction regulator was an early device used to control the voltage
of electric networks. Since the 1930s it has been replaced in
distribution network applications by the tap transformer. Its usage is now mostly confined to electrical laboratories, electrochemical processes and arc welding. With minor variations, its setup can be used as a phase-shifting power transformer.
https://en.wikipedia.org/wiki/Induction_regulator
Magnet wire or enameled wire is a copper (Cu) or aluminium (Al) wire coated with a very thin layer of insulation. It is used in the construction of transformers, inductors, motors, generators,
speakers, hard disk head actuators, electromagnets, electric guitar pickups and other applications that require tight coils of insulated wire.
The wire itself is most often fully annealed,
electrolytically refined copper. Aluminium magnet wire is sometimes
used for large transformers and motors. The insulation is typically made
of tough polymer film materials rather than vitreous enamel, as the name might suggest.
https://en.wikipedia.org/wiki/Magnet_wire
In electronics, a center tap (CT) is a contact made to a point halfway along a winding of a transformer or inductor, or along the element of a resistor or a potentiometer.
Taps are sometimes used on inductors for the coupling of signals,
and may not necessarily be at the half-way point, but rather, closer to
one end. A common application of this is in the Hartley oscillator. Inductors with taps also permit the transformation of the amplitude of alternating current (AC) voltages for the purpose of power conversion, in which case, they are referred to as autotransformers, since there is only one winding. An example of an autotransformer is an automobile ignition coil.
Potentiometer tapping provides one or more connections along the
device's element, along with the usual connections at each of the two
ends of the element, and the slider connection. Potentiometer taps allow
for circuit functions that would otherwise not be available with the
usual construction of just the two end connections and one slider
connection.
https://en.wikipedia.org/wiki/Center_tap
A relief valve or pressure relief valve (PRV) is a type of safety valve used to control or limit the pressure
in a system; excessive pressure might otherwise build up and create a
process upset, instrument or equipment failure, explosion, or fire.
https://en.wikipedia.org/wiki/Relief_valve
The open-circuit test, or no-load test, is one of the methods used in electrical engineering to determine the no-load impedance in the excitation branch of a transformer.
The no load is represented by the open circuit, which is represented on
the right side of the figure as the "hole" or incomplete part of the
circuit.
https://en.wikipedia.org/wiki/Open-circuit_test
Electrical insulation papers are paper types that are used as electrical insulation in many applications due to pure cellulose having outstanding electrical properties. Cellulose is a good insulator and is also polar,[clarification needed] having a dielectric constant significantly greater than one.[1]
Electrical paper products are classified by their thickness, with tissue
considered papers less than 1.5 mils (0.0381 mm) thickness, and board considered more than 20 mils (0.508 mm) thickness.[2]
https://en.wikipedia.org/wiki/Electrical_insulation_paper
A balun (from "balanced to unbalanced", originally, but now dated from "balancing unit")[1] is an electrical device that allows balanced and unbalanced lines to be interfaced without disturbing the impedance arrangement of either line.[2] A balun can take many forms and may include devices that also transform impedances but need not do so. Sometimes, in the case of transformer baluns, they use magnetic coupling but need not do so. Common-mode chokes are also used as baluns and work by eliminating, rather than rejecting, common mode signals.
https://en.wikipedia.org/wiki/Balun
In electrical engineering, the method of symmetrical components simplifies analysis of unbalanced three-phase power systems under both normal and abnormal conditions. The basic idea is that an asymmetrical set of N phasors can be expressed as a linear combination of N symmetrical sets of phasors by means of a complex linear transformation.[1] Fortescue's theorem (symmetrical components) is based on superposition principle,[2] so it is applicable to linear power systems only, or to linear approximations of non-linear power systems.
In the most common case of three-phase systems, the resulting "symmetrical" components are referred to as direct (or positive), inverse (or negative) and zero (or homopolar).
The analysis of power system is much simpler in the domain of
symmetrical components, because the resulting equations are mutually linearly independent if the circuit itself is balanced.[citation needed]
https://en.wikipedia.org/wiki/Symmetrical_components
A solid-state transformer (SST), power electronic transformer (PET), or electronic power transformer is actually an AC-to-AC converter, a type of electric power converter that replaces a conventional transformer used in AC electric power distribution. It is more complex than a conventional transformer operating at utility frequency,
but it can be smaller and more efficient than a conventional
transformer because it operates at high frequency. The main types are
"true" AC-to-AC converter (with no DC stages) and AC-to-DC-to-DC-to-AC
converter (in which an active rectifier supplies power to a DC-to-DC converter, which supplies power to a power inverter).
A solid-state transformer usually contains a transformer, inside the
AC-to-AC converter or DC-to-DC converter, which provides electrical
isolation and carries the full power. This transformer is smaller due to
smaller DC-DC inverting stages between transformer coils, which
consequently mean smaller transformer coils required to step up or step
down voltages. A solid-state transformer can actively regulate voltage
and current. Some can convert single-phase power to three-phase power
and vice versa. Variations can input or output DC power to reduce the number of conversions, for greater end-to-end efficiency. A Modular Solid-state transformer consists of several high-frequency transformers[1] and is similar to a Multi-level converter.
As a complex electronic circuit, it must be designed to withstand
lightning and other surges. Solid-state transformer is an emerging
technology.
https://en.wikipedia.org/wiki/Solid-state_transformer
A grounding transformer or earthing transformer is a type of auxiliary transformer used in three-phase electric power systems to provide a ground path to either an ungrounded wye or a delta-connected system.[1][2] Grounding transformers are part of an earthing system of the network. They let three-phase (delta connected) systems accommodate phase-to-neutral loads by providing a return path for current to a neutral.
Grounding transformers are typically used to:
- Provide a relatively low-impedance path to ground, thereby maintaining the system neutral at or near ground potential.[3]
- Limit the magnitude of transient overvoltages when restriking ground faults occur.
- Provide a source of ground fault current during line-to-ground faults.
- Permit the connection of phase-to-neutral loads when desired.[2]
Earthing transformer with a zig-zag
Grounding transformers most commonly incorporate a single winding transformer with a zigzag winding configuration, but may also be created with a wye-delta winding transformer.[2][4] Neutral grounding transformers are very common on generators in power plants and wind farms.[2]
Neutral grounding transformers are sometimes applied on high-voltage
(sub-transmission) systems, such as at 33 kV, where the circuit would
otherwise not have a ground; for example, if a system is fed by a
delta-connected transformer. The grounding point of the transformer may
be connected through a resistor or arc suppression coil to limit the
fault current on the system in the event of a line-to-ground fault. [5]
https://en.wikipedia.org/wiki/Grounding_transformer
An autotransformer is an electrical transformer with only one winding. The "auto" (Greek for "self") prefix refers to the single coil acting alone, not to any kind of automatic mechanism. In an autotransformer, portions of the same winding act as both the primary winding and secondary winding
sides of the transformer. In contrast, an ordinary transformer has
separate primary and secondary windings which have no metallic
conducting path between them.
The autotransformer winding has at least three taps
where electrical connections are made. Since part of the winding does
"double duty", autotransformers have the advantages of often being
smaller, lighter, and cheaper than typical dual-winding transformers,
but the disadvantage of not providing electrical isolation between primary and secondary circuits. Other advantages of autotransformers include lower leakage reactance, lower losses, lower excitation current, and increased VA rating for a given size and mass.[1]
An example of an application of an autotransformer is one style
of traveler's voltage converter, that allows 230-volt devices to be used
on 120-volt supply circuits, or the reverse. An autotransformer with
multiple taps may be applied to adjust the voltage at the end of a long
distribution circuit to correct for excess voltage drop; when
automatically controlled, this is one example of a voltage regulator.

Single-phase tapped autotransformer with an output voltage range of 40%–115% of input
https://en.wikipedia.org/wiki/Autotransformer
See also
https://en.wikipedia.org/wiki/Autotransformer
A zigzag transformer is a special-purpose transformer with a zigzag or "interconnected star" winding connection, such that each output is the vector sum of two (2) phases offset by 120°.[1] It is used as a grounding transformer, creating a missing neutral connection from an ungrounded 3-phase system to permit the grounding of that neutral to an earth reference point; to perform harmonic mitigation, as they can suppress triplet (3rd, 9th, 15th, 21st, etc.) harmonic currents;[2] to supply 3-phase power as an autotransformer (serving as the primary and secondary with no isolated circuits);[3] and to supply non-standard, phase-shifted, 3-phase power.[1]
9-winding zigzag transformer
Nine-winding, three-phase transformers typically have three primaries
and six identical secondary windings, which can be used in zigzag
winding connection as pictured.[1] As with the conventional delta or wye winding configuration three-phase
transformer, a standard, stand-alone transformer containing only six
windings on three cores can also be used in zigzag winding connection,
such transformer sometimes being referred to as a zigzag bank.[1]
In all cases, six or nine winding, the first coil on each zigzag
winding core is connected contrariwise to the second coil on the next
core. The second coils are then all tied together to form the neutral,
and the phases are connected to the primary coils. Each phase,
therefore, couples with each other phase, and the voltages cancel out.
As such, there would be negligible current through the neutral point,
which can be tied to ground.[4]
Each of the three "limbs" are split into two sections. The two
halves of each limb have an equal number of turns and are wound in
opposite directions. With the neutral grounded, during a phase-to-ground
short fault, a third of the current returns to the fault current, and
the remainder must go through two of the three phases when used to
derive a grounding point from a delta source.[5]
If one or more phases fault to earth, the voltage applied to each
phase of the transformer is no longer in balance; fluxes in the
windings no longer oppose. (Using symmetrical components, this is Ia0 = Ib0 = Ic0.)
Zero-sequence (earth fault) current exists between the transformer’s
neutral to the faulting phase. The purpose of a zigzag transformer in
this application is to provide a return path for earth faults on
delta-connected systems. With negligible current in the neutral under
normal conditions, an undersized (unable to carry a continuous fault
load) transformer may be used only as short-time rating is required,
provided the defective load will be automatically disconnected in a
fault condition. The transformer's impedance should not be too low for
desired maximum fault current. Impedance can be added after the
secondaries are summed to limit maximum fault currents (the 3Io path).[6]
A combination of Y (wye or star), delta, and zigzag windings may be used to achieve a vector phase shift.
For example, an electrical network may have a transmission network of
110 kV/33 kV star/star transformers, with 33 kV/11 kV delta/star for the
high voltage distribution network. If a transformation is required
directly between the 110 kV/11 kV network an option is to use a 110
kV/11 kV star/delta transformer. The problem is that the 11 kV delta no
longer has an earth reference point. Installing a zigzag transformer
near the secondary side of the 110 kV/11 kV transformer provides the
required earth reference point.[7]
https://en.wikipedia.org/wiki/Zigzag_transformer
Railway electrification systems using alternating current (AC) at 25 kilovolts (kV) are used worldwide, especially for high-speed rail. It is usually supplied at the standard utility frequency (typically 50 or 60 Hz), which simplifies traction substations. The development of 25 kV AC electrification is closely connected with that of successfully using utility frequency.
This electrification is ideal for railways that cover long distances or carry heavy traffic. After some experimentation before World War II in Hungary and in the Black Forest in Germany, it came into widespread use in the 1950s.
One of the reasons why it was not introduced earlier was the lack
of suitable small and lightweight control and rectification equipment
before the development of solid-state rectifiers
and related technology. Another reason was the increased clearance
distances required where it ran under bridges and in tunnels, which
would have required major civil engineering in order to provide the increased clearance to live parts.
Railways using older, lower-capacity direct current systems have introduced or are introducing 25 kV AC instead of 3 kV DC/1.5 kV DC for their new high-speed lines.
https://en.wikipedia.org/wiki/25_kV_AC_railway_electrification
In electronics, impedance matching is the practice of designing or adjusting the input impedance or output impedance of an electrical device for a desired value. Often, the desired value is selected to maximize power transfer or minimize signal reflection.
For example, impedance matching typically is used to improve power
transfer from a radio transmitter via the interconnecting transmission
line to the antenna. Signals on a transmission line will be transmitted without reflections if the transmission line is terminated with a matching impedance.
Techniques of impedance matching include transformers, adjustable networks of lumped resistance, capacitance and inductance,
or properly proportioned transmission lines. Practical
impedance-matching devices will generally provide best results over a
specified frequency band.
The concept of impedance matching is widespread in electrical engineering, but is relevant in other applications in which a form of energy, not necessarily electrical, is transferred between a source and a load, such as in acoustics or optics.

Source and
load impedance circuit
https://en.wikipedia.org/wiki/Impedance_matching
In electronics, electrical termination is the practice of ending a transmission line with a device that matches the characteristic impedance of the line. Termination prevents signals from reflecting off the end of the transmission line. Reflections at the ends of unterminated transmission lines cause distortion, which can produce ambiguous digital signal levels and misoperation of digital systems. Reflections in analog signal systems cause such effects as video ghosting, or power loss in radio transmitter transmission lines.
https://en.wikipedia.org/wiki/Electrical_termination
In telecommunications, signal reflection occurs when a signal is transmitted along a transmission medium, such as a copper cable or an optical fiber.
Some of the signal power may be reflected back to its origin rather
than being carried all the way along the cable to the far end. This
happens because imperfections in the cable cause impedance
mismatches and non-linear changes in the cable characteristics. These
abrupt changes in characteristics cause some of the transmitted signal
to be reflected. In radio frequency (RF) practice this is often measured in a dimensionless ratio known as voltage standing wave ratio (VSWR) with a VSWR bridge. The ratio of energy bounced back depends on the impedance mismatch. Mathematically, it is defined using the reflection coefficient.
Because the principles are the same, this concept is perhaps
easiest to understand when considering an optical fiber. Imperfections
in the glass create mirrors that reflect the light back along the fiber.
Impedance discontinuities cause attenuation, attenuation distortion, standing waves, ringing and other effects because a portion of a transmitted signal will be reflected back to the transmitting device rather than continuing to the receiver, much like an echo.
This effect is compounded if multiple discontinuities cause additional
portions of the remaining signal to be reflected back to the
transmitter. This is a fundamental problem with the daisy chain method of connecting electronic components.
When a returning reflection strikes another discontinuity, some
of the signal rebounds in the original signal direction, creating
multiple echo effects. These forward echoes
strike the receiver at different intervals making it difficult for the
receiver to accurately detect data values on the signal. The effects can
resemble those of jitter.
Because damage to the cable can cause reflections, an instrument called an electrical time-domain reflectometer (ETDR; for electrical cables) or an optical time-domain reflectometer
(OTDR; for optical cables) can be used to locate the damaged part of a
cable. These instruments work by sending a short pulsed signal into the
cable and measuring how long the reflection takes to return. If only
reflection magnitudes are desired, however, and exact fault locations
are not required, VSWR bridges perform a similar but lesser function for
RF cables.
The combination of the effects of signal attenuation and impedance discontinuities on a communications link is called insertion loss. Proper network operation depends on constant characteristic impedance in all cables and connectors, with no impedance discontinuities in the entire cable system. When a sufficient degree of impedance matching is not practical, echo suppressors or echo cancellers, or both, can sometimes reduce the problems.
The Bergeron diagram method, valid for both linear and non-linear models, evaluates the reflection's effects in an electric line.
See also
https://en.wikipedia.org/wiki/Signal_reflection
https://en.wikipedia.org/wiki/Optics
An induction motor or asynchronous motor is an AC electric motor in which the electric current in the rotor needed to produce torque is obtained by electromagnetic induction from the magnetic field of the stator winding.[1] An induction motor can therefore be made without electrical connections to the rotor.[a] An induction motor's rotor can be either wound type or squirrel-cage type.
Three-phase squirrel-cage induction motors are widely used as industrial drives because they are self-starting, reliable, and economical. Single-phase induction motors are used extensively for smaller loads, such as garbage disposals
and stationary power tools. Although traditionally only used for
one-speed service, single- and three-phase induction motors are
increasingly being installed in variable-speed applications using variable-frequency drives (VFD). VFDs offer especially important energy savings
opportunities for existing and prospective induction motors in
applications like fans, pumps and compressors that have a variable load.
https://en.wikipedia.org/wiki/Induction_motor
In telecommunications and electrical engineering in general, an unbalanced line is a pair of conductors intended to carry electrical signals, which have unequal impedances along their lengths and to ground and other circuits. Examples of unbalanced lines are coaxial cable or the historic earth return system invented for the telegraph, but rarely used today. Unbalanced lines are to be contrasted with balanced lines, such as twin-lead or twisted pair
which use two identical conductors to maintain impedance balance
throughout the line. Balanced and unbalanced lines can be interfaced
using a device called a balun.
The chief advantage of the unbalanced line format is cost
efficiency. Multiple unbalanced lines can be provided in the same cable
with one conductor per line plus a single common return conductor,
typically the cable shielding. Likewise, multiple microstrip circuits can all use the same ground plane
for the return path. This compares well with balanced cabling which
requires two conductors for each line, nearly twice as many. Another
benefit of unbalanced lines is that they do not require more expensive,
balanced driver and receiver circuits to operate correctly.
Unbalanced lines are sometimes confused with single-ended signalling,
but these are entirely separate concepts. The former is a cabling
scheme while the latter is a signalling scheme. However, single-ended
signalling is commonly sent over unbalanced lines. Unbalanced lines are
not to be confused with single-wire transmission lines which do not use a return path at all.
General description
Any
line that has a different impedance of the return path may be
considered an unbalanced line. However, unbalanced lines usually
consist of a conductor that is considered the signal line and another
conductor that is grounded, or is ground itself. The ground conductor often takes the form of a ground plane or the screen of a cable.
The ground conductor may be, and often is, common to multiple
independent circuits. For this reason the ground conductor may be
referred to as common.
Telegraph lines
The earliest use of unbalanced transmission lines was for electric telegraph
communications. These consisted of single wires strung between poles.
The return path for the current was originally provided by a separate
conductor. Some early telegraph systems, such as Schilling's experimental needle telegraph (1832) and the Cooke & Wheatstone five-needle telegraph (1837) used by British railways required multiple code wires. Essentially, they were parallel bus
coding. In these systems the cost of the return conductor was not so
significant (one conductor in seven for Schilling's earliest needle
telegraph[1] and one conductor in six for the Cooke and Wheatstone telegraph[2])
but the number of coding conductors was progressively reduced with
improved systems. Soon only one coding wire was required with the data
being transmitted serially. Important examples of these single-wire systems were the Morse telegraph (1837) and the Cooke & Wheatstone single-needle telegraph
(1843). In such systems the cost of a return conductor was fully 50
percent of the cable costs. It was discovered that a return conductor
could be replaced with a return path through the Earth using grounding spikes. Using earth return was a significant cost saving and rapidly became the norm.
Underground telegraph cables into large buildings or between
stations often needed to carry multiple independent telegraph lines.
These cables took the form of multiple insulated conductors enclosed by a
metal screen and overall protective jacket. In such cables the screen
can be used as the return conductor. Undersea telegraph cables were
usually a single conductor protected by steel-wire armour, effectively a coaxial cable. The first transatlantic cable of this kind was completed in 1866.
Early telephone
lines (telephone invented 1876) used the same transmission line scheme
as telegraph of unbalanced single wires. However, telephone
communication started to suffer after the widespread introduction of
electrical power lines. Telephone transmission started to use balanced lines to combat this problem and the modern norm for telephone presentation is the balanced twisted pair cable.
Coaxial lines
A coaxial line
(coax) has a central signal conductor surrounded by a cylindrical
shielding conductor. The shield conductor is normally grounded. The
coaxial format was developed during World War II for use in radar.
It was originally constructed from rigid copper pipes, but the usual
form today is a flexible cable with a braided screen. The advantages of
coax are a theoretically perfect electrostatic screen
and highly predictable transmission parameters. The latter is a result
of the fixed geometry of the format which leads to a precision not
found with loose wires. Open wire systems are also affected by nearby
objects altering the field pattern around the conductor. Coax does not
suffer from this since the field is entirely contained within the cable
due to the surrounding screen.
Coaxial lines are the norm for connections between radio
transmitters and their antennae, for interconnection of electronic
equipment where high frequency or above is involved, and were formerly widely used for forming local area networks before twisted pair became popular for this purpose.
Triaxial cable
(triax) is a variant of coax with a second shield conductor surrounding
the first with a layer of insulation in between. As well as providing
additional shielding, the outer conductors can be used for other
purposes such as providing power to equipment or control signals. Triax is widely used for the connection of cameras in television studios.
Planar technologies
Microstrip parallel-coupled transmission lines. The design forms a
band-pass filterPlanar format transmission lines are flat conductors manufactured by a
number of techniques on to a substrate. They are nearly always an
unbalanced format. At the low transmission speeds of early telegraph it was only necessary to consider transmission line theory for a circuit design when the transmission was over many miles. Similarly, the audio frequencies
used by telephones are relatively low and transmission line theory only
becomes significant for distances of at least between buildings.
However, at the higher radio frequencies and microwave frequencies transmission line considerations can become important inside a device, just a matter of centimetres. At the very high data rates handled by modern computer processors, transmission line considerations can even be important inside an individual integrated circuit.
Planar technologies were developed for these kinds of small size
applications and are not very appropriate for long distance
transmissions.
- Stripline
Stripline
is a flat conductor with a ground plane both above and below the
conductor. The variant of stripline where the space between the two
ground planes is completely filled with a dielectric material is sometimes known as triplate. Stripline can be manufactured by etching the transmission line pattern on to a printed circuit board.
The bottom of this board is left completely covered in copper and
forms the bottom ground plane. A second board is clamped on top of the
first. This second board has no pattern on the bottom and plain copper
on the top to form the top ground plane. A sheet of copper foil may be
wrapped around the two boards to electrically bond the two ground planes
firmly together. On the other hand, stripline for high power
applications such as radar will more likely be made as solid metal
strips with periodic dielectric supports, essentially air dielectric.
- Microstrip
Microstrip
is similar to stripline but is open above the conductor. There is no
dielectric or ground plane above the transmission line, there is only
dielectric and a ground plane below the line. Microstrip is a popular
format, especially in domestic products, because microstrip components
can be made using the established manufacturing techniques of printed
circuit boards. Designers are thus able to mix discrete component
circuits with microstrip components. Furthermore, since the board has
to be made anyway, the microstrip components have no additional
manufacturing cost. For applications where performance is more
important than cost a ceramic substrate might be used instead of a
printed circuit. Microstrip has another small advantage over stripline;
the line widths are wider in microstrip for the same impedance
and thus manufacturing tolerances and minimum width are less critical
on high-impedance lines. A drawback of microstrip is that the mode of
transmission is not entirely transverse.
Strictly speaking, standard transmission line analysis does not apply
because other modes are present, but it can be a usable approximation.
- Integrated circuits
Connections within integrated circuits are normally planar so planar
transmission lines are a natural choice where these are needed. The
need for transmission lines is most frequently found in microwave integrated circuits
(MICs). There are a great many materials and techniques used to make
MICs, and transmission lines can be formed in any of these technologies.
Planar transmission lines are used for far more than merely
connecting components or units together. They can themselves be used as
components and units. Any transmission line format can be used in this
way, but for the planar formats it is often their primary purpose.
Typical circuit blocks implemented by transmission lines include filters, directions couplers and power splitters, and impedance matching.
At microwave frequencies discrete components need to be impractically
small and a transmission line solution is the only viable one. On the
other hand, at low frequencies such as audio applications, transmission
line devices need to be impractically large.
Power transmission
Electric power distribution is normally in the form of balanced
three-phase transmission. However, in some remote locations where a
relatively small amount of power is required, a single-wire earth return system may be used.
References
Huurdeman, p. 54
Bibliography
- Huurdeman, Anton A., The Worldwide History of Telecommunications, John Wiley & Sons, 2003 ISBN 0471205052.
- Curran, J.E.; Jeanes, R.; Sewell, H, "A Technology of Thin-Film Hybrid Microwave Circuits", IEEE Transactions on Parts, Hybrids, and Packaging, vol. 12, iss. 4, December 1976.
https://en.wikipedia.org/wiki/Unbalanced_line
A motor soft starter is a device used with AC electrical motors to temporarily reduce the load and torque in the powertrain and electric current surge of the motor during start-up. This reduces the mechanical stress on the motor and shaft, as well as the electrodynamic stresses on the attached power cables and electrical distribution network, extending the lifespan of the system.[1]: 150
It can consist of mechanical or electrical devices, or a combination of both. Mechanical soft starters include clutches and several types of couplings using a fluid, magnetic forces, or steel shot to transmit torque, similar to other forms of torque limiter. Electrical soft starters can be any control system that reduces the torque by temporarily reducing the voltage or current input, or a device that temporarily alters how the motor is connected in the electric circuit.

Compact soft starter for a 3 phase machine, 15kW/10HP
https://en.wikipedia.org/wiki/Motor_soft_starter
A torque limiter is an automatic device that protects
mechanical equipment, or its work, from damage by mechanical overload. A
torque limiter may limit the torque by slipping (as in a friction plate slip-clutch), or uncouple the load entirely (as in a shear pin). The action of a torque limiter is especially useful to limit any damage due to crash stops and jams.
Torque limiters may be packaged as a shaft coupling or as a hub for sprocket or sheave. A torque limiting device is also known as an overload clutch.
https://en.wikipedia.org/wiki/Torque_limiter
Inverter drives (VFDs)
The popularity of the Variable-frequency drive
(VFD) has increased in the last decade, especially in the home-shop
market. This is because of their relative low cost and ability to
generate three-phase output from single phase input. A VFD converts AC
power to DC and then converts it back to AC through a transistor bridge, a technology that is somewhat analogous to that of a switch-mode power supply.
As the VFD generates its AC output from the DC bus, it is possible to
power a three-phase motor from a single-phase source. Nevertheless,
commercial-grade VFDs are produced that require three-phase input, as
there are some efficiency gains to be had with such an arrangement.
A typical VFD functions by rapidly switching transistors on and
off to "chop" the voltage on the DC bus through what is known as pulse-width modulation
(PWM). Proper use of PWM will result in an AC output whose voltage and
frequency can be varied over a fairly wide range. As an induction motor's
rotational speed is proportional to input frequency, a change in the
VFD's output frequency will cause the motor to change speed. Voltage is
also changed in a way that results in the motor producing a relatively
constant torque over the useful speed range.
The output of a quality VFD is an approximation of a sine wave, with some high frequency harmonic content.
Harmonic content will elevate motor temperature and may produce some
whistling or whining noise that could be objectionable. The effects of
unwanted harmonics can be mitigated by the use of reactive output filtering,
which is incorporated into better quality VFDs. Reactive filtration
impedes the high frequency harmonic content but has little effect on the
fundamental frequency that determines motor speed. The result is an output to the motor that is closer to an ideal sine wave.
In the past, VFDs that have a capacity greater than 3 hp (2.2 kW)
were costly, thus making the rotary phase converter (RPC) an attractive
alternative. However, modern VFDs have dropped considerably in cost,
making them more affordable than comparable RPCs. Also working in the
VFD's favor is its more compact size relative to its electrical
capacity. A plus is many VFDs can produce a "soft start" effect (in
which power is gradually applied to the motor), which reduces the amount
of current that must be delivered at machine start-up.
Use of a VFD may result in motor damage if the motor is not rated
for such an application. This is primarily because most induction
motors are forced-air cooled by a fan or blower driven by the motor
itself. Operating such a motor at a lower-than-normal speed will
substantially reduce the cooling airflow, increasing the likelihood of
overheating and winding damage or failure, especially while operating at
full load. A manufacturer may void the warranty on a motor powered by a
VFD unless the motor is "inverter-rated." As VFDs are the most popular
method of powering motors in new commercial installations, most
three-phase motors sold today are, in fact, inverter-rated.
See also
https://en.wikipedia.org/wiki/Rotary_phase_converter
A shear pin is a mechanical detail designed to allow a specific
outcome to occur once a predetermined force is applied. It can either
function as a safeguard designed to break to protect other parts, or as a
conditional operator that will not allow a mechanical device to operate
until the correct force is applied.
https://en.wikipedia.org/wiki/Shear_pin
Magnetic levitation (maglev) or magnetic suspension is a method by which an object is suspended with no support other than magnetic fields. Magnetic force is used to counteract the effects of the gravitational force and any other forces.
The two primary issues involved in magnetic levitation are lifting forces: providing an upward force sufficient to counteract gravity, and stability: ensuring that the system does not spontaneously slide or flip into a configuration where the lift is neutralized.
Magnetic levitation is used for maglev trains, contactless melting, magnetic bearings, and for product display purposes.
https://en.wikipedia.org/wiki/Magnetic_levitation
In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current (such as electromagnets), permanent magnets, elementary particles (such as electrons), various molecules, and many astronomical objects (such as many planets, some moons, stars, etc).
More precisely, the term magnetic moment normally refers to a system's magnetic dipole moment, the component of the magnetic moment that can be represented by an equivalent magnetic dipole:
a magnetic north and south pole separated by a very small distance. The
magnetic dipole component is sufficient for small enough magnets or for
large enough distances. Higher-order terms (such as the magnetic quadrupole moment) may be needed in addition to the dipole moment for extended objects.
The magnetic dipole moment of an object is readily defined in
terms of the torque that the object experiences in a given magnetic
field. The same applied magnetic field creates larger torques on objects
with larger magnetic moments. The strength (and direction) of this
torque depends not only on the magnitude of the magnetic moment but also
on its orientation relative to the direction of the magnetic field. The
magnetic moment may be considered, therefore, to be a vector. The direction of the magnetic moment points from the south to north pole of the magnet (inside the magnet).
https://en.wikipedia.org/wiki/Magnetic_moment
An electric motor is an electrical machine that converts electrical energy into mechanical energy. Most electric motors operate through the interaction between the motor's magnetic field and electric current in a wire winding to generate force in the form of torque applied on the motor's shaft. An electric generator
is mechanically identical to an electric motor, but operates with a
reversed flow of power, converting mechanical energy into electrical
energy.
Electric motors can be powered by direct current (DC) sources, such as from batteries, or rectifiers, or by alternating current (AC) sources, such as a power grid, inverters or electrical generators.
Electric motors may be classified by considerations such as power
source type, construction, application and type of motion output. They
can be powered by AC or DC, be brushed or brushless, single-phase, two-phase, or three-phase, axial or radial flux, and may be air-cooled or liquid-cooled.
Standardized motors provide convenient mechanical power for
industrial use. The largest are used for ship propulsion, pipeline
compression and pumped-storage applications with output exceeding 100 megawatts.
Applications include industrial fans, blowers and pumps, machine
tools, household appliances, power tools, vehicles, and disk drives.
Small motors may be found in electric watches. In certain applications,
such as in regenerative braking with traction motors, electric motors can be used in reverse as generators to recover energy that might otherwise be lost as heat and friction.
Electric motors produce linear or rotary force (torque)
intended to propel some external mechanism, such as a fan or an
elevator. An electric motor is generally designed for continuous
rotation, or for linear movement over a significant distance compared to
its size. Magnetic solenoids are also transducers that convert electrical power to mechanical motion, but can produce motion over only a limited distance.
https://en.wikipedia.org/wiki/Electric_motor
In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
https://en.wikipedia.org/wiki/Dynamo_theory
Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circular birefringence and circular dichroism are the manifestations of optical activity. Optical activity occurs only in chiral materials, those lacking microscopic mirror symmetry. Unlike other sources of birefringence which alter a beam's state of polarization, optical activity can be observed in fluids. This can include gases or solutions of chiral molecules such as sugars, molecules with helical secondary structure such as some proteins, and also chiral liquid crystals. It can also be observed in chiral solids such as certain crystals with a rotation between adjacent crystal planes (such as quartz) or metamaterials.
When looking at the source of light, the rotation of the plane of polarization may be either to the right (dextrorotatory or dextrorotary — d-rotary, represented by (+), clockwise), or to the left (levorotatory or levorotary — l-rotary, represented by (−), counter-clockwise) depending on which stereoisomer is dominant. For instance, sucrose and camphor are d-rotary whereas cholesterol is l-rotary.
For a given substance, the angle by which the polarization of light of a
specified wavelength is rotated is proportional to the path length
through the material and (for a solution) proportional to its
concentration.
Optical activity is measured using a polarized source and polarimeter. This is a tool particularly used in the sugar industry to measure the sugar concentration of syrup, and generally in chemistry to measure the concentration or enantiomeric ratio of chiral molecules in solution. Modulation of a liquid crystal's optical activity, viewed between two sheet polarizers, is the principle of operation of liquid-crystal displays (used in most modern televisions and computer monitors).
Forms
Dextrorotation and laevorotation (also spelled levorotation)[1][2][3] are terms used in chemistry and physics to describe the optical rotation of plane-polarized light. From the point of view of the observer, dextrorotation refers to clockwise or right-handed rotation, and laevorotation refers to counterclockwise or left-handed rotation.[4][5]
A chemical compound that causes dextrorotation is called dextrorotatory or dextrorotary, while a compound that causes laevorotation is called laevorotatory or laevorotary.[6] Compounds with these properties consist of chiral molecules and are said to have optical activity. If a chiral molecule is dextrorotary, its enantiomer
(geometric mirror image) will be laevorotary, and vice versa.
Enantiomers rotate plane-polarized light the same number of degrees, but
in opposite directions.
Chirality prefixes
A compound may be labeled as dextrorotary by using the "(+)-" or "d-" prefix. Likewise, a laevorotary compound may be labeled using the "(−)-" or "l-" prefix. The lowercase "d-" and "l-" prefixes are obsolete, and are distinct from the SMALL CAPS "D-" and "L-" prefixes. The "D-" and "L-" prefixes are used to specify the enantiomer of chiral organic compounds in biochemistry and are based on the compound's absolute configuration relative to (+)-glyceraldehyde, which is the D-form
by definition. The prefix used to indicate absolute configuration is
not directly related to the (+) or (−) prefix used to indicate optical
rotation in the same molecule. For example, nine of the nineteen L-amino acids naturally occurring in proteins are, despite the L- prefix, actually dextrorotary (at a wavelength of 589 nm), and D-fructose is sometimes called "laevulose" because it is laevorotary.
The D- and L- prefixes describe the molecule as a whole, as do the (+) and (−) prefixes for optical rotation. In contrast, the (R)- and (S)- prefixes from the Cahn–Ingold–Prelog priority rules characterize the absolute configuration of each specific chiral stereocenter
with the molecule, rather than a property of the molecule as a whole. A
molecule having exactly one chiral stereocenter (usually an asymmetric carbon atom) can be labeled (R) or (S), but a molecule having multiple stereocenters needs more than one label. For example, the essential amino acid L-threonine contains two chiral stereocenters and is written (2S,3S)-threonine. There is no strict relationship between the R/S, the D/L, and (+)/(−) designations, although some correlations exist. For example, of the naturally occurring amino acids, all are L, and most are (S). For some molecules the (R)-enantiomer
is the dextrorotary (+) enantiomer, and in other cases it is the
laevorotary (−) enantiomer. The relationship must be determined on a
case-by-case basis with experimental measurements or detailed computer
modeling.[7]
History
The two asymmetric crystal forms, dextrorotatory and levorotatory, of
tartaric acid.
Sucrose solution concentration measuring experiment, demonstrating optical rotation.
The rotation of the orientation of linearly polarized light was first observed in 1811 in quartz by French physicist François Arago.[8] In 1820, the English astronomer Sir John F.W. Herschel
discovered that different individual quartz crystals, whose crystalline
structures are mirror images of each other (see illustration), rotate
linear polarization by equal amounts but in opposite directions.[9] Jean Baptiste Biot also observed the rotation of the axis of polarization in certain liquids[10] and vapors of organic substances such as turpentine.[11] In 1822, Augustin-Jean Fresnel found that optical rotation could be explained as a species of birefringence:
whereas previously known cases of birefringence were due to the
different speeds of light polarized in two perpendicular planes, optical
rotation was due to the different speeds of right-hand and left-hand
circularly polarized light.[12] Simple polarimeters have been used since this time to measure the concentrations of simple sugars, such as glucose, in solution. In fact one name for D-glucose (the biological isomer), is dextrose, referring to the fact that it causes linearly polarized light to rotate to the right or dexter side. In a similar manner, levulose, more commonly known as fructose, causes the plane of polarization to rotate to the left. Fructose is even more strongly levorotatory than glucose is dextrorotatory. Invert sugar syrup, commercially formed by the hydrolysis of sucrose
syrup to a mixture of the component simple sugars, fructose, and
glucose, gets its name from the fact that the conversion causes the
direction of rotation to "invert" from right to left.
In 1849, Louis Pasteur resolved a problem concerning the nature of tartaric acid.[13] A solution of this compound derived from living things (to be specific, wine lees) rotates the plane of polarization of light passing through it, but tartaric acid derived by chemical synthesis
has no such effect, even though its reactions are identical and its
elemental composition is the same. Pasteur noticed that the crystals
come in two asymmetric forms that are mirror images of one another.
Sorting the crystals by hand gave two forms of the compound: Solutions
of one form rotate polarized light clockwise, while the other form
rotate light counterclockwise. An equal mix of the two has no
polarizing effect on light. Pasteur deduced that the molecule in
question is asymmetric and could exist in two different forms that
resemble one another as would left- and right-hand gloves, and that the
organic form of the compound consists of purely the one type.
In 1874, Jacobus Henricus van 't Hoff[14] and Joseph Achille Le Bel[15]
independently proposed that this phenomenon of optical activity in
carbon compounds could be explained by assuming that the 4 saturated
chemical bonds between carbon atoms and their neighbors are directed
towards the corners of a regular tetrahedron. If the 4 neighbors are all
different, then there are two possible orderings of the neighbors
around the tetrahedron, which will be mirror images of each other. This
led to a better understanding of the three-dimensional nature of
molecules.
In 1945, Charles William Bunn[16]
predicted optical activity of achiral structures, if the wave's
propagation direction and the achiral structure form an experimental
arrangement that is different from its mirror image. Such optical
activity due to extrinsic chirality was observed in the 1960s in liquid crystals.[17][18]
In 1950, Sergey Vavilov[19]
predicted optical activity that depends on the intensity of light and
the effect of nonlinear optical activity was observed in 1979 in lithium iodate crystals.[20]
Optical activity is normally observed for transmitted light.
However, in 1988, M. P. Silverman discovered that polarization rotation
can also occur for light reflected from chiral substances.[21]
Shortly after, it was observed that chiral media can also reflect
left-handed and right-handed circularly polarized waves with different
efficiencies.[22]
These phenomena of specular circular birefringence and specular
circular dichroism are jointly known as specular optical activity.
Specular optical activity is very weak in natural materials.
In 1898 Jagadish Chandra Bose described the ability of twisted artificial structures to rotate the polarization of microwaves.[23] Since the early 21st century, the development of artificial materials has led to the prediction[24] and realization[25][26]
of chiral metamaterials with optical activity exceeding that of natural
media by orders of magnitude in the optical part of the spectrum.
Extrinsic chirality associated with oblique illumination of metasurfaces
lacking two-fold rotational symmetry has been observed to lead to large
linear optical activity in transmission[27] and reflection,[28] as well as nonlinear optical activity exceeding that of lithium iodate by 30 million times.[29]
Theory
Optical
activity occurs due to molecules dissolved in a fluid or due to the
fluid itself only if the molecules are one of two (or more) stereoisomers; this is known as an enantiomer. The structure of such a molecule is such that it is not identical to its mirror image
(which would be that of a different stereoisomer, or the "opposite
enantiomer"). In mathematics, this property is also known as chirality. For instance, a metal rod is not chiral, since its appearance in a mirror is not distinct from itself. However a screw or light bulb base (or any sort of helix) is
chiral; an ordinary right-handed screw thread, viewed in a mirror,
would appear as a left-handed screw (very uncommon) which could not
possibly screw into an ordinary (right-handed) nut. A human viewed in a
mirror would have their heart on the right side, clear evidence of
chirality, whereas the mirror reflection of a doll might well be
indistinguishable from the doll itself.
In order to display optical activity, a fluid must contain only
one, or a preponderance of one, stereoisomer. If two enantiomers are
present in equal proportions then their effects cancel out and no
optical activity is observed; this is termed a racemic mixture. But when there is an enantiomeric excess,
more of one enantiomer than the other, the cancellation is incomplete
and optical activity is observed. Many naturally occurring molecules are
present as only one enantiomer (such as many sugars). Chiral molecules
produced within the fields of organic chemistry or inorganic chemistry are racemic unless a chiral reagent was employed in the same reaction.
At the fundamental level, polarization rotation in an optically
active medium is caused by circular birefringence, and can best be
understood in that way. Whereas linear birefringence in a crystal involves a small difference in the phase velocity
of light of two different linear polarizations, circular birefringence
implies a small difference in the velocities between right and
left-handed circular polarizations.[12]
Think of one enantiomer in a solution as a large number of little
helices (or screws), all right-handed, but in random orientations.
Birefringence of this sort is possible even in a fluid because the
handedness of the helices is not dependent on their orientation: even
when the direction of one helix is reversed, it still appears right
handed. And circularly polarized light itself is chiral: as the wave
proceeds in one direction the electric (and magnetic) fields composing
it are rotating clockwise (or counterclockwise for the opposite circular
polarization), tracing out a right (or left) handed screw pattern in
space. In addition to the bulk refractive index which substantially lowers the phase velocity of light in any dielectric (transparent) material compared to the speed of light (in vacuum), there is an additional interaction between the chirality of the wave and the chirality of the molecules.
Where their chiralities are the same, there will be a small additional
effect on the wave's velocity, but the opposite circular polarization
will experience an opposite small effect as its chirality is opposite
that of the molecules.
Unlike linear birefringence, however, natural optical rotation
(in the absence of a magnetic field) cannot be explained in terms of a
local material permittivity
tensor (i.e., a charge response that only depends on the local electric
field vector), as symmetry considerations forbid this. Rather, circular
birefringence only appears when considering nonlocality of the material
response, a phenomenon known as spatial dispersion.[30]
Nonlocality means that electric fields in one location of the material
drive currents in another location of the material. Light travels at a
finite speed, and even though it is much faster than the electrons, it
makes a difference whether the charge response naturally wants to travel
along with the electromagnetic wavefront, or opposite to it. Spatial
dispersion means that light travelling in different directions
(different wavevectors) sees a slightly different permittivity tensor.
Natural optical rotation requires a special material, but it also relies
on the fact that the wavevector of light is nonzero, and a nonzero
wavevector bypasses the symmetry restrictions on the local
(zero-wavevector) response. However, there is still reversal symmetry,
which is why the direction of natural optical rotation must be
'reversed' when the direction of the light is reversed, in contrast to
magnetic Faraday rotation.
All optical phenomena have some nonlocality/wavevector influence but it
is usually negligible; natural optical rotation, rather uniquely,
absolutely requires it.[30]
The phase velocity of light in a medium is commonly expressed using the index of refraction n,
defined as the speed of light (in free space) divided by its speed in
the medium. The difference in the refractive indices between the two
circular polarizations quantifies the strength of the circular
birefringence (polarization rotation),
 .
.
While  is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
The familiar rotation of the axis of linear polarization relies on the understanding that a linearly polarized wave can as well be described as the superposition
(addition) of a left and right circularly polarized wave in equal
proportion. The phase difference between these two waves is dependent on
the orientation of the linear polarization which we'll call  , and their electric fields have a relative phase difference of
, and their electric fields have a relative phase difference of  which then add to produce linear polarization:
which then add to produce linear polarization:

where  is the electric field of the net wave, while
is the electric field of the net wave, while  and
and  are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write
are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write  and
and  in terms of their x and y components as follows:
in terms of their x and y components as follows:


where  and
and  are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by
are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by  and then the actual electric field at any instant is given by the real part of that product.
and then the actual electric field at any instant is given by the real part of that product.
Substituting these expressions for  and
and  into the equation for
into the equation for  we obtain:
we obtain:



The last equation shows that the resulting vector has the x and y components in phase and oriented exactly in the  direction, as we had intended, justifying the representation of any linearly polarized state at angle
direction, as we had intended, justifying the representation of any linearly polarized state at angle  as the superposition of right and left circularly polarized components with a relative phase difference of
as the superposition of right and left circularly polarized components with a relative phase difference of  .
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of
.
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of  . Let us call
. Let us call  the result of passing the original wave linearly polarized at angle
the result of passing the original wave linearly polarized at angle  through this medium. This will apply additional phase factors of
through this medium. This will apply additional phase factors of  and
and  to the right and left circularly polarized components of
to the right and left circularly polarized components of  :
:

Using similar math as above we find:

thus describing a wave linearly polarized at angle  , thus rotated by
, thus rotated by  relative to the incoming wave:
relative to the incoming wave: 
We defined above the difference in the refractive indices for right and left circularly polarized waves of  . Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of
. Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of  (as we used above) given by:
(as we used above) given by:
 ,
,
where  is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by
is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by  as we have shown.
as we have shown.
In general, the refractive index depends on wavelength (see dispersion) and the differential refractive index  will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
So we find that the degree of rotation depends on the color of the light (the yellow sodium D line near 589 nm wavelength is commonly used for measurements), and is directly proportional to the path length  through the substance and the amount of circular birefringence of the material
through the substance and the amount of circular birefringence of the material  which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
Although optical activity is normally thought of as a property of fluids, particularly aqueous solutions, it has also been observed in crystals such as quartz (SiO2). Although quartz has a substantial linear birefringence, that effect is cancelled when propagation is along the optic axis.
In that case, rotation of the plane of polarization is observed due to
the relative rotation between crystal planes, thus making the crystal
formally chiral as we have defined it above. The rotation of the crystal
planes can be right or left-handed, again producing opposite optical
activities. On the other hand, amorphous forms of silica such as fused quartz,
like a racemic mixture of chiral molecules, has no net optical activity
since one or the other crystal structure does not dominate the
substance's internal molecular structure.
Applications
For a pure substance in solution, if the color and path length are fixed and the specific rotation is known, the observed rotation can be used to calculate the concentration. This usage makes a polarimeter a tool of great importance to those trading in or using sugar syrups in bulk.
Comparison to the Faraday effect
Rotation of light's plane of polarization may also occur through the Faraday effect which involves a static magnetic field.
However, this is a distinct phenomenon that is not classified as
"optical activity." Optical activity is reciprocal, i.e. it is the same
for opposite directions of wave propagation through an optically active
medium, for example clockwise polarization rotation from the point of
view of an observer. In case of optically active isotropic media, the
rotation is the same for any direction of wave propagation. In contrast,
the Faraday effect is non-reciprocal, i.e opposite directions of wave
propagation through a Faraday medium will result in clockwise and
anti-clockwise polarization rotation from the point of view of an
observer. Faraday rotation depends on the propagation direction relative
to that of the applied magnetic field. All compounds can exhibit
polarization rotation in the presence of an applied magnetic field,
provided that (a component of) the magnetic field is oriented in the
direction of light propagation. The Faraday effect is one of the first
discoveries of the relationship between light and electromagnetic
effects.
See also
References
The first word component dextro- comes from the Latin word dexter, meaning "right" (as opposed to left). Laevo- or levo- comes from the Latin laevus, meaning "left side".
The equivalent French terms are dextrogyre and levogyre. These are used infrequently in English.
Sebti; Hamilton, eds. (2001). Farnesyltransferase inhibitors in cancer therapy. p. 126. ISBN 9780896036291. Retrieved 2015-10-18.
LibreTexts Chemistry – Polarimetry
"Determination of optical rotation and specific rotation" (PDF). The International Pharmacopoeia. World Health Organization. 2017. ISBN 9789241550031. Archived (PDF) from the original on 2022-10-09.
Solomons, T.W. Graham; Fryhle, Graig B. (2004). Organic Chemistry (8th ed.). Hoboken: John Wiley & Sons, Inc.
See, for example,Stephens,
P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J.; Bortolini, O.;
Besse, P. (2003). "Determination of absolute configuration using
calculation of optical rotation". Chirality. 15: S57–64. doi:10.1002/chir.10270. PMID 12884375.
Arago (1811) "Mémoire
sur une modification remarquable qu'éprouvent les rayons lumineux dans
leur passage à travers certains corps diaphanes et sur quelques autres
nouveaux phénomènes d'optique" (Memoir on a remarkable modification
that light rays experience during their passage through certain
translucent substances and on some other new optical phenomena), Mémoires de la classe des sciences mathématiques et physiques de l'Institut Impérial de France, 1st part : 93–134.
Herschel, J.F.W. (1820) "On
the rotation impressed by plates of rock crystal on the planes of
polarization of the rays of light, as connected with certain
peculiarities in its crystallization," Transactions of the Cambridge Philosophical Society, 1 : 43–51.
Biot, J. B. (1815) "Phenomene de polarisation successive, observés dans des fluides homogenes" (Phenomenon of successive polarization, observed in homogeneous fluids), Bulletin des Sciences, par la Société Philomatique de Paris, 190–192.
Biot
(1818 & 1819) "Extrait d'un mémoire sur les rotations que certaines
substances impriment aux axes de polarisation des rayons lumineux"
(Extract from a memoir on the [optical] rotations that certain
substances impress on the axes of polarization of light rays), Annales de Chimie et de Physique, 2nd series, 9 : 372-389 ; 10 : 63-81 ; for Biot's experiments with turpentine vapor (vapeur d'essence de térébenthine), see pp. 72-81.
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); especially §13.
Pasteur, L. (1850) "Recherches sur les propriétés spécifiques des deux acides qui composent l'acide racémique" (Researches on the specific properties of the two acids that compose the racemic acid), Annales de chimie et de physique, 3rd series, 28 : 56–99 ; see also appendix, pp. 99–117.
van 't Hoff, J.H. (1874) "Sur les formules de structure dans l'espace" (On structural formulas in space), Archives Néerlandaises des Sciences Exactes et Naturelles, 9 : 445–454.
Le Bel, J.-A. (1874) "Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions" (On the relations that exist between the atomic formulas of organic substances and the rotatory power of their solutions), Bulletin de la Société Chimique de Paris, 22 : 337–347.
Bunn, C. W. (1945). Chemical Crystallography. New York: Oxford University Press. p. 88.
R. Williams (1968). "Optical Rotatory Effect in the Nematic Liquid Phase of p-Azoxyanisole". Physical Review Letters. 21 (6): 342. Bibcode:1968PhRvL..21..342W. doi:10.1103/PhysRevLett.21.342.
R. Williams (1969). "Optical-rotary power and linear electro-optic effect in nematic liquid crystals of p-azoxyanisole". Journal of Chemical Physics. 50 (3): 1324. Bibcode:1969JChPh..50.1324W. doi:10.1063/1.1671194.
Vavilov, S. I. (1950). Mikrostruktura Sveta (Microstructure of Light). Moscow: USSR Academy of Sciences Publishing.
Akhmanov,
S. A.; Zhdanov, B. V.; Zheludev, N. I.; Kovrigin, A. I.; Kuznetsov, V.
I. (1979). "Nonlinear optical activity in crystals". JETP Letters. 29: 264.
Silverman,
M.; Ritchie, N.; Cushman, G.; Fisher, B. (1988). "Experimental
configurations using optical phase modulation to measure chiral
asymmetries in light specularly reflected from a naturally gyrotropic
medium". Journal of the Optical Society of America A. 5 (11): 1852. Bibcode:1988JOSAA...5.1852S. doi:10.1364/JOSAA.5.001852.
Silverman, M.; Badoz, J.; Briat, B. (1992). "Chiral reflection from a naturally optically active medium". Optics Letters. 17 (12): 886. Bibcode:1992OptL...17..886S. doi:10.1364/OL.17.000886. PMID 19794663.
Bose, Jagadis Chunder (1898). "On the Rotation of Plane of Polarisation of Electric Waves by a Twisted Structure". Proceedings of the Royal Society. 63 (389–400): 146–152. doi:10.1098/rspl.1898.0019. JSTOR 115973. S2CID 89292757.
Svirko, Y.; Zheludev, N. I.; Osipov, M. (2001). "Layered chiral metallic microstructures with inductive coupling". Applied Physics Letters. 78 (4): 498. Bibcode:2001ApPhL..78..498S. doi:10.1063/1.1342210.
Kuwata-Gonokami,
M.; Saito, N.; Ino, Y.; Kauranen, M.; Jefimovs, K.; Vallius, T.;
Turunen, J.; Svirko, Y. (2005). "Giant Optical Activity in
Quasi-Two-Dimensional Planar Nanostructures". Physical Review Letters. 95 (22): 227401. Bibcode:2005PhRvL..95v7401K. doi:10.1103/PhysRevLett.95.227401. PMID 16384264.
Plum,
E.; Fedotov, V. A.; Schwanecke, A. S.; Zheludev, N. I.; Chen, Y.
(2007). "Giant optical gyrotropy due to electromagnetic coupling". Applied Physics Letters. 90 (22): 223113. Bibcode:2007ApPhL..90v3113P. doi:10.1063/1.2745203.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2008). "Optical activity in extrinsically chiral metamaterial" (PDF). Applied Physics Letters. 93 (19): 191911. arXiv:0807.0523. Bibcode:2008ApPhL..93s1911P. doi:10.1063/1.3021082. S2CID 117891131.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2016). "Specular optical activity of achiral metasurfaces" (PDF). Applied Physics Letters. 108 (14): 141905. Bibcode:2016ApPhL.108n1905P. doi:10.1063/1.4944775. hdl:10220/40854.
Ren, M.; Plum, E.; Xu, J.; Zheludev, N. I. (2012). "Giant nonlinear optical activity in a plasmonic metamaterial". Nature Communications. 3: 833. Bibcode:2012NatCo...3..833R. doi:10.1038/ncomms1805. PMID 22588295.
L.D. Landau; E.M. Lifshitz; L.P. Pitaevskii (1984). Electrodynamics of Continuous Media. Vol. 8 (2nd ed.). Butterworth-Heinemann. pp. 362–365. ISBN 978-0-7506-2634-7.
Plum, E.; Zhou, J.; Dong, J.; Fedotov, V. A.; Koschny, T.; Soukoulis, C. M.; Zheludev, N. I. (2009). "Metamaterial with negative index due to chirality" (PDF). Physical Review B. 79 (3): 035407. Bibcode:2009PhRvB..79c5407P. doi:10.1103/PhysRevB.79.035407. S2CID 119259753.
Further reading
- Eugene Hecht, Optics, 3rd Ed., Addison-Wesley, 1998, ISBN 0-201-30425-2
- Akhlesh Lakhtakia, Beltrami Fields in Chiral Media, World Scientific, Singapore, 1994
- A step by step tutorial on Optical Rotation
- Morrison. Robert. T, and Boyd. Robert. N, "Organic Chemistry (6th ed)". Prentice-Hall Inc (1992).

Operating principle of a
polarimeter
for measuring optical rotation. 1. Light source 2. Unpolarized light
3. Linear polarizer 4. Linearly polarized light 5. Sample tube
containing molecules under study 6. Optical rotation due to molecules 7.
Rotatable linear analyzer 8. Detector
https://en.wikipedia.org/wiki/Optical_rotation
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave.
In electrodynamics, the strength and direction of an electric
field is defined by its electric field vector. In the case of a
circularly polarized wave, the tip of the electric field vector,
at a given point in space, relates to the phase of the light as it
travels through time and space. At any instant of time, the electric
field vector of the wave indicates a point on a helix
oriented along the direction of propagation. A circularly polarized
wave can rotate in one of two possible senses: clockwise or right-handed circular polarization (RHCP) in which the electric field vector rotates in a right-hand sense with respect to the direction of propagation, and counter-clockwise or left-handed circular polarization (LHCP) in which the vector rotates in a left-hand sense.
Circular polarization is a limiting case of elliptical polarization. The other special case is the easier-to-understand linear polarization. All three terms were coined by Augustin-Jean Fresnel, in a memoir read to the French Academy of Sciences on 9 December 1822.[1][2] Fresnel had first described the case of circular polarization, without yet naming it, in 1821.[3]
The phenomenon of polarization arises as a consequence of the fact that light behaves as a two-dimensional transverse wave.
Circular polarization occurs when the two orthogonal electric
field component vectors are of equal magnitude and are out of phase by
exactly 90°, or one-quarter wavelength.
Characteristics
Right-handed/clockwise
circularly polarized light displayed with and without the use of
components. This would be considered left-handed/counterclockwise
circularly polarized if defined from the point of view of the source
rather than the receiver
In a circularly polarized electromagnetic wave, the individual
electric field vectors, as well as their combined vector, have a
constant magnitude, and with changing phase angle. Given that this is a plane wave,
each vector represents the magnitude and direction of the electric
field for an entire plane that is perpendicular to the optical axis.
Specifically, given that this is a circularly polarized plane wave,
these vectors indicate that the electric field, from plane to plane,
has a constant strength while its direction steadily rotates. Refer to these two images[dead link]
in the plane wave article to better appreciate this dynamic. This light
is considered to be right-hand, clockwise circularly polarized if
viewed by the receiver. Since this is an electromagnetic wave, each electric field vector has a corresponding, but not illustrated, magnetic field vector that is at a right angle to the electric field vector and proportional in magnitude to it. As a result, the magnetic field vectors would trace out a second helix if displayed.
Circular polarization is often encountered in the field of optics
and, in this section, the electromagnetic wave will be simply referred
to as light.
The nature of circular polarization and its relationship to other
polarizations is often understood by thinking of the electric field as
being divided into two components
that are perpendicular to each other. The vertical component and its
corresponding plane are illustrated in blue, while the horizontal
component and its corresponding plane are illustrated in green. Notice
that the rightward (relative to the direction of travel) horizontal
component leads the vertical component by one quarter of a wavelength, a 90° phase difference. It is this quadrature phase relationship that creates the helix
and causes the points of maximum magnitude of the vertical component to
correspond with the points of zero magnitude of the horizontal
component, and vice versa. The result of this alignment are select
vectors, corresponding to the helix, which exactly match the maxima of
the vertical and horizontal components.
To appreciate how this quadrature phase
shift corresponds to an electric field that rotates while maintaining a
constant magnitude, imagine a dot traveling clockwise in a circle.
Consider how the vertical and horizontal displacements of the dot, relative to the center of the circle, vary sinusoidally
in time and are out of phase by one quarter of a cycle. The
displacements are said to be out of phase by one quarter of a cycle
because the horizontal maximum displacement (toward the left) is reached
one quarter of a cycle before the vertical maximum displacement is
reached. Now referring again to the illustration, imagine the center of
the circle just described, traveling along the axis from the front to
the back. The circling dot will trace out a helix with the displacement
toward our viewing left, leading the vertical displacement. Just as the
horizontal and vertical displacements of the rotating dot are out of
phase by one quarter of a cycle in time, the magnitude of the horizontal
and vertical components of the electric field are out of phase by one
quarter of a wavelength.
Left-handed/counterclockwise
circularly polarized light displayed with and without the use of
components. This would be considered right-handed/clockwise circularly
polarized if defined from the point of view of the source rather than
the receiver.
The next pair of illustrations is that of left-handed,
counterclockwise circularly polarized light when viewed by the receiver.
Because it is left-handed, the rightward (relative to the direction of
travel) horizontal component is now lagging the vertical component by one quarter of a wavelength, rather than leading it.
Reversal of handedness
Waveplate
To convert circularly polarized light to the other handedness, one can use a half-waveplate.
A half-waveplate shifts a given linear component of light one half of a
wavelength relative to its orthogonal linear component.
Reflection
The
handedness of polarized light is reversed reflected off a surface at
normal incidence. Upon such reflection, the rotation of the plane of polarization of the reflected light is identical to that of the incident field. However, with propagation now in the opposite
direction, the same rotation direction that would be described as
"right-handed" for the incident beam, is "left-handed" for propagation
in the reverse direction, and vice versa. Aside from the reversal of
handedness, the ellipticity of polarization is also preserved (except in
cases of reflection by a birefringent surface).
Note that this principle only holds strictly for light reflected
at normal incidence. For instance, right circularly polarized light
reflected from a dielectric surface at grazing incidence (an angle
beyond the Brewster angle)
will still emerge as right-handed, but elliptically, polarized. Light
reflected by a metal at non-normal incidence will generally have its
ellipticity changed as well. Such situations may be solved by
decomposing the incident circular (or other) polarization into
components of linear polarization parallel and perpendicular to the plane of incidence, commonly denoted p and s respectively. The reflected components in the p and s linear polarizations are found by applying the Fresnel coefficients
of reflection, which are generally different for those two linear
polarizations. Only in the special case of normal incidence, where there
is no distinction between p and s, are the Fresnel coefficients for the two components identical, leading to the above property.
A
3-slide series of pictures taken with and without a pair of MasterImage
3D circularly polarized movie glasses of some dead European rose
chafers (Cetonia aurata) whose shiny green color comes from
left-polarized light. Note that, without glasses, both the beetles and
their images have shiny color. The right-polarizer removes the color of
the beetles but leaves the color of the images. The left-polarizer does
the opposite, showing reversal of handedness of the reflected light.
Conversion to and from linear polarization
Circularly polarized light can be converted into linearly polarized light by passing it through a quarter-waveplate.
Passing linearly polarized light through a quarter-waveplate with its
axes at 45° to its polarization axis will convert it to circular
polarization. In fact, this is the most common way of producing circular
polarization in practice. Note that passing linearly polarized light
through a quarter-waveplate at an angle other than 45° will generally produce elliptical polarization.
Handedness conventions
A
right-handed/clockwise circularly polarized wave as defined from the
point of view of the source. It would be considered
left-handed/anti-clockwise circularly polarized if defined from the
point of view of the receiver.
A
left-handed/anti-clockwise circularly polarized wave as defined from
the point of view of the source. It would be considered
right-handed/clockwise circularly polarized if defined from the point of
view of the receiver.
Circular polarization may be referred to as right-handed or
left-handed, and clockwise or anti-clockwise, depending on the direction
in which the electric field vector rotates. Unfortunately, two opposing
historical conventions exist.
From the point of view of the source
Using
this convention, polarization is defined from the point of view of the
source. When using this convention, left- or right-handedness is
determined by pointing one's left or right thumb away from the source, in the same
direction that the wave is propagating, and matching the curling of
one's fingers to the direction of the temporal rotation of the field at a
given point in space. When determining if the wave is clockwise or
anti-clockwise circularly polarized, one again takes the point of view
of the source, and while looking away from the source and in the same direction of the wave's propagation, one observes the direction of the field's spatial rotation.
Using this convention, the electric field vector of a left-handed circularly polarized wave is as follows:

As a specific example, refer to the circularly polarized wave in
the first animation. Using this convention, that wave is defined as
right-handed because when one points one's right thumb in the same
direction of the wave's propagation, the fingers of that hand curl in
the same direction of the field's temporal rotation. It is considered
clockwise circularly polarized because, from the point of view of the
source, looking in the same direction of the wave's propagation, the
field rotates in the clockwise direction. The second animation is that
of left-handed or anti-clockwise light, using this same convention.
This convention is in conformity with the Institute of Electrical and Electronics Engineers (IEEE) standard and, as a result, it is generally used in the engineering community.[4][5][6]
Quantum physicists also use this convention of handedness because
it is consistent with their convention of handedness for a particle's
spin.[7]
Radio astronomers also use this convention in accordance with an International Astronomical Union (IAU) resolution made in 1973.[8]
From the point of view of the receiver
In
this alternative convention, polarization is defined from the point of
view of the receiver. Using this convention, left- or right-handedness
is determined by pointing one's left or right thumb toward the source, against the direction of propagation, and then matching the curling of one's fingers to the spatial rotation of the field.
When using this convention, in contrast to the other convention,
the defined handedness of the wave matches the handedness of the screw
type nature of the field in space. Specifically, if one freezes a
right-handed wave in time, when one curls the fingers of one's right
hand around the helix, the thumb will point in the direction of
progression for the helix, given the sense of rotation. Note that, in
the context of the nature of all screws and helices, it does not matter
in which direction you point your thumb when determining its handedness.
When determining if the wave is clockwise or anti-clockwise
circularly polarized, one again takes the point of view of the receiver
and, while looking toward the source, against the direction of propagation, one observes the direction of the field's temporal rotation.
Just as in the other convention, right-handedness corresponds to a
clockwise rotation, and left-handedness corresponds to an
anti-clockwise rotation.
Many optics textbooks use this second convention.[9][10] It is also used by SPIE[11] as well as the International Union of Pure and Applied Chemistry (IUPAC).[12]
Uses of the two conventions
As
stated earlier, there is significant confusion with regards to these
two conventions. As a general rule, the engineering, quantum physics,
and radio astronomy communities use the first convention, in which the
wave is observed from the point of view of the source.[5][7][8]
In many physics textbooks dealing with optics, the second convention is
used, in which the light is observed from the point of view of the
receiver.[7][9]
To avoid confusion, it is good practice to specify "as defined
from the point of view of the source" or "as defined from the point of
view of the receiver" when discussing polarization matters.
The archive of the US Federal Standard 1037C proposes two contradictory conventions of handedness.[13]
FM radio
The term "circular polarization" is often used erroneously to describe mixed polarity signals[citation needed] used mostly in FM radio
(87.5 to 108.0 MHz in the USA), in which a vertical and a horizontal
component are propagated simultaneously by a single or a combined array.
This has the effect of producing greater penetration into buildings and
difficult reception areas than a signal with just one plane of
polarization. This would be an instance in which the polarization would
more appropriately be called random polarization because the
polarization at a receiver, although constant, will vary depending on
the direction from the transmitter and other factors in the transmitting
antenna design. See Stokes parameters.
The term "FM radio" above refers to FM broadcasting, not two-way radio (more properly called land mobile radio), which uses vertical polarization almost exclusively.
Dichroism
Circular dichroism (CD) is the differential absorption of left- and right-handed circularly polarized light. Circular dichroism is the basis of a form of spectroscopy that can be used to determine the optical isomerism and secondary structure of molecules.
In general, this phenomenon will be exhibited in absorption bands of any optically active molecule. As a consequence, circular dichroism is exhibited by most biological molecules, because of the dextrorotary (e.g., some sugars) and levorotary (e.g., some amino acids) molecules they contain. Noteworthy as well is that a secondary structure will also impart a distinct CD to its respective molecules. Therefore, the alpha helix, beta sheet and random coil regions of proteins and the double helix of nucleic acids have CD spectral signatures representative of their structures.
Also, under the right conditions, even non-chiral molecules will exhibit magnetic circular dichroism — that is, circular dichroism induced by a magnetic field.
Luminescence
Circularly polarized luminescence (CPL) can occur when either a luminophore or an ensemble of luminophores is chiral. The extent to which emissions are polarized is quantified in the same way it is for circular dichroism, in terms of the dissymmetry factor, also sometimes referred to as the anisotropy factor. This value is given by:

where  corresponds to the quantum yield of left-handed circularly polarized light, and
corresponds to the quantum yield of left-handed circularly polarized light, and  to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
Mathematical description
The classical sinusoidal plane wave solution of the electromagnetic wave equation for the electric and magnetic fields is:
![{\displaystyle {\begin{aligned}\mathbf {E} (\mathbf {r} ,t)&=\left|\,\mathbf {E} \,\right|\mathrm {Re} \left\{\mathbf {Q} \left|\psi \right\rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\\\mathbf {B} (\mathbf {r} ,t)&={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72e6f4e48ffd9eabf206d7664ee54e2e2ba2780c)
where k is the wavenumber;

is the angular frequency of the wave; ![\mathbf{Q} = \left [ \hat{ \mathbf{x}}, \hat{\mathbf{y}} \right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c6f209c9644cf3ab69fd75e6d696bb9278c0c12) is an orthogonal
is an orthogonal  matrix whose columns span the transverse x-y plane; and
matrix whose columns span the transverse x-y plane; and  is the speed of light.
is the speed of light.
Here,

is the amplitude of the field, and

is the normalized Jones vector in the x-y plane.
If  is rotated by
is rotated by  radians with respect to
radians with respect to  and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:
and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:

where the plus sign indicates left circular polarization, and the
minus sign indicates right circular polarization. In the case of
circular polarization, the electric field vector of constant magnitude
rotates in the x-y plane.
If basis vectors are defined such that:

and:

then the polarization state can be written in the "R-L basis" as:

where:

and:

Antennas
A number of different types of antenna elements can be used to
produce circularly polarized (or nearly so) radiation; following
Balanis,[14] one can use dipole elements:
"... two crossed dipoles provide the two orthogonal field
components.... If the two dipoles are identical, the field intensity of
each along zenith ... would be of the same intensity. Also, if the two
dipoles were fed with a 90° degree time-phase difference (phase
quadrature), the polarization along zenith would be circular.... One way
to obtain the 90° time-phase difference between the two orthogonal
field components, radiated respectively by the two dipoles, is by
feeding one of the two dipoles with a transmission line which is 1/4
wavelength longer or shorter than that of the other," p.80;
or helical elements:
"To achieve circular polarization [in axial or end-fire mode] ... the circumference C of the helix must be ... with C/wavelength = 1 near optimum, and the spacing about S = wavelength/4," p.571;
or patch elements:
"... circular and elliptical polarizations can be
obtained using various feed arrangements or slight modifications made to
the elements.... Circular polarization can be obtained if two
orthogonal modes are excited with a 90° time-phase difference between
them. This can be accomplished by adjusting the physical dimensions of
the patch.... For a square patch element, the easiest way to excite
ideally circular polarization is to feed the element at two adjacent
edges.... The quadrature phase difference is obtained by feeding the
element with a 90° power divider," p.859.
In quantum mechanics
In the quantum mechanical view, light is composed of photons. Polarization is a manifestation of the spin angular momentum of light.
More specifically, in quantum mechanics, the direction of spin of a
photon is tied to the handedness of the circularly polarized light, and
the spin of a beam of photons is similar to the spin of a beam of
particles, such as electrons.[15]
In nature
The
rose chafer's external surface reflects almost exclusively left-circularly polarized light.
Only a few mechanisms in nature are known to systematically produce circularly polarized light. In 1911, Albert Abraham Michelson discovered that light reflected from the golden scarab beetle Chrysina resplendens is preferentially left-polarized. Since then, circular polarization has been measured in several other scarab beetles such as Chrysina gloriosa,[16] as well as some crustaceans such as the mantis shrimp. In these cases, the underlying mechanism is the molecular-level helicity of the chitinous cuticle.[17]
The bioluminescence of the larvae of fireflies is also circularly polarized, as reported in 1980 for the species Photuris lucicrescens and Photuris versicolor.
For fireflies, it is more difficult to find a microscopic explanation
for the polarization, because the left and right lanterns of the larvae
were found to emit polarized light of opposite senses. The authors
suggest that the light begins with a linear polarization due to inhomogeneities inside aligned photocytes, and it picks up circular polarization while passing through linearly birefringent tissue.[18]
Water-air interfaces provide another source of circular
polarization. Sunlight that gets scattered back up towards the surface
is linearly polarized. If this light is then totally internally reflected back down, its vertical component undergoes a phase shift. To an underwater observer looking up, the faint light outside Snell's window therefore is (partially) circularly polarized.[19]
Weaker sources of circular polarization in nature include multiple scattering by linear polarizers[dubious – discuss], as in the circular polarization of starlight, and selective absorption by circularly dichroic media.
Radio emission from stars and pulsars can be strongly circularly polarized[citation needed].
Two species of mantis shrimp have been reported to be able to detect circular polarized light.[20][21]
See also
References
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); §§9–10.
Académie des Sciences, Procès-verbaux des séances de l'Académie tenues depuis la fondation de l'Institut jusqu'au mois d'août 1835, vol. 7 (for 1820–23), Hendaye, Basses Pyrénées: Imprimerie de l'Observatoire d'Abbadia, 1916, p. 401.
A. Fresnel, "Note sur le calcul des teintes que la polarisation développe dans les lames cristallisées" et seq., Annales de Chimie et de Physique,
Ser. 2, vol. 17, pp. 102–11 (May 1821), 167–96 (June 1821), 312–15
("Postscript", July 1821); reprinted (with added section nos.) in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 609–48; translated as "On the calculation of the
tints that polarization develops in crystalline plates,
& postscript", Zenodo: 4058004 (Creative Commons), 2021; author's footnote to §16.
IEEE
Std 149-1979 (R2008), "IEEE Standard Test Procedures for Antennas".
Reaffirmed December 10, 2008, Approved December 15, 1977, IEEE-SA
Standards Board. Approved October 9, 2003, American National Standards
Institute. ISBN 0-471-08032-2. doi:10.1109/IEEESTD.1979.120310,
sec. 11.1, p. 61."the sense of polarization, or handedness ... is
called right handed (left handed) if the direction of rotation is
clockwise (anti-clockwise) for an observer looking in the direction of
propagation"
Electromagnetic
Waves & Antennas – S. J. Orfanidis: Footnote p.45, "most
engineering texts use the IEEE convention and most physics texts, the
opposite convention."
Electromagnetic
Waves & Antennas – S. J. Orfanidis Pg 44 "Curl the fingers of your
left and right hands into a fist and point both thumbs towards the direction of propagation"
Lectures
on Physics Feynman (Vol. 1, ch.33-1) "If the end of the electric
vector, when we look at it as the light comes straight toward us, goes
around in an anti-clockwise direction, we call it right-hand circular
polarization. ... Our convention for labeling left-hand and right-hand
circular polarization is consistent with that which is used today for
all the other particles in physics which exhibit polarization (e.g.,
electrons). However, in some books on optics the opposite conventions
are used, so one must be careful."
IAU
General Assembly Meeting, 1973, Commission 40 (Radio
Astronomy/Radioastronomie), 8. POLARIZATION DEFINITIONS -- "A working
Group chaired by Westerhout was convened to discuss the definition of
polarization brightness temperatures used in the description of
polarized extended objects and the galactic
background. The following resolution was adopted by Commissions 25 and
40: 'RESOLVED, that the frame of reference for the Stokes parameters is
that of Right Ascension and Declination with the position angle of
electric-vector maximum, q, starting from North and increasing through
East. Elliptical polarization is defined in conformity with the
definitions of the Institute of Electrical and Electronics Engineers
(IEEE Standard 211, 1969). This means that the polarization of incoming
radiation, for which the position angle, q, of the electric vector,
measured at a fixed point in space, increases with time, is described as
right-handed and positive.'"
Polarization
in Spectral Lines. 2004 E. Landi Degl'innocenti, M Landolfi Section 1.2
"When ... the tip of the electric field vector rotates clockwise for an
observer facing the radiation source, ... (it will be considered)...
positive (or righthanded) circular polarization, Our convention ...
agrees with those proposed in the classical textbooks on polarized light
by Shurcliff (1952) and by Clarke and Grainger (1971). The same
convention is also used, although with some few exceptions, by optical
astronomers working in the field of polarimetry. Many radio astronomers,
on the other hand, use the opposite convention. [1]
HANDBOOK
OPTICS Volume I,Devices, Measurements and Properties,Michael Bass Page
272 Footnote: "Right-circularly polarized light is defined as a
clockwise rotation of the electric vector when the observer is looking against the direction the wave is traveling."
"The Polarization Ellipse". spie.org. Retrieved 13 April 2018.
S. E. Braslavsky (1 January 2009). "Glossary of terms used in photochemistry, 3rd edition (IUPAC Recommendations 2006)" (PDF). Pure and Applied Chemistry. 79 (3): 293–465. doi:10.1351/pac200779030293. S2CID 96601716. Archived (PDF) from the original on 2022-10-09.
In
one location it is stated..."Note 1. ... In general, the figure, i.e.,
polarization, is elliptical and is traced in a clockwise or
anti-clockwise sense, as viewed in the direction of propagation. ...
Rotation of the electric vector in a clockwise sense is designated
right-hand polarization, and rotation in an anti-clockwise sense is
designated left-hand polarization. "[2] Archived 2011-05-14 at the Wayback Machine
In another location it is stated... "Note 4: Circular polarization may
be referred to as "right-hand" or "left-hand", depending on whether the
helix describes the thread of a right-hand or left-hand screw,
respectively". [3] Archived 2011-06-06 at the Wayback Machine
Balanis, Constantine A. "Antenna Theory – Analysis and Design", 2005, 3rd Edition, John Wiley & Sons.
Introduction
to Quantum Theory 2ED David Park Sec 2.2 Pg32 "... the polarization of a
beam of light is exactly the same kind of thing as the spin of a beam
of electrons, the differences of terminology reflecting only the
accidents of the historical order of discovery."
Srinivasarao, Mohan; Park, Jung Ok; Crne, Matija; Sharma, Vivek (July 24, 2009). "Structural Origin of Circularly Polarized Iridescence in Jeweled Beetles". Science. 325 (5939): 449–451. Bibcode:2009Sci...325..449S. doi:10.1126/science.1172051. PMID 19628862. S2CID 206519071 – via science.sciencemag.org.
Hegedüs, Ramón; Győző Szélb; Gábor Horváth (September 2006). "Imaging polarimetry of the circularly polarizing cuticle of scarab beetles (Coleoptera: Rutelidae, Cetoniidae)". Vision Research. 46 (17): 2786–2797. doi:10.1016/j.visres.2006.02.007. PMID 16564066. S2CID 14974820.
Wynberg, Hans; Meijer, E.W.; Hummelen, J.C.; Dekkers, H.P.J.M.; Schippers, P.H.; Carlson, A.D. (7 August 1980). "Circular polarization observed in bioluminescence" (PDF). Nature. 286 (5773): 641–642. Bibcode:1980Natur.286..641W. doi:10.1038/286641a0. S2CID 4324467. Archived from the original (PDF) on 24 July 2011.
Horváth, Gábor; Dezsö Varjú (2003). Polarized Light in Animal Vision: Polarization Patterns in Nature. Springer. pp. 100–103. ISBN 978-3-540-40457-6.
Tsyr-Huei
Chiou; Sonja Kleinlogel; Tom Cronin; Roy Caldwell; Birte Loeffler;
Afsheen Siddiqi; Alan Goldizen; Justin Marshall (2008). "Circular polarization vision in a stomatopod crustacean". Current Biology. 18 (6): 429–34. doi:10.1016/j.cub.2008.02.066. PMID 18356053. S2CID 6925705.
Further reading
External links

The
electric field
vectors of a traveling circularly polarized electromagnetic wave. This
wave is right-circularly-polarized, since the direction of rotation of
the vector is related by the
right-hand rule to the direction the wave is moving; or left-circularly-polarized according to alternative convention.
https://en.wikipedia.org/wiki/Circular_polarization
A stellar magnetic field is a magnetic field generated by the motion of conductive plasma inside a star. This motion is created through convection, which is a form of energy transport involving the physical movement of material. A localized magnetic field
exerts a force on the plasma, effectively increasing the pressure
without a comparable gain in density. As a result, the magnetized region
rises relative to the remainder of the plasma, until it reaches the
star's photosphere. This creates starspots on the surface, and the related phenomenon of coronal loops.[1]
https://en.wikipedia.org/wiki/Stellar_magnetic_field
In solar physics, a coronal loop is a well-defined arch-like structure in the Sun's atmosphere made up of relatively dense plasma confined and isolated from the surrounding medium by magnetic flux tubes. Coronal loops begin and end at two footpoints on the photosphere and project into the transition region and lower corona. They typically form and dissipate over periods of seconds to days[1] and may span anywhere from 1 to 1,000 megametres (621 to 621,000 mi) in length.[2]
Coronal loops are often associated with the strong magnetic fields located within active regions and sunspots. The number of coronal loops varies with the 11 year solar cycle.
https://en.wikipedia.org/wiki/Coronal_loop
The photosphere is a star's outer shell from which light is radiated.
The term itself is derived from Ancient Greek roots, φῶς, φωτός/phos, photos meaning "light" and σφαῖρα/sphaira meaning "sphere", in reference to it being a spherical surface that is perceived to emit light.[citation needed] It extends into a star's surface until the plasma becomes opaque, equivalent to an optical depth of approximately 2⁄3,[1] or equivalently, a depth from which 50% of light will escape without being scattered.
A photosphere is the deepest region of a luminous object, usually a star, that is transparent to photons of certain wavelengths.
https://en.wikipedia.org/wiki/Photosphere
In physics, the magnetomotive force (mmf)  is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:
is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:
where
Φ is the magnetic flux and

is the
reluctance of the circuit. It can be seen that the magnetomotive force plays a role in this equation analogous to the voltage
V in
Ohm's law:
V = IR, since it is the cause of magnetic flux in a magnetic circuit:
[2]
 where N is the number of turns in the coil and I is the electric current through the circuit.
where N is the number of turns in the coil and I is the electric current through the circuit. where Φ is the magnetic flux and
where Φ is the magnetic flux and  is the magnetic reluctance
is the magnetic reluctance where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
https://en.wikipedia.org/wiki/Magnetomotive_force
In physics, mainly quantum mechanics and particle physics, a spin magnetic moment is the magnetic moment caused by the spin of elementary particles. For example, the electron is an elementary spin-1/2 fermion. Quantum electrodynamics gives the most accurate prediction of the anomalous magnetic moment of the electron.
In general, a magnetic moment can be defined in terms of an electric current and the area enclosed by the current loop.
Since angular momentum corresponds to rotational motion, the magnetic
moment can be related to the orbital angular momentum of the charge carriers in the constituting current. However, in magnetic materials, the atomic and molecular dipoles have magnetic moments not just because of their quantized orbital angular momentum, but also due to the spin of elementary particles constituting them.[a][b]
"Spin" is a non-classical property of elementary particles, since classically the "spin angular momentum" of a material object is really just the total orbital angular momenta of the object's constituents about the rotation axis. Elementary particles are conceived as point objects with no axis around which to "spin" (see wave–particle duality).
https://en.wikipedia.org/wiki/Spin_magnetic_moment
Coercivity, also called the magnetic coercivity, coercive field or coercive force, is a measure of the ability of a ferromagnetic material to withstand an external magnetic field without becoming demagnetized. Coercivity is usually measured in oersted or ampere/meter units and is denoted HC.
An analogous property in electrical engineering and materials science, electric coercivity, is the ability of a ferroelectric material to withstand an external electric field without becoming depolarized.
Ferromagnetic materials with high coercivity are called magnetically hard, and are used to make permanent magnets. Materials with low coercivity are said to be magnetically soft. The latter are used in transformer and inductor cores, recording heads, microwave devices, and magnetic shielding.
https://en.wikipedia.org/wiki/Coercivity
Magnetic shielding
Equipment sometimes requires isolation from external magnetic fields.[8]
For static or slowly varying magnetic fields (below about 100 kHz) the
Faraday shielding described above is ineffective. In these cases
shields made of high magnetic permeability metal alloys can be used, such as sheets of permalloy and mu-metal[9][10] or with nanocrystalline grain structure ferromagnetic metal coatings.[11]
These materials do not block the magnetic field, as with electric
shielding, but rather draw the field into themselves, providing a path
for the magnetic field lines
around the shielded volume. The best shape for magnetic shields is
thus a closed container surrounding the shielded volume. The
effectiveness of this type of shielding depends on the material's
permeability, which generally drops off at both very low magnetic field
strengths and high field strengths where the material becomes saturated.
Therefore, to achieve low residual fields, magnetic shields often
consist of several enclosures, one inside the other, each of which
successively reduces the field inside it. Entry holes within shielding
surfaces may degrade their performance significantly.
Because of the above limitations of passive shielding, an
alternative used with static or low-frequency fields is active
shielding, in which a field created by electromagnets cancels the ambient field within a volume.[12] Solenoids and Helmholtz coils
are types of coils that can be used for this purpose, as well as more
complex wire patterns designed using methods adapted from those used in
coil design for magnetic resonance imaging. Active shields may also be designed accounting for the electromagnetic coupling with passive shields,[13][14][15][16][17] referred to as hybrid shielding,[18]
so that there is broadband shielding from the passive shield and
additional cancellation of specific components using the active system.
Additionally, superconducting materials can expel magnetic fields via the Meissner effect.
https://en.wikipedia.org/wiki/Electromagnetic_shielding#Magnetic_shielding
First time-dependent rotation
Consider another (non-inertial) observer (the 2-O) located at the center of the Earth but rotating about the NS-axis by  We establish coordinates attached to this observer as
We establish coordinates attached to this observer as
so that the unit

versor

is mapped to the point

.
For the 2-O neither the Earth nor the barycenter of the gyroscope is
moving. The rotation of 2-O relative to 1-O is performed with angular
velocity

. We suppose that the

axis denotes points with zero longitude (the prime, or Greenwich, meridian).
Second and third fixed rotations
We now rotate about the  axis, so that the
axis, so that the  -axis has the longitude of the barycenter. In this case we have
-axis has the longitude of the barycenter. In this case we have
With the next rotation (about the axis  of an angle
of an angle  , the co-latitude) we bring the
, the co-latitude) we bring the  axis along the local zenith (
axis along the local zenith ( -axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)
-axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)
so that the  versor
versor  is mapped to the point
is mapped to the point 
Constant translation
We
now choose another coordinate basis whose origin is located at the
barycenter of the gyroscope. This can be performed by the following
translation along the zenith axis
so that the origin of the new system,  is located at the point
is located at the point  and
and  is the radius of the Earth. Now the
is the radius of the Earth. Now the  -axis points towards the south direction.
-axis points towards the south direction.
Fourth time-dependent rotation
Now we rotate about the zenith  -axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find
-axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find
The axis of symmetry of the gyrocompass is now along the  -axis.
-axis.
Last time-dependent rotation
The last rotation is a rotation on the axis of symmetry of the gyroscope as in
Dynamics of the system
Since
the height of the gyroscope's barycenter does not change (and the
origin of the coordinate system is located at this same point), its gravitational potential energy is constant. Therefore its Lagrangian  corresponds to its kinetic energy
corresponds to its kinetic energy  only. We have
only. We have
where

is the mass of the gyroscope, and
is the squared inertial speed of the origin of the coordinates of the
final coordinate system (i.e. the center of mass). This constant term
does not affect the dynamics of the gyroscope and it can be neglected.
On the other hand, the tensor of inertia is given by
and
Therefore we find
The Lagrangian can be rewritten as
where
is the part of the Lagrangian responsible for the dynamics of the system. Then, since

, we find
Since the angular momentum  of the gyrocompass is given by
of the gyrocompass is given by  we see that the constant
we see that the constant  is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable
is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable  as
as
or
Particular case: the poles
At the poles we find  and the equations of motion become
and the equations of motion become
This simple solution implies that the gyroscope is uniformly
rotating with constant angular velocity in both the vertical and
symmetrical axis.
The general and physically relevant case
Let us suppose now that  and that
and that  ,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find
,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find
Consider the case that
and, further, we allow for fast gyro-rotations, that is
Therefore, for fast spinning rotations,  implies
implies  In this case, the equations of motion further simplify to
In this case, the equations of motion further simplify to
Therefore we find small oscillations about the north-south line, as  ,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by
,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by
which corresponds to a period for the oscillations given by
Therefore  is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required
is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required  ,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the
,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the  -axis, the axis of symmetry. As a side result, on measuring
-axis, the axis of symmetry. As a side result, on measuring  (and knowing
(and knowing  ), one can deduce the local co-latitude
), one can deduce the local co-latitude 
See also
Notes
- Although
the effect is not visible in the specific case when the gyroscope's
axis is precisely parallel to the Earth's rotational axis.
References
Gade, Kenneth (2016). "The Seven Ways to Find Heading" (PDF). The Journal of Navigation. Cambridge University Press. 69 (5): 955–970. doi:10.1017/S0373463316000096. S2CID 53587934.
Elliott-Laboratories (2003). The Anschutz Gyro-Compass and Gyroscope Engineering. pp. 7–24. ISBN 978-1-929148-12-7. Archived from the original on 2017-03-04.
Time Inc. (Mar 15, 1943). "The gyroscope pilots ships & planes". Life. pp. 80–83. Archived from the original on 2017-02-27.
Galison, Peter (1987). How experiments end. pp. 34–37. ISBN 978-0-226-27915-2. Archived from the original on 2012-03-02.
"Archived copy" (PDF). Archived (PDF) from the original on 2015-06-29. Retrieved 2012-02-19. Standard 22
Anschütz Gyro Compass [sic] System: Gyro Compass [sic] Technology [sic] for over than [sic] 100 years
Chambers of Commerce and Industry in Schleswig-Holstein Archived 2017-02-22 at the Wayback Machine Retrieved on February 22, 2017.
Gyrocompass, Auxiliary Gyrocompass, and Dead Reckoning Analyzing Indicator and Tracer Systems Archived 2013-06-01 at the Wayback Machine, San Francisco Maritime National Park Association.
The Invention of Precision Navigational Instruments for Air and Sea Navigation Archived 2011-07-18 at the Wayback Machine, Weems & Plath.
Collinson, R. P. G. (2003), Introduction to avionics systems, Springer, p. 293, ISBN 978-1-4020-7278-9, archived from the original on 2014-07-07
NASA NASA Callback: Heading for Trouble Archived 2011-07-16 at the Wayback Machine, NASA Callback Safety Bulletin website, December 2005, No. 305. Retrieved August 29, 2010.
Bowditch, Nathaniel. American Practical Navigator Archived 2017-03-07 at the Wayback Machine, Paradise Cay Publications, 2002, pp.93-94, ISBN 978-0-939837-54-0.
Gyrocompass: Steaming Error Archived 2008-12-22 at the Wayback Machine, Navis. Accessed 15 December 2008.
- Seamanship Techniques:Shipboard and Marine Operations, D. J. House, Butterworth-Heinemann, 2004, p. 341
Bibliography
External links
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
This article is about devices used on ships. For the type of gyroscope used to determine aircraft heading, see
Heading indicator.
Cutaway of an Anschütz gyrocompass
A gyrocompass is a type of non-magnetic compass which is based on a fast-spinning disc and the rotation of the Earth (or another planetary body if used elsewhere in the universe) to find geographical direction automatically. The use of a gyrocompass is one of the seven fundamental ways to determine the heading of a vehicle.[1] A gyroscope is an essential component of a gyrocompass, but they are different devices; a gyrocompass is built to use the effect of gyroscopic precession, which is a distinctive aspect of the general gyroscopic effect.[2][3] Gyrocompasses are widely used for navigation on ships, because they have two significant advantages over magnetic compasses:[3]
Aircraft commonly use gyroscopic instruments (but not a gyrocompass) for navigation and altitude monitoring; for details, see Flight instruments and Gyroscopic autopilot.
History
The first, not yet practical,[4] form of gyrocompass was patented in 1885 by Marinus Gerardus van den Bos.[4] A usable gyrocompass was invented in 1906 in Germany by Hermann Anschütz-Kaempfe, and after successful tests in 1908 became widely used in the German Imperial Navy.[2][4][5] Anschütz-Kaempfe founded the company Anschütz & Co. in Kiel, to mass produce gyrocompasses; the company is today Raytheon Anschütz GmbH.[6]
The gyrocompass was an important invention for nautical navigation
because it allowed accurate determination of a vessel’s location at all
times regardless of the vessel’s motion, the weather and the amount of
steel used in the construction of the ship.[7]
In the United States, Elmer Ambrose Sperry produced a workable gyrocompass system (1908: U.S. Patent 1,242,065), and founded the Sperry Gyroscope Company. The unit was adopted by the U.S. Navy (1911[3]),
and played a major role in World War I. The Navy also began using
Sperry's "Metal Mike": the first gyroscope-guided autopilot steering
system. In the following decades, these and other Sperry devices were
adopted by steamships such as the RMS Queen Mary, airplanes, and the warships of World War II. After his death in 1930, the Navy named the USS Sperry after him.
Meanwhile, in 1913, C. Plath (a Hamburg, Germany-based
manufacturer of navigational equipment including sextants and magnetic
compasses) developed the first gyrocompass to be installed on a
commercial vessel. C. Plath sold many gyrocompasses to the Weems’
School for Navigation in Annapolis, MD, and soon the founders of each
organization formed an alliance and became Weems & Plath.[8]
The 1889 Dumoulin-Krebs gyroscope
Before the success of the gyrocompass, several attempts had been made in Europe to use a gyroscope instead. By 1880, William Thomson (Lord Kelvin) tried to propose a gyrostat to the British Navy. In 1889, Arthur Krebs adapted an electric motor to the Dumoulin-Froment marine gyroscope, for the French Navy. That gave the Gymnote submarine the ability to keep a straight line while underwater for several hours, and it allowed her to force a naval block in 1890.
In 1923 Max Schuler published his paper containing his observation that if a gyrocompass possessed Schuler tuning
such that it had an oscillation period of 84.4 minutes (which is the
orbital period of a notional satellite orbiting around the Earth at sea
level), then it could be rendered insensitive to lateral motion and
maintain directional stability.[9]
Operation
A gyroscope, not to be confused with a gyrocompass, is a spinning wheel mounted on a set of gimbals so that its axis is free to orient itself in any way.[3] When it is spun up to speed with its axis pointing in some direction, due to the law of conservation of angular momentum, such a wheel will normally maintain its original orientation to a fixed point in outer space
(not to a fixed point on Earth). Since the Earth rotates, it appears to
a stationary observer on Earth that a gyroscope's axis is completing a
full rotation once every 24 hours.[note 1] Such a rotating gyroscope is used for navigation in some cases, for example on aircraft, where it is known as heading indicator
or directional gyro, but cannot ordinarily be used for long-term marine
navigation. The crucial additional ingredient needed to turn a
gyroscope into a gyrocompass, so it would automatically position to true
north,[2][3] is some mechanism that results in an application of torque whenever the compass's axis is not pointing north.
One method uses friction to apply the needed torque:[7]
the gyroscope in a gyrocompass is not completely free to reorient
itself; if for instance a device connected to the axis is immersed in a
viscous fluid, then that fluid will resist reorientation of the axis.
This friction force caused by the fluid results in a torque acting on the axis, causing the axis to turn in a direction orthogonal to the torque (that is, to precess) along a line of longitude.
Once the axis points toward the celestial pole, it will appear to be
stationary and won't experience any more frictional forces. This is
because true north (or true south) is the only direction for which the
gyroscope can remain on the surface of the earth and not be required to
change. This axis orientation is considered to be a point of minimum potential energy.
Another, more practical, method is to use weights to force the
axis of the compass to remain horizontal (perpendicular to the direction
of the center of the Earth), but otherwise allow it to rotate freely
within the horizontal plane.[2][3]
In this case, gravity will apply a torque forcing the compass's axis
toward true north. Because the weights will confine the compass's axis
to be horizontal with respect to the Earth's surface, the axis can never
align with the Earth's axis (except on the Equator) and must realign
itself as the Earth rotates. But with respect to the Earth's surface,
the compass will appear to be stationary and pointing along the Earth's
surface toward the true North Pole.
Since the gyrocompass's north-seeking function depends on the rotation around the axis of the Earth that causes torque-induced gyroscopic precession,
it will not orient itself correctly to true north if it is moved very
fast in an east to west direction, thus negating the Earth's rotation.
However, aircraft commonly use heading indicators or directional gyros,
which are not gyrocompasses and do not align themselves to north via
precession, but are periodically aligned manually to magnetic north.[10][11]
Errors
A gyrocompass is subject to certain errors. These include steaming error, where rapid changes in course, speed and latitude cause deviation before the gyro can adjust itself.[12] On most modern ships the GPS or other navigational aids feed data to the gyrocompass allowing a small computer to apply a correction.
Alternatively a design based on a strapdown architecture (including a triad of fibre optic gyroscopes, ring laser gyroscopes or hemispherical resonator gyroscopes
and a triad of accelerometers) will eliminate these errors, as they do
not depend upon mechanical parts to determinate rate of rotation.[13]
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
A rotating magnetic field is the resultant magnetic field produced by a system of coils symmetrically placed and supplied with polyphase currents.[1]
A rotating magnetic field can be produced by a poly-phase (two or more
phases) current or by a single phase current provided that, in the
latter case, two field windings are supplied and are so designed that
the two resulting magnetic fields generated thereby are out of phase.[2]
Rotating magnetic fields are often utilized for electromechanical applications, such as induction motors, electric generators and induction regulators.
History
In 1824, the French physicist François Arago formulated the existence of rotating magnetic fields using a rotating copper disk and a needle, termed “Arago's rotations.” English experimenters Charles Babbage and John Herschel found they could induce rotation in Arago's copper disk by spinning a horseshoe magnet under it, with English scientist Michael Faraday later attributing the effect to electromagnetic induction.[3] In 1879, English physicist Walter Baily
replaced the horseshoe magnets with four electromagnets and, by
manually turning switches on and off, demonstrated a primitive induction
motor.[4][5][6][7][8]
The idea of a rotating magnetic field in an AC motor was explored by the Italian physicist and electrical engineer Galileo Ferraris and the Serbian-American inventor and electrical engineer Nikola Tesla.[9] Ferraris wrote about researching the concept and built a working model in 1885.[10]
Tesla attempted several (unsuccessful) designs and working models
through the early 1880s before building a working prototype in 1887[11][12][13]
According to Ferraris principle of rotating magnetic field, Friedrich
August Haselwander developed the first AC 3 phase generator in 1887.[14] In 1888, Ferraris published his research in a paper to the Royal Academy of Sciences in Turin and Tesla obtained a United States patent (U.S. Patent 0,381,968)
for his design. Based on the Haselwander generator, Mikhail
Dolivo-Dobrovolsky will develop a three-phase generator and motor for
the world's first three-phase power plant built in 1891 in Frankfurt,
Germany.[15]
Description
The rotating magnetic field is the key principle in the operation of induction machines. The induction motor consists of a stator and rotor.
In the stator a group of fixed windings are so arranged that a two
phase current, for example, produces a magnetic field which rotates at
an angular velocity determined by the frequency of the alternating current. The rotor or armature consists of coils wound in slots, which are short circuited and in which the changing flux
generated by the field poles induce a current. The flux generated by
the armature current reacts upon the field poles and the armature is set
in rotation in a definite direction.[2]
Rotating fields.
As the direction of the current through the windings changes, the
polarity of the windings changes as well. Since there are two windings
acting in conjunction with each other, the polarity of the main field
will depend upon the polarity of each winding. The arrow or vector below
each diagram indicates the direction of the magnetic field in each
case.
[16] A symmetric rotating magnetic field can be produced with as few as two polar wound coils driven at 90-degree phasing. However, three sets of coils are nearly always used, because it is compatible with a symmetric three-phase AC sine current system. The three coils are driven with each set 120 degrees in phase from the others. For the purpose of this example, the magnetic field is taken to be the linear function of the coil's current.
The result of adding three 120-degree phased sine waves on the axis of the motor is a single rotating vector that always remains constant in magnitude.[17]
The rotor has a constant magnetic field. The north pole of the rotor
will move toward the south pole of the magnetic field of the stator, and
vice versa. This magnetomechanical attraction creates a force that will drive the rotor to follow the rotating magnetic field in a synchronous manner.
Rotating three-phase magnetic field, as indicated by the rotating black arrow
A permanent magnet
in such a field will rotate so as to maintain its alignment with the
external field. This effect was utilized in early alternating-current
electric motors. A rotating magnetic field can be constructed using two
orthogonal coils with a 90-degree phase difference in their alternating
currents. However, in practice, such a system would be supplied through
a three-wire arrangement with unequal currents. This inequality would
cause serious problems in the standardization of the conductor size. In
order to overcome this, three-phase systems are used in which the three
currents are equal in magnitude and have a 120-degree phase difference.
Three similar coils having mutual geometrical angles of 120 degrees will
create the rotating magnetic field in this case. The ability of the
three-phase system to create the rotating field utilized in electric
motors is one of the main reasons why three-phase systems dominate the
world’s electric power-supply systems.
Rotating magnetic fields are also used in induction motors.
Because magnets degrade with time, induction motors use short-circuited
rotors (instead of a magnet), which follow the rotating magnetic field
of a multicoiled stator. In these motors, the short-circuited turns of
the rotor develop eddy currents in the rotating field of the stator, which in turn move the rotor by Lorentz force.
These types of motors are not usually synchronous, but instead
necessarily involve a degree of 'slip' in order that the current may be
produced due to the relative movement of the field and the rotor.
See also
References
Graham, Frank Duncan (1921). Audels Engineers and Mechanics Guide. New York: THEO. AUDEL & CO. p. 594.
The Wireless Age. Vol. 6. New York: Macroni Pub. Corp'n. October 1918. pp. 18–19.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 52–54. ISBN 978-1400846559.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. p. 55. ISBN 978-1400846559.
Babbage, C.; Herschel, J. F. W. (Jan 1825). "Account
of the Repetition of M. Arago's Experiments on the Magnetism Manifested
by Various Substances during the Act of Rotation". Philosophical Transactions of the Royal Society. 115: 467–496. Bibcode:1825RSPT..115..467B. doi:10.1098/rstl.1825.0023. Retrieved 2 December 2012.
Thompson, Silvanus Phillips (1895). Polyphase Electric Currents and Alternate-Current Motors (1st ed.). London: E. & F.N. Spon. p. 261. Retrieved 2 December 2012.
Baily, Walter (June 28, 1879). "A Mode of producing Arago's Rotation". Philosophical Magazine. Taylor & Francis. 3 (1): 115–120. Bibcode:1879PPSL....3..115B. doi:10.1088/1478-7814/3/1/318.
Vučković, Vladan (November 2006). "Interpretation of a Discovery" (PDF). The Serbian Journal of Electrical Engineers. 3 (2). Retrieved 10 February 2013.
Hughes, Thomas Parke (1983). Networks of power: electrification in Western society, 1880-1930. Baltimore: Johns Hopkins University Press. p. 117.
Encyclopedia Americana: Meyer to Nauvoo. Vol. 12. Danbury, Connecticut: Scholastic Library Pub. 2006. p. 558.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 63–68. ISBN 978-1400846559.
Debunking the Tesla Myth
O'Neill, John. Prodigal Genius: The Life of Nikola Tesla. pp. 55–58.
https://ieeexplore.ieee.org/document/4401482?arnumber=4401482 H. Hooshyar; M. Savaghebi; A. Vahedi: Synchronous generator - Past, present and future
AC Power History and Timeline
United States, Bureau of Naval Personnel (1945). Advanced Work In Aircraft Electricity. Washington: U.S. Govt. Print. Off. pp. 149–150.
 This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
Further reading
- C Mackechnie Jarvis (1970). "Nikola Tesla and the induction motor". Phys Educ. 5 (5): 280–7. Bibcode:1970PhyEd...5..280M. doi:10.1088/0031-9120/5/5/306. S2CID 250845406.
- Owen, E.L. (October 1988). "The induction motor's historical past". IEEE Potentials. 7 (3): 27–30. doi:10.1109/45.9969. S2CID 19271710.
- Beckhard, Arthur J., "Electrical genius Nikola Tesla". New York,
Messner, 1959. LCCN 59007009 /L/AC/r85 (ed. 192 p.; 22 cm.; biography
with notes on the inventions of the rotating magnetic field motors for
alternating current.)
- Kline, R. (1987). "Science and Engineering Theory in the Invention and Development of the Induction Motor, 1880–1900". Technology and Culture. 28 (2): 283–313. doi:10.2307/3105568. JSTOR 3105568.
- Cēbers, A. (December 13, 2002). "Dynamics of an elongated magnetic droplet in a rotating field". Phys. Rev. E. 66 (6): 061402. Bibcode:2002PhRvE..66f1402C. doi:10.1103/PhysRevE.66.061402. PMID 12513280.
- Cēbers, A. & I. Javaitis (2004). "Dynamics of a flexible magnetic chain in a rotating magnetic field". Phys. Rev. E. 69 (2): 021404. Bibcode:2004PhRvE..69b1404C. doi:10.1103/PhysRevE.69.021404. PMID 14995441.
- Cēbers, A. & M. Ozols (2006). "Dynamics of an active magnetic particle in a rotating magnetic field". Phys. Rev. E. 73 (2): 021505. Bibcode:2006PhRvE..73b1505C. doi:10.1103/PhysRevE.73.021505. PMID 16605340.
- Tao Song; et al. (June 2004). "Rotating permanent magnetic fields exposure system for in vitro study". IEEE Transactions on Applied Superconductivity. 14 (2): 1643–6. Bibcode:2004ITAS...14.1643S. doi:10.1109/TASC.2004.831024.
- Labzovskii, L.N., A.O. Mitrushchenkov, and A.I. Frenkel, "Parity Nonconserving Current in Conductors of Electricity". 6 July 1987. (ed., Shows that the continuous current arises under the influence of the rotating magnetic field.)
- Naval Electrical Engineering Training Series, Module 05 -
Introduction to Generators and Motors, Chapter 4 Alternating Current
Motors, Rotating magnetic fields (ed. different copy of the NEETS book is available, Add-free version)
- Rotating Magnetic Field, eng.ox.ac.uk
- Tesla's Autobiography, III. My Later Endeavors; The Discovery of the Rotating Magnetic Field
- Nikola Tesla and the electro-magnetic motor, Inventor of the Week Archive.
- Galileo Ferraris: the rotating magnetic field
- Single Phase Induction Motors
- H.Y. Guo, A.L. Hoffman, D. Lotz, S.J. Tobin, W.A. Reass, L.S. Schrank and G.A. Wurden, The Rotating Magnetic Field Oscillator System for Current Drive in the Translation, Confinement and Sustainment Experiment, March 22, 2001.
- Putko, V. F., and V. S. Sobolev, Effect of a rotating magnetic field on the characteristics of a direct-current plasma generator.
External links
Patents
|
|---|
Career and
inventions | | |
|---|
| Writings | |
|---|
| Other | |
|---|
| Related | |
|---|
https://en.wikipedia.org/wiki/Rotating_magnetic_field
Earth's rotation or Earth's spin is the rotation of planet Earth around its own axis, as well as changes in the orientation of the rotation axis in space. Earth rotates eastward, in prograde motion. As viewed from the northern polar star Polaris, Earth turns counterclockwise.
https://en.wikipedia.org/wiki/Earth%27s_rotation
Magnetic hysteresis occurs when an external magnetic field is applied to a ferromagnet such as iron and the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. This is the effect that provides the element of memory in a hard disk drive.
https://en.wikipedia.org/wiki/Magnetic_hysteresis
Magnetic reluctance, or magnetic resistance, is a concept used in the analysis of magnetic circuits. It is defined as the ratio of magnetomotive force (mmf) to magnetic flux. It represents the opposition to magnetic flux, and depends on the geometry and composition of an object.
Magnetic reluctance in a magnetic circuit is analogous to electrical resistance in an electrical circuit in that resistance is a measure of the opposition to the electric current. The definition of magnetic reluctance is analogous to Ohm's law
in this respect. However, magnetic flux passing through a reluctance
does not give rise to dissipation of heat as it does for current through
a resistance. Thus, the analogy cannot be used for modelling energy
flow in systems where energy crosses between the magnetic and electrical
domains. An alternative analogy to the reluctance model which does
correctly represent energy flows is the gyrator–capacitor model.
Magnetic reluctance is a scalar extensive quantity. The unit for magnetic reluctance is inverse henry, H−1.
https://en.wikipedia.org/wiki/Magnetic_reluctance
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model
https://en.wikipedia.org/wiki/Lumped-element_model
The lumped-element model (also called lumped-parameter model, or lumped-component model) simplifies the description of the behaviour of spatially distributed physical systems, such as electrical circuits, into a topology
consisting of discrete entities that approximate the behaviour of the
distributed system under certain assumptions. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc. This may be contrasted to distributed parameter systems or models in which the behaviour is distributed spatially and cannot be considered as localized into discrete entities.
Mathematically speaking, the simplification reduces the state space of the system to a finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters.
https://en.wikipedia.org/wiki/Lumped-element_model
https://en.wikipedia.org/wiki/Utility_frequency#Load-frequency_control
Steam turbine governing is the procedure of controlling the flow rate of steam to a steam turbine
so as to maintain its speed of rotation as constant. The variation in
load during the operation of a steam turbine can have a significant
impact on its performance. In a practical situation the load frequently
varies from the designed or economic load and thus there always exists a
considerable deviation from the desired performance of the turbine.[1]
The primary objective in the steam turbine operation is to maintain a
constant speed of rotation irrespective of the varying load. This can
be achieved by means of governing in a steam turbine. There are many types of governors.
https://en.wikipedia.org/wiki/Steam_turbine_governing
A virtual power plant (VPP) is a cloud-based distributed power plant that aggregates the capacities of heterogeneous distributed energy resources
(DER) for the purposes of enhancing power generation, trading or
selling power on the electricity market, and demand side options for
load reduction.[1]
DER assets in a VPP can include photovoltaic solar, energy
storage, electric vehicle chargers, and demand-responsive devices (such
as water heaters, thermostats, and appliances) with examples of virtual
power plants existing in the United States, Europe, and Australia.
https://en.wikipedia.org/wiki/Virtual_power_plant
Power generation
A virtual power plant is a system that integrates several types of power sources to give a reliable overall power supply.[2]
The sources often form a cluster of different types of dispatchable and
non-dispatchable, controllable or flexible load (CL or FL) distributed generation (DG) systems that are controlled by a central authority and can include microCHPs, natural gas-fired reciprocating engines, small-scale wind power plants (WPP), photovoltaics (PV), run-of-river hydroelectricity plants, small hydro, biomass, backup generators, and energy storage systems (ESS).
This system has benefits such as the ability to deliver peak load electricity or load-following power
generation on short notice. Such a VPP can replace a conventional power
plant while providing higher efficiency and more flexibility, which
allows the system to react better to load fluctuations. The drawback is a
higher complexity of the system, which requires complicated
optimization, control, and secure communications.[3] An interactive simulation on the website of the VPP operator Next Kraftwerke illustrates how the technology works.[4]
According to a 2012 report by Pike Research, VPP capacity would,
from 2011 to 2017, increase by 65%, from 55.6 gigawatts (GW) to 91.7 GW
worldwide, generating from $5.3 billion to $6.5 billion in worldwide
revenue in 2017.[5]
In a more aggressive forecast scenario, the clean-tech market
intelligence firm forecasts that global VPP revenues could reach as high
as $12.7 billion during the same period.[6]
"Virtual power plants represent an 'Internet of Energy'",
said senior analyst Peter Asmus of Pike Research. "These systems tap
existing grid networks to tailor electricity supply and demand services
for a customer. VPPs maximize value for both the end user and the
distribution utility using a sophisticated set of software-based
systems. They are dynamic, deliver value in real time, and can react
quickly to changing customer load conditions."
Ancillary services
Virtual power plants can also be used to provide ancillary services to grid operators in order to help maintain grid stability. Ancillary services include frequency regulation, load following, and providing operating reserve.
These services are primarily used to maintain the instantaneous balance
of electrical supply and demand. Power plants providing ancillary
services must respond to signals from grid operators to increase or
decrease load on the order of seconds to minutes in response to varying
levels of consumer demand.
Since ancillary services are typically provided by controllable
fossil-fuel generators, future carbon-free electrical grids that contain
high percentages of solar and wind must rely on other forms of
controllable power generation or consumption. One of the most well-known
examples of this is Vehicle to Grid
technology. In this case, distributed electrical vehicles connected to
the grid can be controlled together to act as a single virtual power
plant. By selectively controlling the rate at which each individual
vehicle charges, the grid sees a net injection or consumption of energy
as if a large scale battery was providing this service.
Similarly, flexible demand in the form of heat pumps or air conditioners has also been explored to provide ancillary services to the grid.[7]
As long as indoor thermal comfort is maintained, an aggregation of
distributed heat pumps can be selectively turned off and on in order to
vary their aggregate power consumption and follow an ancillary service
signal. Again, the effect on the grid is the same as if a large scale
power plant was providing the service.
Since they operate in parallel, virtual power plants can have the
advantage of higher ramp rates than thermal generators, which is
especially important in grids that experience a duck curve
and have high ramping requirements in the morning and evening. However,
the distributed nature generates communication and latency issues,
which could be problematic for providing fast services like frequency
regulation.
Energy trading
A
virtual power plant is also a cloud-based central or distributed
control center that takes advantage of information and communication
technologies (ICTs) and Internet of things (IoT) devices to aggregate the capacities of heterogeneous Distributed Energy Resources (DERs) to form "a coalition of heterogeneous DERs" for the purpose of energy trading on the wholesale electricity markets or providing ancillary services for system operators on behalf of non-eligible individual DERs.[8][9][10][11][12]
A VPP acts as an intermediary between DERs and the wholesale
electricity market and trades energy on behalf of DER owners who by
themselves are unable to participate in that market.[11]
The VPP behaves as a conventional dispatchable power plant from the
point of view of other market participants, although it is indeed a
cluster of many diverse DERs. Also, in the competitive electricity
markets, a virtual power plant acts as an arbitrageur between diverse
energy trading floors (i.e., bilateral and PPA contracts, forward and
futures markets, and the pool).[8][9][10][12]
So far, for risk management purposes, five different risk-hedging
strategies (i.e., IGDT, RO, CVaR, FSD, and SSD) have been applied to
the decision-making problems of VPPs in the research articles to measure
the level of conservatism of VPPs' decisions in diverse energy trading
floors (e.g., day-ahead electricity market, derivatives exchange market,
and bilateral contracts):
- IGDT : Information Gap Decision Theory[8]
- RO : Robust optimization[9]
- CVaR : Conditional Value at Risk[10]
- FSD : First-order Stochastic Dominance[11]
- SSD : Second-order Stochastic Dominance[12][13]
United States
Energy markets are those commodity markets that deal specifically with the trade and supply of energy.[14]
In the United States, virtual power plants not only deal with the
supply side, but also help manage demand, and ensure reliability of grid
functions through demand response (DR) and other load-shifting approaches, in real time.[15]
An often-reported energy crisis in America[16]
has opened the door for government-subsidized companies to enter an
arena that has only been available to utilities and multinational
billion-dollar companies until now. With the deregulation of markets
around the United States, the wholesale market pricing became the
exclusive domain of large retail suppliers; however local and federal
legislation along with large end-users are beginning to recognize the
advantages of wholesale activities.[17]
Texas is in the stage of developing pilot VPP projects to evaluate the impact on service and reliability.[18]
They have had several meetings of their ADER (Aggregated Distributed
Energy Resources) task force to develop the criteria for pilot projects
to operate.[19]
In California there are two electrical markets: private retail
and wholesale. California Senate Bill 2X—which passed the California
legislature on March 30, 2011—mandates 33% renewables by 2020 without
mandating any particular method to reach that goal.[20] PG&E pays VPP providers $2/kWh during peak times.[21][22]
As of August/September 2022, SunRun VPP inputs 80 MW at peak times,[23] and Tesla VPP inputs 68 MW.[24][25]
Europe
The Institute for Solar Energy Supply Technology of the University of Kassel in Germany pilot-tested a combined power plant that linked solar, wind, biogas, and pumped-storage hydroelectricity to provide load-following power around the clock, completely from renewable sources.[26]
Virtual power station operators are also commonly referred to as aggregators.
To test the effects of micro combined heat and power on a smart grid, 45 natural gas SOFC units (each generating 1.5 kW) from Republiq Power (Ceramic Fuel Cells) will be placed in 2013 on Ameland to function as a virtual power plant.[27]
An example of a real-world virtual power plant can be found on the Scottish Inner Hebrides island of Eigg.[28]
Next Kraftwerke from Cologne, Germany operates a virtual power
plant in seven European countries providing peak-load operation, power
trading and grid balancing services. The company aggregates distributed
energy resources from biogas, solar and wind as well as large-scale
power consumers.[29]
Distribution network operator, UK Power Networks,
and Powervault, a battery manufacturer and power aggregator, created
London's first virtual power plant in 2018, installing a trial fleet of
battery systems on over 40 homes across the London Borough of Barnet,
providing a combined capacity of 0.32 MWh.[30] This scheme was further expanded through a second contract in St Helier, London in 2020.[31]
In September 2019, SMS plc entered the virtual power plant sector
in the United Kingdom following the acquisition of Irish energy tech
start-up, Solo Energy.[32]
In October 2020, Tesla launched its Tesla Energy Plan in the UK in partnership with Octopus Energy,
allowing households to join its UK Tesla Virtual Power Plant. Homes
under the scheme are powered with 100% renewable energy from either
solar panels on the roof or from Octopus Energy.[33]
Australia
Commencing
in August 2020, Tesla will install a 5 kW rooftop solar system and 13.5
kWh Powerwall battery at each Housing SA premises, at no upfront cost
to the tenant. As South Australia's largest virtual power plant, the
battery and solar systems can be centrally managed, collectively
delivering 20 MW of generation capacity and 54 MWh of energy storage.[34]
In August 2016, AGL Energy announced a 5 MW virtual-power-plant scheme for Adelaide, Australia. The company will supply battery and photovoltaic systems from Sunverge Energy, of San Francisco, to 1000 households and businesses. The systems will cost consumers AUD $3500 and are expected to recoup the expense in savings in 7 years under current distribution network tariffs. The scheme is worth AUD $20 million and is being billed as the largest in the world.[35]
See also
References
Zurborg, Aaron (2010). "Unlocking Customer Value: the Virtual Power Plant" (PDF). Energy.gov. Retrieved 15 January 2023.
Feasibility, beneficiality, and institutional compatibility of a micro-CHP virtual power plant in the Netherlands
Smart Grid - The New and Improved Power Grid: A Survey; IEEE Communications Surveys and Tutorials 2011; X. Fang, S. Misra, G. Xue, and D. Yang; doi:10.1109/SURV.2011.101911.00087.
"Manage the Virtual Power and prevent a blackout!". Next Kraftwerke. Retrieved 2 December 2019.
"Revenue from Virtual Power Plants Will Reach $5.3 Billion by 2017, Forecasts Pike Research" (Press release). Navigant Consulting. 18 April 2012. Retrieved 20 November 2017 – via Business Wire.
"Virtual-Power-Plant
Market Capacity Expected To Double By 2015 - Apr 16, 2011 -
renewgridmag.com - Transmission - Technical Articles - Index - Library -
GENI - Global Energy Network Institute". Global Energy Network Institute. 2011-04-16. Retrieved 2022-01-05.
Lee,
Zachary E.; Sun, Qingxuan; Ma, Zhao; Wang, Jiangfeng; MacDonald, Jason
S.; Zhang, K. Max (Feb 2020). "Providing Grid Services With Heat Pumps: A
Review". Journal of Engineering for Sustainable Buildings and Cities. 1 (1). doi:10.1115/1.4045819. S2CID 213898377.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2015). "Decision
Making Tool for Virtual Power Plants Considering Midterm Bilateral
Contracts". 3rd Iranian Regional CIRED Conference and Exhibition on
Electricity Distribution, at Niroo Research Institute (NRI), Tehran,
Iran. 3 (3): 1–6. doi:10.13140/2.1.5086.4969.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (October 2015). "The design
of a risk-hedging tool for virtual power plants via robust optimization
approach". Applied Energy. 155: 766–777. doi:10.1016/j.apenergy.2015.06.059.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (May 2016). "A medium-term
coalition-forming model of heterogeneous DERs for a commercial virtual
power plant". Applied Energy. 169: 663–681. doi:10.1016/j.apenergy.2016.02.058.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2017). "Risk-based
medium-term trading strategy for a virtual power plant with first-order
stochastic dominance constraints". IET Generation, Transmission & Distribution. 11 (2): 520–529. doi:10.1049/iet-gtd.2016.1072. S2CID 114478127.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (April 2016). "Modeling the
cooperation between neighboring VPPs: Cross-regional bilateral
transactions". 2016 Iranian Conference on Renewable Energy & Distributed Generation (ICREDG). 11: 520–529. doi:10.1109/ICREDG.2016.7875909. ISBN 978-1-5090-0857-5. S2CID 16453458.
Shabanzadeh,
Morteza; Sheikh-El-Eslami, Mohammad-Kazem; Haghifam, Mahmoud-Reza
(2017). "An interactive cooperation model for neighboring virtual power
plants". Applied Energy. 200: 273–289. doi:10.1016/j.apenergy.2017.05.066. S2CID 157309706.
JEAN-PHILIPPE TAILLON, CFA (2021-10-14). "Introduction to the World of Electricity Trading". Investopedia. Retrieved 2022-01-04.
Aaron Zurborg (2010). "Unlocking Customer Value: The Virtual Power Plant". WorldPower 2010: 1–5.
"Energy Crisis (1970s) - HISTORY". history.com. 2018-08-21. Retrieved 2022-01-04.
"Electricity Deregulation". PennStation Extension. 2010-06-15. Retrieved 2022-01-05.
https://interchange.puc.texas.gov/Documents/51603_66_1221955.PDF
"Admin Monitor - Texas - Public Utility Commission of Texas".
PATRICK MCGREEVY (2011-04-13). "Gov. Brown signs law requiring 33% of energy be renewable by 2020 - Los Angeles Times". Los Angeles Times. Retrieved 2021-01-05.
"PG&E, Tesla virtual power plant delivers 16.5 MW to California grid amid calls for energy conservation". Utility Dive. 23 August 2022.
"Admin Monitor - Texas - Public Utility Commission of Texas".
Colthorpe, Andy (8 September 2022). "California's fleet of battery storage working to avert energy crisis". Energy Storage News.
Lambert, Fred (2022-09-02). "Tesla virtual power plant is rocketing up, reaches 50 MW". Electrek. Retrieved 2022-09-08.
"Tesla's Virtual Power Plant Tracker". Lastbulb. Retrieved 2022-09-08.
"The Combined Power Plant: the first stage in providing 100% power from renewable energy". SolarServer. January 2008. Retrieved 2008-10-10.
"Bijlage persbericht 010/MK – Verleende subsidies – 3. Methaanbrandstoffen op Ameland" [Press release 010/MK appendix – Granted subsidies – 3. Methane fuels on Ameland] (PDF). Wadden Fund (Press release) (in Dutch). 2013. Archived from the original (PDF) on 1 November 2013. Retrieved 21 November 2017.
BBC Radio 4. Costing the Earth- Electric Island
"Next Kraftwerk Reimagines & Redefines The Electrical Grid With Virtual Power Plants". Clean Technica. October 2016. Retrieved 2019-03-13.
"Electricity network plan to launch London's first virtual power station". UK Power Networks. 22 June 2018. Retrieved 15 October 2021.
"London pioneers first 'virtual power station'". GOV.UK. 6 March 2020. Retrieved 1 July 2021.
Grundy, Alice (27 March 2020). "Smart Metering Systems reveals Solo Energy acquisition as it enters VPP market". Current News. Retrieved 1 July 2021.
Lempriere, Molly (27 October 2020). "Tesla Energy Plan launched inviting homes to become part of Virtual Power Plant". Current News. Retrieved 1 July 2021.
"Social housing added to the Tesla virtual power plant - ARENAWIRE". Australian Renewable Energy Agency. Retrieved 2021-01-06.
External links
|
|---|
| Concepts | | |
|---|
| Sources | |
|---|
| Generation | |
|---|
| |
|---|
| Failure modes | |
|---|
Protective
devices | |
|---|
Economics
and policies | |
|---|
Statistics and
production | |
|---|
|
https://en.wikipedia.org/wiki/Virtual_power_plant
lectrical busbar systems[1] (sometimes simply referred to as busbar systems) are a modular approach to electrical wiring,
where instead of a standard cable wiring to every single electrical
device, the electrical devices are mounted onto an adapter which is
directly fitted to a current carrying busbar. This modular approach is used in distribution boards, automation panels and other kinds of installation in an electrical enclosure.[2]
Busbar systems are subject to safety standards for design and installation along with electrical enclosure according to IEC 61439-1 and vary between countries and regions.[3]
https://en.wikipedia.org/wiki/Electrical_busbar_system
A black start is the process of restoring an electric power station or a part of an electric grid to operation without relying on the external electric power transmission network to recover from a total or partial shutdown.[1]
Power to restart a generating station may come from an on-site
standby generator. Alternatively, where a large amount of power is
required, a tie-line to another generating plant may be used to start
the facility. Once the main generating units are running, the electrical
transmission network can be re-connected and electrical loads restored.
Black-start power may be ensured by an agreement where a
particular energy supplier is paid to make black start power available
when required. Not all generating plants are suitable for providing
black-start power to a network.
https://en.wikipedia.org/wiki/Black_start
A rolling blackout, also referred to as rota or rotational load shedding, rota disconnection, feeder rotation, or a rotating outage, is an intentionally engineered electrical power shutdown in which electricity delivery
is stopped for non-overlapping periods of time over different parts of
the distribution region. Rolling blackouts are a last-resort measure
used by an electric utility company to avoid a total blackout of the power system.
Rolling blackouts are a measure of demand response
if the demand for electricity exceeds the power supply capability of
the network. Rolling blackouts may be localised to a specific part of
the electricity network, or they may be more widespread and affect
entire countries and continents. Rolling blackouts generally result from
two causes: insufficient generation capacity or inadequate transmission infrastructure to deliver power to where it is needed.
Rolling blackouts are also used as a response strategy to cope with reduced output beyond reserve capacity from power stations taken offline unexpectedly.
https://en.wikipedia.org/wiki/Rolling_blackout
A cascading failure is a failure in a system of interconnected parts in which the failure of one or few parts leads to the failure of other parts, growing progressively as a result of positive feedback. This can occur when a single part fails, increasing the probability that other portions of the system fail.[1][2]
Such a failure may happen in many types of systems, including power
transmission, computer networking, finance, transportation systems,
organisms, the human body, and ecosystems.
Cascading failures may occur when one part of the system fails.
When this happens, other parts must then compensate for the failed
component. This in turn overloads these nodes, causing them to fail as
well, prompting additional nodes to fail one after another.
https://en.wikipedia.org/wiki/Cascading_failure
A single point of failure (SPOF) is a part of a system that, if it fails, will stop the entire system from working.[1] SPOFs are undesirable in any system with a goal of high availability or reliability, be it a business practice, software application, or other industrial system.
Overview
Systems can be made robust by adding redundancy in all potential SPOFs. Redundancy can be achieved at various levels.
The assessment of a potential SPOF involves identifying the
critical components of a complex system that would provoke a total
systems failure in case of malfunction. Highly reliable systems should not rely on any such individual component.
For instance, the owner of a small tree care company may only own one woodchipper.
If the chipper breaks, he may be unable to complete his current job and
may have to cancel future jobs until he can obtain a replacement. The
owner of the tree care company may have spare parts
ready for the repair of the wood chipper, in case it fails. At a higher
level, he may have a second wood chipper that he can bring to the job
site. Finally, at the highest level, he may have enough equipment
available to completely replace everything at the work site in the case
of multiple failures.
Possible SPOFs in a simple setup
Using redundancy to avoid some SPOFs
Completely redundant system without SPOFs (note: assumes generator
and grid sources are each rated at N, each UPS is rated at N, and "A/C"
and "Electrical" are in themselves completely fault tolerant systems)
Computing
| This section needs to be updated. The reason given is: Needs updating for public cloud computing. Please help update this article to reflect recent events or newly available information. (May 2022) |
A fault-tolerant computer system can be achieved at the internal component level, at the system level (multiple machines), or site level (replication).
One would normally deploy a load balancer to ensure high availability for a server cluster
at the system level. In a high-availability server cluster, each
individual server may attain internal component redundancy by having
multiple power supplies, hard drives, and other components. System-level
redundancy could be obtained by having spare servers waiting to take on
the work of another server if it fails.
Since a data center is often a support center for other
operations such as business logic, it represents a potential SPOF in
itself. Thus, at the site level, the entire cluster may be replicated at
another location, where it can be accessed in case the primary location
becomes unavailable. This is typically addressed as part of an IT
disaster recovery (resiliency) program.
Paul Baran and Donald Davies developed packet switching, a key part of "survivable communications networks". Such networks – including ARPANET and the Internet –
are designed to have no single point of failure. Multiple paths
between any two points on the network allow those points to continue
communicating with each other, the packets "routing around" damage, even after any single failure of any one particular path or any one intermediate node.
Software engineering
In software engineering, a bottleneck occurs when the capacity of an application
or a computer system is limited by a single component. The bottleneck
has lowest throughput of all parts of the transaction path.
Performance engineering
Tracking down bottlenecks (sometimes known as hot spots – sections of the code that execute most frequently – i.e., have the highest execution count) is called performance analysis.
Reduction is usually achieved with the help of specialized tools, known
as performance analyzers or profilers. The objective is to make those
particular sections of code perform as fast as possible to improve
overall algorithmic efficiency.
Computer security
A vulnerability or security exploit in just one component can compromise an entire system.
Other fields
The
concept of a single point of failure has also been applied to fields
outside of engineering, computers, and networking, such as corporate supply chain management[2] and transportation management.[3]
Design structures that create single points of failure include bottlenecks and series circuits (in contrast to parallel circuits).
In transportation, some noted recent examples of the concept's recent application have included the Nipigon River Bridge in Canada, where a partial bridge failure in January 2016 entirely severed road traffic between Eastern Canada and Western Canada for several days because it is located along a portion of the Trans-Canada Highway where there is no alternate detour route for vehicles to take;[4] and the Norwalk River Railroad Bridge in Norwalk, Connecticut, an aging swing bridge that sometimes gets stuck when opening or closing, disrupting rail traffic on the Northeast Corridor line.[3]
The concept of a single point of failure has also been applied to the fields of intelligence. Edward Snowden talked of the dangers of being what he described as "the single point of failure" – the sole repository of information.[5]
Life-support systems
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion. You can help by adding to it. (October 2019) |
A component of a life-support system that would constitute a single point of failure would be required to be extremely reliable.
See also
Concepts
Applications
- Kill switch – Safety mechanism to quickly shut down a system
- Jesus nut – Slang term for the main rotor-retaining nut of some helicopters
- Reliability engineering – Sub-discipline of systems engineering that emphasizes dependability
- Safety engineering – Engineering discipline which assures that engineered systems provide acceptable levels of safety
- Dead man's switch – Equipment that activates or deactivates upon the incapacitation of operator
In literature
- Achilles' heel – Critical weakness which can lead to downfall in spite of overall strength
- Hamartia – Protagonist's error in Greek dramatic theory
References
1:
Designing Large-scale LANs – Page 31, K. Dooley, O'Reilly, 2002
Gary S. Lynch (Oct 7, 2009). Single Point of Failure: The 10 Essential Laws of Supply Chain Risk Management. Wiley. ISBN 978-0-470-42496-4.
"Crucial, Century-Old, And Sometimes Stuck: Connecticut Bridge Is Key To Northeast Corridor". Connecticut Public Radio, August 8, 2017.
"The Nipigon River Bridge and other Trans-Canada bottlenecks". Global News, January 11, 2016.
https://en.wikipedia.org/wiki/Single_point_of_failure
https://en.wikipedia.org/wiki/Floppy_disk
https://en.wikipedia.org/wiki/Thin-film_memory
https://en.wikipedia.org/wiki/Non-volatile_memory
https://en.wikipedia.org/wiki/Magnetoresistive_RAM
https://en.wikipedia.org/wiki/Gamma_Pegasi
https://en.wikipedia.org/wiki/Thermocouple
https://en.wikipedia.org/wiki/Bubble_memory
https://en.wikipedia.org/wiki/CMC_Magnetics
https://en.wikipedia.org/wiki/Physics_of_magnetic_resonance_imaging
https://en.wikipedia.org/wiki/Drum_memory
https://en.wikipedia.org/wiki/Magnetic-tape_data_storage
https://en.wikipedia.org/wiki/Magnetic-core_memory
https://en.wikipedia.org/wiki/Hard_disk_drive
https://en.wikipedia.org/wiki/Curl_(mathematics)
Data degradation is the gradual corruption of computer data due to an accumulation of non-critical failures in a data storage device. The phenomenon is also known as data decay, data rot or bit rot.
https://en.wikipedia.org/wiki/Data_degradation
https://en.wikipedia.org/wiki/Mini-Cassette
https://en.wikipedia.org/wiki/Semiconductor_memory
https://en.wikipedia.org/wiki/Digital_dark_age
https://en.wikipedia.org/wiki/Linear_Tape-Open
https://en.wikipedia.org/wiki/List_of_The_Muppet_Show_episodes
https://en.wikipedia.org/wiki/Parafilm
https://en.wikipedia.org/wiki/Domino_Recording_Company
https://en.wikipedia.org/wiki/Motor_capacitor
https://en.wikipedia.org/wiki/Starlight
https://en.wikipedia.org/wiki/Non-volatile_random-access_memory
https://en.wikipedia.org/wiki/Eddy-current_testing
https://en.wikipedia.org/wiki/List_of_Ghost_Adventures_episodes
https://en.wikipedia.org/wiki/Stephin_Merritt_discography
https://en.wikipedia.org/wiki/Core_rope_memory
https://en.wikipedia.org/wiki/Pyramid_power
https://en.wikipedia.org/wiki/Data_storage
https://en.wikipedia.org/wiki/Random-access_memory
https://en.wikipedia.org/wiki/Computer_memory
https://en.wikipedia.org/w/index.php?limit=20&offset=20&profile=default&search=magnetic+rot&title=Special:Search&ns0=1&searchToken=cems966l2d75df9ijilqv36hq
Magnetic inductance
Circuit equivalence between a magnetic inductance and an electric capacitance.
In the context of the gyrator-capacitor model of a magnetic circuit, magnetic inductance  (SI unit: F) is the analogy to inductance in an electrical circuit.
(SI unit: F) is the analogy to inductance in an electrical circuit.
For phasor analysis the magnetic inductive reactance is:
where:
In the complex form it is a positive imaginary number:
The magnetic potential energy sustained by magnetic inductance
varies with the frequency of oscillations in electric fields. The
average power in a given period is equal to zero. Due to its dependence
on frequency, magnetic inductance is mainly observable in magnetic
circuits which operate at VHF and/or UHF frequencies.[citation needed]
The notion of magnetic inductance is employed in analysis and
computation of circuit behavior in the gyrator–capacitor model in a way
analogous to inductance in electrical circuits.
A magnetic inductor can represent an electrical capacitor.[4]: 43
A shunt capacitance in the electrical circuit, such as intra-winding
capacitance can be represented as a series inductance in the magnetic
circuit.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
The gyrator–capacitor model[1] - sometimes also the capacitor-permeance model[2] - is a lumped-element model for magnetic circuits, that can be used in place of the more common resistance–reluctance model. The model makes permeance elements analogous to electrical capacitance (see magnetic capacitance section) rather than electrical resistance (see magnetic reluctance). Windings are represented as gyrators, interfacing between the electrical circuit and the magnetic model.
The primary advantage of the gyrator–capacitor model compared to
the magnetic reluctance model is that the model preserves the correct
values of energy flow, storage and dissipation.[3][4] The gyrator–capacitor model is an example of a group of analogies
that preserve energy flow across energy domains by making power
conjugate pairs of variables in the various domains analogous. It fills
the same role as the impedance analogy for the mechanical domain.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
Category:Magnetic circuits
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Magnetic_circuits
Category:Electrical analogies
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Electrical_analogies
Magnetic induction
From Wikipedia, the free encyclopedia
Magnetic induction may refer to:
Category:
https://en.wikipedia.org/wiki/Magnetic_induction
https://en.wikipedia.org/wiki/Synchronization_(alternating_current)
https://en.wikipedia.org/wiki/Category:AC_power
https://en.wikipedia.org/wiki/Category:Three-phase_AC_power
https://en.wikipedia.org/wiki/Symmetrical_components
https://en.wikipedia.org/wiki/Linearly_independent
https://en.wikipedia.org/wiki/Root_mean_square#Voltage
https://en.wikipedia.org/wiki/Droop_speed_control
https://en.wikipedia.org/wiki/Beat_(acoustics)
https://en.wikipedia.org/wiki/Interference_(wave_propagation)
In AC electrical power systems, a synchroscope is a device that indicates the degree to which two systems (generators or power networks) are synchronized with each other.[1]
For two electrical systems to be synchronized, both systems must operate at the same frequency, and the phase angle between the systems must be zero (and two polyphase systems must have the same phase sequence).
Synchroscopes measure and display the frequency difference and phase
angle between two power systems. Only when these two quantities are zero
is it safe to connect the two systems together. Connecting two
unsynchronized AC power systems together is likely to cause high
currents to flow, which will severely damage any equipment not protected
by fuses or circuit breakers.

This synchroscope was used to synchronize a factory's power plant with the utility's power grid.
https://en.wikipedia.org/wiki/Synchroscope
https://en.wikipedia.org/wiki/Three-phase_electric_power#Phase_sequence
https://en.wikipedia.org/wiki/Relay
https://en.wikipedia.org/wiki/Circuit_breaker
https://en.wikipedia.org/wiki/Deformed_power
https://en.wikipedia.org/wiki/Leading_and_lagging_current
A rotary phase converter, abbreviated RPC, is an electrical machine that converts power from one polyphase system to another, converting through rotary motion. Typically, single-phase electric power is used to produce three-phase electric power locally to run three-phase loads in premises where only single-phase is available.

A simple homemade phase converter
https://en.wikipedia.org/wiki/Rotary_phase_converter
In communication theory, time-varying phasors are used for analyzing narrow-band signals, whose signal bandwidths in the frequency domain are considerably smaller than the carrier frequency.[1][2] Time-varying phasors are mostly used for analysis of frequency domain of band-pass systems.[2][1] The method uses classical impulse response.[1]
In electrical power system, phasors are used for transient analysis of the power system keeping the quasi-stationary conditions.[1][3][4] They were introduced to facilitate the computation and analysis of power systems in stationary operation.[3] Time-varying phasors are used in dynamic analysis of a large power system.[1][5] The phasor representation of sinusoidal voltages and currents is generalized to arbitrary waveforms.[2] This mathematical transformation eliminates the 60 Hertz (Hz) carrier which is the only time-varying element in the stationary case.[3]
The longer usage of time-varying phasors in large power systems since
1920s have created many misconceptions. One of the misuses suggest that quasi-stationary
models are always accurate, but only when the system dynamics are slow
as compared to nominal system frequency which is usually 60 Hz.[4]
The concern to study time-varying phasors is raised to understand
in-depth the fast amplitude and phase variations of emerging electrical
power generator technologies.[4] This is because current and voltage signals of latest machines may have harmonic components and they can damage the entire transmission system which is coupled with the machine.[3][4]
However, if we employ quasi-static model, we can accurately model AC
signals by using time-varying phasors as opposed to traditional
quasi-static model which supports constant voltage and current signals
throughout the network.[5]
https://en.wikipedia.org/wiki/Time-varying_phasor
Single-phase generator (also known as single-phase alternator) is an alternating current electrical generator that produces a single, continuously alternating voltage. Single-phase generators can be used to generate power in single-phase electric power systems. However, polyphase generators are generally used to deliver power in three-phase distribution
system and the current is converted to single-phase near the
single-phase loads instead. Therefore, single-phase generators are found
in applications that are most often used when the loads being driven
are relatively light,[1] and not connected to a three-phase distribution, for instance, portable engine-generators. Larger single-phase generators are also used in special applications such as single-phase traction power for railway electrification systems.[2]

Elementary generator is an example of single-phase generators with two poles
https://en.wikipedia.org/wiki/Single-phase_generator
Polyphase coils are electromagnetic coils connected together in a polyphase system such as a generator or motor. In modern systems, the number of phases is usually three or a multiple of three. Each phase carries a sinusoidal alternating current whose phase
is delayed relative to one of its neighbours and advanced relative to
its other neighbour. The phase currents are separated in time evenly
within each period of the alternating current. For example, in a
three-phase system, the phases are separated from each other by
one-third of the period.
Coil construction
Like all coils used in electrical machinery, polyphase coils (made from insulated conducting wire) are wound around ferromagnetic armatures with radial projections and maximum core-surface exposure to the magnetic field.
The windings are physically separated around the circumference of an electrical machine. The result of such an arrangement is a rotating magnetic field that is used to convert electrical power to rotary mechanical work, or vice versa.
https://en.wikipedia.org/wiki/Polyphase_coil
https://en.wikipedia.org/wiki/Category:AC_power
A Scott-T transformer (also called a Scott connection) is a type of circuit used to produce two-phase electric power (2 φ, 90 degree phase rotation)[1] from a three-phase
(3 φ, 120 degree phase rotation) source, or vice versa. The Scott
connection evenly distributes a balanced load between the phases of the
source. The Scott three-phase transformer was invented by a Westinghouse engineer Charles F. Scott in the late 1890s to bypass Thomas Edison's more expensive rotary converter and thereby permit two-phase generator plants to drive three-phase motors.[2]
https://en.wikipedia.org/wiki/Scott-T_transformer
History
The first locomotive with a phase converter (only for demonstration purposes)
The Kandó phase converter (1933)
The "Kandó" locomotive, the first locomotive using a phase converter system
At the beginning of the 20th century, there were two main principles of electric railway traction current systems:
- DC system
- 16⅔ Hz single phase system
These systems used series-wound traction motors. All of them needed a separated supply system or converters to take power from the standard 50 Hz electric network.
https://en.wikipedia.org/wiki/Rotary_phase_converter
Unbalanced loads
Two-phase
motors draw constant power, just as three-phase motors do, so a
balanced two-phase load is converted to a balanced three-phase load.
However if a two-phase load is not balanced (more power drawn from one
phase than the other), no arrangement of transformers (including the
Scott-T transformers) can restore balance: Unbalanced current on the
two-phase side causes unbalanced current on the three-phase side. Since
the typical two-phase load was a motor, the current in the two phases
was presumed inherently equal during the Scott-T development.
In modern times people have tried to revive the Scott connection as a way to power single-phase electric railways
from three-phase Utility supplies. This will not result in balanced
current on the three-phase of being equal. The instantaneous
difference in loading on the two sections will be seen as an imbalance
in the three-phase supply; there is no way to smooth it out with
transformers.[4]
https://en.wikipedia.org/wiki/Scott-T_transformer
Back to back arrangement
Scott Connection 3 φ to 3 φ
The Scott-T transformer connection may also be used in a back-to-back
T-to-T arrangement for a three-phase to three-phase connection. This is
a cost-saving in the lower-power transformers due to the two-coil T
connected to a secondary two-coil T instead of the traditional
three-coil primary to three-coil secondary transformer. In this
arrangement the X0 neutral tap is part way up on the secondary teaser
transformer (see right). The voltage stability of this T-to-T
arrangement as compared to the traditional three-coil primary to
three-coil secondary transformer is questioned, as the "per unit"
impedance of the two windings (primary and secondary, respectively) are not the same in a T-to-T configuration, whereas the three windings (primary and secondary, respectively) are the same in a three transformer configuration, if the three transformers are identical.
Three-phase to three-phase (also called "T-connected")
distribution transformers are seeing increasing applications. The
primary must be delta-connected (Δ), but the secondary may be either delta or "wye"-connected (Y),
at the customer's option, with X0 providing the neutral for the "wye"
case. Taps for either case are usually provided. The customary maximum
capacity of such a distribution transformer is 333 kVA (a third of a
megawatt at unity power factor).[citation needed]
https://en.wikipedia.org/wiki/Scott-T_transformer
An induction regulator is an alternating current electrical machine, somewhat similar to an induction motor, which can provide a continuously variable output voltage.
The induction regulator was an early device used to control the voltage
of electric networks. Since the 1930s it has been replaced in
distribution network applications by the tap transformer. Its usage is now mostly confined to electrical laboratories, electrochemical processes and arc welding. With minor variations, its setup can be used as a phase-shifting power transformer.
https://en.wikipedia.org/wiki/Induction_regulator
Magnet wire or enameled wire is a copper (Cu) or aluminium (Al) wire coated with a very thin layer of insulation. It is used in the construction of transformers, inductors, motors, generators,
speakers, hard disk head actuators, electromagnets, electric guitar pickups and other applications that require tight coils of insulated wire.
The wire itself is most often fully annealed,
electrolytically refined copper. Aluminium magnet wire is sometimes
used for large transformers and motors. The insulation is typically made
of tough polymer film materials rather than vitreous enamel, as the name might suggest.
https://en.wikipedia.org/wiki/Magnet_wire
In electronics, a center tap (CT) is a contact made to a point halfway along a winding of a transformer or inductor, or along the element of a resistor or a potentiometer.
Taps are sometimes used on inductors for the coupling of signals,
and may not necessarily be at the half-way point, but rather, closer to
one end. A common application of this is in the Hartley oscillator. Inductors with taps also permit the transformation of the amplitude of alternating current (AC) voltages for the purpose of power conversion, in which case, they are referred to as autotransformers, since there is only one winding. An example of an autotransformer is an automobile ignition coil.
Potentiometer tapping provides one or more connections along the
device's element, along with the usual connections at each of the two
ends of the element, and the slider connection. Potentiometer taps allow
for circuit functions that would otherwise not be available with the
usual construction of just the two end connections and one slider
connection.
https://en.wikipedia.org/wiki/Center_tap
A relief valve or pressure relief valve (PRV) is a type of safety valve used to control or limit the pressure
in a system; excessive pressure might otherwise build up and create a
process upset, instrument or equipment failure, explosion, or fire.
https://en.wikipedia.org/wiki/Relief_valve
The open-circuit test, or no-load test, is one of the methods used in electrical engineering to determine the no-load impedance in the excitation branch of a transformer.
The no load is represented by the open circuit, which is represented on
the right side of the figure as the "hole" or incomplete part of the
circuit.
https://en.wikipedia.org/wiki/Open-circuit_test
Electrical insulation papers are paper types that are used as electrical insulation in many applications due to pure cellulose having outstanding electrical properties. Cellulose is a good insulator and is also polar,[clarification needed] having a dielectric constant significantly greater than one.[1]
Electrical paper products are classified by their thickness, with tissue
considered papers less than 1.5 mils (0.0381 mm) thickness, and board considered more than 20 mils (0.508 mm) thickness.[2]
https://en.wikipedia.org/wiki/Electrical_insulation_paper
A balun (from "balanced to unbalanced", originally, but now dated from "balancing unit")[1] is an electrical device that allows balanced and unbalanced lines to be interfaced without disturbing the impedance arrangement of either line.[2] A balun can take many forms and may include devices that also transform impedances but need not do so. Sometimes, in the case of transformer baluns, they use magnetic coupling but need not do so. Common-mode chokes are also used as baluns and work by eliminating, rather than rejecting, common mode signals.
https://en.wikipedia.org/wiki/Balun
In electrical engineering, the method of symmetrical components simplifies analysis of unbalanced three-phase power systems under both normal and abnormal conditions. The basic idea is that an asymmetrical set of N phasors can be expressed as a linear combination of N symmetrical sets of phasors by means of a complex linear transformation.[1] Fortescue's theorem (symmetrical components) is based on superposition principle,[2] so it is applicable to linear power systems only, or to linear approximations of non-linear power systems.
In the most common case of three-phase systems, the resulting "symmetrical" components are referred to as direct (or positive), inverse (or negative) and zero (or homopolar).
The analysis of power system is much simpler in the domain of
symmetrical components, because the resulting equations are mutually linearly independent if the circuit itself is balanced.[citation needed]
https://en.wikipedia.org/wiki/Symmetrical_components
A solid-state transformer (SST), power electronic transformer (PET), or electronic power transformer is actually an AC-to-AC converter, a type of electric power converter that replaces a conventional transformer used in AC electric power distribution. It is more complex than a conventional transformer operating at utility frequency,
but it can be smaller and more efficient than a conventional
transformer because it operates at high frequency. The main types are
"true" AC-to-AC converter (with no DC stages) and AC-to-DC-to-DC-to-AC
converter (in which an active rectifier supplies power to a DC-to-DC converter, which supplies power to a power inverter).
A solid-state transformer usually contains a transformer, inside the
AC-to-AC converter or DC-to-DC converter, which provides electrical
isolation and carries the full power. This transformer is smaller due to
smaller DC-DC inverting stages between transformer coils, which
consequently mean smaller transformer coils required to step up or step
down voltages. A solid-state transformer can actively regulate voltage
and current. Some can convert single-phase power to three-phase power
and vice versa. Variations can input or output DC power to reduce the number of conversions, for greater end-to-end efficiency. A Modular Solid-state transformer consists of several high-frequency transformers[1] and is similar to a Multi-level converter.
As a complex electronic circuit, it must be designed to withstand
lightning and other surges. Solid-state transformer is an emerging
technology.
https://en.wikipedia.org/wiki/Solid-state_transformer
A grounding transformer or earthing transformer is a type of auxiliary transformer used in three-phase electric power systems to provide a ground path to either an ungrounded wye or a delta-connected system.[1][2] Grounding transformers are part of an earthing system of the network. They let three-phase (delta connected) systems accommodate phase-to-neutral loads by providing a return path for current to a neutral.
Grounding transformers are typically used to:
- Provide a relatively low-impedance path to ground, thereby maintaining the system neutral at or near ground potential.[3]
- Limit the magnitude of transient overvoltages when restriking ground faults occur.
- Provide a source of ground fault current during line-to-ground faults.
- Permit the connection of phase-to-neutral loads when desired.[2]
Earthing transformer with a zig-zag
Grounding transformers most commonly incorporate a single winding transformer with a zigzag winding configuration, but may also be created with a wye-delta winding transformer.[2][4] Neutral grounding transformers are very common on generators in power plants and wind farms.[2]
Neutral grounding transformers are sometimes applied on high-voltage
(sub-transmission) systems, such as at 33 kV, where the circuit would
otherwise not have a ground; for example, if a system is fed by a
delta-connected transformer. The grounding point of the transformer may
be connected through a resistor or arc suppression coil to limit the
fault current on the system in the event of a line-to-ground fault. [5]
https://en.wikipedia.org/wiki/Grounding_transformer
An autotransformer is an electrical transformer with only one winding. The "auto" (Greek for "self") prefix refers to the single coil acting alone, not to any kind of automatic mechanism. In an autotransformer, portions of the same winding act as both the primary winding and secondary winding
sides of the transformer. In contrast, an ordinary transformer has
separate primary and secondary windings which have no metallic
conducting path between them.
The autotransformer winding has at least three taps
where electrical connections are made. Since part of the winding does
"double duty", autotransformers have the advantages of often being
smaller, lighter, and cheaper than typical dual-winding transformers,
but the disadvantage of not providing electrical isolation between primary and secondary circuits. Other advantages of autotransformers include lower leakage reactance, lower losses, lower excitation current, and increased VA rating for a given size and mass.[1]
An example of an application of an autotransformer is one style
of traveler's voltage converter, that allows 230-volt devices to be used
on 120-volt supply circuits, or the reverse. An autotransformer with
multiple taps may be applied to adjust the voltage at the end of a long
distribution circuit to correct for excess voltage drop; when
automatically controlled, this is one example of a voltage regulator.

Single-phase tapped autotransformer with an output voltage range of 40%–115% of input
https://en.wikipedia.org/wiki/Autotransformer
See also
https://en.wikipedia.org/wiki/Autotransformer
A zigzag transformer is a special-purpose transformer with a zigzag or "interconnected star" winding connection, such that each output is the vector sum of two (2) phases offset by 120°.[1] It is used as a grounding transformer, creating a missing neutral connection from an ungrounded 3-phase system to permit the grounding of that neutral to an earth reference point; to perform harmonic mitigation, as they can suppress triplet (3rd, 9th, 15th, 21st, etc.) harmonic currents;[2] to supply 3-phase power as an autotransformer (serving as the primary and secondary with no isolated circuits);[3] and to supply non-standard, phase-shifted, 3-phase power.[1]
9-winding zigzag transformer
Nine-winding, three-phase transformers typically have three primaries
and six identical secondary windings, which can be used in zigzag
winding connection as pictured.[1] As with the conventional delta or wye winding configuration three-phase
transformer, a standard, stand-alone transformer containing only six
windings on three cores can also be used in zigzag winding connection,
such transformer sometimes being referred to as a zigzag bank.[1]
In all cases, six or nine winding, the first coil on each zigzag
winding core is connected contrariwise to the second coil on the next
core. The second coils are then all tied together to form the neutral,
and the phases are connected to the primary coils. Each phase,
therefore, couples with each other phase, and the voltages cancel out.
As such, there would be negligible current through the neutral point,
which can be tied to ground.[4]
Each of the three "limbs" are split into two sections. The two
halves of each limb have an equal number of turns and are wound in
opposite directions. With the neutral grounded, during a phase-to-ground
short fault, a third of the current returns to the fault current, and
the remainder must go through two of the three phases when used to
derive a grounding point from a delta source.[5]
If one or more phases fault to earth, the voltage applied to each
phase of the transformer is no longer in balance; fluxes in the
windings no longer oppose. (Using symmetrical components, this is Ia0 = Ib0 = Ic0.)
Zero-sequence (earth fault) current exists between the transformer’s
neutral to the faulting phase. The purpose of a zigzag transformer in
this application is to provide a return path for earth faults on
delta-connected systems. With negligible current in the neutral under
normal conditions, an undersized (unable to carry a continuous fault
load) transformer may be used only as short-time rating is required,
provided the defective load will be automatically disconnected in a
fault condition. The transformer's impedance should not be too low for
desired maximum fault current. Impedance can be added after the
secondaries are summed to limit maximum fault currents (the 3Io path).[6]
A combination of Y (wye or star), delta, and zigzag windings may be used to achieve a vector phase shift.
For example, an electrical network may have a transmission network of
110 kV/33 kV star/star transformers, with 33 kV/11 kV delta/star for the
high voltage distribution network. If a transformation is required
directly between the 110 kV/11 kV network an option is to use a 110
kV/11 kV star/delta transformer. The problem is that the 11 kV delta no
longer has an earth reference point. Installing a zigzag transformer
near the secondary side of the 110 kV/11 kV transformer provides the
required earth reference point.[7]
https://en.wikipedia.org/wiki/Zigzag_transformer
Railway electrification systems using alternating current (AC) at 25 kilovolts (kV) are used worldwide, especially for high-speed rail. It is usually supplied at the standard utility frequency (typically 50 or 60 Hz), which simplifies traction substations. The development of 25 kV AC electrification is closely connected with that of successfully using utility frequency.
This electrification is ideal for railways that cover long distances or carry heavy traffic. After some experimentation before World War II in Hungary and in the Black Forest in Germany, it came into widespread use in the 1950s.
One of the reasons why it was not introduced earlier was the lack
of suitable small and lightweight control and rectification equipment
before the development of solid-state rectifiers
and related technology. Another reason was the increased clearance
distances required where it ran under bridges and in tunnels, which
would have required major civil engineering in order to provide the increased clearance to live parts.
Railways using older, lower-capacity direct current systems have introduced or are introducing 25 kV AC instead of 3 kV DC/1.5 kV DC for their new high-speed lines.
https://en.wikipedia.org/wiki/25_kV_AC_railway_electrification
In electronics, impedance matching is the practice of designing or adjusting the input impedance or output impedance of an electrical device for a desired value. Often, the desired value is selected to maximize power transfer or minimize signal reflection.
For example, impedance matching typically is used to improve power
transfer from a radio transmitter via the interconnecting transmission
line to the antenna. Signals on a transmission line will be transmitted without reflections if the transmission line is terminated with a matching impedance.
Techniques of impedance matching include transformers, adjustable networks of lumped resistance, capacitance and inductance,
or properly proportioned transmission lines. Practical
impedance-matching devices will generally provide best results over a
specified frequency band.
The concept of impedance matching is widespread in electrical engineering, but is relevant in other applications in which a form of energy, not necessarily electrical, is transferred between a source and a load, such as in acoustics or optics.

Source and
load impedance circuit
https://en.wikipedia.org/wiki/Impedance_matching
In electronics, electrical termination is the practice of ending a transmission line with a device that matches the characteristic impedance of the line. Termination prevents signals from reflecting off the end of the transmission line. Reflections at the ends of unterminated transmission lines cause distortion, which can produce ambiguous digital signal levels and misoperation of digital systems. Reflections in analog signal systems cause such effects as video ghosting, or power loss in radio transmitter transmission lines.
https://en.wikipedia.org/wiki/Electrical_termination
In telecommunications, signal reflection occurs when a signal is transmitted along a transmission medium, such as a copper cable or an optical fiber.
Some of the signal power may be reflected back to its origin rather
than being carried all the way along the cable to the far end. This
happens because imperfections in the cable cause impedance
mismatches and non-linear changes in the cable characteristics. These
abrupt changes in characteristics cause some of the transmitted signal
to be reflected. In radio frequency (RF) practice this is often measured in a dimensionless ratio known as voltage standing wave ratio (VSWR) with a VSWR bridge. The ratio of energy bounced back depends on the impedance mismatch. Mathematically, it is defined using the reflection coefficient.
Because the principles are the same, this concept is perhaps
easiest to understand when considering an optical fiber. Imperfections
in the glass create mirrors that reflect the light back along the fiber.
Impedance discontinuities cause attenuation, attenuation distortion, standing waves, ringing and other effects because a portion of a transmitted signal will be reflected back to the transmitting device rather than continuing to the receiver, much like an echo.
This effect is compounded if multiple discontinuities cause additional
portions of the remaining signal to be reflected back to the
transmitter. This is a fundamental problem with the daisy chain method of connecting electronic components.
When a returning reflection strikes another discontinuity, some
of the signal rebounds in the original signal direction, creating
multiple echo effects. These forward echoes
strike the receiver at different intervals making it difficult for the
receiver to accurately detect data values on the signal. The effects can
resemble those of jitter.
Because damage to the cable can cause reflections, an instrument called an electrical time-domain reflectometer (ETDR; for electrical cables) or an optical time-domain reflectometer
(OTDR; for optical cables) can be used to locate the damaged part of a
cable. These instruments work by sending a short pulsed signal into the
cable and measuring how long the reflection takes to return. If only
reflection magnitudes are desired, however, and exact fault locations
are not required, VSWR bridges perform a similar but lesser function for
RF cables.
The combination of the effects of signal attenuation and impedance discontinuities on a communications link is called insertion loss. Proper network operation depends on constant characteristic impedance in all cables and connectors, with no impedance discontinuities in the entire cable system. When a sufficient degree of impedance matching is not practical, echo suppressors or echo cancellers, or both, can sometimes reduce the problems.
The Bergeron diagram method, valid for both linear and non-linear models, evaluates the reflection's effects in an electric line.
See also
https://en.wikipedia.org/wiki/Signal_reflection
https://en.wikipedia.org/wiki/Optics
An induction motor or asynchronous motor is an AC electric motor in which the electric current in the rotor needed to produce torque is obtained by electromagnetic induction from the magnetic field of the stator winding.[1] An induction motor can therefore be made without electrical connections to the rotor.[a] An induction motor's rotor can be either wound type or squirrel-cage type.
Three-phase squirrel-cage induction motors are widely used as industrial drives because they are self-starting, reliable, and economical. Single-phase induction motors are used extensively for smaller loads, such as garbage disposals
and stationary power tools. Although traditionally only used for
one-speed service, single- and three-phase induction motors are
increasingly being installed in variable-speed applications using variable-frequency drives (VFD). VFDs offer especially important energy savings
opportunities for existing and prospective induction motors in
applications like fans, pumps and compressors that have a variable load.
https://en.wikipedia.org/wiki/Induction_motor
In telecommunications and electrical engineering in general, an unbalanced line is a pair of conductors intended to carry electrical signals, which have unequal impedances along their lengths and to ground and other circuits. Examples of unbalanced lines are coaxial cable or the historic earth return system invented for the telegraph, but rarely used today. Unbalanced lines are to be contrasted with balanced lines, such as twin-lead or twisted pair
which use two identical conductors to maintain impedance balance
throughout the line. Balanced and unbalanced lines can be interfaced
using a device called a balun.
The chief advantage of the unbalanced line format is cost
efficiency. Multiple unbalanced lines can be provided in the same cable
with one conductor per line plus a single common return conductor,
typically the cable shielding. Likewise, multiple microstrip circuits can all use the same ground plane
for the return path. This compares well with balanced cabling which
requires two conductors for each line, nearly twice as many. Another
benefit of unbalanced lines is that they do not require more expensive,
balanced driver and receiver circuits to operate correctly.
Unbalanced lines are sometimes confused with single-ended signalling,
but these are entirely separate concepts. The former is a cabling
scheme while the latter is a signalling scheme. However, single-ended
signalling is commonly sent over unbalanced lines. Unbalanced lines are
not to be confused with single-wire transmission lines which do not use a return path at all.
General description
Any
line that has a different impedance of the return path may be
considered an unbalanced line. However, unbalanced lines usually
consist of a conductor that is considered the signal line and another
conductor that is grounded, or is ground itself. The ground conductor often takes the form of a ground plane or the screen of a cable.
The ground conductor may be, and often is, common to multiple
independent circuits. For this reason the ground conductor may be
referred to as common.
Telegraph lines
The earliest use of unbalanced transmission lines was for electric telegraph
communications. These consisted of single wires strung between poles.
The return path for the current was originally provided by a separate
conductor. Some early telegraph systems, such as Schilling's experimental needle telegraph (1832) and the Cooke & Wheatstone five-needle telegraph (1837) used by British railways required multiple code wires. Essentially, they were parallel bus
coding. In these systems the cost of the return conductor was not so
significant (one conductor in seven for Schilling's earliest needle
telegraph[1] and one conductor in six for the Cooke and Wheatstone telegraph[2])
but the number of coding conductors was progressively reduced with
improved systems. Soon only one coding wire was required with the data
being transmitted serially. Important examples of these single-wire systems were the Morse telegraph (1837) and the Cooke & Wheatstone single-needle telegraph
(1843). In such systems the cost of a return conductor was fully 50
percent of the cable costs. It was discovered that a return conductor
could be replaced with a return path through the Earth using grounding spikes. Using earth return was a significant cost saving and rapidly became the norm.
Underground telegraph cables into large buildings or between
stations often needed to carry multiple independent telegraph lines.
These cables took the form of multiple insulated conductors enclosed by a
metal screen and overall protective jacket. In such cables the screen
can be used as the return conductor. Undersea telegraph cables were
usually a single conductor protected by steel-wire armour, effectively a coaxial cable. The first transatlantic cable of this kind was completed in 1866.
Early telephone
lines (telephone invented 1876) used the same transmission line scheme
as telegraph of unbalanced single wires. However, telephone
communication started to suffer after the widespread introduction of
electrical power lines. Telephone transmission started to use balanced lines to combat this problem and the modern norm for telephone presentation is the balanced twisted pair cable.
Coaxial lines
A coaxial line
(coax) has a central signal conductor surrounded by a cylindrical
shielding conductor. The shield conductor is normally grounded. The
coaxial format was developed during World War II for use in radar.
It was originally constructed from rigid copper pipes, but the usual
form today is a flexible cable with a braided screen. The advantages of
coax are a theoretically perfect electrostatic screen
and highly predictable transmission parameters. The latter is a result
of the fixed geometry of the format which leads to a precision not
found with loose wires. Open wire systems are also affected by nearby
objects altering the field pattern around the conductor. Coax does not
suffer from this since the field is entirely contained within the cable
due to the surrounding screen.
Coaxial lines are the norm for connections between radio
transmitters and their antennae, for interconnection of electronic
equipment where high frequency or above is involved, and were formerly widely used for forming local area networks before twisted pair became popular for this purpose.
Triaxial cable
(triax) is a variant of coax with a second shield conductor surrounding
the first with a layer of insulation in between. As well as providing
additional shielding, the outer conductors can be used for other
purposes such as providing power to equipment or control signals. Triax is widely used for the connection of cameras in television studios.
Planar technologies
Microstrip parallel-coupled transmission lines. The design forms a
band-pass filterPlanar format transmission lines are flat conductors manufactured by a
number of techniques on to a substrate. They are nearly always an
unbalanced format. At the low transmission speeds of early telegraph it was only necessary to consider transmission line theory for a circuit design when the transmission was over many miles. Similarly, the audio frequencies
used by telephones are relatively low and transmission line theory only
becomes significant for distances of at least between buildings.
However, at the higher radio frequencies and microwave frequencies transmission line considerations can become important inside a device, just a matter of centimetres. At the very high data rates handled by modern computer processors, transmission line considerations can even be important inside an individual integrated circuit.
Planar technologies were developed for these kinds of small size
applications and are not very appropriate for long distance
transmissions.
- Stripline
Stripline
is a flat conductor with a ground plane both above and below the
conductor. The variant of stripline where the space between the two
ground planes is completely filled with a dielectric material is sometimes known as triplate. Stripline can be manufactured by etching the transmission line pattern on to a printed circuit board.
The bottom of this board is left completely covered in copper and
forms the bottom ground plane. A second board is clamped on top of the
first. This second board has no pattern on the bottom and plain copper
on the top to form the top ground plane. A sheet of copper foil may be
wrapped around the two boards to electrically bond the two ground planes
firmly together. On the other hand, stripline for high power
applications such as radar will more likely be made as solid metal
strips with periodic dielectric supports, essentially air dielectric.
- Microstrip
Microstrip
is similar to stripline but is open above the conductor. There is no
dielectric or ground plane above the transmission line, there is only
dielectric and a ground plane below the line. Microstrip is a popular
format, especially in domestic products, because microstrip components
can be made using the established manufacturing techniques of printed
circuit boards. Designers are thus able to mix discrete component
circuits with microstrip components. Furthermore, since the board has
to be made anyway, the microstrip components have no additional
manufacturing cost. For applications where performance is more
important than cost a ceramic substrate might be used instead of a
printed circuit. Microstrip has another small advantage over stripline;
the line widths are wider in microstrip for the same impedance
and thus manufacturing tolerances and minimum width are less critical
on high-impedance lines. A drawback of microstrip is that the mode of
transmission is not entirely transverse.
Strictly speaking, standard transmission line analysis does not apply
because other modes are present, but it can be a usable approximation.
- Integrated circuits
Connections within integrated circuits are normally planar so planar
transmission lines are a natural choice where these are needed. The
need for transmission lines is most frequently found in microwave integrated circuits
(MICs). There are a great many materials and techniques used to make
MICs, and transmission lines can be formed in any of these technologies.
Planar transmission lines are used for far more than merely
connecting components or units together. They can themselves be used as
components and units. Any transmission line format can be used in this
way, but for the planar formats it is often their primary purpose.
Typical circuit blocks implemented by transmission lines include filters, directions couplers and power splitters, and impedance matching.
At microwave frequencies discrete components need to be impractically
small and a transmission line solution is the only viable one. On the
other hand, at low frequencies such as audio applications, transmission
line devices need to be impractically large.
Power transmission
Electric power distribution is normally in the form of balanced
three-phase transmission. However, in some remote locations where a
relatively small amount of power is required, a single-wire earth return system may be used.
References
Huurdeman, p. 54
Bibliography
- Huurdeman, Anton A., The Worldwide History of Telecommunications, John Wiley & Sons, 2003 ISBN 0471205052.
- Curran, J.E.; Jeanes, R.; Sewell, H, "A Technology of Thin-Film Hybrid Microwave Circuits", IEEE Transactions on Parts, Hybrids, and Packaging, vol. 12, iss. 4, December 1976.
https://en.wikipedia.org/wiki/Unbalanced_line
A motor soft starter is a device used with AC electrical motors to temporarily reduce the load and torque in the powertrain and electric current surge of the motor during start-up. This reduces the mechanical stress on the motor and shaft, as well as the electrodynamic stresses on the attached power cables and electrical distribution network, extending the lifespan of the system.[1]: 150
It can consist of mechanical or electrical devices, or a combination of both. Mechanical soft starters include clutches and several types of couplings using a fluid, magnetic forces, or steel shot to transmit torque, similar to other forms of torque limiter. Electrical soft starters can be any control system that reduces the torque by temporarily reducing the voltage or current input, or a device that temporarily alters how the motor is connected in the electric circuit.

Compact soft starter for a 3 phase machine, 15kW/10HP
https://en.wikipedia.org/wiki/Motor_soft_starter
A torque limiter is an automatic device that protects
mechanical equipment, or its work, from damage by mechanical overload. A
torque limiter may limit the torque by slipping (as in a friction plate slip-clutch), or uncouple the load entirely (as in a shear pin). The action of a torque limiter is especially useful to limit any damage due to crash stops and jams.
Torque limiters may be packaged as a shaft coupling or as a hub for sprocket or sheave. A torque limiting device is also known as an overload clutch.
https://en.wikipedia.org/wiki/Torque_limiter
Inverter drives (VFDs)
The popularity of the Variable-frequency drive
(VFD) has increased in the last decade, especially in the home-shop
market. This is because of their relative low cost and ability to
generate three-phase output from single phase input. A VFD converts AC
power to DC and then converts it back to AC through a transistor bridge, a technology that is somewhat analogous to that of a switch-mode power supply.
As the VFD generates its AC output from the DC bus, it is possible to
power a three-phase motor from a single-phase source. Nevertheless,
commercial-grade VFDs are produced that require three-phase input, as
there are some efficiency gains to be had with such an arrangement.
A typical VFD functions by rapidly switching transistors on and
off to "chop" the voltage on the DC bus through what is known as pulse-width modulation
(PWM). Proper use of PWM will result in an AC output whose voltage and
frequency can be varied over a fairly wide range. As an induction motor's
rotational speed is proportional to input frequency, a change in the
VFD's output frequency will cause the motor to change speed. Voltage is
also changed in a way that results in the motor producing a relatively
constant torque over the useful speed range.
The output of a quality VFD is an approximation of a sine wave, with some high frequency harmonic content.
Harmonic content will elevate motor temperature and may produce some
whistling or whining noise that could be objectionable. The effects of
unwanted harmonics can be mitigated by the use of reactive output filtering,
which is incorporated into better quality VFDs. Reactive filtration
impedes the high frequency harmonic content but has little effect on the
fundamental frequency that determines motor speed. The result is an output to the motor that is closer to an ideal sine wave.
In the past, VFDs that have a capacity greater than 3 hp (2.2 kW)
were costly, thus making the rotary phase converter (RPC) an attractive
alternative. However, modern VFDs have dropped considerably in cost,
making them more affordable than comparable RPCs. Also working in the
VFD's favor is its more compact size relative to its electrical
capacity. A plus is many VFDs can produce a "soft start" effect (in
which power is gradually applied to the motor), which reduces the amount
of current that must be delivered at machine start-up.
Use of a VFD may result in motor damage if the motor is not rated
for such an application. This is primarily because most induction
motors are forced-air cooled by a fan or blower driven by the motor
itself. Operating such a motor at a lower-than-normal speed will
substantially reduce the cooling airflow, increasing the likelihood of
overheating and winding damage or failure, especially while operating at
full load. A manufacturer may void the warranty on a motor powered by a
VFD unless the motor is "inverter-rated." As VFDs are the most popular
method of powering motors in new commercial installations, most
three-phase motors sold today are, in fact, inverter-rated.
See also
https://en.wikipedia.org/wiki/Rotary_phase_converter
A shear pin is a mechanical detail designed to allow a specific
outcome to occur once a predetermined force is applied. It can either
function as a safeguard designed to break to protect other parts, or as a
conditional operator that will not allow a mechanical device to operate
until the correct force is applied.
https://en.wikipedia.org/wiki/Shear_pin
Magnetic levitation (maglev) or magnetic suspension is a method by which an object is suspended with no support other than magnetic fields. Magnetic force is used to counteract the effects of the gravitational force and any other forces.
The two primary issues involved in magnetic levitation are lifting forces: providing an upward force sufficient to counteract gravity, and stability: ensuring that the system does not spontaneously slide or flip into a configuration where the lift is neutralized.
Magnetic levitation is used for maglev trains, contactless melting, magnetic bearings, and for product display purposes.
https://en.wikipedia.org/wiki/Magnetic_levitation
In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current (such as electromagnets), permanent magnets, elementary particles (such as electrons), various molecules, and many astronomical objects (such as many planets, some moons, stars, etc).
More precisely, the term magnetic moment normally refers to a system's magnetic dipole moment, the component of the magnetic moment that can be represented by an equivalent magnetic dipole:
a magnetic north and south pole separated by a very small distance. The
magnetic dipole component is sufficient for small enough magnets or for
large enough distances. Higher-order terms (such as the magnetic quadrupole moment) may be needed in addition to the dipole moment for extended objects.
The magnetic dipole moment of an object is readily defined in
terms of the torque that the object experiences in a given magnetic
field. The same applied magnetic field creates larger torques on objects
with larger magnetic moments. The strength (and direction) of this
torque depends not only on the magnitude of the magnetic moment but also
on its orientation relative to the direction of the magnetic field. The
magnetic moment may be considered, therefore, to be a vector. The direction of the magnetic moment points from the south to north pole of the magnet (inside the magnet).
https://en.wikipedia.org/wiki/Magnetic_moment
An electric motor is an electrical machine that converts electrical energy into mechanical energy. Most electric motors operate through the interaction between the motor's magnetic field and electric current in a wire winding to generate force in the form of torque applied on the motor's shaft. An electric generator
is mechanically identical to an electric motor, but operates with a
reversed flow of power, converting mechanical energy into electrical
energy.
Electric motors can be powered by direct current (DC) sources, such as from batteries, or rectifiers, or by alternating current (AC) sources, such as a power grid, inverters or electrical generators.
Electric motors may be classified by considerations such as power
source type, construction, application and type of motion output. They
can be powered by AC or DC, be brushed or brushless, single-phase, two-phase, or three-phase, axial or radial flux, and may be air-cooled or liquid-cooled.
Standardized motors provide convenient mechanical power for
industrial use. The largest are used for ship propulsion, pipeline
compression and pumped-storage applications with output exceeding 100 megawatts.
Applications include industrial fans, blowers and pumps, machine
tools, household appliances, power tools, vehicles, and disk drives.
Small motors may be found in electric watches. In certain applications,
such as in regenerative braking with traction motors, electric motors can be used in reverse as generators to recover energy that might otherwise be lost as heat and friction.
Electric motors produce linear or rotary force (torque)
intended to propel some external mechanism, such as a fan or an
elevator. An electric motor is generally designed for continuous
rotation, or for linear movement over a significant distance compared to
its size. Magnetic solenoids are also transducers that convert electrical power to mechanical motion, but can produce motion over only a limited distance.
https://en.wikipedia.org/wiki/Electric_motor
In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
https://en.wikipedia.org/wiki/Dynamo_theory
Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circular birefringence and circular dichroism are the manifestations of optical activity. Optical activity occurs only in chiral materials, those lacking microscopic mirror symmetry. Unlike other sources of birefringence which alter a beam's state of polarization, optical activity can be observed in fluids. This can include gases or solutions of chiral molecules such as sugars, molecules with helical secondary structure such as some proteins, and also chiral liquid crystals. It can also be observed in chiral solids such as certain crystals with a rotation between adjacent crystal planes (such as quartz) or metamaterials.
When looking at the source of light, the rotation of the plane of polarization may be either to the right (dextrorotatory or dextrorotary — d-rotary, represented by (+), clockwise), or to the left (levorotatory or levorotary — l-rotary, represented by (−), counter-clockwise) depending on which stereoisomer is dominant. For instance, sucrose and camphor are d-rotary whereas cholesterol is l-rotary.
For a given substance, the angle by which the polarization of light of a
specified wavelength is rotated is proportional to the path length
through the material and (for a solution) proportional to its
concentration.
Optical activity is measured using a polarized source and polarimeter. This is a tool particularly used in the sugar industry to measure the sugar concentration of syrup, and generally in chemistry to measure the concentration or enantiomeric ratio of chiral molecules in solution. Modulation of a liquid crystal's optical activity, viewed between two sheet polarizers, is the principle of operation of liquid-crystal displays (used in most modern televisions and computer monitors).
Forms
Dextrorotation and laevorotation (also spelled levorotation)[1][2][3] are terms used in chemistry and physics to describe the optical rotation of plane-polarized light. From the point of view of the observer, dextrorotation refers to clockwise or right-handed rotation, and laevorotation refers to counterclockwise or left-handed rotation.[4][5]
A chemical compound that causes dextrorotation is called dextrorotatory or dextrorotary, while a compound that causes laevorotation is called laevorotatory or laevorotary.[6] Compounds with these properties consist of chiral molecules and are said to have optical activity. If a chiral molecule is dextrorotary, its enantiomer
(geometric mirror image) will be laevorotary, and vice versa.
Enantiomers rotate plane-polarized light the same number of degrees, but
in opposite directions.
Chirality prefixes
A compound may be labeled as dextrorotary by using the "(+)-" or "d-" prefix. Likewise, a laevorotary compound may be labeled using the "(−)-" or "l-" prefix. The lowercase "d-" and "l-" prefixes are obsolete, and are distinct from the SMALL CAPS "D-" and "L-" prefixes. The "D-" and "L-" prefixes are used to specify the enantiomer of chiral organic compounds in biochemistry and are based on the compound's absolute configuration relative to (+)-glyceraldehyde, which is the D-form
by definition. The prefix used to indicate absolute configuration is
not directly related to the (+) or (−) prefix used to indicate optical
rotation in the same molecule. For example, nine of the nineteen L-amino acids naturally occurring in proteins are, despite the L- prefix, actually dextrorotary (at a wavelength of 589 nm), and D-fructose is sometimes called "laevulose" because it is laevorotary.
The D- and L- prefixes describe the molecule as a whole, as do the (+) and (−) prefixes for optical rotation. In contrast, the (R)- and (S)- prefixes from the Cahn–Ingold–Prelog priority rules characterize the absolute configuration of each specific chiral stereocenter
with the molecule, rather than a property of the molecule as a whole. A
molecule having exactly one chiral stereocenter (usually an asymmetric carbon atom) can be labeled (R) or (S), but a molecule having multiple stereocenters needs more than one label. For example, the essential amino acid L-threonine contains two chiral stereocenters and is written (2S,3S)-threonine. There is no strict relationship between the R/S, the D/L, and (+)/(−) designations, although some correlations exist. For example, of the naturally occurring amino acids, all are L, and most are (S). For some molecules the (R)-enantiomer
is the dextrorotary (+) enantiomer, and in other cases it is the
laevorotary (−) enantiomer. The relationship must be determined on a
case-by-case basis with experimental measurements or detailed computer
modeling.[7]
History
The two asymmetric crystal forms, dextrorotatory and levorotatory, of
tartaric acid.
Sucrose solution concentration measuring experiment, demonstrating optical rotation.
The rotation of the orientation of linearly polarized light was first observed in 1811 in quartz by French physicist François Arago.[8] In 1820, the English astronomer Sir John F.W. Herschel
discovered that different individual quartz crystals, whose crystalline
structures are mirror images of each other (see illustration), rotate
linear polarization by equal amounts but in opposite directions.[9] Jean Baptiste Biot also observed the rotation of the axis of polarization in certain liquids[10] and vapors of organic substances such as turpentine.[11] In 1822, Augustin-Jean Fresnel found that optical rotation could be explained as a species of birefringence:
whereas previously known cases of birefringence were due to the
different speeds of light polarized in two perpendicular planes, optical
rotation was due to the different speeds of right-hand and left-hand
circularly polarized light.[12] Simple polarimeters have been used since this time to measure the concentrations of simple sugars, such as glucose, in solution. In fact one name for D-glucose (the biological isomer), is dextrose, referring to the fact that it causes linearly polarized light to rotate to the right or dexter side. In a similar manner, levulose, more commonly known as fructose, causes the plane of polarization to rotate to the left. Fructose is even more strongly levorotatory than glucose is dextrorotatory. Invert sugar syrup, commercially formed by the hydrolysis of sucrose
syrup to a mixture of the component simple sugars, fructose, and
glucose, gets its name from the fact that the conversion causes the
direction of rotation to "invert" from right to left.
In 1849, Louis Pasteur resolved a problem concerning the nature of tartaric acid.[13] A solution of this compound derived from living things (to be specific, wine lees) rotates the plane of polarization of light passing through it, but tartaric acid derived by chemical synthesis
has no such effect, even though its reactions are identical and its
elemental composition is the same. Pasteur noticed that the crystals
come in two asymmetric forms that are mirror images of one another.
Sorting the crystals by hand gave two forms of the compound: Solutions
of one form rotate polarized light clockwise, while the other form
rotate light counterclockwise. An equal mix of the two has no
polarizing effect on light. Pasteur deduced that the molecule in
question is asymmetric and could exist in two different forms that
resemble one another as would left- and right-hand gloves, and that the
organic form of the compound consists of purely the one type.
In 1874, Jacobus Henricus van 't Hoff[14] and Joseph Achille Le Bel[15]
independently proposed that this phenomenon of optical activity in
carbon compounds could be explained by assuming that the 4 saturated
chemical bonds between carbon atoms and their neighbors are directed
towards the corners of a regular tetrahedron. If the 4 neighbors are all
different, then there are two possible orderings of the neighbors
around the tetrahedron, which will be mirror images of each other. This
led to a better understanding of the three-dimensional nature of
molecules.
In 1945, Charles William Bunn[16]
predicted optical activity of achiral structures, if the wave's
propagation direction and the achiral structure form an experimental
arrangement that is different from its mirror image. Such optical
activity due to extrinsic chirality was observed in the 1960s in liquid crystals.[17][18]
In 1950, Sergey Vavilov[19]
predicted optical activity that depends on the intensity of light and
the effect of nonlinear optical activity was observed in 1979 in lithium iodate crystals.[20]
Optical activity is normally observed for transmitted light.
However, in 1988, M. P. Silverman discovered that polarization rotation
can also occur for light reflected from chiral substances.[21]
Shortly after, it was observed that chiral media can also reflect
left-handed and right-handed circularly polarized waves with different
efficiencies.[22]
These phenomena of specular circular birefringence and specular
circular dichroism are jointly known as specular optical activity.
Specular optical activity is very weak in natural materials.
In 1898 Jagadish Chandra Bose described the ability of twisted artificial structures to rotate the polarization of microwaves.[23] Since the early 21st century, the development of artificial materials has led to the prediction[24] and realization[25][26]
of chiral metamaterials with optical activity exceeding that of natural
media by orders of magnitude in the optical part of the spectrum.
Extrinsic chirality associated with oblique illumination of metasurfaces
lacking two-fold rotational symmetry has been observed to lead to large
linear optical activity in transmission[27] and reflection,[28] as well as nonlinear optical activity exceeding that of lithium iodate by 30 million times.[29]
Theory
Optical
activity occurs due to molecules dissolved in a fluid or due to the
fluid itself only if the molecules are one of two (or more) stereoisomers; this is known as an enantiomer. The structure of such a molecule is such that it is not identical to its mirror image
(which would be that of a different stereoisomer, or the "opposite
enantiomer"). In mathematics, this property is also known as chirality. For instance, a metal rod is not chiral, since its appearance in a mirror is not distinct from itself. However a screw or light bulb base (or any sort of helix) is
chiral; an ordinary right-handed screw thread, viewed in a mirror,
would appear as a left-handed screw (very uncommon) which could not
possibly screw into an ordinary (right-handed) nut. A human viewed in a
mirror would have their heart on the right side, clear evidence of
chirality, whereas the mirror reflection of a doll might well be
indistinguishable from the doll itself.
In order to display optical activity, a fluid must contain only
one, or a preponderance of one, stereoisomer. If two enantiomers are
present in equal proportions then their effects cancel out and no
optical activity is observed; this is termed a racemic mixture. But when there is an enantiomeric excess,
more of one enantiomer than the other, the cancellation is incomplete
and optical activity is observed. Many naturally occurring molecules are
present as only one enantiomer (such as many sugars). Chiral molecules
produced within the fields of organic chemistry or inorganic chemistry are racemic unless a chiral reagent was employed in the same reaction.
At the fundamental level, polarization rotation in an optically
active medium is caused by circular birefringence, and can best be
understood in that way. Whereas linear birefringence in a crystal involves a small difference in the phase velocity
of light of two different linear polarizations, circular birefringence
implies a small difference in the velocities between right and
left-handed circular polarizations.[12]
Think of one enantiomer in a solution as a large number of little
helices (or screws), all right-handed, but in random orientations.
Birefringence of this sort is possible even in a fluid because the
handedness of the helices is not dependent on their orientation: even
when the direction of one helix is reversed, it still appears right
handed. And circularly polarized light itself is chiral: as the wave
proceeds in one direction the electric (and magnetic) fields composing
it are rotating clockwise (or counterclockwise for the opposite circular
polarization), tracing out a right (or left) handed screw pattern in
space. In addition to the bulk refractive index which substantially lowers the phase velocity of light in any dielectric (transparent) material compared to the speed of light (in vacuum), there is an additional interaction between the chirality of the wave and the chirality of the molecules.
Where their chiralities are the same, there will be a small additional
effect on the wave's velocity, but the opposite circular polarization
will experience an opposite small effect as its chirality is opposite
that of the molecules.
Unlike linear birefringence, however, natural optical rotation
(in the absence of a magnetic field) cannot be explained in terms of a
local material permittivity
tensor (i.e., a charge response that only depends on the local electric
field vector), as symmetry considerations forbid this. Rather, circular
birefringence only appears when considering nonlocality of the material
response, a phenomenon known as spatial dispersion.[30]
Nonlocality means that electric fields in one location of the material
drive currents in another location of the material. Light travels at a
finite speed, and even though it is much faster than the electrons, it
makes a difference whether the charge response naturally wants to travel
along with the electromagnetic wavefront, or opposite to it. Spatial
dispersion means that light travelling in different directions
(different wavevectors) sees a slightly different permittivity tensor.
Natural optical rotation requires a special material, but it also relies
on the fact that the wavevector of light is nonzero, and a nonzero
wavevector bypasses the symmetry restrictions on the local
(zero-wavevector) response. However, there is still reversal symmetry,
which is why the direction of natural optical rotation must be
'reversed' when the direction of the light is reversed, in contrast to
magnetic Faraday rotation.
All optical phenomena have some nonlocality/wavevector influence but it
is usually negligible; natural optical rotation, rather uniquely,
absolutely requires it.[30]
The phase velocity of light in a medium is commonly expressed using the index of refraction n,
defined as the speed of light (in free space) divided by its speed in
the medium. The difference in the refractive indices between the two
circular polarizations quantifies the strength of the circular
birefringence (polarization rotation),
 .
.
While  is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
The familiar rotation of the axis of linear polarization relies on the understanding that a linearly polarized wave can as well be described as the superposition
(addition) of a left and right circularly polarized wave in equal
proportion. The phase difference between these two waves is dependent on
the orientation of the linear polarization which we'll call  , and their electric fields have a relative phase difference of
, and their electric fields have a relative phase difference of  which then add to produce linear polarization:
which then add to produce linear polarization:

where  is the electric field of the net wave, while
is the electric field of the net wave, while  and
and  are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write
are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write  and
and  in terms of their x and y components as follows:
in terms of their x and y components as follows:


where  and
and  are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by
are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by  and then the actual electric field at any instant is given by the real part of that product.
and then the actual electric field at any instant is given by the real part of that product.
Substituting these expressions for  and
and  into the equation for
into the equation for  we obtain:
we obtain:



The last equation shows that the resulting vector has the x and y components in phase and oriented exactly in the  direction, as we had intended, justifying the representation of any linearly polarized state at angle
direction, as we had intended, justifying the representation of any linearly polarized state at angle  as the superposition of right and left circularly polarized components with a relative phase difference of
as the superposition of right and left circularly polarized components with a relative phase difference of  .
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of
.
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of  . Let us call
. Let us call  the result of passing the original wave linearly polarized at angle
the result of passing the original wave linearly polarized at angle  through this medium. This will apply additional phase factors of
through this medium. This will apply additional phase factors of  and
and  to the right and left circularly polarized components of
to the right and left circularly polarized components of  :
:

Using similar math as above we find:

thus describing a wave linearly polarized at angle  , thus rotated by
, thus rotated by  relative to the incoming wave:
relative to the incoming wave: 
We defined above the difference in the refractive indices for right and left circularly polarized waves of  . Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of
. Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of  (as we used above) given by:
(as we used above) given by:
 ,
,
where  is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by
is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by  as we have shown.
as we have shown.
In general, the refractive index depends on wavelength (see dispersion) and the differential refractive index  will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
So we find that the degree of rotation depends on the color of the light (the yellow sodium D line near 589 nm wavelength is commonly used for measurements), and is directly proportional to the path length  through the substance and the amount of circular birefringence of the material
through the substance and the amount of circular birefringence of the material  which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
Although optical activity is normally thought of as a property of fluids, particularly aqueous solutions, it has also been observed in crystals such as quartz (SiO2). Although quartz has a substantial linear birefringence, that effect is cancelled when propagation is along the optic axis.
In that case, rotation of the plane of polarization is observed due to
the relative rotation between crystal planes, thus making the crystal
formally chiral as we have defined it above. The rotation of the crystal
planes can be right or left-handed, again producing opposite optical
activities. On the other hand, amorphous forms of silica such as fused quartz,
like a racemic mixture of chiral molecules, has no net optical activity
since one or the other crystal structure does not dominate the
substance's internal molecular structure.
Applications
For a pure substance in solution, if the color and path length are fixed and the specific rotation is known, the observed rotation can be used to calculate the concentration. This usage makes a polarimeter a tool of great importance to those trading in or using sugar syrups in bulk.
Comparison to the Faraday effect
Rotation of light's plane of polarization may also occur through the Faraday effect which involves a static magnetic field.
However, this is a distinct phenomenon that is not classified as
"optical activity." Optical activity is reciprocal, i.e. it is the same
for opposite directions of wave propagation through an optically active
medium, for example clockwise polarization rotation from the point of
view of an observer. In case of optically active isotropic media, the
rotation is the same for any direction of wave propagation. In contrast,
the Faraday effect is non-reciprocal, i.e opposite directions of wave
propagation through a Faraday medium will result in clockwise and
anti-clockwise polarization rotation from the point of view of an
observer. Faraday rotation depends on the propagation direction relative
to that of the applied magnetic field. All compounds can exhibit
polarization rotation in the presence of an applied magnetic field,
provided that (a component of) the magnetic field is oriented in the
direction of light propagation. The Faraday effect is one of the first
discoveries of the relationship between light and electromagnetic
effects.
See also
References
The first word component dextro- comes from the Latin word dexter, meaning "right" (as opposed to left). Laevo- or levo- comes from the Latin laevus, meaning "left side".
The equivalent French terms are dextrogyre and levogyre. These are used infrequently in English.
Sebti; Hamilton, eds. (2001). Farnesyltransferase inhibitors in cancer therapy. p. 126. ISBN 9780896036291. Retrieved 2015-10-18.
LibreTexts Chemistry – Polarimetry
"Determination of optical rotation and specific rotation" (PDF). The International Pharmacopoeia. World Health Organization. 2017. ISBN 9789241550031. Archived (PDF) from the original on 2022-10-09.
Solomons, T.W. Graham; Fryhle, Graig B. (2004). Organic Chemistry (8th ed.). Hoboken: John Wiley & Sons, Inc.
See, for example,Stephens,
P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J.; Bortolini, O.;
Besse, P. (2003). "Determination of absolute configuration using
calculation of optical rotation". Chirality. 15: S57–64. doi:10.1002/chir.10270. PMID 12884375.
Arago (1811) "Mémoire
sur une modification remarquable qu'éprouvent les rayons lumineux dans
leur passage à travers certains corps diaphanes et sur quelques autres
nouveaux phénomènes d'optique" (Memoir on a remarkable modification
that light rays experience during their passage through certain
translucent substances and on some other new optical phenomena), Mémoires de la classe des sciences mathématiques et physiques de l'Institut Impérial de France, 1st part : 93–134.
Herschel, J.F.W. (1820) "On
the rotation impressed by plates of rock crystal on the planes of
polarization of the rays of light, as connected with certain
peculiarities in its crystallization," Transactions of the Cambridge Philosophical Society, 1 : 43–51.
Biot, J. B. (1815) "Phenomene de polarisation successive, observés dans des fluides homogenes" (Phenomenon of successive polarization, observed in homogeneous fluids), Bulletin des Sciences, par la Société Philomatique de Paris, 190–192.
Biot
(1818 & 1819) "Extrait d'un mémoire sur les rotations que certaines
substances impriment aux axes de polarisation des rayons lumineux"
(Extract from a memoir on the [optical] rotations that certain
substances impress on the axes of polarization of light rays), Annales de Chimie et de Physique, 2nd series, 9 : 372-389 ; 10 : 63-81 ; for Biot's experiments with turpentine vapor (vapeur d'essence de térébenthine), see pp. 72-81.
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); especially §13.
Pasteur, L. (1850) "Recherches sur les propriétés spécifiques des deux acides qui composent l'acide racémique" (Researches on the specific properties of the two acids that compose the racemic acid), Annales de chimie et de physique, 3rd series, 28 : 56–99 ; see also appendix, pp. 99–117.
van 't Hoff, J.H. (1874) "Sur les formules de structure dans l'espace" (On structural formulas in space), Archives Néerlandaises des Sciences Exactes et Naturelles, 9 : 445–454.
Le Bel, J.-A. (1874) "Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions" (On the relations that exist between the atomic formulas of organic substances and the rotatory power of their solutions), Bulletin de la Société Chimique de Paris, 22 : 337–347.
Bunn, C. W. (1945). Chemical Crystallography. New York: Oxford University Press. p. 88.
R. Williams (1968). "Optical Rotatory Effect in the Nematic Liquid Phase of p-Azoxyanisole". Physical Review Letters. 21 (6): 342. Bibcode:1968PhRvL..21..342W. doi:10.1103/PhysRevLett.21.342.
R. Williams (1969). "Optical-rotary power and linear electro-optic effect in nematic liquid crystals of p-azoxyanisole". Journal of Chemical Physics. 50 (3): 1324. Bibcode:1969JChPh..50.1324W. doi:10.1063/1.1671194.
Vavilov, S. I. (1950). Mikrostruktura Sveta (Microstructure of Light). Moscow: USSR Academy of Sciences Publishing.
Akhmanov,
S. A.; Zhdanov, B. V.; Zheludev, N. I.; Kovrigin, A. I.; Kuznetsov, V.
I. (1979). "Nonlinear optical activity in crystals". JETP Letters. 29: 264.
Silverman,
M.; Ritchie, N.; Cushman, G.; Fisher, B. (1988). "Experimental
configurations using optical phase modulation to measure chiral
asymmetries in light specularly reflected from a naturally gyrotropic
medium". Journal of the Optical Society of America A. 5 (11): 1852. Bibcode:1988JOSAA...5.1852S. doi:10.1364/JOSAA.5.001852.
Silverman, M.; Badoz, J.; Briat, B. (1992). "Chiral reflection from a naturally optically active medium". Optics Letters. 17 (12): 886. Bibcode:1992OptL...17..886S. doi:10.1364/OL.17.000886. PMID 19794663.
Bose, Jagadis Chunder (1898). "On the Rotation of Plane of Polarisation of Electric Waves by a Twisted Structure". Proceedings of the Royal Society. 63 (389–400): 146–152. doi:10.1098/rspl.1898.0019. JSTOR 115973. S2CID 89292757.
Svirko, Y.; Zheludev, N. I.; Osipov, M. (2001). "Layered chiral metallic microstructures with inductive coupling". Applied Physics Letters. 78 (4): 498. Bibcode:2001ApPhL..78..498S. doi:10.1063/1.1342210.
Kuwata-Gonokami,
M.; Saito, N.; Ino, Y.; Kauranen, M.; Jefimovs, K.; Vallius, T.;
Turunen, J.; Svirko, Y. (2005). "Giant Optical Activity in
Quasi-Two-Dimensional Planar Nanostructures". Physical Review Letters. 95 (22): 227401. Bibcode:2005PhRvL..95v7401K. doi:10.1103/PhysRevLett.95.227401. PMID 16384264.
Plum,
E.; Fedotov, V. A.; Schwanecke, A. S.; Zheludev, N. I.; Chen, Y.
(2007). "Giant optical gyrotropy due to electromagnetic coupling". Applied Physics Letters. 90 (22): 223113. Bibcode:2007ApPhL..90v3113P. doi:10.1063/1.2745203.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2008). "Optical activity in extrinsically chiral metamaterial" (PDF). Applied Physics Letters. 93 (19): 191911. arXiv:0807.0523. Bibcode:2008ApPhL..93s1911P. doi:10.1063/1.3021082. S2CID 117891131.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2016). "Specular optical activity of achiral metasurfaces" (PDF). Applied Physics Letters. 108 (14): 141905. Bibcode:2016ApPhL.108n1905P. doi:10.1063/1.4944775. hdl:10220/40854.
Ren, M.; Plum, E.; Xu, J.; Zheludev, N. I. (2012). "Giant nonlinear optical activity in a plasmonic metamaterial". Nature Communications. 3: 833. Bibcode:2012NatCo...3..833R. doi:10.1038/ncomms1805. PMID 22588295.
L.D. Landau; E.M. Lifshitz; L.P. Pitaevskii (1984). Electrodynamics of Continuous Media. Vol. 8 (2nd ed.). Butterworth-Heinemann. pp. 362–365. ISBN 978-0-7506-2634-7.
Plum, E.; Zhou, J.; Dong, J.; Fedotov, V. A.; Koschny, T.; Soukoulis, C. M.; Zheludev, N. I. (2009). "Metamaterial with negative index due to chirality" (PDF). Physical Review B. 79 (3): 035407. Bibcode:2009PhRvB..79c5407P. doi:10.1103/PhysRevB.79.035407. S2CID 119259753.
Further reading
- Eugene Hecht, Optics, 3rd Ed., Addison-Wesley, 1998, ISBN 0-201-30425-2
- Akhlesh Lakhtakia, Beltrami Fields in Chiral Media, World Scientific, Singapore, 1994
- A step by step tutorial on Optical Rotation
- Morrison. Robert. T, and Boyd. Robert. N, "Organic Chemistry (6th ed)". Prentice-Hall Inc (1992).

Operating principle of a
polarimeter
for measuring optical rotation. 1. Light source 2. Unpolarized light
3. Linear polarizer 4. Linearly polarized light 5. Sample tube
containing molecules under study 6. Optical rotation due to molecules 7.
Rotatable linear analyzer 8. Detector
https://en.wikipedia.org/wiki/Optical_rotation
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave.
In electrodynamics, the strength and direction of an electric
field is defined by its electric field vector. In the case of a
circularly polarized wave, the tip of the electric field vector,
at a given point in space, relates to the phase of the light as it
travels through time and space. At any instant of time, the electric
field vector of the wave indicates a point on a helix
oriented along the direction of propagation. A circularly polarized
wave can rotate in one of two possible senses: clockwise or right-handed circular polarization (RHCP) in which the electric field vector rotates in a right-hand sense with respect to the direction of propagation, and counter-clockwise or left-handed circular polarization (LHCP) in which the vector rotates in a left-hand sense.
Circular polarization is a limiting case of elliptical polarization. The other special case is the easier-to-understand linear polarization. All three terms were coined by Augustin-Jean Fresnel, in a memoir read to the French Academy of Sciences on 9 December 1822.[1][2] Fresnel had first described the case of circular polarization, without yet naming it, in 1821.[3]
The phenomenon of polarization arises as a consequence of the fact that light behaves as a two-dimensional transverse wave.
Circular polarization occurs when the two orthogonal electric
field component vectors are of equal magnitude and are out of phase by
exactly 90°, or one-quarter wavelength.
Characteristics
Right-handed/clockwise
circularly polarized light displayed with and without the use of
components. This would be considered left-handed/counterclockwise
circularly polarized if defined from the point of view of the source
rather than the receiver
In a circularly polarized electromagnetic wave, the individual
electric field vectors, as well as their combined vector, have a
constant magnitude, and with changing phase angle. Given that this is a plane wave,
each vector represents the magnitude and direction of the electric
field for an entire plane that is perpendicular to the optical axis.
Specifically, given that this is a circularly polarized plane wave,
these vectors indicate that the electric field, from plane to plane,
has a constant strength while its direction steadily rotates. Refer to these two images[dead link]
in the plane wave article to better appreciate this dynamic. This light
is considered to be right-hand, clockwise circularly polarized if
viewed by the receiver. Since this is an electromagnetic wave, each electric field vector has a corresponding, but not illustrated, magnetic field vector that is at a right angle to the electric field vector and proportional in magnitude to it. As a result, the magnetic field vectors would trace out a second helix if displayed.
Circular polarization is often encountered in the field of optics
and, in this section, the electromagnetic wave will be simply referred
to as light.
The nature of circular polarization and its relationship to other
polarizations is often understood by thinking of the electric field as
being divided into two components
that are perpendicular to each other. The vertical component and its
corresponding plane are illustrated in blue, while the horizontal
component and its corresponding plane are illustrated in green. Notice
that the rightward (relative to the direction of travel) horizontal
component leads the vertical component by one quarter of a wavelength, a 90° phase difference. It is this quadrature phase relationship that creates the helix
and causes the points of maximum magnitude of the vertical component to
correspond with the points of zero magnitude of the horizontal
component, and vice versa. The result of this alignment are select
vectors, corresponding to the helix, which exactly match the maxima of
the vertical and horizontal components.
To appreciate how this quadrature phase
shift corresponds to an electric field that rotates while maintaining a
constant magnitude, imagine a dot traveling clockwise in a circle.
Consider how the vertical and horizontal displacements of the dot, relative to the center of the circle, vary sinusoidally
in time and are out of phase by one quarter of a cycle. The
displacements are said to be out of phase by one quarter of a cycle
because the horizontal maximum displacement (toward the left) is reached
one quarter of a cycle before the vertical maximum displacement is
reached. Now referring again to the illustration, imagine the center of
the circle just described, traveling along the axis from the front to
the back. The circling dot will trace out a helix with the displacement
toward our viewing left, leading the vertical displacement. Just as the
horizontal and vertical displacements of the rotating dot are out of
phase by one quarter of a cycle in time, the magnitude of the horizontal
and vertical components of the electric field are out of phase by one
quarter of a wavelength.
Left-handed/counterclockwise
circularly polarized light displayed with and without the use of
components. This would be considered right-handed/clockwise circularly
polarized if defined from the point of view of the source rather than
the receiver.
The next pair of illustrations is that of left-handed,
counterclockwise circularly polarized light when viewed by the receiver.
Because it is left-handed, the rightward (relative to the direction of
travel) horizontal component is now lagging the vertical component by one quarter of a wavelength, rather than leading it.
Reversal of handedness
Waveplate
To convert circularly polarized light to the other handedness, one can use a half-waveplate.
A half-waveplate shifts a given linear component of light one half of a
wavelength relative to its orthogonal linear component.
Reflection
The
handedness of polarized light is reversed reflected off a surface at
normal incidence. Upon such reflection, the rotation of the plane of polarization of the reflected light is identical to that of the incident field. However, with propagation now in the opposite
direction, the same rotation direction that would be described as
"right-handed" for the incident beam, is "left-handed" for propagation
in the reverse direction, and vice versa. Aside from the reversal of
handedness, the ellipticity of polarization is also preserved (except in
cases of reflection by a birefringent surface).
Note that this principle only holds strictly for light reflected
at normal incidence. For instance, right circularly polarized light
reflected from a dielectric surface at grazing incidence (an angle
beyond the Brewster angle)
will still emerge as right-handed, but elliptically, polarized. Light
reflected by a metal at non-normal incidence will generally have its
ellipticity changed as well. Such situations may be solved by
decomposing the incident circular (or other) polarization into
components of linear polarization parallel and perpendicular to the plane of incidence, commonly denoted p and s respectively. The reflected components in the p and s linear polarizations are found by applying the Fresnel coefficients
of reflection, which are generally different for those two linear
polarizations. Only in the special case of normal incidence, where there
is no distinction between p and s, are the Fresnel coefficients for the two components identical, leading to the above property.
A
3-slide series of pictures taken with and without a pair of MasterImage
3D circularly polarized movie glasses of some dead European rose
chafers (Cetonia aurata) whose shiny green color comes from
left-polarized light. Note that, without glasses, both the beetles and
their images have shiny color. The right-polarizer removes the color of
the beetles but leaves the color of the images. The left-polarizer does
the opposite, showing reversal of handedness of the reflected light.
Conversion to and from linear polarization
Circularly polarized light can be converted into linearly polarized light by passing it through a quarter-waveplate.
Passing linearly polarized light through a quarter-waveplate with its
axes at 45° to its polarization axis will convert it to circular
polarization. In fact, this is the most common way of producing circular
polarization in practice. Note that passing linearly polarized light
through a quarter-waveplate at an angle other than 45° will generally produce elliptical polarization.
Handedness conventions
A
right-handed/clockwise circularly polarized wave as defined from the
point of view of the source. It would be considered
left-handed/anti-clockwise circularly polarized if defined from the
point of view of the receiver.
A
left-handed/anti-clockwise circularly polarized wave as defined from
the point of view of the source. It would be considered
right-handed/clockwise circularly polarized if defined from the point of
view of the receiver.
Circular polarization may be referred to as right-handed or
left-handed, and clockwise or anti-clockwise, depending on the direction
in which the electric field vector rotates. Unfortunately, two opposing
historical conventions exist.
From the point of view of the source
Using
this convention, polarization is defined from the point of view of the
source. When using this convention, left- or right-handedness is
determined by pointing one's left or right thumb away from the source, in the same
direction that the wave is propagating, and matching the curling of
one's fingers to the direction of the temporal rotation of the field at a
given point in space. When determining if the wave is clockwise or
anti-clockwise circularly polarized, one again takes the point of view
of the source, and while looking away from the source and in the same direction of the wave's propagation, one observes the direction of the field's spatial rotation.
Using this convention, the electric field vector of a left-handed circularly polarized wave is as follows:

As a specific example, refer to the circularly polarized wave in
the first animation. Using this convention, that wave is defined as
right-handed because when one points one's right thumb in the same
direction of the wave's propagation, the fingers of that hand curl in
the same direction of the field's temporal rotation. It is considered
clockwise circularly polarized because, from the point of view of the
source, looking in the same direction of the wave's propagation, the
field rotates in the clockwise direction. The second animation is that
of left-handed or anti-clockwise light, using this same convention.
This convention is in conformity with the Institute of Electrical and Electronics Engineers (IEEE) standard and, as a result, it is generally used in the engineering community.[4][5][6]
Quantum physicists also use this convention of handedness because
it is consistent with their convention of handedness for a particle's
spin.[7]
Radio astronomers also use this convention in accordance with an International Astronomical Union (IAU) resolution made in 1973.[8]
From the point of view of the receiver
In
this alternative convention, polarization is defined from the point of
view of the receiver. Using this convention, left- or right-handedness
is determined by pointing one's left or right thumb toward the source, against the direction of propagation, and then matching the curling of one's fingers to the spatial rotation of the field.
When using this convention, in contrast to the other convention,
the defined handedness of the wave matches the handedness of the screw
type nature of the field in space. Specifically, if one freezes a
right-handed wave in time, when one curls the fingers of one's right
hand around the helix, the thumb will point in the direction of
progression for the helix, given the sense of rotation. Note that, in
the context of the nature of all screws and helices, it does not matter
in which direction you point your thumb when determining its handedness.
When determining if the wave is clockwise or anti-clockwise
circularly polarized, one again takes the point of view of the receiver
and, while looking toward the source, against the direction of propagation, one observes the direction of the field's temporal rotation.
Just as in the other convention, right-handedness corresponds to a
clockwise rotation, and left-handedness corresponds to an
anti-clockwise rotation.
Many optics textbooks use this second convention.[9][10] It is also used by SPIE[11] as well as the International Union of Pure and Applied Chemistry (IUPAC).[12]
Uses of the two conventions
As
stated earlier, there is significant confusion with regards to these
two conventions. As a general rule, the engineering, quantum physics,
and radio astronomy communities use the first convention, in which the
wave is observed from the point of view of the source.[5][7][8]
In many physics textbooks dealing with optics, the second convention is
used, in which the light is observed from the point of view of the
receiver.[7][9]
To avoid confusion, it is good practice to specify "as defined
from the point of view of the source" or "as defined from the point of
view of the receiver" when discussing polarization matters.
The archive of the US Federal Standard 1037C proposes two contradictory conventions of handedness.[13]
FM radio
The term "circular polarization" is often used erroneously to describe mixed polarity signals[citation needed] used mostly in FM radio
(87.5 to 108.0 MHz in the USA), in which a vertical and a horizontal
component are propagated simultaneously by a single or a combined array.
This has the effect of producing greater penetration into buildings and
difficult reception areas than a signal with just one plane of
polarization. This would be an instance in which the polarization would
more appropriately be called random polarization because the
polarization at a receiver, although constant, will vary depending on
the direction from the transmitter and other factors in the transmitting
antenna design. See Stokes parameters.
The term "FM radio" above refers to FM broadcasting, not two-way radio (more properly called land mobile radio), which uses vertical polarization almost exclusively.
Dichroism
Circular dichroism (CD) is the differential absorption of left- and right-handed circularly polarized light. Circular dichroism is the basis of a form of spectroscopy that can be used to determine the optical isomerism and secondary structure of molecules.
In general, this phenomenon will be exhibited in absorption bands of any optically active molecule. As a consequence, circular dichroism is exhibited by most biological molecules, because of the dextrorotary (e.g., some sugars) and levorotary (e.g., some amino acids) molecules they contain. Noteworthy as well is that a secondary structure will also impart a distinct CD to its respective molecules. Therefore, the alpha helix, beta sheet and random coil regions of proteins and the double helix of nucleic acids have CD spectral signatures representative of their structures.
Also, under the right conditions, even non-chiral molecules will exhibit magnetic circular dichroism — that is, circular dichroism induced by a magnetic field.
Luminescence
Circularly polarized luminescence (CPL) can occur when either a luminophore or an ensemble of luminophores is chiral. The extent to which emissions are polarized is quantified in the same way it is for circular dichroism, in terms of the dissymmetry factor, also sometimes referred to as the anisotropy factor. This value is given by:

where  corresponds to the quantum yield of left-handed circularly polarized light, and
corresponds to the quantum yield of left-handed circularly polarized light, and  to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
Mathematical description
The classical sinusoidal plane wave solution of the electromagnetic wave equation for the electric and magnetic fields is:
![{\displaystyle {\begin{aligned}\mathbf {E} (\mathbf {r} ,t)&=\left|\,\mathbf {E} \,\right|\mathrm {Re} \left\{\mathbf {Q} \left|\psi \right\rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\\\mathbf {B} (\mathbf {r} ,t)&={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72e6f4e48ffd9eabf206d7664ee54e2e2ba2780c)
where k is the wavenumber;

is the angular frequency of the wave; ![\mathbf{Q} = \left [ \hat{ \mathbf{x}}, \hat{\mathbf{y}} \right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c6f209c9644cf3ab69fd75e6d696bb9278c0c12) is an orthogonal
is an orthogonal  matrix whose columns span the transverse x-y plane; and
matrix whose columns span the transverse x-y plane; and  is the speed of light.
is the speed of light.
Here,

is the amplitude of the field, and

is the normalized Jones vector in the x-y plane.
If  is rotated by
is rotated by  radians with respect to
radians with respect to  and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:
and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:

where the plus sign indicates left circular polarization, and the
minus sign indicates right circular polarization. In the case of
circular polarization, the electric field vector of constant magnitude
rotates in the x-y plane.
If basis vectors are defined such that:

and:

then the polarization state can be written in the "R-L basis" as:

where:

and:

Antennas
A number of different types of antenna elements can be used to
produce circularly polarized (or nearly so) radiation; following
Balanis,[14] one can use dipole elements:
"... two crossed dipoles provide the two orthogonal field
components.... If the two dipoles are identical, the field intensity of
each along zenith ... would be of the same intensity. Also, if the two
dipoles were fed with a 90° degree time-phase difference (phase
quadrature), the polarization along zenith would be circular.... One way
to obtain the 90° time-phase difference between the two orthogonal
field components, radiated respectively by the two dipoles, is by
feeding one of the two dipoles with a transmission line which is 1/4
wavelength longer or shorter than that of the other," p.80;
or helical elements:
"To achieve circular polarization [in axial or end-fire mode] ... the circumference C of the helix must be ... with C/wavelength = 1 near optimum, and the spacing about S = wavelength/4," p.571;
or patch elements:
"... circular and elliptical polarizations can be
obtained using various feed arrangements or slight modifications made to
the elements.... Circular polarization can be obtained if two
orthogonal modes are excited with a 90° time-phase difference between
them. This can be accomplished by adjusting the physical dimensions of
the patch.... For a square patch element, the easiest way to excite
ideally circular polarization is to feed the element at two adjacent
edges.... The quadrature phase difference is obtained by feeding the
element with a 90° power divider," p.859.
In quantum mechanics
In the quantum mechanical view, light is composed of photons. Polarization is a manifestation of the spin angular momentum of light.
More specifically, in quantum mechanics, the direction of spin of a
photon is tied to the handedness of the circularly polarized light, and
the spin of a beam of photons is similar to the spin of a beam of
particles, such as electrons.[15]
In nature
The
rose chafer's external surface reflects almost exclusively left-circularly polarized light.
Only a few mechanisms in nature are known to systematically produce circularly polarized light. In 1911, Albert Abraham Michelson discovered that light reflected from the golden scarab beetle Chrysina resplendens is preferentially left-polarized. Since then, circular polarization has been measured in several other scarab beetles such as Chrysina gloriosa,[16] as well as some crustaceans such as the mantis shrimp. In these cases, the underlying mechanism is the molecular-level helicity of the chitinous cuticle.[17]
The bioluminescence of the larvae of fireflies is also circularly polarized, as reported in 1980 for the species Photuris lucicrescens and Photuris versicolor.
For fireflies, it is more difficult to find a microscopic explanation
for the polarization, because the left and right lanterns of the larvae
were found to emit polarized light of opposite senses. The authors
suggest that the light begins with a linear polarization due to inhomogeneities inside aligned photocytes, and it picks up circular polarization while passing through linearly birefringent tissue.[18]
Water-air interfaces provide another source of circular
polarization. Sunlight that gets scattered back up towards the surface
is linearly polarized. If this light is then totally internally reflected back down, its vertical component undergoes a phase shift. To an underwater observer looking up, the faint light outside Snell's window therefore is (partially) circularly polarized.[19]
Weaker sources of circular polarization in nature include multiple scattering by linear polarizers[dubious – discuss], as in the circular polarization of starlight, and selective absorption by circularly dichroic media.
Radio emission from stars and pulsars can be strongly circularly polarized[citation needed].
Two species of mantis shrimp have been reported to be able to detect circular polarized light.[20][21]
See also
References
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); §§9–10.
Académie des Sciences, Procès-verbaux des séances de l'Académie tenues depuis la fondation de l'Institut jusqu'au mois d'août 1835, vol. 7 (for 1820–23), Hendaye, Basses Pyrénées: Imprimerie de l'Observatoire d'Abbadia, 1916, p. 401.
A. Fresnel, "Note sur le calcul des teintes que la polarisation développe dans les lames cristallisées" et seq., Annales de Chimie et de Physique,
Ser. 2, vol. 17, pp. 102–11 (May 1821), 167–96 (June 1821), 312–15
("Postscript", July 1821); reprinted (with added section nos.) in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 609–48; translated as "On the calculation of the
tints that polarization develops in crystalline plates,
& postscript", Zenodo: 4058004 (Creative Commons), 2021; author's footnote to §16.
IEEE
Std 149-1979 (R2008), "IEEE Standard Test Procedures for Antennas".
Reaffirmed December 10, 2008, Approved December 15, 1977, IEEE-SA
Standards Board. Approved October 9, 2003, American National Standards
Institute. ISBN 0-471-08032-2. doi:10.1109/IEEESTD.1979.120310,
sec. 11.1, p. 61."the sense of polarization, or handedness ... is
called right handed (left handed) if the direction of rotation is
clockwise (anti-clockwise) for an observer looking in the direction of
propagation"
Electromagnetic
Waves & Antennas – S. J. Orfanidis: Footnote p.45, "most
engineering texts use the IEEE convention and most physics texts, the
opposite convention."
Electromagnetic
Waves & Antennas – S. J. Orfanidis Pg 44 "Curl the fingers of your
left and right hands into a fist and point both thumbs towards the direction of propagation"
Lectures
on Physics Feynman (Vol. 1, ch.33-1) "If the end of the electric
vector, when we look at it as the light comes straight toward us, goes
around in an anti-clockwise direction, we call it right-hand circular
polarization. ... Our convention for labeling left-hand and right-hand
circular polarization is consistent with that which is used today for
all the other particles in physics which exhibit polarization (e.g.,
electrons). However, in some books on optics the opposite conventions
are used, so one must be careful."
IAU
General Assembly Meeting, 1973, Commission 40 (Radio
Astronomy/Radioastronomie), 8. POLARIZATION DEFINITIONS -- "A working
Group chaired by Westerhout was convened to discuss the definition of
polarization brightness temperatures used in the description of
polarized extended objects and the galactic
background. The following resolution was adopted by Commissions 25 and
40: 'RESOLVED, that the frame of reference for the Stokes parameters is
that of Right Ascension and Declination with the position angle of
electric-vector maximum, q, starting from North and increasing through
East. Elliptical polarization is defined in conformity with the
definitions of the Institute of Electrical and Electronics Engineers
(IEEE Standard 211, 1969). This means that the polarization of incoming
radiation, for which the position angle, q, of the electric vector,
measured at a fixed point in space, increases with time, is described as
right-handed and positive.'"
Polarization
in Spectral Lines. 2004 E. Landi Degl'innocenti, M Landolfi Section 1.2
"When ... the tip of the electric field vector rotates clockwise for an
observer facing the radiation source, ... (it will be considered)...
positive (or righthanded) circular polarization, Our convention ...
agrees with those proposed in the classical textbooks on polarized light
by Shurcliff (1952) and by Clarke and Grainger (1971). The same
convention is also used, although with some few exceptions, by optical
astronomers working in the field of polarimetry. Many radio astronomers,
on the other hand, use the opposite convention. [1]
HANDBOOK
OPTICS Volume I,Devices, Measurements and Properties,Michael Bass Page
272 Footnote: "Right-circularly polarized light is defined as a
clockwise rotation of the electric vector when the observer is looking against the direction the wave is traveling."
"The Polarization Ellipse". spie.org. Retrieved 13 April 2018.
S. E. Braslavsky (1 January 2009). "Glossary of terms used in photochemistry, 3rd edition (IUPAC Recommendations 2006)" (PDF). Pure and Applied Chemistry. 79 (3): 293–465. doi:10.1351/pac200779030293. S2CID 96601716. Archived (PDF) from the original on 2022-10-09.
In
one location it is stated..."Note 1. ... In general, the figure, i.e.,
polarization, is elliptical and is traced in a clockwise or
anti-clockwise sense, as viewed in the direction of propagation. ...
Rotation of the electric vector in a clockwise sense is designated
right-hand polarization, and rotation in an anti-clockwise sense is
designated left-hand polarization. "[2] Archived 2011-05-14 at the Wayback Machine
In another location it is stated... "Note 4: Circular polarization may
be referred to as "right-hand" or "left-hand", depending on whether the
helix describes the thread of a right-hand or left-hand screw,
respectively". [3] Archived 2011-06-06 at the Wayback Machine
Balanis, Constantine A. "Antenna Theory – Analysis and Design", 2005, 3rd Edition, John Wiley & Sons.
Introduction
to Quantum Theory 2ED David Park Sec 2.2 Pg32 "... the polarization of a
beam of light is exactly the same kind of thing as the spin of a beam
of electrons, the differences of terminology reflecting only the
accidents of the historical order of discovery."
Srinivasarao, Mohan; Park, Jung Ok; Crne, Matija; Sharma, Vivek (July 24, 2009). "Structural Origin of Circularly Polarized Iridescence in Jeweled Beetles". Science. 325 (5939): 449–451. Bibcode:2009Sci...325..449S. doi:10.1126/science.1172051. PMID 19628862. S2CID 206519071 – via science.sciencemag.org.
Hegedüs, Ramón; Győző Szélb; Gábor Horváth (September 2006). "Imaging polarimetry of the circularly polarizing cuticle of scarab beetles (Coleoptera: Rutelidae, Cetoniidae)". Vision Research. 46 (17): 2786–2797. doi:10.1016/j.visres.2006.02.007. PMID 16564066. S2CID 14974820.
Wynberg, Hans; Meijer, E.W.; Hummelen, J.C.; Dekkers, H.P.J.M.; Schippers, P.H.; Carlson, A.D. (7 August 1980). "Circular polarization observed in bioluminescence" (PDF). Nature. 286 (5773): 641–642. Bibcode:1980Natur.286..641W. doi:10.1038/286641a0. S2CID 4324467. Archived from the original (PDF) on 24 July 2011.
Horváth, Gábor; Dezsö Varjú (2003). Polarized Light in Animal Vision: Polarization Patterns in Nature. Springer. pp. 100–103. ISBN 978-3-540-40457-6.
Tsyr-Huei
Chiou; Sonja Kleinlogel; Tom Cronin; Roy Caldwell; Birte Loeffler;
Afsheen Siddiqi; Alan Goldizen; Justin Marshall (2008). "Circular polarization vision in a stomatopod crustacean". Current Biology. 18 (6): 429–34. doi:10.1016/j.cub.2008.02.066. PMID 18356053. S2CID 6925705.
Further reading
External links

The
electric field
vectors of a traveling circularly polarized electromagnetic wave. This
wave is right-circularly-polarized, since the direction of rotation of
the vector is related by the
right-hand rule to the direction the wave is moving; or left-circularly-polarized according to alternative convention.
https://en.wikipedia.org/wiki/Circular_polarization
A stellar magnetic field is a magnetic field generated by the motion of conductive plasma inside a star. This motion is created through convection, which is a form of energy transport involving the physical movement of material. A localized magnetic field
exerts a force on the plasma, effectively increasing the pressure
without a comparable gain in density. As a result, the magnetized region
rises relative to the remainder of the plasma, until it reaches the
star's photosphere. This creates starspots on the surface, and the related phenomenon of coronal loops.[1]
https://en.wikipedia.org/wiki/Stellar_magnetic_field
In solar physics, a coronal loop is a well-defined arch-like structure in the Sun's atmosphere made up of relatively dense plasma confined and isolated from the surrounding medium by magnetic flux tubes. Coronal loops begin and end at two footpoints on the photosphere and project into the transition region and lower corona. They typically form and dissipate over periods of seconds to days[1] and may span anywhere from 1 to 1,000 megametres (621 to 621,000 mi) in length.[2]
Coronal loops are often associated with the strong magnetic fields located within active regions and sunspots. The number of coronal loops varies with the 11 year solar cycle.
https://en.wikipedia.org/wiki/Coronal_loop
The photosphere is a star's outer shell from which light is radiated.
The term itself is derived from Ancient Greek roots, φῶς, φωτός/phos, photos meaning "light" and σφαῖρα/sphaira meaning "sphere", in reference to it being a spherical surface that is perceived to emit light.[citation needed] It extends into a star's surface until the plasma becomes opaque, equivalent to an optical depth of approximately 2⁄3,[1] or equivalently, a depth from which 50% of light will escape without being scattered.
A photosphere is the deepest region of a luminous object, usually a star, that is transparent to photons of certain wavelengths.
https://en.wikipedia.org/wiki/Photosphere
In physics, the magnetomotive force (mmf)  is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:
is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:
where
Φ is the magnetic flux and

is the
reluctance of the circuit. It can be seen that the magnetomotive force plays a role in this equation analogous to the voltage
V in
Ohm's law:
V = IR, since it is the cause of magnetic flux in a magnetic circuit:
[2]
 where N is the number of turns in the coil and I is the electric current through the circuit.
where N is the number of turns in the coil and I is the electric current through the circuit. where Φ is the magnetic flux and
where Φ is the magnetic flux and  is the magnetic reluctance
is the magnetic reluctance where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
https://en.wikipedia.org/wiki/Magnetomotive_force
In physics, mainly quantum mechanics and particle physics, a spin magnetic moment is the magnetic moment caused by the spin of elementary particles. For example, the electron is an elementary spin-1/2 fermion. Quantum electrodynamics gives the most accurate prediction of the anomalous magnetic moment of the electron.
In general, a magnetic moment can be defined in terms of an electric current and the area enclosed by the current loop.
Since angular momentum corresponds to rotational motion, the magnetic
moment can be related to the orbital angular momentum of the charge carriers in the constituting current. However, in magnetic materials, the atomic and molecular dipoles have magnetic moments not just because of their quantized orbital angular momentum, but also due to the spin of elementary particles constituting them.[a][b]
"Spin" is a non-classical property of elementary particles, since classically the "spin angular momentum" of a material object is really just the total orbital angular momenta of the object's constituents about the rotation axis. Elementary particles are conceived as point objects with no axis around which to "spin" (see wave–particle duality).
https://en.wikipedia.org/wiki/Spin_magnetic_moment
Coercivity, also called the magnetic coercivity, coercive field or coercive force, is a measure of the ability of a ferromagnetic material to withstand an external magnetic field without becoming demagnetized. Coercivity is usually measured in oersted or ampere/meter units and is denoted HC.
An analogous property in electrical engineering and materials science, electric coercivity, is the ability of a ferroelectric material to withstand an external electric field without becoming depolarized.
Ferromagnetic materials with high coercivity are called magnetically hard, and are used to make permanent magnets. Materials with low coercivity are said to be magnetically soft. The latter are used in transformer and inductor cores, recording heads, microwave devices, and magnetic shielding.
https://en.wikipedia.org/wiki/Coercivity
Magnetic shielding
Equipment sometimes requires isolation from external magnetic fields.[8]
For static or slowly varying magnetic fields (below about 100 kHz) the
Faraday shielding described above is ineffective. In these cases
shields made of high magnetic permeability metal alloys can be used, such as sheets of permalloy and mu-metal[9][10] or with nanocrystalline grain structure ferromagnetic metal coatings.[11]
These materials do not block the magnetic field, as with electric
shielding, but rather draw the field into themselves, providing a path
for the magnetic field lines
around the shielded volume. The best shape for magnetic shields is
thus a closed container surrounding the shielded volume. The
effectiveness of this type of shielding depends on the material's
permeability, which generally drops off at both very low magnetic field
strengths and high field strengths where the material becomes saturated.
Therefore, to achieve low residual fields, magnetic shields often
consist of several enclosures, one inside the other, each of which
successively reduces the field inside it. Entry holes within shielding
surfaces may degrade their performance significantly.
Because of the above limitations of passive shielding, an
alternative used with static or low-frequency fields is active
shielding, in which a field created by electromagnets cancels the ambient field within a volume.[12] Solenoids and Helmholtz coils
are types of coils that can be used for this purpose, as well as more
complex wire patterns designed using methods adapted from those used in
coil design for magnetic resonance imaging. Active shields may also be designed accounting for the electromagnetic coupling with passive shields,[13][14][15][16][17] referred to as hybrid shielding,[18]
so that there is broadband shielding from the passive shield and
additional cancellation of specific components using the active system.
Additionally, superconducting materials can expel magnetic fields via the Meissner effect.
https://en.wikipedia.org/wiki/Electromagnetic_shielding#Magnetic_shielding
First time-dependent rotation
Consider another (non-inertial) observer (the 2-O) located at the center of the Earth but rotating about the NS-axis by  We establish coordinates attached to this observer as
We establish coordinates attached to this observer as
so that the unit

versor

is mapped to the point

.
For the 2-O neither the Earth nor the barycenter of the gyroscope is
moving. The rotation of 2-O relative to 1-O is performed with angular
velocity

. We suppose that the

axis denotes points with zero longitude (the prime, or Greenwich, meridian).
Second and third fixed rotations
We now rotate about the  axis, so that the
axis, so that the  -axis has the longitude of the barycenter. In this case we have
-axis has the longitude of the barycenter. In this case we have
With the next rotation (about the axis  of an angle
of an angle  , the co-latitude) we bring the
, the co-latitude) we bring the  axis along the local zenith (
axis along the local zenith ( -axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)
-axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)
so that the  versor
versor  is mapped to the point
is mapped to the point 
Constant translation
We
now choose another coordinate basis whose origin is located at the
barycenter of the gyroscope. This can be performed by the following
translation along the zenith axis
so that the origin of the new system,  is located at the point
is located at the point  and
and  is the radius of the Earth. Now the
is the radius of the Earth. Now the  -axis points towards the south direction.
-axis points towards the south direction.
Fourth time-dependent rotation
Now we rotate about the zenith  -axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find
-axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find
The axis of symmetry of the gyrocompass is now along the  -axis.
-axis.
Last time-dependent rotation
The last rotation is a rotation on the axis of symmetry of the gyroscope as in
Dynamics of the system
Since
the height of the gyroscope's barycenter does not change (and the
origin of the coordinate system is located at this same point), its gravitational potential energy is constant. Therefore its Lagrangian  corresponds to its kinetic energy
corresponds to its kinetic energy  only. We have
only. We have
where

is the mass of the gyroscope, and
is the squared inertial speed of the origin of the coordinates of the
final coordinate system (i.e. the center of mass). This constant term
does not affect the dynamics of the gyroscope and it can be neglected.
On the other hand, the tensor of inertia is given by
and
Therefore we find
The Lagrangian can be rewritten as
where
is the part of the Lagrangian responsible for the dynamics of the system. Then, since

, we find
Since the angular momentum  of the gyrocompass is given by
of the gyrocompass is given by  we see that the constant
we see that the constant  is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable
is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable  as
as
or
Particular case: the poles
At the poles we find  and the equations of motion become
and the equations of motion become
This simple solution implies that the gyroscope is uniformly
rotating with constant angular velocity in both the vertical and
symmetrical axis.
The general and physically relevant case
Let us suppose now that  and that
and that  ,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find
,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find
Consider the case that
and, further, we allow for fast gyro-rotations, that is
Therefore, for fast spinning rotations,  implies
implies  In this case, the equations of motion further simplify to
In this case, the equations of motion further simplify to
Therefore we find small oscillations about the north-south line, as  ,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by
,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by
which corresponds to a period for the oscillations given by
Therefore  is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required
is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required  ,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the
,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the  -axis, the axis of symmetry. As a side result, on measuring
-axis, the axis of symmetry. As a side result, on measuring  (and knowing
(and knowing  ), one can deduce the local co-latitude
), one can deduce the local co-latitude 
See also
Notes
- Although
the effect is not visible in the specific case when the gyroscope's
axis is precisely parallel to the Earth's rotational axis.
References
Gade, Kenneth (2016). "The Seven Ways to Find Heading" (PDF). The Journal of Navigation. Cambridge University Press. 69 (5): 955–970. doi:10.1017/S0373463316000096. S2CID 53587934.
Elliott-Laboratories (2003). The Anschutz Gyro-Compass and Gyroscope Engineering. pp. 7–24. ISBN 978-1-929148-12-7. Archived from the original on 2017-03-04.
Time Inc. (Mar 15, 1943). "The gyroscope pilots ships & planes". Life. pp. 80–83. Archived from the original on 2017-02-27.
Galison, Peter (1987). How experiments end. pp. 34–37. ISBN 978-0-226-27915-2. Archived from the original on 2012-03-02.
"Archived copy" (PDF). Archived (PDF) from the original on 2015-06-29. Retrieved 2012-02-19. Standard 22
Anschütz Gyro Compass [sic] System: Gyro Compass [sic] Technology [sic] for over than [sic] 100 years
Chambers of Commerce and Industry in Schleswig-Holstein Archived 2017-02-22 at the Wayback Machine Retrieved on February 22, 2017.
Gyrocompass, Auxiliary Gyrocompass, and Dead Reckoning Analyzing Indicator and Tracer Systems Archived 2013-06-01 at the Wayback Machine, San Francisco Maritime National Park Association.
The Invention of Precision Navigational Instruments for Air and Sea Navigation Archived 2011-07-18 at the Wayback Machine, Weems & Plath.
Collinson, R. P. G. (2003), Introduction to avionics systems, Springer, p. 293, ISBN 978-1-4020-7278-9, archived from the original on 2014-07-07
NASA NASA Callback: Heading for Trouble Archived 2011-07-16 at the Wayback Machine, NASA Callback Safety Bulletin website, December 2005, No. 305. Retrieved August 29, 2010.
Bowditch, Nathaniel. American Practical Navigator Archived 2017-03-07 at the Wayback Machine, Paradise Cay Publications, 2002, pp.93-94, ISBN 978-0-939837-54-0.
Gyrocompass: Steaming Error Archived 2008-12-22 at the Wayback Machine, Navis. Accessed 15 December 2008.
- Seamanship Techniques:Shipboard and Marine Operations, D. J. House, Butterworth-Heinemann, 2004, p. 341
Bibliography
External links
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
This article is about devices used on ships. For the type of gyroscope used to determine aircraft heading, see
Heading indicator.
Cutaway of an Anschütz gyrocompass
A gyrocompass is a type of non-magnetic compass which is based on a fast-spinning disc and the rotation of the Earth (or another planetary body if used elsewhere in the universe) to find geographical direction automatically. The use of a gyrocompass is one of the seven fundamental ways to determine the heading of a vehicle.[1] A gyroscope is an essential component of a gyrocompass, but they are different devices; a gyrocompass is built to use the effect of gyroscopic precession, which is a distinctive aspect of the general gyroscopic effect.[2][3] Gyrocompasses are widely used for navigation on ships, because they have two significant advantages over magnetic compasses:[3]
Aircraft commonly use gyroscopic instruments (but not a gyrocompass) for navigation and altitude monitoring; for details, see Flight instruments and Gyroscopic autopilot.
History
The first, not yet practical,[4] form of gyrocompass was patented in 1885 by Marinus Gerardus van den Bos.[4] A usable gyrocompass was invented in 1906 in Germany by Hermann Anschütz-Kaempfe, and after successful tests in 1908 became widely used in the German Imperial Navy.[2][4][5] Anschütz-Kaempfe founded the company Anschütz & Co. in Kiel, to mass produce gyrocompasses; the company is today Raytheon Anschütz GmbH.[6]
The gyrocompass was an important invention for nautical navigation
because it allowed accurate determination of a vessel’s location at all
times regardless of the vessel’s motion, the weather and the amount of
steel used in the construction of the ship.[7]
In the United States, Elmer Ambrose Sperry produced a workable gyrocompass system (1908: U.S. Patent 1,242,065), and founded the Sperry Gyroscope Company. The unit was adopted by the U.S. Navy (1911[3]),
and played a major role in World War I. The Navy also began using
Sperry's "Metal Mike": the first gyroscope-guided autopilot steering
system. In the following decades, these and other Sperry devices were
adopted by steamships such as the RMS Queen Mary, airplanes, and the warships of World War II. After his death in 1930, the Navy named the USS Sperry after him.
Meanwhile, in 1913, C. Plath (a Hamburg, Germany-based
manufacturer of navigational equipment including sextants and magnetic
compasses) developed the first gyrocompass to be installed on a
commercial vessel. C. Plath sold many gyrocompasses to the Weems’
School for Navigation in Annapolis, MD, and soon the founders of each
organization formed an alliance and became Weems & Plath.[8]
The 1889 Dumoulin-Krebs gyroscope
Before the success of the gyrocompass, several attempts had been made in Europe to use a gyroscope instead. By 1880, William Thomson (Lord Kelvin) tried to propose a gyrostat to the British Navy. In 1889, Arthur Krebs adapted an electric motor to the Dumoulin-Froment marine gyroscope, for the French Navy. That gave the Gymnote submarine the ability to keep a straight line while underwater for several hours, and it allowed her to force a naval block in 1890.
In 1923 Max Schuler published his paper containing his observation that if a gyrocompass possessed Schuler tuning
such that it had an oscillation period of 84.4 minutes (which is the
orbital period of a notional satellite orbiting around the Earth at sea
level), then it could be rendered insensitive to lateral motion and
maintain directional stability.[9]
Operation
A gyroscope, not to be confused with a gyrocompass, is a spinning wheel mounted on a set of gimbals so that its axis is free to orient itself in any way.[3] When it is spun up to speed with its axis pointing in some direction, due to the law of conservation of angular momentum, such a wheel will normally maintain its original orientation to a fixed point in outer space
(not to a fixed point on Earth). Since the Earth rotates, it appears to
a stationary observer on Earth that a gyroscope's axis is completing a
full rotation once every 24 hours.[note 1] Such a rotating gyroscope is used for navigation in some cases, for example on aircraft, where it is known as heading indicator
or directional gyro, but cannot ordinarily be used for long-term marine
navigation. The crucial additional ingredient needed to turn a
gyroscope into a gyrocompass, so it would automatically position to true
north,[2][3] is some mechanism that results in an application of torque whenever the compass's axis is not pointing north.
One method uses friction to apply the needed torque:[7]
the gyroscope in a gyrocompass is not completely free to reorient
itself; if for instance a device connected to the axis is immersed in a
viscous fluid, then that fluid will resist reorientation of the axis.
This friction force caused by the fluid results in a torque acting on the axis, causing the axis to turn in a direction orthogonal to the torque (that is, to precess) along a line of longitude.
Once the axis points toward the celestial pole, it will appear to be
stationary and won't experience any more frictional forces. This is
because true north (or true south) is the only direction for which the
gyroscope can remain on the surface of the earth and not be required to
change. This axis orientation is considered to be a point of minimum potential energy.
Another, more practical, method is to use weights to force the
axis of the compass to remain horizontal (perpendicular to the direction
of the center of the Earth), but otherwise allow it to rotate freely
within the horizontal plane.[2][3]
In this case, gravity will apply a torque forcing the compass's axis
toward true north. Because the weights will confine the compass's axis
to be horizontal with respect to the Earth's surface, the axis can never
align with the Earth's axis (except on the Equator) and must realign
itself as the Earth rotates. But with respect to the Earth's surface,
the compass will appear to be stationary and pointing along the Earth's
surface toward the true North Pole.
Since the gyrocompass's north-seeking function depends on the rotation around the axis of the Earth that causes torque-induced gyroscopic precession,
it will not orient itself correctly to true north if it is moved very
fast in an east to west direction, thus negating the Earth's rotation.
However, aircraft commonly use heading indicators or directional gyros,
which are not gyrocompasses and do not align themselves to north via
precession, but are periodically aligned manually to magnetic north.[10][11]
Errors
A gyrocompass is subject to certain errors. These include steaming error, where rapid changes in course, speed and latitude cause deviation before the gyro can adjust itself.[12] On most modern ships the GPS or other navigational aids feed data to the gyrocompass allowing a small computer to apply a correction.
Alternatively a design based on a strapdown architecture (including a triad of fibre optic gyroscopes, ring laser gyroscopes or hemispherical resonator gyroscopes
and a triad of accelerometers) will eliminate these errors, as they do
not depend upon mechanical parts to determinate rate of rotation.[13]
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
A rotating magnetic field is the resultant magnetic field produced by a system of coils symmetrically placed and supplied with polyphase currents.[1]
A rotating magnetic field can be produced by a poly-phase (two or more
phases) current or by a single phase current provided that, in the
latter case, two field windings are supplied and are so designed that
the two resulting magnetic fields generated thereby are out of phase.[2]
Rotating magnetic fields are often utilized for electromechanical applications, such as induction motors, electric generators and induction regulators.
History
In 1824, the French physicist François Arago formulated the existence of rotating magnetic fields using a rotating copper disk and a needle, termed “Arago's rotations.” English experimenters Charles Babbage and John Herschel found they could induce rotation in Arago's copper disk by spinning a horseshoe magnet under it, with English scientist Michael Faraday later attributing the effect to electromagnetic induction.[3] In 1879, English physicist Walter Baily
replaced the horseshoe magnets with four electromagnets and, by
manually turning switches on and off, demonstrated a primitive induction
motor.[4][5][6][7][8]
The idea of a rotating magnetic field in an AC motor was explored by the Italian physicist and electrical engineer Galileo Ferraris and the Serbian-American inventor and electrical engineer Nikola Tesla.[9] Ferraris wrote about researching the concept and built a working model in 1885.[10]
Tesla attempted several (unsuccessful) designs and working models
through the early 1880s before building a working prototype in 1887[11][12][13]
According to Ferraris principle of rotating magnetic field, Friedrich
August Haselwander developed the first AC 3 phase generator in 1887.[14] In 1888, Ferraris published his research in a paper to the Royal Academy of Sciences in Turin and Tesla obtained a United States patent (U.S. Patent 0,381,968)
for his design. Based on the Haselwander generator, Mikhail
Dolivo-Dobrovolsky will develop a three-phase generator and motor for
the world's first three-phase power plant built in 1891 in Frankfurt,
Germany.[15]
Description
The rotating magnetic field is the key principle in the operation of induction machines. The induction motor consists of a stator and rotor.
In the stator a group of fixed windings are so arranged that a two
phase current, for example, produces a magnetic field which rotates at
an angular velocity determined by the frequency of the alternating current. The rotor or armature consists of coils wound in slots, which are short circuited and in which the changing flux
generated by the field poles induce a current. The flux generated by
the armature current reacts upon the field poles and the armature is set
in rotation in a definite direction.[2]
Rotating fields.
As the direction of the current through the windings changes, the
polarity of the windings changes as well. Since there are two windings
acting in conjunction with each other, the polarity of the main field
will depend upon the polarity of each winding. The arrow or vector below
each diagram indicates the direction of the magnetic field in each
case.
[16] A symmetric rotating magnetic field can be produced with as few as two polar wound coils driven at 90-degree phasing. However, three sets of coils are nearly always used, because it is compatible with a symmetric three-phase AC sine current system. The three coils are driven with each set 120 degrees in phase from the others. For the purpose of this example, the magnetic field is taken to be the linear function of the coil's current.
The result of adding three 120-degree phased sine waves on the axis of the motor is a single rotating vector that always remains constant in magnitude.[17]
The rotor has a constant magnetic field. The north pole of the rotor
will move toward the south pole of the magnetic field of the stator, and
vice versa. This magnetomechanical attraction creates a force that will drive the rotor to follow the rotating magnetic field in a synchronous manner.
Rotating three-phase magnetic field, as indicated by the rotating black arrow
A permanent magnet
in such a field will rotate so as to maintain its alignment with the
external field. This effect was utilized in early alternating-current
electric motors. A rotating magnetic field can be constructed using two
orthogonal coils with a 90-degree phase difference in their alternating
currents. However, in practice, such a system would be supplied through
a three-wire arrangement with unequal currents. This inequality would
cause serious problems in the standardization of the conductor size. In
order to overcome this, three-phase systems are used in which the three
currents are equal in magnitude and have a 120-degree phase difference.
Three similar coils having mutual geometrical angles of 120 degrees will
create the rotating magnetic field in this case. The ability of the
three-phase system to create the rotating field utilized in electric
motors is one of the main reasons why three-phase systems dominate the
world’s electric power-supply systems.
Rotating magnetic fields are also used in induction motors.
Because magnets degrade with time, induction motors use short-circuited
rotors (instead of a magnet), which follow the rotating magnetic field
of a multicoiled stator. In these motors, the short-circuited turns of
the rotor develop eddy currents in the rotating field of the stator, which in turn move the rotor by Lorentz force.
These types of motors are not usually synchronous, but instead
necessarily involve a degree of 'slip' in order that the current may be
produced due to the relative movement of the field and the rotor.
See also
References
Graham, Frank Duncan (1921). Audels Engineers and Mechanics Guide. New York: THEO. AUDEL & CO. p. 594.
The Wireless Age. Vol. 6. New York: Macroni Pub. Corp'n. October 1918. pp. 18–19.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 52–54. ISBN 978-1400846559.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. p. 55. ISBN 978-1400846559.
Babbage, C.; Herschel, J. F. W. (Jan 1825). "Account
of the Repetition of M. Arago's Experiments on the Magnetism Manifested
by Various Substances during the Act of Rotation". Philosophical Transactions of the Royal Society. 115: 467–496. Bibcode:1825RSPT..115..467B. doi:10.1098/rstl.1825.0023. Retrieved 2 December 2012.
Thompson, Silvanus Phillips (1895). Polyphase Electric Currents and Alternate-Current Motors (1st ed.). London: E. & F.N. Spon. p. 261. Retrieved 2 December 2012.
Baily, Walter (June 28, 1879). "A Mode of producing Arago's Rotation". Philosophical Magazine. Taylor & Francis. 3 (1): 115–120. Bibcode:1879PPSL....3..115B. doi:10.1088/1478-7814/3/1/318.
Vučković, Vladan (November 2006). "Interpretation of a Discovery" (PDF). The Serbian Journal of Electrical Engineers. 3 (2). Retrieved 10 February 2013.
Hughes, Thomas Parke (1983). Networks of power: electrification in Western society, 1880-1930. Baltimore: Johns Hopkins University Press. p. 117.
Encyclopedia Americana: Meyer to Nauvoo. Vol. 12. Danbury, Connecticut: Scholastic Library Pub. 2006. p. 558.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 63–68. ISBN 978-1400846559.
Debunking the Tesla Myth
O'Neill, John. Prodigal Genius: The Life of Nikola Tesla. pp. 55–58.
https://ieeexplore.ieee.org/document/4401482?arnumber=4401482 H. Hooshyar; M. Savaghebi; A. Vahedi: Synchronous generator - Past, present and future
AC Power History and Timeline
United States, Bureau of Naval Personnel (1945). Advanced Work In Aircraft Electricity. Washington: U.S. Govt. Print. Off. pp. 149–150.
 This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
Further reading
- C Mackechnie Jarvis (1970). "Nikola Tesla and the induction motor". Phys Educ. 5 (5): 280–7. Bibcode:1970PhyEd...5..280M. doi:10.1088/0031-9120/5/5/306. S2CID 250845406.
- Owen, E.L. (October 1988). "The induction motor's historical past". IEEE Potentials. 7 (3): 27–30. doi:10.1109/45.9969. S2CID 19271710.
- Beckhard, Arthur J., "Electrical genius Nikola Tesla". New York,
Messner, 1959. LCCN 59007009 /L/AC/r85 (ed. 192 p.; 22 cm.; biography
with notes on the inventions of the rotating magnetic field motors for
alternating current.)
- Kline, R. (1987). "Science and Engineering Theory in the Invention and Development of the Induction Motor, 1880–1900". Technology and Culture. 28 (2): 283–313. doi:10.2307/3105568. JSTOR 3105568.
- Cēbers, A. (December 13, 2002). "Dynamics of an elongated magnetic droplet in a rotating field". Phys. Rev. E. 66 (6): 061402. Bibcode:2002PhRvE..66f1402C. doi:10.1103/PhysRevE.66.061402. PMID 12513280.
- Cēbers, A. & I. Javaitis (2004). "Dynamics of a flexible magnetic chain in a rotating magnetic field". Phys. Rev. E. 69 (2): 021404. Bibcode:2004PhRvE..69b1404C. doi:10.1103/PhysRevE.69.021404. PMID 14995441.
- Cēbers, A. & M. Ozols (2006). "Dynamics of an active magnetic particle in a rotating magnetic field". Phys. Rev. E. 73 (2): 021505. Bibcode:2006PhRvE..73b1505C. doi:10.1103/PhysRevE.73.021505. PMID 16605340.
- Tao Song; et al. (June 2004). "Rotating permanent magnetic fields exposure system for in vitro study". IEEE Transactions on Applied Superconductivity. 14 (2): 1643–6. Bibcode:2004ITAS...14.1643S. doi:10.1109/TASC.2004.831024.
- Labzovskii, L.N., A.O. Mitrushchenkov, and A.I. Frenkel, "Parity Nonconserving Current in Conductors of Electricity". 6 July 1987. (ed., Shows that the continuous current arises under the influence of the rotating magnetic field.)
- Naval Electrical Engineering Training Series, Module 05 -
Introduction to Generators and Motors, Chapter 4 Alternating Current
Motors, Rotating magnetic fields (ed. different copy of the NEETS book is available, Add-free version)
- Rotating Magnetic Field, eng.ox.ac.uk
- Tesla's Autobiography, III. My Later Endeavors; The Discovery of the Rotating Magnetic Field
- Nikola Tesla and the electro-magnetic motor, Inventor of the Week Archive.
- Galileo Ferraris: the rotating magnetic field
- Single Phase Induction Motors
- H.Y. Guo, A.L. Hoffman, D. Lotz, S.J. Tobin, W.A. Reass, L.S. Schrank and G.A. Wurden, The Rotating Magnetic Field Oscillator System for Current Drive in the Translation, Confinement and Sustainment Experiment, March 22, 2001.
- Putko, V. F., and V. S. Sobolev, Effect of a rotating magnetic field on the characteristics of a direct-current plasma generator.
External links
Patents
|
|---|
Career and
inventions | | |
|---|
| Writings | |
|---|
| Other | |
|---|
| Related | |
|---|
https://en.wikipedia.org/wiki/Rotating_magnetic_field
Earth's rotation or Earth's spin is the rotation of planet Earth around its own axis, as well as changes in the orientation of the rotation axis in space. Earth rotates eastward, in prograde motion. As viewed from the northern polar star Polaris, Earth turns counterclockwise.
https://en.wikipedia.org/wiki/Earth%27s_rotation
Magnetic hysteresis occurs when an external magnetic field is applied to a ferromagnet such as iron and the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. This is the effect that provides the element of memory in a hard disk drive.
https://en.wikipedia.org/wiki/Magnetic_hysteresis
Magnetic reluctance, or magnetic resistance, is a concept used in the analysis of magnetic circuits. It is defined as the ratio of magnetomotive force (mmf) to magnetic flux. It represents the opposition to magnetic flux, and depends on the geometry and composition of an object.
Magnetic reluctance in a magnetic circuit is analogous to electrical resistance in an electrical circuit in that resistance is a measure of the opposition to the electric current. The definition of magnetic reluctance is analogous to Ohm's law
in this respect. However, magnetic flux passing through a reluctance
does not give rise to dissipation of heat as it does for current through
a resistance. Thus, the analogy cannot be used for modelling energy
flow in systems where energy crosses between the magnetic and electrical
domains. An alternative analogy to the reluctance model which does
correctly represent energy flows is the gyrator–capacitor model.
Magnetic reluctance is a scalar extensive quantity. The unit for magnetic reluctance is inverse henry, H−1.
https://en.wikipedia.org/wiki/Magnetic_reluctance
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model
https://en.wikipedia.org/wiki/Lumped-element_model
The lumped-element model (also called lumped-parameter model, or lumped-component model) simplifies the description of the behaviour of spatially distributed physical systems, such as electrical circuits, into a topology
consisting of discrete entities that approximate the behaviour of the
distributed system under certain assumptions. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc. This may be contrasted to distributed parameter systems or models in which the behaviour is distributed spatially and cannot be considered as localized into discrete entities.
Mathematically speaking, the simplification reduces the state space of the system to a finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters.
https://en.wikipedia.org/wiki/Lumped-element_model
https://en.wikipedia.org/wiki/Utility_frequency#Load-frequency_control
Steam turbine governing is the procedure of controlling the flow rate of steam to a steam turbine
so as to maintain its speed of rotation as constant. The variation in
load during the operation of a steam turbine can have a significant
impact on its performance. In a practical situation the load frequently
varies from the designed or economic load and thus there always exists a
considerable deviation from the desired performance of the turbine.[1]
The primary objective in the steam turbine operation is to maintain a
constant speed of rotation irrespective of the varying load. This can
be achieved by means of governing in a steam turbine. There are many types of governors.
https://en.wikipedia.org/wiki/Steam_turbine_governing
A virtual power plant (VPP) is a cloud-based distributed power plant that aggregates the capacities of heterogeneous distributed energy resources
(DER) for the purposes of enhancing power generation, trading or
selling power on the electricity market, and demand side options for
load reduction.[1]
DER assets in a VPP can include photovoltaic solar, energy
storage, electric vehicle chargers, and demand-responsive devices (such
as water heaters, thermostats, and appliances) with examples of virtual
power plants existing in the United States, Europe, and Australia.
https://en.wikipedia.org/wiki/Virtual_power_plant
Power generation
A virtual power plant is a system that integrates several types of power sources to give a reliable overall power supply.[2]
The sources often form a cluster of different types of dispatchable and
non-dispatchable, controllable or flexible load (CL or FL) distributed generation (DG) systems that are controlled by a central authority and can include microCHPs, natural gas-fired reciprocating engines, small-scale wind power plants (WPP), photovoltaics (PV), run-of-river hydroelectricity plants, small hydro, biomass, backup generators, and energy storage systems (ESS).
This system has benefits such as the ability to deliver peak load electricity or load-following power
generation on short notice. Such a VPP can replace a conventional power
plant while providing higher efficiency and more flexibility, which
allows the system to react better to load fluctuations. The drawback is a
higher complexity of the system, which requires complicated
optimization, control, and secure communications.[3] An interactive simulation on the website of the VPP operator Next Kraftwerke illustrates how the technology works.[4]
According to a 2012 report by Pike Research, VPP capacity would,
from 2011 to 2017, increase by 65%, from 55.6 gigawatts (GW) to 91.7 GW
worldwide, generating from $5.3 billion to $6.5 billion in worldwide
revenue in 2017.[5]
In a more aggressive forecast scenario, the clean-tech market
intelligence firm forecasts that global VPP revenues could reach as high
as $12.7 billion during the same period.[6]
"Virtual power plants represent an 'Internet of Energy'",
said senior analyst Peter Asmus of Pike Research. "These systems tap
existing grid networks to tailor electricity supply and demand services
for a customer. VPPs maximize value for both the end user and the
distribution utility using a sophisticated set of software-based
systems. They are dynamic, deliver value in real time, and can react
quickly to changing customer load conditions."
Ancillary services
Virtual power plants can also be used to provide ancillary services to grid operators in order to help maintain grid stability. Ancillary services include frequency regulation, load following, and providing operating reserve.
These services are primarily used to maintain the instantaneous balance
of electrical supply and demand. Power plants providing ancillary
services must respond to signals from grid operators to increase or
decrease load on the order of seconds to minutes in response to varying
levels of consumer demand.
Since ancillary services are typically provided by controllable
fossil-fuel generators, future carbon-free electrical grids that contain
high percentages of solar and wind must rely on other forms of
controllable power generation or consumption. One of the most well-known
examples of this is Vehicle to Grid
technology. In this case, distributed electrical vehicles connected to
the grid can be controlled together to act as a single virtual power
plant. By selectively controlling the rate at which each individual
vehicle charges, the grid sees a net injection or consumption of energy
as if a large scale battery was providing this service.
Similarly, flexible demand in the form of heat pumps or air conditioners has also been explored to provide ancillary services to the grid.[7]
As long as indoor thermal comfort is maintained, an aggregation of
distributed heat pumps can be selectively turned off and on in order to
vary their aggregate power consumption and follow an ancillary service
signal. Again, the effect on the grid is the same as if a large scale
power plant was providing the service.
Since they operate in parallel, virtual power plants can have the
advantage of higher ramp rates than thermal generators, which is
especially important in grids that experience a duck curve
and have high ramping requirements in the morning and evening. However,
the distributed nature generates communication and latency issues,
which could be problematic for providing fast services like frequency
regulation.
Energy trading
A
virtual power plant is also a cloud-based central or distributed
control center that takes advantage of information and communication
technologies (ICTs) and Internet of things (IoT) devices to aggregate the capacities of heterogeneous Distributed Energy Resources (DERs) to form "a coalition of heterogeneous DERs" for the purpose of energy trading on the wholesale electricity markets or providing ancillary services for system operators on behalf of non-eligible individual DERs.[8][9][10][11][12]
A VPP acts as an intermediary between DERs and the wholesale
electricity market and trades energy on behalf of DER owners who by
themselves are unable to participate in that market.[11]
The VPP behaves as a conventional dispatchable power plant from the
point of view of other market participants, although it is indeed a
cluster of many diverse DERs. Also, in the competitive electricity
markets, a virtual power plant acts as an arbitrageur between diverse
energy trading floors (i.e., bilateral and PPA contracts, forward and
futures markets, and the pool).[8][9][10][12]
So far, for risk management purposes, five different risk-hedging
strategies (i.e., IGDT, RO, CVaR, FSD, and SSD) have been applied to
the decision-making problems of VPPs in the research articles to measure
the level of conservatism of VPPs' decisions in diverse energy trading
floors (e.g., day-ahead electricity market, derivatives exchange market,
and bilateral contracts):
- IGDT : Information Gap Decision Theory[8]
- RO : Robust optimization[9]
- CVaR : Conditional Value at Risk[10]
- FSD : First-order Stochastic Dominance[11]
- SSD : Second-order Stochastic Dominance[12][13]
United States
Energy markets are those commodity markets that deal specifically with the trade and supply of energy.[14]
In the United States, virtual power plants not only deal with the
supply side, but also help manage demand, and ensure reliability of grid
functions through demand response (DR) and other load-shifting approaches, in real time.[15]
An often-reported energy crisis in America[16]
has opened the door for government-subsidized companies to enter an
arena that has only been available to utilities and multinational
billion-dollar companies until now. With the deregulation of markets
around the United States, the wholesale market pricing became the
exclusive domain of large retail suppliers; however local and federal
legislation along with large end-users are beginning to recognize the
advantages of wholesale activities.[17]
Texas is in the stage of developing pilot VPP projects to evaluate the impact on service and reliability.[18]
They have had several meetings of their ADER (Aggregated Distributed
Energy Resources) task force to develop the criteria for pilot projects
to operate.[19]
In California there are two electrical markets: private retail
and wholesale. California Senate Bill 2X—which passed the California
legislature on March 30, 2011—mandates 33% renewables by 2020 without
mandating any particular method to reach that goal.[20] PG&E pays VPP providers $2/kWh during peak times.[21][22]
As of August/September 2022, SunRun VPP inputs 80 MW at peak times,[23] and Tesla VPP inputs 68 MW.[24][25]
Europe
The Institute for Solar Energy Supply Technology of the University of Kassel in Germany pilot-tested a combined power plant that linked solar, wind, biogas, and pumped-storage hydroelectricity to provide load-following power around the clock, completely from renewable sources.[26]
Virtual power station operators are also commonly referred to as aggregators.
To test the effects of micro combined heat and power on a smart grid, 45 natural gas SOFC units (each generating 1.5 kW) from Republiq Power (Ceramic Fuel Cells) will be placed in 2013 on Ameland to function as a virtual power plant.[27]
An example of a real-world virtual power plant can be found on the Scottish Inner Hebrides island of Eigg.[28]
Next Kraftwerke from Cologne, Germany operates a virtual power
plant in seven European countries providing peak-load operation, power
trading and grid balancing services. The company aggregates distributed
energy resources from biogas, solar and wind as well as large-scale
power consumers.[29]
Distribution network operator, UK Power Networks,
and Powervault, a battery manufacturer and power aggregator, created
London's first virtual power plant in 2018, installing a trial fleet of
battery systems on over 40 homes across the London Borough of Barnet,
providing a combined capacity of 0.32 MWh.[30] This scheme was further expanded through a second contract in St Helier, London in 2020.[31]
In September 2019, SMS plc entered the virtual power plant sector
in the United Kingdom following the acquisition of Irish energy tech
start-up, Solo Energy.[32]
In October 2020, Tesla launched its Tesla Energy Plan in the UK in partnership with Octopus Energy,
allowing households to join its UK Tesla Virtual Power Plant. Homes
under the scheme are powered with 100% renewable energy from either
solar panels on the roof or from Octopus Energy.[33]
Australia
Commencing
in August 2020, Tesla will install a 5 kW rooftop solar system and 13.5
kWh Powerwall battery at each Housing SA premises, at no upfront cost
to the tenant. As South Australia's largest virtual power plant, the
battery and solar systems can be centrally managed, collectively
delivering 20 MW of generation capacity and 54 MWh of energy storage.[34]
In August 2016, AGL Energy announced a 5 MW virtual-power-plant scheme for Adelaide, Australia. The company will supply battery and photovoltaic systems from Sunverge Energy, of San Francisco, to 1000 households and businesses. The systems will cost consumers AUD $3500 and are expected to recoup the expense in savings in 7 years under current distribution network tariffs. The scheme is worth AUD $20 million and is being billed as the largest in the world.[35]
See also
References
Zurborg, Aaron (2010). "Unlocking Customer Value: the Virtual Power Plant" (PDF). Energy.gov. Retrieved 15 January 2023.
Feasibility, beneficiality, and institutional compatibility of a micro-CHP virtual power plant in the Netherlands
Smart Grid - The New and Improved Power Grid: A Survey; IEEE Communications Surveys and Tutorials 2011; X. Fang, S. Misra, G. Xue, and D. Yang; doi:10.1109/SURV.2011.101911.00087.
"Manage the Virtual Power and prevent a blackout!". Next Kraftwerke. Retrieved 2 December 2019.
"Revenue from Virtual Power Plants Will Reach $5.3 Billion by 2017, Forecasts Pike Research" (Press release). Navigant Consulting. 18 April 2012. Retrieved 20 November 2017 – via Business Wire.
"Virtual-Power-Plant
Market Capacity Expected To Double By 2015 - Apr 16, 2011 -
renewgridmag.com - Transmission - Technical Articles - Index - Library -
GENI - Global Energy Network Institute". Global Energy Network Institute. 2011-04-16. Retrieved 2022-01-05.
Lee,
Zachary E.; Sun, Qingxuan; Ma, Zhao; Wang, Jiangfeng; MacDonald, Jason
S.; Zhang, K. Max (Feb 2020). "Providing Grid Services With Heat Pumps: A
Review". Journal of Engineering for Sustainable Buildings and Cities. 1 (1). doi:10.1115/1.4045819. S2CID 213898377.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2015). "Decision
Making Tool for Virtual Power Plants Considering Midterm Bilateral
Contracts". 3rd Iranian Regional CIRED Conference and Exhibition on
Electricity Distribution, at Niroo Research Institute (NRI), Tehran,
Iran. 3 (3): 1–6. doi:10.13140/2.1.5086.4969.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (October 2015). "The design
of a risk-hedging tool for virtual power plants via robust optimization
approach". Applied Energy. 155: 766–777. doi:10.1016/j.apenergy.2015.06.059.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (May 2016). "A medium-term
coalition-forming model of heterogeneous DERs for a commercial virtual
power plant". Applied Energy. 169: 663–681. doi:10.1016/j.apenergy.2016.02.058.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2017). "Risk-based
medium-term trading strategy for a virtual power plant with first-order
stochastic dominance constraints". IET Generation, Transmission & Distribution. 11 (2): 520–529. doi:10.1049/iet-gtd.2016.1072. S2CID 114478127.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (April 2016). "Modeling the
cooperation between neighboring VPPs: Cross-regional bilateral
transactions". 2016 Iranian Conference on Renewable Energy & Distributed Generation (ICREDG). 11: 520–529. doi:10.1109/ICREDG.2016.7875909. ISBN 978-1-5090-0857-5. S2CID 16453458.
Shabanzadeh,
Morteza; Sheikh-El-Eslami, Mohammad-Kazem; Haghifam, Mahmoud-Reza
(2017). "An interactive cooperation model for neighboring virtual power
plants". Applied Energy. 200: 273–289. doi:10.1016/j.apenergy.2017.05.066. S2CID 157309706.
JEAN-PHILIPPE TAILLON, CFA (2021-10-14). "Introduction to the World of Electricity Trading". Investopedia. Retrieved 2022-01-04.
Aaron Zurborg (2010). "Unlocking Customer Value: The Virtual Power Plant". WorldPower 2010: 1–5.
"Energy Crisis (1970s) - HISTORY". history.com. 2018-08-21. Retrieved 2022-01-04.
"Electricity Deregulation". PennStation Extension. 2010-06-15. Retrieved 2022-01-05.
https://interchange.puc.texas.gov/Documents/51603_66_1221955.PDF
"Admin Monitor - Texas - Public Utility Commission of Texas".
PATRICK MCGREEVY (2011-04-13). "Gov. Brown signs law requiring 33% of energy be renewable by 2020 - Los Angeles Times". Los Angeles Times. Retrieved 2021-01-05.
"PG&E, Tesla virtual power plant delivers 16.5 MW to California grid amid calls for energy conservation". Utility Dive. 23 August 2022.
"Admin Monitor - Texas - Public Utility Commission of Texas".
Colthorpe, Andy (8 September 2022). "California's fleet of battery storage working to avert energy crisis". Energy Storage News.
Lambert, Fred (2022-09-02). "Tesla virtual power plant is rocketing up, reaches 50 MW". Electrek. Retrieved 2022-09-08.
"Tesla's Virtual Power Plant Tracker". Lastbulb. Retrieved 2022-09-08.
"The Combined Power Plant: the first stage in providing 100% power from renewable energy". SolarServer. January 2008. Retrieved 2008-10-10.
"Bijlage persbericht 010/MK – Verleende subsidies – 3. Methaanbrandstoffen op Ameland" [Press release 010/MK appendix – Granted subsidies – 3. Methane fuels on Ameland] (PDF). Wadden Fund (Press release) (in Dutch). 2013. Archived from the original (PDF) on 1 November 2013. Retrieved 21 November 2017.
BBC Radio 4. Costing the Earth- Electric Island
"Next Kraftwerk Reimagines & Redefines The Electrical Grid With Virtual Power Plants". Clean Technica. October 2016. Retrieved 2019-03-13.
"Electricity network plan to launch London's first virtual power station". UK Power Networks. 22 June 2018. Retrieved 15 October 2021.
"London pioneers first 'virtual power station'". GOV.UK. 6 March 2020. Retrieved 1 July 2021.
Grundy, Alice (27 March 2020). "Smart Metering Systems reveals Solo Energy acquisition as it enters VPP market". Current News. Retrieved 1 July 2021.
Lempriere, Molly (27 October 2020). "Tesla Energy Plan launched inviting homes to become part of Virtual Power Plant". Current News. Retrieved 1 July 2021.
"Social housing added to the Tesla virtual power plant - ARENAWIRE". Australian Renewable Energy Agency. Retrieved 2021-01-06.
External links
|
|---|
| Concepts | | |
|---|
| Sources | |
|---|
| Generation | |
|---|
| |
|---|
| Failure modes | |
|---|
Protective
devices | |
|---|
Economics
and policies | |
|---|
Statistics and
production | |
|---|
|
https://en.wikipedia.org/wiki/Virtual_power_plant
lectrical busbar systems[1] (sometimes simply referred to as busbar systems) are a modular approach to electrical wiring,
where instead of a standard cable wiring to every single electrical
device, the electrical devices are mounted onto an adapter which is
directly fitted to a current carrying busbar. This modular approach is used in distribution boards, automation panels and other kinds of installation in an electrical enclosure.[2]
Busbar systems are subject to safety standards for design and installation along with electrical enclosure according to IEC 61439-1 and vary between countries and regions.[3]
https://en.wikipedia.org/wiki/Electrical_busbar_system
A black start is the process of restoring an electric power station or a part of an electric grid to operation without relying on the external electric power transmission network to recover from a total or partial shutdown.[1]
Power to restart a generating station may come from an on-site
standby generator. Alternatively, where a large amount of power is
required, a tie-line to another generating plant may be used to start
the facility. Once the main generating units are running, the electrical
transmission network can be re-connected and electrical loads restored.
Black-start power may be ensured by an agreement where a
particular energy supplier is paid to make black start power available
when required. Not all generating plants are suitable for providing
black-start power to a network.
https://en.wikipedia.org/wiki/Black_start
A rolling blackout, also referred to as rota or rotational load shedding, rota disconnection, feeder rotation, or a rotating outage, is an intentionally engineered electrical power shutdown in which electricity delivery
is stopped for non-overlapping periods of time over different parts of
the distribution region. Rolling blackouts are a last-resort measure
used by an electric utility company to avoid a total blackout of the power system.
Rolling blackouts are a measure of demand response
if the demand for electricity exceeds the power supply capability of
the network. Rolling blackouts may be localised to a specific part of
the electricity network, or they may be more widespread and affect
entire countries and continents. Rolling blackouts generally result from
two causes: insufficient generation capacity or inadequate transmission infrastructure to deliver power to where it is needed.
Rolling blackouts are also used as a response strategy to cope with reduced output beyond reserve capacity from power stations taken offline unexpectedly.
https://en.wikipedia.org/wiki/Rolling_blackout
A cascading failure is a failure in a system of interconnected parts in which the failure of one or few parts leads to the failure of other parts, growing progressively as a result of positive feedback. This can occur when a single part fails, increasing the probability that other portions of the system fail.[1][2]
Such a failure may happen in many types of systems, including power
transmission, computer networking, finance, transportation systems,
organisms, the human body, and ecosystems.
Cascading failures may occur when one part of the system fails.
When this happens, other parts must then compensate for the failed
component. This in turn overloads these nodes, causing them to fail as
well, prompting additional nodes to fail one after another.
https://en.wikipedia.org/wiki/Cascading_failure
A single point of failure (SPOF) is a part of a system that, if it fails, will stop the entire system from working.[1] SPOFs are undesirable in any system with a goal of high availability or reliability, be it a business practice, software application, or other industrial system.
Overview
Systems can be made robust by adding redundancy in all potential SPOFs. Redundancy can be achieved at various levels.
The assessment of a potential SPOF involves identifying the
critical components of a complex system that would provoke a total
systems failure in case of malfunction. Highly reliable systems should not rely on any such individual component.
For instance, the owner of a small tree care company may only own one woodchipper.
If the chipper breaks, he may be unable to complete his current job and
may have to cancel future jobs until he can obtain a replacement. The
owner of the tree care company may have spare parts
ready for the repair of the wood chipper, in case it fails. At a higher
level, he may have a second wood chipper that he can bring to the job
site. Finally, at the highest level, he may have enough equipment
available to completely replace everything at the work site in the case
of multiple failures.
Possible SPOFs in a simple setup
Using redundancy to avoid some SPOFs
Completely redundant system without SPOFs (note: assumes generator
and grid sources are each rated at N, each UPS is rated at N, and "A/C"
and "Electrical" are in themselves completely fault tolerant systems)
Computing
| This section needs to be updated. The reason given is: Needs updating for public cloud computing. Please help update this article to reflect recent events or newly available information. (May 2022) |
A fault-tolerant computer system can be achieved at the internal component level, at the system level (multiple machines), or site level (replication).
One would normally deploy a load balancer to ensure high availability for a server cluster
at the system level. In a high-availability server cluster, each
individual server may attain internal component redundancy by having
multiple power supplies, hard drives, and other components. System-level
redundancy could be obtained by having spare servers waiting to take on
the work of another server if it fails.
Since a data center is often a support center for other
operations such as business logic, it represents a potential SPOF in
itself. Thus, at the site level, the entire cluster may be replicated at
another location, where it can be accessed in case the primary location
becomes unavailable. This is typically addressed as part of an IT
disaster recovery (resiliency) program.
Paul Baran and Donald Davies developed packet switching, a key part of "survivable communications networks". Such networks – including ARPANET and the Internet –
are designed to have no single point of failure. Multiple paths
between any two points on the network allow those points to continue
communicating with each other, the packets "routing around" damage, even after any single failure of any one particular path or any one intermediate node.
Software engineering
In software engineering, a bottleneck occurs when the capacity of an application
or a computer system is limited by a single component. The bottleneck
has lowest throughput of all parts of the transaction path.
Performance engineering
Tracking down bottlenecks (sometimes known as hot spots – sections of the code that execute most frequently – i.e., have the highest execution count) is called performance analysis.
Reduction is usually achieved with the help of specialized tools, known
as performance analyzers or profilers. The objective is to make those
particular sections of code perform as fast as possible to improve
overall algorithmic efficiency.
Computer security
A vulnerability or security exploit in just one component can compromise an entire system.
Other fields
The
concept of a single point of failure has also been applied to fields
outside of engineering, computers, and networking, such as corporate supply chain management[2] and transportation management.[3]
Design structures that create single points of failure include bottlenecks and series circuits (in contrast to parallel circuits).
In transportation, some noted recent examples of the concept's recent application have included the Nipigon River Bridge in Canada, where a partial bridge failure in January 2016 entirely severed road traffic between Eastern Canada and Western Canada for several days because it is located along a portion of the Trans-Canada Highway where there is no alternate detour route for vehicles to take;[4] and the Norwalk River Railroad Bridge in Norwalk, Connecticut, an aging swing bridge that sometimes gets stuck when opening or closing, disrupting rail traffic on the Northeast Corridor line.[3]
The concept of a single point of failure has also been applied to the fields of intelligence. Edward Snowden talked of the dangers of being what he described as "the single point of failure" – the sole repository of information.[5]
Life-support systems
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion. You can help by adding to it. (October 2019) |
A component of a life-support system that would constitute a single point of failure would be required to be extremely reliable.
See also
Concepts
Applications
- Kill switch – Safety mechanism to quickly shut down a system
- Jesus nut – Slang term for the main rotor-retaining nut of some helicopters
- Reliability engineering – Sub-discipline of systems engineering that emphasizes dependability
- Safety engineering – Engineering discipline which assures that engineered systems provide acceptable levels of safety
- Dead man's switch – Equipment that activates or deactivates upon the incapacitation of operator
In literature
- Achilles' heel – Critical weakness which can lead to downfall in spite of overall strength
- Hamartia – Protagonist's error in Greek dramatic theory
References
1:
Designing Large-scale LANs – Page 31, K. Dooley, O'Reilly, 2002
Gary S. Lynch (Oct 7, 2009). Single Point of Failure: The 10 Essential Laws of Supply Chain Risk Management. Wiley. ISBN 978-0-470-42496-4.
"Crucial, Century-Old, And Sometimes Stuck: Connecticut Bridge Is Key To Northeast Corridor". Connecticut Public Radio, August 8, 2017.
"The Nipigon River Bridge and other Trans-Canada bottlenecks". Global News, January 11, 2016.
https://en.wikipedia.org/wiki/Single_point_of_failure
https://en.wikipedia.org/wiki/Floppy_disk
https://en.wikipedia.org/wiki/Thin-film_memory
https://en.wikipedia.org/wiki/Non-volatile_memory
https://en.wikipedia.org/wiki/Magnetoresistive_RAM
https://en.wikipedia.org/wiki/Gamma_Pegasi
https://en.wikipedia.org/wiki/Thermocouple
https://en.wikipedia.org/wiki/Bubble_memory
https://en.wikipedia.org/wiki/CMC_Magnetics
https://en.wikipedia.org/wiki/Physics_of_magnetic_resonance_imaging
https://en.wikipedia.org/wiki/Drum_memory
https://en.wikipedia.org/wiki/Magnetic-tape_data_storage
https://en.wikipedia.org/wiki/Magnetic-core_memory
https://en.wikipedia.org/wiki/Hard_disk_drive
https://en.wikipedia.org/wiki/Curl_(mathematics)
Data degradation is the gradual corruption of computer data due to an accumulation of non-critical failures in a data storage device. The phenomenon is also known as data decay, data rot or bit rot.
https://en.wikipedia.org/wiki/Data_degradation
https://en.wikipedia.org/wiki/Mini-Cassette
https://en.wikipedia.org/wiki/Semiconductor_memory
https://en.wikipedia.org/wiki/Digital_dark_age
https://en.wikipedia.org/wiki/Linear_Tape-Open
https://en.wikipedia.org/wiki/List_of_The_Muppet_Show_episodes
https://en.wikipedia.org/wiki/Parafilm
https://en.wikipedia.org/wiki/Domino_Recording_Company
https://en.wikipedia.org/wiki/Motor_capacitor
https://en.wikipedia.org/wiki/Starlight
https://en.wikipedia.org/wiki/Non-volatile_random-access_memory
https://en.wikipedia.org/wiki/Eddy-current_testing
https://en.wikipedia.org/wiki/List_of_Ghost_Adventures_episodes
https://en.wikipedia.org/wiki/Stephin_Merritt_discography
https://en.wikipedia.org/wiki/Core_rope_memory
https://en.wikipedia.org/wiki/Pyramid_power
https://en.wikipedia.org/wiki/Data_storage
https://en.wikipedia.org/wiki/Random-access_memory
https://en.wikipedia.org/wiki/Computer_memory
https://en.wikipedia.org/w/index.php?limit=20&offset=20&profile=default&search=magnetic+rot&title=Special:Search&ns0=1&searchToken=cems966l2d75df9ijilqv36hq
Magnetic inductance
Circuit equivalence between a magnetic inductance and an electric capacitance.
In the context of the gyrator-capacitor model of a magnetic circuit, magnetic inductance  (SI unit: F) is the analogy to inductance in an electrical circuit.
(SI unit: F) is the analogy to inductance in an electrical circuit.
For phasor analysis the magnetic inductive reactance is:
where:
In the complex form it is a positive imaginary number:
The magnetic potential energy sustained by magnetic inductance
varies with the frequency of oscillations in electric fields. The
average power in a given period is equal to zero. Due to its dependence
on frequency, magnetic inductance is mainly observable in magnetic
circuits which operate at VHF and/or UHF frequencies.[citation needed]
The notion of magnetic inductance is employed in analysis and
computation of circuit behavior in the gyrator–capacitor model in a way
analogous to inductance in electrical circuits.
A magnetic inductor can represent an electrical capacitor.[4]: 43
A shunt capacitance in the electrical circuit, such as intra-winding
capacitance can be represented as a series inductance in the magnetic
circuit.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
The gyrator–capacitor model[1] - sometimes also the capacitor-permeance model[2] - is a lumped-element model for magnetic circuits, that can be used in place of the more common resistance–reluctance model. The model makes permeance elements analogous to electrical capacitance (see magnetic capacitance section) rather than electrical resistance (see magnetic reluctance). Windings are represented as gyrators, interfacing between the electrical circuit and the magnetic model.
The primary advantage of the gyrator–capacitor model compared to
the magnetic reluctance model is that the model preserves the correct
values of energy flow, storage and dissipation.[3][4] The gyrator–capacitor model is an example of a group of analogies
that preserve energy flow across energy domains by making power
conjugate pairs of variables in the various domains analogous. It fills
the same role as the impedance analogy for the mechanical domain.
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model#Magnetic_inductance
Category:Magnetic circuits
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Magnetic_circuits
Category:Electrical analogies
From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Category:Electrical_analogies
Magnetic induction
From Wikipedia, the free encyclopedia
Magnetic induction may refer to:
Category:
https://en.wikipedia.org/wiki/Magnetic_induction
https://en.wikipedia.org/wiki/Synchronization_(alternating_current)
https://en.wikipedia.org/wiki/Category:AC_power
https://en.wikipedia.org/wiki/Category:Three-phase_AC_power
https://en.wikipedia.org/wiki/Symmetrical_components
https://en.wikipedia.org/wiki/Linearly_independent
https://en.wikipedia.org/wiki/Root_mean_square#Voltage
https://en.wikipedia.org/wiki/Droop_speed_control
https://en.wikipedia.org/wiki/Beat_(acoustics)
https://en.wikipedia.org/wiki/Interference_(wave_propagation)
In AC electrical power systems, a synchroscope is a device that indicates the degree to which two systems (generators or power networks) are synchronized with each other.[1]
For two electrical systems to be synchronized, both systems must operate at the same frequency, and the phase angle between the systems must be zero (and two polyphase systems must have the same phase sequence).
Synchroscopes measure and display the frequency difference and phase
angle between two power systems. Only when these two quantities are zero
is it safe to connect the two systems together. Connecting two
unsynchronized AC power systems together is likely to cause high
currents to flow, which will severely damage any equipment not protected
by fuses or circuit breakers.

This synchroscope was used to synchronize a factory's power plant with the utility's power grid.
https://en.wikipedia.org/wiki/Synchroscope
https://en.wikipedia.org/wiki/Three-phase_electric_power#Phase_sequence
https://en.wikipedia.org/wiki/Relay
https://en.wikipedia.org/wiki/Circuit_breaker
https://en.wikipedia.org/wiki/Deformed_power
https://en.wikipedia.org/wiki/Leading_and_lagging_current
A rotary phase converter, abbreviated RPC, is an electrical machine that converts power from one polyphase system to another, converting through rotary motion. Typically, single-phase electric power is used to produce three-phase electric power locally to run three-phase loads in premises where only single-phase is available.

A simple homemade phase converter
https://en.wikipedia.org/wiki/Rotary_phase_converter
In communication theory, time-varying phasors are used for analyzing narrow-band signals, whose signal bandwidths in the frequency domain are considerably smaller than the carrier frequency.[1][2] Time-varying phasors are mostly used for analysis of frequency domain of band-pass systems.[2][1] The method uses classical impulse response.[1]
In electrical power system, phasors are used for transient analysis of the power system keeping the quasi-stationary conditions.[1][3][4] They were introduced to facilitate the computation and analysis of power systems in stationary operation.[3] Time-varying phasors are used in dynamic analysis of a large power system.[1][5] The phasor representation of sinusoidal voltages and currents is generalized to arbitrary waveforms.[2] This mathematical transformation eliminates the 60 Hertz (Hz) carrier which is the only time-varying element in the stationary case.[3]
The longer usage of time-varying phasors in large power systems since
1920s have created many misconceptions. One of the misuses suggest that quasi-stationary
models are always accurate, but only when the system dynamics are slow
as compared to nominal system frequency which is usually 60 Hz.[4]
The concern to study time-varying phasors is raised to understand
in-depth the fast amplitude and phase variations of emerging electrical
power generator technologies.[4] This is because current and voltage signals of latest machines may have harmonic components and they can damage the entire transmission system which is coupled with the machine.[3][4]
However, if we employ quasi-static model, we can accurately model AC
signals by using time-varying phasors as opposed to traditional
quasi-static model which supports constant voltage and current signals
throughout the network.[5]
https://en.wikipedia.org/wiki/Time-varying_phasor
Single-phase generator (also known as single-phase alternator) is an alternating current electrical generator that produces a single, continuously alternating voltage. Single-phase generators can be used to generate power in single-phase electric power systems. However, polyphase generators are generally used to deliver power in three-phase distribution
system and the current is converted to single-phase near the
single-phase loads instead. Therefore, single-phase generators are found
in applications that are most often used when the loads being driven
are relatively light,[1] and not connected to a three-phase distribution, for instance, portable engine-generators. Larger single-phase generators are also used in special applications such as single-phase traction power for railway electrification systems.[2]

Elementary generator is an example of single-phase generators with two poles
https://en.wikipedia.org/wiki/Single-phase_generator
Polyphase coils are electromagnetic coils connected together in a polyphase system such as a generator or motor. In modern systems, the number of phases is usually three or a multiple of three. Each phase carries a sinusoidal alternating current whose phase
is delayed relative to one of its neighbours and advanced relative to
its other neighbour. The phase currents are separated in time evenly
within each period of the alternating current. For example, in a
three-phase system, the phases are separated from each other by
one-third of the period.
Coil construction
Like all coils used in electrical machinery, polyphase coils (made from insulated conducting wire) are wound around ferromagnetic armatures with radial projections and maximum core-surface exposure to the magnetic field.
The windings are physically separated around the circumference of an electrical machine. The result of such an arrangement is a rotating magnetic field that is used to convert electrical power to rotary mechanical work, or vice versa.
https://en.wikipedia.org/wiki/Polyphase_coil
https://en.wikipedia.org/wiki/Category:AC_power
A Scott-T transformer (also called a Scott connection) is a type of circuit used to produce two-phase electric power (2 φ, 90 degree phase rotation)[1] from a three-phase
(3 φ, 120 degree phase rotation) source, or vice versa. The Scott
connection evenly distributes a balanced load between the phases of the
source. The Scott three-phase transformer was invented by a Westinghouse engineer Charles F. Scott in the late 1890s to bypass Thomas Edison's more expensive rotary converter and thereby permit two-phase generator plants to drive three-phase motors.[2]
https://en.wikipedia.org/wiki/Scott-T_transformer
History
The first locomotive with a phase converter (only for demonstration purposes)
The Kandó phase converter (1933)
The "Kandó" locomotive, the first locomotive using a phase converter system
At the beginning of the 20th century, there were two main principles of electric railway traction current systems:
- DC system
- 16⅔ Hz single phase system
These systems used series-wound traction motors. All of them needed a separated supply system or converters to take power from the standard 50 Hz electric network.
https://en.wikipedia.org/wiki/Rotary_phase_converter
Unbalanced loads
Two-phase
motors draw constant power, just as three-phase motors do, so a
balanced two-phase load is converted to a balanced three-phase load.
However if a two-phase load is not balanced (more power drawn from one
phase than the other), no arrangement of transformers (including the
Scott-T transformers) can restore balance: Unbalanced current on the
two-phase side causes unbalanced current on the three-phase side. Since
the typical two-phase load was a motor, the current in the two phases
was presumed inherently equal during the Scott-T development.
In modern times people have tried to revive the Scott connection as a way to power single-phase electric railways
from three-phase Utility supplies. This will not result in balanced
current on the three-phase of being equal. The instantaneous
difference in loading on the two sections will be seen as an imbalance
in the three-phase supply; there is no way to smooth it out with
transformers.[4]
https://en.wikipedia.org/wiki/Scott-T_transformer
Back to back arrangement
Scott Connection 3 φ to 3 φ
The Scott-T transformer connection may also be used in a back-to-back
T-to-T arrangement for a three-phase to three-phase connection. This is
a cost-saving in the lower-power transformers due to the two-coil T
connected to a secondary two-coil T instead of the traditional
three-coil primary to three-coil secondary transformer. In this
arrangement the X0 neutral tap is part way up on the secondary teaser
transformer (see right). The voltage stability of this T-to-T
arrangement as compared to the traditional three-coil primary to
three-coil secondary transformer is questioned, as the "per unit"
impedance of the two windings (primary and secondary, respectively) are not the same in a T-to-T configuration, whereas the three windings (primary and secondary, respectively) are the same in a three transformer configuration, if the three transformers are identical.
Three-phase to three-phase (also called "T-connected")
distribution transformers are seeing increasing applications. The
primary must be delta-connected (Δ), but the secondary may be either delta or "wye"-connected (Y),
at the customer's option, with X0 providing the neutral for the "wye"
case. Taps for either case are usually provided. The customary maximum
capacity of such a distribution transformer is 333 kVA (a third of a
megawatt at unity power factor).[citation needed]
https://en.wikipedia.org/wiki/Scott-T_transformer
An induction regulator is an alternating current electrical machine, somewhat similar to an induction motor, which can provide a continuously variable output voltage.
The induction regulator was an early device used to control the voltage
of electric networks. Since the 1930s it has been replaced in
distribution network applications by the tap transformer. Its usage is now mostly confined to electrical laboratories, electrochemical processes and arc welding. With minor variations, its setup can be used as a phase-shifting power transformer.
https://en.wikipedia.org/wiki/Induction_regulator
Magnet wire or enameled wire is a copper (Cu) or aluminium (Al) wire coated with a very thin layer of insulation. It is used in the construction of transformers, inductors, motors, generators,
speakers, hard disk head actuators, electromagnets, electric guitar pickups and other applications that require tight coils of insulated wire.
The wire itself is most often fully annealed,
electrolytically refined copper. Aluminium magnet wire is sometimes
used for large transformers and motors. The insulation is typically made
of tough polymer film materials rather than vitreous enamel, as the name might suggest.
https://en.wikipedia.org/wiki/Magnet_wire
In electronics, a center tap (CT) is a contact made to a point halfway along a winding of a transformer or inductor, or along the element of a resistor or a potentiometer.
Taps are sometimes used on inductors for the coupling of signals,
and may not necessarily be at the half-way point, but rather, closer to
one end. A common application of this is in the Hartley oscillator. Inductors with taps also permit the transformation of the amplitude of alternating current (AC) voltages for the purpose of power conversion, in which case, they are referred to as autotransformers, since there is only one winding. An example of an autotransformer is an automobile ignition coil.
Potentiometer tapping provides one or more connections along the
device's element, along with the usual connections at each of the two
ends of the element, and the slider connection. Potentiometer taps allow
for circuit functions that would otherwise not be available with the
usual construction of just the two end connections and one slider
connection.
https://en.wikipedia.org/wiki/Center_tap
A relief valve or pressure relief valve (PRV) is a type of safety valve used to control or limit the pressure
in a system; excessive pressure might otherwise build up and create a
process upset, instrument or equipment failure, explosion, or fire.
https://en.wikipedia.org/wiki/Relief_valve
The open-circuit test, or no-load test, is one of the methods used in electrical engineering to determine the no-load impedance in the excitation branch of a transformer.
The no load is represented by the open circuit, which is represented on
the right side of the figure as the "hole" or incomplete part of the
circuit.
https://en.wikipedia.org/wiki/Open-circuit_test
Electrical insulation papers are paper types that are used as electrical insulation in many applications due to pure cellulose having outstanding electrical properties. Cellulose is a good insulator and is also polar,[clarification needed] having a dielectric constant significantly greater than one.[1]
Electrical paper products are classified by their thickness, with tissue
considered papers less than 1.5 mils (0.0381 mm) thickness, and board considered more than 20 mils (0.508 mm) thickness.[2]
https://en.wikipedia.org/wiki/Electrical_insulation_paper
A balun (from "balanced to unbalanced", originally, but now dated from "balancing unit")[1] is an electrical device that allows balanced and unbalanced lines to be interfaced without disturbing the impedance arrangement of either line.[2] A balun can take many forms and may include devices that also transform impedances but need not do so. Sometimes, in the case of transformer baluns, they use magnetic coupling but need not do so. Common-mode chokes are also used as baluns and work by eliminating, rather than rejecting, common mode signals.
https://en.wikipedia.org/wiki/Balun
In electrical engineering, the method of symmetrical components simplifies analysis of unbalanced three-phase power systems under both normal and abnormal conditions. The basic idea is that an asymmetrical set of N phasors can be expressed as a linear combination of N symmetrical sets of phasors by means of a complex linear transformation.[1] Fortescue's theorem (symmetrical components) is based on superposition principle,[2] so it is applicable to linear power systems only, or to linear approximations of non-linear power systems.
In the most common case of three-phase systems, the resulting "symmetrical" components are referred to as direct (or positive), inverse (or negative) and zero (or homopolar).
The analysis of power system is much simpler in the domain of
symmetrical components, because the resulting equations are mutually linearly independent if the circuit itself is balanced.[citation needed]
https://en.wikipedia.org/wiki/Symmetrical_components
A solid-state transformer (SST), power electronic transformer (PET), or electronic power transformer is actually an AC-to-AC converter, a type of electric power converter that replaces a conventional transformer used in AC electric power distribution. It is more complex than a conventional transformer operating at utility frequency,
but it can be smaller and more efficient than a conventional
transformer because it operates at high frequency. The main types are
"true" AC-to-AC converter (with no DC stages) and AC-to-DC-to-DC-to-AC
converter (in which an active rectifier supplies power to a DC-to-DC converter, which supplies power to a power inverter).
A solid-state transformer usually contains a transformer, inside the
AC-to-AC converter or DC-to-DC converter, which provides electrical
isolation and carries the full power. This transformer is smaller due to
smaller DC-DC inverting stages between transformer coils, which
consequently mean smaller transformer coils required to step up or step
down voltages. A solid-state transformer can actively regulate voltage
and current. Some can convert single-phase power to three-phase power
and vice versa. Variations can input or output DC power to reduce the number of conversions, for greater end-to-end efficiency. A Modular Solid-state transformer consists of several high-frequency transformers[1] and is similar to a Multi-level converter.
As a complex electronic circuit, it must be designed to withstand
lightning and other surges. Solid-state transformer is an emerging
technology.
https://en.wikipedia.org/wiki/Solid-state_transformer
A grounding transformer or earthing transformer is a type of auxiliary transformer used in three-phase electric power systems to provide a ground path to either an ungrounded wye or a delta-connected system.[1][2] Grounding transformers are part of an earthing system of the network. They let three-phase (delta connected) systems accommodate phase-to-neutral loads by providing a return path for current to a neutral.
Grounding transformers are typically used to:
- Provide a relatively low-impedance path to ground, thereby maintaining the system neutral at or near ground potential.[3]
- Limit the magnitude of transient overvoltages when restriking ground faults occur.
- Provide a source of ground fault current during line-to-ground faults.
- Permit the connection of phase-to-neutral loads when desired.[2]
Earthing transformer with a zig-zag
Grounding transformers most commonly incorporate a single winding transformer with a zigzag winding configuration, but may also be created with a wye-delta winding transformer.[2][4] Neutral grounding transformers are very common on generators in power plants and wind farms.[2]
Neutral grounding transformers are sometimes applied on high-voltage
(sub-transmission) systems, such as at 33 kV, where the circuit would
otherwise not have a ground; for example, if a system is fed by a
delta-connected transformer. The grounding point of the transformer may
be connected through a resistor or arc suppression coil to limit the
fault current on the system in the event of a line-to-ground fault. [5]
https://en.wikipedia.org/wiki/Grounding_transformer
An autotransformer is an electrical transformer with only one winding. The "auto" (Greek for "self") prefix refers to the single coil acting alone, not to any kind of automatic mechanism. In an autotransformer, portions of the same winding act as both the primary winding and secondary winding
sides of the transformer. In contrast, an ordinary transformer has
separate primary and secondary windings which have no metallic
conducting path between them.
The autotransformer winding has at least three taps
where electrical connections are made. Since part of the winding does
"double duty", autotransformers have the advantages of often being
smaller, lighter, and cheaper than typical dual-winding transformers,
but the disadvantage of not providing electrical isolation between primary and secondary circuits. Other advantages of autotransformers include lower leakage reactance, lower losses, lower excitation current, and increased VA rating for a given size and mass.[1]
An example of an application of an autotransformer is one style
of traveler's voltage converter, that allows 230-volt devices to be used
on 120-volt supply circuits, or the reverse. An autotransformer with
multiple taps may be applied to adjust the voltage at the end of a long
distribution circuit to correct for excess voltage drop; when
automatically controlled, this is one example of a voltage regulator.

Single-phase tapped autotransformer with an output voltage range of 40%–115% of input
https://en.wikipedia.org/wiki/Autotransformer
See also
https://en.wikipedia.org/wiki/Autotransformer
A zigzag transformer is a special-purpose transformer with a zigzag or "interconnected star" winding connection, such that each output is the vector sum of two (2) phases offset by 120°.[1] It is used as a grounding transformer, creating a missing neutral connection from an ungrounded 3-phase system to permit the grounding of that neutral to an earth reference point; to perform harmonic mitigation, as they can suppress triplet (3rd, 9th, 15th, 21st, etc.) harmonic currents;[2] to supply 3-phase power as an autotransformer (serving as the primary and secondary with no isolated circuits);[3] and to supply non-standard, phase-shifted, 3-phase power.[1]
9-winding zigzag transformer
Nine-winding, three-phase transformers typically have three primaries
and six identical secondary windings, which can be used in zigzag
winding connection as pictured.[1] As with the conventional delta or wye winding configuration three-phase
transformer, a standard, stand-alone transformer containing only six
windings on three cores can also be used in zigzag winding connection,
such transformer sometimes being referred to as a zigzag bank.[1]
In all cases, six or nine winding, the first coil on each zigzag
winding core is connected contrariwise to the second coil on the next
core. The second coils are then all tied together to form the neutral,
and the phases are connected to the primary coils. Each phase,
therefore, couples with each other phase, and the voltages cancel out.
As such, there would be negligible current through the neutral point,
which can be tied to ground.[4]
Each of the three "limbs" are split into two sections. The two
halves of each limb have an equal number of turns and are wound in
opposite directions. With the neutral grounded, during a phase-to-ground
short fault, a third of the current returns to the fault current, and
the remainder must go through two of the three phases when used to
derive a grounding point from a delta source.[5]
If one or more phases fault to earth, the voltage applied to each
phase of the transformer is no longer in balance; fluxes in the
windings no longer oppose. (Using symmetrical components, this is Ia0 = Ib0 = Ic0.)
Zero-sequence (earth fault) current exists between the transformer’s
neutral to the faulting phase. The purpose of a zigzag transformer in
this application is to provide a return path for earth faults on
delta-connected systems. With negligible current in the neutral under
normal conditions, an undersized (unable to carry a continuous fault
load) transformer may be used only as short-time rating is required,
provided the defective load will be automatically disconnected in a
fault condition. The transformer's impedance should not be too low for
desired maximum fault current. Impedance can be added after the
secondaries are summed to limit maximum fault currents (the 3Io path).[6]
A combination of Y (wye or star), delta, and zigzag windings may be used to achieve a vector phase shift.
For example, an electrical network may have a transmission network of
110 kV/33 kV star/star transformers, with 33 kV/11 kV delta/star for the
high voltage distribution network. If a transformation is required
directly between the 110 kV/11 kV network an option is to use a 110
kV/11 kV star/delta transformer. The problem is that the 11 kV delta no
longer has an earth reference point. Installing a zigzag transformer
near the secondary side of the 110 kV/11 kV transformer provides the
required earth reference point.[7]
https://en.wikipedia.org/wiki/Zigzag_transformer
Railway electrification systems using alternating current (AC) at 25 kilovolts (kV) are used worldwide, especially for high-speed rail. It is usually supplied at the standard utility frequency (typically 50 or 60 Hz), which simplifies traction substations. The development of 25 kV AC electrification is closely connected with that of successfully using utility frequency.
This electrification is ideal for railways that cover long distances or carry heavy traffic. After some experimentation before World War II in Hungary and in the Black Forest in Germany, it came into widespread use in the 1950s.
One of the reasons why it was not introduced earlier was the lack
of suitable small and lightweight control and rectification equipment
before the development of solid-state rectifiers
and related technology. Another reason was the increased clearance
distances required where it ran under bridges and in tunnels, which
would have required major civil engineering in order to provide the increased clearance to live parts.
Railways using older, lower-capacity direct current systems have introduced or are introducing 25 kV AC instead of 3 kV DC/1.5 kV DC for their new high-speed lines.
https://en.wikipedia.org/wiki/25_kV_AC_railway_electrification
In electronics, impedance matching is the practice of designing or adjusting the input impedance or output impedance of an electrical device for a desired value. Often, the desired value is selected to maximize power transfer or minimize signal reflection.
For example, impedance matching typically is used to improve power
transfer from a radio transmitter via the interconnecting transmission
line to the antenna. Signals on a transmission line will be transmitted without reflections if the transmission line is terminated with a matching impedance.
Techniques of impedance matching include transformers, adjustable networks of lumped resistance, capacitance and inductance,
or properly proportioned transmission lines. Practical
impedance-matching devices will generally provide best results over a
specified frequency band.
The concept of impedance matching is widespread in electrical engineering, but is relevant in other applications in which a form of energy, not necessarily electrical, is transferred between a source and a load, such as in acoustics or optics.

Source and
load impedance circuit
https://en.wikipedia.org/wiki/Impedance_matching
In electronics, electrical termination is the practice of ending a transmission line with a device that matches the characteristic impedance of the line. Termination prevents signals from reflecting off the end of the transmission line. Reflections at the ends of unterminated transmission lines cause distortion, which can produce ambiguous digital signal levels and misoperation of digital systems. Reflections in analog signal systems cause such effects as video ghosting, or power loss in radio transmitter transmission lines.
https://en.wikipedia.org/wiki/Electrical_termination
In telecommunications, signal reflection occurs when a signal is transmitted along a transmission medium, such as a copper cable or an optical fiber.
Some of the signal power may be reflected back to its origin rather
than being carried all the way along the cable to the far end. This
happens because imperfections in the cable cause impedance
mismatches and non-linear changes in the cable characteristics. These
abrupt changes in characteristics cause some of the transmitted signal
to be reflected. In radio frequency (RF) practice this is often measured in a dimensionless ratio known as voltage standing wave ratio (VSWR) with a VSWR bridge. The ratio of energy bounced back depends on the impedance mismatch. Mathematically, it is defined using the reflection coefficient.
Because the principles are the same, this concept is perhaps
easiest to understand when considering an optical fiber. Imperfections
in the glass create mirrors that reflect the light back along the fiber.
Impedance discontinuities cause attenuation, attenuation distortion, standing waves, ringing and other effects because a portion of a transmitted signal will be reflected back to the transmitting device rather than continuing to the receiver, much like an echo.
This effect is compounded if multiple discontinuities cause additional
portions of the remaining signal to be reflected back to the
transmitter. This is a fundamental problem with the daisy chain method of connecting electronic components.
When a returning reflection strikes another discontinuity, some
of the signal rebounds in the original signal direction, creating
multiple echo effects. These forward echoes
strike the receiver at different intervals making it difficult for the
receiver to accurately detect data values on the signal. The effects can
resemble those of jitter.
Because damage to the cable can cause reflections, an instrument called an electrical time-domain reflectometer (ETDR; for electrical cables) or an optical time-domain reflectometer
(OTDR; for optical cables) can be used to locate the damaged part of a
cable. These instruments work by sending a short pulsed signal into the
cable and measuring how long the reflection takes to return. If only
reflection magnitudes are desired, however, and exact fault locations
are not required, VSWR bridges perform a similar but lesser function for
RF cables.
The combination of the effects of signal attenuation and impedance discontinuities on a communications link is called insertion loss. Proper network operation depends on constant characteristic impedance in all cables and connectors, with no impedance discontinuities in the entire cable system. When a sufficient degree of impedance matching is not practical, echo suppressors or echo cancellers, or both, can sometimes reduce the problems.
The Bergeron diagram method, valid for both linear and non-linear models, evaluates the reflection's effects in an electric line.
See also
https://en.wikipedia.org/wiki/Signal_reflection
https://en.wikipedia.org/wiki/Optics
An induction motor or asynchronous motor is an AC electric motor in which the electric current in the rotor needed to produce torque is obtained by electromagnetic induction from the magnetic field of the stator winding.[1] An induction motor can therefore be made without electrical connections to the rotor.[a] An induction motor's rotor can be either wound type or squirrel-cage type.
Three-phase squirrel-cage induction motors are widely used as industrial drives because they are self-starting, reliable, and economical. Single-phase induction motors are used extensively for smaller loads, such as garbage disposals
and stationary power tools. Although traditionally only used for
one-speed service, single- and three-phase induction motors are
increasingly being installed in variable-speed applications using variable-frequency drives (VFD). VFDs offer especially important energy savings
opportunities for existing and prospective induction motors in
applications like fans, pumps and compressors that have a variable load.
https://en.wikipedia.org/wiki/Induction_motor
In telecommunications and electrical engineering in general, an unbalanced line is a pair of conductors intended to carry electrical signals, which have unequal impedances along their lengths and to ground and other circuits. Examples of unbalanced lines are coaxial cable or the historic earth return system invented for the telegraph, but rarely used today. Unbalanced lines are to be contrasted with balanced lines, such as twin-lead or twisted pair
which use two identical conductors to maintain impedance balance
throughout the line. Balanced and unbalanced lines can be interfaced
using a device called a balun.
The chief advantage of the unbalanced line format is cost
efficiency. Multiple unbalanced lines can be provided in the same cable
with one conductor per line plus a single common return conductor,
typically the cable shielding. Likewise, multiple microstrip circuits can all use the same ground plane
for the return path. This compares well with balanced cabling which
requires two conductors for each line, nearly twice as many. Another
benefit of unbalanced lines is that they do not require more expensive,
balanced driver and receiver circuits to operate correctly.
Unbalanced lines are sometimes confused with single-ended signalling,
but these are entirely separate concepts. The former is a cabling
scheme while the latter is a signalling scheme. However, single-ended
signalling is commonly sent over unbalanced lines. Unbalanced lines are
not to be confused with single-wire transmission lines which do not use a return path at all.
General description
Any
line that has a different impedance of the return path may be
considered an unbalanced line. However, unbalanced lines usually
consist of a conductor that is considered the signal line and another
conductor that is grounded, or is ground itself. The ground conductor often takes the form of a ground plane or the screen of a cable.
The ground conductor may be, and often is, common to multiple
independent circuits. For this reason the ground conductor may be
referred to as common.
Telegraph lines
The earliest use of unbalanced transmission lines was for electric telegraph
communications. These consisted of single wires strung between poles.
The return path for the current was originally provided by a separate
conductor. Some early telegraph systems, such as Schilling's experimental needle telegraph (1832) and the Cooke & Wheatstone five-needle telegraph (1837) used by British railways required multiple code wires. Essentially, they were parallel bus
coding. In these systems the cost of the return conductor was not so
significant (one conductor in seven for Schilling's earliest needle
telegraph[1] and one conductor in six for the Cooke and Wheatstone telegraph[2])
but the number of coding conductors was progressively reduced with
improved systems. Soon only one coding wire was required with the data
being transmitted serially. Important examples of these single-wire systems were the Morse telegraph (1837) and the Cooke & Wheatstone single-needle telegraph
(1843). In such systems the cost of a return conductor was fully 50
percent of the cable costs. It was discovered that a return conductor
could be replaced with a return path through the Earth using grounding spikes. Using earth return was a significant cost saving and rapidly became the norm.
Underground telegraph cables into large buildings or between
stations often needed to carry multiple independent telegraph lines.
These cables took the form of multiple insulated conductors enclosed by a
metal screen and overall protective jacket. In such cables the screen
can be used as the return conductor. Undersea telegraph cables were
usually a single conductor protected by steel-wire armour, effectively a coaxial cable. The first transatlantic cable of this kind was completed in 1866.
Early telephone
lines (telephone invented 1876) used the same transmission line scheme
as telegraph of unbalanced single wires. However, telephone
communication started to suffer after the widespread introduction of
electrical power lines. Telephone transmission started to use balanced lines to combat this problem and the modern norm for telephone presentation is the balanced twisted pair cable.
Coaxial lines
A coaxial line
(coax) has a central signal conductor surrounded by a cylindrical
shielding conductor. The shield conductor is normally grounded. The
coaxial format was developed during World War II for use in radar.
It was originally constructed from rigid copper pipes, but the usual
form today is a flexible cable with a braided screen. The advantages of
coax are a theoretically perfect electrostatic screen
and highly predictable transmission parameters. The latter is a result
of the fixed geometry of the format which leads to a precision not
found with loose wires. Open wire systems are also affected by nearby
objects altering the field pattern around the conductor. Coax does not
suffer from this since the field is entirely contained within the cable
due to the surrounding screen.
Coaxial lines are the norm for connections between radio
transmitters and their antennae, for interconnection of electronic
equipment where high frequency or above is involved, and were formerly widely used for forming local area networks before twisted pair became popular for this purpose.
Triaxial cable
(triax) is a variant of coax with a second shield conductor surrounding
the first with a layer of insulation in between. As well as providing
additional shielding, the outer conductors can be used for other
purposes such as providing power to equipment or control signals. Triax is widely used for the connection of cameras in television studios.
Planar technologies
Microstrip parallel-coupled transmission lines. The design forms a
band-pass filterPlanar format transmission lines are flat conductors manufactured by a
number of techniques on to a substrate. They are nearly always an
unbalanced format. At the low transmission speeds of early telegraph it was only necessary to consider transmission line theory for a circuit design when the transmission was over many miles. Similarly, the audio frequencies
used by telephones are relatively low and transmission line theory only
becomes significant for distances of at least between buildings.
However, at the higher radio frequencies and microwave frequencies transmission line considerations can become important inside a device, just a matter of centimetres. At the very high data rates handled by modern computer processors, transmission line considerations can even be important inside an individual integrated circuit.
Planar technologies were developed for these kinds of small size
applications and are not very appropriate for long distance
transmissions.
- Stripline
Stripline
is a flat conductor with a ground plane both above and below the
conductor. The variant of stripline where the space between the two
ground planes is completely filled with a dielectric material is sometimes known as triplate. Stripline can be manufactured by etching the transmission line pattern on to a printed circuit board.
The bottom of this board is left completely covered in copper and
forms the bottom ground plane. A second board is clamped on top of the
first. This second board has no pattern on the bottom and plain copper
on the top to form the top ground plane. A sheet of copper foil may be
wrapped around the two boards to electrically bond the two ground planes
firmly together. On the other hand, stripline for high power
applications such as radar will more likely be made as solid metal
strips with periodic dielectric supports, essentially air dielectric.
- Microstrip
Microstrip
is similar to stripline but is open above the conductor. There is no
dielectric or ground plane above the transmission line, there is only
dielectric and a ground plane below the line. Microstrip is a popular
format, especially in domestic products, because microstrip components
can be made using the established manufacturing techniques of printed
circuit boards. Designers are thus able to mix discrete component
circuits with microstrip components. Furthermore, since the board has
to be made anyway, the microstrip components have no additional
manufacturing cost. For applications where performance is more
important than cost a ceramic substrate might be used instead of a
printed circuit. Microstrip has another small advantage over stripline;
the line widths are wider in microstrip for the same impedance
and thus manufacturing tolerances and minimum width are less critical
on high-impedance lines. A drawback of microstrip is that the mode of
transmission is not entirely transverse.
Strictly speaking, standard transmission line analysis does not apply
because other modes are present, but it can be a usable approximation.
- Integrated circuits
Connections within integrated circuits are normally planar so planar
transmission lines are a natural choice where these are needed. The
need for transmission lines is most frequently found in microwave integrated circuits
(MICs). There are a great many materials and techniques used to make
MICs, and transmission lines can be formed in any of these technologies.
Planar transmission lines are used for far more than merely
connecting components or units together. They can themselves be used as
components and units. Any transmission line format can be used in this
way, but for the planar formats it is often their primary purpose.
Typical circuit blocks implemented by transmission lines include filters, directions couplers and power splitters, and impedance matching.
At microwave frequencies discrete components need to be impractically
small and a transmission line solution is the only viable one. On the
other hand, at low frequencies such as audio applications, transmission
line devices need to be impractically large.
Power transmission
Electric power distribution is normally in the form of balanced
three-phase transmission. However, in some remote locations where a
relatively small amount of power is required, a single-wire earth return system may be used.
References
Huurdeman, p. 54
Bibliography
- Huurdeman, Anton A., The Worldwide History of Telecommunications, John Wiley & Sons, 2003 ISBN 0471205052.
- Curran, J.E.; Jeanes, R.; Sewell, H, "A Technology of Thin-Film Hybrid Microwave Circuits", IEEE Transactions on Parts, Hybrids, and Packaging, vol. 12, iss. 4, December 1976.
https://en.wikipedia.org/wiki/Unbalanced_line
A motor soft starter is a device used with AC electrical motors to temporarily reduce the load and torque in the powertrain and electric current surge of the motor during start-up. This reduces the mechanical stress on the motor and shaft, as well as the electrodynamic stresses on the attached power cables and electrical distribution network, extending the lifespan of the system.[1]: 150
It can consist of mechanical or electrical devices, or a combination of both. Mechanical soft starters include clutches and several types of couplings using a fluid, magnetic forces, or steel shot to transmit torque, similar to other forms of torque limiter. Electrical soft starters can be any control system that reduces the torque by temporarily reducing the voltage or current input, or a device that temporarily alters how the motor is connected in the electric circuit.

Compact soft starter for a 3 phase machine, 15kW/10HP
https://en.wikipedia.org/wiki/Motor_soft_starter
A torque limiter is an automatic device that protects
mechanical equipment, or its work, from damage by mechanical overload. A
torque limiter may limit the torque by slipping (as in a friction plate slip-clutch), or uncouple the load entirely (as in a shear pin). The action of a torque limiter is especially useful to limit any damage due to crash stops and jams.
Torque limiters may be packaged as a shaft coupling or as a hub for sprocket or sheave. A torque limiting device is also known as an overload clutch.
https://en.wikipedia.org/wiki/Torque_limiter
Inverter drives (VFDs)
The popularity of the Variable-frequency drive
(VFD) has increased in the last decade, especially in the home-shop
market. This is because of their relative low cost and ability to
generate three-phase output from single phase input. A VFD converts AC
power to DC and then converts it back to AC through a transistor bridge, a technology that is somewhat analogous to that of a switch-mode power supply.
As the VFD generates its AC output from the DC bus, it is possible to
power a three-phase motor from a single-phase source. Nevertheless,
commercial-grade VFDs are produced that require three-phase input, as
there are some efficiency gains to be had with such an arrangement.
A typical VFD functions by rapidly switching transistors on and
off to "chop" the voltage on the DC bus through what is known as pulse-width modulation
(PWM). Proper use of PWM will result in an AC output whose voltage and
frequency can be varied over a fairly wide range. As an induction motor's
rotational speed is proportional to input frequency, a change in the
VFD's output frequency will cause the motor to change speed. Voltage is
also changed in a way that results in the motor producing a relatively
constant torque over the useful speed range.
The output of a quality VFD is an approximation of a sine wave, with some high frequency harmonic content.
Harmonic content will elevate motor temperature and may produce some
whistling or whining noise that could be objectionable. The effects of
unwanted harmonics can be mitigated by the use of reactive output filtering,
which is incorporated into better quality VFDs. Reactive filtration
impedes the high frequency harmonic content but has little effect on the
fundamental frequency that determines motor speed. The result is an output to the motor that is closer to an ideal sine wave.
In the past, VFDs that have a capacity greater than 3 hp (2.2 kW)
were costly, thus making the rotary phase converter (RPC) an attractive
alternative. However, modern VFDs have dropped considerably in cost,
making them more affordable than comparable RPCs. Also working in the
VFD's favor is its more compact size relative to its electrical
capacity. A plus is many VFDs can produce a "soft start" effect (in
which power is gradually applied to the motor), which reduces the amount
of current that must be delivered at machine start-up.
Use of a VFD may result in motor damage if the motor is not rated
for such an application. This is primarily because most induction
motors are forced-air cooled by a fan or blower driven by the motor
itself. Operating such a motor at a lower-than-normal speed will
substantially reduce the cooling airflow, increasing the likelihood of
overheating and winding damage or failure, especially while operating at
full load. A manufacturer may void the warranty on a motor powered by a
VFD unless the motor is "inverter-rated." As VFDs are the most popular
method of powering motors in new commercial installations, most
three-phase motors sold today are, in fact, inverter-rated.
See also
https://en.wikipedia.org/wiki/Rotary_phase_converter
A shear pin is a mechanical detail designed to allow a specific
outcome to occur once a predetermined force is applied. It can either
function as a safeguard designed to break to protect other parts, or as a
conditional operator that will not allow a mechanical device to operate
until the correct force is applied.
https://en.wikipedia.org/wiki/Shear_pin
Magnetic levitation (maglev) or magnetic suspension is a method by which an object is suspended with no support other than magnetic fields. Magnetic force is used to counteract the effects of the gravitational force and any other forces.
The two primary issues involved in magnetic levitation are lifting forces: providing an upward force sufficient to counteract gravity, and stability: ensuring that the system does not spontaneously slide or flip into a configuration where the lift is neutralized.
Magnetic levitation is used for maglev trains, contactless melting, magnetic bearings, and for product display purposes.
https://en.wikipedia.org/wiki/Magnetic_levitation
In electromagnetism, the magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include loops of electric current (such as electromagnets), permanent magnets, elementary particles (such as electrons), various molecules, and many astronomical objects (such as many planets, some moons, stars, etc).
More precisely, the term magnetic moment normally refers to a system's magnetic dipole moment, the component of the magnetic moment that can be represented by an equivalent magnetic dipole:
a magnetic north and south pole separated by a very small distance. The
magnetic dipole component is sufficient for small enough magnets or for
large enough distances. Higher-order terms (such as the magnetic quadrupole moment) may be needed in addition to the dipole moment for extended objects.
The magnetic dipole moment of an object is readily defined in
terms of the torque that the object experiences in a given magnetic
field. The same applied magnetic field creates larger torques on objects
with larger magnetic moments. The strength (and direction) of this
torque depends not only on the magnitude of the magnetic moment but also
on its orientation relative to the direction of the magnetic field. The
magnetic moment may be considered, therefore, to be a vector. The direction of the magnetic moment points from the south to north pole of the magnet (inside the magnet).
https://en.wikipedia.org/wiki/Magnetic_moment
An electric motor is an electrical machine that converts electrical energy into mechanical energy. Most electric motors operate through the interaction between the motor's magnetic field and electric current in a wire winding to generate force in the form of torque applied on the motor's shaft. An electric generator
is mechanically identical to an electric motor, but operates with a
reversed flow of power, converting mechanical energy into electrical
energy.
Electric motors can be powered by direct current (DC) sources, such as from batteries, or rectifiers, or by alternating current (AC) sources, such as a power grid, inverters or electrical generators.
Electric motors may be classified by considerations such as power
source type, construction, application and type of motion output. They
can be powered by AC or DC, be brushed or brushless, single-phase, two-phase, or three-phase, axial or radial flux, and may be air-cooled or liquid-cooled.
Standardized motors provide convenient mechanical power for
industrial use. The largest are used for ship propulsion, pipeline
compression and pumped-storage applications with output exceeding 100 megawatts.
Applications include industrial fans, blowers and pumps, machine
tools, household appliances, power tools, vehicles, and disk drives.
Small motors may be found in electric watches. In certain applications,
such as in regenerative braking with traction motors, electric motors can be used in reverse as generators to recover energy that might otherwise be lost as heat and friction.
Electric motors produce linear or rotary force (torque)
intended to propel some external mechanism, such as a fan or an
elevator. An electric motor is generally designed for continuous
rotation, or for linear movement over a significant distance compared to
its size. Magnetic solenoids are also transducers that convert electrical power to mechanical motion, but can produce motion over only a limited distance.
https://en.wikipedia.org/wiki/Electric_motor
In physics, the dynamo theory proposes a mechanism by which a celestial body such as Earth or a star generates a magnetic field. The dynamo theory describes the process through which a rotating, convecting, and electrically conducting fluid can maintain a magnetic field over astronomical time scales. A dynamo is thought to be the source of the Earth's magnetic field and the magnetic fields of Mercury and the Jovian planets.
https://en.wikipedia.org/wiki/Dynamo_theory
Optical rotation, also known as polarization rotation or circular birefringence, is the rotation of the orientation of the plane of polarization about the optical axis of linearly polarized light as it travels through certain materials. Circular birefringence and circular dichroism are the manifestations of optical activity. Optical activity occurs only in chiral materials, those lacking microscopic mirror symmetry. Unlike other sources of birefringence which alter a beam's state of polarization, optical activity can be observed in fluids. This can include gases or solutions of chiral molecules such as sugars, molecules with helical secondary structure such as some proteins, and also chiral liquid crystals. It can also be observed in chiral solids such as certain crystals with a rotation between adjacent crystal planes (such as quartz) or metamaterials.
When looking at the source of light, the rotation of the plane of polarization may be either to the right (dextrorotatory or dextrorotary — d-rotary, represented by (+), clockwise), or to the left (levorotatory or levorotary — l-rotary, represented by (−), counter-clockwise) depending on which stereoisomer is dominant. For instance, sucrose and camphor are d-rotary whereas cholesterol is l-rotary.
For a given substance, the angle by which the polarization of light of a
specified wavelength is rotated is proportional to the path length
through the material and (for a solution) proportional to its
concentration.
Optical activity is measured using a polarized source and polarimeter. This is a tool particularly used in the sugar industry to measure the sugar concentration of syrup, and generally in chemistry to measure the concentration or enantiomeric ratio of chiral molecules in solution. Modulation of a liquid crystal's optical activity, viewed between two sheet polarizers, is the principle of operation of liquid-crystal displays (used in most modern televisions and computer monitors).
Forms
Dextrorotation and laevorotation (also spelled levorotation)[1][2][3] are terms used in chemistry and physics to describe the optical rotation of plane-polarized light. From the point of view of the observer, dextrorotation refers to clockwise or right-handed rotation, and laevorotation refers to counterclockwise or left-handed rotation.[4][5]
A chemical compound that causes dextrorotation is called dextrorotatory or dextrorotary, while a compound that causes laevorotation is called laevorotatory or laevorotary.[6] Compounds with these properties consist of chiral molecules and are said to have optical activity. If a chiral molecule is dextrorotary, its enantiomer
(geometric mirror image) will be laevorotary, and vice versa.
Enantiomers rotate plane-polarized light the same number of degrees, but
in opposite directions.
Chirality prefixes
A compound may be labeled as dextrorotary by using the "(+)-" or "d-" prefix. Likewise, a laevorotary compound may be labeled using the "(−)-" or "l-" prefix. The lowercase "d-" and "l-" prefixes are obsolete, and are distinct from the SMALL CAPS "D-" and "L-" prefixes. The "D-" and "L-" prefixes are used to specify the enantiomer of chiral organic compounds in biochemistry and are based on the compound's absolute configuration relative to (+)-glyceraldehyde, which is the D-form
by definition. The prefix used to indicate absolute configuration is
not directly related to the (+) or (−) prefix used to indicate optical
rotation in the same molecule. For example, nine of the nineteen L-amino acids naturally occurring in proteins are, despite the L- prefix, actually dextrorotary (at a wavelength of 589 nm), and D-fructose is sometimes called "laevulose" because it is laevorotary.
The D- and L- prefixes describe the molecule as a whole, as do the (+) and (−) prefixes for optical rotation. In contrast, the (R)- and (S)- prefixes from the Cahn–Ingold–Prelog priority rules characterize the absolute configuration of each specific chiral stereocenter
with the molecule, rather than a property of the molecule as a whole. A
molecule having exactly one chiral stereocenter (usually an asymmetric carbon atom) can be labeled (R) or (S), but a molecule having multiple stereocenters needs more than one label. For example, the essential amino acid L-threonine contains two chiral stereocenters and is written (2S,3S)-threonine. There is no strict relationship between the R/S, the D/L, and (+)/(−) designations, although some correlations exist. For example, of the naturally occurring amino acids, all are L, and most are (S). For some molecules the (R)-enantiomer
is the dextrorotary (+) enantiomer, and in other cases it is the
laevorotary (−) enantiomer. The relationship must be determined on a
case-by-case basis with experimental measurements or detailed computer
modeling.[7]
History
The two asymmetric crystal forms, dextrorotatory and levorotatory, of
tartaric acid.
Sucrose solution concentration measuring experiment, demonstrating optical rotation.
The rotation of the orientation of linearly polarized light was first observed in 1811 in quartz by French physicist François Arago.[8] In 1820, the English astronomer Sir John F.W. Herschel
discovered that different individual quartz crystals, whose crystalline
structures are mirror images of each other (see illustration), rotate
linear polarization by equal amounts but in opposite directions.[9] Jean Baptiste Biot also observed the rotation of the axis of polarization in certain liquids[10] and vapors of organic substances such as turpentine.[11] In 1822, Augustin-Jean Fresnel found that optical rotation could be explained as a species of birefringence:
whereas previously known cases of birefringence were due to the
different speeds of light polarized in two perpendicular planes, optical
rotation was due to the different speeds of right-hand and left-hand
circularly polarized light.[12] Simple polarimeters have been used since this time to measure the concentrations of simple sugars, such as glucose, in solution. In fact one name for D-glucose (the biological isomer), is dextrose, referring to the fact that it causes linearly polarized light to rotate to the right or dexter side. In a similar manner, levulose, more commonly known as fructose, causes the plane of polarization to rotate to the left. Fructose is even more strongly levorotatory than glucose is dextrorotatory. Invert sugar syrup, commercially formed by the hydrolysis of sucrose
syrup to a mixture of the component simple sugars, fructose, and
glucose, gets its name from the fact that the conversion causes the
direction of rotation to "invert" from right to left.
In 1849, Louis Pasteur resolved a problem concerning the nature of tartaric acid.[13] A solution of this compound derived from living things (to be specific, wine lees) rotates the plane of polarization of light passing through it, but tartaric acid derived by chemical synthesis
has no such effect, even though its reactions are identical and its
elemental composition is the same. Pasteur noticed that the crystals
come in two asymmetric forms that are mirror images of one another.
Sorting the crystals by hand gave two forms of the compound: Solutions
of one form rotate polarized light clockwise, while the other form
rotate light counterclockwise. An equal mix of the two has no
polarizing effect on light. Pasteur deduced that the molecule in
question is asymmetric and could exist in two different forms that
resemble one another as would left- and right-hand gloves, and that the
organic form of the compound consists of purely the one type.
In 1874, Jacobus Henricus van 't Hoff[14] and Joseph Achille Le Bel[15]
independently proposed that this phenomenon of optical activity in
carbon compounds could be explained by assuming that the 4 saturated
chemical bonds between carbon atoms and their neighbors are directed
towards the corners of a regular tetrahedron. If the 4 neighbors are all
different, then there are two possible orderings of the neighbors
around the tetrahedron, which will be mirror images of each other. This
led to a better understanding of the three-dimensional nature of
molecules.
In 1945, Charles William Bunn[16]
predicted optical activity of achiral structures, if the wave's
propagation direction and the achiral structure form an experimental
arrangement that is different from its mirror image. Such optical
activity due to extrinsic chirality was observed in the 1960s in liquid crystals.[17][18]
In 1950, Sergey Vavilov[19]
predicted optical activity that depends on the intensity of light and
the effect of nonlinear optical activity was observed in 1979 in lithium iodate crystals.[20]
Optical activity is normally observed for transmitted light.
However, in 1988, M. P. Silverman discovered that polarization rotation
can also occur for light reflected from chiral substances.[21]
Shortly after, it was observed that chiral media can also reflect
left-handed and right-handed circularly polarized waves with different
efficiencies.[22]
These phenomena of specular circular birefringence and specular
circular dichroism are jointly known as specular optical activity.
Specular optical activity is very weak in natural materials.
In 1898 Jagadish Chandra Bose described the ability of twisted artificial structures to rotate the polarization of microwaves.[23] Since the early 21st century, the development of artificial materials has led to the prediction[24] and realization[25][26]
of chiral metamaterials with optical activity exceeding that of natural
media by orders of magnitude in the optical part of the spectrum.
Extrinsic chirality associated with oblique illumination of metasurfaces
lacking two-fold rotational symmetry has been observed to lead to large
linear optical activity in transmission[27] and reflection,[28] as well as nonlinear optical activity exceeding that of lithium iodate by 30 million times.[29]
Theory
Optical
activity occurs due to molecules dissolved in a fluid or due to the
fluid itself only if the molecules are one of two (or more) stereoisomers; this is known as an enantiomer. The structure of such a molecule is such that it is not identical to its mirror image
(which would be that of a different stereoisomer, or the "opposite
enantiomer"). In mathematics, this property is also known as chirality. For instance, a metal rod is not chiral, since its appearance in a mirror is not distinct from itself. However a screw or light bulb base (or any sort of helix) is
chiral; an ordinary right-handed screw thread, viewed in a mirror,
would appear as a left-handed screw (very uncommon) which could not
possibly screw into an ordinary (right-handed) nut. A human viewed in a
mirror would have their heart on the right side, clear evidence of
chirality, whereas the mirror reflection of a doll might well be
indistinguishable from the doll itself.
In order to display optical activity, a fluid must contain only
one, or a preponderance of one, stereoisomer. If two enantiomers are
present in equal proportions then their effects cancel out and no
optical activity is observed; this is termed a racemic mixture. But when there is an enantiomeric excess,
more of one enantiomer than the other, the cancellation is incomplete
and optical activity is observed. Many naturally occurring molecules are
present as only one enantiomer (such as many sugars). Chiral molecules
produced within the fields of organic chemistry or inorganic chemistry are racemic unless a chiral reagent was employed in the same reaction.
At the fundamental level, polarization rotation in an optically
active medium is caused by circular birefringence, and can best be
understood in that way. Whereas linear birefringence in a crystal involves a small difference in the phase velocity
of light of two different linear polarizations, circular birefringence
implies a small difference in the velocities between right and
left-handed circular polarizations.[12]
Think of one enantiomer in a solution as a large number of little
helices (or screws), all right-handed, but in random orientations.
Birefringence of this sort is possible even in a fluid because the
handedness of the helices is not dependent on their orientation: even
when the direction of one helix is reversed, it still appears right
handed. And circularly polarized light itself is chiral: as the wave
proceeds in one direction the electric (and magnetic) fields composing
it are rotating clockwise (or counterclockwise for the opposite circular
polarization), tracing out a right (or left) handed screw pattern in
space. In addition to the bulk refractive index which substantially lowers the phase velocity of light in any dielectric (transparent) material compared to the speed of light (in vacuum), there is an additional interaction between the chirality of the wave and the chirality of the molecules.
Where their chiralities are the same, there will be a small additional
effect on the wave's velocity, but the opposite circular polarization
will experience an opposite small effect as its chirality is opposite
that of the molecules.
Unlike linear birefringence, however, natural optical rotation
(in the absence of a magnetic field) cannot be explained in terms of a
local material permittivity
tensor (i.e., a charge response that only depends on the local electric
field vector), as symmetry considerations forbid this. Rather, circular
birefringence only appears when considering nonlocality of the material
response, a phenomenon known as spatial dispersion.[30]
Nonlocality means that electric fields in one location of the material
drive currents in another location of the material. Light travels at a
finite speed, and even though it is much faster than the electrons, it
makes a difference whether the charge response naturally wants to travel
along with the electromagnetic wavefront, or opposite to it. Spatial
dispersion means that light travelling in different directions
(different wavevectors) sees a slightly different permittivity tensor.
Natural optical rotation requires a special material, but it also relies
on the fact that the wavevector of light is nonzero, and a nonzero
wavevector bypasses the symmetry restrictions on the local
(zero-wavevector) response. However, there is still reversal symmetry,
which is why the direction of natural optical rotation must be
'reversed' when the direction of the light is reversed, in contrast to
magnetic Faraday rotation.
All optical phenomena have some nonlocality/wavevector influence but it
is usually negligible; natural optical rotation, rather uniquely,
absolutely requires it.[30]
The phase velocity of light in a medium is commonly expressed using the index of refraction n,
defined as the speed of light (in free space) divided by its speed in
the medium. The difference in the refractive indices between the two
circular polarizations quantifies the strength of the circular
birefringence (polarization rotation),
 .
.
While  is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
is small in natural materials, examples of giant circular birefringence
resulting in a negative refractive index for one circular polarization
have been reported for chiral metamaterials.[31]
[32]
The familiar rotation of the axis of linear polarization relies on the understanding that a linearly polarized wave can as well be described as the superposition
(addition) of a left and right circularly polarized wave in equal
proportion. The phase difference between these two waves is dependent on
the orientation of the linear polarization which we'll call  , and their electric fields have a relative phase difference of
, and their electric fields have a relative phase difference of  which then add to produce linear polarization:
which then add to produce linear polarization:

where  is the electric field of the net wave, while
is the electric field of the net wave, while  and
and  are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write
are the two circularly polarized basis functions (having zero phase difference). Assuming propagation in the +z direction, we could write  and
and  in terms of their x and y components as follows:
in terms of their x and y components as follows:


where  and
and  are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by
are unit vectors, and i is the imaginary unit, in this case representing the 90 degree phase shift between the x and y components that we have decomposed each circular polarization into. As usual when dealing with phasor notation, it is understood that such quantities are to be multiplied by  and then the actual electric field at any instant is given by the real part of that product.
and then the actual electric field at any instant is given by the real part of that product.
Substituting these expressions for  and
and  into the equation for
into the equation for  we obtain:
we obtain:



The last equation shows that the resulting vector has the x and y components in phase and oriented exactly in the  direction, as we had intended, justifying the representation of any linearly polarized state at angle
direction, as we had intended, justifying the representation of any linearly polarized state at angle  as the superposition of right and left circularly polarized components with a relative phase difference of
as the superposition of right and left circularly polarized components with a relative phase difference of  .
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of
.
Now let us assume transmission through an optically active material
which induces an additional phase difference between the right and left
circularly polarized waves of  . Let us call
. Let us call  the result of passing the original wave linearly polarized at angle
the result of passing the original wave linearly polarized at angle  through this medium. This will apply additional phase factors of
through this medium. This will apply additional phase factors of  and
and  to the right and left circularly polarized components of
to the right and left circularly polarized components of  :
:

Using similar math as above we find:

thus describing a wave linearly polarized at angle  , thus rotated by
, thus rotated by  relative to the incoming wave:
relative to the incoming wave: 
We defined above the difference in the refractive indices for right and left circularly polarized waves of  . Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of
. Considering propagation through a length L in such a material, there will be an additional phase difference induced between them of  (as we used above) given by:
(as we used above) given by:
 ,
,
where  is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by
is the wavelength of the light (in vacuum). This will cause a rotation of the linear axis of polarization by  as we have shown.
as we have shown.
In general, the refractive index depends on wavelength (see dispersion) and the differential refractive index  will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
will also be wavelength dependent. The resulting variation in rotation with the wavelength of the light is called optical rotatory dispersion (ORD). ORD spectra and circular dichroism spectra are related through the Kramers–Kronig relations. Complete knowledge of one spectrum allows the calculation of the other.
So we find that the degree of rotation depends on the color of the light (the yellow sodium D line near 589 nm wavelength is commonly used for measurements), and is directly proportional to the path length  through the substance and the amount of circular birefringence of the material
through the substance and the amount of circular birefringence of the material  which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
which, for a solution, may be computed from the substance's specific rotation and its concentration in solution.
Although optical activity is normally thought of as a property of fluids, particularly aqueous solutions, it has also been observed in crystals such as quartz (SiO2). Although quartz has a substantial linear birefringence, that effect is cancelled when propagation is along the optic axis.
In that case, rotation of the plane of polarization is observed due to
the relative rotation between crystal planes, thus making the crystal
formally chiral as we have defined it above. The rotation of the crystal
planes can be right or left-handed, again producing opposite optical
activities. On the other hand, amorphous forms of silica such as fused quartz,
like a racemic mixture of chiral molecules, has no net optical activity
since one or the other crystal structure does not dominate the
substance's internal molecular structure.
Applications
For a pure substance in solution, if the color and path length are fixed and the specific rotation is known, the observed rotation can be used to calculate the concentration. This usage makes a polarimeter a tool of great importance to those trading in or using sugar syrups in bulk.
Comparison to the Faraday effect
Rotation of light's plane of polarization may also occur through the Faraday effect which involves a static magnetic field.
However, this is a distinct phenomenon that is not classified as
"optical activity." Optical activity is reciprocal, i.e. it is the same
for opposite directions of wave propagation through an optically active
medium, for example clockwise polarization rotation from the point of
view of an observer. In case of optically active isotropic media, the
rotation is the same for any direction of wave propagation. In contrast,
the Faraday effect is non-reciprocal, i.e opposite directions of wave
propagation through a Faraday medium will result in clockwise and
anti-clockwise polarization rotation from the point of view of an
observer. Faraday rotation depends on the propagation direction relative
to that of the applied magnetic field. All compounds can exhibit
polarization rotation in the presence of an applied magnetic field,
provided that (a component of) the magnetic field is oriented in the
direction of light propagation. The Faraday effect is one of the first
discoveries of the relationship between light and electromagnetic
effects.
See also
References
The first word component dextro- comes from the Latin word dexter, meaning "right" (as opposed to left). Laevo- or levo- comes from the Latin laevus, meaning "left side".
The equivalent French terms are dextrogyre and levogyre. These are used infrequently in English.
Sebti; Hamilton, eds. (2001). Farnesyltransferase inhibitors in cancer therapy. p. 126. ISBN 9780896036291. Retrieved 2015-10-18.
LibreTexts Chemistry – Polarimetry
"Determination of optical rotation and specific rotation" (PDF). The International Pharmacopoeia. World Health Organization. 2017. ISBN 9789241550031. Archived (PDF) from the original on 2022-10-09.
Solomons, T.W. Graham; Fryhle, Graig B. (2004). Organic Chemistry (8th ed.). Hoboken: John Wiley & Sons, Inc.
See, for example,Stephens,
P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J.; Bortolini, O.;
Besse, P. (2003). "Determination of absolute configuration using
calculation of optical rotation". Chirality. 15: S57–64. doi:10.1002/chir.10270. PMID 12884375.
Arago (1811) "Mémoire
sur une modification remarquable qu'éprouvent les rayons lumineux dans
leur passage à travers certains corps diaphanes et sur quelques autres
nouveaux phénomènes d'optique" (Memoir on a remarkable modification
that light rays experience during their passage through certain
translucent substances and on some other new optical phenomena), Mémoires de la classe des sciences mathématiques et physiques de l'Institut Impérial de France, 1st part : 93–134.
Herschel, J.F.W. (1820) "On
the rotation impressed by plates of rock crystal on the planes of
polarization of the rays of light, as connected with certain
peculiarities in its crystallization," Transactions of the Cambridge Philosophical Society, 1 : 43–51.
Biot, J. B. (1815) "Phenomene de polarisation successive, observés dans des fluides homogenes" (Phenomenon of successive polarization, observed in homogeneous fluids), Bulletin des Sciences, par la Société Philomatique de Paris, 190–192.
Biot
(1818 & 1819) "Extrait d'un mémoire sur les rotations que certaines
substances impriment aux axes de polarisation des rayons lumineux"
(Extract from a memoir on the [optical] rotations that certain
substances impress on the axes of polarization of light rays), Annales de Chimie et de Physique, 2nd series, 9 : 372-389 ; 10 : 63-81 ; for Biot's experiments with turpentine vapor (vapeur d'essence de térébenthine), see pp. 72-81.
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); especially §13.
Pasteur, L. (1850) "Recherches sur les propriétés spécifiques des deux acides qui composent l'acide racémique" (Researches on the specific properties of the two acids that compose the racemic acid), Annales de chimie et de physique, 3rd series, 28 : 56–99 ; see also appendix, pp. 99–117.
van 't Hoff, J.H. (1874) "Sur les formules de structure dans l'espace" (On structural formulas in space), Archives Néerlandaises des Sciences Exactes et Naturelles, 9 : 445–454.
Le Bel, J.-A. (1874) "Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions" (On the relations that exist between the atomic formulas of organic substances and the rotatory power of their solutions), Bulletin de la Société Chimique de Paris, 22 : 337–347.
Bunn, C. W. (1945). Chemical Crystallography. New York: Oxford University Press. p. 88.
R. Williams (1968). "Optical Rotatory Effect in the Nematic Liquid Phase of p-Azoxyanisole". Physical Review Letters. 21 (6): 342. Bibcode:1968PhRvL..21..342W. doi:10.1103/PhysRevLett.21.342.
R. Williams (1969). "Optical-rotary power and linear electro-optic effect in nematic liquid crystals of p-azoxyanisole". Journal of Chemical Physics. 50 (3): 1324. Bibcode:1969JChPh..50.1324W. doi:10.1063/1.1671194.
Vavilov, S. I. (1950). Mikrostruktura Sveta (Microstructure of Light). Moscow: USSR Academy of Sciences Publishing.
Akhmanov,
S. A.; Zhdanov, B. V.; Zheludev, N. I.; Kovrigin, A. I.; Kuznetsov, V.
I. (1979). "Nonlinear optical activity in crystals". JETP Letters. 29: 264.
Silverman,
M.; Ritchie, N.; Cushman, G.; Fisher, B. (1988). "Experimental
configurations using optical phase modulation to measure chiral
asymmetries in light specularly reflected from a naturally gyrotropic
medium". Journal of the Optical Society of America A. 5 (11): 1852. Bibcode:1988JOSAA...5.1852S. doi:10.1364/JOSAA.5.001852.
Silverman, M.; Badoz, J.; Briat, B. (1992). "Chiral reflection from a naturally optically active medium". Optics Letters. 17 (12): 886. Bibcode:1992OptL...17..886S. doi:10.1364/OL.17.000886. PMID 19794663.
Bose, Jagadis Chunder (1898). "On the Rotation of Plane of Polarisation of Electric Waves by a Twisted Structure". Proceedings of the Royal Society. 63 (389–400): 146–152. doi:10.1098/rspl.1898.0019. JSTOR 115973. S2CID 89292757.
Svirko, Y.; Zheludev, N. I.; Osipov, M. (2001). "Layered chiral metallic microstructures with inductive coupling". Applied Physics Letters. 78 (4): 498. Bibcode:2001ApPhL..78..498S. doi:10.1063/1.1342210.
Kuwata-Gonokami,
M.; Saito, N.; Ino, Y.; Kauranen, M.; Jefimovs, K.; Vallius, T.;
Turunen, J.; Svirko, Y. (2005). "Giant Optical Activity in
Quasi-Two-Dimensional Planar Nanostructures". Physical Review Letters. 95 (22): 227401. Bibcode:2005PhRvL..95v7401K. doi:10.1103/PhysRevLett.95.227401. PMID 16384264.
Plum,
E.; Fedotov, V. A.; Schwanecke, A. S.; Zheludev, N. I.; Chen, Y.
(2007). "Giant optical gyrotropy due to electromagnetic coupling". Applied Physics Letters. 90 (22): 223113. Bibcode:2007ApPhL..90v3113P. doi:10.1063/1.2745203.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2008). "Optical activity in extrinsically chiral metamaterial" (PDF). Applied Physics Letters. 93 (19): 191911. arXiv:0807.0523. Bibcode:2008ApPhL..93s1911P. doi:10.1063/1.3021082. S2CID 117891131.
Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2016). "Specular optical activity of achiral metasurfaces" (PDF). Applied Physics Letters. 108 (14): 141905. Bibcode:2016ApPhL.108n1905P. doi:10.1063/1.4944775. hdl:10220/40854.
Ren, M.; Plum, E.; Xu, J.; Zheludev, N. I. (2012). "Giant nonlinear optical activity in a plasmonic metamaterial". Nature Communications. 3: 833. Bibcode:2012NatCo...3..833R. doi:10.1038/ncomms1805. PMID 22588295.
L.D. Landau; E.M. Lifshitz; L.P. Pitaevskii (1984). Electrodynamics of Continuous Media. Vol. 8 (2nd ed.). Butterworth-Heinemann. pp. 362–365. ISBN 978-0-7506-2634-7.
Plum, E.; Zhou, J.; Dong, J.; Fedotov, V. A.; Koschny, T.; Soukoulis, C. M.; Zheludev, N. I. (2009). "Metamaterial with negative index due to chirality" (PDF). Physical Review B. 79 (3): 035407. Bibcode:2009PhRvB..79c5407P. doi:10.1103/PhysRevB.79.035407. S2CID 119259753.
Further reading
- Eugene Hecht, Optics, 3rd Ed., Addison-Wesley, 1998, ISBN 0-201-30425-2
- Akhlesh Lakhtakia, Beltrami Fields in Chiral Media, World Scientific, Singapore, 1994
- A step by step tutorial on Optical Rotation
- Morrison. Robert. T, and Boyd. Robert. N, "Organic Chemistry (6th ed)". Prentice-Hall Inc (1992).

Operating principle of a
polarimeter
for measuring optical rotation. 1. Light source 2. Unpolarized light
3. Linear polarizer 4. Linearly polarized light 5. Sample tube
containing molecules under study 6. Optical rotation due to molecules 7.
Rotatable linear analyzer 8. Detector
https://en.wikipedia.org/wiki/Optical_rotation
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave.
In electrodynamics, the strength and direction of an electric
field is defined by its electric field vector. In the case of a
circularly polarized wave, the tip of the electric field vector,
at a given point in space, relates to the phase of the light as it
travels through time and space. At any instant of time, the electric
field vector of the wave indicates a point on a helix
oriented along the direction of propagation. A circularly polarized
wave can rotate in one of two possible senses: clockwise or right-handed circular polarization (RHCP) in which the electric field vector rotates in a right-hand sense with respect to the direction of propagation, and counter-clockwise or left-handed circular polarization (LHCP) in which the vector rotates in a left-hand sense.
Circular polarization is a limiting case of elliptical polarization. The other special case is the easier-to-understand linear polarization. All three terms were coined by Augustin-Jean Fresnel, in a memoir read to the French Academy of Sciences on 9 December 1822.[1][2] Fresnel had first described the case of circular polarization, without yet naming it, in 1821.[3]
The phenomenon of polarization arises as a consequence of the fact that light behaves as a two-dimensional transverse wave.
Circular polarization occurs when the two orthogonal electric
field component vectors are of equal magnitude and are out of phase by
exactly 90°, or one-quarter wavelength.
Characteristics
Right-handed/clockwise
circularly polarized light displayed with and without the use of
components. This would be considered left-handed/counterclockwise
circularly polarized if defined from the point of view of the source
rather than the receiver
In a circularly polarized electromagnetic wave, the individual
electric field vectors, as well as their combined vector, have a
constant magnitude, and with changing phase angle. Given that this is a plane wave,
each vector represents the magnitude and direction of the electric
field for an entire plane that is perpendicular to the optical axis.
Specifically, given that this is a circularly polarized plane wave,
these vectors indicate that the electric field, from plane to plane,
has a constant strength while its direction steadily rotates. Refer to these two images[dead link]
in the plane wave article to better appreciate this dynamic. This light
is considered to be right-hand, clockwise circularly polarized if
viewed by the receiver. Since this is an electromagnetic wave, each electric field vector has a corresponding, but not illustrated, magnetic field vector that is at a right angle to the electric field vector and proportional in magnitude to it. As a result, the magnetic field vectors would trace out a second helix if displayed.
Circular polarization is often encountered in the field of optics
and, in this section, the electromagnetic wave will be simply referred
to as light.
The nature of circular polarization and its relationship to other
polarizations is often understood by thinking of the electric field as
being divided into two components
that are perpendicular to each other. The vertical component and its
corresponding plane are illustrated in blue, while the horizontal
component and its corresponding plane are illustrated in green. Notice
that the rightward (relative to the direction of travel) horizontal
component leads the vertical component by one quarter of a wavelength, a 90° phase difference. It is this quadrature phase relationship that creates the helix
and causes the points of maximum magnitude of the vertical component to
correspond with the points of zero magnitude of the horizontal
component, and vice versa. The result of this alignment are select
vectors, corresponding to the helix, which exactly match the maxima of
the vertical and horizontal components.
To appreciate how this quadrature phase
shift corresponds to an electric field that rotates while maintaining a
constant magnitude, imagine a dot traveling clockwise in a circle.
Consider how the vertical and horizontal displacements of the dot, relative to the center of the circle, vary sinusoidally
in time and are out of phase by one quarter of a cycle. The
displacements are said to be out of phase by one quarter of a cycle
because the horizontal maximum displacement (toward the left) is reached
one quarter of a cycle before the vertical maximum displacement is
reached. Now referring again to the illustration, imagine the center of
the circle just described, traveling along the axis from the front to
the back. The circling dot will trace out a helix with the displacement
toward our viewing left, leading the vertical displacement. Just as the
horizontal and vertical displacements of the rotating dot are out of
phase by one quarter of a cycle in time, the magnitude of the horizontal
and vertical components of the electric field are out of phase by one
quarter of a wavelength.
Left-handed/counterclockwise
circularly polarized light displayed with and without the use of
components. This would be considered right-handed/clockwise circularly
polarized if defined from the point of view of the source rather than
the receiver.
The next pair of illustrations is that of left-handed,
counterclockwise circularly polarized light when viewed by the receiver.
Because it is left-handed, the rightward (relative to the direction of
travel) horizontal component is now lagging the vertical component by one quarter of a wavelength, rather than leading it.
Reversal of handedness
Waveplate
To convert circularly polarized light to the other handedness, one can use a half-waveplate.
A half-waveplate shifts a given linear component of light one half of a
wavelength relative to its orthogonal linear component.
Reflection
The
handedness of polarized light is reversed reflected off a surface at
normal incidence. Upon such reflection, the rotation of the plane of polarization of the reflected light is identical to that of the incident field. However, with propagation now in the opposite
direction, the same rotation direction that would be described as
"right-handed" for the incident beam, is "left-handed" for propagation
in the reverse direction, and vice versa. Aside from the reversal of
handedness, the ellipticity of polarization is also preserved (except in
cases of reflection by a birefringent surface).
Note that this principle only holds strictly for light reflected
at normal incidence. For instance, right circularly polarized light
reflected from a dielectric surface at grazing incidence (an angle
beyond the Brewster angle)
will still emerge as right-handed, but elliptically, polarized. Light
reflected by a metal at non-normal incidence will generally have its
ellipticity changed as well. Such situations may be solved by
decomposing the incident circular (or other) polarization into
components of linear polarization parallel and perpendicular to the plane of incidence, commonly denoted p and s respectively. The reflected components in the p and s linear polarizations are found by applying the Fresnel coefficients
of reflection, which are generally different for those two linear
polarizations. Only in the special case of normal incidence, where there
is no distinction between p and s, are the Fresnel coefficients for the two components identical, leading to the above property.
A
3-slide series of pictures taken with and without a pair of MasterImage
3D circularly polarized movie glasses of some dead European rose
chafers (Cetonia aurata) whose shiny green color comes from
left-polarized light. Note that, without glasses, both the beetles and
their images have shiny color. The right-polarizer removes the color of
the beetles but leaves the color of the images. The left-polarizer does
the opposite, showing reversal of handedness of the reflected light.
Conversion to and from linear polarization
Circularly polarized light can be converted into linearly polarized light by passing it through a quarter-waveplate.
Passing linearly polarized light through a quarter-waveplate with its
axes at 45° to its polarization axis will convert it to circular
polarization. In fact, this is the most common way of producing circular
polarization in practice. Note that passing linearly polarized light
through a quarter-waveplate at an angle other than 45° will generally produce elliptical polarization.
Handedness conventions
A
right-handed/clockwise circularly polarized wave as defined from the
point of view of the source. It would be considered
left-handed/anti-clockwise circularly polarized if defined from the
point of view of the receiver.
A
left-handed/anti-clockwise circularly polarized wave as defined from
the point of view of the source. It would be considered
right-handed/clockwise circularly polarized if defined from the point of
view of the receiver.
Circular polarization may be referred to as right-handed or
left-handed, and clockwise or anti-clockwise, depending on the direction
in which the electric field vector rotates. Unfortunately, two opposing
historical conventions exist.
From the point of view of the source
Using
this convention, polarization is defined from the point of view of the
source. When using this convention, left- or right-handedness is
determined by pointing one's left or right thumb away from the source, in the same
direction that the wave is propagating, and matching the curling of
one's fingers to the direction of the temporal rotation of the field at a
given point in space. When determining if the wave is clockwise or
anti-clockwise circularly polarized, one again takes the point of view
of the source, and while looking away from the source and in the same direction of the wave's propagation, one observes the direction of the field's spatial rotation.
Using this convention, the electric field vector of a left-handed circularly polarized wave is as follows:

As a specific example, refer to the circularly polarized wave in
the first animation. Using this convention, that wave is defined as
right-handed because when one points one's right thumb in the same
direction of the wave's propagation, the fingers of that hand curl in
the same direction of the field's temporal rotation. It is considered
clockwise circularly polarized because, from the point of view of the
source, looking in the same direction of the wave's propagation, the
field rotates in the clockwise direction. The second animation is that
of left-handed or anti-clockwise light, using this same convention.
This convention is in conformity with the Institute of Electrical and Electronics Engineers (IEEE) standard and, as a result, it is generally used in the engineering community.[4][5][6]
Quantum physicists also use this convention of handedness because
it is consistent with their convention of handedness for a particle's
spin.[7]
Radio astronomers also use this convention in accordance with an International Astronomical Union (IAU) resolution made in 1973.[8]
From the point of view of the receiver
In
this alternative convention, polarization is defined from the point of
view of the receiver. Using this convention, left- or right-handedness
is determined by pointing one's left or right thumb toward the source, against the direction of propagation, and then matching the curling of one's fingers to the spatial rotation of the field.
When using this convention, in contrast to the other convention,
the defined handedness of the wave matches the handedness of the screw
type nature of the field in space. Specifically, if one freezes a
right-handed wave in time, when one curls the fingers of one's right
hand around the helix, the thumb will point in the direction of
progression for the helix, given the sense of rotation. Note that, in
the context of the nature of all screws and helices, it does not matter
in which direction you point your thumb when determining its handedness.
When determining if the wave is clockwise or anti-clockwise
circularly polarized, one again takes the point of view of the receiver
and, while looking toward the source, against the direction of propagation, one observes the direction of the field's temporal rotation.
Just as in the other convention, right-handedness corresponds to a
clockwise rotation, and left-handedness corresponds to an
anti-clockwise rotation.
Many optics textbooks use this second convention.[9][10] It is also used by SPIE[11] as well as the International Union of Pure and Applied Chemistry (IUPAC).[12]
Uses of the two conventions
As
stated earlier, there is significant confusion with regards to these
two conventions. As a general rule, the engineering, quantum physics,
and radio astronomy communities use the first convention, in which the
wave is observed from the point of view of the source.[5][7][8]
In many physics textbooks dealing with optics, the second convention is
used, in which the light is observed from the point of view of the
receiver.[7][9]
To avoid confusion, it is good practice to specify "as defined
from the point of view of the source" or "as defined from the point of
view of the receiver" when discussing polarization matters.
The archive of the US Federal Standard 1037C proposes two contradictory conventions of handedness.[13]
FM radio
The term "circular polarization" is often used erroneously to describe mixed polarity signals[citation needed] used mostly in FM radio
(87.5 to 108.0 MHz in the USA), in which a vertical and a horizontal
component are propagated simultaneously by a single or a combined array.
This has the effect of producing greater penetration into buildings and
difficult reception areas than a signal with just one plane of
polarization. This would be an instance in which the polarization would
more appropriately be called random polarization because the
polarization at a receiver, although constant, will vary depending on
the direction from the transmitter and other factors in the transmitting
antenna design. See Stokes parameters.
The term "FM radio" above refers to FM broadcasting, not two-way radio (more properly called land mobile radio), which uses vertical polarization almost exclusively.
Dichroism
Circular dichroism (CD) is the differential absorption of left- and right-handed circularly polarized light. Circular dichroism is the basis of a form of spectroscopy that can be used to determine the optical isomerism and secondary structure of molecules.
In general, this phenomenon will be exhibited in absorption bands of any optically active molecule. As a consequence, circular dichroism is exhibited by most biological molecules, because of the dextrorotary (e.g., some sugars) and levorotary (e.g., some amino acids) molecules they contain. Noteworthy as well is that a secondary structure will also impart a distinct CD to its respective molecules. Therefore, the alpha helix, beta sheet and random coil regions of proteins and the double helix of nucleic acids have CD spectral signatures representative of their structures.
Also, under the right conditions, even non-chiral molecules will exhibit magnetic circular dichroism — that is, circular dichroism induced by a magnetic field.
Luminescence
Circularly polarized luminescence (CPL) can occur when either a luminophore or an ensemble of luminophores is chiral. The extent to which emissions are polarized is quantified in the same way it is for circular dichroism, in terms of the dissymmetry factor, also sometimes referred to as the anisotropy factor. This value is given by:

where  corresponds to the quantum yield of left-handed circularly polarized light, and
corresponds to the quantum yield of left-handed circularly polarized light, and  to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
to that of right-handed light. The maximum absolute value of gem,
corresponding to purely left- or right-handed circular polarization, is
therefore 2. Meanwhile, the smallest absolute value that gem can achieve, corresponding to linearly polarized or unpolarized light, is zero.
Mathematical description
The classical sinusoidal plane wave solution of the electromagnetic wave equation for the electric and magnetic fields is:
![{\displaystyle {\begin{aligned}\mathbf {E} (\mathbf {r} ,t)&=\left|\,\mathbf {E} \,\right|\mathrm {Re} \left\{\mathbf {Q} \left|\psi \right\rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\\\mathbf {B} (\mathbf {r} ,t)&={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72e6f4e48ffd9eabf206d7664ee54e2e2ba2780c)
where k is the wavenumber;

is the angular frequency of the wave; ![\mathbf{Q} = \left [ \hat{ \mathbf{x}}, \hat{\mathbf{y}} \right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c6f209c9644cf3ab69fd75e6d696bb9278c0c12) is an orthogonal
is an orthogonal  matrix whose columns span the transverse x-y plane; and
matrix whose columns span the transverse x-y plane; and  is the speed of light.
is the speed of light.
Here,

is the amplitude of the field, and

is the normalized Jones vector in the x-y plane.
If  is rotated by
is rotated by  radians with respect to
radians with respect to  and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:
and the x amplitude equals the y amplitude, the wave is circularly polarized. The Jones vector is:

where the plus sign indicates left circular polarization, and the
minus sign indicates right circular polarization. In the case of
circular polarization, the electric field vector of constant magnitude
rotates in the x-y plane.
If basis vectors are defined such that:

and:

then the polarization state can be written in the "R-L basis" as:

where:

and:

Antennas
A number of different types of antenna elements can be used to
produce circularly polarized (or nearly so) radiation; following
Balanis,[14] one can use dipole elements:
"... two crossed dipoles provide the two orthogonal field
components.... If the two dipoles are identical, the field intensity of
each along zenith ... would be of the same intensity. Also, if the two
dipoles were fed with a 90° degree time-phase difference (phase
quadrature), the polarization along zenith would be circular.... One way
to obtain the 90° time-phase difference between the two orthogonal
field components, radiated respectively by the two dipoles, is by
feeding one of the two dipoles with a transmission line which is 1/4
wavelength longer or shorter than that of the other," p.80;
or helical elements:
"To achieve circular polarization [in axial or end-fire mode] ... the circumference C of the helix must be ... with C/wavelength = 1 near optimum, and the spacing about S = wavelength/4," p.571;
or patch elements:
"... circular and elliptical polarizations can be
obtained using various feed arrangements or slight modifications made to
the elements.... Circular polarization can be obtained if two
orthogonal modes are excited with a 90° time-phase difference between
them. This can be accomplished by adjusting the physical dimensions of
the patch.... For a square patch element, the easiest way to excite
ideally circular polarization is to feed the element at two adjacent
edges.... The quadrature phase difference is obtained by feeding the
element with a 90° power divider," p.859.
In quantum mechanics
In the quantum mechanical view, light is composed of photons. Polarization is a manifestation of the spin angular momentum of light.
More specifically, in quantum mechanics, the direction of spin of a
photon is tied to the handedness of the circularly polarized light, and
the spin of a beam of photons is similar to the spin of a beam of
particles, such as electrons.[15]
In nature
The
rose chafer's external surface reflects almost exclusively left-circularly polarized light.
Only a few mechanisms in nature are known to systematically produce circularly polarized light. In 1911, Albert Abraham Michelson discovered that light reflected from the golden scarab beetle Chrysina resplendens is preferentially left-polarized. Since then, circular polarization has been measured in several other scarab beetles such as Chrysina gloriosa,[16] as well as some crustaceans such as the mantis shrimp. In these cases, the underlying mechanism is the molecular-level helicity of the chitinous cuticle.[17]
The bioluminescence of the larvae of fireflies is also circularly polarized, as reported in 1980 for the species Photuris lucicrescens and Photuris versicolor.
For fireflies, it is more difficult to find a microscopic explanation
for the polarization, because the left and right lanterns of the larvae
were found to emit polarized light of opposite senses. The authors
suggest that the light begins with a linear polarization due to inhomogeneities inside aligned photocytes, and it picks up circular polarization while passing through linearly birefringent tissue.[18]
Water-air interfaces provide another source of circular
polarization. Sunlight that gets scattered back up towards the surface
is linearly polarized. If this light is then totally internally reflected back down, its vertical component undergoes a phase shift. To an underwater observer looking up, the faint light outside Snell's window therefore is (partially) circularly polarized.[19]
Weaker sources of circular polarization in nature include multiple scattering by linear polarizers[dubious – discuss], as in the circular polarization of starlight, and selective absorption by circularly dichroic media.
Radio emission from stars and pulsars can be strongly circularly polarized[citation needed].
Two species of mantis shrimp have been reported to be able to detect circular polarized light.[20][21]
See also
References
A.
Fresnel, "Mémoire sur la double réfraction que les rayons lumineux
éprouvent en traversant les aiguilles de cristal de roche suivant les
directions parallèles à l'axe", read 9 December 1822; printed in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 731–51; translated as "Memoir on the double
refraction that light rays undergo in traversing the needles of quartz
in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); §§9–10.
Académie des Sciences, Procès-verbaux des séances de l'Académie tenues depuis la fondation de l'Institut jusqu'au mois d'août 1835, vol. 7 (for 1820–23), Hendaye, Basses Pyrénées: Imprimerie de l'Observatoire d'Abbadia, 1916, p. 401.
A. Fresnel, "Note sur le calcul des teintes que la polarisation développe dans les lames cristallisées" et seq., Annales de Chimie et de Physique,
Ser. 2, vol. 17, pp. 102–11 (May 1821), 167–96 (June 1821), 312–15
("Postscript", July 1821); reprinted (with added section nos.) in H. de
Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel,
vol. 1 (1866), pp. 609–48; translated as "On the calculation of the
tints that polarization develops in crystalline plates,
& postscript", Zenodo: 4058004 (Creative Commons), 2021; author's footnote to §16.
IEEE
Std 149-1979 (R2008), "IEEE Standard Test Procedures for Antennas".
Reaffirmed December 10, 2008, Approved December 15, 1977, IEEE-SA
Standards Board. Approved October 9, 2003, American National Standards
Institute. ISBN 0-471-08032-2. doi:10.1109/IEEESTD.1979.120310,
sec. 11.1, p. 61."the sense of polarization, or handedness ... is
called right handed (left handed) if the direction of rotation is
clockwise (anti-clockwise) for an observer looking in the direction of
propagation"
Electromagnetic
Waves & Antennas – S. J. Orfanidis: Footnote p.45, "most
engineering texts use the IEEE convention and most physics texts, the
opposite convention."
Electromagnetic
Waves & Antennas – S. J. Orfanidis Pg 44 "Curl the fingers of your
left and right hands into a fist and point both thumbs towards the direction of propagation"
Lectures
on Physics Feynman (Vol. 1, ch.33-1) "If the end of the electric
vector, when we look at it as the light comes straight toward us, goes
around in an anti-clockwise direction, we call it right-hand circular
polarization. ... Our convention for labeling left-hand and right-hand
circular polarization is consistent with that which is used today for
all the other particles in physics which exhibit polarization (e.g.,
electrons). However, in some books on optics the opposite conventions
are used, so one must be careful."
IAU
General Assembly Meeting, 1973, Commission 40 (Radio
Astronomy/Radioastronomie), 8. POLARIZATION DEFINITIONS -- "A working
Group chaired by Westerhout was convened to discuss the definition of
polarization brightness temperatures used in the description of
polarized extended objects and the galactic
background. The following resolution was adopted by Commissions 25 and
40: 'RESOLVED, that the frame of reference for the Stokes parameters is
that of Right Ascension and Declination with the position angle of
electric-vector maximum, q, starting from North and increasing through
East. Elliptical polarization is defined in conformity with the
definitions of the Institute of Electrical and Electronics Engineers
(IEEE Standard 211, 1969). This means that the polarization of incoming
radiation, for which the position angle, q, of the electric vector,
measured at a fixed point in space, increases with time, is described as
right-handed and positive.'"
Polarization
in Spectral Lines. 2004 E. Landi Degl'innocenti, M Landolfi Section 1.2
"When ... the tip of the electric field vector rotates clockwise for an
observer facing the radiation source, ... (it will be considered)...
positive (or righthanded) circular polarization, Our convention ...
agrees with those proposed in the classical textbooks on polarized light
by Shurcliff (1952) and by Clarke and Grainger (1971). The same
convention is also used, although with some few exceptions, by optical
astronomers working in the field of polarimetry. Many radio astronomers,
on the other hand, use the opposite convention. [1]
HANDBOOK
OPTICS Volume I,Devices, Measurements and Properties,Michael Bass Page
272 Footnote: "Right-circularly polarized light is defined as a
clockwise rotation of the electric vector when the observer is looking against the direction the wave is traveling."
"The Polarization Ellipse". spie.org. Retrieved 13 April 2018.
S. E. Braslavsky (1 January 2009). "Glossary of terms used in photochemistry, 3rd edition (IUPAC Recommendations 2006)" (PDF). Pure and Applied Chemistry. 79 (3): 293–465. doi:10.1351/pac200779030293. S2CID 96601716. Archived (PDF) from the original on 2022-10-09.
In
one location it is stated..."Note 1. ... In general, the figure, i.e.,
polarization, is elliptical and is traced in a clockwise or
anti-clockwise sense, as viewed in the direction of propagation. ...
Rotation of the electric vector in a clockwise sense is designated
right-hand polarization, and rotation in an anti-clockwise sense is
designated left-hand polarization. "[2] Archived 2011-05-14 at the Wayback Machine
In another location it is stated... "Note 4: Circular polarization may
be referred to as "right-hand" or "left-hand", depending on whether the
helix describes the thread of a right-hand or left-hand screw,
respectively". [3] Archived 2011-06-06 at the Wayback Machine
Balanis, Constantine A. "Antenna Theory – Analysis and Design", 2005, 3rd Edition, John Wiley & Sons.
Introduction
to Quantum Theory 2ED David Park Sec 2.2 Pg32 "... the polarization of a
beam of light is exactly the same kind of thing as the spin of a beam
of electrons, the differences of terminology reflecting only the
accidents of the historical order of discovery."
Srinivasarao, Mohan; Park, Jung Ok; Crne, Matija; Sharma, Vivek (July 24, 2009). "Structural Origin of Circularly Polarized Iridescence in Jeweled Beetles". Science. 325 (5939): 449–451. Bibcode:2009Sci...325..449S. doi:10.1126/science.1172051. PMID 19628862. S2CID 206519071 – via science.sciencemag.org.
Hegedüs, Ramón; Győző Szélb; Gábor Horváth (September 2006). "Imaging polarimetry of the circularly polarizing cuticle of scarab beetles (Coleoptera: Rutelidae, Cetoniidae)". Vision Research. 46 (17): 2786–2797. doi:10.1016/j.visres.2006.02.007. PMID 16564066. S2CID 14974820.
Wynberg, Hans; Meijer, E.W.; Hummelen, J.C.; Dekkers, H.P.J.M.; Schippers, P.H.; Carlson, A.D. (7 August 1980). "Circular polarization observed in bioluminescence" (PDF). Nature. 286 (5773): 641–642. Bibcode:1980Natur.286..641W. doi:10.1038/286641a0. S2CID 4324467. Archived from the original (PDF) on 24 July 2011.
Horváth, Gábor; Dezsö Varjú (2003). Polarized Light in Animal Vision: Polarization Patterns in Nature. Springer. pp. 100–103. ISBN 978-3-540-40457-6.
Tsyr-Huei
Chiou; Sonja Kleinlogel; Tom Cronin; Roy Caldwell; Birte Loeffler;
Afsheen Siddiqi; Alan Goldizen; Justin Marshall (2008). "Circular polarization vision in a stomatopod crustacean". Current Biology. 18 (6): 429–34. doi:10.1016/j.cub.2008.02.066. PMID 18356053. S2CID 6925705.
Further reading
External links

The
electric field
vectors of a traveling circularly polarized electromagnetic wave. This
wave is right-circularly-polarized, since the direction of rotation of
the vector is related by the
right-hand rule to the direction the wave is moving; or left-circularly-polarized according to alternative convention.
https://en.wikipedia.org/wiki/Circular_polarization
A stellar magnetic field is a magnetic field generated by the motion of conductive plasma inside a star. This motion is created through convection, which is a form of energy transport involving the physical movement of material. A localized magnetic field
exerts a force on the plasma, effectively increasing the pressure
without a comparable gain in density. As a result, the magnetized region
rises relative to the remainder of the plasma, until it reaches the
star's photosphere. This creates starspots on the surface, and the related phenomenon of coronal loops.[1]
https://en.wikipedia.org/wiki/Stellar_magnetic_field
In solar physics, a coronal loop is a well-defined arch-like structure in the Sun's atmosphere made up of relatively dense plasma confined and isolated from the surrounding medium by magnetic flux tubes. Coronal loops begin and end at two footpoints on the photosphere and project into the transition region and lower corona. They typically form and dissipate over periods of seconds to days[1] and may span anywhere from 1 to 1,000 megametres (621 to 621,000 mi) in length.[2]
Coronal loops are often associated with the strong magnetic fields located within active regions and sunspots. The number of coronal loops varies with the 11 year solar cycle.
https://en.wikipedia.org/wiki/Coronal_loop
The photosphere is a star's outer shell from which light is radiated.
The term itself is derived from Ancient Greek roots, φῶς, φωτός/phos, photos meaning "light" and σφαῖρα/sphaira meaning "sphere", in reference to it being a spherical surface that is perceived to emit light.[citation needed] It extends into a star's surface until the plasma becomes opaque, equivalent to an optical depth of approximately 2⁄3,[1] or equivalently, a depth from which 50% of light will escape without being scattered.
A photosphere is the deepest region of a luminous object, usually a star, that is transparent to photons of certain wavelengths.
https://en.wikipedia.org/wiki/Photosphere
In physics, the magnetomotive force (mmf)  is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:
is a quantity appearing in the equation for the magnetic flux in a magnetic circuit, Hopkinson's law.[1] It is the property of certain substances or phenomena that give rise to magnetic fields:
where
Φ is the magnetic flux and

is the
reluctance of the circuit. It can be seen that the magnetomotive force plays a role in this equation analogous to the voltage
V in
Ohm's law:
V = IR, since it is the cause of magnetic flux in a magnetic circuit:
[2]
 where N is the number of turns in the coil and I is the electric current through the circuit.
where N is the number of turns in the coil and I is the electric current through the circuit. where Φ is the magnetic flux and
where Φ is the magnetic flux and  is the magnetic reluctance
is the magnetic reluctance where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
where H is the magnetizing force (the strength of the magnetizing field) and L is the mean length of a solenoid or the circumference of a toroid.
https://en.wikipedia.org/wiki/Magnetomotive_force
In physics, mainly quantum mechanics and particle physics, a spin magnetic moment is the magnetic moment caused by the spin of elementary particles. For example, the electron is an elementary spin-1/2 fermion. Quantum electrodynamics gives the most accurate prediction of the anomalous magnetic moment of the electron.
In general, a magnetic moment can be defined in terms of an electric current and the area enclosed by the current loop.
Since angular momentum corresponds to rotational motion, the magnetic
moment can be related to the orbital angular momentum of the charge carriers in the constituting current. However, in magnetic materials, the atomic and molecular dipoles have magnetic moments not just because of their quantized orbital angular momentum, but also due to the spin of elementary particles constituting them.[a][b]
"Spin" is a non-classical property of elementary particles, since classically the "spin angular momentum" of a material object is really just the total orbital angular momenta of the object's constituents about the rotation axis. Elementary particles are conceived as point objects with no axis around which to "spin" (see wave–particle duality).
https://en.wikipedia.org/wiki/Spin_magnetic_moment
Coercivity, also called the magnetic coercivity, coercive field or coercive force, is a measure of the ability of a ferromagnetic material to withstand an external magnetic field without becoming demagnetized. Coercivity is usually measured in oersted or ampere/meter units and is denoted HC.
An analogous property in electrical engineering and materials science, electric coercivity, is the ability of a ferroelectric material to withstand an external electric field without becoming depolarized.
Ferromagnetic materials with high coercivity are called magnetically hard, and are used to make permanent magnets. Materials with low coercivity are said to be magnetically soft. The latter are used in transformer and inductor cores, recording heads, microwave devices, and magnetic shielding.
https://en.wikipedia.org/wiki/Coercivity
Magnetic shielding
Equipment sometimes requires isolation from external magnetic fields.[8]
For static or slowly varying magnetic fields (below about 100 kHz) the
Faraday shielding described above is ineffective. In these cases
shields made of high magnetic permeability metal alloys can be used, such as sheets of permalloy and mu-metal[9][10] or with nanocrystalline grain structure ferromagnetic metal coatings.[11]
These materials do not block the magnetic field, as with electric
shielding, but rather draw the field into themselves, providing a path
for the magnetic field lines
around the shielded volume. The best shape for magnetic shields is
thus a closed container surrounding the shielded volume. The
effectiveness of this type of shielding depends on the material's
permeability, which generally drops off at both very low magnetic field
strengths and high field strengths where the material becomes saturated.
Therefore, to achieve low residual fields, magnetic shields often
consist of several enclosures, one inside the other, each of which
successively reduces the field inside it. Entry holes within shielding
surfaces may degrade their performance significantly.
Because of the above limitations of passive shielding, an
alternative used with static or low-frequency fields is active
shielding, in which a field created by electromagnets cancels the ambient field within a volume.[12] Solenoids and Helmholtz coils
are types of coils that can be used for this purpose, as well as more
complex wire patterns designed using methods adapted from those used in
coil design for magnetic resonance imaging. Active shields may also be designed accounting for the electromagnetic coupling with passive shields,[13][14][15][16][17] referred to as hybrid shielding,[18]
so that there is broadband shielding from the passive shield and
additional cancellation of specific components using the active system.
Additionally, superconducting materials can expel magnetic fields via the Meissner effect.
https://en.wikipedia.org/wiki/Electromagnetic_shielding#Magnetic_shielding
First time-dependent rotation
Consider another (non-inertial) observer (the 2-O) located at the center of the Earth but rotating about the NS-axis by  We establish coordinates attached to this observer as
We establish coordinates attached to this observer as
so that the unit

versor

is mapped to the point

.
For the 2-O neither the Earth nor the barycenter of the gyroscope is
moving. The rotation of 2-O relative to 1-O is performed with angular
velocity

. We suppose that the

axis denotes points with zero longitude (the prime, or Greenwich, meridian).
Second and third fixed rotations
We now rotate about the  axis, so that the
axis, so that the  -axis has the longitude of the barycenter. In this case we have
-axis has the longitude of the barycenter. In this case we have
With the next rotation (about the axis  of an angle
of an angle  , the co-latitude) we bring the
, the co-latitude) we bring the  axis along the local zenith (
axis along the local zenith ( -axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)
-axis) of the barycenter. This can be achieved by the following orthogonal matrix (with unit determinant)
so that the  versor
versor  is mapped to the point
is mapped to the point 
Constant translation
We
now choose another coordinate basis whose origin is located at the
barycenter of the gyroscope. This can be performed by the following
translation along the zenith axis
so that the origin of the new system,  is located at the point
is located at the point  and
and  is the radius of the Earth. Now the
is the radius of the Earth. Now the  -axis points towards the south direction.
-axis points towards the south direction.
Fourth time-dependent rotation
Now we rotate about the zenith  -axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find
-axis
so that the new coordinate system is attached to the structure of the
gyroscope, so that for an observer at rest in this coordinate system,
the gyrocompass is only rotating about its own axis of symmetry. In this
case we find
The axis of symmetry of the gyrocompass is now along the  -axis.
-axis.
Last time-dependent rotation
The last rotation is a rotation on the axis of symmetry of the gyroscope as in
Dynamics of the system
Since
the height of the gyroscope's barycenter does not change (and the
origin of the coordinate system is located at this same point), its gravitational potential energy is constant. Therefore its Lagrangian  corresponds to its kinetic energy
corresponds to its kinetic energy  only. We have
only. We have
where

is the mass of the gyroscope, and
is the squared inertial speed of the origin of the coordinates of the
final coordinate system (i.e. the center of mass). This constant term
does not affect the dynamics of the gyroscope and it can be neglected.
On the other hand, the tensor of inertia is given by
and
Therefore we find
The Lagrangian can be rewritten as
where
is the part of the Lagrangian responsible for the dynamics of the system. Then, since

, we find
Since the angular momentum  of the gyrocompass is given by
of the gyrocompass is given by  we see that the constant
we see that the constant  is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable
is the component of the angular momentum about the axis of symmetry.
Furthermore, we find the equation of motion for the variable  as
as
or
Particular case: the poles
At the poles we find  and the equations of motion become
and the equations of motion become
This simple solution implies that the gyroscope is uniformly
rotating with constant angular velocity in both the vertical and
symmetrical axis.
The general and physically relevant case
Let us suppose now that  and that
and that  ,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find
,
that is the axis of the gyroscope is approximately along the
north-south line, and let us find the parameter space (if it exists) for
which the system admits stable small oscillations about this same line.
If this situation occurs, the gyroscope will always be approximately
aligned along the north-south line, giving direction. In this case we
find
Consider the case that
and, further, we allow for fast gyro-rotations, that is
Therefore, for fast spinning rotations,  implies
implies  In this case, the equations of motion further simplify to
In this case, the equations of motion further simplify to
Therefore we find small oscillations about the north-south line, as  ,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by
,
where the angular velocity of this harmonic motion of the axis of
symmetry of the gyrocompass about the north-south line is given by
which corresponds to a period for the oscillations given by
Therefore  is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required
is proportional to the geometric mean of the Earth and spinning angular
velocities. In order to have small oscillations we have required  ,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the
,
so that the North is located along the right-hand-rule direction of the
spinning axis, that is along the negative direction of the  -axis, the axis of symmetry. As a side result, on measuring
-axis, the axis of symmetry. As a side result, on measuring  (and knowing
(and knowing  ), one can deduce the local co-latitude
), one can deduce the local co-latitude 
See also
Notes
- Although
the effect is not visible in the specific case when the gyroscope's
axis is precisely parallel to the Earth's rotational axis.
References
Gade, Kenneth (2016). "The Seven Ways to Find Heading" (PDF). The Journal of Navigation. Cambridge University Press. 69 (5): 955–970. doi:10.1017/S0373463316000096. S2CID 53587934.
Elliott-Laboratories (2003). The Anschutz Gyro-Compass and Gyroscope Engineering. pp. 7–24. ISBN 978-1-929148-12-7. Archived from the original on 2017-03-04.
Time Inc. (Mar 15, 1943). "The gyroscope pilots ships & planes". Life. pp. 80–83. Archived from the original on 2017-02-27.
Galison, Peter (1987). How experiments end. pp. 34–37. ISBN 978-0-226-27915-2. Archived from the original on 2012-03-02.
"Archived copy" (PDF). Archived (PDF) from the original on 2015-06-29. Retrieved 2012-02-19. Standard 22
Anschütz Gyro Compass [sic] System: Gyro Compass [sic] Technology [sic] for over than [sic] 100 years
Chambers of Commerce and Industry in Schleswig-Holstein Archived 2017-02-22 at the Wayback Machine Retrieved on February 22, 2017.
Gyrocompass, Auxiliary Gyrocompass, and Dead Reckoning Analyzing Indicator and Tracer Systems Archived 2013-06-01 at the Wayback Machine, San Francisco Maritime National Park Association.
The Invention of Precision Navigational Instruments for Air and Sea Navigation Archived 2011-07-18 at the Wayback Machine, Weems & Plath.
Collinson, R. P. G. (2003), Introduction to avionics systems, Springer, p. 293, ISBN 978-1-4020-7278-9, archived from the original on 2014-07-07
NASA NASA Callback: Heading for Trouble Archived 2011-07-16 at the Wayback Machine, NASA Callback Safety Bulletin website, December 2005, No. 305. Retrieved August 29, 2010.
Bowditch, Nathaniel. American Practical Navigator Archived 2017-03-07 at the Wayback Machine, Paradise Cay Publications, 2002, pp.93-94, ISBN 978-0-939837-54-0.
Gyrocompass: Steaming Error Archived 2008-12-22 at the Wayback Machine, Navis. Accessed 15 December 2008.
- Seamanship Techniques:Shipboard and Marine Operations, D. J. House, Butterworth-Heinemann, 2004, p. 341
Bibliography
External links
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
This article is about devices used on ships. For the type of gyroscope used to determine aircraft heading, see
Heading indicator.
Cutaway of an Anschütz gyrocompass
A gyrocompass is a type of non-magnetic compass which is based on a fast-spinning disc and the rotation of the Earth (or another planetary body if used elsewhere in the universe) to find geographical direction automatically. The use of a gyrocompass is one of the seven fundamental ways to determine the heading of a vehicle.[1] A gyroscope is an essential component of a gyrocompass, but they are different devices; a gyrocompass is built to use the effect of gyroscopic precession, which is a distinctive aspect of the general gyroscopic effect.[2][3] Gyrocompasses are widely used for navigation on ships, because they have two significant advantages over magnetic compasses:[3]
Aircraft commonly use gyroscopic instruments (but not a gyrocompass) for navigation and altitude monitoring; for details, see Flight instruments and Gyroscopic autopilot.
History
The first, not yet practical,[4] form of gyrocompass was patented in 1885 by Marinus Gerardus van den Bos.[4] A usable gyrocompass was invented in 1906 in Germany by Hermann Anschütz-Kaempfe, and after successful tests in 1908 became widely used in the German Imperial Navy.[2][4][5] Anschütz-Kaempfe founded the company Anschütz & Co. in Kiel, to mass produce gyrocompasses; the company is today Raytheon Anschütz GmbH.[6]
The gyrocompass was an important invention for nautical navigation
because it allowed accurate determination of a vessel’s location at all
times regardless of the vessel’s motion, the weather and the amount of
steel used in the construction of the ship.[7]
In the United States, Elmer Ambrose Sperry produced a workable gyrocompass system (1908: U.S. Patent 1,242,065), and founded the Sperry Gyroscope Company. The unit was adopted by the U.S. Navy (1911[3]),
and played a major role in World War I. The Navy also began using
Sperry's "Metal Mike": the first gyroscope-guided autopilot steering
system. In the following decades, these and other Sperry devices were
adopted by steamships such as the RMS Queen Mary, airplanes, and the warships of World War II. After his death in 1930, the Navy named the USS Sperry after him.
Meanwhile, in 1913, C. Plath (a Hamburg, Germany-based
manufacturer of navigational equipment including sextants and magnetic
compasses) developed the first gyrocompass to be installed on a
commercial vessel. C. Plath sold many gyrocompasses to the Weems’
School for Navigation in Annapolis, MD, and soon the founders of each
organization formed an alliance and became Weems & Plath.[8]
The 1889 Dumoulin-Krebs gyroscope
Before the success of the gyrocompass, several attempts had been made in Europe to use a gyroscope instead. By 1880, William Thomson (Lord Kelvin) tried to propose a gyrostat to the British Navy. In 1889, Arthur Krebs adapted an electric motor to the Dumoulin-Froment marine gyroscope, for the French Navy. That gave the Gymnote submarine the ability to keep a straight line while underwater for several hours, and it allowed her to force a naval block in 1890.
In 1923 Max Schuler published his paper containing his observation that if a gyrocompass possessed Schuler tuning
such that it had an oscillation period of 84.4 minutes (which is the
orbital period of a notional satellite orbiting around the Earth at sea
level), then it could be rendered insensitive to lateral motion and
maintain directional stability.[9]
Operation
A gyroscope, not to be confused with a gyrocompass, is a spinning wheel mounted on a set of gimbals so that its axis is free to orient itself in any way.[3] When it is spun up to speed with its axis pointing in some direction, due to the law of conservation of angular momentum, such a wheel will normally maintain its original orientation to a fixed point in outer space
(not to a fixed point on Earth). Since the Earth rotates, it appears to
a stationary observer on Earth that a gyroscope's axis is completing a
full rotation once every 24 hours.[note 1] Such a rotating gyroscope is used for navigation in some cases, for example on aircraft, where it is known as heading indicator
or directional gyro, but cannot ordinarily be used for long-term marine
navigation. The crucial additional ingredient needed to turn a
gyroscope into a gyrocompass, so it would automatically position to true
north,[2][3] is some mechanism that results in an application of torque whenever the compass's axis is not pointing north.
One method uses friction to apply the needed torque:[7]
the gyroscope in a gyrocompass is not completely free to reorient
itself; if for instance a device connected to the axis is immersed in a
viscous fluid, then that fluid will resist reorientation of the axis.
This friction force caused by the fluid results in a torque acting on the axis, causing the axis to turn in a direction orthogonal to the torque (that is, to precess) along a line of longitude.
Once the axis points toward the celestial pole, it will appear to be
stationary and won't experience any more frictional forces. This is
because true north (or true south) is the only direction for which the
gyroscope can remain on the surface of the earth and not be required to
change. This axis orientation is considered to be a point of minimum potential energy.
Another, more practical, method is to use weights to force the
axis of the compass to remain horizontal (perpendicular to the direction
of the center of the Earth), but otherwise allow it to rotate freely
within the horizontal plane.[2][3]
In this case, gravity will apply a torque forcing the compass's axis
toward true north. Because the weights will confine the compass's axis
to be horizontal with respect to the Earth's surface, the axis can never
align with the Earth's axis (except on the Equator) and must realign
itself as the Earth rotates. But with respect to the Earth's surface,
the compass will appear to be stationary and pointing along the Earth's
surface toward the true North Pole.
Since the gyrocompass's north-seeking function depends on the rotation around the axis of the Earth that causes torque-induced gyroscopic precession,
it will not orient itself correctly to true north if it is moved very
fast in an east to west direction, thus negating the Earth's rotation.
However, aircraft commonly use heading indicators or directional gyros,
which are not gyrocompasses and do not align themselves to north via
precession, but are periodically aligned manually to magnetic north.[10][11]
Errors
A gyrocompass is subject to certain errors. These include steaming error, where rapid changes in course, speed and latitude cause deviation before the gyro can adjust itself.[12] On most modern ships the GPS or other navigational aids feed data to the gyrocompass allowing a small computer to apply a correction.
Alternatively a design based on a strapdown architecture (including a triad of fibre optic gyroscopes, ring laser gyroscopes or hemispherical resonator gyroscopes
and a triad of accelerometers) will eliminate these errors, as they do
not depend upon mechanical parts to determinate rate of rotation.[13]
https://en.wikipedia.org/wiki/Gyrocompass#First_time-dependent_rotation
A rotating magnetic field is the resultant magnetic field produced by a system of coils symmetrically placed and supplied with polyphase currents.[1]
A rotating magnetic field can be produced by a poly-phase (two or more
phases) current or by a single phase current provided that, in the
latter case, two field windings are supplied and are so designed that
the two resulting magnetic fields generated thereby are out of phase.[2]
Rotating magnetic fields are often utilized for electromechanical applications, such as induction motors, electric generators and induction regulators.
History
In 1824, the French physicist François Arago formulated the existence of rotating magnetic fields using a rotating copper disk and a needle, termed “Arago's rotations.” English experimenters Charles Babbage and John Herschel found they could induce rotation in Arago's copper disk by spinning a horseshoe magnet under it, with English scientist Michael Faraday later attributing the effect to electromagnetic induction.[3] In 1879, English physicist Walter Baily
replaced the horseshoe magnets with four electromagnets and, by
manually turning switches on and off, demonstrated a primitive induction
motor.[4][5][6][7][8]
The idea of a rotating magnetic field in an AC motor was explored by the Italian physicist and electrical engineer Galileo Ferraris and the Serbian-American inventor and electrical engineer Nikola Tesla.[9] Ferraris wrote about researching the concept and built a working model in 1885.[10]
Tesla attempted several (unsuccessful) designs and working models
through the early 1880s before building a working prototype in 1887[11][12][13]
According to Ferraris principle of rotating magnetic field, Friedrich
August Haselwander developed the first AC 3 phase generator in 1887.[14] In 1888, Ferraris published his research in a paper to the Royal Academy of Sciences in Turin and Tesla obtained a United States patent (U.S. Patent 0,381,968)
for his design. Based on the Haselwander generator, Mikhail
Dolivo-Dobrovolsky will develop a three-phase generator and motor for
the world's first three-phase power plant built in 1891 in Frankfurt,
Germany.[15]
Description
The rotating magnetic field is the key principle in the operation of induction machines. The induction motor consists of a stator and rotor.
In the stator a group of fixed windings are so arranged that a two
phase current, for example, produces a magnetic field which rotates at
an angular velocity determined by the frequency of the alternating current. The rotor or armature consists of coils wound in slots, which are short circuited and in which the changing flux
generated by the field poles induce a current. The flux generated by
the armature current reacts upon the field poles and the armature is set
in rotation in a definite direction.[2]
Rotating fields.
As the direction of the current through the windings changes, the
polarity of the windings changes as well. Since there are two windings
acting in conjunction with each other, the polarity of the main field
will depend upon the polarity of each winding. The arrow or vector below
each diagram indicates the direction of the magnetic field in each
case.
[16] A symmetric rotating magnetic field can be produced with as few as two polar wound coils driven at 90-degree phasing. However, three sets of coils are nearly always used, because it is compatible with a symmetric three-phase AC sine current system. The three coils are driven with each set 120 degrees in phase from the others. For the purpose of this example, the magnetic field is taken to be the linear function of the coil's current.
The result of adding three 120-degree phased sine waves on the axis of the motor is a single rotating vector that always remains constant in magnitude.[17]
The rotor has a constant magnetic field. The north pole of the rotor
will move toward the south pole of the magnetic field of the stator, and
vice versa. This magnetomechanical attraction creates a force that will drive the rotor to follow the rotating magnetic field in a synchronous manner.
Rotating three-phase magnetic field, as indicated by the rotating black arrow
A permanent magnet
in such a field will rotate so as to maintain its alignment with the
external field. This effect was utilized in early alternating-current
electric motors. A rotating magnetic field can be constructed using two
orthogonal coils with a 90-degree phase difference in their alternating
currents. However, in practice, such a system would be supplied through
a three-wire arrangement with unequal currents. This inequality would
cause serious problems in the standardization of the conductor size. In
order to overcome this, three-phase systems are used in which the three
currents are equal in magnitude and have a 120-degree phase difference.
Three similar coils having mutual geometrical angles of 120 degrees will
create the rotating magnetic field in this case. The ability of the
three-phase system to create the rotating field utilized in electric
motors is one of the main reasons why three-phase systems dominate the
world’s electric power-supply systems.
Rotating magnetic fields are also used in induction motors.
Because magnets degrade with time, induction motors use short-circuited
rotors (instead of a magnet), which follow the rotating magnetic field
of a multicoiled stator. In these motors, the short-circuited turns of
the rotor develop eddy currents in the rotating field of the stator, which in turn move the rotor by Lorentz force.
These types of motors are not usually synchronous, but instead
necessarily involve a degree of 'slip' in order that the current may be
produced due to the relative movement of the field and the rotor.
See also
References
Graham, Frank Duncan (1921). Audels Engineers and Mechanics Guide. New York: THEO. AUDEL & CO. p. 594.
The Wireless Age. Vol. 6. New York: Macroni Pub. Corp'n. October 1918. pp. 18–19.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 52–54. ISBN 978-1400846559.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. p. 55. ISBN 978-1400846559.
Babbage, C.; Herschel, J. F. W. (Jan 1825). "Account
of the Repetition of M. Arago's Experiments on the Magnetism Manifested
by Various Substances during the Act of Rotation". Philosophical Transactions of the Royal Society. 115: 467–496. Bibcode:1825RSPT..115..467B. doi:10.1098/rstl.1825.0023. Retrieved 2 December 2012.
Thompson, Silvanus Phillips (1895). Polyphase Electric Currents and Alternate-Current Motors (1st ed.). London: E. & F.N. Spon. p. 261. Retrieved 2 December 2012.
Baily, Walter (June 28, 1879). "A Mode of producing Arago's Rotation". Philosophical Magazine. Taylor & Francis. 3 (1): 115–120. Bibcode:1879PPSL....3..115B. doi:10.1088/1478-7814/3/1/318.
Vučković, Vladan (November 2006). "Interpretation of a Discovery" (PDF). The Serbian Journal of Electrical Engineers. 3 (2). Retrieved 10 February 2013.
Hughes, Thomas Parke (1983). Networks of power: electrification in Western society, 1880-1930. Baltimore: Johns Hopkins University Press. p. 117.
Encyclopedia Americana: Meyer to Nauvoo. Vol. 12. Danbury, Connecticut: Scholastic Library Pub. 2006. p. 558.
Carlson, W. Bernard (2013). Tesla: Inventor of the Electrical Age. Princeton University Press. pp. 63–68. ISBN 978-1400846559.
Debunking the Tesla Myth
O'Neill, John. Prodigal Genius: The Life of Nikola Tesla. pp. 55–58.
https://ieeexplore.ieee.org/document/4401482?arnumber=4401482 H. Hooshyar; M. Savaghebi; A. Vahedi: Synchronous generator - Past, present and future
AC Power History and Timeline
United States, Bureau of Naval Personnel (1945). Advanced Work In Aircraft Electricity. Washington: U.S. Govt. Print. Off. pp. 149–150.
 This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
This article incorporates text from this source, which is in the public domain: The Wireless Age. New York, Marconi Pub. Corporation. 1918.
Further reading
- C Mackechnie Jarvis (1970). "Nikola Tesla and the induction motor". Phys Educ. 5 (5): 280–7. Bibcode:1970PhyEd...5..280M. doi:10.1088/0031-9120/5/5/306. S2CID 250845406.
- Owen, E.L. (October 1988). "The induction motor's historical past". IEEE Potentials. 7 (3): 27–30. doi:10.1109/45.9969. S2CID 19271710.
- Beckhard, Arthur J., "Electrical genius Nikola Tesla". New York,
Messner, 1959. LCCN 59007009 /L/AC/r85 (ed. 192 p.; 22 cm.; biography
with notes on the inventions of the rotating magnetic field motors for
alternating current.)
- Kline, R. (1987). "Science and Engineering Theory in the Invention and Development of the Induction Motor, 1880–1900". Technology and Culture. 28 (2): 283–313. doi:10.2307/3105568. JSTOR 3105568.
- Cēbers, A. (December 13, 2002). "Dynamics of an elongated magnetic droplet in a rotating field". Phys. Rev. E. 66 (6): 061402. Bibcode:2002PhRvE..66f1402C. doi:10.1103/PhysRevE.66.061402. PMID 12513280.
- Cēbers, A. & I. Javaitis (2004). "Dynamics of a flexible magnetic chain in a rotating magnetic field". Phys. Rev. E. 69 (2): 021404. Bibcode:2004PhRvE..69b1404C. doi:10.1103/PhysRevE.69.021404. PMID 14995441.
- Cēbers, A. & M. Ozols (2006). "Dynamics of an active magnetic particle in a rotating magnetic field". Phys. Rev. E. 73 (2): 021505. Bibcode:2006PhRvE..73b1505C. doi:10.1103/PhysRevE.73.021505. PMID 16605340.
- Tao Song; et al. (June 2004). "Rotating permanent magnetic fields exposure system for in vitro study". IEEE Transactions on Applied Superconductivity. 14 (2): 1643–6. Bibcode:2004ITAS...14.1643S. doi:10.1109/TASC.2004.831024.
- Labzovskii, L.N., A.O. Mitrushchenkov, and A.I. Frenkel, "Parity Nonconserving Current in Conductors of Electricity". 6 July 1987. (ed., Shows that the continuous current arises under the influence of the rotating magnetic field.)
- Naval Electrical Engineering Training Series, Module 05 -
Introduction to Generators and Motors, Chapter 4 Alternating Current
Motors, Rotating magnetic fields (ed. different copy of the NEETS book is available, Add-free version)
- Rotating Magnetic Field, eng.ox.ac.uk
- Tesla's Autobiography, III. My Later Endeavors; The Discovery of the Rotating Magnetic Field
- Nikola Tesla and the electro-magnetic motor, Inventor of the Week Archive.
- Galileo Ferraris: the rotating magnetic field
- Single Phase Induction Motors
- H.Y. Guo, A.L. Hoffman, D. Lotz, S.J. Tobin, W.A. Reass, L.S. Schrank and G.A. Wurden, The Rotating Magnetic Field Oscillator System for Current Drive in the Translation, Confinement and Sustainment Experiment, March 22, 2001.
- Putko, V. F., and V. S. Sobolev, Effect of a rotating magnetic field on the characteristics of a direct-current plasma generator.
External links
Patents
|
|---|
Career and
inventions | | |
|---|
| Writings | |
|---|
| Other | |
|---|
| Related | |
|---|
https://en.wikipedia.org/wiki/Rotating_magnetic_field
Earth's rotation or Earth's spin is the rotation of planet Earth around its own axis, as well as changes in the orientation of the rotation axis in space. Earth rotates eastward, in prograde motion. As viewed from the northern polar star Polaris, Earth turns counterclockwise.
https://en.wikipedia.org/wiki/Earth%27s_rotation
Magnetic hysteresis occurs when an external magnetic field is applied to a ferromagnet such as iron and the atomic dipoles align themselves with it. Even when the field is removed, part of the alignment will be retained: the material has become magnetized. Once magnetized, the magnet will stay magnetized indefinitely. To demagnetize it requires heat or a magnetic field in the opposite direction. This is the effect that provides the element of memory in a hard disk drive.
https://en.wikipedia.org/wiki/Magnetic_hysteresis
Magnetic reluctance, or magnetic resistance, is a concept used in the analysis of magnetic circuits. It is defined as the ratio of magnetomotive force (mmf) to magnetic flux. It represents the opposition to magnetic flux, and depends on the geometry and composition of an object.
Magnetic reluctance in a magnetic circuit is analogous to electrical resistance in an electrical circuit in that resistance is a measure of the opposition to the electric current. The definition of magnetic reluctance is analogous to Ohm's law
in this respect. However, magnetic flux passing through a reluctance
does not give rise to dissipation of heat as it does for current through
a resistance. Thus, the analogy cannot be used for modelling energy
flow in systems where energy crosses between the magnetic and electrical
domains. An alternative analogy to the reluctance model which does
correctly represent energy flows is the gyrator–capacitor model.
Magnetic reluctance is a scalar extensive quantity. The unit for magnetic reluctance is inverse henry, H−1.
https://en.wikipedia.org/wiki/Magnetic_reluctance
https://en.wikipedia.org/wiki/Gyrator%E2%80%93capacitor_model
https://en.wikipedia.org/wiki/Lumped-element_model
The lumped-element model (also called lumped-parameter model, or lumped-component model) simplifies the description of the behaviour of spatially distributed physical systems, such as electrical circuits, into a topology
consisting of discrete entities that approximate the behaviour of the
distributed system under certain assumptions. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc. This may be contrasted to distributed parameter systems or models in which the behaviour is distributed spatially and cannot be considered as localized into discrete entities.
Mathematically speaking, the simplification reduces the state space of the system to a finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters.
https://en.wikipedia.org/wiki/Lumped-element_model
https://en.wikipedia.org/wiki/Utility_frequency#Load-frequency_control
Steam turbine governing is the procedure of controlling the flow rate of steam to a steam turbine
so as to maintain its speed of rotation as constant. The variation in
load during the operation of a steam turbine can have a significant
impact on its performance. In a practical situation the load frequently
varies from the designed or economic load and thus there always exists a
considerable deviation from the desired performance of the turbine.[1]
The primary objective in the steam turbine operation is to maintain a
constant speed of rotation irrespective of the varying load. This can
be achieved by means of governing in a steam turbine. There are many types of governors.
https://en.wikipedia.org/wiki/Steam_turbine_governing
A virtual power plant (VPP) is a cloud-based distributed power plant that aggregates the capacities of heterogeneous distributed energy resources
(DER) for the purposes of enhancing power generation, trading or
selling power on the electricity market, and demand side options for
load reduction.[1]
DER assets in a VPP can include photovoltaic solar, energy
storage, electric vehicle chargers, and demand-responsive devices (such
as water heaters, thermostats, and appliances) with examples of virtual
power plants existing in the United States, Europe, and Australia.
https://en.wikipedia.org/wiki/Virtual_power_plant
Power generation
A virtual power plant is a system that integrates several types of power sources to give a reliable overall power supply.[2]
The sources often form a cluster of different types of dispatchable and
non-dispatchable, controllable or flexible load (CL or FL) distributed generation (DG) systems that are controlled by a central authority and can include microCHPs, natural gas-fired reciprocating engines, small-scale wind power plants (WPP), photovoltaics (PV), run-of-river hydroelectricity plants, small hydro, biomass, backup generators, and energy storage systems (ESS).
This system has benefits such as the ability to deliver peak load electricity or load-following power
generation on short notice. Such a VPP can replace a conventional power
plant while providing higher efficiency and more flexibility, which
allows the system to react better to load fluctuations. The drawback is a
higher complexity of the system, which requires complicated
optimization, control, and secure communications.[3] An interactive simulation on the website of the VPP operator Next Kraftwerke illustrates how the technology works.[4]
According to a 2012 report by Pike Research, VPP capacity would,
from 2011 to 2017, increase by 65%, from 55.6 gigawatts (GW) to 91.7 GW
worldwide, generating from $5.3 billion to $6.5 billion in worldwide
revenue in 2017.[5]
In a more aggressive forecast scenario, the clean-tech market
intelligence firm forecasts that global VPP revenues could reach as high
as $12.7 billion during the same period.[6]
"Virtual power plants represent an 'Internet of Energy'",
said senior analyst Peter Asmus of Pike Research. "These systems tap
existing grid networks to tailor electricity supply and demand services
for a customer. VPPs maximize value for both the end user and the
distribution utility using a sophisticated set of software-based
systems. They are dynamic, deliver value in real time, and can react
quickly to changing customer load conditions."
Ancillary services
Virtual power plants can also be used to provide ancillary services to grid operators in order to help maintain grid stability. Ancillary services include frequency regulation, load following, and providing operating reserve.
These services are primarily used to maintain the instantaneous balance
of electrical supply and demand. Power plants providing ancillary
services must respond to signals from grid operators to increase or
decrease load on the order of seconds to minutes in response to varying
levels of consumer demand.
Since ancillary services are typically provided by controllable
fossil-fuel generators, future carbon-free electrical grids that contain
high percentages of solar and wind must rely on other forms of
controllable power generation or consumption. One of the most well-known
examples of this is Vehicle to Grid
technology. In this case, distributed electrical vehicles connected to
the grid can be controlled together to act as a single virtual power
plant. By selectively controlling the rate at which each individual
vehicle charges, the grid sees a net injection or consumption of energy
as if a large scale battery was providing this service.
Similarly, flexible demand in the form of heat pumps or air conditioners has also been explored to provide ancillary services to the grid.[7]
As long as indoor thermal comfort is maintained, an aggregation of
distributed heat pumps can be selectively turned off and on in order to
vary their aggregate power consumption and follow an ancillary service
signal. Again, the effect on the grid is the same as if a large scale
power plant was providing the service.
Since they operate in parallel, virtual power plants can have the
advantage of higher ramp rates than thermal generators, which is
especially important in grids that experience a duck curve
and have high ramping requirements in the morning and evening. However,
the distributed nature generates communication and latency issues,
which could be problematic for providing fast services like frequency
regulation.
Energy trading
A
virtual power plant is also a cloud-based central or distributed
control center that takes advantage of information and communication
technologies (ICTs) and Internet of things (IoT) devices to aggregate the capacities of heterogeneous Distributed Energy Resources (DERs) to form "a coalition of heterogeneous DERs" for the purpose of energy trading on the wholesale electricity markets or providing ancillary services for system operators on behalf of non-eligible individual DERs.[8][9][10][11][12]
A VPP acts as an intermediary between DERs and the wholesale
electricity market and trades energy on behalf of DER owners who by
themselves are unable to participate in that market.[11]
The VPP behaves as a conventional dispatchable power plant from the
point of view of other market participants, although it is indeed a
cluster of many diverse DERs. Also, in the competitive electricity
markets, a virtual power plant acts as an arbitrageur between diverse
energy trading floors (i.e., bilateral and PPA contracts, forward and
futures markets, and the pool).[8][9][10][12]
So far, for risk management purposes, five different risk-hedging
strategies (i.e., IGDT, RO, CVaR, FSD, and SSD) have been applied to
the decision-making problems of VPPs in the research articles to measure
the level of conservatism of VPPs' decisions in diverse energy trading
floors (e.g., day-ahead electricity market, derivatives exchange market,
and bilateral contracts):
- IGDT : Information Gap Decision Theory[8]
- RO : Robust optimization[9]
- CVaR : Conditional Value at Risk[10]
- FSD : First-order Stochastic Dominance[11]
- SSD : Second-order Stochastic Dominance[12][13]
United States
Energy markets are those commodity markets that deal specifically with the trade and supply of energy.[14]
In the United States, virtual power plants not only deal with the
supply side, but also help manage demand, and ensure reliability of grid
functions through demand response (DR) and other load-shifting approaches, in real time.[15]
An often-reported energy crisis in America[16]
has opened the door for government-subsidized companies to enter an
arena that has only been available to utilities and multinational
billion-dollar companies until now. With the deregulation of markets
around the United States, the wholesale market pricing became the
exclusive domain of large retail suppliers; however local and federal
legislation along with large end-users are beginning to recognize the
advantages of wholesale activities.[17]
Texas is in the stage of developing pilot VPP projects to evaluate the impact on service and reliability.[18]
They have had several meetings of their ADER (Aggregated Distributed
Energy Resources) task force to develop the criteria for pilot projects
to operate.[19]
In California there are two electrical markets: private retail
and wholesale. California Senate Bill 2X—which passed the California
legislature on March 30, 2011—mandates 33% renewables by 2020 without
mandating any particular method to reach that goal.[20] PG&E pays VPP providers $2/kWh during peak times.[21][22]
As of August/September 2022, SunRun VPP inputs 80 MW at peak times,[23] and Tesla VPP inputs 68 MW.[24][25]
Europe
The Institute for Solar Energy Supply Technology of the University of Kassel in Germany pilot-tested a combined power plant that linked solar, wind, biogas, and pumped-storage hydroelectricity to provide load-following power around the clock, completely from renewable sources.[26]
Virtual power station operators are also commonly referred to as aggregators.
To test the effects of micro combined heat and power on a smart grid, 45 natural gas SOFC units (each generating 1.5 kW) from Republiq Power (Ceramic Fuel Cells) will be placed in 2013 on Ameland to function as a virtual power plant.[27]
An example of a real-world virtual power plant can be found on the Scottish Inner Hebrides island of Eigg.[28]
Next Kraftwerke from Cologne, Germany operates a virtual power
plant in seven European countries providing peak-load operation, power
trading and grid balancing services. The company aggregates distributed
energy resources from biogas, solar and wind as well as large-scale
power consumers.[29]
Distribution network operator, UK Power Networks,
and Powervault, a battery manufacturer and power aggregator, created
London's first virtual power plant in 2018, installing a trial fleet of
battery systems on over 40 homes across the London Borough of Barnet,
providing a combined capacity of 0.32 MWh.[30] This scheme was further expanded through a second contract in St Helier, London in 2020.[31]
In September 2019, SMS plc entered the virtual power plant sector
in the United Kingdom following the acquisition of Irish energy tech
start-up, Solo Energy.[32]
In October 2020, Tesla launched its Tesla Energy Plan in the UK in partnership with Octopus Energy,
allowing households to join its UK Tesla Virtual Power Plant. Homes
under the scheme are powered with 100% renewable energy from either
solar panels on the roof or from Octopus Energy.[33]
Australia
Commencing
in August 2020, Tesla will install a 5 kW rooftop solar system and 13.5
kWh Powerwall battery at each Housing SA premises, at no upfront cost
to the tenant. As South Australia's largest virtual power plant, the
battery and solar systems can be centrally managed, collectively
delivering 20 MW of generation capacity and 54 MWh of energy storage.[34]
In August 2016, AGL Energy announced a 5 MW virtual-power-plant scheme for Adelaide, Australia. The company will supply battery and photovoltaic systems from Sunverge Energy, of San Francisco, to 1000 households and businesses. The systems will cost consumers AUD $3500 and are expected to recoup the expense in savings in 7 years under current distribution network tariffs. The scheme is worth AUD $20 million and is being billed as the largest in the world.[35]
See also
References
Zurborg, Aaron (2010). "Unlocking Customer Value: the Virtual Power Plant" (PDF). Energy.gov. Retrieved 15 January 2023.
Feasibility, beneficiality, and institutional compatibility of a micro-CHP virtual power plant in the Netherlands
Smart Grid - The New and Improved Power Grid: A Survey; IEEE Communications Surveys and Tutorials 2011; X. Fang, S. Misra, G. Xue, and D. Yang; doi:10.1109/SURV.2011.101911.00087.
"Manage the Virtual Power and prevent a blackout!". Next Kraftwerke. Retrieved 2 December 2019.
"Revenue from Virtual Power Plants Will Reach $5.3 Billion by 2017, Forecasts Pike Research" (Press release). Navigant Consulting. 18 April 2012. Retrieved 20 November 2017 – via Business Wire.
"Virtual-Power-Plant
Market Capacity Expected To Double By 2015 - Apr 16, 2011 -
renewgridmag.com - Transmission - Technical Articles - Index - Library -
GENI - Global Energy Network Institute". Global Energy Network Institute. 2011-04-16. Retrieved 2022-01-05.
Lee,
Zachary E.; Sun, Qingxuan; Ma, Zhao; Wang, Jiangfeng; MacDonald, Jason
S.; Zhang, K. Max (Feb 2020). "Providing Grid Services With Heat Pumps: A
Review". Journal of Engineering for Sustainable Buildings and Cities. 1 (1). doi:10.1115/1.4045819. S2CID 213898377.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2015). "Decision
Making Tool for Virtual Power Plants Considering Midterm Bilateral
Contracts". 3rd Iranian Regional CIRED Conference and Exhibition on
Electricity Distribution, at Niroo Research Institute (NRI), Tehran,
Iran. 3 (3): 1–6. doi:10.13140/2.1.5086.4969.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (October 2015). "The design
of a risk-hedging tool for virtual power plants via robust optimization
approach". Applied Energy. 155: 766–777. doi:10.1016/j.apenergy.2015.06.059.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (May 2016). "A medium-term
coalition-forming model of heterogeneous DERs for a commercial virtual
power plant". Applied Energy. 169: 663–681. doi:10.1016/j.apenergy.2016.02.058.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (January 2017). "Risk-based
medium-term trading strategy for a virtual power plant with first-order
stochastic dominance constraints". IET Generation, Transmission & Distribution. 11 (2): 520–529. doi:10.1049/iet-gtd.2016.1072. S2CID 114478127.
Shabanzadeh
M; Sheikh-El-Eslami, M-K; Haghifam, P; M-R (April 2016). "Modeling the
cooperation between neighboring VPPs: Cross-regional bilateral
transactions". 2016 Iranian Conference on Renewable Energy & Distributed Generation (ICREDG). 11: 520–529. doi:10.1109/ICREDG.2016.7875909. ISBN 978-1-5090-0857-5. S2CID 16453458.
Shabanzadeh,
Morteza; Sheikh-El-Eslami, Mohammad-Kazem; Haghifam, Mahmoud-Reza
(2017). "An interactive cooperation model for neighboring virtual power
plants". Applied Energy. 200: 273–289. doi:10.1016/j.apenergy.2017.05.066. S2CID 157309706.
JEAN-PHILIPPE TAILLON, CFA (2021-10-14). "Introduction to the World of Electricity Trading". Investopedia. Retrieved 2022-01-04.
Aaron Zurborg (2010). "Unlocking Customer Value: The Virtual Power Plant". WorldPower 2010: 1–5.
"Energy Crisis (1970s) - HISTORY". history.com. 2018-08-21. Retrieved 2022-01-04.
"Electricity Deregulation". PennStation Extension. 2010-06-15. Retrieved 2022-01-05.
https://interchange.puc.texas.gov/Documents/51603_66_1221955.PDF
"Admin Monitor - Texas - Public Utility Commission of Texas".
PATRICK MCGREEVY (2011-04-13). "Gov. Brown signs law requiring 33% of energy be renewable by 2020 - Los Angeles Times". Los Angeles Times. Retrieved 2021-01-05.
"PG&E, Tesla virtual power plant delivers 16.5 MW to California grid amid calls for energy conservation". Utility Dive. 23 August 2022.
"Admin Monitor - Texas - Public Utility Commission of Texas".
Colthorpe, Andy (8 September 2022). "California's fleet of battery storage working to avert energy crisis". Energy Storage News.
Lambert, Fred (2022-09-02). "Tesla virtual power plant is rocketing up, reaches 50 MW". Electrek. Retrieved 2022-09-08.
"Tesla's Virtual Power Plant Tracker". Lastbulb. Retrieved 2022-09-08.
"The Combined Power Plant: the first stage in providing 100% power from renewable energy". SolarServer. January 2008. Retrieved 2008-10-10.
"Bijlage persbericht 010/MK – Verleende subsidies – 3. Methaanbrandstoffen op Ameland" [Press release 010/MK appendix – Granted subsidies – 3. Methane fuels on Ameland] (PDF). Wadden Fund (Press release) (in Dutch). 2013. Archived from the original (PDF) on 1 November 2013. Retrieved 21 November 2017.
BBC Radio 4. Costing the Earth- Electric Island
"Next Kraftwerk Reimagines & Redefines The Electrical Grid With Virtual Power Plants". Clean Technica. October 2016. Retrieved 2019-03-13.
"Electricity network plan to launch London's first virtual power station". UK Power Networks. 22 June 2018. Retrieved 15 October 2021.
"London pioneers first 'virtual power station'". GOV.UK. 6 March 2020. Retrieved 1 July 2021.
Grundy, Alice (27 March 2020). "Smart Metering Systems reveals Solo Energy acquisition as it enters VPP market". Current News. Retrieved 1 July 2021.
Lempriere, Molly (27 October 2020). "Tesla Energy Plan launched inviting homes to become part of Virtual Power Plant". Current News. Retrieved 1 July 2021.
"Social housing added to the Tesla virtual power plant - ARENAWIRE". Australian Renewable Energy Agency. Retrieved 2021-01-06.
External links
|
|---|
| Concepts | | |
|---|
| Sources | |
|---|
| Generation | |
|---|
| |
|---|
| Failure modes | |
|---|
Protective
devices | |
|---|
Economics
and policies | |
|---|
Statistics and
production | |
|---|
|
https://en.wikipedia.org/wiki/Virtual_power_plant
lectrical busbar systems[1] (sometimes simply referred to as busbar systems) are a modular approach to electrical wiring,
where instead of a standard cable wiring to every single electrical
device, the electrical devices are mounted onto an adapter which is
directly fitted to a current carrying busbar. This modular approach is used in distribution boards, automation panels and other kinds of installation in an electrical enclosure.[2]
Busbar systems are subject to safety standards for design and installation along with electrical enclosure according to IEC 61439-1 and vary between countries and regions.[3]
https://en.wikipedia.org/wiki/Electrical_busbar_system
A black start is the process of restoring an electric power station or a part of an electric grid to operation without relying on the external electric power transmission network to recover from a total or partial shutdown.[1]
Power to restart a generating station may come from an on-site
standby generator. Alternatively, where a large amount of power is
required, a tie-line to another generating plant may be used to start
the facility. Once the main generating units are running, the electrical
transmission network can be re-connected and electrical loads restored.
Black-start power may be ensured by an agreement where a
particular energy supplier is paid to make black start power available
when required. Not all generating plants are suitable for providing
black-start power to a network.
https://en.wikipedia.org/wiki/Black_start
A rolling blackout, also referred to as rota or rotational load shedding, rota disconnection, feeder rotation, or a rotating outage, is an intentionally engineered electrical power shutdown in which electricity delivery
is stopped for non-overlapping periods of time over different parts of
the distribution region. Rolling blackouts are a last-resort measure
used by an electric utility company to avoid a total blackout of the power system.
Rolling blackouts are a measure of demand response
if the demand for electricity exceeds the power supply capability of
the network. Rolling blackouts may be localised to a specific part of
the electricity network, or they may be more widespread and affect
entire countries and continents. Rolling blackouts generally result from
two causes: insufficient generation capacity or inadequate transmission infrastructure to deliver power to where it is needed.
Rolling blackouts are also used as a response strategy to cope with reduced output beyond reserve capacity from power stations taken offline unexpectedly.
https://en.wikipedia.org/wiki/Rolling_blackout
A cascading failure is a failure in a system of interconnected parts in which the failure of one or few parts leads to the failure of other parts, growing progressively as a result of positive feedback. This can occur when a single part fails, increasing the probability that other portions of the system fail.[1][2]
Such a failure may happen in many types of systems, including power
transmission, computer networking, finance, transportation systems,
organisms, the human body, and ecosystems.
Cascading failures may occur when one part of the system fails.
When this happens, other parts must then compensate for the failed
component. This in turn overloads these nodes, causing them to fail as
well, prompting additional nodes to fail one after another.
https://en.wikipedia.org/wiki/Cascading_failure
A single point of failure (SPOF) is a part of a system that, if it fails, will stop the entire system from working.[1] SPOFs are undesirable in any system with a goal of high availability or reliability, be it a business practice, software application, or other industrial system.
Overview
Systems can be made robust by adding redundancy in all potential SPOFs. Redundancy can be achieved at various levels.
The assessment of a potential SPOF involves identifying the
critical components of a complex system that would provoke a total
systems failure in case of malfunction. Highly reliable systems should not rely on any such individual component.
For instance, the owner of a small tree care company may only own one woodchipper.
If the chipper breaks, he may be unable to complete his current job and
may have to cancel future jobs until he can obtain a replacement. The
owner of the tree care company may have spare parts
ready for the repair of the wood chipper, in case it fails. At a higher
level, he may have a second wood chipper that he can bring to the job
site. Finally, at the highest level, he may have enough equipment
available to completely replace everything at the work site in the case
of multiple failures.
Possible SPOFs in a simple setup
Using redundancy to avoid some SPOFs
Completely redundant system without SPOFs (note: assumes generator
and grid sources are each rated at N, each UPS is rated at N, and "A/C"
and "Electrical" are in themselves completely fault tolerant systems)
Computing
| This section needs to be updated. The reason given is: Needs updating for public cloud computing. Please help update this article to reflect recent events or newly available information. (May 2022) |
A fault-tolerant computer system can be achieved at the internal component level, at the system level (multiple machines), or site level (replication).
One would normally deploy a load balancer to ensure high availability for a server cluster
at the system level. In a high-availability server cluster, each
individual server may attain internal component redundancy by having
multiple power supplies, hard drives, and other components. System-level
redundancy could be obtained by having spare servers waiting to take on
the work of another server if it fails.
Since a data center is often a support center for other
operations such as business logic, it represents a potential SPOF in
itself. Thus, at the site level, the entire cluster may be replicated at
another location, where it can be accessed in case the primary location
becomes unavailable. This is typically addressed as part of an IT
disaster recovery (resiliency) program.
Paul Baran and Donald Davies developed packet switching, a key part of "survivable communications networks". Such networks – including ARPANET and the Internet –
are designed to have no single point of failure. Multiple paths
between any two points on the network allow those points to continue
communicating with each other, the packets "routing around" damage, even after any single failure of any one particular path or any one intermediate node.
Software engineering
In software engineering, a bottleneck occurs when the capacity of an application
or a computer system is limited by a single component. The bottleneck
has lowest throughput of all parts of the transaction path.
Performance engineering
Tracking down bottlenecks (sometimes known as hot spots – sections of the code that execute most frequently – i.e., have the highest execution count) is called performance analysis.
Reduction is usually achieved with the help of specialized tools, known
as performance analyzers or profilers. The objective is to make those
particular sections of code perform as fast as possible to improve
overall algorithmic efficiency.
Computer security
A vulnerability or security exploit in just one component can compromise an entire system.
Other fields
The
concept of a single point of failure has also been applied to fields
outside of engineering, computers, and networking, such as corporate supply chain management[2] and transportation management.[3]
Design structures that create single points of failure include bottlenecks and series circuits (in contrast to parallel circuits).
In transportation, some noted recent examples of the concept's recent application have included the Nipigon River Bridge in Canada, where a partial bridge failure in January 2016 entirely severed road traffic between Eastern Canada and Western Canada for several days because it is located along a portion of the Trans-Canada Highway where there is no alternate detour route for vehicles to take;[4] and the Norwalk River Railroad Bridge in Norwalk, Connecticut, an aging swing bridge that sometimes gets stuck when opening or closing, disrupting rail traffic on the Northeast Corridor line.[3]
The concept of a single point of failure has also been applied to the fields of intelligence. Edward Snowden talked of the dangers of being what he described as "the single point of failure" – the sole repository of information.[5]
Life-support systems
![[icon]](https://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | This section needs expansion. You can help by adding to it. (October 2019) |
A component of a life-support system that would constitute a single point of failure would be required to be extremely reliable.
See also
Concepts
Applications
- Kill switch – Safety mechanism to quickly shut down a system
- Jesus nut – Slang term for the main rotor-retaining nut of some helicopters
- Reliability engineering – Sub-discipline of systems engineering that emphasizes dependability
- Safety engineering – Engineering discipline which assures that engineered systems provide acceptable levels of safety
- Dead man's switch – Equipment that activates or deactivates upon the incapacitation of operator
In literature
- Achilles' heel – Critical weakness which can lead to downfall in spite of overall strength
- Hamartia – Protagonist's error in Greek dramatic theory
References
1:
Designing Large-scale LANs – Page 31, K. Dooley, O'Reilly, 2002
Gary S. Lynch (Oct 7, 2009). Single Point of Failure: The 10 Essential Laws of Supply Chain Risk Management. Wiley. ISBN 978-0-470-42496-4.
"Crucial, Century-Old, And Sometimes Stuck: Connecticut Bridge Is Key To Northeast Corridor". Connecticut Public Radio, August 8, 2017.
"The Nipigon River Bridge and other Trans-Canada bottlenecks". Global News, January 11, 2016.
https://en.wikipedia.org/wiki/Single_point_of_failure
https://en.wikipedia.org/wiki/Floppy_disk
https://en.wikipedia.org/wiki/Thin-film_memory
https://en.wikipedia.org/wiki/Non-volatile_memory
https://en.wikipedia.org/wiki/Magnetoresistive_RAM
https://en.wikipedia.org/wiki/Gamma_Pegasi
https://en.wikipedia.org/wiki/Thermocouple
https://en.wikipedia.org/wiki/Bubble_memory
https://en.wikipedia.org/wiki/CMC_Magnetics
https://en.wikipedia.org/wiki/Physics_of_magnetic_resonance_imaging
https://en.wikipedia.org/wiki/Drum_memory
https://en.wikipedia.org/wiki/Magnetic-tape_data_storage
https://en.wikipedia.org/wiki/Magnetic-core_memory
https://en.wikipedia.org/wiki/Hard_disk_drive
https://en.wikipedia.org/wiki/Curl_(mathematics)
Data degradation is the gradual corruption of computer data due to an accumulation of non-critical failures in a data storage device. The phenomenon is also known as data decay, data rot or bit rot.
https://en.wikipedia.org/wiki/Data_degradation
https://en.wikipedia.org/wiki/Mini-Cassette
https://en.wikipedia.org/wiki/Semiconductor_memory
https://en.wikipedia.org/wiki/Digital_dark_age
https://en.wikipedia.org/wiki/Linear_Tape-Open
https://en.wikipedia.org/wiki/List_of_The_Muppet_Show_episodes
https://en.wikipedia.org/wiki/Parafilm
https://en.wikipedia.org/wiki/Domino_Recording_Company
https://en.wikipedia.org/wiki/Motor_capacitor
https://en.wikipedia.org/wiki/Starlight
https://en.wikipedia.org/wiki/Non-volatile_random-access_memory
https://en.wikipedia.org/wiki/Eddy-current_testing
https://en.wikipedia.org/wiki/List_of_Ghost_Adventures_episodes
https://en.wikipedia.org/wiki/Stephin_Merritt_discography
https://en.wikipedia.org/wiki/Core_rope_memory
https://en.wikipedia.org/wiki/Pyramid_power
https://en.wikipedia.org/wiki/Data_storage
https://en.wikipedia.org/wiki/Random-access_memory
https://en.wikipedia.org/wiki/Computer_memory
https://en.wikipedia.org/w/index.php?limit=20&offset=20&profile=default&search=magnetic+rot&title=Special:Search&ns0=1&searchToken=cems966l2d75df9ijilqv36hq

























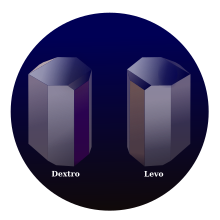

































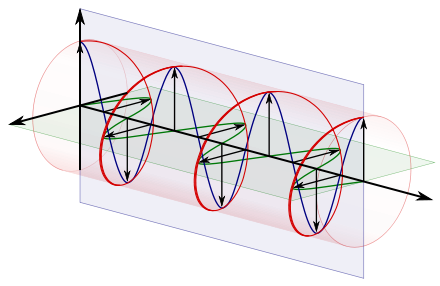


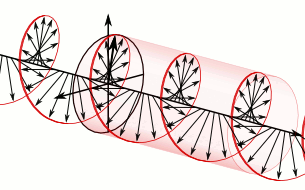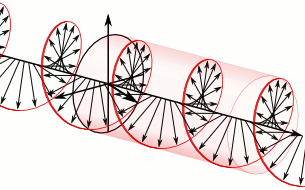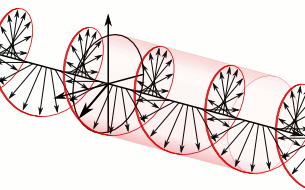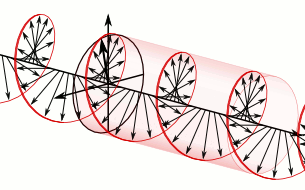




![{\displaystyle {\begin{aligned}\mathbf {E} (\mathbf {r} ,t)&=\left|\,\mathbf {E} \,\right|\mathrm {Re} \left\{\mathbf {Q} \left|\psi \right\rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\\\mathbf {B} (\mathbf {r} ,t)&={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72e6f4e48ffd9eabf206d7664ee54e2e2ba2780c)

![\mathbf{Q} = \left [ \hat{ \mathbf{x}}, \hat{\mathbf{y}} \right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c6f209c9644cf3ab69fd75e6d696bb9278c0c12)






















































![{\displaystyle {\begin{aligned}{\mathcal {L}}&={\frac {1}{2}}\left[I_{1}\omega _{1}^{2}+I_{2}\left(\omega _{2}^{2}+\omega _{3}^{2}\right)\right]\\&={\frac {1}{2}}I_{1}\left({\dot {\psi }}-\Omega \sin \delta \cos \alpha \right)^{2}+{\frac {1}{2}}I_{2}\left\{\left[{\dot {\alpha }}\sin \psi +\Omega (\sin \delta \sin \alpha \cos \psi +\cos \delta \sin \psi )\right]^{2}+\left[{\dot {\alpha }}\cos \psi +\Omega (-\sin \delta \sin \alpha \sin \psi +\cos \delta \cos \psi )\right]^{2}\right\}\\&={\frac {1}{2}}I_{1}\left({\dot {\psi }}-\Omega \sin \delta \cos \alpha \right)^{2}+{\frac {1}{2}}I_{2}\left\{{\dot {\alpha }}^{2}+\Omega ^{2}\left(\cos ^{2}\delta +\sin ^{2}\alpha \sin ^{2}\delta \right)+2{\dot {\alpha }}\Omega \cos \delta \right\}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99ea7fb4d7a5a7959dd44adbf50a88c24e3c5f8c)