05-29-2023-1323 - The semi-major axis (major semiaxis), orbital mechanics, orbital elements, astrodynamics, two-body orbit, eccentricity, celestial mechanics, semi-minor axis (polar radius), geometrical constant, Orbital period, Astronomy, impact parameter, standard gravitational parameter, central body, barycenter, eccentric anomaly, primocentric, geocentric, mass ratio, Semi-major and semi-minor axes of the planets' orbits, reference frame, aphelion, perihelion, Conic sections, Canberra, Australia, 1979, Geocentric gravitational constant, Earth mass, spaceflight in the 1950s, 1960s high-precision measurements, relative uncertainty, Heliocentric gravitational constant, Equatorial (a), polar (b) and mean Earth radii as defined in the 1984 World Geodetic System revision (not to scale), very-long-baseline interferometry (VLBI), collocation, GPS, ITRS, reference ellipsoid, oblateness, arcsecond, zero longitude, IERS Reference Meridian, oblate spheroid, National Geospatial-Intelligence Agency, IGS Antex , horizontal datum, 2D coordinate reference system (CRS), 3D CRS, geocentric 3D CRS, reference ellipsoid, EPSG Geodetic Parameter Dataset, Degree Confluence Project, constant, etc. (draft)

The reference ellipsoid is usually defined by its semi-major axis (equatorial radius) ${\displaystyle a}$ and either its semi-minor axis (polar radius) ${\displaystyle b}$, aspect ratio ${\displaystyle (b/a)}$ or flattening ${\displaystyle f}$, but GRS80 is an exception: For a complete definition, four independent constants are required. GRS80 chooses as these ${\displaystyle a}$, ${\displaystyle GM}$, ${\displaystyle J_2}$ and ${\displaystyle \omega }$, making the geometrical constant ${\displaystyle f}$ a derived quantity. 

https://en.wikipedia.org/wiki/Geodetic_Reference_System_1980

From Wikipedia, the free encyclopedia

(Redirected from Semi-major axis)

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Semi-major and semi-minor axes" – news · newspapers · books · scholar · JSTOR (March 2017) (Learn how and when to remove this template message)

The semi-major (a) and semi-minor axis (b) of an ellipse

Part of a series on
Astrodynamics
Orbital mechanics

Orbital elements

Types of two-body orbits by eccentricity

Equations
Celestial mechanics

Gravitational influences

N-body orbits
Engineering and efficiency

Preflight engineering

Efficiency measures

v t e

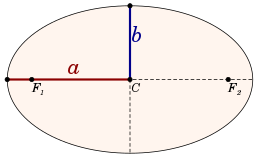
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle.

The length of the semi-major axis a of an ellipse is related to the semi-minor axis's length b through the eccentricity e and the semi-latus rectum ${\displaystyle \ell }$, as follows:

${\displaystyle \begin{array}{rl}b& =a\sqrt{1-e^2},\\ \ell & =a(1-e^2),\\ a\ell & =b^2.\end{array}}$

The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center to either vertex of the hyperbola.

A parabola can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping ${\displaystyle \ell }$ fixed. Thus a and b tend to infinity, a faster than b.

The major and minor axes are the axes of symmetry for the curve: in an ellipse, the minor axis is the shorter one; in a hyperbola, it is the one that does not intersect the hyperbola.

Ellipse

The equation of an ellipse is

${\displaystyle \frac{(x-h{)}^2}{a^2}+\frac{(y-k{)}^2}{b^2}=1,}$

where (h, k) is the center of the ellipse in Cartesian coordinates, in which an arbitrary point is given by (x, y).

The semi-major axis is the mean value of the maximum and minimum distances ${\displaystyle r_{\text{max}}}$ and ${\displaystyle r_{\text{min}}}$ of the ellipse from a focus — that is, of the distances from a focus to the endpoints of the major axis

${\displaystyle a=\frac{r_{\text{max}}+r_{\text{min}}}{2}.}$

In astronomy these extreme points are called apsides.^[1]

The semi-minor axis of an ellipse is the geometric mean of these distances:

${\displaystyle b=\sqrt{r_{\text{max}}{r}_{\text{min}}}.}$

The eccentricity of an ellipse is defined as

${\displaystyle e=\sqrt{1-\frac{b^2}{a^2}},}$

so

${\displaystyle r_{\text{min}}=a(1-e),r_{\text{max}}=a(1+e).}$

Now consider the equation in polar coordinates, with one focus at the origin and the other on the ${\displaystyle \theta =\pi }$ direction:

${\displaystyle r(1+e\cos \theta )=\ell .}$

The mean value of ${\displaystyle r=\ell /(1-e)}$ and ${\displaystyle r=\ell /(1+e)}$, for ${\displaystyle \theta =\pi }$ and ${\displaystyle \theta =0}$ is

${\displaystyle a=\frac{\ell }{1-e^2}.}$

In an ellipse, the semi-major axis is the geometric mean of the distance from the center to either focus and the distance from the center to either directrix.

The semi-minor axis of an ellipse runs from the center of the ellipse (a point halfway between and on the line running between the foci) to the edge of the ellipse. The semi-minor axis is half of the minor axis. The minor axis is the longest line segment perpendicular to the major axis that connects two points on the ellipse's edge.

The semi-minor axis b is related to the semi-major axis a through the eccentricity e and the semi-latus rectum ${\displaystyle \ell }$, as follows:

${\displaystyle \begin{array}{rl}b& =a\sqrt{1-e^2},\\ a\ell & =b^2.\end{array}}$

A parabola can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping ${\displaystyle \ell }$ fixed. Thus a and b tend to infinity, a faster than b.

The length of the semi-minor axis could also be found using the following formula:^[2]

${\displaystyle 2b=\sqrt{(p+q{)}^2-f^2},}$

where f is the distance between the foci, p and q are the distances from each focus to any point in the ellipse.

Hyperbola

The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches; if this is a in the x-direction the equation is:^{[citation needed]}

${\displaystyle \frac{{\left(x-h\right)}^2}{a^2}-\frac{{\left(y-k\right)}^2}{b^2}=1.}$

In terms of the semi-latus rectum and the eccentricity we have

${\displaystyle a=\frac{\ell }{e^2-1}.}$

The transverse axis of a hyperbola coincides with the major axis.^[3]

In a hyperbola, a conjugate axis or minor axis of length ${\displaystyle 2b}$, corresponding to the minor axis of an ellipse, can be drawn perpendicular to the transverse axis or major axis, the latter connecting the two vertices (turning points) of the hyperbola, with the two axes intersecting at the center of the hyperbola. The endpoints ${\displaystyle (0,\pm b)}$ of the minor axis lie at the height of the asymptotes over/under the hyperbola's vertices. Either half of the minor axis is called the semi-minor axis, of length b. Denoting the semi-major axis length (distance from the center to a vertex) as a, the semi-minor and semi-major axes' lengths appear in the equation of the hyperbola relative to these axes as follows:

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1.}$

The semi-minor axis is also the distance from one of focuses of the hyperbola to an asymptote. Often called the impact parameter, this is important in physics and astronomy, and measure the distance a particle will miss the focus by if its journey is unperturbed by the body at the focus.^{[citation needed]}

The semi-minor axis and the semi-major axis are related through the eccentricity, as follows:

${\displaystyle b=a\sqrt{e^2-1}.}$^[4]

Note that in a hyperbola b can be larger than a.^[5]

Astronomy

Orbital period

Log-log plot of period T vs semi-major axis a (average of aphelion and perihelion) of some Solar System orbits (crosses denoting Kepler's values) showing that a³ / T² is constant (green line)

In astrodynamics the orbital period T of a small body orbiting a central body in a circular or elliptical orbit is:^[1]

${\displaystyle T=2\pi \sqrt{\frac{a^3}{\mu }},}$

where:

a is the length of the orbit's semi-major axis,

${\displaystyle \mu }$ is the standard gravitational parameter of the central body.

Note that for all ellipses with a given semi-major axis, the orbital period is the same, disregarding their eccentricity.

The specific angular momentum h of a small body orbiting a central body in a circular or elliptical orbit is^[1]

${\displaystyle h=\sqrt{a\mu (1-e^2)},}$

where:

a and ${\displaystyle \mu }$ are as defined above,

e is the eccentricity of the orbit.

In astronomy, the semi-major axis is one of the most important orbital elements of an orbit, along with its orbital period. For Solar System objects, the semi-major axis is related to the period of the orbit by Kepler's third law (originally empirically derived):^[1]

${\displaystyle T^2\propto a^3,}$

where T is the period, and a is the semi-major axis. This form turns out to be a simplification of the general form for the two-body problem, as determined by Newton:^[1]

${\displaystyle T^2=\frac{4{\pi }^2}{G(M+m)}{a}^3,}$

where G is the gravitational constant, M is the mass of the central body, and m is the mass of the orbiting body. Typically, the central body's mass is so much greater than the orbiting body's, that m may be ignored. Making that assumption and using typical astronomy units results in the simpler form Kepler discovered.

The orbiting body's path around the barycenter and its path relative to its primary are both ellipses.^[1] The semi-major axis is sometimes used in astronomy as the primary-to-secondary distance when the mass ratio of the primary to the secondary is significantly large (${\displaystyle M\gg m}$); thus, the orbital parameters of the planets are given in heliocentric terms. The difference between the primocentric and "absolute" orbits may best be illustrated by looking at the Earth–Moon system. The mass ratio in this case is 81.30059. The Earth–Moon characteristic distance, the semi-major axis of the geocentric lunar orbit, is 384,400 km. (Given the lunar orbit's eccentricity e = 0.0549, its semi-minor axis is 383,800 km. Thus the Moon's orbit is almost circular.) The barycentric lunar orbit, on the other hand, has a semi-major axis of 379,730 km, the Earth's counter-orbit taking up the difference, 4,670 km. The Moon's average barycentric orbital speed is 1.010 km/s, whilst the Earth's is 0.012 km/s. The total of these speeds gives a geocentric lunar average orbital speed of 1.022 km/s; the same value may be obtained by considering just the geocentric semi-major axis value.^{[citation needed]}

Average distance

It is often said that the semi-major axis is the "average" distance between the primary focus of the ellipse and the orbiting body. This is not quite accurate, because it depends on what the average is taken over.

• averaging the distance over the eccentric anomaly indeed results in the semi-major axis.
• averaging over the true anomaly (the true orbital angle, measured at the focus) results in the semi-minor axis ${\displaystyle b=a\sqrt{1-e^2}}$.
• averaging over the mean anomaly (the fraction of the orbital period that has elapsed since pericentre, expressed as an angle) gives the time-average ${\displaystyle a\left(1+\frac{e^2}{2}\right)}$.

The time-averaged value of the reciprocal of the radius, ${\displaystyle r^{-1}}$, is ${\displaystyle a^{-1}}$.

Energy; calculation of semi-major axis from state vectors

In astrodynamics, the semi-major axis a can be calculated from orbital state vectors:

${\displaystyle a=-\frac{\mu }{2\epsilon }}$

for an elliptical orbit and, depending on the convention, the same or

${\displaystyle a=\frac{\mu }{2\epsilon }}$

for a hyperbolic trajectory, and

${\displaystyle \epsilon =\frac{v^2}{2}-\frac{\mu }{|\mathbf{r}|}}$

(specific orbital energy) and

${\displaystyle \mu =GM,}$

(standard gravitational parameter), where:

v is orbital velocity from velocity vector of an orbiting object,

r is a cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentric equatorial for an orbit around Earth, or heliocentric ecliptic for an orbit around the Sun),

G is the gravitational constant,

M is the mass of the gravitating body, and

${\displaystyle \epsilon }$ is the specific energy of the orbiting body.

Note that for a given amount of total mass, the specific energy and the semi-major axis are always the same, regardless of eccentricity or the ratio of the masses. Conversely, for a given total mass and semi-major axis, the total specific orbital energy is always the same. This statement will always be true under any given conditions.^{[citation needed]}

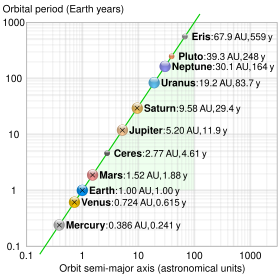
Semi-major and semi-minor axes of the planets' orbits

Planet orbits are always cited as prime examples of ellipses (Kepler's first law). However, the minimal difference between the semi-major and semi-minor axes shows that they are virtually circular in appearance. That difference (or ratio) is based on the eccentricity and is computed as ${\displaystyle \frac{a}{b}=\frac{1}{\sqrt{1-e^2}}}$, which for typical planet eccentricities yields very small results.

The reason for the assumption of prominent elliptical orbits lies probably in the much larger difference between aphelion and perihelion. That difference (or ratio) is also based on the eccentricity and is computed as ${\displaystyle \frac{r_{\text{a}}}{r_{\text{p}}}=\frac{1+e}{1-e}}$. Due to the large difference between aphelion and perihelion, Kepler's second law is easily visualized.

	Eccentricity	Semi-major axis a (AU)	Semi-minor axis b (AU)	Difference (%)	Perihelion (AU)	Aphelion (AU)	Difference (%)
Mercury	0.206	0.38700	0.37870	2.2	0.307	0.467	52
Venus	0.007	0.72300	0.72298	0.002	0.718	0.728	1.4
Earth	0.017	1.00000	0.99986	0.014	0.983	1.017	3.5
Mars	0.093	1.52400	1.51740	0.44	1.382	1.666	21
Jupiter	0.049	5.20440	5.19820	0.12	4.950	5.459	10
Saturn	0.057	9.58260	9.56730	0.16	9.041	10.124	12
Uranus	0.046	19.21840	19.19770	0.11	18.330	20.110	9.7
Neptune	0.010	30.11000	30.10870	0.004	29.820	30.400	1.9

1 AU (astronomical unit) equals 149.6 million km.

References

1. 
   

Lissauer, Jack J.; de Pater, Imke (2019). Fundamental Planetary Sciences: physics, chemistry, and habitability. New York: Cambridge University Press. pp. 24–31. ISBN 9781108411981.

"Major / Minor axis of an ellipse", Math Open Reference, 12 May 2013.

"7.1 Alternative Characterization". www.geom.uiuc.edu. Archived from the original on 2018-10-24. Retrieved 2007-09-06.

"The Geometry of Orbits: Ellipses, Parabolas, and Hyperbolas". www.bogan.ca.

5. "7.1 Alternative Characterization". Archived from the original on 2018-10-24. Retrieved 2007-09-06.

External links

• Semi-major and semi-minor axes of an ellipse With interactive animation

v t e Gravitational orbits

Categories:

• Conic sections
• Orbits

 https://en.wikipedia.org/wiki/Semi-major_and_semi-minor_axes

The 1980 Geodetic Reference System (GRS 80) posited a 6378137 m semi-major axis and a 1⁄298.257222101 flattening. This system was adopted at the XVII General Assembly of the International Union of Geodesy and Geophysics (IUGG) in Canberra, Australia, 1979. 

https://en.wikipedia.org/wiki/Geodetic_Reference_System_1980

Geocentric gravitational constant

Further information: Earth mass

GM_Earth, the gravitational parameter for the Earth as the central body, is called the geocentric gravitational constant. It equals (3.986004418±0.000000008)×10¹⁴ m³ s⁻².^[3]

The value of this constant became important with the beginning of spaceflight in the 1950s, and great effort was expended to determine it as accurately as possible during the 1960s. Sagitov (1969) cites a range of values reported from 1960s high-precision measurements, with a relative uncertainty of the order of 10⁻⁶.^[13]

During the 1970s to 1980s, the increasing number of artificial satellites in Earth orbit further facilitated high-precision measurements, and the relative uncertainty was decreased by another three orders of magnitude, to about 2×10⁻⁹ (1 in 500 million) as of 1992. Measurement involves observations of the distances from the satellite to Earth stations at different times, which can be obtained to high accuracy using radar or laser ranging.^[14]

Heliocentric gravitational constant

Further information: Solar mass

GM_☉, the gravitational parameter for the Sun as the central body, is called the heliocentric gravitational constant or geopotential of the Sun and equals (1.32712440042±0.0000000001)×10²⁰ m³ s⁻².^[15]

The relative uncertainty in GM_☉, cited at below 10⁻¹⁰ as of 2015, is smaller than the uncertainty in GM_Earth because GM_☉ is derived from the ranging of interplanetary probes, and the absolute error of the distance measures to them is about the same as the earth satellite ranging measures, while the absolute distances involved are much bigger.^{[citation needed]}

See also

• Astronomical system of units
• Planetary mass

 https://en.wikipedia.org/wiki/Standard_gravitational_parameter#Geocentric_gravitational_constant

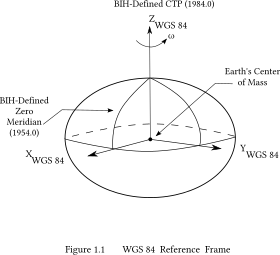
WGS 84

Equatorial (a), polar (b) and mean Earth radii as defined in the 1984 World Geodetic System revision (not to scale)

In the early 1980s, the need for a new world geodetic system was generally recognized by the geodetic community as well as within the US Department of Defense. WGS 72 no longer provided sufficient data, information, geographic coverage, or product accuracy for all then-current and anticipated applications. The means for producing a new WGS were available in the form of improved data, increased data coverage, new data types and improved techniques. Observations from Doppler, satellite laser ranging and very-long-baseline interferometry (VLBI) constituted significant new information. An outstanding new source of data had become available from satellite radar altimetry. Also available was an advanced least squares method called collocation that allowed for a consistent combination solution from different types of measurements all relative to the Earth's gravity field, measurements such as the geoid, gravity anomalies, deflections, and dynamic Doppler.

The new world geodetic system was called WGS 84. It is the reference system used by the Global Positioning System. It is geocentric and globally consistent within 1 m. Current geodetic realizations of the geocentric reference system family International Terrestrial Reference System (ITRS) maintained by the IERS are geocentric, and internally consistent, at the few-cm level, while still being metre-level consistent with WGS 84.

The WGS 84 reference ellipsoid was based on GRS 80, but it contains a very slight variation in the inverse flattening, as it was derived independently and the result was rounded to a different number of significant digits.^[3] This resulted in a tiny difference of 0.105 mm in the semi-minor axis.^[4] The following table compares the primary ellipsoid parameters.

Ellipsoid reference	Semi-major axis a	Semi-minor axis b	Inverse flattening 1/f
GRS 80	6378137.0 m	≈ 6356752.314140 m	298.257222100882711...
WGS 84[5]	6378137.0 m	≈ 6356752.314245 m	298.257223563

Definition

WGS 84 reference frame. The oblateness of the ellipsoid is exaggerated in this image.

The coordinate origin of WGS 84 is meant to be located at the Earth's center of mass; the uncertainty is believed to be less than 2 cm.^[6]

Handheld GPS receiver indicating the Greenwich meridian is 0.089 arcminutes (or 5.34 arcseconds) west to the WGS 84 datum (the IERS Reference Meridian)

The WGS 84 meridian of zero longitude is the IERS Reference Meridian,^[7] 5.3 arc seconds or 102 metres (335 ft) east of the Greenwich meridian at the latitude of the Royal Observatory.^[8][9] (This is related to the fact that the local gravity field at Greenwich doesn't point exactly through the Earth's center of mass, but rather "misses west" of the center of mass by about that 102 meters.) The longitude positions on WGS 84 agree with those on the older North American Datum 1927 at roughly 85° longitude west, in the east-central United States.

The WGS 84 datum surface is an oblate spheroid with equatorial radius a = 6378137 m at the equator and flattening f = 1/298.257223563. The refined value of the WGS 84 gravitational constant (mass of Earth's atmosphere included) is GM = 3986004.418×10¹⁴ m³/s². The angular velocity of the Earth is defined to be ω = 72.92115×10⁻⁶ rad/s.^[10]

This leads to several computed parameters such as the polar semi-minor axis b which equals a × (1 − f) = 6356752.3142 m, and the first eccentricity squared, e² = 6.69437999014×10⁻³.^[10]

Updates and new standards

The original standardization document for WGS 84 was Technical Report 8350.2, published in September 1987 by the Defense Mapping Agency (which later became the National Imagery and Mapping Agency). New editions were published in September 1991 and July 1997; the latter edition was amended twice, in January 2000 and June 2004.^[11] The standardization document was revised again and published in July 2014 by the National Geospatial-Intelligence Agency as NGA.STND.0036.^[12] These updates provide refined descriptions of the Earth and realizations of the system for higher precision.

WGS 84 has most recently been updated to use the reference frame G2139, which was released on January 3, 2021 as an update to G1762' (with a prime).^[13] This frame is aligned with the IGb14 realization of the International Terrestrial Reference Frame (ITRF) 2014 and uses the new IGS Antex standard.^[14][13]

Updates to the original geoid for WGS 84 are now published as a separate Earth Gravitational Model (EGM), with improved resolution and accuracy. Likewise, the World Magnetic Model (WMM) is updated separately. The current version of WGS 84 uses EGM2008 and WMM2020.^[15][16]

Solution for Earth orientation parameters consistent with ITRF2014 is also needed (IERS EOP 14C04).^[17]

Identifiers

Components of WGS 84 are identified by codes in the EPSG Geodetic Parameter Dataset:^[18]

• EPSG:4326 – 2D coordinate reference system (CRS)
• EPSG:4979 – 3D CRS
• EPSG:4978 – geocentric 3D CRS
• EPSG:7030 – reference ellipsoid
• EPSG:6326 – horizontal datum

See also

• Degree Confluence Project
• Earth Gravitational Model
• European Terrestrial Reference System 1989
• geo URI scheme
• Geo (microformat) – for marking up WGS 84 coordinates in (X)HTML
• Geotagging
• North American Datum
• Point of interest
• TRANSIT system
• Geographic information system
• GIS file formats

 

 

 https://en.wikipedia.org/wiki/World_Geodetic_System#WGS84

 

From Wikipedia, the free encyclopedia

For a narrower treatment related to this subject, see Mathematical constant.

In mathematics, the word constant conveys multiple meanings. As an adjective, it refers to non-variance (i.e. unchanging with respect to some other value); as a noun, it has two different meanings:

• A fixed and well-defined number or other non-changing mathematical object. The terms mathematical constant or physical constant are sometimes used to distinguish this meaning.^[1]
• A function whose value remains unchanged (i.e., a constant function).^[2] Such a constant is commonly represented by a variable which does not depend on the main variable(s) in question.

For example, a general quadratic function is commonly written as:

${\displaystyle a{x}^2+bx+c,}$

where a, b and c are constants (or parameters), and x a variable—a placeholder for the argument of the function being studied. A more explicit way to denote this function is

${\displaystyle x\mapsto a{x}^2+bx+c,}$

which makes the function-argument status of x (and by extension the constancy of a, b and c) clear. In this example a, b and c are coefficients of the polynomial. Since c occurs in a term that does not involve x, it is called the constant term of the polynomial and can be thought of as the coefficient of x⁰. More generally, any polynomial term or expression of degree zero (no variable) is a constant.^[3]: 18

Constant function

Main articles: Constant function and Nullary

A constant may be used to define a constant function that ignores its arguments and always gives the same value.^[4] A constant function of a single variable, such as ${\displaystyle f(x)=5}$, has a graph of a horizontal line parallel to the x-axis.^[5] Such a function always takes the same value (in this case 5), because the variable does not appear in the expression defining the function.

Graph of ${\displaystyle f(x)=5}$.

Context-dependence

The context-dependent nature of the concept of "constant" can be seen in this example from elementary calculus:

${\displaystyle \begin{array}{rl}\frac{d}{dx}{2}^x& =\underset{h\to 0}{lim}\frac{2^{x+h}-2^x}{h}=\underset{h\to 0}{lim}{2}^x\frac{2^h-1}{h}\\ & =2^x\underset{h\to 0}{lim}\frac{2^h-1}{h}& & \text{since }x\text{ is constant (i.e. does not depend on }h\text{)}\\ & =2^x\cdot \mathbf{c}\mathbf{o}\mathbf{n}\mathbf{s}\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{t}\mathbf{,}& & \text{where }\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{s}\mathbf{t}\mathbf{a}\mathbf{n}\mathbf{t}\text{ means not depending on }x.\end{array}}$

"Constant" means not depending on some variable; not changing as that variable changes. In the first case above, it means not depending on h; in the second, it means not depending on x. A constant in a narrower context could be regarded as a variable in a broader context.

Notable mathematical constants

Main article: Mathematical constant

Some values occur frequently in mathematics and are conventionally denoted by a specific symbol. These standard symbols and their values are called mathematical constants. Examples include:

• 0 (zero).
• 1 (one), the natural number after zero.
• π (pi), the constant representing the ratio of a circle's circumference to its diameter, approximately equal to 3.141592653589793238462643.^[6]
• e, approximately equal to 2.718281828459045235360287.^[7]
• i, the imaginary unit such that i² = −1.^[8]
• ${\displaystyle \sqrt{2}}$ (square root of 2), the length of the diagonal of a square with unit sides, approximately equal to 1.414213562373095048801688.^[9]
• φ (golden ratio), approximately equal to 1.618033988749894848204586, or algebraically, $\frac{{\displaystyle 1+\sqrt{5}}}{2}$.^[10]

Constants in calculus

In calculus, constants are treated in several different ways depending on the operation. For example, the derivative (rate of change) of a constant function is zero. This is because constants, by definition, do not change. Their derivative is hence zero.

Conversely, when integrating a constant function, the constant is multiplied by the variable of integration.

During the evaluation of a limit, a constant remains the same as it was before and after evaluation.

Integration of a function of one variable often involves a constant of integration. This arises due to the fact that the integral is the inverse (opposite) of the derivative meaning that the aim of integration is to recover the original function before differentiation. The derivative of a constant function is zero, as noted above, and the differential operator is a linear operator, so functions that only differ by a constant term have the same derivative. To acknowledge this, a constant of integration is added to an indefinite integral; this ensures that all possible solutions are included. The constant of integration is generally written as 'c', and represents a constant with a fixed but undefined value.

Examples

If f is the constant function such that ${\displaystyle f(x)=72}$ for every x then

${\displaystyle \begin{array}{rl}{f}^{\prime }(x)& =0\\ \int f(x)dx& =72x+c\\ \underset{x\to 0}{lim}f(x)& =72\end{array}}$

See also

• Constant (disambiguation)
• Expression
• Level set
• List of mathematical constants
• Physical constant

References

1. 
   

"Definition of CONSTANT". www.merriam-webster.com. Retrieved 2021-11-09.

Weisstein, Eric W. "Constant". mathworld.wolfram.com. Retrieved 2020-08-08.

Foerster, Paul A. (2006). Algebra and Trigonometry: Functions and Applications, Teacher's Edition (Classics ed.). Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-165711-9.

Tanton, James (2005). Encyclopedia of mathematics. New York: Facts on File. ISBN 0-8160-5124-0. OCLC 56057904.

"Algebra". tutorial.math.lamar.edu. Retrieved 2021-11-09.

Arndt, Jörg; Haenel, Christoph (2001). Pi – Unleashed. Springer. p. 240. ISBN 978-3540665724.

Weisstein, Eric W. "e". mathworld.wolfram.com. Retrieved 2021-11-09.

Weisstein, Eric W. "i". mathworld.wolfram.com. Retrieved 2021-11-09.

Weisstein, Eric W. "Pythagoras's Constant". mathworld.wolfram.com. Retrieved 2021-11-09.

10. Weisstein, Eric W. "Golden Ratio". mathworld.wolfram.com. Retrieved 2021-11-09.

External links

• Media related to Constants at Wikimedia Commons

Categories:

• Algebra
• Elementary mathematics
• Constants

 

https://en.wikipedia.org/wiki/Constant_(mathematics)