https://en.wikipedia.org/wiki/State_pattern
https://en.wikipedia.org/wiki/Safe_navigation_operator#C.23
C#
C# 6.0 and above have ?., the null-conditional member access operator (which is also called the Elvis operator by Microsoft and is not to be confused with the general usage of the term Elvis operator, whose equivalent in C# is ??, the null coalescing operator) and ?[], the null-conditional element access operator, which performs a null-safe call of an indexer get accessor. If the type of the result of the member access is a value type, the type of the result of a null-conditional access of that member is a nullable version of that value type.[9]
The following example retrieves the name of the author of the
first article in an array of articles (provided that each article has an
Author member and that each author has an Name member), and results in null if the array is null, if its first element is null, if the Author member of that article is null, or if the Name member of that author is null. Note that an IndexOutOfRangeException is still thrown if the array is non-null but empty (i.e. zero-length).
https://en.wikipedia.org/wiki/Safe_navigation_operator#C.23
Nullable types are a feature of some programming languages which allow a value to be set to the special value NULL instead of the usual possible values of the data type. In statically typed languages, a nullable type is an option type[citation needed], while in dynamically typed languages (where values have types, but variables do not), equivalent behavior is provided by having a single null value.
NULL is frequently used to represent a missing value or invalid value, such as from a function that failed to return or a missing field in a database, as in NULL in SQL. In other words NULL is undefined.
Primitive types such as integers and Booleans cannot generally be null, but the corresponding nullable types (nullable integer and nullable Boolean, respectively) can also assume the NULL value.[jargon][citation needed] This can be represented in ternary logic as FALSE,NULL,TRUE as in three-valued logic.
Example
An integer variable may represent integers, but 0 (zero) is a special case because 0 in many programming languages can mean "false". Also this doesn't give us any notion of saying that the variable is empty, a need for which occurs in many circumstances. This need can be achieved with a nullable type. In programming languages like C# 2.0, a nullable integer, for example, can be declared by a question mark (int? x).[1] In programming languages like C# 1.0, nullable types can be defined by an external library[2] as new types (e.g. NullableInteger, NullableBoolean).[3]
A Boolean variable makes the effect more clear. Its values can be either "true" or "false", while a nullable boolean may also contain a representation for "undecided". However, the interpretation or treatment of a logical operation involving such a variable depends on the language.
Compared with null pointers
In contrast, object pointers can be set to NULL by default in most common languages, meaning that the pointer or reference points to nowhere, that no object is assigned (the variable does not point to any object). Nullable references were invented by C. A. R. Hoare in 1965 as part of the Algol W language. Hoare later described his invention as a "billion-dollar mistake".[4] This is because object pointers that can be NULL require the user to check the pointer before using it and require specific code to handle the case when the object pointer is NULL.
Java has classes that correspond to scalar values, such as Integer, Boolean and Float. Combined with autoboxing (automatic usage-driven conversion between object and value), this effectively allows nullable variables for scalar values.[citation needed]
Compared with option types
Nullable type implementations usually adhere to the null object pattern.
There is a more general and formal concept that extend the nullable type concept, it comes from option types, which enforce explicit handling of the exceptional case.
Language support
The following programming languages support nullable types.
Statically typed languages with native null support include:
Statically typed languages with library null support include:
- C# (since version 2)
- Delphi
- Free Pascal
- VB.NET[10]
- Java (since version 8)
- Scala
- Oxygene
- F#
- Statically typed CLI languages
Dynamically-typed languages with null include:
- Perl scalar variables default to
undefand can be set toundef. - PHP with NULL type and is_null() method, native nullable type in version 7.1 [11]
- Python has the
Nonevalue.[12] - Julia has the
nothingvalue (which is of typeNothing) and theUnion{T, Nothing}type idiom.[13] - Ruby with nil value and NilClass type.
- JavaScript has a
nullvalue
See also
References
https://en.wikipedia.org/wiki/Nullable_type
In computer science, a union is a value that may have any of several representations or formats within the same position in memory; that consists of a variable that may hold such a data structure. Some programming languages support special data types, called union types, to describe such values and variables. In other words, a union type definition will specify which of a number of permitted primitive types may be stored in its instances, e.g., "float or long integer". In contrast with a record (or structure), which could be defined to contain both a float and an integer; in a union, there is only one value at any given time.
A union can be pictured as a chunk of memory that is used to store variables of different data types. Once a new value is assigned to a field, the existing data is overwritten with the new data. The memory area storing the value has no intrinsic type (other than just bytes or words of memory), but the value can be treated as one of several abstract data types, having the type of the value that was last written to the memory area.
In type theory, a union has a sum type; this corresponds to disjoint union in mathematics.
Depending on the language and type, a union value may be used in some operations, such as assignment and comparison for equality, without knowing its specific type. Other operations may require that knowledge, either by some external information, or by the use of a tagged union.
Untagged unions
Because of the limitations of their use, untagged unions are generally only provided in untyped languages or in a type-unsafe way (as in C). They have the advantage over simple tagged unions of not requiring space to store a data type tag.
The name "union" stems from the type's formal definition. If a type is considered as the set of all values that that type can take on, a union type is simply the mathematical union of its constituting types, since it can take on any value any of its fields can. Also, because a mathematical union discards duplicates, if more than one field of the union can take on a single common value, it is impossible to tell from the value alone which field was last written.
However, one useful programming function of unions is to map smaller data elements to larger ones for easier manipulation. A data structure consisting, for example, of 4 bytes and a 32-bit integer, can form a union with an unsigned 64-bit integer, and thus be more readily accessed for purposes of comparison etc.
Unions in various programming languages
ALGOL 68
ALGOL 68 has tagged unions, and uses a case clause to distinguish and extract the constituent type at runtime. A union containing another union is treated as the set of all its constituent possibilities, and if the context requires it a union is automatically coerced into the wider union. A union can explicitly contain no value, which can be distinguished at runtime. An example is:
mode node = union (real, int, string, void);
node n := "abc";
case n in
(real r): print(("real:", r)),
(int i): print(("int:", i)),
(string s): print(("string:", s)),
(void): print(("void:", "EMPTY")),
out print(("?:", n))
esac
The syntax of the C/C++ union type and the notion of casts was derived from ALGOL 68, though in an untagged form.[1]
C/C++
In C and C++, untagged unions are expressed nearly exactly like structures (structs), except that each data member begins at the same location in memory. The data members, as in structures, need not be primitive values, and in fact may be structures or even other unions. C++ (since C++11) also allows for a data member to be any type that has a full-fledged constructor/destructor and/or copy constructor, or a non-trivial copy assignment operator. For example, it is possible to have the standard C++ string as a member of a union.
The primary use of a union is allowing access to a common location by different data types, for example hardware input/output access, bitfield and word sharing, or type punning. Unions can also provide low-level polymorphism. However, there is no checking of types, so it is up to the programmer to be sure that the proper fields are accessed in different contexts. The relevant field of a union variable is typically determined by the state of other variables, possibly in an enclosing struct.
One common C programming idiom uses unions to perform what C++ calls a reinterpret_cast, by assigning to one field of a union and reading from another, as is done in code which depends on the raw representation of the values. A practical example is the method of computing square roots using the IEEE representation. This is not, however, a safe use of unions in general.
Structure and union specifiers have the same form. [ . . . ] The size of a union is sufficient to contain the largest of its members. The value of at most one of the members can be stored in a union object at any time. A pointer to a union object, suitably converted, points to each of its members (or if a member is a bit-field, then to the unit in which it resides), and vice versa.
— ANSI/ISO 9899:1990 (the ANSI C standard) Section 6.5.2.1
Anonymous union
In C++, C11, and as a non-standard extension in many compilers, unions can also be anonymous. Their data members do not need to be referenced, are instead accessed directly. They have some restrictions as opposed to traditional unions: in C11, they must be a member of another structure or union,[2] and in C++, they can not have methods or access specifiers.
Simply omitting the class-name portion of the syntax does not make a union an anonymous union. For a union to qualify as an anonymous union, the declaration must not declare an object. Example:
#include <iostream>
#include <cstdint>
int main() {
union {
float f;
std::uint32_t d; // Assumes float is 32 bits wide
};
f = 3.14f;
std::cout << "Hexadecimal representation of 3.14f:"
<< std::hex << d << '\n';
}
Anonymous unions are also useful in C struct definitions to provide a sense of namespacing.[3]
Transparent union
In compilers such as GCC, Clang, and IBM XL C for AIX, a transparent_union
attribute is available for union types. Types contained in the union
can be converted transparently to the union type itself in a function
call, provided that all types have the same size. It is mainly intended
for function with multiple parameter interfaces, a use necessitated by
early Unix extensions and later re-standarisation.[4]
COBOL
In COBOL, union data items are defined in two ways. The first uses the RENAMES (66 level) keyword, which effectively maps a second alphanumeric data item on top of the same memory location as a preceding data item. In the example code below, data item PERSON-REC is defined as a group containing another group and a numeric data item. PERSON-DATA is defined as an alphanumeric data item that renames PERSON-REC, treating the data bytes continued within it as character data.
01 PERSON-REC.
05 PERSON-NAME.
10 PERSON-NAME-LAST PIC X(12).
10 PERSON-NAME-FIRST PIC X(16).
10 PERSON-NAME-MID PIC X.
05 PERSON-ID PIC 9(9) PACKED-DECIMAL.
01 PERSON-DATA RENAMES PERSON-REC.
The second way to define a union type is by using the REDEFINES keyword. In the example code below, data item VERS-NUM is defined as a 2-byte binary integer containing a version number. A second data item VERS-BYTES is defined as a two-character alphanumeric variable. Since the second item is redefined over the first item, the two items share the same address in memory, and therefore share the same underlying data bytes. The first item interprets the two data bytes as a binary value, while the second item interprets the bytes as character values.
01 VERS-INFO.
05 VERS-NUM PIC S9(4) COMP.
05 VERS-BYTES PIC X(2)
REDEFINES VERS-NUM
Pascal
In Pascal, there are two ways to create unions. One is the standard way through a variant record. The second is a nonstandard means of declaring a variable as absolute, meaning it is placed at the same memory location as another variable or at an absolute address. While all Pascal compilers support variant records, only some support absolute variables.
For the purposes of this example, the following are all integer types: a byte is 8-bits, a word is 16-bits, and an integer is 32-bits.
The following example shows the non-standard absolute form:
VAR
A: Integer;
B: Array[1..4] of Byte absolute A;
C: Integer absolute 0;
In the first example, each of the elements of the array B maps to one of the specific bytes of the variable A. In the second example, the variable C is assigned to the exact machine address 0.
In the following example, a record has variants, some of which share the same location as others:
TYPE
Shape = (Circle, Square, Triangle);
Dimensions = record
case Figure: Shape of
Circle: (Diameter: real);
Square: (Width: real);
Triangle: (Side: real; Angle1, Angle2: 0..360)
end;
PL/I
In PL/I then original term for a union was cell,[5] which is still accepted as a synonym for union by several compilers. The union declaration is similar to the structure definition, where elements at the same level within the union declaration occupy the same storage. Elements of the union can be any data type, including structures and array.[6]: pp192–193 Here vers_num and vers_bytes occupy the same storage locations.
1 vers_info union,
5 vers_num fixed binary,
5 vers_bytes pic '(2)A';
An alternative to a union declaration is the DEFINED attribute, which allows alternative declarations of storage, however the data types of the base and defined variables must match.[6]: pp.289–293
Rust
Rust implements both tagged and untagged unions. In Rust, tagged unions are implemented using the enum keyword. Unlike enumerated types
in most other languages, enum variants in Rust can contain additional
data in the form of a tuple or struct, making them tagged unions rather
than simple enumerated types.[7]
Rust also supports untagged unions using the union keyword. The memory layout of unions in Rust is undefined by default,[8] but a union with the #[repr(C)] attribute will be laid out in memory exactly like the equivalent union in C.[9] Reading the fields of a union can only be done within an unsafe
function or block, as the compiler cannot guarantee that the data in
the union will be valid for the type of the field; if this is not the
case, it will result in undefined behavior.[10]
Syntax and example
C/C++
In C and C++, the syntax is:
union <name>
{
<datatype> <1st variable name>;
<datatype> <2nd variable name>;
.
.
.
<datatype> <nth variable name>;
} <union variable name>;
A structure can also be a member of a union, as the following example shows:
union name1
{
struct name2
{
int a;
float b;
char c;
} svar;
int d;
} uvar;
This example defines a variable uvar as a union (tagged as name1), which contains two members, a structure (tagged as name2) named svar (which in turn contains three members), and an integer variable named d.
Unions may occur within structures and arrays, and vice versa:
struct
{
int flags;
char *name;
int utype;
union {
int ival;
float fval;
char *sval;
} u;
} symtab[NSYM];
The number ival is referred to as symtab[i].u.ival and the first character of string sval by either of *symtab[i].u.sval or symtab[i].u.sval[0].
PHP
Union types were introduced in PHP 8.0.[11] The values are implicitly "tagged" with a type by the language, and may be retrieved by "gettype()".
class Example
{
private int|float $foo;
public function squareAndAdd(float|int $bar): int|float
{
return $bar ** 2 + $this->foo;
}
}
Python
Support for typing was introduced in Python 3.5.[12] The new syntax for union types were introduced in Python 3.10.[13]
class Example:
foo = 0
def square_and_add(self, bar: int | float) -> int | float:
return bar ** 2 + self.foo
TypeScript
Union types are supported in TypeScript.[14] The values are implicitly "tagged" with a type by the language, and may be retrieved by "typeof()".
function successor(n: number | bigint): number | bigint {
return ++n
}
Rust
Tagged unions in Rust use the enum keyword, and can contain tuple and struct variants:
enum Foo {
Bar(i32),
Baz { x: String, y: i32 },
}
Untagged unions in Rust use the union keyword:
union Foo {
bar: i32,
baz: bool,
}
Reading from the fields of an untagged union results in undefined behavior if the data in the union is not valid as the type of the field, and thus requires an unsafe block:
let x = Foo { bar: 10 };
let y = unsafe { x.bar }; // This will set y to 10, and does not result in undefined behavior.
let z = unsafe { x.baz }; // This results in undefined behavior, as the value stored in x is not a valid bool.
See also
References
The scheme of type composition adopted by C owes considerable debt to Algol 68, although it did not, perhaps, emerge in a form that Algol's adherents would approve of. The central notion I captured from Algol was a type structure based on atomic types (including structures), composed into arrays, pointers (references), and functions (procedures). Algol 68's concept of unions and casts also had an influence that appeared later.
- "Handbook - Unions and Intersection Types". www.typescriptlang.org. Retrieved 30 November 2020.
- Kernighan, Brian W.; Ritchie, Dennis M. (1978). The C Programming Language (1st ed.). Prentice Hall. p. 138. ISBN 978-0131101630. Retrieved Jan 23, 2018.
External links
- boost::variant, a type-safe alternative to C++ unions
- MSDN: Classes,Structures & Unions, for examples and syntax
- differences, differences between union & structure
- Difference between struct and union in C++
https://en.wikipedia.org/wiki/Union_type
https://en.wikipedia.org/wiki/Category:Composite_data_types
https://en.wikipedia.org/wiki/Object_(computer_science)
https://en.wikipedia.org/wiki/Instance_(computer_science)
https://en.wikipedia.org/wiki/Virtual_machine
https://en.wikipedia.org/wiki/OS-level_virtualization
https://en.wikipedia.org/wiki/Chroot
https://en.wikipedia.org/wiki/Kernel_(operating_system)
https://en.wikipedia.org/wiki/Bootloader
https://en.wikipedia.org/wiki/Input/output
https://en.wikipedia.org/wiki/User_space_and_kernel_space
https://en.wikipedia.org/wiki/Monolithic_kernel
https://en.wikipedia.org/wiki/Memory_management
https://en.wikipedia.org/wiki/Computer_data_storage#Secondary_storage
https://en.wikipedia.org/wiki/Disk_read-and-write_head
https://en.wikipedia.org/wiki/Disk_storage
https://en.wikipedia.org/wiki/Nanometre
https://en.wikipedia.org/wiki/Orders_of_magnitude_(numbers)#10%E2%88%929
10−9
(0.000000001; 1000−3; short scale: one billionth; long scale: one milliardth)
ISO: nano- (n)
- Mathematics – Lottery: The odds of winning the Grand Prize (matching all 6 numbers) in the US Powerball lottery, with a single ticket, under the rules as of October 2015, are 292,201,338 to 1 against, for a probability of 3.422×10−9 (0.0000003422%).
- Mathematics – Lottery: The odds of winning the Grand Prize (matching all 6 numbers) in the Australian Powerball lottery, with a single ticket, under the rules as of April 2018, are 134,490,400 to 1 against, for a probability of 7.435×10−9 (0.0000007435%).
- Mathematics – Lottery: The odds of winning the Jackpot (matching the 6 main numbers) in the UK National Lottery, with
https://en.wikipedia.org/wiki/Orders_of_magnitude_(numbers)#10%E2%88%929
Usage
Nanotechnologies are based on phenomena typically occurring on a scale of nanometres (see nanoscopic scale).[1]
The nanometre is often used to express dimensions on an atomic scale: the diameter of a helium atom, for example, is about 0.06 nm, and that of a ribosome is about 20 nm. The nanometre is also commonly used to specify the wavelength of electromagnetic radiation near the visible part of the spectrum: visible light ranges from around 400 to 700 nm.[4] The ångström, which is equal to 0.1 nm, was formerly used for these purposes.
Since the late 1980s, in usages such as the 32 nm and the 22 nm semiconductor node, it has also been used to describe typical feature sizes in successive generations of the ITRS Roadmap for miniaturized semiconductor device fabrication in the semiconductor industry.
Unicode
The CJK Compatibility block in Unicode has the symbol U+339A ㎚ SQUARE NM.
https://en.wikipedia.org/wiki/Nanometre
https://en.wikipedia.org/wiki/Density_(computer_storage)
https://en.wikipedia.org/wiki/Non-volatile_memory
https://en.wikipedia.org/wiki/Semiconductor_memory
https://en.wikipedia.org/wiki/Memory_cell_(computing)
https://en.wikipedia.org/wiki/Magnetic-core_memory
https://en.wikipedia.org/wiki/Williams_tube
https://en.wikipedia.org/wiki/Delay-line_memory
https://en.wikipedia.org/wiki/Speed_of_sound
https://en.wikipedia.org/wiki/Static_electricity
https://en.wikipedia.org/wiki/Cathode-ray_tube
https://en.wikipedia.org/wiki/Electric_discharge
https://en.wikipedia.org/wiki/Phosphorescence
https://en.wikipedia.org/wiki/Persistent_luminescence
https://en.wikipedia.org/wiki/Forbidden_mechanism
https://en.wikipedia.org/wiki/Radioactive_decay#History
https://en.wikipedia.org/wiki/Phosphorescence
https://en.wikipedia.org/wiki/Vacancy_defect
https://en.wikipedia.org/wiki/Crystallographic_defect
https://en.wikipedia.org/wiki/Crystallographic_defect#Point_defects
https://en.wikipedia.org/wiki/Interstitial_defect
https://en.wikipedia.org/wiki/Interstitial_site
https://en.wikipedia.org/wiki/Sphere_packing
In crystallography, interstitial sites, holes or voids are the empty space that exists between the packing of atoms (spheres) in the crystal structure.[1]
The holes are easy to see if you try to pack circles together; no matter how close you get them or how you arrange them, you will have empty space in between. The same is true in a unit cell; no matter how the atoms are arranged, there will be interstitial sites present between the atoms. These sites or holes can be filled with other atoms (interstitial defect). The picture with packed circles is only a 2D representation. In a crystal lattice, the atoms (spheres) would be packed in a 3D arrangement. This results in different shaped interstitial sites depending on the arrangement of the atoms in the lattice.
https://en.wikipedia.org/wiki/Interstitial_site
Body-centered cubic (BCC)
A body-centered cubic unit cell has six octahedral voids located at the center of each face of the unit cell, and twelve further ones located at the midpoint of each edge of the same cell, for a total of six net octahedral voids. Additionally, there are 24 tetrahedral voids located in a square spacing around each octahedral void, for a total of twelve net tetrahedral voids. These tetrahedral voids are not local maxima and are not technically voids, but they do occasionally appear in multi-atom unit cells.
https://en.wikipedia.org/wiki/Interstitial_site
https://en.wikipedia.org/wiki/Cubic_crystal_system#Multi-element_structures
https://en.wikipedia.org/wiki/Phosphorescence
https://en.wikipedia.org/wiki/Cubic_crystal_system#Zincblende_structure
https://en.wikipedia.org/wiki/Fluorite_structure
https://en.wikipedia.org/wiki/Cubic_crystal_system#Rock-salt_structure
https://en.wikipedia.org/wiki/Cation-anion_radius_ratio
https://en.wikipedia.org/wiki/Chemical_stability
https://en.wikipedia.org/wiki/Hydride
https://en.wikipedia.org/wiki/Coordination_number
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.
There are three main varieties of these crystals:
- Primitive cubic (abbreviated cP and alternatively called simple cubic)
- Body-centered cubic (abbreviated cI or bcc)
- Face-centered cubic (abbreviated cF or fcc)
Note: the term fcc is often used in synonym for the cubic close-packed or ccp structure occurring in metals. However, fcc stands for a face-centered-cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the unit cells in these crystals are conventionally taken to be cubes, the primitive unit cells often are not.
Bravais lattices
The three Bravais lattices in the cubic crystal system are:
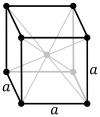
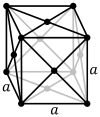
| Bravais lattice | Primitive cubic |
Body-centered cubic |
Face-centered cubic |
|---|---|---|---|
| Pearson symbol | cP | cI | cF |
| Unit cell | 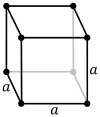
|
|
|
The primitive cubic lattice (cP) consists of one lattice point on each corner of the cube; this means each simple cubic unit cell has in total one lattice point. Each atom at a lattice point is then shared equally between eight adjacent cubes, and the unit cell therefore contains in total one atom (1⁄8 × 8).[1]
The body-centered cubic lattice (cI) has one lattice point in the center of the unit cell in addition to the eight corner points. It has a net total of two lattice points per unit cell (1⁄8 × 8 + 1).[1]
The face-centered cubic lattice (cF) has lattice points on the faces of the cube, that each gives exactly one half contribution, in addition to the corner lattice points, giving a total of 4 lattice points per unit cell (1⁄8 × 8 from the corners plus 1⁄2 × 6 from the faces).
The face-centered cubic lattice is closely related to the hexagonal close packed (hcp) system, where two systems differ only in the relative placements of their hexagonal layers. The [111] plane of a face-centered cubic lattice is a hexagonal grid.
Attempting to create a base-centered cubic lattice (i.e., putting an extra lattice point in the center of each horizontal face) results in a simple tetragonal Bravais lattice.
Coordination number (CN) is the number of nearest neighbors of a central atom in the structure.[1] Each sphere in a cP lattice has coordination number 6, in a cI lattice 8, and in a cF lattice 12.
Atomic packing factor (APF) is the fraction of volume that is occupied by atoms. The cP lattice has an APF of about 0.524 , the cI lattice an APF of about 0.680, and the cF lattice an APF of about 0.740.
Crystal classes
The isometric crystal system class names, point groups (in Schönflies notation, Hermann–Mauguin notation, orbifold, and Coxeter notation), type, examples, international tables for crystallography space group number,[2] and space groups are listed in the table below. There are a total 36 cubic space groups.
| No. | Point group | Type | Example | Space groups | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name[3] | Schön. | Intl | Orb. | Cox. | Primitive | Face-centered | Body-centered | |||
| 195–197 | Tetartoidal | T | 23 | 332 | [3,3]+ | enantiomorphic | Ullmannite, Sodium chlorate | P23 | F23 | I23 |
| 198–199 | P213 |
|
I213 | |||||||
| 200–204 | Diploidal | Th | 2/m3 (m3) |
3*2 | [3+,4] | centrosymmetric | Pyrite | Pm3, Pn3 | Fm3, Fd3 | I3 |
| 205–206 | Pa3 |
|
Ia3 | |||||||
| 207–211 | Gyroidal | O | 432 | 432 | [3,4]+ | enantiomorphic | Petzite | P432, P4232 | F432, F4132 | I432 |
| 212–214 | P4332, P4132 |
|
I4132 | |||||||
| 215–217 | Hextetrahedral | Td | 43m | *332 | [3,3] |
|
Sphalerite | P43m | F43m | I43m |
| 218–220 | P43n | F43c | I43d | |||||||
| 221–230 | Hexoctahedral | Oh | 4/m32/m (m3m) |
*432 | [3,4] | centrosymmetric | Galena, Halite | Pm3m, Pn3n, Pm3n, Pn3m | Fm3m, Fm3c, Fd3m, Fd3c | Im3m, Ia3d |
Other terms for hexoctahedral are: normal class, holohedral, ditesseral central class, galena type.
Single element structures
As a rule, since atoms in a solid attract each other, the more tightly packed arrangements of atoms tend to be more common. (Loosely packed arrangements do occur, though, for example if the orbital hybridization demands certain bond angles.) Accordingly, the primitive cubic structure, with especially low atomic packing factor, is rare in nature, but is found in polonium.[4][5] The bcc and fcc, with their higher densities, are both quite common in nature. Examples of bcc include iron, chromium, tungsten, and niobium. Examples of fcc include aluminium, copper, gold and silver.
Another important cubic crystal structure is the diamond cubic structure, which can appear in carbon, silicon, germanium, and tin. Unlike fcc and bcc, this structure is not a lattice, since it contains multiple atoms in its primitive cell. Other cubic elemental structures include the A15 structure found in tungsten, and the extremely complicated structure of manganese.
Multi-element structures
Compounds that consist of more than one element (e.g. binary compounds) often have crystal structures based on the cubic crystal system. Some of the more common ones are listed here. These structures can be viewed as two or more interpenetrating sublattices where each sublattice occupies the interstitial sites of the others.
Caesium chloride structure
One structure is the "interpenetrating primitive cubic" structure, also called a "caesium chloride" structure. This structure is often confused for a body-centered cubic structure, because the arrangement of atoms is the same. The true structure is shown in the graphic showing two individual primitive cubic structures that are superimposed within each other with the corner of one structure in the center of the cube of the other structure. It helps to convince yourself that it is not body-centered cubic because there is no translational symmetry along the ½, ½, ½, plane, the chloride would be translated into a cesium, not another chloride.[6]
It works the same way for the NaCl structure described in the next section. If you take out the Cl atoms, the leftover Na atoms still form an FCC structure, not a simple cubic structure.
In the unit cell of CsCl, each ion is at the center of a cube of ions of the opposite kind, so the coordination number is eight. The central cation is coordinated to 8 anions on the corners of a cube as shown, and similarly, the central anion is coordinated to 8 cations on the corners of a cube. Alternately, one could view this lattice as a simple cubic structure with a secondary atom in its cubic void.
In addition to caesium chloride itself, the structure also appears in certain other alkali halides when prepared at low temperatures or high pressures.[7] Generally, this structure is more likely to be formed from two elements whose ions are of roughly the same size (for example, ionic radius of Cs+ = 167 pm, and Cl− = 181 pm).
The space group of the caesium chloride (CsCl) structure is called Pm3m (in Hermann–Mauguin notation), or "221" (in the International Tables for Crystallography). The Strukturbericht designation is "B2".[8]
There are nearly a hundred rare earth intermetallic compounds that crystalize in the CsCl structure, including many binary compounds of rare earths with magnesium,[9] and with elements in groups 11, 12,[10][11] and 13. Other compounds showing caesium chloride like structure are CsBr, CsI, high-temperature RbCl, AlCo, AgZn, BeCu, MgCe, RuAl and SrTl.[citation needed]
Rock-salt structure
The space group of the rock-salt or halite (sodium chloride) structure is denoted as Fm3m (in Hermann–Mauguin notation), or "225" (in the International Tables for Crystallography). The Strukturbericht designation is "B1".[12]
In the rock-salt structure, each of the two atom types forms a separate face-centered cubic lattice, with the two lattices interpenetrating so as to form a 3D checkerboard pattern. The rock-salt structure has octahedral coordination: Each atom's nearest neighbors consist of six atoms of the opposite type, positioned like the six vertices of a regular octahedron. In sodium chloride there is a 1:1 ratio of sodium to chlorine atoms. The structure can also be described as an FCC lattice of sodium with chlorine occupying each octahedral void or vice versa.[6]
Examples of compounds with this structure include sodium chloride itself, along with almost all other alkali halides, and "many divalent metal oxides, sulfides, selenides, and tellurides".[7] According to the radius ratio rule, this structure is more likely to be formed if the cation is somewhat smaller than the anion (a cation/anion radius ratio of 0.414 to 0.732).
The interatomic distance (distance between cation and anion, or half the unit cell length a) in some rock-salt-structure crystals are: 2.3 Å (2.3 × 10−10 m) for NaF,[13] 2.8 Å for NaCl,[14] and 3.2 Å for SnTe.[15] Most of the alkali metal hydrides and halides have the rock salt structure, though a few have the caesium chloride structure instead.
Many transition metal monoxides also have the rock salt structure (TiO, VO, CrO, MnO, FeO, CoO, NiO, CdO). The early actinoid monocarbides also have this structure (ThC, PaC, UC, NpC, PuC).[37] Other compounds showing rock salt like structure are TiB,[48] ZrB,[49] PbS, PbSe, PbTe, SnTe, AgF, AgCl, and AgBr.
Fluorite structure
Much like the rock salt structure, the fluorite structure (AB2) is also an Fm3m structure but has 1:2 ratio of ions. The anti-fluorite structure is nearly identical, except the positions of the anions and cations are switched in the structure. They are designated Wyckoff positions 4a and 8c whereas the rock-salt structure positions are 4a and 4b.[50][51]
Zincblende structure
The space group of the Zincblende structure is called F43m (in Hermann–Mauguin notation), or 216.[52][53] The Strukturbericht designation is "B3".[54]
The Zincblende structure (also written "zinc blende") is named after the mineral zincblende (sphalerite), one form of zinc sulfide (β-ZnS). As in the rock-salt structure, the two atom types form two interpenetrating face-centered cubic lattices. However, it differs from rock-salt structure in how the two lattices are positioned relative to one another. The zincblende structure has tetrahedral coordination: Each atom's nearest neighbors consist of four atoms of the opposite type, positioned like the four vertices of a regular tetrahedron. In zinc sulfide the ratio of zinc to sulfur is 1:1.[6] Altogether, the arrangement of atoms in zincblende structure is the same as diamond cubic structure, but with alternating types of atoms at the different lattice sites. The structure can also be described as an FCC lattice of zinc with sulfur atoms occupying half of the tetrahedral voids or vice versa.[6]
Examples of compounds with this structure include zincblende itself, lead(II) nitrate, many compound semiconductors (such as gallium arsenide and cadmium telluride), and a wide array of other binary compounds.[citation needed] The boron group pnictogenides usually have a zincblende structure, though the nitrides are more common in the wurtzite structure, and their zincblende forms are less well known polymorphs.[55][56]
|
|
Fluorides | Chorlorides | Bromides | Iodides |
|---|---|---|---|---|
| Copper | Copper(I) fluoride | Copper(I) chloride | Copper(I) bromide | Copper(I) iodide |
|
|
Sulfides | Selenides | Tellurides | Polonides |
|---|---|---|---|---|
| Beryllium | Beryllium sulfide | Beryllium selenide | Beryllium telluride | Beryllium polonide[57][58] |
| Zinc | Zinc sulfide | Zinc selenide | Zinc telluride | Zinc polonide |
| Cadmium | Cadmium sulfide | Cadmium selenide | Cadmium telluride | Cadmium polonide |
| Mercury | Mercury sulfide | Mercury selenide | Mercury telluride | – |
This group is also known as the II-VI family of compounds, most of which can be made in both the zincblende (cubic) or wurtzite (hexagonal) form.
|
|
Nitrides | Phosphides | Arsenides | Antimonides |
|---|---|---|---|---|
| Boron | Boron nitride* | Boron phosphide | Boron arsenide | Boron antimonide |
| Aluminium | Aluminium nitride* | Aluminium phosphide | Aluminium arsenide | Aluminium antimonide |
| Gallium | Gallium nitride* | Gallium phosphide | Gallium arsenide | Gallium antimonide |
| Indium | Indium nitride* | Indium phosphide | Indium arsenide | Indium antimonide |
This group is also known as the III-V family of compounds.
Heusler structure
The Heusler structure, based on the structure of Cu2MnAl, is a common structure for ternary compounds involving transition metals. It has the space group Fm3m (No. 225), and the Strukturbericht designation is L21. Together with the closely related half-Heusler and inverse-Huesler compounds, there are hundreds of examples.
Iron monosilicide structure
The space group of the iron monosilicide structure is P213 (No. 198), and the Strukturbericht designation is B20. This is a chiral structure, and is sometimes associated with helimagnetic properties. There are four atoms of each element for a total of eight atoms in the unit cell.
Examples occur among the transition metal silicides and germanides, as well as a few other compounds such as gallium palladide.
|
|
Silicides | Germanides |
|---|---|---|
| Manganese | Manganese monosilicide | Manganese germanide |
| Iron | Iron monosilicide | Iron germanide |
| Cobalt | Cobalt monosilicide | Cobalt germanide |
| Chromium | Chromium(IV) silicide | Chromium(IV) germanide |
Weaire–Phelan structure
A Weaire–Phelan structure has Pm3n (223) symmetry.
It has three orientations of stacked tetradecahedrons with pyritohedral cells in the gaps. It is found as a crystal structure in chemistry where it is usually known as a "type I clathrate structure". Gas hydrates formed by methane, propane, and carbon dioxide at low temperatures have a structure in which water molecules lie at the nodes of the Weaire–Phelan structure and are hydrogen bonded together, and the larger gas molecules are trapped in the polyhedral cages.
See also
- Atomium: building which is a model of a bcc unit cell, with vertical body diagonal.
- Close-packing
- Dislocations
- Reciprocal lattice
References
- Moyer, Harvey V. (1956). "Chemical Properties of Polonium". In Moyer, Harvey V. (ed.). Polonium (Report). Oak Ridge, Tenn.: United States Atomic Energy Commission. pp. 33–96. doi:10.2172/4367751. TID-5221..
Further reading
- Hurlbut, Cornelius S.; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed., Wiley, ISBN 0-471-80580-7
External links
- JMol simulations by Graz University:
https://en.wikipedia.org/wiki/Cubic_crystal_system#Rock-salt_structure
https://en.wikipedia.org/wiki/Close-packing_of_equal_spheres
https://en.wikipedia.org/wiki/Unit_cell#Primitive_cell
https://en.wikipedia.org/wiki/Unit_cell#Primitive_cell
https://en.wikipedia.org/wiki/Parallelepiped
https://en.wikipedia.org/wiki/Bravais_lattice
https://en.wikipedia.org/wiki/Voronoi_diagram
https://en.wikipedia.org/wiki/Reciprocal_lattice
https://en.wikipedia.org/wiki/Hexagonal_crystal_family#Multi-element_structures
Multi-element structures
Compounds that consist of more than one element (e.g. binary compounds) often have crystal structures based on the hexagonal crystal family. Some of the more common ones are listed here. These structures can be viewed as two or more interpenetrating sublattices where each sublattice occupies the interstitial sites of the others.
Wurtzite structure
The wurtzite crystal structure is referred to by the Strukturbericht designation B4 and the Pearson symbol hP4. The corresponding space group is No. 186 (in International Union of Crystallography classification) or P63mc (in Hermann–Mauguin notation). The Hermann-Mauguin symbols in P63mc can be read as follows:[13]
- 63.. : a six fold screw rotation around the c-axis
- .m. : a mirror plane with normal {100}
- ..c : glide plane in the c-directions with normal {120}.
Among the compounds that can take the wurtzite structure are wurtzite itself (ZnS with up to 8% iron instead of zinc), silver iodide (AgI), zinc oxide (ZnO), cadmium sulfide (CdS), cadmium selenide (CdSe), silicon carbide (α-SiC), gallium nitride (GaN), aluminium nitride (AlN), boron nitride (w-BN) and other semiconductors.[14] In most of these compounds, wurtzite is not the favored form of the bulk crystal, but the structure can be favored in some nanocrystal forms of the material.
In materials with more than one crystal structure, the prefix "w-" is sometimes added to the empirical formula to denote the wurtzite crystal structure, as in w-BN.
Each of the two individual atom types forms a sublattice which is hexagonal close-packed (HCP-type). When viewed all together, the atomic positions are the same as in lonsdaleite (hexagonal diamond). Each atom is tetrahedrally coordinated. The structure can also be described as an HCP lattice of zinc with sulfur atoms occupying half of the tetrahedral voids or vice versa.
The wurtzite structure is non-centrosymmetric (i.e., lacks inversion symmetry). Due to this, wurtzite crystals can (and generally do) have properties such as piezoelectricity and pyroelectricity, which centrosymmetric crystals lack.[citation needed]
Nickel arsenide structure
The nickel arsenide structure consists of two interpenetrating sublattices: a primitive hexagonal nickel sublattice and a hexagonal close-packed arsenic sublattice. Each nickel atom is octahedrally coordinated to six arsenic atoms, while each arsenic atom is trigonal prismatically coordinated to six nickel atoms.[15] The structure can also be described as an HCP lattice of arsenic with nickel occupying each octahedral void.
Compounds adopting the NiAs structure are generally the chalcogenides, arsenides, antimonides and bismuthides of transition metals.[citation needed]
The following are the members of the nickeline group:[16]
- Achavalite: FeSe
- Breithauptite: NiSb
- Freboldite: CoSe
- Kotulskite: Pd(Te,Bi)
- Langistite: (Co,Ni)As
- Nickeline: NiAs
- Sobolevskite: Pd(Bi,Te)
- Sudburyite: (Pd,Ni)Sb
In two dimensions
There is only one hexagonal Bravais lattice in two dimensions: the hexagonal lattice.
| Bravais lattice | Hexagonal |
|---|---|
| Pearson symbol | hp |
| Unit cell | 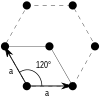
|
See also
References
- http://www.mindat.org/min-2901.html Mindat.org
External links
 Media related to Hexagonal lattices at Wikimedia Commons
Media related to Hexagonal lattices at Wikimedia Commons- Mineralogy database
https://en.wikipedia.org/wiki/Hexagonal_crystal_family#Multi-element_structures
https://en.wikipedia.org/wiki/Amorphous_solid
In crystallography, the triclinic (or anorthic) crystal system is one of the 7 crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. In addition, the angles between these vectors must all be different and may not include 90°.
The triclinic lattice is the least symmetric of the 14 three-dimensional Bravais lattices. It has (itself) the minimum symmetry all lattices have: points of inversion at each lattice point and at 7 more points for each lattice point: at the midpoints of the edges and the faces, and at the center points. It is the only lattice type that itself has no mirror planes.
Crystal classes
The triclinic crystal system class names, examples, Schönflies notation, Hermann-Mauguin notation, point groups, International Tables for Crystallography space group number,[1] orbifold, type, and space groups are listed in the table below. There are a total of 2 space groups.
| # | Point group | Type | Example | Space group | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name[2] | Schönflies | Intl | orbifold | Coxeter | |||||||||||
| 1 | Pedial | C1 | 1 | 11 | [ ]+ | enantiomorphic polar | Tantite | P1 | |||||||
| 2 | Pinacoidal | Ci (S2) | 1 | 1× | [2+,2+] | centrosymmetric | Wollastonite | P1 | |||||||
With each only one space group is associated. Pinacoidal is also known as triclinic normal. Pedial is also triclinic hemihedral.
Mineral examples include plagioclase, microcline, rhodonite, turquoise, wollastonite and amblygonite, all in triclinic normal (1).
See also
References
- "The 32 crystal classes". Retrieved 2018-06-19.
- Hurlbut, Cornelius S.; Klein, Cornelis, 1985, Manual of Mineralogy, 20th ed., pp. 64 – 65, ISBN 0-471-80580-7
External links
 Media related to Triclinic crystal system at Wikimedia Commons
Media related to Triclinic crystal system at Wikimedia Commons
https://en.wikipedia.org/wiki/Triclinic_crystal_system
In crystallography, the hexagonal crystal family is one of the six crystal families, which includes two crystal systems (hexagonal and trigonal) and two lattice systems (hexagonal and rhombohedral). While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent (see section crystal systems below).[1] In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice (such as α-quartz).
The hexagonal crystal family consists of the 12 point groups such that at least one of their space groups has the hexagonal lattice as underlying lattice, and is the union of the hexagonal crystal system and the trigonal crystal system.[2] There are 52 space groups associated with it, which are exactly those whose Bravais lattice is either hexagonal or rhombohedral.
Lattice systems
The hexagonal crystal family consists of two lattice systems: hexagonal and rhombohedral. Each lattice system consists of one Bravais lattice.
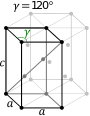
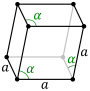
| Bravais lattice | Hexagonal | Rhombohedral |
|---|---|---|
| Pearson symbol | hP | hR |
| Hexagonal unit cell |

|
|
| Rhombohedral unit cell |

|
|
In the hexagonal family, the crystal is conventionally described by a right rhombic prism unit cell with two equal axes (a by a), an included angle of 120° (γ) and a height (c, which can be different from a) perpendicular to the two base axes.
The hexagonal unit cell for the rhombohedral Bravais lattice is the R-centered cell, consisting of two additional lattice points which occupy one body diagonal of the unit cell. There are two ways to do this, which can be thought of as two notations which represent the same structure. In the usual so-called obverse setting, the additional lattice points are at coordinates (2⁄3, 1⁄3, 1⁄3) and (1⁄3, 2⁄3, 2⁄3), whereas in the alternative reverse setting they are at the coordinates (1⁄3,2⁄3,1⁄3) and (2⁄3,1⁄3,2⁄3).[3] In either case, there are 3 lattice points per unit cell in total and the lattice is non-primitive.
The Bravais lattices in the hexagonal crystal family can also be described by rhombohedral axes.[4] The unit cell is a rhombohedron (which gives the name for the rhombohedral lattice). This is a unit cell with parameters a = b = c; α = β = γ ≠ 90°.[5] In practice, the hexagonal description is more commonly used because it is easier to deal with a coordinate system with two 90° angles. However, the rhombohedral axes are often shown (for the rhombohedral lattice) in textbooks because this cell reveals the 3m symmetry of the crystal lattice.
The rhombohedral unit cell for the hexagonal Bravais lattice is the D-centered[1] cell, consisting of two additional lattice points which occupy one body diagonal of the unit cell with coordinates (1⁄3, 1⁄3, 1⁄3) and (2⁄3, 2⁄3, 2⁄3). However, such a description is rarely used.
Crystal systems
| Crystal system | Required symmetries of point group | Point groups | Space groups | Bravais lattices | Lattice system |
|---|---|---|---|---|---|
| Trigonal | 1 threefold axis of rotation | 5 | 7 | 1 | Rhombohedral |
| 18 | 1 | Hexagonal | |||
| Hexagonal | 1 sixfold axis of rotation | 7 | 27 |
The hexagonal crystal family consists of two crystal systems: trigonal and hexagonal. A crystal system is a set of point groups in which the point groups themselves and their corresponding space groups are assigned to a lattice system (see table in Crystal system#Crystal classes).
The trigonal crystal system consists of the 5 point groups that have a single three-fold rotation axis, which includes space groups 143 to 167. These 5 point groups have 7 corresponding space groups (denoted by R) assigned to the rhombohedral lattice system and 18 corresponding space groups (denoted by P) assigned to the hexagonal lattice system. Hence, the trigonal crystal system is the only crystal system whose point groups have more than one lattice system associated with their space groups.
The hexagonal crystal system consists of the 7 point groups that have a single six-fold rotation axis. These 7 point groups have 27 space groups (168 to 194), all of which are assigned to the hexagonal lattice system.
Trigonal crystal system
The 5 point groups in this crystal system are listed below, with their international number and notation, their space groups in name and example crystals.[6][7][8]
| Space group no. | Point group | Type | Examples | Space groups | |||||
|---|---|---|---|---|---|---|---|---|---|
| Name[1] | Intl | Schoen. | Orb. | Cox. | Hexagonal | Rhombohedral | |||
| 143–146 | Trigonal pyramidal | 3 | C3 | 33 | [3]+ | enantiomorphic polar | carlinite, jarosite | P3, P31, P32 | R3 |
| 147–148 | Rhombohedral | 3 | C3i (S6) | 3× | [2+,6+] | centrosymmetric | dolomite, ilmenite | P3 | R3 |
| 149–155 | Trigonal trapezohedral | 32 | D3 | 223 | [2,3]+ | enantiomorphic | abhurite, alpha-quartz (152, 154), cinnabar | P312, P321, P3112, P3121, P3212, P3221 | R32 |
| 156–161 | Ditrigonal pyramidal | 3m | C3v | *33 | [3] | polar | schorl, cerite, tourmaline, alunite, lithium tantalate | P3m1, P31m, P3c1, P31c | R3m, R3c |
| 162–167 | Ditrigonal scalenohedral | 3m | D3d | 2*3 | [2+,6] | centrosymmetric | antimony, hematite, corundum, calcite, bismuth | P31m, P31c, P3m1, P3c1 | R3m, R3c |
Hexagonal crystal system
The 7 point groups (crystal classes) in this crystal system are listed below, followed by their representations in Hermann–Mauguin or international notation and Schoenflies notation, and mineral examples, if they exist.[2][9]
| Space group no. | Point group | Type | Examples | Space groups | ||||
|---|---|---|---|---|---|---|---|---|
| Name[1] | Intl | Schoen. | Orb. | Cox. | ||||
| 168–173 | Hexagonal pyramidal | 6 | C6 | 66 | [6]+ | enantiomorphic polar | nepheline, cancrinite | P6, P61, P65, P62, P64, P63 |
| 174 | Trigonal dipyramidal | 6 | C3h | 3* | [2,3+] |
|
laurelite and boric acid | P6 |
| 175–176 | Hexagonal dipyramidal | 6/m | C6h | 6* | [2,6+] | centrosymmetric | apatite, vanadinite | P6/m, P63/m |
| 177–182 | Hexagonal trapezohedral | 622 | D6 | 226 | [2,6]+ | enantiomorphic | kalsilite and high quartz | P622, P6122, P6522, P6222, P6422, P6322 |
| 183–186 | Dihexagonal pyramidal | 6mm | C6v | *66 | [6] | polar | greenockite, wurtzite[10] | P6mm, P6cc, P63cm, P63mc |
| 187–190 | Ditrigonal dipyramidal | 6m2 | D3h | *223 | [2,3] |
|
benitoite | P6m2, P6c2, P62m, P62c |
| 191–194 | Dihexagonal dipyramidal | 6/mmm | D6h | *226 | [2,6] | centrosymmetric | beryl | P6/mmm, P6/mcc, P63/mcm, P63/mmc |
Hexagonal close packed
Hexagonal close packed (hcp) is one of the two simple types of atomic packing with the highest density, the other being the face-centered cubic (fcc). However, unlike the fcc, it is not a Bravais lattice, as there are two nonequivalent sets of lattice points. Instead, it can be constructed from the hexagonal Bravais lattice by using a two-atom motif (the additional atom at about (2⁄3, 1⁄3, 1⁄2)) associated with each lattice point.[11]
Multi-element structures
Compounds that consist of more than one element (e.g. binary compounds) often have crystal structures based on the hexagonal crystal family. Some of the more common ones are listed here. These structures can be viewed as two or more interpenetrating sublattices where each sublattice occupies the interstitial sites of the others.
Wurtzite structure
The wurtzite crystal structure is referred to by the Strukturbericht designation B4 and the Pearson symbol hP4. The corresponding space group is No. 186 (in International Union of Crystallography classification) or P63mc (in Hermann–Mauguin notation). The Hermann-Mauguin symbols in P63mc can be read as follows:[13]
- 63.. : a six fold screw rotation around the c-axis
- .m. : a mirror plane with normal {100}
- ..c : glide plane in the c-directions with normal {120}.
Among the compounds that can take the wurtzite structure are wurtzite itself (ZnS with up to 8% iron instead of zinc), silver iodide (AgI), zinc oxide (ZnO), cadmium sulfide (CdS), cadmium selenide (CdSe), silicon carbide (α-SiC), gallium nitride (GaN), aluminium nitride (AlN), boron nitride (w-BN) and other semiconductors.[14] In most of these compounds, wurtzite is not the favored form of the bulk crystal, but the structure can be favored in some nanocrystal forms of the material.
In materials with more than one crystal structure, the prefix "w-" is sometimes added to the empirical formula to denote the wurtzite crystal structure, as in w-BN.
Each of the two individual atom types forms a sublattice which is hexagonal close-packed (HCP-type). When viewed all together, the atomic positions are the same as in lonsdaleite (hexagonal diamond). Each atom is tetrahedrally coordinated. The structure can also be described as an HCP lattice of zinc with sulfur atoms occupying half of the tetrahedral voids or vice versa.
The wurtzite structure is non-centrosymmetric (i.e., lacks inversion symmetry). Due to this, wurtzite crystals can (and generally do) have properties such as piezoelectricity and pyroelectricity, which centrosymmetric crystals lack.[citation needed]
Nickel arsenide structure
The nickel arsenide structure consists of two interpenetrating sublattices: a primitive hexagonal nickel sublattice and a hexagonal close-packed arsenic sublattice. Each nickel atom is octahedrally coordinated to six arsenic atoms, while each arsenic atom is trigonal prismatically coordinated to six nickel atoms.[15] The structure can also be described as an HCP lattice of arsenic with nickel occupying each octahedral void.
Compounds adopting the NiAs structure are generally the chalcogenides, arsenides, antimonides and bismuthides of transition metals.[citation needed]
The following are the members of the nickeline group:[16]
- Achavalite: FeSe
- Breithauptite: NiSb
- Freboldite: CoSe
- Kotulskite: Pd(Te,Bi)
- Langistite: (Co,Ni)As
- Nickeline: NiAs
- Sobolevskite: Pd(Bi,Te)
- Sudburyite: (Pd,Ni)Sb
In two dimensions
There is only one hexagonal Bravais lattice in two dimensions: the hexagonal lattice.
| Bravais lattice | Hexagonal |
|---|---|
| Pearson symbol | hp |
| Unit cell | 
|
See also
References
- http://www.mindat.org/min-2901.html Mindat.org
External links
 Media related to Hexagonal lattices at Wikimedia Commons
Media related to Hexagonal lattices at Wikimedia Commons- Mineralogy database
https://en.wikipedia.org/wiki/Hexagonal_crystal_family
On the other hand, persistent phosphorescence occurs when a high-energy photon is absorbed by an atom and its electron becomes trapped in a defect in the lattice of the crystalline or amorphous material. A defect such as a missing atom (vacancy defect) can trap an electron like a pitfall, storing that electron's energy until released by a random spike of thermal (vibrational) energy. Such a substance will then emit light of gradually decreasing intensity, ranging from a few seconds to up to several hours after the original excitation.[4]
https://en.wikipedia.org/wiki/Phosphorescence
Etymology
The term phosphorescence comes from the ancient Greek word φῶς (phos), meaning "light", and the Greek suffix -φόρος (-phoros), meaning "to bear", combined with the Latin suffix -escentem, meaning "becoming of", "having a tendency towards", or "with the essence of".[6] Thus, phosphorescence literally means "having a tendency to bear light". It was first recorded in 1766.[7]
The term phosphor had been used since the Middle Ages to describe minerals that glowed in the dark. One of the most famous, but not the first, was Bolognian phosphor. Around 1604, Vincenzo Casciarolo discovered a "lapis solaris" near Bologna, Italy. Once heated in an oxygen-rich furnace, it thereafter absorbed sunlight and glowed in the dark. In 1677, Hennig Brand isolated a new element that glowed due to a chemiluminescent reaction when exposed to air, and named it "phosphorus".[8]
In contrast, the term luminescence (from the Latin lumen for "light"), was coined by Eilhardt Wiedemann in 1888 as a term to refer to "light without heat", while "fluorescence" by Sir George Stokes in 1852, when he noticed that, when exposing a solution of quinine sulfate to light refracted through a prism, the solution glowed when exposed to the mysterious invisible-light (now known to be UV light) beyond the violet end of the spectrum. Stokes formed the term from a combination of fluorspar and opalescence (preferring to use a mineral instead of a solution), albeit it was later discovered that fluorspar glows due to phosphorescence.[9]
There was much confusion between the meanings of these terms throughout the late nineteenth to mid-twentieth centuries. Whereas the term "fluorescence" tended to refer to luminescence that ceased immediately (by human-eye standards) when removed from excitation, "phosphorescence" referred to virtually any substance that glowed for appreciable periods in darkness, sometimes to include even chemiluminescence (which occasionally produced substantial amounts of heat). Only after the 1950s and 1960s did advances in quantum electronics, spectroscopy, and lasers provide a measure to distinguish between the various processes that emit the light, although in common speech the distinctions are still often rather vague.[10]
https://en.wikipedia.org/wiki/Phosphorescence
https://en.wikipedia.org/wiki/Fluorite
https://en.wikipedia.org/wiki/Phosphorescence
https://en.wikipedia.org/wiki/Opalescence
https://en.wikipedia.org/wiki/Quinine
Conversely, when the stored energy is due to persistent phosphorescence, an entirely different process occurs without a fluorescence precursor. When electrons become trapped within a defect in the atomic or molecular lattice, light is prevented from reemitting until the electron can escape. To escape, the electron needs a boost of thermal energy to help spring it out of the trap and back into orbit around the atom. Only then can the atom emit a photon. Thus, persistent phosphorescence is highly dependent on the temperature of the material.[12]
https://en.wikipedia.org/wiki/Phosphorescence
https://en.wikipedia.org/wiki/Prism_(optics)
https://en.wikipedia.org/wiki/Active_laser_medium
https://en.wikipedia.org/wiki/Uranyl
https://en.wikipedia.org/wiki/Ruby
https://en.wikipedia.org/wiki/Singlet_state
https://en.wikipedia.org/wiki/Triplet_state
Zinc sulfide (or zinc sulphide) is an inorganic compound with the chemical formula of ZnS. This is the main form of zinc found in nature, where it mainly occurs as the mineral sphalerite.
Although this mineral is usually black because of various impurities,
the pure material is white, and it is widely used as a pigment. In its
dense synthetic form, zinc sulfide can be transparent, and it is used as a window for visible optics and infrared optics.
https://en.wikipedia.org/wiki/Zinc_sulfide
https://en.wikipedia.org/wiki/Phosphorescence
https://en.wikipedia.org/wiki/Spectroscopy
The state pattern is a behavioral software design pattern that allows an object to alter its behavior when its internal state changes. This pattern is close to the concept of finite-state machines. The state pattern can be interpreted as a strategy pattern, which is able to switch a strategy through invocations of methods defined in the pattern's interface.
The state pattern is used in computer programming to encapsulate varying behavior for the same object, based on its internal state. This can be a cleaner way for an object to change its behavior at runtime without resorting to conditional statements and thus improve maintainability.[1]: 395
https://en.wikipedia.org/wiki/State_pattern
material state pattern, hardware, processing, source, materials, build, design, etc.. draft [fixed plate]
property, operation, automatic, zero point, baseline, etc.. draft
https://en.wikipedia.org/wiki/State_of_matter
| Gang of Four patterns |
| ||||||
|---|---|---|---|---|---|---|---|
| Concurrency patterns | |||||||
| Architectural patterns | |||||||
| Other patterns | |||||||
| Books | |||||||
| People | |||||||
| Communities | |||||||
| See also |
https://en.wikipedia.org/wiki/State_pattern CL1=L5 usa nac dom et al. humans 2000s 1900s 1500 -10000 0 etc. | ||||||
















No comments:
Post a Comment