| Founded | July 28, 1983[1] |
|---|---|
| Defunct | June 26, 1995[1] |
| Fate | dissolved |
| Headquarters | , |
mt Xinu (from the letters in "Unix™", reversed) was a software company founded in 1983 that produced two operating systems. Its slogan "We know Unix™ backwards and forwards" was an allusion to the company's name and abilities.[2]
mt Xinu offered several products:
- mt Xinu was a commercially licensed version of the BSD Unix operating system for the DEC VAX. The initial version was based on 4.1cBSD; later versions were based on 4.2 and 4.3BSD.
- more/BSD was mt Xinu's version of 4.3BSD-Tahoe for VAX and HP 9000, incorporating code from the University of Utah's HPBSD. It included NFS.
- Mach386 was a hybrid of Mach 2.5/2.6 and 4.3BSD-Tahoe/Reno for 386 and 486-based IBM PC compatibles.
Apart from operating systems, mt Xinu also produced Apple-Unix interoperability software, including an AppleShare server for Unix.[3]
The company's principals were University of California, Berkeley computer science students and graduates, notably Bob Kridle, Alan Tobey, Ed Gould, and Vance Vaughan. Debbie Scherrer was a later contributor.
mt Xinu is also famous for its light-hearted Unix-themed calendars, including:
- Command of the Month (1987–1988)
- Lessons in Art (1989)
- Platform of the Year (1990)
In 1991, a division of mt Xinu broke off to become Xinet.
Notes
References
- Salus, Peter (1994), A Quarter Century of UNIX, Addison-Wesley, p. 209, ISBN 0-201-54777-5
https://en.wikipedia.org/wiki/Mt_Xinu
The Apple Public Source License (APSL) is the open-source and free software license under which Apple's Darwin operating system was released in 2000. A free and open-source software license was voluntarily adopted to further involve the community from which much of Darwin originated.
The first version of the Apple Public Source License was approved by the Open Source Initiative (OSI).[5] Version 2.0, released July 29, 2003, is also approved as a free software license by the Free Software Foundation (FSF) which finds it acceptable for developers to work on projects that are already covered by this license. However, the FSF recommends that developers should not release new projects under this license, because the partial copyleft is not compatible with the GNU General Public License and allows linking with files released entirely as proprietary software.[4] The license does require that if any derivatives of the original source are released externally, their source should be made available; the Free Software Foundation compares this requirement to a similar one in its own GNU Affero General Public License.[4]
Many software releases from Apple have now been relicensed under the more liberal Apache License, such as the Bonjour Zeroconf stack. However, most OS component source code remains under APSL.
See also
References
- Raymond, Eric. "OSI clarifies the status of the APSL". Linux Weekly News. Retrieved February 14, 2013.
External links
https://en.wikipedia.org/wiki/Apple_Public_Source_License
The Cathedral and the Bazaar: Musings on Linux and Open Source by an Accidental Revolutionary (abbreviated CatB) is an essay, and later a book, by Eric S. Raymond on software engineering methods, based on his observations of the Linux kernel development process and his experiences managing an open source project, fetchmail. It examines the struggle between top-down and bottom-up design. The essay was first presented by the author at the Linux Kongress on May 27, 1997 in Würzburg (Germany) and was published as the second chapter of the same‑titled book in 1999.
The illustration on the cover of the book is a 1913 painting by Liubov Popova titled Composition with Figures and belongs to the collection of the State Tretyakov Gallery.[1] The book was released under the Open Publication License v2.0 in 1999.[2]
https://en.wikipedia.org/wiki/The_Cathedral_and_the_Bazaar
In legal terms, a plea is simply an answer to a claim made by someone in a criminal case under common law using the adversarial system. Colloquially, a plea has come to mean the assertion by a defendant at arraignment, or otherwise in response to a criminal charge, whether that person pleaded or pled guilty, not guilty, nolo contendere (a.k.a. no contest), no case to answer (in the United Kingdom), or Alford plea (in the United States).
The concept of the plea is one of the significant differences between criminal procedure under common law and procedure under the civil law system. Under common law, a defendant who pleads guilty is automatically convicted, and the remainder of the trial is used to determine the sentence. This produces a system known as plea bargaining, in which defendants may plead guilty in exchange for a more lenient punishment. In civil law jurisdictions, a confession by the defendant is treated like any other piece of evidence. A full confession does not prevent a full trial or relieve the prosecutor from presenting a case to the court.
https://en.wikipedia.org/wiki/Plea
Limitation may refer to:
- Limitation Act, a list of legislation in Malaysia and the United Kingdom
- A statute of limitations
- Limitations (novel), a 2006 novel by Scott Turow
- A disclaimer for research done in an experiment or study
See also
https://en.wikipedia.org/wiki/Limitation
Limitations and exceptions to copyright are provisions, in local copyright law or the Berne Convention, which allow for copyrighted works to be used without a license from the copyright owner.
Limitations and exceptions to copyright relate to a number of important considerations such as market failure, freedom of speech,[1] education and equality of access (such as by the visually impaired). Some view limitations and exceptions as "user rights"—seeing user rights as providing an essential balance to the rights of the copyright owners. There is no consensus among copyright experts as to whether user rights are rights or simply limitations on copyright. The concept of user rights has been recognised by courts, including the Canadian Supreme Court,[2] which classed "fair dealing" as such a user right. These kinds of disagreements in philosophy are quite common in the philosophy of copyright, where debates about jurisprudential reasoning tend to act as proxies for more substantial disagreements about good policy.
https://en.wikipedia.org/wiki/Limitations_and_exceptions_to_copyright
https://en.wikipedia.org/wiki/Limitations_and_exceptions_to_copyright
| Act of Parliament | |
 | |
| Long title | An Act to consolidate the Limitation Acts 1939 to 1980. |
|---|---|
| Citation | 1980 c. 58 |
| Dates | |
| Royal assent | 13 November 1980 |
| Commencement | 1 May 1981 |
| Other legislation | |
| Repeals/revokes | |
Status: Amended | |
| Text of statute as originally enacted | |
| Revised text of statute as amended | |
The Limitation Act 1980 (c. 58)[1] is an Act of the Parliament of the United Kingdom applicable only to England and Wales. It is a statute of limitations which provides timescales within which action may be taken (by issuing a claim form) for breaches of the law. For example, it provides that breaches of an ordinary contract are actionable for six years after the event[2] whereas breaches of a deed are actionable for twelve years after the event.[3] In most cases, after the expiry of the time periods specified in the Act the remedies available for breaches are extinguished and no action may be taken in the courts in respect of those breaches.
https://en.wikipedia.org/wiki/Limitation_Act_1980
 | |
| Long title | An act to limit the Liability of Ship-Owners, and for other Purposes. |
|---|---|
| Enacted by | the 31st United States Congress |
| Effective | March 3, 1851 |
| Citations | |
| Statutes at Large | 9 Stat. 635 (Ch.43) |
In United States maritime law, the Limitation of Liability Act of 1851, codified as 46 U.S.C. § 30501 since February 1, 2010, states that the owner of a vessel may limit damage claims to the value of the vessel at the end of the voyage plus "pending freight", as long as the owner can prove it lacked knowledge of the problem beforehand. This Act was the subject of a 2001 United States Supreme Court case in Lewis v. Lewis & Clark Marine, Inc.
https://en.wikipedia.org/wiki/Limitation_of_Liability_Act_of_1851
The Limitation Act 1623 (21 Jas 1 c 16), sometimes called the Statute of Limitations 1623, was an Act of the Parliament of England.
The whole Act was repealed by section 1(1) of, and Group 5 of Part I of Schedule 1 to, the Statute Law (Repeals) Act 1986.
https://en.wikipedia.org/wiki/Limitation_Act_1623
 | |
| Citation | 1963 c. 47 |
|---|---|
| Territorial extent | United Kingdom |
| Dates | |
| Royal assent | 31 July 1963 |
| Repealed | 1 May 1981 |
| Other legislation | |
| Repealed by | Prescription and Limitation (Scotland) Act 1973 Northern Ireland Constitution Act 1973 Limitation Act 1975 Limitation Act 1980 |
Status: Repealed | |
| Text of statute as originally enacted | |
The Limitation Act 1963 (c. 47) was an Act of the Parliament of the United Kingdom that amended the statute of limitations to allow actions in some cases where the injured party had not discovered the injury until after the standard date of expiration. The Act was based on the report of the Davies Committee on Limitation of Actions in Cases of Personal Injury, created after the Court of Appeal decision in the case of Cartledge v Jopling, and the Committee notably produced their final report before Cartledge had been heard in the House of Lords. The draft bill was presented to Parliament on 6 May 1963; it was given the Royal Assent on 31 July and came into force on the same day.
The act allowed an injured party to bring a claim outside the normal statute of limitations period if he could show that he was not aware of the injuries himself until after the limitation period had expired and if he gained the permission of the court. After a series of problems emerged, including vagueness on a point even the House of Lords was unable to clarify and poor draftsmanship, the Act was repealed bit by bit during the 1970s, with the Limitation Act 1980 scrapping the last remaining sections.
https://en.wikipedia.org/wiki/Limitation_Act_1963
A limited-slip differential (LSD) is a type of differential that allows its two output shafts to rotate at different speeds but limits the maximum difference between the two shafts. Limited-slip differentials are often known by the generic trademark Positraction, a brand name owned by General Motors.
In an automobile, such limited-slip differentials are sometimes used in place of a standard differential, where they convey certain dynamic advantages, at the expense of greater complexity.
https://en.wikipedia.org/wiki/Limited-slip_differential
https://en.wikipedia.org/wiki/Limited-access_road
https://en.wikipedia.org/wiki/Limitation_of_size
https://en.wikipedia.org/wiki/Conditional_limitation
https://en.wikipedia.org/wiki/Typography
https://en.wikipedia.org/wiki/Time_limit
https://en.wikipedia.org/wiki/Limitation_Act
https://en.wikipedia.org/wiki/Statute_of_limitations
https://en.wikipedia.org/wiki/Scope_limitation
https://en.wikipedia.org/wiki/Collective_self-limitation
https://en.wikipedia.org/wiki/MIT_License
https://en.wikipedia.org/wiki/Exclusion_clause
https://en.wikipedia.org/wiki/Effluent_limitation
https://en.wikipedia.org/wiki/Public_domain
https://en.wikipedia.org/wiki/Hereditary_peer#Limitation_to_heirs_of_the_body
https://en.wikipedia.org/wiki/Act_of_Settlement_1701
https://en.wikipedia.org/wiki/Limitation_Act_1939
https://en.wikipedia.org/wiki/Payment_limitations_(agriculture)
https://en.wikipedia.org/wiki/Copyright#Limitations_and_exceptions
https://en.wikipedia.org/wiki/Definition#Limitations_of_definition
https://en.wikipedia.org/wiki/Term_limit
https://en.wikipedia.org/wiki/Steric_effects
https://en.wikipedia.org/wiki/Words_of_purchase
https://en.wikipedia.org/wiki/Ancient_Greek_accent#Law_of_Limitation
https://en.wikipedia.org/wiki/D%C3%A9tente#Strategic_Arms_Limitations_Talks
https://en.wikipedia.org/wiki/Copyright_infringement#Limitations
https://en.wikipedia.org/wiki/Ground_sample_distance
https://en.wikipedia.org/wiki/Field-of-use_limitation
https://en.wikipedia.org/wiki/List_of_patent_claim_types
https://en.wikipedia.org/wiki/Statistical_disclosure_control
https://en.wikipedia.org/wiki/All_elements_test
https://en.wikipedia.org/wiki/Price_of_Coal_(Limitation)_Act_1915
https://en.wikipedia.org/wiki/AM_broadcasting?wprov=srpw1_119
https://en.wikipedia.org/wiki/Borrowing_statute
https://en.wikipedia.org/wiki/Adverse_possession
https://en.wikipedia.org/wiki/Card_security_code#Benefits_and_limitations
https://en.wikipedia.org/wiki/Self-limiting_(biology)
https://en.wikipedia.org/wiki/Angle_of_arrival#Limitation
https://en.wikipedia.org/wiki/Zero-day_(computing)
https://en.wikipedia.org/wiki/Principle_of_least_privilege
https://en.wikipedia.org/wiki/Cease_and_desist
https://en.wikipedia.org/wiki/Eutrophication
https://en.wikipedia.org/wiki/Central_processing_unit
https://en.wikipedia.org/wiki/Derringer
https://en.wikipedia.org/wiki/Prenuptial_agreement?wprov=srpw1_219
https://en.wikipedia.org/wiki/Executive_(government)
https://en.wikipedia.org/wiki/Paradox_of_tolerance
https://en.wikipedia.org/wiki/Long_mode#Memory_limitations
https://en.wikipedia.org/wiki/Live_USB#Benefits_and_limitations
https://en.wikipedia.org/wiki/Terms_of_service
https://en.wikipedia.org/wiki/Symmetric_mean_absolute_percentage_error
https://en.wikipedia.org/wiki/Immunogold_labelling
https://en.wikipedia.org/wiki/Ankylosing_spondylitis
https://en.wikipedia.org/wiki/Warp_drive
https://en.wikipedia.org/wiki/Flyback_converter#Limitations
https://en.wikipedia.org/wiki/VO2_max
https://en.wikipedia.org/wiki/Unequal_treaty
https://en.wikipedia.org/wiki/Actuator
https://en.wikipedia.org/wiki/Phytoplankton
https://en.wikipedia.org/wiki/Image_resolution
https://en.wikipedia.org/wiki/Chemotroph
https://en.wikipedia.org/wiki/Ultimate_tensile_strength
https://en.wikipedia.org/wiki/Exoskeleton
https://en.wikipedia.org/wiki/Lime_(material)
https://en.wikipedia.org/wiki/Streaming_SIMD_Extensions
https://en.wikipedia.org/wiki/Intercontinental_ballistic_missile
https://en.wikipedia.org/wiki/Cross-licensing
https://en.wikipedia.org/wiki/Medical_grade_silicone#Limitations
https://en.wikipedia.org/wiki/Axonometric_projection#Limitations
https://en.wikipedia.org/wiki/Intel_Graphics_Technology
https://en.wikipedia.org/wiki/Soil_fertility#Light_and_CO2_limitations
https://en.wikipedia.org/wiki/Out-of-band_management
https://en.wikipedia.org/wiki/Defeasible_estate#Fee_simple_subject_to_an_executory_limitation
https://en.wikipedia.org/wiki/Anisogamy
https://en.wikipedia.org/wiki/Stolichnaya
https://en.wikipedia.org/wiki/Count_Dracula#Limitations_of_his_powers
https://en.wikipedia.org/wiki/Pixel
https://en.wikipedia.org/wiki/Traceroute#Limitations
https://en.wikipedia.org/wiki/The_Crown
https://en.wikipedia.org/wiki/Memories_of_Murder
https://en.wikipedia.org/wiki/Russian_Far_East
https://en.wikipedia.org/wiki/Octet_(computing)
https://en.wikipedia.org/wiki/Fixed_deposit
https://en.wikipedia.org/wiki/Passport_validity
https://en.wikipedia.org/wiki/Multitenancy
https://en.wikipedia.org/wiki/Disclaimer
https://en.wikipedia.org/wiki/High_treason_in_the_United_Kingdom
https://en.wikipedia.org/wiki/Gamut#Limitations_of_color_representation
https://en.wikipedia.org/wiki/Fallacy
https://en.wikipedia.org/wiki/OCSP_stapling#Limitations
https://en.wikipedia.org/wiki/Grade_(bouldering)
https://en.wikipedia.org/wiki/Received_signal_strength_indicator
https://en.wikipedia.org/wiki/Everything
https://en.wikipedia.org/wiki/Two-way_radio
https://en.wikipedia.org/wiki/Executive_Order_6102
https://en.wikipedia.org/wiki/Register_(keyword)
https://en.wikipedia.org/wiki/Tar_(computing)?wprov=srpw1_408
https://en.wikipedia.org/wiki/Minimum_viable_product
https://en.wikipedia.org/wiki/Wickerhamomyces_anomalus
https://en.wikipedia.org/wiki/Geiger_counter#Limitations
https://en.wikipedia.org/wiki/IP_fragmentation
https://en.wikipedia.org/wiki/ASCII
https://en.wikipedia.org/wiki/Monopoly_on_violence
https://en.wikipedia.org/wiki/Second_messenger_system
https://en.wikipedia.org/wiki/Maglev
https://en.wikipedia.org/wiki/Bilateral_monopoly
https://en.wikipedia.org/wiki/COM_file
https://en.wikipedia.org/wiki/Shunt_(electrical)
https://en.wikipedia.org/wiki/Doom_engine
https://en.wikipedia.org/wiki/Antinomy
https://en.wikipedia.org/wiki/Utility_clothing
https://en.wikipedia.org/wiki/Decompiler
https://en.wikipedia.org/wiki/Breechloader
https://en.wikipedia.org/wiki/Dimethyl_sulfoxide
https://en.wikipedia.org/wiki/Ion_semiconductor_sequencing
https://en.wikipedia.org/wiki/Ultracopier
https://en.wikipedia.org/wiki/Master_boot_record
https://en.wikipedia.org/wiki/Wildcard_certificate
https://en.wikipedia.org/wiki/Maxims_of_equity
https://en.wikipedia.org/wiki/Remuneration
https://en.wikipedia.org/wiki/Entity%E2%80%93attribute%E2%80%93value_model
https://en.wikipedia.org/wiki/Fire-and-forget
https://en.wikipedia.org/wiki/Typewriter
https://en.wikipedia.org/wiki/Malicious_falsehood
https://en.wikipedia.org/wiki/General_(United_States)
https://en.wikipedia.org/wiki/Three-component_theory_of_stratification
https://en.wikipedia.org/wiki/Lineage_(evolution)
https://en.wikipedia.org/wiki/Wake-on-LAN
https://en.wikipedia.org/wiki/Pilot_in_command
https://en.wikipedia.org/wiki/Isoelectric_focusing
https://en.wikipedia.org/wiki/Conversation
https://en.wikipedia.org/wiki/Bioavailability
https://en.wikipedia.org/wiki/Glossary_of_engineering
https://en.wikipedia.org/wiki/Sewing_needle
https://en.wikipedia.org/wiki/Water%E2%80%93gas_shift_reaction
https://en.wikipedia.org/wiki/Nonelementary_integral
https://en.wikipedia.org/wiki/Digital_potentiometer
https://en.wikipedia.org/wiki/Bedridden
https://en.wikipedia.org/wiki/Posse_comitatus
https://en.wikipedia.org/wiki/Pulsed_rocket_motor
https://en.wikipedia.org/wiki/Manifest_destiny
https://en.wikipedia.org/wiki/Comma-separated_values
https://en.wikipedia.org/wiki/EtherChannel
https://en.wikipedia.org/wiki/V_speeds
https://en.wikipedia.org/wiki/Articles_of_organization
https://en.wikipedia.org/wiki/Dissolution_testing
https://en.wikipedia.org/wiki/Privileges_or_Immunities_Clause
https://en.wikipedia.org/wiki/Identity-based_cryptography
https://en.wikipedia.org/wiki/String_(computer_science)
https://en.wikipedia.org/wiki/Tacking_(sailing)
https://en.wikipedia.org/wiki/Centrifugal_governor
https://en.wikipedia.org/wiki/Locking_differential
https://en.wikipedia.org/wiki/Ploidy
https://en.wikipedia.org/wiki/Optical_disc_image
https://en.wikipedia.org/wiki/FP-45_Liberator
https://en.wikipedia.org/wiki/Pyrosequencing
https://en.wikipedia.org/wiki/Pseudonymization
https://en.wikipedia.org/wiki/CUT%26RUN_sequencing
https://en.wikipedia.org/wiki/Mac_Studio
https://en.wikipedia.org/wiki/Shared_memory
https://en.wikipedia.org/wiki/Scrying
https://en.wikipedia.org/wiki/Tanks_in_World_War_I
https://en.wikipedia.org/wiki/Bomber
https://en.wikipedia.org/wiki/ZX_Spectrum
https://en.wikipedia.org/wiki/Memory_Stick
https://en.wikipedia.org/wiki/GeForce_600_series
https://en.wikipedia.org/wiki/Foreign_key
https://en.wikipedia.org/wiki/Zero-fuel_weight
https://en.wikipedia.org/wiki/Glass_electrode
https://en.wikipedia.org/wiki/Cell_site
https://en.wikipedia.org/wiki/Multiversion_concurrency_control
https://en.wikipedia.org/wiki/Thermocouple
https://en.wikipedia.org/wiki/In-circuit_testing#Limitations
https://en.wikipedia.org/wiki/Printf
https://en.wikipedia.org/wiki/Three_Comrades_(novel)
https://en.wikipedia.org/wiki/Pump_action
https://en.wikipedia.org/wiki/Attitude_indicator
https://en.wikipedia.org/wiki/List_of_common_EMC_test_standards
https://en.wikipedia.org/wiki/Open_source
https://en.wikipedia.org/wiki/American_redstart
https://en.wikipedia.org/wiki/Newton%27s_method_in_optimization
https://en.wikipedia.org/wiki/Stepper_motor
https://en.wikipedia.org/wiki/Slew_rate
https://en.wikipedia.org/wiki/Nuclear_salt-water_rocket
https://en.wikipedia.org/wiki/Limited_government
https://en.wikipedia.org/wiki/Classful_network
https://en.wikipedia.org/wiki/Field_capacity
https://en.wikipedia.org/wiki/Deep_linking
https://en.wikipedia.org/wiki/Statute_of_repose#Difference_from_a_statute_of_limitations
https://en.wikipedia.org/wiki/Cyclotron
https://en.wikipedia.org/wiki/LXC
https://en.wikipedia.org/wiki/Axiomatic_system
https://en.wikipedia.org/wiki/Time-division_multiple_access
https://en.wikipedia.org/wiki/Visigothic_Code
https://en.wikipedia.org/wiki/Avulsion_fracture
https://en.wikipedia.org/wiki/Ostensive_definition
https://en.wikipedia.org/wiki/Gene_knock-in
https://en.wikipedia.org/wiki/Continuous-wave_radar
https://en.wikipedia.org/wiki/Rotary_hook
https://en.wikipedia.org/wiki/Expansion_spring
https://en.wikipedia.org/wiki/Fractionating_column
https://en.wikipedia.org/wiki/Out_of_memory
https://en.wikipedia.org/wiki/Ex_post_facto_law
https://en.wikipedia.org/wiki/Freedom_of_movement
https://en.wikipedia.org/wiki/Open_world
https://en.wikipedia.org/wiki/Joist
https://en.wikipedia.org/wiki/Vacuum_truck
https://en.wikipedia.org/wiki/Elastic_net_regularization
https://en.wikipedia.org/wiki/Heat_deflection_temperature
https://en.wikipedia.org/wiki/Ultimatum
https://en.wikipedia.org/wiki/Indirection
https://en.wikipedia.org/wiki/Limit
https://en.wikipedia.org/wiki/Space_bar
https://en.wikipedia.org/wiki/Maximum_wage
https://en.wikipedia.org/wiki/Time_constraint
https://en.wikipedia.org/wiki/Telescopic_handler
https://en.wikipedia.org/wiki/GNU_parallel
https://en.wikipedia.org/wiki/Fighting_words
https://en.wikipedia.org/wiki/Pseudo-R-squared
https://en.wikipedia.org/wiki/Type_rating
https://en.wikipedia.org/wiki/Image_Composite_Editor
https://en.wikipedia.org/wiki/Durham_tube
https://en.wikipedia.org/wiki/Line_of_hereditary_succession
https://en.wikipedia.org/wiki/Random_amplification_of_polymorphic_DNA
https://en.wikipedia.org/wiki/Inotify#Limitations
https://en.wikipedia.org/wiki/Gateways_to_Annihilation
https://en.wikipedia.org/wiki/Pancake_lens
https://en.wikipedia.org/wiki/Boiling_chip
https://en.wikipedia.org/wiki/Net_reclassification_improvement
https://en.wikipedia.org/wiki/Telephone_number
https://en.wikipedia.org/wiki/Unlicensed_National_Information_Infrastructure
https://en.wikipedia.org/wiki/Warp_and_weft
https://en.wikipedia.org/wiki/Absolute_Infinite
https://en.wikipedia.org/wiki/Variable_capacitor
https://en.wikipedia.org/wiki/Communications_Decency_Act
https://en.wikipedia.org/wiki/Retention_period
https://en.wikipedia.org/wiki/Standstill_agreement
https://en.wikipedia.org/wiki/Search_engine_scraping
https://en.wikipedia.org/wiki/Positive_end-expiratory_pressure
https://en.wikipedia.org/wiki/Title_2_of_the_Swiss_Federal_Constitution
https://en.wikipedia.org/wiki/Inverse_polymerase_chain_reaction
https://en.wikipedia.org/wiki/High-%CE%BA_dielectric
https://en.wikipedia.org/wiki/Pneumococcal_conjugate_vaccine
https://en.wikipedia.org/wiki/True_north
https://en.wikipedia.org/wiki/Earth%27s_circumference
https://en.wikipedia.org/wiki/Proteolysis
https://en.wikipedia.org/wiki/Crocosphaera_watsonii#Phosphorus_limitation
https://en.wikipedia.org/wiki/Borescope
https://en.wikipedia.org/wiki/Submersible_bridge
https://en.wikipedia.org/wiki/Telemetry_intelligence
https://en.wikipedia.org/wiki/Law_of_salvage
https://en.wikipedia.org/wiki/Active_load#Practical_limitations
https://en.wikipedia.org/wiki/Proximate_cause
https://en.wikipedia.org/wiki/Powder_metallurgy
https://en.wikipedia.org/wiki/Proclamation_10043
https://en.wikipedia.org/wiki/Commerce_Clause
https://en.wikipedia.org/wiki/Analog_device
https://en.wikipedia.org/wiki/Earnout#Limitations
https://en.wikipedia.org/wiki/Allotropy
https://en.wikipedia.org/wiki/Parity_bit
https://en.wikipedia.org/wiki/Plenary_power
https://en.wikipedia.org/wiki/Quantum_speed_limit
https://en.wikipedia.org/wiki/Test_light
https://en.wikipedia.org/wiki/Logitech_Unifying_receiver
https://en.wikipedia.org/wiki/Clipping_(audio)
https://en.wikipedia.org/wiki/Cordless_telephone
https://en.wikipedia.org/wiki/Science_of_Logic
https://en.wikipedia.org/wiki/Intersymbol_interference
https://en.wikipedia.org/wiki/Taxing_and_Spending_Clause#Limitations_on_taxing_power
https://en.wikipedia.org/wiki/DDR3_SDRAM
https://en.wikipedia.org/wiki/1933_Datsun_Type_12?wprov=srpw1_1249
https://en.wikipedia.org/wiki/Convective_available_potential_energy
https://en.wikipedia.org/wiki/Accounting_standard#Limitations
https://en.wikipedia.org/wiki/Retrigger
https://en.wikipedia.org/wiki/Relapse
https://en.wikipedia.org/wiki/Public_morality
https://en.wikipedia.org/wiki/Breakpoint
https://en.wikipedia.org/wiki/Freedom_of_thought
https://en.wikipedia.org/wiki/Primum_non_nocere
https://en.wikipedia.org/wiki/Zero_liquid_discharge
https://en.wikipedia.org/wiki/Limited_atonement
https://en.wikipedia.org/wiki/Apitoxin
https://en.wikipedia.org/wiki/Stringent_response
https://en.wikipedia.org/wiki/Tasseography
https://en.wikipedia.org/wiki/ISO_9660
https://en.wikipedia.org/wiki/Nulla_poena_sine_lege
https://en.wikipedia.org/wiki/Property_list
https://en.wikipedia.org/wiki/Crystallization
https://en.wikipedia.org/wiki/Collective_ownership
https://en.wikipedia.org/wiki/Auditor%27s_report
https://en.wikipedia.org/wiki/Jackscrew#Limitations
https://en.wikipedia.org/wiki/Slirp#Limitations
https://en.wikipedia.org/wiki/Heuristic_evaluation
https://en.wikipedia.org/wiki/Immunoprecipitation
https://en.wikipedia.org/wiki/Linear_referencing
https://en.wikipedia.org/wiki/End-to-end_principle
https://en.wikipedia.org/wiki/Handbook_of_Texas
https://en.wikipedia.org/wiki/Simple_triage_and_rapid_treatment
https://en.wikipedia.org/wiki/Maximum_sustainable_yield
https://en.wikipedia.org/wiki/Scanning_tunneling_spectroscopy
https://en.wikipedia.org/wiki/Overlay_(programming)
https://en.wikipedia.org/wiki/Oxygen-15_labelled_water#Limitations
https://en.wikipedia.org/wiki/Res_ipsa_loquitur
https://en.wikipedia.org/wiki/Fuel_gas
https://en.wikipedia.org/wiki/Arable_land
https://en.wikipedia.org/wiki/Cycloid_gear
https://en.wikipedia.org/wiki/Ultra-high_vacuum#Material_limitations
https://en.wikipedia.org/wiki/Contrastive_analysis
https://en.wikipedia.org/wiki/Linear_bounded_automaton
https://en.wikipedia.org/wiki/Run-time_type_information
https://en.wikipedia.org/wiki/Honing_(metalworking)
https://en.wikipedia.org/wiki/MessagePack
https://en.wikipedia.org/wiki/Architectural_pattern
https://en.wikipedia.org/wiki/Electrokinetic_remediation
https://en.wikipedia.org/wiki/Tokenization_(data_security)
https://en.wikipedia.org/wiki/The_Capitalist_Manifesto
https://en.wikipedia.org/wiki/ZX_Spectrum_graphic_modes
https://en.wikipedia.org/wiki/Vito_Badalamenti
https://en.wikipedia.org/wiki/International_taxation
https://en.wikipedia.org/wiki/Eurasier
https://en.wikipedia.org/wiki/Declaratory_judgment
https://en.wikipedia.org/wiki/Fascia_of_Scarpa
https://en.wikipedia.org/wiki/Rupture_disc
https://en.wikipedia.org/wiki/Mister_Mxyzptlk
https://en.wikipedia.org/wiki/Gas_Agility
https://en.wikipedia.org/wiki/Resistor%E2%80%93transistor_logic
https://en.wikipedia.org/wiki/Cylinder_1024
https://en.wikipedia.org/wiki/Black_Knight_(vehicle)
https://en.wikipedia.org/wiki/Stratification_(clinical_trials)
https://en.wikipedia.org/wiki/Forge_welding
https://en.wikipedia.org/wiki/Field_experiment
https://en.wikipedia.org/wiki/Radical_cyclization
https://en.wikipedia.org/wiki/Industrial_process_control
https://en.wikipedia.org/wiki/Delta_Force_(video_game)
https://en.wikipedia.org/wiki/Gas_Vitality
https://en.wikipedia.org/wiki/Sideloading
https://en.wikipedia.org/wiki/Trap_(plumbing)
https://en.wikipedia.org/wiki/Network_throughput#Analog_limitations
https://en.wikipedia.org/wiki/Network_throughput
https://en.wikipedia.org/wiki/TRIAC
https://en.wikipedia.org/wiki/Hold-And-Modify
https://en.wikipedia.org/wiki/Line_code
https://en.wikipedia.org/wiki/DIN_1.0/2.3
https://en.wikipedia.org/wiki/Ohmic_contact
https://en.wikipedia.org/wiki/Protected_mode
https://en.wikipedia.org/wiki/7.92%C3%9794mm_Patronen
https://en.wikipedia.org/wiki/File_format
https://en.wikipedia.org/wiki/Shift_key
https://en.wikipedia.org/wiki/Loop_heat_pipe
https://en.wikipedia.org/wiki/Logical_block_addressing
https://en.wikipedia.org/wiki/Artificial_stupidity
https://en.wikipedia.org/wiki/The_Songs_of_Distant_Earth
https://en.wikipedia.org/wiki/Spirometry
https://en.wikipedia.org/wiki/Taylor_Manifest_Anxiety_Scale
https://en.wikipedia.org/wiki/Rotary_compression_pump
https://en.wikipedia.org/wiki/K-6_(missile)
https://en.wikipedia.org/wiki/K-6_(missile)
https://en.wikipedia.org/wiki/K-6_(missile)
https://en.wikipedia.org/wiki/K-6_(missile)
https://en.wikipedia.org/wiki/K-6_(missile)
https://en.wikipedia.org/wiki/K-6_(missile)
https://en.wikipedia.org/wiki/Ballistic_missile
https://en.wikipedia.org/wiki/church
https://en.wikipedia.org/wiki/illyo
https://en.wikipedia.org/wiki/su
https://en.wikipedia.org/wiki/f
https://en.wikipedia.org/wiki/Congressional_staff
https://en.wikipedia.org/wiki/Everything_Louder_than_Everyone_Else
https://en.wikipedia.org/wiki/Personal_property
https://en.wikipedia.org/wiki/Read%E2%80%93write_memory
https://en.wikipedia.org/wiki/End-to-end_delay
https://en.wikipedia.org/wiki/Peripheral_vascular_system
https://en.wikipedia.org/wiki/Obstructive_lung_disease
https://en.wikipedia.org/wiki/Dragon_Age:_Redemption
https://en.wikipedia.org/wiki/Glossary_of_law
https://en.wikipedia.org/wiki/ATP_test
https://en.wikipedia.org/wiki/Near%E2%80%93far_problem
https://en.wikipedia.org/wiki/Laser-guided_bomb?wprov=srpw1_1562
https://en.wikipedia.org/wiki/Mathematical_formulation_of_quantum_mechanics
https://en.wikipedia.org/wiki/Free_cooling
https://en.wikipedia.org/wiki/Bluetooth_mesh_networking
https://en.wikipedia.org/wiki/Establishment_Clause
https://en.wikipedia.org/wiki/Preposition_and_postposition
https://en.wikipedia.org/wiki/Evidence-based_medicine
https://en.wikipedia.org/wiki/RollerCoaster_Tycoon
https://en.wikipedia.org/wiki/Quantitative_Descriptive_Analysis
https://en.wikipedia.org/wiki/USS_Brooklyn_(CL-40)
https://en.wikipedia.org/wiki/Noise_measurement
https://en.wikipedia.org/wiki/Pulse_shaping
https://en.wikipedia.org/wiki/Sicherheitspolizei
The twisted nematic effect (TN-effect) was a main technology breakthrough that made LCDs practical. Unlike earlier displays, TN-cells did not require a current to flow for operation and used low operating voltages suitable for use with batteries. The introduction of TN-effect displays led to their rapid expansion in the display field, quickly pushing out other common technologies like monolithic LEDs and CRTs for most electronics. By the 1990s, TN-effect LCDs were largely universal in portable electronics, although since then, many applications of LCDs adopted alternatives to the TN-effect such as in-plane switching (IPS) or vertical alignment (VA).
Many monochrome alphanumerical displays without picture information still use TN LCDs.
TN displays benefit from fast pixel response times and less smearing than other LCD display technology, but suffer from poor color reproduction and limited viewing angles, especially in the vertical direction. Colors will shift, potentially to the point of completely inverting, when viewed at an angle that is not perpendicular to the display.
https://en.wikipedia.org/wiki/Twisted_nematic_field_effect
https://en.wikipedia.org/wiki/Keyword_research
https://en.wikipedia.org/wiki/Sound_Blaster_Audigy
https://en.wikipedia.org/wiki/Digital_sculpting
https://en.wikipedia.org/wiki/Cerebrospinal_fluid_flow_MRI
https://en.wikipedia.org/wiki/Osteochondrodysplasia
https://en.wikipedia.org/wiki/Comprehensive_metabolic_panel
https://en.wikipedia.org/wiki/Fdisk
https://en.wikipedia.org/wiki/Process_chemistry
https://en.wikipedia.org/wiki/Hardware-assisted_virtualization
https://en.wikipedia.org/wiki/Cantonment_board
https://en.wikipedia.org/wiki/Electroforming
https://en.wikipedia.org/wiki/Magnetohydrodynamic_drive
https://en.wikipedia.org/wiki/Phosphate_solubilizing_bacteria
https://en.wikipedia.org/wiki/Channel_spacing
https://en.wikipedia.org/wiki/RAM_drive
https://en.wikipedia.org/wiki/Nationally_determined_contribution
https://en.wikipedia.org/wiki/Toll
https://en.wikipedia.org/wiki/Reflector_(cipher_machine)
https://en.wikipedia.org/wiki/Enforced_disappearance
https://en.wikipedia.org/wiki/Neural_efficiency_hypothesis
https://en.wikipedia.org/wiki/Electrically_small_antenna
https://en.wikipedia.org/wiki/Stoping
https://en.wikipedia.org/wiki/Similitude
https://en.wikipedia.org/wiki/Redfield_ratio
https://en.wikipedia.org/wiki/Thomas_Hooker
https://en.wikipedia.org/wiki/Norfolk_and_Western_Railway_class_J_(1941)
https://en.wikipedia.org/wiki/Smelting
https://en.wikipedia.org/wiki/Artificial_brain
https://en.wikipedia.org/wiki/Loudspeakers_in_mosques
https://en.wikipedia.org/wiki/Blade_server
https://en.wikipedia.org/wiki/Richard%27s_paradox
https://en.wikipedia.org/wiki/JACK_Audio_Connection_Kit
https://en.wikipedia.org/wiki/Aircraft_compass_turns
https://en.wikipedia.org/wiki/Ext2
https://en.wikipedia.org/wiki/Liquid_resistor
https://en.wikipedia.org/wiki/Response_spectrum
https://en.wikipedia.org/wiki/Stored-value_card
https://en.wikipedia.org/wiki/British_S-class_submarine_(1931)
https://en.wikipedia.org/wiki/Titan_Fighting_Championships
https://en.wikipedia.org/wiki/Application_binary_interface
https://en.wikipedia.org/wiki/SBC_(codec)
https://en.wikipedia.org/wiki/Quattro_(four-wheel-drive_system)
https://en.wikipedia.org/wiki/Identifier
https://en.wikipedia.org/wiki/Codeshare_agreement
https://en.wikipedia.org/wiki/Side_looking_airborne_radar
https://en.wikipedia.org/wiki/Broadcast_Wave_Format
https://en.wikipedia.org/wiki/Font_family_(HTML)
https://en.wikipedia.org/wiki/Extraterritoriality
https://en.wikipedia.org/wiki/Russia%E2%80%93Korea_Treaty_of_1884
https://en.wikipedia.org/wiki/Power_shuttle
https://en.wikipedia.org/wiki/Reverse_short-channel_effect
https://en.wikipedia.org/wiki/See-through_display
https://en.wikipedia.org/wiki/Combined_track_and_field_events
https://en.wikipedia.org/wiki/Hereditary_monarchy
https://en.wikipedia.org/wiki/Henry_Howard,_15th_Earl_of_Arundel
https://en.wikipedia.org/wiki/Light_Airborne_Multi-Purpose_System
https://en.wikipedia.org/wiki/Gear_bearing
https://en.wikipedia.org/wiki/Personal_god
https://en.wikipedia.org/wiki/Refugee_Act
https://en.wikipedia.org/wiki/Publication
https://en.wikipedia.org/wiki/32-bit_computing
https://en.wikipedia.org/wiki/Genesis_Lynea
https://en.wikipedia.org/wiki/Wireless_local_loop
https://en.wikipedia.org/wiki/AppImage
https://en.wikipedia.org/wiki/Synchronous_circuit?wprov=srpw1_1842
https://en.wikipedia.org/wiki/Unfilmability
https://en.wikipedia.org/wiki/Metal_injection_molding
https://en.wikipedia.org/wiki/Discrete_global_grid
https://en.wikipedia.org/wiki/Emic_and_etic
https://en.wikipedia.org/wiki/Liquid_scintillation_counting
Caveat emptor (/ˈɛmptɔːr/; from caveat, "may he/she beware", a subjunctive form of cavēre, "to beware" + ēmptor, "buyer") is Latin for "Let the buyer beware".[1] It has become a proverb in English. Generally, caveat emptor is the contract law principle that controls the sale of real property after the date of closing, but may also apply to sales of other goods. The phrase caveat emptor and its use as a disclaimer of warranties arises from the fact that buyers typically have less information than the seller about the good or service they are purchasing. This quality of the situation is known as 'information asymmetry'. Defects in the good or service may be hidden from the buyer, and only known to the seller.
It is a short form of Caveat emptor, quia ignorare non debuit quod jus alienum emit ("Let a purchaser beware, for he ought not to be ignorant of the nature of the property which he is buying from another party.")[2] I.e. the buyer should assure himself that the product is good and that the seller had the right to sell it, as opposed to receiving stolen property.
A common way that information asymmetry between seller and buyer has been addressed is through a legally binding warranty, such as a guarantee of satisfaction.
https://en.wikipedia.org/wiki/Caveat_emptor
https://en.wikipedia.org/wiki/Loss_of_clerical_state
https://en.wikipedia.org/wiki/Belgium%E2%80%93Korea_Treaty_of_1901
https://en.wikipedia.org/wiki/Charge-off
https://en.wikipedia.org/wiki/Multi-link_trunking
https://en.wikipedia.org/wiki/Downs%E2%80%93Thomson_paradox
https://en.wikipedia.org/wiki/ISO_22324
https://en.wikipedia.org/wiki/High-IQ_society
https://en.wikipedia.org/wiki/PICO-8
https://en.wikipedia.org/wiki/Wishful_Identification
https://en.wikipedia.org/wiki/Speckle_imaging
https://en.wikipedia.org/wiki/Missile_defense
https://en.wikipedia.org/wiki/Sixth_nerve_palsy
https://en.wikipedia.org/wiki/Battery_management_system
https://en.wikipedia.org/wiki/Magic_systems_in_games
https://en.wikipedia.org/wiki/Weather_warfare
https://en.wikipedia.org/wiki/Glan%E2%80%93Thompson_prism
https://en.wikipedia.org/wiki/Ggplot2
https://en.wikipedia.org/wiki/Function_point
https://en.wikipedia.org/wiki/National_Labor_Relations_Act_of_1935
https://en.wikipedia.org/wiki/Tumor_suppressor_gene
https://en.wikipedia.org/wiki/ISO/IEC_19770
https://en.wikipedia.org/wiki/Rotary_engine
https://en.wikipedia.org/wiki/Crypthecodinium_cohnii
https://en.wikipedia.org/wiki/Unreal_Tournament
https://en.wikipedia.org/wiki/Nullum_tempus_occurrit_regi
https://en.wikipedia.org/wiki/Plate_count_agar
https://en.wikipedia.org/wiki/Government-granted_monopoly
https://en.wikipedia.org/wiki/Thirty-year_rule
https://en.wikipedia.org/wiki/Sampling_(signal_processing)
https://en.wikipedia.org/wiki/Psychoacoustics
https://en.wikipedia.org/wiki/Extremely_high_frequency
https://en.wikipedia.org/wiki/Elephant_gun
https://en.wikipedia.org/wiki/Russian_Socialist_Movement
https://en.wikipedia.org/wiki/Exmor
https://en.wikipedia.org/wiki/Title_8_of_the_United_States_Code
https://en.wikipedia.org/wiki/Primitive_recursive_function
https://en.wikipedia.org/wiki/Rubidium-82
https://en.wikipedia.org/wiki/Electronic_centralised_aircraft_monitor
https://en.wikipedia.org/wiki/Digital_learning
https://en.wikipedia.org/wiki/Wound_healing_assay
https://en.wikipedia.org/wiki/National_Assembly_(French_Revolution)
https://en.wikipedia.org/wiki/Cambridge_Optical_Aperture_Synthesis_Telescope
https://en.wikipedia.org/wiki/Amazon_SimpleDB#Limitations
https://en.wikipedia.org/wiki/Aircraft_maintenance_engineer
https://en.wikipedia.org/wiki/Debt_evasion
https://en.wikipedia.org/wiki/Eigenmode_expansion
https://en.wikipedia.org/wiki/Os_de_Civ%C3%ADs
https://en.wikipedia.org/wiki/Science_fantasy?wprov=srpw1_1922
https://en.wikipedia.org/wiki/Doctrine_of_colourability
https://en.wikipedia.org/wiki/Future_interest
https://en.wikipedia.org/wiki/List_of_governors_of_Texas
https://en.wikipedia.org/wiki/Future_interest
https://en.wikipedia.org/wiki/Animal_hoarding
https://en.wikipedia.org/wiki/Metaphysics_of_presence
https://en.wikipedia.org/wiki/Constant_angular_velocity
https://en.wikipedia.org/wiki/Terminate-and-stay-resident_program
https://en.wikipedia.org/wiki/Notice_of_Claimed_Infringement
https://en.wikipedia.org/wiki/Injunction
https://en.wikipedia.org/wiki/Sivas_massacre
https://en.wikipedia.org/wiki/Optical_disc_authoring
https://en.wikipedia.org/wiki/Ticket_(admission)
https://en.wikipedia.org/wiki/Ultra-royalist
https://en.wikipedia.org/wiki/Remainder_(law)
https://en.wikipedia.org/wiki/Limitations_on_exclusive_rights:_Computer_programs
https://en.wikipedia.org/wiki/200_Cigarettes
https://en.wikipedia.org/wiki/Data_transformation_(computing)
https://en.wikipedia.org/wiki/1790_United_States_census
https://en.wikipedia.org/wiki/Exome_sequencing
https://en.wikipedia.org/wiki/Daily_call_sheet
https://en.wikipedia.org/wiki/Priming_(media)
https://en.wikipedia.org/wiki/First-rate
https://en.wikipedia.org/wiki/Famicom_3D_System
https://en.wikipedia.org/wiki/Passive_matrix_addressing
https://en.wikipedia.org/wiki/Olympus_M.Zuiko_Digital_ED_40-150mm_f/2.8_PRO
https://en.wikipedia.org/wiki/Road_signs_in_Russia?wprov=srpw1_2036
https://en.wikipedia.org/wiki/Military_service
https://en.wikipedia.org/wiki/Molecular_phylogenetics
https://en.wikipedia.org/wiki/Southern_California_freeways
https://en.wikipedia.org/wiki/Rogerian_argument#Limitations
https://en.wikipedia.org/wiki/Space_weapon
https://en.wikipedia.org/wiki/Dry_lubricant
https://en.wikipedia.org/wiki/RF64
https://en.wikipedia.org/wiki/Wideband_audio
https://en.wikipedia.org/wiki/Trickle_charging
https://en.wikipedia.org/wiki/Critique
https://en.wikipedia.org/wiki/Solothurn_S-18/1000
https://en.wikipedia.org/wiki/Divided_visual_field_paradigm
https://en.wikipedia.org/wiki/Faldstool
https://en.wikipedia.org/wiki/Neural_efficiency_hypothesis
https://en.wikipedia.org/wiki/Pro%E2%80%93am
https://en.wikipedia.org/wiki/Doc_(computing)
https://en.wikipedia.org/wiki/Unlock
https://en.wikipedia.org/wiki/Temporal_resolution
https://en.wikipedia.org/wiki/The_Greatest_(1977_film)
https://en.wikipedia.org/wiki/Range_(music)
https://en.wikipedia.org/wiki/MACRS
https://en.wikipedia.org/wiki/Double_data_rate
https://en.wikipedia.org/wiki/Half-Earth
https://en.wikipedia.org/wiki/Explosively_formed_penetrator
https://en.wikipedia.org/wiki/Integrator
https://en.wikipedia.org/wiki/Freely_redistributable_software
https://en.wikipedia.org/wiki/Aphanizomenon#Overcoming_phosphate_limitation
https://en.wikipedia.org/wiki/Betamovie
https://en.wikipedia.org/wiki/Thermal_degradation_of_polymers
https://en.wikipedia.org/wiki/Network_Information_Service
https://en.wikipedia.org/wiki/Traversal_Using_Relays_around_NAT
https://en.wikipedia.org/wiki/SRAAM
https://en.wikipedia.org/wiki/Wedge_strategy_(diplomacy)
https://en.wikipedia.org/wiki/AGM-78_Standard_ARM
https://en.wikipedia.org/wiki/Expert_system
https://en.wikipedia.org/wiki/Linkspan
https://en.wikipedia.org/wiki/Nocticron
https://en.wikipedia.org/wiki/Wedge_strategy_(diplomacy)
https://en.wikipedia.org/wiki/Street_artist
https://en.wikipedia.org/wiki/Mid-air_collision
https://en.wikipedia.org/wiki/UDP_flood_attack
https://en.wikipedia.org/wiki/Pulled_elbow
https://en.wikipedia.org/wiki/Heat_engine
https://en.wikipedia.org/wiki/Winkler_index
https://en.wikipedia.org/wiki/Spatial_multiplexing
https://en.wikipedia.org/wiki/Economic_efficiency
https://en.wikipedia.org/wiki/BL_8-inch_Mk_VIII_naval_gun
https://en.wikipedia.org/wiki/Capacity_factor
https://en.wikipedia.org/wiki/Certified_Emission_Reduction
https://en.wikipedia.org/wiki/Trash_culture
https://en.wikipedia.org/wiki/California_Unfair_Competition_Law
https://en.wikipedia.org/wiki/United_States_Copyright_Office
https://en.wikipedia.org/wiki/Extreme_Fighting_Championship
https://en.wikipedia.org/wiki/Enumerated_powers_(United_States)
https://en.wikipedia.org/wiki/German_underground_horror
https://en.wikipedia.org/wiki/De_novo_protein_structure_prediction
https://en.wikipedia.org/wiki/Equal_temperament
https://en.wikipedia.org/wiki/Positive_and_negative_predictive_values
https://en.wikipedia.org/wiki/Five-string_violin
https://en.wikipedia.org/wiki/Land_Suitability_classification
https://en.wikipedia.org/wiki/Fire_safety
https://en.wikipedia.org/wiki/Medical_identification_tag
https://en.wikipedia.org/wiki/Shewanella
https://en.wikipedia.org/wiki/Tracing_in_English_law
https://en.wikipedia.org/wiki/Outline_of_intellectual_property
https://en.wikipedia.org/wiki/Process_modeling
https://en.wikipedia.org/wiki/Gauntlet_track
https://en.wikipedia.org/wiki/Encumbrance
https://en.wikipedia.org/wiki/Kernel-based_Virtual_Machine
https://en.wikipedia.org/w/index.php?search=bezio&title=Special%3ASearch&ns0=1
https://en.wikipedia.org/wiki/Dexlansoprazole
https://en.wikipedia.org/wiki/Fat-tailed_distribution
https://en.wikipedia.org/wiki/Phase_problem
https://en.wikipedia.org/wiki/Magnetic_resonance_velocimetry
https://en.wikipedia.org/wiki/Industrial_wastewater_treatment
https://en.wikipedia.org/wiki/Network_performance
https://en.wikipedia.org/wiki/Brevetoxin
https://en.wikipedia.org/wiki/Ether#Polyethers
https://en.wikipedia.org/wiki/Full-range_speaker
https://en.wikipedia.org/wiki/Redline
https://en.wikipedia.org/wiki/Characters_per_line
https://en.wikipedia.org/wiki/Shemya
https://en.wikipedia.org/wiki/Java_Card
https://en.wikipedia.org/wiki/Rail_transport_modelling_scales
https://en.wikipedia.org/wiki/EMD_GP20
https://en.wikipedia.org/wiki/Improved_Mobile_Telephone_Service
https://en.wikipedia.org/wiki/Law_of_agency
https://en.wikipedia.org/wiki/Value_change_dump
https://en.wikipedia.org/wiki/Icing_conditions
https://en.wikipedia.org/wiki/Rechargeable_alkaline_battery
https://en.wikipedia.org/wiki/Graphisoft
https://en.wikipedia.org/wiki/Filler_(materials)
https://en.wikipedia.org/wiki/Automatic_target_recognition
https://en.wikipedia.org/wiki/Standard_form_contract
https://en.wikipedia.org/wiki/Digimon_Battle_Spirit
https://en.wikipedia.org/wiki/United_Nations_Disengagement_Observer_Force
https://en.wikipedia.org/wiki/Focke-Wulf_Fw_61
https://en.wikipedia.org/wiki/Electronic_viewfinder
https://en.wikipedia.org/wiki/Halazone
https://en.wikipedia.org/wiki/Nook_Simple_Touch
https://en.wikipedia.org/wiki/Backplane
https://en.wikipedia.org/wiki/Franklin_(automobile)
https://en.wikipedia.org/wiki/Private_pilot_licence
https://en.wikipedia.org/wiki/Monocrystalline_silicon
https://en.wikipedia.org/wiki/Load-bearing_wall
https://en.wikipedia.org/wiki/Irregardless
https://en.wikipedia.org/wiki/Gene_targeting
https://en.wikipedia.org/wiki/Non-linear_editing
https://en.wikipedia.org/wiki/Rafter
https://en.wikipedia.org/wiki/TeXworks
https://en.wikipedia.org/wiki/Isotachophoresis
https://en.wikipedia.org/wiki/Bendix_AN/FPS-20
https://en.wikipedia.org/wiki/Emergency_communication_system
https://en.wikipedia.org/wiki/Gold_mining_in_the_United_States
https://en.wikipedia.org/wiki/Divided_visual_field_paradigm
https://en.wikipedia.org/wiki/Rotary_transformer
https://en.wikipedia.org/wiki/Federal_Department_of_Foreign_Affairs
https://en.wikipedia.org/wiki/Simple-As-Possible_computer
https://en.wikipedia.org/wiki/Display_PostScript
https://en.wikipedia.org/wiki/Noir:_A_Shadowy_Thriller
https://en.wikipedia.org/wiki/Scope_clause
https://en.wikipedia.org/wiki/Homo_Hierarchicus
https://en.wikipedia.org/wiki/Call_of_Duty:_World_at_War_%E2%80%93_Final_Fronts
https://en.wikipedia.org/wiki/Deadly_weapon
https://en.wikipedia.org/wiki/Power_factor_(shooting_sports)
https://en.wikipedia.org/wiki/Certified_Emission_Reduction
https://en.wikipedia.org/wiki/Spinodal
https://en.wikipedia.org/wiki/Criteria_of_truth
https://en.wikipedia.org/wiki/Teleplay
https://en.wikipedia.org/wiki/The_Dead_Past
https://en.wikipedia.org/wiki/Tube_sound
https://en.wikipedia.org/wiki/Persistence_(computer_science)
https://en.wikipedia.org/wiki/Subject_matter_limitations_in_copyright_law_in_Canada
https://en.wikipedia.org/wiki/Non-well-founded_set_theory
https://en.wikipedia.org/wiki/Coleopter
https://en.wikipedia.org/wiki/X-ray_welding
https://en.wikipedia.org/wiki/Diplexer
https://en.wikipedia.org/wiki/Airspace
https://en.wikipedia.org/wiki/Tire_code
https://en.wikipedia.org/wiki/WireGuard
https://en.wikipedia.org/wiki/Cerebral_organoid
https://en.wikipedia.org/wiki/Position-sensing_hydraulic_cylinder
https://en.wikipedia.org/wiki/Mass_spectrometry_data_format
https://en.wikipedia.org/wiki/Power-line_flicker
https://en.wikipedia.org/wiki/Stream_ripping
https://en.wikipedia.org/wiki/Symphysiotomy
https://en.wikipedia.org/wiki/MOS_Technology_8502
https://en.wikipedia.org/wiki/War_2410
https://en.wikipedia.org/wiki/Anguimorpha
https://en.wikipedia.org/wiki/Macintosh_LC
https://en.wikipedia.org/wiki/The_Tower_(poetry_collection)
https://en.wikipedia.org/wiki/Criminal_conversation
https://en.wikipedia.org/wiki/Dynamic_braking
https://en.wikipedia.org/wiki/Marble_Madness
https://en.wikipedia.org/wiki/Vignetting
https://en.wikipedia.org/wiki/Plasma_speaker
https://en.wikipedia.org/wiki/On-balance_volume
https://en.wikipedia.org/wiki/Atmosphere-breathing_electric_propulsion
https://en.wikipedia.org/wiki/Hashgraph
https://en.wikipedia.org/wiki/Kill_All_Normies
https://en.wikipedia.org/wiki/Freight_claim
https://en.wikipedia.org/wiki/Static_Context_Header_Compression
https://en.wikipedia.org/wiki/Nipkow_disk
https://en.wikipedia.org/wiki/Board_International
https://en.wikipedia.org/wiki/Right_to_rest_and_leisure
https://en.wikipedia.org/wiki/Maximum_landing_weight
https://en.wikipedia.org/wiki/Spinal_posture
https://en.wikipedia.org/wiki/Bishop_(artillery)
https://en.wikipedia.org/wiki/Nuke_(software)
https://en.wikipedia.org/wiki/TextEdit_(API)
https://en.wikipedia.org/wiki/Motion_simulator
https://en.wikipedia.org/wiki/Publius_Volumnius_Amintinus_Gallus
https://en.wikipedia.org/wiki/Scrub_typhus
https://en.wikipedia.org/wiki/Protein_mass_spectrometry
https://en.wikipedia.org/wiki/Intellectual_humility
https://en.wikipedia.org/wiki/Instruction-level_parallelism
https://en.wikipedia.org/wiki/Multi-level_cell
https://en.wikipedia.org/wiki/Automatic_generation_control
https://en.wikipedia.org/wiki/Tied_aid
https://en.wikipedia.org/wiki/Shelf_(storage)
https://en.wikipedia.org/wiki/The_Black_Pirate
https://en.wikipedia.org/wiki/Electronic_circuit
https://en.wikipedia.org/wiki/Establishing_shot
https://en.wikipedia.org/wiki/Cranial_ultrasound
https://en.wikipedia.org/wiki/Mathematical_chess_problem
https://en.wikipedia.org/wiki/Gross_Motor_Function_Classification_System
https://en.wikipedia.org/wiki/The_Number_Ones
https://en.wikipedia.org/wiki/U.S._Fire_Arms_Manufacturing_Company
https://en.wikipedia.org/wiki/Broad-gauge_railway
https://en.wikipedia.org/wiki/Magnetic_survey_(archaeology)
https://en.wikipedia.org/wiki/Gleysol
https://en.wikipedia.org/wiki/Flip-flop_(programming)
https://en.wikipedia.org/wiki/Western_Latin_character_sets_(computing)
https://en.wikipedia.org/wiki/Public_property
https://en.wikipedia.org/wiki/FBI_method_of_profiling
https://en.wikipedia.org/wiki/Loading_screen
https://en.wikipedia.org/wiki/Live_looping
https://en.wikipedia.org/wiki/The_Demon%27s_Rook
https://en.wikipedia.org/wiki/Price%E2%80%93Anderson_Nuclear_Industries_Indemnity_Act
https://en.wikipedia.org/wiki/6-meter_band
https://en.wikipedia.org/wiki/Public_Opinion_(book)
https://en.wikipedia.org/wiki/Duplex_sequencing
https://en.wikipedia.org/wiki/Duplex_sequencing
War Order No. 154 was issued during World War II at the end of November or the beginning of December 1939. It was the first explicit instruction by Nazi Germany's Kriegsmarine (navy) to use the tactics of unrestricted submarine warfare.
https://en.wikipedia.org/wiki/War_Order_No._154
https://en.wikipedia.org/wiki/Character_flaw
https://en.wikipedia.org/wiki/High-nutrient,_low-chlorophyll_regions
https://en.wikipedia.org/wiki/Murder_in_Russian_law
https://en.wikipedia.org/wiki/Error-tolerant_design
https://en.wikipedia.org/wiki/Exhaustion_doctrine_under_U.S._law
https://en.wikipedia.org/wiki/Against_the_Murderous,_Thieving_Hordes_of_Peasants
https://en.wikipedia.org/wiki/Attentional_blink
https://en.wikipedia.org/wiki/Holga
https://en.wikipedia.org/wiki/Thermal_imaging_camera
https://en.wikipedia.org/wiki/Fractal_analysis
https://en.wikipedia.org/wiki/Retroshare
https://en.wikipedia.org/wiki/Orbit_insertion
https://en.wikipedia.org/wiki/Mobile_workstation
https://en.wikipedia.org/wiki/Harvest:_Massive_Encounter
https://en.wikipedia.org/wiki/Perfluoroheptane
https://en.wikipedia.org/wiki/Size-exclusion_chromatography
https://en.wikipedia.org/wiki/Deep_learning_speech_synthesis
https://en.wikipedia.org/wiki/Novelty_(patent)
https://en.wikipedia.org/wiki/Optical_lens_design
https://en.wikipedia.org/wiki/Wildfire_Games
https://en.wikipedia.org/wiki/Extensions_of_Fisher%27s_method
https://en.wikipedia.org/wiki/Eupatridae
https://en.wikipedia.org/wiki/Tarsal_coalition
https://en.wikipedia.org/wiki/1977_Constitution_of_the_Soviet_Union
https://en.wikipedia.org/wiki/Respiratory_compensation
https://en.wikipedia.org/wiki/Skandia
https://en.wikipedia.org/wiki/Figure_painting
https://en.wikipedia.org/wiki/Nokia_M1122
https://en.wikipedia.org/wiki/Media_bias
https://en.wikipedia.org/wiki/Diffuser-augmented_wind_turbine
https://en.wikipedia.org/wiki/Valeriana_dioica
https://en.wikipedia.org/wiki/Special_Category_Visa
https://en.wikipedia.org/wiki/Petit_Le_Mans
https://en.wikipedia.org/wiki/Biocultural_anthropology
https://en.wikipedia.org/wiki/Red_Hand_of_Doom
https://en.wikipedia.org/wiki/Academic_grading_in_Denmark
https://en.wikipedia.org/wiki/Monetized_Installment_Sale
https://en.wikipedia.org/wiki/IEEE_1284
https://en.wikipedia.org/wiki/Statute_of_Frauds_Amendment_Act_1828
https://en.wikipedia.org/wiki/Cordon_sanitaire_(medicine)
https://en.wikipedia.org/wiki/Aqua_(satellite)
https://en.wikipedia.org/wiki/F._Matthias_Alexander
https://en.wikipedia.org/wiki/SAFARI-1
https://en.wikipedia.org/wiki/May_Swenson
https://en.wikipedia.org/wiki/386BSD
https://en.wikipedia.org/wiki/Ademption
https://en.wikipedia.org/wiki/Protein_nanoparticles
https://en.wikipedia.org/wiki/Control_banding#Limitations_of_Control_Banding
https://en.wikipedia.org/wiki/Oil_Pollution_Act_of_1973
https://en.wikipedia.org/wiki/Geological_compass
https://en.wikipedia.org/wiki/Novation_CAT
https://en.wikipedia.org/wiki/Rdiff-backup
https://en.wikipedia.org/wiki/Alienation_of_affections
https://en.wikipedia.org/wiki/Deep_Space_Habitat
https://en.wikipedia.org/wiki/Twin_registry
https://en.wikipedia.org/wiki/Optical_cross-connect
https://en.wikipedia.org/wiki/Personal_firewall
https://en.wikipedia.org/wiki/Power_Tab_Editor
https://en.wikipedia.org/wiki/Greatest_Fits
https://en.wikipedia.org/wiki/Erythropoiesis-stimulating_agent
https://en.wikipedia.org/wiki/Digital_piano
https://en.wikipedia.org/wiki/Odour_of_sanctity
https://en.wikipedia.org/wiki/Rotation_method
https://en.wikipedia.org/wiki/Clinostat
https://en.wikipedia.org/wiki/Attendant_circumstance
https://en.wikipedia.org/wiki/Treasury_Agreement
https://en.wikipedia.org/wiki/Packaged_metering_manhole
https://en.wikipedia.org/wiki/Restricted_shell
https://en.wikipedia.org/wiki/Emancipist
https://en.wikipedia.org/wiki/Phaeodactylum_tricornutum
https://en.wikipedia.org/wiki/Zoning
https://en.wikipedia.org/wiki/Fiber_roll
https://en.wikipedia.org/wiki/Probabilistic_semantics
https://en.wikipedia.org/wiki/Conformance_checking
https://en.wikipedia.org/wiki/SoundBridge
https://en.wikipedia.org/wiki/Reading_machine
https://en.wikipedia.org/wiki/Artificial_white_blood_cells#Limitations
https://en.wikipedia.org/wiki/Block_code
https://en.wikipedia.org/wiki/Vinyl_cutter
https://en.wikipedia.org/wiki/Correctness_(computer_science)
https://en.wikipedia.org/wiki/Species%E2%80%93area_relationship
https://en.wikipedia.org/wiki/Evidence-based_dentistry#Limitations_and_criticism
https://en.wikipedia.org/wiki/Data_drilling
https://en.wikipedia.org/wiki/Flash_synchronization
https://en.wikipedia.org/wiki/Retrocession_(kickback)
https://en.wikipedia.org/wiki/List_of_ISIRI_standards
https://en.wikipedia.org/wiki/Ilford_XP
https://en.wikipedia.org/wiki/Tamperproofing
https://en.wikipedia.org/wiki/Thermoluminescence_dating
https://en.wikipedia.org/wiki/Curtailment
https://en.wikipedia.org/wiki/Heterotopic_ossification
https://en.wikipedia.org/wiki/Worldwide_Governance_Indicators
https://en.wikipedia.org/wiki/Siberian_crane
https://en.wikipedia.org/wiki/Christmas_tree#Artificial_trees
https://en.wikipedia.org/wiki/Artificial_general_intelligence
https://en.wikipedia.org/wiki/Artificial_cranial_deformation
https://en.wikipedia.org/wiki/Artificial_stone
https://en.wikipedia.org/wiki/Artificial_rice
https://en.wikipedia.org/wiki/Artificial_sky
https://en.wikipedia.org/wiki/Bacterial_artificial_chromosome
https://en.wikipedia.org/wiki/Food_coloring
https://en.wikipedia.org/wiki/Artificial_Soldier
https://en.wikipedia.org/wiki/Artificial_crowd_noise
https://en.wikipedia.org/wiki/Sea_glass#Artificial
https://en.wikipedia.org/wiki/Cloning_vector
https://en.wikipedia.org/wiki/Winter_white_dwarf_hamster
https://en.wikipedia.org/wiki/White_box_(software_engineering)
https://en.wikipedia.org/wiki/List_of_artificial_radiation_belts
https://en.wikipedia.org/wiki/Artificial_hair_integrations
https://en.wikipedia.org/wiki/Misaligned_goals_in_artificial_intelligence
https://en.wikipedia.org/wiki/Artificial_urinary_sphincter
https://en.wikipedia.org/wiki/Human_hair_color#Gray_and_white_hair
https://en.wikipedia.org/wiki/Onyx
https://en.wikipedia.org/wiki/Largest_artificial_non-nuclear_explosions
https://en.wikipedia.org/wiki/Ruby#Synthesis_and_imitation
https://en.wikipedia.org/wiki/Ultramarine
https://en.wikipedia.org/wiki/Peach
https://en.wikipedia.org/wiki/Nitric_acid#Anhydrous_nitric_acid
https://en.wikipedia.org/wiki/Indian_prawn
https://en.wikipedia.org/wiki/Beluga_whale
https://en.wikipedia.org/wiki/Artificial_structures_visible_from_space
https://en.wikipedia.org/wiki/Synthetic_diamond
https://en.wikipedia.org/wiki/Nacre#Manufactured_nacre
https://en.wikipedia.org/wiki/Castling#Artificial_castling
https://en.wikipedia.org/wiki/Artificial_butter_flavoring
https://en.wikipedia.org/wiki/Horse_markings
https://en.wikipedia.org/wiki/Skyglow
https://en.wikipedia.org/wiki/White_and_Black_in_chess
https://en.wikipedia.org/wiki/Dentures
https://en.wikipedia.org/wiki/Northern_bobwhite
https://en.wikipedia.org/wiki/Hericium_erinaceus
https://en.wikipedia.org/wiki/N,N%27-Dicyclohexylcarbodiimide
https://en.wikipedia.org/wiki/Hip_replacement
https://en.wikipedia.org/wiki/Giant_panda
https://en.wikipedia.org/wiki/Ornithopter
https://en.wikipedia.org/wiki/Otter_Pops
https://en.wikipedia.org/wiki/Orbital_plane
https://en.wikipedia.org/wiki/Picea_glauca
https://en.wikipedia.org/wiki/Acesulfame_potassium
https://en.wikipedia.org/wiki/Monochrome_photography
https://en.wikipedia.org/wiki/Color_balance
https://en.wikipedia.org/wiki/Artificial_Intelligence_Cold_War
https://en.wikipedia.org/wiki/Computational_mathematics
https://en.wikipedia.org/wiki/Light_pollution
https://en.wikipedia.org/wiki/Parian_marble
https://en.wikipedia.org/wiki/Exo_Planet_3_%E2%80%93_The_Exo%27rdium
https://en.wikipedia.org/wiki/Quantum_dot
https://en.wikipedia.org/wiki/Snowmaking
https://en.wikipedia.org/wiki/Naphthalene
https://en.wikipedia.org/wiki/Day_for_night
https://en.wikipedia.org/wiki/OpenAI_Codex
https://en.wikipedia.org/wiki/Academa
https://en.wikipedia.org/wiki/Sodium_benzoate
https://en.wikipedia.org/wiki/Photographic_lighting
https://en.wikipedia.org/wiki/Lead_white
https://en.wikipedia.org/wiki/Deepfake
https://en.wikipedia.org/wiki/In_vitro_fertilisation
https://en.wikipedia.org/wiki/Supernormal_stimulus
https://en.wikipedia.org/wiki/Edible_mushroom
https://en.wikipedia.org/wiki/Albinism
https://en.wikipedia.org/wiki/Wonder_Bread
https://en.wikipedia.org/wiki/Tell_(archaeology)#Middle_East
https://en.wikipedia.org/wiki/Mrs._Davis
https://en.wikipedia.org/wiki/Embodied_cognition
https://en.wikipedia.org/wiki/Rice_paper
https://en.wikipedia.org/wiki/White-winged_chough
https://en.wikipedia.org/wiki/Do_not_feed_the_animals
https://en.wikipedia.org/wiki/Belgian_Blue
https://en.wikipedia.org/wiki/Batman:_Beyond_the_White_Knight
https://en.wikipedia.org/wiki/Megastructure
https://en.wikipedia.org/wiki/IBM
https://en.wikipedia.org/wiki/Broiler
https://en.wikipedia.org/wiki/White_Suffolk
https://en.wikipedia.org/wiki/Domestic_sheep_reproduction#Artificial_insemination_and_embryo_transfer
https://en.wikipedia.org/wiki/Self-replicating_machine
https://en.wikipedia.org/wiki/Bat#Artificial_roosts
https://en.wikipedia.org/wiki/List_of_St._Elsewhere_characters
https://en.wikipedia.org/wiki/Macrocephali
https://en.wikipedia.org/wiki/Rhinoceros#Artificial_substitute_for_rhinoceros_horn
https://en.wikipedia.org/wiki/Universal_approximation_theorem
https://en.wikipedia.org/wiki/Diet_drink#Amount_of_artificial_sweeteners_in_diet_soft_drinks
https://en.wikipedia.org/wiki/Australian_pelican
https://en.wikipedia.org/wiki/Carbon_sink
https://en.wikipedia.org/wiki/Blood_cell#White_blood_cells
https://en.wikipedia.org/wiki/All_Hallows_Lombard_Street
https://en.wikipedia.org/wiki/Laugh_track
https://en.wikipedia.org/wiki/Machine_ethics
https://en.wikipedia.org/wiki/Artificial_Sons_(film)
https://en.wikipedia.org/wiki/Chess_symbols_in_Unicode
https://en.wikipedia.org/wiki/Syslog
https://en.wikipedia.org/wiki/Night_sky
Category:Threshold temperatures Category Talk Read Edit View history Tools Help From Wikipedia, the free encyclopedia Wikimedia Commons has media related to Threshold temperatures. Category for critical temperatures of physical materials, at points of phase change. Pages in category "Threshold temperatures" The following 28 pages are in this category, out of 28 total. This list may not reflect recent changes. A Adiabatic flame temperature Autoignition temperature B Boiling point C Critical point (thermodynamics) Critical temperature D Dew point Doppler cooling limit Ductile-brittle transition temperature E Eutectic Eutectoid F Flash point Freezing point G Glass transition H Hagedorn temperature Heat deflection temperature Hydrocarbon dew point L Lambda point Liquidus M Melting point Minimum design metal temperature O Operating temperature Orders of magnitude (temperature) P Pour point R Relative thermal index S Slip melting point Solidus (chemistry) T Transition temperature Triple point Categories: Phase transitionsState functionsTemperature Hidden category: Commons category link from Wikidata https://en.wikipedia.org/wiki/Category:Threshold_temperatures The lambda point is the temperature at which normal fluid helium (helium I) makes the transition to superfluid helium II (approximately 2.17 K at 1 atmosphere). The lowest pressure at which He-I and He-II can coexist is the vapor−He-I−He-II triple point at 2.1768 K (−270.9732 °C) and 5.0418 kPa (0.049759 atm), which is the "saturated vapor pressure" at that temperature (pure helium gas in thermal equilibrium over the liquid surface, in a hermetic container).[1] The highest pressure at which He-I and He-II can coexist is the bcc−He-I−He-II triple point with a helium solid at 1.762 K (−271.388 °C), 29.725 atm (3,011.9 kPa).[2] The point's name derives from the graph (pictured) that results from plotting the specific heat capacity as a function of temperature (for a given pressure in the above range, in the example shown, at 1 atmosphere), which resembles the Greek letter lambda λ \lambda . The specific heat capacity has a sharp peak as the temperature approaches the lambda point. The tip of the peak is so sharp that a critical exponent characterizing the divergence of the heat capacity can be measured precisely only in zero gravity, to provide a uniform density over a substantial volume of fluid. Hence the heat capacity was measured within 2 nK below the transition in an experiment included in a Space Shuttle payload in 1992.[3] Unsolved problem in physics: Explain the discrepancy between the experimental and theoretical determinations of the heat capacity critical exponent α for the superfluid transition in helium-4.[4] (more unsolved problems in physics) Although the heat capacity has a peak, it does not tend towards infinity (contrary to what the graph may suggest), but has finite limiting values when approaching the transition from above and below.[3] The behavior of the heat capacity near the peak is described by the formula C ≈ A ± t − α + B ± {\displaystyle C\approx A_{\pm }t^{-\alpha }+B_{\pm }} where t = | 1 − T / T c | {\displaystyle t=|1-T/T_{c}|} is the reduced temperature, T c T_{c} is the Lambda point temperature, A ± , B ± {\displaystyle A_{\pm },B_{\pm }} are constants (different above and below the transition temperature), and α is the critical exponent: α = − 0.0127 ( 3 ) {\displaystyle \alpha =-0.0127(3)}.[3][5] Since this exponent is negative for the superfluid transition, specific heat remains finite.[6] The quoted experimental value of α is in a significant disagreement[7][4] with the most precise theoretical determinations[8][9][10] coming from high temperature expansion techniques, Monte Carlo methods and the conformal bootstrap. See also Lambda point refrigerator References Donnelly, Russell J.; Barenghi, Carlo F. (1998). "The Observed Properties of Liquid Helium at the Saturated Vapor Pressure". Journal of Physical and Chemical Reference Data. 27 (6): 1217–1274. Bibcode:1998JPCRD..27.1217D. doi:10.1063/1.556028. Hoffer, J. K.; Gardner, W. R.; Waterfield, C. G.; Phillips, N. E. (April 1976). "Thermodynamic properties of 4He. II. The bcc phase and the P-T and VT phase diagrams below 2 K". Journal of Low Temperature Physics. 23 (1): 63–102. Bibcode:1976JLTP...23...63H. doi:10.1007/BF00117245. S2CID 120473493. Lipa, J.A.; Swanson, D. R.; Nissen, J. A.; Chui, T. C. P.; Israelsson, U. E. (1996). "Heat Capacity and Thermal Relaxation of Bulk Helium very near the Lambda Point". Physical Review Letters. 76 (6): 944–7. Bibcode:1996PhRvL..76..944L. doi:10.1103/PhysRevLett.76.944. hdl:2060/19950007794. PMID 10061591. S2CID 29876364. Rychkov, Slava (2020-01-31). "Conformal bootstrap and the λ-point specific heat experimental anomaly". Journal Club for Condensed Matter Physics. doi:10.36471/JCCM_January_2020_02. Lipa, J. A.; Nissen, J. A.; Stricker, D. A.; Swanson, D. R.; Chui, T. C. P. (2003-11-14). "Specific heat of liquid helium in zero gravity very near the lambda point". Physical Review B. 68 (17): 174518. arXiv:cond-mat/0310163. Bibcode:2003PhRvB..68q4518L. doi:10.1103/PhysRevB.68.174518. S2CID 55646571. For other phase transitions α \alpha may be negative (e.g. α ≈ + 0.1 {\displaystyle \alpha \approx +0.1} for the liquid-vapor critical point which has Ising critical exponents). For those phase transitions specific heat does tend to infinity. Vicari, Ettore (2008-03-21). "Critical phenomena and renormalization-group flow of multi-parameter Phi4 theories". Proceedings of the XXV International Symposium on Lattice Field Theory — PoS(LATTICE 2007). Regensburg, Germany: Sissa Medialab. 42: 023. doi:10.22323/1.042.0023. Campostrini, Massimo; Hasenbusch, Martin; Pelissetto, Andrea; Vicari, Ettore (2006-10-06). "Theoretical estimates of the critical exponents of the superfluid transition in $^{4}\mathrm{He}$ by lattice methods". Physical Review B. 74 (14): 144506. arXiv:cond-mat/0605083. doi:10.1103/PhysRevB.74.144506. S2CID 118924734. Hasenbusch, Martin (2019-12-26). "Monte Carlo study of an improved clock model in three dimensions". Physical Review B. 100 (22): 224517. arXiv:1910.05916. Bibcode:2019PhRvB.100v4517H. doi:10.1103/PhysRevB.100.224517. ISSN 2469-9950. S2CID 204509042. Chester, Shai M.; Landry, Walter; Liu, Junyu; Poland, David; Simmons-Duffin, David; Su, Ning; Vichi, Alessandro (2020). "Carving out OPE space and precise O(2) model critical exponents". Journal of High Energy Physics. 2020 (6): 142. arXiv:1912.03324. Bibcode:2020JHEP...06..142C. doi:10.1007/JHEP06(2020)142. S2CID 208910721. External links What is superfluidity? vte States of matter (list) State Solid Liquid Gas / Vapor Plasma Phase change - en.svg Low energy Bose–Einstein condensate Fermionic condensate Degenerate matter Quantum Hall Rydberg matter Rydberg polaron Strange matter Superfluid Supersolid Photonic molecule High energy QCD matter Lattice QCD Quark–gluon plasma Color-glass condensate Supercritical fluid Other states Colloid Glass Crystal Liquid crystal Time crystal Quantum spin liquid Exotic matter Programmable matter Dark matter Antimatter Magnetically ordered Antiferromagnet Ferrimagnet Ferromagnet String-net liquid Superglass Transitions Boiling Boiling point Condensation Critical line Critical point Crystallization Deposition Evaporation Flash evaporation Freezing Chemical ionization Ionization Lambda point Melting Melting point Recombination Regelation Saturated fluid Sublimation Supercooling Triple point Vaporization Vitrification Quantities Enthalpy of fusion Enthalpy of sublimation Enthalpy of vaporization Latent heat Latent internal energy Trouton's rule Volatility Concepts Baryonic matter Binodal Compressed fluid Cooling curve Equation of state Leidenfrost effect Macroscopic quantum phenomena Mpemba effect Order and disorder (physics) Spinodal Superconductivity Superheated vapor Superheating Thermo-dielectric effect Categories: Threshold temperaturesSuperfluidity https://en.wikipedia.org/wiki/Lambda_point From Wikipedia, the free encyclopedia Beyond the Standard Model CMS Higgs-event.jpg Simulated Large Hadron Collider CMS particle detector data depicting a Higgs boson produced by colliding protons decaying into hadron jets and electrons Standard Model Evidence Theories Supersymmetry Quantum gravity Experiments vte In condensed matter physics, a string-net is an extended object whose collective behavior has been proposed as a physical mechanism for topological order by Michael A. Levin and Xiao-Gang Wen. A particular string-net model may involve only closed loops; or networks of oriented, labeled strings obeying branching rules given by some gauge group; or still more general networks.[1] Overview The string-net model is claimed to show the derivation of photons, electrons, and U(1) gauge charge, small (relative to the Planck mass) but nonzero masses, and suggestions that the leptons, quarks, and gluons can be modeled in the same way. In other words, string-net condensation provides a unified origin for photons and electrons (or gauge bosons and fermions). It can be viewed as an origin of light and electron (or gauge interactions and Fermi statistics). However, their model does not account for the chiral coupling between the fermions and the SU(2) gauge bosons in the standard model. For strings labeled by the positive integers, string-nets are the spin networks studied in loop quantum gravity. This has led to the proposal by Levin and Wen,[2] and Smolin, Markopoulou and Konopka[3] that loop quantum gravity's spin networks can give rise to the standard model of particle physics through this mechanism, along with fermi statistics and gauge interactions. To date, a rigorous derivation from LQG's spin networks to Levin and Wen's spin lattice has yet to be done, but the project to do so is called quantum graphity, and in a more recent paper, Tomasz Konopka, Fotini Markopoulou, Simone Severini argued that there are some similarities to spin networks (but not necessarily an exact equivalence) that gives rise to U(1) gauge charge and electrons in the string net mechanism.[4] Herbertsmithite may be an example of string-net matter.[5][6] Examples Z2 spin liquid Z2 spin liquid obtained using slave-particle approach may be the first theoretical example of string-net liquid.[7][8] The toric code The toric code is a two-dimensional spin-lattice that acts as a quantum error-correcting code. It is defined on a two-dimensional lattice with toric boundary conditions with a spin-1/2 on each link. It can be shown that the ground-state of the standard toric code Hamiltonian is an equal-weight superposition of closed-string states.[9] Such a ground-state is an example of a string-net condensate[10] which has the same topological order as the Z2 spin liquid above. References Levin, Michael A. & Xiao-Gang Wen (12 January 2005). "String-net condensation: A physical mechanism for topological phases". Physical Review B. 71 (45110): 21. arXiv:cond-mat/0404617. Bibcode:2005PhRvB..71d5110L. doi:10.1103/PhysRevB.71.045110. S2CID 51962817. Levin, Michael; Wen, Xiao-Gang (2005). "Photons and electrons as emergent phenomena". Rev. Mod. Phys. 77: 871–879 [878]. arXiv:cond-mat/0407140. Bibcode:2005RvMP...77..871L. doi:10.1103/RevModPhys.77.871. S2CID 117563047. "loop quantum gravity appears to be a string net condensation ..." Konopka, Tomasz; Markopoulou, Fotini; Smolin, Lee (2006). "Quantum Graphity". arXiv:hep-th/0611197. "We argue (but do not prove) that under certain conditions the spins in the system can arrange themselves in regular, lattice-like patterns at low temperatures." Konopka, Tomasz; Markopoulou, Fotini; Severini, Simone (May 2008). "Quantum graphity: A model of emergent locality". Phys. Rev. D. 77 (10): 19. arXiv:0801.0861. Bibcode:2008PhRvD..77j4029K. doi:10.1103/PhysRevD.77.104029. S2CID 6959359. "The characterization of the string-condensed ground state is difficult but its excitations are expected to be that of a U(1) gauge theory, ... The two main differences between this model and the original string-net condensation model proposed by Levin and Wen are that in the present case the background lattice is dynamical and has hexagonal rather than square plaquettes." Bowles, Claire. "Have researchers found a new state of matter?". Eureka Alert. Retrieved 29 January 2012. Merali, Zeeya (2007-03-17). "The universe is a string-net liquid". New Scientist. 193 (2595): 8–9. doi:10.1016/s0262-4079(07)60640-x. Retrieved 29 January 2012. Read, N.; Sachdev, Subir (1 March 1991). "Large-Nexpansion for frustrated quantum antiferromagnets". Physical Review Letters. American Physical Society (APS). 66 (13): 1773–1776. Bibcode:1991PhRvL..66.1773R. doi:10.1103/physrevlett.66.1773. ISSN 0031-9007. PMID 10043303. Xiao-Gang Wen, Mean Field Theory of Spin Liquid States with Finite Energy Gaps and Topological Orders, Phys. Rev. B44, 2664 (1991). Kitaev, Alexei, Y.; Chris Laumann (2009). "Topological phases and quantum computation". arXiv:0904.2771 [cond-mat.mes-hall]. Morimae, Tomoyuki (2012). "Quantum computational tensor network on string-net condensate". Physical Review A. 85 (6): 062328. arXiv:1012.1000. Bibcode:2012PhRvA..85f2328M. doi:10.1103/PhysRevA.85.062328. S2CID 118522495. vte States of matter (list) Categories: Quantum phasesCondensed matter physicsChemical engineeringPhases of matter https://en.wikipedia.org/wiki/String-net_liquid States of matter (list) State Solid Liquid Gas / Vapor Plasma Phase change - en.svg Low energy Bose–Einstein condensate Fermionic condensate Degenerate matter Quantum Hall Rydberg matter Rydberg polaron Strange matter Superfluid Supersolid Photonic molecule High energy QCD matter Lattice QCD Quark–gluon plasma Color-glass condensate Supercritical fluid Other states Colloid Glass Crystal Liquid crystal Time crystal Quantum spin liquid Exotic matter Programmable matter Dark matter Antimatter Magnetically ordered Antiferromagnet Ferrimagnet Ferromagnet String-net liquid Superglass Transitions Boiling Boiling point Condensation Critical line Critical point Crystallization Deposition Evaporation Flash evaporation Freezing Chemical ionization Ionization Lambda point Melting Melting point Recombination Regelation Saturated fluid Sublimation Supercooling Triple point Vaporization Vitrification Quantities Enthalpy of fusion Enthalpy of sublimation Enthalpy of vaporization Latent heat Latent internal energy Trouton's rule Volatility Concepts Baryonic matter Binodal Compressed fluid Cooling curve Equation of state Leidenfrost effect Macroscopic quantum phenomena Mpemba effect Order and disorder (physics) Spinodal Superconductivity Superheated vapor Superheating Thermo-dielectric effect Categories: Threshold temperaturesSuperfluidity https://en.wikipedia.org/wiki/Lambda_point The glass–liquid transition, or glass transition, is the gradual and reversible transition in amorphous materials (or in amorphous regions within semicrystalline materials) from a hard and relatively brittle "glassy" state into a viscous or rubbery state as the temperature is increased.[1][2] An amorphous solid that exhibits a glass transition is called a glass. The reverse transition, achieved by supercooling a viscous liquid into the glass state, is called vitrification. The glass-transition temperature Tg of a material characterizes the range of temperatures over which this glass transition occurs (as an experimental definition, typically marked as 100 s of relaxation time). It is always lower than the melting temperature, Tm, of the crystalline state of the material, if one exists. Hard plastics like polystyrene and poly(methyl methacrylate) are used well below their glass transition temperatures, i.e., when they are in their glassy state. Their Tg values are both at around 100 °C (212 °F). Rubber elastomers like polyisoprene and polyisobutylene are used above their Tg, that is, in the rubbery state, where they are soft and flexible; crosslinking prevents free flow of their molecules, thus endowing rubber with a set shape at room temperature (as opposed to a viscous liquid).[3] Despite the change in the physical properties of a material through its glass transition, the transition is not considered a phase transition; rather it is a phenomenon extending over a range of temperature and defined by one of several conventions.[2][4][5] Such conventions include a constant cooling rate (20 kelvins per minute (36 °F/min))[1] and a viscosity threshold of 1012 Pa·s, among others. Upon cooling or heating through this glass-transition range, the material also exhibits a smooth step in the thermal-expansion coefficient and in the specific heat, with the location of these effects again being dependent on the history of the material.[6] The question of whether some phase transition underlies the glass transition is a matter of ongoing research.[4][5][7][when?] IUPAC definition Glass transition (in polymer science): process in which a polymer melt changes on cooling to a polymer glass or a polymer glass changes on heating to a polymer melt.[8] Phenomena occurring at the glass transition of polymers are still subject to ongoing scientific investigation and debate. The glass transition presents features of a second-order transition since thermal studies often indicate that the molar Gibbs energies, molar enthalpies, and the molar volumes of the two phases, i.e., the melt and the glass, are equal, while the heat capacity and the expansivity are discontinuous. However, the glass transition is generally not regarded as a thermodynamic transition in view of the inherent difficulty in reaching equilibrium in a polymer glass or in a polymer melt at temperatures close to the glass-transition temperature. In the case of polymers, conformational changes of segments, typically consisting of 10–20 main-chain atoms, become infinitely slow below the glass transition temperature. In a partially crystalline polymer the glass transition occurs only in the amorphous parts of the material. The definition is different from that in ref.[9] The commonly used term “glass-rubber transition” for glass transition is not recommended.[8] Introduction The glass transition of a liquid to a solid-like state may occur with either cooling or compression.[10] The transition comprises a smooth increase in the viscosity of a material by as much as 17 orders of magnitude within a temperature range of 500 K without any pronounced change in material structure.[2][11] The consequence of this dramatic increase is a glass exhibiting solid-like mechanical properties on the timescale of practical observation.[clarification needed] This transition is in contrast to the freezing or crystallization transition, which is a first-order phase transition in the Ehrenfest classification and involves discontinuities in thermodynamic and dynamic properties such as volume, energy, and viscosity. In many materials that normally undergo a freezing transition, rapid cooling will avoid this phase transition and instead result in a glass transition at some lower temperature. Other materials, such as many polymers, lack a well defined crystalline state and easily form glasses, even upon very slow cooling or compression. The tendency for a material to form a glass while quenched is called glass forming ability. This ability depends on the composition of the material and can be predicted by the rigidity theory.[12] Below the transition temperature range, the glassy structure does not relax in accordance with the cooling rate used. The expansion coefficient for the glassy state is roughly equivalent to that of the crystalline solid. If slower cooling rates are used, the increased time for structural relaxation (or intermolecular rearrangement) to occur may result in a higher density glass product. Similarly, by annealing (and thus allowing for slow structural relaxation) the glass structure in time approaches an equilibrium density corresponding to the supercooled liquid at this same temperature. Tg is located at the intersection between the cooling curve (volume versus temperature) for the glassy state and the supercooled liquid.[2][13][14][15][16][17] The configuration of the glass in this temperature range changes slowly with time towards the equilibrium structure.[18] The principle of the minimization of the Gibbs free energy provides the thermodynamic driving force necessary for the eventual change. At somewhat higher temperatures than Tg, the structure corresponding to equilibrium at any temperature is achieved quite rapidly. In contrast, at considerably lower temperatures, the configuration of the glass remains sensibly stable over increasingly extended periods of time. Thus, the liquid-glass transition is not a transition between states of thermodynamic equilibrium. It is widely believed that the true equilibrium state is always crystalline. Glass is believed to exist in a kinetically locked state, and its entropy, density, and so on, depend on the thermal history. Therefore, the glass transition is primarily a dynamic phenomenon. Time and temperature are interchangeable quantities (to some extent) when dealing with glasses, a fact often expressed in the time–temperature superposition principle. On cooling a liquid, internal degrees of freedom successively fall out of equilibrium. However, there is a longstanding debate whether there is an underlying second-order phase transition in the hypothetical limit of infinitely long relaxation times.[clarification needed][6][19][20][21] In a more recent model of glass transition, the glass transition temperature corresponds to the temperature at which the largest openings between the vibrating elements in the liquid matrix become smaller than the smallest cross-sections of the elements or parts of them when the temperature is decreasing. As a result of the fluctuating input of thermal energy into the liquid matrix, the harmonics of the oscillations are constantly disturbed and temporary cavities ("free volume") are created between the elements, the number and size of which depend on the temperature. The glass transition temperature Tg0 defined in this way is a fixed material constant of the disordered (non-crystalline) state that is dependent only on the pressure. As a result of the increasing inertia of the molecular matrix when approaching Tg0, the setting of the thermal equilibrium is successively delayed, so that the usual measuring methods for determining the glass transition temperature in principle deliver Tg values that are too high. In principle, the slower the temperature change rate is set during the measurement, the closer the measured Tg value Tg0 approaches.[22] Techniques such as dynamic mechanical analysis can be used to measure the glass transition temperature.[23] Transition temperature Tg This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (July 2009) (Learn how and when to remove this template message) Determination of Tg by dilatometry. Measurement of Tg (the temperature at the point A) by differential scanning calorimetry Refer to the figure on the bottom right plotting the heat capacity as a function of temperature. In this context, Tg is the temperature corresponding to point A on the curve.[24] Different operational definitions of the glass transition temperature Tg are in use, and several of them are endorsed as accepted scientific standards. Nevertheless, all definitions are arbitrary, and all yield different numeric results: at best, values of Tg for a given substance agree within a few kelvins. One definition refers to the viscosity, fixing Tg at a value of 1013 poise (or 1012 Pa·s). As evidenced experimentally, this value is close to the annealing point of many glasses.[25] In contrast to viscosity, the thermal expansion, heat capacity, shear modulus, and many other properties of inorganic glasses show a relatively sudden change at the glass transition temperature. Any such step or kink can be used to define Tg. To make this definition reproducible, the cooling or heating rate must be specified. The most frequently used definition of Tg uses the energy release on heating in differential scanning calorimetry (DSC, see figure). Typically, the sample is first cooled with 10 K/min and then heated with that same speed. Yet another definition of Tg uses the kink in dilatometry (a.k.a. thermal expansion): refer to the figure on the top right. Here, heating rates of 3–5 K/min (5.4–9.0 °F/min) are common. The linear sections below and above Tg are colored green. Tg is the temperature at the intersection of the red regression lines.[24] Summarized below are Tg values characteristic of certain classes of materials. Polymers Material Tg (°C) Tg (°F) Commercial name Tire rubber −70 −94[26] Polyvinylidene fluoride (PVDF) −35 −31[27] Polypropylene (PP atactic) −20 −4[28] Polyvinyl fluoride (PVF) −20 −4[27] Polypropylene (PP isotactic) 0 32[28] Poly-3-hydroxybutyrate (PHB) 15 59[28] Poly(vinyl acetate) (PVAc) 30 86[28] Polychlorotrifluoroethylene (PCTFE) 45 113[27] Polyamide (PA) 47–60 117–140 Nylon-6,x Polylactic acid (PLA) 60–65 140–149 Polyethylene terephthalate (PET) 70 158[28] Poly(vinyl chloride) (PVC) 80 176[28] Poly(vinyl alcohol) (PVA) 85 185[28] Polystyrene (PS) 95 203[28] Poly(methyl methacrylate) (PMMA atactic) 105 221[28] Plexiglas, Perspex Acrylonitrile butadiene styrene (ABS) 105 221[29] Polytetrafluoroethylene (PTFE) 115 239[30] Teflon Poly(carbonate) (PC) 145 293[28] Lexan Polysulfone 185 365 Polynorbornene 215 419[28] Dry nylon-6 has a glass transition temperature of 47 °C (117 °F).[31] Nylon-6,6 in the dry state has a glass transition temperature of about 70 °C (158 °F).[32][33] Whereas polyethene has a glass transition range of −130 to −80 °C (−202 to −112 °F)[34] The above are only mean values, as the glass transition temperature depends on the cooling rate and molecular weight distribution and could be influenced by additives. For a semi-crystalline material, such as polyethene that is 60–80% crystalline at room temperature, the quoted glass transition refers to what happens to the amorphous part of the material upon cooling. Silicates and other covalent network glasses Material Tg (°C) Tg (°F) Chalcogenide GeSbTe 150 302[35] Chalcogenide AsGeSeTe 245 473 ZBLAN fluoride glass 235 455 Tellurium dioxide 280 536 Fluoroaluminate 400 752 Soda-lime glass 520–600 968–1,112 Fused quartz (approximate) 1,200 2,200[36] Kauzmann's paradox Entropy difference between crystal and undercooled melt As a liquid is supercooled, the difference in entropy between the liquid and solid phase decreases. By extrapolating the heat capacity of the supercooled liquid below its glass transition temperature, it is possible to calculate the temperature at which the difference in entropies becomes zero. This temperature has been named the Kauzmann temperature.[2] If a liquid could be supercooled below its Kauzmann temperature, and it did indeed display a lower entropy than the crystal phase, the consequences would be paradoxical. This Kauzmann paradox has been the subject of much debate and many publications since it was first put forward by Walter Kauzmann in 1948.[37][38] One resolution of the Kauzmann paradox is to say that there must be a phase transition before the entropy of the liquid decreases. In this scenario, the transition temperature is known as the calorimetric ideal glass transition temperature T0c. In this view, the glass transition is not merely a kinetic effect, i.e. merely the result of fast cooling of a melt, but there is an underlying thermodynamic basis for glass formation. The glass transition temperature: T g → T 0 c as d T d t → 0. T_{g}\to T_{{0c}}{\text{ as }}{\frac {dT}{dt}}\to 0. The Gibbs–DiMarzio model from 1958[39] specifically predicts that a supercooled liquid's configurational entropy disappears in the limit T → T K + {\displaystyle T\to T_{K}^{+}}, where the liquid's existence regime ends, its microstructure becomes identical to the crystal's, and their property curves intersect in a true second-order phase transition. This has never been experimentally verified due to the difficulty of realizing a slow enough cooling rate while avoiding accidental crystallization. The Adam–Gibbs model from 1965[40] suggested a resolution of the Kauzmann paradox according to which the relaxation time diverges at the Kauzmann temperature, implying that one can never equilibrate the metastable supercooled liquid here. A critical discussion of the Kauzmann paradox and the Adam–Gibbs model was given in 2009.[41] Data on several supercooled organic liquids do not confirm the Adam–Gibbs prediction of a diverging relaxation time at any finite temperature, e.g. the Kauzmann temperature.[42] Alternative resolutions There are at least three other possible resolutions to the Kauzmann paradox. It could be that the heat capacity of the supercooled liquid near the Kauzmann temperature smoothly decreases to a smaller value. It could also be that a first order phase transition to another liquid state occurs before the Kauzmann temperature with the heat capacity of this new state being less than that obtained by extrapolation from higher temperature. Finally, Kauzmann himself resolved the entropy paradox by postulating that all supercooled liquids must crystallize before the Kauzmann temperature is reached. In specific materials Silica, SiO2 Silica (the chemical compound SiO2) has a number of distinct crystalline forms in addition to the quartz structure. Nearly all of the crystalline forms involve tetrahedral SiO4 units linked together by shared vertices in different arrangements (stishovite, composed of linked SiO6 octahedra, is the main exception). Si-O bond lengths vary between the different crystal forms. For example, in α-quartz the bond length is 161 picometres (6.3×10−9 in), whereas in α-tridymite it ranges from 154–171 pm (6.1×10−9–6.7×10−9 in). The Si-O-Si bond angle also varies from 140° in α-tridymite to 144° in α-quartz to 180° in β-tridymite. Any deviations from these standard parameters constitute microstructural differences or variations that represent an approach to an amorphous, vitreous or glassy solid. The transition temperature Tg in silicates is related to the energy required to break and re-form covalent bonds in an amorphous (or random network) lattice of covalent bonds. The Tg is clearly influenced by the chemistry of the glass. For example, addition of elements such as B, Na, K or Ca to a silica glass, which have a valency less than 4, helps in breaking up the network structure, thus reducing the Tg. Alternatively, P, which has a valency of 5, helps to reinforce an ordered lattice, and thus increases the Tg.[43] Tg is directly proportional to bond strength, e.g. it depends on quasi-equilibrium thermodynamic parameters of the bonds e.g. on the enthalpy Hd and entropy Sd of configurons – broken bonds: Tg = Hd / [Sd + R ln[(1 − fc)/ fc] where R is the gas constant and fc is the percolation threshold. For strong melts such as SiO2 the percolation threshold in the above equation is the universal Scher–Zallen critical density in the 3-D space e.g. fc = 0.15, however for fragile materials the percolation thresholds are material-dependent and fc ≪ 1.[44] The enthalpy Hd and the entropy Sd of configurons – broken bonds can be found from available experimental data on viscosity.[45] Polymers In polymers the glass transition temperature, Tg, is often expressed as the temperature at which the Gibbs free energy is such that the activation energy for the cooperative movement of 50 or so elements of the polymer is exceeded[citation needed]. This allows molecular chains to slide past each other when a force is applied. From this definition, we can see that the introduction of relatively stiff chemical groups (such as benzene rings) will interfere with the flowing process and hence increase Tg.[46] The stiffness of thermoplastics decreases due to this effect (see figure.) When the glass temperature has been reached, the stiffness stays the same for a while, i.e., at or near E2, until the temperature exceeds Tm, and the material melts. This region is called the rubber plateau. In ironing, a fabric is heated through the glass-rubber transition. Coming from the low-temperature side, the shear modulus drops by many orders of magnitude at the glass transition temperature Tg. A molecular-level mathematical relation for the temperature-dependent shear modulus of the polymer glass on approaching Tg from below has been developed by Alessio Zaccone and Eugene Terentjev.[47] Even though the shear modulus does not really drop to zero (it drops down to the much lower value of the rubber plateau), upon setting the shear modulus to zero in the Zaccone–Terentjev formula, an expression for Tg is obtained which recovers the Flory–Fox equation, and also shows that Tg is inversely proportional to the thermal expansion coefficient in the glass state. This procedure provides yet another operational protocol to define the Tg of polymer glasses by identifying it with the temperature at which the shear modulus drops by many orders of magnitude down to the rubbery plateau. In ironing, a fabric is heated through this transition so that the polymer chains become mobile. The weight of the iron then imposes a preferred orientation. Tg can be significantly decreased by addition of plasticizers into the polymer matrix. Smaller molecules of plasticizer embed themselves between the polymer chains, increasing the spacing and free volume, and allowing them to move past one another even at lower temperatures. Addition of plasticizer can effectively take control over polymer chain dynamics and dominate the amounts of the associated free volume so that the increased mobility of polymer ends is not apparent.[48] The addition of nonreactive side groups to a polymer can also make the chains stand off from one another, reducing Tg. If a plastic with some desirable properties has a Tg that is too high, it can sometimes be combined with another in a copolymer or composite material with a Tg below the temperature of intended use. Note that some plastics are used at high temperatures, e.g., in automobile engines, and others at low temperatures.[28] Stiffness versus temperature In viscoelastic materials, the presence of liquid-like behavior depends on the properties of and so varies with rate of applied load, i.e., how quickly a force is applied. The silicone toy Silly Putty behaves quite differently depending on the time rate of applying a force: pull slowly and it flows, acting as a heavily viscous liquid; hit it with a hammer and it shatters, acting as a glass. On cooling, rubber undergoes a liquid-glass transition, which has also been called a rubber-glass transition. Mechanics of vitrification Main article: Vitrification Molecular motion in condensed matter can be represented by a Fourier series whose physical interpretation consists of a superposition of longitudinal and transverse waves of atomic displacement with varying directions and wavelengths. In monatomic systems, these waves are called density fluctuations. (In polyatomic systems, they may also include compositional fluctuations.)[49] Thus, thermal motion in liquids can be decomposed into elementary longitudinal vibrations (or acoustic phonons) while transverse vibrations (or shear waves) were originally described only in elastic solids exhibiting the highly ordered crystalline state of matter. In other words, simple liquids cannot support an applied force in the form of a shearing stress, and will yield mechanically via macroscopic plastic deformation (or viscous flow). Furthermore, the fact that a solid deforms locally while retaining its rigidity – while a liquid yields to macroscopic viscous flow in response to the application of an applied shearing force – is accepted by many as the mechanical distinction between the two.[50][51] The inadequacies of this conclusion, however, were pointed out by Frenkel in his revision of the kinetic theory of solids and the theory of elasticity in liquids. This revision follows directly from the continuous characteristic of the viscoelastic crossover from the liquid state into the solid one when the transition is not accompanied by crystallization—ergo the supercooled viscous liquid. Thus we see the intimate correlation between transverse acoustic phonons (or shear waves) and the onset of rigidity upon vitrification, as described by Bartenev in his mechanical description of the vitrification process.[52][53] This concept leads to defining the glass transition in terms of the vanishing or significant lowering of the low-frequency shear modulus, as shown quantitatively in the work of Zaccone and Terentjev[47] on the example of polymer glass. In fact, the shoving model stipulates that the activation energy of the relaxation time is proportional to the high-frequency plateau shear modulus,[2][54] a quantity that increases upon cooling thus explaining the ubiquitous non-Arrhenius temperature dependence of the relaxation time in glass-forming liquids. The velocities of longitudinal acoustic phonons in condensed matter are directly responsible for the thermal conductivity that levels out temperature differentials between compressed and expanded volume elements. Kittel proposed that the behavior of glasses is interpreted in terms of an approximately constant "mean free path" for lattice phonons, and that the value of the mean free path is of the order of magnitude of the scale of disorder in the molecular structure of a liquid or solid. The thermal phonon mean free paths or relaxation lengths of a number of glass formers have been plotted versus the glass transition temperature, indicating a linear relationship between the two. This has suggested a new criterion for glass formation based on the value of the phonon mean free path.[55] It has often been suggested that heat transport in dielectric solids occurs through elastic vibrations of the lattice, and that this transport is limited by elastic scattering of acoustic phonons by lattice defects (e.g. randomly spaced vacancies).[56] These predictions were confirmed by experiments on commercial glasses and glass ceramics, where mean free paths were apparently limited by "internal boundary scattering" to length scales of 10–100 micrometres (0.00039–0.00394 in).[57][58] The relationship between these transverse waves and the mechanism of vitrification has been described by several authors who proposed that the onset of correlations between such phonons results in an orientational ordering or "freezing" of local shear stresses in glass-forming liquids, thus yielding the glass transition.[59] Electronic structure The influence of thermal phonons and their interaction with electronic structure is a topic that was appropriately introduced in a discussion of the resistance of liquid metals. Lindemann's theory of melting is referenced,[60] and it is suggested that the drop in conductivity in going from the crystalline to the liquid state is due to the increased scattering of conduction electrons as a result of the increased amplitude of atomic vibration. Such theories of localization have been applied to transport in metallic glasses, where the mean free path of the electrons is very small (on the order of the interatomic spacing).[61][62] The formation of a non-crystalline form of a gold-silicon alloy by the method of splat quenching from the melt led to further considerations of the influence of electronic structure on glass forming ability, based on the properties of the metallic bond.[63][64][65][66][67] Other work indicates that the mobility of localized electrons is enhanced by the presence of dynamic phonon modes. One claim against such a model is that if chemical bonds are important, the nearly free electron models should not be applicable. However, if the model includes the buildup of a charge distribution between all pairs of atoms just like a chemical bond (e.g., silicon, when a band is just filled with electrons) then it should apply to solids.[68] Thus, if the electrical conductivity is low, the mean free path of the electrons is very short. The electrons will only be sensitive to the short-range order in the glass since they do not get a chance to scatter from atoms spaced at large distances. Since the short-range order is similar in glasses and crystals, the electronic energies should be similar in these two states. For alloys with lower resistivity and longer electronic mean free paths, the electrons could begin to sense[dubious – discuss] that there is disorder in the glass, and this would raise their energies and destabilize the glass with respect to crystallization. Thus, the glass formation tendencies of certain alloys may therefore be due in part to the fact that the electron mean free paths are very short, so that only the short-range order is ever important for the energy of the electrons. It has also been argued that glass formation in metallic systems is related to the "softness" of the interaction potential between unlike atoms. Some authors, emphasizing the strong similarities between the local structure of the glass and the corresponding crystal, suggest that chemical bonding helps to stabilize the amorphous structure.[69][70] Other authors have suggested that the electronic structure yields its influence on glass formation through the directional properties of bonds. Non-crystallinity is thus favored in elements with a large number of polymorphic forms and a high degree of bonding anisotropy. Crystallization becomes more unlikely as bonding anisotropy is increased from isotropic metallic to anisotropic metallic to covalent bonding, thus suggesting a relationship between the group number in the periodic table and the glass forming ability in elemental solids.[71] Testing for glass transition. Temperatures may have to be tested such as glass quartz around 2000 degrees Fahrenheit as shown above. Glass structure can be determined using infrared and Raman spectroscopy. IR rays are good mostly for silicate glasses and helps find water impurities. IR limited penetration to 1 to 25 micrometers. Electron microscopes and transmission electron microscopes can see structures to around 5 to 10 nanometers, however sample needs to be very smooth and have to interpret glass cluster variations due to electron interactions with differing terrain of glass at that scale. Chemical treatment and analysis is also used but is quite complex and prone to mistakes or contamination.[72] See also Gardner transition Glass formation References ISO 11357-2: Plastics – Differential scanning calorimetry – Part 2: Determination of glass transition temperature (1999). Dyre, Jeppe C. (2006). "Colloquium : The glass transition and elastic models of glass-forming liquids". Reviews of Modern Physics. 78 (3): 953–972. Bibcode:2006RvMP...78..953D. doi:10.1103/RevModPhys.78.953. ISSN 0034-6861. "The Glass Transition". Polymer Science Learning Center. Archived from the original on 2019-01-15. Retrieved 2009-10-15. Debenedetti, P. G.; Stillinger (2001). "Supercooled liquids and the glass transition". Nature. 410 (6825): 259–267. Bibcode:2001Natur.410..259D. doi:10.1038/35065704. PMID 11258381. S2CID 4404576. Angell, C. A.; Ngai, K. L.; McKenna, G. B.; McMillan, P. F.; Martin, S. W. (2000). "Relaxation in glassforming liquids and amorphous solids". Appl. Phys. Rev. 88 (6): 3113–3157. Bibcode:2000JAP....88.3113A. doi:10.1063/1.1286035. Archived from the original on 2020-03-07. Retrieved 2018-09-06. Zarzycki, J. (1991). Glasses and the Vitreous State. Cambridge University Press. ISBN 978-0521355827. Archived from the original on 2020-08-02. Retrieved 2016-09-23. Ojovan, M. I. (2004). "Glass formation in amorphous SiO2 as a percolation phase transition in a system of network defects". Journal of Experimental and Theoretical Physics Letters. 79 (12): 632–634. Bibcode:2004JETPL..79..632O. doi:10.1134/1.1790021. S2CID 124299526. Meille Stefano, V.; Allegra, G.; Geil Phillip, H.; He, J.; Hess, M.; Jin, J.-I.; Kratochvíl, P.; Mormann, W.; Stepto, R. (2011). "Definitions of terms relating to crystalline polymers (IUPAC Recommendations 2011)" (PDF). Pure and Applied Chemistry. 83 (10): 1831. doi:10.1351/PAC-REC-10-11-13. S2CID 98823962. Archived (PDF) from the original on 2018-06-25. Retrieved 2018-06-25. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "glass transition". doi:10.1351/goldbook.G02640 Hansen, J.-P.; McDonald, I. R. (2007). Theory of Simple Liquids. Elsevier. pp. 250–254. ISBN 978-0123705358. Archived from the original on 2013-09-21. Retrieved 2016-09-23. Adam, J-L; Zhang, X. (14 February 2014). Chalcogenide Glasses: Preparation, Properties and Applications. Elsevier Science. p. 94. ISBN 978-0-85709-356-1. Archived from the original on 17 July 2017. Retrieved 2 May 2017. Phillips, J.C. (1979). "Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys". Journal of Non-Crystalline Solids. 34 (2): 153. Bibcode:1979JNCS...34..153P. doi:10.1016/0022-3093(79)90033-4. Moynihan, C. et al. (1976) in The Glass Transition and the Nature of the Glassy State, M. Goldstein and R. Simha (Eds.), Ann. N.Y. Acad. Sci., Vol. 279. ISBN 0890720533. Angell, C. A. (1988). "Perspective on the glass transition". Journal of Physics and Chemistry of Solids. 49 (8): 863–871. Bibcode:1988JPCS...49..863A. doi:10.1016/0022-3697(88)90002-9. Ediger, M. D.; Angell, C. A.; Nagel, Sidney R. (1996). "Supercooled Liquids and Glasses". The Journal of Physical Chemistry. 100 (31): 13200. doi:10.1021/jp953538d. Angell, C. A. (1995). "Formation of Glasses from Liquids and Biopolymers". Science. 267 (5206): 1924–35. Bibcode:1995Sci...267.1924A. doi:10.1126/science.267.5206.1924. PMID 17770101. S2CID 927260. Stillinger, F. H. (1995). "A Topographic View of Supercooled Liquids and Glass Formation". Science. 267 (5206): 1935–9. Bibcode:1995Sci...267.1935S. doi:10.1126/science.267.5206.1935. PMID 17770102. S2CID 30407650. Riechers, Birte; Roed, Lisa A.; Mehri, Saeed; Ingebrigtsen, Trond S.; Hecksher, Tina; Dyre, Jeppe C.; Niss, Kristine (2022-03-18). "Predicting nonlinear physical aging of glasses from equilibrium relaxation via the material time". Science Advances. 8 (11): eabl9809. arXiv:2109.11832. Bibcode:2022SciA....8L9809R. doi:10.1126/sciadv.abl9809. ISSN 2375-2548. PMC 8926348. PMID 35294250. Nemilov SV (1994). Thermodynamic and Kinetic Aspects of the Vitreous State. CRC Press. ISBN 978-0849337826. Gibbs, J. H. (1960). MacKenzie, J. D. (ed.). Modern Aspects of the Vitreous State. Butterworth. OCLC 1690554. Ojovan, Michael I; Lee, William (Bill) E (2010). "Connectivity and glass transition in disordered oxide systems". Journal of Non-Crystalline Solids. 356 (44–49): 2534. Bibcode:2010JNCS..356.2534O. doi:10.1016/j.jnoncrysol.2010.05.012. Sturm, Karl Günter (2017). "Microscopic-Phenomenological Model of Glass Transition I. Foundations of the model (Revised and enhanced version) (Former title: Microscopic Model of Glass Transformation and Molecular Translations in Liquids I. Foundations of the Model-October 2015)". doi:10.13140/RG.2.2.19831.73121. "What is Dynamic Mechanical Testing (DMA)?". 2018. Archived from the original on 2020-11-17. Retrieved 2020-12-09. Tg measurement of glasses Archived 2009-04-17 at the Wayback Machine. Glassproperties.com. Retrieved on 2012-06-29. IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "glass-transition temperature". doi:10.1351/goldbook.G02641 Galimberti, Maurizio; Caprio, Michela; Fino, Luigi (2001-12-21). "Tyre comprising a cycloolefin polymer, tread band and elasomeric composition used therein" (published 2003-03-07). Archived from the original on 2013-09-13. Retrieved 2013-09-10. "country-code =EU, patent-number =WO03053721" Ibeh, Christopher C. (2011). THERMOPLASTIC MATERIALS Properties, Manufacturing Methods, and Applications. CRC Press. pp. 491–497. ISBN 978-1-4200-9383-4. Wilkes, C. E. (2005). PVC Handbook. Hanser Verlag. ISBN 978-1-56990-379-7. Archived from the original on 2022-04-03. Retrieved 2016-09-23. ABS. nrri.umn.edu Nicholson, John W. (2011). The Chemistry of Polymers (4, Revised ed.). Royal Society of Chemistry. p. 50. ISBN 9781849733915. Archived from the original on 10 April 2022. Retrieved 10 September 2013. nylon-6 information and properties Archived 2012-01-10 at the Wayback Machine. Polymerprocessing.com (2001-04-15). Retrieved on 2012-06-29. Jones, A (2014). "Supplementary Materials for Artificial Muscles from Fishing Line and Sewing Thread". Science. 343 (6173): 868–72. Bibcode:2014Sci...343..868H. doi:10.1126/science.1246906. PMID 24558156. S2CID 16577662. Measurement of Moisture Effects on the Mechanical Properties of 66 Nylon. TA Instruments Thermal Analysis Application Brief TA-133 PCL | Applications and End Uses | Polythene Archived 2013-06-05 at the Wayback Machine. Polyesterconverters.com. Retrieved on 2012-06-29. EPCOS 2007: Glass Transition and Crystallization in Phase Change Materials Archived 2011-07-26 at the Wayback Machine . Retrieved on 2012-06-29. Bucaro, J. A. (1974). "High-temperature Brillouin scattering in fused quartz". Journal of Applied Physics. 45 (12): 5324–5329. Bibcode:1974JAP....45.5324B. doi:10.1063/1.1663238. Kauzmann, Walter (1948). "The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures". Chemical Reviews. 43 (2): 219–256. doi:10.1021/cr60135a002. Wolchover, Natalie (11 March 2020). "Ideal Glass Would Explain Why Glass Exists at All". Quanta Magazine. Archived from the original on 7 April 2020. Retrieved 3 April 2020. Gibbs, Julian H.; DiMarzio, Edmund A. (1958). "Nature of the Glass Transition and the Glassy State". The Journal of Chemical Physics. 28 (3): 373–383. Bibcode:1958JChPh..28..373G. doi:10.1063/1.1744141. ISSN 0021-9606. S2CID 97800386. Adam, Gerold; Gibbs, Julian H. (1965). "On the Temperature Dependence of Cooperative Relaxation Properties in Glass‐Forming Liquids". The Journal of Chemical Physics. 43 (1): 139–146. Bibcode:1965JChPh..43..139A. doi:10.1063/1.1696442. ISSN 0021-9606. Dyre, Jeppe C.; Hechsher, Tina; Niss, Kristine (2009). "A brief critique of the Adam–Gibbs entropy model". Journal of Non-Crystalline Solids. 355 (10–12): 624–627. arXiv:0901.2104. Bibcode:2009JNCS..355..624D. doi:10.1016/j.jnoncrysol.2009.01.039. S2CID 53051058. Hecksher, Tina; Nielsen, Albena I.; Olsen, Niels Boye; Dyre, Jeppe C. (2008). "Little evidence for dynamic divergences in ultraviscous molecular liquids". Nature Physics. 4 (9): 737–741. Bibcode:2008NatPh...4..673H. doi:10.1038/nphys1033. ISSN 1745-2473. Archived from the original on 2021-11-04. Retrieved 2020-08-02. Ojovan M.I. (2008). "Configurons: thermodynamic parameters and symmetry changes at glass transition" (PDF). Entropy. 10 (3): 334–364. Bibcode:2008Entrp..10..334O. doi:10.3390/e10030334. Archived (PDF) from the original on 2009-07-11. Retrieved 2009-09-25. Ojovan, M.I. (2008). "Configurons: thermodynamic parameters and symmetry changes at glass transition" (PDF). Entropy. 10 (3): 334–364. Bibcode:2008Entrp..10..334O. doi:10.3390/e10030334. Archived (PDF) from the original on 2009-07-11. Retrieved 2009-09-25. Ojovan, Michael I; Travis, Karl P; Hand, Russell J (2007). "Thermodynamic parameters of bonds in glassy materials from viscosity–temperature relationships" (PDF). Journal of Physics: Condensed Matter. 19 (41): 415107. Bibcode:2007JPCM...19O5107O. doi:10.1088/0953-8984/19/41/415107. PMID 28192319. S2CID 24724512. Archived (PDF) from the original on 2018-07-25. Retrieved 2019-07-06. Cowie, J. M. G. and Arrighi, V., Polymers: Chemistry and Physics of Modern Materials, 3rd Edn. (CRC Press, 2007) ISBN 0748740732 Zaccone, A.; Terentjev, E. (2013). "Disorder-Assisted Melting and the Glass Transition in Amorphous Solids". Physical Review Letters. 110 (17): 178002. arXiv:1212.2020. Bibcode:2013PhRvL.110q8002Z. doi:10.1103/PhysRevLett.110.178002. PMID 23679782. S2CID 15600577. Capponi, S.; Alvarez, F.; Racko, D. (2020), "Free Volume in a PVME Polymer–Water Solution", Macromolecules, 53 (12): 4770–4782, Bibcode:2020MaMol..53.4770C, doi:10.1021/acs.macromol.0c00472, hdl:10261/218380, S2CID 219911779 Slater, J.C., Introduction to Chemical Physics (3rd Ed., Martindell Press, 2007) ISBN 1178626598 Born, Max (2008). "On the stability of crystal lattices. I". Mathematical Proceedings of the Cambridge Philosophical Society. 36 (2): 160–172. Bibcode:1940PCPS...36..160B. doi:10.1017/S0305004100017138. S2CID 104272002. Born, Max (1939). "Thermodynamics of Crystals and Melting". The Journal of Chemical Physics. 7 (8): 591–603. Bibcode:1939JChPh...7..591B. doi:10.1063/1.1750497. Frenkel, J. (1946). Kinetic Theory of Liquids. Clarendon Press, Oxford. Bartenev, G. M., Structure and Mechanical Properties of Inorganic Glasses (Wolters – Noordhoof, 1970) ISBN 9001054501 Dyre, Jeppe C.; Olsen, Niels Boye; Christensen, Tage (1996). "Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids". Physical Review B. 53 (5): 2171–2174. Bibcode:1996PhRvB..53.2171D. doi:10.1103/PhysRevB.53.2171. ISSN 0163-1829. PMID 9983702. Reynolds, C. L. Jr. (1979). "Correlation between the low temperature phonon mean free path and glass transition temperature in amorphous solids". J. Non-Cryst. Solids. 30 (3): 371. Bibcode:1979JNCS...30..371R. doi:10.1016/0022-3093(79)90174-1. Rosenburg, H. M. (1963) Low Temperature Solid State Physics. Clarendon Press, Oxford. Kittel, C. (1946). "Ultrasonic Propagation in Liquids". J. Chem. Phys. 14 (10): 614. Bibcode:1946JChPh..14..614K. doi:10.1063/1.1724073. hdl:1721.1/5041. Kittel, C. (1949). "Interpretation of the Thermal Conductivity of Glasses". Phys. Rev. 75 (6): 972. Bibcode:1949PhRv...75..972K. doi:10.1103/PhysRev.75.972. Chen, Shao-Ping; Egami, T.; Vitek, V. (1985). "Orientational ordering of local shear stresses in liquids: A phase transition?". Journal of Non-Crystalline Solids. 75 (1–3): 449. Bibcode:1985JNCS...75..449C. doi:10.1016/0022-3093(85)90256-X. Sorkin, Viacheslav (2005). "Lindemann criterion" (PDF). Point Defects, Lattice Structure and Melting (MSc). Israel Institute of Technology. pp. 5–8. Archived (PDF) from the original on 19 August 2019. Retrieved 6 January 2022. Mott, N. F. (1934). "The Resistance of Liquid Metals". Proceedings of the Royal Society A. 146 (857): 465. Bibcode:1934RSPSA.146..465M. doi:10.1098/rspa.1934.0166. Lindemann, C. (1911). "On the calculation of molecular natural frequencies". Phys. Z. 11: 609. Klement, W.; Willens, R. H.; Duwez, POL (1960). "Non-crystalline Structure in Solidified Gold–Silicon Alloys". Nature. 187 (4740): 869. Bibcode:1960Natur.187..869K. doi:10.1038/187869b0. S2CID 4203025. Duwez, Pol; Willens, R. H.; Klement, W. (1960). "Continuous Series of Metastable Solid Solutions in Silver-Copper Alloys" (PDF). Journal of Applied Physics. 31 (6): 1136. Bibcode:1960JAP....31.1136D. doi:10.1063/1.1735777. Archived (PDF) from the original on 2017-12-02. Retrieved 2018-05-16. Duwez, Pol; Willens, R. H.; Klement, W. (1960). "Metastable Electron Compound in Ag-Ge Alloys" (PDF). Journal of Applied Physics. 31 (6): 1137. Bibcode:1960JAP....31.1137D. doi:10.1063/1.1735778. Archived (PDF) from the original on 2020-04-18. Retrieved 2019-07-06. Chaudhari, P; Turnbull, D (1978). "Structure and properties of metallic glasses". Science. 199 (4324): 11–21. Bibcode:1978Sci...199...11C. doi:10.1126/science.199.4324.11. PMID 17841932. S2CID 7786426. Chen, J. S. (1980). "Glassy metals". Reports on Progress in Physics. 43 (4): 353. Bibcode:1980RPPh...43..353C. doi:10.1088/0034-4885/43/4/001. S2CID 250804009. Jonson, M.; Girvin, S. M. (1979). "Electron-Phonon Dynamics and Transport Anomalies in Random Metal Alloys". Phys. Rev. Lett. 43 (19): 1447. Bibcode:1979PhRvL..43.1447J. doi:10.1103/PhysRevLett.43.1447. Turnbull, D. (1974). "Amorphous Solid Formation and Interstitial Solution Behavior in Metallic Alloy System". J. Phys. C. 35 (C4): C4–1. CiteSeerX 10.1.1.596.7462. doi:10.1051/jphyscol:1974401. S2CID 52102270. Chen, H. S.; Park, B. K. (1973). "Role of chemical bonding in metallic glasses". Acta Metall. 21 (4): 395. doi:10.1016/0001-6160(73)90196-X. Wang, R.; Merz, D. (1977). "Polymorphic bonding and thermal stability of elemental noncrystalline solids". Physica Status Solidi A. 39 (2): 697. Bibcode:1977PSSAR..39..697W. doi:10.1002/pssa.2210390240. Scholze, Horst (1991). Glass : nature, structure, and properties (Revised English translation ed.). New York. ISBN 0-387-97396-6. OCLC 22889723. External links Wikimedia Commons has media related to Glass-liquid transitions. Fragility Archived 2007-06-28 at the Wayback Machine VFT Eqn. Polymers I Polymers II Archived 2010-01-11 at the Wayback Machine Angell: Aqueous media DoITPoMS Teaching and Learning Package- "The Glass Transition in Polymers" Glass Transition Temperature short overview vte Glass science topics Authority control: National Edit this at Wikidata Israel United States Categories: CryobiologyGlass engineering and scienceGlass physicsPhase transitionsPolymer chemistryRubber propertiesThreshold temperatures https://en.wikipedia.org/wiki/Glass_transition From Wikipedia, the free encyclopedia The autoignition temperature or self-ignition temperature, often called spontaneous ignition temperature or minimum ignition temperature (or shortly ignition temperature) and formerly also known as kindling point, of a substance is the lowest temperature in which it spontaneously ignites in a normal atmosphere without an external source of ignition, such as a flame or spark.[1] This temperature is required to supply the activation energy needed for combustion. The temperature at which a chemical ignites decreases as the pressure is increased. Substances which spontaneously ignite in a normal atmosphere at naturally ambient temperatures are termed pyrophoric. Autoignition temperatures of liquid chemicals are typically measured using a 500-millilitre (18 imp fl oz; 17 US fl oz) flask placed in a temperature-controlled oven in accordance with the procedure described in ASTM E659.[2] When measured for plastics, autoignition temperature can be also measured under elevated pressure and at 100% oxygen concentration. The resulting value is used as a predictor of viability for high-oxygen service. The main testing standard for this is ASTM G72.[3] Autoignition time equation The time t ig {\displaystyle t_{\text{ig}}} it takes for a material to reach its autoignition temperature T ig {\displaystyle T_{\text{ig}}} when exposed to a heat flux q ″ {\displaystyle q''} is given by the following equation:[4] t ig = π 4 k ρ c [ T ig − T 0 q ″ ] 2 , {\displaystyle t_{\text{ig}}={\frac {\pi }{4}}k\rho c\left[{\frac {T_{\text{ig}}-T_{0}}{q''}}\right]^{2},} where k = thermal conductivity, ρ = density, and c = specific heat capacity of the material of interest, T 0 T_{0} is the initial temperature of the material (or the temperature of the bulk material). Autoignition temperature of selected substances Temperatures vary widely in the literature and should only be used as estimates. Factors that may cause variation include partial pressure of oxygen, altitude, humidity, and amount of time required for ignition. Generally the autoignition temperature for hydrocarbon/air mixtures decreases with increasing molecular mass and increasing chain length. The autoignition temperature is also higher for branched-chain hydrocarbons than for straight-chain hydrocarbons.[5] Substance Autoignition[D] Note Barium 550 °C (1,022 °F) 550±90[1][C] Bismuth 735 °C (1,355 °F) 735±20[1][C] Butane 405 °C (761 °F) [6] Calcium 790 °C (1,450 °F) 790±10[1][C] Carbon disulfide 90 °C (194 °F) [7] Diesel or Jet A-1 210 °C (410 °F) [8] Diethyl ether 160 °C (320 °F) [9] Ethanol 365 °C (689 °F) [7] Gasoline (Petrol) 247–280 °C (477–536 °F) [7] Hydrogen 535 °C (995 °F) [10] Iron 1,315 °C (2,399 °F) 1315±20[1][C] Lead 850 °C (1,560 °F) 850±5[1][C] Leather / parchment 200–212 °C (392–414 °F) [8][11] Magnesium 635 °C (1,175 °F) 635±5[1][B][C] Magnesium 473 °C (883 °F) [7][B] Molybdenum 780 °C (1,440 °F) 780±5[1][C] Paper 218–246 °C (424–475 °F) [8][12] Phosphorus (white) 34 °C (93 °F) [7][A][B] Silane 21 °C (70 °F) [7] or below Strontium 1,075 °C (1,967 °F) 1075±120[1][C] Tin 940 °C (1,720 °F) 940±25[1][C] Triethylborane −20 °C (−4 °F) [7] A On contact with an organic substance, melts otherwise. B There are two distinct results in the published literature. Both are separately listed in this table. C At 1 atm. The ignition temperature depends on the air pressure. D Under standard conditions for pressure. See also Fire point Flash point Gas burner (for flame temperatures, combustion heat energy values and ignition temperatures) Spontaneous combustion References Laurendeau, N. M.; Glassman, I. (1971-04-01). "Ignition Temperatures of Metals in Oxygen Atmospheres". Combustion Science and Technology. 3 (2): 77–82. doi:10.1080/00102207108952274. E659 – 78 (Reapproved 2000), "Standard Test Method for Autoignition Temperature of Liquid Chemicals", ASTM, 100 Barr Harbor Drive, West Conshohocken, PA 19428-2959. S. Grynko, "Material Properties Explained" (2012), ISBN 1-4700-7991-7, p. 46. Principles of Fire Behavior. ISBN 0-8273-7732-0. 1998. Zabetakis, M. G. (1965), Flammability characteristics of combustible gases and vapours, U.S. Department of Mines, Bulletin 627. "Butane - Safety Properties". Wolfram|Alpha. Fuels and Chemicals - Autoignition Temperatures, engineeringtoolbox.com Cafe, Tony. "PHYSICAL CONSTANTS FOR INVESTIGATORS". tcforensic.com.au. TC Forensic P/L. Retrieved 11 February 2015. "Diethyl Ether - Safety Properties". Wolfram|Alpha. "Hydrogen – Autoignition Point". Wolfram|Alpha. "Flammability and flame retardancy of leather". leathermag.com. Leather International / Global Trade Media. Retrieved 11 February 2015. Tony Cafe. "Physical Constants for Investigators". Journal of Australian Fire Investigators. (Reproduced from "Firepoint" magazine) External links Analysis of Effective Thermal Properties of Thermally Thick Materials. vte Firelighting Campfire Bonfire Glossary Components Ember Fire triangle Firewood Spark Tinder Wood ash Wood fuel Topics Autoignition temperature Combustion Friction fire Minimum ignition energy Smouldering Early starters Burning glass (Solar Spark Lighter) Fire piston Fire plough Fire-saw Fire striker Flint Fire drill Hand drill Bow drill Pump drill Modern starters Match Black match Electric match Ferrocerium Lighter Blowtorch Other equipment Char cloth Feather stick Fire pan Fire pit Fire ring Matchbook Matchbox Punk Tinderbox Torch Chuckmuck Related articles Arson Control of fire by early humans Native American use of fire in ecosystems Outdoor cooking Firem'n Chit Pyrolysis Pyromania Survival skills Authority control: National Edit this at Wikidata Germany Categories: Chemical propertiesFireThreshold temperatures https://en.wikipedia.org/wiki/Autoignition_temperature From Wikipedia, the free encyclopedia (Redirected from Doppler cooling limit) Simplified principle of Doppler laser cooling: 1 A stationary atom sees the laser neither red- nor blue-shifted and does not absorb the photon. 2 An atom moving away from the laser sees it red-shifted and does not absorb the photon. 3.1 An atom moving towards the laser sees it blue-shifted and absorbs the photon, slowing the atom. 3.2 The photon excites the atom, moving an electron to a higher quantum state. 3.3 The atom re-emits a photon. As its direction is random, there is no net change in momentum over many photons. Doppler cooling is a mechanism that can be used to trap and slow the motion of atoms to cool a substance. The term is sometimes used synonymously with laser cooling, though laser cooling includes other techniques. History Doppler cooling was simultaneously proposed by two groups in 1975, the first being David J. Wineland and Hans Georg Dehmelt[1] and the second being Theodor W. Hänsch and Arthur Leonard Schawlow.[2] It was first demonstrated by Wineland, Drullinger, and Walls in 1978[3] and shortly afterwards by Neuhauser, Hohenstatt, Toschek and Dehmelt. One conceptually simple form of Doppler cooling is referred to as optical molasses, since the dissipative optical force resembles the viscous drag on a body moving through molasses. Steven Chu, Claude Cohen-Tannoudji and William D. Phillips were awarded the 1997 Nobel Prize in Physics for their work in laser cooling and atom trapping. Brief explanation Doppler cooling involves light with frequency tuned slightly below an electronic transition in an atom. Because the light is detuned to the "red" (i.e. at lower frequency) of the transition, the atoms will absorb more photons if they move towards the light source, due to the Doppler effect. Consider the simplest case of 1D motion on the x axis. Let the photon be traveling in the +x direction and the atom in the −x direction. In each absorption event, the atom loses a momentum equal to the momentum of the photon. The atom, which is now in the excited state, emits a photon spontaneously but randomly along +x or −x. Momentum is returned to the atom. If the photon was emitted along +x then there is no net change; however, if the photon was emitted along −x, then the atom is moving more slowly in either −x or +x. The net result of the absorption and emission process is a reduced speed of the atom, on the condition that its initial speed is larger than the recoil velocity from scattering a single photon. If the absorption and emission are repeated many times, the mean velocity, and therefore the kinetic energy of the atom, will be reduced. Since the temperature of an ensemble of atoms is a measure of the random internal kinetic energy, this is equivalent to cooling the atoms. The Doppler cooling limit is the minimum temperature achievable with Doppler cooling. Detailed explanation The vast majority of photons that come anywhere near a particular atom are almost[4] completely unaffected by that atom. The atom is almost completely transparent to most frequencies (colors) of photons. A few photons happen to "resonate" with the atom in a few very narrow bands of frequencies (a single color rather than a mixture like white light). When one of those photons comes close to the atom, the atom typically absorbs that photon (absorption spectrum) for a brief period of time, then emits an identical photon (emission spectrum) in some random, unpredictable direction. (Other sorts of interactions between atoms and photons exist, but are not relevant to this article.) The popular idea that lasers increase the thermal energy of matter is not the case when examining individual atoms. If a given atom is practically motionless (a "cold" atom), and the frequency of a laser focused upon it can be controlled, most frequencies do not affect the atom—it is invisible at those frequencies. There are only a few points of electromagnetic frequency that have any effect on that atom. At those frequencies, the atom can absorb a photon from the laser, while transitioning to an excited electronic state, and pick up the momentum of that photon. Since the atom now has the photon's momentum, the atom must begin to drift in the direction the photon was traveling. A short time later, the atom will spontaneously emit a photon in a random direction as it relaxes to a lower electronic state. If that photon is emitted in the direction of the original photon, the atom will give up its momentum to the photon and will become motionless again. If the photon is emitted in the opposite direction, the atom will have to provide momentum in that opposite direction, which means the atom will pick up even more momentum in the direction of the original photon (to conserve momentum), with double its original velocity. But usually the photon speeds away in some other direction, giving the atom at least some sideways thrust. Another way of changing frequencies is to change the positioning of the laser, for example, by using a monochromatic (single-color) laser that has a frequency that is a little below one of the "resonant" frequencies of this atom (at which frequency the laser will not directly affect the atom's state). If the laser were to be positioned so that it was moving towards the observed atoms, then the Doppler effect would raise its frequency. At one specific velocity, the frequency would be precisely correct for said atoms to begin absorbing photons. Something very similar happens in a laser cooling apparatus, except such devices start with a warm cloud of atoms moving in numerous directions at variable velocity. Starting with a laser frequency well below the resonant frequency, photons from any one laser pass right through the majority of atoms. However, atoms moving rapidly towards a particular laser catch the photons for that laser, slowing those atoms down until they become transparent again. (Atoms rapidly moving away from that laser are transparent to that laser's photons—but they are rapidly moving towards the laser directly opposite it). This utilization of a specific velocity to induce absorption is also seen in Mössbauer spectroscopy. On a graph of atom velocities (atoms moving rapidly to the right correspond with stationary dots far to the right, atoms moving rapidly to the left correspond with stationary dots far to the left), there is a narrow band on the left edge corresponding to the speed at which those atoms start absorbing photons from the left laser. Atoms in that band are the only ones that interact with the left laser. When a photon from the left laser slams into one of those atoms, it suddenly slows down an amount corresponding to the momentum of that photon (the dot would be redrawn some fixed "quantum" distance further to the right). If the atom releases the photon directly to the right, then the dot is redrawn that same distance to the left, putting it back in the narrow band of interaction. But usually the atom releases the photon in some other random direction, and the dot is redrawn that quantum distance in the opposite direction. Such an apparatus would be constructed with many lasers, corresponding to many boundary lines that completely surround that cloud of dots. As the laser frequency is increased, the boundary contracts, pushing all the dots on that graph towards zero velocity, the given definition of "cold". Limits Minimum temperature The Doppler temperature is the minimum temperature achievable with Doppler cooling. When a photon is absorbed by an atom counter-propagating to the light source, its velocity is decreased by momentum conservation. When the absorbed photon is spontaneously emitted by the excited atom, the atom receives a momentum kick in a random direction. The spontaneous emissions are isotropic and therefore these momentum kicks average to zero for the mean velocity. On the other hand, the mean squared velocity, ⟨ v 2 ⟩ \langle v^{2}\rangle , is not zero in the random process, and thus heat is supplied to the atom.[5] At equilibrium, the heating and cooling rates are equal, which sets a limit on the amount by which the atom can be cooled. As the transitions used for Doppler cooling have broad natural linewidths γ \gamma (measured in radians per second), this sets the lower limit to the temperature of the atoms after cooling to be[6] T D o p p l e r = ℏ γ / ( 2 k B ) , {\displaystyle T_{\mathrm {Doppler} }=\hbar \gamma /(2k_{\text{B}}),} where k B k_{\text{B}} is the Boltzmann constant and ℏ \hbar is the reduced Planck constant. This is usually much higher than the recoil temperature, which is the temperature associated with the momentum gained from the spontaneous emission of a photon. The Doppler limit has been verified with a gas of metastable helium.[7] Sub-Doppler cooling Main article: Sub-Doppler cooling Temperatures well below the Doppler limit have been achieved with various laser cooling methods, including Sisyphus cooling, evaporative cooling, and resolved sideband cooling. The theory of Doppler cooling assumes an atom with a simple two level structure, whereas most atomic species which are laser cooled have complicated hyperfine structure. Mechanisms such as Sisyphus cooling due to multiple ground states lead to temperatures lower than the Doppler limit. Maximum concentration The concentration must be minimal to prevent the absorption of the photons into the gas in the form of heat. This absorption happens when two atoms collide with each other while one of them has an excited electron. There is then a possibility of the excited electron dropping back to the ground state with its extra energy liberated in additional kinetic energy to the colliding atoms—which heats the atoms. This works against the cooling process and therefore limits the maximum concentration of gas that can be cooled using this method. Atomic structure Only certain atoms and ions have optical transitions amenable to laser cooling, since it is extremely difficult to generate the amounts of laser power needed at wavelengths much shorter than 300 nm. Furthermore, the more hyperfine structure an atom has, the more ways there are for it to emit a photon from the upper state and not return to its original state, putting it in a dark state and removing it from the cooling process. It is possible to use other lasers to optically pump those atoms back into the excited state and try again, but the more complex the hyperfine structure is, the more (narrow-band, frequency locked) lasers are required. Since frequency-locked lasers are both complex and expensive, atoms which need more than one extra repump laser are rarely cooled; the common rubidium magneto-optical trap, for example, requires one repump laser. This is also the reason why molecules are in general difficult to laser cool: in addition to hyperfine structure, molecules also have rovibronic couplings and so can also decay into excited rotational or vibrational states. However, laser cooling of molecules has been demonstrated, first with SrF molecules,[8] and subsequently with other diatomics such as CaF[9][10] and YO.[11] Configurations Counter-propagating sets of laser beams in all three Cartesian dimensions may be used to cool the three motional degrees of freedom of the atom. Common laser-cooling configurations include optical molasses, the magneto-optical trap, and the Zeeman slower. Atomic ions, trapped in an ion trap, can be cooled with a single laser beam as long as that beam has a component along all three motional degrees of freedom. This is in contrast to the six beams required to trap neutral atoms. The original laser cooling experiments were performed on ions in ion traps. (In theory, neutral atoms could be cooled with a single beam if they could be trapped in a deep trap, but in practice neutral traps are much shallower than ion traps and a single recoil event can be enough to kick a neutral atom out of the trap.) Applications One use for Doppler cooling is the optical molasses technique. This process itself forms a part of the magneto-optical trap but it can be used independently. Doppler cooling is also used in spectroscopy and metrology, where cooling allows narrower spectroscopic features. For example, all of the best atomic clock technologies involve Doppler cooling at some point. See also Magneto-optical trap Resolved sideband cooling References Wineland, D. J.; Dehmelt, H. (1975). "Proposed 1014 Δν < ν Laser Fluorescence Spectroscopy on Tl+ Mono-Ion Oscillator III" (PDF). Bulletin of the American Physical Society. 20: 637. Hänsch, T. W.; Shawlow, A. L. (1975). "Cooling of Gases by Laser Radiation". Optics Communications. 13 (1): 68. Bibcode:1975OptCo..13...68H. doi:10.1016/0030-4018(75)90159-5. Wineland, D. J.; Drullinger, R. E.; Walls, F. L. (1978). "Radiation-Pressure Cooling of Bound Resonant Absorbers". Physical Review Letters. 40 (25): 1639. Bibcode:1978PhRvL..40.1639W. doi:10.1103/PhysRevLett.40.1639. There are processes, such as Rayleigh and Raman scattering, by which atoms and molecules will scatter non-resonant photons; see, e.g., Hecht, E.; Zajac, A. (1974). Optics. Addison-Wesley. ISBN 978-0-201-02835-5. This type of scattering, however, is normally very weak in comparison to resonant absorption and emission (i.e., fluorescence). Lett, P. D.; Phillips, W. D.; Rolston, S. L.; Tanner, C. E.; Watts, R. N.; Westbrook, C. I. (1989). "Optical molasses". Journal of the Optical Society of America B. 6 (11): 2084–2107. Bibcode:1989JOSAB...6.2084L. doi:10.1364/JOSAB.6.002084. Letokhov, V. S.; Minogin, V. G.; Pavlik, B. D. (1977). "Cooling and capture of atoms and molecules by a resonant light field". Soviet Physics JETP. 45: 698. Bibcode:1977JETP...45..698L. Chang, R.; Hoendervanger, A. L.; Bouton, Q.; Fang, Y.; Klafka, T.; Audo, K.; Aspect, A.; Westbrook, C. I.; Clément, D. (2014). "Three-dimensional laser cooling at the Doppler limit". Physical Review A. 90 (6): 063407. arXiv:1409.2519. Bibcode:2014PhRvA..90f3407C. doi:10.1103/PhysRevA.90.063407. S2CID 55013080. Shuman, E. S.; Barry, J. F.; DeMille, D. (2010). "Laser cooling of a diatomic molecule". Nature. 467 (7317): 820–823. arXiv:1103.6004. Bibcode:2010Natur.467..820S. doi:10.1038/nature09443. PMID 20852614. S2CID 4430586. "Laser Cooling CaF". doylegroup.harvard.edu/. Doyle Group, Harvard University. Retrieved 9 November 2015. Zhelyazkova, V.; Cournol, A.; Wall, T. E.; Matsushima, A.; Hudson, J. J.; Hinds, E. A.; Tarbutt, M. R.; Sauer, B. E. (2014). "Laser cooling and slowing of CaF molecules". Physical Review A. 89 (5): 053416. arXiv:1308.0421. Bibcode:2014PhRvA..89e3416Z. doi:10.1103/PhysRevA.89.053416. S2CID 119285667. Hummon, M. T.; Yeo, M.; Stuhl, B. K.; Collopy, A. L.; Xia, Y.; Ye, J. (2013). "2D Magneto-Optical Trapping of Diatomic Molecules". Physical Review Letters. 110 (14): 143001. arXiv:1209.4069. Bibcode:2013PhRvL.110n3001H. doi:10.1103/PhysRevLett.110.143001. PMID 25166984. S2CID 13718902. Further reading Foot, C. J. (2005). Atomic Physics. Oxford University Press. pp. 182–213. ISBN 978-0-19-850696-6. Metcalf, H. J.; van der Straten, P. (1999). Laser Cooling and Trapping. Springer-Verlag. ISBN 978-0-387-98728-6. Phillips, W. D. (1997). "Laser Cooling and Trapping of Atoms" (PDF). Nobel Lecture. Nobel Foundation. pp. 199–237. vte Lasers Categories: Atomic physicsCooling technologyDoppler effects https://en.wikipedia.org/wiki/Doppler_cooling#Limits Ductile–brittle transition temperature Schematic appearance of round metal bars after tensile testing. (a) Brittle fracture (b) Ductile fracture (c) Completely ductile fracture Metals can undergo two different types of fractures: brittle fracture or ductile fracture. Failure propagation occurs faster in brittle materials due to the ability for ductile materials to undergo plastic deformation. Thus, ductile materials are able to sustain more stress due to their ability to absorb more energy prior to failure than brittle materials are. The plastic deformation results in the material following a modification of the Griffith equation, where the critical fracture stress increases due to the plastic work required to extend the crack adding to the work necessary to form the crack - work corresponding to the increase in surface energy that results from the formation of an addition crack surface.[26] The plastic deformation of ductile metals is important as it can be a sign of the potential failure of the metal. Yet, the point at which the material exhibits a ductile behavior versus a brittle behavior is not only dependent on the material itself but also on the temperature at which the stress is being applied to the material. The temperature where the material changes from brittle to ductile or vice versa is crucial for the design of load-bearing metallic products. The minimum temperature at which the metal transitions from a brittle behavior to a ductile behavior, or from a ductile behavior to a brittle behavior, is known as the ductile-brittle transition temperature (DBTT). Below the DBTT, the material will not be able to plastically deform, and the crack propagation rate increases rapidly leading to the material undergoing brittle failure rapidly. Furthermore, DBTT is important since, once a material is cooled below the DBTT, it has a much greater tendency to shatter on impact instead of bending or deforming (low temperature embrittlement). Thus, the DBTT indicates the temperature at which, as temperature decreases, a material's ability to deform in a ductile manner decreases and so the rate of crack propagation drastically increases. In other words, solids are very brittle at very low temperatures, and their toughness becomes much higher at elevated temperatures. For more general applications, it is preferred to have a lower DBTT to ensure the material has a wider ductility range. This ensures that sudden cracks are inhibited so that failures in the metal body are prevented. It has been determined that the more slip systems a material has, the wider the range of temperatures ductile behavior is exhibited at. This is due to the slip systems allowing for more motion of dislocations when a stress is applied to the material. Thus, in materials with a lower amount of slip systems, dislocations are often pinned by obstacles leading to strain hardening, which increases the materials strength which makes the material more brittle. For this reason, FCC (face centered cubic) structures are ductile over a wide range of temperatures, BCC (body centered cubic) structures are ductile only at high temperatures, and HCP (hexagonal closest packed) structures are often brittle over wide ranges of temperatures. This leads to each of these structures having different performances as they approach failure (fatigue, overload, and stress cracking) under various temperatures, and shows the importance of the DBTT in selecting the correct material for a specific application. For example, zamak 3 exhibits good ductility at room temperature but shatters when impacted at sub-zero temperatures. DBTT is a very important consideration in selecting materials that are subjected to mechanical stresses. A similar phenomenon, the glass transition temperature, occurs with glasses and polymers, although the mechanism is different in these amorphous materials. The DBTT is also dependent on the size of the grains within the metal, as typically smaller grain size leads to an increase in tensile strength, resulting in an increase in ductility and decrease in the DBTT. This increase in tensile strength is due to the smaller grain sizes resulting in grain boundary hardening occurring within the material, where the dislocations require a larger stress to cross the grain boundaries and continue to propagate throughout the material. It has been shown that by continuing to refine ferrite grains to reduce their size, from 40 microns down to 1.3 microns, that it is possible to eliminate the DBTT entirely so that a brittle fracture never occurs in ferritic steel (as the DBTT required would be below absolute zero).[27] In some materials, the transition is sharper than others and typically requires a temperature-sensitive deformation mechanism. For example, in materials with a body-centered cubic (bcc) lattice the DBTT is readily apparent, as the motion of screw dislocations is very temperature sensitive because the rearrangement of the dislocation core prior to slip requires thermal activation. This can be problematic for steels with a high ferrite content. This famously resulted in serious hull cracking in Liberty ships in colder waters during World War II, causing many sinkings. DBTT can also be influenced by external factors such as neutron radiation, which leads to an increase in internal lattice defects and a corresponding decrease in ductility and increase in DBTT. The most accurate method of measuring the DBTT of a material is by fracture testing. Typically four-point bend testing at a range of temperatures is performed on pre-cracked bars of polished material. Two fracture tests are typically utilized to determine the DBTT of specific metals: the Charpy V-Notch test and the Izod test. The Charpy V-notch test determines the impact energy absorption ability or toughness of the specimen by measuring the potential energy difference resulting from the collision between a mass on a free-falling pendulum and the machined V-shaped notch in the sample, resulting in the pendulum breaking through the sample. The DBTT is determined by repeating this test over a variety of temperatures and noting when the resulting fracture changes to a brittle behavior which occurs when the absorbed energy is dramatically decreased. The Izod test is essentially the same as the Charpy test, with the only differentiating factor being the placement of the sample; In the former the sample is placed vertically, while in the latter the sample is placed horizontally with respect to the bottom of the base. [28] For experiments conducted at higher temperatures, dislocation activity[clarification needed] increases. At a certain temperature, dislocations shield[clarification needed] the crack tip to such an extent that the applied deformation rate is not sufficient for the stress intensity at the crack-tip to reach the critical value for fracture (KiC). The temperature at which this occurs is the ductile–brittle transition temperature. If experiments are performed at a higher strain rate, more dislocation shielding is required to prevent brittle fracture, and the transition temperature is raised.[citation needed] See also Deformation Work hardening, which improves ductility in uniaxial tension by delaying the onset of instability Strength of materials References Brande, William Thomas (1853). A Dictionary of Science, Literature, and Art: Comprising the History, Description, and Scientific Principles of Every Branch of Human Knowledge : with the Derivation and Definition of All the Terms in General Use. Harper & Brothers. p. 369. Kalpakjian, Serope, 1928- (1984). Manufacturing processes for engineering materials. Reading, Mass.: Addison-Wesley. p. 30. ISBN 0-201-11690-1. OCLC 9783323. "Ductility - What is Ductile Material". Nuclear Power. Retrieved 2020-11-14. Budynas, Richard G. (2015). Shigley's Mechanical Engineering Design—10th ed. McGraw Hill. p. 233. ISBN 978-0-07-339820-4.. Chandler Roberts-Austen, William (1894). An Introduction to the Study of Metallurgy. London: C. Griffin. p. 16. Ductility and its effect on material failure. The Engineering Archive. (n.d.). https://theengineeringarchive.com/material-science/page-ductility-material-failure.html "Malleability - Malleable Materials". Nuclear Power. Archived from the original on 2020-09-25. Retrieved 2020-11-14. DOE FUNDAMENTALS HANDBOOK MATERIAL SCIENCE. Vol. 1, Module 2 – Properties of Metals. U.S. Department of Energy. January 1993. p. 25. Rich, Jack C. (1988). The Materials and Methods of Sculpture. Courier Dover Publications. p. 129. ISBN 978-0-486-25742-6.. Masuda, Hideki (2016). "Combined Transmission Electron Microscopy – In situ Observation of the Formation Process and Measurement of Physical Properties for Single Atomic-Sized Metallic Wires". In Janecek, Milos; Kral, Robert (eds.). Modern Electron Microscopy in Physical and Life Sciences. InTech. doi:10.5772/62288. ISBN 978-953-51-2252-4. S2CID 58893669. Vaccaro, John (2002) Materials handbook, Mc Graw-Hill handbooks, 15th ed. Schwartz, M. (2002) CRC encyclopedia of materials parts and finishes, 2nd ed. Lah, Che; Akmal, Nurul; Trigueros, Sonia (2019). "Synthesis and modelling of the mechanical properties of Ag, Au and Cu nanowires". Sci. Technol. Adv. Mater. 20 (1): 225–261. Bibcode:2019STAdM..20..225L. doi:10.1080/14686996.2019.1585145. PMC 6442207. PMID 30956731. Dieter, G. (1986) Mechanical Metallurgy, McGraw-Hill, ISBN 978-0-07-016893-0 "Ductility Review - Strength Mechanics of Materials - Engineers Edge". www.engineersedge.com. Retrieved 2020-07-14. Askeland, Donald R. (2016). "6-4 Properties Obtained from the Tensile Test". The science and engineering of materials. Wright, Wendelin J. (Seventh ed.). Boston, MA. p. 195. ISBN 978-1-305-07676-1. OCLC 903959750. Callister, William D. Jr. (2010). "6.6 Tensile Properties". Materials science and engineering : an introduction. Rethwisch, David G. (8th ed.). Hoboken, NJ. p. 166. ISBN 978-0-470-41997-7. OCLC 401168960. Matic, P (1988). "The Relation of Tensile Specimen Size and Geometry Effects to Unique Constitutive Parameters for Ductile Materials". Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences. 417 (1853): 309–333. Bibcode:1988RSPSA.417..309M. doi:10.1098/rspa.1988.0063. S2CID 43033448. Havner, K (2004). "On the Onset of Necking in the Tensile Test". International Journal of Plasticity. 20 (4–5): 965–978. doi:10.1016/j.ijplas.2003.05.004. Kim, H (2005). "Finite Element Analysis of the Onset of Necking and the Post-Necking Behaviour During Uniaxial Tensile Testing". Materials Transactions. 46 (10): 2159–2163. doi:10.2320/matertrans.46.2159. Joun, M (2007). "Finite Element Analysis of Tensile Testing with Emphasis on Necking". Computational Materials Science. 41 (1): 63–69. doi:10.1016/j.commatsci.2007.03.002. Osovski, S (2013). "Dynamic Tensile Necking: Influence of Specimen Geometry and Boundary Conditions". Mechanics of Materials. 62: 1–13. doi:10.1016/j.mechmat.2013.03.002. hdl:10016/17020. Choung, J (2008). "Study on True Stress Correction from Tensile Tests". Journal of Mechanical Science and Technology. 22 (6): 1039–1051. doi:10.1007/s12206-008-0302-3. S2CID 108776720. Ho, H (2019). "Modelling Tensile Tests on High Strength S690 Steel Materials Undergoing Large Deformations". Engineering Structures. 192: 305–322. doi:10.1016/j.engstruct.2019.04.057. S2CID 182744244. Samuel, E (2008). "Inter-Relation between True Stress at the Onset of Necking and True Uniform Strain in Steels - a Manifestation of Onset to Plastic Instability". Materials Science and Engineering A-Structural Materials Properties Microstructure and Processing. 480 (1–2): 506–509. doi:10.1016/j.msea.2007.07.074. "FRACTURE OF MATERIALS" (PDF). U.S. Naval Academy. Archived (PDF) from the original on 2022-10-09. Retrieved 2 July 2022. Qiu, Hai; Hanamura, Toshihiro; Torizuka, Shiro (2014). "Influence of Grain Size on the Ductile Fracture Toughness of Ferritic Steel". ISIJ International. 54 (8): 1958–1964. doi:10.2355/isijinternational.54.1958. "Ductile-Brittle Transition Temperature and Impact Energy Tests - Yena Engineering". 18 November 2020. External links Look up ductility in Wiktionary, the free dictionary. Look up malleability in Wiktionary, the free dictionary. Ductility definition at engineersedge.com DoITPoMS Teaching and Learning Package- "The Ductile-Brittle Transition Categories: Continuum mechanicsDeformation (mechanics) https://en.wikipedia.org/wiki/Ductility#Ductile%E2%80%93brittle_transition_temperature MDMT is one of the design conditions for pressure vessels engineering calculations, design and manufacturing according to the ASME Boilers and Pressure Vessels Code. Each pressure vessel that conforms to the ASME code has its own MDMT, and this temperature is stamped on the vessel nameplate. The precise definition can sometimes be a little elaborate, but in simple terms the MDMT is a temperature arbitrarily selected by the user of type of fluid and the temperature range the vessel is going to handle. The so-called arbitrary MDMT must be lower than or equal to the CET (which is an environmental or "process" property, see below) and must be higher than or equal to the (MDMT)M (which is a material property). Critical exposure temperature (CET) is the lowest anticipated temperature to which the vessel will be subjected, taking into consideration lowest operating temperature, operational upsets, autorefrigeration, atmospheric temperature, and any other sources of cooling. In some cases it may be the lowest temperature at which significant stresses will occur and not the lowest possible temperature. (MDMT)M is the lowest temperature permitted according to the metallurgy of the vessel fabrication materials and the thickness of the vessel component, that is, according to the low temperature embrittlement range and the charpy impact test requirements per temperature and thickness, for each one of the vessel's components. References ASME, Boilers and Pressure Vessels Code Dennis R. Moss, Pressure Vessel Design Manual, 1997 (2nd ed.) Stub icon This article about a mechanical engineering topic is a stub. You can help Wikipedia by expanding it. Categories: Pressure vesselsThreshold temperaturesMechanical engineering stubs https://en.wikipedia.org/wiki/Minimum_design_metal_temperature From Wikipedia, the free encyclopedia Ethanol burning with its spectrum depicted In the study of combustion, the adiabatic flame temperature is the temperature reached by a flame under ideal conditions. It is an upper bound of the temperature that is reached in actual processes. There are two types adiabatic flame temperature: constant volume and constant pressure, depending on how the process is completed. The constant volume adiabatic flame temperature is the temperature that results from a complete combustion process that occurs without any work, heat transfer or changes in kinetic or potential energy. Its temperature is higher than in the constant pressure process because no energy is utilized to change the volume of the system (i.e., generate work). Common flames Propane Iso-Octane (2,2,4-Trimethylpentane) In daily life, the vast majority of flames one encounters are those caused by rapid oxidation of hydrocarbons in materials such as wood, wax, fat, plastics, propane, and gasoline. The constant-pressure adiabatic flame temperature of such substances in air is in a relatively narrow range around 1950 °C. This is mostly because the heat of combustion of these compounds is roughly proportional to the amount of oxygen consumed, which proportionally increases the amount of air that has to be heated, so the effect of a larger heat of combustion on the flame temperature is offset. Incomplete reaction at higher temperature further curtails the effect of a larger heat of combustion. Because most combustion processes that happen naturally occur in the open air, there is nothing that confines the gas to a particular volume like the cylinder in an engine. As a result, these substances will burn at a constant pressure, which allows the gas to expand during the process. Common flame temperatures Assuming initial atmospheric conditions (1 bar and 20 °C), the following table[1] lists the flame temperature for various fuels under constant pressure conditions. The temperatures mentioned here are for a stoichiometric fuel-oxidizer mixture (i.e. equivalence ratio φ = 1). Note that these are theoretical, not actual, flame temperatures produced by a flame that loses no heat. The closest will be the hottest part of a flame, where the combustion reaction is most efficient. This also assumes complete combustion (e.g. perfectly balanced, non-smoky, usually bluish flame). Several values in the table significantly disagree with the literature[1] or predictions by online calculators. Adiabatic flame temperature (constant pressure) of common fuels Fuel Oxidizer T ad {\displaystyle T_{\text{ad}}} (°C) (°F) Acetylene (C2H2) Air 2500 4532 Oxygen 3480 6296 Butane (C4H10) Air 2231 4074[2] Cyanogen (C2N2) Oxygen 4525 8177 Dicyanoacetylene (C4N2) Oxygen 4990 9010 Ethane (C2H6) Air 1955 3551 Ethanol (C2H5OH) Air 2082 3779[3] Gasoline Air 2138 3880[3] Hydrogen (H2) Air 2254 4089[3] Magnesium (Mg) Air 1982 3600[4] Methane (CH4) Air 1963 3565[5] Methanol (CH3OH) Air 1949 3540[5] Naphtha Air 2533 4591[2] Natural gas Air 1960 3562[6] Pentane (C5H12) Air 1977 3591[5] Propane (C3H8) Air 1980 3596[7] Methylacetylene (CH3CCH) Air 2010 3650 Oxygen 2927 5301 Toluene (C7H8) Air 2071 3760[5] Wood Air 1980 3596 Kerosene Air 2093[8] 3801 Light fuel oil Air 2104[8] 3820 Medium fuel oil Air 2101[8] 3815 Heavy fuel oil Air 2102[8] 3817 Bituminous Coal Air 2172[8] 3943 Anthracite Air 2180[8] 3957 Oxygen ≈3500[9] ≈6332 Aluminium Oxygen 3732 6750[5] Lithium Oxygen 2438 4420[5] Phosphorus (white) Oxygen 2969 5376[5] Zirconium Oxygen 4005 7241[5] Thermodynamics First law of thermodynamics for a closed reacting system From the first law of thermodynamics for a closed reacting system we have R Q P − R W P = U P − U R {}_{R}Q_{P}-{}_{R}W_{P}=U_{P}-U_{R} where, R Q P {}_{R}Q_{P} and R W P {}_{R}W_{P} are the heat and work transferred from the system to the surroundings during the process, respectively, and U R U_{R} and U P U_{P} are the internal energy of the reactants and products, respectively. In the constant volume adiabatic flame temperature case, the volume of the system is held constant and hence there is no work occurring: R W P = ∫ R P p d V = 0 {}_{R}W_{P}=\int \limits _{R}^{P}{pdV}=0 There is also no heat transfer because the process is defined to be adiabatic: R Q P = 0 {}_{R}Q_{P}=0. As a result, the internal energy of the products is equal to the internal energy of the reactants: U P = U R U_{P}=U_{R}. Because this is a closed system, the mass of the products and reactants is constant and the first law can be written on a mass basis, U P = U R ⇒ m P u P = m R u R ⇒ u P = u R U_{P}=U_{R}\Rightarrow m_{P}u_{P}=m_{R}u_{R}\Rightarrow u_{P}=u_{R}. Enthalpy versus temperature diagram illustrating closed system calculation In the case of the constant pressure adiabatic flame temperature, the pressure of the system is held constant, which results in the following equation for the work: R W P = ∫ R P p d V = p ( V P − V R ) {}_{R}W_{P}=\int \limits _{R}^{P}{pdV}=p\left({V_{P}-V_{R}}\right) Again there is no heat transfer occurring because the process is defined to be adiabatic: R Q P = 0 {}_{R}Q_{P}=0. From the first law, we find that, − p ( V P − V R ) = U P − U R ⇒ U P + p V P = U R + p V R -p\left({V_{P}-V_{R}}\right)=U_{P}-U_{R}\Rightarrow U_{P}+pV_{P}=U_{R}+pV_{R} Recalling the definition of enthalpy we obtain H P = H R H_{P}=H_{R}. Because this is a closed system, the mass of the products and reactants is the same and the first law can be written on a mass basis: H P = H R ⇒ m P h P = m R h R ⇒ h P = h R H_{P}=H_{R}\Rightarrow m_{P}h_{P}=m_{R}h_{R}\Rightarrow h_{P}=h_{R}. We see that the adiabatic flame temperature of the constant pressure process is lower than that of the constant volume process. This is because some of the energy released during combustion goes, as work, into changing the volume of the control system. Adiabatic flame temperatures and pressures as a function of ratio of air to iso-octane. A ratio of 1 corresponds to the stoichiometric ratio Constant volume flame temperature of a number of fuels, with air If we make the assumption that combustion goes to completion (i.e. forming only CO 2 and H 2O), we can calculate the adiabatic flame temperature by hand either at stoichiometric conditions or lean of stoichiometry (excess air). This is because there are enough variables and molar equations to balance the left and right hand sides, C α H β O γ N δ + ( a O 2 + b N 2 ) → ν 1 C O 2 + ν 2 H 2 O + ν 3 N 2 + ν 4 O 2 {{\rm {{C}}}}_{\alpha }{{\rm {{H}}}}_{\beta }{{\rm {{O}}}}_{\gamma }{{\rm {{N}}}}_{\delta }+\left({a{{\rm {{O}}}}_{{{\rm {{2}}}}}+b{{\rm {{N}}}}_{{{\rm {{2}}}}}}\right)\to \nu _{1}{{\rm {{CO}}}}_{{{\rm {{2}}}}}+\nu _{2}{{\rm {{H}}}}_{{{\rm {{2}}}}}{{\rm {{O}}}}+\nu _{3}{{\rm {{N}}}}_{{{\rm {{2}}}}}+\nu _{4}{{\rm {{O}}}}_{{{\rm {{2}}}}} Rich of stoichiometry there are not enough variables because combustion cannot go to completion with at least CO and H 2 needed for the molar balance (these are the most common products of incomplete combustion), C α H β O γ N δ + ( a O 2 + b N 2 ) → ν 1 C O 2 + ν 2 H 2 O + ν 3 N 2 + ν 5 C O + ν 6 H 2 {{\rm {{C}}}}_{\alpha }{{\rm {{H}}}}_{\beta }{{\rm {{O}}}}_{\gamma }{{\rm {{N}}}}_{\delta }+\left({a{{\rm {{O}}}}_{{{\rm {{2}}}}}+b{{\rm {{N}}}}_{{{\rm {{2}}}}}}\right)\to \nu _{1}{{\rm {{CO}}}}_{{{\rm {{2}}}}}+\nu _{2}{{\rm {{H}}}}_{{{\rm {{2}}}}}{{\rm {{O}}}}+\nu _{3}{{\rm {{N}}}}_{{{\rm {{2}}}}}+\nu _{5}{{\rm {{CO}}}}+\nu _{6}{{\rm {{H}}}}_{{{\rm {{2}}}}} However, if we include the water gas shift reaction, C O 2 + H 2 ⇔ C O + H 2 O {{\rm {{CO}}}}_{{{\rm {{2}}}}}+H_{2}\Leftrightarrow {{\rm {{CO}}}}+{{\rm {{H}}}}_{{{\rm {{2}}}}}{{\rm {{O}}}} and use the equilibrium constant for this reaction, we will have enough variables to complete the calculation. Different fuels with different levels of energy and molar constituents will have different adiabatic flame temperatures. Constant pressure flame temperature of a number of fuels, with air Nitromethane versus isooctane flame temperature and pressure We can see by the following figure why nitromethane (CH3NO2) is often used as a power boost for cars. Since each molecule of nitromethane contains an oxidant with relatively high-energy bonds between nitrogen and oxygen, it can burn much hotter than hydrocarbons or oxygen-containing methanol. This is analogous to adding pure oxygen, which also raises the adiabatic flame temperature. This in turn allows it to build up more pressure during a constant volume process. The higher the pressure, the more force upon the piston creating more work and more power in the engine. It stays relatively hot rich of stoichiometry because it contains its own oxidant. However, continual running of an engine on nitromethane will eventually melt the piston and/or cylinder because of this higher temperature. Effects of dissociation on adiabatic flame temperature In real world applications, complete combustion does not typically occur. Chemistry dictates that dissociation and kinetics will change the composition of the products. There are a number of programs available that can calculate the adiabatic flame temperature taking into account dissociation through equilibrium constants (Stanjan, NASA CEA, AFTP). The following figure illustrates that the effects of dissociation tend to lower the adiabatic flame temperature. This result can be explained through Le Chatelier's principle. See also Flame speed References See under "Tables" in the external references below. Libal, Angela (27 April 2018). "What Temperatures Do Lighters Burn At?". Leaf Group Ltd. / Leaf Group Media. Sciencing. Flame Temperature Analysis and NOx Emissions for Different Fuels "How hot does magnesium burn? | Reference.com". Archived from the original on 2017-09-17. Retrieved 2017-09-17. CRC Handbook of Chemistry and Physics, 96th Edition, p. 15-51 "North American Combustion Handbook, Volume 1, 3rd edition, North American Mfg Co., 1986". Archived from the original on 2011-07-16. Retrieved 2009-12-09. "Archived copy" (PDF). Archived from the original (PDF) on 2015-09-24. Retrieved 2013-05-19. Power Point Presentation: Flame Temperature, Hsin Chu, Department of Environmental Engineering, National Cheng Kung University, Taiwan Analysis of oxy-fuel combustion power cycle utilizing a pressurized coal combustor by Jongsup Hong et al., MIT, which cites IPCC Special Report on Carbon Dioxide Capture and Storage (PDF). Intergovernmental Panel on Climate Change. 2005. p. 122.. But the IPCC report actually gives a much less precise statement: "The direct combustion of fuel and oxygen has been practised for many years in the metallurgical and glass industries where burners operate at near stoichiometric conditions with flame temperatures of up to 3500°C." The temperature may depend on pressure, because at lower pressure there will be more dissociation of the combustion products, implying a lower adiabatic temperature. External links General information Babrauskas, Vytenis (2006-02-25). "Temperatures in flames and fires". Fire Science and Technology Inc. Archived from the original on 12 January 2008. Retrieved 2008-01-27. Computation of adiabatic flame temperature Adiabatic flame temperature Tables "Adiabatic Flame Temperature". The Engineering Toolbox. Archived from the original on 28 January 2008. Retrieved 2008-01-27. adiabatic flame temperature of hydrogen, methane, propane and octane with oxygen or air as oxidizers "Flame Temperatures for some Common Gases". The Engineering Toolbox. Archived from the original on 7 January 2008. Retrieved 2008-01-27. Temperature of a blue flame and common materials Calculators Online adiabatic flame temperature calculator using Cantera Adiabatic flame temperature program Gaseq, program for performing chemical equilibrium calculations. Flame Temperature Calculator - Constant pressure bipropellant adiabatic combustion Adiabatic Flame Temperature calculator Categories: CombustionTemperatureThreshold temperatures https://en.wikipedia.org/wiki/Adiabatic_flame_temperature Category:State functions Category Talk Read Edit View history Tools Help From Wikipedia, the free encyclopedia Wikimedia Commons has media related to State functions. The main article for this category is State function. Subcategories This category has the following 3 subcategories, out of 3 total. T Thermodynamic entropy (1 C, 41 P) Thermodynamic free energy (9 P) Threshold temperatures (28 P) Pages in category "State functions" The following 15 pages are in this category, out of 15 total. This list may not reflect recent changes. State function E Enthalpy Entropy Entropy (order and disorder) Exergy F Fugacity G Gibbs free energy H Helmholtz free energy I Internal energy P Particle number Pressure T Temperature Thermodynamic free energy Thermodynamic temperature V Volume (thermodynamics) Categories: Thermodynamic propertiesContinuum mechanics Hidden category: Commons category link from Wikidata https://en.wikipedia.org/wiki/Category:State_functions From Wikipedia, the free encyclopedia (Redirected from Eutectoid) "Eutectic" redirects here. For the sports mascot, see St. Louis College of Pharmacy § Mascot. A phase diagram for a fictitious binary chemical mixture (with the two components denoted by A and B) used to depict the eutectic composition, temperature, and point. (L denotes the liquid state.) A eutectic system or eutectic mixture (/juːˈtɛktɪk/ yoo-TEK-tik)[1] is a homogeneous mixture that has a melting point lower than those of the constituents.[2] The lowest possible melting point over all of the mixing ratios of the constituents is called the eutectic temperature. On a phase diagram, the eutectic temperature is seen as the eutectic point (see plot on the right).[3] Non-eutectic mixture ratios would have different melting temperatures for their different constituents, since one component's lattice will melt at a lower temperature than the other's. Conversely, as a non-eutectic mixture cools down, each of its components would solidify (form a lattice) at a different temperature, until the entire mass is solid. Not all binary alloys have eutectic points, since the valence electrons of the component species are not always compatible,[clarification needed] in any mixing ratio, to form a new type of joint crystal lattice. For example, in the silver-gold system the melt temperature (liquidus) and freeze temperature (solidus) "meet at the pure element endpoints of the atomic ratio axis while slightly separating in the mixture region of this axis".[4] The term eutectic was coined in 1884 by British physicist and chemist Frederick Guthrie (1833–1886). The word originates from the Greek εὐ- (eû 'well') and τῆξῐς (têxis 'melting').[2] Eutectic phase transition Four eutectic structures: A) lamellar B) rod-like C) globular D) acicular. The eutectic solidification is defined as follows:[5] Liquid → cooling eutectic temperature α solid solution + β solid solution \text{Liquid} \xrightarrow[\text{cooling}]{\text{eutectic temperature}} \alpha \,\, \text{solid solution} + \beta \,\, \text{solid solution} This type of reaction is an invariant reaction, because it is in thermal equilibrium; another way to define this is the change in Gibbs free energy equals zero. Tangibly, this means the liquid and two solid solutions all coexist at the same time and are in chemical equilibrium. There is also a thermal arrest for the duration of the change of phase during which the temperature of the system does not change.[5] The resulting solid macrostructure from a eutectic reaction depends on a few factors, with the most important factor being how the two solid solutions nucleate and grow. The most common structure is a lamellar structure, but other possible structures include rodlike, globular, and acicular.[6] Non-eutectic compositions Compositions of eutectic systems that are not at the eutectic point can be classified as hypoeutectic or hypereutectic. Hypoeutectic compositions are those with a smaller percent composition of species β and a greater composition of species α than the eutectic composition (E) while hypereutectic solutions are characterized as those with a higher composition of species β and a lower composition of species α than the eutectic composition. As the temperature of a non-eutectic composition is lowered the liquid mixture will precipitate one component of the mixture before the other. In a hypereutectic solution, there will be a proeutectoid phase of species β whereas a hypoeutectic solution will have a proeutectic α phase.[5] Types Alloys Eutectic alloys have two or more materials and have a eutectic composition. When a non-eutectic alloy solidifies, its components solidify at different temperatures, exhibiting a plastic melting range. Conversely, when a well-mixed, eutectic alloy melts, it does so at a single, sharp temperature. The various phase transformations that occur during the solidification of a particular alloy composition can be understood by drawing a vertical line from the liquid phase to the solid phase on the phase diagram for that alloy. Some uses include: NEMA Eutectic Alloy Overload Relays for electrical protection of 3-phase motors for pumps, fans, conveyors, and other factory process equipment.[7] Eutectic alloys for soldering, both traditional alloys composed of lead (Pb) and tin (Sn), sometimes with additional silver (Ag) or gold (Au) — especially Sn63Pb37 and Sn62Pb36Ag2 alloy formula for electronics - and newer lead-free soldering alloys, in particular ones composed of tin (Sn), silver (Ag), and copper (Cu) such as Sn96.5Ag3.5. Casting alloys, such as aluminium-silicon and cast iron (at the composition of 4.3% carbon in iron producing an austenite-cementite eutectic) Silicon chips are bonded to gold-plated substrates through a silicon-gold eutectic by the application of ultrasonic energy to the chip. See eutectic bonding. Brazing, where diffusion can remove alloying elements from the joint, so that eutectic melting is only possible early in the brazing process Temperature response, e.g., Wood's metal and Field's metal for fire sprinklers Non-toxic mercury replacements, such as galinstan Experimental glassy metals, with extremely high strength and corrosion resistance Eutectic alloys of sodium and potassium (NaK) that are liquid at room temperature and used as coolant in experimental fast neutron nuclear reactors. Others Solid–liquid phase change of ethanol–water mixtures Sodium chloride and water form a eutectic mixture whose eutectic point is −21.2 °C[8] and 23.3% salt by mass.[9] The eutectic nature of salt and water is exploited when salt is spread on roads to aid snow removal, or mixed with ice to produce low temperatures (for example, in traditional ice cream making). Ethanol–water has an unusually biased eutectic point, i.e. it is close to pure ethanol, which sets the maximum proof obtainable by fractional freezing. "Solar salt", 60% NaNO3 and 40% KNO3, forms a eutectic molten salt mixture which is used for thermal energy storage in concentrated solar power plants.[10] To reduce the eutectic melting point in the solar molten salts, calcium nitrate is used in the following proportion: 42% Ca(NO3)2, 43% KNO3, and 15% NaNO3. Lidocaine and prilocaine—both are solids at room temperature—form a eutectic that is an oil with a 16 °C (61 °F) melting point that is used in eutectic mixture of local anesthetic (EMLA) preparations. Menthol and camphor, both solids at room temperature, form a eutectic that is a liquid at room temperature in the following proportions: 8:2, 7:3, 6:4, and 5:5. Both substances are common ingredients in pharmacy extemporaneous preparations.[11] Minerals may form eutectic mixtures in igneous rocks, giving rise to characteristic intergrowth textures exhibited, for example, by granophyre.[12] Some inks are eutectic mixtures, allowing inkjet printers to operate at lower temperatures.[13] Choline chloride produces eutectic mixtures with many natural products such as citric acid, malic acid and sugars. These liquid mixtures can be used, for example, to obtain antioxidant and antidiabetic extracts from natural products.[14] Strengthening Mechanisms Alloys The primary strengthening mechanism of the eutectic structure in metals is composite strengthening (See strengthening mechanisms of materials). This deformation mechanism works through load transfer between the two constituent phases where the more compliant phase transfers stress to the stiffer phase[15]. By taking advantage of the strength of the stiff phase and the ductility of the compliant phase, the overall toughness of the material increases. As the composition is varied to either hypoeutectic or hypereutectic formations, the load transfer mechanism becomes more complex as there is now load transfer between the eutectic phase and the secondary phase as well as the load transfer within the eutectic phase itself. A second tunable strengthening mechanism of eutectic structures is the spacing of the secondary phase. By changing the spacing of the secondary phase, the fraction of contact between the two phases through shared phase boundaries is also changed. By decreasing the spacing of the eutectic phase, creating a fine eutectic structure, more surface area is shared between the two constituent phases resulting in more effective load transfer[16]. On the micro-scale, the additional boundary area acts as a barrier to dislocations further strengthening the material. As a result of this strengthening mechanism, coarse eutectic structures tend to be less stiff but more ductile while fine eutectic structures are stiffer but more brittle[16]. The spacing of the eutectic phase can be controlled during processing as it is directly related to the cooling rate during solidification of the eutectic structure. For example, for a simple lamellar eutectic structure, the minimal lamellae spacing is[17]: λ ∗ = 2 γ V m T E Δ H ∗ Δ T 0 {\displaystyle \lambda ^{*}={\frac {2\gamma V_{m}T_{E}}{\Delta H*\Delta T_{0}}}} Where is γ \gamma is the surface energy of the two-phase boundary, V m V_{m} is the molar volume of the eutectic phase, T E T_{E} is the solidification temperature of the eutectic phase, Δ H \Delta H is the enthalpy of formation of the eutectic phase, and Δ T 0 {\displaystyle \Delta T_{0}} is the undercooling of the material. So, by altering the undercooling, and by extension the cooling rate, the minimal achievable spacing of the secondar phase is controlled. Strengthening metallic eutectic phases to resist deformation at high temperatures (see creep deformation) is more convoluted as the primary deformation mechanism changes depending on the level of stress applied. At high temperatures where deformation is dominated by dislocation movement, the strengthening from load transfer and secondary phase spacing remain as they continue to resist dislocation motion. At lower strains where Nabarro-Herring creep is dominant, the shape and size of the eutectic phase structure plays a significant role in material deformation as it affects the available boundary area for vacancy diffusion to occur[18]. Other critical points Iron–carbon phase diagram, showing the eutectoid transformation between austenite (γ) and pearlite. Eutectoid When the solution above the transformation point is solid, rather than liquid, an analogous eutectoid transformation can occur. For instance, in the iron-carbon system, the austenite phase can undergo a eutectoid transformation to produce ferrite and cementite, often in lamellar structures such as pearlite and bainite. This eutectoid point occurs at 723 °C (1,333 °F) and 0.76 wt% carbon.[19] Peritectoid A peritectoid transformation is a type of isothermal reversible reaction that has two solid phases reacting with each other upon cooling of a binary, ternary, ..., n-ary alloy to create a completely different and single solid phase.[20] The reaction plays a key role in the order and decomposition of quasicrystalline phases in several alloy types.[21] A similar structural transition is also predicted for rotating columnar crystals. Peritectic Gold–aluminium phase diagram Peritectic transformations are also similar to eutectic reactions. Here, a liquid and solid phase of fixed proportions react at a fixed temperature to yield a single solid phase. Since the solid product forms at the interface between the two reactants, it can form a diffusion barrier and generally causes such reactions to proceed much more slowly than eutectic or eutectoid transformations. Because of this, when a peritectic composition solidifies it does not show the lamellar structure that is found with eutectic solidification. Such a transformation exists in the iron-carbon system, as seen near the upper-left corner of the figure. It resembles an inverted eutectic, with the δ phase combining with the liquid to produce pure austenite at 1,495 °C (2,723 °F) and 0.17% carbon. At the peritectic decomposition temperature the compound, rather than melting, decomposes into another solid compound and a liquid. The proportion of each is determined by the lever rule. In the Al-Au phase diagram, for example, it can be seen that only two of the phases melt congruently, AuAl2 and Au2Al , while the rest peritectically decompose. Eutectic calculation The composition and temperature of a eutectic can be calculated from enthalpy and entropy of fusion of each components.[22] The Gibbs free energy G depends on its own differential: G = H − T S ⇒ { H = G + T S ( ∂ G ∂ T ) P = − S ⇒ H = G − T ( ∂ G ∂ T ) P . {\displaystyle G=H-TS\Rightarrow {\begin{cases}H=G+TS\\\left({\frac {\partial G}{\partial T}}\right)_{P}=-S\end{cases}}\Rightarrow H=G-T\left({\frac {\partial G}{\partial T}}\right)_{P}.} Thus, the G/T derivative at constant pressure is calculated by the following equation: ( ∂ G / T ∂ T ) P = 1 T ( ∂ G ∂ T ) P − 1 T 2 G = − 1 T 2 ( G − T ( ∂ G ∂ T ) P ) = − H T 2 . {\displaystyle \left({\frac {\partial G/T}{\partial T}}\right)_{P}={\frac {1}{T}}\left({\frac {\partial G}{\partial T}}\right)_{P}-{\frac {1}{T^{2}}}G=-{\frac {1}{T^{2}}}\left(G-T\left({\frac {\partial G}{\partial T}}\right)_{P}\right)=-{\frac {H}{T^{2}}}.} The chemical potential μ i \mu _{i} is calculated if we assume that the activity is equal to the concentration: μ i = μ i ∘ + R T ln a i a ≈ μ i ∘ + R T ln x i . {\displaystyle \mu _{i}=\mu _{i}^{\circ }+RT\ln {\frac {a_{i}}{a}}\approx \mu _{i}^{\circ }+RT\ln x_{i}.} At the equilibrium, μ i = 0 {\displaystyle \mu _{i}=0}, thus μ i ∘ \mu_i^\circ is obtained as μ i = μ i ∘ + R T ln x i = 0 ⇒ μ i ∘ = − R T ln x i . {\displaystyle \mu _{i}=\mu _{i}^{\circ }+RT\ln x_{i}=0\Rightarrow \mu _{i}^{\circ }=-RT\ln x_{i}.} Using[clarification needed] and integrating gives ( ∂ μ i / T ∂ T ) P = ∂ ∂ T ( R ln x i ) ⇒ R ln x i = − H i ∘ T + K . {\displaystyle \left({\frac {\partial \mu _{i}/T}{\partial T}}\right)_{P}={\frac {\partial }{\partial T}}\left(R\ln x_{i}\right)\Rightarrow R\ln x_{i}=-{\frac {H_{i}^{\circ }}{T}}+K.} The integration constant K may be determined for a pure component with a melting temperature T ∘ T^\circ and an enthalpy of fusion H ∘ H^\circ: x i = 1 ⇒ T = T i ∘ ⇒ K = H i ∘ T i ∘ . {\displaystyle x_{i}=1\Rightarrow T=T_{i}^{\circ }\Rightarrow K={\frac {H_{i}^{\circ }}{T_{i}^{\circ }}}.} We obtain a relation that determines the molar fraction as a function of the temperature for each component: R ln x i = − H i ∘ T + H i ∘ T i ∘ . {\displaystyle R\ln x_{i}=-{\frac {H_{i}^{\circ }}{T}}+{\frac {H_{i}^{\circ }}{T_{i}^{\circ }}}.} The mixture of n components is described by the system { ln x i + H i ∘ R T − H i ∘ R T i ∘ = 0 , ∑ i = 1 n x i = 1. {\displaystyle {\begin{cases}\ln x_{i}+{\frac {H_{i}^{\circ }}{RT}}-{\frac {H_{i}^{\circ }}{RT_{i}^{\circ }}}=0,\\\sum \limits _{i=1}^{n}x_{i}=1.\end{cases}}} { ∀ i < n ⇒ ln x i + H i ∘ R T − H i ∘ R T i ∘ = 0 , ln ( 1 − ∑ i = 1 n − 1 x i ) + H n ∘ R T − H n ∘ R T n ∘ = 0 , {\displaystyle {\begin{cases}\forall i

Battle of a French ship of the line and two galleys of the Barbary corsairs
https://en.wikipedia.org/wiki/Barbary_pirates#/media/File:Th%C3%A9odore_Gudin-Combat_d'un_vaisseau_fran%C3%A7ais_et_de_deux_gal%C3%A8res_barbaresques_mg_5061.jpg
https://en.wikipedia.org/wiki/Valencia
https://en.wikipedia.org/wiki/Spain
https://en.wikipedia.org/wiki/Fall_of_the_Western_Roman_Empire
https://en.wikipedia.org/wiki/Visigothic_Kingdom
https://en.wikipedia.org/wiki/Hispania
https://en.wikipedia.org/wiki/Galicia_(Spain)
https://en.wikipedia.org/wiki/Atlantic_Europe
https://en.wikipedia.org/wiki/Bell_Beaker_culture
https://en.wikipedia.org/wiki/Maghreb
https://en.wikipedia.org/wiki/Barbary_Coast
https://en.wikipedia.org/wiki/Tunisian_navy_(1705%E2%80%931881)
https://en.wikipedia.org/wiki/Bronze_Age_Europe
https://en.wikipedia.org/wiki/Bronze_Age_in_Romania
https://en.wikipedia.org/wiki/Inverted_bell
https://en.wikipedia.org/wiki/Corinthian_order
https://en.wikipedia.org/wiki/Trajan
https://en.wikipedia.org/wiki/Haplogroup_R1b
| Haplogroup R1b | |
|---|---|
| Possible time of origin | Probably soon after R1, possibly between 18,000-14,000 BC[1] |
| Possible place of origin | Western Asia, North Eurasia or Eastern Europe[2] |
| Ancestor | R1 |
| Descendants |
|
| Defining mutations | M343 |
Haplogroup R1b (R-M343), previously known as Hg1 and Eu18, is a human Y-chromosome haplogroup.
It is the most frequently occurring paternal lineage in Western Europe, as well as some parts of Russia (e.g. the Bashkirs) and pockets of Central Africa (e.g. parts of Chad and among the Chadic-speaking minority ethnic groups of Cameroon). The clade is also present at lower frequencies throughout Eastern Europe, Western Asia, as well as parts of North Africa, South Asia and Central Asia.
https://en.wikipedia.org/wiki/Haplogroup_R1b
https://en.wikipedia.org/wiki/Samara
https://en.wikipedia.org/wiki/Novokuybyshevsk
https://en.wikipedia.org/wiki/Russia
2000 1900 1500 0 -1500 -3000 3000 6000 9000 -10000 -20000 -100000 -1m -3m -6m -b
5b 5quint exp
1cent -1cent inf unk unc n/a -inf 0
universe age unk earth age unk est.
The Neanderthals continued to use Mousterian stone tool technology and possibly Châtelperronian technology. These tools disappeared from the archeological record at around the same time the Neanderthals themselves disappeared from the fossil record, about 40,000 cal BP.[6]
https://en.wikipedia.org/wiki/Upper_Paleolithic
The peopling of Australia most likely took place before c. 60 ka. Europe was peopled after c. 45 ka. Anatomically modern humans are known to have expanded northward into Siberia as far as the 58th parallel by about 45 ka (Ust'-Ishim man). The Upper Paleolithic is divided by the Last Glacial Maximum (LGM), from about 25 to 15 ka. The peopling of the Americas occurred during this time, with East and Central Asia populations reaching the Bering land bridge after about 35 ka, and expanding into the Americas by about 15 ka. In Western Eurasia, the Paleolithic eases into the so-called Epipaleolithic or Mesolithic from the end of the LGM, beginning 15 ka. The Holocene glacial retreat begins 11.7 ka (10th millennium BC), falling well into the Old World Epipaleolithic, and marking the beginning of the earliest forms of farming in the Fertile Crescent.
https://en.wikipedia.org/wiki/Upper_Paleolithic
 | |
| Geographical range | Western Europe |
|---|---|
| Period | Upper Paleolithic Mesolithic |
| Dates | c. 17,000 – c. 12,000 BP[a][is this date calibrated?] |
| Type site | Abri de la Madeleine |
| Major sites | Cave of Altamira, Kents Cavern, Lascaux |
| Preceded by | Solutrean |
| Followed by | Azilian, Ahrensburg culture |
Magdalenian cave painting
https://en.wikipedia.org/wiki/Magdalenian
Chronology
The culture spans from approximately 17,000 to 12,000 BP,[is this date calibrated?] toward the end of the most recent ice age. Magdalenian tool culture is characterised by regular blade industries struck from carinated cores.
The Magdalenian epoch is divided into six phases generally agreed to have chronological significance (Magdalenian I through VI, I being the earliest and VI being the latest). The earliest phases are recognised by the varying proportion of blades and specific varieties of scrapers, the middle phases marked by the emergence of a microlithic component (particularly the distinctive denticulated microliths), and the later phases by the presence of uniserial (phase 5) and biserial 'harpoons' (phase 6) made of bone, antler and ivory.[3]
Debate continues about the nature of the earliest Magdalenian assemblages, and it remains questionable whether the Badegoulian culture is the earliest phase of Magdalenian culture. Similarly, finds from the forest of Beauregard near Paris have been suggested as belonging to the earliest Magdalenian.[5] The earliest Magdalenian sites are in France. The Epigravettian is a similar culture appearing at the same time. Its known range extends from southeast France to the western shores of the Volga River, Russia, with many sites in Italy.
The later phases of Magdalenian culture are contemporaneous with the human re-settlement of north-western Europe after the Last Glacial Maximum during the Late Glacial Maximum.[6][7] As hunter gatherers, Magdalenians did not re-settle permanently in northwest Europe, instead following herds and seasons.
By the end of the Magdalenian epoch, lithic technology shows a pronounced trend toward increased microlithisation. The bone harpoons and points have the most distinctive chronological markers within the typological sequence. As well as flint tools, Magdalenians are known for their elaborate worked bone, antler and ivory that served both functional and aesthetic purposes, including perforated batons.
The sea shells and fossils found in Magdalenian sites may be sourced to relatively precise areas and have been used to support hypotheses of Magdalenian hunter-gatherer seasonal ranges, and perhaps trade routes.
In northern Spain and south-west France this tool culture was superseded by the Azilian culture. In northern Europe it was followed by variants of the Tjongerian techno-complex. It has been suggested that key Late-glacial sites in south-western Britain may be attributed to Magdalenian culture, including Kent's Cavern.
Art
Bones, reindeer antlers and animal teeth display crude pictures carved or etched on them of seals, fish, reindeer, mammoths and other creatures.
The best of Magdalenian artworks are a mammoth engraved on a fragment of its own ivory;[dubious ] a dagger of reindeer antler, with a handle in form of a reindeer; a cave-bear cut on a flat piece of schist; a seal on a bear's tooth; a fish drawn on a reindeer antler; and a complete picture, also on reindeer antler, showing horses, an aurochs, trees, and a snake biting a man's leg. The man is naked, which, together with the snake, suggests a warm climate in spite of the presence of the reindeer.
In the Tuc d'Audoubert cave, an 18-inch clay statue of two bison sculpted in relief was discovered in the deepest room, now known as the Room of the Bisons.[8]
Examples of Magdalenian portable art include batons, figurines, and intricately engraved projectile points, as well as items of personal adornment including sea shells, perforated carnivore teeth (presumably necklaces), and fossils.
Cave sites such as Lascaux contain the best known examples of Magdalenian cave art. The site of Altamira in Spain, with its extensive and varied forms of Magdalenian mobiliary art has been suggested to be an agglomeration site where groups of Magdalenian hunter-gatherers congregated.[9]
Gallery
Treatment of the dead
Some skulls were cleaned of soft tissues, then had the facial regions removed, with the remaining brain case retouched, possibly to make the broken edges more regular. This manipulation suggests the shaping of skulls to produce skull cups.[10]
Genetics
The genes of seven Magdalenians, the El Miron Cluster in Iberia, have shown close relationship to a population who had lived in Northern Europe some 20,000 years previously. The analyses suggested that 70-80% of the ancestry of these individuals was from the population represented by Goyet Q116-1, associated with the Aurignacian culture of about 35,000 BP, from the Goyet Caves in modern Belgium.[11]
The three samples of Y-DNA included two samples of haplogroup I and one sample of HIJK. All samples of mtDNA belonged to U, including five samples of U8b and one sample of U5b.
https://en.wikipedia.org/wiki/Magdalenian
It is unclear whether radiocarbon dates in this article are calibrated or not. (August 2018) |
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (May 2021) |
 | |
| Geographical range | Western Europe |
|---|---|
| Period | Upper Paleolithic Mesolithic |
| Dates | c. 17,000 – c. 12,000 BP[a][is this date calibrated?] |
| Type site | Abri de la Madeleine |
| Major sites | Cave of Altamira, Kents Cavern, Lascaux |
| Preceded by | Solutrean |
| Followed by | Azilian, Ahrensburg culture |
The Magdalenian cultures (also Madelenian; French: Magdalénien) are later cultures of the Upper Paleolithic and Mesolithic in western Europe. They date from around 17,000 to 12,000 years ago.[a][is this date calibrated?] It is named after the type site of La Madeleine, a rock shelter located in the Vézère valley, commune of Tursac, in France's Dordogne department.
Édouard Lartet and Henry Christy originally termed the period L'âge du renne (the Age of the Reindeer). They conducted the first systematic excavations of the type site, publishing in 1875. The Magdalenian epoch is associated with reindeer hunters, although Magdalenian sites contain extensive evidence for the hunting of red deer, horses, and other large mammals present in Europe toward the end of the last glacial period. The culture was geographically widespread, and later Magdalenian sites stretched from Portugal in the west to Poland in the east, and as far north as France, the Channel Islands, England, and Wales. It is the third epoch of Gabriel de Mortillet's cave chronology system, corresponding roughly to the Late Pleistocene. Besides La Madeleine, the chief stations of the epoch are Les Eyzies, Laugerie-Basse, and Gorges d'Enfer in the Dordogne; Grotte du Placard in Charente and others in south-west France.
Period biology
The Magdalenian epoch is represented by numerous sites, whose contents show progress in arts and culture. It was characterized by a cold and dry climate, humans in association with the reindeer, and the extinction of the mammoth. The use of bone and ivory as implements, begun in the preceding Solutrean epoch, increased, making the period essentially a bone period. Bone instruments are quite varied: spear-points, harpoon-heads, borers, hooks and needles.[citation needed]
The fauna of the Magdalenian epoch seems to have included tigers and other tropical species along with reindeer, arctic foxes, arctic hares, and other polar creatures. Magdalenian humans appear to have been of short stature, dolichocephalic, with a low retreating forehead and prominent brow ridges.[citation needed]
Chronology
The culture spans from approximately 17,000 to 12,000 BP,[is this date calibrated?] toward the end of the most recent ice age. Magdalenian tool culture is characterised by regular blade industries struck from carinated cores.
The Magdalenian epoch is divided into six phases generally agreed to have chronological significance (Magdalenian I through VI, I being the earliest and VI being the latest). The earliest phases are recognised by the varying proportion of blades and specific varieties of scrapers, the middle phases marked by the emergence of a microlithic component (particularly the distinctive denticulated microliths), and the later phases by the presence of uniserial (phase 5) and biserial 'harpoons' (phase 6) made of bone, antler and ivory.[3]
Debate continues about the nature of the earliest Magdalenian assemblages, and it remains questionable whether the Badegoulian culture is the earliest phase of Magdalenian culture. Similarly, finds from the forest of Beauregard near Paris have been suggested as belonging to the earliest Magdalenian.[5] The earliest Magdalenian sites are in France. The Epigravettian is a similar culture appearing at the same time. Its known range extends from southeast France to the western shores of the Volga River, Russia, with many sites in Italy.
The later phases of Magdalenian culture are contemporaneous with the human re-settlement of north-western Europe after the Last Glacial Maximum during the Late Glacial Maximum.[6][7] As hunter gatherers, Magdalenians did not re-settle permanently in northwest Europe, instead following herds and seasons.
By the end of the Magdalenian epoch, lithic technology shows a pronounced trend toward increased microlithisation. The bone harpoons and points have the most distinctive chronological markers within the typological sequence. As well as flint tools, Magdalenians are known for their elaborate worked bone, antler and ivory that served both functional and aesthetic purposes, including perforated batons.
The sea shells and fossils found in Magdalenian sites may be sourced to relatively precise areas and have been used to support hypotheses of Magdalenian hunter-gatherer seasonal ranges, and perhaps trade routes.
In northern Spain and south-west France this tool culture was superseded by the Azilian culture. In northern Europe it was followed by variants of the Tjongerian techno-complex. It has been suggested that key Late-glacial sites in south-western Britain may be attributed to Magdalenian culture, including Kent's Cavern.
Art
Bones, reindeer antlers and animal teeth display crude pictures carved or etched on them of seals, fish, reindeer, mammoths and other creatures.
The best of Magdalenian artworks are a mammoth engraved on a fragment of its own ivory;[dubious ] a dagger of reindeer antler, with a handle in form of a reindeer; a cave-bear cut on a flat piece of schist; a seal on a bear's tooth; a fish drawn on a reindeer antler; and a complete picture, also on reindeer antler, showing horses, an aurochs, trees, and a snake biting a man's leg. The man is naked, which, together with the snake, suggests a warm climate in spite of the presence of the reindeer.
In the Tuc d'Audoubert cave, an 18-inch clay statue of two bison sculpted in relief was discovered in the deepest room, now known as the Room of the Bisons.[8]
Examples of Magdalenian portable art include batons, figurines, and intricately engraved projectile points, as well as items of personal adornment including sea shells, perforated carnivore teeth (presumably necklaces), and fossils.
Cave sites such as Lascaux contain the best known examples of Magdalenian cave art. The site of Altamira in Spain, with its extensive and varied forms of Magdalenian mobiliary art has been suggested to be an agglomeration site where groups of Magdalenian hunter-gatherers congregated.[9]
Gallery
Treatment of the dead
Some skulls were cleaned of soft tissues, then had the facial regions removed, with the remaining brain case retouched, possibly to make the broken edges more regular. This manipulation suggests the shaping of skulls to produce skull cups.[10]
Genetics
The genes of seven Magdalenians, the El Miron Cluster in Iberia, have shown close relationship to a population who had lived in Northern Europe some 20,000 years previously. The analyses suggested that 70-80% of the ancestry of these individuals was from the population represented by Goyet Q116-1, associated with the Aurignacian culture of about 35,000 BP, from the Goyet Caves in modern Belgium.[11]
The three samples of Y-DNA included two samples of haplogroup I and one sample of HIJK. All samples of mtDNA belonged to U, including five samples of U8b and one sample of U5b.
See also
| The Paleolithic |
|---|
| ↑ Pliocene (before Homo) |
|
|
|
|
|
|
| ↓ Mesolithic |
- Magdalenian Girl
- Swimming Reindeer
- Art of the Upper Paleolithic
- List of Stone Age art
- Haplogroup I (Y-DNA)
- Pre-Celtic
References
Notes
Footnotes
Bibliography
- This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed. (1911). "Madelenian". Encyclopædia Britannica. Vol. 17 (11th ed.). Cambridge University Press. pp. 283–284.
- Charles, Ruth (1996). "Back into the North: the Radiocarbon Evidence for the Human Recolonisation of the North-Western Ardennes after the Last Glacial Maximum". Proceedings of the Prehistoric Society. 62: 1–17. doi:10.1017/s0079497x00002711. ISSN 0079-497X. S2CID 128580542.
- Conkey, M.W.; Beltrán, A.; Clark, G.A.; Echegaray, J.G.; Guenther, M.G.; Hahn, J.; Hayden, B.; Paddayya, K.; Straus, L.G.; Valoch, K. (October 1980). "The Identification of Prehistoric Hunter-Gatherer Aggregation Sites: The Case of Altamira [and Comments and Reply]". Current Anthropology. 21 (5): 609–630. doi:10.1086/202540. ISSN 0011-3204. S2CID 145367811.
- Enloe, J. (2001). "Magdalenian". In Peregrine, P.N.; Ember, M. (eds.). Encyclopedia of Prehistory. Boston, MA: Springer. pp. 198–209. doi:10.1007/978-1-4615-1187-8_16. ISBN 978-1-4684-7131-1.
- Fu, Q.; Posth, C.; Hajdinjak, M.; et al. (May 2, 2016). "The genetic history of Ice Age Europe". Nature. 534 (7606): 200–205. Bibcode:2016Natur.534..200F. doi:10.1038/nature17993. PMC 4943878. PMID 27135931.
- Hemingway, M.F. (1980). The Initial Magdalenian in France. B.A.R. ISBN 0860541045. OCLC 7368169.
- Housley, R.A.; Gamble, C.S.; Street, M.; Pettitt, P. (1997). "Radiocarbon evidence for the Lateglacial Human Recolonisation of Northern Europe". Proceedings of the Prehistoric Society. 63: 25–54. doi:10.1017/s0079497x0000236x. ISSN 0079-497X. S2CID 130323509.
- Lartet, E.; Christy, H. (1875). Reliquae Aquitanicae: being contributions to the archaeology of Périgord and adjoining provinces of Southern France. London: Williams & Norgate.
- de Sonneville-Bordes, D.; Perrot, J. (1956). "Lexique typologique du Paléolithique supérieur". Bulletin de la Société préhistorique de France. 53 (7): 408–412. doi:10.3406/bspf.1956.3357. ISSN 0037-9514.
- Straus, Lawrence Guy (1992). Iberia Before the Iberians. University of New Mexico Press.
External links
- "Pictures and description of the La Madeleine site". 2009-03-01. Archived from the original on 2009-03-01. Retrieved 2019-09-28.
- Picture Gallery of the Paleolithic (reconstructional palaeoethnology), Libor Balák at the Czech Academy of Sciences, the Institute of Archaeology in Brno, The Center for Paleolithic and Paleoethnological Research
https://en.wikipedia.org/wiki/Magdalenian
Knapping is the shaping of flint, chert, obsidian, or other conchoidal fracturing stone through the process of lithic reduction to manufacture stone tools, strikers for flintlock firearms, or to produce flat-faced stones for building or facing walls, and flushwork decoration. The original Germanic term knopp meant to strike, shape, or work, so it could theoretically have referred equally well to making statues or dice. Modern usage is more specific, referring almost exclusively to the hand-tool pressure-flaking process pictured. It is distinguished from the more general verb "chip" (to break up into small pieces, or unintentionally break off a piece of something) and is different from "carve" (removing only part of a face), and "cleave" (breaking along a natural plane).
https://en.wikipedia.org/wiki/Knapping
Flint jewelry was known in the prehistoric, protodynastic, and early dynastic periods of ancient Egypt. Ancient Egyptians skillfully made bracelets[1][2] and armlets[3][4] out of flint.
The flint came from locations that include Giza and Upper Egypt.[5] The exact technique used to form rings is not known, but there are several theories based on the examples that have been found in graves and workshops.
Flint bracelets can be found in collections such as those in the Cairo Museum of Egyptian Antiquities,[6] the Fitzwilliam Museum,[7] the Pitt Rivers Museum,[8] the Metropolitan Museum of Art,[9] and the Brooklyn Museum.[10]
See also
- Clothing in ancient Egypt
- Eccentric flint (archaeology)
- Knapping
- Lithic reduction
- Oldowan, the earliest stone tool industry in prehistory
References
- "Flint bracelet". Brooklyn Museum. Retrieved 11 June 2012.
- Predynastic Egypt
- Art of ancient Egypt
- Egyptian artefact types
- Jewellery making
- Egyptian inventions
- Flint (rock)
- Visual arts stubs
- Ancient Egypt stubs
https://en.wikipedia.org/wiki/Ancient_Egyptian_flint_jewelry
Naqada III is the last phase of the Naqada culture of ancient Egyptian prehistory, dating from approximately 3200 to 3000 BC.[2] It is the period during which the process of state formation, which began in Naqada II, became highly visible, with named kings heading powerful polities. Naqada III is often referred to as Dynasty 0 or the Protodynastic Period[2] to reflect the presence of kings at the head of influential states, although, in fact, the kings involved would not have been a part of a dynasty. In this period, those kings' names were inscribed in the form of serekhs on a variety of surfaces including pottery and tombs.
https://en.wikipedia.org/wiki/Naqada_III
In archaeology, in particular of the Stone Age, lithic reduction is the process of fashioning stones or rocks from their natural state into tools or weapons by removing some parts. It has been intensely studied and many archaeological industries are identified almost entirely by the lithic analysis of the precise style of their tools and the chaîne opératoire of the reduction techniques they used.
Normally the starting point is the selection of a piece of tool stone that has been detached by natural geological processes, and is an appropriate size and shape. In some cases solid rock or larger boulders may be quarried and broken into suitable smaller pieces, and in others the starting point may be a piece of the debitage, a flake removed from a previous operation to make a larger tool. The selected piece is called the lithic core (also known as the "objective piece"). A basic distinction is that between flaked or knapped stone, the main subject here, and ground stone objects made by grinding. Flaked stone reduction involves the use of a hard hammer percussor, such as a hammerstone, a soft hammer fabricator (made of wood, bone or antler), or a wood or antler punch to detach lithic flakes from the lithic core. As flakes are detached in sequence, the original mass of stone is reduced; hence the term for this process. Lithic reduction may be performed in order to obtain sharp flakes, of which a variety of tools can be made, or to rough out a blank for later refinement into a projectile point, knife, or other object. Flakes of regular size that are at least twice as long as they are broad are called blades. Lithic tools produced this way may be bifacial (exhibiting flaking on both sides) or unifacial (exhibiting flaking on one side only).
Cryptocrystalline or amorphous stone such as chert, flint, obsidian, and chalcedony, as well as other fine-grained stone material, such as rhyolite, felsite, and quartzite, were used as a source material for producing stone tools. As these materials lack natural planes of separation, conchoidal fractures occur when they are struck with sufficient force; for these stones this process is called knapping. The propagation of force through the material takes the form of a Hertzian cone that originates from the point of impact and results in the separation of material from the objective piece, usually in the form of a partial cone, commonly known as a lithic flake. This process is predictable, and allows the flintknapper to control and direct the application of force so as to shape the material being worked. Controlled experiments may be performed using glass cores and consistent applied force in order to determine how varying factors affect core reduction.[1]
It has been shown that stages in the lithic reduction sequence may be misleading and that a better way to assess the data is by looking at it as a continuum. The assumptions that archaeologists sometimes make regarding the reduction sequence based on the placement of a flake into a stage can be unfounded. For example, a significant amount of cortex can be present on a flake taken off near the very end of the reduction sequence.[2] Removed flakes exhibit features characteristic of conchoidal fracturing, including striking platforms, bulbs of force, and occasionally eraillures (small secondary flakes detached from the flake's bulb of force). Flakes are often quite sharp, with distal edges only a few molecules thick when they have a feather termination. These flakes can be used directly as tools or modified into other utilitarian implements, such as spokeshaves and scrapers.
Reduction index
By understanding the complex processes of lithic reduction, archaeologists recognize that the pattern and amount of reduction contribute tremendous effect to lithic assemblage compositions. One of the measurements is the geometric index of reduction. There are two elements in this index: 't' and 'T'. The 'T' is the 'height' of maximum blank thickness and the 't' is the height of retouched scar from the ventral surface. The ratio between t and T is the geometric index of reduction. In theory this ratio shall range between 0 and 1.[3] The bigger the number is the larger amount of lost weight from lithic flake. By using a logarithmic scale, a linear relationship between the geometric index and the percentage of original flake weight lost through retouch is confirmed.[4] In choosing a reduction index, it is important to understand the strengths and weaknesses of each method, and how they fit to the intended research question, as different indices provide different levels of information.[5] For example, Kuhn's geometric index of unifacial reduction (GIUR), which describes the ratio of scar height relative to the flake thickness, is highly influenced by the morphology of the flake blank which limits the applicability of this reduction index.[5]
Techniques
Alongside the various percussion and manipulation techniques described below, there is evidence that heat was at least sometimes used. Experimental archaeology has demonstrated that heated stones are sometimes much easier to flake, with larger flakes being produced in flint, for example. In some cases the heating changes the colour of the stone.[6]
Percussion reduction
Percussion reduction, or percussion flaking, refers to removal of flakes by impact. Generally, a core or other objective piece, such as a partially formed tool, is held in one hand, and struck with a hammer or percussor. Alternatively, the objective piece can also be struck between a stationary anvil-stone, known as bipolar percussion. Percussion can also be done by throwing the objective piece at an anvil stone. This is sometimes called projectile percussion. Percussors are traditionally either a stone cobble or pebble, often referred to as a hammerstone, or a billet made of bone, antler, or wood.[7] Often, flakes are struck from a core using a punch, in which case the percussor never actually makes contact with the objective piece. This technique is referred to as indirect percussion.[8]
Projectile percussion
Projectile percussion is so basic as to not be considered a technique. It involves throwing the toolstone at a stationary anvil stone. This method provides virtually no control over how the toolstone will fragment, and therefore produces a great deal of shatter, and few flakes. It is difficult to be sure whether or not this method of lithic reduction was ever a commonplace practice, although noting sharp edges on a broken rock might have led early humans to first recognize the value of lithic reduction.
Bipolar percussion
In bipolar percussion the objective piece of toolstone is placed on an anvil stone, and then the percussion force is applied to the tool stone.[9] Like projectile percussion, the tool stone is likely to shatter, rather than producing a single flake. Unlike projectile percussion, the technique has some degree of control to it. Bipolar percussion is not popular with hobbyists, but there is evidence that bipolar percussion was the preferred way of dealing with certain problems. Bipolar percussion has the benefit of producing many sharp flakes, and triangular pieces of stone which can be useful as drills. Bipolar percussion also does not require the manufacturer to locate a platform before setting to work, and bipolar percussion can produce sharp flakes almost the size of the original piece of tool stone. The lack of control makes bipolar percussion undesirable in many situations, but the benefits mean that it often has a use, especially if workable material is rare. Bipolar percussion is often used to break open small cobbles, or to have a second chance with spent lithic cores, broken bifaces, and tools that have been reworked so much that it is impossible to make further useful tools using traditional lithic reduction. The end result of bipolar percussion is often a big mess, with only a few pieces that can be useful as cores or flakes for further working, but if other methods would result in a total dead-end, bipolar percussion may be desirable.
An alternative view of the bipolar reduction technique is offered by Jan Willem Van der Drift which contradicts the suggestion that there is little control over fracturing. The characteristics of bipolar reduction are different from that occurring in conchoidal fracture and are therefore often misinterpreted by archaeologists and lithic experts.
Hard-hammer percussion
Hard hammer techniques are generally used to remove large flakes of stone. Early flintknappers and hobbyists replicating their methods often use cobbles of very hard stone, such as quartzite. This technique can be used by flintknappers to remove broad flakes that can be made into smaller tools. This method of manufacture is believed to have been used to make some of the earliest stone tools ever found, some of which date from over 2 million years ago.[10]
It is the use of hard-hammer percussion that most often results in the formation of the typical features of conchoidal fracture on the detached flake, such as the bulb of percussion and compression rings.[11]
Soft-hammer percussion
Soft-hammer percussion involves the use of a billet, usually made of wood, bone or antler as the percussor. These softer materials are easier to shape than stone hammers, and therefore can be made into more precise tools. Soft hammers also deform around the sharp edges of worked stone, rather than shattering through them, making it desirable for working tool stone that already has been worked to some degree before. Soft hammers of course also do not have as much force behind them as hard hammers do. Flakes produced by soft hammers are generally smaller and thinner than those produced by hard-hammer flaking; thus, soft-hammer flaking is often used after hard-hammer flaking in a lithic reduction sequence to do finer work.[12] As well as this, soft-hammers can produce longer flakes which aid in the conservation of materials because they produce a longer cutting edge per unit of mass lost.[13]
In most cases, the amount of pressure applied to the objective piece in soft-hammer percussion is not enough for the formation of a typical conchoidal fracture. Rather, soft-hammer flakes are most often produced by what is referred to as a bending fracture, so-called because the flake is quite literally bent or "peeled" from the objective piece. A bending fracture can be produced with a hard hammer.[14] Flakes removed in this manner lack a bulb of percussion, and are distinguished instead by the presence of a small lip where the flake's striking platform has separated from the objective piece.[15]
Indirect percussion
Indirect percussion involves the use of a punch and hammer. The punch and hammer make it possible to apply large force to very small areas of a stone tool. Indirect percussion is therefore often used to achieve detail work on smaller tools. Some modern hobbyists make use of indirect percussion almost exclusively, with little or no pressure flaking to finish their work.
Since indirect percussion can be so precisely placed, the platform is often much smaller on flakes produced in this way than in other methods of flake removal. Of course, indirect percussion requires two hands to hold the percussing tool set. One holds the hammer, and one holds the punch. Therefore, modern hobbyists must use a third object in order to hold the targeted piece of tool stone while they strike it. Often, some sort of clamp or vise is used. No evidence for such devices has yet been found in the archaeological record, but this is partly because they would normally be made of perishable materials, and partly because they can have great variation in design.
Pressure flaking
Pressure flaking is a method of trimming the edge of a stone tool by removing small lithic flakes by pressing on the stone with a sharp instrument rather than striking it with a percussor. This method, which often uses punches made from bone or antler tines (or, among modern hobbyists, copper punches or even nails), provides a greater means of controlling the direction and quantity of the applied force than when using even the most careful percussive flaking. Copper retoucheurs to facilitate this process were widely employed in the Early Bronze Age – and may therefore be associated with Beaker Culture in northwestern Europe.
Usually, the objective piece is held clasped in the flintknapper's hand, with a durable piece of fabric or leather protecting the flintknapper's palm from the sharpness of the flakes removed. The tip of the flaking tool is placed against the edge of the stone tool and pressed hard, removing a small linear or lunate flake from the opposite side. The process also involves frequent preparation of the edge to form better platforms for pressing off flakes. This is usually accomplished with abraiders made from a coarse-grained stone such as basalt or quartzite. Great care must be taken during pressure flaking so that perverse fractures that break the entire tool do not occur. Occasionally, outrepasse breaks occur when the force propagates across and through the tool in such a way that the entire opposite margin is removed.[16]
The use of pressure flaking facilitated the early production of sharper and more finely detailed tools. Pressure flaking also gave toolmakers the ability to create notches where the objective piece could be bound more securely to the shaft of the weapon or tool and increasing the object's utility.
An archaeological discovery in 2010 in Blombos Cave, South Africa, places the use of pressure flaking by early humans to make stone tools back to 73,000 BCE, 55,000 years earlier than previously accepted. The previously accepted date, "no more than 20,000 years ago",[17] was based upon the earliest evidence previously available, which derived from findings of the Upper Paleolithic Solutrean culture in France and Spain.[18]
Blanks and preforms
A blank is a stone of suitable size and shape to be worked into a stone tool. Blanks are the starting point of a lithic reduction process, and during prehistoric times were often transported or traded for later refinement at another location. Blanks might be stones or cobbles, just as natural processes have left them, or might be quarried pieces, or flakes that are debitage from making another piece. Whatever their origin, on most definitions no further steps have yet been taken to shape them, or they become a preform.[19]
The next stage creates a preform, or roughly shaped piece of stone, that probably reveals the final form of the tool, but is not complete.[19] Preforms might also be transported or traded. Typically, a preform is the shaped remnant of a lithic core. Larger and thicker than the intended tool, it lacks the final trimming and refinement that is present in the completed artifact. Sometimes basic features such as stems and notches have been initiated. In most cases, the term refers to an incomplete projectile point.
See also
Notes
- Kooyman (2000), p. 47
References
- Andrefsky, W. (2005). Lithics: Macroscopic Approaches to Analysis. Cambridge: Cambridge University Press. ISBN 0-521-61500-3.
- Cotterell, B.; Kamminga, J. (1987). "The Formation of Flakes". American Antiquity. 52: 675–708. doi:10.2307/281378. JSTOR 281378. S2CID 163565502.
- Kooyman, Brian Patrick (2000). Understanding Stone Tools and Archaeological Sites. UNM Press. ISBN 9780826323330.
- Macgregor, O.J. (2005). "Abrupt Terminations and stone artefact reduction potential". In Clarkson, C.; Lamb, L. (eds.). Lithics ‘Down Under’: Australian Approaches to Lithic Reduction, Use and Classification. British Archaeological Reports International Monograph Series S1408. Oxford: Archaeopress.
Further reading
- Waldorf, D. C. (1994). The Art of Flint Knapping (Paperback) (Fourth ed.). Mound Builder Books, Branson MO, USA. p. 76. ISBN 9780943917016. (Excellent illustrations by Valerie Waldorf of processes, techniques, hand tools, ancient and modern knapped artifacts [mostly North American]. On front and rear cover are photos of precisely made replicas of prehistoric points and within the text are B&W photos including two full-scale [12⅝ inch and 10¾ inch] "Danish dagger" replicas made by the author.)
- Inizan, M. L.; et al. (1999). Technology and Terminology of Knapped Stone. C.R.E.P., Meudon, France. p. 193.
https://en.wikipedia.org/wiki/Lithic_reduction
The Oldowan (or Mode I) was a widespread stone tool archaeological industry (style) in prehistory. These early tools were simple, usually made with one or a few flakes chipped off with another stone. Oldowan tools were used during the Lower Paleolithic period, 2.9 million years ago up until at least 1.7 million years ago (Ma), by ancient Hominins (early humans) across much of Africa. This technological industry was followed by the more sophisticated Acheulean industry (two sites associated with Homo erectus at Gona in the Afar Region of Ethiopia dating from 1.5 and 1.26 million years ago have both Oldowan and Acheulean tools[2]).
The term Oldowan is taken from the site of Olduvai Gorge in Tanzania, where the first Oldowan stone tools were discovered by the archaeologist Louis Leakey in the 1930s. However, some contemporary archaeologists and palaeoanthropologists prefer to use the term Mode 1 tools to designate pebble tool industries (including Oldowan), with Mode 2 designating bifacially worked tools (including Acheulean handaxes), Mode 3 designating prepared-core tools, and so forth.[3]
Classification of Oldowan tools is still somewhat contentious. Mary Leakey was the first to create a system to classify Oldowan assemblages, and built her system based on prescribed use. The system included choppers, scrapers, and pounders.[4][5] However, more recent classifications of Oldowan assemblages have been made that focus primarily on manufacture due to the problematic nature of assuming use from stone artefacts. An example is Isaac et al.'s tri-modal categories of "Flaked Pieces" (cores/choppers), "Detached Pieces" (flakes and fragments), "Pounded Pieces" (cobbles utilized as hammerstones, etc.) and "Unmodified Pieces" (manuports, stones transported to sites).[6] Oldowan tools are sometimes called "pebble tools", so named because the blanks chosen for their production already resemble, in pebble form, the final product.[7]
It is not known for sure which hominin species created and used Oldowan tools. Its emergence is often associated with the species Australopithecus garhi[8] and its flourishing with early species of Homo such as H. habilis and H. ergaster. Early Homo erectus appears to inherit Oldowan technology and refines it into the Acheulean industry beginning 1.7 million years ago.[9]
Dates and ranges
The oldest known Oldowan tools have been found at Nyayanga on the Homa Peninsula in Kenya and are dated to ~2.9 Ma.[10] The Oldowan tools were associated with Paranthropus teeth and two butchered hippo skeletons.[10] Early Oldowan tools are also known from Gona in Ethiopia (near the Awash River), and are dated to about 2.6 Ma.[11]
The use of tools by apes including chimpanzees[12] and orangutans[13] can be used to argue in favour of tool-use as an ancestral feature of the hominin family.[14] Tools made from bone, wood, or other organic materials were therefore in all probability used before the Oldowan.[15] Oldowan stone tools are simply the oldest recognisable tools which have been preserved in the archaeological record.
There is a flourishing of Oldowan tools in eastern Africa, spreading to southern Africa, between 2.4 and 1.7 Ma. At 1.7 Ma., the first Acheulean tools appear even as Oldowan assemblages continue to be produced. Both technologies are occasionally found in the same areas, dating to the same time periods. This realisation required a rethinking of old cultural sequences in which the more "advanced" Acheulean was supposed to have succeeded the Oldowan. The different traditions may have been used by different species of hominins living in the same area, or multiple techniques may have been used by an individual species in response to different circumstances.
Sometime before 1.8 Ma Homo erectus had spread outside of Africa, reaching as far east as Java by 1.8 Ma[16] and in Northern China by 1.66 Ma.[17] In these newly colonised areas, no Acheulean assemblages have been found. In China, only "Mode 1" Oldowan assemblages were produced, while in Indonesia stone tools from this age are unknown.
By 1.8 Ma early Homo was present in Europe, as shown by the discovery of fossil remains and Oldowan tools in Dmanisi, Georgia.[18] Remains of their activities have also been excavated in Spain at sites in the Guadix-Baza basin[19] and near Atapuerca.[20] Most early European sites yield "Mode 1" or Oldowan assemblages. The earliest Acheulean sites in Europe only appear around 0.5 Ma. In addition, the Acheulean tradition does not seem to spread to Eastern Asia.[21] It is unclear from the archaeological record when the production of Oldowan technologies ended. Other tool-making traditions seem to have supplanted Oldowan technologies by 0.25 Ma.
The discovery of stone tools that predate the Oldowan, dated to as early as 3.3 Ma, at the Lomekwi site in Kenya, was announced in 2015.[22]
This age pre-dates the current estimates for the age of the genus Homo by half a million years, and would fall into the pre-human period, associated with the direct australopithecine ancestors of genus Homo. It is not clear whether the tools of such a "Lomekwian industry" bear any relation to the Oldowan industry.[23]
Tools
Manufacture
There are articles that address how some Oldowan tools may have been found as stones with naturally occurring shapes that dictate their ideal use, or formed as such.[24] To form the general shape of an Oldowan tool, a roughly spherical hammerstone is struck on the edge, or striking platform, of a suitable core rock to produce a conchoidal fracture with sharp edges useful for various purposes. The process is often called lithic reduction. The chip removed by the blow is the flake. Some of these flakes can be used as tools, provided the aforementioned conditions for the initial stone are met before modification.[25] Below the point of impact on the core is a characteristic bulb with fine fissures on the fracture surface. The flake evidences ripple marks.
The materials of the tools were for the most part quartz, quartzite, basalt, or obsidian, and later flint and chert. Any rock that can hold an edge will do. The main source of these rocks is river cobbles, which provide both hammer stones and striking platforms. The earliest tools were simply split cobbles. It is not always clear which is the flake. Later tool-makers clearly identified and reworked flakes. Complaints that artifacts could not be distinguished from naturally fractured stone have helped spark careful studies of Oldowan techniques. These techniques have now been duplicated many times by archaeologists and other knappers, making misidentification of archaeological finds less likely.
Use of bone tools by hominins also producing Oldowan tools is known from Swartkrans, where a bone shaft with a polished point was discovered in Member (layer) I, dated 1.8–1.5 Ma. The Osteodontokeratic industry, the "bone-tooth-horn" industry hypothesized by Raymond Dart, is less certain.
Shapes and uses
Mary Leakey classified the Oldowan tools as Heavy Duty, Light Duty, Utilized Pieces and Debitage, or waste.[26] Heavy-duty tools are mainly cores. A chopper has an edge on one side. It is unifacial if the edge was created by flaking on one face of the core, or bifacial if on two. Discoid tools are roughly circular with a peripheral edge. Polyhedral tools are edged in the shape of a polyhedron. In addition there are spheroidal hammer stones.
Light-duty tools are mainly flakes. There are scrapers, awls (with points for boring) and burins (with points for engraving). Some of these functions belong also to heavy-duty tools. For example, there are heavy-duty scrapers.
Utilized pieces are tools that began with one purpose in mind but were utilized opportunistically. Because of their use and variation, opportunities lead to the frequent modification of tools for either labor or forms of signaling has been proposed as a cause for the different shapes of similar tools.[27]
Oldowan tools were probably used for many purposes, which have been discovered from observation of modern apes and hunter-gatherers. Nuts and bones are cracked by hitting them with hammer stones on a stone used as an anvil. Battered and pitted stones testify to this possible use.
Heavy-duty tools could be used as axes for woodworking. Both choppers and large flakes were probably used for this purpose. Once a branch was separated, it could be scraped clean with a scraper, or hollowed with pointed tools. Such uses are attested by characteristic microscopic alterations of edges used to scrape wood. Oldowan tools could also have been used for preparing hides. Hides must be cut by slicing, piercing and scraping them clean of residues. Flakes are most suitable for this purpose.
Lawrence Keeley, following in the footsteps of Sergei Semenov, conducted microscopic studies (with a high-powered optical microscope) on the edges of tools manufactured de novo and used for the originally speculative purposes described above. He found that the marks were characteristic of the use and matched marks on prehistoric tools. Studies of the cut marks on bones using an electron microscope produce a similar result.
Abbevillian
Abbevillian is a currently obsolescent name for a tool tradition that is increasingly coming to be called Oldowan. The label Abbevillian prevailed until the Leakey family discovered older (yet similar) artifacts at Olduvai Gorge and promoted the African origin of man. Oldowan soon replaced Abbevillian in describing African and Asian lithics. The term Abbevillian is still used but is now restricted to Europe. The label, however, continues to lose popularity as a scientific designation.
In the late 20th century, discovery of the discrepancies in date caused a crisis of definition. Because Abbevillian did not necessarily precede Acheulean and both traditions had flakes and bifaces, it became difficult to differentiate the two. It was in this spirit that many artifacts formerly considered Abbevillian were labeled Acheulean. In consideration of the difficulty, some preferred to name both phases Acheulean. When the topic of Abbevillian came up, it was simply put down as a phase of Acheulean. Whatever was from Africa was Oldowan, and whatever from Europe, Acheulean.
The solution to the definition problem is to define the types in terms of complexity. Simply struck tools are Oldowan. Retouched, or reworked tools are Acheulean. Retouching is a second working of the artifact. The manufacturer first creates an Oldowan tool. Then he reworks or retouches the edges by removing very small chips so as to straighten and sharpen the edge. Typically but not necessarily the reworking is accomplished by pressure flaking.
Tool users
This section needs additional citations for verification. (January 2010) |
While the exact hominid is up for debate, it is believed that some of the first Oldowan makers did fall within the Homo line.[24] However, fossil evidence showed evolutionary features for human precision grip capabilities in Australopithecines.[28] This leads to current anthropological thinking in which Oldowan tools were made by late Australopithecus and early Homo. Homo habilis was named "skillful" because it was considered the earliest tool-using human ancestor. Indeed, the genus Homo was in origin intended to separate tool-using species from their tool-less predecessors, hence the name of Australopithecus garhi, garhi meaning "surprise", a tool-using Australopithecine discovered in 1996 and described as the "missing link" between the genera Australopithecus and Homo. There is also evidence that some species of Paranthropus utilized stone tools.[29]
There is presently no evidence to show that Oldowan tools were the sole creation of members of the Homo line or that the ability to produce them was a special characteristic of only our ancestors. Research on tool use by modern wild chimpanzees in West Africa shows there is an operational sequence when chimpanzees use lithic implements to crack nuts. In the course of nut cracking, sometimes they will create unintentional flakes. Although the morphology of the chimpanzees' hammer is different from the Oldowan hammer, chimpanzees' ability to use stone tools indicates that the earliest lithic industries were probably not produced by only one kind of hominin species.[30]
Findings from fossil evidence and experimental replication of stone-tool users and manufacturers suggest the presence of physical characteristics of hand morphology for precise stone tool making.[24][28] The makers of Oldowan tools were mainly right-handed.[31] "Handedness" (lateralization) had thus already evolved, though it is not clear how related to modern lateralization it was, since other animals show handedness as well.[clarification needed]
In the mid-1970s, Glynn Isaac touched off a debate by proposing that human ancestors of this period had a "place of origin" and that they foraged outward from this home base, returning with high-quality food to share and to be processed. Over the course of the last 30 years, a variety of competing theories about how foraging occurred have been proposed, each one implying certain kinds of social strategy. The available evidence from the distribution of tools and remains is not enough to decide which theories are the most probable. However, three main groups of theories predominate.
- Glynn Isaac's model became the Central Forage Point, as he responded to critics that accused him of attributing too much "modern" behavior to early hominins with relatively free-form searches outward.
- A second group of models took modern chimpanzee behavior as a starting point, having the hominids use relatively fixed routes of foraging, and leaving tools where it was best to do so on a constant track.
- A third group of theories had relatively loose bands scouring the range, taking care to move carcasses from dangerous death sites and leaving tools more or less at random.
Each group of models implies different grouping and social strategies, from the relative altruism of central base models to the relatively disjointed search models. (See also central foraging theory and Lewis Binford)
Hominins probably lived in social groups that had contact with others. This conclusion is supported by the large number of bones at many sites, too large to be the work of one individual, and all of the scatter patterns implying many different individuals. Since modern primates in Africa have fluid boundaries between groups, as individuals enter, become the focus of bands, and others leave, it is also probable that the tools we find are the result of many overlapping groups working the same territories, and perhaps competing over them. Because of the huge expanse of time and the multiplicity of species associated with possible Oldowan tools, it is difficult to be more precise than this, since it is almost certain that different social groupings were used at different times and in different places.
There is also the question of what mix of hunting, gathering and scavenging the tool users employed. Early models focused on the tool users as hunters. The animals butchered by the tools include waterbuck, hartebeest, springbok, pig and zebra. However, the disposition of the bones allows some question about hominin methods of obtaining meat. That they were omnivores is unquestioned, as the digging implement and the probable use of hammer stones to smash nuts indicate. Lewis Binford first noticed that the bones at Olduvai contained a disproportionately high incidence of extremities, which are low in food substance. He concluded other predators had taken the best meat, and the hominins had only scavenged. The counter view is that while hunting many large animals would be beyond the reach of an individual human, groups could bring down larger game, as pack hunting animals are capable of doing. Moreover, since many animals both hunt and scavenge, it is possible that hominins hunted smaller animals, but were not above driving carnivores from larger kills, as they probably were driven from kills themselves from time to time.
Sites and archaeologists
A complete catalog of Oldowan sites would be too extensive for listing here. Some of the better-known sites include the following:
Africa
Ethiopia
Afar Triangle
Sites in the Gona river system in the Hadar region of the Afar triangle, excavated by Helene Roche, J. W. Harris and Sileshi Semaw, yielded some of the oldest known Oldowan assemblages, dating to about 2.6 million years ago. Raw material analysis done by Semaw showed that some assemblages in this region are biased towards a certain material (e.g.: 70% of the artifacts at sites EG10 and EG12 were composed of trachyte) indicating a selectivity in the quality of stone used.[32] Recent excavations have yielded tools in association with cut-marked bones, indicating that Oldowan were used in meat-processing or -acquiring activities.
Omo River basin
The second oldest known Oldowan tool site comes from the Shungura formation of the Omo River basin. This formation documents the sediments of the Plio-Pleistocene and provides a record of the hominins that lived there. Lithic assemblages have been classified as Oldowan in members E and F in the lower Omo basin. Although there have been lithic assemblages found in multiple sites in these areas, only the Omo sites 57 and 123 in member F are accepted as hominin lithic remains. The assemblages at Omo sites 71 and 84 in member E do not show evidence of hominin modification and are therefore classified as natural assemblages.[33]
The tools are never found in direct association with the hominins, but archaeologists believe that they would be the strongest candidates for tool manufacture. There are no hominins in those layers, but the same layers elsewhere in the Omo valley contain Paranthropus and early Homo fossils. Paranthropus occurs in the preceding layers. In the last layer at 1.4 million years ago is only Homo erectus.
Egypt
Along the Nile River, within the 100-foot terrace, evidence of Chellean or Oldowan cultures has been found.[34]
Algeria
In November 2018 Science published a report of Oldowan artefacts in a secure dating context of 1.9 to 2.4 Ma from Ain Boucherit (Ain Hanech) in Setif.[35]
Kenya
Homa Peninsula
Kanjera South, part of the Kanjera site complex, and Nyayanga are located on the Homa Peninsula.[36] Kanjera South is estimated to around 2 Ma.[37] while Nyayanga is estimated to 2.9 Ma. One of the significant excavations, in the area, is Leakey's expedition in 1932-35.[36] In 1995, Oldowan and Plio-Pleistocene faunal remains surfaced from the site.[36] and in 2015 excavations led to the discovery of the earliest Oldowan ston tool technology in association with Paranthropus fossils and butchered hippo remains from Nyayanga.[10]
East Turkana
The numerous Koobi Fora sites on the east side of Lake Turkana are now part of Sibiloi National Park. Sites were initially excavated by Richard Leakey, Meave Leakey, Jack Harris, Glynn Isaac and others. Currently the artifacts found are classified as Oldowan or KBS Oldowan dated from 1.9–1.7 Ma, Karari (or "advanced Oldowan") dated to 1.6–1.4 Ma, and some early Acheulean at the end of the Karari. Over 200 hominins have been found, including Australopithecus and Homo.
West Turkana
In the Nachukui site in West Turkana, around 500 stone tools were found at a site named Naiyena Engol 2, or NY2. The assemblage at NY2 dates back to 1.8-1.7 Ma, around the peak of the Oldowan period.[38] At the site, freehand flaking was observed to be the most common type of technique for making these tools.[39] A common theme among sites in West Turkana is the high percentage of small flake tools gathered in the assemblages. However, NY2 seems to lack many of these tools, indicating a low productivity rate of flakes.[39]
Kilombe
Acheulian stone tools have been known about at Kilombe Main site in the central rift of Kenya since the 1970s with excavations by Prof John Gowlett for his PhD. More recently, Oldowan technology has also been discovered in Kilombe Caldera in an unusual high altitude setting. The stone tools are associated with fossils and have been dated to 1.8 Ma, with Acheulian stone tools occurring in overlying levels.[40]
Tanzania
Olduvai Gorge
The Oldowan industry is named after discoveries made in the Olduvai Gorge of Tanzania in east Africa by the Leakey family, primarily Mary Leakey, but also her husband Louis and their son, Richard.[41] Mary Leakey organized a typology of Early Pleistocene stone tools, which developed Oldowan tools into three chronological variants, A, B and C. Developed Oldowan B is of particular interest due to changes in morphology that appear to have been driven mostly by the short term availability of a chert resource from 1.65 to 1.53 Ma.[42] The flaking properties of this new resource resulted in considerably more core reduction and a higher prevalence of flake retouch. Similar tools had already been found in various locations in Europe and Asia for some time, where they were called Chellean and Abbevillian.
The oldest tool sites are in the East African Rift system, on the sediments of ancient streams and lakes. This is consistent with what we surmise of the evolution of man.[43]
South Africa
Abbé Breuil was the first recognized archaeologist to go on record to assert the existence of Oldowan tools. While his description was for "Chello-Abbevillean" tools, and post-dated Leakey's finds at Olduvai Gorge by at least ten years, his descriptions nonetheless represented the scholarly acceptance of this technology as legitimate. These findings were cited as being from the location of the Vaal River, at Vereeniging, and Breuil noted the distinct absence of a significant number of cores, suggesting a "portable culture". At the time, this was considered very significant, as portability supported the conclusion that the Oldowan tool-makers were capable of planning for future needs, by creating the tools in a location which was distant from their use.[44]
Swartkrans
The Swartkrans site is a cave filled with layered fossil-bearing limestone deposits. Oldowan is found in Member 1 Lower Bank at 2.2-1.8 Ma in association with Paranthropus robustus and a single fossil attributed to Homo . The Member I assemblage also includes a shaft of pointed bone polished at the pointed end. Member I contained a high percentage of primate remains compared to other animal remains, which did not fit the hypothesis that H. habilis or P. robustus lived in the cave. C. K. Brain conducted a more detailed study and discovered the cave had been the abode of leopards, who preyed on the hominins.[45]
Sterkfontein
Another site of limestone caves is Sterkfontein, found in South Africa. This site contains a large number of not only Oldowan tools, but also early Acheulean technology. [46]
Drimolen
The cave site of Drimolen has yielded 6 stone tools attributed to the Oldowan as well as 65 bone tools, along with specimens of Paranthropus robustus and Homo erectus [47][48]
Europe
Georgia
In 1999 and 2002, two Homo erectus skulls (H. georgicus) were discovered at Dmanisi in southern Georgia. The archaeological layer in which the human remains, hundreds of Oldowan stone tools, and numerous animal bones were unearthed is dated approximately 1.83-1.6 Ma. The site yields the earliest unequivocal evidence for presence of early humans outside the African continent.[49]
Bulgaria
At Kozarnika, in the ground layers, dated to 1.6-1.4 Ma, archaeologists have discovered a human molar tooth, lower palaeolithic assemblages that belong to a core-and-flake non-Acheulian industry and incised bones that may be the earliest example of human symbolic behaviour.[citation needed]
Russia
Ainikab-1 and Muhkay-2[50] (North Caucasus, Daghestan) are the extraordinary sites in relation to date and the culture. Geological and geomorphological data, palynological studies and paleomagnetic testing unequivocally point to Early Pleistocene (Eopleistocene), indicating the age of the sites as being within the range of 1.8 – 1.2 Ma.[51][50]
Spain
Oldowan tools have been found at the following sites: Fuente Nueva 3, Barranco del Leon, Sima del Elefante, Atapuerca TD 6.
France
Oldowan tools have been found at: Lézignan-la-Cèbe, 1.5 Ma; Abbeville, 1–0.5 Ma; Vallonnet cave, French Riviera; Soleihac, open-air site in Massif Central. Oldowan tools have also been found at Tautavel in the foothills of the Pyrenees. These were discovered by Henry de Lumbley alongside human remains (cranium). The tools are of limestone and quartz.
Elsewhere
Oldowan tools have been found in Italy at the Monte Poggiolo open air site dated to approximately 850 ka, making them the oldest evidence of human habitation in Italy. In Germany tools have been found in river gravels at Kärlich dating from 300 ka. In the Czech Republic tools have been found in ancient lake deposits at Przeletice and a cave site at Stranska Skala, dated no later than 500 ka. In Hungary tools have been found at a spring site at Vértesszőlős dating from 500 ka.
Asia
This section needs additional citations for verification. (December 2011) |
China
At the Xihoudu site in China, 32 stone tools were found, including choppers, scrapers, and 3-edged tools. These tools were dated back to 1.8 Ma. This site also included cultural artifacts, such as animal fossils, burnt bones, and cut antlers.[52] The presence of numerous fish and beaver fossils near the stone tools indicate the existence of a body of water at the site.
Pakistan
In Pakistan, Oldowan tools have been found at Riwat during a 1980s excavation. Many of the stones found at this site were considered waste products of stone tool production, as they were small flakes chipped off of larger stones. In total, 1,479 tools and flakes were discovered at this site.[53]
Syria
An excavated site at El Kowm (Aïn al Fil, (de:Aïn al Fil)), Syria revealed a plethora of Oldowan tools. In a 2m2 test pit excavated in 2008, 790 artifacts were found, with many pebble tools, cores, flakes, manuports, and flake debris. Although many of these tools show little sign of modification, several of the pebble tools are distinctly-shaped bifacial and trifacial choppers. Dated between 2.0-1.8 Ma, these stone tools are some of the earliest Near East finds.[54]
Because of their location in the Syrian desert, these tools have raised questions about the path of early hominin dispersal. The predominant theory that early hominins traveled along the Mediterranean, through what is now Israel, into Europe has been challenged, as the presence of these Olowan tools indicate that an alternate route may have been taken.[43]
Iran
In Iran, 80 tools of different assemblages have been discovered at 7 sites in the Kashafrud Basin.[43] Although many of the artifacts found here, dated at 1.8 Ma, were pre-Acheulean, some are of the Oldowan tradition, resembling East African Oldowan finds. Containing cores, choppers, flake, chunks, and hammer stones made predominately of quartz, this site displayed the ability of early toolmakers to work skillfully with fragile stones.
Israel
The site at Bizat Ruhama (near kibbutz Ruhama) has shown evidence that the complexity of the stone tool-making process was more complex than researchers previously thought,[55] leading to a new perspective on the capabilities of invention and adaptability of Oldowan hominin populations.
Another key find at the Bizat Ruhama site was that of the secondary flakes. The discovery of these secondary flakes have led researchers to believe that this was an intentional response to a raw material constraint.
According to the micro-morphological studies at the Bizat Ruhama site, the archaeological assemblages represent one or several occupations of the site in a relatively short time frame.
Notes
{{cite web}}: Missing or empty |url= (help)
- Zaidner, Yossi (2013-06-20). "Adaptive Flexibility of Oldowan Hominins: Secondary Use of Flakes at Bizat Ruhama, Israel". PLOS ONE. 8 (6): e66851. Bibcode:2013PLoSO...866851Z. doi:10.1371/journal.pone.0066851. ISSN 1932-6203. PMC 3689005. PMID 23840539.
Sources
- Braidwood, Robert J., Prehistoric Men, many editions.
- Domínguez-Rodrigo, M.; Pickering, T. R.; Semaw, S.; Rogers, M. J. (2005). "Cutmarked bones from Pliocene archaeological sites at Gona, Afar, Ethiopia: Implications for the function of the world's oldest stone tools". Journal of Human Evolution. 48 (2): 109–121. doi:10.1016/j.jhevol.2004.09.004. PMID 15701526.
- Edey, Maitland A., The Missing Link, Time-Life Books, 1972.
- Schick, Kathy D.; Toth, Nicholas, Making Silent Stones Speak', Simon & Schuster, 1993, ISBN 0-671-69371-9
- Semaw, Sileshi (2000). "The World's Oldest Stone Artefacts from Gona, Ethiopia: Their Implications for Understanding Stone Technology and Patterns of Human Evolution Between 2·6–1·5 Million Years Ago". Journal of Archaeological Science. 27 (12): 1197–1214. doi:10.1006/jasc.1999.0592. S2CID 1490212.
- Isaac, Glynn and Harris, JWK The Scatter between the Patches 1975
- Isaac, Glynn (1978). "The Food Sharing Behavior of Protohuman Hominids". Scientific American. 238 (4): 90–108. Bibcode:1978SciAm.238d..90I. doi:10.1038/scientificamerican0478-90. PMID 418504.
- Binford, Lewis R. (1987). "Searching for Camps and Missing the Evidence?". The Pleistocene Old World. Interdisciplinary Contributions to Archaeology. pp. 17–31. doi:10.1007/978-1-4613-1817-0_2. ISBN 978-1-4612-9016-2.
- Toth, Nicholas (1985). "The oldowan reassessed: A close look at early stone artifacts". Journal of Archaeological Science. 12 (2): 101–120. doi:10.1016/0305-4403(85)90056-1.
- Susman, Randall L. (1991). "Who Made the Oldowan Tools? Fossil Evidence for Tool Behavior in Plio-Pleistocene Hominids". Journal of Anthropological Research. 47 (2): 129–151. doi:10.1086/jar.47.2.3630322. JSTOR 3630322. S2CID 159678644.
- Susman, Randall L. (1998). "Hand function and tool behavior in early hominids". Journal of Human Evolution. 35 (1): 23–46. doi:10.1006/jhev.1998.0220. PMID 9680465.
- Hayden, Brian (2015). "Insights into early lithic technologies from ethnography". Philosophical Transactions of the Royal Society B: Biological Sciences. 370 (1682). doi:10.1098/rstb.2014.0356. PMC 4614719. PMID 26483534.
- Shea, John J. (2010). "Stone Age Visiting Cards Revisited: A Strategic Perspective on the Lithic Technology of Early Hominin Dispersal". Out of Africa I. Vertebrate Paleobiology and Paleoanthropology. pp. 47–64. doi:10.1007/978-90-481-9036-2_4. ISBN 978-90-481-9036-2.
- Marzke, Mary W. (1997). "Precision grips, hand morphology, and tools". American Journal of Physical Anthropology. 102 (1): 91–110. doi:10.1002/(sici)1096-8644(199701)102:1<91::aid-ajpa8>3.0.co;2-g. PMID 9034041.
External links
- Oldowan Pebble Tools of Europe
- Oldowan Pebble Tools of Africa
- Oldowan Flake Tool
- Stone Age Hand-axes at the Wayback Machine (archived February 4, 2007)
- Early Palaeolithic
- Stone Age Reference Collection
- Microwear polishes on early stone tools from Koobi Fora, Kenya, article in Nature 293, 464–465 (8 October 1981). The summary and the references are displayed at no charge at the Nature site.
- Geoarchaeology of the earliest paleolithic sites (Oldowan) in the north Caucasus and the East Europe
- An Ape's View of the Oldowan at the Wayback Machine (archived May 21, 2008), T. Wynn and W.C. McGrew, Man 24:383–398; 1989.
- Plummer, Thomas (2004). "Flaked Stones and Old Bones: Biological and Cultural Evolution at the Dawn of Technology" (PDF). Yearbook of Physical Anthropology. 47: 118–164. doi:10.1002/ajpa.20157. PMID 15605391.
- Lower Paleolithic
- Paleolithic cultures of Africa
- Pliocene
- Industries (archaeology)
- Archaeology of Eastern Africa
- Archaeology of Southern Africa
https://en.wikipedia.org/wiki/Oldowan
This timeline of prehistory covers the time from the appearance of Homo sapiens 315,000 years ago in Africa to the invention of writing, over 5,000 years ago, with the earliest records going back to 3,200 BC. Prehistory covers the time from the Paleolithic (Old Stone Age) to the beginning of ancient history.
All dates are approximate and subject to revision based on new discoveries or analyses.
Middle Paleolithic
- See Timeline of human evolution, Timeline of natural history for earlier evolutionary history.
- ∼320,000 to 305,000 years ago: Populations at Olorgesailie in Southern Kenya undergo technological improvements in tool making and engage in long-distance trade.[1]
- 315,000 years ago: approximate date of appearance of Homo sapiens (Jebel Irhoud, Morocco).
- 270,000 years ago: age of Y-DNA haplogroup A00 ("Y-chromosomal Adam").
- 250,000 years ago: first appearance of Homo neanderthalensis (Saccopastore skulls).
- 230,000–150,000 years ago: age of mt-DNA haplogroup L ("Mitochondrial Eve").
- 210,000 years ago: modern human presence in southeast Europe (Apidima, Greece).[2]
- 200,000 years ago: oldest known grass bedding, including insect-repellent plants and ash layers beneath (possibly for a dirt-free, insulated base and to keep away arthropods).[3][4][5]
- 195,000 years ago: Omo remains (Ethiopia).[6]
- 194,000–177,000 years ago: modern human presence in West Asia (Misliya cave in Israel).
- 170,000 years ago: humans are wearing clothing by this date.[7]
- ∼164,000 years ago: humans diet expands to include marine resources[8]
- 160,000 years ago: Homo sapiens idaltu.
- 150,000 years ago: Peopling of Africa: Khoisanid separation, age of mtDNA haplogroup L0.
- 130,000 years ago: oldest evidence of ancient seafaring, from Crete (an island isolated from land for millions of years prior to human arrival).[9]
- 125,000 years ago: the peak of the Eemian interglacial period.
- ~120,000 years ago: possibly the earliest evidence of use of symbols etched onto bone.[10][11]
- ~120,000 years ago: use of marine shells for personal decoration by humans, including Neandertals.[12][13][14]
- 120,000–90,000 years ago: Abbassia Pluvial in North Africa—the Sahara desert region is wet and fertile.
- 120,000–75,000 years ago: Khoisanid back-migration from Southern Africa to East Africa.[15]
- 100,000 years ago: Earliest structures in the world (sandstone blocks set in a semi-circle with an oval foundation) built in Egypt close to Wadi Halfa near the modern border with Sudan.[16]
- 82,000 years ago: small perforated seashell beads from Taforalt in Morocco are the earliest evidence of personal adornment found anywhere in the world.[17]
- 80,000–70,000 years ago: Recent African origin: separation of sub-Saharan Africans and non-Africans.
- 75,000 years ago: Toba Volcano supereruption that may have contributed to human populations being lowered to about 15,000 people.[18]
- 70,000 years ago: earliest example of abstract art or symbolic art from Blombos Cave, South Africa—stones engraved with grid or cross-hatch patterns.[19]
Upper Paleolithic
"Epipaleolithic" or "Mesolithic" are terms for a transitional period between the Last Glacial Maximum and the Neolithic Revolution in Old World (Eurasian) cultures.
- 80,000–40,000: Evidence of Australian Aboriginal Culture.[20][21]
- 67,000–40,000 years ago: Neanderthal admixture to Eurasians.
- 50,000 years ago: earliest evidence of a sewing needle. Made and used by Denisovans.[22]
- 50,000–30,000 years ago: Mousterian Pluvial in North Africa. The Sahara desert region is wet and fertile. Late Stone Age begins in Africa.
- 45,000–43,000 years ago: Early European modern humans.[23]
- 45,000–40,000 years ago: Châtelperronian cultures in France.[24]
- 42,000 years ago: Laschamps event, a geomagnetic excursion with major implications for humans at the time.[25][26]
- 42,000 years ago: Paleolithic flutes in Germany.[27]
- 42,000 years ago: earliest evidence of advanced deep sea fishing technology at the Jerimalai cave site in East Timor—demonstrates high-level maritime skills and by implication the technology needed to make ocean crossings to reach Australia and other islands, as they were catching and consuming large numbers of big deep sea fish such as tuna.[28][29]
- 41,000 years ago: Denisova hominin lives in the Altai Mountains.
- 40,000 years ago: extinction of Homo neanderthalensis.[24]
- 40,000 years ago: Aurignacian culture begins in Europe.[30]
- 40,000 years ago: oldest known figurative art the zoomorphic Löwenmensch figurine.[31]
- 40,000–30,000 years ago: First human settlements formed by Aboriginal Australians in several areas that are today the cities of Sydney,[32][33] Perth[34] and Melbourne.[35]
- 40,000–20,000 years ago: oldest known ritual cremation, the Mungo Lady, in Lake Mungo, Australia.
- 35,000 years ago: oldest known figurative art of a human figure as opposed to a zoomorphic figure (Venus of Hohle Fels).
- 33,000 years ago: earliest evidence of humanoids in Ireland.[36]
- 31,000–16,000 years ago: Last Glacial Maximum (peak at 26,500 years ago).
- 30,000 years ago: rock paintings tradition begins in Bhimbetka rock shelters in India, which presently as a collection is the densest known concentration of rock art. In an area about 10 km2, there are about 800 rock shelters of which 500 contain paintings.[37]
- 29,000 years ago: The earliest ovens found.
- 28,500 years ago: New Guinea is populated by colonists from Asia or Australia.[38]
- 28,000 years ago: oldest known twisted rope.
- 28,000–24,000 years ago: oldest known pottery—used to make figurines rather than cooking or storage vessels (Venus of Dolní Věstonice).
- 28,000–20,000 years ago: Gravettian period in Europe. Harpoons and saws invented.
- 26,000 years ago: people around the world use fibers to make baby carriers, clothes, bags, baskets, and nets.
- 25,000 years ago: a hamlet consisting of huts built of rocks and of mammoth bones is founded in what is now Dolní Věstonice in Moravia in the Czech Republic. Dolní Věstonice (archaeological site) is the oldest human permanent settlement that has yet been found by archaeologists.[39]
- 24,000 years ago: The cave bear is thought to have become extinct.[40]
- 24,000 years ago: Evidence suggests humans living in Alaska and Yukon North America.[41]
- 23,000–21,000 years ago: The earliest known human footprints in North America are left at what is now White Sands National Park, New Mexico.[42] It is also the earliest known evidence of the Oasisamerica civilizations, which eventually became the cultures in modern Northern Mexico and Southwestern United States.
- 21,000 years ago: artifacts suggest early human activity occurred in Canberra, the capital city of Australia.[43]
- 20,000 years ago: Kebaran culture in the Levant: beginning of the Epipalaeolithic in the Levant.
- 20,000 years ago: theorized earliest date of development of traditional Inuit skin clothing.[44]
- 20,000–10,000 years ago: Khoisanid expansion to Central Africa.[15]
- 20,000–19,000 years ago: earliest pottery use, in Xianren Cave, China.[45]
- 18,000–12,000 years ago: Though estimations vary widely, it is believed by scholars that Afro-Asiatic was spoken as a single language around this time period.[46]
- 16,000–14,000 years ago: Minatogawa Man (Proto-Mongoloid phenotype) in Okinawa, Japan.
- 16,000–11,000 years ago: Caucasus hunter-gatherer expansion to Europe.
- 16,000 years ago: Wisent (European bison) sculpted in clay deep inside the cave now known as Le Tuc d'Audoubert in the French Pyrenees near what is now the border of Spain.[47][48]
- 15,000–14,700 years ago (13,000 BC to 12,700 BC): Earliest supposed date for the domestication of the pig.
- 14,200 years ago: The oldest agreed domestic dog remains belongs to the Bonn-Oberkassel dog that was buried with two humans.
- 14,000–12,000 years ago: Oldest evidence for prehistoric warfare (Jebel Sahaba, Natufian culture).
- 13,000–10,000 years ago: Last Glacial Maximum, end of the Last Glacial Period, climate warms, glaciers recede.
- 13,000 years ago: A major water outbreak occurs on Lake Agassiz in central North America, which at the time could have been the size of the current Black Sea and the largest lake on Earth. Much of the lake is drained in the Arctic Ocean through the Mackenzie River.
- 13,000–11,000 years ago: Earliest dates suggested for the domestication of the sheep.
- 12,900–11,700 years ago: The Younger Dryas, a period of sudden cooling and return to glacial conditions.
- c. 12,000 years ago: Volcanic eruptions in the Virunga Mountains blocked Lake Kivu outflow into Lake Edward and the Nile system, diverting the water to Lake Tanganyika. Nile's total length is shortened and Lake Tanganyika's surface is increased.
- 12,000 years ago: Earliest dates suggested for the domestication of the goat.
Holocene
The terms "Neolithic" and "Bronze Age" are culture-specific and are mostly limited to cultures of the Old World. Many populations of the New World remain in the Mesolithic cultural stage until European contact in the modern period.
- 11,600 years ago (9,600 BC): An abrupt period of global warming accelerates the glacial retreat; taken as the beginning of the Holocene geological epoch.
- 11,600 years ago: Jericho has evidence of settlement dating back to 9,600 BC. Jericho was a popular camping ground for Natufian hunter-gatherer groups, who left a scattering of crescent microlith tools behind them.[50]
- 11,200–11,000 years ago: Meltwater pulse 1B, a sudden rise of sea level by 7.5 m (25 ft) within about 160 years.
- 11,000 years ago (9,000 BC): Earliest date recorded for construction of temenoi ceremonial structures at Göbekli Tepe in southern Turkey, as possibly the oldest surviving proto-religious site on Earth.[51]
- 11,000 years ago (9,000 BC): Giant short-faced bears and giant ground sloths go extinct. Equidae goes extinct in North America.
- 11,000–8,000 years ago (9,000 BC to 7,000 BC): the Ancestral Puebloans, in modern day New Mexico and the Southwestern United States, begin their Archaic–Early Basketmaker Era, leading to art styles in pottery and basketmaking that are still used in the region, as well as early structures in the Pueblo architecture style, including some of those seen at Chaco Culture National Historical Park.
- 10,500 years ago (8,500 BC): Earliest supposed date for the domestication of cattle.
- 10,000 years ago (8,000 BC): The Quaternary extinction event, which has been ongoing since the mid-Pleistocene, concludes. Many of the ice age megafauna go extinct, including the megatherium, woolly rhinoceros, Irish elk, cave bear, cave lion, and the last of the sabre-toothed cats. The mammoth goes extinct in Eurasia and North America, but is preserved in small island populations until ~1650 BC.
- 10,800–9,000 years ago: Byblos appears to have been settled during the PPNB period, approximately 8800 to 7000 BC. Neolithic remains of some buildings can be observed at the site.[52][53]
- 10,000–8,000 years ago (8000 BC to 6000 BC): The post-glacial sea level rise decelerates, slowing the submersion of landmasses that had taken place over the previous 10,000 years.
- 10,000–9,000 years ago (8000 BC to 7000 BC): In northern Mesopotamia, now northern Iraq, cultivation of barley and wheat begins. At first they are used for beer, gruel, and soup, eventually for bread.[54] In early agriculture at this time, the planting stick is used, but it is replaced by a primitive plow in subsequent centuries.[55] Around this time, a round stone tower, now preserved to about 8.5 metres (28 ft) high and 8.5 metres (28 ft) in diameter is built in Jericho.[56]
- 10,000–5,000 years ago (8,000–3,000 BC) Identical ancestors point: sometime in this period lived the latest subgroup of human population consisting of those that were all common ancestors of all present day humans, the rest having no present day descendants.[57]
- 9,500–5,500 years ago: Neolithic Subpluvial in North Africa. The Sahara desert region supports a savanna-like environment. Lake Chad is larger than the current Caspian Sea. An African culture develops across the current Sahel region.
- 9,500 years ago (7500 BC): Çatalhöyük urban settlement founded in Anatolia. Earliest supposed date for the domestication of the cat.
- 9,200 years ago: First human settlement in Amman, Jordan; ʿAin Ghazal Neolithic settlement was built spanning over an area of 15 hectares (37 acres).[58]
- 9,000 years ago (7000 BC): Jiahu culture begins in China.
- 9,000 years ago: First large-scale fish fermentation in southern Sweden.[59]
- 9,000 years ago: Human settlement of Mehrgarh, one of the earliest sites with evidence of farming and herding in South Asia. In April 2006, Nature note that the oldest (and first early Neolithic) evidence for the drilling of human teeth in vivo (i.e. in a living person) was found in Mehrgarh.[60]
- 8,200–8,000 years ago: 8.2-kiloyear event: a sudden decrease of global temperatures, probably caused by the final collapse of the Laurentide Ice Sheet, which leads to drier conditions in East Africa and Mesopotamia.
- 8,200–7,600 years ago (6200–5600 BC): sudden rise in sea level (Meltwater pulse 1C) by 6.5 m (21 ft) in less than 140 years; this concludes the early Holocene sea level rise and sea level remains largely stable throughout the Neolithic.[61]
- 8,000–5,000 years ago: (6000 BC–3000 BC) development of proto-writing in China, Southeast Europe (Vinca symbols) and West Asia (proto-literate cuneiform).
- 8,000 years ago: Evidence of habitation at the current site of Aleppo dates to about c. 8,000 years ago, although excavations at Tell Qaramel, 25 kilometres (16 mi) north of the city show the area was inhabited about 13,000 years ago,[62] Carbon-14 dating at Tell Ramad, on the outskirts of Damascus, suggests that the site may have been occupied since the second half of the seventh millennium BC, possibly around 6300 BC.[63] However, evidence of settlement in the wider Barada basin dating back to 9000 BC exists.[64]
- 7,500 years ago (5500 BC): Copper smelting in evidence in Pločnik and other locations.
- 7,700–6,500 years ago (5700–4500 BC): Vinča culture.
- 7,200–6,000 years ago: 5200–4000 BC:Għar Dalam phase on Malta. First farming settlements on the island.[65][66]
- 6300 or 6350 years ago: Akahoya eruption creates the Kikai Caldera and ends the earliest homogeneous Jomon culture in Japan. When the Jomon culture recovers, it shows regional differences.[67][verification needed]
- 6,100–5,800 years ago: 4100–3800 BC: Żebbuġ phase, Malta.
- 6,070–6,000 years ago (4050–4000 BC): Trypillian build in Nebelivka (Ukraine) settlement which reached 15,000–18,000 inhabitants.[68][69]
- 6,500 years ago: The oldest known gold hoard deposited at Varna Necropolis, Bulgaria.
- 6,000 years ago (4000 BC): Civilizations develop in the Mesopotamia/Fertile Crescent region (around the location of modern-day Iraq). Earliest supposed dates for the domestication of the horse and for the domestication of the chicken, invention of the potter's wheel.
4th millennium BC
- 5,840–5,800 years ago (3840–3800 BC): The Post Track and Sweet Track causeways are constructed in the Somerset Levels.
- 5,800 years ago (3800 BC): Trypillian build in Talianki (Ukraine) settlement which reached 15,600–21,000 inhabitants.[70]
- 5,800–5,600 years ago: (3800–3600 BC): Mġarr phase A short transitional period in Malta's prehistory. It is characterized by pottery consisting of mainly curved lines.
- 5,700 years ago (3700 BC): mass graves at Tell Brak in Syria.
- 5,700 years ago (3700 BC): Trypillian build in Maidanets (Ukraine) settlement which reached 12,000–46,000 inhabitants,[71] and built three-story building.[72]
- 5,700 years ago (3700 BC): Minoan culture begins on Crete.
- 5,600–5,200 years ago (3600–3200 BC): Ġgantija phase on Malta. Characterized by a change in the way the prehistoric inhabitants of Malta lived.
- 5,500 years ago (3500 BC): Uruk period in Sumer. First evidence of mummification in Egypt.
- 5,500 years ago (3500 BC): oldest known depiction of a wheeled vehicle (Bronocice pot, Funnelbeaker culture).
- 5,500 years ago (3500 BC): Earliest conjectured date for the still-undeciphered Indus script.
- 5,500 years ago (3500 BC): End of the African humid period possibly linked to the Piora Oscillation: a rapid and intense aridification event, which probably started the current Sahara Desert dry phase and a population increase in the Nile Valley due to migrations from nearby regions. It is also believed this event contributed to the end of the Ubaid period in Mesopotamia.
- 5,400 years ago (3400 BC): Waun Mawn is built in West Wales.
- 5,300 years ago (3300 BC): Bronze Age begins in the Near East[73] Newgrange is built in Ireland. Ness of Brodgar is built in Orkney[74] Hakra Phase of the Indus Valley civilisation begins in the Indian subcontinent.
- 5,300–5,000 years ago (3300–3000 BC): Saflieni phase in Maltese prehistory.
- 5,200 years ago (3200 BC): The Bronze Age begins on Crete, signaling the beginning of the Early Minoan Period.
3rd millennium BC
- 5,000 years ago (3000 BC): Settlement of Skara Brae built in Orkney.[75]
- 4,600 years ago (2600 BC): Writing is developed in Sumer and Egypt, triggering the beginning of recorded history.
Research
Researchers deduced in a scientific review that "no specific point in time can currently be identified at which modern human ancestry was confined to a limited birthplace" and that current knowledge about long, continuous and complex – e.g. often non-singular, parallel, nonsimultaneous and/or gradual – emergences of characteristics is consistent with a range of evolutionary histories.[76][77] A timeline dating first occurrences and earliest evidence may therefore be an often inadequate approach for describing humanity's (pre-)history.
Post-historical prehistories
- 3,800 years ago (1800 BC): Currently undeciphered Minoan script (Linear A) and Cypro-Minoan script developed on Crete and Cyprus.
- 3,450 years ago (1450 BC): Mycenaean Greece, first deciphered writing in Europe
- 3,200 years ago (1200 BC): Oracle bone script, first written records in Old Chinese
- 3,050–2,800 years ago (1050–800 BC): Alphabetic writing; the Phoenician alphabet spreads around the Mediterranean
- 2,300 years ago (300 BC): Maya script, the only known full writing system developed in the Americas, emerges.
- 2,260 years ago (260 BC): Earliest deciphered written records in South Asia (Middle Indo-Aryan)
- 1800s AD: Undeciphered Rongorongo script on Easter Island may mark the latest independent development of writing.
See also
- Prehistory by world region
- Near East
- Prehistoric Mesopotamia (before 3000 BC)
- Prehistoric Egypt (before 3000 BC)
- Prehistory of Anatolia (before 2000 BC)
- Prehistory of Iran (before 1000 BC)
- Prehistoric Caucasus (before 1000 BC)
- Prehistoric China (before 1000 BC)
- Prehistoric Europe (before 800 BC)
- Prehistory of Central Asia (before 600 BC)
- Prehistoric Siberia (before AD 500)
- Pre-Columbian Americas (before 1492)
- Prehistory of Australia (before 1788)
References
- Bergström, Anders; Stringer, Chris; Hajdinjak, Mateja; Scerri, Eleanor M. L.; Skoglund, Pontus (February 2021). "Origins of modern human ancestry". Nature. 590 (7845): 229–237. Bibcode:2021Natur.590..229B. doi:10.1038/s41586-021-03244-5. ISSN 1476-4687. PMID 33568824. S2CID 231883210. Retrieved 7 March 2021.
Bibliography
- Kristian Kristiansen; Thomas B. Larsson (2005). The Rise of Bronze Age Society: Travels, Transmissions and Transformations. Cambridge University Press. ISBN 978-0521843638.
- Ross Burns (2005). Damascus : A History. Routledge. ISBN 978-1134488506.
External links
- Human Timeline (Interactive) – Smithsonian, National Museum of Natural History (August 2016).
https://en.wikipedia.org/wiki/Timeline_of_prehistory
Two naming scales for large numbers have been used in English and other European languages since the early modern era: the long and short scales. Most English variants use the short scale today, but the long scale remains dominant in many non-English-speaking areas, including continental Europe and Spanish-speaking countries in Latin America. These naming procedures are based on taking the number n occurring in 103n+3 (short scale) or 106n (long scale) and concatenating Latin roots for its units, tens, and hundreds place, together with the suffix -illion.
Names of numbers above a trillion are rarely used in practice; such large numbers have practical usage primarily in the scientific domain, where powers of ten are expressed as 10 with a numeric superscript.
Indian English does not use millions, but has its own system of large numbers including lakhs and crores.[1] English also has many words, such as "zillion", used informally to mean large but unspecified amounts; see indefinite and fictitious numbers.
Standard dictionary numbers
| x | Name (SS/LS, LS) |
SS (103x+3) |
LS (106x, 106x+3) |
Authorities | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AHD4[2] | CED[3] | COD[4] | OED2[5] | OEDweb[6] | RHD2[7] | SOED3[8] | W3[9] | HM[10] | ||||
| 1 | Million | 106 | 106 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Milliard | 109 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| 2 | Billion | 109 | 1012 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 3 | Trillion | 1012 | 1018 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 4 | Quadrillion | 1015 | 1024 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 5 | Quintillion | 1018 | 1030 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 6 | Sextillion | 1021 | 1036 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 7 | Septillion | 1024 | 1042 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 8 | Octillion | 1027 | 1048 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 9 | Nonillion | 1030 | 1054 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 10 | Decillion | 1033 | 1060 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 11 | Undecillion | 1036 | 1066 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 12 | Duodecillion | 1039 | 1072 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 13 | Tredecillion | 1042 | 1078 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 14 | Quattuordecillion | 1045 | 1084 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 15 | Quindecillion | 1048 | 1090 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 16 | Sexdecillion | 1051 | 1096 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 17 | Septendecillion | 1054 | 10102 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 18 | Octodecillion | 1057 | 10108 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 19 | Novemdecillion | 1060 | 10114 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 20 | Vigintillion | 1063 | 10120 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 100 | Centillion | 10303 | 10600 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||
Usage:
- Short scale: US, English Canada, modern British, Australia, and Eastern Europe
- Long scale: French Canada, older British, Western & Central Europe
Apart from million, the words in this list ending with -illion are all derived by adding prefixes (bi-, tri-, etc., derived from Latin) to the stem -illion.[11] Centillion[12] appears to be the highest name ending in -"illion" that is included in these dictionaries. Trigintillion, often cited as a word in discussions of names of large numbers, is not included in any of them, nor are any of the names that can easily be created by extending the naming pattern (unvigintillion, duovigintillion, duoquinquagintillion, etc.).
| Name | Value | Authorities | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AHD4 | CED | COD | OED2 | OEDnew | RHD2 | SOED3 | W3 | UM | ||
| Googol | 10100 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Googolplex | 10googol (1010100) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
All of the dictionaries included googol and googolplex, generally crediting it to the Kasner and Newman book and to Kasner's nephew (see below). None include any higher names in the googol family (googolduplex, etc.). The Oxford English Dictionary comments that googol and googolplex are "not in formal mathematical use".
Usage of names of large numbers
Some names of large numbers, such as million, billion, and trillion, have real referents in human experience, and are encountered in many contexts. At times, the names of large numbers have been forced into common usage as a result of hyperinflation. The highest numerical value banknote ever printed was a note for 1 sextillion pengő (1021 or 1 milliard bilpengő as printed) printed in Hungary in 1946. In 2009, Zimbabwe printed a 100 trillion (1014) Zimbabwean dollar note, which at the time of printing was worth about US$30.[13]
Names of larger numbers, however, have a tenuous, artificial existence, rarely found outside definitions, lists, and discussions of how large numbers are named. Even well-established names like sextillion are rarely used, since in the context of science, including astronomy, where such large numbers often occur, they are nearly always written using scientific notation. In this notation, powers of ten are expressed as 10 with a numeric superscript, e.g. "The X-ray emission of the radio galaxy is 1.3×1045 joules." When a number such as 1045 needs to be referred to in words, it is simply read out as "ten to the forty-fifth". This is easier to say and less ambiguous than "quattuordecillion", which means something different in the long scale and the short scale.
When a number represents a quantity rather than a count, SI prefixes can be used—thus "femtosecond", not "one quadrillionth of a second"—although often powers of ten are used instead of some of the very high and very low prefixes. In some cases, specialized units are used, such as the astronomer's parsec and light year or the particle physicist's barn.
Nevertheless, large numbers have an intellectual fascination and are of mathematical interest, and giving them names is one way people try to conceptualize and understand them.
One of the earliest examples of this is The Sand Reckoner, in which Archimedes gave a system for naming large numbers. To do this, he called the numbers up to a myriad myriad (108) "first numbers" and called 108 itself the "unit of the second numbers". Multiples of this unit then became the second numbers, up to this unit taken a myriad myriad times, 108·108=1016. This became the "unit of the third numbers", whose multiples were the third numbers, and so on. Archimedes continued naming numbers in this way up to a myriad myriad times the unit of the 108-th numbers, i.e. and embedded this construction within another copy of itself to produce names for numbers up to Archimedes then estimated the number of grains of sand that would be required to fill the known universe, and found that it was no more than "one thousand myriad of the eighth numbers" (1063).
Since then, many others have engaged in the pursuit of conceptualizing and naming numbers that have no existence outside the imagination. One motivation for such a pursuit is that attributed to the inventor of the word googol, who was certain that any finite number "had to have a name". Another possible motivation is competition between students in computer programming courses, where a common exercise is that of writing a program to output numbers in the form of English words.[citation needed]
Most names proposed for large numbers belong to systematic schemes which are extensible. Thus, many names for large numbers are simply the result of following a naming system to its logical conclusion—or extending it further.[citation needed]
Origins of the "standard dictionary numbers"
The words bymillion and trimillion were first recorded in 1475 in a manuscript of Jehan Adam. Subsequently, Nicolas Chuquet wrote a book Triparty en la science des nombres which was not published during Chuquet's lifetime. However, most of it was copied by Estienne de La Roche for a portion of his 1520 book, L'arismetique. Chuquet's book contains a passage in which he shows a large number marked off into groups of six digits, with the comment:
Ou qui veult le premier point peult signiffier million Le second point byllion Le tiers point tryllion Le quart quadrillion Le cinqe quyllion Le sixe sixlion Le sept.e septyllion Le huyte ottyllion Le neufe nonyllion et ainsi des ault's se plus oultre on vouloit preceder
(Or if you prefer the first mark can signify million, the second mark byllion, the third mark tryllion, the fourth quadrillion, the fifth quyillion, the sixth sixlion, the seventh septyllion, the eighth ottyllion, the ninth nonyllion and so on with others as far as you wish to go).
Adam and Chuquet used the long scale of powers of a million; that is, Adam's bymillion (Chuquet's byllion) denoted 1012, and Adam's trimillion (Chuquet's tryllion) denoted 1018.
The googol family
The names googol and googolplex were invented by Edward Kasner's nephew Milton Sirotta and introduced in Kasner and Newman's 1940 book Mathematics and the Imagination[14] in the following passage:
The name "googol" was invented by a child (Dr. Kasner's nine-year-old nephew) who was asked to think up a name for a very big number, namely 1 with one hundred zeroes after it. He was very certain that this number was not infinite, and therefore equally certain that it had to have a name. At the same time that he suggested "googol" he gave a name for a still larger number: "googolplex." A googolplex is much larger than a googol, but is still finite, as the inventor of the name was quick to point out. It was first suggested that a googolplex should be 1, followed by writing zeros until you got tired. This is a description of what would happen if one tried to write a googolplex, but different people get tired at different times and it would never do to have Carnera a better mathematician than Dr. Einstein, simply because he had more endurance. The googolplex is, then, a specific finite number, equal to 1 with a googol zeros after it.
| Value | Name | Authority |
|---|---|---|
| 10100 | Googol | Kasner and Newman, dictionaries (see above) |
| 10googol = 1010100 | Googolplex | Kasner and Newman, dictionaries (see above) |
John Horton Conway and Richard K. Guy[15] have suggested that N-plex be used as a name for 10N. This gives rise to the name googolplexplex for 10googolplex = 101010100. Conway and Guy[15] have proposed that N-minex be used as a name for 10−N, giving rise to the name googolminex for the reciprocal of a googolplex, which is written as 10-(10100). None of these names are in wide use.
The names googol and googolplex inspired the name of the Internet company Google and its corporate headquarters, the Googleplex, respectively.
Extensions of the standard dictionary numbers
This section illustrates several systems for naming large numbers, and shows how they can be extended past vigintillion.
Traditional British usage assigned new names for each power of one million (the long scale): 1,000,000 = 1 million; 1,000,0002 = 1 billion; 1,000,0003 = 1 trillion; and so on. It was adapted from French usage, and is similar to the system that was documented or invented by Chuquet.
Traditional American usage (which was also adapted from French usage but at a later date), Canadian, and modern British usage assign new names for each power of one thousand (the short scale.) Thus, a billion is 1000 × 10002 = 109; a trillion is 1000 × 10003 = 1012; and so forth. Due to its dominance in the financial world (and by the US dollar), this was adopted for official United Nations documents.
Traditional French usage has varied; in 1948, France, which had originally popularized the short scale worldwide, reverted to the long scale.
The term milliard is unambiguous and always means 109. It is seldom seen in American usage and rarely in British usage, but frequently in continental European usage. The term is sometimes attributed to French mathematician Jacques Peletier du Mans circa 1550 (for this reason, the long scale is also known as the Chuquet-Peletier system), but the Oxford English Dictionary states that the term derives from post-Classical Latin term milliartum, which became milliare and then milliart and finally our modern term.
Concerning names ending in -illiard for numbers 106n+3, milliard is certainly in widespread use in languages other than English, but the degree of actual use of the larger terms is questionable. The terms "Milliarde" in German, "miljard" in Dutch, "milyar" in Turkish, and "миллиард," milliard (transliterated) in Russian, are standard usage when discussing financial topics.
For additional details, see billion and long and short scale.
The naming procedure for large numbers is based on taking the number n occurring in 103n+3 (short scale) or 106n (long scale) and concatenating Latin roots for its units, tens, and hundreds place, together with the suffix -illion. In this way, numbers up to 103·999+3 = 103000 (short scale) or 106·999 = 105994 (long scale) may be named. The choice of roots and the concatenation procedure is that of the standard dictionary numbers if n is 9 or smaller. For larger n (between 10 and 999), prefixes can be constructed based on a system described by Conway and Guy.[15] Today, sexdecillion and novemdecillion are standard dictionary numbers and, using the same reasoning as Conway and Guy did for the numbers up to nonillion, could probably be used to form acceptable prefixes. The Conway–Guy system for forming prefixes:
|
|
Units | Tens | Hundreds |
|---|---|---|---|
| 1 | Un | N Deci | NX Centi |
| 2 | Duo | MS Viginti | N Ducenti |
| 3 | Tre (*) | NS Triginta | NS Trecenti |
| 4 | Quattuor | NS Quadraginta | NS Quadringenti |
| 5 | Quinqua | NS Quinquaginta | NS Quingenti |
| 6 | Se (*) | N Sexaginta | N Sescenti |
| 7 | Septe (*) | N Septuaginta | N Septingenti |
| 8 | Octo | MX Octoginta | MX Octingenti |
| 9 | Nove (*) | Nonaginta | Nongenti |
- (*) ^ When preceding a component marked S or X, "tre" changes to "tres" and "se" to "ses" or "sex"; similarly, when preceding a component marked M or N, "septe" and "nove" change to "septem" and "novem" or "septen" and "noven".
Since the system of using Latin prefixes will become ambiguous for numbers with exponents of a size which the Romans rarely counted to, like 106,000,258, Conway and Guy co-devised with Allan Wechsler the following set of consistent conventions that permit, in principle, the extension of this system indefinitely to provide English short-scale names for any integer whatsoever.[15] The name of a number 103n+3, where n is greater than or equal to 1000, is formed by concatenating the names of the numbers of the form 103m+3, where m represents each group of comma-separated digits of n, with each but the last "-illion" trimmed to "-illi-", or, in the case of m = 0, either "-nilli-" or "-nillion".[15] For example, 103,000,012, the 1,000,003rd "-illion" number, equals one "millinillitrillion"; 1033,002,010,111, the 11,000,670,036th "-illion" number, equals one "undecillinilliseptuagintasescentillisestrigintillion"; and 1029,629,629,633, the 9,876,543,210th "-illion" number, equals one "nonilliseseptuagintaoctingentillitresquadragintaquingentillideciducentillion".[15]
The following table shows number names generated by the system described by Conway and Guy for the short and long scales.[16]
| Base -illion (short scale) |
Base -illion (long scale) |
Value | US, Canada and modern British (short scale) |
Traditional British (long scale) |
Traditional European (Peletier) (long scale) |
SI Symbol |
SI Prefix |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 106 | Million | Million | Million | M | Mega- |
| 2 | 1 | 109 | Billion | Thousand million | Milliard | G | Giga- |
| 3 | 2 | 1012 | Trillion | Billion | Billion | T | Tera- |
| 4 | 2 | 1015 | Quadrillion | Thousand billion | Billiard | P | Peta- |
| 5 | 3 | 1018 | Quintillion | Trillion | Trillion | E | Exa- |
| 6 | 3 | 1021 | Sextillion | Thousand trillion | Trilliard | Z | Zetta- |
| 7 | 4 | 1024 | Septillion | Quadrillion | Quadrillion | Y | Yotta- |
| 8 | 4 | 1027 | Octillion | Thousand quadrillion | Quadrilliard | R | Ronna- |
| 9 | 5 | 1030 | Nonillion | Quintillion | Quintillion | Q | Quetta- |
| 10 | 5 | 1033 | Decillion | Thousand quintillion | Quintilliard | ||
| 11 | 6 | 1036 | Undecillion | Sextillion | Sextillion | ||
| 12 | 6 | 1039 | Duodecillion | Thousand sextillion | Sextilliard | ||
| 13 | 7 | 1042 | Tredecillion | Septillion | Septillion | ||
| 14 | 7 | 1045 | Quattuordecillion | Thousand septillion | Septilliard | ||
| 15 | 8 | 1048 | Quindecillion | Octillion | Octillion | ||
| 16 | 8 | 1051 | Sedecillion | Thousand octillion | Octilliard | ||
| 17 | 9 | 1054 | Septendecillion | Nonillion | Nonillion | ||
| 18 | 9 | 1057 | Octodecillion | Thousand nonillion | Nonilliard | ||
| 19 | 10 | 1060 | Novendecillion | Decillion | Decillion | ||
| 20 | 10 | 1063 | Vigintillion | Thousand decillion | Decilliard | ||
| 21 | 11 | 1066 | Unvigintillion | Undecillion | Undecillion | ||
| 22 | 11 | 1069 | Duovigintillion | Thousand undecillion | Undecilliard | ||
| 23 | 12 | 1072 | Tresvigintillion | Duodecillion | Duodecillion | ||
| 24 | 12 | 1075 | Quattuorvigintillion | Thousand duodecillion | Duodecilliard | ||
| 25 | 13 | 1078 | Quinvigintillion | Tredecillion | Tredecillion | ||
| 26 | 13 | 1081 | Sesvigintillion | Thousand tredecillion | Tredecilliard | ||
| 27 | 14 | 1084 | Septemvigintillion | Quattuordecillion | Quattuordecillion | ||
| 28 | 14 | 1087 | Octovigintillion | Thousand quattuordecillion | Quattuordecilliard | ||
| 29 | 15 | 1090 | Novemvigintillion | Quindecillion | Quindecillion | ||
| 30 | 15 | 1093 | Trigintillion | Thousand quindecillion | Quindecilliard | ||
| 31 | 16 | 1096 | Untrigintillion | Sedecillion | Sedecillion | ||
| 32 | 16 | 1099 | Duotrigintillion | Thousand sedecillion | Sedecilliard | ||
| 33 | 17 | 10102 | Trestrigintillion | Septendecillion | Septendecillion | ||
| 34 | 17 | 10105 | Quattuortrigintillion | Thousand septendecillion | Septendecilliard | ||
| 35 | 18 | 10108 | Quintrigintillion | Octodecillion | Octodecillion | ||
| 36 | 18 | 10111 | Sestrigintillion | Thousand octodecillion | Octodecilliard | ||
| 37 | 19 | 10114 | Septentrigintillion | Novendecillion | Novendecillion | ||
| 38 | 19 | 10117 | Octotrigintillion | Thousand novendecillion | Novendecilliard | ||
| 39 | 20 | 10120 | Noventrigintillion | Vigintillion | Vigintillion | ||
| 40 | 20 | 10123 | Quadragintillion | Thousand vigintillion | Vigintilliard | ||
| 50 | 25 | 10153 | Quinquagintillion | Thousand quinvigintillion | Quinvigintilliard | ||
| 60 | 30 | 10183 | Sexagintillion | Thousand trigintillion | Trigintilliard | ||
| 70 | 35 | 10213 | Septuagintillion | Thousand quintrigintillion | Quintrigintilliard | ||
| 80 | 40 | 10243 | Octogintillion | Thousand quadragintillion | Quadragintilliard | ||
| 90 | 45 | 10273 | Nonagintillion | Thousand quinquadragintillion | Quinquadragintilliard | ||
| 100 | 50 | 10303 | Centillion | Thousand quinquagintillion | Quinquagintilliard | ||
| 101 | 51 | 10306 | Uncentillion | Unquinquagintillion | Unquinquagintillion | ||
| 110 | 55 | 10333 | Decicentillion | Thousand quinquinquagintillion | Quinquinquagintilliard | ||
| 111 | 56 | 10336 | Undecicentillion | Sesquinquagintillion | Sesquinquagintillion | ||
| 120 | 60 | 10363 | Viginticentillion | Thousand sexagintillion | Sexagintilliard | ||
| 121 | 61 | 10366 | Unviginticentillion | Unsexagintillion | Unsexagintillion | ||
| 130 | 65 | 10393 | Trigintacentillion | Thousand quinsexagintillion | Quinsexagintilliard | ||
| 140 | 70 | 10423 | Quadragintacentillion | Thousand septuagintillion | Septuagintilliard | ||
| 150 | 75 | 10453 | Quinquagintacentillion | Thousand quinseptuagintillion | Quinseptuagintilliard | ||
| 160 | 80 | 10483 | Sexagintacentillion | Thousand octogintillion | Octogintilliard | ||
| 170 | 85 | 10513 | Septuagintacentillion | Thousand quinoctogintillion | Quinoctogintilliard | ||
| 180 | 90 | 10543 | Octogintacentillion | Thousand nonagintillion | Nonagintilliard | ||
| 190 | 95 | 10573 | Nonagintacentillion | Thousand quinnonagintillion | Quinnonagintilliard | ||
| 200 | 100 | 10603 | Ducentillion | Thousand centillion | Centilliard | ||
| 300 | 150 | 10903 | Trecentillion | Thousand quinquagintacentillion | Quinquagintacentilliard | ||
| 400 | 200 | 101203 | Quadringentillion | Thousand ducentillion | Ducentilliard | ||
| 500 | 250 | 101503 | Quingentillion | Thousand quinquagintaducentillion | Quinquagintaducentilliard | ||
| 600 | 300 | 101803 | Sescentillion | Thousand trecentillion | Trecentilliard | ||
| 700 | 350 | 102103 | Septingentillion | Thousand quinquagintatrecentillion | Quinquagintatrecentilliard | ||
| 800 | 400 | 102403 | Octingentillion | Thousand quadringentillion | Quadringentilliard | ||
| 900 | 450 | 102703 | Nongentillion | Thousand quinquagintaquadringentillion | Quinquagintaquadringentilliard | ||
| 1000 | 500 | 103003 | Millillion (alt. millinillion)[17] | Thousand quingentillion | Quingentilliard | ||
| Value | Name | Equivalent | ||
|---|---|---|---|---|
| US, Canadian and modern British (short scale) |
Traditional British (long scale) |
Traditional European (Peletier) (long scale) | ||
| 10100 | Googol | Ten duotrigintillion | Ten thousand sedecillion | Ten sedecilliard |
| 1010100 | Googolplex | [1] Ten trillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentillitrestrigintatrecentilliduotrigintatrecentillion | [2] Ten thousand millisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillion | [2] Ten millisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentillisesexagintasescentilliard |
- ^[1] Googolplex's short scale name is derived from it equal to ten of the 3,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,333,332nd "-illion"s (This is the value of n when 10 X 10(3n + 3) = 1010100)
- ^[2] Googolplex's long scale name (both traditional British and traditional European) is derived from it being equal to ten thousand of the 1,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666,666th "-illion"s (This is the value of n when 10,000 X 106n = 1010100).
Binary prefixes
The International System of Quantities (ISQ) defines a series of prefixes denoting integer powers of 1024 between 10241 and 10248.[18]
| Power | Value | ISQ symbol |
ISQ prefix |
|---|---|---|---|
| 1 | 10241 | Ki | Kibi- |
| 2 | 10242 | Mi | Mebi- |
| 3 | 10243 | Gi | Gibi- |
| 4 | 10244 | Ti | Tebi- |
| 5 | 10245 | Pi | Pebi- |
| 6 | 10246 | Ei | Exbi- |
| 7 | 10247 | Zi | Zebi- |
| 8 | 10248 | Yi | Yobi- |
Other large numbers used in mathematics, physics and chemistry
See also
- -yllion – Mathematical notation
- Asaṃkhyeya – Buddhist name for a large number
- Chinese numerals – Words and characters used to denote numbers in Chinese
- History of large numbers
- Indefinite and fictitious numbers – Terms expressing unspecified and made up numbers
- Indian numbering system – Indian methods of naming large numbers
- Knuth's up-arrow notation – Method of notation of very large integers
- Law of large numbers – Averages of repeated trials converge to the expected value
- List of numbers – Notable numbers
- Long and short scale – Two meanings of "billion" and "trillion"
- Metric prefix – Order of magnitude indicator
- Names of small numbers – Usage and derivation of names
- Number names – Word or phrase which describes a numerical quantity
- Number prefix – Prefix derived from numerals or other numbers
- Orders of magnitude – Scale of numbers with a fixed ratio
- Orders of magnitude (data) – Computer data measurements and scales.
- Orders of magnitude (numbers) – Scale of numbers of interest arranged from small to large
- Power of 10 – Ten raised to an integer power
References
- "IEC 80000-13:2008". International Organization for Standardization. Retrieved 25 September 2022.
https://en.wikipedia.org/wiki/Names_of_large_numbers#Quintillion
The Grzegorczyk hierarchy (/ɡrɛˈɡɔːrtʃək/, Polish pronunciation: [ɡʐɛˈɡɔrt͡ʂɨk]), named after the Polish logician Andrzej Grzegorczyk, is a hierarchy of functions used in computability theory.[1] Every function in the Grzegorczyk hierarchy is a primitive recursive function, and every primitive recursive function appears in the hierarchy at some level. The hierarchy deals with the rate at which the values of the functions grow; intuitively, functions in lower levels of the hierarchy grow slower than functions in the higher levels.
https://en.wikipedia.org/wiki/Grzegorczyk_hierarchy
In mathematics, transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. These include the transfinite cardinals, which are cardinal numbers used to quantify the size of infinite sets, and the transfinite ordinals, which are ordinal numbers used to provide an ordering of infinite sets.[1][2] The term transfinite was coined by Georg Cantor in 1895,[3][4][5][6] who wished to avoid some of the implications of the word infinite in connection with these objects, which were, nevertheless, not finite.[citation needed] Few contemporary writers share these qualms; it is now accepted usage to refer to transfinite cardinals and ordinals as infinite numbers. Nevertheless, the term "transfinite" also remains in use.
Notable work on transfinite numbers was done by Wacław Sierpiński: Leçons sur les nombres transfinis (1928 book) much expanded into Cardinal and Ordinal Numbers (1958,[7] 2nd ed. 1965[8]).
Definition
Any finite natural number can be used in at least two ways: as an ordinal and as a cardinal. Cardinal numbers specify the size of sets (e.g., a bag of five marbles), whereas ordinal numbers specify the order of a member within an ordered set[9] (e.g., "the third man from the left" or "the twenty-seventh day of January"). When extended to transfinite numbers, these two concepts are no longer in one-to-one correspondence. A transfinite cardinal number is used to describe the size of an infinitely large set,[2] while a transfinite ordinal is used to describe the location within an infinitely large set that is ordered.[9][failed verification] The most notable ordinal and cardinal numbers are, respectively:
- (Omega): the lowest transfinite ordinal number. It is also the order type of the natural numbers under their usual linear ordering.
- (Aleph-null): the first transfinite cardinal number. It is also the cardinality of the natural numbers. If the axiom of choice holds, the next higher cardinal number is aleph-one, If not, there may be other cardinals which are incomparable with aleph-one and larger than aleph-null. Either way, there are no cardinals between aleph-null and aleph-one.
The continuum hypothesis is the proposition that there are no intermediate cardinal numbers between and the cardinality of the continuum (the cardinality of the set of real numbers):[2] or equivalently that is the cardinality of the set of real numbers. In Zermelo–Fraenkel set theory, neither the continuum hypothesis nor its negation can be proved.
Some authors, including P. Suppes and J. Rubin, use the term transfinite cardinal to refer to the cardinality of a Dedekind-infinite set in contexts where this may not be equivalent to "infinite cardinal"; that is, in contexts where the axiom of countable choice is not assumed or is not known to hold. Given this definition, the following are all equivalent:
- is a transfinite cardinal. That is, there is a Dedekind infinite set such that the cardinality of is
- There is a cardinal such that
Although transfinite ordinals and cardinals both generalize only the natural numbers, other systems of numbers, including the hyperreal numbers and surreal numbers, provide generalizations of the real numbers.[10]
Examples
In Cantor's theory of ordinal numbers, every integer number must have a successor.[11] The next integer after all the regular ones, that is the first infinite integer, is named . In this context, is larger than , and , and are larger still. Arithmetic expressions containing specify an ordinal number, and can be thought of as the set of all integers up to that number. A given number generally has multiple expressions that represent it, however, there is a unique Cantor normal form that represents it,[11] essentially a finite sequence of digits that give coefficients of descending powers of .
Not all infinite integers can be represented by a Cantor normal form however, and the first one that cannot is given by the limit and is termed .[11] is the smallest solution to , and the following solutions give larger ordinals still, and can be followed until one reaches the limit , which is the first solution to . This means that in order to be able to specify all transfinite integers, one must think up an infinite sequence of names: because if one were to specify a single largest integer, one would then always be able to mention its larger successor. But as noted by Cantor,[citation needed] even this only allows one to reach the lowest class of transfinite numbers: those whose size of sets correspond to the cardinal number .
See also
References
- John Horton Conway, (1976) On Numbers and Games. Academic Press, ISBN 0-12-186350-6. (See Chapter 3.)
Bibliography
- Levy, Azriel, 2002 (1978) Basic Set Theory. Dover Publications. ISBN 0-486-42079-5
- O'Connor, J. J. and E. F. Robertson (1998) "Georg Ferdinand Ludwig Philipp Cantor," MacTutor History of Mathematics archive.
- Rubin, Jean E., 1967. "Set Theory for the Mathematician". San Francisco: Holden-Day. Grounded in Morse–Kelley set theory.
- Rudy Rucker, 2005 (1982) Infinity and the Mind. Princeton Univ. Press. Primarily an exploration of the philosophical implications of Cantor's paradise. ISBN 978-0-691-00172-2.
- Patrick Suppes, 1972 (1960) "Axiomatic Set Theory". Dover. ISBN 0-486-61630-4. Grounded in ZFC.
https://en.wikipedia.org/wiki/Transfinite_number
https://en.wikipedia.org/wiki/Long_and_short_scales
| Joseph Smith | |
|---|---|
 Portrait, c. 1842 | |
|
| |
| 1st President of the Church of Christ (later the Church of Jesus Christ of Latter Day Saints)[a] | |
| April 6, 1830 – June 27, 1844 |
https://en.wikipedia.org/wiki/Joseph_Smith
https://en.wikipedia.org/wiki/Category:1805_births
The Cascade Tunnel refers to two railroad tunnels (original and its replacement) in the northwest United States, east of the Seattle metropolitan area in the Cascade Range of Washington, at Stevens Pass. It is approximately 65 miles (105 km) east of Everett, with both portals adjacent to U.S. Route 2. Both single-track tunnels were constructed by the Great Northern Railway.
The first was 2.63 miles (4.23 km) in length and opened in 1900 to avoid problems caused by heavy winter snowfalls on the original line that had eight zig zags (switchbacks). The current tunnel is 7.8 miles (12.6 km) in length and entered service in early 1929,[1][2] approximately 1.5 miles (2.4 km) south of and 500 feet (150 m) lower in elevation than the original. The present east portal is nearly four miles (6.5 km) east of the original's and is at 2,881 feet (878 m) above sea level, 1,180 feet (360 m) below the pass. The tunnel connects Berne in Chelan County on its east with Scenic Hot Springs in King County on its west and is the longest railroad tunnel in the United States.
https://en.wikipedia.org/wiki/Cascade_Tunnel
A hairpin turn (also hairpin bend or hairpin corner) is a bend in a road with a very acute inner angle, making it necessary for an oncoming vehicle to turn about 180° to continue on the road. It is named for its resemblance to a bent metal hairpin. Such turns in ramps and trails may be called switchbacks in American English, by analogy with switchback railways.
https://en.wikipedia.org/wiki/Hairpin_turn
https://geohack.toolforge.org/geohack.php?pagename=Hairpin_turn¶ms=21_10_52_S_55_27_17_E_
A hairpin turn (also hairpin bend or hairpin corner) is a bend in a road with a very acute inner angle, making it necessary for an oncoming vehicle to turn about 180° to continue on the road. It is named for its resemblance to a bent metal hairpin. Such turns in ramps and trails may be called switchbacks in American English, by analogy with switchback railways.
Description
Hairpin turns are often built when a route climbs up or down a steep slope, so that it can travel mostly across the slope with only moderate steepness, and are often arrayed in a zigzag pattern. Highways with repeating hairpin turns allow easier, safer ascents and descents of mountainous terrain than a direct, steep climb and descent, at the price of greater distances of travel and usually lower speed limits, due to the sharpness of the turn. Highways of this style are also generally less costly to build and maintain than highways with tunnels.
On occasion, the road may loop completely, using a tunnel or bridge to cross itself at a different elevation (example on Reunion Island: 21°10′52″S 55°27′17″E). When this routing geometry is used for a rail line, it is called a spiral, or spiral loop.
In trail building, an alternative to switchbacks is the stairway.
https://en.wikipedia.org/wiki/Hairpin_turn
Réunion
La Réunion (French) | |
|---|---|
| Motto(s): | |
| Anthem: La Marseillaise (National) P'tite fleur aimée (Regional) | |
 | |
| Coordinates: 21°06′52″S 55°31′57″ECoordinates: 21°06′52″S 55°31′57″E | |
| Country | France |
| Prefecture | Saint-Denis |
| Departments | 1 |
| Government | |
| • President of Regional Council | Huguette Bello (PLR) |
| • President of Departmental Council | Cyrille Melchior (LR) |
| Area | |
| • Total | 2,511 km2 (970 sq mi) |
| • Rank | 15th region |
| Population (January 2023)[1] | |
| • Total | 873,102 |
| • Density | 350/km2 (900/sq mi) |
| Demonym | Réunionese |
| Time zone | UTC+04:00 (RET) |
| ISO 3166 code | |
| GDP (nominal) (2019)[2] | Ranked 13th |
| Total | €19.5 billion (US$21.8 bn) |
| Per capita | €22,629 (US$25,333) |
| NUTS Region | FRY4 |
| Website | Prefecture Regional Council Departmental Council |
Réunion,[note 1] officially Department of Réunion,[note 2] is an island in the Indian Ocean that is an overseas department and region of France. Part of the Mascarene Islands, it is located approximately 679 km (422 mi) east of the island of Madagascar and 175 km (109 mi) southwest of the island of Mauritius. As of January 2023, it had a population of 873,102.[1] Its capital and largest city is Saint-Denis.
Réunion was uninhabited until French immigrants and colonial subjects settled the island in the 17th century. Its tropical climate led to the development of a plantation economy focused primarily on sugar; slaves from East Africa were imported as fieldworkers, followed by Malays, Vietnamese, Chinese, and Indians as indentured laborers. Today, the greatest proportion of the population is of mixed descent, while the predominant language is Réunion Creole, though French remains the sole official language.
Since 1946, Réunion has been governed as a French region and is thus politically indistinguishable from its counterparts in Metropolitan France. Consequently, it is the outermost region of the European Union and part of the eurozone;[3] along with the French overseas department of Mayotte it is the only eurozone area in the Southern Hemisphere. Owing to its strategic location, France maintains a large military presence.
Toponymy
When France took possession of the island in the seventeenth century, it was named Bourbon, after the dynasty that then ruled France. To break with this name, which was too attached to the Ancien Régime, the National Convention decided on 23 March 1793,[4] to rename the territory Réunion Island. ("Réunion", in French, usually means "meeting" or "assembly" rather than "reunion". This name was presumably chosen in homage to the meeting of the fédérés of Marseilles and the Paris National Guards that preceded the insurrection of 10 August 1792. No document establishes this and the use of the word "meeting" could have been purely symbolic.)[5]
The island changed its name again in the 19th century: in 1806, under the First Empire, General Decaen named it Île Bonaparte (after Napoleon), and in 1810 it became Île Bourbon again. It was permanently renamed Réunion after the fall of the July monarchy by a decree of the provisional government on 7 March 1848.[6]
In accordance with the original spelling and the classical spelling and typographical rules,[7] "la Réunion" was written with a lower case in the article, but during the end of the 20th century, the spelling "La Réunion" with a capital letter was developed in many writings to emphasize the integration of the article in the name. This last spelling corresponds to the recommendations of the Commission nationale de toponymie[8] and appears in the current Constitution of the French Republic in articles 72-3 and 73.
History
The island has been inhabited since the 17th century, when people from France and Madagascar settled there. Slavery was abolished on 20 December 1848 (a date celebrated yearly on the island), when the Second Republic abolished slavery in the French colonies. However, indentured workers continued to be brought to Réunion from South India, among other places. The island became an overseas department of France in 1946.
Not much is known of Réunion's history prior to the arrival of the Portuguese in the early 16th century.[9] Arab traders were familiar with it by the name Dina Morgabin, "Western Island".[10] The island is possibly featured on a map from 1153 AD by Al Sharif el-Edrisi.[citation needed] The island might also have been visited by Swahili or Austronesian (Ancient Indonesian–Malaysian) sailors on their journey to the west from the Malay Archipelago to Madagascar.[9]
The first European discovery of the area was made around 1507 by Portuguese explorer Diogo Fernandes Pereira, but the specifics are unclear. The uninhabited island might have been first sighted by the expedition led by Dom Pedro Mascarenhas, who gave his name to the island group around Réunion, the Mascarenes.[11] Réunion itself was dubbed Santa Apolónia after a favourite saint,[10] which suggests that the date of the Portuguese discovery could have been 9 February, her feast day. Diogo Lopes de Sequeira is said to have landed on the islands of Réunion and Rodrigues in 1509.[citation needed]
By the early 1600s, nominal Portuguese rule had left Santa Apolónia virtually untouched.[11] The island was then occupied by France and administered from Port Louis, Mauritius. Although the first French claims date from 1638, when François Cauche and Salomon Goubert visited in June 1638,[12] the island was officially claimed by Jacques Pronis of France in 1642, when he deported a dozen French mutineers to the island from Madagascar. The convicts were returned to France several years later, and in 1649, the island was named Île Bourbon after the French royal House of Bourbon. Colonisation started in 1665, when the French East India Company sent the first settlers.[11]
Revolutionary revolts
On 19 March 1793, during the French Revolution, the island's name was changed to "Réunion Island" in homage to the meeting of the Federates of Marseille and the National Guards of Paris, during the march on the Tuileries Palace on 10 August 1792, and to erase the name of the Bourbon dynasty.[13]
The abolition of slavery voted by the National Convention on 4 February 1794, was rejected by Réunion, as well as by Île de France (Mauritius). A delegation accompanied by military forces, charged with imposing the liberation of slaves, arrived on the island of Bourbon on 18 June 1796, only to be immediately expelled without mercy. There followed a period of unrest and challenges to the power of the metropolis, which no longer had any authority over the two islands. The First Consul of the Republic, Napoleon Bonaparte, maintained slavery there, which was never abolished in practice, with the law of 20 May 1802. On 26 September 1806, the island took the name of Bonaparte and found itself in the front line of the Franco-British conflict for the control of the Indian Ocean.
During the Napoleonic Wars, the island was invaded by British forces and its governor, General Sainte-Suzanne, was forced to capitulate on 9 July 1810. The island then came under British rule and was returned to the French under the Treaty of Paris of 1814.
Following climatic catastrophes of 1806-1807 (cyclones, floods), coffee cultivation declined rapidly and was replaced by sugar cane, whose demand in France increased, due to France's recent loss of Saint-Domingue, and soon of the Île-de-France (Mauritius). Because of its growth cycle, sugarcane is not affected by cyclones. In 1841, Edmond Albius' discovery of hand-pollination of vanilla flowers enabled the island to soon become the world's leading vanilla producer. The cultivation of geranium, whose essence is widely used in perfumery, also took off.
From 1838 to 1841, Rear Admiral Anne Chrétien Louis de Hell was governor of the island. A profound change of society and mentality linked to the events of the last ten years led the governor to present three emancipation projects to the Colonial Council.
On 20 December 1848, Sarda Garriga finally proclaimed the abolition of slavery (20 December was a holiday in Réunion). Louis Henri Hubert Delisle became its first Creole governor on 8 August 1852, and remained in this position until 8 January 1858. Europe increasingly turned to sugar beet to meet its sugar needs. Despite the development policy of the local authorities and the recourse to compromise, the economic crisis became evident from the 1870s onwards. Subsequently, the opening of the Suez Canal caused a shift in commercial traffic away from the island. However, this economic depression did not prevent the modernization of the island, with the development of the road network, the creation of the railroad and the construction of the artificial harbor of the Pointe des Galets. These major construction projects offered a welcome alternative for agricultural workers.
Modern history
From the 17th to the 19th centuries, French colonisation, supplemented by importing Africans, Chinese and Indians as workers, contributed to ethnic diversity in the population. From 1690, most of the non-Europeans on the island were enslaved. The colony abolished slavery on 20 December 1848. Afterwards, many of the foreign workers came as indentured workers. The opening of the Suez Canal in 1869 reduced the importance of the island as a stopover on the East Indies trade route.[citation needed]
During the Second World War, Réunion was under the authority of the Vichy regime until 30 November 1942, when Free French forces took over the island with the destroyer Léopard.[citation needed]
Réunion became a département d'outre-mer (overseas département) of France on 19 March 1946. INSEE assigned to Réunion the department code 974, and the region code 04
when regional councils were created in 1982 in France, including in
existing overseas departments which also became overseas regions.
Over about two decades in the late 20th century (1963–1982), 1,630 children from Réunion were relocated to rural areas of metropolitan France, particularly to Creuse, ostensibly for education and work opportunities. That program was led by influential Gaullist politician Michel Debré, who was an MP for Réunion at the time. Many of these children were abused or disadvantaged by the families with whom they were placed. Known as the Children of Creuse, they and their fate came to light in 2002 when one of them, Jean-Jacques Martial, filed suit against the French state for kidnapping and deportation of a minor.[14] Other similar lawsuits were filed over the following years, but all were dismissed by French courts and finally by the European Court of Human Rights in 2011.[15]
In 2005 and 2006, Réunion was hit by a crippling epidemic of chikungunya, a disease spread by mosquitoes. According to the BBC News, 255,000 people on Réunion had contracted the disease as of 26 April 2006.[16] The neighbouring islands of Mauritius and Madagascar also suffered epidemics of this disease during the same year.[17][18] A few cases also appeared in mainland France, carried by people travelling by airline. The French government of Dominique de Villepin sent an emergency aid package worth €36 million and deployed about 500 troops in an effort to eradicate mosquitoes on the island.[citation needed]
Politics
Réunion sends seven deputies to the French National Assembly and three senators to the Senate.
Status
Réunion is an Overseas department and region of France (known in French as a Département et Région d'Outre-Mer, DROM) governed by Article 73 of the Constitution of France, under which the laws and regulations are applicable as of right, as in metropolitan France.[19]
Thus, Réunion has a regional council and a departmental council. These territorial entities have the same general powers as the departments and regions of metropolitan France, albeit with some adaptations. Article 73 of the Constitution provides for the possibility of replacing the region and the department by a single territorial entity, but, unlike French Guiana or Martinique, there are currently no plans to do so. Unlike the other DROMs, the Constitution explicitly excludes Réunion from the possibility of receiving authorization from Parliament to set certain rules itself, either by law or by the national executive.[19] The State is represented in Réunion by a prefect. The territory is divided into four districts (Saint-Benoît, Saint-Denis, Saint-Paul and Saint-Pierre). Réunion has 24 municipalities organized into 5 agglomeration communities. From the point of view of the European Union, Réunion is considered an "outermost region.”
Geopolitics
The positioning of Réunion Island has given it a more or less important strategic role depending on the period.
Already at the time of the India Route or Route des Indes, Réunion was a French possession located between Cape Town and the Indian trading posts, although far from the Mozambique Channel. Île de Bourbon (its name under the Ancien Régime) was not, however, the preferred position for trade and military. Governor Labourdonnais claimed that Île de France (Mauritius) was a land of opportunity, thanks to its topography and the presence of two natural harbours. He intended Île de Bourbon to be a depot or an emergency base for Île de France.[20]
The opening of the Suez Canal diverted much of the maritime traffic from the southern Indian Ocean and reduced the strategic importance of the island. This decline is confirmed by the importance given to Madagascar, which was later colonized.[21]
Today, the island, the seat of a defense and security zone, is the headquarters of the French Armed Forces of the Southern Indian Ocean Zone (FAZSOI), which brings together French Army units stationed in La Réunion and Mayotte. Réunion is also a base for the so-called Frenchelon signal intelligence system, whose infrastructure includes a mobile listening and automatic search unit. Saint-Pierre is also the headquarters of the mostly uninhabited French Southern and Antarctic Lands (Terres australes et antarctiques françaises, TAAF). Because of France's possession of Réunion, France is a member of the Indian Ocean Commission, which also includes the Comoros, Madagascar, Mauritius and the Seychelles.
Administrative divisions
Administratively, Réunion is divided into 24 communes (municipalities) grouped into four arrondissements. It is also subdivided into 25 cantons, meaningful only for electoral purposes at the departmental or regional level.[22] It is a French overseas department, hence a French overseas region. The low number of communes, compared with French metropolitan departments of similar size and population, is unique: most of its communes encompass several localities, sometimes separated by significant distances.
Municipalities (communes)
| Name | Area (km2) | Population (2019)[23] | Coat of arms | Arrondissement | Map |
|---|---|---|---|---|---|
| Les Avirons | 26.27 | 11,440 | Saint-Pierre | ||
| Bras-Panon | 88.55 | 13,057 | Saint-Benoît | ||
| Cilaos | 84.4 | 5,538 | Saint-Pierre | ||
| Entre-Deux | 66.83 | 6,927 | Saint-Pierre | ||
| L'Étang-Salé | 38.65 | 14,059 | Saint-Pierre | ||
| Petite-Île | 33.93 | 12,395 | Saint-Pierre | ||
| La Plaine-des-Palmistes | 83.19 | 6,626 |
|
Saint-Benoît | |
| Le Port | 16.62 | 32,977 | Saint-Paul | ||
| La Possession | 118.35 | 32,985 | Saint-Paul | ||
| Saint-André | 53.07 | 56,902 |
|
Saint-Benoît | |
| Saint-Benoît | 229.61 | 37,036 |
|
Saint-Benoît | |
| Saint-Denis | 142.79 | 153,810 | Saint-Denis | ||
| Saint-Joseph | 178.5 | 37,918 | Saint-Pierre | ||
| Saint-Leu | 118.37 | 34,586 | Saint-Paul | ||
| Saint-Louis | 98.9 | 53,120 | Saint-Pierre | ||
| Saint-Paul | 241.28 | 103,208 | Saint-Paul | ||
| Saint-Philippe | 153.94 | 5,198 |
|
Saint-Pierre | |
| Saint-Pierre | 95.99 | 84,982 | Saint-Pierre | ||
| Sainte-Marie | 87.21 | 34,061 | Saint-Denis | ||
| Sainte-Rose | 177.6 | 6,345 |
|
Saint-Benoît | |
| Sainte-Suzanne | 58.84 | 24,065 |
|
Saint-Denis | |
| Salazie | 103.82 | 7,136 | Saint-Benoît | ||
| Le Tampon | 165.43 | 79,824 | Saint-Pierre | ||
| Les Trois-Bassins | 42.58 | 7,015 |
|
Saint-Paul |
The communes voluntarily grouped themselves into five groups for cooperating in some domains, apart from the four arrondissements to which they belong for purposes of national laws and executive regulation. After some changes in their composition, name and status, all of them operate with the status of agglomeration communities, and apply their own local taxation (in addition to national, regional, departmental, and municipal taxes) and have an autonomous budget decided by the assembly representing all member communes. This budget is also partly funded by the state, the region, the department, and the European Union for some development and investment programs. Every commune in Réunion is now a member of such an intercommunality, with its own taxation, to which member communes have delegated their authority in various areas.
Foreign relations
Although diplomacy, military, and French government matters are handled by Paris, Réunion is a member of La Francophonie, the Indian Ocean Commission, the International Trade Union Confederation, the Universal Postal Union, the Port Management Association of Eastern and Southern Africa, and the World Federation of Trade Unions in its own right.
Defence
The French Armed Forces are responsible for the defence of the department. These forces also contribute to the defence of other French territories in the region, including Mayotte and the French Southern and Antarctic Lands. A total of some 2,000 French troops are deployed in the region - mostly in Réunion centred on the 2nd Marine Infantry Parachute Regiment. Two CASA CN 235 aircraft, forming air detachment 181 and drawn from the 50th Air Transport squadron, provide a modest air transport and surveillance capability.[24][25] In 2022, the French Air Force demonstrated a capacity to reinforce the territory by deploying two Rafale fighter aircraft, supported by an A330 MRTT Phénix tanker, from France to Réunion for a regional exercise.[26]
The French naval presence includes: two Floréal-class frigates, Floréal and Nivôse, the icebreaker L'Astrolabe, the patrol and support ship Champlain and the coast guard vessel Le Malin. The naval aviation element includes Eurocopter AS565 Panther helicopters from Flottille 36F able to embark on the Floréal-class frigates as required.[27][24] By 2024, Le Malin is to be replaced by Auguste Techer, a vessel of the new Félix Éboué class of patrol vessels. The French Navy will further reinforce its offshore patrol capabilities in the region by deploying a second vessel of the class (Félix Éboué) to Réunion by 2025.[28]
About 800 National Gendarmerie, including one mobile squadron and one high mountain platoon, are also stationed in Réunion.[29] The Maritime Gendarmerie operates the patrol boat Verdon in the territory[30] (though she was reported forward-deployed in Mayotte as of 2022).[31]
Geography
The island is 63 km (39 mi) long; 45 km (28 mi) wide; and covers 2,512 km2 (970 sq mi). It is above a hotspot in the Earth's crust. The Piton de la Fournaise, a shield volcano on the eastern end of Réunion Island, rises more than 2,631 m (8,632 ft) above sea level and is sometimes called a sister to Hawaiian volcanoes because of the similarity of climate and volcanic nature. It has erupted more than 100 times since 1640, and is under constant monitoring, most recently erupting on 19 September 2022.[32] During another eruption in April 2007, the lava flow was estimated at 3,000,000 m3 (3,900,000 cu yd) per day.[33] The hotspot that fuels Piton de la Fournaise also created the islands of Mauritius and Rodrigues.
The Piton des Neiges volcano, the highest point on the island at 3,070 m (10,070 ft) above sea level, is northwest of the Piton de la Fournaise. Collapsed calderas and canyons are south west of the mountain. While the Piton de la Fournaise is one of Earth's most active volcanoes, the Piton des Neiges is dormant. Its name is French for "peak of snows", but snowfall on the summit of the mountain is rare. The slopes of both volcanoes are heavily forested. Cultivated land and cities like the capital city of Saint-Denis are concentrated on the surrounding coastal lowlands. Offshore, part of the west coast is characterised by a coral reef system. Réunion also has three calderas: the Cirque de Salazie, the Cirque de Cilaos and the Cirque de Mafate. The last is accessible only on foot or by helicopter.
Cirque de Mafate is a caldera formed from the collapse of the large shield volcano the Piton des Neiges.
Lava flow emitted in 2005 by the Piton de la Fournaise
Geology and relief
Reunion Island is a volcanic island born some three million years ago[34] with the emergence of the Piton des Neiges volcano.It has an altitude of 3,070.50 m, the highest peak in the Mascarene Islands and the Indian Ocean. The eastern part of the island is constituted by the Piton de la Fournaise, a much more recent volcano (500,000 years old) which is considered one of the most active on the planet. The emerged part of the island represents only a small percentage (about 3%) of the underwater mountain that forms it.
In addition to volcanism, the relief of the island is very uneven due to active erosion. The center shelters three vast cirques dug by erosion (Salazie, Mafate and Cilaos) and the slopes of the island are furrowed by numerous rivers digging gullies, estimated at least 600,[35] generally deep and whose torrents cut the sides of the mountains up to several hundreds of meters deep.
The ancient massif of the Piton des Neiges is separated from the massif of La Fournaise by a gap formed by the plaine des Palmistes and the plaine des Cafres, a passageway between the East and the South of the island. Apart from the plains, the coastal areas are generally the flattest regions, especially in the north and west of the island. The coastline of the wild south is however steeper.
Between the coastal fringe and the Hauts, there is a steep transitional zone whose gradient varies considerably before arriving at the ridge lines setting the cirques or the Enclos, the caldera of the Piton de la Fournaise.
Climate
The island of Reunion is characterized by a humid tropical climate, tempered by the oceanic influence of the trade winds blowing from east to west. The climate of Reunion is characterized by its great variability, mainly due to the imposing relief of the island, which is at the origin of numerous microclimates.
As a result, there are strong disparities in rainfall between the windward coast in the east and the leeward coast in the west, and in temperature between the warmer coastal areas and the relatively cooler highland areas.
In Réunion there are two distinct seasons, defined by the rainfall regime:
- a rainy season from January to March, during which most of the year's rain falls;
- a dry season from May to November. However, in the eastern part and in the foothills of the volcano, rainfall can be significant even in the dry season;
April and December are transition months, sometimes very rainy but also very dry.
Pointe des Trois Bassins, located on the coast of the commune of Trois-Bassins (West), is the driest season, with a normal annual precipitation of 447.7 mm (17.63 in), while Le Baril, in Saint-Philippe (Southeast), is the wettest coastal season, with a normal annual precipitation of 4,256.2 mm (167.57 in).[36]
However, the wettest station is in the highlands of Sainte-Rose, with an average annual rainfall of almost 11,000 mm (430 in), making it one of the wettest places in the world.
Temperatures in Reunion are characterized by their great mildness throughout the year. In fact, the thermal amplitude from one season to another is relatively small (rarely exceeding 10 °C or 18 °F), although it is perceptible:
- In the warm season (November to April): average minimums usually range between 21 and 24 °C (70 and 75 °F), and average maximums between 28 and 31 °C (82 and 88 °F), on the coast. At 1,000 m (3,300 ft), average minimums fluctuate between 10 and 14 °C (50 and 57 °F) and average maximums between 21 and 24 °C (70 and 75 °F);
- In the cold season (May to October): temperatures at sea level vary from 17 to 20 °C (63 to 68 °F) for average minimums and from 26 to 28 °C (79 to 82 °F) for average maximums. At 1,000 m (3,300 ft), average minimums range from 8 to 10 °C (46 to 50 °F) and average maximums from 17 to 21 °C (63 to 70 °F).
In mountain towns, such as Cilaos or La Plaine-des-Palmistes, average temperatures range between 12 and 22 °C (54 and 72 °F). The highest parts of the habitat and the natural areas at altitude may suffer some winter frosts. Snow was even observed on the Piton des Neiges and Piton de la Fournaise in 2003 and 2006.[37]
The warmest day on record set on 30 January 2022. In the cold pole of the Reunion Island (all-time low -5C) Gite de Bellecombe (2245m asl) with a max. temperature of 25.4C on 30 January. It beats the previous record of 25.1C set in 2021 and 2021.
While a growing number of islands (including "non-sovereign" islands) in the world are concerned about the effects of climate change, the island of Reunion was chosen (along with Gran Canaria in Spain) as an example for a case study of an affected ultra-European peripheral territory, for a study on the adequacy of urban and regional planning tools to the needs and characteristics of these islands (including land use and population density and the regulatory framework).
This work confirmed that urban and peri-urban land use pressures are high, and that adaptation strategies are incompletely integrated into land use planning. According to the Institute of Island Studies, there is a dysfunction: "island planning tools often do not take climate change adaptation into account and there is too much top-down management in the decision-making process".[38] Réunion holds the world records for the most rainfall in 12-, 24-, 72- and 96-hour periods,[39] including nearly 6 ft (1.8 meters) in 24 hours.[40]
Beaches
Réunion hosts many tropical and unique beaches. They are often equipped with barbecues, amenities, and parking spaces. Hermitage Beach is the most extensive and best-preserved lagoon in Réunion Island and a popular snorkelling location.[41] It is a white sand beach lined with casuarina trees under which the locals often organise picnics. La Plage des Brisants is a well-known surfing spot, with many athletic and leisurely activities taking place. Each November, a film festival is also organised in La Plage des Brisant's. Movies are projected on a large screen in front of a crowd. Beaches at Boucan Canot are surrounded by a stretch of restaurants that particularly cater to tourists. L'Étang-Salé on the west coast is a particularly unique beach as it is covered in black sand consisting of tiny fragments of basalt. This occurs when lava contacts water, it cools rapidly and shatters into the sand and fragmented debris of various size. Much of the debris is small enough to be considered sand. Grand Anse is a tropical white-sand beach lined with coconut trees in the south of Réunion, with a rock pool built for swimmers, a pétanque playground, and a picnic area. Le Vieux Port in Saint Philippe is a green-sand beach consisting of tiny olivine crystals, formed by the 2007 lava flow, making it one of the youngest beaches on Earth.[42]
Restaurants along Boucan Canot beach[43]
Environment
Flora
The tropical and insular flora of Reunion Island is characterized by its diversity, a very high rate of endemism and a very specific structure. The flora of Reunion presents a great diversity of natural environments and species (up to 40 tree species/ha, compared to a temperate forest which has an average of 5/ha). This diversity is even more remarkable, but fragile, as it differs according to the environment (coastal, low, medium and high mountain).
Reunion has a very high rate of endemic species, with more than 850 native plants (of natural origin and present before the arrival of humans), of which 232 are endemic to the island of Reunion (only present on the island), as well as numerous species endemic to the Mascarene archipelago. Finally, the flora of Reunion is distinguished from that of equatorial tropical forests by the low height and density of the canopy, probably due to adaptation to cyclones, and by a very specific vegetation, in particular a strong presence of epiphytic plants (growing on other plants), such as orchids, bromeliads[citation needed] and cacti[citation needed], but also ferns, lichens and mosses.[44]
Wildlife
Like its prodigious floral diversity, Réunion is home to a variety of birds such as the white-tailed tropicbird (French: paille en queue).[45] Many of these birds species are endemic to the island, such as the Réunion harrier and Réunion cuckooshrike. Its largest land animal is the panther chameleon, Furcifer pardalis. Much of the west coast is ringed by coral reef which harbours, among other animals, sea urchins, conger eels, and parrot fish. Sea turtles and dolphins also inhabit the coastal waters. Humpback whales migrate north to the island from the Antarctic waters annually during the Southern Hemisphere winter (June–September) to breed and feed, and can be routinely observed from the shores of Réunion during this season. At least 19 species formerly endemic to Réunion have become extinct following human colonisation. For example, the Réunion giant tortoise became extinct after being slaughtered in vast numbers by sailors and settlers of the island.
A juvenile Emperor angelfish
A white-tailed Tropicbird
A Humpback whale off St-Gilles
Marine biodiversity
Despite the small area of coral reefs, the marine biodiversity of Reunion Island is comparable to that of other islands in the area, which has earned the Mascarene archipelago its inclusion among the top ten global biodiversity "hotspots".[46] Reunion's coral reefs, both flat and barrier, are dominated mainly by fast-growing branching coral species of the genus Acropora (family Acroporidae), which provide shelter and food for many tropical species.
Recent scientific research in Reunion Island indicates that there are more than 190 species of corals, more than 1,300 species of mollusks, more than 500 species of crustaceans,[47] more than 130 species of echinoderms and more than 1,000 species of fish.[48]
Reunion's deeper waters are home to dolphins, killer whales, humpback whales, blue sharks and a variety of shark species, including whale sharks, coral sharks, bull sharks, tiger sharks, blacktip sharks and great white sharks. Several species of sea turtles live and breed here.
Between 2010 and 2017, 23 shark attacks occurred in the waters of Réunion, of which nine were fatal.[49] In July 2013, the Prefect of Réunion Michel Lalande announced a ban on swimming, surfing, and bodyboarding off more than half of the coast. Lalande also said 45 bull sharks and 45 tiger sharks would be culled, in addition to the 20 already killed as part of scientific research into the illness ciguatera.[50]
Migrations of humpback whales contributed to a boom of whale watching industries on Réunion, and watching rules have been governed by the OMAR (Observatoire Marin de la Réunion) and Globice (Groupe local d'observation et d'identification des cétacés).
Coral reef
Because the island is relatively young (3 million years old),[34] the coral formations (8,000 years old) are not well developed and occupy a small area compared to older islands, mostly in the form of fringing reefs.[34]
These formations define shallow "lagoons" (rather "reef depressions"), the largest of which is no more than 200 m (660 ft) wide and about 1–2 m (3.3–6.6 ft) deep.[51] These lagoons, which form a discontinuous reef belt 25 km (16 mi) long (i.e. 12% of the island's coastline) with a total area of 12 km2 (4.6 sq mi), are located on the west and southwest coast of the island. The most important are those of L'Ermitage (St-Gilles), St-Leu, L'Étang-Salé and St-Pierre.
Management
Since 2010, Réunion is home to a UNESCO World Heritage Site that covers about 40% of the island's area and coincides with the central zone of the Réunion National Park.[52] The island is part of the Mascarene forests terrestrial ecoregion.[53]
Gardening and Bourbon roses
The first members of the "Bourbon" group of garden roses originated on this island (then still Île Bourbon, hence the name) from a spontaneous hybridisation between Damask roses and Rosa chinensis,[54] which had been brought there by the colonists. The first Bourbon roses were discovered on the island in 1817.[55]
Threats to the environment
Among coastal ecosystems, coral reefs are among the richest in biodiversity, but they are also the most fragile.[56]
Nearly one-third of fish species were already considered threatened or vulnerable in 2009, with coral degradation in many places. The causes of this state of affairs are pollution, overfishing and poaching, as well as anthropogenic pressure, especially linked to the densification of urbanization in coastal areas and the discharge of sewage.[57]
15 species living on Réunion were included in the Red List published by the International Union for Conservation of Nature (IUCN).[58]
Demographics
Historical population
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Local population estimates and censuses up to 1946.[59][60] INSEE censuses between 1954 and 2019.[61][62] Last INSEE 2022 estimate.[1] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Major metropolitan areas
The most populous metropolitan area is Saint-Denis, which covers 6 communes (Saint-Denis, Sainte-Marie, La Possession, Sainte-Suzanne, Saint-André, and Bras-Panon) in the north of the island.[63] The three largest metropolitan areas are:[64]
| Urban unit | Population (2020) |
|---|---|
| Saint-Denis | 315,080 |
| Saint-Pierre-Le Tampon | 222,614 |
| Saint-Paul | 171,109 |
Migrations and ethnic groups
At the 2019 census, 82.4% of the inhabitants of Réunion were born on the island, 11.7% were born in Metropolitan France, 1.0% were born in Mayotte, 0.3% were born in the rest of Overseas France, and 4.6% were born in foreign countries (46% of them children of French expatriates and settlers born in foreign countries, such as children of Réunionese settlers born in Madagascar during colonial times; the other 54% immigrants, i.e. people born in foreign countries with no French citizenship at birth).[65]
In recent decades, the number of Metropolitan Frenchmen living on the island of Réunion has increased markedly: only 5,664 natives of Metropolitan France lived in Réunion at the 1967 census, but their numbers were multiplied by more than 6 in 23 years, reaching 37,516 at the 1990 census, and then nearly tripled in the next 29 years, reaching 100,493 at the 2019 census.[66][67][65] Native Réunionese, meanwhile, have emigrated increasingly to Metropolitan France: the number of natives of Réunion living in Metropolitan France rose from 16,548 at the 1968 census to 92,354 at the 1990 census to 130,662 at the 2019 census, by which date 15.7% of the natives of Réunion lived outside of Réunion.[67][65]
Réunion has experienced extremely little immigration of foreigners since World War Two, and by the 2019 census only 2.5% of the inhabitants of Réunion were immigrants. This is in contrast to the situation that prevailed from the middle of the 19th century until World War Two when many migrants from India (especially from Tamil Nadu and Gujarat),[68] Eastern Asia (particularly China), and Africa came to Réunion to work in the plantation economy. Their descendants have now become French citizens.
| Census | Born in Réunion |
Born in Metropolitan France |
Born in Mayotte |
Born in the rest of Overseas France |
Born in foreign countries with French citizenship at birth¹ |
Immigrants² |
| 2019 | 82.4% | 11.7% | 1.0% | 0.3% | 2.1% | 2.5% |
| 2013 | 83.7% | 11.1% | 0.7% | 0.3% | 2.2% | 2.0% |
| 2008 | 84.6% | 10.3% | 0.8% | 0.2% | 2.4% | 1.8% |
| 1999 | 86.1% | 9.1% | 0.9% | 0.4% | 2.0% | 1.4% |
| 1990 | 90.4% | 6.3% | 0.2% | 0.1% | 1.9% | 1.0% |
| 1982 | 93.1% | 4.1% | 2.8% | |||
| 1967 | 96.8% | 1.4% | 1.8% | |||
| ¹Persons born abroad of French parents, such as Pieds-Noirs and children of French expatriates. ²An immigrant is by French definition a person born in a foreign country and who didn't have French citizenship at birth. Note that an immigrant may have acquired French citizenship since moving to France, but is still listed as an immigrant in French statistics. On the other hand, persons born in France with foreign citizenship (the children of immigrants) are not listed as immigrants. | ||||||
| Source: IRD,[66] INSEE[67][65] | ||||||
Ethnic groups present include people of African, Indian, European, Malagasy and Chinese origin. Local names for these are Yabs, Cafres, Malbars and Chinois. All of the ethnic groups on the island are immigrant populations that have come to Réunion from Europe, Asia and Africa over the centuries. There are no indigenous people on the island, as it was originally deserted.[69] These populations have mixed from the earliest days of the island's colonial history (the first settlers married women from Madagascar and of Indo-Portuguese heritage), resulting in a majority population of mixed race and of "Creole" culture.
It is not known exactly how many people of each ethnicity live in Réunion, since the French census does not ask questions about ethnic origin,[70] which applies in Réunion because it is a part of France in accordance with the 1958 constitution. The extent of racial mixing on the island also makes ethnic estimates difficult. According to estimates, Whites make up roughly one quarter of the population,[71] Malbars make up more than 25% of the population and people of Chinese ancestry form roughly 3%.[72] The percentages for those of African and mixed-race origins vary widely in estimates. Also, some people of Vietnamese ancestry live on the island, though they are very few in number.[73][74][75]
Tamils are the largest group among the Indian community.[76] The island's community of Muslims from northwestern India, particularly Gujarat, and elsewhere is commonly referred to as zarabes.
Creoles (a name given to those born on the island, regardless of ethnic origins) make up the majority of the population. Groups that are not Creole include people recently arrived from Metropolitan France (known as zoreilles) and those from Mayotte and the Comoros as well as immigrants from Madagascar and Sri Lankan Tamil refugees.
Religion
Religious affiliation (2000 censuses)[77]
The predominant religion is Christianity, notably Roman Catholicism, with a single (Latin Rite) jurisdiction, the Roman Catholic Diocese of Saint-Denis-de-La Réunion. Religious Intelligence estimates Christians to be 84.9% of the population, followed by Hindus (6.7%) and Muslims (2.15%).[75] Chinese folk religion and Buddhism are also represented, among others.
Most large towns have a Hindu temple and a mosque.[78]
Culture
Réunionese culture is a blend (métissage) of European, African, Indian, Chinese and insular traditions. The most widely spoken language, Réunion Creole, derives from French.
Language
French is the sole official language of Réunion. Though not official, Réunion Creole is widely spoken alongside French. Creole is commonly used for informal purposes, whereas the official language for administrative purposes, as well as education, is French.[79]
Other languages spoken on Réunion include: Comorian varieties (especially Shimaore) and Malagasy, by recent immigrants from Mayotte and Madagascar; Mandarin, Hakka and Cantonese by members of the Chinese community; Indian languages, mostly Tamil, Gujarati and Hindi; and Arabic, spoken by a small community of Muslims. These languages are generally spoken by immigrants, as those born on the island tend to use French and Creole.
Cantonese, Arabic and Tamil are offered as optional languages in some schools.[76]
Music
There are two music genres which originated in Réunion: sega, which originated earlier and is also traditional in Mauritius, Rodrigues and Seychelles, and maloya, which originated in the 19th century and is only found in Réunion. Every 20 December, the inhabitants of Reunion Island celebrate Reunion Freedom Day. This celebration, also known as the Fête des Cafres or "Fet' Kaf'", commemorates the proclamation of the abolition of slavery by the Second Republic (France) in 1848. The term "cafre" refers to the Africans of the "Cafrerie" (a part of southern Africa). It derives from the Afrikaans word "kaffer", which is similar to the American slang "nigger" or "nègre", originating in colonial France.[80]
Today, in the 21st century, Reunionese celebrate with joy the end of a long period of oppression. Cafres, Malagasy, Comorians, Indians, Yabs, Z'oreilles and metropolitans gather in the streets dancing to the rhythm of the sega and the maloya, the two great musical genres of Reunion.[81] Numerous concerts are organized, most of them free, as well as costume parades and dance shows such as merengue, for example.
Cuisine
Always accompanied by rice, the most common dishes are carry (sometimes spelled cari), a local version of Indian curry, rougail and civets. Curry is made with a base of onion, garlic and spices such as turmeric (called "safran péi" on the island),[82] on which fish, meat and eggs are fried; tomato is then added. Dishes can also be flavoured with ginger; the peel of a combava is often prized. Chop suey (with rice, not pasta) and other Asian dishes such as pork with pineapple[83]
Some examples of popular réunionese dishes include:
- Achards (inspired by achaar)
- Cabri massalé
- Cari poulet
- Rougail dakatine
- Rougail morue
- Rougail saucisse
- Bouchon
In general, there are few dishes without meat or fish, so there are few vegetarian options. One of them is chouchou chayote gratin. Otherwise, mainly poultry is consumed. One of the local specialties is tangue[84] civet (of the hedgehog family).
Sport
Moringue is a popular combat/dance sport similar to capoeira.
There are several famous Réunionese sportsmen and women like the handballer Jackson Richardson, as well as the karateka Lucie Ignace.
Réunion has a number of contributions to worldwide professional surfing. It has been home to notable pro surfers including Jeremy Flores, Johanne Defay and Justine Mauvin. Famous break St Leu has been host to several world surfing championship competitions.
Since 1992, Réunion has hosted a number of ultramarathons under the umbrella name of the Grand Raid. As of 2018, four different races compose the Grand Raid: the Diagonale des Fous, The Trail de Bourbon, the Mascareignes, and the Zembrocal Trail.[85]
Annual athletics Meeting de la Réunion is held at the Stade Paul Julius Bénard by the governing body Ligue Réunionnaise d'athlétisme.[86]
Football
Football is the most popular sport. With more than 30,000 licensed players for a population exceeding 850,000 inhabitants, it remains the sport of choice for young people. Although the highest level of competition called the First Division of Réunion is equivalent to a division d'honneur in metropolitan France (DH), all the youngsters hope to play at the highest level one day.
This has been the case for players such as Laurent Robert, Florent Sinama-Pongolle, Guillaume Hoarau, Dimitri Payet, Benoit Tremoulinas (the only five Reunionese to have played for the French national team), Bertrand Robert, Thomas Fontaine, Ludovic Ajorque, Fabrice Abriel (of Reunion descent) and Wilfried Moimbe (of Reunion descent), to name but a few. The territory has its own team, the Réunion national football team.
Architecture
Structurally, the local Creole house is said to be symmetrical.[87] In fact, in the absence of an architect, workers would draw a line on the ground and build two identical parts on each side, resulting in houses of essentially rectangular shape. The veranda is an important element of the house. It is an outdoor terrace built on the front of the house, as it allowed to show its richness to the street. A Creole garden completes the house. It is composed of local plants, found in the forest. There is usually a greenhouse with orchids, anthuriums and different types of ferns.
The Villa Déramond-Barre is a Creole architectural model of great heritage interest.[88]
Traditions
Two forms of musical expression historically make up the folkloric tradition of Reunion Island. One, the sega, is a Creole variant of the quadrille, the other, the maloya, like the American blues, comes from Africa, carried by the nostalgia and pain of slaves uprooted and deported from their homeland.
The sega, a disguised ballroom dance to the rhythm of traditional Western instruments (accordion, harmonica, guitar, etc.), is a testament to the fun of colonial society at the time. Today, it is still the typical ballroom dance of the island of Réunion and the Mascarene archipelago in general, along with the Mauritian sega and the Rhodesian sega.
The slaves' maloya, a ritual dance full of melodies and gestures, was performed almost clandestinely at night around a bonfire; the few instruments that accompanied it were made of plants (bamboo, gourds, etc.).
Beyond their taste for this musical art form, the maloya troupes wanted to perpetuate the memory of the slaves, their suffering and their uprooting. Through sometimes controversial texts, they remind France of its slave-owning past and underline the damage that this colonial era did to human beings; in the course of the island's history, maloya artists and kabars (gatherings) were sometimes banned by the authorities.
With the institution of a public holiday to celebrate the abolition of slavery (fête caf', 20 December), maloya has received official recognition; it is regularly played on public radio and many discotheques and dance parties programme it regularly; it is even enjoying a revival: groups have begun to make modern versions, styles and arrangements, such as maloggae and other electric maloya.
Some of Reunion Island's emblematic musical groups include: Groupe folklorique de La Réunion, Kalou Pilé, Baster, Ousanousava, Ziskakan, Pat'Jaune, Danyèl Waro, Tisours, etc. We can also mention one of the greatest Maloya singers: Lo Rwa Kaf. Born in Sainte-Suzanne, he was one of the first to sing Maloya. When he died in 2004, many people were present at his funeral.
In 2008, the artist Brice Guilbert made a video clip entitled La Réunion. In this clip, we see him crossing all the landscapes of the island.
In the field of contemporary dance, we can mention the choreographer Pascal Montrouge, who directs the only company in France that has a double headquarters in Saint-Denis de La Réunion and Hyères, which reinforces the sense of his vision of identity. In 2007, the city of Saint-Denis de La Réunion entrusted him with the artistic direction of its Saint-Denis Danses festival.
The island is home to the regional conservatory of La Réunion, which has four teaching centres and was created in 1987 under the impetus of the then president of the region, Pierre Lagourgue. Today, although traditional dances are not forgotten in the conservatoires (which teach dance, music and theatre), the dances taught are classical dance, contemporary dance and Bharata natyam dance. These students regularly have the opportunity to dance with choreographers from Reunion such as Didier Boutiana cie "konpani Soul city "98, Soraya Thomas cie "Morphose "99or Éric Languet cie "danse en l'R "100. These different local companies allow the inhabitants of Reunion to dance professionally.
Urban culture has also made its appearance, following the trends and influences of metropolitan France and the United States. Thus, hip-hop culture is developing, but also ragga dancehall, with KM David or Kaf Malbar being the figurehead of this new movement, influencing the young generation all over the island, with their songs spread by mp3 or internet. Many young artists are trying to "break through" in this music, whose industry is developing reasonably well, locally but also internationally, and has nothing to envy from the precursors of French dancehall.
Media
Broadcasting
Réunion has a local public television channel, Réunion 1ère, which now forms part of France Télévision, and also receives France 2, France 3, France 4, France 5 and France 24 from metropolitan France, as well as France Ô, which shows programming from all of the overseas departments and territories. There are also two local private channels, Télé Kréol and Antenne Réunion.
It has a local public radio station, formerly Radio Réunion, but now known as Réunion 1ère, like its television counterpart. It also receives the Radio France networks France Inter, France Musique and France Culture. The first private local radio station, Radio Freedom, was introduced in 1981. They broadcast daily content about weather and local services.
Newspapers
Two main newspapers:
Cinema
Present on the island since 1896, is marked by its insularity and its geographical distance from metropolitan France. In the absence of the Centre national de la cinématographie (CNC), it has developed specific distribution and dissemination networks. Its landscapes first served as a natural backdrop for many film and television productions, and film events, such as festivals, multiplied there. Digital technology now facilitates the development of local productions, most of which reflect the particularities of a multicultural and multilingual society.
The Réunion Film festival (festival du film de La Réunion) was created in 2005 and is chaired by Fabienne Redt. The festival presented first and second feature films by French directors. The 10th and last edition took place in 2014 in partnership mainly with the TEAT Champ Fleuri (Saint-Denis) and the city of Saint-Paul.
In the Port, the International Film Festival of Africa and the Reunion Islands (Festival international du film d'Afrique et des îles de La Réunion) was also held.
Among the existing film festivals is the Reunion Island Adventure Film Festival (13 editions), which awards prizes to adventure films.
In Saint-Philippe, the Festival Même pas peur, Réunion's international fantasy film festival, has been held since 2010.
In Saint-Pierre, there are two festivals: Écran jeunes (25th edition in 2019) and the Festival du Film Court de Saint-Pierre, directed by Armand Dauphin (3rd edition in 2019).
Film
- Adama (animated there)
- Mississippi Mermaid (1969) (filmed there)
Blogs
- Reunion Island Tourism blog (English/French tourism blog)
- Visit Reunion (English language blog and Instagram page)[89][non-primary source needed]
Internet
The Internet situation in Réunion was once marked by its insularity and remoteness from mainland France, which caused some technological delays. Today, the trend has been reversed and the region has a relatively efficient Internet connection and is one of the departments most connected by fibre optics in France.
Internet connection can be provided by ADSL (offered by four operators), fibre optic (three operators), or by cellular data on 4G and 5G networks (currently being tested in Saint-Denis).
Reunion domain names have the suffix .re. The Reunion region has deployed a regional fibre-optic network for operators. This network is based partly on EDF's very high voltage cables - G@zelle network, partly on the region's own fibre and partly on Hertzian links for the most isolated areas. This network is managed by a public service company called La Réunion Numérique.[90]
Economy
In 2019, the GDP of Réunion at market exchange rates, not at PPP, was estimated at 19.5 billion euros (US$21.8 bn) and the GDP per capita (also at market exchange rates) was 22,629 euros (US$25,333), the highest in sub-Saharan Africa,[91] but only 61.7% of metropolitan France's GDP per capita that year, and 73.5% of the metropolitan French regions outside the Paris Region.[2]
Before the Global Financial Crisis of 2008, the economy of Réunion was in a process of catching up with the rest of France. From 1997 to 2007, the economy of Réunion grew by an average of +4.6% per year in real terms,[92] and the GDP per capita rose from 53.7% of metropolitan France's level in 2000 to 61.6% of metropolitan France in 2007.[2] The Great Recession that followed the financial crisis greatly affected Réunion whose economy came to a standstill in 2008, then experienced two years of recession in 2009 and 2010, followed by three years of stagnation (2011-2013).[92] By 2013, the GDP per capita of Réunion had fallen back to 60.6% of metropolitan France's level.[2]
Economic growth returned in 2014. The economy grew by an average of +2.9% per year in real terms from 2014 to 2017, and the GDP per capita of Réunion rose to 62.4% of metropolitan France's GDP per capita by 2017, its highest level ever.[2] The economy slowed down in 2018, growing at only +1.7% due in part to the yellow vests protests which paralyzed the Réunionese economy in the end of 2018, before recovering to +2.2% in 2019.[92] As a result of this slower growth since 2018, the GDP per capita of Réunion fell back slightly compared to metropolitan France's, standing at 61.7% of metropolitan France's level in 2019.[2]
Réunion was affected by the COVID-19 pandemic in 2020, leading to a massive recession of -4.2% that year according to provisional estimates, the largest on record,[92] although less severe than in metropolitan France (-7.9% for metropolitan France in 2020).[2]
| 2000 | 2007 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
|---|---|---|---|---|---|---|---|---|---|
| Nominal GDP (€ bn) | 9.55 | 15.17 | 16.53 | 16.97 | 17.55 | 18.07 | 18.56 | 19.00 | 19.51 |
| GDP per capita (euros) | 13,218 | 18,937 | 19,701 | 20,045 | 20,608 | 21,171 | 21,707 | 22,128 | 22,629 |
| GDP per capita as a % of Metropolitan France's |
53.7% | 61.6% | 60.6% | 61.0% | 61.5% | 62.4% | 62.4% | 62.0% | 61.7% |
| Source: INSEE.[2] | |||||||||
Sugar was traditionally the chief agricultural product and export. Tourism is now an important source of income.[93] The island's remote location combined with its stable political alignment with Europe makes it a key location for satellite receiving stations[94] and naval navigation.[95]
GDP sector composition in 2017 (contribution of each sector to the total gross value added):[96]
| Sector | % of total GVA | ||
|---|---|---|---|
| Agriculture, forestry and fishing | 1.9% | ||
|
| |||
| |||
| Mining and quarrying | 0.0% | ||
| Manufacturing | 4.6% | ||
|
| |||
| |||
| Utilities | 1.6% | ||
| Construction | 5.8% | ||
| Market services | 49.8% | ||
|
| |||
| |||
| Non-market services | 36.2% | ||
|
| |||
|
Unemployment is a major problem on Réunion, although the situation has improved markedly since the beginning of the 2000s: the unemployment rate, which stood above 30% from the early 1980s to the early 2000s, declined to 24.6% in 2007, then rebounded to 30.0% in 2011 due to the 2008 global financial crisis and subsequent Great Recession, but declined again after 2011, reaching 21.5% in 2019,[97] its lowest level in 40 years.[98]
In 2014, 40% of the population lived below the poverty line (defined by INSEE as 60% of Metropolitan France's median income; in 2014 the poverty line for a family of two parents and two young children was €2,064 (US$2,743) per month).[99]
Rum distillation contributes to the island's economy. A "Product of France", it is shipped to Europe for bottling, then shipped to consumers around the world.
Brasseries de Bourbon is the main brewery of the island, with Heineken as shareholder.
Tourism
Income from tourism is Reunion Island's primary economic resource, ahead of sugarcane production and processing, which has allowed the development of large Reunionese groups such as Quartier Français, Groupe Bourbon ex-Sucreries Bourbon, a large international company now listed on the stock exchange, but based outside the island and which has abandoned the sugar sector for the off-shore maritime sector. With the reduction of subsidies, this culture is threatened. Therefore, the development of fishing in the French Southern Territories has been promoted.
The tertiary sector, particularly the commercial sector, is by far the most developed, and import distribution has taken off in the mid-1980s through affiliation and franchising agreements with metropolitan groups. The advent of franchised distribution has transformed the commercial apparatus, which historically was characterized by the geographic dispersion of small grocery-type units; the few "Chinese stores" still in operation are limited to mid-range towns and, as relics of a bygone era, have more of a tourist and educational appeal, even if they retain a convenience store function.
Despite its economic dynamism, the island is unable to absorb its significant unemployment, which is explained in particular by a very strong demographic growth. Many Réunioners are forced to move to metropolitan France for their studies or to find work.
Agriculture
Agriculture in Réunion is an important activity in the island's economy:[100] the agricultural territory covering 20% of the island's surface area employs 10% of the active population, generates 5% of the gross regional product and provides the island's main export. Formerly centered on coffee and clove cultivation, it has focused on sugar cane since the events of the early 19th century, namely the Great Avalanches and the seizure of Reunion by the British. Today it faces important issues related to the decisions of the World Trade Organization at the international level and the development of the urban fact at the local level.
Reunion Island has about 7,000 farms, 5,000 of which are professional. These farms mobilize almost 11,000 AWU (annual workload of one person on a full-time basis).
Ninety-seven percent of the farms in Réunion are less than 20 hectares in size, compared to an average of 78 hectares in mainland France.
The most common status is that of individual farmer (97%).
In 2005, more than 60% of farm managers were between 40 and 59 years old.
Public services
Health
In 2005–2006, Réunion experienced an epidemic of chikungunya, a viral disease similar to dengue fever brought in from East Africa, which infected almost a third of the population because of its transmission through mosquitoes. The epidemic has since been eradicated. See the History section for more details.
Transport
Roland Garros Airport serves the island, handling flights to mainland France, India, Madagascar, Mauritius, Tanzania, Comoros, Seychelles, South Africa, China and Thailand. Pierrefonds Airport, a smaller airport, has some flights to Mauritius and Madagascar. In 2019 a light rail system was proposed to link Le Barachois with the airport.[101]
Education
Reunion Island has its own education system. Chantal Manès-Bonnisseau, Inspector General of Education, Sport and Research, was appointed Rector of the Académie de la Réunion and Chancellor of Universities at the Council of Ministers on 29 July 2020.
She succeeds Vêlayoudom Marimoutou, who took office as secretary general of the Indian Ocean Commission on 16 July.
The Rectorate is located in the main city, in the Moufia district of Saint-Denis. At the start of the 2012 school year, the island had 522 pre-school and/or primary schools, including 26 private schools, for 120,230 students at the primary level, 82 secondary schools, including six private schools, for 61,300 students, 32 general and technological high schools, including three private schools, for 23,650 students, and 15 vocational schools, including two private schools, for 16,200 students.
Reunion's priority education zones affect slightly more than half of the primary and secondary school students.[102]
Baccalaureate results are relatively close to the national average with a rate of 81.4% in 2012 compared to 82.4% in 2011 (respectively: 84.5% and 85.6% in the national average).
In higher education, the University of Reunion has 11,600 students spread across the various sites, especially in Saint-Denis and Le Tampon. A further 5,800 students are divided between the post-baccalaureate courses of secondary education and other higher studies.[103]
Energy
Energy on Réunion depends on oil and is limited by the island's insularity, which forces it to produce electricity locally and import fossil fuels. Faced with increasing demand and environmental requirements, the energy produced on the island is tending to increasingly exploit its great renewable energy potential through the development of wind farms, solar farms and other experimental projects. Although 35% of Réunion's electricity came from renewable sources in 2013, the department's energy dependency rate exceeds 85%. Saving electricity and optimising energy efficiency are two major areas of work for the authorities responsible for energy issues.
Hydroelectric power
Due to the large volumes of rainfall, the flow of surface water allows the installation of hydroelectric infrastructures, especially as erosion has carved out narrow and very deep ravines. The Sainte-Rose plant (22 MW) and the Takamaka plant (17.5 MW) are the two largest. In total, the island's six hydroelectric infrastructures have a capacity of 133 MW.
Symbols
Réunion has no official coat of arms or flag.
Former Governor Merwart created a coat of arms for the island on the occasion of the 1925 colonial exhibition organised on Petite-Île. Merwart, a member of the Reunion Island Society of Sciences and Arts, wanted to include the island's history:
- the bees evoke the Empire;
- the central coat of arms evokes the French Republican flag;
- the fleurs-de-lis evoke the royal era;
- The motto "Florebo quocumque ferar" is that of the French East India Company and means "I will bloom wherever they take me", while the vanilla vines honour a flourishing harvest.
- The Roman numeral "MMM" evokes the altitude of the highest peaks;
- the ship Saint-Alexis is the one that first took possession of the island;
The most commonly used flag in Réunion is that of the "radiant volcano", designed by Guy Pignolet in 1975, sometimes called "Lo Mavéli":[104] it represents the volcano of Piton de la Fournaise in the form of a simplified red triangle on a navy blue background, while five sunbeams symbolise the arrival of the populations that have converged on the island over the centuries.[105]
See also
Notes
- French: Département de la Réunion
References
- "Saint-Philippe: Le drapeau Lo Mavéli adopté par la mairie". Zinfos 974, l'actualité de l'île de La Réunion (in French). Archived from the original on 26 September 2021. Retrieved 8 July 2021.
Bibliography
- James Rogers and Luis Simón. The Status and Location of the Military Installations of the Member States of the European Union and Their Potential Role for the European Security and Defence Policy (ESDP). Brussels: European Parliament, 2009. 25 pp.
External links
Government
- Departmental Council website (in French)
- Prefecture website (in French)
- Regional Council website (in French)
General information
- Réunion at Curlie
- Official tourism website
- UNESCO World Heritage Site datasheet
 Wikimedia Atlas of Réunion
Wikimedia Atlas of Réunion
- Réunion
- Mascarene Islands
- Island countries
- Island countries of the Indian Ocean
- Dependent territories in Africa
- Islands of Overseas France
- Overseas departments of France
- East African countries
- Southeast African countries
- Volcanic islands
- Former colonies in Africa
- Former French colonies
- French colonisation in Africa
- French East India Company
- Outermost regions of the European Union
- Regions of France
- French-speaking countries and territories
- Pirate dens and locations
- States and territories established in 1946
- 1946 establishments in Africa
- 1946 establishments in the French colonial empire
https://en.wikipedia.org/wiki/R%C3%A9union

















































































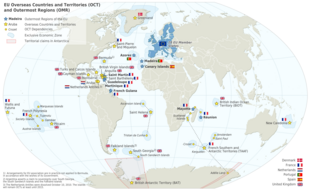









![Restaurants along Boucan Canot beach[43]](https://upload.wikimedia.org/wikipedia/commons/thumb/8/8a/Lunch_on_the_beach.jpg/120px-Lunch_on_the_beach.jpg)


























No comments:
Post a Comment