In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in time exhausts all that can be predicted about the system's behavior. A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states. A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers,[1][2] while mixed states are represented by density matrices, which are positive semidefinite operatorsthat act on Hilbert spaces.[3][4]
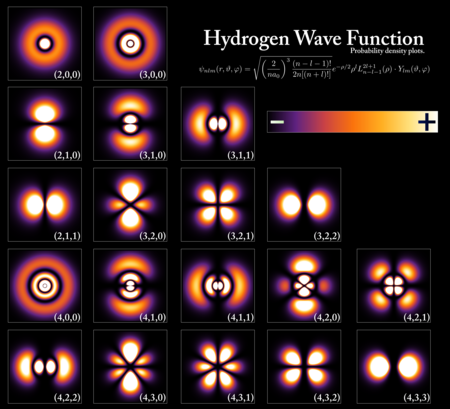
Pure states are also known as state vectors or wave functions, the latter term applying particularly when they are represented as functions of position or momentum. For example, when dealing with the energy spectrum of the electron in a hydrogen atom, the relevant state vectors are identified by the principal quantum number n, the angular momentum quantum number l, the magnetic quantum number m, and the spin z-component sz. For another example, if the spin of an electron is measured in any direction, e.g. with a Stern–Gerlach experiment, there are two possible results: up or down. The Hilbert space for the electron's spin is therefore two-dimensional, constituting a qubit. A pure state here is represented by a two-dimensional complex vector , with a length of one; that is, with
where and are the absolute values of and . A mixed state, in this case, has the structure of a matrix that is Hermitian and positive semi-definite, and has trace 1.[5] A more complicated case is given (in bra–ket notation) by the singlet state, which exemplifies quantum entanglement:
which involves superposition of joint spin states for two particles with spin 1⁄2. The singlet state satisfies the property that if the particles' spins are measured along the same direction then either the spin of the first particle is observed up and the spin of the second particle is observed down, or the first one is observed down and the second one is observed up, both possibilities occurring with equal probability.
A mixed quantum state corresponds to a probabilistic mixture of pure states; however, different distributions of pure states can generate equivalent (i.e., physically indistinguishable) mixed states. The Schrödinger–HJW theorem classifies the multitude of ways to write a given mixed state as a convex combination of pure states.[6] Before a particular measurement is performed on a quantum system, the theory gives only a probability distribution for the outcome, and the form that this distribution takes is completely determined by the quantum state and the linear operators describing the measurement. Probability distributions for different measurements exhibit tradeoffs exemplified by the uncertainty principle: a state that implies a narrow spread of possible outcomes for one experiment necessarily implies a wide spread of possible outcomes for another.
Conceptual description[edit]
Pure states[edit]
In the mathematical formulation of quantum mechanics, pure quantum states correspond to vectors in a Hilbert space, while each observable quantity (such as the energy or momentum of a particle) is associated with a mathematical operator. The operator serves as a linear function which acts on the states of the system. The eigenvalues of the operator correspond to the possible values of the observable. For example, it is possible to observe a particle with a momentum of 1 kg⋅m/s if and only if one of the eigenvalues of the momentum operator is 1 kg⋅m/s. The corresponding eigenvector (which physicists call an eigenstate) with eigenvalue 1 kg⋅m/s would be a quantum state with a definite, well-defined value of momentum of 1 kg⋅m/s, with no quantum uncertainty. If its momentum were measured, the result is guaranteed to be 1 kg⋅m/s.
On the other hand, a system in a superposition of multiple different eigenstates does in general have quantum uncertainty for the given observable. We can represent this linear combination of eigenstates as:
The coefficient which corresponds to a particular state in the linear combination is a complex number, thus allowing interference effects between states. The coefficients are time dependent. How a quantum state changes in time is governed by the time evolution operator. The symbols and [a] surrounding the are part of bra–ket notation.
Statistical mixtures of states are a different type of linear combination. A statistical mixture of states is a statistical ensemble of independent systems. Statistical mixtures represent the degree of knowledge whilst the uncertainty within quantum mechanics is fundamental. Mathematically, a statistical mixture is not a combination using complex coefficients, but rather a combination using real-valued, positive probabilities of different states . A number represents the probability of a randomly selected system being in the state . Unlike the linear combination case each system is in a definite eigenstate.[7][8]
The expectation value of an observable A is a statistical mean of measured values of the observable. It is this mean, and the distribution of probabilities, that is predicted by physical theories.
There is no state which is simultaneously an eigenstate for all observables. For example, we cannot prepare a state such that both the position measurement Q(t) and the momentum measurement P(t) (at the same time t) are known exactly; at least one of them will have a range of possible values.[b] This is the content of the Heisenberg uncertainty relation.
Moreover, in contrast to classical mechanics, it is unavoidable that performing a measurement on the system generally changes its state.[9][10][c] More precisely: After measuring an observable A, the system will be in an eigenstate of A; thus the state has changed, unless the system was already in that eigenstate. This expresses a kind of logical consistency: If we measure A twice in the same run of the experiment, the measurements being directly consecutive in time,[d] then they will produce the same results. This has some strange consequences, however, as follows.
Consider two incompatible observables, A and B, where A corresponds to a measurement earlier in time than B.[e] Suppose that the system is in an eigenstate of B at the experiment's beginning. If we measure only B, all runs of the experiment will yield the same result. If we measure first A and then B in the same run of the experiment, the system will transfer to an eigenstate of A after the first measurement, and we will generally notice that the results of B are statistical. Thus: Quantum mechanical measurements influence one another, and the order in which they are performed is important.
Another feature of quantum states becomes relevant if we consider a physical system that consists of multiple subsystems; for example, an experiment with two particles rather than one. Quantum physics allows for certain states, called entangled states, that show certain statistical correlations between measurements on the two particles which cannot be explained by classical theory. For details, see entanglement. These entangled states lead to experimentally testable properties (Bell's theorem) that allow us to distinguish between quantum theory and alternative classical (non-quantum) models.
Schrödinger picture vs. Heisenberg picture
https://en.wikipedia.org/wiki/Quantum_state#Pure_states
https://en.wikipedia.org/wiki/Quantum_state
Pages in category "Subatomic particles with spin 0"
The following 14 pages are in this category, out of 14 total. This list may not reflect recent changes (learn more).
S
Because of the uncertainty principle, statements about both the position and momentum of particles can only assign a probabilitythat the position or momentum will have some numerical value. The uncertainty principle also says that eliminating uncertainty about position maximises uncertainty about momentum, and eliminating uncertainty about momentum maximizes uncertainty about position. A probability distribution assigns probabilities to all possible values of position and momentum. Schrödinger's wave equation gives wavefunction solutions, the squares of which are probabilities of where the electron might be, just as Heisenberg's probability distribution does.[1][2][3]
In the everyday world, it is natural and intuitive to think of every object being in its own eigenstate. This is another way of saying that every object appears to have a definite position, a definite momentum, a definite measured value, and a definite time of occurrence. However, the uncertainty principle says that it is impossible to measure the exact value for the momentum of a particle like an electron, given that its position has been determined at a given instant. Likewise, it is impossible to determine the exact location of that particle once its momentum has been measured at a particular instant.[1]
Therefore, it became necessary to formulate clearly the difference between the state of something that is uncertain in the way just described, such as an electron in a probability cloud, and the state of something having a definite value. When an object can definitely be "pinned down" in some respect, it is said to possess an eigenstate. As stated above, when the wavefunction collapses because the position of an electron has been determined, the electron's state becomes an "eigenstate of position", meaning that its position has a known value, an eigenvalue of the eigenstate of position.[4]
The word "eigenstate" is derived from the German/Dutch word "eigen", meaning "inherent" or "characteristic". An eigenstate is the measured state of some object possessing quantifiable characteristics such as position, momentum, etc. The state being measured and described must be observable (i.e. something such as position or momentum that can be experimentally measured either directly or indirectly), and must have a definite value, called an eigenvalue. ("Eigenvalue" also refers to a mathematical property of square matrices, a usage pioneered by the mathematician David Hilbert in 1904. Some such matrices are called self-adjoint operators, and represent observables in quantum mechanics.)[5]
See also[edit]
| Composition | Elementary particle |
|---|---|
| Interactions | |
| Status | Hypothetical |
| Theorized |
|
| Mass | ? |
| Electric charge | 0 |
| Spin | 0 |
Mathematical formulation[edit]
The action of the scalar-tensor theory that involves the pressuron can be written as
![S= \frac{1}{c}\int d^4x \sqrt{-g} \left[ \sqrt{\Phi} \mathcal{L}_m (g_{\mu \nu}, \Psi) +
\frac{1}{2\kappa}\left(\Phi R-\frac{\omega(\Phi)}{\Phi} (\partial_\sigma \Phi)^2-V(\Phi) \right) \right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b792cc75047b36b7ffb86e28d2fb78648090c6a)
where is the Ricci scalar constructed from the metric , is the metric determinant, , with the gravitational constant[4] and the velocity of light in vacuum, is the pressuron potential and is the matter Lagrangian[5] and represents the non-gravitational fields. The gravitational field equations therefore write[2]
![R_{\mu \nu}-\frac{1}{2}g_{\mu \nu}R= \kappa~ \frac{1}{\sqrt{\Phi}}T_{\mu \nu}+ \frac{1}{\Phi} [\nabla_{\mu} \nabla_{\nu} -g_{\mu \nu}\Box]\Phi
+\frac{\omega(\Phi)}{\Phi^2}\left[\partial_{\mu} \Phi \partial_{\nu} \Phi - \frac{1}{2}g_{\mu \nu}(\partial_{\alpha}\Phi)^2\right]-g_{\mu \nu} \frac{V(\Phi)}{2 \Phi} ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/87c270f92414bd946f4ef43a97973552b5897805)
and
- .
where is the stress–energy tensor of the matter field, and is its trace.
Decoupling mechanism[edit]
If one considers a pressure-free perfect fluid (also known as a "dust"), the effective material Lagrangian becomes ,[6] where is the mass of the ith particle, its position, and the Dirac delta function, while at the same time the trace of the stress-energy tensor reduces to . Thus, there is an exact cancellation of the pressuron material source term , and hence the pressuron effectively decouples from pressure-free matter fields.
In other words, the specific coupling between the scalar field and the material fields in the Lagrangian leads to a decoupling between the scalar field and the matter fields in the limit that the matter field is exerting zero pressure.
Link to string theory[edit]
The pressuron shares some characteristics with the hypothetical string dilaton,[3][7] and can actually be viewed as a special case of the wider family of possible dilatons.[8] Since perturbative string theory cannot currently give the expected coupling of the string dilaton with material fields in the effective 4-dimension action, it seems conceivable that the pressuron may be the string dilaton in the 4-dimension effective action.
Experimental search[edit]
Solar System[edit]
According to Minazzoli and Hees,[1] post-Newtonian tests of gravitation in the Solar System should lead to the same results as what is expected from general relativity, except for gravitational redshift experiments, which should deviate from general relativity with a relative magnitude of the order of , where is the current cosmological value of the scalar-field function , and and are respectively the mean pressure and density of the Earth (for instance). Current best constraints on the gravitational redshift come from gravity probe A and are at the level only. Therefore, the scalar-tensor theory that involves the pressuron is weakly constrained by Solar System experiments.
Cosmological variation of the fundamental coupling constants[edit]
Because of its non-minimal couplings, the pressuron leads to a variation of the fundamental coupling constants[9] in regimes where it effectively couples to matter.[2] However, since the pressuron decouples in both the matter-dominated era (which is essentially driven by pressure-less material fields) and the dark-energy-dominated era (which is essentially driven by dark energy[10]), the pressuron is also weakly constrained by current cosmological tests on the variation of the coupling constants.
Test with binary pulsars[edit]
Although no calculations seem to have been performed regarding this issue, it has been argued that binary pulsars should give greater constraints on the existence of the pressuron because of the high pressure of bodies involved in such systems.[1]
No comments:
Post a Comment