In physics, action at a distance is the concept that an object can be moved, changed, or otherwise affected without being physically touched (as in mechanical contact) by another object. That is, it is the non-local interaction of objects that are separated in space.
This term was used most often in the context of early theories of gravity and electromagnetism to describe how an object responds to the influence of distant objects. For example, Coulomb's law and Newton's law of universal gravitation are such early theories.
More generally "action at a distance" describes the failure of early atomistic and mechanistic theories which sought to reduce all physical interaction to collision. The exploration and resolution of this problematic phenomenon led to significant developments in physics, from the concept of a field, to descriptions of quantum entanglement and the mediator particles of the Standard Model.[1]
https://en.wikipedia.org/wiki/Action_at_a_distance
In physics, action is a numerical value describing how a physical system has changed over time. Action is significant because the equations of motion of the system can be derived through the principle of stationary action. In the simple case of a single particle moving with a specified velocity, the action is the momentum of the particle times the distance it moves, added up along its path, or equivalently, twice its kinetic energy times the length of time for which it has that amount of energy, added up over the period of time under consideration. For more complicated systems, all such quantities are added together. More formally, action is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Generally, the action takes different values for different paths.[1] Action has dimensions of energy × time or momentum × length, and its SI unit is joule-second (like the Planck constant h).[2]
https://en.wikipedia.org/wiki/Action_(physics)
chamillionaire hip hop police instrumental
Friday, September 17, 2021
Jaffe and Low[5] suggested that the exotic hadrons manifest themselves as poles of the P matrix, and not of the S matrix. Experimental P-matrix poles are determined reliably in both the meson-meson channels and nucleon-nucleon channels.
https://en.wikipedia.org/wiki/Exotic_hadron
https://en.wikipedia.org/wiki/Spin_glass
Friday, September 17, 2021
09-17-2021-0206 - CALorimetric Electron Telescope (CALET)
The CALorimetric Electron Telescope (CALET) is a space telescope being mainly used to perform high precision observations of electrons and gamma rays. It tracks the trajectory of electrons, protons, nuclei, and gamma rays and measures their direction, charge and energy, which may help understand the nature of dark matter or nearby sources of high-energy particle acceleration.[2]
The mission was developed and sponsored by the Japan Aerospace Exploration Agency (JAXA), involving teams from Japan, Italy, and the United States. CALET was launched aboard JAXA's H-II Transfer Vehicle Kounotori 5 (HTV-5) on 19 August 2015, and was placed on the International Space Station's Japanese Kibo module.
https://en.wikipedia.org/wiki/Calorimetric_Electron_Telescope
Friday, September 17, 2021
09-17-2021-0208 - Light dark matter
Light dark matter, in astronomy and cosmology, are dark matter weakly interacting massive particles (WIMPS) candidates with masses less than 1 GeV.[1] These particles are heavier than warm dark matter and hot dark matter, but are lighter than the traditional forms of cold dark matter, such as Massive Compact Halo Objects(MACHOs). The Lee-Weinberg bound [2] limits the mass of the favored dark matter candidate, WIMPs, that interact via the weak interaction to GeV. This bound arises as follows. The lower the mass of WIMPs is, the lower the annihilation cross section, which is of the order , where m is the WIMP mass and M the mass of the Z-boson. This means that low mass WIMPs, which would be abundantly produced in the early universe, freeze out (i.e. stop interacting) much earlier and thus at a higher temperature, than higher mass WIMPs. This leads to a higher relic WIMP density. If the mass is lower than GeV the WIMP relic density would overclose the universe.
Some of the few loopholes allowing one to avoid the Lee-Weinberg bound without introducing new forces below the electroweak scale have been ruled out by accelerator experiments (i.e. CERN, Tevatron), and in decays of B mesons.[3]
A viable way of building light dark matter models is thus by postulating new light bosons. This increases the annihilation cross section and reduces the coupling of dark matter particles to the Standard Model making them consistent with accelerator experiments.[4][5][6]
https://en.wikipedia.org/wiki/Light_dark_matter
The ΛCDM (Lambda cold dark matter) or Lambda-CDM model is a parameterizationof the Big Bang cosmological model in which the universe contains three major components: first, a cosmological constant denoted by Lambda (Greek Λ) associated with dark energy; second, the postulated cold dark matter (abbreviated CDM); and third, ordinary matter. It is frequently referred to as the standard model of Big Bang cosmology because it is the simplest model that provides a reasonably good account of the following properties of the cosmos:
- the existence and structure of the cosmic microwave background
- the large-scale structure in the distribution of galaxies
- the observed abundances of hydrogen (including deuterium), helium, and lithium
- the accelerating expansion of the universe observed in the light from distant galaxies and supernovae
The model assumes that general relativity is the correct theory of gravity on cosmological scales. It emerged in the late 1990s as a concordance cosmology, after a period of time when disparate observed properties of the universe appeared mutually inconsistent, and there was no consensus on the makeup of the energy density of the universe.
The ΛCDM model can be extended by adding cosmological inflation, quintessenceand other elements that are current areas of speculation and research in cosmology.
Some alternative models challenge the assumptions of the ΛCDM model. Examples of these are modified Newtonian dynamics, entropic gravity, modified gravity, theories of large-scale variations in the matter density of the universe, bimetric gravity, scale invariance of empty space, and decaying dark matter (DDM).[1][2][3][4][5]
Most modern cosmological models are based on the cosmological principle, which states that our observational location in the universe is not unusual or special; on a large-enough scale, the universe looks the same in all directions (isotropy) and from every location (homogeneity).[6]
The model includes an expansion of metric space that is well documented both as the red shift of prominent spectral absorption or emission lines in the light from distant galaxies and as the time dilation in the light decay of supernova luminosity curves. Both effects are attributed to a Doppler shift in electromagnetic radiation as it travels across expanding space. Although this expansion increases the distance between objects that are not under shared gravitational influence, it does not increase the size of the objects (e.g. galaxies) in space. It also allows for distant galaxies to recede from each other at speeds greater than the speed of light; local expansion is less than the speed of light, but expansion summed across great distances can collectively exceed the speed of light.
The letter (lambda) represents the cosmological constant, which is currently associated with a vacuum energy or dark energy in empty space that is used to explain the contemporary accelerating expansion of space against the attractive effects of gravity. A cosmological constant has negative pressure, , which contributes to the stress–energy tensor that, according to the general theory of relativity, causes accelerating expansion. The fraction of the total energy density of our (flat or almost flat) universe that is dark energy, , is estimated to be 0.669 ± 0.038 based on the 2018 Dark Energy Survey results using Type Ia Supernovae[7] or 0.6847 ± 0.0073 based on the 2018 release of Planck satellite data, or more than 68.3% (2018 estimate) of the mass-energy density of the universe.[8]
Dark matter is postulated in order to account for gravitational effects observed in very large-scale structures (the "flat" rotation curves of galaxies; the gravitational lensing of light by galaxy clusters; and enhanced clustering of galaxies) that cannot be accounted for by the quantity of observed matter.
Cold dark matter as currently hypothesized is:
- non-baryonic
- It consists of matter other than protons and neutrons (and electrons, by convention, although electrons are not baryons).
- cold
- Its velocity is far less than the speed of light at the epoch of radiation-matter equality (thus neutrinos are excluded, being non-baryonic but not cold).
- dissipationless
- It cannot cool by radiating photons.
- collisionless
- The dark matter particles interact with each other and other particles only through gravity and possibly the weak force.
Dark matter constitutes about 26.5%[9] of the mass-energy density of the universe. The remaining 4.9%[9] comprises all ordinary matter observed as atoms, chemical elements, gas and plasma, the stuff of which visible planets, stars and galaxies are made. The great majority of ordinary matter in the universe is unseen, since visible stars and gas inside galaxies and clusters account for less than 10% of the ordinary matter contribution to the mass-energy density of the universe.[10]
Also, the energy density includes a very small fraction (~ 0.01%) in cosmic microwave background radiation, and not more than 0.5% in relic neutrinos. Although very small today, these were much more important in the distant past, dominating the matter at redshift > 3200.
The model includes a single originating event, the "Big Bang", which was not an explosion but the abrupt appearance of expanding space-time containing radiation at temperatures of around 1015 K. This was immediately (within 10−29 seconds) followed by an exponential expansion of space by a scale multiplier of 1027 or more, known as cosmic inflation. The early universe remained hot (above 10,000 K) for several hundred thousand years, a state that is detectable as a residual cosmic microwave background, or CMB, a very low energy radiation emanating from all parts of the sky. The "Big Bang" scenario, with cosmic inflation and standard particle physics, is the only current cosmological model consistent with the observed continuing expansion of space, the observed distribution of lighter elements in the universe (hydrogen, helium, and lithium), and the spatial texture of minute irregularities (anisotropies) in the CMB radiation. Cosmic inflation also addresses the "horizon problem" in the CMB; indeed, it seems likely that the universe is larger than the observable particle horizon.
The model uses the Friedmann–Lemaître–Robertson–Walker metric, the Friedmann equations and the cosmological equations of state to describe the observable universe from right after the inflationary epoch to present and future.
https://en.wikipedia.org/wiki/Lambda-CDM_model
Friday, September 17, 2021
09-17-2021-0057 - Causal dynamical triangulation (abbreviated as CDT)
Causal dynamical triangulation (abbreviated as CDT) theorized by Renate Loll, Jan Ambjørn and Jerzy Jurkiewicz, is an approach to quantum gravity that like loop quantum gravity is background independent.
This means that it does not assume any pre-existing arena (dimensional space), but rather attempts to show how the spacetime fabric itself evolves.
There is evidence [1] that at large scales CDT approximates the familiar 4-dimensional spacetime, but shows spacetime to be 2-dimensional near the Planck scale, and reveals a fractal structure on slices of constant time. These interesting results agree with the findings of Lauscher and Reuter, who use an approach called Quantum Einstein Gravity, and with other recent theoretical work.
https://en.wikipedia.org/wiki/Causal_dynamical_triangulation
Friday, September 17, 2021
09-17-2021-0055 - Cold Dark Matter CDM
In cosmology and physics, cold dark matter (CDM) is a hypothetical type of dark matter. Observations indicate that approximately 85% of the matter in the universe is dark matter, with only a small fraction being the ordinary baryonic matter that composes stars, planets, and living organisms. Cold refers to the fact that the dark matter moves slowly compared to the speed of light, while darkindicates that it interacts very weakly with ordinary matter and electromagnetic radiation.
The physical nature of CDM is currently unknown, and there are a wide variety of possibilities. Among them are a new type of weakly interacting massive particle, primordial black holes, and axions.
https://en.wikipedia.org/wiki/Cold_dark_matter
Friday, September 17, 2021
09-17-2021-0041 - Superfluid vacuum theory (SVT) BEC vacuum theory, theoretical physics
Superfluid vacuum theory (SVT), sometimes known as the BEC vacuum theory, is an approach in theoretical physics and quantum mechanics where the fundamental physical vacuum (non-removable background) is viewed as superfluid or as a Bose–Einstein condensate (BEC).
The microscopic structure of this physical vacuum is currently unknown and is a subject of intensive studies in SVT. An ultimate goal of this approach is to develop scientific models that unify quantum mechanics (which describes three of the four known fundamental interactions) with gravity, making SVT a candidate for the theory of quantum gravity and describes all known interactions in the Universe, at both microscopic and astronomic scales, as different manifestations of the same entity, superfluid vacuum.
https://en.wikipedia.org/wiki/Superfluid_vacuum_theory
Friday, September 17, 2021
09-17-2021-0035 - coordinate-free, or component-free
A coordinate-free, or component-free, treatment of a scientific theory or mathematical topic develops its concepts on any form of manifold without reference to any particular coordinate system.
https://en.wikipedia.org/wiki/Coordinate-free
Friday, September 17, 2021
09-17-2021-0032 - Background independence
Background independence is a condition in theoretical physics, that requires the defining equations of a theory to be independent of the actual shape of the spacetime and the value of various fields within the spacetime. In particular this means that it must be possible not to refer to a specific coordinate system—the theory must be coordinate-free. In addition, the different spacetime configurations (or backgrounds) should be obtained as different solutions of the underlying equations.
https://en.wikipedia.org/wiki/Background_independence
Friday, September 17, 2021
09-17-2021-0031 - Loop quantum gravity (LQG)
Loop quantum gravity (LQG) is a theory of quantum gravity, which aims to merge quantum mechanics and general relativity, incorporating matter of the Standard Modelinto the framework established for the pure quantum gravity case. It is an attempt to develop a quantum theory of gravity based directly on Einstein's geometric formulation rather than the treatment of gravity as a force. As a theory LQG postulates that the structure of space and time is composed of finite loops woven into an extremely fine fabric or network. These networks of loops are called spin networks. The evolution of a spin network, or spin foam, has a scale on the order of a Planck length, approximately 10−35 meters, and smaller scales are meaningless. Consequently, not just matter, but space itself, prefers an atomic structure.
The areas of research, which involves about 30 research groups worldwide,[1] share the basic physical assumptions and the mathematical description of quantum space. Research has evolved in two directions: the more traditional canonical loop quantum gravity, and the newer covariant loop quantum gravity, called spin foam theory. The most well-developed theory that has been advanced as a direct result of loop quantum gravity is called loop quantum cosmology (LQC). LQC advances the study of the early universe, incorporating the concept of the Big Bang into the broader theory of the Big Bounce, which envisions the Big Bang as the beginning of a period of expansion that follows a period of contraction, which one could talk of as the Big Crunch.
Beyond the Standard Model
CMS Higgs-event.jpg
Simulated Large Hadron Collider CMS particle detector data depicting a Higgs boson produced by colliding protons decaying into hadron jets and electrons
Standard Model
hide
Evidence
Hierarchy problem Dark matter Dark energy Quintessence Phantom energy Dark radiation Dark photon Cosmological constant problem Strong CP problem Neutrino oscillation
hide
Theories
Brans–Dicke theory Cosmic censorship hypothesis Fifth force F-theory Theory of everything Unified field theory Grand Unified Theory Technicolor Kaluza–Klein theory Topological quantum field theory Local quantum field theory Liouville field theory 6D (2,0) superconformal field theory Noncommutative quantum field theory Quantum cosmology Brane cosmology String theory Superstring theory M-theory Mathematical universe hypothesis Mirror matter Randall–Sundrum model Yang–Mills theory N = 4 supersymmetric Yang–Mills theory Twistor string theory Dark fluid Doubly special relativity de Sitter invariant special relativity Causal fermion systems Black hole thermodynamics Unparticle physics Graviphoton Graviscalar Graviton Gravitino Massive gravity Gauge gravitation theory Gauge theory gravity CPT symmetry
hide
Supersymmetry
MSSM NMSSM Superstring theory M-theory Supergravity Supersymmetry breaking Extra dimensions Large extra dimensions
hide
Quantum gravity
False vacuum String theory Spin foam Quantum foam Quantum geometry Loop quantum gravity Quantum cosmology Loop quantum cosmology Causal dynamical triangulation Causal fermion systems Causal sets Canonical quantum gravity Semiclassical gravity Superfluid vacuum theory
hide
Experiments
ANNIE Gran Sasso INO LHC SNO Super-K Tevatron NOvA
https://en.wikipedia.org/wiki/Loop_quantum_gravity
Theories of gravitation
showvte
Quantum gravity
showvte
Standard Model
Categories: Loop quantum gravityPhysics beyond the Standard ModelTheories of gravitation
Friday, September 17, 2021
09-17-2021-0000 - supersymmetric theory supersymmetry
In a supersymmetric theory the equations for force and the equations for matter are identical. In theoretical and mathematical physics, any theory with this property has the principle of supersymmetry (SUSY). Dozens of supersymmetric theories exist.[1]Supersymmetry is a spacetime symmetry between two basic classes of particles: bosons, which have an integer-valued spin and follow Bose–Einstein statistics, and fermions, which have a half-integer-valued spin and follow Fermi-Dirac statistics.[2][3] In supersymmetry, each particle from one class would have an associated particle in the other, known as its superpartner, the spin of which differs by a half-integer. For example, if the electron exists in a supersymmetric theory, then there would be a particle called a "selectron" (superpartner electron), a bosonic partner of the electron. In the simplest supersymmetry theories, with perfectly "unbroken" supersymmetry, each pair of superpartners would share the same mass and internal quantum numbers besides spin. More complex supersymmetry theories have a spontaneously broken symmetry, allowing superpartners to differ in mass.[4][5][6]
Supersymmetry has various applications to different areas of physics, such as quantum mechanics, statistical mechanics, quantum field theory, condensed matter physics, nuclear physics, optics, stochastic dynamics, particle physics, astrophysics, quantum gravity, string theory, and cosmology. Supersymmetry has also been applied outside of physics, such as in finance. In particle physics, a supersymmetric extension of the Standard Model is a possible candidate for physics beyond the Standard Model, and in cosmology, supersymmetry could explain the issue of cosmological inflation.
In quantum field theory, supersymmetry is motivated by solutions to several theoretical problems, for generally providing many desirable mathematical properties, and for ensuring sensible behavior at high energies. Supersymmetric quantum field theory is often much easier to analyze, as many more problems become mathematically tractable. When supersymmetry is imposed as a local symmetry, Einstein's theory of general relativity is included automatically, and the result is said to be a theory of supergravity. Another theoretically appealing property of supersymmetry is that it offers the only "loophole" to the Coleman–Mandula theorem, which prohibits spacetime and internal symmetries from being combined in any nontrivial way, for quantum field theories with very general assumptions. The Haag–Łopuszański–Sohnius theorem demonstrates that supersymmetry is the only way spacetime and internal symmetries can be combined consistently.[7]
https://en.wikipedia.org/wiki/Supersymmetry
Friday, September 17, 2021
09-16-2021-2359 - angular acceleration
In physics, angular acceleration refers to the time rate of change of angular velocity. As there are two types of angular velocity, namely spin angular velocity and orbital angular velocity, there are naturally also two types of angular acceleration, called spin angular acceleration and orbital angular acceleration respectively. Spin angular acceleration refers to the angular acceleration of a rigid body about its centre of rotation, and orbital angular acceleration refers to the angular acceleration of a point particle about a fixed origin.
Angular acceleration is measured in units of angle per unit time squared (which in SIunits is radians per second squared), and is usually represented by the symbol alpha(α). In two dimensions, angular acceleration is a pseudoscalar whose sign is taken to be positive if the angular speed increases counterclockwise or decreases clockwise, and is taken to be negative if the angular speed increases clockwise or decreases counterclockwise. In three dimensions, angular acceleration is a pseudovector.[1]
For rigid bodies, angular acceleration must be caused by a net external torque. However, this is not so for non-rigid bodies: For example, a figure skater can speed up her rotation (thereby obtaining an angular acceleration) simply by contracting her arms and legs inwards, which involves no external torque.
https://en.wikipedia.org/wiki/Angular_acceleration
Friday, September 17, 2021
09-16-2021-2358 - dark energy
In physical cosmology and astronomy, dark energy is an unknown form of energy that affects the universe on the largest scales. The first observational evidence for its existence came from measurements of supernovae, which showed that the universe does not expand at a constant rate; rather, the expansion of the universe is accelerating.[1][2] Understanding the evolution of the universe requires knowledge of its starting conditions and its composition. Prior to these observations, it was thought that all forms of matter and energy in the universe would only cause the expansion to slow down over time. Measurements of the cosmic microwave background suggest the universe began in a hot Big Bang, from which general relativity explains its evolution and the subsequent large-scale motion. Without introducing a new form of energy, there was no way to explain how an accelerating universe could be measured. Since the 1990s, dark energy has been the most accepted premise to account for the accelerated expansion. As of 2021, there are active areas of cosmology researchaimed at understanding the fundamental nature of dark energy.[3]
Assuming that the lambda-CDM model of cosmology is correct, the best current measurements indicate that dark energy contributes 68% of the total energy in the present-day observable universe. The mass–energy of dark matter and ordinary (baryonic) matter contributes 26% and 5%, respectively, and other components such as neutrinos and photons contribute a very small amount.[4][5][6][7] The density of dark energy is very low (~ 7 × 10−30 g/cm3), much less than the density of ordinary matter or dark matter within galaxies. However, it dominates the mass–energy of the universe because it is uniform across space.[8][9][10]
Two proposed forms of dark energy are the cosmological constant,[11][12] representing a constant energy density filling space homogeneously, and scalar fields such as quintessence or moduli, dynamic quantities having energy densities that can vary in time and space. Contributions from scalar fields that are constant in space are usually also included in the cosmological constant. The cosmological constant can be formulated to be equivalent to the zero-point radiation of space i.e. the vacuum energy.[13] Scalar fields that change in space can be difficult to distinguish from a cosmological constant because the change may be extremely slow.
Due to the toy model nature of concordance cosmology, some experts believe[14] that a more accurate general relativistic treatment of the structures that exist on all scales[15] in the real universe may do away with the need to invoke dark energy. Inhomogeneous cosmologies, which attempt to account for the back-reaction of structure formation on the metric, generally do not acknowledge any dark energy contribution to the energy density of the Universe.
https://en.wikipedia.org/wiki/Dark_energy
https://en.wikipedia.org/wiki/Standard_Model
Friday, September 17, 2021
09-17-2021-0229 - Space-division multiple access (SDMA)
Space-division multiple access (SDMA) is a channel access method based on creating parallel spatial pipes (focused signal beams) using advanced antenna technology next to higher capacity pipes through spatial multiplexing and/or diversity, by which it is able to offer superior performance in radio multiple access communication systems (where multiple users may need to use the communication media simultaneously).[1] In traditional mobile cellular network systems, the base station has no information on the position of the mobile units within the cell and radiates the signal in all directions within the cell in order to provide radio coverage. This method results in wasting power on transmissions when there are no mobile units to reach, in addition to causing interferencefor adjacent cells using the same frequency, so called co-channel cells. Likewise, in reception, the antenna receives signals coming from all directions including noise and interference signals. By using smart antenna technology and differing spatial locations of mobile units within the cell, space-division multiple access techniques offer attractive performance enhancements. The radiation pattern of the base station, both in transmission and reception, is adapted to each user to obtain highest gain in the direction of that user. This is often done using phased array techniques.
https://en.wikipedia.org/wiki/Space-division_multiple_access
Friday, September 17, 2021
09-17-2021-0234 - Measure Observable Universe Observer Quantum Foundations Unobservable Impalpable Incompatibility of observables in quantum mechanics Physics
The measure in quantum physics is the integration measure used for performing a path integral.
In quantum field theory, one must sum over all possible histories of a system. When summing over possible histories, which may be very similar to each other, one has to decide when two histories are to be considered different, and when they are to be considered the same, in order not to count the same history twice. This decision is coded within the concept of the measure by an observer.
In fact, the possible histories can be deformed continuously, and therefore the sum is in fact an integral, known as path integral.
In the limit where the sum is becoming an integral, the concept of the measure described above is replaced by an integration measure.
See also[edit]
Action (physics)
Measure (mathematics)
Observable
https://en.wikipedia.org/wiki/Measure_(physics)
Friday, September 17, 2021
09-17-2021-0232 - Eigenstaten Eigen Eigenstate
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in time exhausts all that can be predicted about the system's behavior. A mixture of quantum states is again a quantum state. Quantum states that cannot be written as a mixture of other states are called pure quantum states, while all other states are called mixed quantum states. A pure quantum state can be represented by a ray in a Hilbert space over the complex numbers,[1][2] while mixed states are represented by density matrices, which are positive semidefinite operatorsthat act on Hilbert spaces.[3][4]
Pure states are also known as state vectors or wave functions, the latter term applying particularly when they are represented as functions of position or momentum. For example, when dealing with the energy spectrum of the electron in a hydrogen atom, the relevant state vectors are identified by the principal quantum number n, the angular momentum quantum number l, the magnetic quantum number m, and the spin z-component sz. For another example, if the spin of an electron is measured in any direction, e.g. with a Stern–Gerlach experiment, there are two possible results: up or down. The Hilbert space for the electron's spin is therefore two-dimensional, constituting a qubit. A pure state here is represented by a two-dimensional complex vector (\alpha ,\beta ), with a length of one; that is, with
|\alpha |^{2}+|\beta |^{2}=1,
where |\alpha | and |\beta | are the absolute values of \alpha and \beta. A mixed state, in this case, has the structure of a 2\times 2 matrix that is Hermitian and positive semi-definite, and has trace 1.[5] A more complicated case is given (in bra–ket notation) by the singlet state, which exemplifies quantum entanglement:
{\displaystyle \left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\big (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\big )},}
which involves superposition of joint spin states for two particles with spin 1⁄2. The singlet state satisfies the property that if the particles' spins are measured along the same direction then either the spin of the first particle is observed up and the spin of the second particle is observed down, or the first one is observed down and the second one is observed up, both possibilities occurring with equal probability.
A mixed quantum state corresponds to a probabilistic mixture of pure states; however, different distributions of pure states can generate equivalent (i.e., physically indistinguishable) mixed states. The Schrödinger–HJW theorem classifies the multitude of ways to write a given mixed state as a convex combination of pure states.[6] Before a particular measurement is performed on a quantum system, the theory gives only a probability distribution for the outcome, and the form that this distribution takes is completely determined by the quantum state and the linear operators describing the measurement. Probability distributions for different measurements exhibit tradeoffs exemplified by the uncertainty principle: a state that implies a narrow spread of possible outcomes for one experiment necessarily implies a wide spread of possible outcomes for another.
Conceptual description[edit]
Pure states[edit]
See also: Introduction to eigenstates
Probability densities for the electron of a hydrogen atom in different quantum states.
In the mathematical formulation of quantum mechanics, pure quantum states correspond to vectors in a Hilbert space, while each observable quantity (such as the energy or momentum of a particle) is associated with a mathematical operator. The operator serves as a linear function which acts on the states of the system. The eigenvalues of the operator correspond to the possible values of the observable. For example, it is possible to observe a particle with a momentum of 1 kg⋅m/s if and only if one of the eigenvalues of the momentum operator is 1 kg⋅m/s. The corresponding eigenvector (which physicists call an eigenstate) with eigenvalue 1 kg⋅m/s would be a quantum state with a definite, well-defined value of momentum of 1 kg⋅m/s, with no quantum uncertainty. If its momentum were measured, the result is guaranteed to be 1 kg⋅m/s.
On the other hand, a system in a superposition of multiple different eigenstates does in general have quantum uncertainty for the given observable. We can represent this linear combination of eigenstates as:
{\displaystyle |\Psi (t)\rangle =\sum _{n}C_{n}(t)|\Phi _{n}\rangle .}
The coefficient which corresponds to a particular state in the linear combination is a complex number, thus allowing interference effects between states. The coefficients are time dependent. How a quantum state changes in time is governed by the time evolution operator. The symbols | and \rangle[a] surrounding the \Psi are part of bra–ket notation.
Statistical mixtures of states are a different type of linear combination. A statistical mixture of states is a statistical ensemble of independent systems. Statistical mixtures represent the degree of knowledge whilst the uncertainty within quantum mechanics is fundamental. Mathematically, a statistical mixture is not a combination using complex coefficients, but rather a combination using real-valued, positive probabilities of different states \Phi _{n}. A number P_{n} represents the probability of a randomly selected system being in the state \Phi _{n}. Unlike the linear combination case each system is in a definite eigenstate.[7][8]
The expectation value \langle A\rangle _{\sigma } of an observable A is a statistical mean of measured values of the observable. It is this mean, and the distribution of probabilities, that is predicted by physical theories.
There is no state which is simultaneously an eigenstate for all observables. For example, we cannot prepare a state such that both the position measurement Q(t) and the momentum measurement P(t) (at the same time t) are known exactly; at least one of them will have a range of possible values.[b] This is the content of the Heisenberg uncertainty relation.
Moreover, in contrast to classical mechanics, it is unavoidable that performing a measurement on the system generally changes its state.[9][10][c] More precisely: After measuring an observable A, the system will be in an eigenstate of A; thus the state has changed, unless the system was already in that eigenstate. This expresses a kind of logical consistency: If we measure A twice in the same run of the experiment, the measurements being directly consecutive in time,[d] then they will produce the same results. This has some strange consequences, however, as follows.
Consider two incompatible observables, A and B, where A corresponds to a measurement earlier in time than B.[e] Suppose that the system is in an eigenstate of B at the experiment's beginning. If we measure only B, all runs of the experiment will yield the same result. If we measure first A and then B in the same run of the experiment, the system will transfer to an eigenstate of A after the first measurement, and we will generally notice that the results of B are statistical. Thus: Quantum mechanical measurements influence one another, and the order in which they are performed is important.
Another feature of quantum states becomes relevant if we consider a physical system that consists of multiple subsystems; for example, an experiment with two particles rather than one. Quantum physics allows for certain states, called entangled states, that show certain statistical correlations between measurements on the two particles which cannot be explained by classical theory. For details, see entanglement. These entangled states lead to experimentally testable properties (Bell's theorem) that allow us to distinguish between quantum theory and alternative classical (non-quantum) models.
Schrödinger picture vs. Heisenberg picture
https://en.wikipedia.org/wiki/Quantum_state#Pure_states
https://en.wikipedia.org/wiki/Quantum_state
Pages in category "Subatomic particles with spin 0"
The following 14 pages are in this category, out of 14 total. This list may not reflect recent changes (learn more).
A
Alpha particle
Axion
C
Chameleon particle
E
Even-even nucleus
G
Goldstone boson
H
Higgs boson
M
Majoron
P
Pressuron
Pseudoscalar meson
S
Scalar boson
Scalar meson
Sfermion
Sgoldstino
Stop squark
Categories: Bosons
https://en.wikipedia.org/wiki/Category:Subatomic_particles_with_spin_0
This article is a non-technical introduction to the subject. For the main encyclopedia article, see Eigenstates.
Because of the uncertainty principle, statements about both the position and momentum of particles can only assign a probabilitythat the position or momentum will have some numerical value. The uncertainty principle also says that eliminating uncertainty about position maximises uncertainty about momentum, and eliminating uncertainty about momentum maximizes uncertainty about position. A probability distribution assigns probabilities to all possible values of position and momentum. Schrödinger's wave equation gives wavefunction solutions, the squares of which are probabilities of where the electron might be, just as Heisenberg's probability distribution does.[1][2][3]
In the everyday world, it is natural and intuitive to think of every object being in its own eigenstate. This is another way of saying that every object appears to have a definite position, a definite momentum, a definite measured value, and a definite time of occurrence. However, the uncertainty principle says that it is impossible to measure the exact value for the momentum of a particle like an electron, given that its position has been determined at a given instant. Likewise, it is impossible to determine the exact location of that particle once its momentum has been measured at a particular instant.[1]
Therefore, it became necessary to formulate clearly the difference between the state of something that is uncertain in the way just described, such as an electron in a probability cloud, and the state of something having a definite value. When an object can definitely be "pinned down" in some respect, it is said to possess an eigenstate. As stated above, when the wavefunction collapses because the position of an electron has been determined, the electron's state becomes an "eigenstate of position", meaning that its position has a known value, an eigenvalue of the eigenstate of position.[4]
The word "eigenstate" is derived from the German/Dutch word "eigen", meaning "inherent" or "characteristic". An eigenstate is the measured state of some object possessing quantifiable characteristics such as position, momentum, etc. The state being measured and described must be observable (i.e. something such as position or momentum that can be experimentally measured either directly or indirectly), and must have a definite value, called an eigenvalue. ("Eigenvalue" also refers to a mathematical property of square matrices, a usage pioneered by the mathematician David Hilbert in 1904. Some such matrices are called self-adjoint operators, and represent observables in quantum mechanics.)[5]
See also[edit]
Superposition principle
List of textbooks on classical and quantum mechanics
Introductory science articles
Introduction to eigenstates Introduction to electromagnetism Introduction to entropy Introduction to evolution Introduction to gauge theory Introduction to general relativity Introduction to genetics Introduction to M-theory Introduction to the mathematics of general relativity Introduction to quantum mechanics Introduction to systolic geometry Introduction to the heaviest elements Introduction to viruses
Categories: Quantum mechanics
https://en.wikipedia.org/wiki/Introduction_to_eigenstates
The pressuron is a hypothetical scalar particle which couples to both gravity and matter theorised in 2013.[1] Although originally postulated without self-interaction potential, the pressuron is also a dark energy candidate when it has such a potential.[2] The pressuron takes its name from the fact that it decouples from matter in pressure-less regimes,[2] allowing the scalar-tensor theory of gravity involving it to pass solar system tests, as well as tests on the equivalence principle, even though it is fundamentally coupled to matter. Such a decoupling mechanism could explain why gravitation seems to be well described by general relativity at present epoch, while it could actually be more complex than that. Because of the way it couples to matter, the pressuron is a special case of the hypothetical string dilaton.[3] Therefore, it is one of the possible solutions to the present non-observation of various signals coming from massless or light scalar fields that are generically predicted in string theory.
Pressuron
Composition Elementary particle
Interactions
GravityElectroweakStrong
Status Hypothetical
Theorized
O. MinazzoliA. Hees[1]
Mass ?
Electric charge 0
Spin 0
Mathematical formulation[edit]
The action of the scalar-tensor theory that involves the pressuron \Phi can be written as
S= \frac{1}{c}\int d^4x \sqrt{-g} \left[ \sqrt{\Phi} \mathcal{L}_m (g_{\mu \nu}, \Psi) +
\frac{1}{2\kappa}\left(\Phi R-\frac{\omega(\Phi)}{\Phi} (\partial_\sigma \Phi)^2-V(\Phi) \right) \right],
where R is the Ricci scalar constructed from the metric g_{\mu \nu }, g is the metric determinant, \kappa=\frac{8\pi G}{c^4}, with G the gravitational constant[4] and c the velocity of light in vacuum, V(\Phi) is the pressuron potential and \mathcal{L}_m is the matter Lagrangian[5] and \Psi represents the non-gravitational fields. The gravitational field equations therefore write[2]
R_{\mu \nu}-\frac{1}{2}g_{\mu \nu}R= \kappa~ \frac{1}{\sqrt{\Phi}}T_{\mu \nu}+ \frac{1}{\Phi} [\nabla_{\mu} \nabla_{\nu} -g_{\mu \nu}\Box]\Phi
+\frac{\omega(\Phi)}{\Phi^2}\left[\partial_{\mu} \Phi \partial_{\nu} \Phi - \frac{1}{2}g_{\mu \nu}(\partial_{\alpha}\Phi)^2\right]-g_{\mu \nu} \frac{V(\Phi)}{2 \Phi} ,
and
\frac{2\omega(\Phi)+3}{\Phi}\Box \Phi= \kappa \frac{1}{\sqrt{\Phi}} \left( T - \mathcal{L}_m \right) - \frac{\omega'(\Phi)}{\Phi} (\partial_\sigma \Phi)^2 + V'(\Phi) - 2 \frac{V(\Phi)}{\Phi}.
where T_{\mu \nu } is the stress–energy tensor of the matter field, and {\displaystyle T=g^{\mu \nu }T_{\mu \nu }} is its trace.
Decoupling mechanism[edit]
If one considers a pressure-free perfect fluid (also known as a "dust"), the effective material Lagrangian becomes \mathcal{L}_m = - c^2 \sum_i \mu_i \delta(x^\alpha_i),[6] where \mu _{i} is the mass of the ith particle, x^\alpha_i its position, and \delta(x^\alpha_i) the Dirac delta function, while at the same time the trace of the stress-energy tensor reduces to T = - c^2 \sum_i \mu_i \delta(x^\alpha_i). Thus, there is an exact cancellation of the pressuron material source term \left( T - \mathcal{L}_m \right) , and hence the pressuron effectively decouples from pressure-free matter fields.
In other words, the specific coupling between the scalar field and the material fields in the Lagrangian leads to a decoupling between the scalar field and the matter fields in the limit that the matter field is exerting zero pressure.
Link to string theory[edit]
The pressuron shares some characteristics with the hypothetical string dilaton,[3][7] and can actually be viewed as a special case of the wider family of possible dilatons.[8] Since perturbative string theory cannot currently give the expected coupling of the string dilaton with material fields in the effective 4-dimension action, it seems conceivable that the pressuron may be the string dilaton in the 4-dimension effective action.
Experimental search[edit]
Solar System[edit]
According to Minazzoli and Hees,[1] post-Newtonian tests of gravitation in the Solar System should lead to the same results as what is expected from general relativity, except for gravitational redshift experiments, which should deviate from general relativity with a relative magnitude of the order of \frac{1}{\omega_0} \frac{P}{c^2 \rho} \sim \frac{10^{-6}}{\omega_0}, where \omega _{0} is the current cosmological value of the scalar-field function \omega(\Phi), and P and \rho are respectively the mean pressure and density of the Earth (for instance). Current best constraints on the gravitational redshift come from gravity probe A and are at the 10^{-4} level only. Therefore, the scalar-tensor theory that involves the pressuron is weakly constrained by Solar System experiments.
Cosmological variation of the fundamental coupling constants[edit]
Because of its non-minimal couplings, the pressuron leads to a variation of the fundamental coupling constants[9] in regimes where it effectively couples to matter.[2] However, since the pressuron decouples in both the matter-dominated era (which is essentially driven by pressure-less material fields) and the dark-energy-dominated era (which is essentially driven by dark energy[10]), the pressuron is also weakly constrained by current cosmological tests on the variation of the coupling constants.
Test with binary pulsars[edit]
Although no calculations seem to have been performed regarding this issue, it has been argued that binary pulsars should give greater constraints on the existence of the pressuron because of the high pressure of bodies involved in such systems.[1]
Theories of gravitation
Categories: BosonsGravityHypothetical elementary particlesPhysical cosmologyPhysics beyond the Standard ModelString theoryTheories of gravitationSubatomic particles with spin 0
https://en.wikipedia.org/wiki/Pressuron
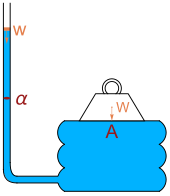
Vertical pressure variation is the variation in pressure as a function of elevation. Depending on the fluid in question and the context being referred to, it may also vary significantly in dimensions perpendicular to elevation as well, and these variations have relevance in the context of pressure gradient force and its effects. However, the vertical variation is especially significant, as it results from the pull of gravity on the fluid; namely, for the same given fluid, a decrease in elevation within it corresponds to a taller column of fluid weighing down on that point.
Hydrostatic paradox[edit]
| Wikimedia Commons has media related to Hydrostatic paradox. |
The barometric formula depends only on the height of the fluid chamber, and not on its width or length. Given a large enough height, any pressure may be attained. This feature of hydrostatics has been called the hydrostatic paradox. As expressed by W. H. Besant,[2]
- Any quantity of liquid, however small, may be made to support any weight, however large.
The Dutch scientist Simon Stevin was the first to explain the paradox mathematically.[3] In 1916 Richard Glazebrook mentioned the hydrostatic paradox as he described an arrangement he attributed to Pascal: a heavy weight W rests on a board with area A resting on a fluid bladder connected to a vertical tube with cross-sectional area α. Pouring water of weight w down the tube will eventually raise the heavy weight. Balance of forces leads to the equation
Glazebrook says, "By making the area of the board considerable and that of the tube small, a large weight W can be supported by a small weight w of water. This fact is sometimes described as the hydrostatic paradox."[4]
Demonstrations of the hydrostatic paradox are used in teaching the phenomenon.[5][6]
https://en.wikipedia.org/wiki/Vertical_pressure_variation#Hydrostatic_paradox
A gravitational singularity, spacetime singularity or simply singularity is a location in spacetime where the density and gravitational field of a celestial body is predicted to become infinite by general relativity in a way that does not depend on the coordinate system. The quantities used to measure gravitational field strength are the scalar invariant curvatures of spacetime, which includes a measure of the density of matter. Since such quantities become infinite at the singularity point, the laws of normal spacetime break down.[1][2]
https://en.wikipedia.org/wiki/Gravitational_singularity
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.[1] As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions (i.e., leptons and quarks), and force fields, whose quanta are bosons (e.g., photons and gluons). All these fields have zero-point energy.[2] These fluctuating zero-point fields lead to a kind of reintroduction of an aether in physics[1][3] since some systems can detect the existence of this energy. However, this aether cannot be thought of as a physical medium if it is to be Lorentz invariant such that there is no contradiction with Einstein's theory of special relativity.[1]
https://en.wikipedia.org/wiki/Zero-point_energy
The quantum vacuum state or simply quantum vacuum refers to the quantum state with the lowest possible energy.
Quantum vacuum may also refer to:
Quantum chromodynamic vacuum (QCD vacuum), a non-perturbative vacuum
Quantum electrodynamic vacuum (QED vacuum), a field-theoretic vacuum
Quantum vacuum (ground state), the state of lowest energy of a quantum system
Quantum vacuum collapse, a hypothetical vacuum metastability event
Quantum vacuum expectation value, an operator's average, expected value in a quantum vacuum
Quantum vacuum energy, an underlying background energy that exists in space throughout the entire Universe
The Quantum Vacuum, a physics textbook by Peter W. Milonni
See also[edit]
Quantum fluctuation
Quantum foam
Quantum vacuum thruster
Virtual particle
Zero-point energy
https://en.wikipedia.org/wiki/Quantum_vacuum_(disambiguation)
In astronomy, the Zero Point in a photometric system is defined as the magnitude of an object that produces 1 count per second on the detector.[1] The zero point is used to calibrate a system to the standard magnitude system, as the flux detected from stars will vary from detector to detector.[2] Traditionally, Vega is used as the calibration star for the zero point magnitude in specific pass bands (U, B, and V), although often, an average of multiple stars is used for higher accuracy.[3] It is not often practical to find Vega in the sky to calibrate the detector, so for general purposes, any star may be used in the sky that has a known apparent magnitude.[4]
https://en.wikipedia.org/wiki/Zero_Point_(photometry)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space.
In physical problems, the choice of origin is often arbitrary, meaning any choice of origin will ultimately give the same answer. This allows one to pick an origin point that makes the mathematics as simple as possible, often by taking advantage of some kind of geometric symmetry.
https://en.wikipedia.org/wiki/Origin_(mathematics)
ee also[edit]
Zero-point energy, the minimum energy a quantum mechanical system may have
Zero-point field, a synonym for the vacuum state in quantum field theory
Hofstadter zero-point, a special point associated with every plane triangle
Point of origin (disambiguation)
Triple zero (disambiguation)
Point Zero (disambiguation)
https://en.wikipedia.org/wiki/Zero_point







No comments:
Post a Comment