Gravitational time dilation is a form of time dilation, an actual difference of elapsed time between two events as measured by observers situated at varying distances from a gravitating mass. The lower the gravitational potential (the closer the clock is to the source of gravitation), the slower time passes, speeding up as the gravitational potential increases (the clock getting away from the source of gravitation). Albert Einstein originally predicted this effect in his theory of relativityand it has since been confirmed by tests of general relativity.[1]
This has been demonstrated by noting that atomic clocks at differing altitudes (and thus different gravitational potential) will eventually show different times. The effects detected in such Earth-bound experiments are extremely small, with differences being measured in nanoseconds. Relative to Earth's age in billions of years, Earth's core is effectively 2.5 years younger than its surface.[2] Demonstrating larger effects would require greater distances from the Earth or a larger gravitational source.
Gravitational time dilation was first described by Albert Einstein in 1907[3] as a consequence of special relativity in accelerated frames of reference. In general relativity, it is considered to be a difference in the passage of proper time at different positions as described by a metric tensor of space-time. The existence of gravitational time dilation was first confirmed directly by the Pound–Rebka experiment in 1959, and later refined by Gravity Probe A and other experiments.
https://en.wikipedia.org/wiki/Gravitational_time_dilation
Time dilation caused by a relative velocity[edit]
Special relativity indicates that, for an observer in an inertial frame of reference, a clock that is moving relative to them will be measured to tick slower than a clock that is at rest in their frame of reference. This case is sometimes called special relativistic time dilation. The faster the relative velocity, the greater the time dilation between one another, with time slowing to a stop as one approaches the speed of light (299,792,458 m/s).
Theoretically, time dilation would make it possible for passengers in a fast-moving vehicle to advance further into the future in a short period of their own time. For sufficiently high speeds, the effect is dramatic. For example, one year of travel might correspond to ten years on Earth. Indeed, a constant 1 gacceleration would permit humans to travel through the entire known Universe in one human lifetime.[9]
With current technology severely limiting the velocity of space travel, however, the differences experienced in practice are minuscule: after 6 months on the International Space Station (ISS), orbiting Earth at a speed of about 7,700 m/s, an astronaut would have aged about 0.005 seconds less than those on Earth.[10] The cosmonauts Sergei Krikalev and Sergei Avdeyev both experienced time dilation of about 20 milliseconds compared to time that passed on Earth.[11][12]
https://en.wikipedia.org/wiki/Time_dilation#Velocity_time_dilation
In classical mechanics, the gravitational potential at a location is equal to the work (energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electric potential with mass playing the role of charge. The reference location, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance.
In mathematics, the gravitational potential is also known as the Newtonian potential and is fundamental in the study of potential theory. It may also be used for solving the electrostatic and magnetostatic fields generated by uniformly charged or polarized ellipsoidal bodies.[1]
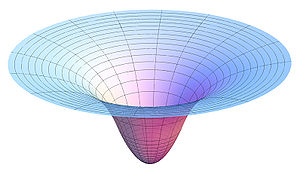
Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body.https://en.wikipedia.org/wiki/Gravitational_potential
Light deflection and gravitational time delay
General relativity predicts that the path of light will follow the curvature of spacetime as it passes near a star. This effect was initially confirmed by observing the light of stars or distant quasars being deflected as it passes the Sun.[70]
This and related predictions follow from the fact that light follows what is called a light-like or null geodesic—a generalization of the straight lines along which light travels in classical physics. Such geodesics are the generalization of the invariance of lightspeed in special relativity.[71] As one examines suitable model spacetimes (either the exterior Schwarzschild solution or, for more than a single mass, the post-Newtonian expansion),[72] several effects of gravity on light propagation emerge. Although the bending of light can also be derived by extending the universality of free fall to light,[73] the angle of deflection resulting from such calculations is only half the value given by general relativity.[74]
Closely related to light deflection is the gravitational time delay (or Shapiro delay), the phenomenon that light signals take longer to move through a gravitational field than they would in the absence of that field. There have been numerous successful tests of this prediction.[75] In the parameterized post-Newtonian formalism (PPN), measurements of both the deflection of light and the gravitational time delay determine a parameter called γ, which encodes the influence of gravity on the geometry of space.[76]
Astrophysical applications[edit]
Gravitational lensing[edit]
The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing.[108]Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an Einstein ring, or partial rings called arcs.[109] The earliest example was discovered in 1979;[110] since then, more than a hundred gravitational lenses have been observed.[111] Even if the multiple images are too close to each other to be resolved, the effect can still be measured, e.g., as an overall brightening of the target object; a number of such "microlensing events" have been observed.[112]
Gravitational lensing has developed into a tool of observational astronomy. It is used to detect the presence and distribution of dark matter, provide a "natural telescope" for observing distant galaxies, and to obtain an independent estimate of the Hubble constant. Statistical evaluations of lensing data provide valuable insight into the structural evolution of galaxies.[113]
https://en.wikipedia.org/wiki/General_relativity#Light_deflection_and_gravitational_time_delay
https://en.wikipedia.org/wiki/Wormhole#Traversable_wormholes
https://en.wikipedia.org/wiki/Tipler_cylinder
https://en.wikipedia.org/wiki/Category:Lorentzian_manifolds
https://en.wikipedia.org/wiki/Supramolecular_chemistry
https://en.wikipedia.org/wiki/Molecular_self-assembly
https://en.wikipedia.org/wiki/Supersymmetry
https://en.wikipedia.org/wiki/Spacetime_symmetries
https://en.wikipedia.org/wiki/Symmetry_(physics)
https://en.wikipedia.org/wiki/Rotation
https://en.wikipedia.org/wiki/Reflection_(physics)
https://en.wikipedia.org/wiki/General_covariance
https://en.wikipedia.org/wiki/Cosmological_principle
https://en.wikipedia.org/wiki/Accretion_(astrophysics)
https://en.wikipedia.org/wiki/Astrophysical_jet#Relativistic_jet
https://en.wikipedia.org/wiki/Physical_cosmology
https://en.wikipedia.org/wiki/Thermal_radiation
https://en.wikipedia.org/wiki/Closed_timelike_curve#Contractible_versus_noncontractible
https://en.wikipedia.org/wiki/Supersymmetry
https://en.wikipedia.org/wiki/Spherically_symmetric_spacetime
https://en.wikipedia.org/wiki/Gravitational_potential
https://en.wikipedia.org/wiki/Gravitational_lens
https://en.wikipedia.org/wiki/Time_dilation#Velocity_time_dilation
https://en.wikipedia.org/wiki/Gravitational_redshift
https://en.wikipedia.org/wiki/Vector_field
https://en.wikipedia.org/wiki/Local_diffeomorphism
https://en.wikipedia.org/wiki/Killing_vector_field
https://en.wikipedia.org/wiki/Homothetic_vector_field
https://en.wikipedia.org/wiki/Affine_vector_field
https://en.wikipedia.org/wiki/Conformal_Killing_vector_field
https://en.wikipedia.org/wiki/Curvature_collineation
https://en.wikipedia.org/wiki/Matter_collineation
https://en.wikipedia.org/wiki/Static_spacetime
https://en.wikipedia.org/wiki/Field_(physics)
https://en.wikipedia.org/wiki/Symmetry_in_quantum_mechanics
https://en.wikipedia.org/wiki/Spontaneous_symmetry_breaking
https://en.wikipedia.org/wiki/Light_cone
https://en.wikipedia.org/wiki/Vacuum_solution_(general_relativity)
https://en.wikipedia.org/wiki/Equations_of_motion
https://en.wikipedia.org/wiki/Dimension
Rotation as possible energy source[edit]
Because of the enormous amount of energy needed to launch a relativistic jet, some jets are possibly powered by spinning black holes. However, the frequency of high-energy astrophysical sources with jets suggest combinations of different mechanisms indirectly identified with the energy within the associated accretion disk and X-ray emissions from the generating source. Two early theories have been used to explain how energy can be transferred from a black hole into an astrophysical jet:
- Blandford–Znajek process.[14] This theory explains the extraction of energy from magnetic fields around an accretion disk, which are dragged and twisted by the spin of the black hole. Relativistic material is then feasibly launched by the tightening of the field lines.
- Penrose mechanism.[15] Here energy is extracted from a rotating black hole by frame dragging, which was later theoretically proven to be able to extract relativistic particle energy and momentum,[16] and subsequently shown to be a possible mechanism for jet formation.[17] This effect may also be explained in terms of gravitoelectromagnetism.
In mathematical physics, a closed timelike curve (CTC) is a world line in a Lorentzian manifold, of a material particle in spacetime that is "closed", returning to its starting point. This possibility was first discovered by Willem Jacob van Stockum in 1937[1] and later confirmed by Kurt Gödel in 1949,[2] who discovered a solution to the equations of general relativity (GR) allowing CTCs known as the Gödel metric; and since then other GR solutions containing CTCs have been found, such as the Tipler cylinder and traversable wormholes. If CTCs exist, their existence would seem to imply at least the theoretical possibility of time travel backwards in time, raising the spectre of the grandfather paradox, although the Novikov self-consistency principle seems to show that such paradoxes could be avoided. Some physicists speculate that the CTCs which appear in certain GR solutions might be ruled out by a future theory of quantum gravity which would replace GR, an idea which Stephen Hawking has labeled the chronology protection conjecture. Others note that if every closed timelike curve in a given space-time passes through an event horizon, a property which can be called chronological censorship, then that space-time with event horizons excised would still be causally well behaved and an observer might not be able to detect the causal violation.[3]
Light cones[edit]
When discussing the evolution of a system in general relativity, or more specifically Minkowski space, physicists often refer to a "light cone". A light cone represents any possible future evolution of an object given its current state, or every possible location given its current location. An object's possible future locations are limited by the speed that the object can move, which is at best the speed of light. For instance, an object located at position p at time t0 can only move to locations within p + c(t1 − t0) by time t1.
This is commonly represented on a graph with physical locations along the horizontal axis and time running vertically, with units of for time and ct for space. Light cones in this representation appear as lines at 45 degrees centered on the object, as light travels at per . On such a diagram, every possible future location of the object lies within the cone. Additionally, every space location has a future time, implying that an object may stay at any location in space indefinitely.
Any single point on such a diagram is known as an event. Separate events are considered to be timelike separated if they differ along the time axis, or spacelike separated if they differ along the space axis. If the object were in free fall, it would travel up the t-axis; if it accelerates, it moves across the x axis as well. The actual path an object takes through spacetime, as opposed to the ones it could take, is known as the worldline. Another definition is that the light cone represents all possible worldlines.
In "simple" examples of spacetime metrics the light cone is directed forward in time. This corresponds to the common case that an object cannot be in two places at once, or alternately that it cannot move instantly to another location. In these spacetimes, the worldlines of physical objects are, by definition, timelike. However this orientation is only true of "locally flat" spacetimes. In curved spacetimes the light cone will be "tilted" along the spacetime's geodesic. For instance, while moving in the vicinity of a star, the star's gravity will "pull" on the object, affecting its worldline, so its possible future positions lie closer to the star. This appears as a slightly tilted lightcone on the corresponding spacetime diagram. An object in free fall in this circumstance continues to move along its local axis, but to an external observer it appears it is accelerating in space as well—a common situation if the object is in orbit, for instance.
In extreme examples, in spacetimes with suitably high-curvature metrics, the light cone can be tilted beyond 45 degrees. That means there are potential "future" positions, from the object's frame of reference, that are spacelike separated to observers in an external rest frame. From this outside viewpoint, the object can move instantaneously through space. In these situations the object would have to move, since its present spatial location would not be in its own future light cone. Additionally, with enough of a tilt, there are event locations that lie in the "past" as seen from the outside. With a suitable movement of what appears to it its own space axis, the object appears to travel through time as seen externally.
A closed timelike curve can be created if a series of such light cones are set up so as to loop back on themselves, so it would be possible for an object to move around this loop and return to the same place and time that it started. An object in such an orbit would repeatedly return to the same point in spacetime if it stays in free fall. Returning to the original spacetime location would be only one possibility; the object's future light cone would include spacetime points both forwards and backwards in time, and so it should be possible for the object to engage in time travel under these conditions.
General relativity[edit]
CTCs appear in locally unobjectionable exact solutions to the Einstein field equation of general relativity, including some of the most important solutions. These include:
- the Misner space (which is Minkowski space orbifolded by a discrete boost)
- the Kerr vacuum (which models a rotating uncharged black hole)
- the interior of a rotating BTZ black hole
- the van Stockum dust (which models a cylindrically symmetric configuration of dust)
- the Gödel lambdadust (which models a dust with a carefully chosen cosmological constant term)
- the Tipler cylinder (a cylindrically symmetric metric with CTCs)
- Bonnor-Steadman solutions describing laboratory situations such as two spinning balls
- J. Richard Gott has proposed a mechanism for creating CTCs using cosmic strings.
Some of these examples are, like the Tipler cylinder, rather artificial, but the exterior part of the Kerr solution is thought to be in some sense generic, so it is rather unnerving to learn that its interior contains CTCs. Most physicists feel that CTCs in such solutions are artifacts.[citation needed]
Consequences[edit]
One feature of a CTC is that it opens the possibility of a worldline which is not connected to earlier times, and so the existence of events that cannot be traced to an earlier cause. Ordinarily, causalitydemands that each event in spacetime is preceded by its cause in every rest frame. This principle is critical in determinism, which in the language of general relativity states complete knowledge of the universe on a spacelike Cauchy surface can be used to calculate the complete state of the rest of spacetime. However, in a CTC, causality breaks down, because an event can be "simultaneous" with its cause—in some sense an event may be able to cause itself. It is impossible to determine based only on knowledge of the past whether or not something exists in the CTC that can interfere with other objects in spacetime. A CTC therefore results in a Cauchy horizon, and a region of spacetime that cannot be predicted from perfect knowledge of some past time.
No CTC can be continuously deformed as a CTC to a point (that is, a CTC and a point are not timelike homotopic), as the manifold would not be causally well behaved at that point. The topological feature which prevents the CTC from being deformed to a point is known as a timelike topological feature.
The existence of CTCs would arguably place restrictions on physically allowable states of matter-energy fields in the universe. Propagating a field configuration along the family of closed timelike worldlines must, according to such arguments, eventually result in the state that is identical to the original one. This idea has been explored by some scientists as a possible approach towards disproving the existence of CTCs.
While quantum formulations of CTCs have been proposed,[4][5] a strong challenge to them is their ability to freely create entanglement,[6] which quantum theory predicts is impossible. Existence of these CTCs implies also equivalence of quantum and classical computation (both in PSPACE).[7]
Contractible versus noncontractible[edit]
There are two classes of CTCs. We have CTCs contractible to a point (if we no longer insist it has to be future-directed timelike everywhere), and we have CTCs which are not contractible. For the latter, we can always go to the universal covering space, and reestablish causality. For the former, such a procedure is not possible. No closed timelike curve is contractible to a point by a timelike homotopy among timelike curves, as that point would not be causally well behaved.[3]
Cauchy horizon[edit]
The chronology violating set is the set of points through which CTCs pass. The boundary of this set is the Cauchy horizon. The Cauchy horizon is generated by closed null geodesics. Associated with each closed null geodesic is a redshift factor describing the rescaling of the rate of change of the affine parameter around a loop. Because of this redshift factor, the affine parameter terminates at a finite value after infinitely many revolutions because the geometric series converges.
See also[edit]
Time[edit]
A temporal dimension, or time dimension, is a dimension of time. Time is often referred to as the "fourth dimension" for this reason, but that is not to imply that it is a spatial dimension. A temporal dimension is one way to measure physical change. It is perceived differently from the three spatial dimensions in that there is only one of it, and that we cannot move freely in time but subjectively move in one direction.
The equations used in physics to model reality do not treat time in the same way that humans commonly perceive it. The equations of classical mechanics are symmetric with respect to time, and equations of quantum mechanics are typically symmetric if both time and other quantities (such as charge and parity) are reversed. In these models, the perception of time flowing in one direction is an artifact of the laws of thermodynamics (we perceive time as flowing in the direction of increasing entropy).
The best-known treatment of time as a dimension is Poincaré and Einstein's special relativity (and extended to general relativity), which treats perceived space and time as components of a four-dimensional manifold, known as spacetime, and in the special, flat case as Minkowski space. Time is different from other spatial dimensions as time is operates in all spacial dimensions. Time operates in the first, second and third as well as theoretical spacial dimensions such as a fourth spatial dimension. Time is not however present in a single point of absolute infinite singularity as defined as a geometric point, as an infinitely small point can have no change and therefore no time. Just as when an object moves through positions in space, it also moves through positions in time. In this sense the force moving any object to change is time.[9][10][11][12]
https://en.wikipedia.org/wiki/Dimension
https://en.wikipedia.org/wiki/Gravitational_wave
https://en.wikipedia.org/wiki/Time_translation_symmetry
https://en.wikipedia.org/wiki/Thermal_time_hypothesis
https://en.wikipedia.org/wiki/Thermodynamics
https://en.wikipedia.org/wiki/Loop_quantum_gravity
https://en.wikipedia.org/wiki/Causal_dynamical_triangulation
https://en.wikipedia.org/wiki/Spin_foam
https://en.wikipedia.org/wiki/Superfluid_vacuum_theory
https://en.wikipedia.org/wiki/Dark_radiation
https://en.wikipedia.org/wiki/T-symmetry
https://en.wikipedia.org/wiki/Fourth,_fifth,_and_sixth_derivatives_of_position
https://en.wikipedia.org/wiki/Relaxation_(physics)
https://en.wikipedia.org/wiki/Baryonic_dark_matter
https://en.wikipedia.org/wiki/Antimatter
https://en.wikipedia.org/wiki/Negative_mass
https://en.wikipedia.org/wiki/Energy_condition
https://en.wikipedia.org/wiki/Space
https://en.wikipedia.org/wiki/Stress–energy_tensor
https://en.wikipedia.org/wiki/Self-interacting_dark_matter
https://en.wikipedia.org/wiki/Scalar_field_dark_matter
https://en.wikipedia.org/wiki/Minimal_Supersymmetric_Standard_Model
https://en.wikipedia.org/wiki/Neutralino
https://en.wikipedia.org/wiki/Fuzzy_cold_dark_matter
https://en.wikipedia.org/wiki/Cosmic_microwave_background
https://en.wikipedia.org/wiki/Superfluidity
https://en.wikipedia.org/wiki/Supercritical_fluid
https://en.wikipedia.org/wiki/Supercritical_flow
https://en.wikipedia.org/wiki/Sonic_black_hole
https://en.wikipedia.org/wiki/Optical_black_hole
https://en.wikipedia.org/wiki/Analog_models_of_gravity
https://en.wikipedia.org/wiki/Transformation_optics
https://en.wikipedia.org/wiki/Black_hole
https://en.wikipedia.org/wiki/Cold_dark_matter
https://en.wikipedia.org/wiki/Primordial_black_hole
https://en.wikipedia.org/wiki/Neutrino_oscillation
https://en.wikipedia.org/wiki/Rotating_black_hole
https://en.wikipedia.org/wiki/Spin-flip
https://en.wikipedia.org/wiki/Black_hole_bomb
https://en.wikipedia.org/wiki/Neutron_reflector
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Photofission
In physics, mirror matter, also called shadow matter or Alice matter, is a hypothetical counterpart to ordinary matter.[1]
Modern physics deals with three basic types of spatial symmetry: reflection, rotation, and translation. The known elementary particles respect rotation and translation symmetry but do not respect mirror reflection symmetry (also called P-symmetry or parity). Of the four fundamental interactions—electromagnetism, the strong interaction, the weak interaction, and gravity—only the weak interaction breaks parity.
Parity violation in weak interactions was first postulated by Tsung Dao Lee and Chen Ning Yang[2] in 1956 as a solution to the τ-θ puzzle. They suggested a number of experiments to test if the weak interaction is invariant under parity. These experiments were performed half a year later and they confirmed that the weak interactions of the known particles violate parity.[3][4][5]
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Neutron_supermirror
https://en.wikipedia.org/wiki/Neutron_flux
https://en.wikipedia.org/wiki/Plane_mirror
https://en.wikipedia.org/wiki/Mirror_nuclei
https://en.wikipedia.org/wiki/Interacting_boson_model
https://en.wikipedia.org/wiki/Nuclear_binding_energy
https://en.wikipedia.org/wiki/Valley_of_stability
https://en.wikipedia.org/wiki/Neutron–proton_ratio
https://en.wikipedia.org/wiki/Isotope#Variation_in_properties_between_isotopes
https://en.wikipedia.org/wiki/Neutron_emission
https://en.wikipedia.org/wiki/Decay_chain
https://en.wikipedia.org/wiki/Bateman_equation
https://en.wikipedia.org/wiki/Island_of_stability
https://en.wikipedia.org/wiki/Photofission
https://en.wikipedia.org/wiki/List_of_equations_in_nuclear_and_particle_physics
https://en.wikipedia.org/wiki/Secular_equilibrium
https://en.wikipedia.org/wiki/Transient_equilibrium
https://en.wikipedia.org/wiki/Scalar_(physics)
In physics and relativity, time dilation is the difference in the elapsed time as measured by two clocks. It is either due to a relative velocity between them (special relativistic "kinetic" time dilation) or to a difference in gravitational potential between their locations (general relativistic gravitational time dilation). When unspecified, "time dilation" usually refers to the effect due to velocity.
After compensating for varying signal delays due to the changing distance between an observer and a moving clock (i.e. Doppler effect), the observer will measure the moving clock as ticking slower than a clock that is at rest in the observer's own reference frame. In addition, a clock that is close to a massive body (and which therefore is at lower gravitational potential) will record less elapsed time than a clock situated further from the said massive body (and which is at a higher gravitational potential).
These predictions of the theory of relativity have been repeatedly confirmed by experiment, and they are of practical concern, for instance in the operation of satellite navigation systems such as GPS and Galileo.[1] Time dilation has also been the subject of science fiction works.
https://en.wikipedia.org/wiki/Time_dilation
The axion (/ˈæksiɒn/) is a hypothetical elementary particle postulated by the Peccei–Quinn theory in 1977 to resolve the strong CP problem in quantum chromodynamics (QCD). If axions exist and have low mass within a specific range, they are of interest as a possible component of cold dark matter.
https://en.wikipedia.org/wiki/Axion
Because dark matter has not yet been observed directly, if it exists, it must barely interact with ordinary baryonic matter and radiation, except through gravity. Most dark matter is thought to be non-baryonic in nature; it may be composed of some as-yet undiscovered subatomic particles.[b] The primary candidate for dark matter is some new kind of elementary particle that has not yet been discovered, in particular, weakly interacting massive particles(WIMPs).[14] Many experiments to directly detect and study dark matter particles are being actively undertaken, but none have yet succeeded.[15] Dark matter is classified as "cold", "warm", or "hot" according to its velocity (more precisely, its free streaming length). Current models favor a cold dark matterscenario, in which structures emerge by gradual accumulation of particles.
https://en.wikipedia.org/wiki/Dark_matter
Forward used the properties of negative-mass matter to create the concept of diametric drive, a design for spacecraft propulsion using negative mass that requires no energy input and no reaction mass to achieve arbitrarily high acceleration.
Forward also coined a term, "nullification", to describe what happens when ordinary matter and negative matter meet: they are expected to be able to cancel out or nullify each other's existence. An interaction between equal quantities of positive mass matter (hence of positive energy E = mc2) and negative mass matter (of negative energy −E = −mc2) would release no energy, but because the only configuration of such particles that has zero momentum (both particles moving with the same velocity in the same direction) does not produce a collision, such interactions would leave a surplus of momentum.
https://en.wikipedia.org/wiki/Negative_mass
https://en.wikipedia.org/wiki/Antimatter
https://en.wikipedia.org/wiki/Mirror_matter
https://en.wikipedia.org/wiki/Effective_mass_(spring–mass_system)
https://en.wikipedia.org/wiki/Lambda-CDM_model
https://en.wikipedia.org/wiki/Negative_mass
https://en.wikipedia.org/wiki/Linear_induction_accelerator
https://en.wikipedia.org/wiki/Angular_acceleration
https://en.wikipedia.org/wiki/0
https://en.wikipedia.org/wiki/Magnetic_scalar_potential
https://en.wikipedia.org/wiki/Accelerator_physics
https://en.wikipedia.org/wiki/Pyrolytic_carbon
https://en.wikipedia.org/wiki/Bismuth
https://en.wikipedia.org/wiki/Hyperloop
https://en.wikipedia.org/wiki/Electrodynamic_suspension#Levitation_melting
https://en.wikipedia.org/wiki/Aerodynamic_levitation
https://en.wikipedia.org/wiki/Electrostatic_levitation
Magnetic levitation
https://en.wikipedia.org/wiki/Launch_loop
https://en.wikipedia.org/wiki/Synchronous_motor
https://en.wikipedia.org/wiki/Linear_stage
https://en.wikipedia.org/wiki/Skew-symmetric_matrix
Supramolecular chemistry
09-18-2021-0806 - Spiro compounds
https://en.wikipedia.org/wiki/Compressible_flow
https://en.wikipedia.org/wiki/Shear_rate
https://en.wikipedia.org/wiki/Hyperfine_structure
https://en.wikipedia.org/wiki/Void_(astronomy)
https://en.wikipedia.org/wiki/Quintessence_(physics)
https://en.wikipedia.org/wiki/Scalar_field
https://en.wikipedia.org/wiki/Symmetric_matrix
https://en.wikipedia.org/wiki/Quadrupole
https://en.wikipedia.org/wiki/Vector_field
https://en.wikipedia.org/wiki/Preon
https://en.wikipedia.org/wiki/Pressuron
https://en.wikipedia.org/wiki/Spinor
Saturday, September 18, 2021
09-18-2021-0754 - ferrite core Magnetic-core memoryhttps://en.wikipedia.org/wiki/Ferrite_core
https://en.wikipedia.org/wiki/Magnetic-core_memory
https://en.wikipedia.org/wiki/Prussian_blue
https://en.wikipedia.org/wiki/Sodium_ferrocyanide
Qubit in ion-trap quantum computing[edit]
The hyperfine states of a trapped ion are commonly used for storing qubits in ion-trap quantum computing. They have the advantage of having very long lifetimes, experimentally exceeding ~10 minutes (compared to ~1 s for metastable electronic levels).
The frequency associated with the states' energy separation is in the microwave region, making it possible to drive hyperfine transitions using microwave radiation. However, at present no emitter is available that can be focused to address a particular ion from a sequence. Instead, a pair of laser pulses can be used to drive the transition, by having their frequency difference (detuning) equal to the required transition's frequency. This is essentially a stimulated Raman transition. In addition, near-field gradients have been exploited to individually address two ions separated by approximately 4.3 micrometers directly with microwave radiation.[16]
See also[edit]
Dynamic nuclear polarisation
Electron paramagnetic resonance
https://en.wikipedia.org/wiki/Hyperfine_structure





No comments:
Post a Comment