https://en.wikipedia.org/wiki/Triple_point
https://en.wikipedia.org/wiki/Tritium
https://en.wikipedia.org/wiki/Implosion
The proton–proton chain, also commonly referred to as the p–p chain, is one of two known sets of nuclear fusion reactions by which stars convert hydrogen to helium. It dominates in stars with masses less than or equal to that of the Sun,[2] whereas the CNO cycle, the other known reaction, is suggested by theoretical models to dominate in stars with masses greater than about 1.3 times that of the Sun.[3]
In general, proton–proton fusion can occur only if the kinetic energy (i.e. temperature) of the protons is high enough to overcome their mutual electrostatic repulsion.[4]
In the Sun, deuteron-producing events are rare. Diprotons are the much more common result of proton–proton reactions within the star, and diprotons almost immediately decay back into two protons. Since the conversion of hydrogen to helium is slow, the complete conversion of the hydrogen initially in the core of the Sun is calculated to take more than ten billion years.[5]
Although sometimes called the "proton–proton chain reaction", it is not a chain reaction in the normal sense. In most nuclear reactions, a chain reaction designates a reaction that produces a product, such as neutrons given off during fission, that quickly induces another such reaction. The proton–proton chain is, like a decay chain, a series of reactions. The product of one reaction is the starting material of the next reaction. There are two main chains leading from hydrogen to helium in the Sun. One chain has five reactions, the other chain has six.
History of the theory
The theory that proton–proton reactions are the basic principle by which the Sun and other stars burn was advocated by Arthur Eddington in the 1920s. At the time, the temperature of the Sun was considered to be too low to overcome the Coulomb barrier. After the development of quantum mechanics, it was discovered that tunneling of the wavefunctions of the protons through the repulsive barrier allows for fusion at a lower temperature than the classical prediction.
In 1939, Hans Bethe attempted to calculate the rates of various reactions in stars. Starting with two protons combining to give a deuterium nucleus and a positron he found what we now call Branch II of the proton–proton chain. But he did not consider the reaction of two 3
He nuclei (Branch I) which we now know to be important.[6] This was part of the body of work in stellar nucleosynthesis for which Bethe won the Nobel Prize in Physics in 1967.
The proton–proton chain
The first step in all the branches is the fusion of two protons into a deuteron. As the protons fuse, one of them undergoes beta plus decay, converting into a neutron by emitting a positron and an electron neutrino[7] (though a small amount of deuterium nuclei is produced by the "pep" reaction, see below):
The positron will annihilate with an electron from the environment into two gamma rays. Including this annihilation and the energy of the neutrino, the net reaction
(which is the same as the PEP reaction, see below) has a Q value (released energy) of 1.442 MeV:[7] The relative amounts of energy going to the neutrino and to the other products is variable.
This is the rate-limiting reaction and is extremely slow due to it being initiated by the weak nuclear force. The average proton in the core of the Sun waits 9 billion years before it successfully fuses with another proton. It has not been possible to measure the cross-section of this reaction experimentally because it is so low[8] but it can be calculated from theory.[1]
After it is formed, the deuteron produced in the first stage can fuse with another proton to produce the light isotope of helium, 3
He
:
This process, mediated by the strong nuclear force rather than the weak force, is extremely fast by comparison to the first step. It is estimated that, under the conditions in the Sun's core, each newly created deuterium nucleus exists for only about one second before it is converted into helium-3.[1]
In the Sun, each helium-3 nucleus produced in these reactions
exists for only about 400 years before it is converted into helium-4.[9] Once the helium-3 has been produced, there are four possible paths to generate 4
He
. In p–p I, helium-4 is produced by fusing two helium-3 nuclei; the p–p II and p–p III branches fuse 3
He
with pre-existing 4
He
to form beryllium-7, which undergoes further reactions to produce two helium-4 nuclei.
About 99% of the energy output of the sun comes from the various p–p chains, with the other 1% coming from the CNO cycle. According to one model of the sun, 83.3 percent of the 4
He
produced by the various p–p branches is produced via branch I while p–p II produces 16.68 percent and p–p III 0.02 percent.[1]
Since half the neutrinos produced in branches II and III are produced
in the first step (synthesis of a deuteron), only about 8.35 percent of
neutrinos come from the later steps (see below), and about 91.65 percent
are from deuteron synthesis. However, another solar model from around
the same time gives only 7.14 percent of neutrinos from the later steps
and 92.86 percent from the synthesis of deuterium nuclei.[10] The difference is apparently due to slightly different assumptions about the composition and metallicity of the sun.
There is also the extremely rare p–p IV branch. Other even rarer reactions may occur. The rate of these reactions is very low due to very small cross-sections, or because the number of reacting particles is so low that any reactions that might happen are statistically insignificant.
The overall reaction is:
- 4 1H+ + 2 e- → 4He2+ + 2 νe
releasing 26.73 MeV of energy, some of which is lost to the neutrinos.
The p–p I branch
The complete chain releases a net energy of 26.732 MeV[11] but 2.2 percent of this energy (0.59 MeV) is lost to the neutrinos that are produced.[12]
The p–p I branch is dominant at temperatures of 10 to 18 MK.[13]
Below 10 MK, the p–p chain proceeds at slow rate, resulting in a low production of 4
He
.[14]
The p–p II branch
3
2He
+ 4
2He
→ 7
4Be+
γ
+ 1.59 MeV 7
4Be
+
e−
→ 7
3Li+
ν
e+ 0.861 MeV / 0.383 MeV 7
3Li
+ 1
1H
→ 24
2He
+ 17.35 MeV
The p–p II branch is dominant at temperatures of 18 to 25 MK.[13]
Note that the energies in the second reaction above are the
energies of the neutrinos that are produced by the reaction. 90 percent
of the neutrinos produced in the reaction of 7
Be
to 7
Li
carry an energy of 0.861 MeV, while the remaining 10 percent carry 0.383 MeV. The difference is whether the lithium-7 produced is in the ground state or an excited (metastable) state, respectively. The total energy released going from 7
Be to stable 7
Li is about 0.862 MeV, almost all of which is lost to the neutrino if the decay goes directly to the stable lithium.
The p–p III branch
The last three stages of this chain, plus the positron annihilation, contribute a total of 18.209 MeV, though much of this is lost to the neutrino.
The p–p III chain is dominant if the temperature exceeds 25 MK.[13]
The p–p III chain is not a major source of energy in the Sun, but it was very important in the solar neutrino problem because it generates very high energy neutrinos (up to 14.06 MeV).
The p–p IV (Hep) branch
This reaction is predicted theoretically, but it has never been observed due to its rarity (about 0.3 ppm in the Sun). In this reaction, helium-3 captures a proton directly to give helium-4, with an even higher possible neutrino energy (up to 18.8 MeV[citation needed]).
The mass–energy relationship gives 19.795 MeV for the energy released by this reaction plus the ensuing annihilation, some of which is lost to the neutrino.
Energy release
Comparing the mass of the final helium-4 atom with the masses of the four protons reveals that 0.7 percent of the mass of the original protons has been lost. This mass has been converted into energy, in the form of kinetic energy of produced particles, gamma rays, and neutrinos released during each of the individual reactions. The total energy yield of one whole chain is 26.73 MeV.
Energy released as gamma rays will interact with electrons and
protons and heat the interior of the Sun. Also kinetic energy of fusion
products (e.g. of the two protons and the 4
2He
from the p–p I reaction) adds energy to the plasma in the Sun. This heating keeps the core of the Sun hot and prevents it from collapsing under its own weight as it would if the sun were to cool down.
Neutrinos do not interact significantly with matter and therefore do not heat the interior and thereby help support the Sun against gravitational collapse. Their energy is lost: the neutrinos in the p–p I, p–p II, and p–p III chains carry away 2.0%, 4.0%, and 28.3% of the energy in those reactions, respectively.[15]
The following table calculates the amount of energy lost to neutrinos and the amount of "solar luminosity" coming from the three branches. "Luminosity" here means the amount of energy given off by the Sun as electromagnetic radiation rather than as neutrinos. The starting figures used are the ones mentioned higher in this article. The table concerns only the 99% of the power and neutrinos that come from the p–p reactions, not the 1% coming from the CNO cycle.
| Branch | Percent of helium-4 produced | Percent loss due to neutrino production | Relative amount of energy lost | Relative amount of luminosity produced | Percentage of total luminosity |
|---|---|---|---|---|---|
| Branch I | 83.3 | 2 | 1.67 | 81.6 | 83.6 |
| Branch II | 16.68 | 4 | 0.67 | 16.0 | 16.4 |
| Branch III | 0.02 | 28.3 | 0.0057 | 0.014 | 0.015 |
| Total | 100 | 2.34 | 97.7 | 100 |
The PEP reaction
A deuteron can also be produced by the rare pep (proton–electron–proton) reaction (electron capture):
In the Sun, the frequency ratio of the pep reaction versus the p–p reaction is 1:400. However, the neutrinos released by the pep reaction are far more energetic: while neutrinos produced in the first step of the p–p reaction range in energy up to 0.42 MeV, the pep reaction produces sharp-energy-line neutrinos of 1.44 MeV. Detection of solar neutrinos from this reaction were reported by the Borexino collaboration in 2012.[16]
Both the pep and p–p reactions can be seen as two different Feynman representations of the same basic interaction, where the electron passes to the right side of the reaction as a positron. This is represented in the figure of proton–proton and electron-capture reactions in a star, available at the NDM'06 web site.[17]
See also
References
- Int'l Conference on Neutrino and Dark Matter, 7 Sept 2006, Session 14.
External links
 Media related to Proton-proton chain reaction at Wikimedia Commons
Media related to Proton-proton chain reaction at Wikimedia Commons
https://en.wikipedia.org/wiki/Proton%E2%80%93proton_chain
https://en.wikipedia.org/wiki/Nucleon_magnetic_moment
https://en.wikipedia.org/wiki/Coulomb%27s_law
The nucleon magnetic moments are the intrinsic magnetic dipole moments of the proton and neutron, symbols μp and μn. The nucleus of atoms comprises protons and neutrons, both nucleons that behave as small magnets. Their magnetic strengths are measured by their magnetic moments. The nucleons interact with normal matter through either the nuclear force or their magnetic moments, with the charged proton also interacting by the Coulomb force.
The proton's magnetic moment, surprisingly large, was directly measured in 1933, while the neutron was determined to have a magnetic moment by indirect methods in the mid 1930s. Luis Alvarez and Felix Bloch made the first accurate, direct measurement of the neutron's magnetic moment in 1940. The proton's magnetic moment is exploited to make measurements of molecules by proton nuclear magnetic resonance. The neutron's magnetic moment is exploited to probe the atomic structure of materials using scattering methods and to manipulate the properties of neutron beams in particle accelerators.
The existence of the neutron's magnetic moment and the large value for the proton magnetic moment indicate the nucleons are not elementary particles. For an elementary particle to have an intrinsic magnetic moment, it must have both spin and electric charge. The nucleons have spin-1/2 ħ, but the neutron has no net charge. Their magnetic moments were puzzling and defied a valid explanation until the quark model for hadron particles was developed in the 1960s. The nucleons are composed of three quarks, and the magnetic moments of these elementary particles combine to give the nucleons their magnetic moments.
https://en.wikipedia.org/wiki/Nucleon_magnetic_moment
https://en.wikipedia.org/wiki/Magnets
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, steel, nickel, cobalt, etc. and attracts or repels other magnets.
A permanent magnet is an object made from a material that is magnetized and creates its own persistent magnetic field. An everyday example is a refrigerator magnet used to hold notes on a refrigerator door. Materials that can be magnetized, which are also the ones that are strongly attracted to a magnet, are called ferromagnetic (or ferrimagnetic). These include the elements iron, nickel and cobalt and their alloys, some alloys of rare-earth metals, and some naturally occurring minerals such as lodestone. Although ferromagnetic (and ferrimagnetic) materials are the only ones attracted to a magnet strongly enough to be commonly considered magnetic, all other substances respond weakly to a magnetic field, by one of several other types of magnetism.
Ferromagnetic materials can be divided into magnetically "soft" materials like annealed iron, which can be magnetized but do not tend to stay magnetized, and magnetically "hard" materials, which do. Permanent magnets are made from "hard" ferromagnetic materials such as alnico and ferrite that are subjected to special processing in a strong magnetic field during manufacture to align their internal microcrystalline structure, making them very hard to demagnetize. To demagnetize a saturated magnet, a certain magnetic field must be applied, and this threshold depends on coercivity of the respective material. "Hard" materials have high coercivity, whereas "soft" materials have low coercivity. The overall strength of a magnet is measured by its magnetic moment or, alternatively, the total magnetic flux it produces. The local strength of magnetism in a material is measured by its magnetization.
An electromagnet is made from a coil of wire that acts as a magnet when an electric current passes through it but stops being a magnet when the current stops. Often, the coil is wrapped around a core of "soft" ferromagnetic material such as mild steel, which greatly enhances the magnetic field produced by the coil.
Discovery and development
Ancient people learned about magnetism from lodestones (or magnetite) which are naturally magnetized pieces of iron ore. The word magnet was adopted in Middle English from Latin magnetum "lodestone", ultimately from Greek μαγνῆτις [λίθος] (magnētis [lithos])[1] meaning "[stone] from Magnesia",[2] a place in Anatolia where lodestones were found (today Manisa in modern-day Turkey). Lodestones, suspended so they could turn, were the first magnetic compasses. The earliest known surviving descriptions of magnets and their properties are from Anatolia, India, and China around 2500 years ago.[3][4][5] The properties of lodestones and their affinity for iron were written of by Pliny the Elder in his encyclopedia Naturalis Historia.[6]
In the 11th century in China, it was discovered that quenching red hot iron in the Earth's magnetic field would leave the iron permanently magnetized. This led to the development of the navigational compass, as described in Dream Pool Essays in 1088.[7][8] By the 12th to 13th centuries AD, magnetic compasses were used in navigation in China, Europe, the Arabian Peninsula and elsewhere.[9]
A straight iron magnet tends to demagnetize itself by its own magnetic field. To overcome this, the horseshoe magnet was invented by Daniel Bernoulli in 1743.[7][10] A horseshoe magnet avoids demagnetization by returning the magnetic field lines to the opposite pole.[11]
In 1820, Hans Christian Ørsted discovered that a compass needle is deflected by a nearby electric current. In the same year André-Marie Ampère showed that iron can be magnetized by inserting it in an electrically fed solenoid. This led William Sturgeon to develop an iron-cored electromagnet in 1824.[7] Joseph Henry further developed the electromagnet into a commercial product in 1830–1831, giving people access to strong magnetic fields for the first time. In 1831 he built an ore separator with an electromagnet capable of lifting 750 pounds (340 kg).[12]
Physics
Magnetic field
The magnetic flux density (also called magnetic B field or just magnetic field, usually denoted B) is a vector field. The magnetic B field vector at a given point in space is specified by two properties:
- Its direction, which is along the orientation of a compass needle.
- Its magnitude (also called strength), which is proportional to how strongly the compass needle orients along that direction.
In SI units, the strength of the magnetic B field is given in teslas.[13]
Magnetic moment
A magnet's magnetic moment (also called magnetic dipole moment and usually denoted μ) is a vector that characterizes the magnet's overall magnetic properties. For a bar magnet, the direction of the magnetic moment points from the magnet's south pole to its north pole,[14] and the magnitude relates to how strong and how far apart these poles are. In SI units, the magnetic moment is specified in terms of A·m2 (amperes times meters squared).
A magnet both produces its own magnetic field and responds to magnetic fields. The strength of the magnetic field it produces is at any given point proportional to the magnitude of its magnetic moment. In addition, when the magnet is put into an external magnetic field, produced by a different source, it is subject to a torque tending to orient the magnetic moment parallel to the field.[15] The amount of this torque is proportional both to the magnetic moment and the external field. A magnet may also be subject to a force driving it in one direction or another, according to the positions and orientations of the magnet and source. If the field is uniform in space, the magnet is subject to no net force, although it is subject to a torque.[16]
A wire in the shape of a circle with area A and carrying current I has a magnetic moment of magnitude equal to IA.
Magnetization
The magnetization of a magnetized material is the local value of its magnetic moment per unit volume, usually denoted M, with units A/m.[17] It is a vector field, rather than just a vector (like the magnetic moment), because different areas in a magnet can be magnetized with different directions and strengths (for example, because of domains, see below). A good bar magnet may have a magnetic moment of magnitude 0.1 A·m2 and a volume of 1 cm3, or 1×10−6 m3, and therefore an average magnetization magnitude is 100,000 A/m. Iron can have a magnetization of around a million amperes per meter. Such a large value explains why iron magnets are so effective at producing magnetic fields.
Modelling magnets
Two different models exist for magnets: magnetic poles and atomic currents.
Although for many purposes it is convenient to think of a magnet as having distinct north and south magnetic poles, the concept of poles should not be taken literally: it is merely a way of referring to the two different ends of a magnet. The magnet does not have distinct north or south particles on opposing sides. If a bar magnet is broken into two pieces, in an attempt to separate the north and south poles, the result will be two bar magnets, each of which has both a north and south pole. However, a version of the magnetic-pole approach is used by professional magneticians to design permanent magnets.[citation needed]
In this approach, the divergence of the magnetization ∇·M inside a magnet is treated as a distribution of magnetic monopoles. This is a mathematical convenience and does not imply that there are actually monopoles in the magnet. If the magnetic-pole distribution is known, then the pole model gives the magnetic field H. Outside the magnet, the field B is proportional to H, while inside the magnetization must be added to H. An extension of this method that allows for internal magnetic charges is used in theories of ferromagnetism.
Another model is the Ampère model, where all magnetization is due to the effect of microscopic, or atomic, circular bound currents, also called Ampèrian currents, throughout the material. For a uniformly magnetized cylindrical bar magnet, the net effect of the microscopic bound currents is to make the magnet behave as if there is a macroscopic sheet of electric current flowing around the surface, with local flow direction normal to the cylinder axis.[18] Microscopic currents in atoms inside the material are generally canceled by currents in neighboring atoms, so only the surface makes a net contribution; shaving off the outer layer of a magnet will not destroy its magnetic field, but will leave a new surface of uncancelled currents from the circular currents throughout the material.[19] The right-hand rule tells which direction positively-charged current flows. However, current due to negatively-charged electricity is far more prevalent in practice.[citation needed]
Polarity
The north pole of a magnet is defined as the pole that, when the magnet is freely suspended, points towards the Earth's North Magnetic Pole in the Arctic (the magnetic and geographic poles do not coincide, see magnetic declination). Since opposite poles (north and south) attract, the North Magnetic Pole is actually the south pole of the Earth's magnetic field.[20][21][22][23] As a practical matter, to tell which pole of a magnet is north and which is south, it is not necessary to use the Earth's magnetic field at all. For example, one method would be to compare it to an electromagnet, whose poles can be identified by the right-hand rule. The magnetic field lines of a magnet are considered by convention to emerge from the magnet's north pole and reenter at the south pole.[23]
Magnetic materials
The term magnet is typically reserved for objects that produce their own persistent magnetic field even in the absence of an applied magnetic field. Only certain classes of materials can do this. Most materials, however, produce a magnetic field in response to an applied magnetic field – a phenomenon known as magnetism. There are several types of magnetism, and all materials exhibit at least one of them.
The overall magnetic behavior of a material can vary widely, depending on the structure of the material, particularly on its electron configuration. Several forms of magnetic behavior have been observed in different materials, including:
- Ferromagnetic and ferrimagnetic materials are the ones normally thought of as magnetic; they are attracted to a magnet strongly enough that the attraction can be felt. These materials are the only ones that can retain magnetization and become magnets; a common example is a traditional refrigerator magnet. Ferrimagnetic materials, which include ferrites and the longest used and naturally occurring magnetic materials magnetite and lodestone, are similar to but weaker than ferromagnetics. The difference between ferro- and ferrimagnetic materials is related to their microscopic structure, as explained in Magnetism.
- Paramagnetic substances, such as platinum, aluminum, and oxygen, are weakly attracted to either pole of a magnet. This attraction is hundreds of thousands of times weaker than that of ferromagnetic materials, so it can only be detected by using sensitive instruments or using extremely strong magnets. Magnetic ferrofluids, although they are made of tiny ferromagnetic particles suspended in liquid, are sometimes considered paramagnetic since they cannot be magnetized.
- Diamagnetic means repelled by both poles. Compared to paramagnetic and ferromagnetic substances, diamagnetic substances, such as carbon, copper, water, and plastic, are even more weakly repelled by a magnet. The permeability of diamagnetic materials is less than the permeability of a vacuum. All substances not possessing one of the other types of magnetism are diamagnetic; this includes most substances. Although force on a diamagnetic object from an ordinary magnet is far too weak to be felt, using extremely strong superconducting magnets, diamagnetic objects such as pieces of lead and even mice[24] can be levitated, so they float in mid-air. Superconductors repel magnetic fields from their interior and are strongly diamagnetic.
There are various other types of magnetism, such as spin glass, superparamagnetism, superdiamagnetism, and metamagnetism.
Common uses
- Magnetic recording media: VHS tapes contain a reel of magnetic tape. The information that makes up the video and sound is encoded on the magnetic coating on the tape. Common audio cassettes also rely on magnetic tape. Similarly, in computers, floppy disks and hard disks record data on a thin magnetic coating.[25]
- Credit, debit, and automatic teller machine cards: All of these cards have a magnetic strip on one side. This strip encodes the information to contact an individual's financial institution and connect with their account(s).[26]
- Older types of televisions (non flat screen) and older large computer monitors: TV and computer screens containing a cathode ray tube employ an electromagnet to guide electrons to the screen.[27]
- Speakers and microphones: Most speakers employ a permanent magnet and a current-carrying coil to convert electric energy (the signal) into mechanical energy (movement that creates the sound). The coil is wrapped around a bobbin attached to the speaker cone and carries the signal as changing current that interacts with the field of the permanent magnet. The voice coil feels a magnetic force and in response, moves the cone and pressurizes the neighboring air, thus generating sound. Dynamic microphones employ the same concept, but in reverse. A microphone has a diaphragm or membrane attached to a coil of wire. The coil rests inside a specially shaped magnet. When sound vibrates the membrane, the coil is vibrated as well. As the coil moves through the magnetic field, a voltage is induced across the coil. This voltage drives a current in the wire that is characteristic of the original sound.
- Electric guitars use magnetic pickups to transduce the vibration of guitar strings into electric current that can then be amplified. This is different from the principle behind the speaker and dynamic microphone because the vibrations are sensed directly by the magnet, and a diaphragm is not employed. The Hammond organ used a similar principle, with rotating tonewheels instead of strings.
- Electric motors and generators: Some electric motors rely upon a combination of an electromagnet and a permanent magnet, and, much like loudspeakers, they convert electric energy into mechanical energy. A generator is the reverse: it converts mechanical energy into electric energy by moving a conductor through a magnetic field.
- Medicine: Hospitals use magnetic resonance imaging to spot problems in a patient's organs without invasive surgery.
- Chemistry: Chemists use nuclear magnetic resonance to characterize synthesized compounds.
- Chucks are used in the metalworking field to hold objects. Magnets are also used in other types of fastening devices, such as the magnetic base, the magnetic clamp and the refrigerator magnet.
- Compasses: A compass (or mariner's compass) is a magnetized pointer free to align itself with a magnetic field, most commonly Earth's magnetic field.
- Art: Vinyl magnet sheets may be attached to paintings, photographs, and other ornamental articles, allowing them to be attached to refrigerators and other metal surfaces. Objects and paint can be applied directly to the magnet surface to create collage pieces of art. Metal magnetic boards, strips, doors, microwave ovens, dishwashers, cars, metal I beams, and any metal surface can be used magnetic vinyl art.
- Science projects: Many topic questions are based on magnets, including the repulsion of current-carrying wires, the effect of temperature, and motors involving magnets.[28]
- Toys: Given their ability to counteract the force of gravity at close range, magnets are often employed in children's toys, such as the Magnet Space Wheel and Levitron, to amusing effect.
- Refrigerator magnets are used to adorn kitchens, as a souvenir, or simply to hold a note or photo to the refrigerator door.
- Magnets can be used to make jewelry. Necklaces and bracelets can have a magnetic clasp, or may be constructed entirely from a linked series of magnets and ferrous beads.
- Magnets can pick up magnetic items (iron nails, staples, tacks, paper clips) that are either too small, too hard to reach, or too thin for fingers to hold. Some screwdrivers are magnetized for this purpose.
- Magnets can be used in scrap and salvage operations to separate magnetic metals (iron, cobalt, and nickel) from non-magnetic metals (aluminum, non-ferrous alloys, etc.). The same idea can be used in the so-called "magnet test", in which a car chassis is inspected with a magnet to detect areas repaired using fiberglass or plastic putty.
- Magnets are found in process industries, food manufacturing especially, in order to remove metal foreign bodies from materials entering the process (raw materials) or to detect a possible contamination at the end of the process and prior to packaging. They constitute an important layer of protection for the process equipment and for the final consumer.[29]
- Magnetic levitation transport, or maglev, is a form of transportation that suspends, guides and propels vehicles (especially trains) through electromagnetic force. Eliminating rolling resistance increases efficiency. The maximum recorded speed of a maglev train is 581 kilometers per hour (361 mph).
- Magnets may be used to serve as a fail-safe device for some cable connections. For example, the power cords of some laptops are magnetic to prevent accidental damage to the port when tripped over. The MagSafe power connection to the Apple MacBook is one such example.
Medical issues and safety
Because human tissues have a very low level of susceptibility to static magnetic fields, there is little mainstream scientific evidence showing a health effect associated with exposure to static fields. Dynamic magnetic fields may be a different issue, however; correlations between electromagnetic radiation and cancer rates have been postulated due to demographic correlations (see Electromagnetic radiation and health).
If a ferromagnetic foreign body is present in human tissue, an external magnetic field interacting with it can pose a serious safety risk.[30]
A different type of indirect magnetic health risk exists involving pacemakers. If a pacemaker has been embedded in a patient's chest (usually for the purpose of monitoring and regulating the heart for steady electrically induced beats), care should be taken to keep it away from magnetic fields. It is for this reason that a patient with the device installed cannot be tested with the use of a magnetic resonance imaging device.
Children sometimes swallow small magnets from toys, and this can be hazardous if two or more magnets are swallowed, as the magnets can pinch or puncture internal tissues.[31]
Magnetic imaging devices (e.g. MRIs) generate enormous magnetic fields, and therefore rooms intended to hold them exclude ferrous metals. Bringing objects made of ferrous metals (such as oxygen canisters) into such a room creates a severe safety risk, as those objects may be powerfully thrown about by the intense magnetic fields.
Magnetizing ferromagnets
Ferromagnetic materials can be magnetized in the following ways:
- Heating the object higher than its Curie temperature, allowing it to cool in a magnetic field and hammering it as it cools. This is the most effective method and is similar to the industrial processes used to create permanent magnets.
- Placing the item in an external magnetic field will result in the item retaining some of the magnetism on removal. Vibration has been shown to increase the effect. Ferrous materials aligned with the Earth's magnetic field that are subject to vibration (e.g., frame of a conveyor) have been shown to acquire significant residual magnetism. Likewise, striking a steel nail held by fingers in a N-S direction with a hammer will temporarily magnetize the nail.
- Stroking: An existing magnet is moved from one end of the item to the other repeatedly in the same direction (single touch method) or two magnets are moved outwards from the center of a third (double touch method).[32]
- Electric Current: The magnetic field produced by passing an electric current through a coil can get domains to line up. Once all of the domains are lined up, increasing the current will not increase the magnetization.[33]
Demagnetizing ferromagnets
Magnetized ferromagnetic materials can be demagnetized (or degaussed) in the following ways:
- Heating a magnet past its Curie temperature; the molecular motion destroys the alignment of the magnetic domains. This always removes all magnetization.
- Placing the magnet in an alternating magnetic field with intensity above the material's coercivity and then either slowly drawing the magnet out or slowly decreasing the magnetic field to zero. This is the principle used in commercial demagnetizers to demagnetize tools, erase credit cards, hard disks, and degaussing coils used to demagnetize CRTs.
- Some demagnetization or reverse magnetization will occur if any part of the magnet is subjected to a reverse field above the magnetic material's coercivity.
- Demagnetization progressively occurs if the magnet is subjected to cyclic fields sufficient to move the magnet away from the linear part on the second quadrant of the B–H curve of the magnetic material (the demagnetization curve).
- Hammering or jarring: mechanical disturbance tends to randomize the magnetic domains and reduce magnetization of an object, but may cause unacceptable damage.
Types of permanent magnets
Magnetic metallic elements
Many materials have unpaired electron spins, and the majority of these materials are paramagnetic. When the spins interact with each other in such a way that the spins align spontaneously, the materials are called ferromagnetic (what is often loosely termed as magnetic). Because of the way their regular crystalline atomic structure causes their spins to interact, some metals are ferromagnetic when found in their natural states, as ores. These include iron ore (magnetite or lodestone), cobalt and nickel, as well as the rare earth metals gadolinium and dysprosium (when at a very low temperature). Such naturally occurring ferromagnets were used in the first experiments with magnetism. Technology has since expanded the availability of magnetic materials to include various man-made products, all based, however, on naturally magnetic elements.
Composites
Ceramic, or ferrite, magnets are made of a sintered composite of powdered iron oxide and barium/strontium carbonate ceramic. Given the low cost of the materials and manufacturing methods, inexpensive magnets (or non-magnetized ferromagnetic cores, for use in electronic components such as portable AM radio antennas) of various shapes can be easily mass-produced. The resulting magnets are non-corroding but brittle and must be treated like other ceramics.
Alnico magnets are made by casting or sintering a combination of aluminium, nickel and cobalt with iron and small amounts of other elements added to enhance the properties of the magnet. Sintering offers superior mechanical characteristics, whereas casting delivers higher magnetic fields and allows for the design of intricate shapes. Alnico magnets resist corrosion and have physical properties more forgiving than ferrite, but not quite as desirable as a metal. Trade names for alloys in this family include: Alni, Alcomax, Hycomax, Columax, and Ticonal.[34]
Injection-molded magnets are a composite of various types of resin and magnetic powders, allowing parts of complex shapes to be manufactured by injection molding. The physical and magnetic properties of the product depend on the raw materials, but are generally lower in magnetic strength and resemble plastics in their physical properties.
Flexible magnet
Flexible magnets are composed of a high-coercivity ferromagnetic compound (usually ferric oxide) mixed with a resinous polymer binder.[35] This is extruded as a sheet and passed over a line of powerful cylindrical permanent magnets. These magnets are arranged in a stack with alternating magnetic poles facing up (N, S, N, S...) on a rotating shaft. This impresses the plastic sheet with the magnetic poles in an alternating line format. No electromagnetism is used to generate the magnets. The pole-to-pole distance is on the order of 5 mm, but varies with manufacturer. These magnets are lower in magnetic strength but can be very flexible, depending on the binder used.[36]
For magnetic compounds (e.g. Nd2Fe14B) that are vulnerable to a grain boundary corrosion problem it gives additional protection.[35]
Rare-earth magnets
Rare earth (lanthanoid) elements have a partially occupied f electron shell (which can accommodate up to 14 electrons). The spin of these electrons can be aligned, resulting in very strong magnetic fields, and therefore, these elements are used in compact high-strength magnets where their higher price is not a concern. The most common types of rare-earth magnets are samarium–cobalt and neodymium–iron–boron (NIB) magnets.
Single-molecule magnets (SMMs) and single-chain magnets (SCMs)
In the 1990s, it was discovered that certain molecules containing paramagnetic metal ions are capable of storing a magnetic moment at very low temperatures. These are very different from conventional magnets that store information at a magnetic domain level and theoretically could provide a far denser storage medium than conventional magnets. In this direction, research on monolayers of SMMs is currently under way. Very briefly, the two main attributes of an SMM are:
- a large ground state spin value (S), which is provided by ferromagnetic or ferrimagnetic coupling between the paramagnetic metal centres
- a negative value of the anisotropy of the zero field splitting (D)
Most SMMs contain manganese but can also be found with vanadium, iron, nickel and cobalt clusters. More recently, it has been found that some chain systems can also display a magnetization that persists for long times at higher temperatures. These systems have been called single-chain magnets.
Nano-structured magnets
Some nano-structured materials exhibit energy waves, called magnons, that coalesce into a common ground state in the manner of a Bose–Einstein condensate.[37][38]
Rare-earth-free permanent magnets
The United States Department of Energy has identified a need to find substitutes for rare-earth metals in permanent-magnet technology, and has begun funding such research. The Advanced Research Projects Agency-Energy (ARPA-E) has sponsored a Rare Earth Alternatives in Critical Technologies (REACT) program to develop alternative materials. In 2011, ARPA-E awarded 31.6 million dollars to fund Rare-Earth Substitute projects.[39]
Costs
The current cheapest permanent magnets, allowing for field strengths, are flexible and ceramic magnets, but these are also among the weakest types. The ferrite magnets are mainly low-cost magnets since they are made from cheap raw materials: iron oxide and Ba- or Sr-carbonate. However, a new low cost magnet, Mn–Al alloy,[35][non-primary source needed][40] has been developed and is now dominating the low-cost magnets field.[citation needed] It has a higher saturation magnetization than the ferrite magnets. It also has more favorable temperature coefficients, although it can be thermally unstable. Neodymium–iron–boron (NIB) magnets are among the strongest. These cost more per kilogram than most other magnetic materials but, owing to their intense field, are smaller and cheaper in many applications.[41]
Temperature
Temperature sensitivity varies, but when a magnet is heated to a temperature known as the Curie point, it loses all of its magnetism, even after cooling below that temperature. The magnets can often be remagnetized, however.
Additionally, some magnets are brittle and can fracture at high temperatures.
The maximum usable temperature is highest for alnico magnets at over 540 °C (1,000 °F), around 300 °C (570 °F) for ferrite and SmCo, about 140 °C (280 °F) for NIB and lower for flexible ceramics, but the exact numbers depend on the grade of material.
Electromagnets
An electromagnet, in its simplest form, is a wire that has been coiled into one or more loops, known as a solenoid. When electric current flows through the wire, a magnetic field is generated. It is concentrated near (and especially inside) the coil, and its field lines are very similar to those of a magnet. The orientation of this effective magnet is determined by the right hand rule. The magnetic moment and the magnetic field of the electromagnet are proportional to the number of loops of wire, to the cross-section of each loop, and to the current passing through the wire.[42]
If the coil of wire is wrapped around a material with no special magnetic properties (e.g., cardboard), it will tend to generate a very weak field. However, if it is wrapped around a soft ferromagnetic material, such as an iron nail, then the net field produced can result in a several hundred- to thousandfold increase of field strength.
Uses for electromagnets include particle accelerators, electric motors, junkyard cranes, and magnetic resonance imaging machines. Some applications involve configurations more than a simple magnetic dipole; for example, quadrupole and sextupole magnets are used to focus particle beams.
Units and calculations
For most engineering applications, MKS (rationalized) or SI (Système International) units are commonly used. Two other sets of units, Gaussian and CGS-EMU, are the same for magnetic properties and are commonly used in physics.[citation needed]
In all units, it is convenient to employ two types of magnetic field, B and H, as well as the magnetization M, defined as the magnetic moment per unit volume.
- The magnetic induction field B is given in SI units of teslas (T). B is the magnetic field whose time variation produces, by Faraday's Law, circulating electric fields (which the power companies sell). B also produces a deflection force on moving charged particles (as in TV tubes). The tesla is equivalent to the magnetic flux (in webers) per unit area (in meters squared), thus giving B the unit of a flux density. In CGS, the unit of B is the gauss (G). One tesla equals 104 G.
- The magnetic field H is given in SI units of ampere-turns per meter (A-turn/m). The turns appear because when H is produced by a current-carrying wire, its value is proportional to the number of turns of that wire. In CGS, the unit of H is the oersted (Oe). One A-turn/m equals 4π×10−3 Oe.
- The magnetization M is given in SI units of amperes per meter (A/m). In CGS, the unit of M is the oersted (Oe). One A/m equals 10−3 emu/cm3. A good permanent magnet can have a magnetization as large as a million amperes per meter.
- In SI units, the relation B = μ0(H + M) holds, where μ0 is the permeability of space, which equals 4π×10−7 T•m/A. In CGS, it is written as B = H + 4πM. (The pole approach gives μ0H in SI units. A μ0M term in SI must then supplement this μ0H to give the correct field within B, the magnet. It will agree with the field B calculated using Ampèrian currents).
Materials that are not permanent magnets usually satisfy the relation M = χH in SI, where χ is the (dimensionless) magnetic susceptibility. Most non-magnetic materials have a relatively small χ (on the order of a millionth), but soft magnets can have χ on the order of hundreds or thousands. For materials satisfying M = χH, we can also write B = μ0(1 + χ)H = μ0μrH = μH, where μr = 1 + χ is the (dimensionless) relative permeability and μ =μ0μr is the magnetic permeability. Both hard and soft magnets have a more complex, history-dependent, behavior described by what are called hysteresis loops, which give either B vs. H or M vs. H. In CGS, M = χH, but χSI = 4πχCGS, and μ = μr.
Caution: in part because there are not enough Roman and Greek symbols, there is no commonly agreed-upon symbol for magnetic pole strength and magnetic moment. The symbol m has been used for both pole strength (unit A•m, where here the upright m is for meter) and for magnetic moment (unit A•m2). The symbol μ has been used in some texts for magnetic permeability and in other texts for magnetic moment. We will use μ for magnetic permeability and m for magnetic moment. For pole strength, we will employ qm. For a bar magnet of cross-section A with uniform magnetization M along its axis, the pole strength is given by qm = MA, so that M can be thought of as a pole strength per unit area.
Fields of a magnet
Far away from a magnet, the magnetic field created by that magnet is almost always described (to a good approximation) by a dipole field characterized by its total magnetic moment. This is true regardless of the shape of the magnet, so long as the magnetic moment is non-zero. One characteristic of a dipole field is that the strength of the field falls off inversely with the cube of the distance from the magnet's center.
Closer to the magnet, the magnetic field becomes more complicated and more dependent on the detailed shape and magnetization of the magnet. Formally, the field can be expressed as a multipole expansion: A dipole field, plus a quadrupole field, plus an octupole field, etc.
At close range, many different fields are possible. For example, for a long, skinny bar magnet with its north pole at one end and south pole at the other, the magnetic field near either end falls off inversely with the square of the distance from that pole.
Calculating the magnetic force
Pull force of a single magnet
The strength of a given magnet is sometimes given in terms of its pull force — its ability to pull ferromagnetic objects.[43] The pull force exerted by either an electromagnet or a permanent magnet with no air gap (i.e., the ferromagnetic object is in direct contact with the pole of the magnet[44]) is given by the Maxwell equation:[45]
- ,
where
- F is force (SI unit: newton)
- A is the cross section of the area of the pole in square meters
- B is the magnetic induction exerted by the magnet
This result can be easily derived using Gilbert model, which assumes that the pole of magnet is charged with magnetic monopoles that induces the same in the ferromagnetic object.
If a magnet is acting vertically, it can lift a mass m in kilograms given by the simple equation:
where g is the gravitational acceleration.
Force between two magnetic poles
Classically, the force between two magnetic poles is given by:[46]
where
- F is force (SI unit: newton)
- qm1 and qm2 are the magnitudes of magnetic poles (SI unit: ampere-meter)
- μ is the permeability of the intervening medium (SI unit: tesla meter per ampere, henry per meter or newton per ampere squared)
- r is the separation (SI unit: meter).
The pole description is useful to the engineers designing real-world magnets, but real magnets have a pole distribution more complex than a single north and south. Therefore, implementation of the pole idea is not simple. In some cases, one of the more complex formulae given below will be more useful.
Force between two nearby magnetized surfaces of area A
The mechanical force between two nearby magnetized surfaces can be calculated with the following equation. The equation is valid only for cases in which the effect of fringing is negligible and the volume of the air gap is much smaller than that of the magnetized material:[47][48]
where:
- A is the area of each surface, in m2
- H is their magnetizing field, in A/m
- μ0 is the permeability of space, which equals 4π×10−7 T•m/A
- B is the flux density, in T.
Force between two bar magnets
The force between two identical cylindrical bar magnets placed end to end at large distance is approximately:[dubious ],[47]
where:
- B0 is the magnetic flux density very close to each pole, in T,
- A is the area of each pole, in m2,
- L is the length of each magnet, in m,
- R is the radius of each magnet, in m, and
- z is the separation between the two magnets, in m.
- relates the flux density at the pole to the magnetization of the magnet.
Note that all these formulations are based on Gilbert's model, which is usable in relatively great distances. In other models (e.g., Ampère's model), a more complicated formulation is used that sometimes cannot be solved analytically. In these cases, numerical methods must be used.
Force between two cylindrical magnets
For two cylindrical magnets with radius and length , with their magnetic dipole aligned, the force can be asymptotically approximated at large distance by,[49]
where is the magnetization of the magnets and is the gap between the magnets. A measurement of the magnetic flux density very close to the magnet is related to approximately by the formula
The effective magnetic dipole can be written as
Where is the volume of the magnet. For a cylinder, this is .
When , the point dipole approximation is obtained,
which matches the expression of the force between two magnetic dipoles.
See also
Notes
- David Vokoun; Marco Beleggia; Ludek Heller; Petr Sittner (2009). "Magnetostatic interactions and forces between cylindrical permanent magnets". Journal of Magnetism and Magnetic Materials. 321 (22): 3758–3763. Bibcode:2009JMMM..321.3758V. doi:10.1016/j.jmmm.2009.07.030.
References
- "The Early History of the Permanent Magnet". Edward Neville Da Costa Andrade, Endeavour, Volume 17, Number 65, January 1958. Contains an excellent description of early methods of producing permanent magnets.
- "positive pole n". The Concise Oxford English Dictionary. Catherine Soanes and Angus Stevenson. Oxford University Press, 2004. Oxford Reference Online. Oxford University Press.
- Wayne M. Saslow, Electricity, Magnetism, and Light, Academic (2002). ISBN 0-12-619455-6. Chapter 9 discusses magnets and their magnetic fields using the concept of magnetic poles, but it also gives evidence that magnetic poles do not really exist in ordinary matter. Chapters 10 and 11, following what appears to be a 19th-century approach, use the pole concept to obtain the laws describing the magnetism of electric currents.
- Edward P. Furlani, Permanent Magnet and Electromechanical Devices:Materials, Analysis and Applications, Academic Press Series in Electromagnetism (2001). ISBN 0-12-269951-3.
External links
- How magnets are made Archived 2013-03-16 at the Wayback Machine (video)
- Floating Ring Magnets, Bulletin of the IAPT, Volume 4, No. 6, 145 (June 2012). (Publication of the Indian Association of Physics Teachers).
- A brief history of electricity and magnetism
https://en.wikipedia.org/wiki/Magnet
https://en.wikipedia.org/wiki/Dipole_magnet
A dipole magnet is the simplest type of magnet. It has two poles, one north and one south. Its magnetic field lines form simple closed loops which emerge from the north pole, re-enter at the south pole, then pass through the body of the magnet. The simplest example of a dipole magnet is a bar magnet.[1]
https://en.wikipedia.org/wiki/Dipole_magnet
A dipole magnet is the simplest type of magnet. It has two poles, one north and one south. Its magnetic field lines form simple closed loops which emerge from the north pole, re-enter at the south pole, then pass through the body of the magnet. The simplest example of a dipole magnet is a bar magnet.[1]
Dipole magnets in accelerators
In particle accelerators, a dipole magnet is the electromagnet used to create a homogeneous magnetic field over some distance. Particle motion in that field will be circular in a plane perpendicular to the field and collinear to the direction of particle motion and free in the direction orthogonal to it. Thus, a particle injected into a dipole magnet will travel on a circular or helical trajectory. By adding several dipole sections on the same plane, the bending radial effect of the beam increases.
In accelerator physics, dipole magnets are used to realize bends in the design trajectory (or 'orbit') of the particles, as in circular accelerators. Other uses include:
- Injection of particles into the accelerator
- Ejection of particles from the accelerator
- Correction of orbit errors
- Production of synchrotron radiation
The force on a charged particle in a particle accelerator from a dipole magnet can be described by the Lorentz force law, where a charged particle experiences a force of
(in SI units). In the case of a particle accelerator dipole magnet, the charged particle beam is bent via the cross product of the particle's velocity and the magnetic field vector, with direction also being dependent on the charge of the particle.
The amount of force that can be applied to a charged particle by a dipole magnet is one of the limiting factors for modern synchrotron and cyclotron proton and ion accelerators. As the energy of the accelerated particles increases, they require more force to change direction and require larger B fields to be steered. Limitations on the amount of B field that can be produced with modern dipole electromagnets require synchrotrons/cyclotrons to increase in size (thus increasing the number of dipole magnets used) to compensate for increases in particle velocity. In the largest modern synchrotron, the Large Hadron Collider, there are 1232 main dipole magnets used for bending the path of the particle beam, each weighing 35 metric tons.[2]
Other uses
Other uses of dipole magnets to deflect moving particles include isotope mass measurement in mass spectrometry, and particle momentum measurement in particle physics.
Such magnets are also used in traditional televisions, which contain a cathode ray tube, which is essentially a small particle accelerator. Their magnets are called deflecting coils. The magnets move a single spot on the screen of the TV tube in a controlled way all over the screen.
See also
- Accelerator physics
- Beam line
- Cyclotron
- Electromagnetism
- Linear particle accelerator
- Particle accelerator
- Quadrupole magnet
- Sextupole magnet
- Multipole magnet
- Storage ring
References
- ["Pulling together: Superconducting electromagnets" CERN; https://home.cern/science/engineering/pulling-together-superconducting-electromagnets]
External links
 Media related to Dipole magnet at Wikimedia Commons
Media related to Dipole magnet at Wikimedia Commons
https://en.wikipedia.org/wiki/Dipole_magnet
https://en.wikipedia.org/wiki/Proton%E2%80%93proton_chain
https://en.wikipedia.org/wiki/Carbon-burning_process
https://en.wikipedia.org/wiki/Hydrostatic_equilibrium
https://en.wikipedia.org/wiki/Proton_nuclear_magnetic_resonance
https://en.wikipedia.org/wiki/Acetone
https://en.wikipedia.org/wiki/Properties_of_water
https://en.wikipedia.org/wiki/Color_of_water
https://en.wikipedia.org/wiki/Scattering
https://en.wikipedia.org/wiki/Diffuse_reflection
https://en.wikipedia.org/wiki/Crystallite
https://en.wikipedia.org/wiki/Single_crystal
https://en.wikipedia.org/wiki/Half-space_(geometry)
https://en.wikipedia.org/wiki/Paracrystallinity
https://en.wikipedia.org/wiki/Grain_boundary
https://en.wikipedia.org/wiki/Misorientation
https://en.wikipedia.org/wiki/Dislocation
https://en.wikipedia.org/wiki/Slip_(materials_science)
In materials science, slip is the large displacement of one part of a crystal relative to another part along crystallographic planes and directions.[1] Slip occurs by the passage of dislocations on close/packed planes, which are planes containing the greatest number of atoms per area and in close-packed directions (most atoms per length). Close-packed planes are known as slip or glide planes. A slip system describes the set of symmetrically identical slip planes and associated family of slip directions for which dislocation motion can easily occur and lead to plastic deformation. The magnitude and direction of slip are represented by the Burgers vector, b.
An external force makes parts of the crystal lattice glide along each other, changing the material's geometry. A critical resolved shear stress is required to initiate a slip.[2]
https://en.wikipedia.org/wiki/Slip_(materials_science)
https://en.wikipedia.org/wiki/Critical_resolved_shear_stress
https://en.wikipedia.org/wiki/Miller_index#Crystallographic_planes_and_directions
https://en.wikipedia.org/wiki/Axis%E2%80%93angle_representation
https://en.wikipedia.org/wiki/Amorphous_solid
https://en.wikipedia.org/wiki/Crystal_structure
https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation
https://en.wikipedia.org/wiki/Electron_microscope
https://en.wikipedia.org/wiki/Scanning_tunneling_microscope
https://en.wikipedia.org/wiki/Absolute_zero
https://en.wikipedia.org/wiki/Proton_spin_crisis
https://en.wikipedia.org/wiki/Neutron%E2%80%93proton_ratio
https://en.wikipedia.org/wiki/Proton_radius_puzzle
https://en.wikipedia.org/wiki/Proton-exchange_membrane_fuel_cell
https://en.wikipedia.org/wiki/Proton-to-electron_mass_ratio
https://en.wikipedia.org/wiki/Proton_ATPase
https://en.wikipedia.org/wiki/Electron_transport_chain#Proton_pumps
https://en.wikipedia.org/wiki/Electrochemical_gradient
https://en.wikipedia.org/wiki/Atomic_number
https://en.wikipedia.org/wiki/Isotopes_of_hydrogen
https://en.wikipedia.org/wiki/Proton_Synchrotron
https://en.wikipedia.org/wiki/Large_Hadron_Collider
https://en.wikipedia.org/wiki/Particle-induced_X-ray_emission
https://en.wikipedia.org/wiki/Proton_(satellite_program)
https://en.wikipedia.org/wiki/Super_Proton%E2%80%93Antiproton_Synchrotron
https://en.wikipedia.org/wiki/Proton_Synchrotron
https://en.wikipedia.org/wiki/Hydronium
https://en.wikipedia.org/wiki/Strong_interaction
https://en.wikipedia.org/wiki/Odderon
https://en.wikipedia.org/wiki/Annihilation#Proton-antiproton_annihilation
https://en.wikipedia.org/wiki/Nucleon_magnetic_moment
https://en.wikipedia.org/wiki/Stellar_structure
https://en.wikipedia.org/wiki/Nuclear_fusion
https://en.wikipedia.org/wiki/Combustion
https://en.wikipedia.org/wiki/Dredge-up
- The third dredge-up
- The third dredge-up occurs after a star enters the asymptotic giant branch, after a flash occurs in a helium-burning shell. The third dredge-up brings helium, carbon, and the s-process products to the surface, increasing the abundance of carbon relative to oxygen; in some larger stars this is the process that turns the star into a carbon star.[2]
https://en.wikipedia.org/wiki/Dredge-up
https://en.wikipedia.org/wiki/Beryllium
https://en.wikipedia.org/wiki/CNO_cycle
https://en.wikipedia.org/wiki/Smoke
https://en.wikipedia.org/wiki/Positron
https://en.wikipedia.org/wiki/Positron_emission
Positron emission, beta plus decay, or β+ decay is a subtype of radioactive decay called beta decay, in which a proton inside a radionuclide nucleus is converted into a neutron while releasing a positron and an electron neutrino (νe).[1] Positron emission is mediated by the weak force. The positron is a type of beta particle (β+), the other beta particle being the electron (β−) emitted from the β− decay of a nucleus.
https://en.wikipedia.org/wiki/Positron_emission
https://en.wikipedia.org/wiki/Radioactive_decay
https://en.wikipedia.org/wiki/Beta_decay
https://en.wikipedia.org/wiki/Radionuclide
https://en.wikipedia.org/wiki/Internal_conversion
https://en.wikipedia.org/wiki/Radionucleotide
https://en.wikipedia.org/wiki/Gamma_ray
https://en.wikipedia.org/wiki/Radio_wave
https://en.wikipedia.org/wiki/Black-body_radiation
https://en.wikipedia.org/wiki/Microwave
https://en.wikipedia.org/wiki/Terahertz_radiation
https://en.wikipedia.org/wiki/Ionosphere
https://en.wikipedia.org/wiki/Ground_wave
https://en.wikipedia.org/wiki/Electromagnetic_radiation
https://en.wikipedia.org/wiki/Far_infrared
https://en.wikipedia.org/wiki/Gauge_boson
https://en.wikipedia.org/wiki/Virtual_particle
https://en.wikipedia.org/wiki/Quantum_vacuum_(disambiguation)
https://en.wikipedia.org/wiki/Antiparticle
https://en.wikipedia.org/wiki/Uncertainty_principle
https://en.wikipedia.org/wiki/Gauge_boson
https://en.wikipedia.org/wiki/Initial_condition
https://en.wikipedia.org/wiki/S-matrix
https://en.wikipedia.org/wiki/Perturbation_theory_(quantum_mechanics)
https://en.wikipedia.org/wiki/Electromagnetism#repel
https://en.wikipedia.org/wiki/Graviton
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Higgs_mechanism
https://en.wikipedia.org/wiki/1964_PRL_symmetry_breaking_papers
https://en.wikipedia.org/wiki/Glueball
https://en.wikipedia.org/wiki/Cosmic_microwave_background
The cosmic microwave background (CMB, CMBR) is microwave radiation that fills all space. It is a remnant that provides an important source of data on the primordial universe.[1] With a standard optical telescope, the background space between stars and galaxies is almost completely dark. However, a sufficiently sensitive radio telescope detects a faint background glow that is almost uniform and is not associated with any star, galaxy, or other object. This glow is strongest in the microwave region of the radio spectrum. The accidental discovery of the CMB in 1965 by American radio astronomers Arno Penzias and Robert Wilson was the culmination of work initiated in the 1940s.[2][3]
CMB is landmark evidence of the Big Bang theory for the origin of the universe. In the Big Bang cosmological models, during the earliest periods, the universe was filled with an opaque fog of dense, hot plasma of sub-atomic particles. As the universe expanded, this plasma cooled to the point where protons and electrons combined to form neutral atoms of mostly hydrogen. Unlike the plasma, these atoms could not scatter thermal radiation by Thomson scattering, and so the universe became transparent.[4] Known as the recombination epoch, this decoupling event released photons to travel freely through space – sometimes referred to as relic radiation.[1] However, the photons have grown less energetic, since the expansion of space causes their wavelength to increase. The surface of last scattering refers to a shell at the right distance in space so photons are now received that were originally emitted at the time of decoupling.
The CMB is not completely smooth and uniform, showing a faint anisotropy that can be mapped by sensitive detectors. Ground and space-based experiments such as COBE and WMAP have been used to measure these temperature inhomogeneties. The anisotropy structure is determined by various interactions of matter and photons up to the point of decoupling, which results in a characteristic lumpy pattern that varies with angular scale. The distribution of the anisotropy across the sky has frequency components that can be represented by a power spectrum displaying a sequence of peaks and valleys. The peak values of this spectrum hold important information about the physical properties of the early universe: the first peak determines the overall curvature of the universe, while the second and third peak detail the density of normal matter and so-called dark matter, respectively. Extracting fine details from the CMB data can be challenging, since the emission has undergone modification by foreground features such as galaxy clusters.
Importance of precise measurement
Precise measurements of the CMB are critical to cosmology, since any proposed model of the universe must explain this radiation. The CMB has a thermal black body spectrum at a temperature of 2.72548±0.00057 K.[5] The spectral radiance dEν/dν peaks at 160.23 GHz, in the microwave range of frequencies, corresponding to a photon energy of about 6.626×10−4 eV. Alternatively, if spectral radiance is defined as dEλ/dλ, then the peak wavelength is 1.063 mm (282 GHz, 1.168×10−3 eV photons). The glow is very nearly uniform in all directions, but the tiny residual variations show a very specific pattern, the same as that expected of a fairly uniformly distributed hot gas that has expanded to the current size of the universe. In particular, the spectral radiance at different angles of observation in the sky contains small anisotropies, or irregularities, which vary with the size of the region examined. They have been measured in detail, and match what would be expected if small thermal variations, generated by quantum fluctuations of matter in a very tiny space, had expanded to the size of the observable universe we see today. This is a very active field of study, with scientists seeking both better data (for example, the Planck spacecraft) and better interpretations of the initial conditions of expansion. Although many different processes might produce the general form of a black body spectrum, no model other than the Big Bang has yet explained the fluctuations. As a result, most cosmologists consider the Big Bang model of the universe to be the best explanation for the CMB.
The high degree of uniformity throughout the observable universe and its faint but measured anisotropy lend strong support for the Big Bang model in general and the ΛCDM ("Lambda Cold Dark Matter") model in particular. Moreover, the fluctuations are coherent on angular scales that are larger than the apparent cosmological horizon at recombination. Either such coherence is acausally fine-tuned, or cosmic inflation occurred.[6][7]
Other than the temperature and polarization anisotropy, the CMB frequency spectrum is expected to feature tiny departures from the black-body law known as spectral distortions. These are also at the focus of an active research effort with the hope of a first measurement within the forthcoming decades, as they contain a wealth of information about the primordial universe and the formation of structures at late time.[8]
Features
The cosmic microwave background radiation is an emission of uniform, black body thermal energy coming from all parts of the sky. The radiation is isotropic to roughly one part in 100,000: the root mean square variations are only 18 μK,[10] after subtracting out a dipole anisotropy from the Doppler shift of the background radiation. The latter is caused by the peculiar velocity of the Sun relative to the comoving cosmic rest frame as it moves at some 369.82 ± 0.11 km/s towards the constellation Leo (galactic longitude 264.021 ± 0.011, galactic latitude 48.253 ± 0.005).[11] The CMB dipole and aberration at higher multipoles have been measured, consistent with galactic motion.[12]
In the Big Bang model for the formation of the universe, inflationary cosmology predicts that after about 10−37 seconds[13] the nascent universe underwent exponential growth that smoothed out nearly all irregularities. The remaining irregularities were caused by quantum fluctuations in the inflation field that caused the inflation event.[14] Long before the formation of stars and planets, the early universe was smaller, much hotter and, starting 10−6 seconds after the Big Bang, filled with a uniform glow from its white-hot fog of interacting plasma of photons, electrons, and baryons.
As the universe expanded, adiabatic cooling caused the energy density of the plasma to decrease until it became favorable for electrons to combine with protons, forming hydrogen atoms. This recombination event happened when the temperature was around 3000 K or when the universe was approximately 379,000 years old.[15] As photons did not interact with these electrically neutral atoms, the former began to travel freely through space, resulting in the decoupling of matter and radiation.[16]
The color temperature of the ensemble of decoupled photons has continued to diminish ever since; now down to 2.7260±0.0013 K,[5] it will continue to drop as the universe expands. The intensity of the radiation corresponds to black-body radiation at 2.726 K because red-shifted black-body radiation is just like black-body radiation at a lower temperature. According to the Big Bang model, the radiation from the sky we measure today comes from a spherical surface called the surface of last scattering. This represents the set of locations in space at which the decoupling event is estimated to have occurred[17] and at a point in time such that the photons from that distance have just reached observers. Most of the radiation energy in the universe is in the cosmic microwave background,[18] making up a fraction of roughly 6×10−5 of the total density of the universe.[19]
Two of the greatest successes of the Big Bang theory are its prediction of the almost perfect black body spectrum and its detailed prediction of the anisotropies in the cosmic microwave background. The CMB spectrum has become the most precisely measured black body spectrum in nature.[9]
The energy density of the CMB is 0.260 eV/cm3 (4.17×10−14 J/m3) which yields about 411 photons/cm3.[20]
History
The cosmic microwave background was first predicted in 1948 by Ralph Alpher and Robert Herman, in close relation to work performed by Alpher's PhD advisor George Gamow.[21][22][23][24] Alpher and Herman were able to estimate the temperature of the cosmic microwave background to be 5 K, though two years later they re-estimated it at 28 K. This high estimate was due to a misestimate of the Hubble constant by Alfred Behr, which could not be replicated and was later abandoned for the earlier estimate. Although there were several previous estimates of the temperature of space, these estimates had two flaws. First, they were measurements of the effective temperature of space and did not suggest that space was filled with a thermal Planck spectrum. Next, they depend on our being at a special spot at the edge of the Milky Way galaxy and they did not suggest the radiation is isotropic. The estimates would yield very different predictions if Earth happened to be located elsewhere in the universe.[25]
The 1948 results of Alpher and Herman were discussed in many physics settings through about 1955, when both left the Applied Physics Laboratory at Johns Hopkins University. The mainstream astronomical community, however, was not intrigued at the time by cosmology. Alpher and Herman's prediction was rediscovered by Yakov Zel'dovich in the early 1960s, and independently predicted by Robert Dicke at the same time. The first published recognition of the CMB radiation as a detectable phenomenon appeared in a brief paper by Soviet astrophysicists A. G. Doroshkevich and Igor Novikov, in the spring of 1964.[26] In 1964, David Todd Wilkinson and Peter Roll, Dicke's colleagues at Princeton University, began constructing a Dicke radiometer to measure the cosmic microwave background.[27] In 1964, Arno Penzias and Robert Woodrow Wilson at the Crawford Hill location of Bell Telephone Laboratories in nearby Holmdel Township, New Jersey had built a Dicke radiometer that they intended to use for radio astronomy and satellite communication experiments. On 20 May 1964 they made their first measurement clearly showing the presence of the microwave background,[28] with their instrument having an excess 4.2K antenna temperature which they could not account for. After receiving a telephone call from Crawford Hill, Dicke said "Boys, we've been scooped."[2][29][30] A meeting between the Princeton and Crawford Hill groups determined that the antenna temperature was indeed due to the microwave background. Penzias and Wilson received the 1978 Nobel Prize in Physics for their discovery.[31]
The interpretation of the cosmic microwave background was a controversial issue in the 1960s with some proponents of the steady state theory arguing that the microwave background was the result of scattered starlight from distant galaxies.[32] Using this model, and based on the study of narrow absorption line features in the spectra of stars, the astronomer Andrew McKellar wrote in 1941: "It can be calculated that the 'rotational temperature' of interstellar space is 2 K."[33] However, during the 1970s the consensus was established that the cosmic microwave background is a remnant of the big bang. This was largely because new measurements at a range of frequencies showed that the spectrum was a thermal, black body spectrum, a result that the steady state model was unable to reproduce.[34]
Harrison, Peebles, Yu and Zel'dovich realized that the early universe would require inhomogeneities at the level of 10−4 or 10−5.[35][36][37] Rashid Sunyaev later calculated the observable imprint that these inhomogeneities would have on the cosmic microwave background.[38] Increasingly stringent limits on the anisotropy of the cosmic microwave background were set by ground-based experiments during the 1980s. RELIKT-1, a Soviet cosmic microwave background anisotropy experiment on board the Prognoz 9 satellite (launched 1 July 1983) gave upper limits on the large-scale anisotropy. The NASA COBE mission clearly confirmed the primary anisotropy with the Differential Microwave Radiometer instrument, publishing their findings in 1992.[39][40] The team received the Nobel Prize in physics for 2006 for this discovery.
Inspired by the COBE results, a series of ground and balloon-based experiments measured cosmic microwave background anisotropies on smaller angular scales over the next decade. The primary goal of these experiments was to measure the scale of the first acoustic peak, which COBE did not have sufficient resolution to resolve. This peak corresponds to large scale density variations in the early universe that are created by gravitational instabilities, resulting in acoustical oscillations in the plasma.[41] The first peak in the anisotropy was tentatively detected by the Toco experiment and the result was confirmed by the BOOMERanG and MAXIMA experiments.[42][43][44] These measurements demonstrated that the geometry of the universe is approximately flat, rather than curved.[45] They ruled out cosmic strings as a major component of cosmic structure formation and suggested cosmic inflation was the right theory of structure formation.[46]
The second peak was tentatively detected by several experiments before being definitively detected by WMAP, which has tentatively detected the third peak.[47] As of 2010, several experiments to improve measurements of the polarization and the microwave background on small angular scales are ongoing.[needs update] These include DASI, WMAP, BOOMERanG, QUaD, Planck spacecraft, Atacama Cosmology Telescope, South Pole Telescope and the QUIET telescope.
Relationship to the Big Bang
−13 — – −12 — – −11 — – −10 — – −9 — – −8 — – −7 — – −6 — – −5 — – −4 — – −3 — – −2 — – −1 — – 0 — |
| |||||||||||||||||||||||||||||||||||||||
The cosmic microwave background radiation and the cosmological redshift-distance relation are together regarded as the best available evidence for the Big Bang event. Measurements of the CMB have made the inflationary Big Bang model the Standard Cosmological Model.[48] The discovery of the CMB in the mid-1960s curtailed interest in alternatives such as the steady state theory.[49]
In the late 1940s Alpher and Herman reasoned that if there was a Big Bang, the expansion of the universe would have stretched the high-energy radiation of the very early universe into the microwave region of the electromagnetic spectrum, and down to a temperature of about 5 K. They were slightly off with their estimate, but they had the right idea. They predicted the CMB. It took another 15 years for Penzias and Wilson to discover that the microwave background was actually there.[50]
According to standard cosmology, the CMB gives a snapshot of the hot early universe at the point in time when the temperature dropped enough to allow electrons and protons to form hydrogen atoms. This event made the universe nearly transparent to radiation because light was no longer being scattered off free electrons. When this occurred some 380,000 years after the Big Bang, the temperature of the universe was about 3,000 K. This corresponds to an ambient energy of about 0.26 eV, which is much less than the 13.6 eV ionization energy of hydrogen.[51] This epoch is generally known as the "time of last scattering" or the period of recombination or decoupling.[52]
Since decoupling, the color temperature of the background radiation has dropped by an average factor of 1,089[53] due to the expansion of the universe. As the universe expands, the CMB photons are redshifted, causing them to decrease in energy. The color temperature of this radiation stays inversely proportional to a parameter that describes the relative expansion of the universe over time, known as the scale length. The color temperature Tr of the CMB as a function of redshift, z, can be shown to be proportional to the color temperature of the CMB as observed in the present day (2.725 K or 0.2348 meV):[54]
- Tr = 2.725 K × (1 + z)
For details about the reasoning that the radiation is evidence for the Big Bang, see Cosmic background radiation of the Big Bang.
Primary anisotropy
The anisotropy, or directional dependency, of the cosmic microwave background is divided into two types: primary anisotropy, due to effects that occur at the surface of last scattering and before; and secondary anisotropy, due to effects such as interactions of the background radiation with intervening hot gas or gravitational potentials, which occur between the last scattering surface and the observer.
The structure of the cosmic microwave background anisotropies is principally determined by two effects: acoustic oscillations and diffusion damping (also called collisionless damping or Silk damping). The acoustic oscillations arise because of a conflict in the photon–baryon plasma in the early universe. The pressure of the photons tends to erase anisotropies, whereas the gravitational attraction of the baryons, moving at speeds much slower than light, makes them tend to collapse to form overdensities. These two effects compete to create acoustic oscillations, which give the microwave background its characteristic peak structure. The peaks correspond, roughly, to resonances in which the photons decouple when a particular mode is at its peak amplitude.
The peaks contain interesting physical signatures. The angular scale of the first peak determines the curvature of the universe (but not the topology of the universe). The next peak—ratio of the odd peaks to the even peaks—determines the reduced baryon density.[55] The third peak can be used to get information about the dark-matter density.[56]
The locations of the peaks give important information about the nature of the primordial density perturbations. There are two fundamental types of density perturbations called adiabatic and isocurvature. A general density perturbation is a mixture of both, and different theories that purport to explain the primordial density perturbation spectrum predict different mixtures.
- Adiabatic density perturbations
- In an adiabatic density perturbation, the fractional additional number density of each type of particle (baryons, photons, etc.) is the same. That is, if at one place there is a 1% higher number density of baryons than average, then at that place there is a 1% higher number density of photons (and a 1% higher number density in neutrinos) than average. Cosmic inflation predicts that the primordial perturbations are adiabatic.
- Isocurvature density perturbations
- In an isocurvature density perturbation, the sum (over different types of particle) of the fractional additional densities is zero. That is, a perturbation where at some spot there is 1% more energy in baryons than average, 1% more energy in photons than average, and 2% less energy in neutrinos than average, would be a pure isocurvature perturbation. Hypothetical cosmic strings would produce mostly isocurvature primordial perturbations.
The CMB spectrum can distinguish between these two because these two types of perturbations produce different peak locations. Isocurvature density perturbations produce a series of peaks whose angular scales (ℓ values of the peaks) are roughly in the ratio 1 : 3 : 5 : ..., while adiabatic density perturbations produce peaks whose locations are in the ratio 1 : 2 : 3 : ...[57] Observations are consistent with the primordial density perturbations being entirely adiabatic, providing key support for inflation, and ruling out many models of structure formation involving, for example, cosmic strings.
Collisionless damping is caused by two effects, when the treatment of the primordial plasma as fluid begins to break down:
- the increasing mean free path of the photons as the primordial plasma becomes increasingly rarefied in an expanding universe,
- the finite depth of the last scattering surface (LSS), which causes the mean free path to increase rapidly during decoupling, even while some Compton scattering is still occurring.
These effects contribute about equally to the suppression of anisotropies at small scales and give rise to the characteristic exponential damping tail seen in the very small angular scale anisotropies.
The depth of the LSS refers to the fact that the decoupling of the photons and baryons does not happen instantaneously, but instead requires an appreciable fraction of the age of the universe up to that era. One method of quantifying how long this process took uses the photon visibility function (PVF). This function is defined so that, denoting the PVF by P(t), the probability that a CMB photon last scattered between time t and t + dt is given by P(t) dt.
The maximum of the PVF (the time when it is most likely that a given CMB photon last scattered) is known quite precisely. The first-year WMAP results put the time at which P(t) has a maximum as 372,000 years.[58] This is often taken as the "time" at which the CMB formed. However, to figure out how long it took the photons and baryons to decouple, we need a measure of the width of the PVF. The WMAP team finds that the PVF is greater than half of its maximal value (the "full width at half maximum", or FWHM) over an interval of 115,000 years. By this measure, decoupling took place over roughly 115,000 years, and when it was complete, the universe was roughly 487,000 years old.[citation needed]
Late time anisotropy
Since the CMB came into existence, it has apparently been modified by several subsequent physical processes, which are collectively referred to as late-time anisotropy, or secondary anisotropy. When the CMB photons became free to travel unimpeded, ordinary matter in the universe was mostly in the form of neutral hydrogen and helium atoms. However, observations of galaxies today seem to indicate that most of the volume of the intergalactic medium (IGM) consists of ionized material (since there are few absorption lines due to hydrogen atoms). This implies a period of reionization during which some of the material of the universe was broken into hydrogen ions.
The CMB photons are scattered by free charges such as electrons that are not bound in atoms. In an ionized universe, such charged particles have been liberated from neutral atoms by ionizing (ultraviolet) radiation. Today these free charges are at sufficiently low density in most of the volume of the universe that they do not measurably affect the CMB. However, if the IGM was ionized at very early times when the universe was still denser, then there are two main effects on the CMB:
- Small scale anisotropies are erased. (Just as when looking at an object through fog, details of the object appear fuzzy.)
- The physics of how photons are scattered by free electrons (Thomson scattering) induces polarization anisotropies on large angular scales. This broad angle polarization is correlated with the broad angle temperature perturbation.
Both of these effects have been observed by the WMAP spacecraft, providing evidence that the universe was ionized at very early times, at a redshift more than 17.[clarification needed] The detailed provenance of this early ionizing radiation is still a matter of scientific debate. It may have included starlight from the very first population of stars (population III stars), supernovae when these first stars reached the end of their lives, or the ionizing radiation produced by the accretion disks of massive black holes.
The time following the emission of the cosmic microwave background—and before the observation of the first stars—is semi-humorously referred to by cosmologists as the Dark Age, and is a period which is under intense study by astronomers (see 21 centimeter radiation).
Two other effects which occurred between reionization and our observations of the cosmic microwave background, and which appear to cause anisotropies, are the Sunyaev–Zeldovich effect, where a cloud of high-energy electrons scatters the radiation, transferring some of its energy to the CMB photons, and the Sachs–Wolfe effect, which causes photons from the Cosmic Microwave Background to be gravitationally redshifted or blueshifted due to changing gravitational fields.
Polarization
The cosmic microwave background is polarized at the level of a few microkelvin. There are two types of polarization, called E-modes and B-modes. This is in analogy to electrostatics, in which the electric field (E-field) has a vanishing curl and the magnetic field (B-field) has a vanishing divergence. The E-modes arise naturally from Thomson scattering in a heterogeneous plasma. The B-modes are not produced by standard scalar type perturbations. Instead they can be created by two mechanisms: the first one is by gravitational lensing of E-modes, which has been measured by the South Pole Telescope in 2013;[59] the second one is from gravitational waves arising from cosmic inflation. Detecting the B-modes is extremely difficult, particularly as the degree of foreground contamination is unknown, and the weak gravitational lensing signal mixes the relatively strong E-mode signal with the B-mode signal.[60]
E-modes
E-modes were first seen in 2002 by the Degree Angular Scale Interferometer (DASI).
B-modes
Cosmologists predict two types of B-modes, the first generated during cosmic inflation shortly after the big bang,[61][62][63] and the second generated by gravitational lensing at later times.[64]
Primordial gravitational waves
Primordial gravitational waves are gravitational waves that could be observed in the polarisation of the cosmic microwave background and having their origin in the early universe. Models of cosmic inflation predict that such gravitational waves should appear; thus, their detection supports the theory of inflation, and their strength can confirm and exclude different models of inflation. It is the result of three things: inflationary expansion of space itself, reheating after inflation, and turbulent fluid mixing of matter and radiation. [65]
On 17 March 2014, it was announced that the BICEP2 instrument had detected the first type of B-modes, consistent with inflation and gravitational waves in the early universe at the level of r = 0.20+0.07
−0.05, which is the amount of power present in gravitational waves
compared to the amount of power present in other scalar density
perturbations in the very early universe. Had this been confirmed it
would have provided strong evidence for cosmic inflation and the Big
Bang[66][67][68][69][70][71][72] and against the ekpyrotic model of Paul Steinhardt and Neil Turok.[73] However, on 19 June 2014, considerably lowered confidence in confirming the findings was reported[71][74][75]
and on 19 September 2014, new results of the Planck experiment reported that the results of BICEP2 can be fully attributed to cosmic dust.[76][77]
Gravitational lensing
The second type of B-modes was discovered in 2013 using the South Pole Telescope with help from the Herschel Space Observatory.[78] In October 2014, a measurement of the B-mode polarization at 150 GHz was published by the POLARBEAR experiment.[79] Compared to BICEP2, POLARBEAR focuses on a smaller patch of the sky and is less susceptible to dust effects. The team reported that POLARBEAR's measured B-mode polarization was of cosmological origin (and not just due to dust) at a 97.2% confidence level.[80]
Microwave background observations
Subsequent to the discovery of the CMB, hundreds of cosmic microwave background experiments have been conducted to measure and characterize the signatures of the radiation. The most famous experiment is probably the NASA Cosmic Background Explorer (COBE) satellite that orbited in 1989–1996 and which detected and quantified the large scale anisotropies at the limit of its detection capabilities. Inspired by the initial COBE results of an extremely isotropic and homogeneous background, a series of ground- and balloon-based experiments quantified CMB anisotropies on smaller angular scales over the next decade. The primary goal of these experiments was to measure the angular scale of the first acoustic peak, for which COBE did not have sufficient resolution. These measurements were able to rule out cosmic strings as the leading theory of cosmic structure formation, and suggested cosmic inflation was the right theory.
During the 1990s, the first peak was measured with increasing sensitivity and by 2000 the BOOMERanG experiment reported that the highest power fluctuations occur at scales of approximately one degree. Together with other cosmological data, these results implied that the geometry of the universe is flat. A number of ground-based interferometers provided measurements of the fluctuations with higher accuracy over the next three years, including the Very Small Array, Degree Angular Scale Interferometer (DASI), and the Cosmic Background Imager (CBI). DASI made the first detection of the polarization of the CMB and the CBI provided the first E-mode polarization spectrum with compelling evidence that it is out of phase with the T-mode spectrum.
In June 2001, NASA launched a second CMB space mission, WMAP, to make much more precise measurements of the large scale anisotropies over the full sky. WMAP used symmetric, rapid-multi-modulated scanning, rapid switching radiometers to minimize non-sky signal noise.[53] The first results from this mission, disclosed in 2003, were detailed measurements of the angular power spectrum at a scale of less than one degree, tightly constraining various cosmological parameters. The results are broadly consistent with those expected from cosmic inflation as well as various other competing theories, and are available in detail at NASA's data bank for Cosmic Microwave Background (CMB) (see links below). Although WMAP provided very accurate measurements of the large scale angular fluctuations in the CMB (structures about as broad in the sky as the moon), it did not have the angular resolution to measure the smaller scale fluctuations which had been observed by former ground-based interferometers.
A third space mission, the ESA (European Space Agency) Planck Surveyor, was launched in May 2009 and performed an even more detailed investigation until it was shut down in October 2013. Planck employed both HEMT radiometers and bolometer technology and measured the CMB at a smaller scale than WMAP. Its detectors were trialled in the Antarctic Viper telescope as ACBAR (Arcminute Cosmology Bolometer Array Receiver) experiment—which has produced the most precise measurements at small angular scales to date—and in the Archeops balloon telescope.
On 21 March 2013, the European-led research team behind the Planck cosmology probe released the mission's all-sky map (565x318 jpeg, 3600x1800 jpeg) of the cosmic microwave background.[81][82] The map suggests the universe is slightly older than researchers expected. According to the map, subtle fluctuations in temperature were imprinted on the deep sky when the cosmos was about 370000 years old. The imprint reflects ripples that arose as early, in the existence of the universe, as the first nonillionth of a second. Apparently, these ripples gave rise to the present vast cosmic web of galaxy clusters and dark matter. Based on the 2013 data, the universe contains 4.9% ordinary matter, 26.8% dark matter and 68.3% dark energy. On 5 February 2015, new data was released by the Planck mission, according to which the age of the universe is 13.799±0.021 billion years old and the Hubble constant was measured to be 67.74±0.46 (km/s)/Mpc.[83]
Additional ground-based instruments such as the South Pole Telescope in Antarctica and the proposed Clover Project, Atacama Cosmology Telescope and the QUIET telescope in Chile will provide additional data not available from satellite observations, possibly including the B-mode polarization.
Data reduction and analysis
This section may be too technical for most readers to understand. (February 2023) |
Raw CMBR data, even from space vehicles such as WMAP or Planck, contain foreground effects that completely obscure the fine-scale structure of the cosmic microwave background. The fine-scale structure is superimposed on the raw CMBR data but is too small to be seen at the scale of the raw data. The most prominent of the foreground effects is the dipole anisotropy caused by the Sun's motion relative to the CMBR background. The dipole anisotropy and others due to Earth's annual motion relative to the Sun and numerous microwave sources in the galactic plane and elsewhere must be subtracted out to reveal the extremely tiny variations characterizing the fine-scale structure of the CMBR background.
The detailed analysis of CMBR data to produce maps, an angular power spectrum, and ultimately cosmological parameters is a complicated, computationally difficult problem. Although computing a power spectrum from a map is in principle a simple Fourier transform, decomposing the map of the sky into spherical harmonics,[84]
By applying the angular correlation function, the sum can be reduced to an expression that only involves ℓ and power spectrum term The angled brackets indicate the average with respect to all observers in the universe; since the universe is homogeneous and isotropic, therefore there is an absence of preferred observing direction. Thus, C is independent of m. Different choices of ℓ correspond to multipole moments of CMB.
In practice it is hard to take the effects of noise and foreground sources into account. In particular, these foregrounds are dominated by galactic emissions such as Bremsstrahlung, synchrotron, and dust that emit in the microwave band; in practice, the galaxy has to be removed, resulting in a CMB map that is not a full-sky map. In addition, point sources like galaxies and clusters represent another source of foreground which must be removed so as not to distort the short scale structure of the CMB power spectrum.
Constraints on many cosmological parameters can be obtained from their effects on the power spectrum, and results are often calculated using Markov chain Monte Carlo sampling techniques.
CMBR monopole term (ℓ = 0)
When ℓ = 0, the term reduced to 1, and what we have left here is just the mean temperature of the CMB. This "mean" is called CMB monopole, and it is observed to have an average temperature of about Tγ = 2.7255±0.0006 K[84] with one standard deviation confidence. The accuracy of this mean temperature may be impaired by the diverse measurements done by different mapping measurements. Such measurements demand absolute temperature devices, such as the FIRAS instrument on the COBE satellite. The measured kTγ is equivalent to 0.234 meV or 4.6×10−10 mec2. The photon number density of a blackbody having such temperature is . Its energy density is , and the ratio to the critical density is Ωγ = 5.38 × 10−5.[84]
CMBR dipole anisotropy (ℓ = 1)
CMB dipole represents the largest anisotropy, which is in the first spherical harmonic (ℓ = 1). When ℓ = 1, the term reduces to one cosine function and thus encodes amplitude fluctuation. The amplitude of CMB dipole is around 3.3621±0.0010 mK.[84] Since the universe is presumed to be homogeneous and isotropic, an observer should see the blackbody spectrum with temperature T at every point in the sky. The spectrum of the dipole has been confirmed to be the differential of a blackbody spectrum.
CMB dipole is frame-dependent. The CMB dipole moment could also be interpreted as the peculiar motion of the Earth toward the CMB. Its amplitude depends on the time due to the Earth's orbit about the barycenter of the solar system. This enables us to add a time-dependent term to the dipole expression. The modulation of this term is 1 year,[84][85] which fits the observation done by COBE FIRAS.[85][86] The dipole moment does not encode any primordial information.
From the CMB data, it is seen that the Sun appears to be moving at 368±2 km/s relative to the reference frame of the CMB (also called the CMB rest frame, or the frame of reference in which there is no motion through the CMB). The Local Group — the galaxy group that includes our own Milky Way galaxy — appears to be moving at 627±22 km/s in the direction of galactic longitude ℓ = 276°±3°, b = 30°±3°.[84][12] This motion results in an anisotropy of the data (CMB appearing slightly warmer in the direction of movement than in the opposite direction).[84] The standard interpretation of this temperature variation is a simple velocity redshift and blueshift due to motion relative to the CMB, but alternative cosmological models can explain some fraction of the observed dipole temperature distribution in the CMB.
A 2021 study of Wide-field Infrared Survey Explorer questions the kinematic interpretation of CMB anisotropy with high statistical confidence.[87]
Multipole (ℓ ≥ 2)
The temperature variation in the CMB temperature maps at higher multipoles, or ℓ ≥ 2, is considered to be the result of perturbations of the density in the early Universe, before the recombination epoch. Before recombination, the Universe consisted of a hot, dense plasma of electrons and baryons. In such a hot dense environment, electrons and protons could not form any neutral atoms. The baryons in such early Universe remained highly ionized and so were tightly coupled with photons through the effect of Thompson scattering. These phenomena caused the pressure and gravitational effects to act against each other, and triggered fluctuations in the photon-baryon plasma. Quickly after the recombination epoch, the rapid expansion of the universe caused the plasma to cool down and these fluctuations are "frozen into" the CMB maps we observe today. The said procedure happened at a redshift of around z ⋍ 1100.[84]
Other anomalies
With the increasingly precise data provided by WMAP, there have been a number of claims that the CMB exhibits anomalies, such as very large scale anisotropies, anomalous alignments, and non-Gaussian distributions.[88][89][90] The most longstanding of these is the low-ℓ multipole controversy. Even in the COBE map, it was observed that the quadrupole (ℓ = 2, spherical harmonic) has a low amplitude compared to the predictions of the Big Bang. In particular, the quadrupole and octupole (ℓ = 3) modes appear to have an unexplained alignment with each other and with both the ecliptic plane and equinoxes.[91][92][93] A number of groups have suggested that this could be the signature of new physics at the greatest observable scales; other groups suspect systematic errors in the data.[94][95][96]
Ultimately, due to the foregrounds and the cosmic variance problem, the greatest modes will never be as well measured as the small angular scale modes. The analyses were performed on two maps that have had the foregrounds removed as far as possible: the "internal linear combination" map of the WMAP collaboration and a similar map prepared by Max Tegmark and others.[47][53][97] Later analyses have pointed out that these are the modes most susceptible to foreground contamination from synchrotron, dust, and Bremsstrahlung emission, and from experimental uncertainty in the monopole and dipole.
A full Bayesian analysis of the WMAP power spectrum demonstrates that the quadrupole prediction of Lambda-CDM cosmology is consistent with the data at the 10% level and that the observed octupole is not remarkable.[98] Carefully accounting for the procedure used to remove the foregrounds from the full sky map further reduces the significance of the alignment by ~5%.[99][100][101][102] Recent observations with the Planck telescope, which is very much more sensitive than WMAP and has a larger angular resolution, record the same anomaly, and so instrumental error (but not foreground contamination) appears to be ruled out.[103] Coincidence is a possible explanation, chief scientist from WMAP, Charles L. Bennett suggested coincidence and human psychology were involved, "I do think there is a bit of a psychological effect; people want to find unusual things."[104]
Future evolution
Assuming the universe keeps expanding and it does not suffer a Big Crunch, a Big Rip, or another similar fate, the cosmic microwave background will continue redshifting until it will no longer be detectable,[105] and will be superseded first by the one produced by starlight, and perhaps, later by the background radiation fields of processes that may take place in the far future of the universe such as proton decay, evaporation of black holes, and positronium decay.[106]
Timeline of prediction, discovery and interpretation
Thermal (non-microwave background) temperature predictions
- 1896 – Charles Édouard Guillaume estimates the "radiation of the stars" to be 5–6 K.[107]
- 1926 – Sir Arthur Eddington estimates the non-thermal radiation of starlight in the galaxy "... by the formula E = σT4 the effective temperature corresponding to this density is 3.18° absolute ... black body".[108]
- 1930s – Cosmologist Erich Regener calculates that the non-thermal spectrum of cosmic rays in the galaxy has an effective temperature of 2.8 K.
- 1931 – Term microwave first used in print: "When trials with wavelengths as low as 18 cm. were made known, there was undisguised surprise+that the problem of the micro-wave had been solved so soon." Telegraph & Telephone Journal XVII. 179/1
- 1934 – Richard Tolman shows that black-body radiation in an expanding universe cools but remains thermal.
- 1938 – Nobel Prize winner (1920) Walther Nernst reestimates the cosmic ray temperature as 0.75 K.
- 1946 – Robert Dicke predicts "... radiation from cosmic matter" at < 20 K, but did not refer to background radiation.[109]
- 1946 – George Gamow calculates a temperature of 50 K (assuming a 3-billion year old universe),[110] commenting it "... is in reasonable agreement with the actual temperature of interstellar space", but does not mention background radiation.[111]
- 1953 – Erwin Finlay-Freundlich in support of his tired light theory, derives a blackbody temperature for intergalactic space of 2.3 K[112] with comment from Max Born suggesting radio astronomy as the arbitrator between expanding and infinite cosmologies.
Microwave background radiation predictions and measurements
- 1941 – Andrew McKellar detected the cosmic microwave background as the coldest component of the interstellar medium by using the excitation of CN doublet lines measured by W. S. Adams in a B star, finding an "effective temperature of space" (the average bolometric temperature) of 2.3 K.[33][113]
- 1946 – George Gamow calculates a temperature of 50 K (assuming a 3-billion year old universe),[110] commenting it "... is in reasonable agreement with the actual temperature of interstellar space", but does not mention background radiation.
- 1948 – Ralph Alpher and Robert Herman estimate "the temperature in the universe" at 5 K. Although they do not specifically mention microwave background radiation, it may be inferred.[114]
- 1949 – Ralph Alpher and Robert Herman re-re-estimate the temperature at 28 K.
- 1953 – George Gamow estimates 7 K.[109]
- 1956 – George Gamow estimates 6 K.[109]
- 1955 – Émile Le Roux of the Nançay Radio Observatory, in a sky survey at λ = 33 cm, reported a near-isotropic background radiation of 3 kelvins, plus or minus 2.[109]
- 1957 – Tigran Shmaonov reports that "the absolute effective temperature of the radioemission background ... is 4±3 K".[115] It is noted that the "measurements showed that radiation intensity was independent of either time or direction of observation ... it is now clear that Shmaonov did observe the cosmic microwave background at a wavelength of 3.2 cm"[116][117]
- 1960s – Robert Dicke re-estimates a microwave background radiation temperature of 40 K[109][118]
- 1964 – A. G. Doroshkevich and Igor Dmitrievich Novikov publish a brief paper suggesting microwave searches for the black-body radiation predicted by Gamow, Alpher, and Herman, where they name the CMB radiation phenomenon as detectable.[119]
- 1964–65 – Arno Penzias and Robert Woodrow Wilson measure the temperature to be approximately 3 K. Robert Dicke, James Peebles, P. G. Roll, and D. T. Wilkinson interpret this radiation as a signature of the Big Bang.
- 1966 – Rainer K. Sachs and Arthur M. Wolfe theoretically predict microwave background fluctuation amplitudes created by gravitational potential variations between observers and the last scattering surface (see Sachs–Wolfe effect).
- 1968 – Martin Rees and Dennis Sciama theoretically predict microwave background fluctuation amplitudes created by photons traversing time-dependent wells of potential.
- 1969 – R. A. Sunyaev and Yakov Zel'dovich study the inverse Compton scattering of microwave background photons by hot electrons (see Sunyaev–Zel'dovich effect).
- 1983 – Researchers from the Cambridge Radio Astronomy Group and the Owens Valley Radio Observatory first detect the Sunyaev–Zel'dovich effect from clusters of galaxies.
- 1983 – RELIKT-1 Soviet CMB anisotropy experiment was launched.
- 1990 – FIRAS on the Cosmic Background Explorer (COBE) satellite measures the black body form of the CMB spectrum with exquisite precision, and shows that the microwave background has a nearly perfect black-body spectrum and thereby strongly constrains the density of the intergalactic medium.
- January 1992 – Scientists that analysed data from the RELIKT-1 report the discovery of anisotropy in the cosmic microwave background at the Moscow astrophysical seminar.[120]
- 1992 – Scientists that analysed data from COBE DMR report the discovery of anisotropy in the cosmic microwave background.[121]
- 1995 – The Cosmic Anisotropy Telescope performs the first high resolution observations of the cosmic microwave background.
- 1999 – First measurements of acoustic oscillations in the CMB anisotropy angular power spectrum from the TOCO, BOOMERANG, and Maxima Experiments. The BOOMERanG experiment makes higher quality maps at intermediate resolution, and confirms that the universe is "flat".
- 2002 – Polarization discovered by DASI.[122]
- 2003 – E-mode polarization spectrum obtained by the CBI.[123] The CBI and the Very Small Array produces yet higher quality maps at high resolution (covering small areas of the sky).
- 2003 – The Wilkinson Microwave Anisotropy Probe spacecraft produces an even higher quality map at low and intermediate resolution of the whole sky (WMAP provides no high-resolution data, but improves on the intermediate resolution maps from BOOMERanG).
- 2004 – E-mode polarization spectrum obtained by the CBI.[124]
- 2004 – The Arcminute Cosmology Bolometer Array Receiver produces a higher quality map of the high resolution structure not mapped by WMAP.
- 2005 – The Arcminute Microkelvin Imager and the Sunyaev–Zel'dovich Array begin the first surveys for very high redshift clusters of galaxies using the Sunyaev–Zel'dovich effect.
- 2005 – Ralph A. Alpher is awarded the National Medal of Science for his groundbreaking work in nucleosynthesis and prediction that the universe expansion leaves behind background radiation, thus providing a model for the Big Bang theory.
- 2006 – The long-awaited three-year WMAP results are released, confirming previous analysis, correcting several points, and including polarization data.
- 2006 – Two of COBE's principal investigators, George Smoot and John Mather, received the Nobel Prize in Physics in 2006 for their work on precision measurement of the CMBR.
- 2006–2011 – Improved measurements from WMAP, new supernova surveys ESSENCE and SNLS, and baryon acoustic oscillations from SDSS and WiggleZ, continue to be consistent with the standard Lambda-CDM model.
- 2010 – The first all-sky map from the Planck telescope is released.
- 2013 – An improved all-sky map from the Planck telescope is released, improving the measurements of WMAP and extending them to much smaller scales.
- 2014 – On March 17, 2014, astrophysicists of the BICEP2 collaboration announced the detection of inflationary gravitational waves in the B-mode power spectrum, which if confirmed, would provide clear experimental evidence for the theory of inflation.[66][67][68][69][71][125] However, on 19 June 2014, lowered confidence in confirming the cosmic inflation findings was reported.[71][74][75]
- 2015 – On January 30, 2015, the same team of astronomers from BICEP2 withdrew the claim made on the previous year. Based on the combined data of BICEP2 and Planck, the European Space Agency announced that the signal can be entirely attributed to dust in the Milky Way.[126]
- 2018 – The final data and maps from the Planck telescope is released, with improved measurements of the polarization on large scales.[127]
- 2019 – Planck telescope analyses of their final 2018 data continue to be released.[128]
In popular culture
- In the Stargate Universe TV series (2009–2011), an ancient spaceship, Destiny, was built to study patterns in the CMBR which is a sentient message left over from the beginning of time.[129]
- In Wheelers, a novel (2000) by Ian Stewart & Jack Cohen, CMBR is explained as the encrypted transmissions of an ancient civilization. This allows the Jovian "blimps" to have a society older than the currently-observed age of the universe.[citation needed]
- In The Three-Body Problem, a 2008 novel by Liu Cixin, a probe from an alien civilization compromises instruments monitoring the CMBR in order to deceive a character into believing the civilization has the power to manipulate the CMBR itself.[130]
- The 2017 issue of the Swiss 20 francs bill lists several astronomical objects with their distances – the CMB is mentioned with 430 · 1015 light-seconds.[131]
- In the 2021 Marvel series WandaVision, a mysterious television broadcast is discovered within the Cosmic Microwave Background.[132]
See also
- List of cosmological computation software
- Cosmic neutrino background – relic of the big bang
- Cosmic microwave background spectral distortions – Fluctuations in the energy spectrum of the microwave background
- Cosmological perturbation theory – theory by which the evolution of structure is understood in the big bang model
- Axis of evil (cosmology) – Name given to an anomaly in astronomical observations of the Cosmic Microwave Background
- Gravitational wave background – Random gravitational-wave signal potentially detectable by gravitational wave experiments
- Heat death of the universe – Possible fate of the universe
- Horizons: Exploring the Universe
- Lambda-CDM model – Model of Big Bang cosmology
- Observational cosmology – Study of the origin of the universe (structure and evolution)
- Observation history of galaxies – Large gravitationally bound system of stars and interstellar matter
- Physical cosmology – Branch of cosmology which studies mathematical models of the universe
- Timeline of cosmological theories – Timeline of theories about physical cosmology
References
- "WandaVision's 'cosmic microwave background radiation' is real, actually". SYFY Official Site. 2021-02-03. Retrieved 2023-01-23.
Further reading
- Balbi, Amedeo (2008). The music of the big bang : the cosmic microwave background and the new cosmology. Berlin: Springer. ISBN 978-3-540-78726-6.
- Durrer, Ruth (2008). The Cosmic Microwave Background. Cambridge University Press. ISBN 978-0-521-84704-9.
- Evans, Rhodri (2015). The Cosmic Microwave Background: How It Changed Our Understanding of the Universe. Springer. ISBN 978-3-319-09927-9.
External links
- Student Friendly Intro to the CMB A pedagogic, step-by-step introduction to the cosmic microwave background power spectrum analysis suitable for those with an undergraduate physics background. More in depth than typical online sites. Less dense than cosmology texts.
- CMBR Theme on arxiv.org
- Audio: Fraser Cain and Dr. Pamela Gay – Astronomy Cast. The Big Bang and Cosmic Microwave Background – October 2006
- Visualization of the CMB data from the Planck mission
- Copeland, Ed. "CMBR: Cosmic Microwave Background Radiation". Sixty Symbols. Brady Haran for the University of Nottingham.
https://en.wikipedia.org/wiki/Cosmic_microwave_background
https://en.wikipedia.org/wiki/Cosmic_microwave_background
https://en.wikipedia.org/wiki/Big_Bang_nucleosynthesis
https://en.wikipedia.org/wiki/Inflation_(cosmology)
https://en.wikipedia.org/wiki/Lambda-CDM_model
https://en.wikipedia.org/wiki/Dark_matter
https://en.wikipedia.org/wiki/Galaxy_filament
https://en.wikipedia.org/wiki/Observable_universe#Large-scale_structure
Seen another way, the photon can be considered as its own antiparticle (thus an "antiphoton" is simply a normal photon with opposite momentum, equal polarization, and 180° out of phase). The reverse process, pair production, is the dominant mechanism by which high-energy photons such as gamma rays lose energy while passing through matter.[29] That process is the reverse of "annihilation to one photon" allowed in the electric field of an atomic nucleus.
https://en.wikipedia.org/wiki/Photon
https://en.wikipedia.org/wiki/Spin_angular_momentum_of_light
https://en.wikipedia.org/wiki/Photoelectric_effect
https://en.wikipedia.org/wiki/Spacetime
https://en.wikipedia.org/wiki/Spin_(particle_physics)
https://en.wikipedia.org/wiki/Medical_optical_imaging
https://en.wikipedia.org/wiki/Electron%E2%80%93positron_annihilation
https://en.wikipedia.org/wiki/Synchrotron_radiation
https://en.wikipedia.org/wiki/Photon_polarization
https://en.wikipedia.org/wiki/Plane_wave
https://en.wikipedia.org/wiki/Photon_polarization
https://en.wikipedia.org/wiki/Linear_polarization
https://en.wikipedia.org/wiki/Helicity_(particle_physics)
https://en.wikipedia.org/wiki/Pauli%E2%80%93Lubanski_pseudovector#Massless_fields
https://en.wikipedia.org/wiki/Three-photon_microscopy
https://en.wikipedia.org/wiki/Two-photon_excitation_microscopy
https://en.wikipedia.org/wiki/Second-harmonic_imaging_microscopy
https://en.wikipedia.org/wiki/Centrosymmetry
https://en.wikipedia.org/wiki/Absorbance
Second-harmonic imaging microscopy (SHIM) is based on a nonlinear optical effect known as second-harmonic generation (SHG). SHIM has been established as a viable microscope imaging contrast mechanism for visualization of cell and tissue structure and function.[1] A second-harmonic microscope obtains contrasts from variations in a specimen's ability to generate second-harmonic light from the incident light while a conventional optical microscope obtains its contrast by detecting variations in optical density, path length, or refractive index of the specimen. SHG requires intense laser light passing through a material with a noncentrosymmetric molecular structure, either inherent or induced externally, for example by an electric field.[2]
https://en.wikipedia.org/wiki/Second-harmonic_imaging_microscopy
Second-harmonic imaging microscopy (SHIM) is based on a nonlinear optical effect known as second-harmonic generation (SHG). SHIM has been established as a viable microscope imaging contrast mechanism for visualization of cell and tissue structure and function.[1] A second-harmonic microscope obtains contrasts from variations in a specimen's ability to generate second-harmonic light from the incident light while a conventional optical microscope obtains its contrast by detecting variations in optical density, path length, or refractive index of the specimen. SHG requires intense laser light passing through a material with a noncentrosymmetric molecular structure, either inherent or induced externally, for example by an electric field.[2]
Second-harmonic light emerging from an SHG material is exactly half the wavelength (frequency doubled) of the light entering the material. While two-photon-excited fluorescence (TPEF) is also a two photon process, TPEF loses some energy during the relaxation of the excited state, while SHG is energy conserving. Typically, an inorganic crystal is used to produce SHG light such as lithium niobate (LiNbO3), potassium titanyl phosphate (KTP = KTiOPO4), and lithium triborate (LBO = LiB3O5). Though SHG requires a material to have specific molecular orientation in order for the incident light to be frequency doubled, some biological materials can be highly polarizable, and assemble into fairly ordered, large noncentrosymmetric structures. While some biological materials such as collagen, microtubules, and muscle myosin[3] can produce SHG signals, even water can become ordered and produce second-harmonic signal under certain conditions, which allows SH microscopy to image surface potentials without any labeling molecules.[2] The SHG pattern is mainly determined by the phase matching condition. A common setup for an SHG imaging system will have a laser scanning microscope with a titanium sapphire mode-locked laser as the excitation source. The SHG signal is propagated in the forward direction. However, some experiments have shown that objects on the order of about a tenth of the wavelength of the SHG produced signal will produce nearly equal forward and backward signals.
Advantages
SHIM offers several advantages for live cell and tissue imaging. SHG does not involve the excitation of molecules like other techniques such as fluorescence microscopy therefore, the molecules shouldn't suffer the effects of phototoxicity or photobleaching. Also, since many biological structures produce strong SHG signals, the labeling of molecules with exogenous probes is not required which can also alter the way a biological system functions. By using near infrared wavelengths for the incident light, SHIM has the ability to construct three-dimensional images of specimens by imaging deeper into thick tissues.
Difference and complementarity with two-photon fluorescence (2PEF)
Two-photons fluorescence (2PEF) is a very different process from SHG: it involves excitation of electrons to higher energy levels, and subsequent de-excitation by photon emission (unlike SHG, although it is also a 2-photon process). Thus, 2PEF is a non coherent process, spatially (emitted isotropically) and temporally (broad, sample-dependent spectrum). It is also not specific to certain structure, unlike SHG.[4]
It can therefore be coupled to SHG in multiphoton imaging to reveal some molecules that do produce autofluorescence, like elastin in tissues (while SHG reveals collagen or myosin for instance).[4]
History
Before SHG was used for imaging, the first demonstration of SHG was performed in 1961 by P. A. Franken, G. Weinreich, C. W. Peters, and A. E. Hill at the University of Michigan, Ann Arbor using a quartz sample.[5] In 1968, SHG from interfaces was discovered by Bloembergen [6] and has since been used as a tool for characterizing surfaces and probing interface dynamics. In 1971, Fine and Hansen reported the first observation of SHG from biological tissue samples.[7] In 1974, Hellwarth and Christensen first reported the integration of SHG and microscopy by imaging SHG signals from polycrystalline ZnSe.[8] In 1977, Colin Sheppard imaged various SHG crystals with a scanning optical microscope. The first biological imaging experiments were done by Freund and Deutsch in 1986 to study the orientation of collagen fibers in rat tail tendon.[9] In 1993, Lewis examined the second-harmonic response of styryl dyes in electric fields. He also showed work on imaging live cells. In 2006, Goro Mizutani group developed a non-scanning SHG microscope that significantly shortens the time required for observation of large samples, even if the two-photons wide-field microscope was published in 1996 [10] and could have been used to detect SHG. The non-scanning SHG microscope was used for observation of plant starch,[11][12] megamolecule,[13] spider silk[14][15] and so on. In 2010 SHG was extended to whole-animal in vivo imaging.[16][17] In 2019, SHG applications widened when it was applied to the use of selectively imaging agrochemicals directly on leaf surfaces to provide a way to evaluate the effectiveness of pesticides.[18]
Quantitative measurements
Orientational anisotropy
SHG polarization anisotropy can be used to determine the orientation and degree of organization of proteins in tissues since SHG signals have well-defined polarizations. By using the anisotropy equation:[19]
and acquiring the intensities of the polarizations in the parallel and perpendicular directions. A high value indicates an anisotropic orientation whereas a low value indicates an isotropic structure. In work done by Campagnola and Loew,[19] it was found that collagen fibers formed well-aligned structures with an value.
Forward over backward SHG
SHG being a coherent process (spatially and temporally), it keeps information on the direction of the excitation and is not emitted isotropically. It is mainly emitted in forward direction (same as excitation), but can also be emitted in backward direction depending on the phase-matching condition. Indeed, the coherence length beyond which the conversion of the signal decreases is:
with for forward, but for backward such that >> . Therefore, thicker structures will appear preferentially in forward, and thinner ones in backward: since the SHG conversion depends at first approximation on the square of the number of nonlinear converters, the signal will be higher if emitted by thick structures, thus the signal in forward direction will be higher than in backward. However, the tissue can scatter the generated light, and a part of the SHG in forward can be retro-reflected in the backward direction.[20] Then, the forward-over-backward ratio F/B can be calculated,[20] and is a metric of the global size and arrangement of the SHG converters (usually collagen fibrils). It can also be shown that the higher the out-of-plane angle of the scatterer, the higher its F/B ratio (see fig. 2.14 of [21]).
Polarization-resolved SHG
The advantages of polarimetry were coupled to SHG in 2002 by Stoller et al.[22] Polarimetry can measure the orientation and order at molecular level, and coupled to SHG it can do so with the specificity to certain structures like collagen: polarization-resolved SHG microscopy (p-SHG) is thus an expansion of SHG microscopy.[23] p-SHG defines another anisotropy parameter, as:[24]
which is, like r, a measure of the principal orientation and disorder of the structure being imaged. Since it is often performed in long cylindrical filaments (like collagen), this anisotropy is often equal to ,[25] where is the nonlinear susceptibility tensor and X the direction of the filament (or main direction of the structure), Y orthogonal to X and Z the propagation of the excitation light. The orientation ϕ of the filaments in the plane XY of the image can also be extracted from p-SHG by FFT analysis, and put in a map.[25][26]
Fibrosis quantization
Collagen (particular case, but widely studied in SHG microscopy), can exist in various forms : 28 different types, of which 5 are fibrillar. One of the challenge is to determine and quantify the amount of fibrillar collagen in a tissue, to be able to see its evolution and relationship with other non-collagenous materials.[27]
To that end, a SHG microscopy image has to be corrected to remove the small amount of residual fluorescence or noise that exist at the SHG wavelength. After that, a mask can be applied to quantify the collagen inside the image.[27] Among other quantization techniques, it is probably the one with the highest specificity, reproductibility and applicability despite being quite complex.[27]
Others
It has also been used to prove that backpropagating action potentials invade dendritic spines without voltage attenuation, establishing a sound basis for future work on Long-term potentiation. Its use here was that it provided a way to accurately measure the voltage in the tiny dendritic spines with an accuracy unattainable with standard two-photon microscopy.[28] Meanwhile, SHG can efficiently convert near-infrared light to visible light to enable imaging-guided photodynamic therapy, overcoming the penetration depth limitations.[29]
Materials that can be imaged
SHG microscopy and its expansions can be used to study various tissues: some example images are reported in the figure below: collagen inside the extracellular matrix remains the main application. It can be found in tendon, skin, bone, cornea, aorta, fascia, cartilage, meniscus, intervertebral disks...
Myosin can also be imaged in skeletal muscle or cardiac muscle.
| Type | Material | Found in | SHG signal | Specificity |
|---|---|---|---|---|
| Carbohydrate | Cellulose | Wood, green plant, algae. | Quite weak in normal cellulose,[18] but substantial in crystalline or nanocrystalline cellulose. | - |
| Starch | Staple foods, green plant | Quite intense signal [30] | chirality is at micro and macro level, and the SHG is different under right or left-handed circular polarization | |
| Megamolecular polysaccharide sacran | Cyanobactery | From sacran cotton-like lump, fibers, and cast films | signal from films is weaker [13] | |
| Protein | Fibroin and sericin | Spider silk | Quite weak | [14] |
| Collagen[9] | tendon, skin, bone, cornea, aorta, fascia, cartilage, meniscus, intervertebral disks ; connective tissues | Quite strong, depends on the type of the collagen (does it form fibrils, fibers ?) | nonlinear susceptibility tensor components are , , , with ~ and / ~ 1.4 in most cases | |
| Myosin | Skeletal or cardiac muscle[3] | Quite strong | nonlinear susceptibility tensor components are , , with ~ but / ~ 0.6 < 1 contrary to collagen | |
| Tubulin | Microtubules in mitosis or meiosis,[31] or in neurites (mainly axons)[32] | Quite weak | The microtubules have to be aligned to efficiently generate | |
| Minerals | Piezoelectric crystals | Also called nonlinear crystals | Strong if phase-matched | Different types of phase-matching, critical of non-critical |
| Polar liquids | Water | Most living organisms | Barely detectable (requires wide-field geometry and ultra-short laser pulses [33]) | Directly probing electrostatic fields, since oriented water molecules satisfy phase-matching condition [34] |
Coupling with THG microscopy
Third-Harmonic Generation (THG) microscopy can be complementary to SHG microscopy, as it is sensitive to the transverse interfaces, and to the 3rd order nonlinear susceptibility [35] · [36]
Applications
Cancer progression, tumor characterization
The mammographic density is correlated with the collagen density, thus SHG can be used for identifying breast cancer.[37] SHG is usually coupled to other nonlinear techniques such as Coherent anti-Stokes Raman Scattering or Two-photon excitation microscopy, as part of a routine called multiphoton microscopy (or tomography) that provides a non-invasive and rapid in vivo histology of biopsies that may be cancerous.[38]
Breast cancer
The comparison of forward and backward SHG images gives insight about the microstructure of collagen, itself related to the grade and stage of a tumor, and its progression in breast.[39] Comparison of SHG and 2PEF can also show the change of collagen orientation in tumors.[40] Even if SHG microscopy has contributed a lot to breast cancer research, it is not yet established as a reliable technique in hospitals, or for diagnostic of this pathology in general.[39]
Ovarian cancer
Healthy ovaries present in SHG a uniform epithelial layer and well-organized collagen in their stroma, whereas abnormal ones show an epithelium with large cells and a changed collagen structure.[39] The r ratio is also used [41] to show that the alignment of fibrils is slightly higher for cancerous than for normal tissues.
Skin cancer
SHG is, again, combined to 2PEF is used to calculate the ratio:
where shg (resp. tpef) is the number of thresholded pixels in the SHG (resp. 2PEF) image,[42] a high MFSI meaning a pure SHG image (with no fluorescence). The highest MFSI is found in cancerous tissues,[39] which provides a contrast mode to differentiate from normal tissues.
SHG was also combined to Third-Harmonic Generation (THG) to show that backward THG is higher in tumors.[43]
Pancreatic cancer
Changes in collagen ultrastructure in pancreatic cancer can be investigated by multiphoton fluorescence and polarization-resolved SHIM.[44]
Other cancers
SHG microscopy was reported for the study of lung, colonic, esophageal stroma and cervical cancers.[39]
Pathologies detection
Alterations in the organization or polarity of the collagen fibrils can be signs of pathology,.[45][46]
In particular, the anisotropy of alignment of collagen fibers allowed to discriminate healthy dermis against pathological scars in skin.[47] Also, pathologies in cartilage such as osteoarthritis can be probed by polarization-resolved SHG microscopy,.[48][49] SHIM was later extended to fibro-cartilage (meniscus).[50]
Tissue engineering
The ability of SHG to image specific molecules can reveal the structure of a certain tissue one material at a time, and at various scales (from macro to micro) using microscopy. For instance, the collagen (type I) is specifically imaged from the extracellular matrix (ECM) of cells, or when it serves as a scaffold or conjonctive material in tissues.[51] SHG also reveals fibroin in silk, myosin in muscles and biosynthetized cellulose. All of this imaging capability can be used to design artificials tissues, by targeting specific points of the tissue : SHG can indeed quantitatively measure some orientations, and material quantity and arrangement.[51] Also, SHG coupled to other multiphoton techniques can serve to monitor the development of engineered tissues, when the sample is relatively thin however.[52] Of course, they can finally be used as a quality control of the fabricated tissues.[52]
Structure of the eye
Cornea, at the surface of the eye, is considered to be made of plywood-like structure of collagen, due to the self-organization properties of sufficiently dense collagen.[53] Yet, the collagenous orientation in lamellae is still under debate in this tissue.[54] Keratoconus cornea can also be imaged by SHG to reveal morphological alterations of the collagen.[55] Third-Harmonic Generation (THG) microscopy is moreover used to image the cornea, which is complementary to SHG signal as THG and SHG maxima in this tissue are often at different places.[56]
See also
Sources
- Schmitt, Michael; Mayerhöfer, Thomas; Popp, Jürgen; Kleppe, Ingo; Weisshartannée, Klaus (2013). Handbook of Biophotonics, Chap.3 Light–Matter Interaction. Wiley. doi:10.1002/9783527643981.bphot003. ISBN 9783527643981. S2CID 93908151.
- Pavone, Francesco S.; Campagnola, Paul J. (2016). Second Harmonic Generation Imaging, 2nd edition. CRC Taylor&Francis. ISBN 978-1-4398-4914-9.
- Campagnola, Paul J.; Clark, Heather A.; Mohler, William A.; Lewis, Aaron; Loew, Leslie M. (2001). "Second harmonic imaging microscopy of living cells" (PDF). Journal of Biomedical Optics. 6 (3): 277–286. Bibcode:2001JBO.....6..277C. doi:10.1117/1.1383294. hdl:2047/d20000323. PMID 11516317. S2CID 2376695.
- Campagnola, Paul J.; Loew, Leslie M (2003). "Second-harmonic imaging microscopy for visualizing biomolecular arrays in cells, tissues and organisms" (PDF). Nature Biotechnology. 21 (11): 1356–1360. doi:10.1038/nbt894. PMID 14595363. S2CID 18701570. Archived from the original (PDF) on 2016-03-04.
- Stoller, P.; Reiser, K.M.; Celliers, P.M.; Rubenchik, A.M. (2002). "Polarization-modulated second harmonic generation in collagen". Biophys. J. 82 (6): 3330–3342. Bibcode:2002BpJ....82.3330S. doi:10.1016/s0006-3495(02)75673-7. PMC 1302120. PMID 12023255.
- Han, M.; Giese, G.; Bille, J. F. (2005). "Second harmonic generation imaging of collagen fibrils in cornea and sclera". Opt. Express. 13 (15): 5791–5797. Bibcode:2005OExpr..13.5791H. doi:10.1364/opex.13.005791. PMID 19498583.
- König, Karsten (2018). Multiphoton Microscopy and Fluorescence Lifetime Imaging - Applications in Biology and Medicine. De Gruyter. ISBN 978-3-11-042998-5.

- Keikhosravi, Adib; Bredfeldt, Jeremy S.; Sagar, Abdul Kader; Eliceiri, Kevin W. (2014). "Second-harmonic generation imaging of cancer (from "Quantitative Imaging in Cell Biology by Jennifer C. Waters, Torsten Wittman")". Methods in Cell Biology. 123: 531–546. doi:10.1016/B978-0-12-420138-5.00028-8. ISSN 0091-679X. PMID 24974046.
- Hanry Yu; Nur Aida Abdul Rahim (2013). Imaging in Cellular and Tissue Engineering, 1st edition. CRC Taylor&Francis. ISBN 9780367445867.
- Cicchi, Riccardo; Vogler, Nadine; Kapsokalyvas, Dimitrios; Dietzek, Benjamin; Popp, Jürgen; Pavone, Francesco Saverio (2013). "From molecular structure to tissue architecture: collagen organization probed by SHG microscopy". Journal of Biophotonics. 6 (2): 129–142. doi:10.1002/jbio.201200092. PMID 22791562.

- Roesel, D.; Eremchev, M.; Schönfeldová, T.; Lee, S.; Roke, S. (2022-04-18). "Water
as a contrast agent to quantify surface chemistry and physics using
second harmonic scattering and imaging: A perspective". Applied Physics Letters. AIP Publishing. 120 (16): 160501. Bibcode:2022ApPhL.120p0501R. doi:10.1063/5.0085807. ISSN 0003-6951. S2CID 248252664.

References
- Olivier, N.; Débarre, D.; Beaurepaire, E. (2016). "THG Microscopy of Cells and Tissues: Contrast Mechanisms and Applications". Second Harmonic Generation Imaging, 2nd edition. CRC Taylor&Francis. ISBN 978-1-4398-4914-9.
https://en.wikipedia.org/wiki/Second-harmonic_imaging_microscopy
https://en.wikipedia.org/wiki/Lithium_triborate
https://en.wikipedia.org/wiki/Transparency_and_translucency
https://en.wikipedia.org/wiki/Nd:YAG_laser
https://en.wikipedia.org/wiki/Nonlinear_optics#Phase_matching
Coupling with other multiphoton techniques
Correlative images can be obtained using different multiphoton schemes such as 2PEF, 3PEF, and Third harmonic generation (THG), in parallel (since the corresponding wavelengths are different, they can be easily separated onto different detectors). A multichannel image is then constructed.[9]
3PEF is also compared to 2PEF: it generally gives a smaller degradation of the signal-to-background ratio (SBR) with depth, even if the emitted signal is smaller than with 2PEF.[9]
https://en.wikipedia.org/wiki/Three-photon_microscopy
https://en.wikipedia.org/wiki/Mode_locking
https://en.wikipedia.org/wiki/Two-photon_absorption
https://en.wikipedia.org/wiki/Point_spread_function
https://en.wikipedia.org/wiki/Confocal_microscopy
https://en.wikipedia.org/wiki/Spatial_filter
https://en.wikipedia.org/wiki/Transverse_mode
https://en.wikipedia.org/wiki/Active_laser_medium
https://en.wikipedia.org/wiki/Rare-earth_element
https://en.wikipedia.org/wiki/Optical_cavity
https://en.wikipedia.org/wiki/Boundary_value_problem
https://en.wikipedia.org/wiki/Eigenfunction
https://en.wikipedia.org/wiki/Scalar_(mathematics)
https://en.wikipedia.org/wiki/Total_internal_reflection
https://en.wikipedia.org/wiki/Scalar_matrix
https://en.wikipedia.org/wiki/Nonlinear_optics
https://en.wikipedia.org/wiki/Optical_parametric_amplifier
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
Spontaneous parametric down-conversion (also known as SPDC, parametric fluorescence or parametric scattering) is a nonlinear instant optical process that converts one photon of higher energy (namely, a pump photon), into a pair of photons (namely, a signal photon, and an idler photon) of lower energy, in accordance with the law of conservation of energy and law of conservation of momentum. It is an important process in quantum optics, for the generation of entangled photon pairs, and of single photons.
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
Type I down converter is a squeezed vacuum that contains only even photon number terms. The nondegenerate output of the Type II down converter is a two-mode squeezed vacuum.
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
An SPDC scheme with the Type I output
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
https://en.wikipedia.org/wiki/Barium_borate
1 - Incident light
2 - 50% transmitted light
3 - 50% reflected light
In practice, the reflective layer absorbs some light.
https://en.wikipedia.org/wiki/Beam_splitter
https://en.wikipedia.org/wiki/Total_internal_reflection#FTIR_(Frustrated_Total_Internal_Reflection)
Designs
In its most common form, a cube, a beam splitter is made from two triangular glass prisms which are glued together at their base using polyester, epoxy, or urethane-based adhesives. (Before these synthetic resins, natural ones were used, e.g. Canada balsam.) The thickness of the resin layer is adjusted such that (for a certain wavelength) half of the light incident through one "port" (i.e., face of the cube) is reflected and the other half is transmitted due to FTIR (Frustrated Total Internal Reflection). Polarizing beam splitters, such as the Wollaston prism, use birefringent materials to split light into two beams of orthogonal polarization states.
Another design is the use of a half-silvered mirror. This is composed of an optical substrate, which is often a sheet of glass or plastic, with a partially transparent thin coating of metal. The thin coating can be aluminium deposited from aluminium vapor using a physical vapor deposition method. The thickness of the deposit is controlled so that part (typically half) of the light, which is incident at a 45-degree angle and not absorbed by the coating or substrate material, is transmitted and the remainder is reflected. A very thin half-silvered mirror used in photography is often called a pellicle mirror. To reduce loss of light due to absorption by the reflective coating, so-called "Swiss-cheese" beam-splitter mirrors have been used. Originally, these were sheets of highly polished metal perforated with holes to obtain the desired ratio of reflection to transmission. Later, metal was sputtered onto glass so as to form a discontinuous coating, or small areas of a continuous coating were removed by chemical or mechanical action to produce a very literally "half-silvered" surface.
Instead of a metallic coating, a dichroic optical coating may be used. Depending on its characteristics, the ratio of reflection to transmission will vary as a function of the wavelength of the incident light. Dichroic mirrors are used in some ellipsoidal reflector spotlights to split off unwanted infrared (heat) radiation, and as output couplers in laser construction.
A third version of the beam splitter is a dichroic mirrored prism assembly which uses dichroic optical coatings to divide an incoming light beam into a number of spectrally distinct output beams. Such a device was used in three-pickup-tube color television cameras and the three-strip Technicolor movie camera. It is currently used in modern three-CCD cameras. An optically similar system is used in reverse as a beam-combiner in three-LCD projectors, in which light from three separate monochrome LCD displays is combined into a single full-color image for projection.
Beam splitters with single-mode[clarification needed] fiber for PON networks use the single-mode behavior to split the beam.[citation needed] The splitter is done by physically splicing two fibers "together" as an X.
Arrangements of mirrors or prisms used as camera attachments to photograph stereoscopic image pairs with one lens and one exposure are sometimes called "beam splitters", but that is a misnomer, as they are effectively a pair of periscopes redirecting rays of light which are already non-coincident. In some very uncommon attachments for stereoscopic photography, mirrors or prism blocks similar to beam splitters perform the opposite function, superimposing views of the subject from two different perspectives through color filters to allow the direct production of an anaglyph 3D image, or through rapidly alternating shutters to record sequential field 3D video.
Phase shift
Beam splitters are sometimes used to recombine beams of light, as in a Mach–Zehnder interferometer. In this case there are two incoming beams, and potentially two outgoing beams. But the amplitudes of the two outgoing beams are the sums of the (complex) amplitudes calculated from each of the incoming beams, and it may result that one of the two outgoing beams has amplitude zero. In order for energy to be conserved (see next section), there must be a phase shift in at least one of the outgoing beams. For example (see red arrows in picture on the right), if a polarized light wave in air hits a dielectric surface such as glass, and the electric field of the light wave is in the plane of the surface, then the reflected wave will have a phase shift of π, while the transmitted wave will not have a phase shift; the blue arrow does not pick up a phase-shift, because it is reflected from a medium with a lower refractive index. The behavior is dictated by the Fresnel equations.[1] This does not apply to partial reflection by conductive (metallic) coatings, where other phase shifts occur in all paths (reflected and transmitted). In any case, the details of the phase shifts depend on the type and geometry of the beam splitter.
Classical lossless beam splitter
For beam splitters with two incoming beams, using a classical, lossless beam splitter with electric fields Ea and Eb each incident at one of the inputs, the two output fields Ec and Ed are linearly related to the inputs through
where the 2×2 element is the beam-splitter transfer matrix and r and t are the reflectance and transmittance along a particular path through the beam splitter, that path being indicated by the subscripts. (The values depend on the polarization of the light.)
If the beam splitter removes no energy from the light beams, the total output energy can be equated with the total input energy, reading
Inserting the results from the transfer equation above with produces
and similarly for then
When both and are non-zero, and using these two results we obtain
where "" indicates the complex conjugate. It is now easy to show that where is the identity, i.e. the beam-splitter transfer matrix is a unitary matrix.
Expanding, it can be written each r and t as a complex number having an amplitude and phase factor; for instance, . The phase factor accounts for possible shifts in phase of a beam as it reflects or transmits at that surface. Then is obtained
Further simplifying, the relationship becomes
which is true when and the exponential term reduces to -1. Applying this new condition and squaring both sides, it becomes
where substitutions of the form were made. This leads to the result
and similarly,
It follows that .
Having determined the constraints describing a lossless beam splitter, the initial expression can be rewritten as
Applying different values for the amplitudes and phases can account for many different forms of the beam splitter that can be seen widely used.
The transfer matrix appears to have 6 amplitude and phase parameters, but it also has 2 constraints: and . To include the constraints and simplify to 4 independent parameters, we may write[3] (and from the constraint ), so that
where is the phase difference between the transmitted beams and similarly for , and is a global phase. Lastly using the other constraint that we define so that , hence
A 50:50 beam splitter is produced when . The dielectric beam splitter above, for example, has
i.e. , while the "symmetric" beam splitter of Loudon [2] has
i.e. .
Use in experiments
Beam splitters have been used in both thought experiments and real-world experiments in the area of quantum theory and relativity theory and other fields of physics. These include:
- The Fizeau experiment of 1851 to measure the speeds of light in water
- The Michelson–Morley experiment of 1887 to measure the effect of the (hypothetical) luminiferous aether on the speed of light
- The Hammar experiment of 1935 to refute Dayton Miller's claim of a positive result from repetitions of the Michelson-Morley experiment
- The Kennedy–Thorndike experiment of 1932 to test the independence of the speed of light and the velocity of the measuring apparatus
- Bell test experiments (from ca. 1972) to demonstrate consequences of quantum entanglement and exclude local hidden-variable theories
- Wheeler's delayed choice experiment of 1978, 1984 etc., to test what makes a photon behave as a wave or a particle and when it happens
- The FELIX experiment (proposed in 2000) to test the Penrose interpretation that quantum superposition depends on spacetime curvature
- The Mach–Zehnder interferometer, used in various experiments, including the Elitzur–Vaidman bomb tester involving interaction-free measurement; and in others in the area of quantum computation
Quantum mechanical description
In quantum mechanics, the electric fields are operators as explained by second quantization and Fock states. Each electrical field operator can further be expressed in terms of modes representing the wave behavior and amplitude operators, which are typically represented by the dimensionless creation and annihilation operators. In this theory, the four ports of the beam splitter are represented by a photon number state and the action of a creation operation is . The following is a simplified version of Ref.[3] The relation between the classical field amplitudes , and produced by the beam splitter is translated into the same relation of the corresponding quantum creation (or annihilation) operators , and , so that
where the transfer matrix is given in classical lossless beam splitter section above:
Since is unitary, , i.e.
This is equivalent to saying that if we start from the vacuum state and add a photon in port a to produce
then the beam splitter creates a superposition on the outputs of
The probabilities for the photon to exit at ports c and d are therefore and , as might be expected.
Likewise, for any input state
and the output is
Using the multi-binomial theorem, this can be written
where and the is a binomial coefficient and it is to be understood that the coefficient is zero if etc.
The transmission/reflection coefficient factor in the last equation may be written in terms of the reduced parameters that ensure unitarity:
where it can be seen that if the beam splitter is 50:50 then and the only factor that depends on j is the term. This factor causes interesting interference cancellations. For example, if and the beam splitter is 50:50, then
where the term has cancelled. Therefore the output states always have even numbers of photons in each arm. A famous example of this is the Hong–Ou–Mandel effect, in which the input has , the output is always or , i.e. the probability of output with a photon in each mode (a coincidence event) is zero. Note that this is true for all types of 50:50 beam splitter irrespective of the details of the phases, and the photons need only be indistinguishable. This contrasts with the classical result, in which equal output in both arms for equal inputs on a 50:50 beam splitter does appear for specific beam splitter phases (e.g. a symmetric beam splitter ), and for other phases where the output goes to one arm (e.g. the dielectric beam splitter ) the output is always in the same arm, not random in either arm as is the case here. From the correspondence principle we might expect the quantum results to tend to the classical one in the limits of large n, but the appearance of large numbers of indistinguishable photons at the input is a non-classical state that does not correspond to a classical field pattern, which instead produces a statistical mixture of different known as Poissonian light.
Rigorous derivation is given in the Fearn–Loudon 1987 paper[4] and extended in Ref [3] to include statistical mixtures with the density matrix.
Non-symmetric beam-splitter
In general, for a non-symmetric beam-splitter, namely a beam-splitter for which the transmission and reflection coefficients are not equal, one can define an angle such that
where and are the reflection and transmission coefficients. Then the unitary operation associated with the beam-splitter is then
Application for quantum computing
In 2000 Knill, Laflamme and Milburn (KLM protocol) proved that it is possible to create a universal quantum computer solely with beam splitters, phase shifters, photodetectors and single photon sources. The states that form a qubit in this protocol are the one-photon states of two modes, i.e. the states |01⟩ and |10⟩ in the occupation number representation (Fock state) of two modes. Using these resources it is possible to implement any single qubit gate and 2-qubit probabilistic gates. The beam splitter is an essential component in this scheme since it is the only one that creates entanglement between the Fock states.
Similar settings exist for continuous-variable quantum information processing. In fact, it is possible to simulate arbitrary Gaussian (Bogoliubov) transformations of a quantum state of light by means of beam splitters, phase shifters and photodetectors, given two-mode squeezed vacuum states are available as a prior resource only (this setting hence shares certain similarities with a Gaussian counterpart of the KLM protocol).[5] The building block of this simulation procedure is the fact that a beam splitter is equivalent to a squeezing transformation under partial time reversal.
Diffractive beam splitter
The diffractive beam splitter[6][7]
(also known as multispot beam generator or array beam generator) is a single optical element that divides an input beam into multiple output beams.[8] Each output beam retains the same optical characteristics as the input beam, such as size, polarization and phase. A diffractive beam splitter can generate either a 1-dimensional beam array (1xN) or a 2-dimensional beam matrix (MxN), depending on the diffractive pattern on the element. The diffractive beam splitter is used with monochromatic light such as a laser beam, and is designed for a specific wavelength and angle of separation between output beams.See also
References
https://en.wikipedia.org/wiki/Beam_splitter
https://en.wikipedia.org/wiki/Category:Mirrors
https://en.wikipedia.org/wiki/Ferrofluid_mirror
https://en.wikipedia.org/wiki/Ethylene_glycol
https://en.wikipedia.org/wiki/Colligative_properties
https://en.wikipedia.org/wiki/Grotthuss_mechanism
https://en.wikipedia.org/wiki/Lithium_atom
https://en.wikipedia.org/wiki/Buffer_solution
https://en.wikipedia.org/wiki/Buffer_solution
https://en.wikipedia.org/wiki/Baryon
https://en.wikipedia.org/wiki/Annihilation#Proton-antiproton_annihilation
https://en.wikipedia.org/wiki/Trihydrogen_cation
https://en.wikipedia.org/wiki/Positron_emission
Ice IX is a form of solid water stable at temperatures below 140 K or -133.15 C and pressures between 200 and 400 MPa. It has a tetragonal crystal lattice and a density of 1.16 g/cm3, 26% higher than ordinary ice. It is formed by cooling ice III from 208 K to 165 K (rapidly—to avoid forming ice II). Its structure is identical to ice III other than being completely proton-ordered.[1]
Ordinary water ice is known as ice Ih in the Bridgman nomenclature. Different types of ice, from ice II to ice XIX, have been created in the laboratory at different temperatures and pressures.
Ice in general becomes different kinds of ice based on situation and temperature. Some ice crystals are colder than others. One big difference in the different kinds of ice besides temperature is formation of the ice crystal. Each kind of crystal holds a different shape.
Cultural References
Additionally, a version of Ice IX is introduced in the book Cat's Cradle by Kurt Vonnegut. In the book, Ice IX is a theoretical ice crystal formation that freezes all water it comes into contact with.
See also
- Ice, for other crystalline forms of ice.
References
- La Placa, Sam J.; Hamilton, Walter C.; Kamb, Barclay; Prakash, Anand (1973-01-15). "On a nearly proton‐ordered structure for ice IX". The Journal of Chemical Physics. 58 (2): 567–580. doi:10.1063/1.1679238. ISSN 0021-9606.
- Chaplin, Martin (2007-11-11). "Ice-three and ice-nine structures". Water Structure and Science. Retrieved 2008-01-02.
External links
https://en.wikipedia.org/wiki/Ice_IX
https://en.wikipedia.org/wiki/Diethynylbenzene_dianion
https://en.wikipedia.org/wiki/Nuclear_drip_line#Proton_drip_line
https://en.wikipedia.org/wiki/Aurora
https://en.wikipedia.org/wiki/Magnetosphere
https://en.wikipedia.org/wiki/Halo_nucleus
https://en.wikipedia.org/wiki/Phosphotungstic_acid#Composite_proton_exchange_membranes
https://en.wikipedia.org/wiki/Proton_conductor
https://en.wikipedia.org/wiki/Desiccation
https://en.wikipedia.org/wiki/Decussation
https://en.wikipedia.org/wiki/Compressor
https://en.wikipedia.org/wiki/Category:Patterned_grounds
https://en.wikipedia.org/wiki/Category:Broadcast_engineering
https://en.wikipedia.org/wiki/Linear_timecode
https://en.wikipedia.org/wiki/Loop_recording
https://en.wikipedia.org/wiki/Phosphoric_acid
https://en.wikipedia.org/wiki/Phosphate
Pyrophosphoric acid, also known as diphosphoric acid, is the inorganic compound with the formula H4P2O7 or, more descriptively, [(HO)2P(O)]2O. Colorless and odorless, it is soluble in water, diethyl ether, and ethyl alcohol. The anhydrous acid crystallizes in two polymorphs, which melt at 54.3 and 71.5 °C. The compound is a component of polyphosphoric acid, an important source of phosphoric acid.[1] Anions, salts, and esters of pyrophosphoric acid are called pyrophosphates.
https://en.wikipedia.org/wiki/Pyrophosphoric_acid
https://en.wikipedia.org/wiki/Phosphoryl_chloride
https://en.wikipedia.org/wiki/Phosphorus_pentachloride
https://en.wikipedia.org/wiki/Phosphoryl_fluoride
https://en.wikipedia.org/wiki/Difluorophosphoric_acid
https://en.wikipedia.org/wiki/Difluorophosphate
https://en.wikipedia.org/wiki/Orthosilicate
https://en.wikipedia.org/wiki/Tetraethyl_orthosilicate
https://en.wikipedia.org/wiki/Silicic_acid
https://en.wikipedia.org/wiki/Category:Ethyl_esters
https://en.wikipedia.org/wiki/Seawater
https://en.wikipedia.org/wiki/Ethyl_acetate
https://en.wikipedia.org/wiki/Ethanol
https://en.wikipedia.org/wiki/Autoionization
https://en.wikipedia.org/wiki/Titanium_tetrachloride
https://en.wikipedia.org/wiki/Distillation
https://en.wikipedia.org/wiki/Dry_distillation
https://en.wikipedia.org/wiki/Condensation
https://en.wikipedia.org/wiki/Nanocluster#Atom_clusters
https://en.wikipedia.org/wiki/Isocyanide
https://en.wikipedia.org/wiki/Resonance_(chemistry)
https://en.wikipedia.org/wiki/Carbon_monoxide
https://en.wikipedia.org/wiki/Ligand
https://en.wikipedia.org/wiki/Denticity
https://en.wikipedia.org/wiki/Bridging_ligand
https://en.wikipedia.org/wiki/Three-center_two-electron_bond
https://en.wikipedia.org/wiki/Dihydrogen_complex
https://en.wikipedia.org/wiki/Chlorobis(dppe)iron_hydride
https://en.wikipedia.org/wiki/Sodium_borohydride
https://en.wikipedia.org/wiki/Protic_solvent
https://en.wikipedia.org/wiki/Eutectic_system
Silicon chips are bonded to gold-plated substrates through a silicon-gold eutectic by the application of ultrasonic energy to the chip. See eutectic bonding.
https://en.wikipedia.org/wiki/Eutectic_system
https://en.wikipedia.org/wiki/Amorphous_metal
https://en.wikipedia.org/wiki/Category:Dehydrating_agents
https://en.wikipedia.org/wiki/Cyanuric_chloride
https://en.wikipedia.org/wiki/1,3,5-Triazine
https://en.wikipedia.org/wiki/Trimer_(chemistry)
https://en.wikipedia.org/wiki/Cyanuric_bromide
https://en.wikipedia.org/wiki/Hydrogen_bromide
https://en.wikipedia.org/wiki/Triple_point
https://en.wikipedia.org/wiki/Tritium
https://en.wikipedia.org/wiki/Implosion
The proton–proton chain, also commonly referred to as the p–p chain, is one of two known sets of nuclear fusion reactions by which stars convert hydrogen to helium. It dominates in stars with masses less than or equal to that of the Sun,[2] whereas the CNO cycle, the other known reaction, is suggested by theoretical models to dominate in stars with masses greater than about 1.3 times that of the Sun.[3]
In general, proton–proton fusion can occur only if the kinetic energy (i.e. temperature) of the protons is high enough to overcome their mutual electrostatic repulsion.[4]
In the Sun, deuteron-producing events are rare. Diprotons are the much more common result of proton–proton reactions within the star, and diprotons almost immediately decay back into two protons. Since the conversion of hydrogen to helium is slow, the complete conversion of the hydrogen initially in the core of the Sun is calculated to take more than ten billion years.[5]
Although sometimes called the "proton–proton chain reaction", it is not a chain reaction in the normal sense. In most nuclear reactions, a chain reaction designates a reaction that produces a product, such as neutrons given off during fission, that quickly induces another such reaction. The proton–proton chain is, like a decay chain, a series of reactions. The product of one reaction is the starting material of the next reaction. There are two main chains leading from hydrogen to helium in the Sun. One chain has five reactions, the other chain has six.
History of the theory
The theory that proton–proton reactions are the basic principle by which the Sun and other stars burn was advocated by Arthur Eddington in the 1920s. At the time, the temperature of the Sun was considered to be too low to overcome the Coulomb barrier. After the development of quantum mechanics, it was discovered that tunneling of the wavefunctions of the protons through the repulsive barrier allows for fusion at a lower temperature than the classical prediction.
In 1939, Hans Bethe attempted to calculate the rates of various reactions in stars. Starting with two protons combining to give a deuterium nucleus and a positron he found what we now call Branch II of the proton–proton chain. But he did not consider the reaction of two 3
He nuclei (Branch I) which we now know to be important.[6] This was part of the body of work in stellar nucleosynthesis for which Bethe won the Nobel Prize in Physics in 1967.
The proton–proton chain
The first step in all the branches is the fusion of two protons into a deuteron. As the protons fuse, one of them undergoes beta plus decay, converting into a neutron by emitting a positron and an electron neutrino[7] (though a small amount of deuterium nuclei is produced by the "pep" reaction, see below):
The positron will annihilate with an electron from the environment into two gamma rays. Including this annihilation and the energy of the neutrino, the net reaction
(which is the same as the PEP reaction, see below) has a Q value (released energy) of 1.442 MeV:[7] The relative amounts of energy going to the neutrino and to the other products is variable.
This is the rate-limiting reaction and is extremely slow due to it being initiated by the weak nuclear force. The average proton in the core of the Sun waits 9 billion years before it successfully fuses with another proton. It has not been possible to measure the cross-section of this reaction experimentally because it is so low[8] but it can be calculated from theory.[1]
After it is formed, the deuteron produced in the first stage can fuse with another proton to produce the light isotope of helium, 3
He
:
This process, mediated by the strong nuclear force rather than the weak force, is extremely fast by comparison to the first step. It is estimated that, under the conditions in the Sun's core, each newly created deuterium nucleus exists for only about one second before it is converted into helium-3.[1]
In the Sun, each helium-3 nucleus produced in these reactions
exists for only about 400 years before it is converted into helium-4.[9] Once the helium-3 has been produced, there are four possible paths to generate 4
He
. In p–p I, helium-4 is produced by fusing two helium-3 nuclei; the p–p II and p–p III branches fuse 3
He
with pre-existing 4
He
to form beryllium-7, which undergoes further reactions to produce two helium-4 nuclei.
About 99% of the energy output of the sun comes from the various p–p chains, with the other 1% coming from the CNO cycle. According to one model of the sun, 83.3 percent of the 4
He
produced by the various p–p branches is produced via branch I while p–p II produces 16.68 percent and p–p III 0.02 percent.[1]
Since half the neutrinos produced in branches II and III are produced
in the first step (synthesis of a deuteron), only about 8.35 percent of
neutrinos come from the later steps (see below), and about 91.65 percent
are from deuteron synthesis. However, another solar model from around
the same time gives only 7.14 percent of neutrinos from the later steps
and 92.86 percent from the synthesis of deuterium nuclei.[10] The difference is apparently due to slightly different assumptions about the composition and metallicity of the sun.
There is also the extremely rare p–p IV branch. Other even rarer reactions may occur. The rate of these reactions is very low due to very small cross-sections, or because the number of reacting particles is so low that any reactions that might happen are statistically insignificant.
The overall reaction is:
- 4 1H+ + 2 e- → 4He2+ + 2 νe
releasing 26.73 MeV of energy, some of which is lost to the neutrinos.
The p–p I branch
The complete chain releases a net energy of 26.732 MeV[11] but 2.2 percent of this energy (0.59 MeV) is lost to the neutrinos that are produced.[12]
The p–p I branch is dominant at temperatures of 10 to 18 MK.[13]
Below 10 MK, the p–p chain proceeds at slow rate, resulting in a low production of 4
He
.[14]
The p–p II branch
3
2He
+ 4
2He
→ 7
4Be+
γ
+ 1.59 MeV 7
4Be
+
e−
→ 7
3Li+
ν
e+ 0.861 MeV / 0.383 MeV 7
3Li
+ 1
1H
→ 24
2He
+ 17.35 MeV
The p–p II branch is dominant at temperatures of 18 to 25 MK.[13]
Note that the energies in the second reaction above are the
energies of the neutrinos that are produced by the reaction. 90 percent
of the neutrinos produced in the reaction of 7
Be
to 7
Li
carry an energy of 0.861 MeV, while the remaining 10 percent carry 0.383 MeV. The difference is whether the lithium-7 produced is in the ground state or an excited (metastable) state, respectively. The total energy released going from 7
Be to stable 7
Li is about 0.862 MeV, almost all of which is lost to the neutrino if the decay goes directly to the stable lithium.
The p–p III branch
The last three stages of this chain, plus the positron annihilation, contribute a total of 18.209 MeV, though much of this is lost to the neutrino.
The p–p III chain is dominant if the temperature exceeds 25 MK.[13]
The p–p III chain is not a major source of energy in the Sun, but it was very important in the solar neutrino problem because it generates very high energy neutrinos (up to 14.06 MeV).
The p–p IV (Hep) branch
This reaction is predicted theoretically, but it has never been observed due to its rarity (about 0.3 ppm in the Sun). In this reaction, helium-3 captures a proton directly to give helium-4, with an even higher possible neutrino energy (up to 18.8 MeV[citation needed]).
The mass–energy relationship gives 19.795 MeV for the energy released by this reaction plus the ensuing annihilation, some of which is lost to the neutrino.
Energy release
Comparing the mass of the final helium-4 atom with the masses of the four protons reveals that 0.7 percent of the mass of the original protons has been lost. This mass has been converted into energy, in the form of kinetic energy of produced particles, gamma rays, and neutrinos released during each of the individual reactions. The total energy yield of one whole chain is 26.73 MeV.
Energy released as gamma rays will interact with electrons and
protons and heat the interior of the Sun. Also kinetic energy of fusion
products (e.g. of the two protons and the 4
2He
from the p–p I reaction) adds energy to the plasma in the Sun. This heating keeps the core of the Sun hot and prevents it from collapsing under its own weight as it would if the sun were to cool down.
Neutrinos do not interact significantly with matter and therefore do not heat the interior and thereby help support the Sun against gravitational collapse. Their energy is lost: the neutrinos in the p–p I, p–p II, and p–p III chains carry away 2.0%, 4.0%, and 28.3% of the energy in those reactions, respectively.[15]
The following table calculates the amount of energy lost to neutrinos and the amount of "solar luminosity" coming from the three branches. "Luminosity" here means the amount of energy given off by the Sun as electromagnetic radiation rather than as neutrinos. The starting figures used are the ones mentioned higher in this article. The table concerns only the 99% of the power and neutrinos that come from the p–p reactions, not the 1% coming from the CNO cycle.
| Branch | Percent of helium-4 produced | Percent loss due to neutrino production | Relative amount of energy lost | Relative amount of luminosity produced | Percentage of total luminosity |
|---|---|---|---|---|---|
| Branch I | 83.3 | 2 | 1.67 | 81.6 | 83.6 |
| Branch II | 16.68 | 4 | 0.67 | 16.0 | 16.4 |
| Branch III | 0.02 | 28.3 | 0.0057 | 0.014 | 0.015 |
| Total | 100 | 2.34 | 97.7 | 100 |
The PEP reaction
A deuteron can also be produced by the rare pep (proton–electron–proton) reaction (electron capture):
In the Sun, the frequency ratio of the pep reaction versus the p–p reaction is 1:400. However, the neutrinos released by the pep reaction are far more energetic: while neutrinos produced in the first step of the p–p reaction range in energy up to 0.42 MeV, the pep reaction produces sharp-energy-line neutrinos of 1.44 MeV. Detection of solar neutrinos from this reaction were reported by the Borexino collaboration in 2012.[16]
Both the pep and p–p reactions can be seen as two different Feynman representations of the same basic interaction, where the electron passes to the right side of the reaction as a positron. This is represented in the figure of proton–proton and electron-capture reactions in a star, available at the NDM'06 web site.[17]
See also
References
- Int'l Conference on Neutrino and Dark Matter, 7 Sept 2006, Session 14.
External links
 Media related to Proton-proton chain reaction at Wikimedia Commons
Media related to Proton-proton chain reaction at Wikimedia Commons
https://en.wikipedia.org/wiki/Proton%E2%80%93proton_chain
https://en.wikipedia.org/wiki/Nucleon_magnetic_moment
https://en.wikipedia.org/wiki/Coulomb%27s_law
The nucleon magnetic moments are the intrinsic magnetic dipole moments of the proton and neutron, symbols μp and μn. The nucleus of atoms comprises protons and neutrons, both nucleons that behave as small magnets. Their magnetic strengths are measured by their magnetic moments. The nucleons interact with normal matter through either the nuclear force or their magnetic moments, with the charged proton also interacting by the Coulomb force.
The proton's magnetic moment, surprisingly large, was directly measured in 1933, while the neutron was determined to have a magnetic moment by indirect methods in the mid 1930s. Luis Alvarez and Felix Bloch made the first accurate, direct measurement of the neutron's magnetic moment in 1940. The proton's magnetic moment is exploited to make measurements of molecules by proton nuclear magnetic resonance. The neutron's magnetic moment is exploited to probe the atomic structure of materials using scattering methods and to manipulate the properties of neutron beams in particle accelerators.
The existence of the neutron's magnetic moment and the large value for the proton magnetic moment indicate the nucleons are not elementary particles. For an elementary particle to have an intrinsic magnetic moment, it must have both spin and electric charge. The nucleons have spin-1/2 ħ, but the neutron has no net charge. Their magnetic moments were puzzling and defied a valid explanation until the quark model for hadron particles was developed in the 1960s. The nucleons are composed of three quarks, and the magnetic moments of these elementary particles combine to give the nucleons their magnetic moments.
https://en.wikipedia.org/wiki/Nucleon_magnetic_moment
https://en.wikipedia.org/wiki/Magnets
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, steel, nickel, cobalt, etc. and attracts or repels other magnets.
A permanent magnet is an object made from a material that is magnetized and creates its own persistent magnetic field. An everyday example is a refrigerator magnet used to hold notes on a refrigerator door. Materials that can be magnetized, which are also the ones that are strongly attracted to a magnet, are called ferromagnetic (or ferrimagnetic). These include the elements iron, nickel and cobalt and their alloys, some alloys of rare-earth metals, and some naturally occurring minerals such as lodestone. Although ferromagnetic (and ferrimagnetic) materials are the only ones attracted to a magnet strongly enough to be commonly considered magnetic, all other substances respond weakly to a magnetic field, by one of several other types of magnetism.
Ferromagnetic materials can be divided into magnetically "soft" materials like annealed iron, which can be magnetized but do not tend to stay magnetized, and magnetically "hard" materials, which do. Permanent magnets are made from "hard" ferromagnetic materials such as alnico and ferrite that are subjected to special processing in a strong magnetic field during manufacture to align their internal microcrystalline structure, making them very hard to demagnetize. To demagnetize a saturated magnet, a certain magnetic field must be applied, and this threshold depends on coercivity of the respective material. "Hard" materials have high coercivity, whereas "soft" materials have low coercivity. The overall strength of a magnet is measured by its magnetic moment or, alternatively, the total magnetic flux it produces. The local strength of magnetism in a material is measured by its magnetization.
An electromagnet is made from a coil of wire that acts as a magnet when an electric current passes through it but stops being a magnet when the current stops. Often, the coil is wrapped around a core of "soft" ferromagnetic material such as mild steel, which greatly enhances the magnetic field produced by the coil.
Discovery and development
Ancient people learned about magnetism from lodestones (or magnetite) which are naturally magnetized pieces of iron ore. The word magnet was adopted in Middle English from Latin magnetum "lodestone", ultimately from Greek μαγνῆτις [λίθος] (magnētis [lithos])[1] meaning "[stone] from Magnesia",[2] a place in Anatolia where lodestones were found (today Manisa in modern-day Turkey). Lodestones, suspended so they could turn, were the first magnetic compasses. The earliest known surviving descriptions of magnets and their properties are from Anatolia, India, and China around 2500 years ago.[3][4][5] The properties of lodestones and their affinity for iron were written of by Pliny the Elder in his encyclopedia Naturalis Historia.[6]
In the 11th century in China, it was discovered that quenching red hot iron in the Earth's magnetic field would leave the iron permanently magnetized. This led to the development of the navigational compass, as described in Dream Pool Essays in 1088.[7][8] By the 12th to 13th centuries AD, magnetic compasses were used in navigation in China, Europe, the Arabian Peninsula and elsewhere.[9]
A straight iron magnet tends to demagnetize itself by its own magnetic field. To overcome this, the horseshoe magnet was invented by Daniel Bernoulli in 1743.[7][10] A horseshoe magnet avoids demagnetization by returning the magnetic field lines to the opposite pole.[11]
In 1820, Hans Christian Ørsted discovered that a compass needle is deflected by a nearby electric current. In the same year André-Marie Ampère showed that iron can be magnetized by inserting it in an electrically fed solenoid. This led William Sturgeon to develop an iron-cored electromagnet in 1824.[7] Joseph Henry further developed the electromagnet into a commercial product in 1830–1831, giving people access to strong magnetic fields for the first time. In 1831 he built an ore separator with an electromagnet capable of lifting 750 pounds (340 kg).[12]
Physics
Magnetic field
The magnetic flux density (also called magnetic B field or just magnetic field, usually denoted B) is a vector field. The magnetic B field vector at a given point in space is specified by two properties:
- Its direction, which is along the orientation of a compass needle.
- Its magnitude (also called strength), which is proportional to how strongly the compass needle orients along that direction.
In SI units, the strength of the magnetic B field is given in teslas.[13]
Magnetic moment
A magnet's magnetic moment (also called magnetic dipole moment and usually denoted μ) is a vector that characterizes the magnet's overall magnetic properties. For a bar magnet, the direction of the magnetic moment points from the magnet's south pole to its north pole,[14] and the magnitude relates to how strong and how far apart these poles are. In SI units, the magnetic moment is specified in terms of A·m2 (amperes times meters squared).
A magnet both produces its own magnetic field and responds to magnetic fields. The strength of the magnetic field it produces is at any given point proportional to the magnitude of its magnetic moment. In addition, when the magnet is put into an external magnetic field, produced by a different source, it is subject to a torque tending to orient the magnetic moment parallel to the field.[15] The amount of this torque is proportional both to the magnetic moment and the external field. A magnet may also be subject to a force driving it in one direction or another, according to the positions and orientations of the magnet and source. If the field is uniform in space, the magnet is subject to no net force, although it is subject to a torque.[16]
A wire in the shape of a circle with area A and carrying current I has a magnetic moment of magnitude equal to IA.
Magnetization
The magnetization of a magnetized material is the local value of its magnetic moment per unit volume, usually denoted M, with units A/m.[17] It is a vector field, rather than just a vector (like the magnetic moment), because different areas in a magnet can be magnetized with different directions and strengths (for example, because of domains, see below). A good bar magnet may have a magnetic moment of magnitude 0.1 A·m2 and a volume of 1 cm3, or 1×10−6 m3, and therefore an average magnetization magnitude is 100,000 A/m. Iron can have a magnetization of around a million amperes per meter. Such a large value explains why iron magnets are so effective at producing magnetic fields.
Modelling magnets
Two different models exist for magnets: magnetic poles and atomic currents.
Although for many purposes it is convenient to think of a magnet as having distinct north and south magnetic poles, the concept of poles should not be taken literally: it is merely a way of referring to the two different ends of a magnet. The magnet does not have distinct north or south particles on opposing sides. If a bar magnet is broken into two pieces, in an attempt to separate the north and south poles, the result will be two bar magnets, each of which has both a north and south pole. However, a version of the magnetic-pole approach is used by professional magneticians to design permanent magnets.[citation needed]
In this approach, the divergence of the magnetization ∇·M inside a magnet is treated as a distribution of magnetic monopoles. This is a mathematical convenience and does not imply that there are actually monopoles in the magnet. If the magnetic-pole distribution is known, then the pole model gives the magnetic field H. Outside the magnet, the field B is proportional to H, while inside the magnetization must be added to H. An extension of this method that allows for internal magnetic charges is used in theories of ferromagnetism.
Another model is the Ampère model, where all magnetization is due to the effect of microscopic, or atomic, circular bound currents, also called Ampèrian currents, throughout the material. For a uniformly magnetized cylindrical bar magnet, the net effect of the microscopic bound currents is to make the magnet behave as if there is a macroscopic sheet of electric current flowing around the surface, with local flow direction normal to the cylinder axis.[18] Microscopic currents in atoms inside the material are generally canceled by currents in neighboring atoms, so only the surface makes a net contribution; shaving off the outer layer of a magnet will not destroy its magnetic field, but will leave a new surface of uncancelled currents from the circular currents throughout the material.[19] The right-hand rule tells which direction positively-charged current flows. However, current due to negatively-charged electricity is far more prevalent in practice.[citation needed]
Polarity
The north pole of a magnet is defined as the pole that, when the magnet is freely suspended, points towards the Earth's North Magnetic Pole in the Arctic (the magnetic and geographic poles do not coincide, see magnetic declination). Since opposite poles (north and south) attract, the North Magnetic Pole is actually the south pole of the Earth's magnetic field.[20][21][22][23] As a practical matter, to tell which pole of a magnet is north and which is south, it is not necessary to use the Earth's magnetic field at all. For example, one method would be to compare it to an electromagnet, whose poles can be identified by the right-hand rule. The magnetic field lines of a magnet are considered by convention to emerge from the magnet's north pole and reenter at the south pole.[23]
Magnetic materials
The term magnet is typically reserved for objects that produce their own persistent magnetic field even in the absence of an applied magnetic field. Only certain classes of materials can do this. Most materials, however, produce a magnetic field in response to an applied magnetic field – a phenomenon known as magnetism. There are several types of magnetism, and all materials exhibit at least one of them.
The overall magnetic behavior of a material can vary widely, depending on the structure of the material, particularly on its electron configuration. Several forms of magnetic behavior have been observed in different materials, including:
- Ferromagnetic and ferrimagnetic materials are the ones normally thought of as magnetic; they are attracted to a magnet strongly enough that the attraction can be felt. These materials are the only ones that can retain magnetization and become magnets; a common example is a traditional refrigerator magnet. Ferrimagnetic materials, which include ferrites and the longest used and naturally occurring magnetic materials magnetite and lodestone, are similar to but weaker than ferromagnetics. The difference between ferro- and ferrimagnetic materials is related to their microscopic structure, as explained in Magnetism.
- Paramagnetic substances, such as platinum, aluminum, and oxygen, are weakly attracted to either pole of a magnet. This attraction is hundreds of thousands of times weaker than that of ferromagnetic materials, so it can only be detected by using sensitive instruments or using extremely strong magnets. Magnetic ferrofluids, although they are made of tiny ferromagnetic particles suspended in liquid, are sometimes considered paramagnetic since they cannot be magnetized.
- Diamagnetic means repelled by both poles. Compared to paramagnetic and ferromagnetic substances, diamagnetic substances, such as carbon, copper, water, and plastic, are even more weakly repelled by a magnet. The permeability of diamagnetic materials is less than the permeability of a vacuum. All substances not possessing one of the other types of magnetism are diamagnetic; this includes most substances. Although force on a diamagnetic object from an ordinary magnet is far too weak to be felt, using extremely strong superconducting magnets, diamagnetic objects such as pieces of lead and even mice[24] can be levitated, so they float in mid-air. Superconductors repel magnetic fields from their interior and are strongly diamagnetic.
There are various other types of magnetism, such as spin glass, superparamagnetism, superdiamagnetism, and metamagnetism.
Common uses
- Magnetic recording media: VHS tapes contain a reel of magnetic tape. The information that makes up the video and sound is encoded on the magnetic coating on the tape. Common audio cassettes also rely on magnetic tape. Similarly, in computers, floppy disks and hard disks record data on a thin magnetic coating.[25]
- Credit, debit, and automatic teller machine cards: All of these cards have a magnetic strip on one side. This strip encodes the information to contact an individual's financial institution and connect with their account(s).[26]
- Older types of televisions (non flat screen) and older large computer monitors: TV and computer screens containing a cathode ray tube employ an electromagnet to guide electrons to the screen.[27]
- Speakers and microphones: Most speakers employ a permanent magnet and a current-carrying coil to convert electric energy (the signal) into mechanical energy (movement that creates the sound). The coil is wrapped around a bobbin attached to the speaker cone and carries the signal as changing current that interacts with the field of the permanent magnet. The voice coil feels a magnetic force and in response, moves the cone and pressurizes the neighboring air, thus generating sound. Dynamic microphones employ the same concept, but in reverse. A microphone has a diaphragm or membrane attached to a coil of wire. The coil rests inside a specially shaped magnet. When sound vibrates the membrane, the coil is vibrated as well. As the coil moves through the magnetic field, a voltage is induced across the coil. This voltage drives a current in the wire that is characteristic of the original sound.
- Electric guitars use magnetic pickups to transduce the vibration of guitar strings into electric current that can then be amplified. This is different from the principle behind the speaker and dynamic microphone because the vibrations are sensed directly by the magnet, and a diaphragm is not employed. The Hammond organ used a similar principle, with rotating tonewheels instead of strings.
- Electric motors and generators: Some electric motors rely upon a combination of an electromagnet and a permanent magnet, and, much like loudspeakers, they convert electric energy into mechanical energy. A generator is the reverse: it converts mechanical energy into electric energy by moving a conductor through a magnetic field.
- Medicine: Hospitals use magnetic resonance imaging to spot problems in a patient's organs without invasive surgery.
- Chemistry: Chemists use nuclear magnetic resonance to characterize synthesized compounds.
- Chucks are used in the metalworking field to hold objects. Magnets are also used in other types of fastening devices, such as the magnetic base, the magnetic clamp and the refrigerator magnet.
- Compasses: A compass (or mariner's compass) is a magnetized pointer free to align itself with a magnetic field, most commonly Earth's magnetic field.
- Art: Vinyl magnet sheets may be attached to paintings, photographs, and other ornamental articles, allowing them to be attached to refrigerators and other metal surfaces. Objects and paint can be applied directly to the magnet surface to create collage pieces of art. Metal magnetic boards, strips, doors, microwave ovens, dishwashers, cars, metal I beams, and any metal surface can be used magnetic vinyl art.
- Science projects: Many topic questions are based on magnets, including the repulsion of current-carrying wires, the effect of temperature, and motors involving magnets.[28]
- Toys: Given their ability to counteract the force of gravity at close range, magnets are often employed in children's toys, such as the Magnet Space Wheel and Levitron, to amusing effect.
- Refrigerator magnets are used to adorn kitchens, as a souvenir, or simply to hold a note or photo to the refrigerator door.
- Magnets can be used to make jewelry. Necklaces and bracelets can have a magnetic clasp, or may be constructed entirely from a linked series of magnets and ferrous beads.
- Magnets can pick up magnetic items (iron nails, staples, tacks, paper clips) that are either too small, too hard to reach, or too thin for fingers to hold. Some screwdrivers are magnetized for this purpose.
- Magnets can be used in scrap and salvage operations to separate magnetic metals (iron, cobalt, and nickel) from non-magnetic metals (aluminum, non-ferrous alloys, etc.). The same idea can be used in the so-called "magnet test", in which a car chassis is inspected with a magnet to detect areas repaired using fiberglass or plastic putty.
- Magnets are found in process industries, food manufacturing especially, in order to remove metal foreign bodies from materials entering the process (raw materials) or to detect a possible contamination at the end of the process and prior to packaging. They constitute an important layer of protection for the process equipment and for the final consumer.[29]
- Magnetic levitation transport, or maglev, is a form of transportation that suspends, guides and propels vehicles (especially trains) through electromagnetic force. Eliminating rolling resistance increases efficiency. The maximum recorded speed of a maglev train is 581 kilometers per hour (361 mph).
- Magnets may be used to serve as a fail-safe device for some cable connections. For example, the power cords of some laptops are magnetic to prevent accidental damage to the port when tripped over. The MagSafe power connection to the Apple MacBook is one such example.
Medical issues and safety
Because human tissues have a very low level of susceptibility to static magnetic fields, there is little mainstream scientific evidence showing a health effect associated with exposure to static fields. Dynamic magnetic fields may be a different issue, however; correlations between electromagnetic radiation and cancer rates have been postulated due to demographic correlations (see Electromagnetic radiation and health).
If a ferromagnetic foreign body is present in human tissue, an external magnetic field interacting with it can pose a serious safety risk.[30]
A different type of indirect magnetic health risk exists involving pacemakers. If a pacemaker has been embedded in a patient's chest (usually for the purpose of monitoring and regulating the heart for steady electrically induced beats), care should be taken to keep it away from magnetic fields. It is for this reason that a patient with the device installed cannot be tested with the use of a magnetic resonance imaging device.
Children sometimes swallow small magnets from toys, and this can be hazardous if two or more magnets are swallowed, as the magnets can pinch or puncture internal tissues.[31]
Magnetic imaging devices (e.g. MRIs) generate enormous magnetic fields, and therefore rooms intended to hold them exclude ferrous metals. Bringing objects made of ferrous metals (such as oxygen canisters) into such a room creates a severe safety risk, as those objects may be powerfully thrown about by the intense magnetic fields.
Magnetizing ferromagnets
Ferromagnetic materials can be magnetized in the following ways:
- Heating the object higher than its Curie temperature, allowing it to cool in a magnetic field and hammering it as it cools. This is the most effective method and is similar to the industrial processes used to create permanent magnets.
- Placing the item in an external magnetic field will result in the item retaining some of the magnetism on removal. Vibration has been shown to increase the effect. Ferrous materials aligned with the Earth's magnetic field that are subject to vibration (e.g., frame of a conveyor) have been shown to acquire significant residual magnetism. Likewise, striking a steel nail held by fingers in a N-S direction with a hammer will temporarily magnetize the nail.
- Stroking: An existing magnet is moved from one end of the item to the other repeatedly in the same direction (single touch method) or two magnets are moved outwards from the center of a third (double touch method).[32]
- Electric Current: The magnetic field produced by passing an electric current through a coil can get domains to line up. Once all of the domains are lined up, increasing the current will not increase the magnetization.[33]
Demagnetizing ferromagnets
Magnetized ferromagnetic materials can be demagnetized (or degaussed) in the following ways:
- Heating a magnet past its Curie temperature; the molecular motion destroys the alignment of the magnetic domains. This always removes all magnetization.
- Placing the magnet in an alternating magnetic field with intensity above the material's coercivity and then either slowly drawing the magnet out or slowly decreasing the magnetic field to zero. This is the principle used in commercial demagnetizers to demagnetize tools, erase credit cards, hard disks, and degaussing coils used to demagnetize CRTs.
- Some demagnetization or reverse magnetization will occur if any part of the magnet is subjected to a reverse field above the magnetic material's coercivity.
- Demagnetization progressively occurs if the magnet is subjected to cyclic fields sufficient to move the magnet away from the linear part on the second quadrant of the B–H curve of the magnetic material (the demagnetization curve).
- Hammering or jarring: mechanical disturbance tends to randomize the magnetic domains and reduce magnetization of an object, but may cause unacceptable damage.
Types of permanent magnets
Magnetic metallic elements
Many materials have unpaired electron spins, and the majority of these materials are paramagnetic. When the spins interact with each other in such a way that the spins align spontaneously, the materials are called ferromagnetic (what is often loosely termed as magnetic). Because of the way their regular crystalline atomic structure causes their spins to interact, some metals are ferromagnetic when found in their natural states, as ores. These include iron ore (magnetite or lodestone), cobalt and nickel, as well as the rare earth metals gadolinium and dysprosium (when at a very low temperature). Such naturally occurring ferromagnets were used in the first experiments with magnetism. Technology has since expanded the availability of magnetic materials to include various man-made products, all based, however, on naturally magnetic elements.
Composites
Ceramic, or ferrite, magnets are made of a sintered composite of powdered iron oxide and barium/strontium carbonate ceramic. Given the low cost of the materials and manufacturing methods, inexpensive magnets (or non-magnetized ferromagnetic cores, for use in electronic components such as portable AM radio antennas) of various shapes can be easily mass-produced. The resulting magnets are non-corroding but brittle and must be treated like other ceramics.
Alnico magnets are made by casting or sintering a combination of aluminium, nickel and cobalt with iron and small amounts of other elements added to enhance the properties of the magnet. Sintering offers superior mechanical characteristics, whereas casting delivers higher magnetic fields and allows for the design of intricate shapes. Alnico magnets resist corrosion and have physical properties more forgiving than ferrite, but not quite as desirable as a metal. Trade names for alloys in this family include: Alni, Alcomax, Hycomax, Columax, and Ticonal.[34]
Injection-molded magnets are a composite of various types of resin and magnetic powders, allowing parts of complex shapes to be manufactured by injection molding. The physical and magnetic properties of the product depend on the raw materials, but are generally lower in magnetic strength and resemble plastics in their physical properties.
Flexible magnet
Flexible magnets are composed of a high-coercivity ferromagnetic compound (usually ferric oxide) mixed with a resinous polymer binder.[35] This is extruded as a sheet and passed over a line of powerful cylindrical permanent magnets. These magnets are arranged in a stack with alternating magnetic poles facing up (N, S, N, S...) on a rotating shaft. This impresses the plastic sheet with the magnetic poles in an alternating line format. No electromagnetism is used to generate the magnets. The pole-to-pole distance is on the order of 5 mm, but varies with manufacturer. These magnets are lower in magnetic strength but can be very flexible, depending on the binder used.[36]
For magnetic compounds (e.g. Nd2Fe14B) that are vulnerable to a grain boundary corrosion problem it gives additional protection.[35]
Rare-earth magnets
Rare earth (lanthanoid) elements have a partially occupied f electron shell (which can accommodate up to 14 electrons). The spin of these electrons can be aligned, resulting in very strong magnetic fields, and therefore, these elements are used in compact high-strength magnets where their higher price is not a concern. The most common types of rare-earth magnets are samarium–cobalt and neodymium–iron–boron (NIB) magnets.
Single-molecule magnets (SMMs) and single-chain magnets (SCMs)
In the 1990s, it was discovered that certain molecules containing paramagnetic metal ions are capable of storing a magnetic moment at very low temperatures. These are very different from conventional magnets that store information at a magnetic domain level and theoretically could provide a far denser storage medium than conventional magnets. In this direction, research on monolayers of SMMs is currently under way. Very briefly, the two main attributes of an SMM are:
- a large ground state spin value (S), which is provided by ferromagnetic or ferrimagnetic coupling between the paramagnetic metal centres
- a negative value of the anisotropy of the zero field splitting (D)
Most SMMs contain manganese but can also be found with vanadium, iron, nickel and cobalt clusters. More recently, it has been found that some chain systems can also display a magnetization that persists for long times at higher temperatures. These systems have been called single-chain magnets.
Nano-structured magnets
Some nano-structured materials exhibit energy waves, called magnons, that coalesce into a common ground state in the manner of a Bose–Einstein condensate.[37][38]
Rare-earth-free permanent magnets
The United States Department of Energy has identified a need to find substitutes for rare-earth metals in permanent-magnet technology, and has begun funding such research. The Advanced Research Projects Agency-Energy (ARPA-E) has sponsored a Rare Earth Alternatives in Critical Technologies (REACT) program to develop alternative materials. In 2011, ARPA-E awarded 31.6 million dollars to fund Rare-Earth Substitute projects.[39]
Costs
The current cheapest permanent magnets, allowing for field strengths, are flexible and ceramic magnets, but these are also among the weakest types. The ferrite magnets are mainly low-cost magnets since they are made from cheap raw materials: iron oxide and Ba- or Sr-carbonate. However, a new low cost magnet, Mn–Al alloy,[35][non-primary source needed][40] has been developed and is now dominating the low-cost magnets field.[citation needed] It has a higher saturation magnetization than the ferrite magnets. It also has more favorable temperature coefficients, although it can be thermally unstable. Neodymium–iron–boron (NIB) magnets are among the strongest. These cost more per kilogram than most other magnetic materials but, owing to their intense field, are smaller and cheaper in many applications.[41]
Temperature
Temperature sensitivity varies, but when a magnet is heated to a temperature known as the Curie point, it loses all of its magnetism, even after cooling below that temperature. The magnets can often be remagnetized, however.
Additionally, some magnets are brittle and can fracture at high temperatures.
The maximum usable temperature is highest for alnico magnets at over 540 °C (1,000 °F), around 300 °C (570 °F) for ferrite and SmCo, about 140 °C (280 °F) for NIB and lower for flexible ceramics, but the exact numbers depend on the grade of material.
Electromagnets
An electromagnet, in its simplest form, is a wire that has been coiled into one or more loops, known as a solenoid. When electric current flows through the wire, a magnetic field is generated. It is concentrated near (and especially inside) the coil, and its field lines are very similar to those of a magnet. The orientation of this effective magnet is determined by the right hand rule. The magnetic moment and the magnetic field of the electromagnet are proportional to the number of loops of wire, to the cross-section of each loop, and to the current passing through the wire.[42]
If the coil of wire is wrapped around a material with no special magnetic properties (e.g., cardboard), it will tend to generate a very weak field. However, if it is wrapped around a soft ferromagnetic material, such as an iron nail, then the net field produced can result in a several hundred- to thousandfold increase of field strength.
Uses for electromagnets include particle accelerators, electric motors, junkyard cranes, and magnetic resonance imaging machines. Some applications involve configurations more than a simple magnetic dipole; for example, quadrupole and sextupole magnets are used to focus particle beams.
Units and calculations
For most engineering applications, MKS (rationalized) or SI (Système International) units are commonly used. Two other sets of units, Gaussian and CGS-EMU, are the same for magnetic properties and are commonly used in physics.[citation needed]
In all units, it is convenient to employ two types of magnetic field, B and H, as well as the magnetization M, defined as the magnetic moment per unit volume.
- The magnetic induction field B is given in SI units of teslas (T). B is the magnetic field whose time variation produces, by Faraday's Law, circulating electric fields (which the power companies sell). B also produces a deflection force on moving charged particles (as in TV tubes). The tesla is equivalent to the magnetic flux (in webers) per unit area (in meters squared), thus giving B the unit of a flux density. In CGS, the unit of B is the gauss (G). One tesla equals 104 G.
- The magnetic field H is given in SI units of ampere-turns per meter (A-turn/m). The turns appear because when H is produced by a current-carrying wire, its value is proportional to the number of turns of that wire. In CGS, the unit of H is the oersted (Oe). One A-turn/m equals 4π×10−3 Oe.
- The magnetization M is given in SI units of amperes per meter (A/m). In CGS, the unit of M is the oersted (Oe). One A/m equals 10−3 emu/cm3. A good permanent magnet can have a magnetization as large as a million amperes per meter.
- In SI units, the relation B = μ0(H + M) holds, where μ0 is the permeability of space, which equals 4π×10−7 T•m/A. In CGS, it is written as B = H + 4πM. (The pole approach gives μ0H in SI units. A μ0M term in SI must then supplement this μ0H to give the correct field within B, the magnet. It will agree with the field B calculated using Ampèrian currents).
Materials that are not permanent magnets usually satisfy the relation M = χH in SI, where χ is the (dimensionless) magnetic susceptibility. Most non-magnetic materials have a relatively small χ (on the order of a millionth), but soft magnets can have χ on the order of hundreds or thousands. For materials satisfying M = χH, we can also write B = μ0(1 + χ)H = μ0μrH = μH, where μr = 1 + χ is the (dimensionless) relative permeability and μ =μ0μr is the magnetic permeability. Both hard and soft magnets have a more complex, history-dependent, behavior described by what are called hysteresis loops, which give either B vs. H or M vs. H. In CGS, M = χH, but χSI = 4πχCGS, and μ = μr.
Caution: in part because there are not enough Roman and Greek symbols, there is no commonly agreed-upon symbol for magnetic pole strength and magnetic moment. The symbol m has been used for both pole strength (unit A•m, where here the upright m is for meter) and for magnetic moment (unit A•m2). The symbol μ has been used in some texts for magnetic permeability and in other texts for magnetic moment. We will use μ for magnetic permeability and m for magnetic moment. For pole strength, we will employ qm. For a bar magnet of cross-section A with uniform magnetization M along its axis, the pole strength is given by qm = MA, so that M can be thought of as a pole strength per unit area.
Fields of a magnet
Far away from a magnet, the magnetic field created by that magnet is almost always described (to a good approximation) by a dipole field characterized by its total magnetic moment. This is true regardless of the shape of the magnet, so long as the magnetic moment is non-zero. One characteristic of a dipole field is that the strength of the field falls off inversely with the cube of the distance from the magnet's center.
Closer to the magnet, the magnetic field becomes more complicated and more dependent on the detailed shape and magnetization of the magnet. Formally, the field can be expressed as a multipole expansion: A dipole field, plus a quadrupole field, plus an octupole field, etc.
At close range, many different fields are possible. For example, for a long, skinny bar magnet with its north pole at one end and south pole at the other, the magnetic field near either end falls off inversely with the square of the distance from that pole.
Calculating the magnetic force
Pull force of a single magnet
The strength of a given magnet is sometimes given in terms of its pull force — its ability to pull ferromagnetic objects.[43] The pull force exerted by either an electromagnet or a permanent magnet with no air gap (i.e., the ferromagnetic object is in direct contact with the pole of the magnet[44]) is given by the Maxwell equation:[45]
- ,
where
- F is force (SI unit: newton)
- A is the cross section of the area of the pole in square meters
- B is the magnetic induction exerted by the magnet
This result can be easily derived using Gilbert model, which assumes that the pole of magnet is charged with magnetic monopoles that induces the same in the ferromagnetic object.
If a magnet is acting vertically, it can lift a mass m in kilograms given by the simple equation:
where g is the gravitational acceleration.
Force between two magnetic poles
Classically, the force between two magnetic poles is given by:[46]
where
- F is force (SI unit: newton)
- qm1 and qm2 are the magnitudes of magnetic poles (SI unit: ampere-meter)
- μ is the permeability of the intervening medium (SI unit: tesla meter per ampere, henry per meter or newton per ampere squared)
- r is the separation (SI unit: meter).
The pole description is useful to the engineers designing real-world magnets, but real magnets have a pole distribution more complex than a single north and south. Therefore, implementation of the pole idea is not simple. In some cases, one of the more complex formulae given below will be more useful.
Force between two nearby magnetized surfaces of area A
The mechanical force between two nearby magnetized surfaces can be calculated with the following equation. The equation is valid only for cases in which the effect of fringing is negligible and the volume of the air gap is much smaller than that of the magnetized material:[47][48]
where:
- A is the area of each surface, in m2
- H is their magnetizing field, in A/m
- μ0 is the permeability of space, which equals 4π×10−7 T•m/A
- B is the flux density, in T.
Force between two bar magnets
The force between two identical cylindrical bar magnets placed end to end at large distance is approximately:[dubious ],[47]
where:
- B0 is the magnetic flux density very close to each pole, in T,
- A is the area of each pole, in m2,
- L is the length of each magnet, in m,
- R is the radius of each magnet, in m, and
- z is the separation between the two magnets, in m.
- relates the flux density at the pole to the magnetization of the magnet.
Note that all these formulations are based on Gilbert's model, which is usable in relatively great distances. In other models (e.g., Ampère's model), a more complicated formulation is used that sometimes cannot be solved analytically. In these cases, numerical methods must be used.
Force between two cylindrical magnets
For two cylindrical magnets with radius and length , with their magnetic dipole aligned, the force can be asymptotically approximated at large distance by,[49]
where is the magnetization of the magnets and is the gap between the magnets. A measurement of the magnetic flux density very close to the magnet is related to approximately by the formula
The effective magnetic dipole can be written as
Where is the volume of the magnet. For a cylinder, this is .
When , the point dipole approximation is obtained,
which matches the expression of the force between two magnetic dipoles.
See also
Notes
- David Vokoun; Marco Beleggia; Ludek Heller; Petr Sittner (2009). "Magnetostatic interactions and forces between cylindrical permanent magnets". Journal of Magnetism and Magnetic Materials. 321 (22): 3758–3763. Bibcode:2009JMMM..321.3758V. doi:10.1016/j.jmmm.2009.07.030.
References
- "The Early History of the Permanent Magnet". Edward Neville Da Costa Andrade, Endeavour, Volume 17, Number 65, January 1958. Contains an excellent description of early methods of producing permanent magnets.
- "positive pole n". The Concise Oxford English Dictionary. Catherine Soanes and Angus Stevenson. Oxford University Press, 2004. Oxford Reference Online. Oxford University Press.
- Wayne M. Saslow, Electricity, Magnetism, and Light, Academic (2002). ISBN 0-12-619455-6. Chapter 9 discusses magnets and their magnetic fields using the concept of magnetic poles, but it also gives evidence that magnetic poles do not really exist in ordinary matter. Chapters 10 and 11, following what appears to be a 19th-century approach, use the pole concept to obtain the laws describing the magnetism of electric currents.
- Edward P. Furlani, Permanent Magnet and Electromechanical Devices:Materials, Analysis and Applications, Academic Press Series in Electromagnetism (2001). ISBN 0-12-269951-3.
External links
- How magnets are made Archived 2013-03-16 at the Wayback Machine (video)
- Floating Ring Magnets, Bulletin of the IAPT, Volume 4, No. 6, 145 (June 2012). (Publication of the Indian Association of Physics Teachers).
- A brief history of electricity and magnetism
https://en.wikipedia.org/wiki/Magnet
https://en.wikipedia.org/wiki/Dipole_magnet
A dipole magnet is the simplest type of magnet. It has two poles, one north and one south. Its magnetic field lines form simple closed loops which emerge from the north pole, re-enter at the south pole, then pass through the body of the magnet. The simplest example of a dipole magnet is a bar magnet.[1]
https://en.wikipedia.org/wiki/Dipole_magnet
A dipole magnet is the simplest type of magnet. It has two poles, one north and one south. Its magnetic field lines form simple closed loops which emerge from the north pole, re-enter at the south pole, then pass through the body of the magnet. The simplest example of a dipole magnet is a bar magnet.[1]
Dipole magnets in accelerators
In particle accelerators, a dipole magnet is the electromagnet used to create a homogeneous magnetic field over some distance. Particle motion in that field will be circular in a plane perpendicular to the field and collinear to the direction of particle motion and free in the direction orthogonal to it. Thus, a particle injected into a dipole magnet will travel on a circular or helical trajectory. By adding several dipole sections on the same plane, the bending radial effect of the beam increases.
In accelerator physics, dipole magnets are used to realize bends in the design trajectory (or 'orbit') of the particles, as in circular accelerators. Other uses include:
- Injection of particles into the accelerator
- Ejection of particles from the accelerator
- Correction of orbit errors
- Production of synchrotron radiation
The force on a charged particle in a particle accelerator from a dipole magnet can be described by the Lorentz force law, where a charged particle experiences a force of
(in SI units). In the case of a particle accelerator dipole magnet, the charged particle beam is bent via the cross product of the particle's velocity and the magnetic field vector, with direction also being dependent on the charge of the particle.
The amount of force that can be applied to a charged particle by a dipole magnet is one of the limiting factors for modern synchrotron and cyclotron proton and ion accelerators. As the energy of the accelerated particles increases, they require more force to change direction and require larger B fields to be steered. Limitations on the amount of B field that can be produced with modern dipole electromagnets require synchrotrons/cyclotrons to increase in size (thus increasing the number of dipole magnets used) to compensate for increases in particle velocity. In the largest modern synchrotron, the Large Hadron Collider, there are 1232 main dipole magnets used for bending the path of the particle beam, each weighing 35 metric tons.[2]
Other uses
Other uses of dipole magnets to deflect moving particles include isotope mass measurement in mass spectrometry, and particle momentum measurement in particle physics.
Such magnets are also used in traditional televisions, which contain a cathode ray tube, which is essentially a small particle accelerator. Their magnets are called deflecting coils. The magnets move a single spot on the screen of the TV tube in a controlled way all over the screen.
See also
- Accelerator physics
- Beam line
- Cyclotron
- Electromagnetism
- Linear particle accelerator
- Particle accelerator
- Quadrupole magnet
- Sextupole magnet
- Multipole magnet
- Storage ring
References
- ["Pulling together: Superconducting electromagnets" CERN; https://home.cern/science/engineering/pulling-together-superconducting-electromagnets]
External links
 Media related to Dipole magnet at Wikimedia Commons
Media related to Dipole magnet at Wikimedia Commons
https://en.wikipedia.org/wiki/Dipole_magnet
https://en.wikipedia.org/wiki/Proton%E2%80%93proton_chain
https://en.wikipedia.org/wiki/Carbon-burning_process
https://en.wikipedia.org/wiki/Hydrostatic_equilibrium
https://en.wikipedia.org/wiki/Proton_nuclear_magnetic_resonance
https://en.wikipedia.org/wiki/Acetone
https://en.wikipedia.org/wiki/Properties_of_water
https://en.wikipedia.org/wiki/Color_of_water
https://en.wikipedia.org/wiki/Scattering
https://en.wikipedia.org/wiki/Diffuse_reflection
https://en.wikipedia.org/wiki/Crystallite
https://en.wikipedia.org/wiki/Single_crystal
https://en.wikipedia.org/wiki/Half-space_(geometry)
https://en.wikipedia.org/wiki/Paracrystallinity
https://en.wikipedia.org/wiki/Grain_boundary
https://en.wikipedia.org/wiki/Misorientation
https://en.wikipedia.org/wiki/Dislocation
https://en.wikipedia.org/wiki/Slip_(materials_science)
In materials science, slip is the large displacement of one part of a crystal relative to another part along crystallographic planes and directions.[1] Slip occurs by the passage of dislocations on close/packed planes, which are planes containing the greatest number of atoms per area and in close-packed directions (most atoms per length). Close-packed planes are known as slip or glide planes. A slip system describes the set of symmetrically identical slip planes and associated family of slip directions for which dislocation motion can easily occur and lead to plastic deformation. The magnitude and direction of slip are represented by the Burgers vector, b.
An external force makes parts of the crystal lattice glide along each other, changing the material's geometry. A critical resolved shear stress is required to initiate a slip.[2]
https://en.wikipedia.org/wiki/Slip_(materials_science)
https://en.wikipedia.org/wiki/Critical_resolved_shear_stress
https://en.wikipedia.org/wiki/Miller_index#Crystallographic_planes_and_directions
https://en.wikipedia.org/wiki/Axis%E2%80%93angle_representation
https://en.wikipedia.org/wiki/Amorphous_solid
https://en.wikipedia.org/wiki/Crystal_structure
https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation
https://en.wikipedia.org/wiki/Electron_microscope
https://en.wikipedia.org/wiki/Scanning_tunneling_microscope
https://en.wikipedia.org/wiki/Absolute_zero
https://en.wikipedia.org/wiki/Proton_spin_crisis
https://en.wikipedia.org/wiki/Neutron%E2%80%93proton_ratio
https://en.wikipedia.org/wiki/Proton_radius_puzzle
https://en.wikipedia.org/wiki/Proton-exchange_membrane_fuel_cell
https://en.wikipedia.org/wiki/Proton-to-electron_mass_ratio
https://en.wikipedia.org/wiki/Proton_ATPase
https://en.wikipedia.org/wiki/Electron_transport_chain#Proton_pumps
https://en.wikipedia.org/wiki/Electrochemical_gradient
https://en.wikipedia.org/wiki/Atomic_number
https://en.wikipedia.org/wiki/Isotopes_of_hydrogen
https://en.wikipedia.org/wiki/Proton_Synchrotron
https://en.wikipedia.org/wiki/Large_Hadron_Collider
https://en.wikipedia.org/wiki/Particle-induced_X-ray_emission
https://en.wikipedia.org/wiki/Proton_(satellite_program)
https://en.wikipedia.org/wiki/Super_Proton%E2%80%93Antiproton_Synchrotron
https://en.wikipedia.org/wiki/Proton_Synchrotron
https://en.wikipedia.org/wiki/Hydronium
https://en.wikipedia.org/wiki/Strong_interaction
https://en.wikipedia.org/wiki/Odderon
https://en.wikipedia.org/wiki/Annihilation#Proton-antiproton_annihilation
https://en.wikipedia.org/wiki/Nucleon_magnetic_moment
https://en.wikipedia.org/wiki/Stellar_structure
https://en.wikipedia.org/wiki/Nuclear_fusion
https://en.wikipedia.org/wiki/Combustion
https://en.wikipedia.org/wiki/Dredge-up
- The third dredge-up
- The third dredge-up occurs after a star enters the asymptotic giant branch, after a flash occurs in a helium-burning shell. The third dredge-up brings helium, carbon, and the s-process products to the surface, increasing the abundance of carbon relative to oxygen; in some larger stars this is the process that turns the star into a carbon star.[2]
https://en.wikipedia.org/wiki/Dredge-up
https://en.wikipedia.org/wiki/Beryllium
https://en.wikipedia.org/wiki/CNO_cycle
https://en.wikipedia.org/wiki/Smoke
https://en.wikipedia.org/wiki/Positron
https://en.wikipedia.org/wiki/Positron_emission
Positron emission, beta plus decay, or β+ decay is a subtype of radioactive decay called beta decay, in which a proton inside a radionuclide nucleus is converted into a neutron while releasing a positron and an electron neutrino (νe).[1] Positron emission is mediated by the weak force. The positron is a type of beta particle (β+), the other beta particle being the electron (β−) emitted from the β− decay of a nucleus.
https://en.wikipedia.org/wiki/Positron_emission
https://en.wikipedia.org/wiki/Radioactive_decay
https://en.wikipedia.org/wiki/Beta_decay
https://en.wikipedia.org/wiki/Radionuclide
https://en.wikipedia.org/wiki/Internal_conversion
https://en.wikipedia.org/wiki/Radionucleotide
https://en.wikipedia.org/wiki/Gamma_ray
https://en.wikipedia.org/wiki/Radio_wave
https://en.wikipedia.org/wiki/Black-body_radiation
https://en.wikipedia.org/wiki/Microwave
https://en.wikipedia.org/wiki/Terahertz_radiation
https://en.wikipedia.org/wiki/Ionosphere
https://en.wikipedia.org/wiki/Ground_wave
https://en.wikipedia.org/wiki/Electromagnetic_radiation
https://en.wikipedia.org/wiki/Far_infrared
https://en.wikipedia.org/wiki/Gauge_boson
https://en.wikipedia.org/wiki/Virtual_particle
https://en.wikipedia.org/wiki/Quantum_vacuum_(disambiguation)
https://en.wikipedia.org/wiki/Antiparticle
https://en.wikipedia.org/wiki/Uncertainty_principle
https://en.wikipedia.org/wiki/Gauge_boson
https://en.wikipedia.org/wiki/Initial_condition
https://en.wikipedia.org/wiki/S-matrix
https://en.wikipedia.org/wiki/Perturbation_theory_(quantum_mechanics)
https://en.wikipedia.org/wiki/Electromagnetism#repel
https://en.wikipedia.org/wiki/Graviton
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Gauge_theory
https://en.wikipedia.org/wiki/Higgs_mechanism
https://en.wikipedia.org/wiki/1964_PRL_symmetry_breaking_papers
https://en.wikipedia.org/wiki/Glueball
https://en.wikipedia.org/wiki/Cosmic_microwave_background
The cosmic microwave background (CMB, CMBR) is microwave radiation that fills all space. It is a remnant that provides an important source of data on the primordial universe.[1] With a standard optical telescope, the background space between stars and galaxies is almost completely dark. However, a sufficiently sensitive radio telescope detects a faint background glow that is almost uniform and is not associated with any star, galaxy, or other object. This glow is strongest in the microwave region of the radio spectrum. The accidental discovery of the CMB in 1965 by American radio astronomers Arno Penzias and Robert Wilson was the culmination of work initiated in the 1940s.[2][3]
CMB is landmark evidence of the Big Bang theory for the origin of the universe. In the Big Bang cosmological models, during the earliest periods, the universe was filled with an opaque fog of dense, hot plasma of sub-atomic particles. As the universe expanded, this plasma cooled to the point where protons and electrons combined to form neutral atoms of mostly hydrogen. Unlike the plasma, these atoms could not scatter thermal radiation by Thomson scattering, and so the universe became transparent.[4] Known as the recombination epoch, this decoupling event released photons to travel freely through space – sometimes referred to as relic radiation.[1] However, the photons have grown less energetic, since the expansion of space causes their wavelength to increase. The surface of last scattering refers to a shell at the right distance in space so photons are now received that were originally emitted at the time of decoupling.
The CMB is not completely smooth and uniform, showing a faint anisotropy that can be mapped by sensitive detectors. Ground and space-based experiments such as COBE and WMAP have been used to measure these temperature inhomogeneties. The anisotropy structure is determined by various interactions of matter and photons up to the point of decoupling, which results in a characteristic lumpy pattern that varies with angular scale. The distribution of the anisotropy across the sky has frequency components that can be represented by a power spectrum displaying a sequence of peaks and valleys. The peak values of this spectrum hold important information about the physical properties of the early universe: the first peak determines the overall curvature of the universe, while the second and third peak detail the density of normal matter and so-called dark matter, respectively. Extracting fine details from the CMB data can be challenging, since the emission has undergone modification by foreground features such as galaxy clusters.
Importance of precise measurement
Precise measurements of the CMB are critical to cosmology, since any proposed model of the universe must explain this radiation. The CMB has a thermal black body spectrum at a temperature of 2.72548±0.00057 K.[5] The spectral radiance dEν/dν peaks at 160.23 GHz, in the microwave range of frequencies, corresponding to a photon energy of about 6.626×10−4 eV. Alternatively, if spectral radiance is defined as dEλ/dλ, then the peak wavelength is 1.063 mm (282 GHz, 1.168×10−3 eV photons). The glow is very nearly uniform in all directions, but the tiny residual variations show a very specific pattern, the same as that expected of a fairly uniformly distributed hot gas that has expanded to the current size of the universe. In particular, the spectral radiance at different angles of observation in the sky contains small anisotropies, or irregularities, which vary with the size of the region examined. They have been measured in detail, and match what would be expected if small thermal variations, generated by quantum fluctuations of matter in a very tiny space, had expanded to the size of the observable universe we see today. This is a very active field of study, with scientists seeking both better data (for example, the Planck spacecraft) and better interpretations of the initial conditions of expansion. Although many different processes might produce the general form of a black body spectrum, no model other than the Big Bang has yet explained the fluctuations. As a result, most cosmologists consider the Big Bang model of the universe to be the best explanation for the CMB.
The high degree of uniformity throughout the observable universe and its faint but measured anisotropy lend strong support for the Big Bang model in general and the ΛCDM ("Lambda Cold Dark Matter") model in particular. Moreover, the fluctuations are coherent on angular scales that are larger than the apparent cosmological horizon at recombination. Either such coherence is acausally fine-tuned, or cosmic inflation occurred.[6][7]
Other than the temperature and polarization anisotropy, the CMB frequency spectrum is expected to feature tiny departures from the black-body law known as spectral distortions. These are also at the focus of an active research effort with the hope of a first measurement within the forthcoming decades, as they contain a wealth of information about the primordial universe and the formation of structures at late time.[8]
Features
The cosmic microwave background radiation is an emission of uniform, black body thermal energy coming from all parts of the sky. The radiation is isotropic to roughly one part in 100,000: the root mean square variations are only 18 μK,[10] after subtracting out a dipole anisotropy from the Doppler shift of the background radiation. The latter is caused by the peculiar velocity of the Sun relative to the comoving cosmic rest frame as it moves at some 369.82 ± 0.11 km/s towards the constellation Leo (galactic longitude 264.021 ± 0.011, galactic latitude 48.253 ± 0.005).[11] The CMB dipole and aberration at higher multipoles have been measured, consistent with galactic motion.[12]
In the Big Bang model for the formation of the universe, inflationary cosmology predicts that after about 10−37 seconds[13] the nascent universe underwent exponential growth that smoothed out nearly all irregularities. The remaining irregularities were caused by quantum fluctuations in the inflation field that caused the inflation event.[14] Long before the formation of stars and planets, the early universe was smaller, much hotter and, starting 10−6 seconds after the Big Bang, filled with a uniform glow from its white-hot fog of interacting plasma of photons, electrons, and baryons.
As the universe expanded, adiabatic cooling caused the energy density of the plasma to decrease until it became favorable for electrons to combine with protons, forming hydrogen atoms. This recombination event happened when the temperature was around 3000 K or when the universe was approximately 379,000 years old.[15] As photons did not interact with these electrically neutral atoms, the former began to travel freely through space, resulting in the decoupling of matter and radiation.[16]
The color temperature of the ensemble of decoupled photons has continued to diminish ever since; now down to 2.7260±0.0013 K,[5] it will continue to drop as the universe expands. The intensity of the radiation corresponds to black-body radiation at 2.726 K because red-shifted black-body radiation is just like black-body radiation at a lower temperature. According to the Big Bang model, the radiation from the sky we measure today comes from a spherical surface called the surface of last scattering. This represents the set of locations in space at which the decoupling event is estimated to have occurred[17] and at a point in time such that the photons from that distance have just reached observers. Most of the radiation energy in the universe is in the cosmic microwave background,[18] making up a fraction of roughly 6×10−5 of the total density of the universe.[19]
Two of the greatest successes of the Big Bang theory are its prediction of the almost perfect black body spectrum and its detailed prediction of the anisotropies in the cosmic microwave background. The CMB spectrum has become the most precisely measured black body spectrum in nature.[9]
The energy density of the CMB is 0.260 eV/cm3 (4.17×10−14 J/m3) which yields about 411 photons/cm3.[20]
History
The cosmic microwave background was first predicted in 1948 by Ralph Alpher and Robert Herman, in close relation to work performed by Alpher's PhD advisor George Gamow.[21][22][23][24] Alpher and Herman were able to estimate the temperature of the cosmic microwave background to be 5 K, though two years later they re-estimated it at 28 K. This high estimate was due to a misestimate of the Hubble constant by Alfred Behr, which could not be replicated and was later abandoned for the earlier estimate. Although there were several previous estimates of the temperature of space, these estimates had two flaws. First, they were measurements of the effective temperature of space and did not suggest that space was filled with a thermal Planck spectrum. Next, they depend on our being at a special spot at the edge of the Milky Way galaxy and they did not suggest the radiation is isotropic. The estimates would yield very different predictions if Earth happened to be located elsewhere in the universe.[25]
The 1948 results of Alpher and Herman were discussed in many physics settings through about 1955, when both left the Applied Physics Laboratory at Johns Hopkins University. The mainstream astronomical community, however, was not intrigued at the time by cosmology. Alpher and Herman's prediction was rediscovered by Yakov Zel'dovich in the early 1960s, and independently predicted by Robert Dicke at the same time. The first published recognition of the CMB radiation as a detectable phenomenon appeared in a brief paper by Soviet astrophysicists A. G. Doroshkevich and Igor Novikov, in the spring of 1964.[26] In 1964, David Todd Wilkinson and Peter Roll, Dicke's colleagues at Princeton University, began constructing a Dicke radiometer to measure the cosmic microwave background.[27] In 1964, Arno Penzias and Robert Woodrow Wilson at the Crawford Hill location of Bell Telephone Laboratories in nearby Holmdel Township, New Jersey had built a Dicke radiometer that they intended to use for radio astronomy and satellite communication experiments. On 20 May 1964 they made their first measurement clearly showing the presence of the microwave background,[28] with their instrument having an excess 4.2K antenna temperature which they could not account for. After receiving a telephone call from Crawford Hill, Dicke said "Boys, we've been scooped."[2][29][30] A meeting between the Princeton and Crawford Hill groups determined that the antenna temperature was indeed due to the microwave background. Penzias and Wilson received the 1978 Nobel Prize in Physics for their discovery.[31]
The interpretation of the cosmic microwave background was a controversial issue in the 1960s with some proponents of the steady state theory arguing that the microwave background was the result of scattered starlight from distant galaxies.[32] Using this model, and based on the study of narrow absorption line features in the spectra of stars, the astronomer Andrew McKellar wrote in 1941: "It can be calculated that the 'rotational temperature' of interstellar space is 2 K."[33] However, during the 1970s the consensus was established that the cosmic microwave background is a remnant of the big bang. This was largely because new measurements at a range of frequencies showed that the spectrum was a thermal, black body spectrum, a result that the steady state model was unable to reproduce.[34]
Harrison, Peebles, Yu and Zel'dovich realized that the early universe would require inhomogeneities at the level of 10−4 or 10−5.[35][36][37] Rashid Sunyaev later calculated the observable imprint that these inhomogeneities would have on the cosmic microwave background.[38] Increasingly stringent limits on the anisotropy of the cosmic microwave background were set by ground-based experiments during the 1980s. RELIKT-1, a Soviet cosmic microwave background anisotropy experiment on board the Prognoz 9 satellite (launched 1 July 1983) gave upper limits on the large-scale anisotropy. The NASA COBE mission clearly confirmed the primary anisotropy with the Differential Microwave Radiometer instrument, publishing their findings in 1992.[39][40] The team received the Nobel Prize in physics for 2006 for this discovery.
Inspired by the COBE results, a series of ground and balloon-based experiments measured cosmic microwave background anisotropies on smaller angular scales over the next decade. The primary goal of these experiments was to measure the scale of the first acoustic peak, which COBE did not have sufficient resolution to resolve. This peak corresponds to large scale density variations in the early universe that are created by gravitational instabilities, resulting in acoustical oscillations in the plasma.[41] The first peak in the anisotropy was tentatively detected by the Toco experiment and the result was confirmed by the BOOMERanG and MAXIMA experiments.[42][43][44] These measurements demonstrated that the geometry of the universe is approximately flat, rather than curved.[45] They ruled out cosmic strings as a major component of cosmic structure formation and suggested cosmic inflation was the right theory of structure formation.[46]
The second peak was tentatively detected by several experiments before being definitively detected by WMAP, which has tentatively detected the third peak.[47] As of 2010, several experiments to improve measurements of the polarization and the microwave background on small angular scales are ongoing.[needs update] These include DASI, WMAP, BOOMERanG, QUaD, Planck spacecraft, Atacama Cosmology Telescope, South Pole Telescope and the QUIET telescope.
Relationship to the Big Bang
−13 — – −12 — – −11 — – −10 — – −9 — – −8 — – −7 — – −6 — – −5 — – −4 — – −3 — – −2 — – −1 — – 0 — |
| |||||||||||||||||||||||||||||||||||||||
The cosmic microwave background radiation and the cosmological redshift-distance relation are together regarded as the best available evidence for the Big Bang event. Measurements of the CMB have made the inflationary Big Bang model the Standard Cosmological Model.[48] The discovery of the CMB in the mid-1960s curtailed interest in alternatives such as the steady state theory.[49]
In the late 1940s Alpher and Herman reasoned that if there was a Big Bang, the expansion of the universe would have stretched the high-energy radiation of the very early universe into the microwave region of the electromagnetic spectrum, and down to a temperature of about 5 K. They were slightly off with their estimate, but they had the right idea. They predicted the CMB. It took another 15 years for Penzias and Wilson to discover that the microwave background was actually there.[50]
According to standard cosmology, the CMB gives a snapshot of the hot early universe at the point in time when the temperature dropped enough to allow electrons and protons to form hydrogen atoms. This event made the universe nearly transparent to radiation because light was no longer being scattered off free electrons. When this occurred some 380,000 years after the Big Bang, the temperature of the universe was about 3,000 K. This corresponds to an ambient energy of about 0.26 eV, which is much less than the 13.6 eV ionization energy of hydrogen.[51] This epoch is generally known as the "time of last scattering" or the period of recombination or decoupling.[52]
Since decoupling, the color temperature of the background radiation has dropped by an average factor of 1,089[53] due to the expansion of the universe. As the universe expands, the CMB photons are redshifted, causing them to decrease in energy. The color temperature of this radiation stays inversely proportional to a parameter that describes the relative expansion of the universe over time, known as the scale length. The color temperature Tr of the CMB as a function of redshift, z, can be shown to be proportional to the color temperature of the CMB as observed in the present day (2.725 K or 0.2348 meV):[54]
- Tr = 2.725 K × (1 + z)
For details about the reasoning that the radiation is evidence for the Big Bang, see Cosmic background radiation of the Big Bang.
Primary anisotropy
The anisotropy, or directional dependency, of the cosmic microwave background is divided into two types: primary anisotropy, due to effects that occur at the surface of last scattering and before; and secondary anisotropy, due to effects such as interactions of the background radiation with intervening hot gas or gravitational potentials, which occur between the last scattering surface and the observer.
The structure of the cosmic microwave background anisotropies is principally determined by two effects: acoustic oscillations and diffusion damping (also called collisionless damping or Silk damping). The acoustic oscillations arise because of a conflict in the photon–baryon plasma in the early universe. The pressure of the photons tends to erase anisotropies, whereas the gravitational attraction of the baryons, moving at speeds much slower than light, makes them tend to collapse to form overdensities. These two effects compete to create acoustic oscillations, which give the microwave background its characteristic peak structure. The peaks correspond, roughly, to resonances in which the photons decouple when a particular mode is at its peak amplitude.
The peaks contain interesting physical signatures. The angular scale of the first peak determines the curvature of the universe (but not the topology of the universe). The next peak—ratio of the odd peaks to the even peaks—determines the reduced baryon density.[55] The third peak can be used to get information about the dark-matter density.[56]
The locations of the peaks give important information about the nature of the primordial density perturbations. There are two fundamental types of density perturbations called adiabatic and isocurvature. A general density perturbation is a mixture of both, and different theories that purport to explain the primordial density perturbation spectrum predict different mixtures.
- Adiabatic density perturbations
- In an adiabatic density perturbation, the fractional additional number density of each type of particle (baryons, photons, etc.) is the same. That is, if at one place there is a 1% higher number density of baryons than average, then at that place there is a 1% higher number density of photons (and a 1% higher number density in neutrinos) than average. Cosmic inflation predicts that the primordial perturbations are adiabatic.
- Isocurvature density perturbations
- In an isocurvature density perturbation, the sum (over different types of particle) of the fractional additional densities is zero. That is, a perturbation where at some spot there is 1% more energy in baryons than average, 1% more energy in photons than average, and 2% less energy in neutrinos than average, would be a pure isocurvature perturbation. Hypothetical cosmic strings would produce mostly isocurvature primordial perturbations.
The CMB spectrum can distinguish between these two because these two types of perturbations produce different peak locations. Isocurvature density perturbations produce a series of peaks whose angular scales (ℓ values of the peaks) are roughly in the ratio 1 : 3 : 5 : ..., while adiabatic density perturbations produce peaks whose locations are in the ratio 1 : 2 : 3 : ...[57] Observations are consistent with the primordial density perturbations being entirely adiabatic, providing key support for inflation, and ruling out many models of structure formation involving, for example, cosmic strings.
Collisionless damping is caused by two effects, when the treatment of the primordial plasma as fluid begins to break down:
- the increasing mean free path of the photons as the primordial plasma becomes increasingly rarefied in an expanding universe,
- the finite depth of the last scattering surface (LSS), which causes the mean free path to increase rapidly during decoupling, even while some Compton scattering is still occurring.
These effects contribute about equally to the suppression of anisotropies at small scales and give rise to the characteristic exponential damping tail seen in the very small angular scale anisotropies.
The depth of the LSS refers to the fact that the decoupling of the photons and baryons does not happen instantaneously, but instead requires an appreciable fraction of the age of the universe up to that era. One method of quantifying how long this process took uses the photon visibility function (PVF). This function is defined so that, denoting the PVF by P(t), the probability that a CMB photon last scattered between time t and t + dt is given by P(t) dt.
The maximum of the PVF (the time when it is most likely that a given CMB photon last scattered) is known quite precisely. The first-year WMAP results put the time at which P(t) has a maximum as 372,000 years.[58] This is often taken as the "time" at which the CMB formed. However, to figure out how long it took the photons and baryons to decouple, we need a measure of the width of the PVF. The WMAP team finds that the PVF is greater than half of its maximal value (the "full width at half maximum", or FWHM) over an interval of 115,000 years. By this measure, decoupling took place over roughly 115,000 years, and when it was complete, the universe was roughly 487,000 years old.[citation needed]
Late time anisotropy
Since the CMB came into existence, it has apparently been modified by several subsequent physical processes, which are collectively referred to as late-time anisotropy, or secondary anisotropy. When the CMB photons became free to travel unimpeded, ordinary matter in the universe was mostly in the form of neutral hydrogen and helium atoms. However, observations of galaxies today seem to indicate that most of the volume of the intergalactic medium (IGM) consists of ionized material (since there are few absorption lines due to hydrogen atoms). This implies a period of reionization during which some of the material of the universe was broken into hydrogen ions.
The CMB photons are scattered by free charges such as electrons that are not bound in atoms. In an ionized universe, such charged particles have been liberated from neutral atoms by ionizing (ultraviolet) radiation. Today these free charges are at sufficiently low density in most of the volume of the universe that they do not measurably affect the CMB. However, if the IGM was ionized at very early times when the universe was still denser, then there are two main effects on the CMB:
- Small scale anisotropies are erased. (Just as when looking at an object through fog, details of the object appear fuzzy.)
- The physics of how photons are scattered by free electrons (Thomson scattering) induces polarization anisotropies on large angular scales. This broad angle polarization is correlated with the broad angle temperature perturbation.
Both of these effects have been observed by the WMAP spacecraft, providing evidence that the universe was ionized at very early times, at a redshift more than 17.[clarification needed] The detailed provenance of this early ionizing radiation is still a matter of scientific debate. It may have included starlight from the very first population of stars (population III stars), supernovae when these first stars reached the end of their lives, or the ionizing radiation produced by the accretion disks of massive black holes.
The time following the emission of the cosmic microwave background—and before the observation of the first stars—is semi-humorously referred to by cosmologists as the Dark Age, and is a period which is under intense study by astronomers (see 21 centimeter radiation).
Two other effects which occurred between reionization and our observations of the cosmic microwave background, and which appear to cause anisotropies, are the Sunyaev–Zeldovich effect, where a cloud of high-energy electrons scatters the radiation, transferring some of its energy to the CMB photons, and the Sachs–Wolfe effect, which causes photons from the Cosmic Microwave Background to be gravitationally redshifted or blueshifted due to changing gravitational fields.
Polarization
The cosmic microwave background is polarized at the level of a few microkelvin. There are two types of polarization, called E-modes and B-modes. This is in analogy to electrostatics, in which the electric field (E-field) has a vanishing curl and the magnetic field (B-field) has a vanishing divergence. The E-modes arise naturally from Thomson scattering in a heterogeneous plasma. The B-modes are not produced by standard scalar type perturbations. Instead they can be created by two mechanisms: the first one is by gravitational lensing of E-modes, which has been measured by the South Pole Telescope in 2013;[59] the second one is from gravitational waves arising from cosmic inflation. Detecting the B-modes is extremely difficult, particularly as the degree of foreground contamination is unknown, and the weak gravitational lensing signal mixes the relatively strong E-mode signal with the B-mode signal.[60]
E-modes
E-modes were first seen in 2002 by the Degree Angular Scale Interferometer (DASI).
B-modes
Cosmologists predict two types of B-modes, the first generated during cosmic inflation shortly after the big bang,[61][62][63] and the second generated by gravitational lensing at later times.[64]
Primordial gravitational waves
Primordial gravitational waves are gravitational waves that could be observed in the polarisation of the cosmic microwave background and having their origin in the early universe. Models of cosmic inflation predict that such gravitational waves should appear; thus, their detection supports the theory of inflation, and their strength can confirm and exclude different models of inflation. It is the result of three things: inflationary expansion of space itself, reheating after inflation, and turbulent fluid mixing of matter and radiation. [65]
On 17 March 2014, it was announced that the BICEP2 instrument had detected the first type of B-modes, consistent with inflation and gravitational waves in the early universe at the level of r = 0.20+0.07
−0.05, which is the amount of power present in gravitational waves
compared to the amount of power present in other scalar density
perturbations in the very early universe. Had this been confirmed it
would have provided strong evidence for cosmic inflation and the Big
Bang[66][67][68][69][70][71][72] and against the ekpyrotic model of Paul Steinhardt and Neil Turok.[73] However, on 19 June 2014, considerably lowered confidence in confirming the findings was reported[71][74][75]
and on 19 September 2014, new results of the Planck experiment reported that the results of BICEP2 can be fully attributed to cosmic dust.[76][77]
Gravitational lensing
The second type of B-modes was discovered in 2013 using the South Pole Telescope with help from the Herschel Space Observatory.[78] In October 2014, a measurement of the B-mode polarization at 150 GHz was published by the POLARBEAR experiment.[79] Compared to BICEP2, POLARBEAR focuses on a smaller patch of the sky and is less susceptible to dust effects. The team reported that POLARBEAR's measured B-mode polarization was of cosmological origin (and not just due to dust) at a 97.2% confidence level.[80]
Microwave background observations
Subsequent to the discovery of the CMB, hundreds of cosmic microwave background experiments have been conducted to measure and characterize the signatures of the radiation. The most famous experiment is probably the NASA Cosmic Background Explorer (COBE) satellite that orbited in 1989–1996 and which detected and quantified the large scale anisotropies at the limit of its detection capabilities. Inspired by the initial COBE results of an extremely isotropic and homogeneous background, a series of ground- and balloon-based experiments quantified CMB anisotropies on smaller angular scales over the next decade. The primary goal of these experiments was to measure the angular scale of the first acoustic peak, for which COBE did not have sufficient resolution. These measurements were able to rule out cosmic strings as the leading theory of cosmic structure formation, and suggested cosmic inflation was the right theory.
During the 1990s, the first peak was measured with increasing sensitivity and by 2000 the BOOMERanG experiment reported that the highest power fluctuations occur at scales of approximately one degree. Together with other cosmological data, these results implied that the geometry of the universe is flat. A number of ground-based interferometers provided measurements of the fluctuations with higher accuracy over the next three years, including the Very Small Array, Degree Angular Scale Interferometer (DASI), and the Cosmic Background Imager (CBI). DASI made the first detection of the polarization of the CMB and the CBI provided the first E-mode polarization spectrum with compelling evidence that it is out of phase with the T-mode spectrum.
In June 2001, NASA launched a second CMB space mission, WMAP, to make much more precise measurements of the large scale anisotropies over the full sky. WMAP used symmetric, rapid-multi-modulated scanning, rapid switching radiometers to minimize non-sky signal noise.[53] The first results from this mission, disclosed in 2003, were detailed measurements of the angular power spectrum at a scale of less than one degree, tightly constraining various cosmological parameters. The results are broadly consistent with those expected from cosmic inflation as well as various other competing theories, and are available in detail at NASA's data bank for Cosmic Microwave Background (CMB) (see links below). Although WMAP provided very accurate measurements of the large scale angular fluctuations in the CMB (structures about as broad in the sky as the moon), it did not have the angular resolution to measure the smaller scale fluctuations which had been observed by former ground-based interferometers.
A third space mission, the ESA (European Space Agency) Planck Surveyor, was launched in May 2009 and performed an even more detailed investigation until it was shut down in October 2013. Planck employed both HEMT radiometers and bolometer technology and measured the CMB at a smaller scale than WMAP. Its detectors were trialled in the Antarctic Viper telescope as ACBAR (Arcminute Cosmology Bolometer Array Receiver) experiment—which has produced the most precise measurements at small angular scales to date—and in the Archeops balloon telescope.
On 21 March 2013, the European-led research team behind the Planck cosmology probe released the mission's all-sky map (565x318 jpeg, 3600x1800 jpeg) of the cosmic microwave background.[81][82] The map suggests the universe is slightly older than researchers expected. According to the map, subtle fluctuations in temperature were imprinted on the deep sky when the cosmos was about 370000 years old. The imprint reflects ripples that arose as early, in the existence of the universe, as the first nonillionth of a second. Apparently, these ripples gave rise to the present vast cosmic web of galaxy clusters and dark matter. Based on the 2013 data, the universe contains 4.9% ordinary matter, 26.8% dark matter and 68.3% dark energy. On 5 February 2015, new data was released by the Planck mission, according to which the age of the universe is 13.799±0.021 billion years old and the Hubble constant was measured to be 67.74±0.46 (km/s)/Mpc.[83]
Additional ground-based instruments such as the South Pole Telescope in Antarctica and the proposed Clover Project, Atacama Cosmology Telescope and the QUIET telescope in Chile will provide additional data not available from satellite observations, possibly including the B-mode polarization.
Data reduction and analysis
This section may be too technical for most readers to understand. (February 2023) |
Raw CMBR data, even from space vehicles such as WMAP or Planck, contain foreground effects that completely obscure the fine-scale structure of the cosmic microwave background. The fine-scale structure is superimposed on the raw CMBR data but is too small to be seen at the scale of the raw data. The most prominent of the foreground effects is the dipole anisotropy caused by the Sun's motion relative to the CMBR background. The dipole anisotropy and others due to Earth's annual motion relative to the Sun and numerous microwave sources in the galactic plane and elsewhere must be subtracted out to reveal the extremely tiny variations characterizing the fine-scale structure of the CMBR background.
The detailed analysis of CMBR data to produce maps, an angular power spectrum, and ultimately cosmological parameters is a complicated, computationally difficult problem. Although computing a power spectrum from a map is in principle a simple Fourier transform, decomposing the map of the sky into spherical harmonics,[84]
By applying the angular correlation function, the sum can be reduced to an expression that only involves ℓ and power spectrum term The angled brackets indicate the average with respect to all observers in the universe; since the universe is homogeneous and isotropic, therefore there is an absence of preferred observing direction. Thus, C is independent of m. Different choices of ℓ correspond to multipole moments of CMB.
In practice it is hard to take the effects of noise and foreground sources into account. In particular, these foregrounds are dominated by galactic emissions such as Bremsstrahlung, synchrotron, and dust that emit in the microwave band; in practice, the galaxy has to be removed, resulting in a CMB map that is not a full-sky map. In addition, point sources like galaxies and clusters represent another source of foreground which must be removed so as not to distort the short scale structure of the CMB power spectrum.
Constraints on many cosmological parameters can be obtained from their effects on the power spectrum, and results are often calculated using Markov chain Monte Carlo sampling techniques.
CMBR monopole term (ℓ = 0)
When ℓ = 0, the term reduced to 1, and what we have left here is just the mean temperature of the CMB. This "mean" is called CMB monopole, and it is observed to have an average temperature of about Tγ = 2.7255±0.0006 K[84] with one standard deviation confidence. The accuracy of this mean temperature may be impaired by the diverse measurements done by different mapping measurements. Such measurements demand absolute temperature devices, such as the FIRAS instrument on the COBE satellite. The measured kTγ is equivalent to 0.234 meV or 4.6×10−10 mec2. The photon number density of a blackbody having such temperature is . Its energy density is , and the ratio to the critical density is Ωγ = 5.38 × 10−5.[84]
CMBR dipole anisotropy (ℓ = 1)
CMB dipole represents the largest anisotropy, which is in the first spherical harmonic (ℓ = 1). When ℓ = 1, the term reduces to one cosine function and thus encodes amplitude fluctuation. The amplitude of CMB dipole is around 3.3621±0.0010 mK.[84] Since the universe is presumed to be homogeneous and isotropic, an observer should see the blackbody spectrum with temperature T at every point in the sky. The spectrum of the dipole has been confirmed to be the differential of a blackbody spectrum.
CMB dipole is frame-dependent. The CMB dipole moment could also be interpreted as the peculiar motion of the Earth toward the CMB. Its amplitude depends on the time due to the Earth's orbit about the barycenter of the solar system. This enables us to add a time-dependent term to the dipole expression. The modulation of this term is 1 year,[84][85] which fits the observation done by COBE FIRAS.[85][86] The dipole moment does not encode any primordial information.
From the CMB data, it is seen that the Sun appears to be moving at 368±2 km/s relative to the reference frame of the CMB (also called the CMB rest frame, or the frame of reference in which there is no motion through the CMB). The Local Group — the galaxy group that includes our own Milky Way galaxy — appears to be moving at 627±22 km/s in the direction of galactic longitude ℓ = 276°±3°, b = 30°±3°.[84][12] This motion results in an anisotropy of the data (CMB appearing slightly warmer in the direction of movement than in the opposite direction).[84] The standard interpretation of this temperature variation is a simple velocity redshift and blueshift due to motion relative to the CMB, but alternative cosmological models can explain some fraction of the observed dipole temperature distribution in the CMB.
A 2021 study of Wide-field Infrared Survey Explorer questions the kinematic interpretation of CMB anisotropy with high statistical confidence.[87]
Multipole (ℓ ≥ 2)
The temperature variation in the CMB temperature maps at higher multipoles, or ℓ ≥ 2, is considered to be the result of perturbations of the density in the early Universe, before the recombination epoch. Before recombination, the Universe consisted of a hot, dense plasma of electrons and baryons. In such a hot dense environment, electrons and protons could not form any neutral atoms. The baryons in such early Universe remained highly ionized and so were tightly coupled with photons through the effect of Thompson scattering. These phenomena caused the pressure and gravitational effects to act against each other, and triggered fluctuations in the photon-baryon plasma. Quickly after the recombination epoch, the rapid expansion of the universe caused the plasma to cool down and these fluctuations are "frozen into" the CMB maps we observe today. The said procedure happened at a redshift of around z ⋍ 1100.[84]
Other anomalies
With the increasingly precise data provided by WMAP, there have been a number of claims that the CMB exhibits anomalies, such as very large scale anisotropies, anomalous alignments, and non-Gaussian distributions.[88][89][90] The most longstanding of these is the low-ℓ multipole controversy. Even in the COBE map, it was observed that the quadrupole (ℓ = 2, spherical harmonic) has a low amplitude compared to the predictions of the Big Bang. In particular, the quadrupole and octupole (ℓ = 3) modes appear to have an unexplained alignment with each other and with both the ecliptic plane and equinoxes.[91][92][93] A number of groups have suggested that this could be the signature of new physics at the greatest observable scales; other groups suspect systematic errors in the data.[94][95][96]
Ultimately, due to the foregrounds and the cosmic variance problem, the greatest modes will never be as well measured as the small angular scale modes. The analyses were performed on two maps that have had the foregrounds removed as far as possible: the "internal linear combination" map of the WMAP collaboration and a similar map prepared by Max Tegmark and others.[47][53][97] Later analyses have pointed out that these are the modes most susceptible to foreground contamination from synchrotron, dust, and Bremsstrahlung emission, and from experimental uncertainty in the monopole and dipole.
A full Bayesian analysis of the WMAP power spectrum demonstrates that the quadrupole prediction of Lambda-CDM cosmology is consistent with the data at the 10% level and that the observed octupole is not remarkable.[98] Carefully accounting for the procedure used to remove the foregrounds from the full sky map further reduces the significance of the alignment by ~5%.[99][100][101][102] Recent observations with the Planck telescope, which is very much more sensitive than WMAP and has a larger angular resolution, record the same anomaly, and so instrumental error (but not foreground contamination) appears to be ruled out.[103] Coincidence is a possible explanation, chief scientist from WMAP, Charles L. Bennett suggested coincidence and human psychology were involved, "I do think there is a bit of a psychological effect; people want to find unusual things."[104]
Future evolution
Assuming the universe keeps expanding and it does not suffer a Big Crunch, a Big Rip, or another similar fate, the cosmic microwave background will continue redshifting until it will no longer be detectable,[105] and will be superseded first by the one produced by starlight, and perhaps, later by the background radiation fields of processes that may take place in the far future of the universe such as proton decay, evaporation of black holes, and positronium decay.[106]
Timeline of prediction, discovery and interpretation
Thermal (non-microwave background) temperature predictions
- 1896 – Charles Édouard Guillaume estimates the "radiation of the stars" to be 5–6 K.[107]
- 1926 – Sir Arthur Eddington estimates the non-thermal radiation of starlight in the galaxy "... by the formula E = σT4 the effective temperature corresponding to this density is 3.18° absolute ... black body".[108]
- 1930s – Cosmologist Erich Regener calculates that the non-thermal spectrum of cosmic rays in the galaxy has an effective temperature of 2.8 K.
- 1931 – Term microwave first used in print: "When trials with wavelengths as low as 18 cm. were made known, there was undisguised surprise+that the problem of the micro-wave had been solved so soon." Telegraph & Telephone Journal XVII. 179/1
- 1934 – Richard Tolman shows that black-body radiation in an expanding universe cools but remains thermal.
- 1938 – Nobel Prize winner (1920) Walther Nernst reestimates the cosmic ray temperature as 0.75 K.
- 1946 – Robert Dicke predicts "... radiation from cosmic matter" at < 20 K, but did not refer to background radiation.[109]
- 1946 – George Gamow calculates a temperature of 50 K (assuming a 3-billion year old universe),[110] commenting it "... is in reasonable agreement with the actual temperature of interstellar space", but does not mention background radiation.[111]
- 1953 – Erwin Finlay-Freundlich in support of his tired light theory, derives a blackbody temperature for intergalactic space of 2.3 K[112] with comment from Max Born suggesting radio astronomy as the arbitrator between expanding and infinite cosmologies.
Microwave background radiation predictions and measurements
- 1941 – Andrew McKellar detected the cosmic microwave background as the coldest component of the interstellar medium by using the excitation of CN doublet lines measured by W. S. Adams in a B star, finding an "effective temperature of space" (the average bolometric temperature) of 2.3 K.[33][113]
- 1946 – George Gamow calculates a temperature of 50 K (assuming a 3-billion year old universe),[110] commenting it "... is in reasonable agreement with the actual temperature of interstellar space", but does not mention background radiation.
- 1948 – Ralph Alpher and Robert Herman estimate "the temperature in the universe" at 5 K. Although they do not specifically mention microwave background radiation, it may be inferred.[114]
- 1949 – Ralph Alpher and Robert Herman re-re-estimate the temperature at 28 K.
- 1953 – George Gamow estimates 7 K.[109]
- 1956 – George Gamow estimates 6 K.[109]
- 1955 – Émile Le Roux of the Nançay Radio Observatory, in a sky survey at λ = 33 cm, reported a near-isotropic background radiation of 3 kelvins, plus or minus 2.[109]
- 1957 – Tigran Shmaonov reports that "the absolute effective temperature of the radioemission background ... is 4±3 K".[115] It is noted that the "measurements showed that radiation intensity was independent of either time or direction of observation ... it is now clear that Shmaonov did observe the cosmic microwave background at a wavelength of 3.2 cm"[116][117]
- 1960s – Robert Dicke re-estimates a microwave background radiation temperature of 40 K[109][118]
- 1964 – A. G. Doroshkevich and Igor Dmitrievich Novikov publish a brief paper suggesting microwave searches for the black-body radiation predicted by Gamow, Alpher, and Herman, where they name the CMB radiation phenomenon as detectable.[119]
- 1964–65 – Arno Penzias and Robert Woodrow Wilson measure the temperature to be approximately 3 K. Robert Dicke, James Peebles, P. G. Roll, and D. T. Wilkinson interpret this radiation as a signature of the Big Bang.
- 1966 – Rainer K. Sachs and Arthur M. Wolfe theoretically predict microwave background fluctuation amplitudes created by gravitational potential variations between observers and the last scattering surface (see Sachs–Wolfe effect).
- 1968 – Martin Rees and Dennis Sciama theoretically predict microwave background fluctuation amplitudes created by photons traversing time-dependent wells of potential.
- 1969 – R. A. Sunyaev and Yakov Zel'dovich study the inverse Compton scattering of microwave background photons by hot electrons (see Sunyaev–Zel'dovich effect).
- 1983 – Researchers from the Cambridge Radio Astronomy Group and the Owens Valley Radio Observatory first detect the Sunyaev–Zel'dovich effect from clusters of galaxies.
- 1983 – RELIKT-1 Soviet CMB anisotropy experiment was launched.
- 1990 – FIRAS on the Cosmic Background Explorer (COBE) satellite measures the black body form of the CMB spectrum with exquisite precision, and shows that the microwave background has a nearly perfect black-body spectrum and thereby strongly constrains the density of the intergalactic medium.
- January 1992 – Scientists that analysed data from the RELIKT-1 report the discovery of anisotropy in the cosmic microwave background at the Moscow astrophysical seminar.[120]
- 1992 – Scientists that analysed data from COBE DMR report the discovery of anisotropy in the cosmic microwave background.[121]
- 1995 – The Cosmic Anisotropy Telescope performs the first high resolution observations of the cosmic microwave background.
- 1999 – First measurements of acoustic oscillations in the CMB anisotropy angular power spectrum from the TOCO, BOOMERANG, and Maxima Experiments. The BOOMERanG experiment makes higher quality maps at intermediate resolution, and confirms that the universe is "flat".
- 2002 – Polarization discovered by DASI.[122]
- 2003 – E-mode polarization spectrum obtained by the CBI.[123] The CBI and the Very Small Array produces yet higher quality maps at high resolution (covering small areas of the sky).
- 2003 – The Wilkinson Microwave Anisotropy Probe spacecraft produces an even higher quality map at low and intermediate resolution of the whole sky (WMAP provides no high-resolution data, but improves on the intermediate resolution maps from BOOMERanG).
- 2004 – E-mode polarization spectrum obtained by the CBI.[124]
- 2004 – The Arcminute Cosmology Bolometer Array Receiver produces a higher quality map of the high resolution structure not mapped by WMAP.
- 2005 – The Arcminute Microkelvin Imager and the Sunyaev–Zel'dovich Array begin the first surveys for very high redshift clusters of galaxies using the Sunyaev–Zel'dovich effect.
- 2005 – Ralph A. Alpher is awarded the National Medal of Science for his groundbreaking work in nucleosynthesis and prediction that the universe expansion leaves behind background radiation, thus providing a model for the Big Bang theory.
- 2006 – The long-awaited three-year WMAP results are released, confirming previous analysis, correcting several points, and including polarization data.
- 2006 – Two of COBE's principal investigators, George Smoot and John Mather, received the Nobel Prize in Physics in 2006 for their work on precision measurement of the CMBR.
- 2006–2011 – Improved measurements from WMAP, new supernova surveys ESSENCE and SNLS, and baryon acoustic oscillations from SDSS and WiggleZ, continue to be consistent with the standard Lambda-CDM model.
- 2010 – The first all-sky map from the Planck telescope is released.
- 2013 – An improved all-sky map from the Planck telescope is released, improving the measurements of WMAP and extending them to much smaller scales.
- 2014 – On March 17, 2014, astrophysicists of the BICEP2 collaboration announced the detection of inflationary gravitational waves in the B-mode power spectrum, which if confirmed, would provide clear experimental evidence for the theory of inflation.[66][67][68][69][71][125] However, on 19 June 2014, lowered confidence in confirming the cosmic inflation findings was reported.[71][74][75]
- 2015 – On January 30, 2015, the same team of astronomers from BICEP2 withdrew the claim made on the previous year. Based on the combined data of BICEP2 and Planck, the European Space Agency announced that the signal can be entirely attributed to dust in the Milky Way.[126]
- 2018 – The final data and maps from the Planck telescope is released, with improved measurements of the polarization on large scales.[127]
- 2019 – Planck telescope analyses of their final 2018 data continue to be released.[128]
In popular culture
- In the Stargate Universe TV series (2009–2011), an ancient spaceship, Destiny, was built to study patterns in the CMBR which is a sentient message left over from the beginning of time.[129]
- In Wheelers, a novel (2000) by Ian Stewart & Jack Cohen, CMBR is explained as the encrypted transmissions of an ancient civilization. This allows the Jovian "blimps" to have a society older than the currently-observed age of the universe.[citation needed]
- In The Three-Body Problem, a 2008 novel by Liu Cixin, a probe from an alien civilization compromises instruments monitoring the CMBR in order to deceive a character into believing the civilization has the power to manipulate the CMBR itself.[130]
- The 2017 issue of the Swiss 20 francs bill lists several astronomical objects with their distances – the CMB is mentioned with 430 · 1015 light-seconds.[131]
- In the 2021 Marvel series WandaVision, a mysterious television broadcast is discovered within the Cosmic Microwave Background.[132]
See also
- List of cosmological computation software
- Cosmic neutrino background – relic of the big bang
- Cosmic microwave background spectral distortions – Fluctuations in the energy spectrum of the microwave background
- Cosmological perturbation theory – theory by which the evolution of structure is understood in the big bang model
- Axis of evil (cosmology) – Name given to an anomaly in astronomical observations of the Cosmic Microwave Background
- Gravitational wave background – Random gravitational-wave signal potentially detectable by gravitational wave experiments
- Heat death of the universe – Possible fate of the universe
- Horizons: Exploring the Universe
- Lambda-CDM model – Model of Big Bang cosmology
- Observational cosmology – Study of the origin of the universe (structure and evolution)
- Observation history of galaxies – Large gravitationally bound system of stars and interstellar matter
- Physical cosmology – Branch of cosmology which studies mathematical models of the universe
- Timeline of cosmological theories – Timeline of theories about physical cosmology
References
- "WandaVision's 'cosmic microwave background radiation' is real, actually". SYFY Official Site. 2021-02-03. Retrieved 2023-01-23.
Further reading
- Balbi, Amedeo (2008). The music of the big bang : the cosmic microwave background and the new cosmology. Berlin: Springer. ISBN 978-3-540-78726-6.
- Durrer, Ruth (2008). The Cosmic Microwave Background. Cambridge University Press. ISBN 978-0-521-84704-9.
- Evans, Rhodri (2015). The Cosmic Microwave Background: How It Changed Our Understanding of the Universe. Springer. ISBN 978-3-319-09927-9.
External links
- Student Friendly Intro to the CMB A pedagogic, step-by-step introduction to the cosmic microwave background power spectrum analysis suitable for those with an undergraduate physics background. More in depth than typical online sites. Less dense than cosmology texts.
- CMBR Theme on arxiv.org
- Audio: Fraser Cain and Dr. Pamela Gay – Astronomy Cast. The Big Bang and Cosmic Microwave Background – October 2006
- Visualization of the CMB data from the Planck mission
- Copeland, Ed. "CMBR: Cosmic Microwave Background Radiation". Sixty Symbols. Brady Haran for the University of Nottingham.
https://en.wikipedia.org/wiki/Cosmic_microwave_background
https://en.wikipedia.org/wiki/Cosmic_microwave_background
https://en.wikipedia.org/wiki/Big_Bang_nucleosynthesis
https://en.wikipedia.org/wiki/Inflation_(cosmology)
https://en.wikipedia.org/wiki/Lambda-CDM_model
https://en.wikipedia.org/wiki/Dark_matter
https://en.wikipedia.org/wiki/Galaxy_filament
https://en.wikipedia.org/wiki/Observable_universe#Large-scale_structure
Seen another way, the photon can be considered as its own antiparticle (thus an "antiphoton" is simply a normal photon with opposite momentum, equal polarization, and 180° out of phase). The reverse process, pair production, is the dominant mechanism by which high-energy photons such as gamma rays lose energy while passing through matter.[29] That process is the reverse of "annihilation to one photon" allowed in the electric field of an atomic nucleus.
https://en.wikipedia.org/wiki/Photon
https://en.wikipedia.org/wiki/Spin_angular_momentum_of_light
https://en.wikipedia.org/wiki/Photoelectric_effect
https://en.wikipedia.org/wiki/Spacetime
https://en.wikipedia.org/wiki/Spin_(particle_physics)
https://en.wikipedia.org/wiki/Medical_optical_imaging
https://en.wikipedia.org/wiki/Electron%E2%80%93positron_annihilation
https://en.wikipedia.org/wiki/Synchrotron_radiation
https://en.wikipedia.org/wiki/Photon_polarization
https://en.wikipedia.org/wiki/Plane_wave
https://en.wikipedia.org/wiki/Photon_polarization
https://en.wikipedia.org/wiki/Linear_polarization
https://en.wikipedia.org/wiki/Helicity_(particle_physics)
https://en.wikipedia.org/wiki/Pauli%E2%80%93Lubanski_pseudovector#Massless_fields
https://en.wikipedia.org/wiki/Three-photon_microscopy
https://en.wikipedia.org/wiki/Two-photon_excitation_microscopy
https://en.wikipedia.org/wiki/Second-harmonic_imaging_microscopy
https://en.wikipedia.org/wiki/Centrosymmetry
https://en.wikipedia.org/wiki/Absorbance
Second-harmonic imaging microscopy (SHIM) is based on a nonlinear optical effect known as second-harmonic generation (SHG). SHIM has been established as a viable microscope imaging contrast mechanism for visualization of cell and tissue structure and function.[1] A second-harmonic microscope obtains contrasts from variations in a specimen's ability to generate second-harmonic light from the incident light while a conventional optical microscope obtains its contrast by detecting variations in optical density, path length, or refractive index of the specimen. SHG requires intense laser light passing through a material with a noncentrosymmetric molecular structure, either inherent or induced externally, for example by an electric field.[2]
https://en.wikipedia.org/wiki/Second-harmonic_imaging_microscopy
Second-harmonic imaging microscopy (SHIM) is based on a nonlinear optical effect known as second-harmonic generation (SHG). SHIM has been established as a viable microscope imaging contrast mechanism for visualization of cell and tissue structure and function.[1] A second-harmonic microscope obtains contrasts from variations in a specimen's ability to generate second-harmonic light from the incident light while a conventional optical microscope obtains its contrast by detecting variations in optical density, path length, or refractive index of the specimen. SHG requires intense laser light passing through a material with a noncentrosymmetric molecular structure, either inherent or induced externally, for example by an electric field.[2]
Second-harmonic light emerging from an SHG material is exactly half the wavelength (frequency doubled) of the light entering the material. While two-photon-excited fluorescence (TPEF) is also a two photon process, TPEF loses some energy during the relaxation of the excited state, while SHG is energy conserving. Typically, an inorganic crystal is used to produce SHG light such as lithium niobate (LiNbO3), potassium titanyl phosphate (KTP = KTiOPO4), and lithium triborate (LBO = LiB3O5). Though SHG requires a material to have specific molecular orientation in order for the incident light to be frequency doubled, some biological materials can be highly polarizable, and assemble into fairly ordered, large noncentrosymmetric structures. While some biological materials such as collagen, microtubules, and muscle myosin[3] can produce SHG signals, even water can become ordered and produce second-harmonic signal under certain conditions, which allows SH microscopy to image surface potentials without any labeling molecules.[2] The SHG pattern is mainly determined by the phase matching condition. A common setup for an SHG imaging system will have a laser scanning microscope with a titanium sapphire mode-locked laser as the excitation source. The SHG signal is propagated in the forward direction. However, some experiments have shown that objects on the order of about a tenth of the wavelength of the SHG produced signal will produce nearly equal forward and backward signals.
Advantages
SHIM offers several advantages for live cell and tissue imaging. SHG does not involve the excitation of molecules like other techniques such as fluorescence microscopy therefore, the molecules shouldn't suffer the effects of phototoxicity or photobleaching. Also, since many biological structures produce strong SHG signals, the labeling of molecules with exogenous probes is not required which can also alter the way a biological system functions. By using near infrared wavelengths for the incident light, SHIM has the ability to construct three-dimensional images of specimens by imaging deeper into thick tissues.
Difference and complementarity with two-photon fluorescence (2PEF)
Two-photons fluorescence (2PEF) is a very different process from SHG: it involves excitation of electrons to higher energy levels, and subsequent de-excitation by photon emission (unlike SHG, although it is also a 2-photon process). Thus, 2PEF is a non coherent process, spatially (emitted isotropically) and temporally (broad, sample-dependent spectrum). It is also not specific to certain structure, unlike SHG.[4]
It can therefore be coupled to SHG in multiphoton imaging to reveal some molecules that do produce autofluorescence, like elastin in tissues (while SHG reveals collagen or myosin for instance).[4]
History
Before SHG was used for imaging, the first demonstration of SHG was performed in 1961 by P. A. Franken, G. Weinreich, C. W. Peters, and A. E. Hill at the University of Michigan, Ann Arbor using a quartz sample.[5] In 1968, SHG from interfaces was discovered by Bloembergen [6] and has since been used as a tool for characterizing surfaces and probing interface dynamics. In 1971, Fine and Hansen reported the first observation of SHG from biological tissue samples.[7] In 1974, Hellwarth and Christensen first reported the integration of SHG and microscopy by imaging SHG signals from polycrystalline ZnSe.[8] In 1977, Colin Sheppard imaged various SHG crystals with a scanning optical microscope. The first biological imaging experiments were done by Freund and Deutsch in 1986 to study the orientation of collagen fibers in rat tail tendon.[9] In 1993, Lewis examined the second-harmonic response of styryl dyes in electric fields. He also showed work on imaging live cells. In 2006, Goro Mizutani group developed a non-scanning SHG microscope that significantly shortens the time required for observation of large samples, even if the two-photons wide-field microscope was published in 1996 [10] and could have been used to detect SHG. The non-scanning SHG microscope was used for observation of plant starch,[11][12] megamolecule,[13] spider silk[14][15] and so on. In 2010 SHG was extended to whole-animal in vivo imaging.[16][17] In 2019, SHG applications widened when it was applied to the use of selectively imaging agrochemicals directly on leaf surfaces to provide a way to evaluate the effectiveness of pesticides.[18]
Quantitative measurements
Orientational anisotropy
SHG polarization anisotropy can be used to determine the orientation and degree of organization of proteins in tissues since SHG signals have well-defined polarizations. By using the anisotropy equation:[19]
and acquiring the intensities of the polarizations in the parallel and perpendicular directions. A high value indicates an anisotropic orientation whereas a low value indicates an isotropic structure. In work done by Campagnola and Loew,[19] it was found that collagen fibers formed well-aligned structures with an value.
Forward over backward SHG
SHG being a coherent process (spatially and temporally), it keeps information on the direction of the excitation and is not emitted isotropically. It is mainly emitted in forward direction (same as excitation), but can also be emitted in backward direction depending on the phase-matching condition. Indeed, the coherence length beyond which the conversion of the signal decreases is:
with for forward, but for backward such that >> . Therefore, thicker structures will appear preferentially in forward, and thinner ones in backward: since the SHG conversion depends at first approximation on the square of the number of nonlinear converters, the signal will be higher if emitted by thick structures, thus the signal in forward direction will be higher than in backward. However, the tissue can scatter the generated light, and a part of the SHG in forward can be retro-reflected in the backward direction.[20] Then, the forward-over-backward ratio F/B can be calculated,[20] and is a metric of the global size and arrangement of the SHG converters (usually collagen fibrils). It can also be shown that the higher the out-of-plane angle of the scatterer, the higher its F/B ratio (see fig. 2.14 of [21]).
Polarization-resolved SHG
The advantages of polarimetry were coupled to SHG in 2002 by Stoller et al.[22] Polarimetry can measure the orientation and order at molecular level, and coupled to SHG it can do so with the specificity to certain structures like collagen: polarization-resolved SHG microscopy (p-SHG) is thus an expansion of SHG microscopy.[23] p-SHG defines another anisotropy parameter, as:[24]
which is, like r, a measure of the principal orientation and disorder of the structure being imaged. Since it is often performed in long cylindrical filaments (like collagen), this anisotropy is often equal to ,[25] where is the nonlinear susceptibility tensor and X the direction of the filament (or main direction of the structure), Y orthogonal to X and Z the propagation of the excitation light. The orientation ϕ of the filaments in the plane XY of the image can also be extracted from p-SHG by FFT analysis, and put in a map.[25][26]
Fibrosis quantization
Collagen (particular case, but widely studied in SHG microscopy), can exist in various forms : 28 different types, of which 5 are fibrillar. One of the challenge is to determine and quantify the amount of fibrillar collagen in a tissue, to be able to see its evolution and relationship with other non-collagenous materials.[27]
To that end, a SHG microscopy image has to be corrected to remove the small amount of residual fluorescence or noise that exist at the SHG wavelength. After that, a mask can be applied to quantify the collagen inside the image.[27] Among other quantization techniques, it is probably the one with the highest specificity, reproductibility and applicability despite being quite complex.[27]
Others
It has also been used to prove that backpropagating action potentials invade dendritic spines without voltage attenuation, establishing a sound basis for future work on Long-term potentiation. Its use here was that it provided a way to accurately measure the voltage in the tiny dendritic spines with an accuracy unattainable with standard two-photon microscopy.[28] Meanwhile, SHG can efficiently convert near-infrared light to visible light to enable imaging-guided photodynamic therapy, overcoming the penetration depth limitations.[29]
Materials that can be imaged
SHG microscopy and its expansions can be used to study various tissues: some example images are reported in the figure below: collagen inside the extracellular matrix remains the main application. It can be found in tendon, skin, bone, cornea, aorta, fascia, cartilage, meniscus, intervertebral disks...
Myosin can also be imaged in skeletal muscle or cardiac muscle.
| Type | Material | Found in | SHG signal | Specificity |
|---|---|---|---|---|
| Carbohydrate | Cellulose | Wood, green plant, algae. | Quite weak in normal cellulose,[18] but substantial in crystalline or nanocrystalline cellulose. | - |
| Starch | Staple foods, green plant | Quite intense signal [30] | chirality is at micro and macro level, and the SHG is different under right or left-handed circular polarization | |
| Megamolecular polysaccharide sacran | Cyanobactery | From sacran cotton-like lump, fibers, and cast films | signal from films is weaker [13] | |
| Protein | Fibroin and sericin | Spider silk | Quite weak | [14] |
| Collagen[9] | tendon, skin, bone, cornea, aorta, fascia, cartilage, meniscus, intervertebral disks ; connective tissues | Quite strong, depends on the type of the collagen (does it form fibrils, fibers ?) | nonlinear susceptibility tensor components are , , , with ~ and / ~ 1.4 in most cases | |
| Myosin | Skeletal or cardiac muscle[3] | Quite strong | nonlinear susceptibility tensor components are , , with ~ but / ~ 0.6 < 1 contrary to collagen | |
| Tubulin | Microtubules in mitosis or meiosis,[31] or in neurites (mainly axons)[32] | Quite weak | The microtubules have to be aligned to efficiently generate | |
| Minerals | Piezoelectric crystals | Also called nonlinear crystals | Strong if phase-matched | Different types of phase-matching, critical of non-critical |
| Polar liquids | Water | Most living organisms | Barely detectable (requires wide-field geometry and ultra-short laser pulses [33]) | Directly probing electrostatic fields, since oriented water molecules satisfy phase-matching condition [34] |
Coupling with THG microscopy
Third-Harmonic Generation (THG) microscopy can be complementary to SHG microscopy, as it is sensitive to the transverse interfaces, and to the 3rd order nonlinear susceptibility [35] · [36]
Applications
Cancer progression, tumor characterization
The mammographic density is correlated with the collagen density, thus SHG can be used for identifying breast cancer.[37] SHG is usually coupled to other nonlinear techniques such as Coherent anti-Stokes Raman Scattering or Two-photon excitation microscopy, as part of a routine called multiphoton microscopy (or tomography) that provides a non-invasive and rapid in vivo histology of biopsies that may be cancerous.[38]
Breast cancer
The comparison of forward and backward SHG images gives insight about the microstructure of collagen, itself related to the grade and stage of a tumor, and its progression in breast.[39] Comparison of SHG and 2PEF can also show the change of collagen orientation in tumors.[40] Even if SHG microscopy has contributed a lot to breast cancer research, it is not yet established as a reliable technique in hospitals, or for diagnostic of this pathology in general.[39]
Ovarian cancer
Healthy ovaries present in SHG a uniform epithelial layer and well-organized collagen in their stroma, whereas abnormal ones show an epithelium with large cells and a changed collagen structure.[39] The r ratio is also used [41] to show that the alignment of fibrils is slightly higher for cancerous than for normal tissues.
Skin cancer
SHG is, again, combined to 2PEF is used to calculate the ratio:
where shg (resp. tpef) is the number of thresholded pixels in the SHG (resp. 2PEF) image,[42] a high MFSI meaning a pure SHG image (with no fluorescence). The highest MFSI is found in cancerous tissues,[39] which provides a contrast mode to differentiate from normal tissues.
SHG was also combined to Third-Harmonic Generation (THG) to show that backward THG is higher in tumors.[43]
Pancreatic cancer
Changes in collagen ultrastructure in pancreatic cancer can be investigated by multiphoton fluorescence and polarization-resolved SHIM.[44]
Other cancers
SHG microscopy was reported for the study of lung, colonic, esophageal stroma and cervical cancers.[39]
Pathologies detection
Alterations in the organization or polarity of the collagen fibrils can be signs of pathology,.[45][46]
In particular, the anisotropy of alignment of collagen fibers allowed to discriminate healthy dermis against pathological scars in skin.[47] Also, pathologies in cartilage such as osteoarthritis can be probed by polarization-resolved SHG microscopy,.[48][49] SHIM was later extended to fibro-cartilage (meniscus).[50]
Tissue engineering
The ability of SHG to image specific molecules can reveal the structure of a certain tissue one material at a time, and at various scales (from macro to micro) using microscopy. For instance, the collagen (type I) is specifically imaged from the extracellular matrix (ECM) of cells, or when it serves as a scaffold or conjonctive material in tissues.[51] SHG also reveals fibroin in silk, myosin in muscles and biosynthetized cellulose. All of this imaging capability can be used to design artificials tissues, by targeting specific points of the tissue : SHG can indeed quantitatively measure some orientations, and material quantity and arrangement.[51] Also, SHG coupled to other multiphoton techniques can serve to monitor the development of engineered tissues, when the sample is relatively thin however.[52] Of course, they can finally be used as a quality control of the fabricated tissues.[52]
Structure of the eye
Cornea, at the surface of the eye, is considered to be made of plywood-like structure of collagen, due to the self-organization properties of sufficiently dense collagen.[53] Yet, the collagenous orientation in lamellae is still under debate in this tissue.[54] Keratoconus cornea can also be imaged by SHG to reveal morphological alterations of the collagen.[55] Third-Harmonic Generation (THG) microscopy is moreover used to image the cornea, which is complementary to SHG signal as THG and SHG maxima in this tissue are often at different places.[56]
See also
Sources
- Schmitt, Michael; Mayerhöfer, Thomas; Popp, Jürgen; Kleppe, Ingo; Weisshartannée, Klaus (2013). Handbook of Biophotonics, Chap.3 Light–Matter Interaction. Wiley. doi:10.1002/9783527643981.bphot003. ISBN 9783527643981. S2CID 93908151.
- Pavone, Francesco S.; Campagnola, Paul J. (2016). Second Harmonic Generation Imaging, 2nd edition. CRC Taylor&Francis. ISBN 978-1-4398-4914-9.
- Campagnola, Paul J.; Clark, Heather A.; Mohler, William A.; Lewis, Aaron; Loew, Leslie M. (2001). "Second harmonic imaging microscopy of living cells" (PDF). Journal of Biomedical Optics. 6 (3): 277–286. Bibcode:2001JBO.....6..277C. doi:10.1117/1.1383294. hdl:2047/d20000323. PMID 11516317. S2CID 2376695.
- Campagnola, Paul J.; Loew, Leslie M (2003). "Second-harmonic imaging microscopy for visualizing biomolecular arrays in cells, tissues and organisms" (PDF). Nature Biotechnology. 21 (11): 1356–1360. doi:10.1038/nbt894. PMID 14595363. S2CID 18701570. Archived from the original (PDF) on 2016-03-04.
- Stoller, P.; Reiser, K.M.; Celliers, P.M.; Rubenchik, A.M. (2002). "Polarization-modulated second harmonic generation in collagen". Biophys. J. 82 (6): 3330–3342. Bibcode:2002BpJ....82.3330S. doi:10.1016/s0006-3495(02)75673-7. PMC 1302120. PMID 12023255.
- Han, M.; Giese, G.; Bille, J. F. (2005). "Second harmonic generation imaging of collagen fibrils in cornea and sclera". Opt. Express. 13 (15): 5791–5797. Bibcode:2005OExpr..13.5791H. doi:10.1364/opex.13.005791. PMID 19498583.
- König, Karsten (2018). Multiphoton Microscopy and Fluorescence Lifetime Imaging - Applications in Biology and Medicine. De Gruyter. ISBN 978-3-11-042998-5.

- Keikhosravi, Adib; Bredfeldt, Jeremy S.; Sagar, Abdul Kader; Eliceiri, Kevin W. (2014). "Second-harmonic generation imaging of cancer (from "Quantitative Imaging in Cell Biology by Jennifer C. Waters, Torsten Wittman")". Methods in Cell Biology. 123: 531–546. doi:10.1016/B978-0-12-420138-5.00028-8. ISSN 0091-679X. PMID 24974046.
- Hanry Yu; Nur Aida Abdul Rahim (2013). Imaging in Cellular and Tissue Engineering, 1st edition. CRC Taylor&Francis. ISBN 9780367445867.
- Cicchi, Riccardo; Vogler, Nadine; Kapsokalyvas, Dimitrios; Dietzek, Benjamin; Popp, Jürgen; Pavone, Francesco Saverio (2013). "From molecular structure to tissue architecture: collagen organization probed by SHG microscopy". Journal of Biophotonics. 6 (2): 129–142. doi:10.1002/jbio.201200092. PMID 22791562.

- Roesel, D.; Eremchev, M.; Schönfeldová, T.; Lee, S.; Roke, S. (2022-04-18). "Water
as a contrast agent to quantify surface chemistry and physics using
second harmonic scattering and imaging: A perspective". Applied Physics Letters. AIP Publishing. 120 (16): 160501. Bibcode:2022ApPhL.120p0501R. doi:10.1063/5.0085807. ISSN 0003-6951. S2CID 248252664.

References
- Olivier, N.; Débarre, D.; Beaurepaire, E. (2016). "THG Microscopy of Cells and Tissues: Contrast Mechanisms and Applications". Second Harmonic Generation Imaging, 2nd edition. CRC Taylor&Francis. ISBN 978-1-4398-4914-9.
https://en.wikipedia.org/wiki/Second-harmonic_imaging_microscopy
https://en.wikipedia.org/wiki/Lithium_triborate
https://en.wikipedia.org/wiki/Transparency_and_translucency
https://en.wikipedia.org/wiki/Nd:YAG_laser
https://en.wikipedia.org/wiki/Nonlinear_optics#Phase_matching
Coupling with other multiphoton techniques
Correlative images can be obtained using different multiphoton schemes such as 2PEF, 3PEF, and Third harmonic generation (THG), in parallel (since the corresponding wavelengths are different, they can be easily separated onto different detectors). A multichannel image is then constructed.[9]
3PEF is also compared to 2PEF: it generally gives a smaller degradation of the signal-to-background ratio (SBR) with depth, even if the emitted signal is smaller than with 2PEF.[9]
https://en.wikipedia.org/wiki/Three-photon_microscopy
https://en.wikipedia.org/wiki/Mode_locking
https://en.wikipedia.org/wiki/Two-photon_absorption
https://en.wikipedia.org/wiki/Point_spread_function
https://en.wikipedia.org/wiki/Confocal_microscopy
https://en.wikipedia.org/wiki/Spatial_filter
https://en.wikipedia.org/wiki/Transverse_mode
https://en.wikipedia.org/wiki/Active_laser_medium
https://en.wikipedia.org/wiki/Rare-earth_element
https://en.wikipedia.org/wiki/Optical_cavity
https://en.wikipedia.org/wiki/Boundary_value_problem
https://en.wikipedia.org/wiki/Eigenfunction
https://en.wikipedia.org/wiki/Scalar_(mathematics)
https://en.wikipedia.org/wiki/Total_internal_reflection
https://en.wikipedia.org/wiki/Scalar_matrix
https://en.wikipedia.org/wiki/Nonlinear_optics
https://en.wikipedia.org/wiki/Optical_parametric_amplifier
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
Spontaneous parametric down-conversion (also known as SPDC, parametric fluorescence or parametric scattering) is a nonlinear instant optical process that converts one photon of higher energy (namely, a pump photon), into a pair of photons (namely, a signal photon, and an idler photon) of lower energy, in accordance with the law of conservation of energy and law of conservation of momentum. It is an important process in quantum optics, for the generation of entangled photon pairs, and of single photons.
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
Type I down converter is a squeezed vacuum that contains only even photon number terms. The nondegenerate output of the Type II down converter is a two-mode squeezed vacuum.
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
An SPDC scheme with the Type I output
https://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion
https://en.wikipedia.org/wiki/Barium_borate
1 - Incident light
2 - 50% transmitted light
3 - 50% reflected light
In practice, the reflective layer absorbs some light.
https://en.wikipedia.org/wiki/Beam_splitter
https://en.wikipedia.org/wiki/Total_internal_reflection#FTIR_(Frustrated_Total_Internal_Reflection)
Designs
In its most common form, a cube, a beam splitter is made from two triangular glass prisms which are glued together at their base using polyester, epoxy, or urethane-based adhesives. (Before these synthetic resins, natural ones were used, e.g. Canada balsam.) The thickness of the resin layer is adjusted such that (for a certain wavelength) half of the light incident through one "port" (i.e., face of the cube) is reflected and the other half is transmitted due to FTIR (Frustrated Total Internal Reflection). Polarizing beam splitters, such as the Wollaston prism, use birefringent materials to split light into two beams of orthogonal polarization states.
Another design is the use of a half-silvered mirror. This is composed of an optical substrate, which is often a sheet of glass or plastic, with a partially transparent thin coating of metal. The thin coating can be aluminium deposited from aluminium vapor using a physical vapor deposition method. The thickness of the deposit is controlled so that part (typically half) of the light, which is incident at a 45-degree angle and not absorbed by the coating or substrate material, is transmitted and the remainder is reflected. A very thin half-silvered mirror used in photography is often called a pellicle mirror. To reduce loss of light due to absorption by the reflective coating, so-called "Swiss-cheese" beam-splitter mirrors have been used. Originally, these were sheets of highly polished metal perforated with holes to obtain the desired ratio of reflection to transmission. Later, metal was sputtered onto glass so as to form a discontinuous coating, or small areas of a continuous coating were removed by chemical or mechanical action to produce a very literally "half-silvered" surface.
Instead of a metallic coating, a dichroic optical coating may be used. Depending on its characteristics, the ratio of reflection to transmission will vary as a function of the wavelength of the incident light. Dichroic mirrors are used in some ellipsoidal reflector spotlights to split off unwanted infrared (heat) radiation, and as output couplers in laser construction.
A third version of the beam splitter is a dichroic mirrored prism assembly which uses dichroic optical coatings to divide an incoming light beam into a number of spectrally distinct output beams. Such a device was used in three-pickup-tube color television cameras and the three-strip Technicolor movie camera. It is currently used in modern three-CCD cameras. An optically similar system is used in reverse as a beam-combiner in three-LCD projectors, in which light from three separate monochrome LCD displays is combined into a single full-color image for projection.
Beam splitters with single-mode[clarification needed] fiber for PON networks use the single-mode behavior to split the beam.[citation needed] The splitter is done by physically splicing two fibers "together" as an X.
Arrangements of mirrors or prisms used as camera attachments to photograph stereoscopic image pairs with one lens and one exposure are sometimes called "beam splitters", but that is a misnomer, as they are effectively a pair of periscopes redirecting rays of light which are already non-coincident. In some very uncommon attachments for stereoscopic photography, mirrors or prism blocks similar to beam splitters perform the opposite function, superimposing views of the subject from two different perspectives through color filters to allow the direct production of an anaglyph 3D image, or through rapidly alternating shutters to record sequential field 3D video.
Phase shift
Beam splitters are sometimes used to recombine beams of light, as in a Mach–Zehnder interferometer. In this case there are two incoming beams, and potentially two outgoing beams. But the amplitudes of the two outgoing beams are the sums of the (complex) amplitudes calculated from each of the incoming beams, and it may result that one of the two outgoing beams has amplitude zero. In order for energy to be conserved (see next section), there must be a phase shift in at least one of the outgoing beams. For example (see red arrows in picture on the right), if a polarized light wave in air hits a dielectric surface such as glass, and the electric field of the light wave is in the plane of the surface, then the reflected wave will have a phase shift of π, while the transmitted wave will not have a phase shift; the blue arrow does not pick up a phase-shift, because it is reflected from a medium with a lower refractive index. The behavior is dictated by the Fresnel equations.[1] This does not apply to partial reflection by conductive (metallic) coatings, where other phase shifts occur in all paths (reflected and transmitted). In any case, the details of the phase shifts depend on the type and geometry of the beam splitter.
Classical lossless beam splitter
For beam splitters with two incoming beams, using a classical, lossless beam splitter with electric fields Ea and Eb each incident at one of the inputs, the two output fields Ec and Ed are linearly related to the inputs through
where the 2×2 element is the beam-splitter transfer matrix and r and t are the reflectance and transmittance along a particular path through the beam splitter, that path being indicated by the subscripts. (The values depend on the polarization of the light.)
If the beam splitter removes no energy from the light beams, the total output energy can be equated with the total input energy, reading
Inserting the results from the transfer equation above with produces
and similarly for then
When both and are non-zero, and using these two results we obtain
where "" indicates the complex conjugate. It is now easy to show that where is the identity, i.e. the beam-splitter transfer matrix is a unitary matrix.
Expanding, it can be written each r and t as a complex number having an amplitude and phase factor; for instance, . The phase factor accounts for possible shifts in phase of a beam as it reflects or transmits at that surface. Then is obtained
Further simplifying, the relationship becomes
which is true when and the exponential term reduces to -1. Applying this new condition and squaring both sides, it becomes
where substitutions of the form were made. This leads to the result
and similarly,
It follows that .
Having determined the constraints describing a lossless beam splitter, the initial expression can be rewritten as
Applying different values for the amplitudes and phases can account for many different forms of the beam splitter that can be seen widely used.
The transfer matrix appears to have 6 amplitude and phase parameters, but it also has 2 constraints: and . To include the constraints and simplify to 4 independent parameters, we may write[3] (and from the constraint ), so that
where is the phase difference between the transmitted beams and similarly for , and is a global phase. Lastly using the other constraint that we define so that , hence
A 50:50 beam splitter is produced when . The dielectric beam splitter above, for example, has
i.e. , while the "symmetric" beam splitter of Loudon [2] has
i.e. .
Use in experiments
Beam splitters have been used in both thought experiments and real-world experiments in the area of quantum theory and relativity theory and other fields of physics. These include:
- The Fizeau experiment of 1851 to measure the speeds of light in water
- The Michelson–Morley experiment of 1887 to measure the effect of the (hypothetical) luminiferous aether on the speed of light
- The Hammar experiment of 1935 to refute Dayton Miller's claim of a positive result from repetitions of the Michelson-Morley experiment
- The Kennedy–Thorndike experiment of 1932 to test the independence of the speed of light and the velocity of the measuring apparatus
- Bell test experiments (from ca. 1972) to demonstrate consequences of quantum entanglement and exclude local hidden-variable theories
- Wheeler's delayed choice experiment of 1978, 1984 etc., to test what makes a photon behave as a wave or a particle and when it happens
- The FELIX experiment (proposed in 2000) to test the Penrose interpretation that quantum superposition depends on spacetime curvature
- The Mach–Zehnder interferometer, used in various experiments, including the Elitzur–Vaidman bomb tester involving interaction-free measurement; and in others in the area of quantum computation
Quantum mechanical description
In quantum mechanics, the electric fields are operators as explained by second quantization and Fock states. Each electrical field operator can further be expressed in terms of modes representing the wave behavior and amplitude operators, which are typically represented by the dimensionless creation and annihilation operators. In this theory, the four ports of the beam splitter are represented by a photon number state and the action of a creation operation is . The following is a simplified version of Ref.[3] The relation between the classical field amplitudes , and produced by the beam splitter is translated into the same relation of the corresponding quantum creation (or annihilation) operators , and , so that
where the transfer matrix is given in classical lossless beam splitter section above:
Since is unitary, , i.e.
This is equivalent to saying that if we start from the vacuum state and add a photon in port a to produce
then the beam splitter creates a superposition on the outputs of
The probabilities for the photon to exit at ports c and d are therefore and , as might be expected.
Likewise, for any input state
and the output is
Using the multi-binomial theorem, this can be written
where and the is a binomial coefficient and it is to be understood that the coefficient is zero if etc.
The transmission/reflection coefficient factor in the last equation may be written in terms of the reduced parameters that ensure unitarity:
where it can be seen that if the beam splitter is 50:50 then and the only factor that depends on j is the term. This factor causes interesting interference cancellations. For example, if and the beam splitter is 50:50, then
where the term has cancelled. Therefore the output states always have even numbers of photons in each arm. A famous example of this is the Hong–Ou–Mandel effect, in which the input has , the output is always or , i.e. the probability of output with a photon in each mode (a coincidence event) is zero. Note that this is true for all types of 50:50 beam splitter irrespective of the details of the phases, and the photons need only be indistinguishable. This contrasts with the classical result, in which equal output in both arms for equal inputs on a 50:50 beam splitter does appear for specific beam splitter phases (e.g. a symmetric beam splitter ), and for other phases where the output goes to one arm (e.g. the dielectric beam splitter ) the output is always in the same arm, not random in either arm as is the case here. From the correspondence principle we might expect the quantum results to tend to the classical one in the limits of large n, but the appearance of large numbers of indistinguishable photons at the input is a non-classical state that does not correspond to a classical field pattern, which instead produces a statistical mixture of different known as Poissonian light.
Rigorous derivation is given in the Fearn–Loudon 1987 paper[4] and extended in Ref [3] to include statistical mixtures with the density matrix.
Non-symmetric beam-splitter
In general, for a non-symmetric beam-splitter, namely a beam-splitter for which the transmission and reflection coefficients are not equal, one can define an angle such that
where and are the reflection and transmission coefficients. Then the unitary operation associated with the beam-splitter is then
Application for quantum computing
In 2000 Knill, Laflamme and Milburn (KLM protocol) proved that it is possible to create a universal quantum computer solely with beam splitters, phase shifters, photodetectors and single photon sources. The states that form a qubit in this protocol are the one-photon states of two modes, i.e. the states |01⟩ and |10⟩ in the occupation number representation (Fock state) of two modes. Using these resources it is possible to implement any single qubit gate and 2-qubit probabilistic gates. The beam splitter is an essential component in this scheme since it is the only one that creates entanglement between the Fock states.
Similar settings exist for continuous-variable quantum information processing. In fact, it is possible to simulate arbitrary Gaussian (Bogoliubov) transformations of a quantum state of light by means of beam splitters, phase shifters and photodetectors, given two-mode squeezed vacuum states are available as a prior resource only (this setting hence shares certain similarities with a Gaussian counterpart of the KLM protocol).[5] The building block of this simulation procedure is the fact that a beam splitter is equivalent to a squeezing transformation under partial time reversal.
Diffractive beam splitter
The diffractive beam splitter[6][7]
(also known as multispot beam generator or array beam generator) is a single optical element that divides an input beam into multiple output beams.[8] Each output beam retains the same optical characteristics as the input beam, such as size, polarization and phase. A diffractive beam splitter can generate either a 1-dimensional beam array (1xN) or a 2-dimensional beam matrix (MxN), depending on the diffractive pattern on the element. The diffractive beam splitter is used with monochromatic light such as a laser beam, and is designed for a specific wavelength and angle of separation between output beams.See also
References
https://en.wikipedia.org/wiki/Beam_splitter
https://en.wikipedia.org/wiki/Category:Mirrors
https://en.wikipedia.org/wiki/Ferrofluid_mirror
https://en.wikipedia.org/wiki/Ethylene_glycol
https://en.wikipedia.org/wiki/Colligative_properties
https://en.wikipedia.org/wiki/Grotthuss_mechanism
https://en.wikipedia.org/wiki/Lithium_atom
https://en.wikipedia.org/wiki/Buffer_solution
https://en.wikipedia.org/wiki/Buffer_solution
https://en.wikipedia.org/wiki/Baryon
https://en.wikipedia.org/wiki/Annihilation#Proton-antiproton_annihilation
https://en.wikipedia.org/wiki/Trihydrogen_cation
https://en.wikipedia.org/wiki/Positron_emission
Ice IX is a form of solid water stable at temperatures below 140 K or -133.15 C and pressures between 200 and 400 MPa. It has a tetragonal crystal lattice and a density of 1.16 g/cm3, 26% higher than ordinary ice. It is formed by cooling ice III from 208 K to 165 K (rapidly—to avoid forming ice II). Its structure is identical to ice III other than being completely proton-ordered.[1]
Ordinary water ice is known as ice Ih in the Bridgman nomenclature. Different types of ice, from ice II to ice XIX, have been created in the laboratory at different temperatures and pressures.
Ice in general becomes different kinds of ice based on situation and temperature. Some ice crystals are colder than others. One big difference in the different kinds of ice besides temperature is formation of the ice crystal. Each kind of crystal holds a different shape.
Cultural References
Additionally, a version of Ice IX is introduced in the book Cat's Cradle by Kurt Vonnegut. In the book, Ice IX is a theoretical ice crystal formation that freezes all water it comes into contact with.
See also
- Ice, for other crystalline forms of ice.
References
- La Placa, Sam J.; Hamilton, Walter C.; Kamb, Barclay; Prakash, Anand (1973-01-15). "On a nearly proton‐ordered structure for ice IX". The Journal of Chemical Physics. 58 (2): 567–580. doi:10.1063/1.1679238. ISSN 0021-9606.
- Chaplin, Martin (2007-11-11). "Ice-three and ice-nine structures". Water Structure and Science. Retrieved 2008-01-02.
External links
https://en.wikipedia.org/wiki/Ice_IX
https://en.wikipedia.org/wiki/Diethynylbenzene_dianion
https://en.wikipedia.org/wiki/Nuclear_drip_line#Proton_drip_line
https://en.wikipedia.org/wiki/Aurora
https://en.wikipedia.org/wiki/Magnetosphere
https://en.wikipedia.org/wiki/Halo_nucleus
https://en.wikipedia.org/wiki/Phosphotungstic_acid#Composite_proton_exchange_membranes
https://en.wikipedia.org/wiki/Proton_conductor
https://en.wikipedia.org/wiki/Desiccation
https://en.wikipedia.org/wiki/Decussation
https://en.wikipedia.org/wiki/Compressor
https://en.wikipedia.org/wiki/Category:Patterned_grounds
https://en.wikipedia.org/wiki/Category:Broadcast_engineering
https://en.wikipedia.org/wiki/Linear_timecode
https://en.wikipedia.org/wiki/Loop_recording
https://en.wikipedia.org/wiki/Phosphoric_acid
https://en.wikipedia.org/wiki/Phosphate
Pyrophosphoric acid, also known as diphosphoric acid, is the inorganic compound with the formula H4P2O7 or, more descriptively, [(HO)2P(O)]2O. Colorless and odorless, it is soluble in water, diethyl ether, and ethyl alcohol. The anhydrous acid crystallizes in two polymorphs, which melt at 54.3 and 71.5 °C. The compound is a component of polyphosphoric acid, an important source of phosphoric acid.[1] Anions, salts, and esters of pyrophosphoric acid are called pyrophosphates.
https://en.wikipedia.org/wiki/Pyrophosphoric_acid
https://en.wikipedia.org/wiki/Phosphoryl_chloride
https://en.wikipedia.org/wiki/Phosphorus_pentachloride
https://en.wikipedia.org/wiki/Phosphoryl_fluoride
https://en.wikipedia.org/wiki/Difluorophosphoric_acid
https://en.wikipedia.org/wiki/Difluorophosphate
https://en.wikipedia.org/wiki/Orthosilicate
https://en.wikipedia.org/wiki/Tetraethyl_orthosilicate
https://en.wikipedia.org/wiki/Silicic_acid
https://en.wikipedia.org/wiki/Category:Ethyl_esters
https://en.wikipedia.org/wiki/Seawater
https://en.wikipedia.org/wiki/Ethyl_acetate
https://en.wikipedia.org/wiki/Ethanol
https://en.wikipedia.org/wiki/Autoionization
https://en.wikipedia.org/wiki/Titanium_tetrachloride
https://en.wikipedia.org/wiki/Distillation
https://en.wikipedia.org/wiki/Dry_distillation
https://en.wikipedia.org/wiki/Condensation
https://en.wikipedia.org/wiki/Nanocluster#Atom_clusters
https://en.wikipedia.org/wiki/Isocyanide
https://en.wikipedia.org/wiki/Resonance_(chemistry)
https://en.wikipedia.org/wiki/Carbon_monoxide
https://en.wikipedia.org/wiki/Ligand
https://en.wikipedia.org/wiki/Denticity
https://en.wikipedia.org/wiki/Bridging_ligand
https://en.wikipedia.org/wiki/Three-center_two-electron_bond
https://en.wikipedia.org/wiki/Dihydrogen_complex
https://en.wikipedia.org/wiki/Chlorobis(dppe)iron_hydride
https://en.wikipedia.org/wiki/Sodium_borohydride
https://en.wikipedia.org/wiki/Protic_solvent
https://en.wikipedia.org/wiki/Eutectic_system
Silicon chips are bonded to gold-plated substrates through a silicon-gold eutectic by the application of ultrasonic energy to the chip. See eutectic bonding.
https://en.wikipedia.org/wiki/Eutectic_system
https://en.wikipedia.org/wiki/Amorphous_metal
https://en.wikipedia.org/wiki/Category:Dehydrating_agents
https://en.wikipedia.org/wiki/Cyanuric_chloride
https://en.wikipedia.org/wiki/1,3,5-Triazine
https://en.wikipedia.org/wiki/Trimer_(chemistry)
https://en.wikipedia.org/wiki/Cyanuric_bromide
https://en.wikipedia.org/wiki/Hydrogen_bromide
https://en.wikipedia.org/wiki/Azeotrope
https://en.wikipedia.org/wiki/Halothane
https://en.wikipedia.org/wiki/Sevoflurane
https://en.wikipedia.org/wiki/Nitrous_oxide
https://en.wikipedia.org/wiki/Chlorofluorocarbon
https://en.wikipedia.org/wiki/Supramolecular_polymer#Hydrogen_bonding_interaction
https://en.wikipedia.org/wiki/Fluorosulfuric_acid
https://en.wikipedia.org/wiki/Glovebox
https://en.wikipedia.org/wiki/Potential_applications_of_carbon_nanotubes
https://en.wikipedia.org/wiki/Metabolism
https://en.wikipedia.org/wiki/Cellulose_fiber
https://en.wikipedia.org/wiki/Silk#Regenerated_silk_fiber
https://en.wikipedia.org/wiki/Scramjet
https://en.wikipedia.org/wiki/Halobacterium_salinarum
https://en.wikipedia.org/wiki/Primordial_nuclide
https://en.wikipedia.org/wiki/Coal_gasification
https://en.wikipedia.org/wiki/Cyanohydrin
https://en.wikipedia.org/wiki/Timeline_of_motor_and_engine_technology
https://en.wikipedia.org/wiki/Turbomolecular_pump
https://en.wikipedia.org/wiki/Compressed-air_vehicle
https://en.wikipedia.org/wiki/Direct_borohydride_fuel_cell
https://en.wikipedia.org/wiki/Renal_physiology
https://en.wikipedia.org/wiki/Liquid-propellant_rocket
https://en.wikipedia.org/wiki/Flue_gas
https://en.wikipedia.org/wiki/Reductive_elimination
https://en.wikipedia.org/wiki/Neon-burning_process
https://en.wikipedia.org/wiki/Lithium_chloride
https://en.wikipedia.org/wiki/Dehydrogenation
https://en.wikipedia.org/wiki/Industrial_processes
https://en.wikipedia.org/wiki/Electric_multiple_unit
https://en.wikipedia.org/wiki/Ionic_hydrogenation
https://en.wikipedia.org/wiki/Stoichiometry
https://en.wikipedia.org/wiki/Aluminium_hydride#High_pressure_hydrogenation_of_aluminium_metal
https://en.wikipedia.org/wiki/Vacuum_pump
https://en.wikipedia.org/wiki/Activated_alumina
https://en.wikipedia.org/wiki/Activated_alumina
https://en.wikipedia.org/wiki/Photoelectrochemical_cell
https://en.wikipedia.org/wiki/Photocatalysis
https://en.wikipedia.org/wiki/Acid_gas
https://en.wikipedia.org/wiki/Iodine#Hydrogen_iodide
https://en.wikipedia.org/wiki/Sorption_enhanced_water_gas_shift
https://en.wikipedia.org/wiki/Energy_density
https://en.wikipedia.org/wiki/Forming_gas
https://en.wikipedia.org/wiki/Hydrail
https://en.wikipedia.org/wiki/Glass_melting_furnace
https://en.wikipedia.org/wiki/Self-healing_hydrogels#Hydrogen_bonding
https://en.wikipedia.org/wiki/Exhaust_gas_recirculation
https://en.wikipedia.org/wiki/Nicotinamide_adenine_dinucleotide_phosphate
https://en.wikipedia.org/wiki/Unitized_regenerative_fuel_cell
https://en.wikipedia.org/wiki/Liquid-propellant_rocket
A unitized regenerative fuel cell (URFC) is a fuel cell based on the proton exchange membrane which can do the electrolysis of water in regenerative mode and function in the other mode as a fuel cell recombining oxygen and hydrogen gas to produce electricity. Both modes are done with the same fuel cell stack[1]
By definition, the process of any fuel cell could be reversed. However, a given device is usually optimized for operating in one mode and may not be built in such a way that it can be operated backwards. Fuel cells operated backwards generally do not make very efficient systems unless they are purpose-built to do so as in high pressure electrolyzers, unitized regenerative fuel cells and regenerative fuel cells.
https://en.wikipedia.org/wiki/Unitized_regenerative_fuel_cell
https://en.wikipedia.org/wiki/Electrodeionization
https://en.wikipedia.org/wiki/Pyrolysis#Methane_pyrolysis_for_hydrogen
https://en.wikipedia.org/wiki/High-pressure_electrolysis
https://en.wikipedia.org/wiki/Anoxygenic_photosynthesis
https://en.wikipedia.org/wiki/Absorption_refrigerator
https://en.wikipedia.org/wiki/Hydrogen_spillover
https://en.wikipedia.org/wiki/Ion_exchange#Waste_water_produced_by_resin_regeneration
https://en.wikipedia.org/wiki/Calvin_cycle
https://en.wikipedia.org/wiki/Power-to-gas
https://en.wikipedia.org/wiki/Cellular_respiration
https://en.wikipedia.org/wiki/NOx_adsorber
https://en.wikipedia.org/wiki/Pressure_swing_adsorption
https://en.wikipedia.org/wiki/Glycolysis#Anoxic_regeneration_of_NAD+
https://en.wikipedia.org/wiki/Frustrated_Lewis_pair#Hydrogen
https://en.wikipedia.org/wiki/Glycolysis
https://en.wikipedia.org/wiki/Heavy_water
https://en.wikipedia.org/wiki/Transfer_hydrogenation
https://en.wikipedia.org/wiki/Radiolysis#Hydrogen_production
https://en.wikipedia.org/wiki/Solid_oxide_electrolyzer_cell
https://en.wikipedia.org/wiki/Amine_gas_treating
https://en.wikipedia.org/wiki/Hydrogen%E2%80%93bromine_battery
https://en.wikipedia.org/wiki/Hydrogen_halide
https://en.wikipedia.org/wiki/Activated_carbon#Reactivation_and_regeneration
https://en.wikipedia.org/wiki/Catalytic_reforming
https://en.wikipedia.org/wiki/Regenerative_fuel_cell
https://en.wikipedia.org/wiki/Chronic_periodontitis#Guided_tissue_regeneration
https://en.wikipedia.org/wiki/Phlogiston_theory
Maximum life span (or, for humans, maximum reported age at death) is a measure of the maximum amount of time one or more members of a population have been observed to survive between birth and death. The term can also denote an estimate of the maximum amount of time that a member of a given species could survive between birth and death, provided circumstances that are optimal to that member's longevity.
Most living species have an upper limit on the number of times somatic cells not expressing telomerase can divide. This is called the Hayflick limit, although this number of cell divisions does not strictly control lifespan.
Definition
In animal studies, maximum span is often taken to be the mean life span of the most long-lived 10% of a given cohort. By another definition, however, maximum life span corresponds to the age at which the oldest known member of a species or experimental group has died. Calculation of the maximum life span in the latter sense depends upon the initial sample size.[1]
Maximum life span contrasts with mean life span (average life span, life expectancy), and longevity. Mean life span varies with susceptibility to disease, accident, suicide and homicide, whereas maximum life span is determined by "rate of aging".[2][3][failed verification] Longevity refers only to the characteristics of the especially long lived members of a population, such as infirmities as they age or compression of morbidity, and not the specific life span of an individual.
In humans
Demographic evidence
The longest living person whose dates of birth and death were verified according to the modern norms of Guinness World Records and the Gerontology Research Group was Jeanne Calment (1875–1997), a French woman who is verified to have lived to 122. The oldest male lifespan has only been verified as 116, by Japanese man Jiroemon Kimura. Reduction of infant mortality has accounted for most of the increased average life span longevity, but since the 1960s mortality rates among those over 80 years have decreased by about 1.5% per year. "The progress being made in lengthening lifespans and postponing senescence is entirely due to medical and public-health efforts, rising standards of living, better education, healthier nutrition and more salubrious lifestyles."[4] Animal studies suggest that further lengthening of median human lifespan as well as maximum lifespan could be achieved through "calorie restriction mimetic" drugs or by directly reducing food consumption.[5] Although calorie restriction has not been proven to extend the maximum human life span as of 2014, results in ongoing primate studies have demonstrated that the assumptions derived from rodents are valid in primates.[6][7]
It has been proposed that no fixed theoretical limit to human longevity is apparent today.[8][9] Studies in the biodemography of human longevity indicate a late-life mortality deceleration law: that death rates level off at advanced ages to a late-life mortality plateau. That is, there is no fixed upper limit to human longevity, or fixed maximal human lifespan.[10] This law was first quantified in 1939, when researchers found that the one-year probability of death at advanced age asymptotically approaches a limit of 44% for women and 54% for men.[11]
However, this evidence depends on the existence of a late-life plateaus and deceleration that can be explained, in humans and other species, by the existence of very rare errors.[12][13] Age-coding error rates below 1 in 10,000 are sufficient to make artificial late-life plateaus, and errors below 1 in 100,000 can generate late-life mortality deceleration. These error rates cannot be ruled out by examining documents[13] (the standard) because of successful pension fraud, identity theft, forgeries and errors that leave no documentary evidence. This capacity for errors to explain late-life plateaus solves the "fundamental question in aging research is whether humans and other species possess an immutable life-span limit" and suggests that a limit to human life span exists.[14] A theoretical study suggested the maximum human lifespan to be around 125 years using a modified stretched exponential function for human survival curves.[15] In another study, researchers claimed that there exists a maximum lifespan for humans, and that the human maximal lifespan has been declining since the 1990s.[16] A theoretical study also suggested that the maximum human life expectancy at birth is limited by the human life characteristic value δ, which is around 104 years.[17]
The United Nations has undertaken an important Bayesian sensitivity analysis of global population burden based on life expectancy projection at birth in future decades. The 2017 95% prediction interval of 2090 average life expectancy rises as high as +6 (106, in Century Representation Form) by 2090, with dramatic, ongoing, layered consequences on world population and demography should that happen. The prediction interval is extremely wide, and the United Nations cannot be certain. Organizations like the Methuselah Foundation are working toward an end to senescence and practically unlimited human lifespan. If successful, the demographic implications for human population will be greater in effective multiplier terms than any experienced in the last five centuries if maximum lifespan or the birthrate remain unlimited by law. Modern Malthusian predictions of overpopulation based on increased longevity have been criticized on the same basis as general population alarmism (see Malthusianism).
Non-demographic evidence
Evidence for maximum lifespan is also provided by the dynamics of physiological indices with age. For example, scientists have observed that a person's VO2max value (a measure of the volume of oxygen flow to the cardiac muscle) decreases as a function of age. Therefore, the maximum lifespan of a person could be determined by calculating when the person's VO2max value drops below the basal metabolic rate necessary to sustain life, which is approximately 3 ml per kg per minute.[18][page needed] On the basis of this hypothesis, athletes with a VO2max value between 50 and 60 at age 20 would be expected "to live for 100 to 125 years, provided they maintained their physical activity so that their rate of decline in VO2max remained constant".[19]
https://en.wikipedia.org/wiki/Maximum_life_span
https://en.wikipedia.org/wiki/Industrial_catalysts
https://en.wikipedia.org/wiki/Microplasma
https://en.wikipedia.org/wiki/Dental_pulp_stem_cell
https://en.wikipedia.org/wiki/Photoinitiator
https://en.wikipedia.org/wiki/Solid_oxide_fuel_cell
https://en.wikipedia.org/wiki/Indigo_dye
https://en.wikipedia.org/wiki/VRLA_battery
https://en.wikipedia.org/wiki/International_Chemical_Identifier
https://en.wikipedia.org/wiki/RD-0126
https://en.wikipedia.org/wiki/Pyrimethamine
https://en.wikipedia.org/wiki/Thermal_runaway
https://en.wikipedia.org/wiki/Electronic_oscillator
https://en.wikipedia.org/wiki/World_War_I
https://en.wikipedia.org/wiki/Nanogel#Tissue_Regeneration
https://en.wikipedia.org/wiki/Nanogel#Tissue_Regeneration
https://en.wikipedia.org/wiki/Nanocomposite_hydrogels
https://en.wikipedia.org/wiki/Chain-growth_polymerization
https://en.wikipedia.org/wiki/Silica_gel
https://en.wikipedia.org/wiki/Artificial_cartilage
https://en.wikipedia.org/wiki/Artificial_cartilage
https://en.wikipedia.org/wiki/Artificial_cartilage#Cell_and_scaffold-based_cartilage_regeneration
https://en.wikipedia.org/wiki/Chain_reaction#Detailed_example%3A_the_hydrogen-bromine_reaction
https://en.wikipedia.org/wiki/Insertion_reaction
https://en.wikipedia.org/wiki/Bacterial_cellulose
https://en.wikipedia.org/wiki/Displacement_chromatography
https://en.wikipedia.org/wiki/Chemical_looping_reforming_and_gasification
https://en.wikipedia.org/wiki/On-water_reaction
https://en.wikipedia.org/wiki/Chlorine_trifluoride
https://en.wikipedia.org/wiki/Hofmann%E2%80%93L%C3%B6ffler_reaction#Selectivity_of_hydrogen_transfer
https://en.wikipedia.org/wiki/Black_Sea
https://en.wikipedia.org/wiki/Polyethylene
https://en.wikipedia.org/wiki/Hyaluronic_acid
https://en.wikipedia.org/wiki/Flue-gas_desulfurization
https://en.wikipedia.org/wiki/Cationic_polymerization
https://en.wikipedia.org/wiki/History_of_rail_transport
https://en.wikipedia.org/wiki/Carbon_capture_and_storage
https://en.wikipedia.org/wiki/Coherent_turbulent_structure
https://en.wikipedia.org/wiki/Oxidative_phosphorylation
https://en.wikipedia.org/wiki/Carbon_fibers
https://en.wikipedia.org/wiki/Glass_fiber
https://en.wikipedia.org/wiki/Basalt_fiber



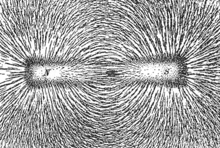
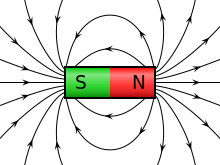





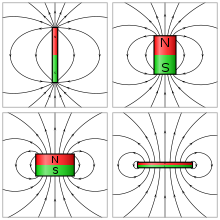





![{\displaystyle F\simeq \left[{\frac {B_{0}^{2}A^{2}\left(L^{2}+R^{2}\right)}{\pi \mu _{0}L^{2}}}\right]\left[{\frac {1}{z^{2}}}+{\frac {1}{(z+2L)^{2}}}-{\frac {2}{(z+L)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92025ea3ce20ac6022e6d9c4677bde62daf6764e)



![{\displaystyle F(z)\simeq {\frac {\pi \mu _{0}}{4}}M^{2}R^{4}\left[{\frac {1}{z^{2}}}+{\frac {1}{(z+2L)^{2}}}-{\frac {2}{(z+L)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02185a720de327d3e9296e2678217ceef559a2cc)














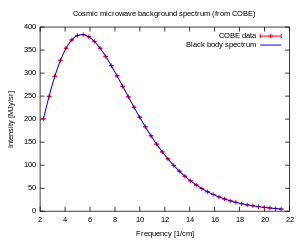




























































































![{\displaystyle r_{ac}^{\ast j}t_{ad}^{\ast (n-j)}t_{bc}^{\ast (N-j)}r_{bd}^{\ast (m-N+j)}=(-1)^{j}\tan ^{2j}\theta (-\tan \theta )^{m-N}\cos ^{n+m}\theta \exp -i\left[(n+m)(\phi _{0}+\phi _{T})-m(\phi _{R}+\phi _{T})+N(\phi _{R}-\phi _{T})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb1f62cbb2a6678b2bf9d1ec9f464a7a8ce3007)



![{\displaystyle {\begin{aligned}\left({\hat {a}}_{a}^{\dagger }\right)^{n}\left({\hat {a}}_{b}^{\dagger }\right)^{m}&\to \left[{\hat {a}}_{a}^{\dagger }{\hat {a}}_{b}^{\dagger }\right]^{n}\\&=\left[\left(r_{ac}^{\ast }{\hat {a}}_{c}^{\dagger }+t_{ad}^{\ast }{\hat {a}}_{d}^{\dagger }\right)\left(t_{bc}^{\ast }{\hat {a}}_{c}^{\dagger }+r_{bd}^{\ast }{\hat {a}}_{d}^{\dagger }\right)\right]^{n}\\&=\left[{\frac {e^{-i\phi _{0}}}{\sqrt {2}}}\right]^{2n}\left[\left(e^{-i\phi _{R}}{\hat {a}}_{c}^{\dagger }+e^{-i\phi _{T}}{\hat {a}}_{d}^{\dagger }\right)\left(e^{i\phi _{T}}{\hat {a}}_{c}^{\dagger }-e^{i\phi _{R}}{\hat {a}}_{d}^{\dagger }\right)\right]^{n}\\&={\frac {e^{-2in\phi _{0}}}{2^{n}}}\left[e^{i(\phi _{T}-\phi _{R})}\left({\hat {a}}_{c}^{\dagger }\right)^{2}+e^{-i(\phi _{T}-\phi _{R})}\left({\hat {a}}_{d}^{\dagger }\right)^{2}\right]^{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/783a4f6750281ed27d3a5929dc0dcbf1023797a0)













No comments:
Post a Comment