The Williams tube, or the Williams–Kilburn tube named after inventors Freddie Williams and Tom Kilburn, is an early form of computer memory.[1][2] It was the first random-access digital storage device, and was used successfully in several early computers.[3]
The Williams tube works by displaying a grid of dots on a cathode-ray tube (CRT). Due to the way CRTs work, this creates a small charge of static electricity over each dot. The charge at the location of each of the dots is read by a thin metal sheet just in front of the display. Since the display faded over time, it was periodically refreshed. It operates faster than earlier acoustic delay-line memory, at the speed of the electrons inside the vacuum tube, rather than at the speed of sound. The system was adversely affected by nearby electrical fields, and required frequent adjustment to remain operational. Williams–Kilburn tubes were used primarily on high-speed computer designs.
Williams and Kilburn applied for British patents on 11 December 1946,[4] and 2 October 1947,[5] followed by United States patent applications on 10 December 1947,[6] and 16 May 1949.[7]
https://en.wikipedia.org/wiki/Williams_tube
Delay-line memory is a form of computer memory, now obsolete, that was used on some of the earliest digital computers. Like many modern forms of electronic computer memory, delay-line memory was a refreshable memory, but as opposed to modern random-access memory, delay-line memory was sequential-access.
Analog delay line technology had been used since the 1920s to delay the propagation of analog signals. When a delay line is used as a memory device, an amplifier and a pulse shaper are connected between the output of the delay line and the input. These devices recirculate the signals from the output back into the input, creating a loop that maintains the signal as long as power is applied. The shaper ensures the pulses remain well-formed, removing any degradation due to losses in the medium.
The memory capacity is determined by dividing the time taken to transmit one bit into the time it takes for data to circulate through the delay line. Early delay-line memory systems had capacities of a few thousand bits, with recirculation times measured in microseconds. To read or write a particular bit stored in such a memory, it is necessary to wait for that bit to circulate through the delay line into the electronics. The delay to read or write any particular bit is no longer than the recirculation time.
Use of a delay line for a computer memory was invented by J. Presper Eckert in the mid-1940s for use in computers such as the EDVAC and the UNIVAC I. Eckert and John Mauchly applied for a patent for a delay-line memory system on October 31, 1947; the patent was issued in 1953.[1] This patent focused on mercury delay lines, but it also discussed delay lines made of strings of inductors and capacitors, magnetostrictive delay lines, and delay lines built using rotating disks to transfer data to a read head at one point on the circumference from a write head elsewhere around the circumference.
https://en.wikipedia.org/wiki/Delay-line_memory
Mellon optical memory was an early form of computer memory invented at the Mellon Institute (today part of Carnegie Mellon University) in 1951.[1][2] The device used a combination of photoemissive and phosphorescent materials to produce a "light loop" between two surfaces. The presence or lack of light, detected by a photocell, represented a one or zero. Although promising, the system was rendered obsolete with the introduction of magnetic-core memory in the early 1950s. It appears that the system was never used in production.
| Computer memory and data storage types |
|---|
|
|
| Volatile |
|---|
|
|
|
|
| Non-volatile |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Description
The main memory element of the Mellon device consisted of a very large (television sized) square vacuum tube consisting of two slightly separated flat glass plates. The inner side of one of the plates was coated with a photoemissive material that released electrons when struck by light. The inside of the other plate was coated with a phosphorescent material, that would release light when struck by electrons.
The tube was charged with a high electrical voltage. When an external source of light struck the photoemissive layer, it would release a shower of electrons. The electrons would be pulled toward the positive charge on the phosphorescent layer, traveling through the vacuum. When they struck the phosphorescent layer, they would release a shower of photons (light) travelling in all directions. Some of these photons would travel back to the photoemissive layer, where they would cause a second shower of electrons to be released. To ensure that the light did not activate nearby areas of the photoemissive material, a baffle was used inside the tube, dividing the device up into a grid of cells.
The process of electron emission causing photoemission in turn causing electron emission is what provided the memory action. This process would continue for a short time; the light emitted by the phosphorescent layer was much smaller than the amount of energy absorbed by it from the electrons, so the total amount of light in the cell faded away at a rate determined by the characteristics of the phosphorescent material.
Overall the system was similar to the better-known Williams tube. The Williams tube used the phosphorescent front of a single CRT to create small spots of static electricity on a plate arranged in front of the tube. However, the stability of these dots proved difficult to maintain in the presence of external electrical signals, which were common in computer settings. The Mellon system replaced the static charges with light, which was much more resistant to external influence.
Writing
Writing to the cell was accomplished by an external cathode ray tube (CRT) arranged in front of the photoemissive side of the grid. Cells were activated by using the deflection coils in the CRT to pull the beam into position in front of the cell, lighting up the front of the tube in that location. This initial pulse of light, focussed through a lens, would set the cell to the "on" state. Due to the way the photoemissive layer worked, focusing light on it again when it was already "lit up" would overload the material, stopping electrons from flowing out the other side into the interior of the cell. When the external light was then removed, the cell was dark, turning it off.
Reading
Reading the cells was accomplished by a grid of photocells arranged behind the phosphorescent layer, which emitted photons omnidirectionally. This allowed the cells to be read from the back of the device, as long as the phosphorescent layer was thin enough. To form a complete memory the system was arranged to be regenerative, with the output of the photocells being amplified and sent back into the CRT to refresh the cells periodically.
References
- Echert Jr., J.P., "A Survey of Digital Computer Memory Systems", Proceedings of the IRE, October 1953. Reprinted in IEEE Annals of the History of Computing, Vol.20, No.4, 1998
https://en.wikipedia.org/wiki/Mellon_optical_memory
The Selectron was an early form of digital computer memory developed by Jan A. Rajchman and his group at the Radio Corporation of America (RCA) under the direction of Vladimir K. Zworykin. It was a vacuum tube that stored digital data as electrostatic charges using technology similar to the Williams tube storage device. The team was never able to produce a commercially viable form of Selectron before magnetic-core memory became almost universal.
Development
Development of Selectron started in 1946 at the behest of John von Neumann of the Institute for Advanced Study,[1] who was in the midst of designing the IAS machine and was looking for a new form of high-speed memory.
RCA's original design concept had a capacity of 4096 bits, with a planned production of 200 by the end of 1946. They found the device to be much more difficult to build than expected, and they were still not available by the middle of 1948. As development dragged on, the IAS machine was forced to switch to Williams tubes for storage, and the primary customer for Selectron disappeared. RCA lost interest in the design and assigned its engineers to improve televisions[2]
A contract from the US Air Force led to a re-examination of the device in a 256-bit form. Rand Corporation took advantage of this project to switch their own IAS machine, the JOHNNIAC, to this new version of the Selectron, using 80 of them to provide 512 40-bit words of main memory. They signed a development contract with RCA to produce enough tubes for their machine at a projected cost of $500 per tube ($5631 in 2021).[2]
Around this time IBM expressed an interest in the Selectron as well, but this did not lead to additional production. As a result, RCA assigned their engineers to color television development, and put the Selectron in the hands of "the mothers-in-law of two deserving employees (the Chairman of the Board and the President)."[2]
Both the Selectron and the Williams tube were superseded in the market by the compact and cost-effective magnetic-core memory, in the early 1950s. The JOHNNIAC developers had decided to switch to core even before the first Selectron-based version had been completed.[2]
Principle of operation
Electrostatic storage
The Williams tube was an example of a general class of cathode ray tube (CRT) devices known as storage tubes.
The primary function of a conventional CRT is to display an image by lighting phosphor using a beam of electrons fired at it from an electron gun at the back of the tube. The target point of the beam is steered around the front of the tube though the use of deflection magnets or electrostatic plates.
Storage tubes were based on CRTs, sometimes unmodified. They relied on two normally undesirable principles of phosphor used in the tubes. One was that when electrons from the CRT's electron gun struck the phosphor to light it, some of the electrons "stuck" to the tube and caused a localized static electric charge to build up. The second was that the phosphor, like many materials, also released new electrons when struck by an electron beam, a process known as secondary emission.[3]
Secondary emission had the useful feature that the rate of electron release was significantly non-linear. When a voltage was applied that crossed a certain threshold, the rate of emission increased dramatically. This caused the lit spot to rapidly decay, which also caused any stuck electrons to be released as well. Visual systems used this process to erase the display, causing any stored pattern to rapidly fade. For computer uses it was the rapid release of the stuck charge that allowed it to be used for storage.
In the Williams tube, the electron gun at the back of an otherwise typical CRT is used to deposit a series of small patterns representing a 1 or 0 on the phosphor in a grid representing memory locations. To read the display, the beam scanned the tube again, this time set to a voltage very close to that of the secondary emission threshold. The patterns were selected to bias the tube very slightly positive or negative. When the stored static electricity was added to the voltage of the beam, the total voltage either crossed the secondary emission threshold or didn't. If it crossed the threshold, a burst of electrons was released as the dot decayed. This burst was read capacitively on a metal plate placed just in front of the display side of the tube.[4]
There were four general classes of storage tubes; the "surface redistribution type" represented by the Williams tube, the "barrier grid" system, which was unsuccessfully commercialized by RCA as the Radechon tube, the "sticking potential" type which was not used commercially, and the "holding beam" concept, of which the Selectron is a specific example.[5]
Holding beam concept
In the most basic implementation, the holding beam tube uses three electron guns; one for writing, one for reading, and a third "holding gun" that maintains the pattern. The general operation is very similar to the Williams tube in concept. The main difference was the holding gun, which fired continually and unfocussed so it covered the entire storage area on the phosphor. This caused the phosphor to be continually charged to a selected voltage, somewhat below that of the secondary emission threshold.[6]
Writing was accomplished by firing the writing gun at low voltage in a fashion similar to the Williams tube, adding a further voltage to the phosphor. Thus the storage pattern was the slight difference between two voltages stored on the tube, typically only a few tens of volts different.[6] In comparison, the Williams tube used much higher voltages, producing a pattern that could only be stored for a short period before it decayed below readability.
Reading was accomplished by scanning the reading gun across the storage area. This gun was set to a voltage that would cross the secondary emission threshold for the entire display. If the scanned area held the holding gun potential a certain number of electrons would be released, if it held the writing gun potential the number would be higher. The electrons were read on a grid of fine wires placed behind the display, making the system entirely self-contained. In contrast, the Williams tube's read plate was in front of the tube, and required continual mechanical adjustment to work properly.[6] The grid also had the advantage of breaking the display into individual spots without requiring the tight focus of the Williams system.
General operation was the same as the Williams system, but the holding concept had two major advantages. One was that it operated at much lower voltage differences and was thus able to safely store data for a longer period of time. The other was that the same deflection magnet drivers could be sent to several electron guns to produce a single larger device with no increase in complexity of the electronics.
Design
The Selectron further modified the basic holding gun concept through the use of individual metal eyelets that were used to store additional charge in a more predictable and long-lasting fashion.
Unlike a CRT where the electron gun is a single point source consisting of a filament and single charged accelerator, in the Selectron the "gun" is a plate and the accelerator is a grid of wires (thus borrowing some design notes from the barrier-grid tube). Switching circuits allow voltages to be applied to the wires to turn them on or off. When the gun fires through the eyelets, it is slightly defocussed. Some of the electrons strike the eyelet and deposit a charge on it.
The original 4096-bit Selectron[7] was a 10-inch-long (250 mm) by 3-inch-diameter (76 mm) vacuum tube configured as 1024 by 4 bits. It had an indirectly heated cathode running up the middle, surrounded by two separate sets of wires — one radial, one axial — forming a cylindrical grid array, and finally a dielectric storage material coating on the inside of four segments of an enclosing metal cylinder, called the signal plates. The bits were stored as discrete regions of charge on the smooth surfaces of the signal plates.
The two sets of orthogonal grid wires were normally "biased" slightly positive, so that the electrons from the cathode were accelerated through the grid to reach the dielectric. The continuous flow of electrons allowed the stored charge to be continuously regenerated by the secondary emission of electrons. To select a bit to be read from or written to, all but two adjacent wires on each of the two grids were biased negative, allowing current to flow to the dielectric at one location only.
In this respect, the Selectron works in the opposite sense of the Williams tube. In the Williams tube, the beam is continually scanning in a read/write cycle which is also used to regenerate data. In contrast, the Selectron is almost always regenerating the entire tube, only breaking this periodically to do actual reads and writes. This not only made operation faster due to the lack of required pauses but also meant the data was much more reliable as it was constantly refreshed.
Writing was accomplished by selecting a bit, as above, and then sending a pulse of potential, either positive or negative, to the signal plate. With a bit selected, electrons would be pulled onto (with a positive potential) or pushed from (negative potential) the dielectric. When the bias on the grid was dropped, the electrons were trapped on the dielectric as a spot of static electricity.
To read from the device, a bit location was selected and a pulse sent from the cathode. If the dielectric for that bit contained a charge, the electrons would be pushed off the dielectric and read as a brief pulse of current in the signal plate. No such pulse meant that the dielectric must not have held a charge.
The smaller capacity 256-bit (128 by 2 bits) "production" device[8] was in a similar vacuum-tube envelope. It was built with two storage arrays of discrete "eyelets" on a rectangular plate, separated by a row of eight cathodes. The pin count was reduced from 44 for the 4096-bit device down to 31 pins and two coaxial signal output connectors. This version included visible green phosphors in each eyelet[citation needed] so that the bit status could also be read by eye.
Patents
- U.S. Patent 2,494,670 Cylindrical 4096-bit Selectron
- U.S. Patent 2,604,606 Planar 256-bit Selectron
References
Citations
- Rajchman, JA (1951). "The Selective Electrostatic Storage Tube". RCA Review. 12 (1): 53–97.
Bibliography
- Eckert Jr., J. Presper (October 1953). "A Survey of Digital Computer Memory Systems" (PDF). Proceedings of the IRE. 41 (10): 1393–1406. doi:10.1109/jrproc.1953.274316. S2CID 8564797. Republished in IEEE Annals of the History of Computing, Volume 20 Number 4 (October 1988), pp. 11–28 doi:10.1109/85.728227
- Knoll, Max; Kazan, B. (1952). Storage Tubes and Their Basic Principles (PDF). John Wiley and Sons.
External links
- The Selectron
- Early Devices display: Memories — has a picture of a 256-bit Selectron about halfway down the page
- More pictures
- History of the RCA Selectron
https://en.wikipedia.org/wiki/Selectron_tube
Thyristor RAM (T-RAM) is a type of random-access memory dating from 2009 invented and developed by T-RAM Semiconductor, which departs from the usual designs of memory cells, combining the strengths of the DRAM and SRAM: high density and high speed.[citation needed] This technology, which exploits the electrical property known as negative differential resistance and is called thin capacitively-coupled thyristor,[1] is used to create memory cells capable of very high packing densities. Due to this, the memory is highly scalable, and already has a storage density that is several times higher than found in conventional 6T SRAM. It was expected that the next generation of T-RAM memory will have the same density as DRAM.[by whom?]
This technology exploits the electrical property known as negative differential resistor and is characterized by the way in which its memory cells are built, combining DRAM efficiency in terms of space with that of SRAM in terms of speed. Very similar to the current 6T-SRAM, or SRAM memories with 6 cell transistors, is substantially different because the SRAM latch CMOS, consisting of 4 of the 6 transistors of each cell, is replaced by a bipolar latch PNP -NPN of a single Thyristor. The result is to significantly reduce the area occupied by each cell, thus obtaining a highly scalable memory that has already reached storage density several times higher than the current SRAM.
The Thyristor-RAM provides the best density / performance ratio available between the various integrated memories, matching the performance of an SRAM memory, but allowing 2-3 times greater storage density and lower power consumption. It is expected that the new generation of T-RAM memory will have the same storage density as DRAMs.
Related items
References
- "T - R a M". Archived from the original on 2009-05-23. Retrieved 2009-09-19. Description of the technology
External links
- T-RAM Semiconductor
- T-RAM Description
- Farid Nemati (T-RAM Semiconductor), Thyristor RAM (T-RAM): A High-Speed High-Density Embedded Memory. Technology for Nano-scale CMOS / 2007 Hot Chips Conference, August 21, 2007
- EE Times: GlobalFoundries to apply thyristor-RAM at 32-nm node
- Semiconductor International: GlobalFoundries Outlines 22 nm Roadmap[permanent dead link]
https://en.wikipedia.org/wiki/T-RAM
To filter out static objects, two pulses were compared, and returns with the same delay times were removed. To do this, the signal sent from the receiver to the display was split in two, with one path leading directly to the display and the second leading to a delay unit. The delay was carefully tuned to be some multiple of the time between pulses, or "pulse repetition frequency". This resulted in the delayed signal from an earlier pulse exiting the delay unit the same time that the signal from a newer pulse was received from the antenna. One of the signals was electrically inverted, typically the one from the delay, and the two signals were then combined and sent to the display. Any signal that was at the same location was nullified by the inverted signal from a previous pulse, leaving only the moving objects on the display.
Several different types of delay systems were invented for this purpose, with one common principle being that the information was stored acoustically in a medium. MIT experimented with a number of systems, including glass, quartz, steel and lead. The Japanese deployed a system consisting of a quartz element with a powdered glass coating that reduced surface waves that interfered with proper reception. The United States Naval Research Laboratory used steel rods wrapped into a helix, but this was useful only for low frequencies under 1 MHz. Raytheon used a magnesium alloy originally developed for making bells.[2]
https://en.wikipedia.org/wiki/Delay-line_memory
Magnetostriction (cf. electrostriction) is a property of magnetic materials that causes them to change their shape or dimensions during the process of magnetization. The variation of materials' magnetization due to the applied magnetic field changes the magnetostrictive strain until reaching its saturation value, λ. The effect was first identified in 1842 by James Joule when observing a sample of iron.[1]
This effect causes energy loss due to frictional heating in susceptible ferromagnetic cores. The effect is also responsible for the low-pitched humming sound that can be heard coming from transformers, where oscillating AC currents produce a changing magnetic field.[2]
https://en.wikipedia.org/wiki/Magnetostriction
Explanation
Internally, ferromagnetic materials have a structure that is divided into domains, each of which is a region of uniform magnetization. When a magnetic field is applied, the boundaries between the domains shift and the domains rotate; both of these effects cause a change in the material's dimensions. The reason that a change in the magnetic domains of a material results in a change in the material's dimensions is a consequence of magnetocrystalline anisotropy; it takes more energy to magnetize a crystalline material in one direction than in another. If a magnetic field is applied to the material at an angle to an easy axis of magnetization, the material will tend to rearrange its structure so that an easy axis is aligned with the field to minimize the free energy of the system. Since different crystal directions are associated with different lengths, this effect induces a strain in the material.[3]
The reciprocal effect, the change of the magnetic susceptibility (response to an applied field) of a material when subjected to a mechanical stress, is called the Villari effect. Two other effects are related to magnetostriction: the Matteucci effect is the creation of a helical anisotropy of the susceptibility of a magnetostrictive material when subjected to a torque and the Wiedemann effect is the twisting of these materials when a helical magnetic field is applied to them.
The Villari reversal is the change in sign of the magnetostriction of iron from positive to negative when exposed to magnetic fields of approximately 40 kA/m.
On magnetization, a magnetic material undergoes changes in volume which are small: of the order 10−6.
Magnetostrictive hysteresis loop
Like flux density, the magnetostriction also exhibits hysteresis versus the strength of the magnetizing field. The shape of this hysteresis loop (called "dragonfly loop") can be reproduced using the Jiles-Atherton model.[4]
Magnetostrictive materials
Magnetostrictive materials can convert magnetic energy into kinetic energy, or the reverse, and are used to build actuators and sensors.
The property can be quantified by the magnetostrictive coefficient, λ,
which may be positive or negative and is defined as the fractional
change in length as the magnetization of the material increases from
zero to the saturation value. The effect is responsible for the familiar "electric hum" (![]() Listen (help·info)) which can be heard near transformers and high power electrical devices.
Listen (help·info)) which can be heard near transformers and high power electrical devices.
Cobalt exhibits the largest room-temperature magnetostriction of a pure element at 60 microstrains. Among alloys, the highest known magnetostriction is exhibited by Terfenol-D, (Ter for terbium, Fe for iron, NOL for Naval Ordnance Laboratory, and D for dysprosium). Terfenol-D, TbxDy1−xFe2, exhibits about 2,000 microstrains in a field of 160 kA/m (2 kOe) at room temperature and is the most commonly used engineering magnetostrictive material.[5] Galfenol, FexGa1−x, and Alfer, FexAl1−x, are newer alloys that exhibit 200-400 microstrains at lower applied fields (~200 Oe) and have enhanced mechanical properties from the brittle Terfenol-D. Both of these alloys have <100> easy axes for magnetostriction and demonstrate sufficient ductility for sensor and actuator applications.[6]
Another very common magnetostrictive composite is the amorphous alloy Fe81Si3.5B13.5C2 with its trade name Metglas 2605SC. Favourable properties of this material are its high saturation-magnetostriction constant, λ, of about 20 microstrains and more, coupled with a low magnetic-anisotropy field strength, HA, of less than 1 kA/m (to reach magnetic saturation). Metglas 2605SC also exhibits a very strong ΔE-effect with reductions in the effective Young's modulus up to about 80% in bulk. This helps build energy-efficient magnetic MEMS.[citation needed]
Cobalt ferrite, CoFe2O4 (CoO·Fe2O3), is also mainly used for its magnetostrictive applications like sensors and actuators, thanks to its high saturation magnetostriction (~200 parts per million).[7] In the absence of rare-earth elements, it is a good substitute for Terfenol-D.[8] Moreover, its magnetostrictive properties can be tuned by inducing a magnetic uniaxial anisotropy.[9] This can be done by magnetic annealing,[10] magnetic field assisted compaction,[11] or reaction under uniaxial pressure.[12] This last solution has the advantage of being ultrafast (20 min), thanks to the use of spark plasma sintering.
In early sonar transducers during World War II, nickel was used as a magnetostrictive material. To alleviate the shortage of nickel, the Japanese navy used an iron-aluminium alloy from the Alperm family.
Mechanical behaviors of magnetostrictive alloys
Effect of microstructure on elastic strain
Single-crystal alloys exhibit superior microstrain, but are vulnerable to yielding due to the anisotropic mechanical properties of most metals. It has been observed that for polycrystalline alloys with a high area coverage of preferential grains for microstrain, the mechanical properties (ductility) of magnetostrictive alloys can be significantly improved. Targeted metallurgical processing steps promote abnormal grain growth of {011} grains in galfenol and alfenol thin sheets, which contain two easy axes for magnetic domain alignment during magnetostriction. This can be accomplished by adding particles such as boride species [13] and niobium carbide (NbC) [14] during initial chill casting of the ingot.
For a polycrystalline alloy, an established formula for the magnetostriction, λ, from known directional microstrain measurements is:[15]
λs = 1/5(2λ100+3λ111)
During subsequent hot rolling and recrystallization steps, particle strengthening occurs in which the particles introduce a “pinning” force at grain boundaries that hinders normal (stochastic) grain growth in an annealing step assisted by a H2S atmosphere. Thus, single-crystal-like texture (~90% {011} grain coverage) is attainable, reducing the interference with magnetic domain alignment and increasing microstrain attainable for polycrystalline alloys as measured by semiconducting strain gauges.[16] These surface textures can be visualized using electron backscatter diffraction (EBSD) or related diffraction techniques.
Compressive stress to induce domain alignment
For actuator applications, maximum rotation of magnetic moments leads to the highest possible magnetostriction output. This can be achieved by processing techniques such as stress annealing and field annealing. However, mechanical pre-stresses can also be applied to thin sheets to induce alignment perpendicular to actuation as long as the stress is below the buckling limit. For example, it has been demonstrated that applied compressive pre-stress of up to ~50 MPa can result in an increase of magnetostriction by ~90%. This is hypothesized to be due to a "jump" in initial alignment of domains perpendicular to applied stress and improved final alignment parallel to applied stress.[17]
Constitutive behavior of magnetostrictive materials
These materials generally show non-linear behavior with a change in applied magnetic field or stress. For small magnetic fields, linear piezomagnetic constitutive[18] behavior is enough. Non-linear magnetic behavior is captured using a classical macroscopic model such as the Preisach model[19] and Jiles-Atherton model.[20] For capturing magneto-mechanical behavior, Armstrong[21] proposed an "energy average" approach. More recently, Wahi et al.[22] have proposed a computationally efficient constitutive model wherein constitutive behavior is captured using a "locally linearizing" scheme.
Applications
- Electronic article surveillance – using magnetostriction to prevent shoplifting
- Magnetostrictive delay lines - an earlier form of computer memory
- Magnetostrictive loudspeakers and headphones
See also
- Electromagnetically induced acoustic noise and vibration
- Inverse magnetostrictive effect
- Wiedemann effect – a torsional force caused by magnetostriction
- Magnetomechanical effects for a collection of similar effects
- Magnetocaloric effect
- Electrostriction
- Piezoelectricity
- Piezomagnetism
- SoundBug
- FeONIC – developer of audio products using magnetostriction
- Terfenol-D
- Galfenol
References
- Wahi, Sajan K.; Kumar, Manik; Santapuri, Sushma; Dapino, Marcelo J. (2019-06-07). "Computationally efficient locally linearized constitutive model for magnetostrictive materials". Journal of Applied Physics. 125 (21): 215108. Bibcode:2019JAP...125u5108W. doi:10.1063/1.5086953. ISSN 0021-8979. S2CID 189954942.
External links
- Magnetostriction
- "Magnetostriction and transformer noise" (PDF). Archived from the original (PDF) on 2006-05-10.
- Invisible Speakers from Feonic that use Magnetostriction
- Magnetostrictive alloy maker: REMA-CN Archived 2017-03-21 at the Wayback Machine
https://en.wikipedia.org/wiki/Magnetostriction
https://en.wikipedia.org/wiki/Alternating_current
Alternating current (AC) is an electric current which periodically reverses direction and changes its magnitude continuously with time in contrast to direct current (DC), which flows only in one direction. Alternating current is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans and electric lamps into a wall socket. A common source of DC power is a battery cell in a flashlight. The abbreviations AC and DC are often used to mean simply alternating and direct, respectively, as when they modify current or voltage.[1][2]
The usual waveform of alternating current in most electric power circuits is a sine wave, whose positive half-period corresponds with positive direction of the current and vice versa. In certain applications, like guitar amplifiers, different waveforms are used, such as triangular waves or square waves. Audio and radio signals carried on electrical wires are also examples of alternating current. These types of alternating current carry information such as sound (audio) or images (video) sometimes carried by modulation of an AC carrier signal. These currents typically alternate at higher frequencies than those used in power transmission.
https://en.wikipedia.org/wiki/Alternating_current
The pulse repetition frequency (PRF) is the number of pulses of a repeating signal in a specific time unit. The term is used within a number of technical disciplines, notably radar.
In radar, a radio signal of a particular carrier frequency is turned on and off; the term "frequency" refers to the carrier, while the PRF refers to the number of switches. Both are measured in terms of cycle per second, or hertz. The PRF is normally much lower than the frequency. For instance, a typical World War II radar like the Type 7 GCI radar had a basic carrier frequency of 209 MHz (209 million cycles per second) and a PRF of 300 or 500 pulses per second. A related measure is the pulse width, the amount of time the transmitter is turned on during each pulse.
After producing a brief pulse of radio signal, the transmitter is turned off in order for the receiver units to hear the reflections of that signal off distant targets. Since the radio signal has to travel out to the target and back again, the required inter-pulse quiet period is a function of the radar's desired range. Longer periods are required for longer range signals, requiring lower PRFs. Conversely, higher PRFs produce shorter maximum ranges, but broadcast more pulses, and thus radio energy, in a given time. This creates stronger reflections that make detection easier. Radar systems must balance these two competing requirements.
Using older electronics, PRFs were generally fixed to a specific value, or might be switched among a limited set of possible values. This gives each radar system a characteristic PRF, which can be used in electronic warfare to identify the type or class of a particular platform such as a ship or aircraft, or in some cases, a particular unit. Radar warning receivers in aircraft include a library of common PRFs which can identify not only the type of radar, but in some cases the mode of operation. This allowed pilots to be warned when an SA-2 SAM battery had "locked on", for instance. Modern radar systems are generally able to smoothly change their PRF, pulse width and carrier frequency, making identification much more difficult.
Sonar and lidar systems also have PRFs, as does any pulsed system. In the case of sonar, the term pulse repetition rate (PRR) is more common, although it refers to the same concept.
Introduction
Electromagnetic (e.g. radio or light) waves are conceptually pure single frequency phenomena while pulses may be mathematically thought of as composed of a number of pure frequencies that sum and nullify in interactions that create a pulse train of the specific amplitudes, PRRs, base frequencies, phase characteristics, et cetera (See Fourier Analysis). The first term (PRF) is more common in device technical literature (Electrical Engineering and some sciences), and the latter (PRR) more commonly used in military-aerospace terminology (especially United States armed forces terminologies) and equipment specifications such as training and technical manuals for radar and sonar systems.
The reciprocal of PRF (or PRR) is called the pulse repetition time (PRT), pulse repetition interval (PRI), or inter-pulse period (IPP), which is the elapsed time from the beginning of one pulse to the beginning of the next pulse. The IPP term is normally used when referring to the quantity of PRT periods to be processed digitally. Each PRT having a fixed number of range gates, but not all of them being used. For example, the APY-1 radar used 128 IPP's with a fixed 50 range gates, producing 128 Doppler filters using an FFT. The different number of range gates on each of the five PRF's all being less than 50.
Within radar technology PRF is important since it determines the maximum target range (Rmax) and maximum Doppler velocity (Vmax) that can be accurately determined by the radar.[1] Conversely, a high PRR/PRF can enhance target discrimination of nearer objects, such as a periscope or fast moving missile. This leads to use of low PRRs for search radar, and very high PRFs for fire control radars. Many dual-purpose and navigation radars—especially naval designs with variable PRRs—allow a skilled operator to adjust PRR to enhance and clarify the radar picture—for example in bad sea states where wave action generates false returns, and in general for less clutter, or perhaps a better return signal off a prominent landscape feature (e.g., a cliff).
https://en.wikipedia.org/wiki/Pulse_repetition_frequency
A radar system consists principally of an antenna, a transmitter, a receiver, and a display. The antenna is connected to the transmitter, which sends out a brief pulse of radio energy before being disconnected again. The antenna is then connected to the receiver, which amplifies any reflected signals and sends them to the display. Objects farther from the radar return echos later than those closer to the radar, which the display indicates visually as a "blip", which can be measured against a scale.
https://en.wikipedia.org/wiki/Delay-line_memory
The first practical de-cluttering system based on the concept was developed by J. Presper Eckert at the University of Pennsylvania's Moore School of Electrical Engineering. His solution used a column of mercury with piezo crystal transducers (a combination of speaker and microphone) at either end. Signals from the radar amplifier were sent to the transducer at one end of the tube, which would generate a small wave in the mercury. The wave would quickly travel to the far end of the tube, where it would be read back out by the other transducer, inverted, and sent to the display. Careful mechanical arrangement was needed to ensure that the delay time matched the inter-pulse timing of the radar being used.
All of these systems were suitable for conversion into a computer memory. The key was to recycle the signals within the memory system, so they would not disappear after traveling through the delay. This was relatively easy to arrange with simple electronics.
https://en.wikipedia.org/wiki/Delay-line_memory
Mercury was used because its acoustic impedance is close to that of the piezoelectric quartz crystals; this minimized the energy loss and the echoes when the signal was transmitted from crystal to medium and back again. The high speed of sound in mercury (1450 m/s) meant that the time needed to wait for a pulse to arrive at the receiving end was less than it would have been with a slower medium, such as air (343.2 m/s), but it also meant that the total number of pulses that could be stored in any reasonably sized column of mercury was limited. Other technical drawbacks of mercury included its weight, its cost, and its toxicity. Moreover, to get the acoustic impedances to match as closely as possible, the mercury had to be kept at a constant temperature. The system heated the mercury to a uniform above-room temperature setting of 40 °C (104 °F), which made servicing the tubes hot and uncomfortable work. (Alan Turing proposed the use of gin as an ultrasonic delay medium, claiming that it had the necessary acoustic properties.[3])
A considerable amount of engineering was needed to maintain a "clean" signal inside the tube. Large transducers were used to generate a very tight "beam" of sound that would not touch the walls of the tube, and care had to be taken to eliminate reflections from the far end of the tubes. The tightness of the beam then required considerable tuning to make sure that both transducers were pointed directly at each other. Since the speed of sound changes with temperature, the tubes were heated in large ovens to keep them at a precise temperature. Other systems[specify] instead adjusted the computer clock rate according to the ambient temperature to achieve the same effect.
EDSAC, the second full-scale stored-program digital computer, began operation with 256 35-bit words of memory, stored in 16 delay lines holding 560 bits each (words in the delay line were composed from 36 pulses, one pulse was used as a space between consecutive numbers).[4] The memory was later expanded to 512 words by adding a second set of 16 delay lines. In the UNIVAC I the capacity of an individual delay line was smaller, each column stored 120 bits (although the term "bit" was not in popular use at the time), requiring 7 large memory units with 18 columns each to make up a 1000-word store. Combined with their support circuitry and amplifiers, the memory subsystem formed its own walk-in room. The average access time was about 222 microseconds, which was considerably faster than the mechanical systems used on earlier computers.
CSIRAC, completed in November 1949, also used delay-line memory.
Some mercury delay-line memory devices produced audible sounds, which were described as akin to a human voice mumbling. This property gave rise to the slang term "mumble-tub" for these devices.
Magnetostrictive delay lines
A later version of the delay line used steel wires as the storage medium. Transducers were built by applying the magnetostrictive effect; small pieces of a magnetostrictive material, typically nickel, were attached to either side of the end of the wire, inside an electromagnet. When bits from the computer entered the magnets, the nickel would contract or expand (based on the polarity) and twist the end of the wire. The resulting torsional wave would then move down the wire just as the sound wave did down the mercury column.
Unlike the compressive wave used in earlier devices, torsional waves are considerably more resistant to problems caused by mechanical imperfections, so much that the wires could be wound into a loose coil and pinned to a board. Due to their ability to be coiled, the wire-based systems could be built as "long" as needed and tended to hold considerably more data per unit; 1 kbit units were typical on a board only 1 foot square (~30 cm × 30 cm). Of course, this also meant that the time needed to find a particular bit was somewhat longer as it travelled through the wire, and access times on the order of 500 microseconds were typical.
Delay-line memory was far less expensive and far more reliable per bit than flip-flops made from tubes, and yet far faster than a latching relay. It was used right into the late 1960s, notably on commercial machines like the LEO I, Highgate Wood Telephone Exchange, various Ferranti machines, and the IBM 2848 Display Control. Delay-line memory was also used for video memory in early terminals, where one delay line would typically store 4 lines of characters (4 lines × 40 characters per line × 6 bits per character = 960 bits in one delay line). They were also used very successfully in several models of early desktop electronic calculator, including the Friden EC-130 (1964) and EC-132, the Olivetti Programma 101 desktop programmable calculator introduced in 1965, and the Litton Monroe Epic 2000 and 3000 programmable calculators of 1967.
Piezoelectric delay lines
A similar solution to the magnetostrictive system was to use delay lines made entirely of a piezoelectric material, typically quartz. Current fed into one end of the crystal would generate a compressive wave that would flow to the other end, where it could be read. In effect, piezoelectric material simply replaced the mercury and transducers of a conventional mercury delay line with a single unit combining both. However, these solutions were fairly rare; growing crystals of the required quality in large sizes was not easy, which limited them to small sizes and thus small amounts of data storage.[5]
A better and more widespread use of piezoelectric delay lines was in European television sets. The European PAL standard for color broadcasts compares the signal from two successive lines of the image in order to avoid color shifting due to small phase shifts. By comparing two lines, one of which is inverted, the shifting is averaged, and the resulting signal more closely matches the original signal, even in the presence of interference. In order to compare the two lines, a piezoelectric delay unit to delay the signal by a time that is equal to the duration of each line, 64 µs, is inserted in one of the two signal paths that are compared.[6] In order to produce the required delay in a crystal of convenient size, the delay unit is shaped to reflect the signal multiple times through the crystal, thereby greatly reducing the required size of the crystal and thus producing a small, rectangular-shaped device.
Electric delay lines
Electric delay lines are used for shorter delay times (nanoseconds to several microseconds). They consist of a long electric line or are made of discrete inductors and capacitors, which are arranged in a chain. To shorten the total length of the line, it can be wound around a metal tube, getting some more capacitance against ground and also more inductance due to the wire windings, which are lying close together.
Other examples are:
- short coaxial or microstrip lines for phase matching in high-frequency circuits or antennas,
- hollow resonator lines in magnetrons and klystrons as helices in travelling-wave tubes to match the velocity of the electrons to the velocity of the electromagnetic waves,
- undulators in free-electron lasers.
Another way to create a delay time is to implement a delay line in an integrated circuit storage device. This can be done digitally or with a discrete analogue method. The analogue one uses bucket-brigade devices or charge-coupled devices (CCD), which transport a stored electric charge stepwise from one end to the other. Both digital and analog methods are bandwidth limited at the upper end to the half of the clock frequency, which determines the steps of transportation.
In modern computers operating at gigahertz speeds, millimeter differences in the length of conductors in a parallel data bus can cause data-bit skew, which can lead to data corruption or reduced processing performance. This is remedied by making all conductor paths of similar length, delaying the arrival time for what would otherwise be shorter travel distances by using zig-zagging traces.
References
- Backers, F.T. (1968). Ultrasonic delay lines for the PAL colour-television system (PDF) (Ph.D.). Eindhoven, Netherlands: Technische Universiteit. pp. 7–8.
Backers, F. Th. (1968). "A delay line for PAL colour television receivers" (PDF). Philips Technical Review. 29: 243–251.
External links
- Acoustic Delay Line Memory – has an image of a Ferranti wire-based system about halfway down the page
- Delay line memories – contains a diagram of the magnetostrictive transducer
- Litton Monroe Epic 3000 - Shows details of the torsion delay lines inside this electronic calculator of 1967
- Magnetostrictive memory, still used in a German computer museum
- U.S. Patent 2,629,827 "Memory System", Eckert–Mauchly Computer Corporation, filed October 1947, patented February 1953
- Display Terminal built with 32 TV delay lines Complete description
- "What store for EDSAC?". The National Museum of Computing. 13 September 2013. How nickel delay line memory works, some information about the construction
- Nickel delay line for EDSAC replica
https://en.wikipedia.org/wiki/Delay-line_memory
An analog delay line is a network of electrical components connected in cascade[dubious ], where each individual element creates a time difference between its input and output. It operates on analog signals whose amplitude varies continuously. In the case of a periodic signal, the time difference can be described in terms of a change in the phase of the signal. One example of an analog delay line is a bucket-brigade device.[1]
Other types of delay line include acoustic (usually ultrasonic), magnetostrictive, and surface acoustic wave devices. A series of resistor–capacitor circuits (RC circuits) can be cascaded to form a delay. A long transmission line can also provide a delay element. The delay time of an analog delay line may be only a few nanoseconds or several milliseconds, limited by the practical size of the physical medium used to delay the signal and the propagation speed of impulses in the medium.
Analog delay lines are applied in many types of signal processing circuits; for example the PAL television standard uses an analog delay line to store an entire video scanline. Acoustic and electromechanical delay lines are used to provide a "reverberation" effect in musical instrument amplifiers, or to simulate an echo. High-speed oscilloscopes used an analog delay line to allow observation of waveforms just before some triggering event.
With the growing use of digital signal processing techniques, digital forms of delay are practical and eliminate some of the problems with dissipation and noise in analog systems.
History
Inductor–capacitor ladder networks were used as analog delay lines in the 1920s. For example, Francis Hubbard's sonar direction finder patent filed in 1921.[2] Hubbard referred to this as an Artificial transmission line. In 1941, Gerald Tawney of Sperry Gyroscope Company filed for a patent on a compact packaging of an inductor–capacitor ladder network that he explicitly referred to as a time delay line.[3]
In 1924, Robert Mathes of Bell Telephone Laboratories filed a broad patent covering essentially all electromechanical delay lines, but focusing on acoustic delay lines where an air column confined to a pipe served as the mechanical medium, and a telephone receiver at one end and a telephone transmitter at the other end served as the electromechanical transducers.[4] Mathes was motivated by the problem of echo suppression on long-distance telephone lines, and his patent clearly explained the fundamental relationship between inductor–capacitor ladder networks and mechanical elastic delay lines such as his acoustic line.
In 1938, William Spencer Percival of Electrical & Musical Industries (later EMI) applied for a patent on an acoustical delay line using piezoelectric transducers and a liquid medium. He used water or kerosene, with a 10 MHz carrier frequency, with multiple baffles and reflectors in the delay tank to create a long acoustic path in a relatively small tank.[5]
In 1939, Laurens Hammond applied electromechanical delay lines to the problem of creating artificial reverberation for his Hammond organ.[6] Hammond used coil springs to transmit mechanical waves between voice-coil transducers.
The problem of suppressing multipath interference in television reception motivated Clarence Hansell of RCA to use delay lines in his 1939 patent application. He used "delay cables" for this, relatively short pieces of coaxial cable used as delay lines, but he recognized the possibility of using magnetostrictive or piezoelectric delay lines.[7]
By 1943, compact delay lines with distributed capacitance and inductance were devised. Typical early designs involved winding an enamel insulated wire on an insulating core and then surrounding that with a grounded conductive jacket. Richard Nelson of General Electric filed a patent for such a line that year.[8] Other GE employees, John Rubel and Roy Troell, concluded that the insulated wire could be wound around a conducting core to achieve the same effect.[9] Much of the development of delay lines during World War II was motivated by the problems encountered in radar systems.
In 1944, Madison G. Nicholson applied for a general patent on magnetostrictive delay lines. He recommended their use for applications requiring delays or measurement of intervals in the 10 to 1000 microseconds time range.[10]
In 1945, Gordon D. Forbes and Herbert Shapiro filed a patent for the mercury delay line with piezoelectric transducers.[11] This delay line technology would play an important role, serving as the basis of the delay-line memory used in several first-generation computers.
In 1946, David Arenberg filed patents covering the use of piezoelectric transducers attached to single crystal solid delay lines. He tried using quartz as a delay medium and reported that anisotropy in the quartz crystals caused problems. He reported success with single crystals of lithium bromide, sodium chloride and aluminum.[12][13] Arlenberg developed the idea of complex 2- and 3-dimensional folding of the acoustic path in the solid medium in order to package long delays into a compact crystal.[14] The delay lines used to decode PAL television signals follow the outline of this patent, using quartz glass as a medium instead of a single crystal.
See also
References
- David L. Arenberg, Solid Delay Line, U.S. Patent 2,624,804, granted Jan. 6, 1953.
https://en.wikipedia.org/wiki/Analog_delay_line
An amplifier, electronic amplifier or (informally) amp is an electronic device that can increase the magnitude of a signal (a time-varying voltage or current). A power amplifier is similarly used to deliver output power (AF or RF), controlled by an input signal. It is a two-port electronic circuit that uses electric power from a power supply to increase the amplitude (magnitude of the voltage or current) of a signal applied to its input terminals, producing a proportionally greater amplitude signal at its output. The amount of amplification provided by an amplifier is measured by its gain: the ratio of output voltage, current, or power to input. An amplifier is a circuit that has a power gain greater than one.[2][3][4]
An amplifier can either be a separate piece of equipment or an electrical circuit contained within another device. Amplification is fundamental to modern electronics, and amplifiers are widely used in almost all electronic equipment. Amplifiers can be categorized in different ways. One is by the frequency of the electronic signal being amplified. For example, audio amplifiers amplify signals in the audio (sound) range of less than 20 kHz, RF amplifiers amplify frequencies in the radio frequency range between 20 kHz and 300 GHz, and servo amplifiers and instrumentation amplifiers may work with very low frequencies down to direct current. Amplifiers can also be categorized by their physical placement in the signal chain; a preamplifier may precede other signal processing stages, for example.[5] The first practical electrical device which could amplify was the triode vacuum tube, invented in 1906 by Lee De Forest, which led to the first amplifiers around 1912. Today most amplifiers use transistors.
History
Vacuum tubes
The first practical prominent device that could amplify was the triode vacuum tube, invented in 1906 by Lee De Forest, which led to the first amplifiers around 1912. Vacuum tubes were used in almost all amplifiers until the 1960s–1970s when transistors replaced them. Today, most amplifiers use transistors, but vacuum tubes continue to be used in some applications.
The development of audio communication technology in form of the telephone, first patented in 1876, created the need to increase the amplitude of electrical signals to extend the transmission of signals over increasingly long distances. In telegraphy, this problem had been solved with intermediate devices at stations that replenished the dissipated energy by operating a signal recorder and transmitter back-to-back, forming a relay, so that a local energy source at each intermediate station powered the next leg of transmission. For duplex transmission, i.e. sending and receiving in both directions, bi-directional relay repeaters were developed starting with the work of C. F. Varley for telegraphic transmission. Duplex transmission was essential for telephony and the problem was not satisfactorily solved until 1904, when H. E. Shreeve of the American Telephone and Telegraph Company improved existing attempts at constructing a telephone repeater consisting of back-to-back carbon-granule transmitter and electrodynamic receiver pairs.[6] The Shreeve repeater was first tested on a line between Boston and Amesbury, MA, and more refined devices remained in service for some time. After the turn of the century it was found that negative resistance mercury lamps could amplify, and were also tried in repeaters, with little success.[7]
The development of thermionic valves starting around 1902, provided an entirely electronic method of amplifying signals. The first practical version of such devices was the Audion triode, invented in 1906 by Lee De Forest,[8][9][10] which led to the first amplifiers around 1912.[11] Since the only previous device which was widely used to strengthen a signal was the relay used in telegraph systems, the amplifying vacuum tube was first called an electron relay.[12][13][14][15] The terms amplifier and amplification, derived from the Latin amplificare, (to enlarge or expand),[16] were first used for this new capability around 1915 when triodes became widespread.[16]
The amplifying vacuum tube revolutionized electrical technology, creating the new field of electronics, the technology of active electrical devices.[11] It made possible long-distance telephone lines, public address systems, radio broadcasting, talking motion pictures, practical audio recording, radar, television, and the first computers. For 50 years virtually all consumer electronic devices used vacuum tubes. Early tube amplifiers often had positive feedback (regeneration), which could increase gain but also make the amplifier unstable and prone to oscillation. Much of the mathematical theory of amplifiers was developed at Bell Telephone Laboratories during the 1920s to 1940s. Distortion levels in early amplifiers were high, usually around 5%, until 1934, when Harold Black developed negative feedback; this allowed the distortion levels to be greatly reduced, at the cost of lower gain. Other advances in the theory of amplification were made by Harry Nyquist and Hendrik Wade Bode.[17]
The vacuum tube was virtually the only amplifying device, other than specialized power devices such as the magnetic amplifier and amplidyne, for 40 years. Power control circuitry used magnetic amplifiers until the latter half of the twentieth century when power semiconductor devices became more economical, with higher operating speeds. The old Shreeve electroacoustic carbon repeaters were used in adjustable amplifiers in telephone subscriber sets for the hearing impaired until the transistor provided smaller and higher quality amplifiers in the 1950s.[18]
Transistors
The first working transistor was a point-contact transistor invented by John Bardeen and Walter Brattain in 1947 at Bell Labs, where William Shockley later invented the bipolar junction transistor (BJT) in 1948. They were followed by the invention of the metal–oxide–semiconductor field-effect transistor (MOSFET) by Mohamed M. Atalla and Dawon Kahng at Bell Labs in 1959. Due to MOSFET scaling, the ability to scale down to increasingly small sizes, the MOSFET has since become the most widely used amplifier.[19]
The replacement of bulky electron tubes with transistors during the 1960s and 1970s created a revolution in electronics, making possible a large class of portable electronic devices, such as the transistor radio developed in 1954. Today, use of vacuum tubes is limited for some high power applications, such as radio transmitters.
Beginning in the 1970s, more and more transistors were connected on a single chip thereby creating higher scales of integration (such as small-scale, medium-scale and large-scale integration) in integrated circuits. Many amplifiers commercially available today are based on integrated circuits.
For special purposes, other active elements have been used. For example, in the early days of the satellite communication, parametric amplifiers were used. The core circuit was a diode whose capacitance was changed by an RF signal created locally. Under certain conditions, this RF signal provided energy that was modulated by the extremely weak satellite signal received at the earth station.
Advances in digital electronics since the late 20th century provided new alternatives to the traditional linear-gain amplifiers by using digital switching to vary the pulse-shape of fixed amplitude signals, resulting in devices such as the Class-D amplifier.
Ideal
In principle, an amplifier is an electrical two-port network that produces a signal at the output port that is a replica of the signal applied to the input port, but increased in magnitude.
The input port can be idealized as either being a voltage input, which takes no current, with the output proportional to the voltage across the port; or a current input, with no voltage across it, in which the output is proportional to the current through the port. The output port can be idealized as being either a dependent voltage source, with zero source resistance and its output voltage dependent on the input; or a dependent current source, with infinite source resistance and the output current dependent on the input. Combinations of these choices lead to four types of ideal amplifiers.[5] In idealized form they are represented by each of the four types of dependent source used in linear analysis, as shown in the figure, namely:
| Input | Output | Dependent source | Amplifier type | Gain units |
|---|---|---|---|---|
| I | I | Current controlled current source, CCCS | Current amplifier | Unitless |
| I | V | Current controlled voltage source, CCVS | Transresistance amplifier | Ohm |
| V | I | Voltage controlled current source, VCCS | Transconductance amplifier | Siemens |
| V | V | Voltage controlled voltage source, VCVS | Voltage amplifier | Unitless |
Each type of amplifier in its ideal form has an ideal input and output resistance that is the same as that of the corresponding dependent source:[20]
| Amplifier type | Dependent source | Input impedance | Output impedance |
|---|---|---|---|
| Current | CCCS | 0 | ∞ |
| Transresistance | CCVS | 0 | 0 |
| Transconductance | VCCS | ∞ | ∞ |
| Voltage | VCVS | ∞ | 0 |
In real amplifiers the ideal impedances are not possible to achieve, but these ideal elements can be used to construct equivalent circuits of real amplifiers by adding impedances (resistance, capacitance and inductance) to the input and output. For any particular circuit, a small-signal analysis is often used to find the actual impedance. A small-signal AC test current Ix is applied to the input or output node, all external sources are set to AC zero, and the corresponding alternating voltage Vx across the test current source determines the impedance seen at that node as R = Vx / Ix.[21]
Amplifiers designed to attach to a transmission line at input and output, especially RF amplifiers, do not fit into this classification approach. Rather than dealing with voltage or current individually, they ideally couple with an input or output impedance matched to the transmission line impedance, that is, match ratios of voltage to current. Many real RF amplifiers come close to this ideal. Although, for a given appropriate source and load impedance, RF amplifiers can be characterized as amplifying voltage or current, they fundamentally are amplifying power.[22]
Properties
Amplifier properties are given by parameters that include:
- Gain, the ratio between the magnitude of output and input signals
- Bandwidth, the width of the useful frequency range
- Efficiency, the ratio between the power of the output and total power consumption
- Linearity, the extent to which the proportion between input and output amplitude is the same for high amplitude and low amplitude input
- Noise, a measure of undesired noise mixed into the output
- Output dynamic range, the ratio of the largest and the smallest useful output levels
- Slew rate, the maximum rate of change of the output
- Rise time, settling time, ringing and overshoot that characterize the step response
- Stability, the ability to avoid self-oscillation
Amplifiers are described according to the properties of their inputs, their outputs, and how they relate.[23] All amplifiers have gain, a multiplication factor that relates the magnitude of some property of the output signal to a property of the input signal. The gain may be specified as the ratio of output voltage to input voltage (voltage gain), output power to input power (power gain), or some combination of current, voltage, and power. In many cases the property of the output that varies is dependent on the same property of the input, making the gain unitless (though often expressed in decibels (dB)).
Most amplifiers are designed to be linear. That is, they provide constant gain for any normal input level and output signal. If an amplifier's gain is not linear, the output signal can become distorted. There are, however, cases where variable gain is useful. Certain signal processing applications use exponential gain amplifiers.[5]
Amplifiers are usually designed to function well in a specific application, for example: radio and television transmitters and receivers, high-fidelity ("hi-fi") stereo equipment, microcomputers and other digital equipment, and guitar and other instrument amplifiers. Every amplifier includes at least one active device, such as a vacuum tube or transistor.
Negative feedback
Negative feedback is a technique used in most modern amplifiers to improve bandwidth and distortion and control gain. In a negative feedback amplifier part of the output is fed back and added to the input in opposite phase, subtracting from the input. The main effect is to reduce the overall gain of the system. However, any unwanted signals introduced by the amplifier, such as distortion are also fed back. Since they are not part of the original input, they are added to the input in opposite phase, subtracting them from the input. In this way, negative feedback also reduces nonlinearity, distortion and other errors introduced by the amplifier. Large amounts of negative feedback can reduce errors to the point that the response of the amplifier itself becomes almost irrelevant as long as it has a large gain, and the output performance of the system (the "closed loop performance") is defined entirely by the components in the feedback loop. This technique is particularly used with operational amplifiers (op-amps).
Non-feedback amplifiers can only achieve about 1% distortion for audio-frequency signals. With negative feedback, distortion can typically be reduced to 0.001%. Noise, even crossover distortion, can be practically eliminated. Negative feedback also compensates for changing temperatures, and degrading or nonlinear components in the gain stage, but any change or nonlinearity in the components in the feedback loop will affect the output. Indeed, the ability of the feedback loop to define the output is used to make active filter circuits.
Another advantage of negative feedback is that it extends the bandwidth of the amplifier. The concept of feedback is used in operational amplifiers to precisely define gain, bandwidth, and other parameters entirely based on the components in the feedback loop.
Negative feedback can be applied at each stage of an amplifier to stabilize the operating point of active devices against minor changes in power-supply voltage or device characteristics.
Some feedback, positive or negative, is unavoidable and often undesirable—introduced, for example, by parasitic elements, such as inherent capacitance between input and output of devices such as transistors, and capacitive coupling of external wiring. Excessive frequency-dependent positive feedback can produce parasitic oscillation and turn an amplifier into an oscillator.
Categories
Active devices
All amplifiers include some form of active device: this is the device that does the actual amplification. The active device can be a vacuum tube, discrete solid state component, such as a single transistor, or part of an integrated circuit, as in an op-amp).
Transistor amplifiers (or solid state amplifiers) are the most common type of amplifier in use today. A transistor is used as the active element. The gain of the amplifier is determined by the properties of the transistor itself as well as the circuit it is contained within.
Common active devices in transistor amplifiers include bipolar junction transistors (BJTs) and metal oxide semiconductor field-effect transistors (MOSFETs).
Applications are numerous, some common examples are audio amplifiers in a home stereo or public address system, RF high power generation for semiconductor equipment, to RF and microwave applications such as radio transmitters.
Transistor-based amplification can be realized using various configurations: for example a bipolar junction transistor can realize common base, common collector or common emitter amplification; a MOSFET can realize common gate, common source or common drain amplification. Each configuration has different characteristics.
Vacuum-tube amplifiers (also known as tube amplifiers or valve amplifiers) use a vacuum tube as the active device. While semiconductor amplifiers have largely displaced valve amplifiers for low-power applications, valve amplifiers can be much more cost effective in high power applications such as radar, countermeasures equipment, and communications equipment. Many microwave amplifiers are specially designed valve amplifiers, such as the klystron, gyrotron, traveling wave tube, and crossed-field amplifier, and these microwave valves provide much greater single-device power output at microwave frequencies than solid-state devices.[24] Vacuum tubes remain in use in some high end audio equipment, as well as in musical instrument amplifiers, due to a preference for "tube sound".
Magnetic amplifiers are devices somewhat similar to a transformer where one winding is used to control the saturation of a magnetic core and hence alter the impedance of the other winding.[25]
They have largely fallen out of use due to development in semiconductor amplifiers but are still useful in HVDC control, and in nuclear power control circuitry due to not being affected by radioactivity.
Negative resistances can be used as amplifiers, such as the tunnel diode amplifier.[26][27]
Power amplifiers
A power amplifier is an amplifier designed primarily to increase the power available to a load. In practice, amplifier power gain depends on the source and load impedances, as well as the inherent voltage and current gain. A radio frequency (RF) amplifier design typically optimizes impedances for power transfer, while audio and instrumentation amplifier designs normally optimize input and output impedance for least loading and highest signal integrity. An amplifier that is said to have a gain of 20 dB might have a voltage gain of 20 dB and an available power gain of much more than 20 dB (power ratio of 100)—yet actually deliver a much lower power gain if, for example, the input is from a 600 Ω microphone and the output connects to a 47 kΩ input socket for a power amplifier. In general, the power amplifier is the last 'amplifier' or actual circuit in a signal chain (the output stage) and is the amplifier stage that requires attention to power efficiency. Efficiency considerations lead to the various classes of power amplifiers based on the biasing of the output transistors or tubes: see power amplifier classes below.
Audio power amplifiers are typically used to drive loudspeakers. They will often have two output channels and deliver equal power to each. An RF power amplifier is found in radio transmitter final stages. A Servo motor controller: amplifies a control voltage to adjust the speed of a motor, or the position of a motorized system.
Operational amplifiers (op-amps)
An operational amplifier is an amplifier circuit which typically has very high open loop gain and differential inputs. Op amps have become very widely used as standardized "gain blocks" in circuits due to their versatility; their gain, bandwidth and other characteristics can be controlled by feedback through an external circuit. Though the term today commonly applies to integrated circuits, the original operational amplifier design used valves, and later designs used discrete transistor circuits.
A fully differential amplifier is similar to the operational amplifier, but also has differential outputs. These are usually constructed using BJTs or FETs.
Distributed amplifiers
These use balanced transmission lines to separate individual single stage amplifiers, the outputs of which are summed by the same transmission line. The transmission line is a balanced type with the input at one end and on one side only of the balanced transmission line and the output at the opposite end is also the opposite side of the balanced transmission line. The gain of each stage adds linearly to the output rather than multiplies one on the other as in a cascade configuration. This allows a higher bandwidth to be achieved than could otherwise be realised even with the same gain stage elements.
Switched mode amplifiers
These nonlinear amplifiers have much higher efficiencies than linear amps, and are used where the power saving justifies the extra complexity. Class-D amplifiers are the main example of this type of amplification.
Negative resistance amplifier
Negative Resistance Amplifier is a type of Regenerative Amplifier [28] that can use the feedback between the transistor's source and gate to transform a capacitive impedance on the transistor's source to a negative resistance on its gate. Compared to other types of amplifiers, this "negative resistance amplifier" will only require a tiny amount of power to achieve very high gain, maintaining a good noise figure at the same time.
Applications
Video amplifiers
Video amplifiers are designed to process video signals and have varying bandwidths depending on whether the video signal is for SDTV, EDTV, HDTV 720p or 1080i/p etc.. The specification of the bandwidth itself depends on what kind of filter is used—and at which point (−1 dB or −3 dB for example) the bandwidth is measured. Certain requirements for step response and overshoot are necessary for an acceptable TV image.[29]
Microwave amplifiers
Traveling wave tube amplifiers (TWTAs) are used for high power amplification at low microwave frequencies. They typically can amplify across a broad spectrum of frequencies; however, they are usually not as tunable as klystrons.[30]
Klystrons are specialized linear-beam vacuum-devices, designed to provide high power, widely tunable amplification of millimetre and sub-millimetre waves. Klystrons are designed for large scale operations and despite having a narrower bandwidth than TWTAs, they have the advantage of coherently amplifying a reference signal so its output may be precisely controlled in amplitude, frequency and phase.
Solid-state devices such as silicon short channel MOSFETs like double-diffused metal–oxide–semiconductor (DMOS) FETs, GaAs FETs, SiGe and GaAs heterojunction bipolar transistors/HBTs, HEMTs, IMPATT diodes, and others, are used especially at lower microwave frequencies and power levels on the order of watts specifically in applications like portable RF terminals/cell phones and access points where size and efficiency are the drivers. New materials like gallium nitride (GaN) or GaN on silicon or on silicon carbide/SiC are emerging in HEMT transistors and applications where improved efficiency, wide bandwidth, operation roughly from few to few tens of GHz with output power of few Watts to few hundred of Watts are needed.[31][32]
Depending on the amplifier specifications and size requirements microwave amplifiers can be realised as monolithically integrated, integrated as modules or based on discrete parts or any combination of those.
The maser is a non-electronic microwave amplifier.
Musical instrument amplifiers
Instrument amplifiers are a range of audio power amplifiers used to increase the sound level of musical instruments, for example guitars, during performances.
Classification of amplifier stages and systems
Common terminal
One set of classifications for amplifiers is based on which device terminal is common to both the input and the output circuit. In the case of bipolar junction transistors, the three classes are common emitter, common base, and common collector. For field-effect transistors, the corresponding configurations are common source, common gate, and common drain; for vacuum tubes, common cathode, common grid, and common plate.
The common emitter (or common source, common cathode, etc.) is most often configured to provide amplification of a voltage applied between base and emitter, and the output signal taken between collector and emitter is inverted, relative to the input. The common collector arrangement applies the input voltage between base and collector, and to take the output voltage between emitter and collector. This causes negative feedback, and the output voltage tends to follow the input voltage. This arrangement is also used as the input presents a high impedance and does not load the signal source, though the voltage amplification is less than one. The common-collector circuit is, therefore, better known as an emitter follower, source follower, or cathode follower.
Unilateral or bilateral
An amplifier whose output exhibits no feedback to its input side is described as 'unilateral'. The input impedance of a unilateral amplifier is independent of load, and output impedance is independent of signal source impedance.[33]
An amplifier that uses feedback to connect part of the output back to the input is a bilateral amplifier. Bilateral amplifier input impedance depends on the load, and output impedance on the signal source impedance. All amplifiers are bilateral to some degree; however they may often be modeled as unilateral under operating conditions where feedback is small enough to neglect for most purposes, simplifying analysis (see the common base article for an example).
Inverting or non-inverting
Another way to classify amplifiers is by the phase relationship of the input signal to the output signal. An 'inverting' amplifier produces an output 180 degrees out of phase with the input signal (that is, a polarity inversion or mirror image of the input as seen on an oscilloscope). A 'non-inverting' amplifier maintains the phase of the input signal waveforms. An emitter follower is a type of non-inverting amplifier, indicating that the signal at the emitter of a transistor is following (that is, matching with unity gain but perhaps an offset) the input signal. Voltage follower is also non inverting type of amplifier having unity gain.
This description can apply to a single stage of an amplifier, or to a complete amplifier system.
Function
Other amplifiers may be classified by their function or output characteristics. These functional descriptions usually apply to complete amplifier systems or sub-systems and rarely to individual stages.
- A servo amplifier indicates an integrated feedback loop to actively control the output at some desired level. A DC servo indicates use at frequencies down to DC levels, where the rapid fluctuations of an audio or RF signal do not occur. These are often used in mechanical actuators, or devices such as DC motors that must maintain a constant speed or torque. An AC servo amp. can do this for some AC motors.
- A linear amplifier responds to different frequency components independently, and does not generate harmonic distortion or intermodulation distortion. No amplifier can provide perfect linearity (even the most linear amplifier has some nonlinearities, since the amplifying devices—transistors or vacuum tubes—follow nonlinear power laws such as square-laws and rely on circuitry techniques to reduce those effects).
- A nonlinear amplifier generates significant distortion and so
changes the harmonic content; there are situations where this is
useful. Amplifier circuits intentionally providing a non-linear transfer function include:
- a device like a silicon controlled rectifier or a transistor used as a switch may be employed to turn either fully on or off a load such as a lamp based on a threshold in a continuously variable input.
- a non-linear amplifier in an analog computer or true RMS converter for example can provide a special transfer function, such as logarithmic or square-law.
- a Class C RF amplifier may be chosen because it can be very efficient—but is non-linear. Following such an amplifier with a so-called tank tuned circuit can reduce unwanted harmonics (distortion) sufficiently to make it useful in transmitters, or some desired harmonic may be selected by setting the resonant frequency of the tuned circuit to a higher frequency rather than fundamental frequency in frequency multiplier circuits.
- Automatic gain control circuits require an amplifier's gain be controlled by the time-averaged amplitude so that the output amplitude varies little when weak stations are being received. The non-linearities are assumed arranged so the relatively small signal amplitude suffers from little distortion (cross-channel interference or intermodulation) yet is still modulated by the relatively large gain-control DC voltage.
- AM detector circuits that use amplification such as anode-bend detectors, precision rectifiers and infinite impedance detectors (so excluding unamplified detectors such as cat's-whisker detectors), as well as peak detector circuits, rely on changes in amplification based on the signal's instantaneous amplitude to derive a direct current from an alternating current input.
- Operational amplifier comparator and detector circuits.
- A wideband amplifier has a precise amplification factor over a wide frequency range, and is often used to boost signals for relay in communications systems. A narrowband amp amplifies a specific narrow range of frequencies, to the exclusion of other frequencies.
- An RF amplifier amplifies signals in the radio frequency range of the electromagnetic spectrum, and is often used to increase the sensitivity of a receiver or the output power of a transmitter.[34]
- An audio amplifier amplifies audio frequencies. This category subdivides into small signal amplification, and power amps that are optimised to driving speakers,
sometimes with multiple amps grouped together as separate or bridgeable
channels to accommodate different audio reproduction requirements.
Frequently used terms within audio amplifiers include:
- Preamplifier (preamp.), which may include a phono preamp with RIAA equalization, or tape head preamps with CCIR equalisation filters. They may include filters or tone control circuitry.
- Power amplifier (normally drives loudspeakers), headphone amplifiers, and public address amplifiers.
- Stereo amplifiers imply two channels of output (left and right), though the term simply means "solid" sound (referring to three-dimensional)—so quadraphonic stereo was used for amplifiers with four channels. 5.1 and 7.1 systems refer to Home theatre systems with 5 or 7 normal spatial channels, plus a subwoofer channel.
- Buffer amplifiers, which may include emitter followers, provide a high impedance input for a device (perhaps another amplifier, or perhaps an energy-hungry load such as lights) that would otherwise draw too much current from the source. Line drivers are a type of buffer that feeds long or interference-prone interconnect cables, possibly with differential outputs through twisted pair cables.
Interstage coupling method
Amplifiers are sometimes classified by the coupling method of the signal at the input, output, or between stages. Different types of these include:
- Resistive-capacitive (RC) coupled amplifier, using a network of resistors and capacitors
- By design these amplifiers cannot amplify DC signals as the capacitors block the DC component of the input signal. RC-coupled amplifiers were used very often in circuits with vacuum tubes or discrete transistors. In the days of the integrated circuit a few more transistors on a chip are much cheaper and smaller than a capacitor.
- Inductive-capacitive (LC) coupled amplifier, using a network of inductors and capacitors
- This kind of amplifier is most often used in selective radio-frequency circuits.
- Transformer coupled amplifier, using a transformer to match impedances or to decouple parts of the circuits
- Quite often LC-coupled and transformer-coupled amplifiers cannot be distinguished as a transformer is some kind of inductor.
- Direct coupled amplifier, using no impedance and bias matching components
- This class of amplifier was very uncommon in the vacuum tube days when the anode (output) voltage was at greater than several hundred volts and the grid (input) voltage at a few volts minus. So they were only used if the gain was specified down to DC (e.g., in an oscilloscope). In the context of modern electronics developers are encouraged to use directly coupled amplifiers whenever possible. In FET and CMOS technologies direct coupling is dominant since gates of MOSFETs theoretically pass no current through themselves. Therefore, DC component of the input signals is automatically filtered.
Frequency range
Depending on the frequency range and other properties amplifiers are designed according to different principles.
Frequency ranges down to DC are only used when this property is needed. Amplifiers for direct current signals are vulnerable to minor variations in the properties of components with time. Special methods, such as chopper stabilized amplifiers are used to prevent objectionable drift in the amplifier's properties for DC. "DC-blocking" capacitors can be added to remove DC and sub-sonic frequencies from audio amplifiers.
Depending on the frequency range specified different design principles must be used. Up to the MHz range only "discrete" properties need be considered; e.g., a terminal has an input impedance.
As soon as any connection within the circuit gets longer than perhaps 1% of the wavelength of the highest specified frequency (e.g., at 100 MHz the wavelength is 3 m, so the critical connection length is approx. 3 cm) design properties radically change. For example, a specified length and width of a PCB trace can be used as a selective or impedance-matching entity. Above a few hundred MHz, it gets difficult to use discrete elements, especially inductors. In most cases, PCB traces of very closely defined shapes are used instead (stripline techniques).
The frequency range handled by an amplifier might be specified in terms of bandwidth (normally implying a response that is 3 dB down when the frequency reaches the specified bandwidth), or by specifying a frequency response that is within a certain number of decibels between a lower and an upper frequency (e.g. "20 Hz to 20 kHz plus or minus 1 dB").
Power amplifier classes
Power amplifier circuits (output stages) are classified as A, B, AB and C for analog designs—and class D and E for switching designs. The power amplifier classes are based on the proportion of each input cycle (conduction angle) during which an amplifying device passes current.[35] The image of the conduction angle derives from amplifying a sinusoidal signal. If the device is always on, the conducting angle is 360°. If it is on for only half of each cycle, the angle is 180°. The angle of flow is closely related to the amplifier power efficiency.
Example amplifier circuit
The practical amplifier circuit shown above could be the basis for a moderate-power audio amplifier. It features a typical (though substantially simplified) design as found in modern amplifiers, with a class-AB push–pull output stage, and uses some overall negative feedback. Bipolar transistors are shown, but this design would also be realizable with FETs or valves.
The input signal is coupled through capacitor C1 to the base of transistor Q1. The capacitor allows the AC signal to pass, but blocks the DC bias voltage established by resistors R1 and R2 so that any preceding circuit is not affected by it. Q1 and Q2 form a differential amplifier (an amplifier that multiplies the difference between two inputs by some constant), in an arrangement known as a long-tailed pair. This arrangement is used to conveniently allow the use of negative feedback, which is fed from the output to Q2 via R7 and R8.
The negative feedback into the difference amplifier allows the amplifier to compare the input to the actual output. The amplified signal from Q1 is directly fed to the second stage, Q3, which is a common emitter stage that provides further amplification of the signal and the DC bias for the output stages, Q4 and Q5. R6 provides the load for Q3 (a better design would probably use some form of active load here, such as a constant-current sink). So far, all of the amplifier is operating in class A. The output pair are arranged in class-AB push–pull, also called a complementary pair. They provide the majority of the current amplification (while consuming low quiescent current) and directly drive the load, connected via DC-blocking capacitor C2. The diodes D1 and D2 provide a small amount of constant voltage bias for the output pair, just biasing them into the conducting state so that crossover distortion is minimized. That is, the diodes push the output stage firmly into class-AB mode (assuming that the base-emitter drop of the output transistors is reduced by heat dissipation).
This design is simple, but a good basis for a practical design because it automatically stabilises its operating point, since feedback internally operates from DC up through the audio range and beyond. Further circuit elements would probably be found in a real design that would roll-off the frequency response above the needed range to prevent the possibility of unwanted oscillation. Also, the use of fixed diode bias as shown here can cause problems if the diodes are not both electrically and thermally matched to the output transistors – if the output transistors turn on too much, they can easily overheat and destroy themselves, as the full current from the power supply is not limited at this stage.
A common solution to help stabilise the output devices is to include some emitter resistors, typically one ohm or so. Calculating the values of the circuit's resistors and capacitors is done based on the components employed and the intended use of the amp.
Notes on implementation
Any real amplifier is an imperfect realization of an ideal amplifier. An important limitation of a real amplifier is that the output it generates is ultimately limited by the power available from the power supply. An amplifier saturates and clips the output if the input signal becomes too large for the amplifier to reproduce or exceeds operational limits for the device. The power supply may influence the output, so must be considered in the design. The power output from an amplifier cannot exceed its input power.
The amplifier circuit has an "open loop" performance. This is described by various parameters (gain, slew rate, output impedance, distortion, bandwidth, signal-to-noise ratio, etc.). Many modern amplifiers use negative feedback techniques to hold the gain at the desired value and reduce distortion. Negative loop feedback has the intended effect of lowering the output impedance and thereby increasing electrical damping of loudspeaker motion at and near the resonance frequency of the speaker.
When assessing rated amplifier power output, it is useful to consider the applied load, the signal type (e.g., speech or music), required power output duration (i.e., short-time or continuous), and required dynamic range (e.g., recorded or live audio). In high-powered audio applications that require long cables to the load (e.g., cinemas and shopping centres) it may be more efficient to connect to the load at line output voltage, with matching transformers at source and loads. This avoids long runs of heavy speaker cables.
To prevent instability or overheating requires care to ensure solid state amplifiers are adequately loaded. Most have a rated minimum load impedance.
All amplifiers generate heat through electrical losses. The amplifier must dissipate this heat via convection or forced air cooling. Heat can damage or reduce electronic component service life. Designers and installers must also consider heating effects on adjacent equipment.
Different power supply types result in many different methods of bias. Bias is a technique by which active devices are set to operate in a particular region, or by which the DC component of the output signal is set to the midpoint between the maximum voltages available from the power supply. Most amplifiers use several devices at each stage; they are typically matched in specifications except for polarity. Matched inverted polarity devices are called complementary pairs. Class-A amplifiers generally use only one device, unless the power supply is set to provide both positive and negative voltages, in which case a dual device symmetrical design may be used. Class-C amplifiers, by definition, use a single polarity supply.
Amplifiers often have multiple stages in cascade to increase gain. Each stage of these designs may be a different type of amp to suit the needs of that stage. For instance, the first stage might be a class-A stage, feeding a class-AB push–pull second stage, which then drives a class-G final output stage, taking advantage of the strengths of each type, while minimizing their weaknesses.
See also
- Charge transfer amplifier
- CMOS amplifiers
- Current sense amplifier
- Distributed amplifier
- Doherty amplifier
- Double-tuned amplifier
- Faithful amplification
- Intermediate power amplifier
- Low-noise amplifier
- Negative feedback amplifier
- Optical amplifier
- Power added efficiency
- Programmable-gain amplifier
- Tuned amplifier
References
- "Understanding Amplifier Operating "Classes"". electronicdesign.com. 2012-03-21. Retrieved 2016-06-20.
External links
- AES guide to amplifier classes
- "Amplifier Anatomy - Part 1" (PDF). Archived from the original (PDF) on 2004-06-10. – contains an explanation of different amplifier classes
- "Reinventing the power amplifier" (PDF). Archived from the original (PDF) on 2013-04-03.
https://en.wikipedia.org/wiki/Amplifier
https://en.wikipedia.org/wiki/Optical_amplifier
https://en.wikipedia.org/wiki/Tuned_amplifier
In electronics and telecommunications, pulse shaping is the process of changing a transmitted pulses' waveform to optimize the signal for its intended purpose or the communication channel. This is often done by limiting the bandwidth of the transmission and filtering the pulses to control intersymbol interference. Pulse shaping is particularly important in RF communication for fitting the signal within a certain frequency band and is typically applied after line coding and modulation.
Need for pulse shaping
Transmitting a signal at high modulation rate through a band-limited channel can create intersymbol interference. The reason for this are Fourier correspondences (see Fourier transform). A bandlimited signal corresponds to an infinite time signal, that causes neighbouring pulses to overlap. As the modulation rate increases, the signal's bandwidth increases.[1] As soon as the spectrum of the signal is a sharp rectangular, this leads to a sinc shape in the time domain. This happens if the bandwidth of the signal is larger than the channel bandwidth, leading to a distortion. This distortion usually manifests itself as intersymbol interference (ISI). Theoretically for sinc shaped pulses, there is no ISI, if neighbouring pulses are perfectly aligned, i.e. in the zero crossings of each other. But this requires a very good synchronization and precise/stable sampling without jitters. As a practical tool to determine ISI, one uses the Eye pattern, that visualizes typical effects of the channel and the synchronization/frequency stability.
The signal's spectrum is determined by the modulation scheme and data rate used by the transmitter, but can be modified with a pulse shaping filter. This pulse shaping will make the spectrum smooth, leading to a time limited signal again. Usually the transmitted symbols are represented as a time sequence of dirac delta pulses multiplied with the symbol. This is the formal transition from the digital to the analog domain. At this point, the bandwidth of the signal is unlimited. This theoretical signal is then filtered with the pulse shaping filter, producing the transmitted signal. If the pulse shaping filter is a rectangular in the time domain (like this is usually done when drawing it), this would lead to an unlimited spectrum.
In many base band communication systems the pulse shaping filter is implicitly a boxcar filter. Its Fourier transform is of the form sin(x)/x, and has significant signal power at frequencies higher than symbol rate. This is not a big problem when optical fibre or even twisted pair cable is used as the communication channel. However, in RF communications this would waste bandwidth, and only tightly specified frequency bands are used for single transmissions. In other words, the channel for the signal is band-limited. Therefore, better filters have been developed, which attempt to minimise the bandwidth needed for a certain symbol rate.
An example in other areas of electronics is the generation of pulses where the rise time need to be short; one way to do this is to start with a slower-rising pulse, and decrease the rise time, for example with a step recovery diode circuit.
These descriptions here provide a working knowledge, that cover most effects, but do not include causality, which would lead to analytical functions/signals. To understand this completely, one needs the Hilbert transform, that induces a direction by the convolution with the Cauchy Kernel. This couples the real and imaginary part of the baseband description, thereby adding structure. This immediately implies, that either the real or the imaginary part are enough to describe an analytical signal. By measuring both in a noisy setting, one has a redundancy, that can be used to better reconstruct the original signal. A physical realization is always causal, since an analytic signal carries the information.
Pulse shaping filters
Not every filter can be used as a pulse shaping filter. The filter itself must not introduce intersymbol interference — it needs to satisfy certain criteria. The Nyquist ISI criterion is a commonly used criterion for evaluation, because it relates the frequency spectrum of the transmitter signal to intersymbol interference.
Examples of pulse shaping filters that are commonly found in communication systems are:
- Sinc shaped filter
- Raised-cosine filter
- Gaussian filter
Sender side pulse shaping is often combined with a receiver side matched filter to achieve optimum tolerance for noise in the system. In this case the pulse shaping is equally distributed between the sender and receiver filters. The filters' amplitude responses are thus pointwise square roots of the system filters.
Other approaches that eliminate complex pulse shaping filters have been invented. In OFDM, the carriers are modulated so slowly that each carrier is virtually unaffected by the bandwidth limitation of the channel.
Sinc filter
It is also called as Boxcar filter as its frequency domain equivalent is a rectangular shape. Theoretically the best pulse shaping filter would be the sinc filter, but it cannot be implemented precisely. It is a non-causal filter with relatively slowly decaying tails. It is also problematic from a synchronisation point of view as any phase error results in steeply increasing intersymbol interference.
Raised-cosine filter
Raised-cosine is similar to sinc, with the tradeoff of smaller sidelobes for a slightly larger spectral width. Raised-cosine filters are practical to implement and they are in wide use. They have a configurable excess bandwidth, so communication systems can choose a trade off between a simpler filter and spectral efficiency.
Gaussian filter
This gives an output pulse shaped like a Gaussian function.
See also
- Nyquist ISI criterion
- Raised-cosine filter
- Matched filter
- Femtosecond pulse shaping
- Pulse (signal processing)
References
- Lathi, B. P. (2009). Modern digital and analog communication systems (4th ed.). New York: Oxford University Press. ISBN 9780195331455.
- John G. Proakis, "Digital Communications, 3rd Edition" Chapter 9, McGraw-Hill Book Co., 1995. ISBN 0-07-113814-5
- National Instruments Signal Generator Tutorial, Pulse Shaping to Improve Spectral Efficiency
- National Instruments Measurement Fundamentals Tutorial, Pulse-Shape Filtering in Communications Systems
- Root Raised Cosine Filters & Pulse Shaping in Communication Systems by Erkin Cubukcu (ntrs.nasa.gov).
https://en.wikipedia.org/wiki/Pulse_shaping
|
Units of information |
| Information-theoretic |
|---|
| Data storage |
| Quantum information |
The bit is the most basic unit of information in computing and digital communications. The name is a portmanteau of binary digit.[1] The bit represents a logical state with one of two possible values. These values are most commonly represented as either "1" or "0", but other representations such as true/false, yes/no, on/off, or +/− are also widely used.
The relation between these values and the physical states of the underlying storage or device is a matter of convention, and different assignments may be used even within the same device or program. It may be physically implemented with a two-state device.
A contiguous group of binary digits is commonly called a bit string, a bit vector, or a single-dimensional (or multi-dimensional) bit array. A group of eight bits is called one byte, but historically the size of the byte is not strictly defined.[2] Frequently, half, full, double and quadruple words consist of a number of bytes which is a low power of two. A string of four bits is a nibble.
In information theory, one bit is the information entropy of a random binary variable that is 0 or 1 with equal probability,[3] or the information that is gained when the value of such a variable becomes known.[4][5] As a unit of information, the bit is also known as a shannon,[6] named after Claude E. Shannon.
The symbol for the binary digit is either "bit" as per the IEC 80000-13:2008 standard, or the lowercase character "b", as per the IEEE 1541-2002 standard. Use of the latter may create confusion with the capital "B" which is the international standard symbol for the byte.
History
The encoding of data by discrete bits was used in the punched cards invented by Basile Bouchon and Jean-Baptiste Falcon (1732), developed by Joseph Marie Jacquard (1804), and later adopted by Semyon Korsakov, Charles Babbage, Hermann Hollerith, and early computer manufacturers like IBM. A variant of that idea was the perforated paper tape. In all those systems, the medium (card or tape) conceptually carried an array of hole positions; each position could be either punched through or not, thus carrying one bit of information. The encoding of text by bits was also used in Morse code (1844) and early digital communications machines such as teletypes and stock ticker machines (1870).
Ralph Hartley suggested the use of a logarithmic measure of information in 1928.[7] Claude E. Shannon first used the word "bit" in his seminal 1948 paper "A Mathematical Theory of Communication".[8][9][10] He attributed its origin to John W. Tukey, who had written a Bell Labs memo on 9 January 1947 in which he contracted "binary information digit" to simply "bit".[8] Vannevar Bush had written in 1936 of "bits of information" that could be stored on the punched cards used in the mechanical computers of that time.[11] The first programmable computer, built by Konrad Zuse, used binary notation for numbers.
Physical representation
A bit can be stored by a digital device or other physical system that exists in either of two possible distinct states. These may be the two stable states of a flip-flop, two positions of an electrical switch, two distinct voltage or current levels allowed by a circuit, two distinct levels of light intensity, two directions of magnetization or polarization, the orientation of reversible double stranded DNA, etc.
Bits can be implemented in several forms. In most modern computing devices, a bit is usually represented by an electrical voltage or current pulse, or by the electrical state of a flip-flop circuit.
For devices using positive logic, a digit value of 1 (or a logical value of true) is represented by a more positive voltage relative to the representation of 0. Different logic families require different voltages, and variations are allowed to account for component aging and noise immunity. For example, in transistor–transistor logic (TTL) and compatible circuits, digit values 0 and 1 at the output of a device are represented by no higher than 0.4 volts and no lower than 2.6 volts, respectively; while TTL inputs are specified to recognize 0.8 volts or below as 0 and 2.2 volts or above as 1.
Transmission and processing
Bits are transmitted one at a time in serial transmission, and by a multiple number of bits in parallel transmission. A bitwise operation optionally processes bits one at a time. Data transfer rates are usually measured in decimal SI multiples of the unit bit per second (bit/s), such as kbit/s.
Storage
In the earliest non-electronic information processing devices, such as Jacquard's loom or Babbage's Analytical Engine, a bit was often stored as the position of a mechanical lever or gear, or the presence or absence of a hole at a specific point of a paper card or tape. The first electrical devices for discrete logic (such as elevator and traffic light control circuits, telephone switches, and Konrad Zuse's computer) represented bits as the states of electrical relays which could be either "open" or "closed". When relays were replaced by vacuum tubes, starting in the 1940s, computer builders experimented with a variety of storage methods, such as pressure pulses traveling down a mercury delay line, charges stored on the inside surface of a cathode-ray tube, or opaque spots printed on glass discs by photolithographic techniques.
In the 1950s and 1960s, these methods were largely supplanted by magnetic storage devices such as magnetic-core memory, magnetic tapes, drums, and disks, where a bit was represented by the polarity of magnetization of a certain area of a ferromagnetic film, or by a change in polarity from one direction to the other. The same principle was later used in the magnetic bubble memory developed in the 1980s, and is still found in various magnetic strip items such as metro tickets and some credit cards.
In modern semiconductor memory, such as dynamic random-access memory, the two values of a bit may be represented by two levels of electric charge stored in a capacitor. In certain types of programmable logic arrays and read-only memory, a bit may be represented by the presence or absence of a conducting path at a certain point of a circuit. In optical discs, a bit is encoded as the presence or absence of a microscopic pit on a reflective surface. In one-dimensional bar codes, bits are encoded as the thickness of alternating black and white lines.
Unit and symbol
The bit is not defined in the International System of Units (SI). However, the International Electrotechnical Commission issued standard IEC 60027, which specifies that the symbol for binary digit should be 'bit', and this should be used in all multiples, such as 'kbit', for kilobit.[12] However, the lower-case letter 'b' is widely used as well and was recommended by the IEEE 1541 Standard (2002). In contrast, the upper case letter 'B' is the standard and customary symbol for byte.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Orders of magnitude of data | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiple bits
Multiple bits may be expressed and represented in several ways. For convenience of representing commonly reoccurring groups of bits in information technology, several units of information have traditionally been used. The most common is the unit byte, coined by Werner Buchholz in June 1956, which historically was used to represent the group of bits used to encode a single character of text (until UTF-8 multibyte encoding took over) in a computer[2][13][14][15][16] and for this reason it was used as the basic addressable element in many computer architectures. The trend in hardware design converged on the most common implementation of using eight bits per byte, as it is widely used today. However, because of the ambiguity of relying on the underlying hardware design, the unit octet was defined to explicitly denote a sequence of eight bits.
Computers usually manipulate bits in groups of a fixed size, conventionally named "words". Like the byte, the number of bits in a word also varies with the hardware design, and is typically between 8 and 80 bits, or even more in some specialized computers. In the 21st century, retail personal or server computers have a word size of 32 or 64 bits.
The International System of Units defines a series of decimal prefixes for multiples of standardized units which are commonly also used with the bit and the byte. The prefixes kilo (103) through yotta (1024) increment by multiples of one thousand, and the corresponding units are the kilobit (kbit) through the yottabit (Ybit).
Information capacity and information compression
This article needs to be updated. The reason given is: it cites a fact about global information content in computers from 2007. (October 2018) |
When the information capacity of a storage system or a communication channel is presented in bits or bits per second, this often refers to binary digits, which is a computer hardware capacity to store binary data (0 or 1, up or down, current or not, etc.).[17] Information capacity of a storage system is only an upper bound to the quantity of information stored therein. If the two possible values of one bit of storage are not equally likely, that bit of storage contains less than one bit of information. If the value is completely predictable, then the reading of that value provides no information at all (zero entropic bits, because no resolution of uncertainty occurs and therefore no information is available). If a computer file that uses n bits of storage contains only m < n bits of information, then that information can in principle be encoded in about m bits, at least on the average. This principle is the basis of data compression technology. Using an analogy, the hardware binary digits refer to the amount of storage space available (like the number of buckets available to store things), and the information content the filling, which comes in different levels of granularity (fine or coarse, that is, compressed or uncompressed information). When the granularity is finer—when information is more compressed—the same bucket can hold more.
For example, it is estimated that the combined technological capacity of the world to store information provides 1,300 exabytes of hardware digits. However, when this storage space is filled and the corresponding content is optimally compressed, this only represents 295 exabytes of information.[18] When optimally compressed, the resulting carrying capacity approaches Shannon information or information entropy.[17]
Bit-based computing
Certain bitwise computer processor instructions (such as bit set) operate at the level of manipulating bits rather than manipulating data interpreted as an aggregate of bits.
In the 1980s, when bitmapped computer displays became popular, some computers provided specialized bit block transfer instructions to set or copy the bits that corresponded to a given rectangular area on the screen.
In most computers and programming languages, when a bit within a group of bits, such as a byte or word, is referred to, it is usually specified by a number from 0 upwards corresponding to its position within the byte or word. However, 0 can refer to either the most or least significant bit depending on the context.
Other information units
Similar to torque and energy in physics; information-theoretic information and data storage size have the same dimensionality of units of measurement, but there is in general no meaning to adding, subtracting or otherwise combining the units mathematically, although one may act as a bound on the other.
Units of information used in information theory include the shannon (Sh), the natural unit of information (nat) and the hartley (Hart). One shannon is the maximum amount of information needed to specify the state of one bit of storage. These are related by 1 Sh ≈ 0.693 nat ≈ 0.301 Hart.
Some authors also define a binit as an arbitrary information unit equivalent to some fixed but unspecified number of bits.[19]
See also
- Byte
- Integer (computer science)
- Primitive data type
- Trit (Trinary digit)
- Qubit (quantum bit)
- Bitstream
- Entropy (information theory)
- Bit rate and baud rate
- Binary numeral system
- Ternary numeral system
- Shannon (unit)
- Nibble
References
[…] With IBM's STRETCH computer as background, handling 64-character words divisible into groups of 8 (I designed the character set for it, under the guidance of Dr. Werner Buchholz, the man who DID coin the term "byte" for an 8-bit grouping). […] The IBM 360 used 8-bit characters, although not ASCII directly. Thus Buchholz's "byte" caught on everywhere. I myself did not like the name for many reasons. […]
The choice of a logarithmic base corresponds to the choice of a unit for measuring information. If the base 2 is used the resulting units may be called binary digits, or more briefly bits, a word suggested by J. W. Tukey.
[…] Most important, from the point of view of editing, will be the ability to handle any characters or digits, from 1 to 6 bits long […] the Shift Matrix to be used to convert a 60-bit word, coming from Memory in parallel, into characters, or "bytes" as we have called them, to be sent to the Adder serially. The 60 bits are dumped into magnetic cores on six different levels. Thus, if a 1 comes out of position 9, it appears in all six cores underneath. […] The Adder may accept all or only some of the bits. […] Assume that it is desired to operate on 4 bit decimal digits, starting at the right. The 0-diagonal is pulsed first, sending out the six bits 0 to 5, of which the Adder accepts only the first four (0-3). Bits 4 and 5 are ignored. Next, the 4 diagonal is pulsed. This sends out bits 4 to 9, of which the last two are again ignored, and so on. […] It is just as easy to use all six bits in alphanumeric work, or to handle bytes of only one bit for logical analysis, or to offset the bytes by any number of bits. […]
[…] The first reference found in the files was contained in an internal memo written in June 1956 during the early days of developing Stretch. A byte was described as consisting of any number of parallel bits from one to six. Thus a byte was assumed to have a length appropriate for the occasion. Its first use was in the context of the input-output equipment of the 1950s, which handled six bits at a time. The possibility of going to 8 bit bytes was considered in August 1956 and incorporated in the design of Stretch shortly thereafter. The first published reference to the term occurred in 1959 in a paper "Processing Data in Bits and Pieces" by G A Blaauw, F P Brooks Jr and W Buchholz in the IRE Transactions on Electronic Computers, June 1959, page 121. The notions of that paper were elaborated in Chapter 4 of Planning a Computer System (Project Stretch), edited by W Buchholz, McGraw-Hill Book Company (1962). The rationale for coining the term was explained there on page 40 as follows:
Byte denotes a group of bits used to encode a character, or the number of bits transmitted in parallel to and from input-output units. A term other than character is used here because a given character may be represented in different applications by more than one code, and different codes may use different numbers of bits (ie, different byte sizes). In input-output transmission the grouping of bits may be completely arbitrary and have no relation to actual characters. (The term is coined from bite, but respelled to avoid accidental mutation to bit.)
System/360 took over many of the Stretch concepts, including the basic byte and word sizes, which are powers of 2. For economy, however, the byte size was fixed at the 8 bit maximum, and addressing at the bit level was replaced by byte addressing. […]
- Bhattacharya, Amitabha (2005). Digital Communication. Tata McGraw-Hill Education. ISBN 978-0-07059117-2. Archived from the original on 2017-03-27.
External links
- Bit Calculator – a tool providing conversions between bit, byte, kilobit, kilobyte, megabit, megabyte, gigabit, gigabyte
- BitXByteConverter – a tool for computing file sizes, storage capacity, and digital information in various units
https://en.wikipedia.org/wiki/Bit
In electromagnetism, electrostriction is a property of all electrical non-conductors, or dielectrics, that causes them to change their shape under the application of an electric field. It is the dual property to magnetostriction.
Explanation
Electrostriction is a property of all dielectric materials, and is caused by displacement of ions in the crystal lattice upon being exposed to an external electric field. Positive ions will be displaced in the direction of the field, while negative ions will be displaced in the opposite direction. This displacement will accumulate throughout the bulk material and result in an overall strain (elongation) in the direction of the field. The thickness will be reduced in the orthogonal directions characterized by Poisson's ratio. All insulating materials consisting of more than one type of atom will be ionic to some extent due to the difference of electronegativity of the atoms, and therefore exhibit electrostriction.
The resulting strain (ratio of deformation to the original dimension) is proportional to the square of the polarization. Reversal of the electric field does not reverse the direction of the deformation.
More formally, the electrostriction coefficient is a fourth rank tensor (), relating the second-order strain tensor () and the first-order electric polarization density ().
The related piezoelectric effect occurs only in a particular class of dielectrics. Electrostriction applies to all crystal symmetries, while the piezoelectric effect only applies to the 20 piezoelectric point groups. Electrostriction is a quadratic effect, unlike piezoelectricity, which is a linear effect.
Materials
Although all dielectrics exhibit some electrostriction, certain engineered ceramics, known as relaxor ferroelectrics, have extraordinarily high electrostrictive constants. The most commonly used are
- lead magnesium niobate (PMN)
- lead magnesium niobate-lead titanate (PMN-PT)
- lead lanthanum zirconate titanate (PLZT)
Magnitude of effect
Electrostriction can produce a strain of 0.1% at a field strength of 2 million volts per meter (2 MV/m) for the material called PMN-15 (TRS website listed in the references below). The effect appears to be quadratic at low field strengths (up to 0.3 MV/m) and roughly linear after that, up to a maximum field strength of 4 MV/m[citation needed]. Therefore, devices made of such materials are normally operated around a bias voltage in order to behave nearly linearly. This will probably cause deformations to lead to a change of electric charge, but this is unconfirmed.
Applications
See also
References
- "Electrostriction." Encyclopædia Britannica.
- Mini dictionary of physics (1988) Oxford University Press
- "Electrostrictive Materials" from TRS Technologies
- "Electronic Materials" by Prof. Dr. Helmut Föll
https://en.wikipedia.org/wiki/Electrostriction
Photoelasticity describes changes in the optical properties of a material under mechanical deformation. It is a property of all dielectric media and is often used to experimentally determine the stress distribution in a material, where it gives a picture of stress distributions around discontinuities in materials. Photoelastic experiments (also informally referred to as photoelasticity) are an important tool for determining critical stress points in a material, and are used for determining stress concentration in irregular geometries.
History
The photoelastic phenomenon was first discovered by the Scottish physicist David Brewster, who immediately recognized it as stress-induced birefringence.[1][2] That diagnosis was confirmed in a direct refraction experiment by Augustin-Jean Fresnel.[3] Experimental frameworks were developed at the beginning of the twentieth century with the works of E. G. Coker and L. N. G. Filon of University of London. Their book Treatise on Photoelasticity, published in 1930 by Cambridge Press, became a standard text on the subject. Between 1930 and 1940, many other books appeared on the subject, including books in Russian, German and French. Max M. Frocht published the classic two volume work, Photoelasticity, in the field.[4] At the same time, much development occurred in the field – great improvements were achieved in technique, and the equipment was simplified. With refinements in the technology, photoelastic experiments were extended to determining three-dimensional states of stress. In parallel to developments in experimental technique, the first phenomenological description of photoelasticity was given in 1890 by Friedrich Pockels,[5] however this was proved inadequate almost a century later by Nelson & Lax[6] as the description by Pockels only considered the effect of mechanical strain on the optical properties of the material.
With the advent of the digital polariscope – made possible by light-emitting diodes – continuous monitoring of structures under load became possible. This led to the development of dynamic photoelasticity, which has contributed greatly to the study of complex phenomena such as fracture of materials.
Applications
Photoelasticity has been used for a variety of stress analyses and even for routine use in design, particularly before the advent of numerical methods, such as finite elements or boundary elements.[7] Digitization of polariscopy enables fast image acquisition and data processing, which allows its industrial applications to control quality of manufacturing process for materials such as glass[8] and polymer.[9] Dentistry utilizes photoelasticity to analyze strain in denture materials.[10]
Photoelasticity can successfully be used to investigate the highly localized stress state within masonry[11][12][13] or in proximity of a rigid line inclusion (stiffener) embedded in an elastic medium.[14] In the former case, the problem is nonlinear due to the contacts between bricks, while in the latter case the elastic solution is singular, so that numerical methods may fail to provide correct results. These can be obtained through photoelastic techniques. Dynamic photoelasticity integrated with high-speed photography is utilized to investigate fracture behavior in materials.[15] Another important application of the photoelasticity experiments is to study the stress field around bi-material notches.[16] Bi-material notches exist in many engineering application like welded or adhesively bonded structures.
Formal definition
For a linear dielectric material the change in the inverse permittivity tensor with respect to the deformation (the gradient of the displacement ) is described by [17]
where is the fourth-rank photoelasticity tensor, is the linear displacement from equilibrium, and denotes differentiation with respect to the Cartesian coordinate . For isotropic materials, this definition simplifies to [18]
where is the symmetric part of the photoelastic tensor (the photoelastic strain tensor), and is the linear strain. The antisymmetric part of is known as the roto-optic tensor. From either definition, it is clear that deformations to the body may induce optical anisotropy, which can cause an otherwise optically isotropic material to exhibit birefringence. Although the symmetric photoelastic tensor is most commonly defined with respect to mechanical strain, it is also possible to express photoelasticity in terms of the mechanical stress.
Experimental principles
The experimental procedure relies on the property of birefringence, as exhibited by certain transparent materials. Birefringence is a phenomenon in which a ray of light passing through a given material experiences two refractive indices. The property of birefringence (or double refraction) is observed in many optical crystals. Upon the application of stresses, photoelastic materials exhibit the property of birefringence, and the magnitude of the refractive indices at each point in the material is directly related to the state of stresses at that point. Information such as maximum shear stress and its orientation are available by analyzing the birefringence with an instrument called a polariscope.
When a ray of light passes through a photoelastic material, its electromagnetic wave components are resolved along the two principal stress directions and each component experiences a different refractive index due to the birefringence. The difference in the refractive indices leads to a relative phase retardation between the two components. Assuming a thin specimen made of isotropic materials, where two-dimensional photoelasticity is applicable, the magnitude of the relative retardation is given by the stress-optic law:[19]
where Δ is the induced retardation, C is the stress-optic coefficient, t is the specimen thickness, λ is the vacuum wavelength, and σ1 and σ2 are the first and second principal stresses, respectively. The retardation changes the polarization of transmitted light. The polariscope combines the different polarization states of light waves before and after passing the specimen. Due to optical interference of the two waves, a fringe pattern is revealed. The number of fringe order N is denoted as
which depends on relative retardation. By studying the fringe pattern one can determine the state of stress at various points in the material.
For materials that do not show photoelastic behavior, it is still possible to study the stress distribution. The first step is to build a model, using photoelastic materials, which has geometry similar to the real structure under investigation. The loading is then applied in the same way to ensure that the stress distribution in the model is similar to the stress in the real structure.
Isoclinics and isochromatics
Isoclinics are the loci of the points in the specimen along which the principal stresses are in the same direction.[citation needed]
Isochromatics are the loci of the points along which the difference in the first and second principal stress remains the same. Thus they are the lines which join the points with equal maximum shear stress magnitude.[20]
Two-dimensional photoelasticity
Photoelasticity can describe both three-dimensional and two-dimensional states of stress. However, examining photoelasticity in three-dimensional systems is more involved than two-dimensional or plane-stress system. So the present section deals with photoelasticity in a plane stress system. This condition is achieved when the thickness of the prototype is much smaller as compared to dimensions in the plane.[citation needed] Thus one is only concerned with stresses acting parallel to the plane of the model, as other stress components are zero. The experimental setup varies from experiment to experiment. The two basic kinds of setup used are plane polariscope and circular polariscope.[citation needed]
The working principle of a two-dimensional experiment allows the measurement of retardation, which can be converted to the difference between the first and second principal stress and their orientation. To further get values of each stress component, a technique called stress-separation is required.[21] Several theoretical and experimental methods are utilized to provide additional information to solve individual stress components.
Plane polariscope setup
The setup consists of two linear polarizers and a light source. The light source can either emit monochromatic light or white light depending upon the experiment. First the light is passed through the first polarizer which converts the light into plane polarized light. The apparatus is set up in such a way that this plane polarized light then passes through the stressed specimen. This light then follows, at each point of the specimen, the direction of principal stress at that point. The light is then made to pass through the analyzer and we finally get the fringe pattern.[citation needed]
The fringe pattern in a plane polariscope setup consists of both the isochromatics and the isoclinics. The isoclinics change with the orientation of the polariscope while there is no change in the isochromatics.[citation needed]
The same device functions as a plane polariscope when quarter wave plates are taken aside or rotated so their axes parallel to polarization axes
Circular polariscope setup
In a circular polariscope setup two quarter-wave plates are added to the experimental setup of the plane polariscope. The first quarter-wave plate is placed in between the polarizer and the specimen and the second quarter-wave plate is placed between the specimen and the analyzer. The effect of adding the quarter-wave plate after the source-side polarizer is that we get circularly polarized light passing through the sample. The analyzer-side quarter-wave plate converts the circular polarization state back to linear before the light passes through the analyzer.[citation needed]
The basic advantage of a circular polariscope over a plane polariscope is that in a circular polariscope setup we only get the isochromatics and not the isoclinics. This eliminates the problem of differentiating between the isoclinics and the isochromatics.[citation needed]
See also
References
- Fernandez M.S-B., Calderon, J. M. A., Diez, P. M. B. and Segura, I. I. C., Stress-separation techniques in photoelasticity: A review. The Journal of Strain Analysis for Engineering Design, 2010, 45:1 [doi:10.1243/03093247JSA583]
External links
https://en.wikipedia.org/wiki/Photoelasticity
An acousto-optic modulator (AOM), also called a Bragg cell or an acousto-optic deflector (AOD), uses the acousto-optic effect to diffract and shift the frequency of light using sound waves (usually at radio-frequency). They are used in lasers for Q-switching, telecommunications for signal modulation, and in spectroscopy for frequency control. A piezoelectric transducer is attached to a material such as glass. An oscillating electric signal drives the transducer to vibrate, which creates sound waves in the material. These can be thought of as moving periodic planes of expansion and compression that change the index of refraction. Incoming light scatters (see Brillouin scattering) off the resulting periodic index modulation and interference occurs similar to Bragg diffraction. The interaction can be thought of as a three-wave mixing process resulting in Sum-frequency generation or Difference-frequency generation between phonons and photons.
Principles of operation
A typical AOM operates under Bragg Condition, where the incident light comes at Bragg angle from the perpendicular of the sound wave's propagation.[1][2]
Diffraction
When the incident light beam is at Bragg angle, a diffraction pattern emerges where an order of diffracted beam occurs at each angle θ that satisfies:
Here, m = ..., −2, −1, 0, +1, +2, ... is the order of diffraction, is the wavelength of light in vacuum, is the refractive index of the crystal material (e.g. quartz), and is the wavelength of the sound.[3] itself is the wavelength of the light in the material. Note that m = 0 order travels in the same direction as the incident beam, and exits at Bragg angle from the perpendicular of the sound wave's propagation.
Diffraction from a sinusoidal modulation in a thin crystal mostly results in the m = −1, 0, +1 diffraction orders. Cascaded diffraction in medium thickness crystals leads to higher orders of diffraction. In thick crystals with weak modulation, only phasematched orders are diffracted; this is called Bragg diffraction. The angular deflection can range from 1 to 5000 beam widths (the number of resolvable spots). Consequently, the deflection is typically limited to tens of milliradians.
The angular separation between adjacent orders is twice the Bragg angle, i.e. .
Intensity
The amount of light diffracted by the sound wave depends on the intensity of the sound. Hence, the intensity of the sound can be used to modulate the intensity of the light in the diffracted beam. Typically, the intensity that is diffracted into m = 0 order can be varied between 15% and 99% of the input light intensity. Likewise, the intensity of the m = +1 order can be varied between 0% and 80%.
An expression of the efficiency in m = +1 order is:[4]
where the external phase excursion .
To obtain the same efficiency for different wavelength, the RF power in the AOM has to be proportional to the square of the wavelength of the optical beam. Note that this formula also tells us that, when we start at a high RF power P, it might be higher than the first peak in the sine squared function, in which case as we increase P, we would settle at the second peak with a very high RF power, leading to overdriving the AOM and potential damage to the crystal or other components. To avoid this problem, one should always start with a very low RF power, and slowly increase it to settle at the first peak.
Note that there are two configurations that satisfies Bragg Condition: If the incident beam's wavevector's component on the sound wave's propagation direction goes against the sound wave, the Bragg diffraction/scattering process will result in the maximum efficiency into m = +1 order, which has a positive frequency shift; However, if the incident beam goes along the sound wave, the maximum diffraction efficiency into m = -1 order is achieved, which has a negative frequency shift.
Frequency
One difference from Bragg diffraction is that the light is scattering from moving planes. A consequence of this is the frequency of the diffracted beam f in order m will be Doppler-shifted by an amount equal to the frequency of the sound wave F.
This frequency shift can be also understood by the fact that energy and momentum (of the photons and phonons) are conserved in the scattering process. A typical frequency shift varies from 27 MHz, for a less-expensive AOM, to 1 GHz, for a state-of-the-art commercial device. In some AOMs, two acoustic waves travel in opposite directions in the material, creating a standing wave. In this case the spectrum of the diffracted beam contains multiple frequency shifts, in any case integer multiples of the frequency of the sound wave.
Phase
In addition, the phase of the diffracted beam will also be shifted by the phase of the sound wave. The phase can be changed by an arbitrary amount.
Polarization
Collinear transverse acoustic waves or perpendicular longitudinal waves can change the polarization. The acoustic waves induce a birefringent phase-shift, much like in a Pockels cell[dubious ]. The acousto-optic tunable filter, especially the dazzler, which can generate variable pulse shapes, is based on this principle.[5]
Modelocking
Acousto-optic modulators are much faster than typical mechanical devices such as tiltable mirrors. The time it takes an AOM to shift the exiting beam in is roughly limited to the transit time of the sound wave across the beam (typically 5 to 100 ns). This is fast enough to create active modelocking in an ultrafast laser. When faster control is necessary electro-optic modulators are used. However, these require very high voltages (e.g. 1...10 kV), whereas AOMs offer more deflection range, simple design, and low power consumption (less than 3 W).[6]
Applications
- Q-switching
- Regenerative amplifiers
- Cavity dumping
- Modelocking
- Laser Doppler vibrometer
- RGB Laser Light Modulation for Digital Imaging of Photographic Film
- Confocal microscopy
- Synthetic array heterodyne detection
- Hyperspectral Imaging
See also
- Acousto-optics
- Acousto-optic deflector
- Electro-optic modulator
- Jeffree cell
- Acousto-optical spectrometer
- Liquid crystal tunable filter
- Photoelasticity
- Pockels effect
- Frequency shifting
External links
References
- Keller, Ursula; Gallmann, Lukas. "Ultrafast Laser Physics" (PDF). ETH Zurich. Retrieved 21 March 2022.
https://en.wikipedia.org/wiki/Acousto-optic_modulator
Electronic filter topology defines electronic filter circuits without taking note of the values of the components used but only the manner in which those components are connected.
Filter design characterises filter circuits primarily by their transfer function rather than their topology. Transfer functions may be linear or nonlinear. Common types of linear filter transfer function are; high-pass, low-pass, bandpass, band-reject or notch and all-pass. Once the transfer function for a filter is chosen, the particular topology to implement such a prototype filter can be selected so that, for example, one might choose to design a Butterworth filter using the Sallen–Key topology.
Filter topologies may be divided into passive and active types. Passive topologies are composed exclusively of passive components: resistors, capacitors, and inductors. Active topologies also include active components (such as transistors, op amps, and other integrated circuits) that require power. Further, topologies may be implemented either in unbalanced form or else in balanced form when employed in balanced circuits. Implementations such as electronic mixers and stereo sound may require arrays of identical circuits.
Passive topologies
Passive filters have been long in development and use. Most are built from simple two-port networks called "sections". There is no formal definition of a section except that it must have at least one series component and one shunt component. Sections are invariably connected in a "cascade" or "daisy-chain" topology, consisting of additional copies of the same section or of completely different sections. The rules of series and parallel impedance would combine two sections consisting only of series components or shunt components into a single section.
Some passive filters, consisting of only one or two filter sections, are given special names including the L-section, T-section and Π-section, which are unbalanced filters, and the C-section, H-section and box-section, which are balanced. All are built upon a very simple "ladder" topology (see below). The chart at the bottom of the page shows these various topologies in terms of general constant k filters.
Filters designed using network synthesis usually repeat the simplest form of L-section topology though component values may change in each section. Image designed filters, on the other hand, keep the same basic component values from section to section though the topology may vary and tend to make use of more complex sections.
L-sections are never symmetrical but two L-sections back-to-back form a symmetrical topology and many other sections are symmetrical in form.
Ladder topologies
Ladder topology, often called Cauer topology after Wilhelm Cauer (inventor of the elliptic filter), was in fact first used by George Campbell (inventor of the constant k filter). Campbell published in 1922 but had clearly been using the topology for some time before this. Cauer first picked up on ladders (published 1926) inspired by the work of Foster (1924). There are two forms of basic ladder topologies: unbalanced and balanced. Cauer topology is usually thought of as an unbalanced ladder topology.
A ladder network consists of cascaded asymmetrical L-sections (unbalanced) or C-sections (balanced). In low pass form the topology would consist of series inductors and shunt capacitors. Other bandforms would have an equally simple topology transformed from the lowpass topology. The transformed network will have shunt admittances that are dual networks of the series impedances if they were duals in the starting network - which is the case with series inductors and shunt capacitors.
| Image filter sections | |||||||
|---|---|---|---|---|---|---|---|
|
| |||||||
|
|||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
Modified ladder topologies
Image filter design commonly uses modifications of the basic ladder topology. These topologies, invented by Otto Zobel,[1] have the same passbands as the ladder on which they are based but their transfer functions are modified to improve some parameter such as impedance matching, stopband rejection or passband-to-stopband transition steepness. Usually the design applies some transform to a simple ladder topology: the resulting topology is ladder-like but no longer obeys the rule that shunt admittances are the dual network of series impedances: it invariably becomes more complex with higher component count. Such topologies include;
The m-type (m-derived) filter is by far the most commonly used modified image ladder topology. There are two m-type topologies for each of the basic ladder topologies; the series-derived and shunt-derived topologies. These have identical transfer functions to each other but different image impedances. Where a filter is being designed with more than one passband, the m-type topology will result in a filter where each passband has an analogous frequency-domain response. It is possible to generalise the m-type topology for filters with more than one passband using parameters m1, m2, m3 etc., which are not equal to each other resulting in general mn-type[2] filters which have bandforms that can differ in different parts of the frequency spectrum.
The mm'-type topology can be thought of as a double m-type design. Like the m-type it has the same bandform but offers further improved transfer characteristics. It is, however, a rarely used design due to increased component count and complexity as well as its normally requiring basic ladder and m-type sections in the same filter for impedance matching reasons. It is normally only found in a composite filter.
Bridged-T topologies
Zobel constant resistance filters[3] use a topology that is somewhat different from other filter types, distinguished by having a constant input resistance at all frequencies and in that they use resistive components in the design of their sections. The higher component and section count of these designs usually limits their use to equalisation applications. Topologies usually associated with constant resistance filters are the bridged-T and its variants, all described in the Zobel network article;
- Bridged-T topology
- Balanced bridged-T topology
- Open-circuit L-section topology
- Short-circuit L-section topology
- Balanced open-circuit C-section topology
- Balanced short-circuit C-section topology
The bridged-T topology is also used in sections intended to produce a signal delay but in this case no resistive components are used in the design.
Lattice topology
Both the T-section (from ladder topology) and the bridge-T (from Zobel topology) can be transformed into a lattice topology filter section but in both cases this results in high component count and complexity. The most common application of lattice filters (X-sections) is in all-pass filters used for phase equalisation.[4]
Although T and bridged-T sections can always be transformed into X-sections the reverse is not always possible because of the possibility of negative values of inductance and capacitance arising in the transform.
Lattice topology is identical to the more familiar bridge topology, the difference being merely the drawn representation on the page rather than any real difference in topology, circuitry or function.
Active topologies
Multiple feedback topology
Multiple feedback topology is an electronic filter topology which is used to implement an electronic filter by adding two poles to the transfer function. A diagram of the circuit topology for a second order low pass filter is shown in the figure on the right.
The transfer function of the multiple feedback topology circuit, like all second-order linear filters, is:
- .
In an MF filter,
For finding suitable component values to achieve the desired filter properties, a similar approach can be followed as in the Design choices section of the alternative Sallen–Key topology.
Biquad filter topology
For the digital implementation of a biquad filter, see Digital biquad filter.
A biquad filter is a type of linear filter that implements a transfer function that is the ratio of two quadratic functions. The name biquad is short for biquadratic. Any second-order filter topology can be referred to as a biquad, such as the MFB or Sallen-Key.[5][6] However, there is also a specific "biquad" topology. It is also sometimes called the 'ring of 3' circuit.[citation needed]
Biquad filters are typically active and implemented with a single-amplifier biquad (SAB) or two-integrator-loop topology.
- The SAB topology uses feedback to generate complex poles and possibly complex zeros. In particular, the feedback moves the real poles of an RC circuit in order to generate the proper filter characteristics.
- The two-integrator-loop topology is derived from rearranging a biquadratic transfer function. The rearrangement will equate one signal with the sum of another signal, its integral, and the integral's integral. In other words, the rearrangement reveals a state variable filter structure. By using different states as outputs, any kind of second-order filter can be implemented.
The SAB topology is sensitive to component choice and can be more difficult to adjust. Hence, usually the term biquad refers to the two-integrator-loop state variable filter topology.
Tow-Thomas filter
For example, the basic configuration in Figure 1 can be used as either a low-pass or bandpass filter depending on where the output signal is taken from.
The second-order low-pass transfer function is given by
where low-pass gain . The second-order bandpass transfer function is given by
- .
with bandpass gain . In both cases, the
- Natural frequency is .
- Quality factor is .
The bandwidth is approximated by , and Q is sometimes expressed as a damping constant . If a noninverting low-pass filter is required, the output can be taken at the output of the second operational amplifier, after the order of the second integrator and the inverter has been switched. If a noninverting bandpass filter is required, the order of the second integrator and the inverter can be switched, and the output taken at the output of the inverter's operational amplifier.
Akerberg-Mossberg filter
Figure 2 shows a variant of the Tow-Thomas topology, known as Akerberg-Mossberg topology, that uses an actively compensated Miller integrator, which improves filter performance.
Sallen–Key topology
The Sallen-Key design is a non-inverting second-order filter with the option of high Q and passband gain.
See also
Notes
This means Sallen-Key filters, state-variable variable filters, multiple feedback filters and other types are all biquads. There also is a "biquad" topology to help further confuse things.
- Moschytz, George S. (2019). Analog
circuit theory and filter design in the digital world : with an
introduction to the morphological method for creative solutions and
design. Cham, Switzerland. ISBN 978-3-030-00096-7. OCLC 1100066185.
plethora of single-amplifier second-order active filter circuits … whose numerator and denominator are of second order, i.e., biquadratic; they are therefore referred to as "biquads"
References
- Campbell, G A, "Physical Theory of the Electric Wave-Filter", Bell System Technical Journal, November 1922, vol. 1, no. 2, pp. 1–32.
- Zobel, O J, "Theory and Design of Uniform and Composite Electric Wave Filters", Bell System Technical Journal, Vol. 2 (1923).
- Foster, R M, "A reactance theorem", Bell System Technical Journal, Vol. 3, pp. 259–267, 1924.
- Cauer, W, "Die Verwirklichung der Wechselstromwiderstande vorgeschriebener Frequenzabhängigkeit", Archiv für Elektrotechnik, 17, pp. 355–388, 1926.
- Zobel, O J, "Distortion correction in electrical networks with constant resistance recurrent networks", Bell System Technical Journal, Vol. 7 (1928), p. 438.
- Zobel, O J, Phase-shifting network, US patent 1 792 523, filed 12 March 1927, issued 17 Feb 1931.
External links
 Media related to Electronic filter topology at Wikimedia Commons
Media related to Electronic filter topology at Wikimedia Commons
https://en.wikipedia.org/wiki/Electronic_filter_topology#Ladder_topologies
| Computer memory and data storage types |
|---|
|
|
| Volatile |
|---|
|
|
|
|
| Non-volatile |
|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Drum memory was a magnetic data storage device invented by Gustav Tauschek in 1932 in Austria.[1][2] Drums were widely used in the 1950s and into the 1960s as computer memory.
Many early computers, called drum computers or drum machines, used drum memory as the main working memory of the computer.[3] Some drums were also used as secondary storage as for example various IBM drum storage drives.
Drums were displaced as primary computer memory by magnetic core memory, which offered a better balance of size, speed, cost, reliability and potential for further improvements.[4] Drums in turn were replaced by hard disk drives for secondary storage, which were both less expensive and offered denser storage. The manufacturing of drums ceased in the 1970s.
Technical design
A drum memory or drum storage unit contained a large metal cylinder, coated on the outside surface with a ferromagnetic recording material. It could be considered the precursor to the hard disk drive (HDD), but in the form of a drum (cylinder) rather than a flat disk. In most designs, one or more rows of fixed read-write heads ran along the long axis of the drum, one for each track. The drum's controller simply selected the proper head and waited for the data to appear under it as the drum turned (rotational latency). Not all drum units were designed with each track having its own head. Some, such as the English Electric DEUCE drum and the UNIVAC FASTRAND had multiple heads moving a short distance on the drum in contrast to modern HDDs, which have one head per platter surface.
Magnetic drum units used as primary memory were addressed by word. Drum units used as secondary storage were addressed by block. Several modes of block addressing were possible, depending on the device.
- Blocks took up an entire track and were addressed by track.
- Tracks were divided into fixed length sectors and addressing was by track and sectors.
- Blocks were variable length, and blocks were addressed by track and record number
- Blocks were variable length with a key, and could be searched by key content.
Some devices were divided into logical cylinders, and addressing by track was actually logical cylinder and track.
The performance of a drum with one head per track is comparable to that of a disk with one head per track and is determined almost entirely by the rotational latency, whereas in an HDD with moving heads its performance includes a rotational latency delay plus the time to position the head over the desired track (seek time). In the era when drums were used as main working memory, programmers often did optimum programming—the programmer—or the assembler, e.g., Symbolic Optimal Assembly Program (SOAP)—positioned code on the drum in such a way as to reduce the amount of time needed for the next instruction to rotate into place under the head.[5] They did this by timing how long it would take after loading an instruction for the computer to be ready to read the next one, then placing that instruction on the drum so that it would arrive under a head just in time. This method of timing-compensation, called the "skip factor" or "interleaving", was used for many years in storage memory controllers.
History
Tauschek's original drum memory (1932) had a capacity of about 500,000 bits (62.5 kilobytes).[2]
One of the earliest functioning computers to employ drum memory was the Atanasoff–Berry computer (1942). It stored 3,000 bits; however, it employed capacitance rather than magnetism to store the information. The outer surface of the drum was lined with electrical contacts leading to capacitors contained within.
Magnetic drums were developed for the U.S. Navy during World War II with the work continuing at Engineering Research Associates (ERA) in 1946 and 1947.[6] An experimental ERA study was completed and reported to the Navy on June 19, 1947.[6] Other early drum storage device development occurred at Birkbeck College (University of London),[7] Harvard University, IBM and the University of Manchester. An ERA drum was the internal memory for the ATLAS-I computer delivered to the U.S. Navy in October 1950 and later sold commercially as the ERA 1101 and UNIVAC_1101. Through mergers, ERA became a division of UNIVAC shipping the Series 1100 drum as a part of the UNIVAC File Computer in 1956; each drum stored 180,000 6-bit characters (135 kilobytes).[8]
The first mass-produced computer, the IBM 650, initially had up to 2,000 10-digit words, about 17.5 kilobytes, of drum memory (later doubled to 4,000 words, about 35 kilobytes, in the Model 4). As late as 1980, PDP-11/45 machines using magnetic core main memory and drums for swapping were still in use at many of the original UNIX sites.
In BSD Unix and its descendants, /dev/drum was the name of the default virtual memory (swap) device, deriving from the use of drum secondary-storage devices as backup storage for pages in virtual memory.[9]
Magnetic drum memory units were used in the Minuteman ICBM launch control centers from the beginning in the early 1960s until the REACT upgrades in the mid-1990s.
See also
- CAB500
- Carousel memory (magnetic rolls)
- Karlqvist gap
- Manchester Mark 1
- Random-access memory
- Wisconsin Integrally Synchronized Computer
References
There was a 1,070-word drum memory for data, stored as twelve 6-bit digits or characters per word
- "FreeBSD drum(4) manpage". Retrieved 2013-01-27.
External links
- The Story of Mel: the classic story about one programmer's drum machine hand-coding antics: Mel Kaye.
- Librascope LGP-30: The drum memory computer referenced in the above story, also referenced on Librascope LGP-30.
- Librascope RPC-4000: Another drum memory computer referenced in the above story
- Oral history interview with Dean Babcock
https://en.wikipedia.org/wiki/Drum_memory
https://en.wikipedia.org/wiki/Carousel_memory
A liquid crystal tunable filter (LCTF) is an optical filter that uses electronically controlled liquid crystal (LC) elements to transmit a selectable wavelength of light and exclude others. Often, the basic working principle is based on the Lyot filter but many other designs can be used.[1] The main difference with the original Lyot filter is that the fixed wave plates are replaced by switchable liquid crystal wave plates.
Optical systems
LCTFs enable high image quality and allowing relatively easy integration with regard to optical system design and software control. However, they emit lower peak transmission values in comparison with conventional fixed-wavelength optical filters due to the use of multiple polarizing elements. This can be mitigated in some instances by using wider bandpass designs, since wider bandpass results in more light traveling through the filter. Some LCTFs are designed to tune to a limited number of fixed wavelengths such as the red, green, and blue (RGB) colors while others can be tuned in small increments over a wide range of wavelengths such as the visible or near-infrared spectrum from 400 to the current limit of 2450 nm. The tuning speed of LCTFs varies by manufacturer and design but is generally several tens of milliseconds, mainly determined by the switching speed of the liquid crystal elements. Higher temperatures can decrease the transition time for the molecules of the liquid crystal material to align themselves and for the filter to tune to a particular wavelength. Lower temperatures increase the viscosity of the liquid crystal material and increase the tuning time of the filter from one wavelength to another.
Recent advances in miniaturized electronic driver circuitry have reduced the size requirement of LCTF enclosures without sacrificing large working aperture sizes. In addition, new materials have allowed the effective wavelength range to be extended to 2450 nm.[2]
Imaging
LCTFs are often used in multispectral imaging or hyperspectral imaging systems because of their high image quality and rapid tuning over a broad spectral range.[3][4][5] Multiple LCTFs in separate imaging paths can be used in optical designs when the required wavelength range exceeds the capabilities of a single filter, such as in astronomy applications.[6]
LCTFs have been utilized for aerospace imaging.[5][7] They can be found integrated into compact but high-performance scientific digital imaging cameras as well as industrial- and military-grade instruments (multispectral and high-resolution color imaging systems).[8] LCTFs can have a long lifespan, usually up to at least 45 years. Environmental factors that can cause degradation of filters are extended exposure to high heat and humidity, thermal and/or mechanical shock (most, but not all, LCTFs utilize standard window glass as the principal base material), and long-term exposure to high photonic energy such as ultraviolet light which can photobleach some of the materials used to construct the filters.
Acousto optic tunable filter
Another type of solid-state tunable filter is the acousto-optic tunable filter (AOTF), based on the principles of the acousto-optic modulator. Compared with LCTFs, AOTFs enjoy a much faster tuning speed (microseconds versus milliseconds) and broader wavelength ranges. However, since they rely on the acousto-optic effect of sound waves to diffract and shift the frequency of light, imaging quality is comparatively poor, and the optical design requirements are more stringent. Indeed, LCTFs are capable of diffraction-limited imaging onto high-resolution imaging sensors. AOTFs have smaller apertures and have narrower angle-of-acceptance specifications compared with LCTFs that can have working aperture sizes up to 35mm and can be placed into positions where light rays travel through the filter at angles of over 7 degrees from the normal.[9][10]
See also
References
- Gebhart, Steven C.; Stokes, David L.; Vo-Dinh, Tuan; Mahadevan-Jansen, Anita (2005). Bearman, Gregory H; Mahadevan-Jansen, Anita; Levenson, Richard M (eds.). "Instrumentation considerations in spectral imaging for tissue demarcation: comparing three methods of spectral resolution". Proceedings of SPIE. Spectral Imaging: Instrumentation, Applications, and Analysis III. 5694: 41. Bibcode:2005SPIE.5694...41G. doi:10.1117/12.611351. S2CID 120372420.
https://en.wikipedia.org/wiki/Liquid_crystal_tunable_filter
https://en.wikipedia.org/wiki/Amplifier
https://en.wikipedia.org/wiki/Distributed_amplifier
https://en.wikipedia.org/wiki/CMOS_amplifier
https://en.wikipedia.org/wiki/Negative-feedback_amplifier
https://en.wikipedia.org/wiki/Charge-transfer_amplifier
https://en.wikipedia.org/wiki/Programmable-gain_amplifier
https://en.wikipedia.org/wiki/Sequential_access
https://en.wikipedia.org/wiki/Read-only_memory
https://en.wikipedia.org/wiki/EEPROM
https://en.wikipedia.org/wiki/Flash_memory
Because erase cycles are slow, the large block sizes used in flash memory erasing give it a significant speed advantage over non-flash EEPROM when writing large amounts of data. As of 2019, flash memory costs much less[by how much?] than byte-programmable EEPROM and had become the dominant memory type wherever a system required a significant amount of non-volatile solid-state storage. EEPROMs, however, are still used in applications that require only small amounts of storage, as in serial presence detect.[5][6]
Flash memory packages can use die stacking with through-silicon vias and several dozen layers of 3D TLC NAND cells (per die) simultaneously to achieve capacities of up to 1 tebibyte per package using 16 stacked dies and an integrated flash controller as a separate die inside the package.[7][8][9][10]
https://en.wikipedia.org/wiki/Flash_memory
Static random-access memory (static RAM or SRAM) is a type of random-access memory (RAM) that uses latching circuitry (flip-flop) to store each bit. SRAM is volatile memory; data is lost when power is removed.
The term static differentiates SRAM from DRAM (dynamic random-access memory) — SRAM will hold its data permanently in the presence of power, while data in DRAM decays in seconds and thus must be periodically refreshed. SRAM is faster than DRAM but it is more expensive in terms of silicon area and cost; it is typically used for the cache and internal registers of a CPU while DRAM is used for a computer's main memory.
https://en.wikipedia.org/wiki/Static_random-access_memory
In April 1969 Intel inc. introduced its first product, Intel 3101, a SRAM memory chip intended to replace bulky magnetic core memory modules; Its capacity was 64 bits (only 63 bits were usable due to a bug)[citation needed] and was based on bipolar junction transistors[6] it was designed by using rubylith.[citation needed]
Characteristics
Though it can be characterized as volatile memory, SRAM exhibits data remanence.[7]
SRAM offers a simple data access model and does not require a refresh circuit. Performance and reliability are good and power consumption is low when idle.[8]
Since SRAM requires more transistors per bit to implement, it is less dense and more expensive than DRAM and also has a higher power consumption during read or write access. The power consumption of SRAM varies widely depending on how frequently it is accessed.[8]
https://en.wikipedia.org/wiki/Static_random-access_memory
Applications
Embedded use
Many categories of industrial and scientific subsystems, automotive electronics, and similar embedded systems, contain SRAM which, in this context, may be referred to as ESRAM.[9] Some amount (kilobytes or less) is also embedded in practically all modern appliances, toys, etc. that implement an electronic user interface.
SRAM in its dual-ported form is sometimes used for real-time digital signal processing circuits.[10]
In computers
SRAM is also used in personal computers, workstations, routers and peripheral equipment: CPU register files, internal CPU caches, internal GPU caches and external burst mode SRAM caches, hard disk buffers, router buffers, etc. LCD screens and printers also normally employ SRAM to hold the image displayed (or to be printed). SRAM was used for the main memory of many early personal computers such as the ZX80, TRS-80 Model 100, and VIC-20.
Hobbyists
Hobbyists, specifically home-built processor enthusiasts,[11] often prefer SRAM due to the ease of interfacing. It is much easier to work with than DRAM as there are no refresh cycles and the address and data buses are often directly accessible.[citation needed] In addition to buses and power connections, SRAM usually requires only three controls: Chip Enable (CE), Write Enable (WE) and Output Enable (OE). In synchronous SRAM, Clock (CLK) is also included.[citation needed]
Types of SRAM
Non-volatile SRAM
Non-volatile SRAM (nvSRAM) has standard SRAM functionality, but they save the data when the power supply is lost, ensuring preservation of critical information. nvSRAMs are used in a wide range of situations – networking, aerospace, and medical, among many others[12] – where the preservation of data is critical and where batteries are impractical.
Pseudostatic RAM
Pseudostatic RAM (PSRAM) is DRAM combined with a self-refresh circuit.[13] It appears externally as slower SRAM, albeit with a density/cost advantage over true SRAM, and without the access complexity of DRAM.
By transistor type
- Bipolar junction transistor (used in TTL and ECL) – very fast but with high power consumption
- MOSFET (used in CMOS) – low power
- Binary SRAM
- Ternary SRAM
By function
- Asynchronous – independent of clock frequency; data in and data out are controlled by address transition. Examples include the ubiquitous 28-pin 8K × 8 and 32K × 8 chips (often but not always named something along the lines of 6264 and 62C256 respectively), as well as similar products up to 16 Mbit per chip.
- Synchronous – all timings are initiated by the clock edges. Address, data in and other control signals are associated with the clock signals.
In the 1990s, asynchronous SRAM used to be employed for fast access time. Asynchronous SRAM was used as main memory for small cache-less embedded processors used in everything from industrial electronics and measurement systems to hard disks and networking equipment, among many other applications. Nowadays, synchronous SRAM (e.g. DDR SRAM) is rather employed similarly to synchronous DRAM – DDR SDRAM memory is rather used than asynchronous DRAM. Synchronous memory interface is much faster as access time can be significantly reduced by employing pipeline architecture. Furthermore, as DRAM is much cheaper than SRAM, SRAM is often replaced by DRAM, especially in the case when a large volume of data is required. SRAM memory is, however, much faster for random (not block / burst) access. Therefore, SRAM memory is mainly used for CPU cache, small on-chip memory, FIFOs or other small buffers.
By feature
- Zero bus turnaround (ZBT) – the turnaround is the number of clock cycles it takes to change access to the SRAM from write to read and vice versa. The turnaround for ZBT SRAMs or the latency between read and write cycle is zero.
- syncBurst (syncBurst SRAM or synchronous-burst SRAM) – features synchronous burst write access to the SRAM to increase write operation to the SRAM.
- DDR SRAM – synchronous, single read/write port, double data rate I/O.
- Quad Data Rate SRAM – synchronous, separate read and write ports, quadruple data rate I/O.
Integrated on chip
SRAM may be integrated as RAM or cache memory in micro-controllers (usually from around 32 bytes up to 128 kilobytes), as the primary caches in powerful microprocessors, such as the x86 family, and many others (from 8 KB, up to many megabytes), to store the registers and parts of the state-machines used in some microprocessors (see register file), on application-specific integrated circuits (ASICs) (usually in the order of kilobytes) and in field-programmable gate arrays (FPGAs) and complex programmable logic devices (CPLDs).
Design
A typical SRAM cell is made up of six MOSFETs, and is often called a 6T SRAM cell. Each bit in the cell is stored on four transistors (M1, M2, M3, M4) that form two cross-coupled inverters. This storage cell has two stable states which are used to denote 0 and 1. Two additional access transistors serve to control the access to a storage cell during read and write operations. In addition to 6T SRAM, other kinds of SRAM chips use 4, 8, 10 (4T, 8T, 10T SRAM), or more transistors per bit.[14][15][16] Four-transistor SRAM is quite common in stand-alone SRAM devices (as opposed to SRAM used for CPU caches), implemented in special processes with an extra layer of polysilicon, allowing for very high-resistance pull-up resistors.[17] The principal drawback of using 4T SRAM is increased static power due to the constant current flow through one of the pull-down transistors (M1 or M2).
This is sometimes used to implement more than one (read and/or write) port, which may be useful in certain types of video memory and register files implemented with multi-ported SRAM circuitry.
Generally, the fewer transistors needed per cell, the smaller each cell can be. Since the cost of processing a silicon wafer is relatively fixed, using smaller cells and so packing more bits on one wafer reduces the cost per bit of memory.
Memory cells that use fewer than four transistors are possible; however, such 3T[18][19] or 1T cells are DRAM, not SRAM (even the so-called 1T-SRAM).
Access to the cell is enabled by the word line (WL in figure) which controls the two access transistors M5 and M6 which, in turn, control whether the cell should be connected to the bit lines: BL and BL. They are used to transfer data for both read and write operations. Although it is not strictly necessary to have two bit lines, both the signal and its inverse are typically provided in order to improve noise margins.
During read accesses, the bit lines are actively driven high and low by the inverters in the SRAM cell. This improves SRAM bandwidth compared to DRAMs – in a DRAM, the bit line is connected to storage capacitors and charge sharing causes the bit line to swing upwards or downwards. The symmetric structure of SRAMs also allows for differential signaling, which makes small voltage swings more easily detectable. Another difference with DRAM that contributes to making SRAM faster is that commercial chips accept all address bits at a time. By comparison, commodity DRAMs have the address multiplexed in two halves, i.e. higher bits followed by lower bits, over the same package pins in order to keep their size and cost down.
The size of an SRAM with m address lines and n data lines is 2m words, or 2m × n bits. The most common word size is 8 bits, meaning that a single byte can be read or written to each of 2m different words within the SRAM chip. Several common SRAM chips have 11 address lines (thus a capacity of 211 = 2,048 = 2k words) and an 8-bit word, so they are referred to as "2k × 8 SRAM".
The dimensions of an SRAM cell on an IC is determined by the minimum feature size of the process used to make the IC.
SRAM operation
This section is written like a manual or guidebook. (January 2023) |
An SRAM cell has three different states: standby (the circuit is idle), reading (the data has been requested) or writing (updating the contents). SRAM operating in read and write modes should have "readability" and "write stability", respectively. The three different states work as follows:
Standby
If the word line is not asserted, the access transistors M5 and M6 disconnect the cell from the bit lines. The two cross-coupled inverters formed by M1 – M4 will continue to reinforce each other as long as they are connected to the supply.
Reading
In theory, reading only requires asserting the word line WL and reading the SRAM cell state by a single access transistor and bit line, e.g. M6, BL. However, bit lines are relatively long and have large parasitic capacitance. To speed up reading, a more complex process is used in practice: The read cycle is started by precharging both bit lines BL and BL, to high (logic 1) voltage. Then asserting the word line WL enables both the access transistors M5 and M6, which causes one bit line BL voltage to slightly drop. Then the BL and BL lines will have a small voltage difference between them. A sense amplifier will sense which line has the higher voltage and thus determine whether there was 1 or 0 stored. The higher the sensitivity of the sense amplifier, the faster the read operation. As the NMOS is more powerful, the pull-down is easier. Therefore, bit lines are traditionally precharged to high voltage. Many researchers are also trying to precharge at a slightly low voltage to reduce the power consumption.[20][21]
Writing
The write cycle begins by applying the value to be written to the bit lines. To write a 0, a 0 is applied to the bit lines, such as setting BL to 1 and BL to 0. This is similar to applying a reset pulse to an SR-latch, which causes the flip flop to change state. A 1 is written by inverting the values of the bit lines. WL is then asserted and the value that is to be stored is latched in. This works because the bit line input-drivers are designed to be much stronger than the relatively weak transistors in the cell itself so they can easily override the previous state of the cross-coupled inverters. In practice, access NMOS transistors M5 and M6 have to be stronger than either bottom NMOS (M1, M3) or top PMOS (M2, M4) transistors. This is easily obtained as PMOS transistors are much weaker than NMOS when same sized. Consequently, when one transistor pair (e.g. M3 and M4) is only slightly overridden by the write process, the opposite transistors pair (M1 and M2) gate voltage is also changed. This means that the M1 and M2 transistors can be easier overridden, and so on. Thus, cross-coupled inverters magnify the writing process.
Bus behavior
RAM with an access time of 70 ns will output valid data within 70 ns from the time that the address lines are valid. Some SRAM cells have a "page mode", where words of a page (256, 512, or 1024 words) can be read sequentially with a significantly shorter access time (typically approximately 30 ns). The page is selected by setting the upper address lines and then words are sequentially read by stepping through the lower address lines.
Production challenges
With the introduction of the FinFET transistor implementation of SRAM cells, they started to suffer from increasing inefficiencies in cell sizes. Over the last 30 years (from 1987 to 2017) with a steadily decreasing transistor size (node size) the footprint-shrinking of the SRAM cell topology itself slowed down, making it harder to pack the cells more densely.[4]
Besides issues with size a significant challenge of modern SRAM cells is a static current leakage. The current, that flows from positive supply (Vdd), through the cell, and to the ground, increases exponentially when the cell's temperature rises. The cell power drain occurs in both active and idle states, thus wasting useful energy without any useful work done. Even though in the last 20 years the issue was partially addressed by the Data Retention Voltage technique (DRV) with reduction rates ranging from 5 to 10, the decrease in node size caused reduction rates to fall to about 2.[4]
With these two issues it became more challenging to develop energy-efficient and dense SRAM memories, prompting semiconductor industry to look for alternatives such as STT-MRAM and F-RAM.[4][22]
Research
In 2019 a French institute reported on a research of an IoT-purposed 28nm fabricated IC.[23] It was based on fully depleted silicon on insulator-transistors (FD-SOI), had two-ported SRAM memory rail for synchronous/asynchronous accesses, and selective virtual ground (SVGND). The study claimed reaching an ultra-low SVGND current in a "sleep" and read modes by finely tuning its voltage.[23]
See also
- Flash memory
- Miniature Card, a discontinued SRAM memory card standard
- In-memory processing
References
- Reda, Boumchedda (May 20, 2019). "Ultra-low voltage and energy efficient SRAM design with new technologies for IoT applications". Grenoble Alpes University.
https://en.wikipedia.org/wiki/Static_random-access_memory
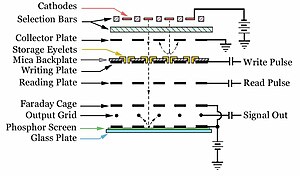










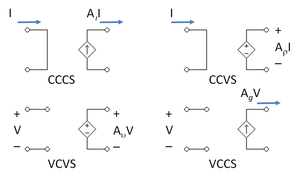



































































No comments:
Post a Comment