Nikiya Anton Bettey 2021: 08-13-2021-1906

Saturday, August 14, 2021

08-13-2021-1906 - The equation of time

The equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of "reconcile a difference". The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with uniform motion along the celestial equator. Apparent solar time can be obtained by measurement of the current position (hour angle) of the Sun, as indicated (with limited accuracy) by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would have a mean of zero.^[1]

The equation of time is the east or west component of the analemma, a curve representing the angular offset of the Sun from its mean position on the celestial sphere as viewed from Earth. The equation of time values for each day of the year, compiled by astronomical observatories, were widely listed in almanacs and ephemerides.^[2]^[3]^:14

The United States Naval Observatory states "the Equation of Time is the difference apparent solar time minus mean solar time", i.e. if the sun is ahead of the clock the sign is positive, and if the clock is ahead of the sun the sign is negative.^[5]^[6] The equation of time is shown in the upper graph above for a period of slightly more than a year. The lower graph (which covers exactly one calendar year) has the same absolute values but the sign is reversed as it shows how far the clock is ahead of the sun. Publications may use either format — in the English-speaking world, the former usage is the more common, but is not always followed. Anyone who makes use of a published table or graph should first check its sign usage. Often, there is a note or caption which explains it. Otherwise, the usage can be determined by knowing that, during the first three months of each year, the clock is ahead of the sundial. The mnemonic "NYSS" (pronounced "nice"), for "new year, sundial slow", can be useful. Some published tables avoid the ambiguity by not using signs, but by showing phrases such as "sundial fast" or "sundial slow" instead.^[7]

In this article, and others in English Wikipedia, a positive value of the equation of time implies that a sundial is ahead of a clock.

Secular effects[edit]

The two above mentioned factors have different wavelengths, amplitudes and phases, so their combined contribution is an irregular wave. At epoch2000 these are the values (in minutes and seconds with UT dates):

Point	Value	Date
minimum	−14 min 15 s	11 February
zero	0 min 0 s	15 April
maximum	+3 min 41 s	14 May
zero	0 min 0 s	13 June
minimum	−6 min 30 s	26 July
zero	0 min 0 s	1 September
maximum	+16 min 25 s	3 November
zero	0 min 0 s	25 December

^{[citation needed]}

E.T. = apparent − mean. Positive means: Sun runs fast and culminates earlier, or the sundial is ahead of mean time. A slight yearly variation occurs due to presence of leap years, resetting itself every 4 years. The exact shape of the equation of time curve and the associated analemma slowly change over the centuries, due to secular variations in both eccentricity and obliquity. At this moment both are slowly decreasing, but they increase and decrease over a timescale of hundreds of thousands of years.^[23]

If the gnomon (the shadow-casting object) is not an edge but a point (e.g., a hole in a plate), the shadow (or spot of light) will trace out a curve during the course of a day. If the shadow is cast on a plane surface, this curve will be a conic section (usually a hyperbola), since the circle of the Sun's motion together with the gnomon point define a cone. At the spring and fall equinoxes, the cone degenerates into a plane and the hyperbola into a line. With a different hyperbola for each day, hour marks can be put on each hyperbola which include any necessary corrections. Unfortunately, each hyperbola corresponds to two different days, one in each half of the year, and these two days will require different corrections. A convenient compromise is to draw the line for the "mean time" and add a curve showing the exact position of the shadow points at noon during the course of the year. This curve will take the form of a figure eight and is known as an analemma. By comparing the analemma to the mean noon line, the amount of correction to be applied generally on that day can be determined.

The equation of time is obtained from a published table, or a graph. For dates in the past such tables are produced from historical measurements, or by calculation; for future dates, of course, tables can only be calculated. In devices such as computer-controlled heliostats the computer is often programmed to calculate the equation of time. The calculation can be numerical or analytical. The former are based on numerical integration of the differential equations of motion, including all significant gravitational and relativistic effects. The results are accurate to better than 1 second and are the basis for modern almanac data. The latter are based on a solution that includes only the gravitational interaction between the Sun and Earth, simpler than but not as accurate as the former. Its accuracy can be improved by including small corrections.

The following discussion describes a reasonably accurate (agreeing with almanac data to within 3 seconds over a wide range of years) algorithm for the equation of time that is well known to astronomers.^[26]^:89 It also shows how to obtain a simple approximate formula (accurate to within 1 minute over a large time interval), that can be easily evaluated with a calculator and provides the simple explanation of the phenomenon that was used previously in this article.

Mathematical description[edit]

The precise definition of the equation of time is^[27]^:1529

EOT = GHA − GMHA

The quantities occurring in this equation are

EOT, the time difference between apparent solar time and mean solar time;
GHA, the Greenwich Hour Angle of the apparent (actual) Sun;
GMHA = Universal Time − Offset, the Greenwich Mean Hour Angle of the mean (fictitious) Sun.

Here time and angle are quantities that are related by factors such as: 2 $π$ radians = 360° = 1 day = 24 hours. The difference, EOT, is measurable since GHA is an angle that can be measured and Universal Time, UT, is a scale for the measurement of time. The offset by $π$ = 180° = 12 hours from UT is needed because UT is zero at mean midnight while GMHA = 0 at mean noon.^{[n 6]} Both GHA and GMHA, like all physical angles, have a mathematical, but not a physical discontinuity at their respective (apparent and mean) noon. Despite the mathematical discontinuities of its components, EOT is defined as a continuous function by adding (or subtracting) 24 hours in the small time interval between the discontinuities in GHA and GMHA.

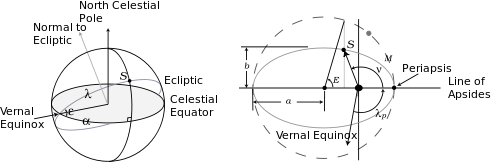
According to the definitions of the angles on the celestial sphere GHA = GAST − $α$ (see hour angle)
where:

GAST is the Greenwich apparent sidereal time (the angle between the apparent vernal equinox and the meridian in the plane of the equator). This is a known function of UT.^[28]
$α$ is the right ascension of the apparent Sun (the angle between the apparent vernal equinox and the actual Sun in the plane of the equator).

On substituting into the equation of time, it is

EOT = GAST −

α

− UT + offset

Like the formula for GHA above, one can write GMHA = GAST − $α M$ , where the last term is the right ascension of the mean Sun. The equation is often written in these terms as^[4]^:275^[29]^:45

EOT =

α M - α

where $α M$ = GAST − UT + offset. In this formulation a measurement or calculation of EOT at a certain value of time depends on a measurement or calculation of $α$ at that time. Both $α$ and $α M$ vary from 0 to 24 hours during the course of a year. The former has a discontinuity at a time that depends on the value of UT, while the latter has its at a slightly later time. As a consequence, when calculated this way EOT has two, artificial, discontinuities. They can both be removed by subtracting 24 hours from the value of EOT in the small time interval after the discontinuity in $α$ and before the one in $α M$ . The resulting EOT is a continuous function of time.

Another definition, denoted $E$ to distinguish it from EOT, is

E

= GMST −

α

− UT + offset

Here GMST = GAST − eqeq, is the Greenwich mean sidereal time (the angle between the mean vernal equinox and the mean Sun in the plane of the equator). Therefore, GMST is an approximation to GAST (and $E$ is an approximation to EOT); eqeq is called the equation of the equinoxes and is due to the wobbling, or nutation of the Earth's axis of rotation about its precessional motion. Since the amplitude of the nutational motion is only about 1.2 s (18″ of longitude) the difference between EOT and $E$ can be ignored unless one is interested in subsecond accuracy.

A third definition, denoted $Δ t$ to distinguish it from EOT and $E$ , and now called the Equation of Ephemeris Time^[27]^:1532 (prior to the distinction that is now made between EOT, $E$ , and $Δ t$ the latter was known as the equation of time) is

Δ t = Λ - α

here $Λ$ is the ecliptic longitude of the mean Sun (the angle from the mean vernal equinox to the mean Sun in the plane of the ecliptic).

The difference $Λ$ − (GMST − UT + offset) is 1.3 s from 1960 to 2040. Therefore, over this restricted range of years $Δ t$ is an approximation to EOT whose error is in the range 0.1 to 2.5 s depending on the longitude correction in the equation of the equinoxes; for many purposes, for example correcting a sundial, this accuracy is more than good enough.

Right ascension calculation[edit]

The right ascension, and hence the equation of time, can be calculated from Newton's two-body theory of celestial motion, in which the bodies (Earth and Sun) describe elliptical orbits about their common mass center. Using this theory, the equation of time becomes

Δ t = M + λ p - α

where the new angles that appear are

$M = 2π(t - t p) / t Y$ , is the mean anomaly, the angle from the periapsis of the elliptical orbit to the mean Sun; its range is from 0 to 2 $π$ as $t$ increases from $t p$ to $t p + t Y$ ;
$t Y$ = 365.2596358 days is the length of time in an anomalistic year: the time interval between two successive passages of the periapsis;
$λ p = Λ - M$ , is the ecliptic longitude of the periapsis;
$t$ is dynamical time, the independent variable in the theory. Here it is taken to be identical with the continuous time based on UT (see above), but in more precise calculations (of $E$ or EOT) the small difference between them must be accounted for^[27]^:1530^[28] as well as the distinction between UT1 and UTC.
$t p$ is the value of $t$ at the periapsis.

To complete the calculation three additional angles are required:

$E$ , the Sun's eccentric anomaly (note that this is different from $M$ );
$ν$ , the Sun's true anomaly;
$λ = ν + λ p$ , the Sun's true longitude on the ecliptic.

The celestial sphere and the Sun's elliptical orbit as seen by a geocentric observer looking normal to the ecliptic showing the 6 angles (

M, λ p, α, ν, λ, E

) needed for the calculation of the equation of time. For the sake of clarity the drawings are not to scale.

All these angles are shown in the figure on the right, which shows the celestial sphere and the Sun's elliptical orbit seen from the Earth (the same as the Earth's orbit seen from the Sun). In this figure $ε$ is the obliquity, while $e = \sqrt 1 - (b / a) 2$ is the eccentricity of the ellipse.

Now given a value of $0 \leq M \leq 2π$ , one can calculate $α (M)$ by means of the following well-known procedure:^[26]^:89

First, given $M$ , calculate $E$ from Kepler's equation:^[30]^:159

M = E - e sin E

Although this equation cannot be solved exactly in closed form, values of $E (M)$ can be obtained from infinite (power or trigonometric) series, graphical, or numerical methods. Alternatively, note that for $e = 0$ , $E = M$ , and by iteration:^[31]^:2

E \approx M + e sin M

This approximation can be improved, for small $e$ , by iterating again,

E \approx M + e sin M + 1 / 2 e 2 sin 2 M

and continued iteration produces successively higher order terms of the power series expansion in $e$ . For small values of $e$ (much less than 1) two or three terms of the series give a good approximation for $E$ ; the smaller $e$ , the better the approximation.

Next, knowing $E$ , calculate the true anomaly $ν$ from an elliptical orbit relation^[30]^:165

\nu =2\tan ^{-1}\left({\sqrt {\frac {1+e}{1-e}}}\tan {\tfrac {1}{2}}E\right)

The correct branch of the multiple valued function $tan -1 x$ to use is the one that makes $ν$ a continuous function of $E (M)$ starting from $ν E =0 = 0$ . Thus for $0 \leq E < π$ use $tan -1 x = Tan -1 x$ , and for $π < E \leq 2π$ use $tan -1 x = Tan -1 x + π$ . At the specific value $E = π$ for which the argument of $tan$ is infinite, use $ν = E$ . Here $Tan -1 x$ is the principal branch, $| Tan -1 x | < π / 2$ ; the function that is returned by calculators and computer applications. Alternatively, this function can be expressed in terms of its Taylor series in $e$ , the first three terms of which are:

ν \approx E + e sin E + 1 / 4 e 2 sin 2 E

For small $e$ this approximation (or even just the first two terms) is a good one. Combining the approximation for $E (M)$ with this one for $ν (E)$ produces

ν \approx M + 2 e sin M + 5 / 4 e 2 sin 2 M

The relation $ν (M)$ is called the equation of the center; the expression written here is a second-order approximation in $e$ . For the small value of $e$ that characterises the Earth's orbit this gives a very good approximation for $ν (M)$ .

Next, knowing $ν$ , calculate $λ$ from its definition:

λ = ν + λ p

The value of $λ$ varies non-linearly with $M$ because the orbit is elliptical and not circular. From the approximation for $ν$ :

λ \approx M + λ p + 2 e sin M + 5 / 4 e 2 sin 2 M

Finally, knowing $λ$ calculate $α$ from a relation for the right triangle on the celestial sphere shown above^[32]^:22

α = tan -1 (cos ε tan λ)

Note that the quadrant of $α$ is the same as that of $λ$ , therefore reduce $λ$ to the range 0 to 2 $π$ and write

α = Tan -1 (cos ε tan λ) + k π

where $k$ is 0 if $λ$ is in quadrant 1, it is 1 if $λ$ is in quadrants 2 or 3 and it is 2 if $λ$ is in quadrant 4. For the values at which tan is infinite, $α = λ$ .

Although approximate values for $α$ can be obtained from truncated Taylor series like those for $ν$ ,^[33]^:32 it is more efficacious to use the equation^[34]^:374

α = λ - sin -1 [y sin (α + λ)]

where $y = tan 2 (ε / 2)$ . Note that for $ε = y = 0$ , $α = λ$ and iterating twice:

α \approx λ - y sin 2 λ + 1 / 2 y 2 sin 4 λ

Equation of time[edit]

The equation of time is obtained by substituting the result of the right ascension calculation into an equation of time formula. Here $Δ t (M) = M + λ p - α [λ (M)]$ is used; in part because small corrections (of the order of 1 second), that would justify using $E$ , are not included, and in part because the goal is to obtain a simple analytical expression. Using two-term approximations for $λ (M)$ and $α (λ)$ allows $Δ t$ to be written as an explicit expression of two terms, which is designated $Δ t ey$ because it is a first order approximation in $e$ and in $y$ .

Δ t ey = -2 e sin M + y sin (2 M + 2 λ p) = -7.659 sin M + 9.863 sin (2 M + 3.5932)

minutes

This equation was first derived by Milne,^[34]^:375 who wrote it in terms of $λ = M + λ p$ . The numerical values written here result from using the orbital parameter values, $e$ = 0.016709, $ε$ = 23.4393° = 0.409093 radians, and $λ p$ = 282.9381° = 4.938201 radians that correspond to the epoch 1 January 2000 at 12 noon UT1. When evaluating the numerical expression for $Δ t ey$ as given above, a calculator must be in radian mode to obtain correct values because the value of $2 λ p - 2π$ in the argument of the second term is written there in radians. Higher order approximations can also be written,^[35]^{:Eqs (45) and (46)} but they necessarily have more terms. For example, the second order approximation in both $e$ and $y$ consists of five terms^[27]^:1535

Δ t e 2 y 2 = Δ t ey - 5 / 4 e 2 sin 2 M + ey sin M cos (2 M + 2 λ p) - 1 / 2 y 2 sin (4 M + 4 λ p)

This approximation has the potential for high accuracy, however, in order to achieve it over a wide range of years, the parameters $e$ , $ε$ , and $λ p$ must be allowed to vary with time.^[26]^:86^[27]^:1531,1535 This creates additional calculational complications. Other approximations have been proposed, for example, $Δ t e$ ^[26]^:86^[36] which uses the first order equation of the center but no other approximation to determine $α$ , and $Δ t e 2$ ^[37] which uses the second order equation of the center.

The time variable, $M$ , can be written either in terms of $n$ , the number of days past perihelion, or $D$ , the number of days past a specific date and time (epoch):

M = 2π / t Y n days = M D + 2π / t Y D days = 6.240 04077 + 0.017 20197 D

Here $M D$ is the value of $M$ at the chosen date and time. For the values given here, in radians, $M D$ is that measured for the actual Sun at the epoch, 1 January 2000 at 12 noon UT1, and $D$ is the number of days past that epoch. At periapsis $M = 2π$ , so solving gives $D = D p$ = 2.508109. This puts the periapsis on 4 January 2000 at 00:11:41 while the actual periapsis is, according to results from the Multiyear Interactive Computer Almanac^[38](abbreviated as MICA), on 3 January 2000 at 05:17:30. This large discrepancy happens because the difference between the orbital radius at the two locations is only 1 part in a million; in other words, radius is a very weak function of time near periapsis. As a practical matter this means that one cannot get a highly accurate result for the equation of time by using $n$ and adding the actual periapsis date for a given year. However, high accuracy can be achieved by using the formulation in terms of $D$ .

Curves of

Δ t

and

Δ t ey

along with symbols locating the daily values at noon (at 10-day intervals) obtained from the Multiyear Interactive Computer Almanac vs

d

for the year 2000

When $D > D p$ , M is greater than 2 $π$ and one must subtract a multiple of 2 $π$ (that depends on the year) from it to bring it into the range 0 to 2 $π$ . Likewise for years prior to 2000 one must add multiples of 2 $π$ . For example, for the year 2010, $D$ varies from 3653 on 1 January at noon to 4017 on 31 December at noon; the corresponding $M$ values are 69.0789468 and 75.3404748 and are reduced to the range 0 to 2 $π$ by subtracting 10 and 11 times 2 $π$ respectively. One can always write $D = n Y + d$ , where $n Y$ is the number of days from the epoch to noon on 1 January of the desired year, and $0 \leq d \leq 364$ (365 if the calculation is for a leap year).

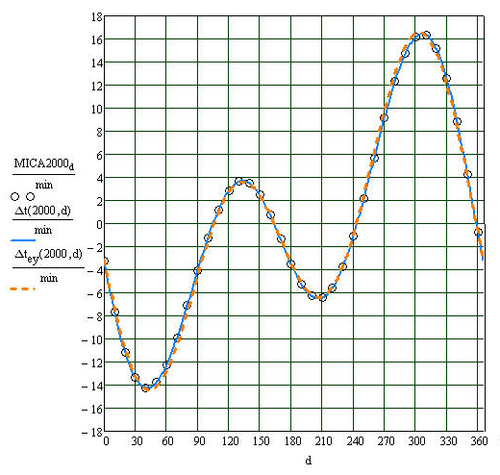
The result of the computations is usually given as either a set of tabular values, or a graph of the equation of time as a function of $d$ . A comparison of plots of $Δ t$ , $Δ t ey$ , and results from MICA all for the year 2000 is shown in the figure on the right. The plot of $Δ t ey$ is seen to be close to the results produced by MICA, the absolute error, Err = | $Δ t ey$ − MICA2000|, is less than 1 minute throughout the year; its largest value is 43.2 seconds and occurs on day 276 (3 October). The plot of $Δ t$ is indistinguishable from the results of MICA, the largest absolute error between the two is 2.46 s on day 324 (20 November).

Remark on the continuity of the equation of time[edit]

For the choice of the appropriate branch of the $arctan$ relation with respect to function continuity a modified version of the arctangent function is helpful. It brings in previous knowledge about the expected value by a parameter. The modified arctangent function is defined as:

arctan η x = arctan x + π round (η - arctan x / π)

It produces a value that is as close to $η$ as possible. The function $round$ rounds to the nearest integer.

Applying this yields:

Δ t (M) = M + λ p - arctan (M + λ p) (cos ε tan λ)

The parameter $M + λ p$ arranges here to set $Δ t$ to the zero nearest value which is the desired one.

Secular effects[edit]

The difference between the MICA and $Δ t$ results was checked every 5 years over the range from 1960 to 2040. In every instance the maximum absolute error was less than 3 s; the largest difference, 2.91 s, occurred on 22 May 1965 (day 141). However, in order to achieve this level of accuracy over this range of years it is necessary to account for the secular change in the orbital parameters with time. The equations that describe this variation are:^[26]^:86^[27]^:1531,1535

{\begin{aligned}e&=1.6709\times 10^{-2}-4.193\times 10^{-5}\left({\frac {D}{36\,525}}\right)-1.26\times 10^{-7}\left({\frac {D}{36525}}\right)^{2}\\\varepsilon &=23.4393-0.013\left({\frac {D}{36\,525}}\right)-2\times 10^{-7}\left({\frac {D}{36\,525}}\right)^{2}+5\times 10^{-7}\left({\frac {D}{36\,525}}\right)^{3}{\mbox{ degrees}}\\\lambda _{\mathrm {p} }&=282.938\,07+1.7195\left({\frac {D}{36\,525}}\right)+3.025\times 10^{-4}\left({\frac {D}{36\,525}}\right)^{2}{\mbox{ degrees}}\end{aligned}}

According to these relations, in 100 years ( $D$ = 36525), $λ p$ increases by about 0.5% (1.7°), $e$ decreases by about 0.25%, and $ε$ decreases by about 0.05%.

As a result, the number of calculations required for any of the higher-order approximations of the equation of time requires a computer to complete them, if one wants to achieve their inherent accuracy over a wide range of time. In this event it is no more difficult to evaluate $Δ t$ using a computer than any of its approximations.

In all this note that $Δ t ey$ as written above is easy to evaluate, even with a calculator, is accurate enough (better than 1 minute over the 80-year range) for correcting sundials, and has the nice physical explanation as the sum of two terms, one due to obliquity and the other to eccentricity that was used previously in the article. This is not true either for $Δ t$ considered as a function of $M$ or for any of its higher-order approximations.

^{https://en.wikipedia.org/wiki/Equation_of_time}

Nikiya Anton Bettey 2021

Blog Archive

Saturday, August 14, 2021

08-13-2021-1906 - The equation of time

Secular effects[edit]

Mathematical description[edit]

Right ascension calculation[edit]

Equation of time[edit]

Remark on the continuity of the equation of time[edit]

Secular effects[edit]

No comments:

Post a Comment