05-15-2023-2007 - two-dimensional electron gas (2DEG), etc. (draft)

https://en.wikipedia.org/wiki/Wigner_crystal

https://en.wikipedia.org/wiki/Metallic_bonding

https://en.wikipedia.org/wiki/Glass_transition

https://en.wikipedia.org/wiki/Electron_beam_texturing

https://en.wikipedia.org/wiki/Density_functional_theory#Electron_smearing

https://en.wikipedia.org/wiki/Electron-beam_freeform_fabrication

https://en.wikipedia.org/wiki/Vitrification

https://en.wikipedia.org/wiki/Melt_inclusion

https://en.wikipedia.org/wiki/Disodium_helide

https://en.wikipedia.org/wiki/Ionic_compound

https://en.wikipedia.org/wiki/Glass

https://en.wikipedia.org/wiki/Solid-state_chemistry#Melt_methods

https://en.wikipedia.org/wiki/Selective_laser_melting

https://en.wikipedia.org/wiki/Aluminium_smelting

https://en.wikipedia.org/wiki/Plasma_(physics)

https://en.wikipedia.org/wiki/Archaeometallurgical_slag

https://en.wikipedia.org/wiki/Metalworking

 

 

https://en.wikipedia.org/wiki/Atmosphere_of_Earth

https://en.wikipedia.org/wiki/Gas

https://en.wikipedia.org/wiki/Surroundings

https://en.wikipedia.org/wiki/System

 

A two-dimensional electron gas (2DEG) is a scientific model in solid-state physics. It is an electron gas that is free to move in two dimensions, but tightly confined in the third. This tight confinement leads to quantized energy levels for motion in the third direction, which can then be ignored for most problems. Thus the electrons appear to be a 2D sheet embedded in a 3D world. The analogous construct of holes is called a two-dimensional hole gas (2DHG), and such systems have many useful and interesting properties.

 

https://en.wikipedia.org/wiki/Two-dimensional_electron_gas

https://en.wikipedia.org/wiki/Local-density_approximation

https://en.wikipedia.org/wiki/Degenerate_matter#Degenerate_gases

https://en.wikipedia.org/wiki/Jellium

https://en.wikipedia.org/wiki/Free_electron

https://en.wikipedia.org/wiki/Plasma_oscillation#%27Cold%27_electrons

https://en.wikipedia.org/wiki/Free_electron_model

https://en.wikipedia.org/wiki/Local-density_approximation#Homogeneous_electron_gas

https://en.wikipedia.org/wiki/Thomas%E2%80%93Fermi_screening#Relation_between_electron_density_and_internal_chemical_potential

https://en.wikipedia.org/wiki/Gas_electron_diffraction

One-dimensional electron gas

Friedel oscillations of the electron density in 1D electron gas occupying the half-space ${\displaystyle x>0}$. Here, ${\displaystyle n_0=2k_{\mathrm{F}}/\pi }$, and ${\displaystyle k_{\mathrm{F}}}$ is the Fermi wave vector.

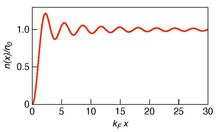
As a simple model, consider one-dimensional electron gas in a half-space ${\displaystyle x>0}$. The electrons do not penetrate into the half-space ${\displaystyle x\le 0}$, so that the boundary condition for the electron wave function is ${\displaystyle \psi (x=0)=0}$. The oscillating wave functions that satisfy this condition are

${\displaystyle {\psi }_k(x)=\sqrt{\frac{2}{L}}\sin kx}$ ,

where ${\displaystyle k>0}$ is the electron wave vector, and ${\displaystyle L}$ is the length of the one-dimensional box (we use the 'box" normalization here). We consider degenerate electron gas, so that the electrons fill states with energies less than the Fermi energy ${\displaystyle E_{\mathrm{F}}}$. Then, the electron density ${\displaystyle n(x)}$ is calculated as

${\displaystyle n(x)=2\sum _{k<k_F}|{\psi }_k(x){|}^2}$,

where summation is taken over all wave vectors less than the Fermi wave vector ${\displaystyle k_{\mathrm{F}}=\sqrt{2m{E}_{\mathrm{F}}/{\hslash }^2}}$, the factor 2 accounts for the spin degeneracy. By transforming the sum over ${\displaystyle k}$ into the integral we obtain

${\displaystyle n(x)=2\frac{L}{\pi }\underset{0}{\overset{k_{\mathrm{F}}}{\int }}|{\psi }_k(x){|}^{2}dk=\frac{2k_{\mathrm{F}}}{\pi }\left(1-\frac{\sin 2k_{\mathrm{F}}x}{2k_{\mathrm{F}}x}\right)}$.

We see that the boundary perturbs the electron density leading to its spatial oscillations with the period ${\displaystyle {\lambda }_{\mathrm{F}}=\pi /k_{\mathrm{F}}}$ near the boundary. These oscillations decay into the bulk with the decay length also given by ${\displaystyle {\lambda }_{\mathrm{F}}}$. At ${\displaystyle x\to +\mathrm{\infty }}$ the electron density equals to the unperturbed density of the one-dimensional electron gas ${\displaystyle 2k_{\mathrm{F}}/\pi }$.

Scattering description

The electrons that move through a metal or semiconductor behave like free electrons of a Fermi gas with a plane wave-like wave function, that is

${\displaystyle {\psi }_{\mathbf{k}}(\mathbf{r})=\frac{1}{\sqrt{\mathrm{\Omega }}}{e}^{i\mathbf{k}\cdot \mathbf{r}}}$.

Electrons in a metal behave differently than particles in a normal gas because electrons are fermions and they obey Fermi–Dirac statistics. This behaviour means that every k-state in the gas can only be occupied by two electrons with opposite spin. The occupied states fill a sphere in the band structure k-space, up to a fixed energy level, the so-called Fermi energy. The radius of the sphere in k-space, k_F, is called the Fermi wave vector.

If there is a foreign atom embedded in the metal or semiconductor, a so-called impurity, the electrons that move freely through the solid are scattered by the deviating potential of the impurity. During the scattering process the initial state wave vector k_i of the electron wave function is scattered to a final state wave vector k_f. Because the electron gas is a Fermi gas only electrons with energies near the Fermi level can participate in the scattering process because there must be empty final states for the scattered states to jump to. Electrons that are too far below the Fermi energy E_F can't jump to unoccupied states. The states around the Fermi level that can be scattered occupy a limited range of k-values or wavelengths. So only electrons within a limited wavelength range near the Fermi energy are scattered resulting in a density modulation around the impurity of the form

${\displaystyle \rho (\mathbf{r})={\rho }_0+\delta n\frac{\cos (2k_{\mathrm{F}}|\mathbf{r}|+\delta )}{|\mathbf{r}{|}^3}}$.^{[further explanation needed]}

https://en.wikipedia.org/wiki/Friedel_oscillations#One-dimensional_electron_gas

Screening of negatively charged particle in a pool of positive ions

Friedel oscillations,^[1] named after French physicist Jacques Friedel, arise from localized perturbations in a metallic or semiconductor system caused by a defect in the Fermi gas or Fermi liquid.^[2] Friedel oscillations are a quantum mechanical analog to electric charge screening of charged species in a pool of ions. Whereas electrical charge screening utilizes a point entity treatment to describe the make-up of the ion pool, Friedel oscillations describing fermions in a Fermi fluid or Fermi gas require a quasi-particle or a scattering treatment. Such oscillations depict a characteristic exponential decay in the fermionic density near the perturbation followed by an ongoing sinusoidal decay resembling sinc function. In 2020, magnetic Friedel oscillations were observed on a metal surface.^[3][4]

https://en.wikipedia.org/wiki/Friedel_oscillations

https://en.wikipedia.org/wiki/Category:Condensed_matter_physics

Basic Faraday disc generator

https://en.wikipedia.org/wiki/Homopolar_generator