05-15-2023-2018 - monogon, also known as a henagon

In geometry, a monogon, also known as a henagon, is a polygon with one edge and one vertex. It has Schläfli symbol {1}.^[1]

In Euclidean geometry

In Euclidean geometry a monogon is a degenerate polygon because its endpoints must coincide, unlike any Euclidean line segment. Most definitions of a polygon in Euclidean geometry do not admit the monogon.

In spherical geometry

In spherical geometry, a monogon can be constructed as a vertex on a great circle (equator). This forms a dihedron, {1,2}, with two hemispherical monogonal faces which share one 360° edge and one vertex. Its dual, a hosohedron, {2,1} has two antipodal vertices at the poles, one 360° lune face, and one edge (meridian) between the two vertices.^[1]

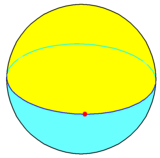Monogonal dihedron, {1,2}

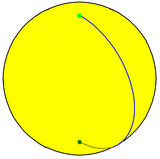Monogonal hosohedron, {2,1}

See also

Look up monogon in Wiktionary, the free dictionary.

• Digon

References

1. 
   

1. Coxeter, Introduction to geometry, 1969, Second edition, sec 21.3 Regular maps, p. 386-388

• Herbert Busemann, The geometry of geodesics. New York, Academic Press, 1955
• Coxeter, H.S.M; Regular Polytopes (third edition). Dover Publications Inc. ISBN 0-486-61480-8

v t e Polygons (List)

v t e Polyhedra

Categories:

• Polygons by the number of sides
• 1 (number)

https://en.wikipedia.org/wiki/Monogon