The gas laws were developed at the end of the 18th century, when scientists began to realize that relationships between pressure, volume and temperature of a sample of gas could be obtained which would hold to approximation for all gases.
Boyle's law[edit]
In 1662 Robert Boyle studied the relationship between volume and pressure of a gas of fixed amount at constant temperature. He observed that volume of a given mass of a gas is inversely proportional to its pressure at a constant temperature. Boyle's law, published in 1662, states that, at constant temperature, the product of the pressure and volume of a given mass of an ideal gas in a closed system is always constant. It can be verified experimentally using a pressure gauge and a variable volume container. It can also be derived from the kinetic theory of gases: if a container, with a fixed number of molecules inside, is reduced in volume, more molecules will strike a given area of the sides of the container per unit time, causing a greater pressure.
A statement of Boyle's law is as follows:
- The volume of a given mass of a gas is inversely related to pressure when the temperature is constant.
The concept can be represented with these formulae:
- , meaning "Volume is inversely proportional to Pressure", or
- , meaning "Pressure is inversely proportional to Volume", or
- , or
- where P is the pressure, and V is the volume of a gas, and k1 is the constant in this equation (and is not the same as the proportionality constants in the other equations in this article).
Charles's law[edit]
Charles's law, or the law of volumes, was found in 1787 by Jacques Charles. It states that, for a given mass of an ideal gas at constant pressure, the volume is directly proportional to its absolute temperature, assuming in a closed system.
The statement of Charles's law is as follows: the volume (V) of a given mass of a gas, at constant pressure (P), is directly proportional to its temperature (T). As a mathematical equation, Charles's law is written as either:
- , or
- , or
- ,
where "V" is the volume of a gas, "T" is the absolute temperature and k2 is a proportionality constant (which is not the same as the proportionality constants in the other equations in this article).
Gay-Lussac's law[edit]
Gay-Lussac's law, Amontons' law or the pressure law was found by Joseph Louis Gay-Lussac in 1808. It states that, for a given mass and constant volume of an ideal gas, the pressure exerted on the sides of its container is directly proportional to its absolute temperature.
As a mathematical equation, Gay-Lussac's law is written as either:
- , or
- , or
- ,
- where P is the pressure, T is the absolute temperature, and k is another proportionality constant.
Avogadro's law[edit]
Avogadro's law (hypothesized in 1811) states that the volume occupied by an ideal gas is directly proportional to the number of molecules of the gas present in the container. This gives rise to the molar volume of a gas, which at STP (273.15 K, 1 atm) is about 22.4 L. The relation is given by
- where n is equal to the number of molecules of gas (or the number of moles of gas).
Combined and ideal gas laws[edit]
The Combined gas law or General Gas Equation is obtained by combining Boyle's Law, Charles's law, and Gay-Lussac's Law. It shows the relationship between the pressure, volume, and temperature for a fixed mass (quantity) of gas:
This can also be written as:
With the addition of Avogadro's law, the combined gas law develops into the ideal gas law:
- where
- P is pressure
- V is volume
- n is the number of moles
- R is the universal gas constant
- T is temperature (K)
- where the proportionality constant, now named R, is the universal gas constant with a value of 8.3144598 (kPa∙L)/(mol∙K). An equivalent formulation of this law is:
- where
- P is the pressure
- V is the volume
- N is the number of gas molecules
- k is the Boltzmann constant (1.381×10−23 J·K−1 in SI units)
- T is the temperature (K)
These equations are exact only for an ideal gas, which neglects various intermolecular effects (see real gas). However, the ideal gas law is a good approximation for most gases under moderate pressure and temperature.
This law has the following important consequences:
- If temperature and pressure are kept constant, then the volume of the gas is directly proportional to the number of molecules of gas.
- If the temperature and volume remain constant, then the pressure of the gas changes is directly proportional to the number of molecules of gas present.
- If the number of gas molecules and the temperature remain constant, then the pressure is inversely proportional to the volume.
- If the temperature changes and the number of gas molecules are kept constant, then either pressure or volume (or both) will change in direct proportion to the temperature.
Other gas laws[edit]
- Graham's law
- states that the rate at which gas molecules diffuse is inversely proportional to the square root of the gas density at constant temperature. Combined with Avogadro's law (i.e. since equal volumes have equal number of molecules) this is the same as being inversely proportional to the root of the molecular weight.
- Dalton's law of partial pressures
- states that the pressure of a mixture of gases simply is the sum of the partial pressures of the individual components. Dalton's law is as follows:
- and all component gases and the mixture are at the same temperature and volume
- where Ptotal is the total pressure of the gas mixture
- Pi is the partial pressure, or pressure of the component gas at the given volume and temperature.
- Amagat's law of partial volumes
- states that the volume of a mixture of gases (or the volume of the container) simply is the sum of the partial volumes of the individual components. Amagat's law is as follows:
- and all component gases and the mixture are at the same temperature and pressure
- where Vtotal is the total volume of the gas mixture, or the volume of the container,
- Vi is the partial volume, or volume of the component gas at the given pressure and temperature.
- Henry's law
- states that At constant temperature, the amount of a given gas dissolved in a given type and volume of liquid is directly proportional to the partial pressure of that gas in equilibrium with that liquid.
- Real gas law
- formulated by Johannes Diderik van der Waals (1873).
References[edit]
- Castka, Joseph F.; Metcalfe, H. Clark; Davis, Raymond E.; Williams, John E. (2002). Modern Chemistry. Holt, Rinehart and Winston. ISBN 0-03-056537-5.
- Guch, Ian (2003). The Complete Idiot's Guide to Chemistry. Alpha, Penguin Group Inc. ISBN 1-59257-101-8.
- Zumdahl, Steven S (1998). Chemical Principles. Houghton Mifflin Company. ISBN 0-395-83995-5.
https://en.wikipedia.org/wiki/Gas_laws
In chemistry and thermodynamics, the Van der Waals equation (or Van der Waals equation of state; named after Dutch physicist Johannes Diderik van der Waals) is an equation of state that generalizes the ideal gas law based on plausible reasons that real gases do not act ideally. The ideal gas law treats gas molecules as point particles that interact with their containers but not each other, meaning they neither take up space nor change kinetic energy during collisions(i.e. all collisions are perfectly elastic).[1] The ideal gas law states that volume (V) occupied by n moles of any gas has a pressure (P) at temperature (T) in kelvinsgiven by the following relationship, where R is the gas constant:
To account for the volume that a real gas molecule takes up, the Van der Waals equation replaces V in the ideal gas law with , where Vm is the molar volume of the gas and b is the volume that is occupied by one mole of the molecules. This leads to:[1]
The second modification made to the ideal gas law accounts for the fact that gas molecules do in fact interact with each other (they usually experience attraction at low pressures and repulsion at high pressures) and that real gases therefore show different compressibility than ideal gases. Van der Waals provided for intermolecular interaction by adding to the observed pressure P in the equation of state a term , where a is a constant whose value depends on the gas. The Van der Waals equation is therefore written as:[1]
and, for n moles of gas, can also be written as the equation below:
where Vm is the molar volume of the gas, R is the universal gas constant, T is temperature, P is pressure, and V is volume. When the molar volume Vm is large, bbecomes negligible in comparison with Vm, a/Vm2 becomes negligible with respect to P, and the Van der Waals equation reduces to the ideal gas law, PVm=RT.[1]
It is available via its traditional derivation (a mechanical equation of state), or via a derivation based in statistical thermodynamics, the latter of which provides the partition function of the system and allows thermodynamic functions to be specified. It successfully approximates the behavior of real fluids above their critical temperatures and is qualitatively reasonable for their liquid and low-pressure gaseous states at low temperatures. However, near the phase transitions between gas and liquid, in the range of p, V, and T where the liquid phase and the gas phase are in equilibrium, the Van der Waals equation fails to accurately model observed experimental behaviour, in particular that p is a constant function of V at given temperatures. As such, the Van der Waals model is not useful only for calculations intended to predict real behavior in regions near the critical point. Corrections to address these predictive deficiencies have since been made, such as the equal area rule or the principle of corresponding states.
https://en.wikipedia.org/wiki/Van_der_Waals_equation
According to van der Waals, the theorem of corresponding states (or principle/law of corresponding states) indicates that all fluids, when compared at the same reduced temperature and reduced pressure, have approximately the same compressibility factor and all deviate from ideal gas behavior to about the same degree.[1][2]
Material constants that vary for each type of material are eliminated, in a recast reduced form of a constitutive equation. The reduced variables are defined in terms of critical variables.
The principle originated with the work of Johannes Diderik van der Waals in about 1873[3] when he used the critical temperature and critical pressure to characterize a fluid.
The most prominent example is the van der Waals equation of state, the reduced form of which applies to all fluids.
Compressibility factor at the critical point[edit]
The compressibility factor at the critical point, which is defined as , where the subscript indicates the critical point, is predicted to be a constant independent of substance by many equations of state; the Van der Waals equation e.g. predicts a value of .
Where:
- : critical temperature [K]
- : critical pressure [Pa]
- : critical specific volume [m3⋅kg−1]
- : gas constant (8.314 J⋅K−1⋅mol−1)
- : Molar mass [kg⋅mol−1]
For example:
| Substance | [Pa] | [K] | [m3/kg] | |
|---|---|---|---|---|
| H2O | 21.817×106 | 647.3 | 3.154×10−3 | 0.23[4] |
| 4He | 0.226×106 | 5.2 | 14.43×10−3 | 0.31[4] |
| He | 0.226×106 | 5.2 | 14.43×10−3 | 0.30[5] |
| H2 | 1.279×106 | 33.2 | 32.3×10−3 | 0.30[5] |
| Ne | 2.73×106 | 44.5 | 2.066×10−3 | 0.29[5] |
| N2 | 3.354×106 | 126.2 | 3.2154×10−3 | 0.29[5] |
| Ar | 4.861×106 | 150.7 | 1.883×10−3 | 0.29[5] |
| Xe | 5.87×106 | 289.7 | 0.9049×10−3 | 0.29 |
| O2 | 5.014×106 | 154.8 | 2.33×10−3 | 0.291 |
| CO2 | 7.290×106 | 304.2 | 2.17×10−3 | 0.275 |
| SO2 | 7.88×106 | 430.0 | 1.900×10−3 | 0.275 |
| CH4 | 4.58×106 | 190.7 | 6.17×10−3 | 0.285 |
| C3H8 | 4.21×106 | 370.0 | 4.425×10−3 | 0.267 |
See also[edit]
- Van der Waals equation
- Equation of state
- Compressibility factors
- Johannes Diderik van der Waals equation
- Noro-Frenkel law of corresponding states
https://en.wikipedia.org/wiki/Theorem_of_corresponding_states
In physics and thermodynamics, an equation of state is a thermodynamic equation relating state variables which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature (PVT), or internal energy.[1] Equations of state are useful in describing the properties of fluids, mixtures of fluids, solids, and the interior of stars.
https://en.wikipedia.org/wiki/Equation_of_state
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, is a correction factor which describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour.[1] In general, deviation from ideal behaviour becomes more significant the closer a gas is to a phase change, the lower the temperature or the larger the pressure. Compressibility factor values are usually obtained by calculation from equations of state (EOS), such as the virial equation which take compound-specific empirical constants as input. For a gas that is a mixture of two or more pure gases (air or natural gas, for example), the gas composition must be known before compressibility can be calculated.
Alternatively, the compressibility factor for specific gases can be read from generalized compressibility charts[1] that plot as a function of pressure at constant temperature.
The compressibility factor should not be confused with the compressibility (also known as coefficient of compressibility or isothermal compressibility) of a material, which is the measure of the relative volume change of a fluid or solid in response to a pressure change.
https://en.wikipedia.org/wiki/Compressibility_factor
In physics and thermodynamics, an equation of state is a thermodynamic equation relating state variables which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature (PVT), or internal energy.[1] Equations of state are useful in describing the properties of fluids, mixtures of fluids, solids, and the interior of stars.
Overview[edit]
At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate for weakly polar gases at low pressures and moderate temperatures. This equation becomes increasingly inaccurate at higher pressures and lower temperatures, and fails to predict condensation from a gas to a liquid.
Another common use is in modeling the interior of stars, including neutron stars, dense matter (quark–gluon plasmas) and radiation fields. A related concept is the perfect fluid equation of state used in cosmology.
Equations of state can also describe solids, including the transition of solids from one crystalline state to another.
In a practical context, equations of state are instrumental for PVT calculations in process engineering problems, such as petroleum gas/liquid equilibrium calculations. A successful PVT model based on a fitted equation of state can be helpful to determine the state of the flow regime, the parameters for handling the reservoir fluids, and pipe sizing.
Measurements of equation-of-state parameters, especially at high pressures, can be made using lasers.[2][3][4]
Historical[edit]
Boyle's law (1662)[edit]
Boyle's Law was perhaps the first expression of an equation of state.[citation needed] In 1662, the Irish physicist and chemist Robert Boyle performed a series of experiments employing a J-shaped glass tube, which was sealed on one end. Mercury was added to the tube, trapping a fixed quantity of air in the short, sealed end of the tube. Then the volume of gas was measured as additional mercury was added to the tube. The pressure of the gas could be determined by the difference between the mercury level in the short end of the tube and that in the long, open end. Through these experiments, Boyle noted that the gas volume varied inversely with the pressure. In mathematical form, this can be stated as:
The above relationship has also been attributed to Edme Mariotte and is sometimes referred to as Mariotte's law. However, Mariotte's work was not published until 1676.
Charles's law or Law of Charles and Gay-Lussac (1787)[edit]
In 1787 the French physicist Jacques Charles found that oxygen, nitrogen, hydrogen, carbon dioxide, and air expand to roughly the same extent over the same 80-kelvin interval. Later, in 1802, Joseph Louis Gay-Lussac published results of similar experiments, indicating a linear relationship between volume and temperature (Charles's Law):
Dalton's law of partial pressures (1801)[edit]
Dalton's Law of partial pressure states that the pressure of a mixture of gases is equal to the sum of the pressures of all of the constituent gases alone.
Mathematically, this can be represented for n species as:
The ideal gas law (1834)[edit]
In 1834, Émile Clapeyron combined Boyle's Law and Charles' law into the first statement of the ideal gas law. Initially, the law was formulated as pVm = R(TC + 267) (with temperature expressed in degrees Celsius), where R is the gas constant. However, later work revealed that the number should actually be closer to 273.2, and then the Celsius scale was defined with 0 °C = 273.15 K, giving:
Van der Waals equation of state (1873)[edit]
In 1873, J. D. van der Waals introduced the first equation of state derived by the assumption of a finite volume occupied by the constituent molecules.[5] His new formula revolutionized the study of equations of state, and was most famously continued via the Redlich–Kwong equation of state[6] and the Soave modification of Redlich-Kwong.[7]
General form of an equation of state[edit]
Thermodynamic systems are specified by an equation of state that constrains the values that the state variables may assume. For a given amount of substance contained in a system, the temperature, volume, and pressure are not independent quantities; they are connected by a relationship of the general form
An equation used to model this relationship is called an equation of state. In the following sections major equations of state are described, and the variables used here are defined as follows. Any consistent set of units may be used, although SI units are preferred. Absolute temperature refers to the use of the Kelvin (K) or Rankine (°R) temperature scales, with zero being absolute zero.
- , pressure (absolute)
- , volume
- , number of moles of a substance
- , , molar volume, the volume of 1 mole of gas or liquid
- , absolute temperature
- , ideal gas constant ≈ 8.3144621 J/mol·K
- , pressure at the critical point
- , molar volume at the critical point
- , absolute temperature at the critical point
Classical ideal gas law[edit]
The classical ideal gas law may be written
In the form shown above, the equation of state is thus
If the calorically perfect gas approximation is used, then the ideal gas law may also be expressed as follows
where is the density, is the (constant) adiabatic index (ratio of specific heats), is the internal energy per unit mass (the "specific internal energy"), is the constant specific heat at constant volume, and is the constant specific heat at constant pressure.
Quantum ideal gas law[edit]
Since for atomic and molecular gases, the classical ideal gas law is well suited in most cases, let us describe the equation of state for elementary particles with mass and spin that takes into account of quantum effects. In the following, the upper sign will always correspond to Fermi-Dirac statistics and the lower sign to Bose–Einstein statistics. The equation of state of such gases with particles occupying a volume with temperature and pressure is given by[8]
where is the Boltzmann constant and the chemical potential is given by the following implicit function
In the limiting case where , this equation of state will reduce to that of the classical ideal gas. It can be shown that the above equation of state in the limit reduces to
With a fixed number density , decreasing the temperature causes in Fermi gas, a increase in the value for pressure from its classical value implying an effective repulsion between particles (this is an apparent repulsion due to quantum exchange effects not because of actual interactions between particles since in ideal gas, interactional forces are neglected) and in Bose gas, a decrease in pressure from its classical value implying an effective attraction.
Cubic equations of state[edit]
Cubic equations of state are called such because they can be rewritten as a cubic function of .
Van der Waals equation of state[edit]
The Van der Waals equation of state may be written:
where is molar volume. The substance-specific constants and can be calculated from the critical properties , , and (noting that is the molar volume at the critical point) as:
Also written as
Proposed in 1873, the van der Waals equation of state was one of the first to perform markedly better than the ideal gas law. In this landmark equation is called the attraction parameter and the repulsion parameter or the effective molecular volume. While the equation is definitely superior to the ideal gas law and does predict the formation of a liquid phase, the agreement with experimental data is limited for conditions where the liquid forms. While the van der Waals equation is commonly referenced in text-books and papers for historical reasons, it is now obsolete. Other modern equations of only slightly greater complexity are much more accurate.
The van der Waals equation may be considered as the ideal gas law, "improved" due to two independent reasons:
- Molecules are thought as particles with volume, not material points. Thus cannot be too little, less than some constant. So we get () instead of .
- While ideal gas molecules do not interact, we consider molecules attracting others within a distance of several molecules' radii. It makes no effect inside the material, but surface molecules are attracted into the material from the surface. We see this as diminishing of pressure on the outer shell (which is used in the ideal gas law), so we write ( something) instead of . To evaluate this ‘something’, let's examine an additional force acting on an element of gas surface. While the force acting on each surface molecule is ~, the force acting on the whole element is ~~.
With the reduced state variables, i.e. , and , the reduced form of the Van der Waals equation can be formulated:
The benefit of this form is that for given and , the reduced volume of the liquid and gas can be calculated directly using Cardano's method for the reduced cubic form:
For and , the system is in a state of vapor–liquid equilibrium. The reduced cubic equation of state yields in that case 3 solutions. The largest and the lowest solution are the gas and liquid reduced volume.
Redlich-Kwong equation of state[6][edit]
Introduced in 1949, the Redlich-Kwong equation of state was a considerable improvement over other equations of the time. It is still of interest primarily due to its relatively simple form. While superior to the van der Waals equation of state, it performs poorly with respect to the liquid phase and thus cannot be used for accurately calculating vapor–liquid equilibria. However, it can be used in conjunction with separate liquid-phase correlations for this purpose.
The Redlich-Kwong equation is adequate for calculation of gas phase properties when the ratio of the pressure to the critical pressure (reduced pressure) is less than about one-half of the ratio of the temperature to the critical temperature (reduced temperature):
Soave modification of Redlich-Kwong[7][edit]
Where ω is the acentric factor for the species.
This formulation for is due to Graboski and Daubert. The original formulation from Soave is:
for hydrogen:
We can also write it in the polynomial form, with:
then we have:
where is the universal gas constant and Z=PV/(RT) is the compressibility factor.
In 1972 G. Soave[9] replaced the 1/√T term of the Redlich-Kwong equation with a function α(T,ω) involving the temperature and the acentric factor (the resulting equation is also known as the Soave-Redlich-Kwong equation of state; SRK EOS). The α function was devised to fit the vapor pressure data of hydrocarbons and the equation does fairly well for these materials.
Note especially that this replacement changes the definition of a slightly, as the is now to the second power.
Volume translation of Peneloux et al. (1982)[edit]
The SRK EOS may be written as
where
where and other parts of the SRK EOS is defined in the SRK EOS section.
A downside of the SRK EOS, and other cubic EOS, is that the liquid molar volume is significantly less accurate than the gas molar volume. Peneloux et alios (1982)[10] proposed a simple correction for this by introducing a volume translation
where is an additional fluid component parameter that translates the molar volume slightly. On the liquid branch of the EOS, a small change in molar volume corresponds to a large change in pressure. On the gas branch of the EOS, a small change in molar volume corresponds to a much smaller change in pressure than for the liquid branch. Thus, the perturbation of the molar gas volume is small. Unfortunately, there are two versions that occur in science and industry.
In the first version only is translated,[11] [12] and the EOS becomes
In the second version both and are translated, or the translation of is followed by a renaming of the composite parameter b − c.[13] This gives
The c-parameter of a fluid mixture is calculated by
The c-parameter of the individual fluid components in a petroleum gas and oil can be estimated by the correlation
where the Rackett compressibility factor can be estimated by
A nice feature with the volume translation method of Peneloux et al. (1982) is that it does not affect the vapor-liquid equilibrium calculations.[14] This method of volume translation can also be applied to other cubic EOSs if the c-parameter correlation is adjusted to match the selected EOS.
Peng–Robinson equation of state[edit]
In polynomial form:
where is the acentric factor of the species, is the universal gas constant and is compressibility factor.
The Peng–Robinson equation of state (PR EOS) was developed in 1976 at The University of Alberta by Ding-Yu Peng and Donald Robinson in order to satisfy the following goals:[15]
- The parameters should be expressible in terms of the critical properties and the acentric factor.
- The model should provide reasonable accuracy near the critical point, particularly for calculations of the compressibility factor and liquid density.
- The mixing rules should not employ more than a single binary interaction parameter, which should be independent of temperature, pressure, and composition.
- The equation should be applicable to all calculations of all fluid properties in natural gas processes.
For the most part the Peng–Robinson equation exhibits performance similar to the Soave equation, although it is generally superior in predicting the liquid densities of many materials, especially nonpolar ones.[16] The departure functions of the Peng–Robinson equation are given on a separate article.
The analytic values of its characteristic constants are:
Peng–Robinson-Stryjek-Vera equations of state[edit]
PRSV1[edit]
A modification to the attraction term in the Peng–Robinson equation of state published by Stryjek and Vera in 1986 (PRSV) significantly improved the model's accuracy by introducing an adjustable pure component parameter and by modifying the polynomial fit of the acentric factor.[17]
The modification is:
where is an adjustable pure component parameter. Stryjek and Vera published pure component parameters for many compounds of industrial interest in their original journal article. At reduced temperatures above 0.7, they recommend to set and simply use . For alcohols and water the value of may be used up to the critical temperature and set to zero at higher temperatures.[17]
PRSV2[edit]
A subsequent modification published in 1986 (PRSV2) further improved the model's accuracy by introducing two additional pure component parameters to the previous attraction term modification.[18]
The modification is:
where , , and are adjustable pure component parameters.
PRSV2 is particularly advantageous for VLE calculations. While PRSV1 does offer an advantage over the Peng–Robinson model for describing thermodynamic behavior, it is still not accurate enough, in general, for phase equilibrium calculations.[17] The highly non-linear behavior of phase-equilibrium calculation methods tends to amplify what would otherwise be acceptably small errors. It is therefore recommended that PRSV2 be used for equilibrium calculations when applying these models to a design. However, once the equilibrium state has been determined, the phase specific thermodynamic values at equilibrium may be determined by one of several simpler models with a reasonable degree of accuracy.[18]
One thing to note is that in the PRSV equation, the parameter fit is done in a particular temperature range which is usually below the critical temperature. Above the critical temperature, the PRSV alpha function tends to diverge and become arbitrarily large instead of tending towards 0. Because of this, alternate equations for alpha should be employed above the critical point. This is especially important for systems containing hydrogen which is often found at temperatures far above its critical point. Several alternate formulations have been proposed. Some well known ones are by Twu et al or by Mathias and Copeman.
Peng-Robinson-Babalola equation of state (PRB)[edit]
Babalola [19] modified the Peng–Robinson Equation of state as:
The attractive force parameter ‘a’, which was considered to be a constant with respect to pressure in Peng–Robinson EOS. The modification, in which parameter ‘a’ was treated as a variable with respect to pressure for multicomponent multi-phase high density reservoir systems was to improve accuracy in the prediction of properties of complex reservoir fluids for PVT modeling. The variation was represented with a linear equation where a1 and a2 represent the slope and the intercept respectively of the straight line obtained when values of parameter ‘a’ are plotted against pressure.
This modification increases the accuracy of Peng–Robinson equation of state for heavier fluids particularly at pressure ranges (>30MPa) and eliminates the need for tuning the original Peng-Robinson equation of state. Values for a
Elliott, Suresh, Donohue equation of state[edit]
The Elliott, Suresh, and Donohue (ESD) equation of state was proposed in 1990.[20] The equation seeks to correct a shortcoming in the Peng–Robinson EOS in that there was an inaccuracy in the van der Waals repulsive term. The EOS accounts for the effect of the shape of a non-polar molecule and can be extended to polymers with the addition of an extra term (not shown). The EOS itself was developed through modeling computer simulations and should capture the essential physics of the size, shape, and hydrogen bonding.
where:
and
- is a "shape factor", with for spherical molecules
- For non-spherical molecules, the following relation is suggested
- where is the acentric factor.
- The reduced number density is defined as
where
- is the characteristic size parameter
- is the number of molecules
- is the volume of the container
The characteristic size parameter is related to the shape parameter through
where
- and is Boltzmann's constant.
Noting the relationships between Boltzmann's constant and the Universal gas constant, and observing that the number of molecules can be expressed in terms of Avogadro's number and the molar mass, the reduced number density can be expressed in terms of the molar volume as
The shape parameter appearing in the Attraction term and the term are given by
- (and is hence also equal to 1 for spherical molecules).
where is the depth of the square-well potential and is given by
- , , and are constants in the equation of state:
- for spherical molecules (c=1)
- for spherical molecules (c=1)
- for spherical molecules (c=1)
The model can be extended to associating components and mixtures of nonassociating components. Details are in the paper by J.R. Elliott, Jr. et al. (1990).[20]
Cubic-Plus-Association[edit]
The Cubic-Plus-Association (CPA) equation of state combines the Soave-Redlich-Kwong equation with the association term from SAFT[21][22] based on Chapman's extensions and simplifications of a theory of associating molecules due to Michael Wertheim.[23] The development of the equation began in 1995 as a research project that was funded by Shell, and in 1996 an article was published which presented the CPA equation of state.[23][24]
In the association term is the mole fraction of molecules not bonded at site A.
Non-cubic equations of state[edit]
Dieterici equation of state[edit]
where a is associated with the interaction between molecules and b takes into account the finite size of the molecules, similar to the Van der Waals equation.
The reduced coordinates are:
Virial equations of state[edit]
Virial equation of state[edit]
Although usually not the most convenient equation of state, the virial equation is important because it can be derived directly from statistical mechanics. This equation is also called the Kamerlingh Onnes equation. If appropriate assumptions are made about the mathematical form of intermolecular forces, theoretical expressions can be developed for each of the coefficients. A is the first virial coefficient, which has a constant value of 1 and makes the statement that when volume is large, all fluids behave like ideal gases. The second virial coefficient B corresponds to interactions between pairs of molecules, C to triplets, and so on. Accuracy can be increased indefinitely by considering higher order terms. The coefficients B, C, D, etc. are functions of temperature only.
One of the most accurate equations of state is that from Benedict-Webb-Rubin-Starling[25] shown next. It was very close to a virial equation of state. If the exponential term in it is expanded to two Taylor terms, a virial equation can be derived:
Note that in this virial equation, the fourth and fifth virial terms are zero. The second virial coefficient is monotonically decreasing as temperature is lowered. The third virial coefficient is monotonically increasing as temperature is lowered.
The BWR equation of state[edit]
where
- p is pressure
- ρ is molar density
Values of the various parameters can be found in reference materials.[26]
Lee-Kesler equation of state[edit]
The Lee-Kesler equation of state is based on the corresponding states principle, and is a modification of the BWR equation of state.[27]
SAFT equations of state[edit]
Statistical associating fluid theory (SAFT) equations of state predict the effect of molecular size and shape and hydrogen bonding on fluid properties and phase behavior. The SAFT equation of state was developed using statistical mechanical methods (in particular perturbation theory) to describe the interactions between molecules in a system.[21][22][28] The idea of a SAFT equation of state was first proposed by Chapman et al. in 1988 and 1989.[21][22][28] Many different versions of the SAFT equation of state have been proposed, but all use the same chain and association terms derived by Chapman.[21][29][30] SAFT equations of state represent molecules as chains of typically spherical particles that interact with one another through short range repulsion, long range attraction, and hydrogen bonding between specific sites.[28] One popular version of the SAFT equation of state includes the effect of chain length on the shielding of the dispersion interactions between molecules (PC-SAFT).[31] In general, SAFT equations give more accurate results than traditional cubic equations of state, especially for systems containing liquids or solids.[32][33]
Multiparameter equations of state[edit]
Helmholtz Function form[edit]
Multiparameter equations of state (MEOS) can be used to represent pure fluids with high accuracy, in both the liquid and gaseous states. MEOS's represent the Helmholtz function of the fluid as the sum of ideal gas and residual terms. Both terms are explicit in reduced temperature and reduced density - thus:
where:
The reduced density and temperature are typically, though not always, the critical values for the pure fluid.
Other thermodynamic functions can be derived from the MEOS by using appropriate derivatives of the Helmholtz function; hence, because integration of the MEOS is not required, there are few restrictions as to the functional form of the ideal or residual terms.[34][35] Typical MEOS use upwards of 50 fluid specific parameters, but are able to represent the fluid's properties with high accuracy. MEOS are available currently for about 50 of the most common industrial fluids including refrigerants. The IAPWS95 reference equation of state for water is also an MEOS.[36] Mixture models for MEOS exist, as well.
One example of such an equation of state is the form proposed by Span and Wagner.[34]
This is a somewhat simpler form that is intended to be used more in technical applications.[34] Reference equations of state require a higher accuracy and use a more complicated form with more terms.[36][35]
Other equations of state of interest[edit]
Stiffened equation of state[edit]
When considering water under very high pressures, in situations such as underwater nuclear explosions, sonic shock lithotripsy, and sonoluminescence, the stiffened equation of state[37] is often used:
where is the internal energy per unit mass, is an empirically determined constant typically taken to be about 6.1, and is another constant, representing the molecular attraction between water molecules. The magnitude of the correction is about 2 gigapascals (20,000 atmospheres).
The equation is stated in this form because the speed of sound in water is given by .
Thus water behaves as though it is an ideal gas that is already under about 20,000 atmospheres (2 GPa) pressure, and explains why water is commonly assumed to be incompressible: when the external pressure changes from 1 atmosphere to 2 atmospheres (100 kPa to 200 kPa), the water behaves as an ideal gas would when changing from 20,001 to 20,002 atmospheres (2000.1 MPa to 2000.2 MPa).
This equation mispredicts the specific heat capacity of water but few simple alternatives are available for severely nonisentropic processes such as strong shocks.
Ultrarelativistic equation of state[edit]
An ultrarelativistic fluid has equation of state
where is the pressure, is the mass density, and is the speed of sound.
Ideal Bose equation of state[edit]
The equation of state for an ideal Bose gas is
where α is an exponent specific to the system (e.g. in the absence of a potential field, α = 3/2), z is exp(μ/kT) where μ is the chemical potential, Li is the polylogarithm, ζ is the Riemann zeta function, and Tc is the critical temperature at which a Bose–Einstein condensate begins to form.
Jones–Wilkins–Lee equation of state for explosives (JWL equation)[edit]
The equation of state from Jones–Wilkins–Lee is used to describe the detonation products of explosives.
The ratio is defined by using = density of the explosive (solid part) and = density of the detonation products. The parameters , , , and are given by several references.[38] In addition, the initial density (solid part) , speed of detonation , Chapman–Jouguet pressure and the chemical energy of the explosive are given in such references. These parameters are obtained by fitting the JWL-EOS to experimental results. Typical parameters for some explosives are listed in the table below.
| Material | (g/cm3) | (m/s) | (GPa) | (GPa) | (GPa) | (GPa) | |||
|---|---|---|---|---|---|---|---|---|---|
| TNT | 1.630 | 6930 | 21.0 | 373.8 | 3.747 | 4.15 | 0.90 | 0.35 | 6.00 |
| Composition B | 1.717 | 7980 | 29.5 | 524.2 | 7.678 | 4.20 | 1.10 | 0.35 | 8.50 |
| PBX 9501[39] | 1.844 | 36.3 | 852.4 | 18.02 | 4.55 | 1.3 | 0.38 | 10.2 |
Equations of state for solids and liquids[edit]
Common abbreviations:
- Tait equation for water and other liquids. Several equations are referred to as the Tait equation.
- Murnaghan equation of state
- Stacey-Brennan-Irvine equation of state[40] (falsely often refer to Rose-Vinet equation of state)
- Adapted Polynomial equation of state[44] (second order form = AP2, adapted for extreme compression)
- with
- where = 0.02337 GPa.nm5. The total number of electrons in the initial volume determines the Fermi gas pressure , which provides for the correct behavior at extreme compression. So far there are no known "simple" solids that require higher order terms.
- Adapted polynomial equation of state[44] (third order form = AP3)
- Mie–Grüneisen equation of state (for a more detailed discussion see refs.[45] [46])
- where is the bulk modulus at equilibrium volume and typically about −2 is often related to the Grüneisen parameter by
See also[edit]
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law.[1] The ideal gas law is often written in an empirical form:
where , and are the pressure, volume and temperature; is the amount of substance; and is the ideal gas constant. It is the same for all gases. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856[2] and Rudolf Clausius in 1857.[3]
Equation[edit]
The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropriate SI unit is the kelvin.[4]
Common forms[edit]
The most frequently introduced forms are:
where:
- is the pressure of the gas,
- is the volume of the gas,
- is the amount of substance of gas (also known as number of moles),
- is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
- is the Boltzmann constant
- is the Avogadro constant
- is the absolute temperature of the gas.
In SI units, p is measured in pascals, V is measured in cubic metres, n is measured in moles, and T in kelvins (the Kelvin scale is a shifted Celsius scale, where 0.00 K = −273.15 °C, the lowest possible temperature). R has the value 8.314 J/(K⋅mol) ≈ 2 cal/(K⋅mol), or 0.0821 L⋅atm/(mol⋅K).
Molar form[edit]
How much gas is present could be specified by giving the mass instead of the chemical amount of gas. Therefore, an alternative form of the ideal gas law may be useful. The chemical amount (n) (in moles) is equal to total mass of the gas (m) (in kilograms) divided by the molar mass (M) (in kilograms per mole):
By replacing n with m/M and subsequently introducing density ρ = m/V, we get:
Defining the specific gas constant Rspecific(r) as the ratio R/M,
This form of the ideal gas law is very useful because it links pressure, density, and temperature in a unique formula independent of the quantity of the considered gas. Alternatively, the law may be written in terms of the specific volume v, the reciprocal of density, as
It is common, especially in engineering and meteorological applications, to represent the specific gas constant by the symbol R. In such cases, the universalgas constant is usually given a different symbol such as or to distinguish it. In any case, the context and/or units of the gas constant should make it clear as to whether the universal or specific gas constant is being referred to.[5]
Statistical mechanics[edit]
In statistical mechanics the following molecular equation is derived from first principles
where P is the absolute pressure of the gas, n is the number density of the molecules (given by the ratio n = N/V, in contrast to the previous formulation in which n is the number of moles), T is the absolute temperature, and kB is the Boltzmann constant relating temperature and energy, given by:
where NA is the Avogadro constant.
From this we notice that for a gas of mass m, with an average particle mass of μ times the atomic mass constant, mu, (i.e., the mass is μ u) the number of molecules will be given by
and since ρ = m/V = nμmu, we find that the ideal gas law can be rewritten as
In SI units, P is measured in pascals, V in cubic metres, T in kelvins, and kB = 1.38×10−23 J⋅K−1 in SI units.
Combined gas law[edit]
Combining the laws of Charles, Boyle and Gay-Lussac gives the combined gas law, which takes the same functional form as the ideal gas law save that the number of moles is unspecified, and the ratio of to is simply taken as a constant:[6]
where is the pressure of the gas, is the volume of the gas, is the absolute temperature of the gas, and is a constant. When comparing the same substance under two different sets of conditions, the law can be written as
Energy associated with a gas[edit]
According to assumptions of the kinetic theory of ideal gases, we assume that there are no intermolecular attractions between the molecules of an ideal gas. In other words, its potential energy is zero. Hence, all the energy possessed by the gas is in the kinetic energy of the molecules of the gas.
This is the kinetic energy of n moles of a monatomic gas having 3 degrees of freedom; x, y, z.
| Energy of gas | Mathematical expression |
|---|---|
| energy associated with one mole of a monatomic gas | |
| energy associated with one gram of a monatomic gas | |
| energy associated with one molecule (or atom) of a monatomic gas |
Applications to thermodynamic processes[edit]
The table below essentially simplifies the ideal gas equation for a particular processes, thus making this equation easier to solve using numerical methods.
A thermodynamic process is defined as a system that moves from state 1 to state 2, where the state number is denoted by subscript. As shown in the first column of the table, basic thermodynamic processes are defined such that one of the gas properties (P, V, T, S, or H) is constant throughout the process.
For a given thermodynamics process, in order to specify the extent of a particular process, one of the properties ratios (which are listed under the column labeled "known ratio") must be specified (either directly or indirectly). Also, the property for which the ratio is known must be distinct from the property held constant in the previous column (otherwise the ratio would be unity, and not enough information would be available to simplify the gas law equation).
In the final three columns, the properties (p, V, or T) at state 2 can be calculated from the properties at state 1 using the equations listed.
| Process | Constant | Known ratio or delta | p2 | V2 | T2 |
|---|---|---|---|---|---|
| Isobaric process | Pressure | p2 = p1 | V2 = V1(V2/V1) | T2 = T1(V2/V1) | |
| p2 = p1 | V2 = V1(T2/T1) | T2 = T1(T2/T1) | |||
| Isochoric process (Isovolumetric process) (Isometric process) | Volume | p2 = p1(p2/p1) | V2 = V1 | T2 = T1(p2/p1) | |
| p2 = p1(T2/T1) | V2 = V1 | T2 = T1(T2/T1) | |||
| Isothermal process | Temperature | p2 = p1(p2/p1) | V2 = V1/(p2/p1) | T2 = T1 | |
| p2 = p1/(V2/V1) | V2 = V1(V2/V1) | T2 = T1 | |||
| Isentropic process (Reversible adiabatic process) | p2 = p1(p2/p1) | V2 = V1(p2/p1)(−1/γ) | T2 = T1(p2/p1)(γ − 1)/γ | ||
| p2 = p1(V2/V1)−γ | V2 = V1(V2/V1) | T2 = T1(V2/V1)(1 − γ) | |||
| p2 = p1(T2/T1)γ/(γ − 1) | V2 = V1(T2/T1)1/(1 − γ) | T2 = T1(T2/T1) | |||
| Polytropic process | P Vn | p2 = p1(p2/p1) | V2 = V1(p2/p1)(−1/n) | T2 = T1(p2/p1)(n − 1)/n | |
| p2 = p1(V2/V1)−n | V2 = V1(V2/V1) | T2 = T1(V2/V1)(1 − n) | |||
| p2 = p1(T2/T1)n/(n − 1) | V2 = V1(T2/T1)1/(1 − n) | T2 = T1(T2/T1) | |||
| Isenthalpic process (Irreversible adiabatic process) | p2 = p1 + (p2 − p1) | T2 = T1 + μJT(p2 − p1) | |||
| p2 = p1 + (T2 − T1)/μJT | T2 = T1 + (T2 − T1) |
^ a. In an isentropic process, system entropy (S) is constant. Under these conditions, p1V1γ = p2V2γ, where γ is defined as the heat capacity ratio, which is constant for a calorifically perfect gas. The value used for γ is typically 1.4 for diatomic gases like nitrogen (N2) and oxygen (O2), (and air, which is 99% diatomic). Also γ is typically 1.6 for mono atomic gases like the noble gases helium (He), and argon (Ar). In internal combustion engines γ varies between 1.35 and 1.15, depending on constitution gases and temperature.
^ b. In an isenthalpic process, system enthalpy (H) is constant. In the case of free expansion for an ideal gas, there are no molecular interactions, and the temperature remains constant. For real gasses, the molecules do interact via attraction or repulsion depending on temperature and pressure, and heating or cooling does occur. This is known as the Joule–Thomson effect. For reference, the Joule–Thomson coefficient μJT for air at room temperature and sea level is 0.22 °C/bar.[7]
Deviations from ideal behavior of real gases[edit]
The equation of state given here (PV = nRT) applies only to an ideal gas, or as an approximation to a real gas that behaves sufficiently like an ideal gas. There are in fact many different forms of the equation of state. Since the ideal gas law neglects both molecular size and inter molecular attractions, it is most accurate for monatomic gases at high temperatures and low pressures. The neglect of molecular size becomes less important for lower densities, i.e. for larger volumes at lower pressures, because the average distance between adjacent molecules becomes much larger than the molecular size. The relative importance of intermolecular attractions diminishes with increasing thermal kinetic energy, i.e., with increasing temperatures. More detailed equations of state, such as the van der Waals equation, account for deviations from ideality caused by molecular size and intermolecular forces.
Derivations[edit]
Empirical[edit]
The empirical laws that led to the derivation of the ideal gas law were discovered with experiments that changed only 2 state variables of the gas and kept every other one constant.
All the possible gas laws that could have been discovered with this kind of setup are:
or |
| (1) known as Boyle's law |
or |
| (2) known as Charles's law |
or |
| (3) known as Avogadro's law |
or |
| (4) known as Gay-Lussac's law |
or |
| (5) |
or |
| (6) |
where P stands for pressure, V for volume, N for number of particles in the gas and T for temperature; where are not actual constants but are in this context because of each equation requiring only the parameters explicitly noted in it changing.
To derive the ideal gas law one does not need to know all 6 formulas, one can just know 3 and with those derive the rest or just one more to be able to get the ideal gas law, which needs 4.
Since each formula only holds when only the state variables involved in said formula change while the others remain constant, we cannot simply use algebra and directly combine them all. I.e. Boyle did his experiments while keeping N and Tconstant and this must be taken into account.
Keeping this in mind, to carry the derivation on correctly, one must imagine the gas being altered by one process at a time. The derivation using 4 formulas can look like this:
at first the gas has parameters
Say, starting to change only pressure and volume, according to Boyle's law, then:
| (7) |
After this process, the gas has parameters
Using then equation (5) to change the number of particles in the gas and the temperature,
| (8) |
After this process, the gas has parameters
Using then equation (6) to change the pressure and the number of particles,
| (9) |
After this process, the gas has parameters
Using then Charles's law to change the volume and temperature of the gas,
| (10) |
After this process, the gas has parameters
Using simple algebra on equations (7), (8), (9) and (10) yields the result:
or
where stands for Boltzmann's constant.
Another equivalent result, using the fact that , where n is the number of moles in the gas and R is the universal gas constant, is:
which is known as the ideal gas law.
If three of the six equations are known, it may be possible to derive the remaining three using the same method. However, because each formula has two variables, this is possible only for certain groups of three. For example, if you were to have equations (1), (2) and (4) you would not be able to get any more because combining any two of them will only give you the third. However, if you had equations (1), (2) and (3) you would be able to get all six equations because combining (1) and (2) will yield (4), then (1) and (3) will yield (6), then (4) and (6) will yield (5), as well as would the combination of (2) and (3) as is explained in the following visual relation:
where the numbers represent the gas laws numbered above.
If you were to use the same method used above on 2 of the 3 laws on the vertices of one triangle that has a "O" inside it, you would get the third.
For example:
Change only pressure and volume first:
| (1') |
then only volume and temperature:
| (2') |
then as we can choose any value for , if we set , equation (2') becomes:
| (3') |
combining equations (1') and (3') yields , which is equation (4), of which we had no prior knowledge until this derivation.
Theoretical[edit]
Kinetic theory[edit]
The ideal gas law can also be derived from first principles using the kinetic theory of gases, in which several simplifying assumptions are made, chief among which are that the molecules, or atoms, of the gas are point masses, possessing mass but no significant volume, and undergo only elastic collisions with each other and the sides of the container in which both linear momentum and kinetic energy are conserved.
The fundamental assumptions of the kinetic theory of gases imply that
Using the Maxwell–Boltzmann distribution, the fraction of molecules that have a speed in the range to is , where
and denotes the Boltzmann constant. The root-mean-square speed can be calculated by
Using the integration formula
it follows that
from which we get the ideal gas law:
Statistical mechanics[edit]
Let q = (qx, qy, qz) and p = (px, py, pz) denote the position vector and momentum vector of a particle of an ideal gas, respectively. Let F denote the net force on that particle. Then the time-averaged kinetic energy of the particle is:
where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition theorem. Summing over a system of Nparticles yields
By Newton's third law and the ideal gas assumption, the net force of the system is the force applied by the walls of the container, and this force is given by the pressure P of the gas. Hence
where dS is the infinitesimal area element along the walls of the container. Since the divergence of the position vector q is
the divergence theorem implies that
where dV is an infinitesimal volume within the container and V is the total volume of the container.
Putting these equalities together yields
which immediately implies the ideal gas law for N particles:
where n = N/NA is the number of moles of gas and R = NAkB is the gas constant.
Other dimensions[edit]
For a d-dimensional system, the ideal gas pressure is:[8]
where is the volume of the d-dimensional domain in which the gas exists. Note that the dimensions of the pressure changes with dimensionality.
See also[edit]
- Boltzmann constant – Physical constant relating particle kinetic energy with temperature
- Configuration integral – Function in thermodynamics and statistical physics
- Dynamic pressure – Concept in fluid dynamics
- Gas laws
- Internal energy – Energy contained in a system, excluding energy due to its position as a body in external force fields or its overall motion
- Van der Waals equation – Gas equation of state which accounts for non-ideal gas behavior
https://en.wikipedia.org/wiki/Ideal_gas_law
A thermodynamic system is a body of matter and/or radiation, confined in space by walls, with defined permeabilities, which separate it from its surroundings. The surroundings may include other thermodynamic systems, or physical systems that are not thermodynamic systems. A wall of a thermodynamic system may be purely notional, when it is described as being 'permeable' to all matter, all radiation, and all forces. A thermodynamic system can be fully described by a definite set of thermodynamic state variables, which always covers both intensive and extensive properties.
A widely used distinction is between isolated, closed, and open thermodynamic systems.
An isolated thermodynamic system has walls that are non-conductive of heat and perfectly reflective of all radiation, that are rigid and immovable, and that are impermeable to all forms of matter and all forces. (Some writers use the word 'closed' when here the word 'isolated' is being used.)
A closed thermodynamic system is confined by walls that are impermeable to matter, but, by thermodynamic operations, alternately can be made permeable (described as 'diathermal') or impermeable ('adiabatic') to heat, and that, for thermodynamic processes (initiated and terminated by thermodynamic operations), alternately can be allowed or not allowed to move, with system volume change or agitation with internal friction in system contents, as in Joule's original demonstration of the mechanical equivalent of heat, and alternately can be made rough or smooth, so as to allow or not allow heating of the system by friction on its surface.
An open thermodynamic system has at least one wall that separates it from another thermodynamic system, which for this purpose is counted as part of the surroundings of the open system, the wall being permeable to at least one chemical substance, as well as to radiation; such a wall, when the open system is in thermodynamic equilibrium, does not sustain a temperature difference across itself.
A thermodynamic system is subject to external interventions called thermodynamic operations; these alter the system's walls or its surroundings; as a result, the system undergoes transient thermodynamic processes according to the principles of thermodynamics. Such operations and processes effect changes in the thermodynamic state of the system.
When the intensive state variables of its content vary in space, a thermodynamic system can be considered as many systems contiguous with each other, each being a different thermodynamical system.
A thermodynamic system may comprise several phases, such as ice, liquid water, and water vapour, in mutual thermodynamic equilibrium, mutually unseparated by any wall. Or it may be homogeneous. Such systems may be regarded as 'simple'.
A 'compound' thermodynamic system may comprise several simple thermodynamic sub-systems, mutually separated by one or several walls of definite respective permeabilities. It is often convenient to consider such a compound system initially isolated in a state of thermodynamic equilibrium, then affected by a thermodynamic operation of increase of some inter-sub-system wall permeability, to initiate a transient thermodynamic process, so as to generate a final new state of thermodynamic equilibrium. This idea was used, and perhaps introduced, by Carathéodory. In a compound system, initially isolated in a state of thermodynamic equilibrium, a reduction of a wall permeability does not effect a thermodynamic process, nor a change of thermodynamic state. This difference expresses the Second Law of thermodynamics. It illustrates that increase in entropy measures increase in dispersal of energy, due to increase of accessibility of microstates.[1]
In equilibrium thermodynamics, the state of a thermodynamic system is a state of thermodynamic equilibrium, as opposed to a non-equilibrium state.
According to the permeabilities of the walls of a system, transfers of energy and matter occur between it and its surroundings, which are assumed to be unchanging over time, until a state of thermodynamic equilibrium is attained. The only states considered in equilibrium thermodynamics are equilibrium states. Classical thermodynamics includes (a) equilibrium thermodynamics; (b) systems considered in terms of cyclic sequences of processes rather than of states of the system; such were historically important in the conceptual development of the subject. Systems considered in terms of continuously persisting processes described by steady flows are important in engineering.
The very existence of thermodynamic equilibrium, defining states of thermodynamic systems, is the essential, characteristic, and most fundamental postulate of thermodynamics, though it is only rarely cited as a numbered law.[2][3][4] According to Bailyn, the commonly rehearsed statement of the zeroth law of thermodynamics is a consequence of this fundamental postulate.[5] In reality, practically nothing in nature is in strict thermodynamic equilibrium, but the postulate of thermodynamic equilibrium often provides very useful idealizations or approximations, both theoretically and experimentally; experiments can provide scenarios of practical thermodynamic equilibrium.
In equilibrium thermodynamics the state variables do not include fluxes because in a state of thermodynamic equilibrium all fluxes have zero values by definition. Equilibrium thermodynamic processes may involve fluxes but these must have ceased by the time a thermodynamic process or operation is complete bringing a system to its eventual thermodynamic state. Non-equilibrium thermodynamics allows its state variables to include non-zero fluxes, that describe transfers of massor energy or entropy between a system and its surroundings.[6]
In 1824 Sadi Carnot described a thermodynamic system as the working substance (such as the volume of steam) of any heat engine under study.
https://en.wikipedia.org/wiki/Thermodynamic_system
In thermodynamics, a thermodynamic state of a system is its condition at a specific time; that is, fully identified by values of a suitable set of parameters known as state variables, state parameters or thermodynamic variables. Once such a set of values of thermodynamic variables has been specified for a system, the values of all thermodynamic properties of the system are uniquely determined. Usually, by default, a thermodynamic state is taken to be one of thermodynamic equilibrium. This means that the state is not merely the condition of the system at a specific time, but that the condition is the same, unchanging, over an indefinitely long duration of time.
Thermodynamics sets up an idealized conceptual structure that can be summarized by a formal scheme of definitions and postulates. Thermodynamic states are amongst the fundamental or primitive objects or notions of the scheme, for which their existence is primary and definitive, rather than being derived or constructed from other concepts.[1][2][3]
A thermodynamic system is not simply a physical system.[4] Rather, in general, infinitely many different alternative physical systems comprise a given thermodynamic system, because in general a physical system has vastly many more microscopic characteristics than are mentioned in a thermodynamic description. A thermodynamic system is a macroscopic object, the microscopic details of which are not explicitly considered in its thermodynamic description. The number of state variables required to specify the thermodynamic state depends on the system, and is not always known in advance of experiment; it is usually found from experimental evidence. The number is always two or more; usually it is not more than some dozen. Though the number of state variables is fixed by experiment, there remains choice of which of them to use for a particular convenient description; a given thermodynamic system may be alternatively identified by several different choices of the set of state variables. The choice is usually made on the basis of the walls and surroundings that are relevant for the thermodynamic processes that are to be considered for the system. For example, if it is intended to consider heat transfer for the system, then a wall of the system should be permeable to heat, and that wall should connect the system to a body, in the surroundings, that has a definite time-invariant temperature.[5][6]
For equilibrium thermodynamics, in a thermodynamic state of a system, its contents are in internal thermodynamic equilibrium, with zero flows of all quantities, both internal and between system and surroundings. For Planck, the primary characteristic of a thermodynamic state of a system that consists of a single phase, in the absence of an externally imposed force field, is spatial homogeneity.[7] For non-equilibrium thermodynamics, a suitable set of identifying state variables includes some macroscopic variables, for example a non-zero spatial gradient of temperature, that indicate departure from thermodynamic equilibrium. Such non-equilibrium identifying state variables indicate that some non-zero flow may be occurring within the system or between system and surroundings.[8]
https://en.wikipedia.org/wiki/Thermodynamic_state
Classical thermodynamics considers three main kinds of thermodynamic process: (1) changes in a system, (2) cycles in a system, and (3) flow processes.
(1) A change in a system is defined by a passage from an initial to a final state of thermodynamic equilibrium. In classical thermodynamics, the actual course of the process is not the primary concern, and often is ignored. A state of thermodynamic equilibrium endures unchangingly unless it is interrupted by a thermodynamic operation that initiates a thermodynamic process. The equilibrium states are each respectively fully specified by a suitable set of thermodynamic state variables, that depend only on the current state of the system, not on the path taken by the processes that produce the state. In general, during the actual course of a thermodynamic process, the system may pass through physical states which are not describable as thermodynamic states, because they are far from internal thermodynamic equilibrium. Non-equilibrium thermodynamics, however, considers processes in which the states of the system are close to thermodynamic equilibrium, and aims to describe the continuous passage along the path, at definite rates of progress.
As a useful theoretical but not actually physically realizable limiting case, a process may be imagined to take place practically infinitely slowly or smoothly enough to allow it to be described by a continuous path of equilibrium thermodynamic states, when it is called a "quasi-static" process. This is a theoretical exercise in differential geometry, as opposed to a description of an actually possible physical process; in this idealized case, the calculation may be exact.
A really possible or actual thermodynamic process, considered closely, involves friction. This contrasts with theoretically idealized, imagined, or limiting, but not actually possible, quasi-static processes which may occur with a theoretical slowness that avoids friction. It also contrasts with idealized frictionless processes in the surroundings, which may be thought of as including 'purely mechanical systems'; this difference comes close to defining a thermodynamic process.[1]
(2) A cyclic process carries the system through a cycle of stages, starting and being completed in some particular state. The descriptions of the staged states of the system are not the primary concern. The primary concern is the sums of matter and energy inputs and outputs to the cycle. Cyclic processes were important conceptual devices in the early days of thermodynamical investigation, while the concept of the thermodynamic state variable was being developed.
(3) Defined by flows through a system, a flow process is a steady state of flows into and out of a vessel with definite wall properties. The internal state of the vessel contents is not the primary concern. The quantities of primary concern describe the states of the inflow and the outflow materials, and, on the side, the transfers of heat, work, and kinetic and potential energies for the vessel. Flow processes are of interest in engineering.
https://en.wikipedia.org/wiki/Thermodynamic_process
A thermodynamic cycle consists of a linked sequence of thermodynamic processes that involve transfer of heatand work into and out of the system, while varying pressure, temperature, and other state variables within the system, and that eventually returns the system to its initial state.[1] In the process of passing through a cycle, the working fluid (system) may convert heat from a warm source into useful work, and dispose of the remaining heat to a cold sink, thereby acting as a heat engine. Conversely, the cycle may be reversed and use work to move heat from a cold source and transfer it to a warm sink thereby acting as a heat pump. At every point in the cycle, the system is in thermodynamic equilibrium, so the cycle is reversible (its entropy change is zero, as entropy is a state function).
During a closed cycle, the system returns to its original thermodynamic state of temperature and pressure. Process quantities (or path quantities), such as heat and work are process dependent. For a cycle for which the system returns to its initial state the first law of thermodynamics applies:
The above states that there is no change of the energy of the system over the cycle. Ein might be the work and heat input during the cycle and Eout would be the work and heat output during the cycle. The first law of thermodynamicsalso dictates that the net heat input is equal to the net work output over a cycle (we account for heat, Qin, as positive and Qout as negative). The repeating nature of the process path allows for continuous operation, making the cycle an important concept in thermodynamics. Thermodynamic cycles are often represented mathematically as quasistatic processes in the modeling of the workings of an actual device.
https://en.wikipedia.org/wiki/Thermodynamic_cycle
A state variable is one of the set of variables that are used to describe the mathematical "state"of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour in the absence of any external forces affecting the system. Models that consist of coupled first-order differential equations are said to be in state-variable form.[1]
Examples[edit]
- In mechanical systems, the position coordinates and velocities of mechanical parts are typical state variables; knowing these, it is possible to determine the future state of the objects in the system.
- In thermodynamics, a state variable is an independent variable of a state function like internal energy, enthalpy, and entropy. Examples include temperature, pressure, and volume. Heat and work are not state functions, but process functions.
- In electronic/electrical circuits, the voltages of the nodes and the currents through components in the circuit are usually the state variables. In any electrical circuit, the number of state variables are equal to the number of storage elements, which are inductors and capacitors. The state variable for an inductor is the current through the inductor, while that for a capacitor is the voltage across the capacitor.
- In ecosystem models, population sizes (or concentrations) of plants, animals and resources (nutrients, organic material) are typical state variables.
Control systems engineering[edit]
In control engineering and other areas of science and engineering, state variables are used to represent the states of a general system. The set of possible combinations of state variable values is called the state space of the system. The equations relating the current state of a system to its most recent input and past states are called the state equations, and the equations expressing the values of the output variables in terms of the state variables and inputs are called the output equations. As shown below, the state equations and output equations for a linear time invariant system can be expressed using coefficient matrices: A, B, C, and D
where N, L and M are the dimensions of the vectors describing the state, input and output, respectively.
Discrete-time systems[edit]
The state vector (vector of state variables) representing the current state of a discrete-time system (i.e. digital system) is , where n is the discrete point in time at which the system is being evaluated. The discrete-time state equations are
which describes the next state of the system (x[n+1]) with respect to current state and inputs u[n] of the system. The output equations are
which describes the output y[n] with respect to current states and inputs u[n] to the system.
Continuous time systems[edit]
The state vector representing the current state of a continuous-time system (i.e. analog system) is , and the continuous-time state equations giving the evolution of the state vector are
which describes the continuous rate of change of the state of the system with respect to current state x(t) and inputs u(t) of the system. The output equations are
which describes the output y(t) with respect to current states x(t) and inputs u(t) to the system.
See also[edit]
https://en.wikipedia.org/wiki/State_variable
In thermodynamics, a critical point (or critical state) is the end point of a phase equilibrium curve. The most prominent example is the liquid–vapor critical point, the end point of the pressure–temperature curve that designates conditions under which a liquid and its vapor can coexist. At higher temperatures, the gas cannot be liquefied by pressure alone. At the critical point, defined by a critical temperature Tc and a critical pressure pc, phase boundaries vanish. Other examples include the liquid–liquid critical points in mixtures.
Liquid–vapor critical point[edit]
Overview[edit]
For simplicity and clarity, the generic notion of critical point is best introduced by discussing a specific example, the vapor-liquid critical point. This was the first critical point to be discovered, and it is still the best known and most studied one.
The figure to the right shows the schematic PT diagram of a pure substance (as opposed to mixtures, which have additional state variables and richer phase diagrams, discussed below). The commonly known phases solid, liquid and vapor are separated by phase boundaries, i.e. pressure–temperature combinations where two phases can coexist. At the triple point, all three phases can coexist. However, the liquid–vapor boundary terminates in an endpoint at some critical temperature Tc and critical pressure pc. This is the critical point.
In water, the critical point occurs at 647.096 K (373.946 °C; 705.103 °F) and 22.064 megapascals (3,200.1 psi; 217.75 atm).[2]
In the vicinity of the critical point, the physical properties of the liquid and the vapor change dramatically, with both phases becoming ever more similar. For instance, liquid water under normal conditions is nearly incompressible, has a low thermal expansion coefficient, has a high dielectric constant, and is an excellent solvent for electrolytes. Near the critical point, all these properties change into the exact opposite: water becomes compressible, expandable, a poor dielectric, a bad solvent for electrolytes, and prefers to mix with nonpolar gases and organic molecules.[3]
At the critical point, only one phase exists. The heat of vaporization is zero. There is a stationary inflection point in the constant-temperature line (critical isotherm) on a PV diagram. This means that at the critical point:[4][5][6]
Above the critical point there exists a state of matter that is continuously connected with (can be transformed without phase transition into) both the liquid and the gaseous state. It is called supercritical fluid. The common textbook knowledge that all distinction between liquid and vapor disappears beyond the critical point has been challenged by Fisher and Widom,[7] who identified a p–T line that separates states with different asymptotic statistical properties (Fisher–Widom line).
Sometimes[ambiguous] the critical point does not manifest in most thermodynamic or mechanical properties, but is "hidden" and reveals itself in the onset of inhomogeneities in elastic moduli, marked changes in the appearance and local properties of non-affine droplets, and a sudden enhancement in defect pair concentration.[8]
History[edit]
The existence of a critical point was first discovered by Charles Cagniard de la Tour in 1822[9][10] and named by Dmitri Mendeleev in 1860[11][12] and Thomas Andrews in 1869.[13] Cagniard showed that CO2 could be liquefied at 31 °C at a pressure of 73 atm, but not at a slightly higher temperature, even under pressures as high as 3000 atm.
Theory[edit]
Solving the above condition for the van der Waals equation, one can compute the critical point as
However, the van der Waals equation, based on a mean-field theory, does not hold near the critical point. In particular, it predicts wrong scaling laws.
To analyse properties of fluids near the critical point, reduced state variables are sometimes defined relative to the critical properties[14]
The principle of corresponding states indicates that substances at equal reduced pressures and temperatures have equal reduced volumes. This relationship is approximately true for many substances, but becomes increasingly inaccurate for large values of pr.
For some gases, there is an additional correction factor, called Newton's correction, added to the critical temperature and critical pressure calculated in this manner. These are empirically derived values and vary with the pressure range of interest.[15]
Table of liquid–vapor critical temperature and pressure for selected substances[edit]
| Substance[16][17] | Critical temperature | Critical pressure (absolute) |
|---|---|---|
| Argon | −122.4 °C (150.8 K) | 48.1 atm (4,870 kPa) |
| Ammonia (NH3)[18] | 132.4 °C (405.5 K) | 111.3 atm (11,280 kPa) |
| R-134a | 101.06 °C (374.21 K) | 40.06 atm (4,059 kPa) |
| R-410A | 72.8 °C (345.9 K) | 47.08 atm (4,770 kPa) |
| Bromine | 310.8 °C (584.0 K) | 102 atm (10,300 kPa) |
| Caesium | 1,664.85 °C (1,938.00 K) | 94 atm (9,500 kPa) |
| Chlorine | 143.8 °C (416.9 K) | 76.0 atm (7,700 kPa) |
| Ethanol (C2H5OH) | 241 °C (514 K) | 62.18 atm (6,300 kPa) |
| Fluorine | −128.85 °C (144.30 K) | 51.5 atm (5,220 kPa) |
| Helium | −267.96 °C (5.19 K) | 2.24 atm (227 kPa) |
| Hydrogen | −239.95 °C (33.20 K) | 12.8 atm (1,300 kPa) |
| Krypton | −63.8 °C (209.3 K) | 54.3 atm (5,500 kPa) |
| Methane (CH4) | −82.3 °C (190.8 K) | 45.79 atm (4,640 kPa) |
| Neon | −228.75 °C (44.40 K) | 27.2 atm (2,760 kPa) |
| Nitrogen | −146.9 °C (126.2 K) | 33.5 atm (3,390 kPa) |
| Oxygen (O2) | −118.6 °C (154.6 K) | 49.8 atm (5,050 kPa) |
| Carbon dioxide (CO2) | 31.04 °C (304.19 K) | 72.8 atm (7,380 kPa) |
| Nitrous oxide (N2O) | 36.4 °C (309.5 K) | 71.5 atm (7,240 kPa) |
| Sulfuric acid (H2SO4) | 654 °C (927 K) | 45.4 atm (4,600 kPa) |
| Xenon | 16.6 °C (289.8 K) | 57.6 atm (5,840 kPa) |
| Lithium | 2,950 °C (3,220 K) | 652 atm (66,100 kPa) |
| Mercury | 1,476.9 °C (1,750.1 K) | 1,720 atm (174,000 kPa) |
| Sulfur | 1,040.85 °C (1,314.00 K) | 207 atm (21,000 kPa) |
| Iron | 8,227 °C (8,500 K) | |
| Gold | 6,977 °C (7,250 K) | 5,000 atm (510,000 kPa) |
| Aluminium | 7,577 °C (7,850 K) | |
| Water (H2O)[2][19] | 373.946 °C (647.096 K) | 217.7 atm (22,060 kPa) |
Mixtures: liquid–liquid critical point[edit]
The liquid–liquid critical point of a solution, which occurs at the critical solution temperature, occurs at the limit of the two-phase region of the phase diagram. In other words, it is the point at which an infinitesimal change in some thermodynamic variable (such as temperature or pressure) leads to separation of the mixture into two distinct liquid phases, as shown in the polymer–solvent phase diagram to the right. Two types of liquid–liquid critical points are the upper critical solution temperature(UCST), which is the hottest point at which cooling induces phase separation, and the lower critical solution temperature (LCST), which is the coldest point at which heating induces phase separation.
Mathematical definition[edit]
From a theoretical standpoint, the liquid–liquid critical point represents the temperature–concentration extremum of the spinodal curve (as can be seen in the figure to the right). Thus, the liquid–liquid critical point in a two-component system must satisfy two conditions: the condition of the spinodal curve (the second derivative of the free energy with respect to concentration must equal zero), and the extremum condition (the third derivative of the free energy with respect to concentration must also equal zero or the derivative of the spinodal temperature with respect to concentration must equal zero).
See also[edit]
- Conformal field theory
- Critical exponents
- Critical phenomena (more advanced article)
- Critical points of the elements (data page)
- Curie point
- Joback method, Klincewicz method, Lydersen method (estimation of critical temperature, pressure, and volume from molecular structure)
- Liquid–liquid critical point
- Lower critical solution temperature
- Néel point
- Percolation thresholds
- Phase transition
- Rushbrooke inequality
- Scale invariance
- Self-organized criticality
- Supercritical fluid, Supercritical drying, Supercritical water oxidation, Supercritical fluid extraction
- Tricritical point
- Triple point
- Upper critical solution temperature
- Widom scaling
https://en.wikipedia.org/wiki/Critical_point_(thermodynamics)
External links[edit]
- "Critical points for some common solvents". ProSciTech. Archived from the original on 2008-01-31.
- "Critical Temperature and Pressure". Department of Chemistry. Purdue University. Retrieved 2006-12-03.
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, is a correction factor which describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour.[1] In general, deviation from ideal behaviour becomes more significant the closer a gas is to a phase change, the lower the temperature or the larger the pressure. Compressibility factor values are usually obtained by calculation from equations of state (EOS), such as the virial equation which take compound-specific empirical constants as input. For a gas that is a mixture of two or more pure gases (air or natural gas, for example), the gas composition must be known before compressibility can be calculated.
Alternatively, the compressibility factor for specific gases can be read from generalized compressibility charts[1] that plot as a function of pressure at constant temperature.
The compressibility factor should not be confused with the compressibility (also known as coefficient of compressibility or isothermal compressibility) of a material, which is the measure of the relative volume change of a fluid or solid in response to a pressure change.
https://en.wikipedia.org/wiki/Compressibility_factor
Supercritical fluid extraction (SFE) is the process of separating one component (the extractant) from another (the matrix) using supercritical fluids as the extracting solvent. Extraction is usually from a solid matrix, but can also be from liquids. SFE can be used as a sample preparation step for analytical purposes, or on a larger scale to either strip unwanted material from a product (e.g. decaffeination) or collect a desired product (e.g. essential oils). These essential oils can include limonene and other straight solvents. Carbon dioxide (CO2) is the most used supercritical fluid, sometimes modified by co-solvents such as ethanol or methanol. Extraction conditions for supercritical carbon dioxide are above the critical temperature of 31 °C and critical pressure of 74 bar. Addition of modifiers may slightly alter this. The discussion below will mainly refer to extraction with CO2, except where specified.
Advantages[edit]
Selectivity[edit]
The properties of the supercritical fluid can be altered by varying the pressure and temperature, allowing selective extraction. For example, volatile oils can be extracted from a plant with low pressures (100 bar), whereas liquid extraction would also remove lipids. Lipids can be removed using pure CO2 at higher pressures, and then phospholipids can be removed by adding ethanol to the solvent.[1] The same principle can be used to extract polyphenols and unsaturated fatty acids separately from wine wastes.[2]
Speed[edit]
Extraction is a diffusion-based process, in which the solvent is required to diffuse into the matrix and the extracted material to diffuse out of the matrix into the solvent. Diffusivities are much faster in supercritical fluids than in liquids, and therefore extraction can occur faster. In addition, due to the lack of surface tensionand negligible viscosities compared to liquids, the solvent can penetrate more into the matrix inaccessible to liquids. An extraction using an organic liquid may take several hours, whereas supercritical fluid extraction can be completed in 10 to 60 minutes.[3]
Limitations[edit]
The requirement for high pressures increases the cost compared to conventional liquid extraction, so SFE will only be used where there are significant advantages. Carbon dioxide itself is non-polar, and has somewhat limited dissolving power, so cannot always be used as a solvent on its own, particularly for polar solutes. The use of modifiers increases the range of materials which can be extracted. Food grade modifiers such as ethanol can often be used, and can also help in the collection of the extracted material, but reduces some of the benefits of using a solvent which is gaseous at room temperature.
Procedure[edit]
The system must contain a pump for the CO2, a pressure cell to contain the sample, a means of maintaining pressure in the system and a collecting vessel. The liquid is pumped to a heating zone, where it is heated to supercritical conditions. It then passes into the extraction vessel, where it rapidly diffuses into the solid matrix and dissolves the material to be extracted. The dissolved material is swept from the extraction cell into a separator at lower pressure, and the extracted material settles out. The CO2 can then be cooled, re-compressed and recycled, or discharged to atmosphere.
Pumps[edit]
Carbon dioxide (CO
2) is usually pumped as a liquid, usually below 5 °C (41 °F) and a pressure of about 50 bar. The solvent is pumped as a liquid as it is then almost incompressible; if it were pumped as a supercritical fluid, much of the pump stroke would be "used up" in compressing the fluid, rather than pumping it. For small scale extractions (up to a few grams / minute), reciprocating CO
2 pumps or syringe pumps are often used. For larger scale extractions, diaphragm pumps are most common. The pump heads will usually require cooling, and the CO2 will also be cooled before entering the pump.
Pressure vessels[edit]
Pressure vessels can range from simple tubing to more sophisticated purpose built vessels with quick release fittings. The pressure requirement is at least 74 bar, and most extractions are conducted at under 350 bar. However, sometimes higher pressures will be needed, such as extraction of vegetable oils, where pressures of 800 bar are sometimes required for complete miscibility of the two phases.[4]
The vessel must be equipped with a means of heating. It can be placed inside an oven for small vessels, or an oil or electrically heated jacket for larger vessels. Care must be taken if rubber seals are used on the vessel, as the supercritical carbon dioxide may dissolve in the rubber, causing swelling, and the rubber will rupture on depressurization.[citation needed]
Pressure maintenance[edit]
The pressure in the system must be maintained from the pump right through the pressure vessel. In smaller systems (up to about 10 mL / min) a simple restrictor can be used. This can be either a capillary tube cut to length, or a needle valve which can be adjusted to maintain pressure at different flow rates. In larger systems a back pressure regulator will be used, which maintains pressure upstream of the regulator by means of a spring, compressed air, or electronically driven valve. Whichever is used, heating must be supplied, as the adiabatic expansion of the CO2 results in significant cooling. This is problematic if water or other extracted material is present in the sample, as this may freeze in the restrictor or valve and cause blockages.
Collection[edit]
The supercritical solvent is passed into a vessel at lower pressure than the extraction vessel. The density, and hence dissolving power, of supercritical fluids varies sharply with pressure, and hence the solubility in the lower density CO2 is much lower, and the material precipitates for collection. It is possible to fractionate the dissolved material using a series of vessels at reducing pressure. The CO2 can be recycled or depressurized to atmospheric pressure and vented. For analytical SFE, the pressure is usually dropped to atmospheric, and the now gaseous carbon dioxide bubbled through a solvent to trap the precipitated components.
Heating and cooling[edit]
This is an important aspect. The fluid is cooled before pumping to maintain liquid conditions, then heated after pressurization. As the fluid is expanded into the separator, heat must be provided to prevent excessive cooling. For small scale extractions, such as for analytical purposes, it is usually sufficient to pre-heat the fluid in a length of tubing inside the oven containing the extraction cell. The restrictor can be electrically heated, or even heated with a hairdryer. For larger systems, the energy required during each stage of the process can be calculated using the thermodynamic properties of the supercritical fluid.[5]
Simple model of SFE[edit]
There are two essential steps to SFE, transport (by diffusion or otherwise) of the solid particles to the surface, and dissolution in the supercritical fluid. Other factors, such as diffusion into the particle by the SF and reversible release such as desorption from an active site are sometimes significant, but not dealt with in detail here. Figure 2 shows the stages during extraction from a spherical particle where at the start of the extraction the level of extractant is equal across the whole sphere (Fig. 2a). As extraction commences, material is initially extracted from the edge of the sphere, and the concentration in the center is unchanged (Fig 2b). As the extraction progresses, the concentration in the center of the sphere drops as the extractant diffuses towards the edge of the sphere (Figure 2c).[6]
The relative rates of diffusion and dissolution are illustrated by two extreme cases in Figure 3. Figure 3a shows a case where dissolution is fast relative to diffusion. The material is carried away from the edge faster than it can diffuse from the center, so the concentration at the edge drops to zero. The material is carried away as fast as it arrives at the surface, and the extraction is completely diffusion limited. Here the rate of extraction can be increased by increasing diffusion rate, for example raising the temperature, but not by increasing the flow rate of the solvent. Figure 3b shows a case where solubility is low relative to diffusion. The extractant is able to diffuse to the edge faster than it can be carried away by the solvent, and the concentration profile is flat. In this case, the extraction rate can be increased by increasing the rate of dissolution, for example by increasing flow rate of the solvent.
The extraction curve of % recovery against time can be used to elucidate the type of extraction occurring. Figure 4(a) shows a typical diffusion controlled curve. The extraction is initially rapid, until the concentration at the surface drops to zero, and the rate then becomes much slower. The % extracted eventually approaches 100%. Figure 4(b) shows a curve for a solubility limited extraction. The extraction rate is almost constant, and only flattens off towards the end of the extraction. Figure 4(c) shows a curve where there are significant matrix effects, where there is some sort of reversible interaction with the matrix, such as desorption from an active site. The recovery flattens off, and if the 100% value is not known, then it is hard to tell that extraction is less than complete.
Optimization[edit]
The optimum will depend on the purpose of the extraction. For an analytical extraction to determine, say, antioxidant content of a polymer, then the essential factors are complete extraction in the shortest time. However, for production of an essential oil extract from a plant, then quantity of CO2 used will be a significant cost, and "complete" extraction not required, a yield of 70 - 80% perhaps being sufficient to provide economic returns. In another case, the selectivity may be more important, and a reduced rate of extraction will be preferable if it provides greater discrimination. Therefore, few comments can be made which are universally applicable. However, some general principles are outlined below.
Maximizing diffusion[edit]
This can be achieved by increasing the temperature, swelling the matrix, or reducing the particle size. Matrix swelling can sometimes be increased by increasing the pressure of the solvent, and by adding modifiers to the solvent. Some polymers and elastomers in particular are swelled dramatically by CO2, with diffusion being increased by several orders of magnitude in some cases.[7]
Maximizing solubility[edit]
Generally, higher pressure will increase solubility. The effect of temperature is less certain, as close to the critical point, increasing the temperature causes decreases in density, and hence dissolving power. At pressures well above the critical pressure, solubility is likely to increase with temperature.[8] Addition of low levels of modifiers (sometimes called entrainers), such as methanol and ethanol, can also significantly increase solubility, particularly of more polar compounds.
Optimizing flow rate[edit]
The flow rate of supercritical carbon dioxide should be measured in terms of mass flow rather than by volume because the density of the CO
2 changes according to the temperature both before entering the pump heads and during compression. Coriolis flow meters are best used to achieve such flow confirmation. To maximize the rate of extraction, the flow rate should be high enough for the extraction to be completely diffusion limited (but this will be very wasteful of solvent). However, to minimize the amount of solvent used, the extraction should be completely solubility limited (which will take a very long time). Flow rate must therefore be determined depending on the competing factors of time and solvent costs, and also capital costs of pumps, heaters and heat exchangers. The optimum flow rate will probably be somewhere in the region where both solubility and diffusion are significant factors.
See also[edit]
https://en.wikipedia.org/wiki/Supercritical_fluid_extraction
The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice modelsof random systems or networks (graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability p, or more generally a critical surface for a group of parameters p1, p2, ..., such that infinite connectivity (percolation) first occurs.
https://en.wikipedia.org/wiki/Percolation_threshold
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) to float on a water surface without becoming even partly submerged.
At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion).[citation needed][further explanation needed]
There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract.[1][2] Second is a tangential force parallel to the surface of the liquid.[2] This tangential force (per unit length) is generally referred to as the surface tension. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane. But this analogy must not be taken too far as the tension in an elastic membrane is dependent on the amount of deformation of the membrane while surface tension is an inherent property of the liquid–air or liquid–vapour interface.[3]
Because of the relatively high attraction of water molecules to each other through a web of hydrogen bonds, water has a higher surface tension (72.8 millinewtons (mN) per meter at 20 °C) than most other liquids. Surface tension is an important factor in the phenomenon of capillarity.
Surface tension has the dimension of force per unit length, or of energy per unit area.[3] The two are equivalent, but when referring to energy per unit of area, it is common to use the term surface energy, which is a more general term in the sense that it applies also to solids.
In materials science, surface tension is used for either surface stress or surface energy.
https://en.wikipedia.org/wiki/Surface_tension
Thermodynamic equilibrium is an axiomatic concept of thermodynamics. It is an internal state of a single thermodynamic system, or a relation between several thermodynamic systems connected by more or less permeable or impermeable walls. In thermodynamic equilibrium there are no net macroscopic flows of matteror of energy, either within a system or between systems.
In a system that is in its own state of internal thermodynamic equilibrium, no macroscopic change occurs.
Systems in mutual thermodynamic equilibrium are simultaneously in mutual thermal, mechanical, chemical, and radiative equilibria. Systems can be in one kind of mutual equilibrium, though not in others. In thermodynamic equilibrium, all kinds of equilibrium hold at once and indefinitely, until disturbed by a thermodynamic operation. In a macroscopic equilibrium, perfectly or almost perfectly balanced microscopic exchanges occur; this is the physical explanation of the notion of macroscopic equilibrium.
A thermodynamic system in a state of internal thermodynamic equilibrium has a spatially uniform temperature. Its intensive properties, other than temperature, may be driven to spatial inhomogeneity by an unchanging long-range force field imposed on it by its surroundings.
In systems that are at a state of non-equilibrium there are, by contrast, net flows of matter or energy. If such changes can be triggered to occur in a system in which they are not already occurring, the system is said to be in a meta-stable equilibrium.
Though not a widely named "law," it is an axiom of thermodynamics that there exist states of thermodynamic equilibrium. The second law of thermodynamicsstates that when a body of material starts from an equilibrium state, in which, portions of it are held at different states by more or less permeable or impermeable partitions, and a thermodynamic operation removes or makes the partitions more permeable and it is isolated, then it spontaneously reaches its own, new state of internal thermodynamic equilibrium, and this is accompanied by an increase in the sum of the entropies of the portions.
https://en.wikipedia.org/wiki/Thermodynamic_equilibrium
The internal energy of a thermodynamic system is the energy contained within it. It is the energy necessary to create or prepare the system in any given internal state. It does not include the kinetic energy of motion of the system as a whole, nor the potential energy of the system as a whole due to external force fields, including the energy of displacement of the surroundings of the system. It keeps account of the gains and losses of energy of the system that are due to changes in its internal state.[1][2] The internal energy is measured as a difference from a reference zero defined by a standard state. The difference is determined by thermodynamic processes that carry the system between the reference state and the current state of interest.
The internal energy is an extensive property, and cannot be measured directly. The thermodynamic processes that define the internal energy are transfers of chemical substances or of energy as heat, and thermodynamic work.[3]These processes are measured by changes in the system's extensive variables, such as entropy, volume, and chemical composition. It is often not necessary to consider all of the system's intrinsic energies, for example, the static rest mass energy of its constituent matter. When mass transfer is prevented by impermeable containing walls, the system is said to be closed and the first law of thermodynamics defines the change in internal energy as the difference between the energy added to the system as heat and the thermodynamic work done by the system on its surroundings. If the containing walls pass neither substance nor energy, the system is said to be isolated and its internal energy cannot change.
The internal energy describes the entire thermodynamic information of a system, and is an equivalent representation to the entropy, both cardinal state functions of only extensive state variables.[4] Thus, its value depends only on the current state of the system and not on the particular choice from the many possible processes by which energy may pass to or from the system. It is a thermodynamic potential. Microscopically, the internal energy can be analyzed in terms of the kinetic energy of microscopic motion of the system's particles from translations, rotations, and vibrations, and of the potential energy associated with microscopic forces, including chemical bonds.
The unit of energy in the International System of Units (SI) is the joule (J). Also defined is a corresponding intensive energy density, called specific internal energy, which is either relative to the mass of the system, with the unit J/kg, or relative to the amount of substance with unit J/mol (molar internal energy).
https://en.wikipedia.org/wiki/Internal_energy
The velocity of an object is the rate of change of its position with respect to a frame of reference, and is a function of time. Velocity is equivalent to a specification of an object's speed and direction of motion (e.g. 60 km/h to the north). Velocity is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of bodies.
Velocity is a physical vector quantity; both magnitude and direction are needed to define it. The scalar absolute value (magnitude) of velocity is called speed, being a coherent derived unit whose quantity is measured in the SI(metric system) as metres per second (m/s or m⋅s−1). For example, "5 metres per second" is a scalar, whereas "5 metres per second east" is a vector. If there is a change in speed, direction or both, then the object has a changing velocity and is said to be undergoing an acceleration.
https://en.wikipedia.org/wiki/Velocity
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction).[1][2] The orientation of an object's acceleration is given by the orientation of the net force acting on that object. The magnitude of an object's acceleration, as described by Newton's Second Law,[3] is the combined effect of two causes:
- the net balance of all external forces acting onto that object — magnitude is directly proportional to this net resulting force;
- that object's mass, depending on the materials out of which it is made — magnitude is inversely proportional to the object's mass.
The SI unit for acceleration is metre per second squared (m⋅s−2, ).
The velocity of a particle moving on a curved path as a function of time can be written as:
with v(t) equal to the speed of travel along the path, and
a unit vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the changing speed v(t) and the changing direction of ut, the acceleration of a particle moving on a curved path can be written using the chain rule of differentiation[5] for the product of two functions of time as:
where un is the unit (inward) normal vector to the particle's trajectory (also called the principal normal), and r is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the normal or radial acceleration (or centripetal acceleration in circular motion, see also circular motion and centripetal force).
Geometrical analysis of three-dimensional space curves, which explains tangent, (principal) normal and binormal, is described by the Frenet–Serret formulas.[6][7]
Uniform acceleration[edit]
Uniform or constant acceleration is a type of motion in which the velocity of an object changes by an equal amount in every equal time period.
A frequently cited example of uniform acceleration is that of an object in free fall in a uniform gravitational field. The acceleration of a falling body in the absence of resistances to motion is dependent only on the gravitational field strength g (also called acceleration due to gravity). By Newton's Second Law the force acting on a body is given by:
Because of the simple analytic properties of the case of constant acceleration, there are simple formulas relating the displacement, initial and time-dependent velocities, and acceleration to the time elapsed:[8]
where
- is the elapsed time,
- is the initial displacement from the origin,
- is the displacement from the origin at time ,
- is the initial velocity,
- is the velocity at time , and
- is the uniform rate of acceleration.
In particular, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, which describes, e. g., the trajectory of a projectile in a vacuum near the surface of Earth.[9]
Circular motion[edit]
In uniform circular motion, that is moving with constant speed along a circular path, a particle experiences an acceleration resulting from the change of the direction of the velocity vector, while its magnitude remains constant. The derivative of the location of a point on a curve with respect to time, i.e. its velocity, turns out to be always exactly tangential to the curve, respectively orthogonal to the radius in this point. Since in uniform motion the velocity in the tangential direction does not change, the acceleration must be in radial direction, pointing to the center of the circle. This acceleration constantly changes the direction of the velocity to be tangent in the neighboring point, thereby rotating the velocity vector along the circle.
- For a given speed , the magnitude of this geometrically caused acceleration (centripetal acceleration) is inversely proportional to the radius of the circle, and increases as the square of this speed:
- Note that, for a given angular velocity , the centripetal acceleration is directly proportional to radius . This is due to the dependence of velocity on the radius .
Expressing centripetal acceleration vector in polar components, where is a vector from the centre of the circle to the particle with magnitude equal to this distance, and considering the orientation of the acceleration towards the center, yields
As usual in rotations, the speed of a particle may be expressed as an angular speed with respect to a point at the distance as
Thus
This acceleration and the mass of the particle determine the necessary centripetal force, directed toward the centre of the circle, as the net force acting on this particle to keep it in this uniform circular motion. The so-called 'centrifugal force', appearing to act outward on the body, is a so-called pseudo force experienced in the frame of reference of the body in circular motion, due to the body's linear momentum, a vector tangent to the circle of motion.
In a nonuniform circular motion, i.e., the speed along the curved path is changing, the acceleration has a non-zero component tangential to the curve, and is not confined to the principal normal, which directs to the center of the osculating circle, that determines the radius for the centripetal acceleration. The tangential component is given by the angular acceleration , i.e., the rate of change of the angular speed times the radius . That is,
The sign of the tangential component of the acceleration is determined by the sign of the angular acceleration (), and the tangent is always directed at right angles to the radius vector.
https://en.wikipedia.org/wiki/Acceleration
https://en.wikipedia.org/wiki/Classical_mechanics
Classical mechanics[note 1] is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical mechanics, if the present state is known, it is possible to predict how it will move in the future (determinism), and how it has moved in the past (reversibility).
The earliest development of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts based on foundational works of Sir Isaac Newton, and the mathematical methods invented by Gottfried Wilhelm Leibniz, Joseph-Louis Lagrange, Leonhard Euler, and other contemporaries, in the 17th century to describe the motion of bodies under the influence of a system of forces. Later, more abstract methods were developed, leading to the reformulations of classical mechanics known as Lagrangian mechanics and Hamiltonian mechanics. These advances, made predominantly in the 18th and 19th centuries, extend substantially beyond earlier works, particularly through their use of analytical mechanics. They are, with some modification, also used in all areas of modern physics.
Classical mechanics provides extremely accurate results when studying large objects that are not extremely massive and speeds not approaching the speed of light. When the objects being examined have about the size of an atom diameter, it becomes necessary to introduce the other major sub-field of mechanics: quantum mechanics. To describe velocities that are not small compared to the speed of light, special relativity is needed. In cases where objects become extremely massive, general relativity becomes applicable. However, a number of modern sources do include relativistic mechanics in classical physics, which in their view represents classical mechanics in its most developed and accurate form.
https://en.wikipedia.org/wiki/Classical_mechanics
In analytic geometry, an asymptote (/ˈæsɪmptoʊt/) of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.[1][2]
The word asymptote is derived from the Greek ἀσύμπτωτος (asumptōtos) which means "not falling together", from ἀ priv. + σύν "together" + πτωτ-ός "fallen".[3] The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve.[4]
https://en.wikipedia.org/wiki/Asymptote
https://en.wikipedia.org/wiki/List_of_thermodynamic_properties
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move.[1][2][3]Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics.[4][5][6] A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.
Kinematics is used in astrophysics to describe the motion of celestial bodies and collections of such bodies. In mechanical engineering, robotics, and biomechanics[7] kinematics is used to describe the motion of systems composed of joined parts (multi-link systems) such as an engine, a robotic arm or the human skeleton.
Geometric transformations, also called rigid transformations, are used to describe the movement of components in a mechanical system, simplifying the derivation of the equations of motion. They are also central to dynamic analysis.
Kinematic analysis is the process of measuring the kinematic quantities used to describe motion. In engineering, for instance, kinematic analysis may be used to find the range of movement for a given mechanism and working in reverse, using kinematic synthesis to design a mechanism for a desired range of motion.[8] In addition, kinematics applies algebraic geometry to the study of the mechanical advantage of a mechanical system or mechanism.
https://en.wikipedia.org/wiki/Kinematics
In physics, the fourth, fifth and sixth derivatives of position are defined as derivatives of the position vector with respect to time – with the first, second, and third derivatives being velocity, acceleration, and jerk, respectively. However, these higher-order derivatives rarely appear,[1] and have little practical use, thus their names are not as standard.
The fourth derivative is often referred to as snap or jounce. The name "snap" for the fourth derivative led to crackle and pop for the fifth and sixth derivatives respectively,[2] inspired by the advertising mascots Snap, Crackle, and Pop.[3]These are occasionally used, though "sometimes somewhat facetiously".[3]
https://en.wikipedia.org/wiki/Fourth,_fifth,_and_sixth_derivatives_of_position#Fourth_derivative_(snap/jounce)
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.
The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable.
Derivatives can be generalized to functions of several real variables. In this generalization, the derivative is reinterpreted as a linear transformation whose graph is (after an appropriate translation) the best linear approximation to the graph of the original function. The Jacobian matrix is the matrix that represents this linear transformation with respect to the basis given by the choice of independent and dependent variables. It can be calculated in terms of the partial derivatives with respect to the independent variables. For a real-valued function of several variables, the Jacobian matrix reduces to the gradient vector.
The process of finding a derivative is called differentiation. The reverse process is called antidifferentiation. The fundamental theorem of calculus relates antidifferentiation with integration. Differentiation and integration constitute the two fundamental operations in single-variable calculus.[Note 1]
https://en.wikipedia.org/wiki/Derivative
In analytic geometry, the direction cosines (or directional cosines) of a vector are the cosines of the angles between the vector and the three positive coordinate axes. Equivalently, they are the contributions of each component of the basis to a unit vector in that direction. Direction cosines are an analogous extension of the usual notion of slope to higher dimensions.
https://en.wikipedia.org/wiki/Direction_cosine
In geometry and linear algebra, a Cartesian tensor uses an orthonormal basis to represent a tensor in a Euclidean space in the form of components. Converting a tensor's components from one such basis to another is through an orthogonal transformation.
The most familiar coordinate systems are the two-dimensional and three-dimensional Cartesian coordinate systems. Cartesian tensors may be used with any Euclidean space, or more technically, any finite-dimensional vector space over the field of real numbers that has an inner product.
Use of Cartesian tensors occurs in physics and engineering, such as with the Cauchy stress tensor and the moment of inertia tensor in rigid body dynamics. Sometimes general curvilinear coordinates are convenient, as in high-deformation continuum mechanics, or even necessary, as in general relativity. While orthonormal bases may be found for some such coordinate systems (e.g. tangent to spherical coordinates), Cartesian tensors may provide considerable simplification for applications in which rotations of rectilinear coordinate axes suffice. The transformation is a passive transformation, since the coordinates are changed and not the physical system.
https://en.wikipedia.org/wiki/Cartesian_tensor
Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized.[1] It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure.[2] Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy.[3] A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory.[4][5]
Optimal control is an extension of the calculus of variations, and is a mathematical optimization method for deriving control policies.[6] The method is largely due to the work of Lev Pontryagin and Richard Bellman in the 1950s, after contributions to calculus of variations by Edward J. McShane.[7] Optimal control can be seen as a control strategy in control theory.[1]
https://en.wikipedia.org/wiki/Optimal_control#General_method
In physics, a collision is any event in which two or more bodies exert forces on each other in a relatively short time. Although the most common use of the word collision refers to incidents in which two or more objects collide with great force, the scientific use of the term implies nothing about the magnitude of the force.
Some examples of physical interactions that scientists would consider collisions are the following:
- When an insect lands on a plant's leaf, its legs are said to collide with the leaf.
- When a cat strides across a lawn, each contact that its paws make with the ground is considered a collision, as well as each brush of its fur against a blade of grass.
- When a boxer throws a punch, their fist is said to collide with the opponent's body.
- When an astronomical object merges with a black hole, they are considered to collide.
Some colloquial uses of the word collision are the following:
- A traffic collision involves at least one automobile.
- A mid-air collision occurs between airplanes.
- A ship collision accurately involves at least two moving maritime vessels hitting each other; the related term, allision, describes when a moving ship strikes a stationary object (often, but not always, another ship).
In physics, collisions can be classified by the change in the total kinetic energy of the system before and after the collision:
- If most or all of the total kinetic energy is lost (dissipated as heat, sound, etc. or absorbed by the objects themselves), the collision is said to be inelastic; such collisions involve objects coming to a full stop. An example of such a collision is a car crash, as cars crumple inward when crashing, rather than bouncing off of each other. This is by design, for the safety of the occupants and bystanders should a crash occur - the frame of the car absorbs the energy of the crash instead.
- If most of the kinetic energy is conserved (i.e. the objects continue moving afterwards), the collision is said to be elastic. An example of this is a baseball bat hitting a baseball - the kinetic energy of the bat is transferred to the ball, greatly increasing the ball's velocity. The sound of the bat hitting the ball represents the loss of energy.
- And if all of the total kinetic energy is conserved (i.e. no energy is released as sound, heat, etc.), the collision is said to be perfectly elastic. Such a system is an idealization and cannot occur in reality, due to the second law of thermodynamics.
Intermolecular forces (IMF) (or secondary forces) are the forces which mediate interaction between molecules, including forces of attraction or repulsion which act between atoms and other types of neighboring particles, e.g. atoms or ions. Intermolecular forces are weak relative to intramolecular forces – the forces which hold a molecule together. For example, the covalent bond, involving sharing electron pairs between atoms, is much stronger than the forces present between neighboring molecules. Both sets of forces are essential parts of force fields frequently used in molecular mechanics.
The investigation of intermolecular forces starts from macroscopic observations which indicate the existence and action of forces at a molecular level. These observations include non-ideal-gas thermodynamic behavior reflected by virial coefficients, vapor pressure, viscosity, superficial tension, and absorption data.
The first reference to the nature of microscopic forces is found in Alexis Clairaut's work Théorie de la figure de la Terre, published in Paris in 1743.[1] Other scientists who have contributed to the investigation of microscopic forces include: Laplace, Gauss, Maxwell and Boltzmann.
Attractive intermolecular forces are categorized into the following types:
- Hydrogen bonding
- Ion–induced dipole forces
- Ion–dipole forces
- van der Waals forces – Keesom force, Debye force, and London dispersion force
Information on intermolecular forces is obtained by macroscopic measurements of properties like viscosity, pressure, volume, temperature (PVT) data. The link to microscopic aspects is given by virial coefficients and Lennard-Jones potentials.
https://en.wikipedia.org/wiki/Intermolecular_force
Vapor pressure (or vapour pressure in British English; see spelling differences) or equilibrium vapor pressure is defined as the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system. The equilibrium vapor pressure is an indication of a liquid's evaporation rate. It relates to the tendency of particles to escape from the liquid (or a solid). A substance with a high vapor pressure at normal temperatures is often referred to as volatile. The pressure exhibited by vapor present above a liquid surface is known as vapor pressure. As the temperature of a liquid increases, the kinetic energy of its molecules also increases. As the kinetic energy of the molecules increases, the number of molecules transitioning into a vapor also increases, thereby increasing the vapor pressure.
The vapor pressure of any substance increases non-linearly with temperature according to the Clausius–Clapeyron relation. The atmospheric pressure boiling point of a liquid (also known as the normal boiling point) is the temperature at which the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form vapor bubbles inside the bulk of the substance. Bubble formation deeper in the liquid requires a higher temperature due to the higher fluid pressure, because fluid pressure increases above the atmospheric pressure as the depth increases. More important at shallow depths is the higher temperature required to start bubble formation. The surface tension of the bubble wall leads to an overpressure in the very small, initial bubbles.
The vapor pressure that a single component in a mixture contributes to the total pressure in the system is called partial pressure. For example, air at sea level, and saturated with water vapor at 20 °C, has partial pressures of about 2.3 kPa of water, 78 kPa of nitrogen, 21 kPa of oxygen and 0.9 kPa of argon, totaling 102.2 kPa, making the basis for standard atmospheric pressure.
https://en.wikipedia.org/wiki/Vapor_pressure
In the physical sciences, a phase is a region of space (a thermodynamic system), throughout which all physical properties of a material are essentially uniform.[1][2]: 86 [3]: 3 Examples of physical properties include density, index of refraction, magnetization and chemical composition. A simple description is that a phase is a region of material that is chemically uniform, physically distinct, and (often) mechanically separable. In a system consisting of ice and water in a glass jar, the ice cubes are one phase, the water is a second phase, and the humid air is a third phase over the ice and water. The glass of the jar is another separate phase. (See state of matter § Glass)
The term phase is sometimes used as a synonym for state of matter, but there can be several immiscible phases of the same state of matter. Also, the term phase is sometimes used to refer to a set of equilibrium states demarcated in terms of state variables such as pressure and temperature by a phase boundary on a phase diagram. Because phase boundaries relate to changes in the organization of matter, such as a change from liquid to solid or a more subtle change from one crystal structure to another, this latter usage is similar to the use of "phase" as a synonym for state of matter. However, the state of matter and phase diagram usages are not commensurate with the formal definition given above and the intended meaning must be determined in part from the context in which the term is used.
https://en.wikipedia.org/wiki/Phase_(matter)
In physics, a state of matter is one of the distinct forms in which matter can exist. Four states of matter are observable in everyday life: solid, liquid, gas, and plasma. Many intermediate states are known to exist, such as liquid crystal, and some states only exist under extreme conditions, such as Bose–Einstein condensates, neutron-degenerate matter, and quark–gluon plasma, which only occur, respectively, in situations of extreme cold, extreme density, and extremely high energy. For a complete list of all exotic states of matter, see the list of states of matter.
Historically, the distinction is made based on qualitative differences in properties. Matter in the solid state maintains a fixed volume and shape, with component particles (atoms, molecules or ions) close together and fixed into place. Matter in the liquid state maintains a fixed volume, but has a variable shape that adapts to fit its container. Its particles are still close together but move freely. Matter in the gaseous state has both variable volume and shape, adapting both to fit its container. Its particles are neither close together nor fixed in place. Matter in the plasma state has variable volume and shape, and contains neutral atoms as well as a significant number of ions and electrons, both of which can move around freely.
The term phase is sometimes used as a synonym for state of matter, but a system can contain several immiscible phases of the same state of matter.
https://en.wikipedia.org/wiki/State_of_matter
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chartused to show conditions (pressure, temperature, volume, etc.) at which thermodynamically distinct phases(such as solid, liquid or gaseous states) occur and coexist at equilibrium.
https://en.wikipedia.org/wiki/Phase_diagram
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. It is the outer product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs.[1]
https://en.wikipedia.org/wiki/Phase_space
Non-classical states
Glass
Glass is a non-crystalline or amorphous solid material that exhibits a glass transition when heated towards the liquid state. Glasses can be made of quite different classes of materials: inorganic networks (such as window glass, made of silicate plus additives), metallic alloys, ionic melts, aqueous solutions, molecular liquids, and polymers. Thermodynamically, a glass is in a metastable state with respect to its crystalline counterpart. The conversion rate, however, is practically zero.
Crystals with some degree of disorder
A plastic crystal is a molecular solid with long-range positional order but with constituent molecules retaining rotational freedom; in an orientational glass this degree of freedom is frozen in a quenched disordered state.
Similarly, in a spin glass magnetic disorder is frozen.
Liquid crystal states
Liquid crystal states have properties intermediate between mobile liquids and ordered solids. Generally, they are able to flow like a liquid, but exhibiting long-range order. For example, the nematic phase consists of long rod-like molecules such as para-azoxyanisole, which is nematic in the temperature range 118–136 °C (244–277 °F).[7] In this state the molecules flow as in a liquid, but they all point in the same direction (within each domain) and cannot rotate freely. Like a crystalline solid, but unlike a liquid, liquid crystals react to polarized light.
Other types of liquid crystals are described in the main article on these states. Several types have technological importance, for example, in liquid crystal displays.
Magnetically ordered
Transition metal atoms often have magnetic moments due to the net spin of electrons that remain unpaired and do not form chemical bonds. In some solids the magnetic moments on different atoms are ordered and can form a ferromagnet, an antiferromagnet or a ferrimagnet.
In a ferromagnet—for instance, solid iron—the magnetic moment on each atom is aligned in the same direction (within a magnetic domain). If the domains are also aligned, the solid is a permanent magnet, which is magnetic even in the absence of an external magnetic field. The magnetization disappears when the magnet is heated to the Curie point, which for iron is 768 °C (1,414 °F).
An antiferromagnet has two networks of equal and opposite magnetic moments, which cancel each other out so that the net magnetization is zero. For example, in nickel(II) oxide (NiO), half the nickel atoms have moments aligned in one direction and half in the opposite direction.
In a ferrimagnet, the two networks of magnetic moments are opposite but unequal, so that cancellation is incomplete and there is a non-zero net magnetization. An example is magnetite (Fe3O4), which contains Fe2+ and Fe3+ ions with different magnetic moments.
A quantum spin liquid (QSL) is a disordered state in a system of interacting quantum spins which preserves its disorder to very low temperatures, unlike other disordered states. It is not a liquid in physical sense, but a solid whose magnetic order is inherently disordered. The name "liquid" is due to an analogy with the molecular disorder in a conventional liquid. A QSL is neither a ferromagnet, where magnetic domains are parallel, nor an antiferromagnet, where the magnetic domains are antiparallel; instead, the magnetic domains are randomly oriented. This can be realized e.g. by geometrically frustrated magnetic moments that cannot point uniformly parallel or antiparallel. When cooling down and settling to a state, the domain must "choose" an orientation, but if the possible states are similar in energy, one will be chosen randomly. Consequently, despite strong short-range order, there is no long-range magnetic order.
Microphase-separated
Copolymers can undergo microphase separation to form a diverse array of periodic nanostructures, as shown in the example of the styrene-butadiene-styrene block copolymer shown at right. Microphase separation can be understood by analogy to the phase separation between oil and water. Due to chemical incompatibility between the blocks, block copolymers undergo a similar phase separation. However, because the blocks are covalently bonded to each other, they cannot demix macroscopically as water and oil can, and so instead the blocks form nanometre-sized structures. Depending on the relative lengths of each block and the overall block topology of the polymer, many morphologies can be obtained, each its own phase of matter.
Ionic liquids also display microphase separation. The anion and cation are not necessarily compatible and would demix otherwise, but electric charge attraction prevents them from separating. Their anions and cations appear to diffuse within compartmentalized layers or micelles instead of freely as in a uniform liquid.[8]
Low-temperature states
Superconductor
Superconductors are materials which have zero electrical resistivity, and therefore perfect conductivity. This is a distinct physical state which exists at low temperature, and the resistivity increases discontinuously to a finite value at a sharply-defined transition temperature for each superconductor.[9]
A superconductor also excludes all magnetic fields from its interior, a phenomenon known as the Meissner effect or perfect diamagnetism.[9] Superconducting magnets are used as electromagnets in magnetic resonance imaging machines.
The phenomenon of superconductivity was discovered in 1911, and for 75 years was only known in some metals and metallic alloys at temperatures below 30 K. In 1986 so-called high-temperature superconductivity was discovered in certain ceramic oxides, and has now been observed in temperatures as high as 164 K.[10]
Superfluid
Close to absolute zero, some liquids form a second liquid state described as superfluid because it has zero viscosity (or infinite fluidity; i.e., flowing without friction). This was discovered in 1937 for helium, which forms a superfluid below the lambda temperature of 2.17 K (−270.98 °C; −455.76 °F). In this state it will attempt to "climb" out of its container.[11] It also has infinite thermal conductivity so that no temperature gradient can form in a superfluid. Placing a superfluid in a spinning container will result in quantized vortices.
These properties are explained by the theory that the common isotope helium-4 forms a Bose–Einstein condensate (see next section) in the superfluid state. More recently, Fermionic condensate superfluids have been formed at even lower temperatures by the rare isotope helium-3 and by lithium-6.[12]
Bose–Einstein condensate
In 1924, Albert Einstein and Satyendra Nath Bose predicted the "Bose–Einstein condensate" (BEC), sometimes referred to as the fifth state of matter. In a BEC, matter stops behaving as independent particles, and collapses into a single quantum state that can be described with a single, uniform wavefunction.
In the gas phase, the Bose–Einstein condensate remained an unverified theoretical prediction for many years. In 1995, the research groups of Eric Cornell and Carl Wieman, of JILA at the University of Colorado at Boulder, produced the first such condensate experimentally. A Bose–Einstein condensate is "colder" than a solid. It may occur when atoms have very similar (or the same) quantum levels, at temperatures very close to absolute zero, −273.15 °C (−459.67 °F).
Fermionic condensate
A fermionic condensate is similar to the Bose–Einstein condensate but composed of fermions. The Pauli exclusion principle prevents fermions from entering the same quantum state, but a pair of fermions can behave as a boson, and multiple such pairs can then enter the same quantum state without restriction.
Rydberg molecule
One of the metastable states of strongly non-ideal plasma are condensates of excited atoms. These atoms can also turn into ions and electrons if they reach a certain temperature. In April 2009, Nature reported the creation of Rydberg molecules from a Rydberg atom and a ground state atom,[13] confirming that such a state of matter could exist.[14] The experiment was performed using ultracold rubidium atoms.
Quantum Hall state
A quantum Hall state gives rise to quantized Hall voltage measured in the direction perpendicular to the current flow. A quantum spin Hall state is a theoretical phase that may pave the way for the development of electronic devices that dissipate less energy and generate less heat. This is a derivation of the Quantum Hall state of matter.
Photonic matter
Photonic matter is a phenomenon where photons interacting with a gas develop apparent mass, and can interact with each other, even forming photonic "molecules". The source of mass is the gas, which is massive. This is in contrast to photons moving in empty space, which have no rest mass, and cannot interact.
Dropleton
A "quantum fog" of electrons and holes that flow around each other and even ripple like a liquid, rather than existing as discrete pairs.[15]
High-energy states
Degenerate matter
Under extremely high pressure, as in the cores of dead stars, ordinary matter undergoes a transition to a series of exotic states of matter collectively known as degenerate matter, which are supported mainly by quantum mechanical effects. In physics, "degenerate" refers to two states that have the same energy and are thus interchangeable. Degenerate matter is supported by the Pauli exclusion principle, which prevents two fermionic particles from occupying the same quantum state. Unlike regular plasma, degenerate plasma expands little when heated, because there are simply no momentum states left. Consequently, degenerate stars collapse into very high densities. More massive degenerate stars are smaller, because the gravitational force increases, but pressure does not increase proportionally.
Electron-degenerate matter is found inside white dwarf stars. Electrons remain bound to atoms but are able to transfer to adjacent atoms. Neutron-degenerate matter is found in neutron stars. Vast gravitational pressure compresses atoms so strongly that the electrons are forced to combine with protons via inverse beta-decay, resulting in a superdense conglomeration of neutrons. Normally free neutrons outside an atomic nucleus will decay with a half life of approximately 10 minutes, but in a neutron star, the decay is overtaken by inverse decay. Cold degenerate matter is also present in planets such as Jupiter and in the even more massive brown dwarfs, which are expected to have a core with metallic hydrogen. Because of the degeneracy, more massive brown dwarfs are not significantly larger. In metals, the electrons can be modeled as a degenerate gas moving in a lattice of non-degenerate positive ions.
Quark matter
In regular cold matter, quarks, fundamental particles of nuclear matter, are confined by the strong force into hadrons that consist of 2–4 quarks, such as protons and neutrons. Quark matter or quantum chromodynamical (QCD) matter is a group of phases where the strong force is overcome and quarks are deconfined and free to move. Quark matter phases occur at extremely high densities or temperatures, and there are no known ways to produce them in equilibrium in the laboratory; in ordinary conditions, any quark matter formed immediately undergoes radioactive decay.
Strange matter is a type of quark matter that is suspected to exist inside some neutron stars close to the Tolman–Oppenheimer–Volkoff limit (approximately 2–3 solar masses), although there is no direct evidence of its existence. In strange matter, part of the energy available manifests as strange quarks, a heavier analogue of the common down quark. It may be stable at lower energy states once formed, although this is not known.
Quark–gluon plasma is a very high-temperature phase in which quarks become free and able to move independently, rather than being perpetually bound into particles, in a sea of gluons, subatomic particles that transmit the strong force that binds quarks together. This is analogous to the liberation of electrons from atoms in a plasma. This state is briefly attainable in extremely high-energy heavy ion collisions in particle accelerators, and allows scientists to observe the properties of individual quarks, and not just theorize. Quark–gluon plasma was discovered at CERN in 2000. Unlike plasma, which flows like a gas, interactions within QGP are strong and it flows like a liquid.
At high densities but relatively low temperatures, quarks are theorized to form a quark liquid whose nature is presently unknown. It forms a distinct color-flavor locked (CFL) phase at even higher densities. This phase is superconductive for color charge. These phases may occur in neutron stars but they are presently theoretical.
Color-glass condensate
Color-glass condensate is a type of matter theorized to exist in atomic nuclei traveling near the speed of light. According to Einstein's theory of relativity, a high-energy nucleus appears length contracted, or compressed, along its direction of motion. As a result, the gluons inside the nucleus appear to a stationary observer as a "gluonic wall" traveling near the speed of light. At very high energies, the density of the gluons in this wall is seen to increase greatly. Unlike the quark–gluon plasma produced in the collision of such walls, the color-glass condensate describes the walls themselves, and is an intrinsic property of the particles that can only be observed under high-energy conditions such as those at RHIC and possibly at the Large Hadron Collider as well.
Very high energy states
Various theories predict new states of matter at very high energies. An unknown state has created the baryon asymmetry in the universe, but little is known about it. In string theory, a Hagedorn temperature is predicted for superstrings at about 1030 K, where superstrings are copiously produced. At Planck temperature(1032 K), gravity becomes a significant force between individual particles. No current theory can describe these states and they cannot be produced with any foreseeable experiment. However, these states are important in cosmology because the universe may have passed through these states in the Big Bang.
The gravitational singularity predicted by general relativity to exist at the center of a black hole is not a phase of matter; it is not a material object at all (although the mass-energy of matter contributed to its creation) but rather a property of spacetime. Because spacetime breaks down there, the singularity should not be thought of as a localized structure, but as a global, topological feature of spacetime.[16] It has been argued that elementary particles are fundamentally not material, either, but are localized properties of spacetime.[17] In quantum gravity, singularities may in fact mark transitions to a new phase of matter.[18]
Other proposed states
Supersolid
A supersolid is a spatially ordered material (that is, a solid or crystal) with superfluid properties. Similar to a superfluid, a supersolid is able to move without friction but retains a rigid shape. Although a supersolid is a solid, it exhibits so many characteristic properties different from other solids that many argue it is another state of matter.[19]
String-net liquid
In a string-net liquid, atoms have apparently unstable arrangement, like a liquid, but are still consistent in overall pattern, like a solid. When in a normal solid state, the atoms of matter align themselves in a grid pattern, so that the spin of any electron is the opposite of the spin of all electrons touching it. But in a string-net liquid, atoms are arranged in some pattern that requires some electrons to have neighbors with the same spin. This gives rise to curious properties, as well as supporting some unusual proposals about the fundamental conditions of the universe itself.
Superglass
A superglass is a phase of matter characterized, at the same time, by superfluidity and a frozen amorphous structure.
Arbitrary definition
Although multiple attempts have been made to create a unified account, ultimately the definitions of what states of matter exist and the point at which states change are arbitrary.[20][21][22] Some authors have suggested that states of matter are better thought of as a spectrum between a solid and plasma instead of being rigidly defined.[23]
See also
- Hidden states of matter
- Classical element
- Condensed matter physics
- Cooling curve
- Phase (matter)
- Supercooling
- Superheating
To From | Solid | Liquid | Gas | Plasma |
|---|---|---|---|---|
| Solid | Melting | Sublimation | ||
| Liquid | Freezing | Vaporization | ||
| Gas | Deposition | Condensation | Ionization | |
| Plasma | Recombination |
A hidden state of matter is a state of matter which cannot be reached under ergodic conditions, and is therefore distinct from known thermodynamic phases of the material.[1][2] Examples exist in condensed matter systems, and are typically reached by the non-ergodic conditions created through laser photo excitation.[3][4] Short-lived hidden states of matter have also been reported in crystals using lasers. Recently a persistent hidden state was discovered in a crystal of Tantalum(IV) sulfide (TaS2), where the state is stable at low temperatures.[2] A hidden state of matter is not to be confused with hidden order, which exists in equilibrium, but is not immediately apparent or easily observed.
Using ultrashort laser pulses impinging on solid state matter,[3] the system may be knocked out of equilibrium so that not only are the individual subsystems out of equilibrium with each other but also internally. Under such conditions, new states of matter may be created which are not otherwise reachable under equilibrium, ergodic system evolution. Such states are usually unstable and decay very rapidly, typically in nanoseconds or less.[4] The difficulty is in distinguishing a genuine hidden state from one which is simply out of thermal equilibrium.[5]
Probably the first instance of a photoinduced state is described for the organic molecular compound TTF-CA, which turns from neutral to ionic species as a result of excitation by laser pulses.[4][6][7] However, a similar transformation is also possible by the application of pressure, so strictly speaking the photoinduced transition is not to a hidden state under the definition given in the introductory paragraph. A few further examples are given in ref.[4] Photoexcitation has been shown to produce persistent states in vanadates[8][9] and manganite materials,[10][11] [12] leading to filamentary paths of a modified charge ordered phase which is sustained by a passing current. Transient superconductivity was also reported in cuprates.[13][14]
A photoexcited transition to an H state[edit]
A hypothetical schematic diagram for the transition to an H state by photo excitation is shown in the Figure (After [4]). An absorbed photon causes an electron from the ground state G to an excited state E (red arrow). State E rapidly relaxes via Frank-Condon relaxation to an intermediate locally reordered state I. Through interactions with others of its kind, this state collectively orders to form a macroscopically ordered metastable state H, further lowering its energy as a result. The new state has a broken symmetry with respect to the G or E state, and may also involve further relaxation compared to the I state. The barrier EBprevents state H from reverting to the ground state G. If the barrier is sufficiently large compared to thermal energy kBT, where kB is the Boltzmann constant, the H state can be stable indefinitely.
https://en.wikipedia.org/wiki/Hidden_states_of_matter
A cooling curve is a line graph that represents the change of phase of matter, typically from a gas to a solid or a liquid to a solid. The independent variable (X-axis) is time and the dependent variable (Y-axis) is temperature.[1] Below is an example of a cooling curve used in castings.
https://en.wikipedia.org/wiki/Cooling_curve
A pressure–volume diagram (or PV diagram, or volume–pressure loop)[1] is used to describe corresponding changes in volume and pressure in a system. They are commonly used in thermodynamics, cardiovascular physiology, and respiratory physiology.
PV diagrams, originally called indicator diagrams, were developed in the 18th century as tools for understanding the efficiency of steam engines.
https://en.wikipedia.org/wiki/Pressure–volume_diagram
In condensed matter physics, dealing with the macroscopic physical properties of matter, a tricritical point is a point in the phase diagram of a system at which three-phase coexistence terminates.[1] This definition is clearly parallel to the definition of an ordinary critical point as the point at which two-phase coexistence terminates.
https://en.wikipedia.org/wiki/Tricritical_point
Critical exponents describe the behavior of physical quantities near continuous phase transitions.
https://en.wikipedia.org/wiki/Critical_exponent
https://en.wikipedia.org/wiki/Critical_points_of_the_elements_(data_page)
A conformal field theory (CFT) is a quantum field theory that is invariant under conformal transformations. In two dimensions, there is an infinite-dimensional algebra of local conformal transformations, and conformal field theories can sometimes be exactly solved or classified.
https://en.wikipedia.org/wiki/Conformal_field_theory
Pages in category "Phase transitions"
The following 112 pages are in this category, out of 112 total. This list may not reflect recent changes (learn more).
B
C
- CALPHAD
- Charge ordering
- Cloud point
- Coffee ring effect
- Computational Fluid Dynamics for Phase Change Materials
- Condensation
- Congruent melting
- Continuous cooling transformation
- Continuum percolation theory
- Critical dimension
- Critical exponent
- Critical opalescence
- Critical point (thermodynamics)
- Critical points of the elements (data page)
- Critical radius
- Cryobiology
- Cryophorus
- Cryoscopic constant
- Crystallization
- Crystallization of polymers
- Curie temperature
D
F
L
M
P
R
S
- Saturation dome
- Schreinemaker's analysis
- Simon–Glatzel equation
- Slip melting point
- Solid
- Solid light
- Solidus (chemistry)
- Spinodal decomposition
- State of matter
- Sublimation (phase transition)
- Sublimation apparatus
- Superconductivity
- Supercritical liquid–gas boundaries
- Superradiant phase transition
- Swendsen–Wang algorithm
- Symplectite
https://en.wikipedia.org/wiki/Category:Phase_transitions
Pages in category "Renormalization group"
The following 36 pages are in this category, out of 36 total. This list may not reflect recent changes (learn more).
C
https://en.wikipedia.org/wiki/Category:Renormalization_group
Pages in category "Threshold temperatures"
The following 27 pages are in this category, out of 27 total. This list may not reflect recent changes (learn more).
T
A eutectic system (/juːˈtɛktɪk/ yoo-TEK-tik)[1] from the Greek "εύ" (eu = well) and "τήξις" (tēxis = melting) is a heterogeneous mixture of substances that melts or solidifies at a single temperature that is lower than the melting point of any of the constituents.[2] This temperature is known as the eutectic temperature, and is the lowest possible melting temperature over all of the mixing ratios for the involved component species. On a phase diagram, the eutectic temperature is seen as the eutectic point (see plot on the right).[3]
Non-eutectic mixture ratios would have different melting temperatures for their different constituents, since one component's lattice will melt at a lower temperature than the other's. Conversely, as a non-eutectic mixture cools down, each of its components would solidify (form a lattice) at a different temperature, until the entire mass is solid.
Not all binary alloys have eutectic points, since the valence electrons of the component species are not always compatible,[clarification needed] in any mixing ratio, to form a new type of joint crystal lattice. For example, in the silver-gold system the melt temperature (liquidus) and freeze temperature (solidus) "meet at the pure element endpoints of the atomic ratio axis while slightly separating in the mixture region of this axis".[4]
The term eutectic was coined in 1884 by British physicist and chemist Frederick Guthrie (1833–1886).[5]
https://en.wikipedia.org/wiki/Eutectic_system
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex(concave upward), or vice versa.
For the graph of a function of differentiability class C2 (f, its first derivative f', and its second derivative f'', exist and are continuous), the condition f'' = 0 can also be used to find an inflection point since a point of f'' = 0 must be passed to change f'' from a positive value (concave upward) to a negative value (concave downward) or vise versa as f'' is continuous; an inflection point of the curve is where f'' = 0 and changes its sign at the point (from positive to negative or from negative to positive).[1] A point where the second derivative vanishes but does not change its sign is sometimes called a point of undulation or undulation point.
In algebraic geometry an inflection point is defined slightly more generally, as a regular point where the tangent meets the curve to order at least 3, and an undulation point or hyperflex is defined as a point where the tangent meets the curve to order at least 4.
https://en.wikipedia.org/wiki/Inflection_point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases (gas, liquid, and solid) of that substance coexist in thermodynamic equilibrium.[1] It is that temperature and pressure at which the sublimation curve, fusion curve and the vaporisation curve meet. For example, the triple point of mercury occurs at a temperature of −38.83440 °C (−37.90192 °F) and a pressure of 0.165 mPa.
In addition to the triple point for solid, liquid, and gas phases, a triple point may involve more than one solid phase, for substances with multiple polymorphs. Helium-4 is a special case that presents a triple point involving two different fluid phases (lambda point).[1]
The triple point of water was used to define the kelvin, the base unit of thermodynamic temperature in the International System of Units (SI).[2] The value of the triple point of water was fixed by definition, rather than measured, but that changed with the 2019 redefinition of SI base units. The triple points of several substances are used to define points in the ITS-90 international temperature scale, ranging from the triple point of hydrogen (13.8033 K) to the triple point of water (273.16 K, 0.01 °C, or 32.018 °F).
The term "triple point" was coined in 1873 by James Thomson, brother of Lord Kelvin.[3]
https://en.wikipedia.org/wiki/Triple_point
In thermodynamics, the limit of local stability with respect to small fluctuations is clearly defined by the condition that the second derivative of Gibbs free energy is zero. The locus of these points (the inflection point within a G-x or G-c curve, Gibbs free energy as a function of composition) is known as the spinodal curve.[1][2][3] For compositions within this curve, infinitesimally small fluctuations in composition and density will lead to phase separation via spinodal decomposition. Outside of the curve, the solution will be at least metastable with respect to fluctuations.[3] In other words, outside the spinodal curve some careful process may obtain a single phase system.[3] Inside it, only processes far from thermodynamic equilibrium, such as physical vapor deposition, will enable one to prepare single phase compositions.[4] The local points of coexisting compositions, defined by the common tangent construction, are known as a binodal (coexistence) curve, which denotes the minimum-energy equilibrium state of the system. Increasing temperature results in a decreasing difference between mixing entropy and mixing enthalpy, and thus the coexisting compositions come closer. The binodal curve forms the basis for the miscibility gap in a phase diagram. The free energy of mixing changes with temperature and concentration, and the binodal and spinodal meet at the critical or consolute temperature and composition.[5]
https://en.wikipedia.org/wiki/Spinodal
In physics, mathematics and statistics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor, and thus represent a universality.
The technical term for this transformation is a dilatation (also known as dilation), and the dilatations can also form part of a larger conformal symmetry.
- In mathematics, scale invariance usually refers to an invariance of individual functions or curves. A closely related concept is self-similarity, where a function or curve is invariant under a discrete subset of the dilations. It is also possible for the probability distributions of random processes to display this kind of scale invariance or self-similarity.
- In classical field theory, scale invariance most commonly applies to the invariance of a whole theory under dilatations. Such theories typically describe classical physical processes with no characteristic length scale.
- In quantum field theory, scale invariance has an interpretation in terms of particle physics. In a scale-invariant theory, the strength of particle interactions does not depend on the energy of the particles involved.
- In statistical mechanics, scale invariance is a feature of phase transitions. The key observation is that near a phase transition or critical point, fluctuations occur at all length scales, and thus one should look for an explicitly scale-invariant theory to describe the phenomena. Such theories are scale-invariant statistical field theories, and are formally very similar to scale-invariant quantum field theories.
- Universality is the observation that widely different microscopic systems can display the same behaviour at a phase transition. Thus phase transitions in many different systems may be described by the same underlying scale-invariant theory.
- In general, dimensionless quantities are scale invariant. The analogous concept in statistics are standardized moments, which are scale invariant statistics of a variable, while the unstandardized moments are not.
In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, is a correction factor which describes the deviation of a real gas from ideal gas behaviour.
https://en.wikipedia.org/wiki/Compressibility_factor
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.[1]
https://en.wikipedia.org/wiki/Viscosity
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in concentration.
https://en.wikipedia.org/wiki/Diffusion
Real gases are nonideal gases whose molecules occupy space and have interactions; consequently, they do not adhere to the ideal gas law. To understand the behaviour of real gases, the following must be taken into account:
- compressibility effects;
- variable specific heat capacity;
- van der Waals forces;
- non-equilibrium thermodynamic effects;
- issues with molecular dissociation and elementary reactions with variable composition
For most applications, such a detailed analysis is unnecessary, and the ideal gas approximation can be used with reasonable accuracy. On the other hand, real-gas models have to be used near the condensation point of gases, near critical points, at very high pressures, to explain the Joule–Thomson effect and in other less usual cases. The deviation from ideality can be described by the compressibility factor Z.
https://en.wikipedia.org/wiki/Real_gas
In science, an empirical relationship or phenomenological relationship is a relationship or correlation that is supported by experiment and observation but not necessarily supported by theory.[1]
Analytical solutions without a theory[edit]
An empirical relationship is supported by confirmatory data irrespective of theoretical basis such as first principles. Sometimes theoretical explanations for what were initially empirical relationships are found, in which case the relationships are no longer considered empirical. An example was the Rydberg formula to predict the wavelengths of hydrogen spectral lines. Proposed in 1876, it perfectly predicted the wavelengths of the Lyman series, but lacked a theoretical basis until Niels Bohr produced his Bohr model of the atom in 1925.[2]
On occasion, what was thought to be an empirical factor is later deemed to be a fundamental physical constant.[citation needed]
Approximations[edit]
Some empirical relationships are merely approximations, often equivalent to the first few terms of the Taylor series of the analytical solution describing the phenomenon.[citation needed] Other relationships only hold under certain specific conditions, reducing them to special cases of more general relationship.[2] Some approximations, in particular phenomenological models, may even contradict theory; they are employed because they are more mathematically tractable than some theories, and are able to yield results.[3]
See also[edit]
- Hall, Carl W.; Hinman, George W. (1983), Dictionary of Energy, CRC Press, p. 84, ISBN 0824717937
- ^ a b McMullin, Ernan (1968), “What Do Physical Models Tell Us?”, in B. van Rootselaar and J. F. Staal (eds.), Logic, Methodology and Science III. Amsterdam: North Holland, 385–396.
- ^ Roman, Frigg; Hartmann, Stephan. "Models in Science". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Fall 2012 ed.). Retrieved 24 July2015.
https://en.wikipedia.org/wiki/Empirical_relationship
The Gas composition of any gas can be characterised by listing the pure substances it contains, and stating for each substance its proportion of the gas mixture's molecule count.
Gas composition of air[edit]
To give a familiar example, air has a composition of:[1]
| Pure Gas Name | Symbol | Percent by Volume |
|---|---|---|
| Nitrogen | N2 | 78.084 |
| Oxygen | O2 | 20.9476 |
| Argon | Ar | 0.934 |
| Carbon Dioxide | CO2 | 0.0314 |
| Neon | Ne | 0.001818 |
| Methane | CH4 | 0.0002 |
| Helium | He | 0.000524 |
| Krypton | Kr | 0.000114 |
| Hydrogen | H2 | 0.00005 |
| Xenon | Xe | 0.0000087 |
Standard Dry Air is the agreed-upon gas composition for air from which all water vapour has been removed. There are various standards bodies which publish documents that define a dry air gas composition. Each standard provides a list of constituent concentrations, a gas density at standard conditions and a molar mass.
It is extremely unlikely that the actual composition of any specific sample of air will completely agree with any definition for standard dry air. While the various definitions for standard dry air all attempt to provide realistic information about the constituents of air, the definitions are important in and of themselves because they establish a standard which can be cited in legal contracts and publications documenting measurement calculation methodologies or equations of state.
The standards below are two examples of commonly used and cited publications that provide a composition for standard dry air:
- ISO TR 29922-2017 provides a definition for standard dry air which specifies an air molar mass of 28,965 46 ± 0,000 17 kg·kmol-1.[2]
- GPA 2145:2009 is published by the Gas Processors Association. It provides a molar mass for air of 28.9625 g/mol, and provides a composition for standard dry air as a footnote.[3]
https://en.wikipedia.org/wiki/Gas_composition
In thermodynamics, the internal energy of a system is expressed in terms of pairs of conjugate variables such as temperature and entropy or pressure and volume. In fact, all thermodynamic potentials are expressed in terms of conjugate pairs. The product of two quantities that are conjugate has units of energy or sometimes power.
For a mechanical system, a small increment of energy is the product of a force times a small displacement. A similar situation exists in thermodynamics. An increment in the energy of a thermodynamic system can be expressed as the sum of the products of certain generalized "forces" that, when unbalanced, cause certain generalized "displacements", and the product of the two is the energy transferred as a result. These forces and their associated displacements are called conjugate variables. The thermodynamic force is always an intensive variable and the displacement is always an extensive variable, yielding an extensive energy transfer. The intensive (force) variable is the derivative of the internal energy with respect to the extensive (displacement) variable, while all other extensive variables are held constant.
The thermodynamic square can be used as a tool to recall and derive some of the thermodynamic potentials based on conjugate variables.
In the above description, the product of two conjugate variables yields an energy. In other words, the conjugate pairs are conjugate with respect to energy. In general, conjugate pairs can be defined with respect to any thermodynamic state function. Conjugate pairs with respect to entropy are often used, in which the product of the conjugate pairs yields an entropy. Such conjugate pairs are particularly useful in the analysis of irreversible processes, as exemplified in the derivation of the Onsager reciprocal relations.
https://en.wikipedia.org/wiki/Conjugate_variables_(thermodynamics)
In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of the chemical equilibrium constant. It is equal to the pressure of an ideal gas which has the same temperature and molar Gibbs free energy as the real gas.[1]
Fugacities are determined experimentally or estimated from various models such as a Van der Waals gas that are closer to reality than an ideal gas. The real gas pressure and fugacity are related through the dimensionless fugacity coefficient φ.[1]
For an ideal gas, fugacity and pressure are equal and so φ = 1. Taken at the same temperature and pressure, the difference between the molar Gibbs free energies of a real gas and the corresponding ideal gas is equal to RT ln φ.
The fugacity is closely related to the thermodynamic activity. For a gas, the activity is simply the fugacity divided by a reference pressure to give a dimensionless quantity. This reference pressure is called the standard state and normally chosen as 1 atmosphere or 1 bar.
Accurate calculations of chemical equilibrium for real gases should use the fugacity rather than the pressure. The thermodynamic condition for chemical equilibrium is that the total chemical potential of reactants is equal to that of products. If the chemical potential of each gas is expressed as a function of fugacity, the equilibrium condition may be transformed into the familiar reaction quotient form (or law of mass action) except that the pressures are replaced by fugacities.
For a condensed phase (liquid or solid) in equilibrium with its vapor phase, the chemical potential is equal to that of the vapor, and therefore the fugacity is equal to the fugacity of the vapor. This fugacity is approximately equal to the vapor pressure when the vapor pressure is not too high.
https://en.wikipedia.org/wiki/Fugacity
In thermodynamics, the internal energy of a system is expressed in terms of pairs of conjugate variables such as temperature and entropy or pressure and volume. In fact, all thermodynamic potentials are expressed in terms of conjugate pairs. The product of two quantities that are conjugate has units of energy or sometimes power.
Pressure/volume and stress/strain pairs[edit]
As an example, consider the conjugate pair. The pressure acts as a generalized force – pressure differences force a change in volume, and their product is the energy lost by the system due to mechanical work. Pressure is the driving force, volume is the associated displacement, and the two form a pair of conjugate variables.
The above holds true only for non-viscous fluids. In the case of viscous fluids, plastic and elastic solids, the pressure force is generalized to the stress tensor, and changes in volume are generalized to the volume multiplied by the strain tensor.[2] These then form a conjugate pair. If is the ij component of the stress tensor, and is the ij component of the strain tensor, then the mechanical work done as the result of a stress-induced infinitesimal strain is:
or, using Einstein notation for the tensors, in which repeated indices are assumed to be summed:
In the case of pure compression (i.e. no shearing forces), the stress tensor is simply the negative of the pressure times the unit tensor so that
The trace of the strain tensor () is the fractional change in volume so that the above reduces to as it should.
Temperature/entropy pair[edit]
In a similar way, temperature differences drive changes in entropy, and their product is the energy transferred by heating. Temperature is the driving force, entropy is the associated displacement, and the two form a pair of conjugate variables. The temperature/entropy pair of conjugate variables is the only heat term; the other terms are essentially all various forms of work.
Chemical potential/particle number pair[edit]
The chemical potential is like a force which pushes an increase in particle number. In cases where there are a mixture of chemicals and phases, this is a useful concept. For example, if a container holds water and water vapor, there will be a chemical potential (which is negative) for the liquid, pushing water molecules into the vapor (evaporation) and a chemical potential for the vapor, pushing vapor molecules into the liquid (condensation). Only when these "forces" equilibrate is equilibrium obtained.
See also[edit]
- Generalized coordinate and generalized force: analogous conjugate variable pairs found in classical mechanics.
- Intensive and extensive properties
- Bond graph
In thermodynamics, a physical property is any property that is measurable, and whose value describes a state of a physical system. Thermodynamic properties are defined as characteristic features of a system, capable of specifying the system's state. Some constants, such as the ideal gas constant, R, do not describe the state of a system, and so are not properties. On the other hand, some constants, such as Kf (the freezing point depression constant, or cryoscopic constant), depend on the identity of a substance, and so may be considered to describe the state of a system, and therefore may be considered physical properties.
"Specific" properties are expressed on a per mass basis. If the units were changed from per mass to, for example, per mole, the property would remain as it was (i.e., intensive or extensive).
Regarding work and heat[edit]
Work and heat are not thermodynamic properties, but rather process quantities: flows of energy across a system boundary. Systems do not contain work, but can perform work, and likewise, in formal thermodynamics, systems do not contain heat, but can transfer heat. Informally, however, a difference in the energy of a system that occurs solely because of a difference in its temperature is commonly called heat, and the energy that flows across a boundary as a result of a temperature difference is "heat".
Altitude (or elevation) is usually not a thermodynamic property. Altitude can help specify the location of a system, but that does not describe the state of the system. An exception would be if the effect of gravity need to be considered in order to describe a state, in which case altitude could indeed be a thermodynamic property.
See also[edit]
- Conjugate variables
- Dimensionless numbers
- Intensive and extensive properties
- Thermodynamic databases for pure substances
- Thermodynamic variable
https://en.wikipedia.org/wiki/List_of_thermodynamic_properties
In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the affine connection. It can also be regarded as the gauge field generated by local Lorentz transformations. In some canonical formulations of general relativity, a spin connection is defined on spatial slices and can also be regarded as the gauge field generated by local rotations.
The spin connection occurs in two common forms: the Levi-Civita spin connection, when it is derived from the Levi-Civita connection, and the affine spin connection, when it is obtained from the affine connection. The difference between the two of these is that the Levi-Civita connection is by definition the unique torsion-free connection, whereas the affine connection (and so the affine spin connection) may contain torsion.
https://en.wikipedia.org/wiki/Spin_connection
https://en.wikipedia.org/wiki/Superionic_water
https://en.wikipedia.org/wiki/Strengthening_mechanisms_of_materials
https://en.wikipedia.org/wiki/Sulfide_stress_cracking
https://en.wikipedia.org/wiki/Lattice_diffusion_coefficient
https://en.wikipedia.org/wiki/Diffusion
https://en.wikipedia.org/wiki/Atomic_diffusion
https://en.wikipedia.org/wiki/Vector
https://en.wikipedia.org/wiki/Calculus
https://en.wikipedia.org/wiki/Oscillation
https://en.wikipedia.org/wiki/Field
https://en.wikipedia.org/wiki/Collapse
Cascade Matrix Magnet Magnetism linear induction magnetic induction gas plane plasma electrostatics hydrostatics air gravity
scale sum scalar
explosives mercury phosphorus iron acid sulfur ; air - oxygen nitrogen hydrogen ; water - salt hydrogen oxygen
mineral boron beryllium helium fusion starter state ground state dark matter ion hole iodine silvers
Atomic diffusion is a diffusion process whereby the random thermally-activated movement of atoms in a solid results in the net transport of atoms. For example, helium atoms inside a balloon can diffuse through the wall of the balloon and escape, resulting in the balloon slowly deflating. Other air molecules (e.g. oxygen, nitrogen) have lower mobilities and thus diffuse more slowly through the balloon wall. There is a concentration gradient in the balloon wall, because the balloon was initially filled with helium, and thus there is plenty of helium on the inside, but there is relatively little helium on the outside (helium is not a major component of air). The rate of transport is governed by the diffusivity and the concentration gradient.
In crystals[edit]
In the crystal solid state, diffusion within the crystal lattice occurs by either interstitial or substitutional mechanisms and is referred to as lattice diffusion.[1] In interstitial lattice diffusion, a diffusant (such as C in an iron alloy), will diffuse in between the lattice structure of another crystalline element. In substitutional lattice diffusion (self-diffusionfor example), the atom can only move by substituting place with another atom. Substitutional lattice diffusion is often contingent upon the availability of point vacancies throughout the crystal lattice. Diffusing particles migrate from point vacancy to point vacancy by the rapid, essentially random jumping about (jump diffusion).
Since the prevalence of point vacancies increases in accordance with the Arrhenius equation, the rate of crystal solid state diffusion increases with temperature.
For a single atom in a defect-free crystal, the movement can be described by the "random walk" model. In 3-dimensions it can be shown that after jumps of length the atom will have moved, on average, a distance of:
If the jump frequency is given by (in jumps per second) and time is given by , then is proportional to the square root of :
Diffusion in polycrystalline materials can involve short circuit diffusion mechanisms. For example, along the grain boundaries and certain crystalline defects such as dislocations there is more open space, thereby allowing for a lower activation energy for diffusion. Atomic diffusion in polycrystalline materials is therefore often modeled using an effective diffusion coefficient, which is a combination of lattice, and grain boundary diffusion coefficients. In general, surface diffusionoccurs much faster than grain boundary diffusion, and grain boundary diffusion occurs much faster than lattice diffusion.
https://en.wikipedia.org/wiki/Atomic_diffusion
https://en.wikipedia.org/wiki/Grain_boundary_diffusion_coefficient
https://en.wikipedia.org/wiki/Drag_(physics)
https://en.wikipedia.org/wiki/Aerodynamic_force
https://en.wikipedia.org/wiki/Laminar_flow
https://en.wikipedia.org/wiki/Fluid_dynamics
https://en.wikipedia.org/wiki/Parasitic_drag#Form_drag
https://en.wikipedia.org/wiki/Parasitic_drag
https://en.wikipedia.org/wiki/Drag_(physics)#Very_low_Reynolds_numbers:_Stokes'_drag
https://en.wikipedia.org/wiki/Shear_force
https://en.wikipedia.org/wiki/Pressure
https://en.wikipedia.org/wiki/Viscosity
https://en.wikipedia.org/wiki/Center_of_pressure_(fluid_mechanics)
https://en.wikipedia.org/wiki/Propeller_(aeronautics)
https://en.wikipedia.org/wiki/Body_force
https://en.wikipedia.org/wiki/Archimedes%27_principle
https://en.wikipedia.org/wiki/Eötvös_number
https://en.wikipedia.org/wiki/Stall_(fluid_dynamics)
https://en.wikipedia.org/wiki/Boundary_layer
https://en.wikipedia.org/wiki/Stokes%27_law
https://en.wikipedia.org/wiki/Cross_section_(geometry)
https://en.wikipedia.org/wiki/Drag_equation
https://en.wikipedia.org/wiki/Square–cube_law
https://en.wikipedia.org/wiki/Drag_equation
https://en.wikipedia.org/wiki/Viscosity#Kinematic_viscosity
https://en.wikipedia.org/wiki/Stokes_radius
https://en.wikipedia.org/wiki/Freestream
https://en.wikipedia.org/wiki/Shock_wave
https://en.wikipedia.org/wiki/Hyperbolic_functions
https://en.wikipedia.org/wiki/Hydrodynamic_radius
https://en.wikipedia.org/wiki/Size-exclusion_chromatography
https://en.wikipedia.org/wiki/Radius_of_gyration
https://en.wikipedia.org/wiki/Centroid
https://en.wikipedia.org/wiki/Barycenter
https://en.wikipedia.org/wiki/Chemical_structure
https://en.wikipedia.org/wiki/Ensemble_average
https://en.wikipedia.org/wiki/Contour_length
https://en.wikipedia.org/wiki/Colloid
https://en.wikipedia.org/wiki/Born_equation
https://en.wikipedia.org/wiki/Capillary_electrophoresis
https://en.wikipedia.org/wiki/Gradient
https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity
https://en.wikipedia.org/wiki/PH
https://en.wikipedia.org/wiki/Electro-osmosis
A fluid that has no resistance to shear stress is known as an ideal or inviscid fluid. Zero viscosity is observed only at very low temperatures in superfluids. Otherwise
https://en.wikipedia.org/wiki/Viscosity
https://en.wikipedia.org/wiki/Capillary_pressure
https://en.wikipedia.org/wiki/Buoyancy
https://en.wikipedia.org/wiki/Continuum_mechanics
https://en.wikipedia.org/wiki/Constitutive_equation
https://en.wikipedia.org/wiki/Strain_energy_density_function
https://en.wikipedia.org/wiki/Finite_strain_theory#Deformation_gradient_tensor
https://en.wikipedia.org/wiki/Linear_map
https://en.wikipedia.org/wiki/Inelastic_collision
https://en.wikipedia.org/wiki/Parameter
https://en.wikipedia.org/wiki/Lambda_calculus
https://en.wikipedia.org/wiki/Combinatory_logic
Computer programming[edit]
In computer programming, two notions of parameter are commonly used, and are referred to as parameters and arguments—or more formally as a formal parameter and an actual parameter.
For example, in the definition of a function such as
- y = f(x) = x + 2,
x is the formal parameter (the parameter) of the defined function.
When the function is evaluated for a given value, as in
- f(3): or, y = f(3) = 3 + 2 = 5,
3 is the actual parameter (the argument) for evaluation by the defined function; it is a given value (actual value) that is substituted for the formal parameter of the defined function. (In casual usage the terms parameter and argument might inadvertently be interchanged, and thereby used incorrectly.)
These concepts are discussed in a more precise way in functional programming and its foundational disciplines, lambda calculus and combinatory logic. Terminology varies between languages; some computer languages such as C define parameter and argument as given here, while Eiffel uses an alternative convention.
https://en.wikipedia.org/wiki/Parameter
https://en.wikipedia.org/wiki/Drag_(physics)
https://en.wikipedia.org/wiki/Ludwig_Prandtl





































































![{\displaystyle pV=Nk_{B}T\left[1\pm {\frac {\pi ^{3/2}}{2(2s+1)}}{\frac {N\hbar ^{3}}{V(mk_{B}T)^{3/2}}}+\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef692eee683dd0f2db91919df6547fdc4e25b180)
























![{\displaystyle {\begin{aligned}p&={\frac {R\,T}{V_{m}-b}}-{\frac {a}{{\sqrt {T}}\,V_{m}\left(V_{m}+b\right)}}\\[3pt]a&\approx 0.42748{\frac {R^{2}\,T_{c}^{\frac {5}{2}}}{p_{c}}}\\[3pt]b&\approx 0.08664{\frac {R\,T_{c}}{p_{c}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76af7621de77a84d9aa661afc810edddcc65fdf4)























![{\displaystyle {\begin{aligned}p&={\frac {R\,T}{V_{m}-b}}-{\frac {a\,\alpha }{V_{m}^{2}+2bV_{m}-b^{2}}}\\[3pt]a&\approx 0.45724{\frac {R^{2}\,T_{c}^{2}}{p_{c}}}\\[3pt]b&\approx 0.07780{\frac {R\,T_{c}}{p_{c}}}\\[3pt]\alpha &=\left(1+\kappa \left(1-T_{r}^{\frac {1}{2}}\right)\right)^{2}\\[3pt]\kappa &\approx 0.37464+1.54226\,\omega -0.26992\,\omega ^{2}\\[3pt]T_{r}&={\frac {T}{T_{c}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76b0fb3bcb60fc74628c1460f5ef109cdad6a7b7)












![{\displaystyle {\begin{aligned}\kappa &=\kappa _{0}+\left[\kappa _{1}+\kappa _{2}\left(\kappa _{3}-T_{r}\right)\left(1-T_{r}^{\frac {1}{2}}\right)\right]\left(1+T_{r}^{\frac {1}{2}}\right)\left(0.7-T_{r}\right)\\\kappa _{0}&=0.378893+1.4897153\,\omega -0.17131848\,\omega ^{2}+0.0196554\,\omega ^{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/839e586ab76a17eede9adbc715084a6b0f0b4ab9)


![{\displaystyle P=\left({\frac {RT}{v-b}}\right)-\left[{\frac {(a_{1}P+a_{2})\alpha }{v(v+b)+b(v-b)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c426907ba2b485be5f0d509d15aabfd49434af9)



























![{\displaystyle P={\frac {RT}{(V-b)}}-{\frac {a}{V(V+b)}}+{\frac {RT}{V}}\rho \sum _{A}\left[{\frac {1}{X^{A}}}-{\frac {1}{2}}\right]{\frac {\partial X^{A}}{\partial \rho }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cbd434d11122538f320972751c749f06e589165)








































![{\displaystyle p(V)={\frac {K_{0}}{K_{0}'}}\left[\eta ^{-3K_{0}'}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/119acc194c6fe4b55cdb04509f35d2de82943be0)

![{\displaystyle p(V)=3K_{0}\left({\frac {1-\eta }{\eta ^{2}}}\right)\exp \left[{\frac {3}{2}}\left(K_{0}'-1\right)(1-\eta )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84b54e6697098407c42a951f4d417f550947640c)
![{\displaystyle p(V)=3K_{0}\left({\frac {1-\eta }{\eta ^{5}}}\right)\exp \left[{\frac {3}{2}}\left(K_{0}'-3\right)(1-\eta )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72f0bf0c52a562fef450596bac5bab2a9ceb64a6)
![{\displaystyle p(V)=3K_{0}\left({\frac {1-\eta }{\eta ^{5}}}\right)\exp \left[c_{0}(1-\eta )\right]\left\{1+c_{2}\eta (1-\eta )\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6a84eadfd547167097d76e43eabe588d3fe49e7)




![{\displaystyle p(V)=3K_{0}\left({\frac {1-\eta }{\eta ^{5}}}\right)\exp \left[c_{0}(1-\eta )\right]\left\{1+c_{2}\eta (1-\eta )+c_{3}\eta (1-\eta )^{2}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d845ea54ae72a8b5098788d19cb3f9c3c1bb1bd2)










 is the
is the 


































































![x[n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)
![{\displaystyle x[n+1]=Ax[n]+Bu[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b3b41ed33294fd2c2d99283bf6e5e132ee92a38)
![{\displaystyle y[n]=Cx[n]+Du[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc61ab54f3baacfb7cb73fb75910c1ae248641a2)







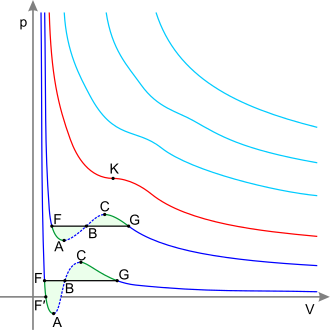




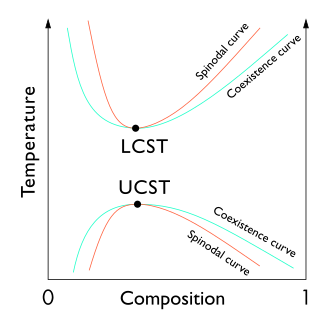












![{\displaystyle {v^{2}}(t)={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {s} (t)-\mathbf {s} _{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dad0ae6651010935bfa411ced51abe128c9e8647)






















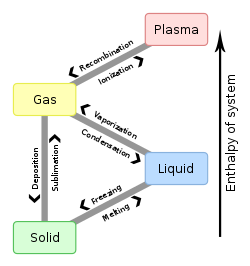















No comments:
Post a Comment