In geometry, a skew apeirohedron is an infinite skew polyhedron consisting of nonplanar faces or nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface.
Skew apeirohedra have also been called polyhedral sponges.
Many are directly related to a convex uniform honeycomb, being the polygonal surface of a honeycomb with some of the cells removed. Characteristically, an infinite skew polyhedron divides 3-dimensional space into two halves. If one half is thought of as solid the figure is sometimes called a partial honeycomb.
Regular skew apeirohedra[edit]
According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to regular skew polyhedra(apeirohedra).[1]
Coxeter and Petrie found three of these that filled 3-space:
| Regular skew apeirohedra | ||
|---|---|---|
 {4,6|4} mucube |  {6,4|4} muoctahedron |  {6,6|3} mutetrahedron |
There also exist chiral skew apeirohedra of types {4,6}, {6,4}, and {6,6}. These skew apeirohedra are vertex-transitive, edge-transitive, and face-transitive, but not mirror symmetric (Schulte 2004).
Beyond Euclidean 3-space, in 1967 C. W. L. Garner published a set of 31 regular skew polyhedra in hyperbolic 3-space.[2]
Gott's regular pseudopolyhedrons[edit]
J. Richard Gott in 1967 published a larger set of seven infinite skew polyhedra which he called regular pseudopolyhedrons, including the three from Coxeter as {4,6}, {6,4}, and {6,6} and four new ones: {5,5}, {4,5}, {3,8}, {3,10}.[3][4]
Gott relaxed the definition of regularity to allow his new figures. Where Coxeter and Petrie had required that the vertices be symmetrical, Gott required only that they be congruent. Thus, Gott's new examples are not regular by Coxeter and Petrie's definition.
Gott called the full set of regular polyhedra, regular tilings, and regular pseudopolyhedra as regular generalized polyhedra, representable by a {p,q} Schläfli symbol, with by p-gonal faces, q around each vertex. However neither the term "pseudopolyhedron" nor Gott's definition of regularity have achieved wide usage.
Crystallographer A.F. Wells in 1960's also published a list of skew apeirohedra. Melinda Green published many more in 1998.
| {p,q} | Cells around a vertex | Vertex faces | Larger pattern | Space group | Related H2 orbifold notation | ||
|---|---|---|---|---|---|---|---|
| Cubic space group | Coxeter notation | Fibrifold notation | |||||
| {4,5} | 3 cubes |  |  | Im3m | [[4,3,4]] | 8°:2 | *4222 |
| {4,5} | 1 truncated octahedron 2 hexagonal prisms |  | I3 | [[4,3+,4]] | 8°:2 | 2*42 | |
| {3,7} | 1 octahedron 1 icosahedron |  |  | Fd3 | [[3[4]]]+ | 2°− | 3222 |
| {3,8} | 2 snub cubes |  |  | Fm3m | [4,(3,4)+] | 2−− | 32* |
| {3,9} | 1 tetrahedron 3 octahedra |  |  | Fd3m | [[3[4]]] | 2+:2 | 2*32 |
| {3,9} | 1 icosahedron 2 octahedra |  | I3 | [[4,3+,4]] | 8°:2 | 22*2 | |
| {3,12} | 5 octahedra |  |  | Im3m | [[4,3,4]] | 8°:2 | 2*32 |
Prismatic forms[edit]
 Prismatic form: {4,5} |
There are two prismatic forms:
- {4,5}: 5 squares on a vertex (Two parallel square tilings connected by cubic holes.)
- {3,8}: 8 triangles on a vertex (Two parallel triangle tilings connected by octahedral holes.)
Other forms[edit]
{3,10} is also formed from parallel planes of triangular tilings, with alternating octahedral holes going both ways.
{5,5} is composed of 3 coplanar pentagons around a vertex and two perpendicular pentagons filling the gap.
Gott also acknowledged that there are other periodic forms of the regular planar tessellations. Both the square tiling {4,4} and triangular tiling {3,6} can be curved into approximating infinite cylinders in 3-space.
Theorems[edit]
He wrote some theorems:
- For every regular polyhedron {p,q}: (p-2)*(q-2)<4. For Every regular tessellation: (p-2)*(q-2)=4. For every regular pseudopolyhedron: (p-2)*(q-2)>4.
- The number of faces surrounding a given face is p*(q-2) in any regular generalized polyhedron.
- Every regular pseudopolyhedron approximates a negatively curved surface.
- The seven regular pseudopolyhedron are repeating structures.
Uniform skew apeirohedra[edit]
There are many other uniform (vertex-transitive) skew apeirohedra. Wachmann, Burt and Kleinmann (1974) discovered many examples but it is not known whether their list is complete.
A few are illustrated here. They can be named by their vertex configuration, although it is not a unique designation for skew forms.
| 4.4.6.6 | 6.6.8.8 | |
|---|---|---|
 |  | 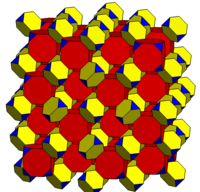 |
| Related to cantitruncated cubic honeycomb, | Related to runcicantic cubic honeycomb, | |
| 4.4.4.6 | 4.8.4.8 | 3.3.3.3.3.3.3 |
 |  |  |
| Related to the omnitruncated cubic honeycomb: | ||
| 4.4.4.6 | 4.4.4.8 | 3.4.4.4.4 |
 | 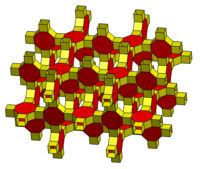 |  Related to the runcitruncated cubic honeycomb. |
| 4.4.4.4.4 | 4.4.4.6 |
|---|---|
 Related to |  Related to |
Others can be constructed as augmented chains of polyhedra:
  |  |
| Uniform Boerdijk–Coxeter helix | Stacks of cubes |
|---|
See also[edit]
John Richard Gott III (born February 8, 1947) is a professor of astrophysical sciences at Princeton University. He is known for his work on time travel and the Doomsday argument.
John Richard Gott III | |
|---|---|
 J. Richard Gott (1989) | |
| Born | February 8, 1947 |
| Nationality | American |
| Scientific career | |
| Fields | Astrophysics, gravitational physics |
| Institutions | Princeton University |
| Notable students | Matthew Headrick[1] |
Copernicus method and Doomsday theory[edit]
Gott first thought of his "Copernicus method" of lifetime estimation in 1969 when stopping at the Berlin Wall and wondering how long it would stand. Gott postulated that the Copernican principle is applicable in cases where nothing is known; unless there was something special about his visit (which he didn't think there was) this gave a 75% chance that he was seeing the wall after the first quarter of its life. Based on its age in 1969 (8 years), Gott left the wall with 50% confidence that it wouldn't be there in 1993 (1969 + 8·(1.5/0.5)).
In fact, the wall was brought down in 1989, and 1993 was the year in which Gott applied his "Copernicus method" to the lifetime of the human race. His paper in Nature was the first to apply the Copernican principle to the survival of humanity; His original prediction gave 95% confidence that the human race would last for between 5100 and 7.8 million years. (Brandon Carter's alternative form of the Doomsday argument was delivered earlier that year, but Gott's derivation was independent.)
He made a major effort subsequently to defend his form of the Doomsday argument from a variety of philosophical attacks, and this debate (like the feasibility of closed time loops) is still ongoing. To popularize the Copernicus method, Gott gave The New Yorker magazine a 95% confidence interval for the closing time of forty-four Broadway and Off Broadway productions based only on their opening dates.[5]
Education work[edit]
He received the President's Award for Distinguished Teaching in acknowledgment of his work on the National Westinghouse/Intel Science Talent Search high school student science competition. He is an active promoter of the public awareness of science at the popular level, and Princeton students have voted him the school's outstanding professor several times.
Gott was born in Louisville, Kentucky. He is a Presbyterian who distinguishes physical from meta-physical questions by their teleology; he believes that his writings are entirely scientific (not trespassing into theology) because the motivation for the way things are (or might be) is never examined.[6]
See also[edit]
- Kip Thorne's writings on wormhole time travel marked the introduction of the subject's serious discussion in physics
- Regular pseudopolyhedrons, infinite periodic polyhedra in 3-space

[edit]
Hermann Bondi named the principle after Copernicus in the mid-20th century, although the principle itself dates back to the 16th-17th century paradigm shift away from the Ptolemaic system, which placed Earth at the center of the universe. Copernicus proposed that the motion of the planets could be explained by reference to an assumption that the Sun is centrally located and stationary in contrast to the then currently upheld belief that the Earth was central. He argued that the apparent retrograde motion of the planets is an illusion caused by Earth's movement around the Sun, which the Copernican model placed at the centre of the universe. Copernicus himself was mainly motivated by technical dissatisfaction with the earlier system and not by support for any mediocrity principle.[3] In fact, although the Copernican heliocentric model is often described as "demoting" Earth from its central role it had in the Ptolemaic geocentric model, it was successors to Copernicus, notably the 16th century Giordano Bruno, who adopted this new perspective. The Earth's central position had been interpreted as being in the "lowest and filthiest parts". Instead, as Galileo said, the Earth is part of the "dance of the stars" rather than the "sump where the universe's filth and ephemera collect".[4][5] In the late 20th Century, Carl Sagan asked, "Who are we? We find that we live on an insignificant planet of a humdrum star lost in a galaxy tucked away in some forgotten corner of a universe in which there are far more galaxies than people."[6]
In cosmology, if one assumes the Copernican principle and observes that the universe appears isotropic or the same in all directions from the vantage point of Earth, then one can infer that the universe is generally homogeneous or the same everywhere (at any given time) and is also isotropic about any given point. These two conditions make up the cosmological principle.[7] In practice, astronomers observe that the universe has heterogeneous or non-uniform structures up to the scale of galactic superclusters, filaments and great voids. It becomes more and more homogeneous and isotropic when observed on larger and larger scales, with little detectable structure on scales of more than about 200 million parsecs. However, on scales comparable to the radius of the observable universe, we see systematic changes with distance from Earth. For instance, galaxies contain more young stars and are less clustered, and quasars appear more numerous. While this might suggest that Earth is at the center of the universe, the Copernican principle requires us to interpret it as evidence for the evolution of the universe with time: this distant light has taken most of the age of the universe to reach Earth and shows the universe when it was young. The most distant light of all, cosmic microwave background radiation, is isotropic to at least one part in a thousand.
Modern mathematical cosmology is based on the assumption that the Cosmological principle is almost, but not exactly, true on the largest scales. The Copernican principle represents the irreducible philosophical assumption needed to justify this, when combined with the observations.
Michael Rowan-Robinson emphasizes the Copernican principle as the threshold test for modern thought, asserting that: "It is evident that in the post-Copernican era of human history, no well-informed and rational person can imagine that the Earth occupies a unique position in the universe."[7]
Bondi and Thomas Gold used the Copernican principle to argue for the perfect cosmological principle which maintains that the universe is also homogeneous in time, and is the basis for the steady-state cosmology.[8] However, this strongly conflicts with the evidence for cosmological evolution mentioned earlier: the universe has progressed from extremely different conditions at the Big Bang, and will continue to progress toward extremely different conditions, particularly under the rising influence of dark energy, apparently toward the Big Freeze or Big Rip.
Since the 1990s the term has been used (interchangeably with "the Copernicus method") for J. Richard Gott's Bayesian-inference-based prediction of duration of ongoing events, a generalized version of the Doomsday argument.[clarification needed]
Tests of the principle[edit]
The Copernican principle has never been proven, and in the most general sense cannot be proven, but it is implicit in many modern theories of physics. Cosmological models are often derived with reference to the cosmological principle, slightly more general than the Copernican principle, and many tests of these models can be considered tests of the Copernican principle.[9]
Historical[edit]
Before the term Copernican principle was even coined, Earth was repeatedly shown not to have any special location in the universe. The Copernican Revolutiondethroned Earth to just one of many planets orbiting the Sun. Proper motion was mentioned by Halley. William Herschel found that the Solar System is moving through space within our disk-shaped Milky Way galaxy. Edwin Hubble showed that the Milky Way galaxy is just one of many galaxies in the universe. Examination of the galaxy's position and motion in the universe led to the Big Bang theory and the whole of modern cosmology.
Modern tests[edit]
Recent and planned tests relevant to the cosmological and Copernican principles include:
- time drift of cosmological redshifts;[10]
- modelling the local gravitational potential using reflection of cosmic microwave background (CMB) photons;[11]
- the redshift dependence of the luminosity of supernovae;[12]
- the kinetic Sunyaev–Zel’dovich effect in relation to dark energy;[13]
- cosmic neutrino background;[14]
- the integrated Sachs–Wolfe effect[15]
- testing the isotropy and homogeneity of the CMB;[16][17][18][19][20]
Physics without the principle[edit]
The standard model of cosmology, the Lambda-CDM model, assumes the Copernican principle and the more general Cosmological principle. The Lambda-CDM model's observations are largely consistent, but there remain unsolved problems. Some cosmologists and theoretical physicists have created models without the Cosmological or Copernican principles to constrain the values of observational results, to address specific known issues, and to propose tests to distinguish between current models and other possible models.
A prominent example in this context is the observed accelerating universe and cosmological constant. Instead of using the current accepted idea of dark energy, this model proposes the universe is much more inhomogeneous than currently assumed, and instead, we are in an extremely large low-density void.[21] To match observations we would have to be very close to the centre of this void, immediately contradicting the Copernican principle.
No comments:
Post a Comment