In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to the direction of the wave.
In electrodynamics, the strength and direction of an electric field is defined by its electric field vector. In the case of a circularly polarized wave, as seen in the accompanying animation, the tip of the electric field vector, at a given point in space, relates to the phase of the light as it travels through time and space. At any instant of time, the electric field vector of the wave indicates a point on a helix oriented along the direction of propagation. A circularly polarized wave can rotate in one of two possible senses: clockwise or right-handed circular polarization (RHCP) in which the electric field vector rotates in a right-hand sense with respect to the direction of propagation, and counter-clockwise or left-handed circular polarization (LHCP) in which the vector rotates in a left-hand sense.
Circular polarization is a limiting case of elliptical polarization. The other special case is the easier-to-understand linear polarization.
The phenomenon of polarization arises as a consequence of the fact that light behaves as a two-dimensional transverse wave.
Circular polarization occurs when the two orthogonal electric field component vectors are of equal magnitude and are out of phase by exactly 90°, or one-quarter wavelength.
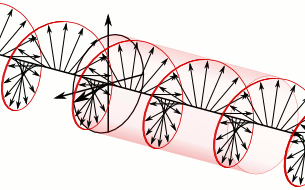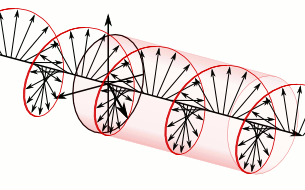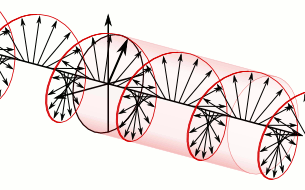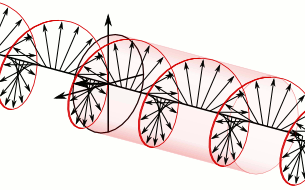
The electric field vectors of a traveling circularly polarized electromagnetic wave. This wave is right-circularly-polarized, since the direction of rotation of the vector is related by the right-hand rule to the direction the wave is moving; or left-circularly-polarized according to alternative convention.
https://en.wikipedia.org/wiki/Circular_polarization
A magneto-optic effect is any one of a number of phenomena in which an electromagnetic wave propagates through a medium that has been altered by the presence of a quasistatic magnetic field. In such a medium, which is also called gyrotropic or gyromagnetic, left- and right-rotating elliptical polarizations can propagate at different speeds, leading to a number of important phenomena. When light is transmitted through a layer of magneto-optic material, the result is called the Faraday effect: the plane of polarization can be rotated, forming a Faraday rotator. The results of reflection from a magneto-optic material are known as the magneto-optic Kerr effect (not to be confused with the nonlinear Kerr effect).
In general, magneto-optic effects break time reversal symmetry locally (i.e. when only the propagation of light, and not the source of the magnetic field, is considered) as well as Lorentz reciprocity, which is a necessary condition to construct devices such as optical isolators (through which light passes in one direction but not the other).
Two gyrotropic materials with reversed rotation directions of the two principal polarizations, corresponding to complex-conjugate ε tensors for lossless media, are called optical isomers.
Kerr Rotation and Kerr Ellipticity[edit]
Kerr Rotation and Kerr Ellipticity are changes in the polarization of incident light which comes in contact with a gyromagnetic material. Kerr Rotation is a rotation in the plane of polarization of transmitted light, and Kerr Ellipticity is the ratio of the major to minor axis of the ellipse traced out by elliptically polarized light on the plane through which it propagates. Changes in the orientation of polarized incident light can be quantified using these two properties.
According to classical physics, the speed of light varies with the permittivity of a material:
where is the velocity of light through the material, is the material permittivity, and is the material permeability. Because the permittivity is anisotropic, polarized light of different orientations will travel at different speeds.
This can be better understood if we consider a wave of light that is circularly polarized (seen to the right). If this wave interacts with a material at which the horizontal component (green sinusoid) travels at a different speed than the vertical component (blue sinusoid), the two components will fall out of the 90 degree phase difference (required for circular polarization) changing the Kerr Ellipticity
A change in Kerr Rotation is most easily recognized in linearly polarized light, which can be separated into two Circularly polarized components: Left-Handed Circular Polarized (LCP) light and Right-Handed Circular Polarized (RCP) light. The anisotropy of the Magneto Optic material permittivity causes a difference in the speed of LCP and RCP light, which will cause a change in the angle of polarized light. Materials that exhibit this property are known as Birefringent.
From this rotation, we can calculate the difference in orthogonal velocity components, find the anisotropic permittivity, find the gyration vector, and calculate the applied magnetic field[1]
https://en.wikipedia.org/wiki/Magneto-optic_effect






No comments:
Post a Comment