09-24-2021-1020 - Coherence physics spatial coherence temporal coherence Optical coherence tomography (OCT)

In physics, two wave sources are coherent if their frequency and waveform are identical. Coherence is an ideal property of waves that enables stationary (i.e. temporally and spatially constant) interference. It contains several distinct concepts, which are limiting cases that never quite occur in reality but allow an understanding of the physics of waves, and has become a very important concept in quantum physics. More generally, coherence describes all properties of the correlation between physical quantities of a single wave, or between several waves or wave packets.

Interference is the addition, in the mathematical sense, of wave functions. A single wave can interfere with itself, but this is still an addition of two waves (see Young's slits experiment). Constructive or destructive interferences are limit cases, and two waves always interfere, even if the result of the addition is complicated or not remarkable. When interfering, two waves can add together to create a wave of greater amplitude than either one (constructive interference) or subtract from each other to create a wave of lesser amplitude than either one (destructive interference), depending on their relative phase. Two waves are said to be coherent if they have a constant relative phase. The amount of coherence can readily be measured by the interference visibility, which looks at the size of the interference fringes relative to the input waves (as the phase offset is varied); a precise mathematical definition of the degree of coherence is given by means of correlation functions.

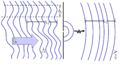
Spatial coherence describes the correlation (or predictable relationship) between waves at different points in space, either lateral or longitudinal.^[1] Temporal coherence describes the correlation between waves observed at different moments in time. Both are observed in the Michelson–Morley experiment and Young's interference experiment. Once the fringes are obtained in the Michelson interferometer, when one of the mirrors is moved away gradually from the beam-splitter, the time for the beam to travel increases and the fringes become dull and finally disappear, showing temporal coherence. Similarly, in a double-slit experiment, if the space between the two slits is increased, the coherence dies gradually and finally the fringes disappear, showing spatial coherence. In both cases, the fr
inge amplitude slowly disappears, as the path difference increases past the coherence length.

Spatial coherence

[edit]

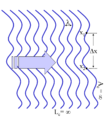
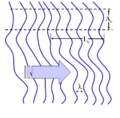
In some systems, such as water waves or optics, wave-like states can extend over one or two dimensions. Spatial coherence describes the ability for two points in space, x₁ and x₂, in the extent of a wave to interfere, when averaged over time. More precisely, the spatial coherence is the cross-correlationbetween two points in a wave for all times. If a wave has only 1 value of amplitude over an infinite length, it is perfectly spatially coherent. The range of separation between the two points over which there is significant interference defines the diameter of the coherence area, A_c^[13] (Coherence length, often a feature of a source, is usually an industrial term related to the coherence time of the source, not the coherence area in the medium.) A_c is the relevant type of coherence for the Young's double-slit interferometer. It is also used in optical imaging systems and particularly in various types of astronomy telescopes. Sometimes people also use "spatial coherence" to refer to the visibility when a wave-like state is combined with a spatially shifted copy of itself.

Examples[edit]

• Spatial coherence
• 

  Figure 5: A plane wave with an infinite coherence length.

 
• 

  Figure 6: A wave with a varying profile (wavefront) and infinite coherence length.

 
• 

  Figure 7: A wave with a varying profile (wavefront) and finite coherence length.

 
• 

  Figure 8: A wave with finite coherence area is incident on a pinhole (small aperture). The wave will diffract out of the pinhole. Far from the pinhole the emerging spherical wavefronts are approximately flat. The coherence area is now infinite while the coherence length is unchanged.

 
• 

  Figure 9: A wave with infinite coherence area is combined with a spatially shifted copy of itself. Some sections in the wave interfere constructively and some will interfere destructively. Averaging over these sections, a detector with length D will measure reduced interference visibility. For example, a misaligned Mach–Zehnder interferometerwill do this.

  
  

  
  

https://en.wikipedia.org/wiki/Coherence_(physics)#Spatial_coherence

Temporal coherence[edit]

Figure 1: The amplitude of a single frequency wave as a function of time t (red) and a copy of the same wave delayed by τ (blue). The coherence time of the wave is infinite since it is perfectly correlated with itself for all delays τ.^[11]: 118

Figure 2: The amplitude of a wave whose phase drifts significantly in time τ_c as a function of time t (red) and a copy of the same wave delayed by 2τ_c(green). At any particular time t the wave can interfere perfectly with its delayed copy. But, since half the time the red and green waves are in phase and half the time out of phase, when averaged over t any interference disappears at this delay.

Temporal coherence is the measure of the average correlation between the value of a wave and itself delayed by τ, at any pair of times. Temporal coherence tells us how monochromatic a source is. In other words, it characterizes how well a wave can interfere with itself at a different time. The delay over which the phase or amplitude wanders by a significant amount (and hence the correlation decreases by significant amount) is defined as the coherence time τ_c. At a delay of τ=0 the degree of coherence is perfect, whereas it drops significantly as the delay passes τ=τ_c. The coherence lengthL_c is defined as the distance the wave travels in time τ_c.^{[9]: 560, 571–573}

One should be careful not to confuse the coherence time with the time duration of the signal, nor the coherence length with the coherence area (see below).

The relationship between coherence time and bandwidth[edit]

It can be shown that the larger the range of frequencies Δf a wave contains, the faster the wave decorrelates (and hence the smaller τ_c is). Thus there is a tradeoff:^{[9]: 358-359, 560}

.

Formally, this follows from the convolution theorem in mathematics, which relates the Fourier transform of the power spectrum (the intensity of each frequency) to its autocorrelation.^[9]: 572

Examples of temporal coherence[edit]

We consider four examples of temporal coherence. 

• A wave containing only a single frequency (monochromatic) is perfectly correlated with itself at all time delays, in accordance with the above relation. (See Figure 1)
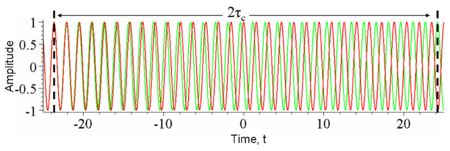
• Conversely, a wave whose phase drifts quickly will have a short coherence time. (See Figure 2)
• Similarly, pulses (wave packets) of waves, which naturally have a broad range of frequencies, also have a short coherence time since the amplitude of the wave changes quickly. (See Figure 3)
• Finally, white light, which has a very broad range of frequencies, is a wave which varies quickly in both amplitude and phase. Since it consequently has a very short coherence time (just 10 periods or so), it is often called incoherent.

The high degree of monochromaticity of lasers implies long coherence lengths (up to hundreds of meters). For example, a stabilized and monomode helium–neon laser can easily produce light with coherence lengths of 300 m.^[12] Not all lasers have a high degree of monochromaticity, however (e.g. for a mode-locked Ti-sapphire laser, Δλ ≈ 2 nm - 70 nm). LEDs are characterized by Δλ ≈ 50 nm, and tungsten filament lights exhibit Δλ ≈ 600 nm, so these sources have shorter coherence times than the most monochromatic lasers.

Holography requires light with a long coherence time. In contrast, optical coherence tomography, in its classical version, uses light with a short coherence time.

Measurement of temporal coherence[edit]

Figure 3: The amplitude of a wavepacket whose amplitude changes significantly in time τ_c (red) and a copy of the same wave delayed by 2τ_c(green) plotted as a function of time t. At any particular time the red and green waves are uncorrelated; one oscillates while the other is constant and so there will be no interference at this delay. Another way of looking at this is the wavepackets are not overlapped in time and so at any particular time there is only one nonzero field so no interference can occur.

Figure 4: The time-averaged intensity (blue) detected at the output of an interferometer plotted as a function of delay τ for the example waves in Figures 2 and 3. As the delay is changed by half a period, the interference switches between constructive and destructive. The black lines indicate the interference envelope, which gives the degree of coherence. Although the waves in Figures 2 and 3 have different time durations, they have the same coherence time.

In optics, temporal coherence is measured in an interferometer such as the Michelson interferometer or Mach–Zehnder interferometer. In these devices, a wave is combined with a copy of itself that is delayed by time τ. A detector measures the time-averaged intensity of the light exiting the interferometer. The resulting visibility of the interference pattern (e.g. see Figure 4) gives the temporal coherence at delay τ. Since for most natural light sources, the coherence time is much shorter than the time resolution of any detector, the detector itself does the time averaging. Consider the example shown in Figure 3. At a fixed delay, here 2τ_c, an infinitely fast detector would measure an intensity that fluctuates significantly over a time t equal to τ_c. In this case, to find the temporal coherence at 2τ_c, one would manually time-average the intensity.

https://en.wikipedia.org/wiki/Coherence_(physics)#Temporal_coherence

Optical coherence tomography (OCT) is an imaging technique that uses low-coherence light to capture micrometer-resolution, two- and three-dimensional images from within optical scattering media (e.g., biological tissue). It is used for medical imaging and industrial nondestructive testing (NDT). Optical coherence tomography is based on low-coherence interferometry, typically employing near-infrared light. The use of relatively long wavelength light allows it to penetrate into the scattering medium. Confocal microscopy, another optical technique, typically penetrates less deeply into the sample but with higher resolution.

Depending on the properties of the light source (superluminescent diodes, ultrashort pulsed lasers, and supercontinuum lasers have been employed), optical coherence tomography has achieved sub-micrometer resolution (with very wide-spectrum sources emitting over a ~100 nm wavelength range).^{[citation needed][verification needed]}

Optical coherence tomography is one of a class of optical tomographic techniques.^{[citation needed]}Commercially available optical coherence tomography systems are employed in diverse applications, including art conservation and diagnostic medicine, notably in ophthalmology and optometry where it can be used to obtain detailed images from within the retina.^{[citation needed]} Recently, it has also begun to be used in interventional cardiology to help diagnose coronary artery disease,^[1] and in dermatology to improve diagnosis.^[2] A relatively recent implementation of optical coherence tomography, frequency-domain optical coherence tomography, provides advantages in the signal-to-noise ratio provided, thus permitting faster signal acquisition.^{[citation needed]}

Optical coherence tomography
Optical coherence tomography (OCT) image of a sarcoma
MeSH	D041623
OPS-301 code	3-300
[edit on Wikidata]

https://en.wikipedia.org/wiki/Optical_coherence_tomography