Nikiya Anton Bettey 2021: 09-24-2021-1208

Friday, September 24, 2021

09-24-2021-1208 - interference

In physics, interference is a phenomenon in which two waves superpose to form a resultant wave of greater, lower, or the same amplitude. Constructive and destructive interference result from the interaction of waves that are correlated or coherent with each other, either because they come from the same source or because they have the same or nearly the same frequency. Interference effects can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity waves, or matter waves. The resulting images or graphs are called interferograms.

The interference of two waves. When in phase, the two lower waves create constructive interference (left), resulting in a wave of greater amplitude. When 180° out of phase, they create destructive interference (right).

Mechanisms[edit]

Interference of right traveling (green) and left traveling (blue) waves in Two-dimensional space, resulting in final (red) wave

Interference of waves from two point sources.

Cropped tomography scan animation of laser light interference passing through two pinholes (side edges).

The principle of superposition of waves states that when two or more propagating waves of the same type are incident on the same point, the resultant amplitude at that point is equal to the vector sum of the amplitudes of the individual waves.^[1] If a crest of a wave meets a crest of another wave of the same frequency at the same point, then the amplitude is the sum of the individual amplitudes—this is constructive interference. If a crest of one wave meets a trough of another wave, then the amplitude is equal to the difference in the individual amplitudes—this is known as destructive interference.

A magnified image of a coloured interference pattern in a soap film. The "black holes" are areas of almost total destructive interference (antiphase).

Constructive interference occurs when the phase difference between the waves is an even multiple of $π$ (180°), whereas destructive interference occurs when the difference is an odd multiple of $π$ . If the difference between the phases is intermediate between these two extremes, then the magnitude of the displacement of the summed waves lies between the minimum and maximum values.

Consider, for example, what happens when two identical stones are dropped into a still pool of water at different locations. Each stone generates a circular wave propagating outwards from the point where the stone was dropped. When the two waves overlap, the net displacement at a particular point is the sum of the displacements of the individual waves. At some points, these will be in phase, and will produce a maximum displacement. In other places, the waves will be in anti-phase, and there will be no net displacement at these points. Thus, parts of the surface will be stationary—these are seen in the figure above and to the right as stationary blue-green lines radiating from the centre.

Interference of light is a common phenomenon that can be explained classically by the superposition of waves, however a deeper understanding of light interference requires knowledge of wave-particle duality of light which is due to quantum mechanics. Prime examples of light interference are the famous double-slit experiment, laser speckle, anti-reflective coatings and interferometers. Traditionally the classical wave model is taught as a basis for understanding optical interference, based on the Huygens–Fresnel principle.

Derivation[edit]

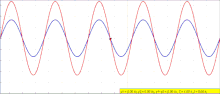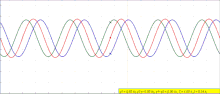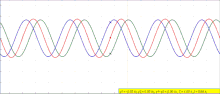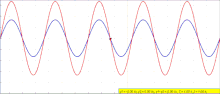
The above can be demonstrated in one dimension by deriving the formula for the sum of two waves. The equation for the amplitude of a sinusoidal wave traveling to the right along the x-axis is

W_{1}(x,t)=A\cos(kx-\omega t)\,

where $A\,$ is the peak amplitude, $k=2\pi /\lambda \,$ is the wavenumber and $\omega = 2\pi f\,$ is the angular frequency of the wave. Suppose a second wave of the same frequency and amplitude but with a different phase is also traveling to the right

W_{2}(x,t)=A\cos(kx-\omega t+\varphi )\,

where $\varphi \,$ is the phase difference between the waves in radians. The two waves will superpose and add: the sum of the two waves is

W_{1}+W_{2}=A[\cos(kx-\omega t)+\cos(kx-\omega t+\varphi )].

Using the trigonometric identity for the sum of two cosines: $\cos a+\cos b=2\cos {\Bigl (}{a-b \over 2}{\Bigr )}\cos {\Bigl (}{a+b \over 2}{\Bigr )},$ this can be written

W_{1}+W_{2}=2A\cos {\Bigl (}{\varphi  \over 2}{\Bigr )}\cos {\Bigl (}kx-\omega t+{\varphi  \over 2}{\Bigr )}.

This represents a wave at the original frequency, traveling to the right like its components, whose amplitude is proportional to the cosine of $\varphi /2$ .

Constructive interference: If the phase difference is an even multiple of $π$ : $\varphi =\ldots ,-4\pi ,-2\pi ,0,2\pi ,4\pi ,\ldots$ then $|\cos(\varphi /2)|=1\,$ , so the sum of the two waves is a wave with twice the amplitude

W_{1}+W_{2}=2A\cos(kx-\omega t)

Destructive interference: If the phase difference is an odd multiple of $π$ : $\varphi =\ldots ,-3\pi ,\,-\pi ,\,\pi ,\,3\pi ,\,5\pi ,\ldots$ then $\cos(\varphi /2)=0\,$ , so the sum of the two waves is zero

W_{1}+W_{2}=0\,

Between two plane waves[edit]

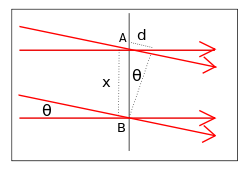
Geometrical arrangement for two plane wave interference

Interference fringes in overlapping plane waves

A simple form of interference pattern is obtained if two plane waves of the same frequency intersect at an angle. Interference is essentially an energy redistribution process. The energy which is lost at the destructive interference is regained at the constructive interference. One wave is travelling horizontally, and the other is travelling downwards at an angle θ to the first wave. Assuming that the two waves are in phase at the point B, then the relative phase changes along the x-axis. The phase difference at the point A is given by

\Delta \varphi ={\frac {2\pi d}{\lambda }}={\frac {2\pi x\sin \theta }{\lambda }}.

It can be seen that the two waves are in phase when

{\frac {x\sin \theta }{\lambda }}=0,\pm 1,\pm 2,\ldots ,

and are half a cycle out of phase when

{\frac {x\sin \theta }{\lambda }}=\pm {\frac {1}{2}},\pm {\frac {3}{2}},\ldots

Constructive interference occurs when the waves are in phase, and destructive interference when they are half a cycle out of phase. Thus, an interference fringe pattern is produced, where the separation of the maxima is

d_f = \frac {\lambda} {\sin \theta}

and $d f$ is known as the fringe spacing. The fringe spacing increases with increase in wavelength, and with decreasing angle $θ$ .

The fringes are observed wherever the two waves overlap and the fringe spacing is uniform throughout.

Between two spherical waves[edit]

Optical interference between two point sources that have different wavelengths and separations of sources.

A point source produces a spherical wave. If the light from two point sources overlaps, the interference pattern maps out the way in which the phase difference between the two waves varies in space. This depends on the wavelength and on the separation of the point sources. The figure to the right shows interference between two spherical waves. The wavelength increases from top to bottom, and the distance between the sources increases from left to right.

When the plane of observation is far enough away, the fringe pattern will be a series of almost straight lines, since the waves will then be almost planar.

Multiple beams[edit]

Interference occurs when several waves are added together provided that the phase differences between them remain constant over the observation time.

It is sometimes desirable for several waves of the same frequency and amplitude to sum to zero (that is, interfere destructively, cancel). This is the principle behind, for example, 3-phase power and the diffraction grating. In both of these cases, the result is achieved by uniform spacing of the phases.

It is easy to see that a set of waves will cancel if they have the same amplitude and their phases are spaced equally in angle. Using phasors, each wave can be represented as $A e^{i \varphi_n}$ for $N$ waves from $n=0$ to $n = N-1$ , where

\varphi _{n}-\varphi _{n-1}={\frac {2\pi }{N}}.

To show that

\sum_{n=0}^{N-1} A e^{i \varphi_n} = 0

one merely assumes the converse, then multiplies both sides by $e^{i{\frac {2\pi }{N}}}.$

The Fabry–Pérot interferometer uses interference between multiple reflections.

A diffraction grating can be considered to be a multiple-beam interferometer; since the peaks which it produces are generated by interference between the light transmitted by each of the elements in the grating; see interference vs. diffraction for further discussion.

Optical interference[edit]

Creation of interference fringes by an optical flat on a reflective surface. Light rays from a monochromatic source pass through the glass and reflect off both the bottom surface of the flat and the supporting surface. The tiny gap between the surfaces means the two reflected rays have different path lengths. In addition the ray reflected from the bottom plate undergoes a 180° phase reversal. As a result, at locations (a)where the path difference is an odd multiple of λ/2, the waves reinforce. At locations (b) where the path difference is an even multiple of λ/2 the waves cancel. Since the gap between the surfaces varies slightly in width at different points, a series of alternating bright and dark bands, interference fringes, are seen.

Because the frequency of light waves (~10¹⁴ Hz) is too high to be detected by currently available detectors, it is possible to observe only the intensity of an optical interference pattern. The intensity of the light at a given point is proportional to the square of the average amplitude of the wave. This can be expressed mathematically as follows. The displacement of the two waves at a point $r$ is:

U_1 (\mathbf r,t) = A_1(\mathbf r) e^{i [\varphi_1 (\mathbf r) - \omega t]}

U_2 (\mathbf r,t) = A_2(\mathbf r) e^{i [\varphi_2 (\mathbf r) - \omega t]}

where $A$ represents the magnitude of the displacement, $φ$ represents the phase and $ω$ represents the angular frequency.

The displacement of the summed waves is

U(\mathbf {r} ,t)=A_{1}(\mathbf {r} )e^{i[\varphi _{1}(\mathbf {r} )-\omega t]}+A_{2}(\mathbf {r} )e^{i[\varphi _{2}(\mathbf {r} )-\omega t]}.

The intensity of the light at $r$ is given by

I(\mathbf {r} )=\int U(\mathbf {r} ,t)U^{*}(\mathbf {r} ,t)\,dt\propto A_{1}^{2}(\mathbf {r} )+A_{2}^{2}(\mathbf {r} )+2A_{1}(\mathbf {r} )A_{2}(\mathbf {r} )\cos[\varphi _{1}(\mathbf {r} )-\varphi _{2}(\mathbf {r} )].

This can be expressed in terms of the intensities of the individual waves as

I(\mathbf {r} )=I_{1}(\mathbf {r} )+I_{2}(\mathbf {r} )+2{\sqrt {I_{1}(\mathbf {r} )I_{2}(\mathbf {r} )}}\cos[\varphi _{1}(\mathbf {r} )-\varphi _{2}(\mathbf {r} )].

Thus, the interference pattern maps out the difference in phase between the two waves, with maxima occurring when the phase difference is a multiple of 2 $π$ . If the two beams are of equal intensity, the maxima are four times as bright as the individual beams, and the minima have zero intensity.

The two waves must have the same polarization to give rise to interference fringes since it is not possible for waves of different polarizations to cancel one another out or add together. Instead, when waves of different polarization are added together, they give rise to a wave of a different polarization state.

https://en.wikipedia.org/wiki/Wave_interference

Nikiya Anton Bettey 2021

Blog Archive