The fundamental plane in a spherical coordinate system is a plane of reference that divides the sphere into two hemispheres. The geocentric latitude of a point is then the angle between the fundamental plane and the line joining the point to the centre of the sphere.[1]
For a geographic coordinate system of the Earth, the fundamental plane is the Equator. Celestial coordinate systems have varying fundamental planes:[2]
- The horizontal coordinate system uses the observer's horizon.
- The Besselian coordinate system uses Earth's terminator (day/night boundary).[citation needed] This is a Cartesian coordinate system (x, y, z).
- The equatorial coordinate system uses the celestial equator.
- The ecliptic coordinate system uses the ecliptic.
- The galactic coordinate system uses the Milky Way's galactic equator.

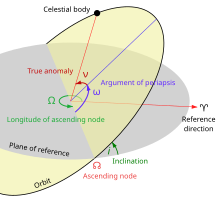
In celestial mechanics, the plane of reference (or reference plane) is the plane used to define orbital elements (positions). The two main orbital elements that are measured with respect to the plane of reference are the inclination and the longitude of the ascending node.
Depending on the type of body being described, there are four different kinds of reference planes that are typically used:
- The ecliptic or invariable plane for planets, asteroids, comets, etc. within the Solar System, as these bodies generally have orbits that lie close to the ecliptic.
- The equatorial plane of the orbited body for satellites with small semi-major axes
- The local Laplace plane for satellites with intermediate-to-large semi-major axes
- The plane tangent to celestial sphere for extrasolar objects
On the plane of reference, a zero-point must be defined from which the angles of longitude are measured. This is usually defined as the point on the celestial sphere where the plane crosses the prime hour circle (the hour circle occupied by the First Point of Aries), also known as the equinox.
See also[edit]

In celestial mechanics, the longitude of the periapsis, also called longitude of the pericenter, of an orbiting body is the longitude (measured from the point of the vernal equinox) at which the periapsis (closest approach to the central body) would occur if the body's orbit inclination were zero. It is usually denoted ϖ.
For the motion of a planet around the Sun, this position is called longitude of perihelion ϖ, which is the sum of the longitude of the ascending node Ω, and the argument of perihelion ω.[1][2]: p.672, etc.
The longitude of periapsis is a compound angle, with part of it being measured in the plane of reference and the rest being measured in the plane of the orbit. Likewise, any angle derived from the longitude of periapsis (e.g., mean longitude and true longitude) will also be compound.
Sometimes, the term longitude of periapsis is used to refer to ω, the angle between the ascending node and the periapsis. That usage of the term is especially common in discussions of binary stars and exoplanets.[3][4] However, the angle ω is less ambiguously known as the argument of periapsis.
https://en.wikipedia.org/wiki/Longitude_of_the_periapsis

Irradiation at the top of the atmosphere[edit]
The distribution of solar radiation at the top of the atmosphere is determined by Earth's sphericityand orbital parameters. This applies to any unidirectional beam incident to a rotating sphere. Insolation is essential for numerical weather prediction and understanding seasons and climatic change. Application to ice ages is known as Milankovitch cycles.
Distribution is based on a fundamental identity from spherical trigonometry, the spherical law of cosines:
where a, b and c are arc lengths, in radians, of the sides of a spherical triangle. C is the angle in the vertex opposite the side which has arc length c. Applied to the calculation of solar zenith angleΘ, the following applies to the spherical law of cosines:
This equation can be also derived from a more general formula:[11]
where β is an angle from the horizontal and γ is an azimuth angle.
The separation of Earth from the sun can be denoted RE and the mean distance can be denoted R0, approximately 1 astronomical unit (AU). The solar constant is denoted S0. The solar flux density (insolation) onto a plane tangent to the sphere of the Earth, but above the bulk of the atmosphere (elevation 100 km or greater) is:
The average of Q over a day is the average of Q over one rotation, or the hour angle progressing from h = π to h = −π:
Let h0 be the hour angle when Q becomes positive. This could occur at sunrise when , or for h0 as a solution of
or
If tan(φ)tan(δ) > 1, then the sun does not set and the sun is already risen at h = π, so ho = π. If tan(φ)tan(δ) < −1, the sun does not rise and .
is nearly constant over the course of a day, and can be taken outside the integral
Therefore:
Let θ be the conventional polar angle describing a planetary orbit. Let θ = 0 at the vernal equinox. The declination δ as a function of orbital position is[12][13]
where ε is the obliquity. The conventional longitude of perihelion ϖ is defined relative to the vernal equinox, so for the elliptical orbit:
or
With knowledge of ϖ, ε and e from astrodynamical calculations[14] and So from a consensus of observations or theory, can be calculated for any latitude φ and θ. Because of the elliptical orbit, and as a consequence of Kepler's second law, θ does not progress uniformly with time. Nevertheless, θ = 0° is exactly the time of the vernal equinox, θ = 90° is exactly the time of the summer solstice, θ = 180° is exactly the time of the autumnal equinox and θ = 270° is exactly the time of the winter solstice.
A simplified equation for irradiance on a given day is:[15]
where n is a number of a day of the year.
https://en.wikipedia.org/wiki/Solar_irradiance









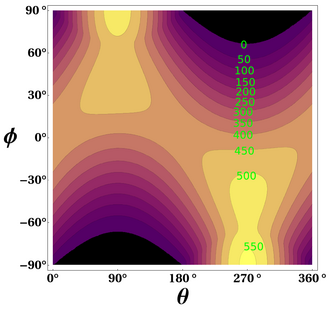








![{\displaystyle {\begin{aligned}\int _{\pi }^{-\pi }Q\,dh&=\int _{h_{o}}^{-h_{o}}Q\,dh\\&=S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\int _{h_{o}}^{-h_{o}}\cos(\Theta )\,dh\\&=S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h)\right]_{h=h_{o}}^{h=-h_{o}}\\&=-2S_{o}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h_{o}\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h_{o})\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcb1dbb45713cbc7a95e25fce752e4807f05f67e)
![{\displaystyle {\overline {Q}}^{\text{day}}={\frac {S_{o}}{\pi }}{\frac {R_{o}^{2}}{R_{E}^{2}}}\left[h_{o}\sin(\phi )\sin(\delta )+\cos(\phi )\cos(\delta )\sin(h_{o})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37e20bedaf32de24aeec5d44dd338414b928ee56)




No comments:
Post a Comment