Magnetic quadrupole[edit]
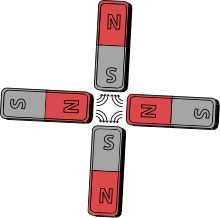
All known magnetic sources give dipole fields. However, it is possible to make a magnetic quadrupole by placing four identical bar magnets perpendicular to each other such that the north pole of one is next to the south of the other. Such a configuration cancels the dipole moment and gives a quadrupole moment, and its field will decrease at large distances faster than that of a dipole.
An example of a magnetic quadrupole, involving permanent magnets, is depicted on the right. Electromagnets of similar conceptual design (called quadrupole magnets) are commonly used to focus beams of charged particles in particle accelerators and beam transport lines, a method known as strong focusing. There are four steel pole tips, two opposing magnetic north poles and two opposing magnetic south poles. The steel is magnetized by a large electric current that flows in the coils of tubing wrapped around the poles. Also, the quadrupole-dipole intersect can be found by multiplying the spin of the unpaired nucleon by its parent atom.
A changing magnetic quadrupole moment produces electromagnetic radiation.
https://en.wikipedia.org/wiki/Quadrupole#magnetic_quadrupole
Just as electric charge and current multipoles contribute to the electromagnetic field, mass and mass-current multipoles contribute to the gravitational field in general relativity, causing the so-called gravitomagnetic effects. Changing mass-current multipoles can also give off gravitational radiation. However, contributions from the current multipoles will typically be much smaller than that of the mass quadrupole.
https://en.wikipedia.org/wiki/Quadrupole#Gravitational_quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.
https://en.wikipedia.org/wiki/Quadrupole
Quadrupole magnets, abbreviated as Q-magnets, consist of groups of four magnets laid out so that in the planar multipole expansion of the field, the dipole terms cancel and where the lowest significant terms in the field equations are quadrupole. Quadrupole magnets are useful as they create a magnetic field whose magnitude grows rapidly with the radial distance from its longitudinal axis. This is used in particle beamfocusing.
The simplest magnetic quadrupole is two identical bar magnets parallel to each other such that the north pole of one is next to the south of the other and vice versa. Such a configuration will have no dipole moment, and its field will decrease at large distances faster than that of a dipole. A stronger version with very little external field involves using a k=3 Halbach cylinder.
In some designs of quadrupoles using electromagnets, there are four steel pole tips: two opposing magnetic north poles and two opposing magnetic south poles. The steel is magnetized by a large electric current in the coils of tubing wrapped around the poles. Another design is a Helmholtz coil layout but with the current in one of the coils reversed.[1]
https://en.wikipedia.org/wiki/Quadrupole_magnet
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ambient space. If a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. This notion can be used in any general space in which the concept of the dimension of a subspace is defined.
In different settings, hyperplanes may have different properties. For instance, a hyperplane of an n-dimensional affine space is a flat subset with dimension n − 1[1] and it separates the space into two half spaces. While a hyperplane of an n-dimensional projective space does not have this property.
The difference in dimension between a subspace S and its ambient space X is known as the codimension of S with respect to X. Therefore, a necessary condition for S to be a hyperplane in X is for S to have codimension one in X.
https://en.wikipedia.org/wiki/Hyperplane
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, . Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on , or less often on for some other .
Multipole expansions are used frequently in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space.[1]
The multipole expansion is expressed as a sum of terms with progressively finer angular features (moments). The first (the zeroth-order) term is called the monopole moment, the second (the first-order) term is called the dipole moment, the third (the second-order) the quadrupole moment, the fourth (third-order) term is called the octupole moment, and so on. Given the limitation of Greek numeral prefixes, terms of higher order are conventionally named by adding "-pole" to the number of poles—e.g., 32-pole (rarely dotriacontapole or triacontadipole) and 64-pole (rarely tetrahexacontapole or hexacontatetrapole).[2][3][4] A multipole moment usually involves powers (or inverse powers) of the distance to the origin, as well as some angular dependence.
In principle, a multipole expansion provides an exact description of the potential, and generally converges under two conditions: (1) if the sources (e.g. charges) are localized close to the origin and the point at which the potential is observed is far from the origin; or (2) the reverse, i.e., if the sources are located far from the origin and the potential is observed close to the origin. In the first (more common) case, the coefficients of the series expansion are called exterior multipole moments or simply multipole moments whereas, in the second case, they are called interior multipole moments.
https://en.wikipedia.org/wiki/Multipole_expansion




No comments:
Post a Comment