
The electric potential (also called the electric field potential, potential drop, the electrostatic potential) is defined as the amount of work energy needed to move a unit of electric charge from a reference point to the specific point in an electric field. More precisely, it is the energy per unit charge for a test charge that is so small that the disturbance of the field under consideration is negligible. Furthermore, the motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is earth or a point at infinity, although any point can be used.
In classical electrostatics, the electrostatic field is a vector quantity which is expressed as the gradient of the electrostatic potential, which is a scalar quantity denoted by V or occasionally φ,[1] equal to the electric potential energy of any charged particle at any location (measured in joules) divided by the charge of that particle (measured in coulombs). By dividing out the charge on the particle a quotient is obtained that is a property of the electric field itself. In short, electric potential is the electric potential energy per unit charge.
This value can be calculated in either a static (time-invariant) or a dynamic (varying with time) electric field at a specific time in units of joules per coulomb (J⋅C−1), or volts (V). The electric potential at infinity is assumed to be zero.
In electrodynamics, when time-varying fields are present, the electric field cannot be expressed only in terms of a scalar potential. Instead, the electric field can be expressed in terms of both the scalar electric potential and the magnetic vector potential.[2] The electric potential and the magnetic vector potential together form a four vector, so that the two kinds of potential are mixed under Lorentz transformations.
Practically, electric potential is always a continuous function in space; Otherwise, the spatial derivative of it will yield a field with infinite magnitude, which is practically impossible. Even an idealized point charge has 1 ⁄ rpotential, which is continuous everywhere except the origin. The electric field is not continuous across an idealized surface charge, but it is not infinite at any point. Therefore, the electric potential is continuous across an idealized surface charge. An idealized linear charge has ln(r) potential, which is continuous everywhere except on the linear charge.
| Electric potential | |
|---|---|
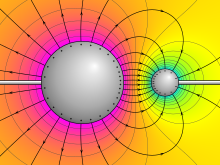 Electric potential around two oppositely charged conducting spheres. Purple represents the highest potential, yellow zero, and cyan the lowest potential. The electric field lines are shown leaving perpendicularly to the surface of each sphere. | |
Common symbols | V, φ |
| SI unit | volt |
Other units | statvolt |
| In SI base units | V = kg⋅m2⋅s−3⋅A−1 |
| Extensive? | yes |
| Dimension | M L2 T−3 I−1 |
https://en.wikipedia.org/wiki/Electric_potential
No comments:
Post a Comment