In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ABCD would be denoted ABCD.[1]
Characterizations
A convex quadrilateral is a square if and only if it is any one of the following:[2][3]
- A rectangle with two adjacent equal sides
- A rhombus with a right vertex angle
- A rhombus with all angles equal
- A parallelogram with one right vertex angle and two adjacent equal sides
- A quadrilateral with four equal sides and four right angles
- A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals)
- A convex quadrilateral with successive sides a, b, c, d whose area is [4]: Corollary 15
Properties
A square is a special case of a rhombus (equal sides, opposite equal angles), a kite (two pairs of adjacent equal sides), a trapezoid (one pair of opposite sides parallel), a parallelogram (all opposite sides parallel), a quadrilateral or tetragon (four-sided polygon), and a rectangle (opposite sides equal, right-angles), and therefore has all the properties of all these shapes, namely:[5]
- All four internal angles of a square are equal (each being 360°/4 = 90°, a right angle).
- The central angle of a square is equal to 90° (360°/4).
- The external angle of a square is equal to 90°.
- The diagonals of a square are equal and bisect each other, meeting at 90°.
- The diagonal of a square bisects its internal angle, forming adjacent angles of 45°.
- All four sides of a square are equal.
- Opposite sides of a square are parallel.
- A square has Schläfli symbol {4}. A truncated square, t{4}, is an octagon, {8}. An alternated square, h{4}, is a digon, {2}.
- The square is the n = 2 case of the families of n-hypercubes and n-orthoplexes.
Perimeter and area
The perimeter of a square whose four sides have length is
and the area A is
Since four squared equals sixteen, a four by four square has an area equal to its perimeter. The only other quadrilateral with such a property is that of a three by six rectangle.
In classical times, the second power was described in terms of the area of a square, as in the above formula. This led to the use of the term square to mean raising to the second power.
The area can also be calculated using the diagonal d according to
In terms of the circumradius R, the area of a square is
since the area of the circle is the square fills of its circumscribed circle.
In terms of the inradius r, the area of the square is
hence the area of the inscribed circle is of that of the square.
Because it is a regular polygon, a square is the quadrilateral of least perimeter enclosing a given area. Dually, a square is the quadrilateral containing the largest area within a given perimeter.[6] Indeed, if A and P are the area and perimeter enclosed by a quadrilateral, then the following isoperimetric inequality holds:
with equality if and only if the quadrilateral is a square.
Other facts
- The diagonals of a square are (about 1.414) times the length of a side of the square. This value, known as the square root of 2 or Pythagoras' constant,[1] was the first number proven to be irrational.
- A square can also be defined as a parallelogram with equal diagonals that bisect the angles.
- If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths), then it is a square.
- A square has a larger area than any other quadrilateral with the same perimeter.[7]
- A square tiling is one of three regular tilings of the plane (the others are the equilateral triangle and the regular hexagon).
- The square is in two families of polytopes in two dimensions: hypercube and the cross-polytope. The Schläfli symbol for the square is {4}.
- The square is a highly symmetric object. There are four lines of reflectional symmetry and it has rotational symmetry of order 4 (through 90°, 180° and 270°). Its symmetry group is the dihedral group D4.
- A square can be inscribed inside any regular polygon. The only other polygon with this property is the equilateral triangle.
- If the inscribed circle of a square ABCD has tangency points E on AB, F on BC, G on CD, and H on DA, then for any point P on the inscribed circle,[8]
- If is the distance from an arbitrary point in the plane to the i-th vertex of a square and is the circumradius of the square, then[9]
- If and are the distances from an arbitrary point in the plane to the centroid of the square and its four vertices respectively, then [10]
- and
- where is the circumradius of the square.
Coordinates and equations
The coordinates for the vertices of a square with vertical and horizontal sides, centered at the origin and with side length 2 are (±1, ±1), while the interior of this square consists of all points (xi, yi) with −1 < xi < 1 and −1 < yi < 1. The equation
specifies the boundary of this square. This equation means "x2 or y2, whichever is larger, equals 1." The circumradius of this square (the radius of a circle drawn through the square's vertices) is half the square's diagonal, and is equal to Then the circumcircle has the equation
Alternatively the equation
can also be used to describe the boundary of a square with center coordinates (a, b), and a horizontal or vertical radius of r. The square is therefore the shape of a topological ball according to the L1 distance metric.
Construction
The following animations show how to construct a square using a compass and straightedge. This is possible as 4 = 22, a power of two.
right angle by using Thales' theorem
Symmetry
The square has Dih4 symmetry, order 8. There are 2 dihedral subgroups: Dih2, Dih1, and 3 cyclic subgroups: Z4, Z2, and Z1.
A square is a special case of many lower symmetry quadrilaterals:
- A rectangle with two adjacent equal sides
- A quadrilateral with four equal sides and four right angles
- A parallelogram with one right angle and two adjacent equal sides
- A rhombus with a right angle
- A rhombus with all angles equal
- A rhombus with equal diagonals
These 6 symmetries express 8 distinct symmetries on a square. John Conway labels these by a letter and group order.[11]
Each subgroup symmetry allows one or more degrees of freedom for irregular quadrilaterals. r8 is full symmetry of the square, and a1 is no symmetry. d4 is the symmetry of a rectangle, and p4 is the symmetry of a rhombus. These two forms are duals of each other, and have half the symmetry order of the square. d2 is the symmetry of an isosceles trapezoid, and p2 is the symmetry of a kite. g2 defines the geometry of a parallelogram.
Only the g4 subgroup has no degrees of freedom, but can seen as a square with directed edges.
Squares inscribed in triangles
Every acute triangle has three inscribed squares (squares in its interior such that all four of a square's vertices lie on a side of the triangle, so two of them lie on the same side and hence one side of the square coincides with part of a side of the triangle). In a right triangle two of the squares coincide and have a vertex at the triangle's right angle, so a right triangle has only two distinct inscribed squares. An obtuse triangle has only one inscribed square, with a side coinciding with part of the triangle's longest side.
The fraction of the triangle's area that is filled by the square is no more than 1/2.
Squaring the circle
Squaring the circle, proposed by ancient geometers, is the problem of constructing a square with the same area as a given circle, by using only a finite number of steps with compass and straightedge.
In 1882, the task was proven to be impossible as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (π) is a transcendental number rather than an algebraic irrational number; that is, it is not the root of any polynomial with rational coefficients.
Non-Euclidean geometry
In non-Euclidean geometry, squares are more generally polygons with 4 equal sides and equal angles.
In spherical geometry, a square is a polygon whose edges are great circle arcs of equal distance, which meet at equal angles. Unlike the square of plane geometry, the angles of such a square are larger than a right angle. Larger spherical squares have larger angles.
In hyperbolic geometry, squares with right angles do not exist. Rather, squares in hyperbolic geometry have angles of less than right angles. Larger hyperbolic squares have smaller angles.
Examples:
 Two squares can tile the sphere with 2 squares around each vertex and 180-degree internal angles. Each square covers an entire hemisphere and their vertices lie along a great circle. This is called a spherical square dihedron. The Schläfli symbol is {4,2}. |
 Six squares can tile the sphere with 3 squares around each vertex and 120-degree internal angles. This is called a spherical cube. The Schläfli symbol is {4,3}. |
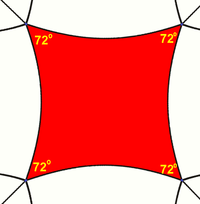 Squares can tile the hyperbolic plane with 5 around each vertex, with each square having 72-degree internal angles. The Schläfli symbol is {4,5}. In fact, for any n ≥ 5 there is a hyperbolic tiling with n squares about each vertex. |
Crossed square
A crossed square is a faceting of the square, a self-intersecting polygon created by removing two opposite edges of a square and reconnecting by its two diagonals. It has half the symmetry of the square, Dih2, order 4. It has the same vertex arrangement as the square, and is vertex-transitive. It appears as two 45-45-90 triangle with a common vertex, but the geometric intersection is not considered a vertex.
A crossed square is sometimes likened to a bow tie or butterfly. the crossed rectangle is related, as a faceting of the rectangle, both special cases of crossed quadrilaterals.[12]
The interior of a crossed square can have a polygon density of ±1 in each triangle, dependent upon the winding orientation as clockwise or counterclockwise.
A square and a crossed square have the following properties in common:
- Opposite sides are equal in length.
- The two diagonals are equal in length.
- It has two lines of reflectional symmetry and rotational symmetry of order 2 (through 180°).
It exists in the vertex figure of a uniform star polyhedra, the tetrahemihexahedron.
Graphs
The K4 complete graph is often drawn as a square with all 6 possible edges connected, hence appearing as a square with both diagonals drawn. This graph also represents an orthographic projection of the 4 vertices and 6 edges of the regular 3-simplex (tetrahedron).
See also
References
- Wells, Christopher J. "Quadrilaterals". www.technologyuk.net. Retrieved 2017-12-12.
External links
- Animated course (Construction, Circumference, Area)
- Definition and properties of a square With interactive applet
- Animated applet illustrating the area of a square
| Square | |
|---|---|
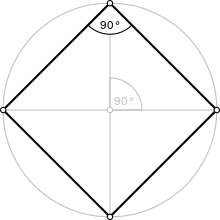 A regular quadrilateral | |
| Type | Regular polygon |
| Edges and vertices | 4 |
| Schläfli symbol | {4} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D4), order 2×4 |
| Internal angle (degrees) | 90° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
https://en.wikipedia.org/wiki/Square
In Euclidean geometry, a tangential trapezoid, also called a circumscribed trapezoid, is a trapezoid whose four sides are all tangent to a circle within the trapezoid: the incircle or inscribed circle. It is the special case of a tangential quadrilateral in which at least one pair of opposite sides are parallel. As for other trapezoids, the parallel sides are called the bases and the other two sides the legs. The legs can be equal (see isosceles tangential trapezoid below), but they don't have to be.
Special cases
Examples of tangential trapezoids are rhombi and squares.
Characterization
If the incircle is tangent to the sides AB and CD at W and Y respectively, then a tangential quadrilateral ABCD is also a trapezoid with parallel sides AB and CD if and only if[1]: Thm. 2
and AD and BC are the parallel sides of a trapezoid if and only if
Area
The formula for the area of a trapezoid can be simplified using Pitot's theorem to get a formula for the area of a tangential trapezoid. If the bases have lengths a, b, and any one of the other two sides has length c, then the area K is given by the formula[2] (This formula can be used only in cases where the bases are parallel.)
The area can be expressed in terms of the tangent lengths e, f, g, h as[3]: p.129
Inradius
Using the same notations as for the area, the radius in the incircle is[2]
The diameter of the incircle is equal to the height of the tangential trapezoid.
The inradius can also be expressed in terms of the tangent lengths as[3]: p.129
Moreover, if the tangent lengths e, f, g, h emanate respectively from vertices A, B, C, D and AB is parallel to DC, then[1]
Properties of the incenter
If the incircle is tangent to the bases at P, Q, then P, I, Q are collinear, where I is the incenter.[4]
The angles ∠ AID and ∠ BIC in a tangential trapezoid ABCD, with bases AB and DC, are right angles.[4]
The incenter lies on the median (also called the midsegment; that is, the segment connecting the midpoints of the legs).[4]
Other properties
The median (midsegment) of a tangential trapezoid equals one fourth of the perimeter of the trapezoid. It also equals half the sum of the bases, as in all trapezoids.
If two circles are drawn, each with a diameter coinciding with the legs of a tangential trapezoid, then these two circles are tangent to each other.[5]
Right tangential trapezoid
A right tangential trapezoid is a tangential trapezoid where two adjacent angles are right angles. If the bases have lengths a, b, then the inradius is[6]
Thus the diameter of the incircle is the harmonic mean of the bases.
The right tangential trapezoid has the area[6]
Isosceles tangential trapezoid
An isosceles tangential trapezoid is a tangential trapezoid where the legs are equal. Since an isosceles trapezoid is cyclic, an isosceles tangential trapezoid is a bicentric quadrilateral. That is, it has both an incircle and a circumcircle.
If the bases are a, b, then the inradius is given by[7]
To derive this formula was a simple Sangaku problem from Japan. From Pitot's theorem it follows that the lengths of the legs are half the sum of the bases. Since the diameter of the incircle is the square root of the product of the bases, an isosceles tangential trapezoid gives a nice geometric interpretation of the arithmetic mean and geometric mean of the bases as the length of a leg and the diameter of the incircle respectively.
The area K of an isosceles tangential trapezoid with bases a, b is given by[8]
References
- Abhijit Guha, CAT Mathematics, PHI Learning Private Limited, 2014, p. 7-73.
https://en.wikipedia.org/wiki/Tangential_trapezoid
In geometry, a chiliagon (/ˈkɪliəɡɒn/) or 1000-gon is a polygon with 1,000 sides. Philosophers commonly refer to chiliagons to illustrate ideas about the nature and workings of thought, meaning, and mental representation.
https://en.wikipedia.org/wiki/Chiliagon
| Regular 65537-gon | |
|---|---|
 A regular 65537-gon | |
| Type | Regular polygon |
| Edges and vertices | 65537 |
| Schläfli symbol | {65537} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D65537), order 2×65537 |
| Internal angle (degrees) | ≈179.994 507° |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | Self |
In geometry, a 65537-gon is a polygon with 65,537 (216 + 1) sides. The sum of the interior angles of any non–self-intersecting 65537-gon is 11796300°.
https://en.wikipedia.org/wiki/65537-gon
In geometry, a hendecagram (also endecagram or endekagram) is a star polygon that has eleven vertices.
The name hendecagram combines a Greek numeral prefix, hendeca-, with the Greek suffix -gram. The hendeca- prefix derives from Greek ἕνδεκα (ἕν + δέκα, one + ten) meaning "eleven". The -gram suffix derives from γραμμῆς (grammēs) meaning a line.[1]
https://en.wikipedia.org/wiki/Hendecagram
A simple polygon that is not convex is called concave,[1] non-convex[2] or reentrant.[3] A concave polygon will always have at least one reflex interior angle—that is, an angle with a measure that is between 180 degrees and 360 degrees exclusive.[4]
https://en.wikipedia.org/wiki/Concave_polygon
In geometry, a polytope (for example, a polygon or a polyhedron) or a tiling is isotoxal (from Greek τόξον 'arc') or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation, and/or reflection that will move one edge to the other while leaving the region occupied by the object unchanged.
https://en.wikipedia.org/wiki/Isotoxal_figure
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is an automorphism of G that maps e1 to e2.[1]
In other words, a graph is edge-transitive if its automorphism group acts transitively on its edges.
https://en.wikipedia.org/wiki/Edge-transitive_graph
A magic polygon is a polygonal magic graph with integers on its vertices.
https://en.wikipedia.org/wiki/Magic_polygon
In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.
Although the words "pseudotriangle" and "pseudotriangulation" have been used with various meanings in mathematics for much longer,[1] the terms as used here were introduced in 1993 by Michel Pocchiola and Gert Vegter in connection with the computation of visibility relations and bitangents among convex obstacles in the plane. Pointed pseudotriangulations were first considered by Ileana Streinu (2000, 2005) as part of her solution to the carpenter's ruler problem, a proof that any simple polygonal path in the plane can be straightened out by a sequence of continuous motions. Pseudotriangulations have also been used for collision detection among moving objects[2] and for dynamic graph drawing and shape morphing.[3] Pointed pseudotriangulations arise in rigidity theory as examples of minimally rigid planar graphs,[4] and in methods for placing guards in connection with the art gallery theorem.[5] The shelling antimatroid of a planar point set gives rise to pointed pseudotriangulations,[6] although not all pointed pseudotriangulations can arise in this way.
For a detailed survey of much of the material discussed here, see Rote, Santos, and Streinu (2008).
https://en.wikipedia.org/wiki/Pseudotriangle
In geometry, an apeirogon (from Ancient Greek ἄπειρος apeiros 'infinite, boundless', and γωνία gonia 'angle') or infinite polygon is a polygon with an infinite number of sides. Apeirogons are the two-dimensional case of infinite polytopes. In some literature, the term "apeirogon" may refer only to the regular apeirogon, with an infinite dihedral group of symmetries.[1]
https://en.wikipedia.org/wiki/Apeirogon
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines.
A geometric polytope is said to be a realization of an abstract polytope in some real N-dimensional space, typically Euclidean. This abstract definition allows more general combinatorial structures than traditional definitions of a polytope, thus allowing new objects that have no counterpart in traditional theory.
https://en.wikipedia.org/wiki/Abstract_polytope
An (simple) arc in finite projective geometry is a set of points which satisfies, in an intuitive way, a feature of curved figures in continuous geometries. Loosely speaking, they are sets of points that are far from "line-like" in a plane or far from "plane-like" in a three-dimensional space. In this finite setting it is typical to include the number of points in the set in the name, so these simple arcs are called k-arcs. An important generalization of the k-arc concept, also referred to as arcs in the literature, are the (k, d)-arcs.
https://en.wikipedia.org/wiki/Arc_(projective_geometry)
In projective geometry, Desargues's theorem, named after Girard Desargues, states:
- Two triangles are in perspective axially if and only if they are in perspective centrally.
Denote the three vertices of one triangle by a, b and c, and those of the other by A, B and C. Axial perspectivity means that lines ab and AB meet in a point, lines ac and AC meet in a second point, and lines bc and BC meet in a third point, and that these three points all lie on a common line called the axis of perspectivity. Central perspectivity means that the three lines Aa, Bb and Cc are concurrent, at a point called the center of perspectivity.
This intersection theorem is true in the usual Euclidean plane but special care needs to be taken in exceptional cases, as when a pair of sides are parallel, so that their "point of intersection" recedes to infinity. Commonly, to remove these exceptions, mathematicians "complete" the Euclidean plane by adding points at infinity, following Jean-Victor Poncelet. This results in a projective plane.
Desargues's theorem is true for the real projective plane and for any projective space defined arithmetically from a field or division ring; that includes any projective space of dimension greater than two or in which Pappus's theorem holds. However, there are many "non-Desarguesian planes", in which Desargues's theorem is false.
History
Desargues never published this theorem, but it appeared in an appendix entitled Universal Method of M. Desargues for Using Perspective (Manière universelle de M. Desargues pour practiquer la perspective) to a practical book on the use of perspective published in 1648.[1] by his friend and pupil Abraham Bosse (1602–1676).[2]
Coordinatization
The importance of Desargues's theorem in abstract projective geometry is due especially to the fact that a projective space satisfies that theorem if and only if it is isomorphic to a projective space defined over a field or division ring.
Projective versus affine spaces
In an affine space such as the Euclidean plane a similar statement is true, but only if one lists various exceptions involving parallel lines. Desargues's theorem is therefore one of the simplest geometric theorems whose natural home is in projective rather than affine space.
Self-duality
By definition, two triangles are perspective if and only if they are in perspective centrally (or, equivalently according to this theorem, in perspective axially). Note that perspective triangles need not be similar.
Under the standard duality of plane projective geometry (where points correspond to lines and collinearity of points corresponds to concurrency of lines), the statement of Desargues's theorem is self-dual: axial perspectivity is translated into central perspectivity and vice versa. The Desargues configuration (below) is a self-dual configuration.[3]
This self-duality in the statement is due to the usual modern way of writing the theorem. Historically, the theorem only read, "In a projective space, a pair of centrally perspective triangles is axially perspective" and the dual of this statement was called the converse of Desargues's theorem and was always referred to by that name.[4]
Proof of Desargues's theorem
Desargues's theorem holds for projective space of any dimension over any field or division ring, and also holds for abstract projective spaces of dimension at least 3. In dimension 2 the planes for which it holds are called Desarguesian planes and are the same as the planes that can be given coordinates over a division ring. There are also many non-Desarguesian planes where Desargues's theorem does not hold.
Three-dimensional proof
Desargues's theorem is true for any projective space of dimension at least 3, and more generally for any projective space that can be embedded in a space of dimension at least 3.
Desargues's theorem can be stated as follows:
- If lines Aa, Bb and Cc are concurrent (meet at a point), then
- the points AB ∩ ab, AC ∩ ac and BC ∩ bc are collinear.
The points A, B, a and b are coplanar (lie in the same plane) because of the assumed concurrency of Aa and Bb. Therefore, the lines AB and ab belong to the same plane and must intersect. Further, if the two triangles lie on different planes, then the point AB ∩ ab belongs to both planes. By a symmetric argument, the points AC ∩ ac and BC ∩ bc also exist and belong to the planes of both triangles. Since these two planes intersect in more than one point, their intersection is a line that contains all three points.
This proves Desargues's theorem if the two triangles are not contained in the same plane. If they are in the same plane, Desargues's theorem can be proved by choosing a point not in the plane, using this to lift the triangles out of the plane so that the argument above works, and then projecting back into the plane. The last step of the proof fails if the projective space has dimension less than 3, as in this case it is not possible to find a point not in the plane.
Monge's theorem also asserts that three points lie on a line, and has a proof using the same idea of considering it in three rather than two dimensions and writing the line as an intersection of two planes.
Two-dimensional proof
As there are non-Desarguesian projective planes in which Desargues's theorem is not true,[5] some extra conditions need to be met in order to prove it. These conditions usually take the form of assuming the existence of sufficiently many collineations of a certain type, which in turn leads to showing that the underlying algebraic coordinate system must be a division ring (skewfield).[6]
Relation to Pappus's theorem
Pappus's hexagon theorem states that, if a hexagon AbCaBc is drawn in such a way that vertices a, b and c lie on a line and vertices A, B and C lie on a second line, then each two opposite sides of the hexagon lie on two lines that meet in a point and the three points constructed in this way are collinear. A plane in which Pappus's theorem is universally true is called Pappian. Hessenberg (1905)[7] showed that Desargues's theorem can be deduced from three applications of Pappus's theorem.[8]
The converse of this result is not true, that is, not all Desarguesian planes are Pappian. Satisfying Pappus's theorem universally is equivalent to having the underlying coordinate system be commutative. A plane defined over a non-commutative division ring (a division ring that is not a field) would therefore be Desarguesian but not Pappian. However, due to Wedderburn's little theorem, which states that all finite division rings are fields, all finite Desarguesian planes are Pappian. There is no known completely geometric proof of this fact, although Bamberg & Penttila (2015) give a proof that uses only "elementary" algebraic facts (rather than the full strength of Wedderburn's little theorem).
The Desargues configuration
The ten lines involved in Desargues's theorem (six sides of triangles, the three lines Aa, Bb and Cc, and the axis of perspectivity) and the ten points involved (the six vertices, the three points of intersection on the axis of perspectivity, and the center of perspectivity) are so arranged that each of the ten lines passes through three of the ten points, and each of the ten points lies on three of the ten lines. Those ten points and ten lines make up the Desargues configuration, an example of a projective configuration. Although Desargues's theorem chooses different roles for these ten lines and points, the Desargues configuration itself is more symmetric: any of the ten points may be chosen to be the center of perspectivity, and that choice determines which six points will be the vertices of triangles and which line will be the axis of perspectivity.
The little Desargues theorem
This restricted version states that if two triangles are perspective from a point on a given line, and two pairs of corresponding sides also meet on this line, then the third pair of corresponding sides meet on the line as well. Thus, it is the specialization of Desargues's Theorem to only the cases in which the center of perspectivity lies on the axis of perspectivity.
A Moufang plane is a projective plane in which the little Desargues theorem is valid for every line.
See also
Notes
- Coxeter 1969, p. 238, section 14.3
References
- Albert, A. Adrian; Sandler, Reuben (2015) [1968], An Introduction to Finite Projective Planes, Dover, ISBN 978-0-486-78994-1
- Bamberg, John; Penttila, Tim (2015), "Completing Segre's proof of Wedderburn's little theorem", Bulletin of the London Mathematical Society, 47 (3): 483–492, doi:10.1112/blms/bdv021, S2CID 123036578
- Casse, Rey (2006), Projective Geometry: An Introduction, Oxford: Oxford University Press, ISBN 0-19-929886-6
- Coxeter, H.S.M. (1964), Projective Geometry, Blaisdell
- Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), Wiley, ISBN 978-0-471-50458-0, MR 0123930
- Cronheim, Arno (1953), "A proof of Hessenberg's theorem", Proceedings of the American Mathematical Society, 4 (2): 219–221, doi:10.2307/2031794, JSTOR 2031794, MR 0053531
- Dembowski, Peter (1968), Finite Geometries, Springer Verlag, ISBN 978-3-540-61786-0
- Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen, Springer, 61 (2): 161–172, doi:10.1007/BF01457558, ISSN 1432-1807, S2CID 120456855
- Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), Chelsea, pp. 119–128, ISBN 0-8284-1087-9
- Hughes, Dan; Piper, Fred (1973), Projective Planes, Springer-Verlag, ISBN 0-387-90044-6
- Kárteszi, Ferenc (1976), Introduction to Finite Geometries, North-Holland, ISBN 0-7204-2832-7
- Katz, Victor J. (1998), A History of Mathematics:An Introduction (2nd ed.), Reading, Mass.: Addison Wesley Longman, ISBN 0-321-01618-1
- Pambuccian, Victor; Schacht, Celia (2019), "The axiomatic destiny of the theorems of Pappus and Desargues", in Dani, S. G.; Papadopoulos, A. (eds.), Geometry in history, Springer, pp. 355–399, ISBN 978-3-030-13611-6
- Room, Thomas G.; Kirkpatrick, P. B. (1971), Miniquaternion Geometry, Cambridge: Cambridge University Press, ISBN 0-521-07926-8
- Smith, David Eugene (1959), A Source Book in Mathematics, Dover, ISBN 0-486-64690-4
- Stevenson, Frederick W. (1972), Projective Planes, W.H. Freeman, ISBN 0-7167-0443-9
- Voitsekhovskii, M.I. (2001) [1994], "Desargues assumption", Encyclopedia of Mathematics, EMS Press
External links
https://en.wikipedia.org/wiki/Desargues%27s_theorem
In projective geometry an oval is a point set in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.
As mentioned, in projective geometry an oval is defined by incidence properties, but in other areas, ovals may be defined to satisfy other criteria, for instance, in differential geometry by differentiability conditions in the real plane.
The higher dimensional analog of an oval is an ovoid in a projective space.
A generalization of the oval concept is an abstract oval, which is a structure that is not necessarily embedded in a projective plane. Indeed, there exist abstract ovals which can not lie in any projective plane.
e: exterior (passing) line,
t: tangent,
s: secant
https://en.wikipedia.org/wiki/Oval_(projective_plane)
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ambient space. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. This notion can be used in any general space in which the concept of the dimension of a subspace is defined.
In different settings, hyperplanes may have different properties. For instance, a hyperplane of an n-dimensional affine space is a flat subset with dimension n − 1[1] and it separates the space into two half spaces. While a hyperplane of an n-dimensional projective space does not have this property.
The difference in dimension between a subspace S and its ambient space X is known as the codimension of S with respect to X. Therefore, a necessary and sufficient condition for S to be a hyperplane in X is for S to have codimension one in X.
https://en.wikipedia.org/wiki/Hyperplane
A maximal arc in a finite projective plane is a largest possible (k,d)-arc in that projective plane. If the finite projective plane has order q (there are q+1 points on any line), then for a maximal arc, k, the number of points of the arc, is the maximum possible (= qd + d - q) with the property that no d+1 points of the arc lie on the same line.
https://en.wikipedia.org/wiki/Maximal_arc
In mathematics, the rational normal curve is a smooth, rational curve C of degree n in projective n-space Pn. It is a simple example of a projective variety; formally, it is the Veronese variety when the domain is the projective line. For n = 2 it is the plane conic Z0Z2 = Z2
1, and for n = 3 it is the twisted cubic. The term "normal" refers to projective normality, not normal schemes. The intersection of the rational normal curve with an affine space is called the moment curve.
https://en.wikipedia.org/wiki/Rational_normal_curve
In mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation (the twisted cubic, therefore). In algebraic geometry, the twisted cubic is a simple example of a projective variety that is not linear or a hypersurface, in fact not a complete intersection. It is the three-dimensional case of the rational normal curve, and is the image of a Veronese map of degree three on the projective line.
https://en.wikipedia.org/wiki/Twisted_cubic
In algebraic geometry the AF+BG theorem (also known as Max Noether's fundamental theorem) is a result of Max Noether that asserts that, if the equation of an algebraic curve in the complex projective plane belongs locally (at each intersection point) to the ideal generated by the equations of two other algebraic curves, then it belongs globally to this ideal.
https://en.wikipedia.org/wiki/AF%2BBG_theorem
In algebraic geometry, the first polar, or simply polar of an algebraic plane curve C of degree n with respect to a point Q is an algebraic curve of degree n−1 which contains every point of C whose tangent line passes through Q. It is used to investigate the relationship between the curve and its dual, for example in the derivation of the Plücker formulas.
https://en.wikipedia.org/wiki/Polar_curve
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation
applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting z = 1 in such an equation. Here F is a non-zero linear combination of the third-degree monomials
These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field K. Each point P imposes a single linear condition on F, if we ask that C pass through P. Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position; compare to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem.
A cubic curve may have a singular point, in which case it has a parametrization in terms of a projective line. Otherwise a non-singular cubic curve is known to have nine points of inflection, over an algebraically closed field such as the complex numbers. This can be shown by taking the homogeneous version of the Hessian matrix, which defines again a cubic, and intersecting it with C; the intersections are then counted by Bézout's theorem. However, only three of these points may be real, so that the others cannot be seen in the real projective plane by drawing the curve. The nine inflection points of a non-singular cubic have the property that every line passing through two of them contains exactly three inflection points.
The real points of cubic curves were studied by Isaac Newton. The real points of a non-singular projective cubic fall into one or two 'ovals'. One of these ovals crosses every real projective line, and thus is never bounded when the cubic is drawn in the Euclidean plane; it appears as one or three infinite branches, containing the three real inflection points. The other oval, if it exists, does not contain any real inflection point and appears either as an oval or as two infinite branches. Like for conic sections, a line cuts this oval at, at most, two points.
A non-singular plane cubic defines an elliptic curve, over any field K for which it has a point defined. Elliptic curves are now normally studied in some variant of Weierstrass's elliptic functions, defining a quadratic extension of the field of rational functions made by extracting the square root of a cubic. This does depend on having a K-rational point, which serves as the point at infinity in Weierstrass form. There are many cubic curves that have no such point, for example when K is the rational number field.
The singular points of an irreducible plane cubic curve are quite limited: one double point, or one cusp. A reducible plane cubic curve is either a conic and a line or three lines, and accordingly have two double points or a tacnode (if a conic and a line), or up to three double points or a single triple point (concurrent lines) if three lines.
Cubic curves in the plane of a triangle
Suppose that △ABC is a triangle with sidelengths Relative to △ABC, many named cubics pass through well-known points. Examples shown below use two kinds of homogeneous coordinates: trilinear and barycentric.
To convert from trilinear to barycentric in a cubic equation, substitute as follows:
to convert from barycentric to trilinear, use
Many equations for cubics have the form
In the examples below, such equations are written more succinctly in "cyclic sum notation", like this:
- .
The cubics listed below can be defined in terms of the isogonal conjugate, denoted by X*, of a point X not on a sideline of △ABC. A construction of X* follows. Let LA be the reflection of line XA about the internal angle bisector of angle A, and define LB and LC analogously. Then the three reflected lines concur in X*. In trilinear coordinates, if then
Neuberg cubic
Trilinear equation:
Barycentric equation:
The Neuberg cubic (named after Joseph Jean Baptiste Neuberg) is the locus of a point X such that X* is on the line EX, where E is the Euler infinity point (X(30) in the Encyclopedia of Triangle Centers). Also, this cubic is the locus of X such that the triangle △XAXBXC is perspective to △ABC, where △XAXBXC is the reflection of X in the lines BC, CA, AB, respectively
The Neuberg cubic passes through the following points: incenter, circumcenter, orthocenter, both Fermat points, both isodynamic points, the Euler infinity point, other triangle centers, the excenters, the reflections of A, B, C in the sidelines of △ABC, and the vertices of the six equilateral triangles erected on the sides of △ABC.
For a graphical representation and extensive list of properties of the Neuberg cubic, see K001 at Berhard Gibert's Cubics in the Triangle Plane.
Thomson cubic
Trilinear equation:
Barycentric equation:
The Thomson cubic is the locus of a point X such that X* is on the line GX, where G is the centroid.
The Thomson cubic passes through the following points: incenter, centroid, circumcenter, orthocenter, symmedian point, other triangle centers, the vertices A, B, C, the excenters, the midpoints of sides BC, CA, AB, and the midpoints of the altitudes of △ABC. For each point P on the cubic but not on a sideline of the cubic, the isogonal conjugate of P is also on the cubic.
For graphs and properties, see K002 at Cubics in the Triangle Plane.
Darboux cubic
Trilinear equation:
Barycentric equation:
The Darboux cubic is the locus of a point X such that X* is on the line LX, where L is the de Longchamps point. Also, this cubic is the locus of X such that the pedal triangle of X is the cevian triangle of some point (which lies on the Lucas cubic). Also, this cubic is the locus of a point X such that the pedal triangle of X and the anticevian triangle of X are perspective; the perspector lies on the Thomson cubic.
The Darboux cubic passes through the incenter, circumcenter, orthocenter, de Longchamps point, other triangle centers, the vertices A, B, C, the excenters, and the antipodes of A, B, C on the circumcircle. For each point P on the cubic but not on a sideline of the cubic, the isogonal conjugate of P is also on the cubic.
For graphics and properties, see K004 at Cubics in the Triangle Plane.
Napoleon–Feuerbach cubic
Trilinear equation:
Barycentric equation:
The Napoleon–Feuerbach cubic is the locus of a point X* is on the line NX, where N is the nine-point center, (N = X(5) in the Encyclopedia of Triangle Centers).
The Napoleon–Feuerbach cubic passes through the incenter, circumcenter, orthocenter, 1st and 2nd Napoleon points, other triangle centers, the vertices A, B, C, the excenters, the projections of the centroid on the altitudes, and the centers of the 6 equilateral triangles erected on the sides of △ABC.
For a graphics and properties, see K005 at Cubics in the Triangle Plane.
Lucas cubic
Trilinear equation:
Barycentric equation:
The Lucas cubic is the locus of a point X such that the cevian triangle of X is the pedal triangle of some point; the point lies on the Darboux cubic.
The Lucas cubic passes through the centroid, orthocenter, Gergonne point, Nagel point, de Longchamps point, other triangle centers, the vertices of the anticomplementary triangle, and the foci of the Steiner circumellipse.
For graphics and properties, see K007 at Cubics in the Triangle Plane.
1st Brocard cubic
Trilinear equation:
Barycentric equation:
Let △A'B'C' be the 1st Brocard triangle. For arbitrary point X, let XA, XB, XC be the intersections of the lines XA′, XB′, XC′ with the sidelines BC, CA, AB, respectively. The 1st Brocard cubic is the locus of X for which the points XA, XB, XC are collinear.
The 1st Brocard cubic passes through the centroid, symmedian point, Steiner point, other triangle centers, and the vertices of the 1st and 3rd Brocard triangles.
For graphics and properties, see K017 at Cubics in the Triangle Plane.
2nd Brocard cubic
Trilinear equation:
Barycentric equation:
The 2nd Brocard cubic is the locus of a point X for which the pole of the line XX* in the circumconic through X and X* lies on the line of the circumcenter and the symmedian point (i.e., the Brocard axis). The cubic passes through the centroid, symmedian point, both Fermat points, both isodynamic points, the Parry point, other triangle centers, and the vertices of the 2nd and 4th Brocard triangles.
For a graphics and properties, see K018 at Cubics in the Triangle Plane.
1st equal areas cubic
Trilinear equation:
Barycentric equation:
The 1st equal areas cubic is the locus of a point X such that area of the cevian triangle of X equals the area of the cevian triangle of X*. Also, this cubic is the locus of X for which X* is on the line S*X, where S is the Steiner point. (S = X(99) in the Encyclopedia of Triangle Centers).
The 1st equal areas cubic passes through the incenter, Steiner point, other triangle centers, the 1st and 2nd Brocard points, and the excenters.
For a graphics and properties, see K021 at Cubics in the Triangle Plane.
2nd equal areas cubic
Trilinear equation:
Barycentric equation:
For any point (trilinears), let and The 2nd equal areas cubic is the locus of X such that the area of the cevian triangle of XY equals the area of the cevian triangle of XZ.
The 2nd equal areas cubic passes through the incenter, centroid, symmedian point, and points in Encyclopedia of Triangle Centers indexed as X(31), X(105), X(238), X(292), X(365), X(672), X(1453), X(1931), X(2053), and others.
For a graphics and properties, see K155 at Cubics in the Triangle Plane.
See also
- Cayley–Bacharach theorem, on the intersection of two cubic plane curves
- Twisted cubic, a cubic space curve
- Elliptic curve
- Witch of Agnesi
- Catalogue of Triangle Cubics
References
- Bix, Robert (1998), Conics and Cubics: A Concrete Introduction to Algebraic Curves, New York: Springer, ISBN 0-387-98401-1.
- Cerin, Zvonko (1998), "Locus properties of the Neuberg cubic", Journal of Geometry, 63 (1–2): 39–56, doi:10.1007/BF01221237, S2CID 116778499.
- Cerin, Zvonko (1999), "On the cubic of Napoleon", Journal of Geometry, 66 (1–2): 55–71, doi:10.1007/BF01225672, S2CID 120174967.
- Cundy, H. M. & Parry, Cyril F. (1995), "Some cubic curves associated with a triangle", Journal of Geometry, 53 (1–2): 41–66, doi:10.1007/BF01224039, S2CID 122633134.
- Cundy, H. M. & Parry, Cyril F. (1999), "Geometrical properties of some Euler and circular cubics (part 1)", Journal of Geometry, 66 (1–2): 72–103, doi:10.1007/BF01225673, S2CID 119886462.
- Cundy, H. M. & Parry, Cyril F. (2000), "Geometrical properties of some Euler and circular cubics (part 2)", Journal of Geometry, 68 (1–2): 58–75, doi:10.1007/BF01221061, S2CID 126542269.
- Ehrmann, Jean-Pierre & Gibert, Bernard (2001), "A Morley configuration", Forum Geometricorum, 1: 51–58.
- Ehrmann, Jean-Pierre & Gibert, Bernard (2001), "The Simson cubic", Forum Geometricorum, 1: 107–114.
- Gibert, Bernard (2003), "Orthocorrespondence and orthopivotal cubics", Forum Geometricorum, 3: 1–27.
- Kimberling, Clark (1998), "Triangle Centers and Central Triangles", Congressus Numerantium, 129: 1–295. See Chapter 8 for cubics.
- Kimberling, Clark (2001), "Cubics associated with triangles of equal areas" (PDF), Forum Geometricorum, 1: 161–171.
- Lang, Fred (2002), "Geometry and group structures of some cubics", Forum Geometricorum, 2: 135–146.
- Pinkernell, Guido M. (1996), "Cubic curves in the triangle plane", Journal of Geometry, 55 (1–2): 142–161, doi:10.1007/BF01223040, S2CID 123411561.
- Salmon, George (1879), Higher Plane Curves (3rd ed.), Dublin: Hodges, Foster, and Figgis.
External links
- A Catalog of Cubic Plane Curves (archived version)
- Points on Cubics
- Cubics in the Triangle Plane
- Special Isocubics in the Triangle Plane (pdf), by Jean-Pierre Ehrmann and Bernard Gibert
- "Real and Complex Cubic Curves - John Milnor, Stony Brook University [2016]". YouTube. Graduate Mathematics. June 27, 2018. lecture on July 2016, ICMS, Edinburgh at conference in honour of Dusa McDuff's 70th birthday
https://en.wikipedia.org/wiki/Cubic_plane_curve
Classification of singularities
Singular points include multiple points where the curve crosses over itself, and also various types of cusp, for example that shown by the curve with equation x3 = y2 at (0,0).
A curve C has at most a finite number of singular points. If it has none, it can be called smooth or non-singular. Commonly, this definition is understood over an algebraically closed field and for a curve C in a projective space (i.e., complete in the sense of algebraic geometry). For example, the plane curve of equation is considered as singular, as having a singular point (a cusp) at infinity.
In the remainder of this section, one considers a plane curve C defined as the zero set of a bivariate polynomial f(x, y). Some of the results, but not all, may be generalized to non-plane curves.
The singular points are classified by means of several invariants. The multiplicity m is defined as the maximum integer such that the derivatives of f to all orders up to m – 1 vanish (also the minimal intersection number between the curve and a straight line at P). Intuitively, a singular point has delta invariant δ if it concentrates δ ordinary double points at P. To make this precise, the blow up process produces so-called infinitely near points, and summing m(m − 1)/2 over the infinitely near points, where m is their multiplicity, produces δ. For an irreducible and reduced curve and a point P we can define δ algebraically as the length of where is the local ring at P and is its integral closure.[1]
The Milnor number μ of a singularity is the degree of the mapping grad f(x,y)/|grad f(x,y)| on the small sphere of radius ε, in the sense of the topological degree of a continuous mapping, where grad f is the (complex) gradient vector field of f. It is related to δ and r by the Milnor–Jung formula,
Here, the branching number r of P is the number of locally irreducible branches at P. For example, r = 1 at an ordinary cusp, and r = 2 at an ordinary double point. The multiplicity m is at least r, and that P is singular if and only if m is at least 2. Moreover, δ is at least m(m-1)/2.
Computing the delta invariants of all of the singularities allows the genus g of the curve to be determined; if d is the degree, then
where the sum is taken over all singular points P of the complex projective plane curve. It is called the genus formula.
Assign the invariants [m, δ, r] to a singularity, where m is the multiplicity, δ is the delta-invariant, and r is the branching number. Then an ordinary cusp is a point with invariants [2,1,1] and an ordinary double point is a point with invariants [2,1,2], and an ordinary m-multiple point is a point with invariants [m, m(m − 1)/2, m].
https://en.wikipedia.org/wiki/Algebraic_curve#delta_invariant
In mathematics, elliptic curve primality testing techniques, or elliptic curve primality proving (ECPP), are among the quickest and most widely used methods in primality proving.[1] It is an idea put forward by Shafi Goldwasser and Joe Kilian in 1986 and turned into an algorithm by A. O. L. Atkin the same year. The algorithm was altered and improved by several collaborators subsequently, and notably by Atkin and François Morain, in 1993.[2] The concept of using elliptic curves in factorization had been developed by H. W. Lenstra in 1985, and the implications for its use in primality testing (and proving) followed quickly.
Primality testing is a field that has been around since the time of Fermat, in whose time most algorithms were based on factoring, which become unwieldy with large input; modern algorithms treat the problems of determining whether a number is prime and what its factors are separately. It became of practical importance with the advent of modern cryptography. Although many current tests result in a probabilistic output (N is either shown composite, or probably prime, such as with the Baillie–PSW primality test or the Miller–Rabin test), the elliptic curve test proves primality (or compositeness) with a quickly verifiable certificate.[3]
Previously-known prime-proving methods such as the Pocklington primality test required at least partial factorization of in order to prove that is prime. As a result, these methods required some luck and are generally slow in practice.
https://en.wikipedia.org/wiki/Elliptic_curve_primality
In algebraic geometry, a stable curve is an algebraic curve that is asymptotically stable in the sense of geometric invariant theory.
This is equivalent to the condition that it is a complete connected curve whose only singularities are ordinary double points and whose automorphism group is finite. The condition that the automorphism group is finite can be replaced by the condition that it is not of arithmetic genus one and every non-singular rational component meets the other components in at least 3 points (Deligne & Mumford 1969).
A semi-stable curve is one satisfying similar conditions, except that the automorphism group is allowed to be reductive rather than finite (or equivalently its connected component may be a torus). Alternatively the condition that non-singular rational components meet the other components in at least three points is replaced by the condition that they meet in at least two points.
Similarly a curve with a finite number of marked points is called stable if it is complete, connected, has only ordinary double points as singularities, and has finite automorphism group. For example, an elliptic curve (a non-singular genus 1 curve with 1 marked point) is stable.
Over the complex numbers, a connected curve is stable if and only if, after removing all singular and marked points, the universal covers of all its components are isomorphic to the unit disk.
https://en.wikipedia.org/wiki/Stable_curve
In the study of the arithmetic of elliptic curves, the j-line over a ring R is the coarse moduli scheme attached to the moduli problem sending a ring to the set of isomorphism classes of elliptic curves over . Since elliptic curves over the complex numbers are isomorphic (over an algebraic closure) if and only if their -invariants agree, the affine space parameterizing j-invariants of elliptic curves yields a coarse moduli space. However, this fails to be a fine moduli space due to the presence of elliptic curves with automorphisms, necessitating the construction of the Moduli stack of elliptic curves.
This is related to the congruence subgroup in the following way:[1]
Here the j-invariant is normalized such that has complex multiplication by , and has complex multiplication by .
The j-line can be seen as giving a coordinatization of the classical modular curve of level 1, , which is isomorphic to the complex projective line .[2]
References
- Gouvêa, Fernando Q. (2001), "Deformations of Galois representations", Arithmetic algebraic geometry (Park City, UT, 1999), IAS/Park City Math. Ser., vol. 9, Amer. Math. Soc., Providence, RI, pp. 233–406, MR 1860043. See in particular p. 378.
https://en.wikipedia.org/wiki/J-line
The age of the captain is a mathematical word problem which cannot be answered even though there seems to be plenty of information supplied. It was given for the first time by Gustave Flaubert in a letter to his sister Caroline in 1841:[1][2]
Puisque tu fais de la géométrie et de la trigonométrie, je vais te donner un problème : Un navire est en mer, il est parti de Boston chargé de coton, il jauge 200 tonneaux. Il fait voile vers le Havre, le grand mât est cassé, il y a un mousse sur le gaillard d’avant, les passagers sont au nombre de douze, le vent souffle N.-E.-E., l’horloge marque 3 heures un quart d’après-midi, on est au mois de mai…. On demande l’âge du capitaine?[1][2] |
Since you are now studying geometry and trigonometry, I will give you a problem. A ship sails the ocean. It left Boston with a cargo of wool. It grosses 200 tons. It is bound for Le Havre. The mainmast is broken, the cabin boy is on deck, there are 12 passengers aboard, the wind is blowing East-North-East, the clock points to a quarter past three in the afternoon. It is the month of May. How old is the captain?[3] |
More recently, a simpler version has been used to study how students react to word problems:
A captain owns 26 sheep and 10 goats. How old is the captain?[4]
Many children in elementary school, from different parts of the world, attempt to "solve" this nonsensical problem by giving the answer 36, obtained by adding the numbers 26 and 10.[4][5] It has been suggested that this indicates schooling and education fail to instill critical thinking in children, and do not teach them that a question may be unsolvable.[4][5] However, others have countered that in education students are taught that all questions have a solution and that giving any answer is better than leaving it blank, hence the attempt to "solve" it.[4][5]
References
- Molina, Natalia; Strohmaier, Anselm; Reiss, Kristina (November 10, 2018). ""I added the numbers, it's math!" How sense-making in "age of the captain" problems differs between a mathematics classroom and a language classroom".
https://en.wikipedia.org/wiki/Age_of_the_captain
In mathematics, an ancient solution to a differential equation is a solution that can be extrapolated backwards to all past times, without singularities. That is, it is a solution "that is defined on a time interval of the form (−∞, T)."[1]
The term was introduced by Richard Hamilton in his work on the Ricci flow.[2] It has since been applied to other geometric flows[3][4][5][6] as well as to other systems such as the Navier–Stokes equations[7][8] and heat equation.[9]
References
- Wang, Meng (2011), "Liouville theorems for the ancient solution of heat flows", Proceedings of the American Mathematical Society, 139 (10): 3491–3496, doi:10.1090/S0002-9939-2011-11170-5, MR 2813381.
https://en.wikipedia.org/wiki/Ancient_solution
Bar recursion is a generalized form of recursion developed by C. Spector in his 1962 paper.[1] It is related to bar induction in the same fashion that primitive recursion is related to ordinary induction, or transfinite recursion is related to transfinite induction.
https://en.wikipedia.org/wiki/Bar_recursion
In mathematics, a canonical map, also called a natural map, is a map or morphism between objects that arises naturally from the definition or the construction of the objects. Often, it is a map which preserves the widest amount of structure. A choice of a canonical map sometimes depends on a convention (e.g., a sign convention).
A closely related notion is a structure map or structure morphism; the map or morphism that comes with the given structure on the object. These are also sometimes called canonical maps.
A canonical isomorphism is a canonical map that is also an isomorphism (i.e., invertible). In some contexts, it might be necessary to address an issue of choices of canonical maps or canonical isomorphisms; for a typical example, see prestack.
For a discussion of the problem of defining a canonical map see Kevin Buzzard's talk at the 2022 Grothendieck conference.[1]
https://en.wikipedia.org/wiki/Canonical_map
In mathematics education, concept image and concept definition are two ways of understanding a mathematical concept.
The terms were introduced by Tall & Vinner (1981). They define a concept image as such:
- "We shall use the term concept image to describe the total cognitive structure that is associated with the concept, which includes all the mental pictures and associated properties and processes. It is built up over the years through experiences of all kinds, changing as the individual meets new stimuli and matures."[1]
A concept definition is similar to the usual notion of a definition in mathematics, with the distinction that it is personal to an individual:
- "a personal concept definition can differ from a formal concept definition, the latter being a concept definition which is accepted by the mathematical community at large."[1]
Bibliography
- Tall, David; Vinner, Shlomo (May 1981), "Concept image and concept definition in mathematics with particular reference to limits and continuity" (PDF), Educational Studies in Mathematics, 12 (2): 151–169, doi:10.1007/BF00305619, S2CID 120226918
References
- Tall & Vinner 1981, p. 152.
External links
https://en.wikipedia.org/wiki/Concept_image_and_concept_definition
The Canon Palmtronic LE-80M is an early hand-held calculator. It was manufactured by Canon inc. Unlike other models which used a processing chip manufactured by Texas Instruments the LE-80M used a Hitachi HD3553 chip.[1] When first released in 1973, it retailed for $138.45.[2]
References
- Kiplinger's Personal Finance; Vol. 27, No. 7. Kiplinger Washington Editors, Inc. 1973. p. 41. 528-9729.
https://en.wikipedia.org/wiki/Canon_Palmtronic_LE-80M
In mathematics, the continuous q-Legendre polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme.Koekoek, Lesky & Swarttouw (2010) give a detailed list of their properties.[1]
https://en.wikipedia.org/wiki/Continuous_q-Legendre_polynomials
The cut locus is a mathematical structure defined for a closed set in a space as the closure of the set of all points that have two or more distinct shortest paths in from to .
Definition in a special case
Let be a metric space, equipped with the metric , and let be a point. The cut locus of in (), is the locus of all the points in for which there exists at least two distinct shortest paths to in . More formally, for a point in if and only if there exists two paths such that , , , and the trajectories of the two paths are distinct.
Examples
For example, let S be the boundary of a simple polygon, and X the interior of the polygon. Then the cut locus is the medial axis of the polygon. The points on the medial axis are centers of maximal disks that touch the polygon boundary at two or more points, corresponding to two or more shortest paths to the disk center.
As a second example, let S be a point x on the surface of a convex polyhedron P, and X the surface itself. Then the cut locus of x is what is known as the ridge tree of P with respect to x. This ridge tree has the property that cutting the surface along its edges unfolds P to a simple planar polygon. This polygon can be viewed as a net for the polyhedron.
Example for the special case
Let , that is the regular 2-sphere. Then the cut locus of every point on the sphere consists of exactly one point, namely the antipodal one.
References
https://en.wikipedia.org/wiki/Cut_locus
Deterministic blockmodeling is an approach in blockmodeling that does not assume a probabilistic model, and instead relies on the exact or approximate algorithms, which are used to find blockmodel(s). This approach typically minimizes some inconsistency that can occur with the ideal block structure.[1] Such analysis is focused on clustering (grouping) of the network (or adjacency matrix) that is obtained with minimizing an objective function, which measures discrepancy from the ideal block structure.[2]
However, some indirect approaches (or methods between direct and indirect approaches, such as CONCOR) do not explicitly minimize inconsistencies or optimize some criterion function. [3]
This approach was popularized in the 1970s, due to the presence of two computer packages (CONCOR and STRUCTURE) that were used to "find a permutation of the rows and columns in the adjacency matrix leading to an approximate block structure".[4]
The opposite approach to deterministic blockmodeling is a stochastic blockmodeling approach.[2]
https://en.wikipedia.org/wiki/Deterministic_blockmodeling
A discontinuous group is a mathematical concept relating to mappings in topological space.
Definition
Let be a topological space of points , and let , , be an open continuous representation of the topological group as a transitive group of homeomorphic mappings of on itself. The representation of the discrete subgroup in is called discontinuous, if no sequence () converges to a point in , as runs over distinct elements of .[1]
References
- Carl Ludwig Siegel (1943), Annals of Mathematics (ed.), Discontinuous groups, vol. 44, pp. 674−689
This article needs additional or more specific categories. (January 2020) |
https://en.wikipedia.org/wiki/Discontinuous_group
In mathematics, a distinguished limit is an appropriately chosen scale factor used in the method of matched asymptotic expansions.
External links
https://en.wikipedia.org/wiki/Distinguished_limit
Early numeracy is a branch of numeracy that aims to enhance numeracy learning for younger learners, particularly those at-risk in the area of mathematics. Usually the mathematical learning begins with simply learning the first digits, 1 through 10. This is done because it acts as an entry way to the expansion of counting. One can keep track of the digits using any of the phalanges[1]
https://en.wikipedia.org/wiki/Early_numeracy
In mathematics, an eigenoperator, A, of a matrix H is a linear operator such that
where is a corresponding scalar called an eigenvalue.[1]
References
- Gardiner, Crispin (2000). Quantum Noise. Springer. p. 85.
https://en.wikipedia.org/wiki/Eigenoperator
https://en.wikipedia.org/wiki/Glossary_of_mathematics
In mathematics the Gould polynomials Gn(x; a,b) are polynomials introduced by H. W. Gould and named by Roman in 1984.[1] They are given by [2]
where
- so
References
- Gould, H. W. (1961), "A series transformation for finding convolution identities", Duke Math. J. Volume 28, Number 2, 193-202.
https://en.wikipedia.org/wiki/Gould_polynomials
In mathematical morphology, the h-maxima transform is a morphological operation used to filter local maxima of an image based on local contrast information. First, all local maxima are defined as connected pixels in a given neighborhood with intensity level greater than pixels outside the neighborhood. Second, all local maxima that have height lower or equal to a given threshold are suppressed. The height f of the remaining maxima is decreased by .
The h-maxima transform is defined as the reconstruction by dilation of from :
References
- Soille, P., "Morphological Image Analysis: Principles and Applications" (Chapter 6), 2nd edition (2003), ISBN 3540429883.
https://en.wikipedia.org/wiki/H-maxima_transform
In the mathematics of graph theory, two graphs, G and H, are called homomorphically equivalent if there exists a graph homomorphism and a graph homomorphism . An example usage of this notion is that any two cores of a graph are homomorphically equivalent.
Homomorphic equivalence also comes up in the theory of databases. Given a database schema, two instances I and J on it are called homomorphically equivalent if there exists an instance homomorphism and an instance homomorphism .
In fact for any category C, one can define homomorphic equivalence. It is used in the theory of accessible categories, where "weak universality" is the best one can hope for in terms of injectivity classes; see [1]
References
- Adamek and Rosicky, "Locally Presentable and Accessible Categories".
https://en.wikipedia.org/wiki/Homomorphic_equivalence
A latent space, also known as a latent feature space or embedding space, is an embedding of a set of items within a manifold in which items resembling each other are positioned closer to one another in the latent space. Position within the latent space can be viewed as being defined by a set of latent variables that emerge from the resemblances from the objects.
In most cases, the dimensionality of the latent space is chosen to be lower than the dimensionality of the feature space from which the data points are drawn, making the construction of a latent space an example of dimensionality reduction, which can also be viewed as a form of data compression.[1] Latent spaces are usually fit via machine learning, and they can then be used as feature spaces in machine learning models, including classifiers and other supervised predictors.
The interpretation of the latent spaces of machine learning models is an active field of study, but latent space interpretation is difficult to achieve. Due to the black-box nature of machine learning models, the latent space may be completely unintuitive. Additionally, the latent space may be high-dimensional, complex, and nonlinear, which may add to the difficulty of interpretation.[2] Some visualization techniques have been developed to connect the latent space to the visual world, but there is often not a direct connection between the latent space interpretation and the model itself. Such techniques include t-distributed stochastic neighbor embedding (t-SNE), where the latent space is mapped to two dimensions for visualization. Latent space distances lack physical units, so the interpretation of these distances may depend on the application.[3]
A number of algorithms exist to create latent space embeddings given a set of data items and a similarity function.
See also
References
- Arvanitidis, Georgios; Hansen, Lars Kai; Hauberg, Søren (13 December 2021). "Latent Space Oddity: on the Curvature of Deep Generative Models". arXiv:1710.11379 [stat.ML].
https://en.wikipedia.org/wiki/Latent_space
In mathematics, specifically in order theory and functional analysis, an element of a vector lattice is called a weak order unit in if and also for all [1]
Examples
- If is a separable Fréchet topological vector lattice then the set of weak order units is dense in the positive cone of [2]
See also
- Quasi-interior point
- Vector lattice – Partially ordered vector space, ordered as a lattice
Citations
- Schaefer & Wolff 1999, pp. 204–214.
References
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
In mathematics, a topological space is called separable if it contains a countable, dense subset; that is, there exists a sequence of elements of the space such that every nonempty open subset of the space contains at least one element of the sequence.
Like the other axioms of countability, separability is a "limitation on size", not necessarily in terms of cardinality (though, in the presence of the Hausdorff axiom, this does turn out to be the case; see below) but in a more subtle topological sense. In particular, every continuous function on a separable space whose image is a subset of a Hausdorff space is determined by its values on the countable dense subset.
Contrast separability with the related notion of second countability, which is in general stronger but equivalent on the class of metrizable spaces.
https://en.wikipedia.org/wiki/Separable_space
In mathematics, specifically in order theory and functional analysis, an element of an ordered topological vector space is called a quasi-interior point of the positive cone of if and if the order interval is a total subset of ; that is, if the linear span of is a dense subset of [1]
Properties
If is a separable metrizable locally convex ordered topological vector space whose positive cone is a complete and total subset of then the set of quasi-interior points of is dense in [1]
Examples
If then a point in is quasi-interior to the positive cone if and only it is a weak order unit, which happens if and only if the element (which recall is an equivalence class of functions) contains a function that is almost everywhere (with respect to ).[1]
A point in is quasi-interior to the positive cone if and only if it is interior to [1]
See also
- Weak order unit
- Vector lattice – Partially ordered vector space, ordered as a lattice
References
- Schaefer & Wolff 1999, pp. 234–242.
Bibliography
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
https://en.wikipedia.org/wiki/Quasi-interior_point
In functional analysis, a state of an operator system is a positive linear functional of norm 1. States in functional analysis generalize the notion of density matrices in quantum mechanics, which represent quantum states, both §§ Mixed states and pure states. Density matrices in turn generalize state vectors, which only represent pure states. For M an operator system in a C*-algebra A with identity, the set of all states of M, sometimes denoted by S(M), is convex, weak-* closed in the Banach dual space M*. Thus the set of all states of M with the weak-* topology forms a compact Hausdorff space, known as the state space of M .
In the C*-algebraic formulation of quantum mechanics, states in this previous sense correspond to physical states, i.e. mappings from physical observables (self-adjoint elements of the C*-algebra) to their expected measurement outcome (real number).
https://en.wikipedia.org/wiki/State_(functional_analysis)
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity.[1] The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire probability space.
Intuitively, the additivity property says that the probability assigned to the union of two disjoint events by the measure should be the sum of the probabilities of the events; for example, the value assigned to "1 or 2" in a throw of a dice should be the sum of the values assigned to "1" and "2".
Probability measures have applications in diverse fields, from physics to finance and biology.
https://en.wikipedia.org/wiki/Probability_measure
In functional analysis, a discipline within mathematics, given a C*-algebra A, the Gelfand–Naimark–Segal construction establishes a correspondence between cyclic *-representations of A and certain linear functionals on A (called states). The correspondence is shown by an explicit construction of the *-representation from the state. It is named for Israel Gelfand, Mark Naimark, and Irving Segal.
States and representations
A *-representation of a C*-algebra A on a Hilbert space H is a mapping π from A into the algebra of bounded operators on H such that
- π is a ring homomorphism which carries involution on A into involution on operators
- π is nondegenerate, that is the space of vectors π(x) ξ is dense as x ranges through A and ξ ranges through H. Note that if A has an identity, nondegeneracy means exactly π is unit-preserving, i.e. π maps the identity of A to the identity operator on H.
A state on a C*-algebra A is a positive linear functional f of norm 1. If A has a multiplicative unit element this condition is equivalent to f(1) = 1.
For a representation π of a C*-algebra A on a Hilbert space H, an element ξ is called a cyclic vector if the set of vectors
is norm dense in H, in which case π is called a cyclic representation. Any non-zero vector of an irreducible representation is cyclic. However, non-zero vectors in a general cyclic representation may fail to be cyclic.
The GNS construction
Let π be a *-representation of a C*-algebra A on the Hilbert space H and ξ be a unit norm cyclic vector for π. Then
is a state of A.
Conversely, every state of A may be viewed as a vector state as above, under a suitable canonical representation.
- Theorem.[1] Given a state ρ of A, there is a *-representation π of A acting on a Hilbert space H with distinguished unit cyclic vector ξ such that for every a in A.
- Proof.
- 1) Construction of the Hilbert space H
- Define on A a semi-definite sesquilinear form
- By the Cauchy–Schwarz inequality, the degenerate elements, a in A satisfying ρ(a* a)= 0, form a vector subspace I of A. By a C*-algebraic argument, one can show that I is a left ideal of A (known as the left kernel of ρ). In fact, it is the largest left ideal in the null space of ρ. The quotient space of A by the vector subspace I is an inner product space with the inner product defined by. The Cauchy completion of A/I in the norm induced by this inner product is a Hilbert space, which we denote by H.
- 2) Construction of the representation π
- Define the action π of A on A/I by π(a)(b+I) = ab+I of A on A/I. The same argument showing I is a left ideal also implies that π(a) is a bounded operator on A/I and therefore can be extended uniquely to the completion. Unravelling the definition of the adjoint of an operator on a Hilbert space, π turns out to be *-preserving. This proves the existence of a *-representation π.
- 3) Identifying the unit norm cyclic vector ξ
- If A has a multiplicative identity 1, then it is immediate that the equivalence class ξ in the GNS Hilbert space H containing 1 is a cyclic vector for the above representation. If A is non-unital, take an approximate identity {eλ} for A. Since positive linear functionals are bounded, the equivalence classes of the net {eλ} converges to some vector ξ in H, which is a cyclic vector for π.
- It is clear from the definition of the inner product on the GNS Hilbert space H that the state ρ can be recovered as a vector state on H. This proves the theorem.
The method used to produce a *-representation from a state of A in the proof of the above theorem is called the GNS construction. For a state of a C*-algebra A, the corresponding GNS representation is essentially uniquely determined by the condition, as seen in the theorem below.
- Theorem.[2] Given a state ρ of A, let π, π' be *-representations of A on Hilbert spaces H, H' respectively each with unit norm cyclic vectors ξ ∈ H, ξ' ∈ H' such that for all . Then π, π' are unitarily equivalent *-representations i.e. there is a unitary operator U from H to H' such that π'(a) = Uπ(a)U* for all a in A. The operator U that implements the unitary equivalence maps π(a)ξ to π'(a)ξ' for all a in A.
Significance of the GNS construction
The GNS construction is at the heart of the proof of the Gelfand–Naimark theorem characterizing C*-algebras as algebras of operators. A C*-algebra has sufficiently many pure states (see below) so that the direct sum of corresponding irreducible GNS representations is faithful.
The direct sum of the corresponding GNS representations of all states is called the universal representation of A. The universal representation of A contains every cyclic representation. As every *-representation is a direct sum of cyclic representations, it follows that every *-representation of A is a direct summand of some sum of copies of the universal representation.
If Φ is the universal representation of a C*-algebra A, the closure of Φ(A) in the weak operator topology is called the enveloping von Neumann algebra of A. It can be identified with the double dual A**.
Irreducibility
Also of significance is the relation between irreducible *-representations and extreme points of the convex set of states. A representation π on H is irreducible if and only if there are no closed subspaces of H which are invariant under all the operators π(x) other than H itself and the trivial subspace {0}.
- Theorem. The set of states of a C*-algebra A with a unit element is a compact convex set under the weak-* topology. In general, (regardless of whether or not A has a unit element) the set of positive functionals of norm ≤ 1 is a compact convex set.
Both of these results follow immediately from the Banach–Alaoglu theorem.
In the unital commutative case, for the C*-algebra C(X) of continuous functions on some compact X, Riesz–Markov–Kakutani representation theorem says that the positive functionals of norm ≤ 1 are precisely the Borel positive measures on X with total mass ≤ 1. It follows from Krein–Milman theorem that the extremal states are the Dirac point-mass measures.
On the other hand, a representation of C(X) is irreducible if and only if it is one-dimensional. Therefore, the GNS representation of C(X) corresponding to a measure μ is irreducible if and only if μ is an extremal state. This is in fact true for C*-algebras in general.
- Theorem. Let A be a C*-algebra. If π is a *-representation of A on the Hilbert space H with unit norm cyclic vector ξ, then π is irreducible if and only if the corresponding state f is an extreme point of the convex set of positive linear functionals on A of norm ≤ 1.
To prove this result one notes first that a representation is irreducible if and only if the commutant of π(A), denoted by π(A)', consists of scalar multiples of the identity.
Any positive linear functionals g on A dominated by f is of the form
for some positive operator Tg in π(A)' with 0 ≤ T ≤ 1 in the operator order. This is a version of the Radon–Nikodym theorem.
For such g, one can write f as a sum of positive linear functionals: f = g + g' . So π is unitarily equivalent to a subrepresentation of πg ⊕ πg' . This shows that π is irreducible if and only if any such πg is unitarily equivalent to π, i.e. g is a scalar multiple of f, which proves the theorem.
Extremal states are usually called pure states. Note that a state is a pure state if and only if it is extremal in the convex set of states.
The theorems above for C*-algebras are valid more generally in the context of B*-algebras with approximate identity.
Generalizations
The Stinespring factorization theorem characterizing completely positive maps is an important generalization of the GNS construction.
History
Gelfand and Naimark's paper on the Gelfand–Naimark theorem was published in 1943.[3] Segal recognized the construction that was implicit in this work and presented it in sharpened form.[4]
In his paper of 1947 Segal showed that it is sufficient, for any physical system that can be described by an algebra of operators on a Hilbert space, to consider the irreducible representations of a C*-algebra. In quantum theory this means that the C*-algebra is generated by the observables. This, as Segal pointed out, had been shown earlier by John von Neumann only for the specific case of the non-relativistic Schrödinger-Heisenberg theory.[5]
See also
References
- William Arveson, An Invitation to C*-Algebra, Springer-Verlag, 1981
- Kadison, Richard, Fundamentals of the Theory of Operator Algebras, Vol. I : Elementary Theory, American Mathematical Society. ISBN 978-0821808191.
- Jacques Dixmier, Les C*-algèbres et leurs Représentations, Gauthier-Villars, 1969.
English translation: Dixmier, Jacques (1982). C*-algebras. North-Holland. ISBN 0-444-86391-5. - Thomas Timmermann, An invitation to quantum groups and duality: from Hopf algebras to multiplicative unitaries and beyond, European Mathematical Society, 2008, ISBN 978-3-03719-043-2 – Appendix 12.1, section: GNS construction (p. 371)
- Stefan Waldmann: On the representation theory of deformation quantization, In: Deformation Quantization: Proceedings of the Meeting of Theoretical Physicists and Mathematicians, Strasbourg, May 31-June 2, 2001 (Studies in Generative Grammar) , Gruyter, 2002, ISBN 978-3-11-017247-8, p. 107–134 – section 4. The GNS construction (p. 113)
- G. Giachetta, L. Mangiarotti, G. Sardanashvily (2005). Geometric and Algebraic Topological Methods in Quantum Mechanics. World Scientific. ISBN 981-256-129-3.
- Inline references
- I. E. Segal (1947). "Irreducible representations of operator algebras" (PDF). Bull. Am. Math. Soc. 53 (2): 73–88. doi:10.1090/s0002-9904-1947-08742-5.
https://en.wikipedia.org/wiki/Gelfand%E2%80%93Naimark%E2%80%93Segal_construction
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using the Born rule. It is a generalization of the more usual state vectors or wavefunctions: while those can only represent pure states, density matrices can also represent mixed states. Mixed states arise in quantum mechanics in two different situations:
- when the preparation of the system is not fully known, and thus one must deal with a statistical ensemble of possible preparations, and
- when one wants to describe a physical system which is entangled with another, without describing their combined state.
Density matrices are thus crucial tools in areas of quantum mechanics that deal with mixed states, such as quantum statistical mechanics, open quantum systems, quantum decoherence, and quantum information.
https://en.wikipedia.org/wiki/Density_matrix
In mathematics, specifically in order theory and functional analysis, a band in a vector lattice is a subspace of that is solid and such that for all such that exists in we have [1] The smallest band containing a subset of is called the band generated by in [1] A band generated by a singleton set is called a principal band.
https://en.wikipedia.org/wiki/Band_(order_theory)
In mathematics, the Freudenthal spectral theorem is a result in Riesz space theory proved by Hans Freudenthal in 1936. It roughly states that any element dominated by a positive element in a Riesz space with the principal projection property can in a sense be approximated uniformly by simple functions.
Numerous well-known results may be derived from the Freudenthal spectral theorem. The well-known Radon–Nikodym theorem, the validity of the Poisson formula and the spectral theorem from the theory of normal operators can all be shown to follow as special cases of the Freudenthal spectral theorem.
https://en.wikipedia.org/wiki/Freudenthal_spectral_theorem
In mathematics, specifically in order theory and functional analysis, a subset of a vector lattice is said to be solid and is called an ideal if for all and if then An ordered vector space whose order is Archimedean is said to be Archimedean ordered.[1] If then the ideal generated by is the smallest ideal in containing An ideal generated by a singleton set is called a principal ideal in
https://en.wikipedia.org/wiki/Solid_set
In mathematics, specifically in order theory and functional analysis, an abstract m-space or an AM-space is a Banach lattice whose norm satisfies for all x and y in the positive cone of X.
We say that an AM-space X is an AM-space with unit if in addition there exists some u ≥ 0 in X such that the interval [−u, u] := { z ∈ X : −u ≤ z and z ≤ u } is equal to the unit ball of X; such an element u is unique and an order unit of X.[1]
https://en.wikipedia.org/wiki/Abstract_m-space
https://en.wikipedia.org/wiki/Quasi-interior_point
In operations research, the makespan of a project is the length of time that elapses from the start of work to the end. This type of multi-mode resource constrained project scheduling problem (MRCPSP) seeks to create the shortest logical project schedule, by efficiently using project resources, adding the lowest number of additional resources as possible to achieve the minimum makespan.[1] The term commonly appears in the context of scheduling.
https://en.wikipedia.org/wiki/Makespan
A mathematical instrument is a tool or device used in the study or practice of mathematics. In geometry, construction of various proofs was done using only a compass and straightedge; arguments in these proofs relied only on idealized properties of these instruments and literal construction was regarded as only an approximation. In applied mathematics, mathematical instruments were used for measuring angles and distances, in astronomy, navigation, surveying and in the measurement of time.[1]
https://en.wikipedia.org/wiki/Mathematical_instrument
In mathematics, a property is any characteristic that applies to a given set.[1] Rigorously, a property p defined for all elements of a set X is usually defined as a function p: X → {true, false}, that is true whenever the property holds; or equivalently, as the subset of X for which p holds; i.e. the set {x | p(x) = true}; p is its indicator function. However, it may be objected that the rigorous definition defines merely the extension of a property, and says nothing about what causes the property to hold for exactly those values.
Examples
Of objects
Of operations
- associative property
- commutative property of binary operations between real and complex numbers
- distributive property.
See also
References
- "Introduction to Sets". www.mathsisfun.com. Retrieved October 15, 2018.
https://en.wikipedia.org/wiki/Property_(mathematics)
In mathematics education, a procept is an amalgam of three components: a "process" which produces a mathematical "object" and a "symbol" which is used to represent either process or object. It derives from the work of Eddie Gray and David O. Tall.
The notion was first published in a paper in the Journal for Research in Mathematics Education in 1994, and is part of the process-object literature. This body of literature suggests that mathematical objects are formed by encapsulating processes, that is to say that the mathematical object 3 is formed by an encapsulation of the process of counting: 1,2,3...
Gray and Tall's notion of procept improved upon the existing literature by noting that mathematical notation is often ambiguous as to whether it refers to process or object. Examples of such notations are:
- : refers to the process of adding as well as the outcome of the process.
- : refers to the process of summing an infinite sequence, and to the outcome of the process.
- : refers to the process of mapping x to 3x+2 as well as the outcome of that process, the function .
References
- Gray, E. & Tall, D. (1994) "Duality, Ambiguity, and Flexibility: A "Proceptual" View of Simple Arithmetic", Journal for Research in Mathematics Education 25(2) p.116-40. Available Online as PDF
External links
https://en.wikipedia.org/wiki/Procept
In the history of mathematics, the principle of permanence, or law of the permanence of equivalent forms, was the idea that algebraic operations like addition and multiplication should behave consistently in every number system, especially when developing extensions to established number systems.[1][2]
Before the advent of modern mathematics and its emphasis on the axiomatic method, the principle of permanence was considered an important tool in mathematical arguments. In modern mathematics, arguments have instead been supplanted by rigorous proofs built upon axioms, and the principle is instead used as a heuristic for discovering new algebraic structures.[3] Additionally, the principle has been formalized into a class of theorems called transfer principles,[3] which state that all statements of some language that are true for some structure are true for another structure.
History
The principle was described by George Peacock in his book A Treatise of Algebra (emphasis in original):[4][page needed]
132. Let us again recur to this principle or law of the permanence of equivalent forms, and consider it when stated in the form of a direct and converse proportion.
"Whatever form is Algebraically equivalent to another, when expressed in general symbols, must be true, whatever those symbols denote."
Conversely, if we discover an equivalent form in Arithmetical Algebra or any other subordinate science, when the symbols are general in form though specific in their nature, the same must be an equivalent form, when the symbols are general in their nature as well as in their form.
The principle was later revised by Hermann Hankel[5][6] and adopted by Giuseppe Peano, Ernst Mach, Hermann Schubert, Alfred Pringsheim, and others.[7]
Around the same time period as A Treatise of Algebra, Augustin-Louis Cauchy published Cours d'Analyse, which used the term "generality of algebra"[8][page needed] to describe (and criticize) a method of argument used by 18th century mathematicians like Euler and Lagrange that was similar to the Principle of Permanence.
Applications
One of the main uses of the principle of permanence is to show that a functional equation that holds for the real numbers also holds for the complex numbers.[9]
As an example, the equation hold for all real numbers s, t. By the principle of permanence for functions of two variables, this suggests that it holds for all complex numbers as well.[10][example needed]
References
- Gamelin, T. Complex Analysis, UTM Series, Springer-Verlag, 2001c
| Basic concepts | |
|---|---|
| Types of orders/spaces | |
| Types of elements/subsets | |
| Topologies/Convergence | |
| Operators | |
| Main results | |
https://en.wikipedia.org/wiki/Principle_of_permanence
In mathematical invariant theory, a perpetuant is informally an irreducible covariant of a form or infinite degree. More precisely, the dimension of the space of irreducible covariants of given degree and weight for a binary form stabilizes provided the degree of the form is larger than the weight of the covariant, and the elements of this space are called perpetuants. Perpetuants were introduced and named by Sylvester (1882, p.105). MacMahon (1884, 1885, 1894) and Stroh (1890) classified the perpetuants. Elliott (1907) describes the early history of perpetuants and gives an annotated bibliography.
MacMahon conjectured and Stroh proved that the dimension of the space of perpetuants of degree n>2 and weight w is the coefficient of xw of
For n=1 there is just one perpetuant, of weight 0, and for n=2 the number is given by the coefficient of xw of x2/(1-x2).
There are very few papers after about 1910 discussing perpetuants; (Littlewood 1944) is one of the few exceptions. (Kraft & Procesi 2020) exhibited an explicit base of the space of perpetuants.
References
- Cayley, Arthur (1884), "A Memoir on Seminvariants", American Journal of Mathematics, The Johns Hopkins University Press, 7 (1): 1–25, doi:10.2307/2369456, ISSN 0002-9327, JSTOR 2369456
- Elliott, Edwin Bailey (1895), "An introduction to the algebra of quantics", Nature, Oxford, Clarendon Press, 53 (1364): 147–148, Bibcode:1895Natur..53..147G, doi:10.1038/053147a0, S2CID 4036717, Reprinted by Chelsea Scientific Books 1964
- Elliott, Edwin Bailey (1907), "On Perpetuants and Contra-Perpetuants", Proc. London Math. Soc., 4 (1): 228–246, doi:10.1112/plms/s2-4.1.228
- Grace, J. H.; Young, Alfred (1903), The algebra of invariants, Cambridge University Press
- Kraft, Hanspeter; Procesi, Claudio (2020-03-11). "Perpetuants: A Lost Treasure". International Mathematics Research Notices. 2021 (5): 3597–3632. arXiv:1810.01131. doi:10.1093/imrn/rnaa032. ISSN 1073-7928.
- Littlewood, D. E. (1944), "Invariant theory, tensors and group characters", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 239 (807): 305–365, Bibcode:1944RSPTA.239..305L, doi:10.1098/rsta.1944.0001, ISSN 0080-4614, JSTOR 91389, MR 0010594
- MacMahon, P. A. (1884), "On Perpetuants", American Journal of Mathematics, The Johns Hopkins University Press, 7 (1): 26–46, doi:10.2307/2369457, ISSN 0002-9327, JSTOR 2369457
- MacMahon, P. A. (1885), "A Second Paper on Perpetuants", American Journal of Mathematics, The Johns Hopkins University Press, 7 (3): 259–263, doi:10.2307/2369271, ISSN 0002-9327, JSTOR 2369271
- MacMahon, P. A. (1894), "The Perpetuant Invariants of Binary Quantics", Proc. London Math. Soc., 26 (1): 262–284, doi:10.1112/plms/s1-26.1.262
- Stroh, E. (1888), "Ueber eine fundamentale Eigenschaft des Ueberschiebungs-processes und deren Verwerthung in der Theorie der binären Formen", Mathematische Annalen, Springer Berlin / Heidelberg, 33: 61–107, doi:10.1007/bf01444111, ISSN 0025-5831, S2CID 121256190
- Stroh, E. (1890), "Ueber die symbolische Darstellung der Grundsyzyganten einer binären Form sechster Ordnung und eine Erweiterung der Symbolik von Clebsch", Mathematische Annalen, Springer Berlin / Heidelberg, 36 (2): 262–303, doi:10.1007/BF01207843, S2CID 121641107
- Sylvester, James Joseph (1882), "On Subvariants, i.e. Semi-Invariants to Binary Quantics of an Unlimited Order", American Journal of Mathematics, The Johns Hopkins University Press, 5 (1): 79–136, doi:10.2307/2369536, ISSN 0002-9327, JSTOR 2369536
https://en.wikipedia.org/wiki/Perpetuant
In mathematics, for example in the study of statistical properties of graphs, a null model is a type of random object that matches one specific object in some of its features, or more generally satisfies a collection of constraints, but which is otherwise taken to be an unbiasedly random structure. The null model is used as a term of comparison, to verify whether the object in question displays some non-trivial features (properties that wouldn't be expected on the basis of chance alone or as a consequence of the constraints), such as community structure in graphs. An appropriate null model behaves in accordance with a reasonable null hypothesis for the behavior of the system under investigation.
One null model of utility in the study of complex networks is that proposed by Newman and Girvan, consisting of a randomized version of an original graph , produced through edges being rewired at random, under the constraint that the expected degree of each vertex matches the degree of the vertex in the original graph.[1]
The null model is the basic concept behind the definition of modularity, a function which evaluates the goodness of partitions of a graph into clusters. In particular, given a graph and a specific community partition (an assignment of a community-index (here taken as an integer from to ) to each vertex in the graph), the modularity measures the difference between the number of links from/to each pair of communities, from that expected in a graph that is completely random in all respects other than the set of degrees of each of the vertices (the degree sequence). In other words, the modularity contrasts the exhibited community structure in with that of a null model, which in this case is the configuration model (the maximally random graph subject to a constraint on the degree of each vertex).
See also
References
- M.E.J, Newman; M.Girvan (2004). "Finding and evaluating community structure in networks". Phys. Rev. E. 69 (2): 026113. arXiv:cond-mat/0308217. Bibcode:2004PhRvE..69b6113N. doi:10.1103/physreve.69.026113. PMID 14995526.
https://en.wikipedia.org/wiki/Null_model
In mathematics, the word null (from German: null[citation needed] meaning "zero", which is from Latin: nullus meaning "none") is often associated with the concept of zero or the concept of nothing.[1][2] It is used in varying context from "having zero members in a set" (e.g., null set)[3] to "having a value of zero" (e.g., null vector).[4]
In a vector space, the null vector is the neutral element of vector addition; depending on the context, a null vector may also be a vector mapped to some null by a function under consideration (such as a quadratic form coming with the vector space, see null vector, a linear mapping given as matrix product or dot product,[4] a seminorm in a Minkowski space, etc.). In set theory, the empty set, that is, the set with zero elements, denoted "{}" or "∅", may also be called null set.[3][5] In measure theory, a null set is a (possibly nonempty) set with zero measure.
A null space of a mapping is the part of the domain that is mapped into the null element of the image (the inverse image of the null element). For example, in linear algebra, the null space of a linear mapping, also known as kernel, is the set of vectors which map to the null vector under that mapping.
In statistics, a null hypothesis is a proposition that no effect or relationship exists between populations and phenomena. It is the hypothesis which is presumed true—unless statistical evidence indicates otherwise.[6]
See also
References
- Helmenstine, Anne Marie. "What Is the Null Hypothesis? Definition and Examples". ThoughtCo. Retrieved 2019-12-09.
https://en.wikipedia.org/wiki/Null_(mathematics)
In mathematics, the normal form of a dynamical system is a simplified form that can be useful in determining the system's behavior.
Normal forms are often used for determining local bifurcations in a system. All systems exhibiting a certain type of bifurcation are locally (around the equilibrium) topologically equivalent to the normal form of the bifurcation. For example, the normal form of a saddle-node bifurcation is
where is the bifurcation parameter. The transcritical bifurcation
near can be converted to the normal form
with the transformation .[1]
See also canonical form for use of the terms canonical form, normal form, or standard form more generally in mathematics.
References
- Strogatz, Steven. "Nonlinear Dynamics and Chaos". Westview Press, 2001. p. 52.
Further reading
- Guckenheimer, John; Holmes, Philip (1983), Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, Section 3.3, ISBN 0-387-90819-6
- Kuznetsov, Yuri A. (1998), Elements of Applied Bifurcation Theory (Second ed.), Springer, Section 2.4, ISBN 0-387-98382-1
- Murdock, James (2006). "Normal forms". Scholarpedia. 1 (10): 1902. Bibcode:2006SchpJ...1.1902M. doi:10.4249/scholarpedia.1902.
- Murdock, James (2003). Normal Forms and Unfoldings for Local Dynamical Systems. Springer. ISBN 978-0-387-21785-7.
https://en.wikipedia.org/wiki/Normal_form_(dynamical_systems)

In mathematics and physics, a non-perturbative function or process is one that cannot be described by perturbation theory. An example is the function
which does not have a Taylor series at x = 0. Every coefficient of the Taylor expansion around x = 0 is exactly zero, but the function is non-zero if x ≠ 0.
In physics, such functions arise for phenomena which are impossible to understand by perturbation theory, at any finite order. In quantum field theory, 't Hooft–Polyakov monopoles, domain walls, flux tubes, and instantons are examples.[1] A concrete, physical example is given by the Schwinger effect,[2] whereby a strong electric field may spontaneously decay into electron-positron pairs. For not too strong fields, the rate per unit volume of this process is given by,
which cannot be expanded in a Taylor series in the electric charge , or the electric field strength . Here is the mass of an electron and we have used units where .
In theoretical physics, a non-perturbative solution is one that cannot be described in terms of perturbations about some simple background, such as empty space. For this reason, non-perturbative solutions and theories yield insights into areas and subjects that perturbative methods cannot reveal.
See also
References
- Schwinger, Julian (1951-06-01). "On Gauge Invariance and Vacuum Polarization". Physical Review. American Physical Society (APS). 82 (5): 664–679. doi:10.1103/physrev.82.664. ISSN 0031-899X.
https://en.wikipedia.org/wiki/Non-perturbative
A network automaton (plural network automata) is a mathematical system consisting of a network of nodes that evolves over time according to predetermined rules. It is similar in concept to a cellular automaton, but much less studied.
Stephen Wolfram's book A New Kind of Science, which is primarily concerned with cellular automata, briefly discusses network automata, and suggests (without positive evidence) that the universe might at the very lowest level be a network automaton.
https://en.wikipedia.org/wiki/Network_automaton
In size theory, the natural pseudodistance between two size pairs , is the value , where varies in the set of all homeomorphisms from the manifold to the manifold and is the supremum norm. If and are not homeomorphic, then the natural pseudodistance is defined to be . It is usually assumed that , are closed manifolds and the measuring functions are . Put another way, the natural pseudodistance measures the infimum of the change of the measuring function induced by the homeomorphisms from to .
The concept of natural pseudodistance can be easily extended to size pairs where the measuring function takes values in .[1] When , the group of all homeomorphisms of can be replaced in the definition of natural pseudodistance by a subgroup of , so obtaining the concept of natural pseudodistance with respect to the group .[2][3] Lower bounds and approximations of the natural pseudodistance with respect to the group can be obtained both by means of -invariant persistent homology[4] and by combining classical persistent homology with the use of G-equivariant non-expansive operators.[2][3]
Main properties
It can be proved [5] that the natural pseudodistance always equals the Euclidean distance between two critical values of the measuring functions (possibly, of the same measuring function) divided by a suitable positive integer . If and are surfaces, the number can be assumed to be , or .[6] If and are curves, the number can be assumed to be or .[7] If an optimal homeomorphism exists (i.e., ), then can be assumed to be .[5] The research concerning optimal homeomorphisms is still at its very beginning .[8][9]
See also
References
- Alessandro De Gregorio, On the set of optimal homeomorphisms for the natural pseudo-distance associated with the Lie group , Topology and its Applications, 229:187-195, 2017.
https://en.wikipedia.org/wiki/Natural_pseudodistance
The Moschovakis coding lemma is a lemma from descriptive set theory involving sets of real numbers under the axiom of determinacy (the principle — incompatible with choice — that every two-player integer game is determined). The lemma was developed and named after the mathematician Yiannis N. Moschovakis.
The lemma may be expressed generally as follows:
- Let Γ be a non-selfdual pointclass closed under real quantification and ∧, and ≺ a Γ-well-founded relation on ωω of rank θ ∈ ON. Let R ⊆ dom(≺) × ωω be such that (∀x∈dom(≺))(∃y)(x R y). Then there is a Γ-set A ⊆ dom(≺) × ωω which is a choice set for R , that is:
- (∀α<θ)(∃x∈dom(≺),y)(|x|≺=α ∧ x A y).
- (∀x,y)(x A y → x R y).
A proof runs as follows: suppose for contradiction θ is a minimal counterexample, and fix ≺, R, and a good universal set U ⊆ (ωω)3 for the Γ-subsets of (ωω)2. Easily, θ must be a limit ordinal.[1] For δ < θ, we say u ∈ ωω codes a δ-choice set provided the property (1) holds for α ≤ δ using A = U u and property (2) holds for A = U u where we replace x ∈ dom(≺) with x ∈ dom(≺) ∧ |x| ≺ [≤δ]. By minimality of θ, for all δ < θ, there are δ-choice sets.
Now, play a game where players I, II select points u,v ∈ ωω and II wins when u coding a δ1-choice set for some δ1 < θ implies v codes a δ2-choice set for some δ2 > δ1. A winning strategy for I defines a Σ1
1 set B of reals encoding δ-choice sets for arbitrarily large δ < θ. Define then
- x A y ↔ (∃w∈B)U(w,x,y),
which easily works. On the other hand, suppose τ is a winning strategy for II. From the s-m-n theorem, let s:(ωω)2 → ωω be continuous such that for all ϵ, x, t, and w,
- U(s(ϵ,x),t,w) ↔ (∃y,z)(y ≺ x ∧ U(ϵ,y,z) ∧ U(z,t,w)).
By the recursion theorem, there exists ϵ0 such that U(ϵ0,x,z) ↔ z = τ(s(ϵ0,x)). A straightforward induction on |x|≺ for x ∈ dom(≺) shows that
- (∀x∈dom(≺))(∃!z)U(ϵ0,x,z),
and
- (∀x∈dom(≺),z)(U(ϵ0,x,z) → z encodes a choice set of ordinal ≥|x|≺).
So let
References
{{cite web}}: |last1= has generic name (help)
- Moschovakis, Yiannis (October 4, 2006). "Ordinal games and playful models". In Alexander S. Kechris; Donald A. Martin; Yiannis N. Moschovakis (eds.). Cabal Seminar 77 – 79: Proceedings, Caltech-UCLA Logic Seminar 1977 – 79. Lecture Notes in Mathematics. Vol. 839. Berlin: Springer. pp. 169–201. doi:10.1007/BFb0090241. ISBN 978-3-540-38422-9.
https://en.wikipedia.org/wiki/Moschovakis_coding_lemma
In control theory, given any transfer function, any state-space model that is both controllable and observable and has the same input-output behaviour as the transfer function is said to be a minimal realization of the transfer function.[1][2] The realization is called "minimal" because it describes the system with the minimum number of states.[2]
The minimum number of state variables required to describe a system equals the order of the differential equation;[3] more state variables than the minimum can be defined. For example, a second order system can be defined by two or more state variables, with two being the minimal realization.
Gilbert's realization
Given a matrix transfer function, it is possible to directly construct a minimal state-space realization by using Gilbert's method (also known as Gilbert's realization).[4]
References
- Mackenroth, Uwe. (17 April 2013). Robust control systems : theory and case studies. Berlin. pp. 114–116. ISBN 978-3-662-09775-5. OCLC 861706617.
https://en.wikipedia.org/wiki/Minimal_realization
In statistics, the terms "mathematical elimination" and "mathematically eliminated" mean to be excluded in a decision, based on numerical counts, due to insufficient total numbers, even if all remaining events were 100% in favor. The excluded outcome is considered to be eliminated due to the mathematical probability being zero (0%).
The term is used in elections when a candidate lacks sufficient votes to win, even if that candidate could garner all remaining votes. In sports, the term "mathematically eliminated" [1] refers to situations where there are not enough future games or competitive events remaining to be played to avoid defeat, even if all future events were won.
History
The term "mathematically eliminated" has been in use for more than 100 years,[2] although the meaning has varied. In a 1904 article, in the American Journal of Psychology, Volume XV, errors of measurement were described as quantifiable to be "mathematically eliminated" from the analysis of the remaining data.[2]
References
- "General Intelligence", Chapter 3, American Journal of Psychology, Volume XV, No. 1, January 1904, p. 226, webpage: Book-Google-AAJ.
https://en.wikipedia.org/wiki/Mathematical_elimination
In mathematics, a univariate object is an expression, equation, function or polynomial involving only one variable. Objects involving more than one variable are multivariate. In some cases the distinction between the univariate and multivariate cases is fundamental; for example, the fundamental theorem of algebra and Euclid's algorithm for polynomials are fundamental properties of univariate polynomials that cannot be generalized to multivariate polynomials.
In statistics, a univariate distribution characterizes one variable, although it can be applied in other ways as well. For example, univariate data are composed of a single scalar component. In time series analysis, the whole time series is the "variable": a univariate time series is the series of values over time of a single quantity. Correspondingly, a "multivariate time series" characterizes the changing values over time of several quantities. In some cases, the terminology is ambiguous, since the values within a univariate time series may be treated using certain types of multivariate statistical analyses and may be represented using multivariate distributions.
In addition to the question of scaling, a criterion (variable) in univariate statistics can be described by two important measures (also key figures or parameters): Location & Variation.[1]
- Measures of Location Scales (e.g. mode, median, arithmetic mean) describe in which area the data is arranged centrally.
- Measures of Variation (e.g. span, interquartile distance, standard deviation) describe how similar or different the data are scattered.
See also
- Arity
- Bivariate (disambiguation)
- Multivariate (disambiguation)
- Univariate analysis
- Univariate binary model
- Univariate distribution
References
- Grünwald, Robert. "Univariate Statistik in SPSS". novustat.com (in German). Retrieved 29 October 2019.
https://en.wikipedia.org/wiki/Univariate
A unary function is a function that takes one argument. A unary operator belongs to a subset of unary functions, in that its range coincides with its domain. In contrast, a unary function's domain may or may not coincide with its range.
Examples
The successor function, denoted , is a unary operator. Its domain and codomain are the natural numbers, its definition is as follows:
In many programming languages such as C, executing this operation is denoted by postfixing to the operand, i.e. the use of is equivalent to executing the assignment .
Many of the elementary functions are unary functions, including the trigonometric functions, logarithm with a specified base, exponentiation to a particular power or base, and hyperbolic functions.
See also
References
https://en.wikipedia.org/wiki/Unary_function
In statistics and computational geometry, the Tukey depth [1] is a measure of the depth of a point in a fixed set of points. The concept is named after its inventor, John Tukey. Given a set of n points in d-dimensional space, Tukey's depth of a point x is the smallest fraction (or number) of points in any closed halfspace that contains x.
Tukey's depth measures how extreme a point is with respect to a point cloud. It is used to define the bagplot, a bivariate generalization of the boxplot.
For example, for any extreme point of the convex hull there is always a (closed) halfspace that contains only that point, and hence its Tukey depth as a fraction is 1/n.
https://en.wikipedia.org/wiki/Tukey_depth
In mathematics and physics, a traveling plane wave is a special case of plane wave, namely a field whose evolution in time can be described as simple translation of its values at a constant wave speed , along a fixed direction of propagation .
Such a field can be written as
where is a function of a single real parameter . The function describes the profile of the wave, namely the value of the field at time , for each displacement . For each displacement , the moving plane perpendicular to at distance from the origin is called a wavefront. This plane too travels along the direction of propagation with velocity ; and the value of the field is then the same, and constant in time, at every one of its points.
The wave may be a scalar or vector field; its values are the values of .
A sinusoidal plane wave is a special case, when is a sinusoidal function of .
Properties
A traveling plane wave can be studied by ignoring the dimensions of space perpendicular to the vector ; that is, by considering the wave on a one-dimensional medium, with a single position coordinate .
For a scalar traveling plane wave in two or three dimensions, the gradient of the field is always collinear with the direction ; specifically, , where is the derivative of . Moreover, a traveling plane wave of any shape satisfies the partial differential equation
Plane traveling waves are also special solutions of the wave equation in an homogeneous medium.
See also
References
https://en.wikipedia.org/wiki/Traveling_plane_wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes.
A tape diagram is a rectangular visual model resembling a piece of tape, that is used to assist with the calculation of ratios and addition, subtraction, and commonly multiplication. It is also known as a divided bar model, fraction strip, length model or strip diagram.[citation needed] In mathematics education, it is used to solve word problems for children in elementary school.[1]
Example
If, for example, a boy has won fifteen games, and the ratio of his wins to losses is 3:2, a tape diagram can be used to determine his number of losses, such as by doing
|
|
15 | ? | |
| Total games lost = ? | |||
|---|---|---|---|
|
|
3 | 2 | |
| Total games lost = ? | |||
|---|---|---|---|
Since the ratio between his wins and losses is 3:2, and he has won fifteen games, it can be concluded that the boy has lost ten of these games.
References
- Lisa Watts-Lawton; Colleen Sheeron (2015). Eureka Math Curriculum Guide: A Story of Units, Grade 2 yes. Wiley. p. 128. ISBN 978-1-118-81261-7.
https://en.wikipedia.org/wiki/Tape_diagram
The tee (⊤, \top in LaTeX) also called down tack (as opposed to the up tack) or verum is a symbol used to represent:
- The top element in lattice theory.
- The truth value of being true in logic, or a sentence (e.g., formula in propositional calculus) which is unconditionally true.[1][2][3] By definition, every tautology is logically equivalent to the verum.
- The top type in type theory.
- Mixed radix encoding in the APL programming language.
A similar-looking superscript T may be used to mean the transpose of a matrix.
Encoding
In Unicode, the tee character is encoded as U+22A4 ⊤ DOWN TACK (⊤, ⊤).[4] The symbol is encoded in LaTeX as \top.
A large variant is encoded as U+27D9 ⟙ LARGE DOWN TACK in the Unicode block Miscellaneous Mathematical Symbols-A.
See also
Notes
- "Mathematical Operators – Unicode" (PDF). Retrieved 2013-07-20.
https://en.wikipedia.org/wiki/Tee_(symbol)
This table of bases gives the values of 0 to 256 in bases 2 to 36, using A−Z for 10−35.
"Base" (or "radix") is a term used in discussions of numeral systems which use place-value notation for representing numbers.
Base 10 is in bold.
https://en.wikipedia.org/wiki/Table_of_bases
In mathematics, the n-th symmetric power of an object X is the quotient of the n-fold product by the permutation action of the symmetric group .
More precisely, the notion exists at least in the following three areas:
- In linear algebra, the n-th symmetric power of a vector space V is the vector subspace of the symmetric algebra of V consisting of degree-n elements (here the product is a tensor product).
- In algebraic topology, the n-th symmetric power of a topological space X is the quotient space , as in the beginning of this article.
- In algebraic geometry, a symmetric power is defined in a way similar to that in algebraic topology. For example, if is an affine variety, then the GIT quotient is the n-th symmetric power of X.
References
- Eisenbud, David; Harris, Joe, 3264 and All That: A Second Course in Algebraic Geometry, Cambridge University Press, ISBN 978-1-107-01708-5
External links
- Hopkins, Michael J. (March 2018). "Symmetric powers of the sphere" (PDF).
https://en.wikipedia.org/wiki/Symmetric_power
In mathematics, a symbolic language is a language that uses characters or symbols to represent concepts, such as mathematical operations, expressions, and statements, and the entities or operands on which the operations are performed.[1] [2]
See also
- Formal language
- Language of mathematics
- List of mathematical symbols
- Mathematical Alphanumeric Symbols
- Mathematical notation
- Notation (general)
- Symbolic language (other)
References
- "A Handbook of Mathematical Discourse". 2009. CiteSeerX 10.1.1.217.5892.
External links
https://en.wikipedia.org/wiki/Symbolic_language_(mathematics)
In mathematics, a strange nonchaotic attractor (SNA) is a form of attractor which, while converging to a limit, is strange, because it is not piecewise differentiable, and also non-chaotic, in that its Lyapunov exponents are non-positive.[1] SNAs were introduced as a topic of study by Grebogi et al. in 1984.[1][2] SNAs can be distinguished from periodic, quasiperiodic and chaotic attractors using the 0-1 test for chaos.[3]
Periodically driven damped nonlinear systems can exhibit complex dynamics characterized by strange chaotic attractors, where strange refers to the fractal geometry of the attractor and chaotic refers to the exponential sensitivity of orbits on the attractor. Quasiperiodically driven systems forced by incommensurate frequencies are natural extensions of periodically driven ones and are phenomenologically richer. In addition to periodic or quasiperiodic motion, they can exhibit chaotic or nonchaotic motion on strange attractors. Although quasiperiodic forcing is not necessary for strange nonchaotic dynamics (e.g., the period doubling accumulation point of a period doubling cascade), if quasiperiodic driving is not present, strange nonchaotic attractors are typically not robust and not expected to occur naturally because they exist only when the system is carefully tuned to a precise critical parameter value. On the other hand, it was shown in the paper of Grebogi et al. that SNAs can be robust when the system is quasiperiodically driven. The first experiment to demonstrate a robust strange nonchaotic attractor involved the buckling of a magnetoelastic ribbon driven quasiperiodically by two incommensurate frequencies in the golden ratio.[4] Strange nonchaotic attractors have been robustly observed in laboratory experiments involving magnetoelastic ribbons, electrochemical cells, electronic circuits, a neon glow discharge and most recently detected in the dynamics of the pulsating RR Lyrae variables KIC 5520878 (as obtained from the Kepler Space Telescope) which may be the first strange nonchaotic dynamical system observed in the wild.[5][6][7][8]
References
- Lindner, John F.; Kohar, Vivek; Kia, Behnam; Hippke, Michael; Learned, John G.; Ditto, William L. (2015). "Stars That Act Irrational". Physical Review Letters. 114 (5): 054101. arXiv:1501.01747. Bibcode:2015PhRvL.114e4101L. doi:10.1103/PhysRevLett.114.054101. PMID 25699444.
https://en.wikipedia.org/wiki/Strange_nonchaotic_attractor
In theoretical physics, stochastic quantization is a method for modelling quantum mechanics, introduced by Edward Nelson in 1966,[1][2][3] and streamlined by Parisi and Wu.[4]
Details
Stochastic quantization serves to quantize Euclidean field theories,[5] and is used for numerical applications, such as numerical simulations of gauge theories with fermions. This serves to address the problem of fermion doubling that usually occurs in these numerical calculations.
Stochastic quantization takes advantage of the fact that a Euclidean quantum field theory can be modeled as the equilibrium limit of a statistical mechanical system coupled to a heat bath. In particular, in the path integral representation of a Euclidean quantum field theory, the path integral measure is closely related to the Boltzmann distribution of a statistical mechanical system in equilibrium. In this relation, Euclidean Green's functions become correlation functions in the statistical mechanical system. A statistical mechanical system in equilibrium can be modeled, via the ergodic hypothesis, as the stationary distribution of a stochastic process. Then the Euclidean path integral measure can also be thought of as the stationary distribution of a stochastic process; hence the name stochastic quantization.
See also
References
- Damgaard, Poul; Helmuth Huffel (1987). "Stochastic Quantization" (PDF). Physics Reports. 152 (5&6): 227–398. Bibcode:1987PhR...152..227D. doi:10.1016/0370-1573(87)90144-X. hdl:1721.1/3101. Retrieved 8 March 2013.
https://en.wikipedia.org/wiki/Stochastic_quantization
In homogenization theory, a branch of mathematics, stochastic homogenization is a technique for understanding solutions to partial differential equations with oscillatory random coefficients.[1]
References
- "Stochastic Homogenization". www.mis.mpg.de. Retrieved 11 June 2018.
https://en.wikipedia.org/wiki/Stochastic_homogenization
In telecommunications, spectral component is any of the waves that range outside the interval of frequencies assigned to a signal. Any waveform can be disassembled into its spectral components by Fourier analysis or Fourier transformation. The length of a pulse thereby is detesitions (spectral phase) of these spectral components.
See also
https://en.wikipedia.org/wiki/Spectral_component
In mathematics graph theory, a single-entry single-exit (SESE) region in a given graph is an ordered edge pair.
For example, with the ordered edge pair, (a, b) of distinct control-flow edges a and b where:
- a dominates b
- b postdominates a
- Every cycle containing a also contains b and vice versa.
where a node x is said to dominate node y in a directed graph if every path from start to y includes x. A node x is said to postdominate a node y if every path from y to end includes x.
So, a and b refer to the entry and exit edge, respectively.
- The first condition ensures that every path from start into the region passes through the region’s entry edge, a.
- The second condition ensures that every path from inside the region to end passes through the region’s exit edge, b.
- The first two conditions are necessary but not enough to characterize SESE regions: since backedges do not alter the dominance or postdominance relationships, the first two conditions alone do not prohibit backedges entering or exiting the region.
- The third condition encodes two constraints: every path from inside the region to a point 'above' a passed through b, and every path from a point 'below' b to a point inside the region passes through a.[1]
References
https://en.wikipedia.org/wiki/Single-entry_single-exit
In mathematics, a simplicial space is a simplicial object in the category of topological spaces. In other words, it is a contravariant functor from the simplex category Δ to the category of topological spaces.[1]
References
- Baues, Hans Joachim (1995), "Homotopy types", in James, I. M. (ed.), Handbook of Algebraic Topology, Amsterdam: North-Holland, pp. 1–72, doi:10.1016/B978-044481779-2/50002-X, ISBN 9780444817792, MR 1361886. See in particular p. 8.
https://en.wikipedia.org/wiki/Simplicial_space
In mathematics, semi-infinite objects are objects which are infinite or unbounded in some but not all possible ways.
In ordered structures and Euclidean spaces
Generally, a semi-infinite set is bounded in one direction, and unbounded in another. For instance, the natural numbers are semi-infinite considered as a subset of the integers; similarly, the intervals and and their closed counterparts are semi-infinite subsets of . Half-spaces are sometimes described as semi-infinite regions.
Semi-infinite regions occur frequently in the study of differential equations.[1][2] For instance, one might study solutions of the heat equation in an idealised semi-infinite metal bar.
A semi-infinite integral is an improper integral over a semi-infinite interval. More generally, objects indexed or parametrised by semi-infinite sets may be described as semi-infinite.[3]
Most forms of semi-infiniteness are boundedness properties, not cardinality or measure properties: semi-infinite sets are typically infinite in cardinality and measure.
In optimization
Many optimization problems involve some set of variables and some set of constraints. A problem is called semi-infinite if one (but not both) of these sets is finite. The study of such problems is known as semi-infinite programming.[4]
References
- Reemsten, Rückmann, Semi-infinite Programming, Kluwer Academic, 1998. ISBN 0-7923-5054-5
https://en.wikipedia.org/wiki/Semi-infinite
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In mathematics, restricted root systems, sometimes called relative root systems, are the root systems associated with a symmetric space. The associated finite reflection group is called the restricted Weyl group. The restricted root system of a symmetric space and its dual can be identified. For symmetric spaces of noncompact type arising as homogeneous spaces of a semisimple Lie group, the restricted root system and its Weyl group are related to the Iwasawa decomposition of the Lie group.
See also
References
- Bump, Daniel (2004), Lie groups, Graduate Texts in Mathematics, vol. 225, Springer, ISBN 0387211543
- Helgason, Sigurdur (1978), Differential geometry, Lie groups, and symmetric spaces, Academic Press, ISBN 0821828487
- Onishchik, A. L.; Vinberg, E. B. (1994), Lie Groups and Lie Algebras III: Structure of Lie Groups and Lie Algebras, Encyclopaedia of Mathematical Sciences, vol. 41, Springer, ISBN 9783540546832
- Wolf, Joseph A. (2010), Spaces of constant curvature, AMS Chelsea Publishing (6th ed.), American Mathematical Society, ISBN 0821852825
- Wolf, Joseph A. (1972), "Fine structure of Hermitian symmetric spaces", in Boothby, William; Weiss, Guido (eds.), Symmetric spaces (Short Courses, Washington University), Pure and Applied Mathematics, vol. 8, Dekker, pp. 271–357, ISBN 978-0-608-30568-4
https://en.wikipedia.org/wiki/Restricted_root_system
The Rankine vortex is a simple mathematical model of a vortex in a viscous fluid. It is named after its discoverer, William John Macquorn Rankine.
The vortices observed in nature are usually modelled with an irrotational (potential or free) vortex. However, in potential vortex, the velocity becomes infinite at the vortex center. In reality, very close to the origin, the motion resembles a solid body rotation. The Rankine vortex model assumes a solid-body rotation inside a cylinder of radius and a potential vortex outside the cylinder. The radius is referred to as the vortex-core radius. The velocity components of the Rankine vortex, expressed in terms of the cylindrical-coordinate system are given by[1]
where is the circulation strength of the Rankine vortex. Since solid-body rotation is characterized by an azimuthal velocity , where is the constant angular velocity, one can also use the parameter to characterize the vortex.
The vorticity field associated with the Rankine vortex is
At all points inside the core of the Rankine vortex, the vorticity is uniform at twice the angular velocity of the core; whereas vorticity is zero at all points outside the core because the flow there is irrotational.
In reality, vortex cores are not always circular; and vorticity is not exactly uniform throughout the vortex core.
See also
- Kaufmann (Scully) vortex – an alternative mathematical simplification for a vortex, with a smoother transition.
- Lamb–Oseen vortex – the exact solution for a free vortex decaying due to viscosity.
- Burgers vortex
External links
- Streamlines vs. Trajectories in a Translating Rankine Vortex: an example of a Rankine vortex imposed on a constant velocity field, with animation.
Notes
- D. J. Acheson (1990). Elementary Fluid Dynamics. Oxford University Press. ISBN 0-19-859679-0.
https://en.wikipedia.org/wiki/Rankine_vortex
In mathematics, quantales are certain partially ordered algebraic structures that generalize locales (point free topologies) as well as various multiplicative lattices of ideals from ring theory and functional analysis (C*-algebras, von Neumann algebras). Quantales are sometimes referred to as complete residuated semigroups.
Overview
A quantale is a complete lattice Q with an associative binary operation ∗ : Q × Q → Q, called its multiplication, satisfying a distributive property such that
and
for all x, yi in Q, i in I (here I is any index set). The quantale is unital if it has an identity element e for its multiplication:
for all x in Q. In this case, the quantale is naturally a monoid with respect to its multiplication ∗.
A unital quantale may be defined equivalently as a monoid in the category Sup of complete join semi-lattices.
A unital quantale is an idempotent semiring under join and multiplication.
A unital quantale in which the identity is the top element of the underlying lattice is said to be strictly two-sided (or simply integral).
A commutative quantale is a quantale whose multiplication is commutative. A frame, with its multiplication given by the meet operation, is a typical example of a strictly two-sided commutative quantale. Another simple example is provided by the unit interval together with its usual multiplication.
An idempotent quantale is a quantale whose multiplication is idempotent. A frame is the same as an idempotent strictly two-sided quantale.
An involutive quantale is a quantale with an involution
that preserves joins:
A quantale homomorphism is a map f : Q1 → Q2 that preserves joins and multiplication for all x, y, xi in Q1, and i in I:
See also
References
- C.J. Mulvey (2001) [1994], "Quantale", Encyclopedia of Mathematics, EMS Press [1]
- J. Paseka, J. Rosicky, Quantales, in: B. Coecke, D. Moore, A. Wilce, (Eds.), Current Research in Operational Quantum Logic: Algebras, Categories and Languages, Fund. Theories Phys., vol. 111, Kluwer Academic Publishers, 2000, pp. 245–262.
- M. Piazza, M. Castellan, Quantales and structural rules. Journal of Logic and Computation, 6 (1996), 709–724.
- K. Rosenthal, Quantales and Their Applications, Pitman Research Notes in Mathematics Series 234, Longman Scientific & Technical, 1990.
https://en.wikipedia.org/wiki/Quantale
Category:Mathematics stubs
| This category is maintained by WikiProject Stub sorting. Please propose new stub templates and categories here before creation. |
| This category is for stub articles relating to mathematical topics. You can help by expanding them. To add an article to this category, use {{math-stub}} instead of {{stub}}. |
Rather the general {{math-stub}}, please consider using one of the following more specific stub types (or even changing articles that use {{math-stub}}):
- Algebra stubs: {{algebra-stub}}
- Applied mathematics stubs: {{applied-math-stub}}
- Category theory stubs: {{categorytheory-stub}}
- Combinatorics stubs: {{combin-stub}}
- Cryptography stubs: {{crypto-stub}}
- Geometry stubs: {{geometry-stub}}
- Mathematical analysis stubs: {{mathanalysis-stub}}
- Mathematical logic stubs: {{mathlogic-stub}}
- Mathematician stubs: {{mathematician-stub}}
- Number stubs: {{num-stub}}
- Number theory stubs: {{numtheory-stub}}
- Statistics stubs: {{statistics-stub}}
- Topology stubs: {{topology-stub}}
- Probability stubs: {{probability-stub}}
- Mathematics literature stubs: {{mathematics-lit-stub}}
- Mathematics competition stubs: {{math-competition-stub}}
Subcategories
This category has the following 18 subcategories, out of 18 total.
- Mathematician stubs (5 C, 269 P)
*
- Topology stubs (1 C, 282 P)
M
- Mathematics stub templates (1 C, 28 P)
Pages in category "Mathematics stubs"
The following 193 pages are in this category, out of 193 total. This list may not reflect recent changes.
A
- A-equivalence
- Absorbing set (random dynamical systems)
- Actuarial polynomials
- Advisory Committee on Mathematics Education
- Age of the captain
- Ahlfors finiteness theorem
- Ahlfors measure conjecture
- AKNS system
- Al-Salam–Ismail polynomials
- ALEKS
- Ancient solution
- Argand system
- Argument of a function
- Arithmetic progression game
- Askey–Wilson polynomials
- Association of Christians in the Mathematical Sciences
B
C
- Canadian Society for History and Philosophy of Mathematics
- Canon Palmtronic LE-80M
- Canonical map
- Canonizant
- Carry operator
- Chihara–Ismail polynomials
- Chisini mean
- Coherent topos
- Concept image and concept definition
- Continuous q-Legendre polynomials
- Contracted Bianchi identities
- Convolution quotient
- Count On
- Counting board
- David Crighton Medal
- Cut locus
D
H
I
K
L
M
- MAA Certificate of Merit
- Maass–Selberg relations
- Macaulay brackets
- Magic polygon
- Makespan
- Mandelbox
- Map (graph theory)
- Math Country
- Math-U-See
- Mathematical elimination
- Mathematical instrument
- Mathematical knowledge management
- Mathematical Society of Japan
- Mathematical theory
- Mathematics and God
- Mathematics mastery
- MathFest
- McShane integral
- Mean square
- Metric lattice
- Minimal K-type
- Minimal realization
- Modular subgroup
- Moschovakis coding lemma
- Mostowski model
N
P
R
S
- School Mathematics Study Group
- Schwarz function
- Self-dissimilarity
- Semi-infinite
- Sequential decision making
- Shephard Prize
- Shimizu L-function
- Siegel parabolic subgroup
- Simplicial group
- Simplicial space
- Single-entry single-exit
- Sister Celine's polynomials
- Somos' quadratic recurrence constant
- Space cardioid
- Specht's theorem
- Spectral component
- Spectral network
- Steinhaus longimeter
- Steklov Institute of Mathematics
- Stochastic homogenization
- Stochastic quantization
- Strange nonchaotic attractor
- Symbolic language (mathematics)
- Symmetric power
- System of differential equations
- Szegő polynomial
T
W
https://en.wikipedia.org/wiki/Category:Mathematics_stubs



























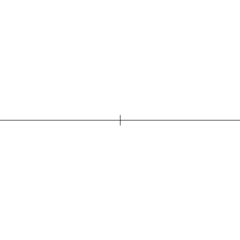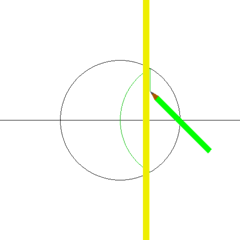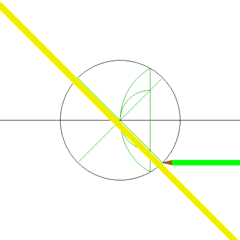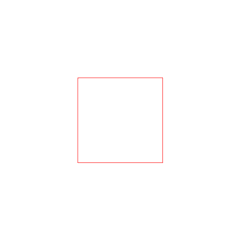


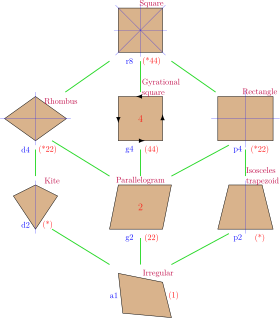







![K={\sqrt[ {4}]{efgh}}(e+f+g+h).](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef723678f235a25b2488c717837a47cb493f9bd)

![r={\sqrt[ {4}]{efgh}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/5760badfbf69d199976db4357edf238b525b132d)










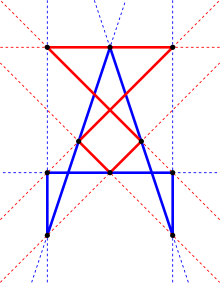
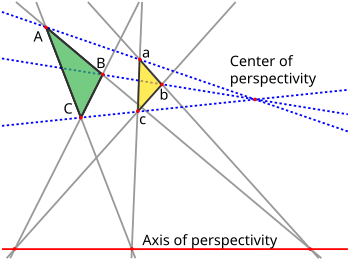
















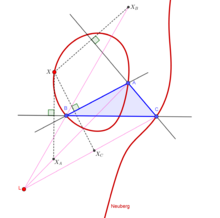




































![{\displaystyle M([\Gamma (1)])=\mathrm {Spec} (R[j])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab23afece9ba02b8ed011358c5c4b852018c234a)

![{\displaystyle \mathbb {Z} [\zeta _{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a43a841d0ccd0abdc772748fc336c157e8185b6)

![\mathbb {Z} [i]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)





























![{\displaystyle [H,A]=\lambda A\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9db727e0515c4fbd9c532ed19f5c9bb8eb9d886d)



















![{\displaystyle [0,x]:=\{z\in Z:0\leq z{\text{ and }}z\leq x\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67f50b3c3653cf1633091a9127ba52c2b6b6aca3)
![{\displaystyle [0,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/725684c883c7ef386e8a0fe4d111e72c565747ed)



























































































































No comments:
Post a Comment