An attic (sometimes referred to as a loft) is a space found directly below the pitched roof of a house or other building; an attic may also be called a sky parlor[1] or a garret. Because attics fill the space between the ceiling of the top floor of a building and the slanted roof, they are known for being awkwardly shaped spaces with exposed rafters and difficult-to-reach corners.
While some attics are converted into bedrooms, home offices, or attic apartments complete with windows and staircases, most remain difficult to access (and are usually entered using a loft hatch and ladder). Attics help control temperatures in a house by providing a large mass of slowly moving air, and are often used for storage. The hot air rising from the lower floors of a building is often retained in attics, further compounding their reputation as inhospitable environments. However, in recent years attics have been insulated to help decrease heating costs, since, on average, uninsulated attics account for 15 percent of the total energy loss in average houses.[2]
A loft is also the uppermost space in a building but is distinguished from an attic in that an attic typically constitutes an entire floor of the building, while a loft covers only a few rooms, leaving one or more sides open to the lower floor.[citation needed]
https://en.wikipedia.org/wiki/Attic
Pyroxferroite (Fe2+,Ca)SiO3 is a single chain inosilicate. It is mostly composed of iron, silicon and oxygen, with smaller fractions of calcium and several other metals.[1] Together with armalcolite and tranquillityite, it is one of the three minerals which were discovered on the Moon. It was then found in Lunar and Martian meteorites as well as a mineral in the Earth's crust. Pyroxferroite can also be produced by annealing synthetic clinopyroxene at high pressures and temperatures. The mineral is metastable and gradually decomposes at ambient conditions, but this process can take billions of years.
https://en.wikipedia.org/wiki/Pyroxferroite
A fusion energy gain factor, usually expressed with the symbol Q, is the ratio of fusion power produced in a nuclear fusion reactor to the power required to maintain the plasma in steady state. The condition of Q = 1, when the power being released by the fusion reactions is equal to the required heating power, is referred to as breakeven, or in some sources, scientific breakeven.
The energy given off by the fusion reactions may be captured within the fuel, leading to self-heating. Most fusion reactions release at least some of their energy in a form that cannot be captured within the plasma, so a system at Q = 1 will cool without external heating. With typical fuels, self-heating in fusion reactors is not expected to match the external sources until at least Q = 5. If Q increases past this point, increasing self-heating eventually removes the need for external heating. At this point the reaction becomes self-sustaining, a condition called ignition. Ignition corresponds to infinite Q, and is generally regarded as highly desirable for practical reactor designs.
Over time, several related terms have entered the fusion lexicon. Energy that is not captured within the fuel can be captured externally to produce electricity. That electricity can be used to heat the plasma to operational temperatures. A system that is self-powered in this way is referred to as running at engineering breakeven. Operating above engineering breakeven, a machine would produce more electricity than it uses and could sell that excess. One that sells enough electricity to cover its operating costs is sometimes known as economic breakeven. Additionally, fusion fuels, especially tritium, are very expensive, so many experiments run on various test gasses like hydrogen or deuterium. A reactor running on these fuels that reaches the conditions for breakeven if tritium was introduced is said to be operating at extrapolated breakeven.
As of 2021, the record for Q is held by the JET tokamak in the UK, at Q = (16 MW)/(24 MW) ≈ 0.67, first attained in 1997. The highest record for extrapolated breakeven was posted by the JT-60 device, with Qext = 1.25, slightly besting JET's earlier 1.14. ITER was originally designed to reach ignition, but is currently designed to reach Q = 10, producing 500 MW of fusion power from 50 MW of injected thermal power.
In the case of neutrons carrying most of the practical energy, as is the case in the D-T fuel, this neutron energy is normally captured in a "blanket" of lithium that produces more tritium that is used to fuel the reactor. Due to various exothermic and endothermic reactions, the blanket may have a power gain factor MR. MR is typically on the order of 1.1 to 1.3, meaning it produces a small amount of energy as well. The net result, the total amount of energy released to the environment and thus available for energy production, is referred to as PR, the net power output of the reactor.[9]
The blanket is then cooled and the cooling fluid used in a heat exchanger driving conventional steam turbines and generators. That electricity is then fed back into the heating system.[9] Each of these steps in the generation chain has an efficiency to consider. In the case of the plasma heating systems, is on the order of 60 to 70%, while modern generator systems based on the Rankine cycle have around 35 to 40%. Combining these we get a net efficiency of the power conversion loop as a whole, , of around 0.20 to 0.25. That is, about 20 to 25% of can be recirculated.[9]
Thus, the fusion energy gain factor required to reach engineering breakeven is defined as:[10]
To understand how is used, consider a reactor operating at 20 MW and Q = 2. Q = 2 at 20 MW implies that Pheat is 10 MW. Of that original 20 MW about 20% is alphas, so assuming complete capture, 4 MW of Pheat is self-supplied. We need a total of 10 MW of heating and get 4 of that through alphas, so we need another 6 MW of power. Of the original 20 MW of output, 4 MW are left in the fuel, so we have 16 MW of net output. Using MR of 1.15 for the blanket, we get PR about 18.4 MW. Assuming a good of 0.25, that requires 24 MW PR, so a reactor at Q = 2 cannot reach engineering breakeven. At Q = 4 one needs 5 MW of heating, 4 of which come from the fusion, leaving 1 MW of external power required, which can easily be generated by the 18.4 MW net output. Thus for this theoretical design the QE is between 2 and 4.
Considering real-world losses and efficiencies, Q values between 5 and 8 are typically listed for magnetic confinement devices,[9] while inertial devices have dramatically lower values for and thus require much higher QE values, on the order of 50 to 100.[11]
Ignition[edit]
As the temperature of the plasma increases, the rate of fusion reactions grows rapidly, and with it, the rate of self-heating. In contrast, non-capturable energy losses like x-rays do not grow at the same rate. Thus, in overall terms, the self-heating process becomes more efficient as the temperature increases, and less energy is needed from external sources to keep it hot.
Eventually Pheat reaches zero, that is, all of the energy needed to keep the plasma at the operational temperature is being supplied by self-heating, and the amount of external energy that needs to be added drops to zero. This point is known as ignition. In the case of D-T fuel, where only 20% of the energy is released as alphas that give rise to self-heating, this cannot occur until the plasma is releasing at least five times the power needed to keep it at its working temperature.
Ignition, by definition, corresponds to an infinite Q, but it does not mean that frecirc drops to zero as the other power sinks in the system, like the magnets and cooling systems, still need to be powered. Generally, however, these are much smaller than the energy in the heaters, and require a much smaller frecirc. More importantly, this number is more likely to be near-constant, meaning that further improvements in plasma performance will result in more energy that can be directly used for commercial generation, as opposed to recirculation.
https://en.wikipedia.org/wiki/Fusion_energy_gain_factor
A field-reversed configuration (FRC) is a type of plasma device studied as a means of producing nuclear fusion. It confines a plasma on closed magnetic field lines without a central penetration.[1]In an FRC, the plasma has the form of a self-stable torus, similar to a smoke ring.
FRCs are closely related to another self-stable magnetic confinement fusion device, the spheromak. Both are considered part of the compact toroid class of fusion devices. FRCs normally have a plasma that is more elongated than spheromaks, having the overall shape of a hollowed out sausage rather than the roughly spherical spheromak.
FRCs were a major area of research in the 1960s and into the 1970s, but had problems scaling up into practical fusion triple products. Interest returned in the 1990s and as of 2019, FRCs were an active research area.
https://en.wikipedia.org/wiki/Field-reversed_configuration
Fusion power, processes and devices
Core topics
Nuclear fusion Timeline List of experiments Nuclear power Nuclear reactor Atomic nucleus Fusion energy gain factor Lawson criterion Magnetohydrodynamics Neutron Plasma
Processes,
methods
Confinement
type
Gravitational
Alpha process Triple-alpha process CNO cycle Fusor Helium flash Nova remnants Proton-proton chain Carbon-burning Lithium burning Neon-burning Oxygen-burning Silicon-burning R-process S-process
Magnetic
Dense plasma focus Field-reversed configuration Levitated dipole Magnetic mirror Bumpy torus Reversed field pinch Spheromak Stellarator Tokamak Spherical Z-pinch
Inertial
Bubble (acoustic) Laser-driven Ion-driven Magnetized Liner Inertial Fusion
Electrostatic
Fusor Polywell
Other forms
Colliding beam Magnetized target Migma Muon-catalyzed Pyroelectric
https://en.wikipedia.org/wiki/nuclear_cascade
https://en.wikipedia.org/wiki/Proton–proton_chain
https://en.wikipedia.org/wiki/CNO_cycle
https://en.wikipedia.org/wiki/Fusor_(astronomy)
https://en.wikipedia.org/wiki/Helium_flash
https://en.wikipedia.org/wiki/Fusion_energy_gain_factor
https://en.wikipedia.org/wiki/Aneutronic_fusion
Candidate reactions[edit]
Several nuclear reactions produce no neutrons on any of their branches. Those with the largest cross sections are these:
| Isotopes | Reaction | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Deuterium - Helium-3 | 2D | + | 3He | → | 4He | + | 1p | + 18.3 MeV | |
| Deuterium - Lithium-6 | 2D | + | 6Li | → | 2 | 4He | + 22.4 MeV | ||
| Proton - Lithium-6 | 1p | + | 6Li | → | 4He | + | 3He | + 4.0 MeV | |
| Helium-3 – Lithium-6 | 3He | + | 6Li | → | 2 | 4He | + | 1p | + 16.9 MeV |
| Helium-3 - Helium-3 | 3He | + | 3He | → | 4He | + | 2 1p | + 12.86 MeV | |
| Proton – Lithium-7 | 1p | + | 7Li | → | 2 | 4He | + 17.2 MeV | ||
| Proton – Boron-11 | 1p | + | 11B | → | 3 | 4He | + 8.7 MeV | ||
| Proton – Nitrogen | 1p | + | 15N | → | 12C | + | 4He | + 5.0 MeV | |
Energy capture[edit]
Aneutronic fusion produces energy in the form of charged particles instead of neutrons. This means that energy from aneutronic fusion could be captured using direct conversion instead of the steam cycle. Direct conversion techniques can either be inductive, based on changes in magnetic fields, electrostatic, based on pitting charged particles against an electric field, or photoelectric, in which light energy is captured. In a pulsed mode.[50]
Electrostatic direct conversion uses the motion of charged particles to create voltage. This voltage drives electricity in a wire. This becomes electrical power, the reverse of most phenomena that use a voltage to put a particle in motion. Direct energy conversion does the opposite, using particle motion to produce a voltage. It has been described as a linear accelerator running backwards.[51] An early supporter of this method was Richard F. Post at Lawrence Livermore. He proposed to capture the kinetic energy of charged particles as they were exhausted from a fusion reactor and convert this into voltage to drive current.[52] Post helped develop the theoretical underpinnings of direct conversion, later demonstrated by Barr and Moir. They demonstrated a 48 percent energy capture efficiency on the Tandem Mirror Experiment in 1981.[53]
Aneutronic fusion loses much of its energy as light. This energy results from the acceleration and deceleration of charged particles. These speed changes can be caused by Bremsstrahlung radiation or cyclotron radiation or synchrotron radiation or electric field interactions. The radiation can be estimated using the Larmor formula and comes in the X-ray, IR, UV and visible spectra. Some of the energy radiated as X-rays may be converted directly to electricity. Because of the photoelectric effect, X-rays passing through an array of conducting foils transfer some of their energy to electrons, which can then be captured electrostatically. Since X-rays can go through far greater material thickness than electrons, many hundreds or thousands of layers are needed to absorb them.[54]
See also[edit]
https://en.wikipedia.org/wiki/Aneutronic_fusion
Direct energy conversion (DEC) or simply direct conversion converts a charged particle's kinetic energy into a voltage. It is a scheme for power extraction from nuclear fusion.
https://en.wikipedia.org/wiki/Direct_energy_conversion
A magnetic mirror, known as a magnetic trap (магнитный захват) in Russia and briefly as a pyrotron in the US, is a type of magnetic confinement device used in fusion power to trap high temperature plasma using magnetic fields. The mirror was one of the earliest major approaches to fusion power, along with the stellaratorand z-pinch machines.
https://en.wikipedia.org/wiki/Magnetic_mirror
The bumpy torus is a class of magnetic fusion energy devices that consist of a series of magnetic mirrorsconnected end-to-end to form a closed torus. It is based on a discovery made by a team headed by Dr. Ray Dandl at Oak Ridge National Laboratory in the 1960s.[1]
https://en.wikipedia.org/wiki/Bumpy_torus
A magnetohydrodynamic generator (MHD generator) is a magnetohydrodynamic converter that utilizes a Brayton cycle to transform thermal energy and kinetic energy directly into electricity. MHD generators are different from traditional electric generators in that they operate without moving parts (e.g. no turbine) to limit the upper temperature. They therefore have the highest known theoretical thermodynamic efficiency of any electrical generation method. MHD has been extensively developed as a topping cycle to increase the efficiency of electric generation, especially when burning coal or natural gas. The hot exhaust gas from an MHD generator can heat the boilers of a steam power plant, increasing overall efficiency.
An MHD generator, like a conventional generator, relies on moving a conductor through a magnetic field to generate electric current. The MHD generator uses hot conductive ionized gas (a plasma) as the moving conductor. The mechanical dynamo, in contrast, uses the motion of mechanical devices to accomplish this.
Practical MHD generators have been developed for fossil fuels, but these were overtaken by less expensive combined cycles in which the exhaust of a gas turbine or molten carbonate fuel cell heats steam to power a steam turbine.
MHD dynamos are the complement of MHD accelerators, which have been applied to pump liquid metals, seawater and plasmas.
Natural MHD dynamos are an active area of research in plasma physics and are of great interest to the geophysics and astrophysics communities, since the magnetic fields of the earth and sun are produced by these natural dynamos.
Disc generator[edit]
The third and, currently, the most efficient design is the Hall effect disc generator. This design currently holds the efficiency and energy density records for MHD generation. A disc generator has fluid flowing between the center of a disc, and a duct wrapped around the edge. (The ducts are not shown.) The magnetic excitation field is made by a pair of circular Helmholtz coils above and below the disk. (The coils are not shown.)
The Faraday currents flow in a perfect dead short around the periphery of the disk.
The Hall effect currents flow between ring electrodes near the center duct and ring electrodes near the periphery duct.
The wide flat gas flow reduced the distance, hence the resistance of the moving fluid. This increases efficiency.
Another significant advantage of this design is that the magnets are more efficient. First, they cause simple parallel field lines. Second, because the fluid is processed in a disk, the magnet can be closer to the fluid, and in this magnetic geometry, magnetic field strengths increase as the 7th power of distance. Finally, the generator is compact for its power, so the magnet is also smaller. The resulting magnet uses a much smaller percentage of the generated power.
Generator efficiency[edit]
The efficiency of the direct energy conversion in MHD power generation increases with the magnetic field strength and the plasma conductivity, which depends directly on the plasma temperature, and more precisely on the electron temperature. As very hot plasmas can only be used in pulsed MHD generators (for example using shock tubes) due to the fast thermal material erosion, it was envisaged to use nonthermal plasmas as working fluids in steady MHD generators, where only free electrons are heated a lot (10,000–20,000 kelvins) while the main gas (neutral atoms and ions) remains at a much lower temperature, typically 2500 kelvins. The goal was to preserve the materials of the generator (walls and electrodes) while improving the limited conductivity of such poor conductors to the same level as a plasma in thermodynamic equilibrium; i.e. completely heated to more than 10,000 kelvins, a temperature that no material could stand.[1][2][3][4]
But Evgeny Velikhov first discovered theoretically in 1962 and experimentally in 1963 that an ionization instability, later called the Velikhov instability or electrothermal instability, quickly arises in any MHD converter using magnetized nonthermal plasmas with hot electrons, when a critical Hall parameteris reached, hence depending on the degree of ionization and the magnetic field.[5][6][7] Such an instability greatly degrades the performance of nonequilibrium MHD generators. The prospects about this technology, which initially predicted awesome efficiencies, crippled MHD programs all over the world as no solution to mitigate the instability was found at that time.[8][9][10][11]
Also, MHDs work better with stronger magnetic fields. The most successful magnets have been superconducting, and very close to the channel. A major difficulty was refrigerating these magnets while insulating them from the channel. The problem is worse because the magnets work better when they are closer to the channel. There are also severe risks of damage to the hot, brittle ceramics from differential thermal cracking. The magnets are usually near absolute zero, while the channel is several thousand degrees.
A magnetohydrodynamic generator might also be the first stage of a gas-cooled nuclear reactor.[12]
Toxic byproducts[edit]
MHD reduces overall production of hazardous fossil fuel wastes because it increases plant efficiency. In MHD coal plants, the patented commercial "Econoseed" process developed by the U.S. (see below) recycles potassium ionization seed from the fly ash captured by the stack-gas scrubber. However, this equipment is an additional expense. If molten metal is the armature fluid of an MHD generator, care must be taken with the coolant of the electromagnetics and channel. The alkali metals commonly used as MHD fluids react violently with water. Also, the chemical byproducts of heated, electrified alkali metals and channel ceramics may be poisonous and environmentally persistent.
History[edit]
The first practical MHD power research was funded in 1938 in the U.S. by Westinghouse in its Pittsburgh, Pennsylvania laboratories, headed by Hungarian Bela Karlovitz. The initial patent on MHD is by B. Karlovitz, U.S. Patent No. 2,210,918, "Process for the Conversion of Energy", August 13, 1940.
Former Yugoslavia development[edit]
Over more than a ten-year span, engineers in former Yugoslavian Institute of Thermal and Nuclear Technology (ITEN), Energoinvest Co., Sarajevo, had built the first experimental Magneto-Hydrodynamic facility power generator in 1989. It was here it was first patented.[16][17]
U.S. development[edit]
In the 1980s, the U.S. Department of Energy began a vigorous multiyear program, culminating in a 1992 50 MW demonstration coal combustor at the Component Development and Integration Facility (CDIF) in Butte, Montana. This program also had significant work at the Coal-Fired-In-Flow-Facility (CFIFF) at University of Tennessee Space Institute.
This program combined four parts:
- An integrated MHD topping cycle, with channel, electrodes and current control units developed by AVCO, later known as Textron Defence of Boston. This system was a Hall effect duct generator heated by pulverized coal, with a potassium ionisation seed. AVCO had developed the famous Mk. V generator, and had significant experience.
- An integrated bottoming cycle, developed at the CDIF.
- A facility to regenerate the ionization seed was developed by TRW. Potassium carbonate is separated from the sulphate in the fly ash from the scrubbers. The carbonate is removed, to regain the potassium.
- A method to integrate MHD into preexisting coal plants. The Department of Energy commissioned two studies. Westinghouse Electric performed a study based on the Scholtz Plant of Gulf Power in Sneads, Florida. The MHD Development Corporation also produced a study based on the J.E. Corrette Plant of the Montana Power Company of Billings, Montana.
Initial prototypes at the CDIF were operated for short durations, with various coals: Montana Rosebud, and a high-sulphur corrosive coal, Illinois No. 6. A great deal of engineering, chemistry and material science was completed. After final components were developed, operational testing completed with 4,000 hours of continuous operation, 2,000 on Montana Rosebud, 2,000 on Illinois No. 6. The testing ended in 1993.[citation needed]
Japanese development[edit]
The Japanese program in the late 1980s concentrated on closed-cycle MHD. The belief was that it would have higher efficiencies, and smaller equipment, especially in the clean, small, economical plant capacities near 100 megawatts (electrical) which are suited to Japanese conditions. Open-cycle coal-powered plants are generally thought to become economical above 200 megawatts.
The first major series of experiments was FUJI-1, a blow-down system powered from a shock tube at the Tokyo Institute of Technology. These experiments extracted up to 30.2% of enthalpy, and achieved power densities near 100 megawatts per cubic meter. This facility was funded by Tokyo Electric Power, other Japanese utilities, and the Department of Education. Some authorities believe this system was a disc generator with a helium and argon carrier gas and potassium ionization seed.
In 1994, there were detailed plans for FUJI-2, a 5 MWe continuous closed-cycle facility, powered by natural gas, to be built using the experience of FUJI-1. The basic MHD design was to be a system with inert gases using a disk generator. The aim was an enthalpy extraction of 30% and an MHD thermal efficiency of 60%. FUJI-2 was to be followed by a retrofit to a 300 MWe natural gas plant.
Australian development[edit]
In 1986, Professor Hugo Karl Messerle at The University of Sydney researched coal-fueled MHD. This resulted in a 28 MWe topping facility that was operated outside Sydney. Messerle also wrote one of the most recent reference works (see below), as part of a UNESCO education program.
A detailed obituary for Hugo is located on the Australian Academy of Technological Sciences and Engineering (ATSE) website.[18]
Italian development[edit]
The Italian program began in 1989 with a budget of about 20 million $US, and had three main development areas:
- MHD Modelling.
- Superconducting magnet development. The goal in 1994 was a prototype 2 m long, storing 66 MJ, for an MHD demonstration 8 m long. The field was to be 5 teslas, with a taper of 0.15 T/m. The geometry was to resemble a saddle shape, with cylindrical and rectangular windings of niobium-titanium copper.
- Retrofits to natural gas powerplants. One was to be at the Enichem-Anic factor in Ravenna. In this plant, the combustion gases from the MHD would pass to the boiler. The other was a 230 MW (thermal) installation for a power station in Brindisi, that would pass steam to the main power plant.
Chinese development[edit]
A joint U.S.-China national programme ended in 1992 by retrofitting the coal-fired No. 3 plant in Asbach.[citation needed] A further eleven-year program was approved in March 1994. This established centres of research in:
- The Institute of Electrical Engineering in the Chinese Academy of Sciences, Beijing, concerned with MHD generator design.
- The Shanghai Power Research Institute, concerned with overall system and superconducting magnet research.
- The Thermoenergy Research Engineering Institute at the Nanjing's Southeast University, concerned with later developments.
The 1994 study proposed a 10 W (electrical, 108 MW thermal) generator with the MHD and bottoming cycle plants connected by steam piping, so either could operate independently.
Russian developments[edit]
In 1971 the natural-gas fired U-25 plant was completed near Moscow, with a designed capacity of 25 megawatts. By 1974 it delivered 6 megawatts of power.[19] By 1994, Russia had developed and operated the coal-operated facility U-25, at the High-Temperature Institute of the Russian Academy of Science in Moscow. U-25's bottoming plant was actually operated under contract with the Moscow utility, and fed power into Moscow's grid. There was substantial interest in Russia in developing a coal-powered disc generator. In 1986 the first industrial power plant with MHD generator was built, but in 1989 the project was cancelled before MHD launch and this power plant later joined to Ryazan Power Station as a 7th unit with ordinary construction.
https://en.wikipedia.org/wiki/Magnetohydrodynamic_generator
Shocks and discontinuities are transition layers where the plasma properties change from one equilibrium state to another. The relation between the plasma properties on both sides of a shock or a discontinuity can be obtained from the conservative form of the magnetohydrodynamic (MHD) equations, assuming conservation of mass, momentum, energy and of .
https://en.wikipedia.org/wiki/Shocks_and_discontinuities_(magnetohydrodynamics)
https://en.wikipedia.org/wiki/Helion_Energy
https://en.wikipedia.org/wiki/Magnetic_pressure
https://en.wikipedia.org/wiki/Tangential_and_normal_components
https://en.wikipedia.org/wiki/Density
https://en.wikipedia.org/wiki/thermodynamics
https://en.wikipedia.org/wiki/Speed_of_sound
https://en.wikipedia.org/wiki/Bow_shock
https://en.wikipedia.org/wiki/Category:Space_plasmas
https://en.wikipedia.org/wiki/Magnetic_confinement_fusion
https://en.wikipedia.org/wiki/Plasma_(physics)
https://en.wikipedia.org/wiki/Neutron
https://en.wikipedia.org/wiki/Levitated_dipole
https://en.wikipedia.org/wiki/Stellarator
https://en.wikipedia.org/wiki/Z-pinch
https://en.wikipedia.org/wiki/Thermonuclear_fusion#Confinement
https://en.wikipedia.org/wiki/Vacuum
https://en.wikipedia.org/wiki/Binding_energy#Nuclear_binding_energy_curve
https://en.wikipedia.org/wiki/R-process
https://en.wikipedia.org/wiki/Voitenko_compressor
https://en.wikipedia.org/wiki/Shear
https://en.wikipedia.org/wiki/conduction
https://en.wikipedia.org/wiki/compression
https://en.wikipedia.org/wiki/Spinor
https://en.wikipedia.org/wiki/Spin_(physics)
https://en.wikipedia.org/wiki/intrinsic_angular_momentum
https://en.wikipedia.org/wiki/scalar
https://en.wikipedia.org/wiki/eigen
https://en.wikipedia.org/wiki/zero
https://en.wikipedia.org/wiki/linear
https://en.wikipedia.org/wiki/Spin–statistics_theorem
https://en.wikipedia.org/wiki/Intrinsically_disordered_proteins
https://en.wikipedia.org/wiki/supramolecular_chemistry
https://en.wikipedia.org/wiki/Folding_(chemistry)
https://en.wikipedia.org/wiki/Category:Self-organization
https://en.wikipedia.org/wiki/Globular_protein
https://en.wikipedia.org/wiki/Scleroprotein
Spinors were introduced in geometry by Élie Cartan in 1913.[1][d] In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.[e]
https://en.wikipedia.org/wiki/Spinor
https://en.wikipedia.org/wiki/Möbius_strip
https://en.wikipedia.org/wiki/Killing_spinor
https://en.wikipedia.org/wiki/Spinor_condensate
https://en.wikipedia.org/wiki/Killing_spinor
https://en.wikipedia.org/wiki/Spin–spin_relaxation
https://en.wikipedia.org/wiki/Spinor_spherical_harmonics
https://en.wikipedia.org/wiki/Orthogonal_group
https://en.wikipedia.org/wiki/Dirac_operator
https://en.wikipedia.org/wiki/Spin-1/2
https://en.wikipedia.org/wiki/Metal_spinning
https://en.wikipedia.org/wiki/Symplectic_spinor_bundle
https://en.wikipedia.org/wiki/Vorticity#Vortex_lines_and_vortex_tubes
https://en.wikipedia.org/wiki/Wingtip_vortices
https://en.wikipedia.org/wiki/Dust_devil
https://en.wikipedia.org/wiki/Negative_temperature#Two-dimensional_vortex_motion
https://en.wikipedia.org/wiki/Strake_(aeronautics)#Anti-spin_strakes
https://en.wikipedia.org/wiki/negative_matter
https://en.wikipedia.org/wiki/negative_resistance
https://en.wikipedia.org/wiki/negative_energy
https://en.wikipedia.org/wiki/Atomic_Age
https://en.wikipedia.org/wiki/Stimulated_emission#Small_signal_gain_equation
https://en.wikipedia.org/wiki/Ion
https://en.wikipedia.org/wiki/Second
https://en.wikipedia.org/wiki/Atomic_layer_deposition
https://en.wikipedia.org/wiki/Gas
https://en.wikipedia.org/wiki/Neon
https://en.wikipedia.org/wiki/Accretion_disk
https://en.wikipedia.org/wiki/astrophysical_jet
Roy Orbison - Oh, Pretty Woman
Above. Flo Rida (ft. Timbaland) - Elevator
Above. White Zombie - Thunder Kiss '65 (Official Video)
Triple-alpha process in stars[edit]
Helium accumulates in the cores of stars as a result of the proton–proton chain reaction and the carbon–nitrogen–oxygen cycle.
https://en.wikipedia.org/wiki/Magnetohydrodynamics
https://en.wikipedia.org/wiki/Fusion_energy_gain_factor
In linguistics, and more precisely in traditional grammar, a cardinal numeral (or cardinal number word) is a part of speechused to count. Examples in English are the words one, two, three, and the compounds three hundred and forty-two and nine hundred and sixty. Cardinal numerals are classified as definite, and are related to ordinal numbers, such as the English first, second, and third, etc.[1][2][3]
See also[edit]
- Arity
- Cardinal number for the related usage in mathematics
- English numerals (in particular the Cardinal numbers section)
- Distributive number
- Multiplier
- Numeral for examples of number systems
- Ordinal number
- Valency
In linguistics, ordinal numerals or ordinal number words are words representing position or rank in a sequential order; the order may be of size, importance, chronology, and so on (e.g., "third", "tertiary"). They differ from cardinal numerals, which represent quantity (e.g., "three") and other types of numerals.
In traditional grammar, all numerals, including ordinal numerals, are grouped into a separate part of speech(Latin: nomen numerale, hence, "noun numeral" in older English grammar books). However, in modern interpretations of English grammar, ordinal numerals are usually conflated with adjectives.
Ordinal numbers may be written in English with numerals and letter suffixes: 1st, 2nd or 2d, 3rd or 3d, 4th, 11th, 21st, 101st, 477th, etc., with the suffix acting as an ordinal indicator. Written dates often omit the suffix, although it is nevertheless pronounced. For example: 5 November 1605 (pronounced "the fifth of November ... "); November 5, 1605, ("November (the) Fifth ..."). When written out in full with "of", however, the suffix is retained: the 5th of November. In other languages, different ordinal indicators are used to write ordinal numbers.
In American Sign Language, the ordinal numbers first through ninth are formed with handshapes similar to those for the corresponding cardinal numbers with the addition of a small twist of the wrist.[1]
https://en.wikipedia.org/wiki/Ordinal_numeral
0 (zero) is a number,[1] and the numerical digit used to represent that number in numerals. It fulfills a central role in mathematics as the additive identity[2] of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems. Names for the number 0 in English include zero, nought (UK), naught (US; /nɔːt/), nil, or—in contexts where at least one adjacent digit distinguishes it from the letter "O"—oh or o (/oʊ/). Informal or slang terms for zero include zilch and zip.[3] Ought and aught (/ɔːt/),[4] as well as cipher,[5] have also been used historically.[6][7]
https://en.wikipedia.org/wiki/0
Zero-point energy (ZPE) is the lowest possible energy that a quantum mechanical system may have. Unlike in classical mechanics, quantum systems constantly fluctuate in their lowest energy state as described by the Heisenberg uncertainty principle.[1] As well as atoms and molecules, the empty space of the vacuum has these properties. According to quantum field theory, the universe can be thought of not as isolated particles but continuous fluctuating fields: matter fields, whose quanta are fermions (i.e., leptons and quarks), and force fields, whose quanta are bosons (e.g., photons and gluons). All these fields have zero-point energy.[2] These fluctuating zero-point fields lead to a kind of reintroduction of an aether in physics[1][3] since some systems can detect the existence of this energy. However, this aether cannot be thought of as a physical medium if it is to be Lorentz invariant such that there is no contradiction with Einstein's theory of special relativity.[1]
Physics currently lacks a full theoretical model for understanding zero-point energy; in particular, the discrepancy between theorized and observed vacuum energy is a source of major contention.[4] Physicists Richard Feynman and John Wheeler calculated the zero-point radiation of the vacuum to be an order of magnitude greater than nuclear energy, with a single light bulb containing enough energy to boil all the world's oceans.[5] Yet according to Einstein's theory of general relativity, any such energy would gravitate and the experimental evidence from both the expansion of the universe, dark energy and the Casimir effect shows any such energy to be exceptionally weak. A popular proposal that attempts to address this issue is to say that the fermion field has a negative zero-point energy, while the boson field has positive zero-point energy and thus these energies somehow cancel each other out.[6][7] This idea would be true if supersymmetry were an exact symmetry of nature; however, the LHC at CERN has so far found no evidence to support it. Moreover, it is known that if supersymmetry is valid at all, it is at most a broken symmetry, only true at very high energies, and no one has been able to show a theory where zero-point cancellations occur in the low energy universe we observe today.[7] This discrepancy is known as the cosmological constant problem and it is one of the greatest unsolved mysteries in physics. Many physicists believe that "the vacuum holds the key to a full understanding of nature".[8]
https://en.wikipedia.org/wiki/Zero-point_energy
Necessity of the vacuum field in QED[edit]
The vacuum state of the "free" electromagnetic field (that with no sources) is defined as the ground state in which nkλ = 0 for all modes (k, λ). The vacuum state, like all stationary states of the field, is an eigenstate of the Hamiltonian but not the electric and magnetic field operators. In the vacuum state, therefore, the electric and magnetic fields do not have definite values. We can imagine them to be fluctuating about their mean value of zero.
In a process in which a photon is annihilated (absorbed), we can think of the photon as making a transition into the vacuum state. Similarly, when a photon is created (emitted), it is occasionally useful to imagine that the photon has made a transition out of the vacuum state.[55] An atom, for instance, can be considered to be "dressed" by emission and reabsorption of "virtual photons" from the vacuum. The vacuum state energy described by ∑kλ ħωk2is infinite. We can make the replacement:
the zero-point energy density is:
or in other words the spectral energy density of the vacuum field:
The zero-point energy density in the frequency range from ω1 to ω2 is therefore:
This can be large even in relatively narrow "low frequency" regions of the spectrum. In the optical region from 400 to 700 nm, for instance, the above equation yields around 220 erg/cm3.
We showed in the above section that the zero-point energy can be eliminated from the Hamiltonian by the normal ordering prescription. However, this elimination does not mean that the vacuum field has been rendered unimportant or without physical consequences. To illustrate this point we consider a linear dipole oscillator in the vacuum. The Hamiltonian for the oscillator plus the field with which it interacts is:
This has the same form as the corresponding classical Hamiltonian and the Heisenberg equations of motion for the oscillator and the field are formally the same as their classical counterparts. For instance the Heisenberg equations for the coordinate x and the canonical momentum p = mẋ +eAc of the oscillator are:
or:
since the rate of change of the vector potential in the frame of the moving charge is given by the convective derivative
For nonrelativistic motion we may neglect the magnetic force and replace the expression for mẍ by:
Above we have made the electric dipole approximation in which the spatial dependence of the field is neglected. The Heisenberg equation for akλ is found similarly from the Hamiltonian to be:
In the electric dipole approximation.
In deriving these equations for x, p, and akλ we have used the fact that equal-time particle and field operators commute. This follows from the assumption that particle and field operators commute at some time (say, t = 0) when the matter-field interpretation is presumed to begin, together with the fact that a Heisenberg-picture operator A(t) evolves in time as A(t) = U†(t)A(0)U(t), where U(t) is the time evolution operator satisfying
Alternatively, we can argue that these operators must commute if we are to obtain the correct equations of motion from the Hamiltonian, just as the corresponding Poisson brackets in classical theory must vanish in order to generate the correct Hamilton equations. The formal solution of the field equation is:
and therefore the equation for ȧkλ may be written:
where:
and:
It can be shown that in the radiation reaction field, if the mass m is regarded as the "observed" mass then we can take:
The total field acting on the dipole has two parts, E0(t) and ERR(t). E0(t) is the free or zero-point field acting on the dipole. It is the homogeneous solution of the Maxwell equation for the field acting on the dipole, i.e., the solution, at the position of the dipole, of the wave equation
satisfied by the field in the (source free) vacuum. For this reason E0(t) is often referred to as the "vacuum field", although it is of course a Heisenberg-picture operator acting on whatever state of the field happens to be appropriate at t = 0. ERR(t) is the source field, the field generated by the dipole and acting on the dipole.
Using the above equation for ERR(t) we obtain an equation for the Heisenberg-picture operator that is formally the same as the classical equation for a linear dipole oscillator:
where τ = 2e23mc3. in this instance we have considered a dipole in the vacuum, without any "external" field acting on it. the role of the external field in the above equation is played by the vacuum electric field acting on the dipole.
Classically, a dipole in the vacuum is not acted upon by any "external" field: if there are no sources other than the dipole itself, then the only field acting on the dipole is its own radiation reaction field. In quantum theory however there is always an "external" field, namely the source-free or vacuum field E0(t).
According to our earlier equation for akλ(t) the free field is the only field in existence at t = 0 as the time at which the interaction between the dipole and the field is "switched on". The state vector of the dipole-field system at t = 0 is therefore of the form
where |vac⟩ is the vacuum state of the field and |ψD⟩ is the initial state of the dipole oscillator. The expectation value of the free field is therefore at all times equal to zero:
since akλ(0)|vac⟩ = 0. however, the energy density associated with the free field is infinite:
The important point of this is that the zero-point field energy HF does not affect the Heisenberg equation for akλ since it is a c-number or constant (i.e. an ordinary number rather than an operator) and commutes with akλ. We can therefore drop the zero-point field energy from the Hamiltonian, as is usually done. But the zero-point field re-emerges as the homogeneous solution for the field equation. A charged particle in the vacuum will therefore always see a zero-point field of infinite density. This is the origin of one of the infinities of quantum electrodynamics, and it cannot be eliminated by the trivial expedient dropping of the term ∑kλ ħωk2 in the field Hamiltonian.
The free field is in fact necessary for the formal consistency of the theory. In particular, it is necessary for the preservation of the commutation relations, which is required by the unitary of time evolution in quantum theory:
We can calculate [z(t),pz(t)] from the formal solution of the operator equation of motion
Using the fact that
and that equal-time particle and field operators commute, we obtain:
For the dipole oscillator under consideration it can be assumed that the radiative damping rate is small compared with the natural oscillation frequency, i.e., τω0 ≪ 1. Then the integrand above is sharply peaked at ω = ω0 and:
the necessity of the vacuum field can also be appreciated by making the small damping approximation in
and
Without the free field E0(t) in this equation the operator x(t) would be exponentially dampened, and commutators like [z(t),pz(t)] would approach zero for t ≫ 1τω2
0. With the vacuum field included, however, the commutator is iħ at all times, as required by unitarity, and as we have just shown. A similar result is easily worked out for the case of a free particle instead of a dipole oscillator.[98]
What we have here is an example of a "fluctuation-dissipation elation". Generally speaking if a system is coupled to a bath that can take energy from the system in an effectively irreversible way, then the bath must also cause fluctuations. The fluctuations and the dissipation go hand in hand we cannot have one without the other. In the current example the coupling of a dipole oscillator to the electromagnetic field has a dissipative component, in the form of the zero-point (vacuum) field; given the existence of radiation reaction, the vacuum field must also exist in order to preserve the canonical commutation rule and all it entails.
The spectral density of the vacuum field is fixed by the form of the radiation reaction field, or vice versa: because the radiation reaction field varies with the third derivative of x, the spectral energy density of the vacuum field must be proportional to the third power of ω in order for [z(t),pz(t)] to hold. In the case of a dissipative force proportional to ẋ, by contrast, the fluctuation force must be proportional to in order to maintain the canonical commutation relation.[98] This relation between the form of the dissipation and the spectral density of the fluctuation is the essence of the fluctuation-dissipation theorem.[77]
The fact that the canonical commutation relation for a harmonic oscillator coupled to the vacuum field is preserved implies that the zero-point energy of the oscillator is preserved. it is easy to show that after a few damping times the zero-point motion of the oscillator is in fact sustained by the driving zero-point field.[99]
https://en.wikipedia.org/wiki/Zero-point_energy#Necessity_of_the_vacuum_field_in_QED
The cosmic microwave background (CMB, CMBR), in Big Bang cosmology, is electromagnetic radiation which is a remnant from an early stage of the universe, also known as "relic radiation".[1] The CMB is faint cosmic background radiation filling all space. It is an important source of data on the early universe because it is the oldest electromagnetic radiation in the universe, dating to the epoch of recombination. With a traditional optical telescope, the space between stars and galaxies (the background) is completely dark. However, a sufficiently sensitive radio telescope shows a faint background noise, or glow, almost isotropic, that is not associated with any star, galaxy, or other object. This glow is strongest in the microwave region of the radio spectrum. The accidental discovery of the CMBin 1965 by American radio astronomers Arno Penzias and Robert Wilson[2][3] was the culmination of work initiated in the 1940s, and earned the discoverers the 1978 Nobel Prize in Physics.
https://en.wikipedia.org/wiki/Cosmic_microwave_background
In quantum physics, a quantum fluctuation (or vacuum state fluctuation or vacuum fluctuation) is the temporary random change in the amount of energy in a point in space,[2] as prescribed by Werner Heisenberg's uncertainty principle. They are tiny random fluctuations in the values of the fields which represent elementary particles, such as electric and magnetic fields which represent the electromagnetic force carried by photons, W and Z fields which carry the weak force, and gluon fields which carry the strong force.[3] Vacuum fluctuations appear as virtual particles, which are always created in particle-antiparticle pairs.[4] Since they are created spontaneously without a source of energy, vacuum fluctuations and virtual particles are said to violate the conservation of energy. This is theoretically allowable because the particles annihilate each other within a time limit determined by the uncertainty principle so they are not directly observable.[4][3] The uncertainty principlestates the uncertainty in energy and time can be related by[5] , where 12ħ ≈ 5,27286×10−35 Js. This means that pairs of virtual particles with energy and lifetime shorter than are continually created and annihilated in empty space. Although the particles are not directly detectable, the cumulative effects of these particles are measurable. For example, without quantum fluctuations the "bare" mass and charge of elementary particles would be infinite; from renormalization theory the shielding effect of the cloud of virtual particles is responsible for the finite mass and charge of elementary particles. Another consequence is the Casimir effect. One of the first observations which was evidence for vacuum fluctuations was the Lamb shift in hydrogen. In July 2020, scientists reported that quantum vacuum fluctuations can influence the motion of macroscopic, human-scale objects by measuring correlations below the standard quantum limitbetween the position/momentum uncertainty of the mirrors of LIGO and the photon number/phase uncertainty of light that they reflect.[6][7][8]
https://en.wikipedia.org/wiki/Quantum_fluctuation
https://en.wikipedia.org/wiki/Quantum_annealing
https://en.wikipedia.org/wiki/Quantum_foam
Vacuum energy is an underlying background energy that exists in space throughout the entire Universe.[1] The vacuum energy is a special case of zero-point energy that relates to the quantum vacuum.[2]
Why does the zero-point energy of the vacuum not cause a large cosmological constant? What cancels it out?
Summing over all possible oscillators at all points in space gives an infinite quantity. To remove this infinity, one may argue that only differences in energy are physically measurable, much as the concept of potential energy has been treated in classical mechanics for centuries. This argument is the underpinning of the theory of renormalization. In all practical calculations, this is how the infinity is handled.
Vacuum energy can also be thought of in terms of virtual particles (also known as vacuum fluctuations) which are created and destroyed out of the vacuum. These particles are always created out of the vacuum in particle–antiparticle pairs, which in most cases shortly annihilate each other and disappear. However, these particles and antiparticles may interact with others before disappearing, a process which can be mapped using Feynman diagrams. Note that this method of computing vacuum energy is mathematically equivalent to having a quantum harmonic oscillator at each point and, therefore, suffers the same renormalization problems.
Additional contributions to the vacuum energy come from spontaneous symmetry breaking in quantum field theory.
https://en.wikipedia.org/wiki/Vacuum_energy
Above. Property of Material , origins, scale, hydrogen emissions spectra, consideration to possibility of fine state no two state match without signal and with proper measure ; consider approximate vac model and limit of math ; actual v. model ; zero absou zero idea zero or number line force zero or concep zero type zero ; heterogenous or control at homogeniety supercession; etc..
Description[edit]
The defining criterion of a shock wave is that the bulk velocity of the plasma drops from "supersonic" to "subsonic", where the speed of sound cs is defined by where is the ratio of specific heats, is the pressure, and is the density of the plasma.
A common complication in astrophysics is the presence of a magnetic field. For instance, the charged particles making up the solar wind follow spiral paths along magnetic field lines. The velocity of each particle as it gyrates around a field line can be treated similarly to a thermal velocity in an ordinary gas, and in an ordinary gas the mean thermal velocity is roughly the speed of sound. At the bow shock, the bulk forward velocity of the wind (which is the component of the velocity parallel to the field lines about which the particles gyrate) drops below the speed at which the particles are gyrating.
https://en.wikipedia.org/wiki/Bow_shock
Comet Grigg–Skjellerup (formally designated 26P/Grigg–Skjellerup) is a periodic comet. It was visited by the Giotto probe in July 1992.[5]

https://en.wikipedia.org/wiki/26P/Grigg–Skjellerup
| Brownleeite | |
|---|---|
| General | |
| Category | Native element class, Fersilicite group |
| Formula (repeating unit) | MnSi |
| Strunz classification | 1.XX.00 |
| Dana classification | 01.01.23.07 |
| Crystal system | Isometric |
| Crystal class | Tetartoidal (23) H-M symbol: (23) |
| Space group | P213 |
| Identification | |
| Crystal habit | Cubic grain in microscopic dust particle (< 2.5 μm) |
| References | [1][2] |
A mirror galvanometer is an ammeter that indicates it has sensed an electric current by deflecting a light beam with a mirror. The beam of light projected on a scale acts as a long massless pointer. In 1826, Johann Christian Poggendorffdeveloped the mirror galvanometer for detecting electric currents. The apparatus is also known as a spot galvanometerafter the spot of light produced in some models.
Mirror galvanometers were used extensively in scientific instruments before reliable, stable electronic amplifiers were available. The most common uses were as recording equipment for seismometers and submarine cables used for telegraphy.
In modern times, the term mirror galvanometer is also used for devices that move laser beams by rotating a mirror through a galvanometer set-up, often with a servo-like control loop. The name is often abbreviated as galvo.
Kelvin's galvanometer[edit]
The mirror galvanometer was improved significantly by William Thomson, later to become Lord Kelvin. He coined the term mirror galvanometer and patented the device in 1858. Thomson intended the instrument to read weak signal currents on very long submarine telegraph cables.[1] This instrument was far more sensitive than any which preceded it, enabling the detection of the slightest defect in the core of a cable during its manufacture and submersion.
Thomson decided that he needed an extremely sensitive instrument after he took part in the failed attempt to lay a transatlantic telegraph cable in 1857. He worked on the device while waiting for a new expedition the following year. He first looked at improving a galvanometer used by Hermann von Helmholtz to measure the speed of nerve signals in 1849. Helmholtz's galvanometer had a mirror fixed to the moving needle, which was used to project a beam of light onto the opposite wall, thus greatly amplifying the signal. Thomson intended to make this more sensitive by reducing the mass of the moving parts, but in a flash of inspiration while watching the light reflected from his monocle suspended around his neck, he realised that he could dispense with the needle and its mounting altogether. He instead used a small piece of mirrored glass with a small piece of magnetised steel glued on the back. This was suspended by a thread in the magnetic field of the fixed sensing coil. In a hurry to try the idea, Thomson first used a hair from his dog, but later used a silk thread from the dress of his niece Agnes.[1]
The following is adapted from a contemporary account of Thomson's instrument:[2]
Moving coil galvanometer
Moving coil galvanometer was developed independently by Marcel Deprez and Jacques-Arsène d'Arsonval about 1880. Deprez's galvanometer was developed for high currents, while D'Arsonval designed his to measure weak currents. Unlike in the Kelvin's galvanometer, in this type of galvanometer the magnet is stationary and the coil is suspended in the magnet gap. The mirror attached to the coil frame rotates together with it. This form of instrument can be more sensitive and accurate and it replaced the Kelvin's galvanometer in most applications. The moving coil galvanometer is practically immune to ambient magnetic fields. Another important feature is self-damping generated by the electro-magnetic forces due to the currents induced in the coil by its movements the magnetic field. These are proportional to the angular velocity of the coil.
In modern times, high-speed mirror galvanometers are employed in laser light shows to move the laser beams and produce colorful geometric patterns in fog around the audience. Such high speed mirror galvanometers have proved to be indispensable in industry for laser marking systems for everything from laser etching hand tools, containers, and parts to batch-coding semiconductor wafers in semiconductor device fabrication. They typically control X and Y directions on Nd:YAG and CO2 laser markers to control the position of the infrared power laser spot. Laser ablation, laser beam machining and wafer dicing are all industrial areas where high-speed mirror galvanometers can be found.
This moving coil galvanometer is mainly used to measure very feeble or low currents of order 10−9 A.
To linearise the magnetic field across the coil throughout the galvanometer's range of movement, the d'Arsonval design of a soft iron cylinder is placed inside the coil without touching it. This gives a consistent radial field, rather than a parallel linear field.
See also[edit]
https://en.wikipedia.org/wiki/Mirror_galvanometer
https://en.wikipedia.org/wiki/String_galvanometer
https://en.wikipedia.org/wiki/Current_mirror
https://en.wikipedia.org/wiki/Cold_mirror
https://en.wikipedia.org/wiki/Index_case
https://en.wikipedia.org/wiki/Disk_mirroring
https://en.wikipedia.org/wiki/Retroreflector
https://en.wikipedia.org/wiki/Retroreflector#Phase-conjugate_mirror
Parity of Zero
Zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": it is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—and x and 0 + x always have the same parity.
Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all.[1]
Among the general public, the parity of zero can be a source of confusion. In reaction time experiments, most people are slower to identify 0 as even than 2, 4, 6, or 8. Some students of mathematics—and some teachers—think that zero is odd, or both even and odd, or neither. Researchers in mathematics education propose that these misconceptions can become learning opportunities. Studying equalities like 0 × 2 = 0 can address students' doubts about calling 0 a number and using it in arithmetic. Class discussions can lead students to appreciate the basic principles of mathematical reasoning, such as the importance of definitions. Evaluating the parity of this exceptional number is an early example of a pervasive theme in mathematics: the abstraction of a familiar concept to an unfamiliar setting.
Mathematical contexts[edit]
Countless results in number theory invoke the fundamental theorem of arithmetic and the algebraic properties of even numbers, so the above choices have far-reaching consequences. For example, the fact that positive numbers have unique factorizations means that one can determine whether a number has an even or odd number of distinct prime factors. Since 1 is not prime, nor does it have prime factors, it is a product of 0 distinct primes; since 0 is an even number, 1 has an even number of distinct prime factors. This implies that the Möbius function takes the value μ(1) = 1, which is necessary for it to be a multiplicative function and for the Möbius inversion formula to work.[14]
Not being odd[edit]
A number n is odd if there is an integer k such that n = 2k + 1. One way to prove that zero is not odd is by contradiction: if 0 = 2k + 1 then k = −1/2, which is not an integer.[15] Since zero is not odd, if an unknown number is proven to be odd, then it cannot be zero. This apparently trivial observation can provide a convenient and revealing proof explaining why an odd number is nonzero.
A classic result of graph theory states that a graph of odd order (having an odd number of vertices) always has at least one vertex of even degree. (The statement itself requires zero to be even: the empty graph has an even order, and an isolated vertex has an even degree.)[16] In order to prove the statement, it is actually easier to prove a stronger result: any odd-order graph has an odd number of even degree vertices. The appearance of this odd number is explained by a still more general result, known as the handshaking lemma: any graph has an even number of vertices of odd degree.[17]Finally, the even number of odd vertices is naturally explained by the degree sum formula.
Sperner's lemma is a more advanced application of the same strategy. The lemma states that a certain kind of coloring on a triangulation of a simplexhas a subsimplex that contains every color. Rather than directly construct such a subsimplex, it is more convenient to prove that there exists an odd number of such subsimplices through an induction argument.[18] A stronger statement of the lemma then explains why this number is odd: it naturally breaks down as (n + 1) + n when one considers the two possible orientations of a simplex.[19]
Even-odd alternation[edit]
The fact that zero is even, together with the fact that even and odd numbers alternate, is enough to determine the parity of every other natural number. This idea can be formalized into a recursive definition of the set of even natural numbers:
- 0 is even.
- (n + 1) is even if and only if n is not even.
This definition has the conceptual advantage of relying only on the minimal foundations of the natural numbers: the existence of 0 and of successors. As such, it is useful for computer logic systems such as LF and the Isabelle theorem prover.[20] With this definition, the evenness of zero is not a theorem but an axiom. Indeed, "zero is an even number" may be interpreted as one of the Peano axioms, of which the even natural numbers are a model.[21] A similar construction extends the definition of parity to transfinite ordinal numbers: every limit ordinal is even, including zero, and successors of even ordinals are odd.[22]
The classic point in polygon test from computational geometry applies the above ideas. To determine if a point lies within a polygon, one casts a ray from infinity to the point and counts the number of times the ray crosses the edge of polygon. The crossing number is even if and only if the point is outside the polygon. This algorithmworks because if the ray never crosses the polygon, then its crossing number is zero, which is even, and the point is outside. Every time the ray does cross the polygon, the crossing number alternates between even and odd, and the point at its tip alternates between outside and inside.[23]
In graph theory, a bipartite graph is a graph whose vertices are split into two colors, such that neighboring vertices have different colors. If a connected graph has no odd cycles, then a bipartition can be constructed by choosing a base vertex v and coloring every vertex black or white, depending on whether its distance from v is even or odd. Since the distance between v and itself is 0, and 0 is even, the base vertex is colored differently from its neighbors, which lie at a distance of 1.[24]
Algebraic patterns[edit]
In abstract algebra, the even integers form various algebraic structuresthat require the inclusion of zero. The fact that the additive identity (zero) is even, together with the evenness of sums and additive inverses of even numbers and the associativity of addition, means that the even integers form a group. Moreover, the group of even integers under addition is a subgroup of the group of all integers; this is an elementary example of the subgroup concept.[16] The earlier observation that the rule "even − even = even" forces 0 to be even is part of a general pattern: any nonempty subset of an additive group that is closed under subtraction must be a subgroup, and in particular, must contain the identity.[25]
Since the even integers form a subgroup of the integers, they partition the integers into cosets. These cosets may be described as the equivalence classes of the following equivalence relation: x ~ y if (x − y) is even. Here, the evenness of zero is directly manifested as the reflexivity of the binary relation ~.[26] There are only two cosets of this subgroup—the even and odd numbers—so it has index 2.
Analogously, the alternating group is a subgroup of index 2 in the symmetric group on n letters. The elements of the alternating group, called even permutations, are the products of even numbers of transpositions. The identity map, an empty product of no transpositions, is an even permutation since zero is even; it is the identity element of the group.[27]
The rule "even × integer = even" means that the even numbers form an ideal in the ring of integers, and the above equivalence relation can be described as equivalence modulo this ideal. In particular, even integers are exactly those integers k where k ≡ 0 (mod 2). This formulation is useful for investigating integer zeroes of polynomials.[28]
2-adic order[edit]
There is a sense in which some multiples of 2 are "more even" than others. Multiples of 4 are called doubly even, since they can be divided by 2 twice. Not only is zero divisible by 4, zero has the unique property of being divisible by every power of 2, so it surpasses all other numbers in "evenness".[1]
One consequence of this fact appears in the bit-reversed ordering of integer data types used by some computer algorithms, such as the Cooley–Tukeyfast Fourier transform. This ordering has the property that the farther to the left the first 1 occurs in a number's binary expansion, or the more times it is divisible by 2, the sooner it appears. Zero's bit reversal is still zero; it can be divided by 2 any number of times, and its binary expansion does not contain any 1s, so it always comes first.[29]
Although 0 is divisible by 2 more times than any other number, it is not straightforward to quantify exactly how many times that is. For any nonzero integer n, one may define the 2-adic order of n to be the number of times n is divisible by 2. This description does not work for 0; no matter how many times it is divided by 2, it can always be divided by 2 again. Rather, the usual convention is to set the 2-order of 0 to be infinity as a special case.[30] This convention is not peculiar to the 2-order; it is one of the axioms of an additive valuation in higher algebra.[31]
The powers of two—1, 2, 4, 8, ...—form a simple sequence of numbers of increasing 2-order. In the 2-adic numbers, such sequences actually convergeto zero.[32]
https://en.wikipedia.org/wiki/Parity_of_zero
In mathematics, the classic Möbius inversion formula is a relation between pairs of arithmetic functions, each defined from the other by sums over divisors. It was introduced into number theory in 1832 by August Ferdinand Möbius.[1]
A large generalization of this formula applies to summation over an arbitrary locally finite partially ordered set, with Möbius' classical formula applying to the set of the natural numbers ordered by divisibility: see incidence algebra.
https://en.wikipedia.org/wiki/Möbius_inversion_formula
In mathematics, the Möbius energy of a knot is a particular knot energy, i.e., a functional on the space of knots. It was discovered by Jun O'Hara, who demonstrated that the energy blows up as the knot's strands get close to one another.[1] This is a useful property because it prevents self-intersection and ensures the result under gradient descent is of the same knot type.
https://en.wikipedia.org/wiki/Möbius_energy
Signed zero is zero with an associated sign. In ordinary arithmetic, the number 0 does not have a sign, so that −0, +0 and 0 are identical. However, in computing, some number representations allow for the existence of two zeros, often denoted by −0 (negative zero) and +0 (positive zero), regarded as equal by the numerical comparison operations but with possible different behaviors in particular operations. This occurs in the sign and magnitudeand ones' complement signed number representations for integers, and in most floating-point number representations. The number 0 is usually encoded as +0, but can be represented by either +0 or −0.
The IEEE 754 standard for floating-point arithmetic (presently used by most computers and programming languages that support floating-point numbers) requires both +0 and −0. Real arithmetic with signed zeros can be considered a variant of the extended real number line such that 1/−0 = −∞and 1/+0 = +∞; division is only undefined for ±0/±0 and ±∞/±∞.
Negatively signed zero echoes the mathematical analysis concept of approaching 0 from below as a one-sided limit, which may be denoted by x → 0−, x → 0−, or x → ↑0. The notation "−0" may be used informally to denote a negative number that has been rounded to zero. The concept of negative zero also has some theoretical applications in statistical mechanics and other disciplines.
It is claimed that the inclusion of signed zero in IEEE 754 makes it much easier to achieve numerical accuracy in some critical problems,[1] in particular when computing with complex elementary functions.[2] On the other hand, the concept of signed zero runs contrary to the general assumption made in most mathematical fields that negative zero is the same thing as zero. Representations that allow negative zero can be a source of errors in programs, if software developers do not take into account that while the two zero representations behave as equal under numeric comparisons, they yield different results in some operations.
https://en.wikipedia.org/wiki/Signed_zero
The zero-energy universe hypothesis proposes that the total amount of energy in the universe is exactly zero: its amount of positive energy in the form of matter is exactly canceled out by its negative energy in the form of gravity.[1] Some physicists, such as Lawrence Krauss, Stephen Hawking or Alexander Vilenkin, call or called this state "a universe from nothingness", although the zero-energy universe model requires both a matter field with positive energy and a gravitational field with negative energy to exist.[2] The hypothesis is broadly discussed in popular sources.[3][4][5]
https://en.wikipedia.org/wiki/Zero-energy_universe
Gravitational energy or gravitational potential energy is the potential energy a massive object has in relation to another massive object due to gravity. It is the potential energy associated with the gravitational field, which is released (converted into kinetic energy) when the objects fall towards each other. Gravitational potential energy increases when two objects are brought further apart.
For two pairwise interacting point particles, the gravitational potential energy is given by
where and are the masses of the two particles, is the distance between them, and is the gravitational constant.[1]
Close to the Earth's surface, the gravitational field is approximately constant, and the gravitational potential energy of an object reduces to
where is the object's mass, is the gravity of Earth, and is the height of the object's center of mass above a chosen reference level.[1]
https://en.wikipedia.org/wiki/Gravitational_energy
Energy
Outline History Index
Fundamental
concepts
Energy Units Conservation of energy Energetics Energy transformation Energy condition Energy transition Energy level Energy system Mass Negative mass Mass–energy equivalence Power Thermodynamics Quantum thermodynamics Laws of thermodynamics Thermodynamic system Thermodynamic state Thermodynamic potential Thermodynamic free energy Irreversible process Thermal reservoir Heat transfer Heat capacity Volume (thermodynamics) Thermodynamic equilibrium Thermal equilibrium Thermodynamic temperature Isolated system Entropy Free entropy Entropic force Negentropy Work Exergy Enthalpy
Types
Kinetic Internal Thermal Potential Gravitational Elastic Electric potential energy Mechanical Interatomic potential Quantum potential Electrical Magnetic Ionization Radiant Binding Nuclear binding energy Gravitational binding energy Quantum chromodynamics binding energy Dark Quintessence Phantom Negative Chemical Rest Sound energy Surface energy Vacuum energy Zero-point energy Quantum potential Quantum fluctuation
Energy carriers
Radiation Enthalpy Mechanical wave Sound wave Fuel fossil fuel Heat Latent heat Work Electricity Battery Capacitor
Primary energy
Fossil fuel Coal Petroleum Natural gas Nuclear fuel Natural uranium Radiant energy Solar Wind Hydropower Marine energy Geothermal Bioenergy Gravitational energy
Energy system
components
Energy engineering Oil refinery Electric power Fossil fuel power station Cogeneration Integrated gasification combined cycle Nuclear power Nuclear power plant Radioisotope thermoelectric generator Solar power Photovoltaic system Concentrated solar power Solar thermal energy Solar power tower Solar furnace Wind power Wind farm Airborne wind energy Hydropower Hydroelectricity Wave farm Tidal power Geothermal power Biomass
Use and
supply
Energy consumption Energy storage World energy consumption Energy security Energy conservation Efficient energy use Transport Agriculture Renewable energy Sustainable energy Energy policy Energy development Worldwide energy supply South America USA Mexico Canada Europe Asia Africa Australia
Misc.
Jevons paradox Carbon footprint
Category Category Commons page Commons Portal Portal WikiProject WikiProject
Categories: Forms of energyGravityConservation lawsTensors in general relativity
https://en.wikipedia.org/wiki/Gravitational_energy
https://en.wikipedia.org/wiki/Outline_of_energy
https://en.wikipedia.org/wiki/Retroreflector
In politics, “poodle” is an insult used to describe a politician who obediently or passively follows the lead of others.[1] It is considered to be equivalent to lackey.[2] Usage of the term is thought to relate to the passive and obedient nature of the type of dog. Colette Avital unsuccessfully tried to have the term’s use banned from the Knesset in June 2001.[3]
During the 2000s, it was used against Tony Blair with regard to his close relationship with George W. Bush and the involvement of the United Kingdom in the Iraq War. The singer George Michael infamously used it in his song “Shoot the Dog” in July 2002, the video of which showed Blair as the “poodle” on the lawn of the White House.[4] However, it has somewhat of a longer history as a label to criticise British Prime Ministers who are perceived to be too close to the United States.[5]
See also[edit]

The Schlenk line (also vacuum gas manifold) is a commonly used chemistry apparatus developed by Wilhelm Schlenk. It consists of a dual manifold with several ports.[1] One manifold is connected to a source of purified inert gas, while the other is connected to a vacuum pump. The inert-gas line is vented through an oil bubbler, while solvent vapors and gaseous reaction products are prevented from contaminating the vacuum pump by a liquid-nitrogen or dry-ice/acetone cold trap. Special stopcocks or Teflon taps allow vacuum or inert gas to be selected without the need for placing the sample on a separate line.
Schlenk lines are useful for safely and successfully manipulating moisture- and air-sensitive compounds. The vacuum is also often used to remove the last traces of solvent from a sample. Vacuum and gas manifolds often have many ports and lines, and with care, it is possible for several reactions or operations to be run simultaneously.
When the reagents are highly susceptible to oxidation, traces of oxygen may pose a problem. Then, for the removal of oxygen below the ppm level, the inert gas needs to be purified by passing it through a deoxygenation catalyst.[2] This is usually a column of copper(I) or manganese(II) oxide, which reacts with oxygen traces present in the inert gas.
Techniques[edit]
The main techniques associated with the use of a Schlenk line include:
- counterflow additions, where air-stable reagents are added to the reaction vessel against a flow of inert gas;
- the use of syringes and rubber septa to transfer liquids and solutions;[3]
- cannula transfer, where liquids or solutions of air-sensitive reagents are transferred between different vessels stoppered with septa using a long thin tube known as a cannula. Liquid flow is supported by vacuum or inert-gas pressure.[4]
Glassware are usually connected by tightly fitting and greased ground glass joints. Round bends of glass tubing with ground glass joints may be used to adjust the orientation of various vessels. Glassware is necessarily purged of outside air by alternating application of vacuum and inert gas. The solvents and reagents that are used are also purged of air and water using various methods.
Filtration under inert conditions poses a special challenge that is usually tackled with specialized glassware. A Schlenk filter consists of sintered glass funnel fitted with joints and stopcocks. By fitting the pre-dried funnel and receiving flask to the reaction flask against a flow of nitrogen, carefully inverting the set-up, and turning on the vacuum appropriately, the filtration may be accomplished with minimal exposure to air.
Dangers[edit]
The main dangers associated with the use of a Schlenk line are the risks of an implosion or explosion. An implosion can occur due to the use of vacuum and flaws in the glass apparatus.
An explosion can occur due to the common use of liquid nitrogen in the cold trap, used to protect the vacuum pump from solvents. If a reasonable amount of air is allowed to enter the Schlenk line, liquid oxygen can condense into the cold trap as a pale blue liquid. An explosion may occur due to reaction of the liquid oxygen with any organic compounds also in the trap.
Gallery[edit]
See also[edit]
- Air-free technique gives a broad overview of methods including:
- Glovebox – used to manipulate air-sensitive (oxygen- or moisture-sensitive) chemicals.
- Schlenk flask – reaction vessel for handling air-sensitive compounds.
- Perkin triangle – used for the distillation of air-sensitive compounds.
Further reading[edit]
- Sella, Andrea (January 2008). "Schlenk Apparatus". Chemistry World: 69. Retrieved 2008-01-30.
- Tidwell, Thomas (2001). "Wilhelm Schlenk: The Man Behind the Flask". Angewandte Chemie International Edition. 40 (2): 331–337. doi:10.1002/1521-3773(20010119)40:2<331::AID-ANIE331>3.0.CO;2-E. PMID 11180319.
- Jürgen Heck. "The Integrated Synthesis Course: Schlenk Technique" (PDF). University of Hamburg. Archived from the original (reprint at Norwegian University of Science and Technology) on 2008-03-09.
- "Handling Air-Sensitive Reagents" (PDF). Sigma-Aldrich.
- "Handling Air-Sensitive Reagents" Sigma-Aldrich.
External links[edit]
- Rob Toreki (25 May 2004). "Schlenk Lines and Vacuum Lines". The Glassware Gallery. Interactive Learning Paradigms Incorporated.
- Preparation of a Manganese oxide column for inert gas purification from oxygen traces
https://en.wikipedia.org/wiki/Schlenk_line
Constituents[edit]
The lower compartment of the desiccator contains lumps of silica gel, freshly calcined quicklime, Drierite or (not as effective) anhydrous calcium chlorideto absorb water vapor. The substance needing desiccation is put in the upper compartment, usually on a glazed, perforated ceramic plate. The ground-glass rim of the desiccator lid must be greased with a thin layer of vacuum grease, petroleum jelly or other lubricant to ensure an airtight seal.
In order to prevent damage to a desiccator the lid should be carefully slid on and off instead of being directly placed onto the base.[1]
Operation[edit]
In laboratory use, the most common desiccators are circular and made of heavy glass. There is usually a removable platform on which the items to be stored are placed. The desiccant, usually an otherwise-inert solid such as silica gel, fills the space under the platform. Colour changing silica may be used to indicate when it should be refreshed. Indication gels typically change from blue to pink as they absorb moisture but other colours may be used.
A stopcock may be included to permit the desiccator to be evacuated. Such models are usually known as vacuum desiccators. When a vacuum is to be applied, it is a common practice to criss-cross the vacuum desiccator with tape, or to place it behind a screen to minimize damage or injury caused by an implosion. To maintain a good seal, vacuum grease is usually applied to the flanges.
See also[edit]

Operation[edit]
The drying pistol consists of two concentric barrels; the inner is connected to a vacuum source via a trap.[3] The outer barrel is connected at the bottom to a round bottom flask, and a condenser. To operate the drying pistol, a sample is placed within the inner barrel, and the barrel is evacuated. The round bottom flask, filled with an appropriate solvent, is heated to a boil. Hot vapors warm the inner barrel; losses are avoided with the condenser. By choosing the appropriate solvent, the temperature at which the sample is dried can be selected.
The trap is filled with an appropriate material: water is removed with phosphorus pentoxide, acidic gases by potassium or sodium hydroxide, and organic solvents by thin pieces of paraffin. However, use of these agents has been shown to have little efficacy. Generally, the main impurity to be removed is water.[2][4]
This set-up allows the desiccation of heat-sensitive compounds under relatively mild conditions. Removing these trace impurities is especially important to give good results for elemental analysis and gravimetric analysis.
Pages in category "Laboratory glassware"
The following 84 pages are in this category, out of 84 total. This list may not reflect recent changes (learn more).
B
C
G
S
W
Subcategories
This category has the following 4 subcategories, out of 4 total.
Pages in category "Vacuum systems"
The following 20 pages are in this category, out of 20 total. This list may not reflect recent changes (learn more).
V
A vacuum furnace is a type of furnace in which the product in the furnace is surrounded by a vacuum during processing. The absence of air or other gases prevents oxidation, heat loss from the product through convection, and removes a source of contamination. This enables the furnace to heat materials (typically metals and ceramics) to temperatures as high as 3,000 °C (5,432 °F) [1] with select materials. Maximum furnace temperatures and vacuum levels depend on melting points and vapor pressures of heated materials. Vacuum furnaces are used to carry out processes such as annealing, brazing, sintering and heat treatment with high consistency and low contamination.
Characteristics of a vacuum furnace are:
- Uniform temperatures in the range. 800–3,000 °C (1,500–5,400 °F)
- Commercially available vacuum pumping systems can reach vacuum levels as low as 1×10−11 torrs (1.3×10−11 mbar; 1.3×10−14 atm)
- Temperature can be controlled within a heated zone, typically surrounded by heat shielding or insulation.
- Low contamination of the product by carbon, oxygen and other gases.
- Vacuum pumping systems remove low temperature by-products from the process materials during heating, resulting in a higher purity end product.
- Quick cooling (quenching) of product can be used to shorten process cycle times.
- The process can be computer controlled to ensure repeatability.
Heating metals to high temperatures in open to atmosphere normally causes rapid oxidation, which is undesirable. A vacuum furnace removes the oxygen and prevents this from happening.
An inert gas, such as Argon, is often used to quickly cool the treated metals back to non-metallurgical levels (below 400 °F [200 °C]) after the desired process in the furnace.[2] This inert gas can be pressurized to two times atmosphere or more, then circulated through the hot zone area to pick up heat before passing through a heat exchanger to remove heat. This process continues until the desired temperature is reached.
Vacuum furnaces are used in a wide range of applications in both production industries and research laboratories.
At temperatures below 1200 °C, a vacuum furnace is commonly used for the heat treatment of steel alloys. Many general heat treating applications involve the hardening and tempering of a steel part to make it strong and tough through service. Hardening involves heating the steel to a predetermined temperature, then cooling it rapidly in water, oil or suitable medium.
A further application for vacuum furnaces is Vacuum Carburizing also known as Low Pressure Carburizing or LPC. In this process, a gas (such as acetylene) is introduced as a partial pressure into the hot zone at temperatures typically between 1,600 and 1,950 °F (870 and 1,070 °C). The gas disassociates into its constituent elements (in this case carbon and hydrogen). The carbon is then diffused into the surface area of the part. This function is typically repeated, varying the duration of gas input and diffusion time. Once the workload is properly "cased", the metal is quenched using oil or high pressure gas (HPGQ). For HPGQ, nitrogen or, for faster quench helium, is commonly used. This process is also known as case hardening.
Another low temperature application of vacuum furnaces is debinding, a process for the removal of binders. Heat is applied under a vacuum in a sealed chamber, melting or vaporizing the binder from the aggregate. The binder is evacuated by the pumping system and collected or purged downstream. The material with a higher melting point is left behind in a purified state and can be further processed.
Vacuum furnaces capable of temperatures above 1200 °C are used in various industry sectors such as electronics, medical, crystal growth, energy and artificial gems. The processing of high temperature materials, both of metals and nonmetals, in a vacuum environment allows annealing, brazing, purification, sintering and other processes to take place in a controlled manner.
https://en.wikipedia.org/wiki/Vacuum_furnace
Goura, Phthiotis was a village located within Phthiotis, Greece.[1] Sometime around the late 19th century, a beehive tomb burial structure constructed from stone was discovered in Goura.[1] Local people converted the tomb into a lime kiln, and it contained rings, gold, silver, painted vases and bones.[1]
https://en.wikipedia.org/wiki/Goura,_Phthiotis
A flue-gas stack, also known as a smoke stack, chimney stack or simply as a stack, is a type of chimney, a vertical pipe, channel or similar structure through which combustion product gases called flue gases are exhausted to the outside air. Flue gases are produced when coal, oil, natural gas, wood or any other fuel is combusted in an industrial furnace, a power plant's steam-generating boiler, or other large combustion device. Flue gas is usually composed of carbon dioxide (CO2) and water vapor as well as nitrogen and excess oxygen remaining from the intake combustion air. It also contains a small percentage of pollutants such as particulate matter, carbon monoxide, nitrogen oxides and sulfur oxides. The flue gas stacks are often quite tall, up to 400 metres (1300 feet) or more, so as to disperse the exhaust pollutants over a greater area and thereby reduce the concentration of the pollutants to the levels required by governmental environmental policy and environmental regulation.
When the flue gases are exhausted from stoves, ovens, fireplaces, heating furnaces and boilers, or other small sources within residential abodes, restaurants, hotels, or other public buildings and small commercial enterprises, their flue gas stacks are referred to as chimneys.
Flue-gas stack draft[edit]
The combustion flue gases inside the flue gas stacks are much hotter than the ambient outside air and therefore less dense than the ambient air. That causes the bottom of the vertical column of hot flue gas to have a lower pressure than the pressure at the bottom of a corresponding column of outside air. That higher pressure outside the chimney is the driving force that moves the required combustion air into the combustion zone and also moves the flue gas up and out of the chimney. That movement or flow of combustion air and flue gas is called "natural draft", "natural ventilation", "chimney effect", or "stack effect". The taller the stack, the more draft is created.
The equation below provides an approximation of the pressure difference, ΔP, (between the bottom and the top of the flue gas stack) that is created by the draft:[3][4]
where:
- ΔP: available pressure difference, in Pa
- C = 0.0342
- a: atmospheric pressure, in Pa
- h: height of the flue gas stack, in m
- To: absolute outside air temperature, in K
- Ti: absolute average temperature of the flue gas inside the stack, in K.
The above equation is an approximation because it assumes that the molar mass of the flue gas and the outside air are equal and that the pressure drop through the flue gas stack is quite small. Both assumptions are fairly good but not exactly accurate.
https://en.wikipedia.org/wiki/Flue-gas_stack
Stack effect or chimney effect is the movement of air into and out of buildings, chimneys, flue-gas stacks, or other containers, resulting from air buoyancy. Buoyancy occurs due to a difference in indoor-to-outdoor air density resulting from temperature and moisture differences. The result is either a positive or negative buoyancy force. The greater the thermal difference and the height of the structure, the greater the buoyancy force, and thus the stack effect. The stack effect helps drive natural ventilation, air infiltration, and fires (e.g. the Kaprun tunnel fire, King's Cross underground station fireand the Grenfell Tower fire).
Stack effect in buildings[edit]
Since buildings are not totally sealed (at the very minimum, there is always a ground level entrance), the stack effect will cause air infiltration. During the heating season, the warmer indoor air rises up through the building and escapes at the top either through open windows, ventilation openings, or unintentional holes in ceilings, like ceiling fans and recessed lights. The rising warm air reduces the pressure in the base of the building, drawing cold air in through either open doors, windows, or other openings and leakage. During the cooling season, the stack effect is reversed, but is typically weaker due to lower temperature differences.[1]
https://en.wikipedia.org/wiki/Stack_effect
The Pressure-Temperature-time path (P-T-t path) is a record of the pressure and temperature(P-T) conditions that a rock experienced in a metamorphic cycle from burial and heating to upliftand exhumation to the surface.[1] Metamorphism is a dynamic process which involves the changes in minerals and textures of the pre-existing rocks (protoliths) under different P-T conditions in solid state.[2] The changes in pressures and temperatures with time experienced by the metamorphic rocks are often investigated by petrological methods, radiometric dating techniques and thermodynamic modeling.[1][2]
Metamorphic minerals are unstable upon changing P-T conditions.[1][3] The original minerals are commonly destroyed during solid state metamorphism and react to grow into new minerals that are relatively stable.[1][3] Water is generally involved in the reaction, either from the surroundings or generated by the reaction itself.[3] Usually, a large amount of fluids (e.g. water vapor, gas etc.) escape under increasing P-T conditions e.g. burial.[1] When the rock is later uplifted, due to the escape of fluids at an earlier stage, there is not enough fluids to permit all the new minerals to react back into the original minerals.[1] Hence, the minerals are not fully in equilibrium when discovered on the surface.[1] Therefore, the mineral assemblages in metamorphic rocks implicitly record the past P-T conditions that the rock has experienced, and investigating these minerals can supply information about the past metamorphic and tectonic history.[1]
The P-T-t paths are generally classified into two types: clockwise P-T-t paths, which are related to collision origin, and involve high pressures followed by high temperatures;[4] and anticlockwise P-T-t paths, which are usually of intrusion origin, and involve high temperatures before high pressures.[4] (The "clockwise" and "anticlockwise" names refer to the apparent direction of the paths in the Cartesian space, where the x-axis is temperature, and the y-axis is pressure.[3])
https://en.wikipedia.org/wiki/Pressure-temperature-time_path
The Antoine equation is a class of semi-empirical correlations describing the relation between vapor pressure and temperature for pure substances. The Antoine equation is derived from the Clausius–Clapeyron relation. The equation was presented in 1888 by the French engineer Louis Charles Antoine (1825–1897).[1]
https://en.wikipedia.org/wiki/Antoine_equation
Internal pressure is a measure of how the internal energy of a system changes when it expands or contracts at constant temperature. It has the same dimensions as pressure, the SI unit of which is the pascal.
Internal pressure is usually given the symbol . It is defined as a partial derivative of internal energy with respect to volume at constant temperature:
https://en.wikipedia.org/wiki/Internal_pressure
Pressure[edit]
The maximum air pressure (weight of the atmosphere) is at sea level and decreases at high altitude because the atmosphere is in hydrostatic equilibrium, wherein the air pressure is equal to the weight of the air above a given point on the planetary surface. The relation between decreased air pressure and high altitude can be equated to the density of a fluid, by way of the following hydrostatic equation:
where:
- gn is the standard gravity
- ρ is the density
- z is the altitude
- P is the pressure
- R is the gas constant
- T is the thermodynamic (absolute) temperature
- m is the molar mass[3]
 The atmosphere of the Earth is in five layers:
The atmosphere of the Earth is in five layers:
(i) the exosphere at 600+ km;
(ii) the thermosphere at 600 km;
(iii) the mesosphere at 95–120 km;
(iv) the stratosphere at 50–60 km; and
(v) the troposphere at 8–15 km.
The scale indicates that the layers’ distances from the planetary surface to the edge of the stratosphere is ±50 km, less than 1.0% of the radius of the Earth.
https://en.wikipedia.org/wiki/Troposphere#Pressure
The tropopause is the atmospheric boundary that demarcates the troposphere from the stratosphere; which are two of the five layers of the atmosphere of Earth. The tropopause is a thermodynamic gradient-stratification layer, that marks the end of the troposphere, and lies approximately 17 kilometres (11 mi) above the equatorial regions, and approximately 9 kilometres (5.6 mi) above the polar regions. The atmosphere of planet Earth:The tropopause is between the troposphere and the stratosphere.
The atmosphere of planet Earth:The tropopause is between the troposphere and the stratosphere.- https://en.wikipedia.org/wiki/Tropopause
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis (the birth and development of a cyclone), especially along the polar front, and in analyzing flow in the ocean.
Potential vorticity (PV) is seen as one of the important theoretical successes of modern meteorology. It is a simplified approach for understanding fluid motions in a rotating system such as the Earth's atmosphere and ocean. Its development traces back to the circulation theorem by Bjerknes in 1898,[1]which is a specialized form of Kelvin's circulation theorem. Starting from Hoskins et al., 1985,[2] PV has been more commonly used in operational weather diagnosis such as tracing dynamics of air parcels and inverting for the full flow field. Even after detailed numerical weather forecasts on finer scales were made possible by increases in computational power, the PV view is still used in academia and routine weather forecasts, shedding light on the synoptic scale features for forecasters and researchers.[3]
Baroclinic instability requires the presence of a potential vorticity gradient along which waves amplify during cyclogenesis.
https://en.wikipedia.org/wiki/Potential_vorticity
In the context of meteorology, a solenoid is a tube-shaped region in the atmosphere where isobaric (constant pressure) and isopycnal (constant density) surfaces intersect, causing vertical circulation.[1][2] They are so-named because they are driven by the solenoid term of the vorticity equation.[3]Examples of solenoids include the sea breeze circulation and the mountain–plains solenoid.[4][5]
https://en.wikipedia.org/wiki/Solenoid_(meteorology)
https://en.wikipedia.org/wiki/Category:Atmospheric_dynamics
A flow tracer is any fluid property used to track flow, magnitude, direction, and circulation patterns. Tracers can be chemical properties, such as radioactive material, or chemical compounds, physical properties, such as density, temperature, salinity, or dyes, and can be natural or artificially induced. Flow tracers are used in many fields, such as physics, hydrology, limnology, oceanography, environmental studies and atmospheric studies.
Conservative tracers remain constant following fluid parcels, whereas reactive tracers (such as compounds undergoing a mutual chemical reaction) grow or decay with time. Active tracersdynamically alter the flow of the fluid by changing fluid properties which appear in the equation of motion such as density or viscosity, while passive tracers have no influence on flow.[1]
https://en.wikipedia.org/wiki/Flow_tracer
Perfluorocarbon tracers (PFTs) are a range of perfluorocarbons used in tracer applications. They are used by releasing the PFT at a certain point, and determining the concentration of that PFT at another set of points, allowing the flow from the source to the points to be determined.
https://en.wikipedia.org/wiki/Perfluorocarbon_tracer
Laser-driven muon sources seem to be the economical tipping point for making muon-catalyzed fusion reactors viable.[citation needed]
Process
[edit]
To create this effect, a stream of negative muons, most often created by decaying pions, is sent to a block that may be made up of all three hydrogen isotopes (protium, deuterium, and/or tritium), where the block is usually frozen, and the block may be at temperatures of about 3 kelvin (−270 degrees Celsius) or so. The muon may bump the electron from one of the hydrogen isotopes. The muon, 207 times more massive than the electron, effectively shields and reduces the electromagnetic repulsion between two nuclei and draws them much closer into a covalent bond than an electron can. Because the nuclei are so close, the strong nuclear force is able to kick in and bind both nuclei together. They fuse, release the catalytic muon (most of the time), and part of the original mass of both nuclei is released as energetic particles, as with any other type of nuclear fusion.
Deuterium-tritium (d-t or dt)[edit]
In the muon-catalyzed fusion of most interest, a positively charged deuteron (d), a positively charged triton (t), and a muon essentially form a positively charged muonic molecular heavy hydrogen ion (d-μ-t)+. The muon, with a rest mass 207 times greater than the rest mass of an electron,[7] is able to drag the more massive triton and deuteron 207 times closer together to each other[1] [2] in the muonic (d-μ-t)+ molecular ion than can an electron in the corresponding electronic (d-e-t)+ molecular ion. The average separation between the triton and the deuteron in the electronic molecular ion is about one angstrom (100 pm),[6][note 4] so the average separation between the triton and the deuteron in the muonic molecular ion is 207 times smaller than that.[note 5] Due to the strong nuclear force, whenever the triton and the deuteron in the muonic molecular ion happen to get even closer to each other during their periodic vibrational motions, the probability is very greatly enhanced that the positively charged triton and the positively charged deuteron would undergo quantum tunnelling through the repulsive Coulomb barrier that acts to keep them apart. Indeed, the quantum mechanical tunnelling probability depends roughly exponentially on the average separation between the triton and the deuteron, allowing a single muon to catalyze the d-t nuclear fusion in less than about half a picosecond, once the muonic molecular ion is formed.[6]
https://en.wikipedia.org/wiki/Muon-catalyzed_fusion
- Railgun
- Plasma railgun
- Coilgun
- Mass driver
- Ram accelerator
- Light-gas gun
- Electrothermal-chemical technology
- Henry Kolm
- Kolm, H.; et al. (1980). "Electromagnetic Guns, Launchers, and Reaction Engines". 2Nd International Pulsed Power Conference. Massachusetts Institute of Technology: 42. Bibcode:1979pupo.conf...42K.
- Specific
- Elastomer items such as O-rings can suffer ozone cracking
- ionization
- thermoionic emission
- electron melt
Colliding beam Magnetized target Migma Muon-catalyzed Pyroelectric
https://en.wikipedia.org/wiki/Magnetohydrodynamics
https://en.wikipedia.org/wiki/Fusion_energy_gain_factor
confinement magnetosphere
magneto
radioactive elements such as plutonium is complicated by the fact that solutions of this element can undergo disproportionation[11] and as a result many different oxidation states can coexist at once.
https://en.wikipedia.org/wiki/Radiochemistry
09-27-2021-1746 - recognised a small spike at an energy of 803 kilo-electron volts (keV) as the gamma ray signal from polonium-210
Scientists at AWE were involved in testing for radioactive poison after the poisoning of Alexander Litvinenko. No gamma rays were detected; however, the BBC reported that a scientist at AWE, who had worked on Britain's early atomic bomb programme decades before, recognised a small spike at an energy of 803 kilo-electron volts (keV) as the gamma ray signal from polonium-210, a critical component of early nuclear bombs, which led to the correct diagnosis. Further tests using spectroscopy designed to detect alpha radiation confirmed the result.[11]
https://en.wikipedia.org/wiki/Atomic_Weapons_Establishment
https://en.wikipedia.org/wiki/Modulated_neutron_initiatorhttps://en.wikipedia.org/wiki/Scaling_(geometry)
https://en.wikipedia.org/wiki/Reflection_(mathematics)
https://en.wikipedia.org/wiki/Norm_(mathematics)#Zero_norm
https://en.wikipedia.org/wiki/Uncorrelatedness_(probability_theory)
https://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation#Quaternion-derived_rotation_matrix
https://en.wikipedia.org/wiki/Reflection_symmetry
https://en.wikipedia.org/wiki/Graphite-moderated_reactor
In Euclidean geometry, uniform scaling (or isotropic scaling[1]) is a linear transformation that enlarges (increases) or shrinks (diminishes) objects by a scale factor that is the same in all directions. The result of uniform scaling is similar (in the geometric sense) to the original. A scale factor of 1 is normally allowed, so that congruent shapes are also classed as similar. Uniform scaling happens, for example, when enlarging or reducing a photograph, or when creating a scale model of a building, car, airplane, etc.
More general is scaling with a separate scale factor for each axis direction. Non-uniform scaling (anisotropic scaling) is obtained when at least one of the scaling factors is different from the others; a special case is directional scaling or stretching (in one direction). Non-uniform scaling changes the shape of the object; e.g. a square may change into a rectangle, or into a parallelogram if the sides of the square are not parallel to the scaling axes (the angles between lines parallel to the axes are preserved, but not all angles). It occurs, for example, when a faraway billboard is viewed from an oblique angle, or when the shadow of a flat object falls on a surface that is not parallel to it.
When the scale factor is larger than 1, (uniform or non-uniform) scaling is sometimes also called dilation or enlargement. When the scale factor is a positive number smaller than 1, scaling is sometimes also called contraction.
In the most general sense, a scaling includes the case in which the directions of scaling are not perpendicular. It also includes the case in which one or more scale factors are equal to zero (projection), and the case of one or more negative scale factors (a directional scaling by -1 is equivalent to a reflection).
Scaling is a linear transformation, and a special case of homothetic transformation. In most cases, the homothetic transformations are non-linear transformations.
https://en.wikipedia.org/wiki/Scaling_(geometry)
Zero norm[edit]
In probability and functional analysis, the zero norm induces a complete metric topology for the space of measurable functions and for the F-spaceof sequences with F–norm [11] Here we mean by F-norm some real-valued function on an F-space with distance d, such that The F-norm described above is not a norm in the usual sense because it lacks the required homogeneity property.
Hamming distance of a vector from zero[edit]
In metric geometry, the discrete metric takes the value one for distinct points and zero otherwise. When applied coordinate-wise to the elements of a vector space, the discrete distance defines the Hamming distance, which is important in coding and information theory. In the field of real or complex numbers, the distance of the discrete metric from zero is not homogeneous in the non-zero point; indeed, the distance from zero remains one as its non-zero argument approaches zero. However, the discrete distance of a number from zero does satisfy the other properties of a norm, namely the triangle inequality and positive definiteness. When applied component-wise to vectors, the discrete distance from zero behaves like a non-homogeneous "norm", which counts the number of non-zero components in its vector argument; again, this non-homogeneous "norm" is discontinuous.
In signal processing and statistics, David Donoho referred to the zero "norm" with quotation marks. Following Donoho's notation, the zero "norm" of x is simply the number of non-zero coordinates of x, or the Hamming distance of the vector from zero. When this "norm" is localized to a bounded set, it is the limit of p-norms as p approaches 0. Of course, the zero "norm" is not truly a norm, because it is not positive homogeneous. Indeed, it is not even an F-norm in the sense described above, since it is discontinuous, jointly and severally, with respect to the scalar argument in scalar–vector multiplication and with respect to its vector argument. Abusing terminology, some engineers[who?] omit Donoho's quotation marks and inappropriately call the number-of-nonzeros function the L0 norm, echoing the notation for the Lebesgue space of measurable functions.
https://en.wikipedia.org/wiki/Norm_(mathematics)#Zero_norm
In mathematics, a reflection (also spelled reflexion)[1] is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as a set of fixed points; this set is called the axis (in dimension 2) or plane (in dimension 3) of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection. For example the mirror image of the small Latin letter p for a reflection with respect to a vertical axis would look like q. Its image by reflection in a horizontal axis would look like b. A reflection is an involution: when applied twice in succession, every point returns to its original location, and every geometrical object is restored to its original state.
The term reflection is sometimes used for a larger class of mappings from a Euclidean space to itself, namely the non-identity isometries that are involutions. Such isometries have a set of fixed points (the "mirror") that is an affine subspace, but is possibly smaller than a hyperplane. For instance a reflection through a point is an involutive isometry with just one fixed point; the image of the letter p under it would look like a d. This operation is also known as a central inversion (Coxeter 1969, §7.2), and exhibits Euclidean space as a symmetric space. In a Euclidean vector space, the reflection in the point situated at the origin is the same as vector negation. Other examples include reflections in a line in three-dimensional space. Typically, however, unqualified use of the term "reflection" means reflection in a hyperplane.
A figure that does not change upon undergoing a reflection is said to have reflectional symmetry.
Some mathematicians use "flip" as a synonym for "reflection".[2][3][4]
https://en.wikipedia.org/wiki/Reflection_(mathematics)
A mass driver or electromagnetic catapult is a proposed method of non-rocket spacelaunch which would use a linear motor to accelerate and catapult payloads up to high speeds. All existing and contemplated mass drivers use coils of wire energized by electricity to make electromagnets. Sequential firing of a row of electromagnets accelerates the payload along a path. After leaving the path, the payload continues to move due to momentum.
https://en.wikipedia.org/wiki/Mass_driver
Monday, September 27, 2021
09-26-2021-2250 - Ferromagnetic resonance
Ferromagnetic resonance, or FMR, is coupling between an electromagnetic wave and the magnetization of a medium through which it passes. This coupling induces a significant loss of power of the wave. The power is absorbed by the precessing magnetization (Larmor precession) of the material and lost as heat. For this coupling to occur, the frequency of the incident wave must be equal to the precession frequency of the magnetization (Larmor frequency) and the polarization of the wave must match the orientation of the magnetization.
This effect can be used for various applications such as spectroscopic techniques or conception of microwave devices.
The FMR spectroscopic technique is used to probe the magnetization of ferromagnetic materials. It is a standard tool for probing spin waves and spin dynamics. FMR is very broadly similar to electron paramagnetic resonance (EPR), and also somewhat similar to nuclear magnetic resonance (NMR), except that FMR probes the sample magnetization resulting from the magnetic moments of dipolar-coupled but unpaired electrons, while NMR probes the magnetic moment of atomic nuclei that are screened by the atomic or molecular orbitals surrounding such nuclei of non-zero nuclear spin.
The FMR resonance is also the basis of various high-frequency electronic devices, such as resonance isolators or circulators.
https://en.wikipedia.org/wiki/Ferromagnetic_resonance
Monday, September 27, 2021
09-26-2021-2303 - Helical railguns
Helical railguns[1] are multi-turn railguns that reduce rail and brush current by a factor equal to the number of turns. Two rails are surrounded by a helical barrel and the projectile or re-usable carrier is cylindrical. The projectile is energized continuously by two brushes sliding along the rails, and two or more additional brushes on the projectile serve to energize and commute several windings of the helical barrel direction in front of and/or behind the projectile. The helical railgun is a cross between a railgun and a coilgun. They do not currently exist in a practical, usable form.
A helical railgun was built at MIT in 1980 and was powered by several banks of, for the time, large capacitors (approximately 4 farads). It was about 3 meters long, consisting of 2 meters of accelerating coil and 1 meter of decelerating coil. It was able to launch a glider or projectile about 500 meters.
See also[edit]
References[edit]
Monday, September 27, 2021
09-26-2021-2252 - Particle Radiation Range, Energy Density Tables, Gravimetry
Monday, September 27, 2021
09-26-2021-2113 - Corona Discharge electrical breakdown conductive leak charge into air, corona ring, ion wind, Hall effect thruster, Magnetohydrodynamic drive, Field-emission electric propulsion, plasma, Air ioniser, ion thruster, plasma actuator, AC, etc..
Theory of operation[edit]
The vapor core reactor (VCR), also called a gas core reactor (GCR), has been studied for some time. It would have a gas or vapor core composed of uranium tetrafluoride (UF4) with some helium (4He) added to increase the electrical conductivity, the vapor core may also have tiny UF4 droplets in it. It has both terrestrial and space based applications. Since the space concept doesn't necessarily have to be economical in the traditional sense, it allows the enrichment to exceed what would be acceptable for a terrestrial system. It also allows for a higher ratio of UF4 to helium, which in the terrestrial version would be kept just high enough to ensure criticality in order to increase the efficiency of direct conversion. The terrestrial version is designed for a vapor core inlet temperature of about 1,500 K and exit temperature of 2,500 K and a UF4 to helium ratio of around 20% to 60%. It is thought that the outlet temperature could be raised to that of the 8,000 K to 15,000 K range where the exhaust would be a fission-generated non-equilibrium electron gas, which would be of much more importance for a rocket design.
Energy production[edit]
For energy production purposes, one might use a container located inside a solenoid. The container is filled with gaseous uranium hexafluoride, where the uranium is enriched, to a level just short of criticality. Afterward, the uranium hexafluoride is compressed by external means, thus initiating a nuclear chain reaction and a great amount of heat, which in turn causes an expansion of the uranium hexafluoride. Since the UF6 is contained within the vessel, it can't escape and thus compresses elsewhere. The result is a plasma wave moving in the container, and the solenoid converts some of its energy into electricity at an efficiency level of about 20%. In addition, the container must be cooled, and one can extract energy from the coolant by passing it through a heat exchanger and turbine system as in an ordinary thermal power plant.
However, there are enormous problems with corrosion during this arrangement, as the uranium hexafluoride is chemically very reactive.
- https://en.wikipedia.org/wiki/Gaseous_fission_reactor
- https://en.wikipedia.org/wiki/Water–gas_shift_reaction
- https://en.wikipedia.org/wiki/Boiling_water_reactor
- https://en.wikipedia.org/wiki/Pressurized_water_reactor
- https://en.wikipedia.org/wiki/Heterogeneous_catalytic_reactor
- https://en.wikipedia.org/wiki/Void_coefficient?wprov=srpw1_42
- https://en.wikipedia.org/wiki/Nuclear_power#Advanced_fission_reactor_designs
- https://en.wikipedia.org/wiki/Continuous_stirred-tank_reactor
- Metalorganic vapour-phase epitaxy (MOVPE), also known as organometallic vapour-phase epitaxy (OMVPE) or metalorganic chemical vapour deposition (MOCVD),[1] is a chemical vapour deposition method used to produce single- or polycrystalline thin films. It is a process for growing crystalline layers to create complex semiconductor multilayer structures.[2] In contrast to molecular-beam epitaxy (MBE), the growth of crystals is by chemical reaction and not physical deposition. This takes place not in vacuum, but from the gas phase at moderate pressures (10 to 760 Torr). As such, this technique is preferred for the formation of devices incorporating thermodynamically metastable alloys,[citation needed] and it has become a major process in the manufacture of optoelectronics, such as Light-emitting diodes. It was invented in 1968 at North American Aviation (later Rockwell International) Science Center by Harold M. Manasevit.
- https://en.wikipedia.org/wiki/Metalorganic_vapour-phase_epitaxy
https://en.wikipedia.org/wiki/Metalorganic_vapour-phase_epitaxy#Reactor_components
- https://en.wikipedia.org/wiki/Pebble_bed_modular_reactor
- https://en.wikipedia.org/wiki/Closed-cycle_gas_turbine
- https://en.wikipedia.org/wiki/Liquid_metal_cooled_reactor
- https://en.wikipedia.org/wiki/Pressurized_heavy-water_reactor
- https://en.wikipedia.org/wiki/Steam-Generating_Heavy_Water_Reactor
- https://en.wikipedia.org/wiki/Internal_circulation_reactor
- https://en.wikipedia.org/wiki/X-energy
- https://en.wikipedia.org/wiki/Fluid_catalytic_cracking
- https://en.wikipedia.org/wiki/Fluid_catalytic_cracking#Reactor_and_regenerator
- https://en.wikipedia.org/wiki/Laminar_flow_reactor
- https://en.wikipedia.org/wiki/Subcritical_reactor
- https://en.wikipedia.org/wiki/Stable_salt_reactor
- https://en.wikipedia.org/wiki/Aqueous_homogeneous_reactor
- https://en.wikipedia.org/wiki/Advanced_boiling_water_reactor
- https://en.wikipedia.org/wiki/Integral_fast_reactor
- https://en.wikipedia.org/wiki/Pressure_reactor
- https://en.wikipedia.org/wiki/Fusion_power
- https://en.wikipedia.org/wiki/Enriched_uranium#Gas_centrifuge
- https://en.wikipedia.org/wiki/Mass_balance#Ideal_tank_reactor%2Fcontinuously_stirred_tank_reactor
- https://en.wikipedia.org/wiki/Bioreactor
Monday, August 9, 2021
08-08-2021-2244 - Plasma Physics
Monday, September 27, 2021
Monday, September 20, 2021
https://en.wikipedia.org/wiki/Rydberg_atom
https://en.wikipedia.org/wiki/Azimuthal_quantum_number
https://en.wikipedia.org/wiki/Binding_energy
https://en.wikipedia.org/wiki/Separation_energy
https://en.wikipedia.org/wiki/Photoionization
https://en.wikipedia.org/wiki/Photodissociation
https://en.wikipedia.org/wiki/Photoelectric_effect
https://en.wikipedia.org/wiki/Photovoltaics
https://en.wikipedia.org/wiki/Bond-dissociation_energy
https://en.wikipedia.org/wiki/Nuclear_physics
https://en.wikipedia.org/wiki/Powder_coating
https://en.wikipedia.org/wiki/Melt_electrospinning
https://en.wikipedia.org/wiki/Electrospinning
https://en.wikipedia.org/wiki/Electret
https://en.wikipedia.org/wiki/Overvoltage
https://en.wikipedia.org/wiki/Gaseous_fission_reactor
https://en.wikipedia.org/wiki/Electron-beam_technology
A gas nuclear reactor (or gas fueled reactor or vapor core reactor) is a proposed kind of nuclear reactor in which the nuclear fuel would be in a gaseous state rather than liquid or solid. In this type of reactor, the only temperature-limiting materials would be the reactor walls. Conventional reactors have stricter limitations because the core would melt if the fuel temperature were to rise too high. It may also be possible to confine gaseous fission fuel magnetically, electrostatically or electrodynamically so that it would not touch (and melt) the reactor walls. A potential benefit of the gaseous reactor core concept is that instead of relying on the traditional Rankine or Brayton conversion cycles, it may be possible to extract electricity magnetohydrodynamically, or with simple direct electrostatic conversion of the charged particles.
https://en.wikipedia.org/wiki/Gaseous_fission_reactor
- https://en.wikipedia.org/wiki/Melt_electrospinning
- https://en.wikipedia.org/wiki/Taylor_cone
- https://en.wikipedia.org/wiki/Spinneret_(polymers)
- https://en.wikipedia.org/wiki/Tissue_engineering#Electrospinning
- https://en.wikipedia.org/wiki/Polydioxanone
- https://en.wikipedia.org/wiki/Electrospray
- https://en.wikipedia.org/wiki/Polymer_nanocomposite#Bio-hybrid_nanofibres_by_electrospinning
- https://en.wikipedia.org/wiki/Aluminium_oxide_nanoparticle
- https://en.wikipedia.org/wiki/Nano-scaffold
- https://en.wikipedia.org/wiki/Dielectric_barrier_discharge
- https://en.wikipedia.org/wiki/Aggregate_(composite)
- https://en.wikipedia.org/wiki/Field_electron_emission
- https://en.wikipedia.org/wiki/Bacteriophage
- https://en.wikipedia.org/wiki/Characteristic_X-ray
- https://en.wikipedia.org/wiki/Flame_ionization_detector
- https://en.wikipedia.org/wiki/Photon_upconversion
- https://en.wikipedia.org/wiki/Bremsstrahlung
- https://en.wikipedia.org/wiki/Forbidden_mechanism
- https://en.wikipedia.org/wiki/Low-energy_ion_scattering
- https://en.wikipedia.org/wiki/Maser
- https://en.wikipedia.org/wiki/Neutron_generator#Ion_sources
- https://en.wikipedia.org/wiki/Thermal_ionization
- https://en.wikipedia.org/wiki/Particle-induced_gamma_emission
- https://en.wikipedia.org/wiki/Helium_hydride_ion
- https://en.wikipedia.org/wiki/Hydrogen_spectral_series
- https://en.wikipedia.org/wiki/Trihydrogen_cation
- https://en.wikipedia.org/wiki/Erwin_Wilhelm_Müller
- https://en.wikipedia.org/wiki/Fluorophore
- https://en.wikipedia.org/wiki/Vacuum_arc
- https://en.wikipedia.org/wiki/Homogeneous_broadening
- https://en.wikipedia.org/wiki/Gallium-68_generator
- https://en.wikipedia.org/wiki/Upconverting_nanoparticles
- https://en.wikipedia.org/wiki/Electron_ionization
- https://en.wikipedia.org/wiki/Cherenkov_radiation#Emission_angle
- ionization, thermal energy electrostatics electron melt air drag neutron drag plasma
- dry thrust dessican vaccume
- ion hydrag
- https://en.wikipedia.org/wiki/Resonance_ionization
- https://en.wikipedia.org/wiki/Self-ionization_of_water
- https://en.wikipedia.org/wiki/Townsend_discharge
- https://en.wikipedia.org/wiki/oxyanion_hole
- https://en.wikipedia.org/wiki/Avalanche_breakdown
- https://en.wikipedia.org/wiki/Electron_avalanche
- https://en.wikipedia.org/wiki/Impact_ionization
- https://en.wikipedia.org/wiki/Electrical_breakdown
- https://en.wikipedia.org/wiki/Chain_reaction
- https://en.wikipedia.org/wiki/Electronegativity
https://en.wikipedia.org/wiki/Magnetic_pressure
https://en.wikipedia.org/wiki/Tangential_and_normal_components
- Spinors were introduced in geometry by Élie Cartan in 1913.[1][d] In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.[e]
- https://en.wikipedia.org/wiki/Spinor
- https://en.wikipedia.org/wiki/Tunnel_ionization
- https://en.wikipedia.org/wiki/Degree_of_ionization
- https://en.wikipedia.org/wiki/Inductive_effect
- https://en.wikipedia.org/wiki/Ion_source
- https://en.wikipedia.org/wiki/Grand_canonical_ensemble
- https://en.wikipedia.org/wiki/Fusion_bonded_epoxy_coating
- Electron-beam welding (EBW) is a fusion welding process in which a beam of high-velocity electrons is applied to two materials to be joined. The workpieces melt and flow together as the kinetic energy of the electrons is transformed into heat upon impact. EBW is often performed under vacuumconditions to prevent dissipation of the electron beam.
- Electrons are elementary particles possessing a mass m = 9.1 · 10−31 kg and a negative electrical charge e = 1.6 · 10−19 C. They exist either bound to an atomic nucleus, as conduction electrons in the atomic lattice of metals, or as free electrons in vacuum.
- https://en.wikipedia.org/wiki/Electron-beam_welding
- https://en.wikipedia.org/wiki/Induction_furnace
- https://en.wikipedia.org/wiki/Nucleic_acid_thermodynamics
- https://en.wikipedia.org/wiki/Fusion_welding
- https://en.wikipedia.org/wiki/Plate_tectonics#Magnetic_striping
- An amorphous metal transformer (AMT) is a type of energy efficient transformer found on electric grids.[1] The magnetic core of this transformer is made with a ferromagnetic amorphous metal. The typical material (Metglas) is an alloy of iron with boron, silicon, and phosphorus in the form of thin (e.g. 25 µm) foils rapidly cooled from melt. These materials have high magnetic susceptibility, very low coercivity and high electrical resistance. The high resistance and thin foils lead to low losses by eddy currents when subjected to alternating magnetic fields. On the downside amorphous alloys have a lower saturation induction and often a higher magnetostriction compared to conventional crystalline iron-silicon electrical steel.[2]
- https://en.wikipedia.org/wiki/Amorphous_metal_transformer
- Seen in some magnetic materials, saturation is the state reached when an increase in applied external magnetic field H cannot increase the magnetization of the material further, so the total magnetic flux density Bmore or less levels off. (Though, magnetization continues to increase very slowly with the field due to paramagnetism.) Saturation is a characteristic of ferromagnetic and ferrimagnetic materials, such as iron, nickel, cobalt and their alloys. Different ferromagnetic materials have different saturation levels.
- https://en.wikipedia.org/wiki/Saturation_(magnetic)
- A saturable reactor in electrical engineering is a special form of inductor where the magnetic core can be deliberately saturated by a direct electric current in a control winding. Once saturated, the inductance of the saturable reactor drops dramatically.[1] This decreases inductive reactance and allows increased flow of the alternating current (AC).
- https://en.wikipedia.org/wiki/Saturable_reactor
- Two brass rings.
- Two steel balls.
- Two ball guides to hold the balls in position.
- A Support to hold the rings, balls and thermometer in position
- A Glass beaker
- Thermometer
- Hot plate
- Magnetic stirrer
- Glycerol or water as heating bath
Ring and Ball Apparatus is used to determine the softening point of bitumen, waxes, LDPE, HDPE/PP blend granules, rosin and solid hydrocarbonresins.[1] The apparatus was first designed way back in the 1910s while ASTM adopted a test method in 1916. This instrument is ideally used for materials having softening point in the range of 30 °C to 157 °C.[2][3][4]
Components[edit]
Procedure[edit]
The solid sample is taken in a Petri dish and melted by heating it on a standard hot plate. The bubble free liquefied sample is poured from the Petri dish and cast into the ring. The brass shouldered rings in this apparatus have 6.4 mm depth. The cast sample in the ring is kept undisturbed for one hour to solidify. Excess material is removed with hot knife. The ring is set with the ball on top with ball guides on the grooved plate within the heating bath. As the temperature rises, the balls begin to sink through the rings carrying a portion of the softened sample with it. The temperature at which the steel balls touch the bottom plate determines the softening point in degrees celsius.[5][6] The bottom plate has a distance of 25 mm from the rings.[7]
https://en.wikipedia.org/wiki/Ring_and_Ball_Apparatus
Metglas is a thin amorphous metal alloy ribbon produced by using rapid solidification process of approximately 1,000,000 °C/s (1,800,000 °F/s; 1,000,000 K/s). This rapid solidification creates unique ferromagnetic properties that allows the ribbon to be magnetized and de-magnetized quickly and effectively with very low core losses of approximately 5 mW/kg[1] at 60 Hz and a maximum relative permeability of approximately 1,000,000.[2]
https://en.wikipedia.org/wiki/Metglas
Fluxgate magnetometer[edit]
The fluxgate magnetometer was invented by H. Aschenbrenner and G. Goubau in 1936.[19][20]: 4 A team at Gulf Research Laboratories led by Victor Vacquier developed airborne fluxgate magnetometers to detect submarines during World War II and after the war confirmed the theory of plate tectonics by using them to measure shifts in the magnetic patterns on the sea floor.[21]
A fluxgate magnetometer consists of a small magnetically susceptible core wrapped by two coils of wire. An alternating electric current is passed through one coil, driving the core through an alternating cycle of magnetic saturation; i.e., magnetised, unmagnetised, inversely magnetised, unmagnetised, magnetised, and so forth. This constantly changing field induces an electric current in the second coil, and this output current is measured by a detector. In a magnetically neutral background, the input and output currents match. However, when the core is exposed to a background field, it is more easily saturated in alignment with that field and less easily saturated in opposition to it. Hence the alternating magnetic field, and the induced output current, are out of step with the input current. The extent to which this is the case depends on the strength of the background magnetic field. Often, the current in the output coil is integrated, yielding an output analog voltage proportional to the magnetic field.
A wide variety of sensors are currently available and used to measure magnetic fields. Fluxgate compassesand gradiometers measure the direction and magnitude of magnetic fields. Fluxgates are affordable, rugged and compact with miniaturization recently advancing to the point of complete sensor solutions in the form of IC chips, including examples from both academia [22] and industry.[23] This, plus their typically low power consumption makes them ideal for a variety of sensing applications. Gradiometers are commonly used for archaeological prospecting and unexploded ordnance (UXO) detection such as the German military's popular Foerster.[24]
The typical fluxgate magnetometer consists of a "sense" (secondary) coil surrounding an inner "drive" (primary) coil that is closely wound around a highly permeable core material, such as mu-metal or permalloy. An alternating current is applied to the drive winding, which drives the core in a continuous repeating cycle of saturation and unsaturation. To an external field, the core is alternately weakly permeable and highly permeable. The core is often a toroidally wrapped ring or a pair of linear elements whose drive windings are each wound in opposing directions. Such closed flux paths minimise coupling between the drive and sense windings. In the presence of an external magnetic field, with the core in a highly permeable state, such a field is locally attracted or gated (hence the name fluxgate) through the sense winding. When the core is weakly permeable, the external field is less attracted. This continuous gating of the external field in and out of the sense winding induces a signal in the sense winding, whose principal frequency is twice that of the drive frequency, and whose strength and phase orientation vary directly with the external-field magnitude and polarity.
There are additional factors that affect the size of the resultant signal. These factors include the number of turns in the sense winding, magnetic permeability of the core, sensor geometry, and the gated flux rate of change with respect to time.
Phase synchronous detection is used to extract these harmonic signals from the sense winding and convert them into a DC voltage proportional to the external magnetic field. Active current feedback may also be employed, such that the sense winding is driven to counteract the external field. In such cases, the feedback current varies linearly with the external magnetic field and is used as the basis for measurement. This helps to counter inherent non-linearity between the applied external field strength and the flux gated through the sense winding.
SQUID magnetometer[edit]
SQUIDs, or superconducting quantum interference devices, measure extremely small changes in magnetic fields. They are very sensitive vector magnetometers, with noise levels as low as 3 fT Hz−½ in commercial instruments and 0.4 fT Hz−½ in experimental devices. Many liquid-helium-cooled commercial SQUIDs achieve a flat noise spectrum from near DC (less than 1 Hz) to tens of kilohertz, making such devices ideal for time-domain biomagnetic signal measurements. SERF atomic magnetometers demonstrated in laboratories so far reach competitive noise floor but in relatively small frequency ranges.
SQUID magnetometers require cooling with liquid helium (4.2 K) or liquid nitrogen (77 K) to operate, hence the packaging requirements to use them are rather stringent both from a thermal-mechanical as well as magnetic standpoint. SQUID magnetometers are most commonly used to measure the magnetic fields produced by laboratory samples, also for brain or heart activity (magnetoencephalography and magnetocardiography, respectively). Geophysical surveys use SQUIDs from time to time, but the logistics of cooling the SQUID are much more complicated than other magnetometers that operate at room temperature.
Spin-exchange relaxation-free (SERF) atomic magnetometers[edit]
At sufficiently high atomic density, extremely high sensitivity can be achieved. Spin-exchange-relaxation-free (SERF) atomic magnetometers containing potassium, caesium, or rubidium vapor operate similarly to the caesium magnetometers described above, yet can reach sensitivities lower than 1 fT Hz−½. The SERF magnetometers only operate in small magnetic fields. The Earth's field is about 50 µT; SERF magnetometers operate in fields less than 0.5 µT.
Large volume detectors have achieved a sensitivity of 200 aT Hz−½.[25] This technology has greater sensitivity per unit volume than SQUIDdetectors.[26] The technology can also produce very small magnetometers that may in the future replace coils for detecting changing magnetic fields.[citation needed] This technology may produce a magnetic sensor that has all of its input and output signals in the form of light on fiber-optic cables.[27] This lets the magnetic measurement be made near high electrical voltages.
Calibration of magnetometers[edit]
The calibration of magnetometers is usually performed by means of coils which are supplied by an electrical current to create a magnetic field. It allows to characterize the sensitivity of the magnetometer (in terms of V/T). In many applications the homogeneity of the calibration coil is an important feature. For this reason, coils like Helmholtz coils are commonly used either in a single axis or a three axis configuration. For demanding applications a high homogeneity magnetic field is mandatory, in such cases magnetic field calibration can be performed using a Maxwell coil, cosine coils,[28] or calibration in the highly homogenous Earth's magnetic field.
https://en.wikipedia.org/wiki/Magnetometer#Fluxgate_magnetometer
https://en.wikipedia.org/wiki/Colloid_vibration_current
https://en.wikipedia.org/wiki/ion_drag
https://en.wikipedia.org/wiki/ion_vibration
https://en.wikipedia.org/wiki/Electrical_mobility
- https://en.wikipedia.org/wiki/Electron_hole
- Electrical resistance, the measure of the degree to which a conductor opposes an electric current through that conductor
- Friction
- Drag (physics) ("air resistance"), fluid or gas forces opposing motion and flow
- Geological resistance, a measure of how well minerals resist erosive factors
- Hydraulic conductivity, the ease with which water can move through pore spaces or fractures in soil or rock
- Hardness, in materials science
- Thermal shock resistance, a measure of resistance of a material to temperature jumps.
- Thermal resistance, a measure of difficulty of heat transfer through a substance
- Thermal conductivity, how well heat is conducted through a substance
- Thermal resistance in electronics, heat considerations in electronics design
- Dry friction is a force that opposes the relative lateral motion of two solid surfaces in contact. Dry friction is subdivided into static friction ("stiction") between non-moving surfaces, and kinetic frictionbetween moving surfaces. With the exception of atomic or molecular friction, dry friction generally arises from the interaction of surface features, known as asperities (see Figure 1).
- is the torque vector and is the magnitude of the torque,
- is the position vector (a vector from the point about which the torque is being measured to the point where the force is applied),
- is the force vector,
- denotes the cross product, which produces a vector that is perpendicular to both r and F following the right-hand rule,
- is the angle between the force vector and the lever arm vector.
- Bryophytes, an informal group that taxonomists now treat as three separate land-plant divisions, namely: Bryophyta (mosses), Marchantiophyta (liverworts), and Anthocerotophyta (hornworts). In all bryophytes, the primary plants are the haploid gametophytes, with the only diploid portion being the attached sporophyte, consisting of a stalk and sporangium. Because these plants lack lignified water-conducting tissues, they can't become as tall as most vascular plants.
- Algae, especially the green algae. The algae consist of several unrelated groups. Only the groups included in the Viridiplantae are still considered relatives of land plants.[1]: 6 [2]
- . Encyclopædia Britannica. 5 (11th ed.). 1911.
- Structure and morphology of cellulose by Serge Pérez and William Mackie, CERMAV-CNRS
- Cellulose, by Martin Chaplin, London South Bank University
- Clear description of a cellulose assay method at the Cotton Fiber Biosciences unit of the USDA.
- Cellulose films could provide flapping wings and cheap artificial muscles for robots – TechnologyReview.com
Physics[edit]
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other.[2] There are several types of friction:
Amperian loop model
In the model developed by Ampere, the elementary magnetic dipole that makes up all magnets is a sufficiently small Amperian loop of current I. The dipole moment of this loop is m = IA where Ais the area of the loop.
These magnetic dipoles produce a magnetic B-field.
The magnetic field of a magnetic dipole is depicted in the figure. From outside, the ideal magnetic dipole is identical to that of an ideal electric dipole of the same strength. Unlike the electric dipole, a magnetic dipole is properly modeled as a current loop having a current I and an area a. Such a current loop has a magnetic moment of:
where the direction of m is perpendicular to the area of the loop and depends on the direction of the current using the right-hand rule. An ideal magnetic dipole is modeled as a real magnetic dipole whose area a has been reduced to zero and its current I increased to infinity such that the product m = Ia is finite. This model clarifies the connection between angular momentum and magnetic moment, which is the basis of the Einstein–de Haas effect rotation by magnetization and its inverse, the Barnett effect or magnetization by rotation.[24] Rotating the loop faster (in the same direction) increases the current and therefore the magnetic moment, for example.
https://en.wikipedia.org/wiki/Magnetic_field#Magnetic_field_lines
In physics and mechanics, torque is the rotational equivalent of linear force.[1] It is also referred to as the moment, moment of force, rotational force or turning effect, depending on the field of study. The concept originated with the studies by Archimedes of the usage of levers. Just as a linear force is a push or a pull, a torque can be thought of as a twist to an object around a specific axis. Another definition of torque is the product of the magnitude of the force and the perpendicular distance of the line of action of a force from the axis of rotation. The symbol for torque is typically or τ, the lowercase Greek letter tau. When being referred to as moment of force, it is commonly denoted by M.
In three dimensions, the torque is a pseudovector; for point particles, it is given by the cross product of the position vector (distance vector) and the force vector. The magnitude of torque of a rigid body depends on three quantities: the force applied, the lever arm vector[2] connecting the point about which the torque is being measured to the point of force application, and the angle between the force and lever arm vectors. In symbols:
where
The SI unit for torque is the newton-metre (N⋅m). For more on the units of torque, see § Units.
https://en.wikipedia.org/wiki/Torque
Remanence or remanent magnetization or residual magnetism is the magnetization left behind in a ferromagnetic material (such as iron) after an external magnetic field is removed.[1] Colloquially, when a magnet is "magnetized" it has remanence.[2] The remanence of magnetic materials provides the magnetic memory in magnetic storage devices, and is used as a source of information on the past Earth's magnetic field in paleomagnetism. The word remanence is from remanent + -ence, meaning "that which remains".[3]
The equivalent term residual magnetization is generally used in engineering applications. In transformers, electric motors and generators a large residual magnetization is not desirable (see also electrical steel) as it is an unwanted contamination, for example a magnetization remaining in an electromagnet after the current in the coil is turned off. Where it is unwanted, it can be removed by degaussing.
Sometimes the term retentivity is used for remanence measured in units of magnetic flux density.[4]
https://en.wikipedia.org/wiki/Remanence
https://en.wikipedia.org/wiki/Magnetic_moment#Effects_of_an_external_magnetic_field
https://en.wikipedia.org/wiki/Magnetic_field
https://en.wikipedia.org/wiki/Conservative_vector_field
Levitation melting[edit]
In the 1950s, a technique was developed where small quantities of metal were levitated and melted by a magnetic field of a few tens of kHz. The coil was a metal pipe, allowing coolant to be circulated through it. The overall form was generally conical, with a flat top. This permitted an inert atmosphere to be employed, and was commercially successful.[1]
Linear induction motor[edit]
Eric Laithwaite and colleagues took the Bedford levitator, and by stages developed and improved it.
First they made the levitator longer along one axis, and were able to make a levitator that was neutrally stable along one axis, and stable along all other axes.
Further development included replacing the single phase energising current with a linear induction motor which combined levitation and thrust.
Later "traverse-flux" systems at his Imperial College laboratory, such as Magnetic river avoided most of the problems of needing to have long, thick iron backing plates when having very long poles, by closing the flux path laterally by arranging the two opposite long poles side by side. They were also able to break the levitator primary into convenient sections which made it easier to build and transport.[2]
Null flux[edit]
Null flux systems work by having coils that are exposed to a magnetic field, but are wound in figure of 8 and similar configurations such that when there is relative movement between the magnet and coils, but centered, no current flows since the potential cancels out. When they are displaced off-center, current flows and a strong field is generated by the coil which tends to restore the spacing.
These schemes were proposed by Powell and Danby in the 1960s, and they suggested that superconducting magnets could be used to generate the high magnetic pressure needed.
HMV: Tigger and Friends - I Wanna Scare Myself - Halloween Music Video Crossover 2019
Lettuce (Lactuca sativa) is an annual plant of the daisy family, Asteraceae. It is most often grown as a leaf vegetable, but sometimes for its stem and seeds. Lettuce is most often used for salads, although it is also seen in other kinds of food, such as soups, sandwiches and wraps; it can also be grilled.[3] One variety, the celtuce(asparagus lettuce), is grown for its stems, which are eaten either raw or cooked. In addition to its main use as a leafy green, it has also gathered religious and medicinal significance over centuries of human consumption. Europe and North America originally dominated the market for lettuce, but by the late 20th century the consumption of lettuce had spread throughout the world. World production of lettuce and chicory for 2017 was 27 million tonnes, 56% of which came from China.[4]
Lettuce was originally farmed by the ancient Egyptians, who transformed it from a plant whose seeds were used to create oil into an important food crop raised for its succulent leaves and oil-rich seeds. Lettuce spread to the Greeks and Romans; the latter gave it the name lactuca, from which the English lettuce is derived. By 50 AD, many types were described, and lettuce appeared often in medieval writings, including several herbals. The 16th through 18th centuries saw the development of many varieties in Europe, and by the mid-18th century cultivars were described that can still be found in gardens.
Generally grown as a hardy annual, lettuce is easily cultivated, although it requires relatively low temperatures to prevent it from flowering quickly. It can be plagued by numerous nutrient deficiencies, as well as insect and mammal pests, and fungal and bacterial diseases. L. sativa crosses easily within the species and with some other species within the genus Lactuca. Although this trait can be a problem to home gardeners who attempt to save seeds, biologists have used it to broaden the gene pool of cultivated lettuce varieties.
Lettuce is a rich source of vitamin K and vitamin A, and a moderate source of folate and iron. Contaminated lettuce is often a source of bacterial, viral, and parasitic outbreaks in humans, including E. coli and Salmonella.
https://en.wikipedia.org/wiki/Lettuce
https://en.wikipedia.org/wiki/Glossary_of_botanical_terms#sensu_amplo
Non-vascular plants are plants without a vascular system consisting of xylem and phloem. Instead, they may possess simpler tissues that have specialized functions for the internal transport of water.
Non-vascular plants include two distantly related groups:
These groups are sometimes called "lower plants", referring to their status as the earliest plant groups to evolve, but the usage is imprecise, since both groups are polyphyletic and may be used to include vascularcryptogams, such as the ferns and fern allies that reproduce using spores. Non-vascular plants are often among the first species to move into new and inhospitable territories, along with prokaryotes and protists, and thus function as pioneer species.
Non-vascular plants do not have a wide variety of specialized tissue types.[citation needed] Mosses and leafy liverworts have structures called phyllids that resemble leaves, but only consist of single sheets of cells with no internal air spaces no cuticle or stomata and no xylem or phloem. Consequently, phyllids are unable to control the rate of water loss from their tissues and are said to be poikilohydric. Some liverworts, such as Marchantia have a cuticle and the sporophytes of mosses have both cuticles and stomata, which were important in the evolution of land plants.[3]
All land plants have a life cycle with an alternation of generations between a diploid sporophyte and a haploid gametophyte, but in all non-vascular land plants the gametophyte generation is dominant. In these plants, the sporophytes grow from and are dependent on gametophytes for taking in water and mineral nutrients and for provision of photosynthate, the products of photosynthesis.
https://en.wikipedia.org/wiki/Non-vascular_plant
Botany
History of botany
Subdisciplines
Plant systematics Ethnobotany Paleobotany Plant anatomy Plant ecology Phytogeography Geobotany Flora Phytochemistry Plant pathology Bryology Phycology Floristics Dendrology Astrobotany
Plant groups
Algae Archaeplastida Bryophyte Non-vascular plants Vascular plants Spermatophytes Pteridophyte Gymnosperm Angiosperm
Plant morphology
(glossary)
Plant cells
Cell wall Phragmoplast Plastid Plasmodesma Vacuole
Tissues
Meristem Vascular tissue Vascular bundle Ground tissue Mesophyll Cork Wood Storage organs
Vegetative
Root Rhizoid Bulb Rhizome Shoot Stem Leaf Petiole Cataphyll Bud Sessility
Reproductive
(Flower)
Flower development Inflorescence Umbel Raceme Bract Pedicellate Flower Aestivation Whorl Floral symmetry Floral diagram Floral formula Receptacle Hypanthium (Floral cup) Perianth Tepal Petal Sepal Sporophyll Gynoecium Ovary Ovule Stigma Archegonium Androecium Stamen Staminode Pollen Tapetum Gynandrium Gametophyte Sporophyte Plant embryo Fruit Fruit anatomy Berry Capsule Seed Seed dispersal Endosperm
Surface structures
Epicuticular wax Plant cuticle Epidermis Stoma Nectary Trichome Prickle
Plant physiologyMaterials
Nutrition Photosynthesis Chlorophyll Plant hormone Transpiration Turgor pressure Bulk flow Aleurone Phytomelanin Sugar Sap Starch Cellulose
Plant growth and habit
Secondary growth Woody plants Herbaceous plants Habit Cushion plants Rosettes Shrubs Prostrate shrubs Subshrubs Succulent plants Trees Vines Lianas
Reproduction
EvolutionEcology
Alternation of generations Sporangium Spore Microsporangia Microspore Megasporangium Megaspore Pollination Artificial Pollinators Pollen tube Self Double fertilization Germination Evolutionary development Evolutionary history timeline
Plant taxonomy
History of plant systematics Herbarium Biological classification Botanical nomenclature Botanical name Correct name Author citation International Code of Nomenclature for algae, fungi, and plants (ICN) International Code of Nomenclature for Cultivated Plants (ICNCP) Taxonomic rank International Association for Plant Taxonomy (IAPT) Plant taxonomy systems Cultivated plant taxonomy Citrus taxonomy Cultigen Cultivar Group Grex
Practice
Agronomy Floriculture Forestry Horticulture
ListsRelated topics
Botanical terms Botanists by author abbreviation Botanical expedition
CategoryCategory WikiProjectWikiProject
showvte
Classification of Archaeplastida or Plantae s.l.
Categories: Plants
Cellulose is an organic compound with the formula (C
6H
10O
5)
n, a polysaccharide consisting of a linear chain of several hundred to many thousands of β(1→4) linked D-glucose units.[3][4] Cellulose is an important structural component of the primary cell wall of green plants, many forms of algae and the oomycetes. Some species of bacteria secrete it to form biofilms.[5] Cellulose is the most abundant organic polymer on Earth.[6] The cellulose content of cotton fiber is 90%, that of wood is 40–50%, and that of dried hemp is approximately 57%.[7][8][9]
Cellulose is mainly used to produce paperboard and paper. Smaller quantities are converted into a wide variety of derivative products such as cellophane and rayon. Conversion of cellulose from energy cropsinto biofuels such as cellulosic ethanol is under development as a renewable fuel source. Cellulose for industrial use is mainly obtained from wood pulp and cotton.[6]
Some animals, particularly ruminants and termites, can digest cellulose with the help of symbiotic micro-organisms that live in their guts, such as Trichonympha. In human nutrition, cellulose is a non-digestible constituent of insoluble dietary fiber...
History[edit]
Cellulose was discovered in 1838 by the French chemist Anselme Payen, who isolated it from plant matter and determined its chemical formula.[3][10][11] Cellulose was used to produce the first successful thermoplastic polymer, celluloid, by Hyatt Manufacturing Company in 1870. Production of rayon ("artificial silk") from cellulose began in the 1890s and cellophane was invented in 1912. Hermann Staudingerdetermined the polymer structure of cellulose in 1920. The compound was first chemically synthesized (without the use of any biologically derived enzymes) in 1992, by Kobayashi and Shoda.[12]
External links[edit]
https://en.wikipedia.org/wiki/Cellulose








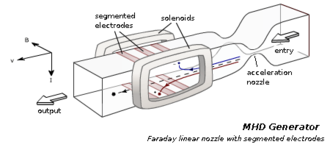
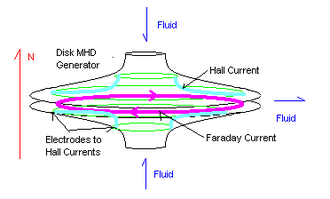







![{\displaystyle {\begin{aligned}\mathbf {\dot {x}} &=(i\hbar )^{-1}[\mathbf {x} .H]={\frac {1}{m}}\left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)\\\mathbf {\dot {p}} &=(i\hbar )^{-1}[\mathbf {p} .H]{\begin{aligned}&={\tfrac {1}{2}}\nabla \left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)^{2}-m\omega _{0}^{2}\mathbf {\dot {x}} \\&=-{\frac {1}{m}}\left[\left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)\cdot \nabla \right]\left[-{\frac {e}{c}}\mathbf {A} \right]-{\frac {1}{m}}\left(\mathbf {p} -{\frac {e}{c}}\mathbf {A} \right)\times \nabla \times \left[-{\frac {e}{c}}\mathbf {A} \right]-m\omega _{0}^{2}\mathbf {\dot {x}} \\&={\frac {e}{c}}(\mathbf {\dot {x}} \cdot \nabla )\mathbf {A} +{\frac {e}{c}}\mathbf {\dot {x}} \times \mathbf {B} -m\omega _{0}^{2}\mathbf {\dot {x}} \end{aligned}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fc7bd73dc1f0fc5519f1427d30efec3b7806a54)
![{\displaystyle {\begin{aligned}m\mathbf {\ddot {x}} &=\mathbf {\dot {p}} -{\frac {e}{c}}\mathbf {\dot {A}} \\&=-{\frac {e}{c}}\left[\mathbf {\dot {A}} -\left(\mathbf {\dot {x}} \cdot \nabla \right)\mathbf {A} \right]+{\frac {e}{c}}\mathbf {\dot {x}} \times \mathbf {B} -m\omega _{0}^{2}\mathbf {x} \\&=e\mathbf {E} +{\frac {e}{c}}\mathbf {\dot {x}} \times \mathbf {B} -m\omega _{0}^{2}\mathbf {x} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b33f34c188c9b38ac5935b2e8777dedbc487dfbd)

![{\displaystyle {\begin{aligned}\mathbf {\ddot {x}} +\omega _{0}^{2}\mathbf {x} &\approx {\frac {e}{m}}\mathbf {E} \\&\approx \sum _{\mathbf {k} \lambda }{\sqrt {\frac {2\pi \hbar \omega _{k}}{V}}}\left[a_{\mathbf {k} \lambda }(t)+a_{\mathbf {k} \lambda }^{\dagger }(t)\right]e_{\mathbf {k} \lambda }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d599af4e0a15961249f4381fd95ca0b826637f4)




![{\displaystyle \mathbf {E} _{0}(t)=i\sum _{\mathbf {k} \lambda }{\sqrt {\frac {2\pi \hbar \omega _{k}}{V}}}\left[a_{\mathbf {k} \lambda }(0)e^{-i\omega _{k}t}-a_{\mathbf {k} \lambda }^{\dagger }(0)e^{i\omega _{k}t}\right]e_{\mathbf {k} \lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79c7762e3d4255c5c4f4d6d0407e36584e3ed596)
![{\displaystyle \mathbf {E} _{RR}(t)=-{\frac {4\pi e}{V}}\sum _{\mathbf {k} \lambda }\int _{0}^{t}dt'\left[e_{\mathbf {k} \lambda }\cdot \mathbf {\dot {x}} \left(t'\right)\right]\cos \omega _{k}\left(t'-t\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66305499878dc5dcb445e9e54a8a3508aab1d37e)

![{\displaystyle \left[\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right]\mathbf {E} =0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eb3f09893b6543462f2067d166cefebbecc7811)





![{\displaystyle {\begin{aligned}\left[z(t),p_{z}(t)\right]&=\left[U^{\dagger }(t)z(0)U(t),U^{\dagger }(t)p_{z}(0)U(t)\right]\\&=U^{\dagger }(t)\left[z(0),p_{z}(0)\right]U(t)\\&=i\hbar U^{\dagger }(t)U(t)\\&=i\hbar \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bd879d669ee3c5c9fae50a1f314e765c58a3635)
![{\displaystyle \left[a_{\mathbf {k} \lambda }(0),a_{\mathbf {k'} \lambda '}^{\dagger }(0)\right]=\delta _{\mathbf {kk'} }^{3},\delta _{\lambda \lambda '}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b319f53134810ccc6a5524bc4cc97a6cd854405)
![{\displaystyle {\begin{aligned}[z(t),p_{z}(t)]&=\left[z(t),m{\dot {z}}(t)\right]+\left[z(t),{\frac {e}{c}}A_{z}(t)\right]\\&=\left[z(t),m{\dot {z}}(t)\right]\\&=\left({\frac {i\hbar e^{2}}{2\pi ^{2}mc^{3}}}\right)\left({\frac {8\pi }{3}}\right)\int _{0}^{\infty }{\frac {d\omega \,\omega ^{4}}{\left(\omega ^{2}-\omega _{0}^{2}\right)^{2}+\tau ^{2}\omega ^{6}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41cf948249a6ae51282a1225d60b45d737e07c12)
![{\displaystyle {\begin{aligned}\left[z(t),p_{z}(t)\right]&\approx {\frac {2i\hbar e^{2}}{3\pi mc^{3}}}\omega _{0}^{3}\int _{-\infty }^{\infty }{\frac {dx}{x^{2}+\tau ^{2}\omega _{0}^{6}}}\\&=\left({\frac {2i\hbar e^{2}\omega _{0}^{3}}{3\pi mc^{3}}}\right)\left({\frac {\pi }{\tau \omega _{0}^{3}}}\right)\\&=i\hbar \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/871074648f797bba79ddb93f1c0a4d7bdafb5378)



















































No comments:
Post a Comment