Nikiya Anton Bettey 2021: 09-23-2021-0538 - Spherical Wave String Consecutive Epochs

Thursday, September 23, 2021

09-23-2021-0538 - Spherical Wave String Consecutive Epochs

Figure 2: The string at 6 consecutive epochs, the first (red) corresponding to the initial time with the string in rest

Figure 3: The string at 6 consecutive epochs

Figure 4: The string at 6 consecutive epochs

Figure 5: The string at 6 consecutive epochs

Figure 6: The string at 6 consecutive epochs

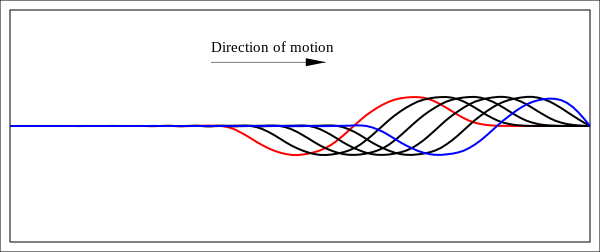
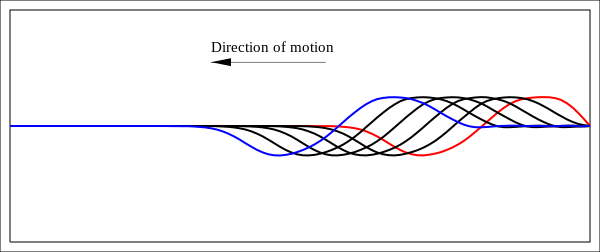
Figure 7: The string at 6 consecutive epochs

A solution of the wave equation in two dimensions with a zero-displacement boundary condition along the entire outer edge.

Figure 1: Three consecutive mass points of the discrete model for a string

1-d standing wave as a superposition of two waves traveling in opposite directions

Spherical waves coming from a point source.

A pulse traveling through a string with fixed endpoints as modeled by the wave equation.

Problems with boundaries[edit]

One space dimension[edit]

The Sturm–Liouville formulation[edit]

A flexible string that is stretched between two points $x = 0$ and $x = L$ satisfies the wave equation for $t > 0$ and $0 < x < L$ . On the boundary points, $u$ may satisfy a variety of boundary conditions. A general form that is appropriate for applications is

-u_{x}(t,0)+au(t,0)=0,

u_{x}(t,L)+bu(t,L)=0,

where $a$ and $b$ are non-negative. The case where u is required to vanish at an endpoint is the limit of this condition when the respective $a$ or $b$ approaches infinity. The method of separation of variables consists in looking for solutions of this problem in the special form

u(t,x)=T(t)v(x).

A consequence is that

{\frac {T''}{c^{2}T}}={\frac {v''}{v}}=-\lambda .

The eigenvalue $λ$ must be determined so that there is a non-trivial solution of the boundary-value problem

v''+\lambda v=0,

-v'(0)+av(0)=0,\quad v'(L)+bv(L)=0.

This is a special case of the general problem of Sturm–Liouville theory. If $a$ and $b$ are positive, the eigenvalues are all positive, and the solutions are trigonometric functions. A solution that satisfies square-integrable initial conditions for $u$ and $u t$ can be obtained from expansion of these functions in the appropriate trigonometric series.

Several space dimensions[edit]

A solution of the wave equation in two dimensions with a zero-displacement boundary condition along the entire outer edge.

The one-dimensional initial-boundary value theory may be extended to an arbitrary number of space dimensions. Consider a domain $D$ in $m$ -dimensional $x$ space, with boundary $B$ . Then the wave equation is to be satisfied if $x$ is in $D$ and $t > 0$ . On the boundary of $D$ , the solution $u$ shall satisfy

{\frac {\partial u}{\partial n}}+au=0,\,

where $n$ is the unit outward normal to $B$ , and $a$ is a non-negative function defined on $B$ . The case where $u$ vanishes on $B$ is a limiting case for $a$ approaching infinity. The initial conditions are

u(0,x) = f(x), \quad u_t(0,x)=g(x), \,

where $f$ and $g$ are defined in $D$ . This problem may be solved by expanding $f$ and $g$ in the eigenfunctions of the Laplacian in $D$ , which satisfy the boundary conditions. Thus the eigenfunction $v$ satisfies

\nabla \cdot \nabla v + \lambda v = 0, \,

in $D$ , and

{\frac {\partial v}{\partial n}}+av=0,\,

on $B$ .

In the case of two space dimensions, the eigenfunctions may be interpreted as the modes of vibration of a drumhead stretched over the boundary $B$ . If $B$ is a circle, then these eigenfunctions have an angular component that is a trigonometric function of the polar angle $θ$ , multiplied by a Bessel function (of integer order) of the radial component. Further details are in Helmholtz equation.

If the boundary is a sphere in three space dimensions, the angular components of the eigenfunctions are spherical harmonics, and the radial components are Bessel functions of half-integer order.

Inhomogeneous wave equation in one dimension[edit]

The inhomogeneous wave equation in one dimension is the following:

u_{tt}(x,t)-c^{2}u_{xx}(x,t)=s(x,t)\,

with initial conditions given by

u(x,0)=f(x) \,

u_t(x,0)=g(x) \,

The function $s (x, t)$ is often called the source function because in practice it describes the effects of the sources of waves on the medium carrying them. Physical examples of source functions include the force driving a wave on a string, or the charge or current density in the Lorenz gauge of electromagnetism.

One method to solve the initial value problem (with the initial values as posed above) is to take advantage of a special property of the wave equation in an odd number of space dimensions, namely that its solutions respect causality. That is, for any point $(x i, t i)$ , the value of $u (x i, t i)$ depends only on the values of $f (x i + ct i)$ and $f (x i - ct i)$ and the values of the function $g (x)$ between $(x i - ct i)$ and $(x i + ct i)$ . This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is $c$ , then no part of the wave that can't propagate to a given point by a given time can affect the amplitude at the same point and time.

In terms of finding a solution, this causality property means that for any given point on the line being considered, the only area that needs to be considered is the area encompassing all the points that could causally affect the point being considered. Denote the area that casually affects point $(x i, t i)$ as $R C$ . Suppose we integrate the inhomogeneous wave equation over this region.

\iint _{R_{C}}\left(c^{2}u_{xx}(x,t)-u_{tt}(x,t)\right)\,\mathrm {d} x\,\mathrm {d} t=\iint _{R_{C}}s(x,t)\,\mathrm {d} x\,\mathrm {d} t.

To simplify this greatly, we can use Green's theorem to simplify the left side to get the following:

\int _{L_{0}+L_{1}+L_{2}}\left(-c^{2}u_{x}(x,t)\,\mathrm {d} t-u_{t}(x,t)\mathrm {d} x\right)=\iint _{R_{C}}s(x,t)\,\mathrm {d} x\,\mathrm {d} t.

The left side is now the sum of three line integrals along the bounds of the causality region. These turn out to be fairly easy to compute

\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}-u_{t}(x,0)\,\mathrm {d} x=-\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,\mathrm {d} x.

In the above, the term to be integrated with respect to time disappears because the time interval involved is zero, thus $d t = 0$ .

For the other two sides of the region, it is worth noting that $x \pm ct$ is a constant, namely $x i \pm ct i$ , where the sign is chosen appropriately. Using this, we can get the relation $d x \pm c d t = 0$ , again choosing the right sign:

{\begin{aligned}\int _{L_{1}}\left(-c^{2}u_{x}(x,t)\,\mathrm {d} t-u_{t}(x,t)\,\mathrm {d} x\right)&=\int _{L_{1}}\left(cu_{x}(x,t)\,\mathrm {d} x+cu_{t}(x,t)\,\mathrm {d} t\right)\\&=c\int _{L_{1}}\,\mathrm {d} u(x,t)\\&=cu(x_{i},t_{i})-cf(x_{i}+ct_{i}).\end{aligned}}

And similarly for the final boundary segment:

{\begin{aligned}\int _{L_{2}}\left(-c^{2}u_{x}(x,t)\,\mathrm {d} t-u_{t}(x,t)\,\mathrm {d} x\right)&=-\int _{L_{2}}\left(cu_{x}(x,t)\,\mathrm {d} x+cu_{t}(x,t)\,\mathrm {d} t\right)\\&=-c\int _{L_{2}}\,\mathrm {d} u(x,t)\\&=cu(x_{i},t_{i})-cf(x_{i}-ct_{i}).\end{aligned}}

Adding the three results together and putting them back in the original integral:

{\begin{aligned}\iint _{R_{C}}s(x,t)\,\mathrm {d} x\,\mathrm {d} t&=-\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,\mathrm {d} x+cu(x_{i},t_{i})-cf(x_{i}+ct_{i})+cu(x_{i},t_{i})-cf(x_{i}-ct_{i})\\&=2cu(x_{i},t_{i})-cf(x_{i}+ct_{i})-cf(x_{i}-ct_{i})-\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,\mathrm {d} x\end{aligned}}

Solving for $u (x i, t i)$ we arrive at

u(x_{i},t_{i})={\frac {f(x_{i}+ct_{i})+f(x_{i}-ct_{i})}{2}}+{\frac {1}{2c}}\int _{x_{i}-ct_{i}}^{x_{i}+ct_{i}}g(x)\,\mathrm {d} x+{\frac {1}{2c}}\int _{0}^{t_{i}}\int _{x_{i}-c\left(t_{i}-t\right)}^{x_{i}+c\left(t_{i}-t\right)}s(x,t)\,\mathrm {d} x\,\mathrm {d} t.

In the last equation of the sequence, the bounds of the integral over the source function have been made explicit. Looking at this solution, which is valid for all choices $(x i, t i)$ compatible with the wave equation, it is clear that the first two terms are simply d'Alembert's formula, as stated above as the solution of the homogeneous wave equation in one dimension. The difference is in the third term, the integral over the source.

Further generalizations[edit]

Elastic waves[edit]

The elastic wave equation (also known as the Navier–Cauchy equation) in three dimensions describes the propagation of waves in an isotropic homogeneous elasticmedium. Most solid materials are elastic, so this equation describes such phenomena as seismic waves in the Earth and ultrasonic waves used to detect flaws in materials. While linear, this equation has a more complex form than the equations given above, as it must account for both longitudinal and transverse motion:

\rho {\ddot {\mathbf {u} }}=\mathbf {f} +(\lambda +2\mu )\nabla (\nabla \cdot \mathbf {u} )-\mu \nabla \times (\nabla \times \mathbf {u} )

where:

$λ$ and $μ$ are the so-called Lamé parameters describing the elastic properties of the medium,
$ρ$ is the density,
$f$ is the source function (driving force),
and $u$ is the displacement vector.

By using $\nabla \times (\nabla \times u) = \nabla(\nabla \cdot u) - \nabla \cdot \nabla u = \nabla(\nabla \cdot u) - ∆ u$ the elastic wave equation can be rewritten into the more common form of the Navier–Cauchy equation.

Note that in the elastic wave equation, both force and displacement are vector quantities. Thus, this equation is sometimes known as the vector wave equation. As an aid to understanding, the reader will observe that if $f$ and $\nabla \cdot u$ are set to zero, this becomes (effectively) Maxwell's equation for the propagation of the electric field $E$ , which has only transverse waves.

Dispersion relation[edit]

In dispersive wave phenomena, the speed of wave propagation varies with the wavelength of the wave, which is reflected by a dispersion relation

\omega =\omega ({\mathbf {k}}),

where $ω$ is the angular frequency and $k$ is the wavevector describing plane wave solutions. For light waves, the dispersion relation is $ω = \pm c | k |$ , but in general, the constant speed $c$ gets replaced by a variable phase velocity:

v_{{\mathrm {p}}}={\frac {\omega (k)}{k}}.

Nikiya Anton Bettey 2021

Blog Archive