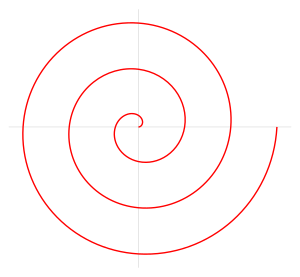
The Archimedean spiral (also known as the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation
with real numbers a and b. Changing the parameter a moves the centerpoint of the spiral outward from the origin (positive a toward θ = 0 and negative a toward θ = π) essentially through a rotation of the spiral, while b controls the distance between loops.
From the above equation, it can thus be stated: the position of particle from the point of start is proportional to the angle θ as time elapses.
Archimedes described such a spiral in his book On Spirals. Conon of Samos was a friend of his and Pappusstates that this spiral was discovered by Conon.[1]
https://en.wikipedia.org/wiki/Archimedean_spiral

No comments:
Post a Comment