Nikiya Anton Bettey 2021: 09-23-2021-0650

Thursday, September 23, 2021

09-23-2021-0650 - Orthogonal Trajectory

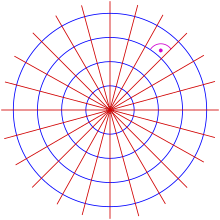
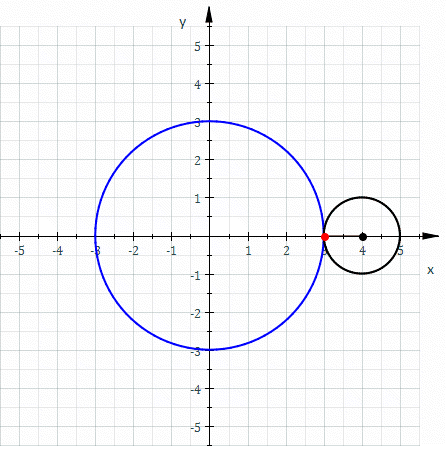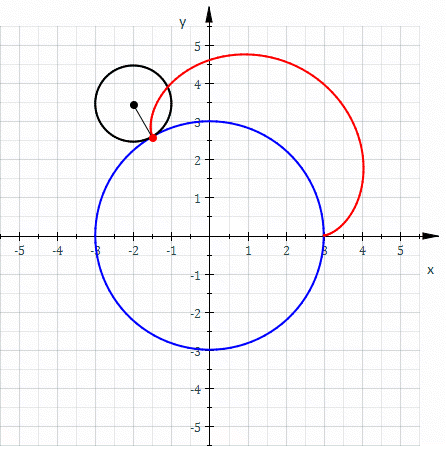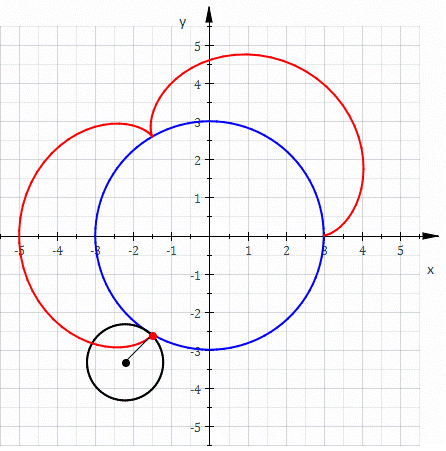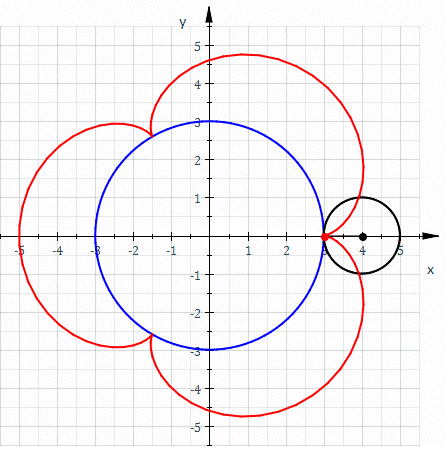
In mathematics an orthogonal trajectory is a curve, which intersects any curve of a given pencil of (planar) curves orthogonally.

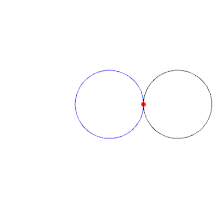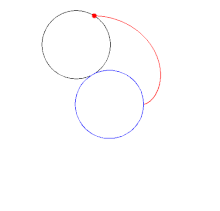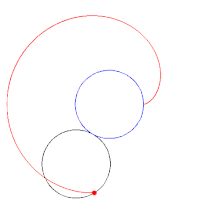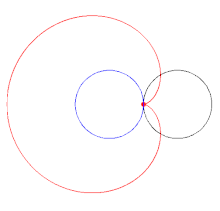
For example, the orthogonal trajectories of a pencil of concentric circles are the lines through their common center (see diagram).

Suitable methods for the determination of orthogonal trajectories are provided by solving differential equations. The standard method establishes a first order ordinary differential equation and solves it by separation of variables. Both steps may be difficult or even impossible. In such cases one has to apply numerical methods.

Orthogonal trajectories are used in mathematics for example as curved coordinate systems (i.e. elliptic coordinates) or appear in physics as electric fields and their equipotential curves.

If the trajectory intersects the given curves by an arbitrary (but fixed) angle, one gets an isogonal trajectory.

Concentric circles with orthogonal trajectories (1. example)

Parabolas with orthogonal trajectories (2. example)

Isogonal trajectories of concentric circles for

\alpha =45^{\circ }

https://en.wikipedia.org/wiki/Orthogonal_trajectory

In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.

https://en.wikipedia.org/wiki/Separation_of_variables

Step 3.

Because the slope of the orthogonal trajectory at a point $(x,y)$ is the negative multiplicative inverse of the slope of the given curve at this point, the orthogonal trajectory satisfies the differential equation of first order

(3)

:\ y'=-{\frac {1}{f(x,y)}}\ ,\qquad

in 1. example

:\ y'=y/x\ ,\qquad

2. example

:\ y'=-{\frac {x}{2y}}\ .

https://en.wikipedia.org/wiki/Orthogonal_trajectory

https://en.wikipedia.org/wiki/Perpendicular#Graph_of_functions

A contour line (also isoline, isopleth, or isarithm) of a function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value.^[1]^[2] It is a plane section of the three-dimensional graph of the function $f(x,y)$ parallel to the $(x,y)$ -plane. More generally, a contour line for a function of two variables is a curve connecting points where the function has the same particular value.^[2]

The bottom part of the diagram shows some contour lines with a straight line running through the location of the maximum value. The curve at the top represents the values along that straight line.

https://en.wikipedia.org/wiki/Contour_line

A cardioid (from the Greek καρδία "heart") is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. The Greek further suggests motion of this rotation mimics the rocking of the heart on an axis defined mathematically as cardioid. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion.^[1] It's also the set of points of reflections of a fixed point on a circle through all tangents to the circle.^[2]

Cardioid generated by a rolling circle on a circle with the same radius

https://en.wikipedia.org/wiki/Cardioid

In geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates

r^{n}=a^{n}\cos(n\theta )\,

where a is a nonzero constant and n is a rational number other than 0. With a rotation about the origin, this can also be written

r^{n}=a^{n}\sin(n\theta ).\,

The term "spiral" is a misnomer, because they are not actually spirals, and often have a flower-like shape. Many well known curves are sinusoidal spirals including:

Rectangular hyperbola (n = −2)
Line (n = −1)
Parabola (n = −1/2)
Tschirnhausen cubic (n = −1/3)
Cayley's sextet (n = 1/3)
Cardioid (n = 1/2)
Circle (n = 1)
Lemniscate of Bernoulli (n = 2)

The curves were first studied by Colin Maclaurin.

https://en.wikipedia.org/wiki/Sinusoidal_spiral

In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an epicycle—which rolls without slipping around a fixed circle. It is a particular kind of roulette.

The red curve is an epicycloid traced as the small circle (radius r = 1) rolls around the outside of the large circle (radius R = 3).

https://en.wikipedia.org/wiki/Epicycloid

In numerical analysis, the Runge–Kutta methods (English: /ˈrʊŋəˈkʊtɑː/ (listen) RUUNG-ə-KUUT-tah^[1]) are a family of implicit and explicit iterative methods, which include the well-known routine called the Euler Method, used in temporal discretization for the approximate solutions of ordinary differential equations.^[2] These methods were developed around 1900 by the German mathematicians Carl Runge and Wilhelm Kutta.

https://en.wikipedia.org/wiki/Runge–Kutta_methods

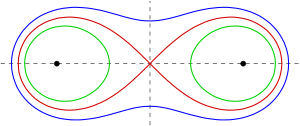
A Cassini oval is a quartic plane curve defined as the locus of points in the plane such that the product of the distances to two fixed points is constant. This may be contrasted with an ellipse, for which thesum of the distances is constant, rather than the product. Cassini ovals are the special case of polynomial lemniscates when the polynomial used has degree 2.

Cassini ovals are named after the astronomer Giovanni Domenico Cassini who studied them in 1680.^[1] Cassini believed that the Sun traveled around the Earth on one of these ovals, with the Earth at one focus of the oval.^{[citation needed]} Other names include Cassinian ovals, Cassinian curves and ovals of Cassini.

Three Cassini ovals, differing by the range within which the parameter e falls: 0 < e < 1 (green); e = 1 (red); 1 < e <

{\sqrt {2}}

(blue). Not shown: e ≥

{\sqrt {2}}

(convex).

https://en.wikipedia.org/wiki/Cassini_oval

In geometry, two conic sections are called confocal, if they have the same foci. Because ellipses and hyperbolas possess two foci, there are confocal ellipses, confocal hyperbolas and confocal mixtures of ellipses and hyperbolas. In the mixture of confocal ellipses and hyperbolas, any ellipse intersects any hyperbola orthogonally (at right angles). Parabolas possess only one focus, so, by convention, confocal parabolas have the same focus and the same axis of symmetry. Consequently, any point not on the axis of symmetry lies on two confocal parabolas which intersect orthogonally (see below).

The formal extension of the concept of confocal conics to surfaces leads to confocal quadrics.

Pencils of confocal ellipses and hyperbolas

https://en.wikipedia.org/wiki/Confocal_conic_sections

Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. They were discovered by Apollonius of Perga, a renowned Greekgeometer.

Some Apollonian circles. Every blue circle intersects every red circle at a right angle. Every red circle passes through the two points, C and D, and every blue circle separates the two points.

https://en.wikipedia.org/wiki/Apollonian_circles

In mathematics, orthogonality is the generalization of the notion of perpendicularity to the linear algebra of bilinear forms. Two elements u and v of a vector space with bilinear form B are orthogonal when B(u, v) = 0. Depending on the bilinear form, the vector space may contain nonzero self-orthogonal vectors. In the case of function spaces, families of orthogonal functions are used to form a basis.

By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in other fields including art and chemistry.

The line segments AB and CD are orthogonal to each other.

Etymology[edit]

The word comes from the Greek ὀρθός (orthos), meaning "upright",^[1] and γωνία (gonia), meaning "angle".^[2] The ancient Greek ὀρθογώνιον orthogōnionand classical Latin orthogonium originally denoted a rectangle.^[3] Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word orthogonalis came to mean a right angle or something related to a right angle.^[4]

Mathematics and physics[edit]

Orthogonality and rotation of coordinate systems compared between left: Euclidean space through circular angle ϕ, right: in Minkowski spacetime through hyperbolic angle ϕ (red lines labelled c denote the worldlines of a light signal, a vector is orthogonal to itself if it lies on this line).^[5]

Definitions[edit]

In geometry, two Euclidean vectors are orthogonal if they are perpendicular, i.e., they form a right angle.
Two vectors, x and y, in an inner product space, V, are orthogonal if their inner product $\langle x, y \rangle$ is zero.^[6] This relationship is denoted $x\perp y$ .
Two vector subspaces, A and B, of an inner product space V, are called orthogonal subspaces if each vector in A is orthogonal to each vector in B. The largest subspace of Vthat is orthogonal to a given subspace is its orthogonal complement.
Given a module M and its dual M^∗, an element m′ of M^∗ and an element m of M are orthogonal if their natural pairing is zero, i.e. ⟨m′, m⟩ = 0. Two sets S′ ⊆ M^∗ and S ⊆ M are orthogonal if each element of S′ is orthogonal to each element of S.^[7]
A term rewriting system is said to be orthogonal if it is left-linear and is non-ambiguous. Orthogonal term rewriting systems are confluent.

A set of vectors in an inner product space is called pairwise orthogonal if each pairing of them is orthogonal. Such a set is called an orthogonal set.

In certain cases, the word normal is used to mean orthogonal, particularly in the geometric sense as in the normal to a surface. For example, the y-axis is normal to the curve y = x² at the origin. However, normal may also refer to the magnitude of a vector. In particular, a set is called orthonormal (orthogonal plus normal) if it is an orthogonal set of unit vectors. As a result, use of the term normal to mean "orthogonal" is often avoided. The word "normal" also has a different meaning in probability and statistics.

A vector space with a bilinear form generalizes the case of an inner product. When the bilinear form applied to two vectors results in zero, then they are orthogonal. The case of a pseudo-Euclidean plane uses the term hyperbolic orthogonality. In the diagram, axes x′ and t′ are hyperbolic-orthogonal for any given ϕ.

Euclidean vector spaces[edit]

In Euclidean space, two vectors are orthogonal if and only if their dot product is zero, i.e. they make an angle of 90° (π/2 radians), or one of the vectors is zero.^[8] Hence orthogonality of vectors is an extension of the concept of perpendicular vectors to spaces of any dimension.

The orthogonal complement of a subspace is the space of all vectors that are orthogonal to every vector in the subspace. In a three-dimensional Euclidean vector space, the orthogonal complement of a line through the origin is the plane through the origin perpendicular to it, and vice versa.^[9]

Note that the geometric concept of two planes being perpendicular does not correspond to the orthogonal complement, since in three dimensions a pair of vectors, one from each of a pair of perpendicular planes, might meet at any angle.

In four-dimensional Euclidean space, the orthogonal complement of a line is a hyperplane and vice versa, and that of a plane is a plane.^[9]

Orthogonal functions[edit]

By using integral calculus, it is common to use the following to define the inner product of two functions f and g with respect to a nonnegative weight functionw over an interval [a, b]:

\langle f, g\rangle_w = \int_a^b f(x)g(x)w(x)\,dx.

In simple cases, w(x) = 1.

We say that functions f and g are orthogonal if their inner product (equivalently, the value of this integral) is zero:

\langle f,g\rangle _{w}=0.

Orthogonality of two functions with respect to one inner product does not imply orthogonality with respect to another inner product.

We write the norm with respect to this inner product as

\|f\|_w = \sqrt{\langle f, f\rangle_w}

The members of a set of functions {f_i : i = 1, 2, 3, ...} are orthogonal with respect to w on the interval [a, b] if

\langle f_{i},f_{j}\rangle _{w}=0\quad i\neq j.

The members of such a set of functions are orthonormal with respect to w on the interval [a, b] if

\langle f_{i},f_{j}\rangle _{w}=\delta _{i,j},

where

\delta _{i,j}=\left\{{\begin{matrix}1,&&i=j\\0,&&i\neq j\end{matrix}}\right.

is the Kronecker delta. In other words, every pair of them (excluding pairing of a function with itself) is orthogonal, and the norm of each is 1. See in particular the orthogonal polynomials.

Examples[edit]

The vectors (1, 3, 2)^T, (3, −1, 0)^T, (1, 3, −5)^T are orthogonal to each other, since (1)(3) + (3)(−1) + (2)(0) = 0, (3)(1) + (−1)(3) + (0)(−5) = 0, and (1)(1) + (3)(3) + (2)(−5) = 0.
The vectors (1, 0, 1, 0, ...)^T and (0, 1, 0, 1, ...)^T are orthogonal to each other. The dot product of these vectors is 0. We can then make the generalization to consider the vectors in Z₂ⁿ: $\mathbf {v} _{k}=\sum _{i=0 \atop ai+k<n}^{n/a}\mathbf {e} _{i}$ for some positive integer a, and for 1 ≤ k ≤ a − 1, these vectors are orthogonal, for example ${\begin{bmatrix}1&0&0&1&0&0&1&0\end{bmatrix}}$ , ${\begin{bmatrix}0&1&0&0&1&0&0&1\end{bmatrix}}$ , ${\begin{bmatrix}0&0&1&0&0&1&0&0\end{bmatrix}}$ are orthogonal.
The functions 2t + 3 and 45t² + 9t − 17 are orthogonal with respect to a unit weight function on the interval from −1 to 1: $\int _{-1}^{1}\left(2t+3\right)\left(45t^{2}+9t-17\right)\,dt=0$
The functions 1, sin(nx), cos(nx) : n = 1, 2, 3, … are orthogonal with respect to Riemann integration on the intervals [0, 2π], [−π, π], or any other closed interval of length 2π. This fact is a central one in Fourier series.

Orthogonal polynomials[edit]

Various polynomial sequences named for mathematicians of the past are sequences of orthogonal polynomials. In particular:

The Hermite polynomials are orthogonal with respect to the Gaussian distribution with zero mean value.
The Legendre polynomials are orthogonal with respect to the uniform distribution on the interval [−1, 1].
The Laguerre polynomials are orthogonal with respect to the exponential distribution. Somewhat more general Laguerre polynomial sequences are orthogonal with respect to gamma distributions.
The Chebyshev polynomials of the first kind are orthogonal with respect to the measure $1/\sqrt{1-x^2}.$
The Chebyshev polynomials of the second kind are orthogonal with respect to the Wigner semicircle distribution.

Orthogonal states in quantum mechanics[edit]

In quantum mechanics, a sufficient (but not necessary) condition that two eigenstates of a Hermitian operator, $\psi_m$ and $\psi _{n}$ , are orthogonal is that they correspond to different eigenvalues. This means, in Dirac notation, that $\langle \psi_m | \psi_n \rangle = 0$ if $\psi_m$ and $\psi _{n}$ correspond to different eigenvalues. This follows from the fact that Schrödinger's equation is a Sturm–Liouville equation (in Schrödinger's formulation) or that observables are given by hermitian operators (in Heisenberg's formulation).^{[citation needed]}

https://en.wikipedia.org/wiki/Orthogonality

Underwater acoustics is the study of the propagation of sound in water and the interaction of the mechanical waves that constitute sound with the water, its contents and its boundaries. The water may be in the ocean, a lake, a river or a tank. Typical frequencies associated with underwater acoustics are between 10 Hz and 1 MHz. The propagation of sound in the ocean at frequencies lower than 10 Hz is usually not possible without penetrating deep into the seabed, whereas frequencies above 1 MHz are rarely used because they are absorbed very quickly. Underwater acoustics is sometimes known as hydroacoustics.

The field of underwater acoustics is closely related to a number of other fields of acoustic study, including sonar, transduction, signal processing, acoustical oceanography, bioacoustics, and physical acoustics.

Absorption of sound[edit]

Absorption of low frequency sound is weak.^[6] (see Technical Guides – Calculation of absorption of sound in seawater for an on-line calculator). The main cause of sound attenuation in fresh water, and at high frequency in sea water (above 100 kHz) is viscosity. Important additional contributions at lower frequency in seawater are associated with the ionic relaxation of boric acid (up to c. 10 kHz)^[6] and magnesium sulfate (c. 10 kHz-100 kHz).^[7]

Sound may be absorbed by losses at the fluid boundaries. Near the surface of the sea losses can occur in a bubble layer or in ice, while at the bottom sound can penetrate into the sediment and be absorbed.

Sound reflection and scattering[edit]

Boundary interactions[edit]

Both the water surface and bottom are reflecting and scattering boundaries.

Surface[edit]

For many purposes the sea-air surface can be thought of as a perfect reflector. The impedance contrast is so great that little energy is able to cross this boundary. Acoustic pressure waves reflected from the sea surface experience a reversal in phase, often stated as either a "pi phase change" or a "180 deg phase change". This is represented mathematically by assigning a reflection coefficient of minus 1 instead of plus one to the sea surface.^[8]

At high frequency (above about 1 kHz) or when the sea is rough, some of the incident sound is scattered, and this is taken into account by assigning a reflection coefficient whose magnitude is less than one. For example, close to normal incidence, the reflection coefficient becomes $R=-e^{{-2k^{{2}}h^{{2}}sin^{2}A}}$ , where h is the rmswave height.^[9]

A further complication is the presence of wind generated bubbles or fish close to the sea surface.^[10] The bubbles can also form plumes that absorb some of the incident and scattered sound, and scatter some of the sound themselves.^[11]

Seabed[edit]

The acoustic impedance mismatch between water and the bottom is generally much less than at the surface and is more complex. It depends on the bottom material types and depth of the layers. Theories have been developed for predicting the sound propagation in the bottom in this case, for example by Biot ^[12] and by Buckingham.^[13]

At target[edit]

The reflection of sound at a target whose dimensions are large compared with the acoustic wavelength depends on its size and shape as well as the impedance of the target relative to that of water. Formulae have been developed for the target strength of various simple shapes as a function of angle of sound incidence. More complex shapes may be approximated by combining these simple ones.^[1]

Particle physics[edit]

A neutrino is a fundamental particle that interacts very weakly with other matter. For this reason, it requires detection apparatus on a very large scale, and the ocean is sometimes used for this purpose. In particular, it is thought that ultra-high energy neutrinos in seawater can be detected acoustically.^[55]

https://en.wikipedia.org/wiki/Underwater_acoustics

Nikiya Anton Bettey 2021

Blog Archive