Nikiya Anton Bettey 2021: 09-23-2021-0748 - rhumb line great-circle distance orthodromic distance sphere Sphere-cylinder intersection cylinder Viviani curve Viviani's Curve

Thursday, September 23, 2021

09-23-2021-0748 - rhumb line great-circle distance orthodromic distance sphere Sphere-cylinder intersection cylinder Viviani curve Viviani's Curve

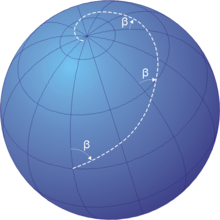
In navigation, a rhumb line, rhumb, (/rʌm/) or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant bearing as measured relative to true north.

Image of a loxodrome, or rhumb line, spiraling towards the North Pole

https://en.wikipedia.org/wiki/Rhumb_line

https://en.wikipedia.org/wiki/Category:Spherical_curves

The great-circle distance, orthodromic distance, or spherical distance is the distance along a great circle.

It is the shortest distance between two points on the surface of a sphere, measured along the surface of the sphere (as opposed to a straight line through the sphere's interior). The distance between two points in Euclidean space is the length of a straight line between them, but on the sphere there are no straight lines. In spaces with curvature, straight lines are replaced by geodesics. Geodesics on the sphere are circles on the sphere whose centers coincide with the center of the sphere, and are called great circles.

The determination of the great-circle distance is part of the more general problem of great-circle navigation, which also computes the azimuths at the end points and intermediate way-points.

Through any two points on a sphere that are not directly opposite each other, there is a unique great circle. The two points separate the great circle into two arcs. The length of the shorter arc is the great-circle distance between the points. A great circle endowed with such a distance is called a Riemannian circle in Riemannian geometry.

Between two points that are directly opposite each other, called antipodal points, there are infinitely many great circles, and all great circle arcs between antipodal points have a length of half the circumference of the circle, or $\pi r$ , where r is the radius of the sphere.

The Earth is nearly spherical, so great-circle distance formulas give the distance between points on the surface of the Earth correct to within about 0.5%.^[1]

The vertex^{[disambiguation needed]} is the highest-latitude point on a great circle.

A diagram illustrating great-circle distance (drawn in red) between two points on a sphere, P and Q. Two nodal^{[disambiguation needed]} points, u and v, which are antipodal, are also shown.

https://en.wikipedia.org/wiki/Great-circle_distance

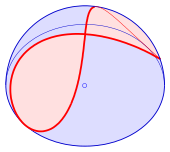
In mathematics, Viviani's curve, also known as Viviani's window, is a figure eight shaped space curve named after the Italian mathematician Vincenzo Viviani. It is the intersection of a sphere with a cylinder that is tangent to the sphere and passes through two poles (a diameter) of the sphere (see diagram). Before Viviani this curve was studied by Simon de La Loubère and Gilles de Roberval.^[1]^[2]

The projection of Viviani's curve onto a plane perpendicular to the line through the crossing point and the sphere center is the lemniscate of Gerono.^[3]

In 1692 Viviani tackled the task: Cut out of a half sphere (radius $r$ ) two windows, such that the remaining surface (of the half sphere) can be squared, i.e. a square with the same area can be constructed using only compasses and ruler. His solution has an area of $4r^{2}$ (see below).

Viviani's curve: intersection of a sphere with a tangent cylinder

The light blue part of the half sphere can be squared

Equations[edit]

cylinder upright.

In order to keep the proof for squaring simple,

the sphere has the equation

\;x^{2}+y^{2}+z^{2}=r^{2}\;

and

the cylinder is upright with equation

\;x^{2}+y^{2}-rx=0\;

The cylinder has radius $r/2$ and is tangent to the sphere at point $(r,0,0)\ .$

Properties of the curve[edit]

Floor plan, elevation and side plan[edit]

Floor plan, elevation and side plan

Elimination of $x$ , $y$ , $z$ respectively yields:

The orthogonal projection of the intersection curve onto the

x

y

-plane is the circle with equation

\;\left(x-{\tfrac {r}{2}}\right)^{2}+y^{2}=\left({\tfrac {r}{2}}\right)^{2}\ .

x

z

-plane the parabola with equation

\;x=-{\tfrac {1}{r}}z^{2}+r\;.

y

z

-plane the algebraic curve with the equation

\;z^{4}+r^{2}(y^{2}-z^{2})=0\;.

Parametric representation[edit]

For parametric representation and the determination of the area

Representing the sphere by

{\begin{array}{cll}x&=&r\cdot \cos \theta \cdot \cos \varphi \\y&=&r\cdot \cos \theta \cdot \sin \varphi \\z&=&r\cdot \sin \theta \qquad \qquad -{\tfrac {\pi }{2}}\leq \theta \leq {\tfrac {\pi }{2}}\ ,\ -\pi \leq \varphi \leq \pi \;,\end{array}}

and setting $\;\varphi =\theta ,\;$ yields the curve

{\begin{array}{cll}x&=&r\cdot \cos \theta \cdot \cos \theta \\y&=&r\cdot \cos \theta \cdot \sin \theta \\z&=&r\cdot \sin \theta \qquad \qquad -{\tfrac {\pi }{2}}\leq \theta \leq {\tfrac {\pi }{2}}\ .\end{array}}

One easily checks that the spherical curve fulfills the equation of the cylinder. But the boundaries allow only the red part (see diagram) of Viviani's curve. The missing second half (green) has the property $\;\color {green}\varphi =-\theta \;.$

With help of this parametric representation it is easy to prove the statement: The area of the half sphere (containing Viviani's curve) minus the area of the two windows is $4r^{2}$ . The area of the upper right part of Viviani's window (see diagram) can be calculated by an integration:

\iint _{S_{sphere}}r^{2}\cos \theta \,\mathrm {d} \theta \mathrm {d} \varphi =r^{2}\int _{0}^{\pi /2}\int _{0}^{\theta }\cos \theta \,\mathrm {d} \varphi \mathrm {d} \theta =r^{2}\left({\frac {\pi }{2}}-1\right)\ .

Hence the total area of the spherical surface included by Viviani's curve is $2\pi r^{2}-4r^{2}$ and the area of the half sphere ( $2\pi r^{2}$ ) minus the area of Viviani's window is $\;4r^{2}\;$ , the area of a square with the sphere's diameter as the length of an edge.

Rational bezier representation[edit]

The quarter of Viviani's curve that lies in the all-positive quadrant of 3D space cannot be represented exactly by a regular bezier curve of any degree.

However, it can be represented exactly by a 3D rational bezier segment of degree 4, and there is an infinite family of rational bezier control points generating that segment.

One possible solution is given by the following five control points:

{\boldsymbol {p0}}={\begin{bmatrix}0\\0\\1\\1\end{bmatrix}}{\boldsymbol {p1}}={\begin{bmatrix}0\\{\frac {1}{2{\sqrt {2}}}}\\{\frac {1}{\sqrt {2}}}\\{\frac {1}{\sqrt {2}}}\end{bmatrix}}{\boldsymbol {p2}}={\begin{bmatrix}{\frac {1}{3}}\\{\frac {1}{2}}\\{\frac {1}{2}}\\{\frac {2}{3}}\end{bmatrix}}{\boldsymbol {p3}}={\begin{bmatrix}{\frac {1}{\sqrt {2}}}\\{\frac {1}{2{\sqrt {2}}}}\\{\frac {1}{2{\sqrt {2}}}}\\{\frac {1}{\sqrt {2}}}\end{bmatrix}}{\boldsymbol {p4}}={\begin{bmatrix}1\\0\\0\\1\end{bmatrix}}

The corresponding rational parametrization is:

\left({\begin{array}{c}{\frac {2\mu ^{2}\left(\mu ^{2}-2\left(2+{\sqrt {2}}\right)\mu +4{\sqrt {2}}+6\right)}{\left(2(\mu -1)\mu +{\sqrt {2}}+2\right)^{2}}}\\{\frac {2(\mu -1)\mu \left((\mu -1)\mu -3{\sqrt {2}}-4\right)}{\left(2(\mu -1)\mu +{\sqrt {2}}+2\right)^{2}}}\\-{\frac {(\mu -1)\left({\sqrt {2}}\mu +{\sqrt {2}}+2\right)}{2(\mu -1)\mu +{\sqrt {2}}+2}}\\\end{array}}\right)\;\mu \in \left[0,1\right]

Relation to other curves[edit]

The 8-shaped elevation (see above) is a Lemniscate of Gerono.
Viviani' curve is a special Clelia curve. For a Clelia curve the relation between the angles is $\;\varphi =c\;\theta \;.$

Viviani's curve (red) as intersection of the sphere and a cone (pink)

Subtracting 2× the cylinder equation from the sphere's equation and applying completing the square leads to the equation

(x-r)^{2}+y^{2}=z^{2}\;,

which describes a right circular cone with its apex at $\;(r,0,0)\;$ , the double point of Viviani's curve. Hence

Viviani's curve can be considered not only as the intersection curve of a sphere and a cylinder but also as

a) the intersection of a sphere and a cone and as

b) the intersection of a cylinder and a cone.

Nikiya Anton Bettey 2021

Blog Archive