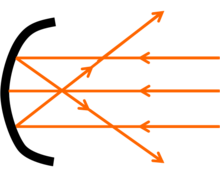
In geometry, the center of curvature of a curve is found at a point that is at a distance from the curve equal to the radius of curvature lying on the normal vector. It is the point at infinity if the curvature is zero. The osculating circle to the curve is centered at the centre of curvature. Cauchy defined the center of curvature C as the intersection point of two infinitely close normal lines to the curve.[1] The locus of centers of curvature for each point on the curve comprise the evolute of the curve. This term is generally used in physics regarding to study of lenses and mirrors.
It can also be defined as the spherical distance between the point at which all the rays falling on a lens or mirror either seems to converge to (in the case of convex lenses and concave mirrors) or diverge from (in the case of concave lenses or convex mirrors) and the lens/mirror itself.[2]
https://en.wikipedia.org/wiki/Center_of_curvature
In mathematics, osculate, meaning to touch (from the Latin osculum meaning kiss), may refer to:
- osculant, an invariant of hypersurfaces
- osculating circle
- osculating curve
- osculating plane
- osculating orbit
The obsolete Quinarian system of biological classification attempted to group creatures into circles which could touch or overlap with adjacent circles, a phenomenon called 'osculation'.
https://en.wikipedia.org/wiki/Osculate
In mathematics, particularly in differential geometry, an osculating plane is a plane in a Euclidean space or affine space which meets a submanifold at a point in such a way as to have a second order of contact at the point. The word osculate is from the Latin osculatus which is a past participle of osculari, meaning to kiss. An osculating plane is thus a plane which "kisses" a submanifold.
The osculating plane in the geometry of Euclidean space curves can be described in terms of the Frenet-Serret formulas as the linear span of the tangent and normal vectors.
https://en.wikipedia.org/wiki/Osculating_plane


No comments:
Post a Comment