In geometry, a negative pedal curve is a plane curve that can be constructed from another plane curve C and a fixed point P on that curve. For each point X ≠ P on the curve C, the negative pedal curve has a tangent that passes through X and is perpendicular to line XP. Constructing the negative pedal curve is the inverse operation to constructing a pedal curve.
https://en.wikipedia.org/wiki/Negative_pedal_curve
In geometry, the center of curvature of a curve is found at a point that is at a distance from the curve equal to the radius of curvature lying on the normal vector. It is the point at infinity if the curvature is zero. The osculating circle to the curve is centered at the centre of curvature. Cauchy defined the center of curvature C as the intersection point of two infinitely close normal lines to the curve.[1] The locus of centers of curvature for each point on the curve comprise the evolute of the curve. This term is generally used in physics regarding to study of lenses and mirrors.
It can also be defined as the spherical distance between the point at which all the rays falling on a lens or mirror either seems to converge to (in the case of convex lenses and concave mirrors) or diverge from (in the case of concave lenses or convex mirrors) and the lens/mirror itself.[2]
https://en.wikipedia.org/wiki/Center_of_curvature
In mathematics, a plane curve is a curve in a plane that may be either a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases are smooth plane curves (including piecewise smooth plane curves), and algebraic plane curves. Plane curves also include the Jordan curves (curves that enclose a region of the plane but need not be smooth) and the graphs of continuous functions.
Examples[edit]
Numerous examples of plane curves are shown in Gallery of curves and listed at List of curves. The algebraic curves of degree 1 or 2 are shown here (an algebraic curve of degree less than 3 is always contained in a plane):
| Name | Implicit equation | Parametric equation | As a function | graph |
|---|---|---|---|---|
| Straight line | 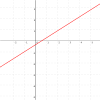 | |||
| Circle | 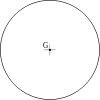 | |||
| Parabola | 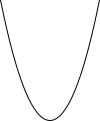 | |||
| Ellipse |  | |||
| Hyperbola |  |
https://en.wikipedia.org/wiki/Plane_curve
In geometry, a sectrix of Maclaurin is defined as the curve swept out by the point of intersection of two lines which are each revolving at constant rates about different points called poles. Equivalently, a sectrix of Maclaurin can be defined as a curve whose equation in biangular coordinates is linear. The name is derived from the trisectrix of Maclaurin (named for Colin Maclaurin), which is a prominent member of the family, and their sectrix property, which means they can be used to divide an angle into a given number of equal parts. There are special cases are also known as arachnida or araneidans because of their spider-like shape, and Plateau curves after Joseph Plateau who studied them.
https://en.wikipedia.org/wiki/Sectrix_of_Maclaurin
In mathematics, biangular coordinates are a coordinate system for the plane where and are two fixed points, and the position of a point P not on the line is determined by the angles and
https://en.wikipedia.org/wiki/Biangular_coordinates
Straightedge and compass construction, also known as ruler-and-compass construction or classical construction, is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.
https://en.wikipedia.org/wiki/Straightedge_and_compass_construction
Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well known toy version was developed by British engineer Denys Fisher and first sold in 1965.
The name has been a registered trademark of Hasbro Inc. since 1998 following purchase of the company that had acquired the Denys Fisher company. The Spirograph brand was relaunched worldwide in 2013, with its original product configurations, by Kahootz Toys.
https://en.wikipedia.org/wiki/Spirograph



















No comments:
Post a Comment