Peter Guthrie Tait FRSE (28 April 1831 – 4 July 1901) was a Scottish mathematical physicist and early pioneer in thermodynamics. He is best known for the mathematical physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory.
His work on knot theory contributed to the eventual formation of topology as a mathematical discipline. His name is known in graph theory mainly for Tait's conjecture. He is also one of the namesakes of the Tait-Kneser theorem on osculating circles.
Peter Guthrie Tait | |
|---|---|
 Peter Guthrie Tait – Scottish physicist, an early pioneer in thermodynamics | |
| Born | 28 April 1831 Dalkeith, Scotland |
| Died | 4 July 1901 (aged 70) Edinburgh, Scotland |
| Nationality | Scottish |
| Citizenship | British |
| Alma mater | University of Edinburgh Peterhouse, Cambridge |
| Known for | Knot theory Ménage problem Snark Tait conjectures Tait equation Tait–Bryan angles Tait–Kneser theorem |
| Awards | Smith's Prize (1852) Keith Medal (1867-69) Royal Medal (1886) |
| Scientific career | |
| Fields | Mathematical physics |
| Institutions | Peterhouse, Cambridge |
| Academic advisors | William Hopkins |
https://en.wikipedia.org/wiki/Peter_Tait_(physicist)
In combinatorial mathematics, the ménage problem or problème des ménages[1] asks for the number of different ways in which it is possible to seat a set of male-female couples at a round dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas and independently, a few years earlier, by Peter Guthrie Tait in connection with knot theory.[2] For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is
Mathematicians have developed formulas and recurrence equations for computing these numbers and related sequences of numbers. Along with their applications to etiquette and knot theory, these numbers also have a graph theoreticinterpretation: they count the numbers of matchings and Hamiltonian cycles in certain families of graphs.
https://en.wikipedia.org/wiki/Ménage_problem
In the mathematical field of graph theory, a snark is a simple, connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, the connectivity is redundant so that removing no one edge would split the graph, and the edges cannot be colored by only three colors without two edges of the same color meeting at a point. (By Vizing's theorem, the chromatic index of a cubic graph is 3 or 4.) In order to avoid trivial cases, snarks are often restricted to have girth at least 5.
Writing in The Electronic Journal of Combinatorics, Miroslav Chladný states that
https://en.wikipedia.org/wiki/Snark_(graph_theory)
In the mathematical field of topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, (in topology, a circle isn't bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself.
Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental problem in knot theory is determining when two descriptions represent the same knot.
A complete algorithmic solution to this problem exists, which has unknown complexity. In practice, knots are often distinguished using a knot invariant, a "quantity" which is the same when computed from different descriptions of a knot. Important invariants include knot polynomials, knot groups, and hyperbolic invariants.
The original motivation for the founders of knot theory was to create a table of knots and links, which are knots of several components entangled with each other. More than six billion knots and links have been tabulated since the beginnings of knot theory in the 19th century.
To gain further insight, mathematicians have generalized the knot concept in several ways. Knots can be considered in other three-dimensional spaces and objects other than circles can be used; see knot (mathematics). Higher-dimensional knots are n-dimensional spheres in m-dimensional Euclidean space.
https://en.wikipedia.org/wiki/Knot_theory
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots.[1] The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
Background[edit]
Tait came up with his conjectures after his attempt to tabulate all knots in the late 19th century. As a founder of the field of knot theory, his work lacks a mathematically rigorous framework, and it is unclear whether he intended the conjectures to apply to all knots, or just to alternating knots. It turns out that most of them are only true for alternating knots.[2] In the Tait conjectures, a knot diagram is called "reduced" if all the "isthmi", or "nugatory crossings" have been removed.
Crossing number of alternating knots[edit]
Tait conjectured that in certain circumstances, crossing number was a knot invariant, specifically:
In other words, the crossing number of a reduced, alternating link is an invariant of the knot. This conjecture was proved by Louis Kauffman, Kunio Murasugi (村杉 邦男), and Morwen Thistlethwaite in 1987, using the Jones polynomial.[3] [4] [5] A geometric proof, not using knot polynomials, was given in 2017 by Joshua Greene.[6]
Writhe and chirality[edit]
A second conjecture of Tait:
This conjecture was also proved by Kauffman and Thistlethwaite.[3][7]
Flyping[edit]
The Tait flyping conjecture can be stated:
The Tait flyping conjecture was proved by Thistlethwaite and William Menasco in 1991.[9] The Tait flyping conjecture implies some more of Tait's conjectures:
This follows because flyping preserves writhe. This was proved earlier by Murasugi and Thistlethwaite.[10][7] It also follows from Greene's work.[6] For non-alternating knots this conjecture is not true; the Perko pair is a counterexample.[2] This result also implies the following conjecture:
This follows because a knot's mirror image has opposite writhe. This conjecture is again only true for alternating knots: non-alternating amphichiral knot with crossing number 15 exist.[11]
See also[edit]
In fluid mechanics, the Tait equation is an equation of state, used to relate liquid density to pressure. The equation was originally published by Peter Guthrie Tait in 1888 in the form[1]
where is the reference pressure (taken to be 1 atmosphere), is the current pressure, is the volume of fresh water at the reference pressure, is the volume at the current pressure, and are experimentally determined parameters.
https://en.wikipedia.org/wiki/Tait_equation
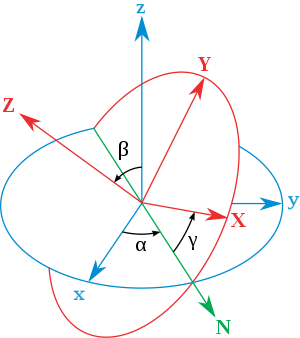
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.[1]
They can also represent the orientation of a mobile frame of reference in physics or the orientation of a general basis in 3-dimensional linear algebra. Alternative forms were later introduced by Peter Guthrie Tait and George H. Bryan intended for use in aeronautics and engineering.
Proper Euler angles[edit]
Assuming a frame with unit vectors (X, Y, Z) given by their coordinates as in the main diagram, it can be seen that:
And, since
for we have
As is the double projection of a unitary vector,
There is a similar construction for , projecting it first over the plane defined by the axis z and the line of nodes. As the angle between the planes is and , this leads to:
and finally, using the inverse cosine function,
Tait–Bryan angles[edit]
Assuming a frame with unit vectors (X, Y, Z) given by their coordinates as in this new diagram (notice that the angle theta is negative), it can be seen that:
As before,
for we have
in a way analogous to the former one:
Looking for similar expressions to the former ones:
Last remarks[edit]
Note that the inverse sine and cosine functions yield two possible values for the argument. In this geometrical description, only one of the solutions is valid. When Euler angles are defined as a sequence of rotations, all the solutions can be valid, but there will be only one inside the angle ranges. This is because the sequence of rotations to reach the target frame is not unique if the ranges are not previously defined.[2]
For computational purposes, it may be useful to represent the angles using atan2(y, x). For example, in the case of proper Euler angles:
https://en.wikipedia.org/wiki/Euler_angles#Tait–Bryan_angles_2
In differential geometry, the Tait–Kneser theorem states that, if a smooth plane curve has monotonic curvature, then the osculating circles of the curve are disjoint and nested within each other.[1] The logarithmic spiral or the pictured Archimedean spiral provide examples of curves whose curvature is monotonic for the entire curve. This monotonicity cannot happen for a simple closed curve (by the four-vertex theorem, there are at least four vertices where the curvature reaches an extreme point)[1] but for such curves the theorem can be applied to the arcs of the curves between its vertices.
The theorem is named after Peter Tait, who published it in 1896, and Adolf Kneser, who rediscovered it and published it in 1912.[1][2][3] Tait's proof follows simply from the properties of the evolute, the curve traced out by the centers of osculating circles. For curves with monotone curvature, the arc length along the evolute between two centers equals the difference in radii of the corresponding circles. This arc length must be greater than the straight-line distance between the same two centers, so the two circles have centers closer together than the difference of their radii, from which the theorem follows.[1][2]
Analogous disjointness theorems can be proved for the family of Taylor polynomials of a given smooth function, and for the osculating conics to a given smooth curve.[1][4]
https://en.wikipedia.org/wiki/Tait–Kneser_theorem








































No comments:
Post a Comment