Chronozone
A chronozone or chron is a unit in chronostratigraphy, defined by events such as geomagnetic reversals (magnetozones), or based on the presence of specific fossils (biozone or biochronozone). According to the International Commission on Stratigraphy, the term "chronozone" refers to the rocks formed during a particular time period, while "chron" refers to that time period.[1]
Although non-hierarchical, chronozones have been recognized as useful markers or benchmarks of time in the rock record. Chronozones are non-hierarchical in that chronozones do not need to correspond across geographic or geologic boundaries, nor be equal in length. Although a former, early constraint required that a chronozone be defined as smaller than a geological stage. Another early use was hierarchical in that Harland et al. (1989) used "chronozone" for the slice of time smaller than a faunal stage defined in biostratigraphy. [2] The ICS superseded these earlier usages in 1994.[3]
The key factor in designating an internationally acceptable chronozone is whether the overall fossil column is clear, unambiguous, and widespread. Some accepted chronozones contain others, and certain larger chronozones have been designated which span whole defined geological time units, both large and small. For example, the chronozone Pliocene is a subset of the chronozone Neogene, and the chronozone Pleistocene is a subset of the chronozone Quaternary.
| Segments of rock (strata) in chronostratigraphy | Time spans in geochronology | Notes to geochronological units |
|---|---|---|
| Eonothem | Eon | 4 total, half a billion years or more |
| Erathem | Era | 10 defined, several hundred million years |
| System | Period | 22 defined, tens to ~one hundred million years |
| Series | Epoch | 34 defined, tens of millions of years |
| Stage | Age | 99 defined, millions of years |
| Chronozone | Chron | subdivision of an age, not used by the ICS timescale |
See also
- Body form
- Chronology (geology)
- European Mammal Neogene
- Geologic time scale
- North American Land Mammal Age
- Type locality (geology)
- List of GSSPs
References
- Cohen, K.M.; Finney, S.; Gibbard, P.L. (2015), International Chronostratigraphic Chart (PDF), International Commission on Stratigraphy.
- Gehling, James; Jensen, Sören; Droser, Mary; Myrow, Paul; Narbonne, Guy (March 2001). "Burrowing below the basal Cambrian GSSP, Fortune Head, Newfoundland". Geological Magazine. 138 (2): 213–218. Bibcode:2001GeoM..138..213G. doi:10.1017/S001675680100509X. S2CID 131211543. 1.
- Hedberg, H.D., (editor), International stratigraphic guide: A guide to stratigraphic classification, terminology, and procedure, New York, John Wiley and Sons, 1976
External links
- International Stratigraphic Chart from the International Commission on Stratigraphy
- USA National Park Service
- Washington State University Archived 2011-07-26 at the Wayback Machine
- Web Geological Time Machine
- Eon or Aeon, Math Words - An alphabetical index
- The Global Boundary Stratotype Section and Point (GSSP): overview
- Chart of The Global Boundary Stratotype Sections and Points (GSSP): chart
- Geotime chart displaying geologic time periods compared to the fossil record
https://en.wikipedia.org/wiki/Chronozone
Magnetic orientations of all samples from a site are then compared and their average magnetic polarity is determined with directional statistics, most commonly Fisher statistics or bootstrapping.[5] The statistical significance of each average is evaluated. The latitudes of the Virtual Geomagnetic Poles from those sites determined to be statistically significant are plotted against the stratigraphic level at which they were collected. These data are then abstracted to the standard black and white magnetostratigraphic columns in which black indicates normal polarity and white is reversed polarity.
https://en.wikipedia.org/wiki/Magnetostratigraphy#Chron
Analytical procedures
Samples are first analyzed in their natural state to obtain their natural remanent magnetization (NRM). The NRM is then stripped away in a stepwise manner using thermal or alternating field demagnetization techniques to reveal the stable magnetic component.
https://en.wikipedia.org/wiki/Magnetostratigraphy#Chron
Because the age of each reversal shown on the GMPTS is relatively well known, the correlation establishes numerous time lines through the stratigraphic section. These ages provide relatively precise dates for features in the rocks such as fossils, changes in sedimentary rock composition, changes in depositional environment, etc. They also constrain the ages of cross-cutting features such as faults, dikes, and unconformities.
https://en.wikipedia.org/wiki/Magnetostratigraphy#Chron
https://en.wikipedia.org/wiki/Volcanic_ash
https://en.wikipedia.org/wiki/Biostratigraphy
These data are also used to model basin subsidence rates. Knowing the depth of a hydrocarbon source rock beneath the basin-filling strata allows calculation of the age at which the source rock passed through the generation window and hydrocarbon migration began. Because the ages of cross-cutting trapping structures can usually be determined from magnetostratigraphic data, a comparison of these ages will assist reservoir geologists in their determination of whether or not a play is likely in a given trap.[6]
https://en.wikipedia.org/wiki/Magnetostratigraphy#Chron
https://en.wikipedia.org/wiki/Magnetostratigraphy#Chron
See also
- Biostratigraphy
- Chemostratigraphy
- Chronostratigraphy
- Cyclostratigraphy
- Lithostratigraphy
- Tectonostratigraphy
- Paleomagnetism
https://en.wikipedia.org/wiki/Magnetostratigraphy#Chron
https://en.wikipedia.org/wiki/Category:Stratigraphy
https://en.wikipedia.org/wiki/Geophysics
Cyclostratigraphy is a subdiscipline of stratigraphy that studies astronomically forced climate cycles within sedimentary successions.[1]
https://en.wikipedia.org/wiki/Cyclostratigraphy
Orbital changes
Astronomical cycles (also known as Milankovitch cycles) are variations of the Earth's orbit around the sun due to the gravitational interaction with other masses within the solar system.[1] Due to this cyclicity, solar irradiation differs through time on different hemispheres and seasonality is affected. These insolation variations have influence on Earth's climate and on the deposition of sedimentary rocks.
The main orbital cycles are precession with main periods of 19 and 23 kyr, obliquity with main periods of 41 kyr, and 1.2 Myr, and eccentricity with main periods of around 100 kyr, 405 kyr, and 2.4 Myr.[2] Precession influences how much insolation each hemisphere receives. Obliquity controls the intensity of the seasons. Eccentricity influences how much insolation the Earth receives altogether. Varied insolation directly influences Earth's climate, and changes in precipitation and weathering are revealed in the sedimentary record. The 405 kyr eccentricity cycle helps correct chronologies in rocks or sediment cores when variable sedimentation makes them difficult to assign.[1] Indicators of these cycles in sediments include rock magnetism, geochemistry, biological composition, and physical features like color and facies changes.[1][3]
https://en.wikipedia.org/wiki/Cyclostratigraphy
Dating methods and applications
To determine the time range of a cyclostratigraphic study, rocks are dated using radiometric dating and other stratigraphic methods. Once the time range is calibrated, the rocks are examined for Milankovitch signals. From there, ages can be assigned to the sediment layers based on the astronomical signals they contain.[3]
Cyclostratigraphic studies of rock records can lead to accurate dating of events in the geological past, to increase understanding of cause and consequences of Earth's (climate) history, and to more control on depositional mechanisms of sediments and the acting of sedimentary systems. Cyclostratigraphy also aids the study of planetary physics, because it provides information of astronomical cycles that extends beyond 50 Ma (astronomical models are not accurate beyond this).[1] Assigning time ranges to these astronomical cycles can be used to calibrate 40Ar/39Ar dating.[3]
Limitations
Uncertainties also arise when using cyclostratigraphy. Using radioisotope dating to set parameters for time scales introduces a degree of uncertainty. There are also stratigraphic uncertainties, uncertainties due to climate forcing, and uncertainty about Earth's rotational effects on its precession. There is also uncertainty in records extending beyond 50 Ma because astronomical models are not accurate beyond 50 Ma due to chaos and uncertainties of initial conditions.[1]
https://en.wikipedia.org/wiki/Cyclostratigraphy
Cyclic sediments (also called rhythmic sediments[1]) are sequences of sedimentary rocks that are characterised by repetitive patterns of different rock types (strata) or facies within the sequence. Processes that generate sedimentary cyclicity can be either autocyclic or allocyclic, and can result in piles of sedimentary cycles hundreds or even thousands of metres thick. The study of sequence stratigraphy was developed from controversies over the causes of cyclic sedimentation.[2]
https://en.wikipedia.org/wiki/Cyclic_sediments
In geology, depositional environment or sedimentary environment describes the combination of physical, chemical, and biological processes associated with the deposition of a particular type of sediment and, therefore, the rock types that will be formed after lithification, if the sediment is preserved in the rock record. In most cases, the environments associated with particular rock types or associations of rock types can be matched to existing analogues. However, the further back in geological time sediments were deposited, the more likely that direct modern analogues are not available (e.g. banded iron formations).
https://en.wikipedia.org/wiki/Depositional_environment
| Sedimentary rock | |
 Banded iron formation, Karijini National Park, Western Australia | |
| Composition | |
|---|---|
| Primary | iron oxides, cherts |
| Secondary | Other |
Banded iron formations (BIFs; also called banded ironstone formations) are distinctive units of sedimentary rock consisting of alternating layers of iron oxides and iron-poor chert. They can be up to several hundred meters in thickness and extend laterally for several hundred kilometers. Almost all of these formations are of Precambrian age and are thought to record the oxygenation of the Earth's oceans. Some of the Earth's oldest rock formations, which formed about 3,700 million years ago (Ma), are associated with banded iron formations.
Banded iron formations are thought to have formed in sea water as the result of oxygen production by photosynthetic cyanobacteria. The oxygen combined with dissolved iron in Earth's oceans to form insoluble iron oxides, which precipitated out, forming a thin layer on the ocean floor. Each band is similar to a varve, resulting from cyclic variations in oxygen production.
Banded iron formations were first discovered in northern Michigan in 1844. Banded iron formations account for more than 60% of global iron reserves and provide most of the iron ore presently mined. Most formations can be found in Australia, Brazil, Canada, India, Russia, South Africa, Ukraine, and the United States.
https://en.wikipedia.org/wiki/Banded_iron_formation
Description
A typical banded iron formation consists of repeated, thin layers (a few millimeters to a few centimeters in thickness) of silver to black iron oxides, either magnetite (Fe3O4) or hematite (Fe2O3), alternating with bands of iron-poor chert, often red in color, of similar thickness.[1][2][3][4] A single banded iron formation can be up to several hundred meters in thickness and extend laterally for several hundred kilometers.[5]
Banded iron formation is more precisely defined as chemically precipitated sedimentary rock containing greater than 15% iron. However, most BIFs have a higher content of iron, typically around 30% by mass, so that roughly half the rock is iron oxides and the other half is silica.[5][6] The iron in BIFs is divided roughly equally between the more oxidized ferric form, Fe(III), and the more reduced ferrous form, Fe(II), so that the ratio Fe(III)/Fe(II+III) typically varies from 0.3 to 0.6. This indicates a predominance of magnetite, in which the ratio is 0.67, over hematite, for which the ratio is 1.[4] In addition to the iron oxides (hematite and magnetite), the iron sediment may contain the iron-rich carbonates siderite and ankerite, or the iron-rich silicates minnesotaite and greenalite. Most BIFs are chemically simple, containing little but iron oxides, silica, and minor carbonate,[5] though some contain significant calcium and magnesium, up to 9% and 6.7% as oxides respectively.[7][8]
When used in the singular, the term banded iron formation refers to the sedimentary lithology just described.[1] The plural form, banded iron formations, is used informally to refer to stratigraphic units that consist primarily of banded iron formation.[9]
A well-preserved banded iron formation typically consists of macrobands several meters thick that are separated by thin shale beds. The macrobands in turn are composed of characteristic alternating layers of chert and iron oxides, called mesobands, that are several millimeters to a few centimeters thick. Many of the chert mesobands contain microbands of iron oxides that are less than a millimeter thick, while the iron mesobands are relatively featureless. BIFs tend to be extremely hard, tough, and dense, making them highly resistant to erosion, and they show fine details of stratification over great distances, suggesting they were deposited in a very low-energy environment; that is, in relatively deep water, undisturbed by wave motion or currents.[2] BIFs only rarely interfinger with other rock types, tending to form sharply bounded discrete units that never grade laterally into other rock types.[5]
Banded iron formations of the Great Lakes region and the Frere Formation of western Australia are somewhat different in character and are sometimes described as granular iron formations or GIFs.[7][5] Their iron sediments are granular to oolitic in character, forming discrete grains about a millimeter in diameter, and they lack microbanding in their chert mesobands. They also show more irregular mesobanding, with indications of ripples and other sedimentary structures, and their mesobands cannot be traced out any great distance. Though they form well-defined, discrete units, these are commonly interbedded with coarse to medium-grained epiclastic sediments (sediments formed by weathering of rock). These features suggest a higher energy depositional environment, in shallower water disturbed by wave motions. However, they otherwise resemble other banded iron formations.[7]
The great majority of banded iron formations are Archean or Paleoproterozoic in age. However, a small number of BIFs are Neoproterozoic in age, and are frequently,[8][10][11] if not universally,[12] associated with glacial deposits, often containing glacial dropstones.[8] They also tend to show a higher level of oxidation, with hematite prevailing over magnetite,[10] and they typically contain a small amount of phosphate, about 1% by mass.[10] Mesobanding is often poor to nonexistent[13] and soft-sediment deformation structures are common. This suggests very rapid deposition.[14] However, like the granular iron formations of the Great Lakes, the Neoproterozoic occurrences are widely described as banded iron formations.[8][10][14][4][15][16]
Banded iron formations are distinct from most Phanerozoic ironstones. Ironstones are relatively rare and are thought to have been deposited in marine anoxic events, in which the depositional basin became depleted in free oxygen. They are composed of iron silicates and oxides without appreciable chert but with significant phosphorus content, which is lacking in BIFs.[11]
No classification scheme for banded iron formations has gained complete acceptance.[5] In 1954, Harold Lloyd James advocated a classification based on four lithological facies (oxide, carbonate, silicate, and sulfide) assumed to represent different depths of deposition,[1] but this speculative model did not hold up.[5] In 1980, Gordon A. Gross advocated a twofold division of BIFs into an Algoma type and a Lake Superior type, based on the character of the depositional basin. Algoma BIFs are found in relatively small basins in association with greywackes and other volcanic rocks and are assumed to be associated with volcanic centers. Lake Superior BIFs are found in larger basins in association with black shales, quartzites, and dolomites, with relatively minor tuffs or other volcanic rocks, and are assumed to have formed on a continental shelf.[17] This classification has been more widely accepted, but the failure to appreciate that it is strictly based on the characteristics of the depositional basin and not the lithology of the BIF itself has led to confusion, and some geologists have advocated for its abandonment.[2][18] However, the classification into Algoma versus Lake Superior types continues to be used.[19][20]
https://en.wikipedia.org/wiki/Banded_iron_formation
A shield is a large area of exposed Precambrian crystalline igneous and high-grade metamorphic rocks that form tectonically stable areas.[1] These rocks are older than 570 million years and sometimes date back to around 2 to 3.5 billion years.[citation needed] They have been little affected by tectonic events following the end of the Precambrian, and are relatively flat regions where mountain building, faulting, and other tectonic processes are minor, compared with the activity at their margins and between tectonic plates. Shields occur on all continents.
https://en.wikipedia.org/wiki/Shield_(geology)
Terminology
The term shield cannot be used interchangeably with the term craton. However, shield can be used interchangeably with the term basement. The difference is that a craton describes a basement overlayed by a sedimentary platform while shield only describes the basement.
The term shield, used to describe this type of geographic region, appears in the 1901 English translation of Eduard Suess's Face of Earth by H. B. C. Sollas, and comes from the shape "not unlike a flat shield"[2] of the Canadian Shield which has an outline that "suggests the shape of the shields carried by soldiers in the days of hand-to-hand combat."[3]
Lithology
A shield is that part of the continental crust in which these usually Precambrian basement rocks crop out extensively at the surface. Shields can be very complex: they consist of vast areas of granitic or granodioritic gneisses, usually of tonalitic composition, and they also contain belts of sedimentary rocks, often surrounded by low-grade volcano-sedimentary sequences, or greenstone belts. These rocks are frequently metamorphosed greenschist, amphibolite, and granulite facies.[citation needed] It is estimated that over 50% of Earth's shields surface is made up of gneiss.[4]
Erosion and landforms
Being relatively stable regions the relief of shields is rather old with elements such as peneplains being shaped in Precambrian times. The oldest peneplain identifiable in a shield is called a "primary peneplain",[5] in the case of the Fennoscandian Shield this is the Sub-Cambrian peneplain.[6]
The landforms and shallow deposits of northern shields that have been subject to Quaternary glaciation and periglaciation are distinct from those found in closer to the equator.[5] Shield relief, including peneplains, can be protected from erosion by various means.[5][7] Shield surfaces exposed to sub-tropical and tropical climate for long enough time can end up being silicified, becoming hard and extremely difficult to erode.[7] Erosion of peneplains by glaciers in shield regions is limited.[7][8] In the Fennoscandian Shield average glacier erosion during the Quaternary amounts to tens of meters, albeit this was not evenly distributed.[8] For glacier erosion to be effective in shields a long "preparation period" of weathering under non-glacial conditions may be a requirement.[7]
In weathered and eroded shields inselbergs are common sights.[9]
List of shields
- The Canadian Shield forms the nucleus of North America and extends from Lake Superior on the south to the Arctic Islands on the north, and from western Canada eastward across to include most of Greenland.[10]
- The Atlantic Shield
- The Amazonian (Brazilian) Shield on the eastern bulge portion of South America. Bordering this is the Guiana Shield to the north, and the Platian Shield to the south.
- The Uruguayan Shield
- The Baltic (Fennoscandian) Shield is located in eastern Norway, Finland and Sweden.
- The African (Ethiopian) Shield is located in Africa.
- The Australian Shield occupies most of the western half of Australia.
- The Arabian-Nubian Shield on the western edge of Arabia.
- The Antarctic Shield.
- In Asia, an area in China and North Korea is sometimes referred to as the China-Korean Shield.
- The Angaran Shield, as it is sometimes called, is bounded by the Yenisey River on the west, the Lena River on the east, the Arctic Ocean on the north, and Lake Baikal on the south.
- The Indian Shield occupies two-thirds of the southern Indian peninsula.
See also
Notes
- Merriam, D. F. (2005). Encyclopedia of Geology. Selley, Richard C., 1939-, Cocks, L. R. M. (Leonard Robert Morrison), 1938-, Plimer, I. R. Amsterdam: Elsevier Academic. p. 21. ISBN 9781601193674. OCLC 183883048.
https://en.wikipedia.org/wiki/Shield_(geology)
In geology, basement and crystalline basement are crystalline rocks lying above the mantle and beneath all other rocks and sediments. They are sometimes exposed at the surface, but often they are buried under miles of rock and sediment.[1] The basement rocks lie below a sedimentary platform or cover, or more generally any rock below sedimentary rocks or sedimentary basins that are metamorphic or igneous in origin. In the same way, the sediments or sedimentary rocks on top of the basement can be called a "cover" or "sedimentary cover".
Crustal rocks are modified several times before they become basement, and these transitions alter their composition.[1]
https://en.wikipedia.org/wiki/Basement_(geology)
Continental crust
Basement rock is the thick foundation of ancient, and oldest, metamorphic and igneous rock that forms the crust of continents, often in the form of granite.[2] Basement rock is contrasted to overlying sedimentary rocks which are laid down on top of the basement rocks after the continent was formed, such as sandstone and limestone. The sedimentary rocks which may be deposited on top of the basement usually form a relatively thin veneer, but can be more than 5 kilometres (3 mi) thick. The basement rock of the crust can be 32–48 kilometres (20–30 mi) thick or more. The basement rock can be located under layers of sedimentary rock, or be visible at the surface.
Basement rock is visible, for example, at the bottom of the Grand Canyon, consisting of 1.7- to 2-billion-year-old granite (Zoroaster Granite) and schist (Vishnu Schist). The Vishnu Schist is believed to be highly metamorphosed igneous rocks and shale, from basalt, mud and clay laid from volcanic eruptions, and the granite is the result of magma intrusions into the Vishnu Schist. An extensive cross section of sedimentary rocks laid down on top of it through the ages is visible as well.
https://en.wikipedia.org/wiki/Basement_(geology)
Age
The basement rocks of the continental crust tend to be much older than the oceanic crust.[3] The oceanic crust can be from 0–340 million years in age, with an average age of 64 million years.[4] Continental crust is older because continental crust is light and thick enough so it is not subducted, while oceanic crust is periodically subducted and replaced at subduction and oceanic rifting areas.
https://en.wikipedia.org/wiki/Basement_(geology)
Complexity
This section needs additional citations for verification. (January 2019) |
The basement rocks are often highly metamorphosed and complex, and are usually crystalline.[5] They may consist of many different types of rock – volcanic, intrusive igneous and metamorphic. They may also contain ophiolites, which are fragments of oceanic crust that became wedged between plates when a terrane was accreted to the edge of the continent. Any of this material may be folded, refolded and metamorphosed. New igneous rock may freshly intrude into the crust from underneath, or may form underplating, where the new igneous rock forms a layer on the underside of the crust. The majority of continental crust on the planet is around 1 to 3 billion years old, and it is theorised that there was at least one period of rapid expansion and accretion to the continents during the Precambrian.
Much of the basement rock may have originally been oceanic crust, but it was highly metamorphosed and converted into continental crust. It is possible for oceanic crust to be subducted down into the Earth's mantle, at subduction fronts, where oceanic crust is being pushed down into the mantle by an overriding plate of oceanic or continental crust.
https://en.wikipedia.org/wiki/Basement_(geology)
Magmatic underplating occurs when basaltic magmas are trapped during their rise to the surface at the Mohorovičić discontinuity or within the crust.[1] Entrapment (or 'stalling out') of magmas within the crust occurs due to the difference in relative densities between the rising magma and the surrounding rock. Magmatic underplating can be responsible for thickening of the crust when the magma cools.[1] Geophysical seismic studies (as well as igneous petrology and geochemistry) utilize the differences in densities to identify underplating that occurs at depth.[1]
https://en.wikipedia.org/wiki/Magmatic_underplating
Cratons
Many continents can consist of several continental cratons – blocks of crust built around an initial original core of continents – that gradually grew and expanded as additional newly created terranes were added to their edges. For instance, Pangea consisted of most of the Earth's continents being accreted into one giant supercontinent. Most continents, such as Asia, Africa and Europe, include several continental cratons, as they were formed by the accretion of many smaller continents.
Usage
In European geology, the basement generally refers to rocks older than the Variscan orogeny. On top of this older basement Permian evaporites and Mesozoic limestones were deposited. The evaporites formed a weak zone on which the harder (stronger) limestone cover was able to move over the hard basement, making the distinction between basement and cover even more pronounced.[citation needed]
In Andean geology the basement refers to the Proterozoic, Paleozoic and early Mesozoic (Triassic to Jurassic) rock units as the basement to the late Mesozoic and Cenozoic Andean sequences developed following the onset of subduction along the western margin of the South American Plate.[7]
When discussing the Trans-Mexican Volcanic Belt of Mexico the basement include Proterozoic, Paleozoic and Mesozoic age rocks for the Oaxaquia, the Mixteco and the Guerrero terranes respectively.[8]
The term basement is used mostly in disciplines of geology like basin geology, sedimentology and petroleum geology in which the (typically Precambrian) crystalline basement is not of interest as it rarely contains petroleum or natural gas.[9] The term economic basement is also used to describe the deeper parts of a cover sequence that are of no economic interest.[10]
https://en.wikipedia.org/wiki/Basement_(geology)
The internal structure of Earth is the solid portion of the Earth,[clarification needed] excluding its atmosphere and hydrosphere. The structure consists of an outer silicate solid crust, a highly viscous asthenosphere and solid mantle, a liquid outer core whose flow generates the Earth's magnetic field, and a solid inner core.
Scientific understanding of the internal structure of Earth is based on observations of topography and bathymetry, observations of rock in outcrop, samples brought to the surface from greater depths by volcanoes or volcanic activity, analysis of the seismic waves that pass through Earth, measurements of the gravitational and magnetic fields of Earth, and experiments with crystalline solids at pressures and temperatures characteristic of Earth's deep interior.
https://en.wikipedia.org/wiki/Internal_structure_of_Earth
Lodestones are naturally magnetized pieces of the mineral magnetite.[1][2] They are naturally occurring magnets, which can attract iron. The property of magnetism was first discovered in antiquity through lodestones.[3] Pieces of lodestone, suspended so they could turn, were the first magnetic compasses,[3][4][5][6] and their importance to early navigation is indicated by the name lodestone, which in Middle English means "course stone" or "leading stone",[7] from the now-obsolete meaning of lode as "journey, way".[8]
Lodestone is one of only a very few minerals that is found naturally magnetized.[1] Magnetite is black or brownish-black, with a metallic luster, a Mohs hardness of 5.5–6.5 and a black streak.
https://en.wikipedia.org/wiki/Lodestone
Geophysics
Geophysics (/ˌdʒiːoʊˈfɪzɪks/) is a subject of natural science concerned with the physical processes and physical properties of the Earth and its surrounding space environment, and the use of quantitative methods for their analysis. Geophysicists, who usually study geophysics, physics, or one of the earth sciences at the graduate level, complete investigations across a wide range of scientific disciplines. The term geophysics classically refers to solid earth applications: Earth's shape; its gravitational, magnetic fields, and electromagnetic fields ; its internal structure and composition; its dynamics and their surface expression in plate tectonics, the generation of magmas, volcanism and rock formation.[3] However, modern geophysics organizations and pure scientists use a broader definition that includes the water cycle including snow and ice; fluid dynamics of the oceans and the atmosphere; electricity and magnetism in the ionosphere and magnetosphere and solar-terrestrial physics; and analogous problems associated with the Moon and other planets.[3][4][5][6][7][8]
Although geophysics was only recognized as a separate discipline in the 19th century, its origins date back to ancient times. The first magnetic compasses were made from lodestones, while more modern magnetic compasses played an important role in the history of navigation. The first seismic instrument was built in 132 AD. Isaac Newton applied his theory of mechanics to the tides and the precession of the equinox; and instruments were developed to measure the Earth's shape, density and gravity field, as well as the components of the water cycle. In the 20th century, geophysical methods were developed for remote exploration of the solid Earth and the ocean, and geophysics played an essential role in the development of the theory of plate tectonics.
Geophysics is applied to societal needs, such as mineral resources, mitigation of natural hazards and environmental protection.[4] In exploration geophysics, geophysical survey data are used to analyze potential petroleum reservoirs and mineral deposits, locate groundwater, find archaeological relics, determine the thickness of glaciers and soils, and assess sites for environmental remediation.
Physical phenomena
Geophysics is a highly interdisciplinary subject, and geophysicists contribute to every area of the Earth sciences and some geophysicists conduct research in planetary sciences. To provide a clearer idea of what constitutes geophysics, this section describes phenomena that are studied in physics and how they relate to the Earth and its surroundings. Geophysicists also investigate the physical processes and properties of the Earth, its fluid layers, and magnetic field along with the near-Earth environment in the Solar System, which includes other planetary bodies.
Gravity
The gravitational pull of the Moon and Sun gives rise to two high tides and two low tides every lunar day, or every 24 hours and 50 minutes. Therefore, there is a gap of 12 hours and 25 minutes between every high tide and between every low tide.[9]
Gravitational forces make rocks press down on deeper rocks, increasing their density as the depth increases.[10] Measurements of gravitational acceleration and gravitational potential at the Earth's surface and above it can be used to look for mineral deposits (see gravity anomaly and gravimetry).[11] The surface gravitational field provides information on the dynamics of tectonic plates. The geopotential surface called the geoid is one definition of the shape of the Earth. The geoid would be the global mean sea level if the oceans were in equilibrium and could be extended through the continents (such as with very narrow canals).[12]
Heat flow
The Earth is cooling, and the resulting heat flow generates the Earth's magnetic field through the geodynamo and plate tectonics through mantle convection.[13] The main sources of heat are the primordial heat and radioactivity, although there are also contributions from phase transitions. Heat is mostly carried to the surface by thermal convection, although there are two thermal boundary layers – the core–mantle boundary and the lithosphere – in which heat is transported by conduction.[14] Some heat is carried up from the bottom of the mantle by mantle plumes. The heat flow at the Earth's surface is about 4.2 × 1013 W, and it is a potential source of geothermal energy.[15]
Vibrations
Seismic waves are vibrations that travel through the Earth's interior or along its surface. The entire Earth can also oscillate in forms that are called normal modes or free oscillations of the Earth. Ground motions from waves or normal modes are measured using seismographs. If the waves come from a localized source such as an earthquake or explosion, measurements at more than one location can be used to locate the source. The locations of earthquakes provide information on plate tectonics and mantle convection.[16][17]
Recording of seismic waves from controlled sources provides information on the region that the waves travel through. If the density or composition of the rock changes, waves are reflected. Reflections recorded using Reflection Seismology can provide a wealth of information on the structure of the earth up to several kilometers deep and are used to increase our understanding of the geology as well as to explore for oil and gas.[11] Changes in the travel direction, called refraction, can be used to infer the deep structure of the Earth.[17]
Earthquakes pose a risk to humans. Understanding their mechanisms, which depend on the type of earthquake (e.g., intraplate or deep focus), can lead to better estimates of earthquake risk and improvements in earthquake engineering.[18]
Electricity
Although we mainly notice electricity during thunderstorms, there is always a downward electric field near the surface that averages 120 volts per meter.[19] Relative to the solid Earth, the atmosphere has a net positive charge due to bombardment by cosmic rays. A current of about 1800 amperes flows in the global circuit.[19] It flows downward from the ionosphere over most of the Earth and back upwards through thunderstorms. The flow is manifested by lightning below the clouds and sprites above.
A variety of electric methods are used in geophysical survey. Some measure spontaneous potential, a potential that arises in the ground because of man-made or natural disturbances. Telluric currents flow in Earth and the oceans. They have two causes: electromagnetic induction by the time-varying, external-origin geomagnetic field and motion of conducting bodies (such as seawater) across the Earth's permanent magnetic field.[20] The distribution of telluric current density can be used to detect variations in electrical resistivity of underground structures. Geophysicists can also provide the electric current themselves (see induced polarization and electrical resistivity tomography).
Electromagnetic waves
Electromagnetic waves occur in the ionosphere and magnetosphere as well as in Earth's outer core. Dawn chorus is believed to be caused by high-energy electrons that get caught in the Van Allen radiation belt. Whistlers are produced by lightning strikes. Hiss may be generated by both. Electromagnetic waves may also be generated by earthquakes (see seismo-electromagnetics).
In the highly conductive liquid iron of the outer core, magnetic fields are generated by electric currents through electromagnetic induction. Alfvén waves are magnetohydrodynamic waves in the magnetosphere or the Earth's core. In the core, they probably have little observable effect on the Earth's magnetic field, but slower waves such as magnetic Rossby waves may be one source of geomagnetic secular variation.[21]
Electromagnetic methods that are used for geophysical survey include transient electromagnetics, magnetotellurics, surface nuclear magnetic resonance and electromagnetic seabed logging.[22]
Magnetism
The Earth's magnetic field protects the Earth from the deadly solar wind and has long been used for navigation. It originates in the fluid motions of the outer core.[21] The magnetic field in the upper atmosphere gives rise to the auroras.[23]
The Earth's field is roughly like a tilted dipole, but it changes over time (a phenomenon called geomagnetic secular variation). Mostly the geomagnetic pole stays near the geographic pole, but at random intervals averaging 440,000 to a million years or so, the polarity of the Earth's field reverses. These geomagnetic reversals, analyzed within a Geomagnetic Polarity Time Scale, contain 184 polarity intervals in the last 83 million years, with change in frequency over time, with the most recent brief complete reversal of the Laschamp event occurring 41,000 years ago during the last glacial period. Geologists observed geomagnetic reversal recorded in volcanic rocks, through magnetostratigraphy correlation (see natural remanent magnetization) and their signature can be seen as parallel linear magnetic anomaly stripes on the seafloor. These stripes provide quantitative information on seafloor spreading, a part of plate tectonics. They are the basis of magnetostratigraphy, which correlates magnetic reversals with other stratigraphies to construct geologic time scales.[24] In addition, the magnetization in rocks can be used to measure the motion of continents.[21]
Radioactivity
Radioactive decay accounts for about 80% of the Earth's internal heat, powering the geodynamo and plate tectonics.[25] The main heat-producing isotopes are potassium-40, uranium-238, uranium-235, and thorium-232.[26] Radioactive elements are used for radiometric dating, the primary method for establishing an absolute time scale in geochronology.
Unstable isotopes decay at predictable rates, and the decay rates of different isotopes cover several orders of magnitude, so radioactive decay can be used to accurately date both recent events and events in past geologic eras.[27] Radiometric mapping using ground and airborne gamma spectrometry can be used to map the concentration and distribution of radioisotopes near the Earth's surface, which is useful for mapping lithology and alteration.[28][29]
Fluid dynamics
Fluid motions occur in the magnetosphere, atmosphere, ocean, mantle and core. Even the mantle, though it has an enormous viscosity, flows like a fluid over long time intervals. This flow is reflected in phenomena such as isostasy, post-glacial rebound and mantle plumes. The mantle flow drives plate tectonics and the flow in the Earth's core drives the geodynamo.[21]
Geophysical fluid dynamics is a primary tool in physical oceanography and meteorology. The rotation of the Earth has profound effects on the Earth's fluid dynamics, often due to the Coriolis effect. In the atmosphere, it gives rise to large-scale patterns like Rossby waves and determines the basic circulation patterns of storms. In the ocean, they drive large-scale circulation patterns as well as Kelvin waves and Ekman spirals at the ocean surface.[30] In the Earth's core, the circulation of the molten iron is structured by Taylor columns.[21]
Waves and other phenomena in the magnetosphere can be modeled using magnetohydrodynamics.
Mineral physics
The physical properties of minerals must be understood to infer the composition of the Earth's interior from seismology, the geothermal gradient and other sources of information. Mineral physicists study the elastic properties of minerals; their high-pressure phase diagrams, melting points and equations of state at high pressure; and the rheological properties of rocks, or their ability to flow. Deformation of rocks by creep make flow possible, although over short times the rocks are brittle. The viscosity of rocks is affected by temperature and pressure, and in turn, determines the rates at which tectonic plates move.[10]
Water is a very complex substance and its unique properties are essential for life.[31] Its physical properties shape the hydrosphere and are an essential part of the water cycle and climate. Its thermodynamic properties determine evaporation and the thermal gradient in the atmosphere. The many types of precipitation involve a complex mixture of processes such as coalescence, supercooling and supersaturation.[32] Some precipitated water becomes groundwater, and groundwater flow includes phenomena such as percolation, while the conductivity of water makes electrical and electromagnetic methods useful for tracking groundwater flow. Physical properties of water such as salinity have a large effect on its motion in the oceans.[30]
The many phases of ice form the cryosphere and come in forms like ice sheets, glaciers, sea ice, freshwater ice, snow, and frozen ground (or permafrost).[33]
Regions of the Earth
Size and form of the Earth
The Earth is roughly spherical, but it bulges towards the Equator, so it is roughly in the shape of an ellipsoid (see Earth ellipsoid). This bulge is due to its rotation and is nearly consistent with an Earth in hydrostatic equilibrium. The detailed shape of the Earth, however, is also affected by the distribution of continents and ocean basins, and to some extent by the dynamics of the plates.[12]
Structure of the interior
Evidence from seismology, heat flow at the surface, and mineral physics is combined with the Earth's mass and moment of inertia to infer models of the Earth's interior – its composition, density, temperature, pressure. For example, the Earth's mean specific gravity (5.515) is far higher than the typical specific gravity of rocks at the surface (2.7–3.3), implying that the deeper material is denser. This is also implied by its low moment of inertia ( 0.33 M R2, compared to 0.4 M R2 for a sphere of constant density). However, some of the density increase is compression under the enormous pressures inside the Earth. The effect of pressure can be calculated using the Adams–Williamson equation. The conclusion is that pressure alone cannot account for the increase in density. Instead, we know that the Earth's core is composed of an alloy of iron and other minerals.[10]
Reconstructions of seismic waves in the deep interior of the Earth show that there are no S-waves in the outer core. This indicates that the outer core is liquid, because liquids cannot support shear. The outer core is liquid, and the motion of this highly conductive fluid generates the Earth's field. Earth's inner core, however, is solid because of the enormous pressure.[12]
Reconstruction of seismic reflections in the deep interior indicates some major discontinuities in seismic velocities that demarcate the major zones of the Earth: inner core, outer core, mantle, lithosphere and crust. The mantle itself is divided into the upper mantle, transition zone, lower mantle and D′′ layer. Between the crust and the mantle is the Mohorovičić discontinuity.[12]
The seismic model of the Earth does not by itself determine the composition of the layers. For a complete model of the Earth, mineral physics is needed to interpret seismic velocities in terms of composition. The mineral properties are temperature-dependent, so the geotherm must also be determined. This requires physical theory for thermal conduction and convection and the heat contribution of radioactive elements. The main model for the radial structure of the interior of the Earth is the preliminary reference Earth model (PREM). Some parts of this model have been updated by recent findings in mineral physics (see post-perovskite) and supplemented by seismic tomography. The mantle is mainly composed of silicates, and the boundaries between layers of the mantle are consistent with phase transitions.[10]
The mantle acts as a solid for seismic waves, but under high pressures and temperatures, it deforms so that over millions of years it acts like a liquid. This makes plate tectonics possible.
Magnetosphere
If a planet's magnetic field is strong enough, its interaction with the solar wind forms a magnetosphere. Early space probes mapped out the gross dimensions of the Earth's magnetic field, which extends about 10 Earth radii towards the Sun. The solar wind, a stream of charged particles, streams out and around the terrestrial magnetic field, and continues behind the magnetic tail, hundreds of Earth radii downstream. Inside the magnetosphere, there are relatively dense regions of solar wind particles called the Van Allen radiation belts.[23]
Methods
Geodesy
Geophysical measurements are generally at a particular time and place. Accurate measurements of position, along with earth deformation and gravity, are the province of geodesy. While geodesy and geophysics are separate fields, the two are so closely connected that many scientific organizations such as the American Geophysical Union, the Canadian Geophysical Union and the International Union of Geodesy and Geophysics encompass both.[34]
Absolute positions are most frequently determined using the global positioning system (GPS). A three-dimensional position is calculated using messages from four or more visible satellites and referred to the 1980 Geodetic Reference System. An alternative, optical astronomy, combines astronomical coordinates and the local gravity vector to get geodetic coordinates. This method only provides the position in two coordinates and is more difficult to use than GPS. However, it is useful for measuring motions of the Earth such as nutation and Chandler wobble. Relative positions of two or more points can be determined using very-long-baseline interferometry.[34][35][36]
Gravity measurements became part of geodesy because they were needed to related measurements at the surface of the Earth to the reference coordinate system. Gravity measurements on land can be made using gravimeters deployed either on the surface or in helicopter flyovers. Since the 1960s, the Earth's gravity field has been measured by analyzing the motion of satellites. Sea level can also be measured by satellites using radar altimetry, contributing to a more accurate geoid.[34] In 2002, NASA launched the Gravity Recovery and Climate Experiment (GRACE), wherein two twin satellites map variations in Earth's gravity field by making measurements of the distance between the two satellites using GPS and a microwave ranging system. Gravity variations detected by GRACE include those caused by changes in ocean currents; runoff and ground water depletion; melting ice sheets and glaciers.[37]
Satellites and space probes
Satellites in space have made it possible to collect data from not only the visible light region, but in other areas of the electromagnetic spectrum. The planets can be characterized by their force fields: gravity and their magnetic fields, which are studied through geophysics and space physics.
Measuring the changes in acceleration experienced by spacecraft as they orbit has allowed fine details of the gravity fields of the planets to be mapped. For example, in the 1970s, the gravity field disturbances above lunar maria were measured through lunar orbiters, which led to the discovery of concentrations of mass, mascons, beneath the Imbrium, Serenitatis, Crisium, Nectaris and Humorum basins.[38]
Global positioning systems (GPS) and geographical information systems (GIS)
Since geophysics is concerned with the shape of the Earth, and by extension the mapping of features around and in the planet, geophysical measurements include high accuracy GPS measurements. These measurements are processed to increase their accuracy through differential GPS processing. Once the geophysical measurements have been processed and inverted, the interpreted results are plotted using GIS. Programs such as ArcGIS and Geosoft were built to meet these needs and include many geophysical functions that are built-in, such as upward continuation, and the calculation of the measurement derivative such as the first-vertical derivative.[11][39] Many geophysics companies have designed in-house geophysics programs that pre-date ArcGIS and GeoSoft in order to meet the visualization requirements of a geophysical dataset.
Remote sensing
Exploration geophysics is applied geophysics that often uses remote sensing platforms such as; satellites, aircraft, ships, boats, rovers, drones, borehole sensing equipment, and seismic receivers.[11] Most correction for data gathered using geophysical methods such as magnetic, gravimetry, electromagnetic, radiometric, radar, laser altimetry, barometry, and Lidar, on remote sensing platforms involves the correction of the geophysical data gathered from that remote sensing platform due to the effects of that platform on the geophysical data.[11] For instance, aeromagnetic data (aircraft gathered magnetic data) gathered using conventional fixed-wing aircraft platforms must be corrected for electromagnetic eddy currents that are created as the aircraft moves through Earth's magnetic field.[11] There are also corrections related to changes in measured potential field intensity as the Earth rotates, as the Earth orbits the Sun, and as the moon orbits the Earth.[11] [39]
Signal processing
Geophysical measurements are often recorded as time-series with GPS location. Signal processing involves the correction of time-series data for unwanted noise or errors introduced by the measurement platform, such as aircraft vibrations in gravity data. It also involves the reduction of sources of noise, such as diurnal corrections in magnetic data.[11][39] In seismic data, electromagnetic data, and gravity data, processing continues after error corrections to include computational geophysics which result in the final interpretation of the geophysical data into a geological interpretation of the geophysical measurements[11][39]
History
Geophysics emerged as a separate discipline only in the 19th century, from the intersection of physical geography, geology, astronomy, meteorology, and physics.[40][41] The first known use of the word geophysics was in german („Geophysik”) by Julius Fröbel in 1834.[42] However, many geophysical phenomena – such as the Earth's magnetic field and earthquakes – have been investigated since the ancient era.
Ancient and classical eras
The magnetic compass existed in China back as far as the fourth century BC. It was used as much for feng shui as for navigation on land. It was not until good steel needles could be forged that compasses were used for navigation at sea; before that, they could not retain their magnetism long enough to be useful. The first mention of a compass in Europe was in 1190 AD.[43]
In circa 240 BC, Eratosthenes of Cyrene deduced that the Earth was round and measured the circumference of Earth with great precision.[44] He developed a system of latitude and longitude.[45]
Perhaps the earliest contribution to seismology was the invention of a seismoscope by the prolific inventor Zhang Heng in 132 AD.[46] This instrument was designed to drop a bronze ball from the mouth of a dragon into the mouth of a toad. By looking at which of eight toads had the ball, one could determine the direction of the earthquake. It was 1571 years before the first design for a seismoscope was published in Europe, by Jean de la Hautefeuille. It was never built.[47]
Beginnings of modern science
One of the publications that marked the beginning of modern science was William Gilbert's De Magnete (1600), a report of a series of meticulous experiments in magnetism. Gilbert deduced that compasses point north because the Earth itself is magnetic.[21]
In 1687 Isaac Newton published his Principia, which not only laid the foundations for classical mechanics and gravitation but also explained a variety of geophysical phenomena such as the tides and the precession of the equinox.[48]
The first seismometer, an instrument capable of keeping a continuous record of seismic activity, was built by James Forbes in 1844.[47]
See also
- International Union of Geodesy and Geophysics (IUGG)
- Sociedade Brasileira de Geofísica
- Earth system science – Scientific study of the Earth's spheres and their natural integrated systems
- List of geophysicists – Famous geophysicists
- Outline of geophysics – Topics in the physics of the Earth and its vicinity
- Geodynamics – Study of dynamics of the Earth
- Planetary science – Science of planets and planetary systems
- Geological Engineering
- Physics
- Space physics
- Geosciences
- Geodesy
Notes
- Newton 1999 Section 3
References
- American Geophysical Union (2011). "Our Science". About AGU. Retrieved 30 September 2011.
- "About IUGG". 2011. Retrieved 30 September 2011.
- "AGUs Cryosphere Focus Group". 2011. Archived from the original on 16 November 2011. Retrieved 30 September 2011.
- Bozorgnia, Yousef; Bertero, Vitelmo V. (2004). Earthquake Engineering: From Engineering Seismology to Performance-Based Engineering. CRC Press. ISBN 978-0-8493-1439-1.
- Chemin, Jean-Yves; Desjardins, Benoit; Gallagher, Isabelle; Grenier, Emmanuel (2006). Mathematical geophysics: an introduction to rotating fluids and the Navier-Stokes equations. Oxford lecture series in mathematics and its applications. Oxford University Press. ISBN 0-19-857133-X.
- Davies, Geoffrey F. (2001). Dynamic Earth: Plates, Plumes and Mantle Convection. Cambridge University Press. ISBN 0-521-59067-1.
- Dewey, James; Byerly, Perry (1969). "The Early History of Seismometry (to 1900)". Bulletin of the Seismological Society of America. 59 (1): 183–227. Archived from the original on 23 November 2011.
- Defense Mapping Agency (1984) [1959]. Geodesy for the Layman (Technical report). National Geospatial-Intelligence Agency. TR 80-003. Retrieved 30 September 2011.
- Eratosthenes (2010). Eratosthenes' "Geography". Fragments collected and translated, with commentary and additional material by Duane W. Roller. Princeton University Press. ISBN 978-0-691-14267-8.
- Fowler, C.M.R. (2005). The Solid Earth: An Introduction to Global Geophysics (2 ed.). Cambridge University Press. ISBN 0-521-89307-0.
- "GRACE: Gravity Recovery and Climate Experiment". University of Texas at Austin Center for Space Research. 2011. Retrieved 30 September 2011.
- Hardy, Shaun J.; Goodman, Roy E. (2005). "Web resources in the history of geophysics". American Geophysical Union. Archived from the original on 27 April 2013. Retrieved 30 September 2011.
- Harrison, R. G.; Carslaw, K. S. (2003). "Ion-aerosol-cloud processes in the lower atmosphere". Reviews of Geophysics. 41 (3): 1012. Bibcode:2003RvGeo..41.1012H. doi:10.1029/2002RG000114. S2CID 123305218.
- Kivelson, Margaret G.; Russell, Christopher T. (1995). Introduction to Space Physics. Cambridge University Press. ISBN 978-0-521-45714-9.
- Lanzerotti, Louis J.; Gregori, Giovanni P. (1986). "Telluric currents: the natural environment and interactions with man-made systems". In Geophysics Study Committee; Geophysics Research Forum; Commission on Physical Sciences, Mathematics and Resources; National Research Council (eds.). The Earth's electrical environment. The Earth's Electrical Environment. National Academy Press. pp. 232–258. ISBN 0-309-03680-1.
- Lowrie, William (2004). Fundamentals of Geophysics. Cambridge University Press. ISBN 0-521-46164-2.
- Merrill, Ronald T.; McElhinny, Michael W.; McFadden, Phillip L. (1998). The Magnetic Field of the Earth: Paleomagnetism, the Core, and the Deep Mantle. International Geophysics Series. Vol. 63. Academic Press. ISBN 978-0124912458.
- Muller, Paul; Sjogren, William (1968). "Mascons: lunar mass concentrations". Science. 161 (3842): 680–684. Bibcode:1968Sci...161..680M. doi:10.1126/science.161.3842.680. PMID 17801458. S2CID 40110502.
- National Research Council (U.S.). Committee on Geodesy (1985). Geodesy: a look to the future (PDF) (Report). National Academies.
- Newton, Isaac (1999). The Principia, Mathematical principles of natural philosophy. A new translation by I Bernard Cohen and Anne Whitman, preceded by "A Guide to Newton's Principia" by I Bernard Cohen. University of California Press. ISBN 978-0-520-08816-0.
- Opdyke, Neil D.; Channell, James T. (1996). Magnetic Stratigraphy. Academic Press. ISBN 0-12-527470-X.
- Pedlosky, Joseph (1987). Geophysical Fluid Dynamics (Second ed.). Springer-Verlag. ISBN 0-387-96387-1.
- Poirier, Jean-Paul (2000). Introduction to the Physics of the Earth's Interior. Cambridge Topics in Mineral Physics & Chemistry. Cambridge University Press. ISBN 0-521-66313-X.
- Pollack, Henry N.; Hurter, Suzanne J.; Johnson, Jeffrey R. (1993). "Heat flow from the Earth's interior: Analysis of the global data set". Reviews of Geophysics. 31 (3): 267–280. Bibcode:1993RvGeo..31..267P. doi:10.1029/93RG01249.
- Renne, P.R.; Ludwig, K.R.; Karner, D.B. (2000). "Progress and challenges in geochronology". Science Progress. 83: 107–121. PMID 10800377.
- Reynolds, John M. (2011). An Introduction to Applied and Environmental Geophysics. Wiley-Blackwell. ISBN 978-0-471-48535-3.
- Richards, M. A.; Duncan, R. A.; Courtillot, V. E. (1989). "Flood Basalts and Hot-Spot Tracks: Plume Heads and Tails". Science. 246 (4926): 103–107. Bibcode:1989Sci...246..103R. doi:10.1126/science.246.4926.103. PMID 17837768. S2CID 9147772.
- Ross, D.A. (1995). Introduction to Oceanography. HarperCollins. ISBN 0-13-491408-2.
- Sadava, David; Heller, H. Craig; Hillis, David M.; Berenbaum, May (2009). Life: The Science of Biology. Macmillan. ISBN 978-1-4292-1962-4.
- Sanders, Robert (10 December 2003). "Radioactive potassium may be major heat source in Earth's core". UC Berkeley News. Retrieved 28 February 2007.
- Sirvatka, Paul (2003). "Cloud Physics: Collision/Coalescence; The Bergeron Process". College of DuPage. Retrieved 31 August 2011.
- Sheriff, Robert E. (1991). "Geophysics". Encyclopedic Dictionary of Exploration Geophysics (3rd ed.). Society of Exploration. ISBN 978-1-56080-018-7.
- Stein, Seth; Wysession, Michael (2003). An introduction to seismology, earthquakes, and earth structure. Wiley-Blackwell. ISBN 0-86542-078-5.
- Telford, William Murray; Geldart, L. P.; Sheriff, Robert E. (1990). Applied geophysics. Cambridge University Press. ISBN 978-0-521-33938-4.
- Temple, Robert (2006). The Genius of China. Andre Deutsch. ISBN 0-671-62028-2.
- Torge, W. (2001). Geodesy (3rd ed.). Walter de Gruyter. ISBN 0-89925-680-5.
- Turcotte, Donald Lawson; Schubert, Gerald (2002). Geodynamics (2nd ed.). Cambridge University Press. ISBN 0-521-66624-4.
- Verhoogen, John (1980). Energetics of the Earth. National Academy Press. ISBN 978-0-309-03076-2.
External links
- A reference manual for near-surface geophysics techniques and applications
- Commission on Geophysical Risk and Sustainability (GeoRisk), International Union of Geodesy and Geophysics (IUGG)
- Study of the Earth's Deep Interior, a Committee of IUGG
- Union Commissions (IUGG)
- USGS Geomagnetism Program
- Career crate: Seismic processor
- Society of Exploration Geophysicists
https://en.wikipedia.org/wiki/Geophysics
Surface nuclear magnetic resonance (SNMR), also known as magnetic resonance Sounding (MRS), is a geophysical technique specially designed for hydrogeology. It is based on the principle of nuclear magnetic resonance (NMR) and measurements can be used to indirectly estimate the water content of saturated and unsaturated zones in the earth's subsurface.[1] SNMR is used to estimate aquifer properties, including the quantity of water contained in the aquifer, porosity, and hydraulic conductivity.
https://en.wikipedia.org/wiki/Surface_nuclear_magnetic_resonance
Magnetotellurics (MT) is an electromagnetic geophysical method for inferring the earth's subsurface electrical conductivity from measurements of natural geomagnetic and geoelectric field variation at the Earth's surface.
Investigation depth ranges from 300 m below ground by recording higher frequencies down to 10,000 m or deeper with long-period soundings. Proposed in Japan in the 1940s, and France and the USSR during the early 1950s, MT is now an international academic discipline and is used in exploration surveys around the world.
Commercial uses include hydrocarbon (oil and gas) exploration, geothermal exploration, carbon sequestration, mining exploration, as well as hydrocarbon and groundwater monitoring. Research applications include experimentation to further develop the MT technique, long-period deep crustal exploration, deep mantle probing, sub-glacial water flow mapping, and earthquake precursor research.
https://en.wikipedia.org/wiki/Magnetotellurics
Transient electromagnetics, (also time-domain electromagnetics / TDEM), is a geophysical exploration technique in which electric and magnetic fields are induced by transient pulses of electric current and the subsequent decay response measured. TEM / TDEM methods are generally able to determine subsurface electrical properties, but are also sensitive to subsurface magnetic properties in applications like UXO detection and characterization. TEM/TDEM surveys are a very common surface EM technique for mineral exploration, groundwater exploration, and for environmental mapping, used throughout the world in both onshore and offshore applications.
https://en.wikipedia.org/wiki/Transient_electromagnetics
Geomagnetic secular variation refers to changes in the Earth's magnetic field on time scales of about a year or more. These changes mostly reflect changes in the Earth's interior, while more rapid changes mostly originate in the ionosphere or magnetosphere.[1]
The geomagnetic field changes on time scales from milliseconds to millions of years. Shorter time scales mostly arise from currents in the ionosphere and magnetosphere, and some changes can be traced to geomagnetic storms or daily variations in currents. Changes over time scales of a year or more mostly reflect changes in the Earth's interior, particularly the iron-rich core. These changes are referred to as secular variation.[1] In most models, the secular variation is the amortized time derivative of the magnetic field , . The second derivative, is the secular acceleration.[2]
https://en.wikipedia.org/wiki/Geomagnetic_secular_variation
In astronomy and planetary science, a magnetosphere is a region of space surrounding an astronomical object in which charged particles are affected by that object's magnetic field.[1][2] It is created by a celestial body with an active interior dynamo.
In the space environment close to a planetary body, the magnetic field resembles a magnetic dipole. Farther out, field lines can be significantly distorted by the flow of electrically conducting plasma, as emitted from the Sun (i.e., the solar wind) or a nearby star.[3][4] Planets having active magnetospheres, like the Earth, are capable of mitigating or blocking the effects of solar radiation or cosmic radiation, that also protects all living organisms from potentially detrimental and dangerous consequences. This is studied under the specialized scientific subjects of plasma physics, space physics, and aeronomy.
https://en.wikipedia.org/wiki/Magnetosphere
Magnetohydrodynamics (MHD; also called magneto-fluid dynamics or hydromagnetics) is the study of the magnetic properties and behaviour of electrically conducting fluids. Examples of such magnetofluids include plasmas, liquid metals, salt water, and electrolytes.[1] The word magnetohydrodynamics is derived from magneto- meaning magnetic field, hydro- meaning water, and dynamics meaning movement. The field of MHD was initiated by Hannes Alfvén,[2] for which he received the Nobel Prize in Physics in 1970.
The fundamental concept behind MHD is that magnetic fields can induce currents in a moving conductive fluid, which in turn polarizes the fluid and reciprocally changes the magnetic field itself. The set of equations that describe MHD is a combination of the Navier–Stokes equations of fluid dynamics and Maxwell’s equations of electromagnetism. These differential equations must be solved simultaneously, either analytically or numerically.
https://en.wikipedia.org/wiki/Magnetohydrodynamics
Seismo-electromagnetics are various electro-magnetic phenomena believed to be generated by tectonic forces acting on the earth's crust, and possibly associated with seismic activity such as earthquakes and volcanoes. Study of these has been prompted by the prospect they might be generated by the increased stress leading up to an earthquake, and might thereby provide a basis for short-term earthquake prediction. However, despite many studies, no form of seismo-electromagnetics has been shown to be effective for earthquake prediction. A key problem is that earthquakes themselves produce relatively weak electromagnetic phenomena, and the effects from any precursory phenomena are likely to be too weak to measure. Close monitoring of the Parkfield earthquake revealed no significant pre-seismic electromagnetic effects. However, some researchers remain optimistic, and searches for seismo-electromagnetic earthquake precursors continue.[citation needed]
https://en.wikipedia.org/wiki/Seismo-electromagnetics
Electromagnetic or magnetic induction is the production of an electromotive force (emf) across an electrical conductor in a changing magnetic field.
Michael Faraday is generally credited with the discovery of induction in 1831, and James Clerk Maxwell mathematically described it as Faraday's law of induction. Lenz's law describes the direction of the induced field. Faraday's law was later generalized to become the Maxwell–Faraday equation, one of the four Maxwell equations in his theory of electromagnetism.
Electromagnetic induction has found many applications, including electrical components such as inductors and transformers, and devices such as electric motors and generators.
https://en.wikipedia.org/wiki/Electromagnetic_induction
Sprites or red sprites are large-scale electric discharges that occur in the mesosphere, high above thunderstorm clouds, or cumulonimbus, giving rise to a varied range of visual shapes flickering in the night sky. They are usually triggered by the discharges of positive lightning between an underlying thundercloud and the ground.
Sprites appear as luminous red-orange flashes. They often occur in clusters above the troposphere at an altitude range of 50–90 km (31–56 mi). Sporadic visual reports of sprites go back at least to 1886 [1] but they were first photographed on July 4, 1989,[2] by scientists from the University of Minnesota and have subsequently been captured in video recordings many thousands of times.
Sprites are sometimes inaccurately called upper-atmospheric lightning. However, sprites are cold plasma phenomena that lack the hot channel temperatures of tropospheric lightning, so they are more akin to fluorescent tube discharges than to lightning discharges. Sprites are associated with various other upper-atmospheric optical phenomena including blue jets and ELVES.[1]
https://en.wikipedia.org/wiki/Sprite_(lightning)
Spontaneous potentials are often measured down boreholes for formation evaluation in the oil and gas industry, and they can also be measured along the Earth's surface for mineral exploration or groundwater investigation. The phenomenon and its application to geology was first recognized by Conrad Schlumberger, Marcel Schlumberger, and E.G. Leonardon in 1931, and the first published examples were from Romanian oil fields.
https://en.wikipedia.org/wiki/Spontaneous_potential
Induced polarization (IP) is a geophysical imaging technique used to identify the electrical chargeability of subsurface materials, such as ore.[1][2]
The polarization effect was originally discovered by Conrad Schlumberger when measuring the resistivity of rock.[3]
The survey method is similar to electrical resistivity tomography (ERT), in that an electric current is transmitted into the subsurface through two electrodes, and voltage is monitored through two other electrodes.
Induced polarization is a geophysical method used extensively in mineral exploration and mine operations. Resistivity and IP methods are often applied on the ground surface using multiple four-electrode sites. In an IP survey, in addition to resistivity measurement, capacitive properties of the subsurface materials are determined as well. As a result, IP surveys provide additional information about the spatial variation in lithology and grain-surface chemistry.
The IP survey can be made in time-domain and frequency-domain mode:
In the time-domain induced polarization method, the voltage response is observed as a function of time after the injected current is switched off or on. [4]
In the frequency-domain induced polarization mode, an alternating current is injected into the ground with variable frequencies. Voltage phase-shifts are measured to evaluate the impedance spectrum at different injection frequencies, which is commonly referred to as spectral IP.
The IP method is one of the most widely used techniques in mineral exploration and mining industry and it has other applications in hydrogeophysical surveys, environmental investigations and geotechnical engineering projects.[5]
https://en.wikipedia.org/wiki/Induced_polarization
A telluric current (from Latin tellūs, "earth"), or Earth current,[1] is an electric current which moves underground or through the sea. Telluric currents result from both natural causes and human activity, and the discrete currents interact in a complex pattern. The currents are extremely low frequency and travel over large areas at or near the surface of the Earth.
https://en.wikipedia.org/wiki/Telluric_current
The term intraplate earthquake refers to a variety of earthquake that occurs within the interior of a tectonic plate; this stands in contrast to an interplate earthquake, which occurs at the boundary of a tectonic plate. Intraplate earthquakes are often called "intraslab earthquakes," especially when occurring in microplates.[1][2]
Intraplate earthquakes are relatively rare compared to the more familiar boundary-located interplate earthquakes. Structures far from plate boundaries tend to lack seismic retrofitting, so large intraplate earthquakes can inflict heavy damage. Examples of damaging intraplate earthquakes are the devastating Gujarat earthquake in 2001, the 2012 Indian Ocean earthquakes, the 2017 Puebla earthquake, the 1811–1812 earthquakes in New Madrid, Missouri, and the 1886 earthquake in Charleston, South Carolina.[3]
https://en.wikipedia.org/wiki/Intraplate_earthquake
The internal structure of Earth is the solid portion of the Earth,[clarification needed] excluding its atmosphere and hydrosphere. The structure consists of an outer silicate solid crust, a highly viscous asthenosphere and solid mantle, a liquid outer core whose flow generates the Earth's magnetic field, and a solid inner core.
Scientific understanding of the internal structure of Earth is based on observations of topography and bathymetry, observations of rock in outcrop, samples brought to the surface from greater depths by volcanoes or volcanic activity, analysis of the seismic waves that pass through Earth, measurements of the gravitational and magnetic fields of Earth, and experiments with crystalline solids at pressures and temperatures characteristic of Earth's deep interior.
https://en.wikipedia.org/wiki/Internal_structure_of_Earth
Reflection seismology (or seismic reflection) is a method of exploration geophysics that uses the principles of seismology to estimate the properties of the Earth's subsurface from reflected seismic waves. The method requires a controlled seismic source of energy, such as dynamite or Tovex blast, a specialized air gun or a seismic vibrator. Reflection seismology is similar to sonar and echolocation. This article is about surface seismic surveys; for vertical seismic profiles, see VSP.
Seismic reflection data
https://en.wikipedia.org/wiki/Reflection_seismology
Normal modes
Free oscillations of the Earth are standing waves, the result of interference between two surface waves traveling in opposite directions. Interference of Rayleigh waves results in spheroidal oscillation S while interference of Love waves gives toroidal oscillation T. The modes of oscillations are specified by three numbers, e.g., nSlm, where l is the angular order number (or spherical harmonic degree, see Spherical harmonics for more details). The number m is the azimuthal order number. It may take on 2l+1 values from −l to +l. The number n is the radial order number. It means the wave with n zero crossings in radius. For spherically symmetric Earth the period for given n and l does not depend on m.
Some examples of spheroidal oscillations are the "breathing" mode 0S0, which involves an expansion and contraction of the whole Earth, and has a period of about 20 minutes; and the "rugby" mode 0S2, which involves expansions along two alternating directions, and has a period of about 54 minutes. The mode 0S1 does not exist because it would require a change in the center of gravity, which would require an external force.[3]
Of the fundamental toroidal modes, 0T1 represents changes in Earth's rotation rate; although this occurs, it is much too slow to be useful in seismology. The mode 0T2 describes a twisting of the northern and southern hemispheres relative to each other; it has a period of about 44 minutes.[3]
The first observations of free oscillations of the Earth were done during the great 1960 earthquake in Chile. Presently periods of thousands of modes are known. These data are used for determining some large scale structures of the Earth interior.
P and S waves in Earth's mantle and core
When an earthquake occurs, seismographs near the epicenter are able to record both P and S waves, but those at a greater distance no longer detect the high frequencies of the first S wave. Since shear waves cannot pass through liquids, this phenomenon was original evidence for the now well-established observation that the Earth has a liquid outer core, as demonstrated by Richard Dixon Oldham. This kind of observation has also been used to argue, by seismic testing, that the Moon has a solid core, although recent geodetic studies suggest the core is still molten[citation needed].
https://en.wikipedia.org/wiki/Seismic_wave#Normal_modes
A mantle plume is a proposed mechanism of convection within the Earth's mantle, hypothesized to explain anomalous volcanism.[2] Because the plume head partially melts on reaching shallow depths, a plume is often invoked as the cause of volcanic hotspots, such as Hawaii or Iceland, and large igneous provinces such as the Deccan and Siberian Traps. Some such volcanic regions lie far from tectonic plate boundaries, while others represent unusually large-volume volcanism near plate boundaries.
https://en.wikipedia.org/wiki/Mantle_plume
Geothermal gradient
Geothermal gradient is the rate of temperature change with respect to increasing depth in Earth's interior. As a general rule, the crust temperature rises with depth due to the heat flow from the much hotter mantle; away from tectonic plate boundaries, temperature rises in about 25–30 °C/km (72–87 °F/mi) of depth near the surface in most of the world.[1] However, in some cases the temperature may drop with increasing depth, especially near the surface, a phenomenon known as inverse or negative geothermal gradient. The effects of weather, sun, and season only reach a depth of approximately 10-20 metres.
Strictly speaking, geo-thermal necessarily refers to Earth but the concept may be applied to other planets. In SI units, the geothermal gradient is expressed as °C/km,[1] K/km,[2] or mK/m.[3] These are all equivalent.
Earth's internal heat comes from a combination of residual heat from planetary accretion, heat produced through radioactive decay, latent heat from core crystallization, and possibly heat from other sources. The major heat-producing nuclides in Earth are potassium-40, uranium-238, uranium-235, and thorium-232.[4] The inner core is thought to have temperatures in the range of 4000 to 7000 K, and the pressure at the centre of the planet is thought to be about 360 GPa (3.6 million atm).[5] (The exact value depends on the density profile in Earth.) Because much of the heat is provided for by radioactive decay, scientists believe that early in Earth's history, before nuclides with short half-lives had been depleted, Earth's heat production would have been much higher. Heat production was twice that of present-day at approximately 3 billion years ago,[6] resulting in larger temperature gradients within Earth, larger rates of mantle convection and plate tectonics, allowing the production of igneous rocks such as komatiites that are no longer formed.[7]
The top of the geothermal gradient is influenced by atmospheric temperature. The uppermost layers of the solid planet are at the temperature produced by the local weather, decaying to approximately the annual mean-average ground temperature (MAGT) at a shallow depth of about 10-20 metres depending on the type of ground, rock etc;[8][9] [10][11][12] it is this depth which is used for many ground-source heat pumps.[13] The top hundreds of meters reflect past climate change;[14] descending further, warmth increases steadily as interior heat sources begin to dominate.
Heat sources
Temperature within Earth increases with depth. Highly viscous or partially molten rock at temperatures between 650 and 1,200 °C (1,200 and 2,200 °F) are found at the margins of tectonic plates, increasing the geothermal gradient in the vicinity, but only the outer core is postulated to exist in a molten or fluid state, and the temperature at Earth's inner core/outer core boundary, around 3,500 kilometres (2,200 mi) deep, is estimated to be 5650 ± 600 Kelvin.[15][16] The heat content of Earth is 1031 joules.[1]
- Much of the heat is created by decay of naturally radioactive elements. An estimated 45 to 90 percent of the heat escaping from Earth originates from radioactive decay of elements mainly located in the mantle.[6][17][18]
- Gravitational potential energy, which can be further divided into:
- Release during the accretion of Earth.
- Heat released during differentiation, as abundant heavy metals (iron, nickel, copper) descended to Earth's core.
- Latent heat released as the liquid outer core crystallizes at the inner core boundary.
- Heat may be generated by tidal forces on Earth as it rotates (conservation of angular momentum). The resulting earth tides dissipate energy in Earth's interior as heat.
In Earth's continental crust, the decay of natural radioactive nuclides makes a significant contribution to geothermal heat production. The continental crust is abundant in lower density minerals but also contains significant concentrations of heavier lithophilic elements such as uranium. Because of this, it holds the most concentrated global reservoir of radioactive elements found in Earth.[19] Naturally occurring radioactive elements are enriched in the granite and basaltic rocks, especially in layers closer to Earth's surface.[20] These high levels of radioactive elements are largely excluded from Earth's mantle due to their inability to substitute in mantle minerals and consequent enrichment in melts during mantle melting processes. The mantle is mostly made up of high density minerals with higher concentrations of elements that have relatively small atomic radii such as magnesium (Mg), titanium (Ti), and calcium (Ca).[19]
| Nuclide | Heat release
[W/kg nuclide] |
Half-life
[years] |
Mean mantle concentration
[kg nuclide/kg mantle] |
Heat release
[W/kg mantle] |
|---|---|---|---|---|
| 238U | 9.46 × 10−5 | 4.47 × 109 | 30.8 × 10−9 | 2.91 × 10−12 |
| 235U | 56.9 × 10−5 | 0.704 × 109 | 0.22 × 10−9 | 0.125 × 10−12 |
| 232Th | 2.64 × 10−5 | 14.0 × 109 | 124 × 10−9 | 3.27 × 10−12 |
| 40K | 2.92 × 10−5 | 1.25 × 109 | 36.9 × 10−9 | 1.08 × 10−12 |
The geothermal gradient is steeper in the lithosphere than in the mantle because the mantle transports heat primarily by convection, leading to a geothermal gradient that is determined by the mantle adiabat, rather than by the conductive heat transfer processes that predominate in the lithosphere, which acts as a thermal boundary layer of the convecting mantle.[citation needed]
Heat flow
Heat flows constantly from its sources within Earth to the surface. Total heat loss from Earth is estimated at 44.2 TW (4.42 × 1013 Watts).[22] Mean heat flow is 65 mW/m2 over continental crust and 101 mW/m2 over oceanic crust.[22] This is 0.087 watt/square metre on average (0.03 percent of solar power absorbed by Earth[23]), but is much more concentrated in areas where the lithosphere is thin, such as along mid-ocean ridges (where new oceanic lithosphere is created) and near mantle plumes.[24] Earth's crust effectively acts as a thick insulating blanket which must be pierced by fluid conduits (of magma, water or other) in order to release the heat underneath. More of the heat in Earth is lost through plate tectonics, by mantle upwelling associated with mid-ocean ridges. Another major mode of heat loss is by conduction through the lithosphere, the majority of which occurs in the oceans due to the crust there being much thinner and younger than under the continents.[22][25]
The heat of Earth is replenished by radioactive decay at a rate of 30 TW.[26] The global geothermal flow rates are more than twice the rate of human energy consumption from all primary sources. Global data on heat-flow density are collected and compiled by the International Heat Flow Commission (IHFC) of the IASPEI/IUGG.[27]
Direct application
Heat from Earth's interior can be used as an energy source, known as geothermal energy. The geothermal gradient has been used for space heating and bathing since ancient Roman times, and more recently for generating electricity. As the human population continues to grow, so does energy use and the correlating environmental impacts that are consistent with global primary sources of energy. This has caused a growing interest in finding sources of energy that are renewable and have reduced greenhouse gas emissions. In areas of high geothermal energy density, current technology allows for the generation of electrical power because of the corresponding high temperatures. Generating electrical power from geothermal resources requires no fuel while providing true baseload energy at a reliability rate that constantly exceeds 90%.[19] In order to extract geothermal energy, it is necessary to efficiently transfer heat from a geothermal reservoir to a power plant, where electrical energy is converted from heat by passing steam through a turbine connected to a generator.[19] The efficiency of converting the geothermal heat into electricity depends on the temperature difference between the heated fluid (water or steam) and the environmental temperature, so it is advantageous to use deep, high-temperature heat sources. On a worldwide scale, the heat stored in Earth's interior provides an energy that is still seen as an exotic source. About 10 GW of geothermal electric capacity is installed around the world as of 2007, generating 0.3% of global electricity demand. An additional 28 GW of direct geothermal heating capacity is installed for district heating, space heating, spas, industrial processes, desalination and agricultural applications.[1]
Variations
The geothermal gradient varies with location and is typically measured by determining the bottom open-hole temperature after borehole drilling. Temperature logs obtained immediately after drilling are however affected due to drilling fluid circulation. To obtain accurate bottom hole temperature estimates, it is necessary for the well to reach stable temperature. This is not always achievable for practical reasons.
In stable tectonic areas in the tropics a temperature-depth plot will converge to the annual average surface temperature. However, in areas where deep permafrost developed during the Pleistocene a low temperature anomaly can be observed that persists down to several hundred metres.[28] The Suwałki cold anomaly in Poland has led to the recognition that similar thermal disturbances related to Pleistocene-Holocene climatic changes are recorded in boreholes throughout Poland, as well as in Alaska, northern Canada, and Siberia.
In areas of Holocene uplift and erosion (Fig. 1) the shallow gradient will be high until it reaches a point (labeled "Inflection point" in the figure) where it reaches the stabilized heat-flow regime. If the gradient of the stabilized regime is projected above this point to its intersection with present-day annual average temperature, the height of this intersection above present-day surface level gives a measure of the extent of Holocene uplift and erosion. In areas of Holocene subsidence and deposition (Fig. 2) the initial gradient will be lower than the average until it reaches a point where it joins the stabilized heat-flow regime.
Variations in surface temperature, whether daily, seasonal, or induced by climate changes and the Milankovitch cycle, penetrate below Earth's surface and produce an oscillation in the geothermal gradient with periods varying from a day to tens of thousands of years, and an amplitude which decreases with depth. The longest-period variations have a scale depth of several kilometers.[29][30] Melt water from the polar ice caps flowing along ocean bottoms tends to maintain a constant geothermal gradient throughout Earth's surface.[29][dubious ][verification needed]
If the rate of temperature increase with depth observed in shallow boreholes were to persist at greater depths, temperatures deep within Earth would soon reach the point where rocks would melt. We know, however, that Earth's mantle is solid because of the transmission of S-waves. The temperature gradient dramatically decreases with depth for two reasons. First, the mechanism of thermal transport changes from conduction, as within the rigid tectonic plates, to convection, in the portion of Earth's mantle that convects. Despite its solidity, most of Earth's mantle behaves over long time-scales as a fluid, and heat is transported by advection, or material transport. Second, radioactive heat production is concentrated within the crust of Earth, and particularly within the upper part of the crust, as concentrations of uranium, thorium, and potassium are highest there: these three elements are the main producers of radioactive heat within Earth. Thus, the geothermal gradient within the bulk of Earth's mantle is of the order of 0.5 kelvin per kilometer, and is determined by the adiabatic gradient associated with mantle material (peridotite in the upper mantle).[31]
Negative geothermal gradient
Negative geothermal gradients occur where temperature decreases with depth. This occurs in the upper few hundreds of meters near the surface. Because of the low thermal diffusivity of rocks, deep underground temperatures are hardly affected by diurnal or even annual surface temperature variations. At depths of a few meters, underground temperatures are therefore similar to the annual average surface temperature. At greater depths, underground temperatures reflect a long-term average over past climate, so that temperatures at the depths of dozens to hundreds of meters contain information about the climate of the last hundreds to thousands of years. Depending on the location, these may be colder than current temperatures due to the colder weather close to the last ice age, or due to more recent climate change.[32][33][14]
Negative geothermal gradients may also occur due to deep aquifers, where heat transfer from deep water by convection and advection results in water at shallower levels heating adjacent rocks to a higher temperature than rocks at a somewhat deeper level.[34]
Negative geothermal gradients are also found at large scales in subduction zones.[35] A subduction zone is a tectonic plate boundary where oceanic crust sinks into the mantle due to the high density of the oceanic plate relative to the underlying mantle. Since the sinking plate enters the mantle at a rate of a few centimeters per year, heat conduction is unable to heat the plate as quickly as it sinks. Therefore, the sinking plate has a lower temperature than the surrounding mantle, resulting in a negative geothermal gradient.[35]
See also
- Temperature gradient
- Earth's internal heat budget
- Geothermal power
- Hydrothermal circulation
- PANGAEA Global Heat Flow Database data set with geothermal gradients for large number of sites around the world
References
- Ernst, W.G., (1976) Petrologic Phase Equilibria, W.H. Freeman, San Francisco.
"Geothermal Resources". DOE/EIA-0603(95) Background Information and 1990 Baseline Data Initially Published in the Renewable Energy Annual 1995. Retrieved May 4, 2005.
https://en.wikipedia.org/wiki/Geothermal_gradient
Category:Spatial gradient
Pages in category "Spatial gradient"
The following 11 pages are in this category, out of 11 total. This list may not reflect recent changes.
https://en.wikipedia.org/wiki/Category:Spatial_gradient
In the field of physics, engineering, and earth sciences, advection is the transport of a substance or quantity by bulk motion of a fluid. The properties of that substance are carried with it. Generally the majority of the advected substance is also a fluid. The properties that are carried with the advected substance are conserved properties such as energy. An example of advection is the transport of pollutants or silt in a river by bulk water flow downstream. Another commonly advected quantity is energy or enthalpy. Here the fluid may be any material that contains thermal energy, such as water or air. In general, any substance or conserved, extensive quantity can be advected by a fluid that can hold or contain the quantity or substance.
During advection, a fluid transports some conserved quantity or material via bulk motion. The fluid's motion is described mathematically as a vector field, and the transported material is described by a scalar field showing its distribution over space. Advection requires currents in the fluid, and so cannot happen in rigid solids. It does not include transport of substances by molecular diffusion.
Advection is sometimes confused with the more encompassing process of convection, which is the combination of advective transport and diffusive transport.
In meteorology and physical oceanography, advection often refers to the transport of some property of the atmosphere or ocean, such as heat, humidity (see moisture) or salinity. Advection is important for the formation of orographic clouds and the precipitation of water from clouds, as part of the hydrological cycle.
https://en.wikipedia.org/wiki/Advection
Geopotential is the potential of the Earth's gravity field. For convenience it is often defined as the negative of the potential energy per unit mass, so that the gravity vector is obtained as the gradient of the geopotential, without the negation. In addition to the actual potential (the geopotential), a hypothetical normal potential and their difference, the disturbing potential, can also be defined.
https://en.wikipedia.org/wiki/Geopotential
Concept
For geophysical applications, gravity is distinguished from gravitation. Gravity is defined as the resultant force of gravitation and the centrifugal force caused by the Earth's rotation. Likewise, the respective scalar potentials can be added to form an effective potential called the geopotential, . The surfaces of constant geopotential or isosurfaces of the geopotential are called equigeopotential surfaces, also known as geopotential surfaces, equipotential surfaces, or simply level surfaces.[1]
Global mean sea surface is close to one equigeopotential called the geoid.[2] How the gravitational force and the centrifugal force add up to a force orthogonal to the geoid is illustrated in the figure (not to scale). At latitude 50 deg the off-set between the gravitational force (red line in the figure) and the local vertical (green line in the figure) is in fact 0.098 deg. For a mass point (atmosphere) in motion the centrifugal force no more matches the gravitational and the vector sum is not exactly orthogonal to the Earth surface. This is the cause of the coriolis effect for atmospheric motion.
The geoid is a gently undulating surface due to the irregular mass distribution inside the Earth; it may be approximated however by an ellipsoid of revolution called the reference ellipsoid. The currently most widely used reference ellipsoid, that of the Geodetic Reference System 1980 (GRS80), approximates the geoid to within a little over ±100 m. One can construct a simple model geopotential that has as one of its equipotential surfaces this reference ellipsoid, with the same model potential as the true potential of the geoid; this model is called a normal potential. The difference is called the disturbing potential. Many observable quantities of the gravity field, such as gravity anomalies and deflections of the plumbline, can be expressed in this disturbing potential.
Formulation
The Earth's gravity field can be derived from a gravity potential (geopotential) field as follows:
which expresses the gravity acceleration vector as the gradient of , the potential of gravity. The vector triad is the orthonormal set of base vectors in space, pointing along the coordinate axes.
Note that both gravity and its potential contain a contribution from the centrifugal pseudo-force due to the Earth's rotation. We can write
where is the potential of the gravitational field, that of the gravity field, and that of the centrifugal force field.
The centrifugal force—per unit of mass, i.e., acceleration—is given by
where
is the vector pointing to the point considered straight from the Earth's rotational axis. It can be shown that this pseudo-force field, in a reference frame co-rotating with the Earth, has a potential associated with it that looks like this:
This can be verified by taking the gradient () operator of this expression.
Here, , and are geocentric coordinates.
Normal potential
To a rough approximation, the Earth is a sphere, or to a much better approximation, an ellipsoid. We can similarly approximate the gravity field of the Earth by a spherically symmetric field:
of which the equipotential surfaces—the surfaces of constant potential value—are concentric spheres.
It is more accurate to approximate the geopotential by a field that has the Earth reference ellipsoid as one of its equipotential surfaces, however. The most recent Earth reference ellipsoid is GRS80, or Geodetic Reference System 1980, which the Global Positioning system uses as its reference. Its geometric parameters are: semi-major axis a = 6378137.0 m, and flattening f = 1/298.257222101.
A geopotential field is constructed, being the sum of a gravitational potential and the known centrifugal potential , that has the GRS80 reference ellipsoid as one of its equipotential surfaces. If we also require that the enclosed mass is equal to the known mass of the Earth (including atmosphere) GM = 3986005 × 108 m3·s−2, we obtain for the potential at the reference ellipsoid:
Obviously, this value depends on the assumption that the potential goes asymptotically to zero at infinity (), as is common in physics. For practical purposes it makes more sense to choose the zero point of normal gravity to be that of the reference ellipsoid, and refer the potentials of other points to this.
Disturbing potential
Once a clean, smooth geopotential field has been constructed matching the known GRS80 reference ellipsoid with an equipotential surface (we call such a field a normal potential) we can subtract it from the true (measured) potential of the real Earth. The result is defined as T, the disturbing potential:
The disturbing potential T is numerically a great deal smaller than U or W, and captures the detailed, complex variations of the true gravity field of the actually existing Earth from point-to-point, as distinguished from the overall global trend captured by the smooth mathematical ellipsoid of the normal potential.
Geopotential number
In practical terrestrial work, e.g., levelling, an alternative version of the geopotential is used called geopotential number , which are reckoned from the geoid upward:
Simple case: sphere
For the purpose of satellite orbital mechanics, the geopotential is typically described by a series expansion into spherical harmonics (spectral representation). In this context the geopotential is taken as the potential of the gravitational field of the Earth, that is, leaving out the centrifugal potential.
Solving for geopotential (Φ) in the simple case of a sphere:[3]
Integrate to get
- G = 6.673×10−11 Nm2/kg2 is the gravitational constant,
- m = 5.975×1024 kg is the mass of the earth,
- a = 6.378×106 m is the average radius of the earth,
- z is the geometric height in meters
- Φ is the geopotential at height z, which is in units of [m2/s2] or [J/kg].
See also
References
- Holton, James R. (2004). An Introduction to Dynamic Meteorology (4th ed.). Burlington: Elsevier. ISBN 0-12-354015-1.
https://en.wikipedia.org/wiki/Geopotential
Gravity anomaly
The gravity anomaly at a location on the Earth's surface is the difference between the observed value of gravity and the value predicted by a theoretical model. If the Earth were an ideal oblate spheroid of uniform density, then the gravity measured at every point on its surface would be given precisely by a simple algebraic expression. However, the Earth has a rugged surface and non-uniform composition, which distorts its gravitational field. The theoretical value of gravity can be corrected for altitude and the effects of nearby terrain, but it usually still differs slightly from the measured value. This gravity anomaly can reveal the presence of subsurface structures of unusual density. For example, a mass of dense ore below the surface will give a positive anomaly due to the increased gravitational attraction of the ore.
Different theoretical models will predict different values of gravity, and so a gravity anomaly is always specified with reference to a particular model. The Bouguer, free-air, and isostatic gravity anomalies are each based on different theoretical corrections to the value of gravity.
A gravity survey is conducted by measuring the gravity anomaly at many locations in a region of interest, using a portable instrument called a gravimeter. Careful analysis of the gravity data allows geologists to make inferences about the subsurface geology.
Definition
The gravity anomaly is the difference between the observed acceleration of an object in free fall (gravity) near a planet's surface, and the corresponding value predicted by a model of the planet's gravitational field.[1] Typically the model is based on simplifying assumptions, such as that, under its self-gravitation and rotational motion, the planet assumes the figure of an ellipsoid of revolution.[2] Gravity on the surface of this reference ellipsoid is then given by a simple formula which only contains the latitude. For Earth, the reference ellipsoid is the International Reference Ellipsoid, and the value of gravity predicted for points on the ellipsoid is the normal gravity, gn.[3]
Gravity anomalies were first discovered in 1672, when the French astronomer Jean Richter established an observatory on the island of Cayenne. Richter was equipped with a highly precise pendulum clock which had been carefully calibrated at Paris before his departure. However, he found that the clock ran too slowly in Cayenne, compared with the apparent motion of the stars. Fifteen years later, Isaac Newton used his newly formulated universal theory of gravitation to explain the anomaly. Newton showed that the measured value of gravity was affected by the rotation of the Earth, which caused the Earth's equator to bulge out slightly relative to its poles. Cayenne, being nearer the equator than Paris, would be both further from the center of Earth (reducing the Earth's bulk gravitational attraction slightly) and subject to stronger centrifugal acceleration from the Earth's rotation. Both these effects reduce the value of gravity, explaining why Richter's pendulum clock, which depended on the value of gravity, ran too slowly. Correcting for these effects removed most of this anomaly.[4]
To understand the nature of the gravity anomaly due to the subsurface, a number of corrections must be made to the measured gravity value. Different theoretical models will include different corrections to the value of gravity, and so a gravity anomaly is always specified with reference to a particular model. The Bouguer, free-air, and isostatic gravity anomalies are each based on different theoretical corrections to the value of gravity.[5]
The model field and corrections
The starting point for the model field is the International Reference Ellipsoid, which gives the normal gravity gn for every point on the Earth's idealized shape. Further refinements of the model field are usually expressed as corrections added to the measured gravity or (equivalently) subtracted from the normal gravity. At a minimum, these include the tidal correction △gtid, the terrain correction △gT, and the free air correction △gFA. Other corrections are added for various gravitational models. The difference between the corrected measured gravity and the normal gravity is the gravity anomaly.[6]
The normal gravity
The normal gravity accounts for the bulk gravitation of the entire Earth, corrected for its idealized shape and rotation. It is given by the formula:
The tidal correction
The Sun and Moon create time-dependent tidal forces that affect the measured value of gravity by about 0.3 mgal. Two-thirds of this is from the Moon. This effect is very well understood and can be calculated precisely for a given time and location using astrophysical data and formulas, to yield the tidal correction △gtid.[8]
The terrain correction
The local topography of the land surface affects the gravity measurement. Both terrain higher than the measurement point and valleys lower than the measurement point reduce the measured value of gravity. This is taken into account by the terrain correction △gT. The terrain correction is calculated from knowledge of the local topography and estimates of the density of the rock making up the high ground. In effect, the terrain correction levels the terrain around the measurement point.[9]
The terrain correction must be calculated for every point at which gravity is measured, taking into account every hill or valley whose difference in elevation from the measurement point is greater than about 5% of its distance from the measurement point. This is tedious and time-consuming but necessary for obtaining a meaningful gravity anomaly.[10]
The free-air correction
The next correction is the free-air correction. This takes into account the fact that the measurement is usually at a different elevation than the reference ellipsoid at the measurement latitude and longitude. For a measurement point above the reference ellipsoid, this means that the gravitational attraction of the bulk mass of the earth is slightly reduced. The free-air correction is simply 0.3086 mgal m−1 times the elevation above the reference ellipsoid.[11]
The remaining gravity anomaly at this point in the reduction is called the free-air anomaly. That is, the free-air anomaly is:[12]
Bouguer plate correction
The free-air anomaly does not take into account the layer of material (after terrain leveling) outside the reference ellipsoid. The gravitational attraction of this layer or plate is taken into account by the Bouguer plate correction, which is −0.0419×10−3 ρ h mgal m2 kg−1. The density of crustal rock, ρ, is usually taken to be 2670 kg m3 so the Bouguer plate correction is usually taken as −0.1119 mgal m−1 h. Here h is the elevation above the reference ellipsoid.[13]
The remaining gravity anomaly at this point in the reduction is called the Bouguer anomaly. That is, the Bouguer anomaly is:[12]
Isostatic correction
The Bouguer anomaly is positive over ocean basins and negative over high continental areas. This shows that the low elevation of ocean basins and high elevation of continents is compensated by the thickness of the crust at depth. The higher terrain is held up by the buoyancy of thicker crust "floating" on the mantle.[14]
The isostatic anomaly is defined as the Bouger anomaly minus the gravity anomaly due to the subsurface compensation, and is a measure of the local departure from isostatic equilibrium, due to dynamic processes in the viscous mantle. At the center of a level plateau, it is approximately equal to the free air anomaly.[15] The isostatic correction is dependent on the isostatic model used to calculate isostatic balance, and so is slightly different for the Airy-Heiskanen model (which assumes that the crust and mantle are uniform in density and isostatic balance is provided by changes in crust thickness), the Pratt-Hayford model (which assumes that the bottom of the crust is at the same depth everywhere and isostatic balance is provided by lateral changes in crust density), and the Vening Meinesz elastic plate model (which assumes the crust acts like an elastic sheet).[16]
Forward modelling is the process of computing the detailed shape of the compensation required by a theoretical model and using this to correct the Bouguer anomaly to yield an isostatic anomaly.[17]
Causes
Lateral variations in gravity anomalies are related to anomalous density distributions within the Earth. Local measurements of the gravity of Earth help us to understand the planet's internal structure.
Regional causes
The Bouguer anomaly over continents is generally negative, especially over mountain ranges.[18] For example, typical Bouguer anomalies in the Central Alps are −150 milligals.[19] By contrast, the Bouguer anomaly is positive over oceans. These anomalies reflect the varying thickness of the Earth's crust. The higher continental terrain is supported by thick, low-density crust that "floats" on the denser mantle, while the ocean basins are floored by much thinner oceanic crust. The free-air and isostatic anomalies are small near the centers of ocean basins or continental plateaus, showing that these are approximately in isostatic equilibrium. The gravitational attraction of the high terrain is balanced by the reduced gravitational attraction of its underlying low-density roots. This brings the free-air anomaly, which omits the correction terms for either, close to zero. The isostatic anomaly includes correction terms for both effects, which reduces it nearly to zero as well. The Bouguer anomaly includes only the negative correction for the high terrain and so is strongly negative.[18]
More generally, the Airy isostatic anomaly is zero over regions where there is complete isostatic compensation. The free-air anomaly is also close to zero except near boundaries of crustal blocks. The Bouger anomaly is very negative over elevated terrain. The opposite is true for the theoretical case of terrain that is completely uncompensated: The Bouger anomaly is zero while the free-air and Airy isostatic anomalies are very positive.[15]
The Bouger anomaly map of the Alps shows additional features besides the expected deep mountain roots. A positive anomaly is associated with the Ivrea body, a wedge of dense mantle rock caught up by an ancient continental collision. The low-density sediments of the Molasse basin produce a negative anomaly. Larger surveys across the region provide evidence of a relict subduction zone.[20] Negative isostatic anomalies in Switzerland correlate with areas of active uplift, while positive anomalies are associated with subsidence.[21]
Over mid-ocean ridges, the free-air anomalies are small and correlate with the ocean bottom topography. The ridge and its flanks appear to be fully isostatically compensated. There is a large Bouger positive, of over 350 mgal, beyond 1,000 kilometers (620 mi) from the ridge axis, which drops to 200 over the axis. This is consistent with seismic data and suggests the presence of a low-density magma chamber under the ridge axis.[22]
There are intense isostatic and free-air anomalies along island arcs. These are indications of strong dynamic effects in subduction zones. The free-air anomaly is around +70 mgal along the Andes coast, and this is attributed to the subducting dense slab. The trench itself is very negative,[23] with values more negative than −250 mgal. This arises from the low-density ocean water and sediments filling the trench.[24]
Gravity anomalies provide clues on other processes taking place deep in the lithosphere. For example, the formation and sinking of a lithospheric root may explain negative isostatic anomalies in eastern Tien Shan.[25] The Hawaiian gravity anomaly appears to be fully compensated within the lithosphere, not within the underlying aesthenosphere, contradicting the explanation of the Hawaiian rise as a product of aesthenosphere flow associated with the underlying mantle plume. The rise may instead be a result of lithosphere thinning: The underlying aesthenosphere is less dense than the lithosphere and it rises to produce the swell. Subsequent cooling thickens the lithosphere again and subsidence takes place.[26]
Local anomalies
Local anomalies are used in applied geophysics. For example, a local positive anomaly may indicate a body of metallic ores. Salt domes are typically expressed in gravity maps as lows, because salt has a low density compared to the rocks the dome intrudes.[27]
At scales between entire mountain ranges and ore bodies, Bouguer anomalies may indicate rock types. For example, the northeast-southwest trending high across central New Jersey represents a graben of Triassic age largely filled with dense basalts.[28]
Satellite measurements
Currently, the static and time-variable Earth's gravity field parameters are being determined using modern satellite missions, such as GOCE, CHAMP, Swarm, GRACE and GRACE-FO.[29][30] The lowest-degree parameters, including the Earth's oblateness and geocenter motion are best determined from Satellite laser ranging.[31]
Large-scale gravity anomalies can be detected from space, as a by-product of satellite gravity missions, e.g., GOCE. These satellite missions aim at the recovery of a detailed gravity field model of the Earth, typically presented in the form of a spherical-harmonic expansion of the Earth's gravitational potential, but alternative presentations, such as maps of geoid undulations or gravity anomalies, are also produced.
The Gravity Recovery and Climate Experiment (GRACE) consists of two satellites that can detect gravitational changes across the Earth. Also these changes can be presented as gravity anomaly temporal variations. The Gravity Recovery and Interior Laboratory (GRAIL) also consisted of two spacecraft orbiting the Moon, which orbited for three years before their deorbit in 2015.See also
- Gravimetry
- Gravity anomalies of Britain and Ireland
- Magnetic anomaly
- Mass concentration (astronomy)
- Physical geodesy
- Vertical deflection
References
- Sośnica, Krzysztof; Jäggi, Adrian; Meyer, Ulrich; Thaller, Daniela; Beutler, Gerhard; Arnold, Daniel; Dach, Rolf (October 2015). "Time variable Earth's gravity field from SLR satellites". Journal of Geodesy. 89 (10): 945–960. Bibcode:2015JGeod..89..945S. doi:10.1007/s00190-015-0825-1.
Further reading
- Heiskanen, Weikko Aleksanteri; Moritz, Helmut (1967). Physical Geodesy. W.H. Freeman.
https://en.wikipedia.org/wiki/Gravity_anomaly
Mass concentration (astronomy)
In astronomy, astrophysics and geophysics, a mass concentration (or mascon) is a region of a planet's or moon's crust that contains a large positive gravity anomaly. In general, the word "mascon" can be used as a noun to refer to an excess distribution of mass on or beneath the surface of an astronomical body (compared to some suitable average), such as is found around Hawaii on Earth.[1] However, this term is most often used to describe a geologic structure that has a positive gravitational anomaly associated with a feature (e.g. depressed basin) that might otherwise have been expected to have a negative anomaly, such as the "mascon basins" on the Moon.
Lunar and Martian mascons
The Moon is the most gravitationally "lumpy" major body known in the Solar System. Its largest mascons can cause a plumb bob to hang about a third of a degree off vertical, pointing toward the mascon, and increase the force of gravity by one-half percent.[2][3]
Typical examples of mascon basins on the Moon are the Imbrium, Serenitatis, Crisium and Orientale impact basins, all of which exhibit significant topographic depressions and positive gravitational anomalies. Examples of mascon basins on Mars are the Argyre, Isidis, and Utopia basins. Theoretical considerations imply that a topographic low in isostatic equilibrium would exhibit a slight negative gravitational anomaly. Thus, the positive gravitational anomalies associated with these impact basins indicate that some form of positive density anomaly must exist within the crust or upper mantle that is currently supported by the lithosphere. One possibility is that these anomalies are due to dense mare basaltic lavas, which might reach up to 6 kilometers in thickness for the Moon. While these lavas certainly contribute to the observed gravitational anomalies, uplift of the crust-mantle interface is also required to account for their magnitude. Indeed, some mascon basins on the Moon do not appear to be associated with any signs of volcanic activity. Theoretical considerations in either case indicate that all the lunar mascons are super-isostatic (that is, supported above their isostatic positions). The huge expanse of mare basaltic volcanism associated with Oceanus Procellarum does not possess a positive gravitational anomaly.
Origin of lunar mascons
Since their identification in 1968 by Doppler tracking of the five Lunar Orbiter spacecraft,[4] the origin of the mascons beneath the surface of the Moon has been subject to much debate, but they are now regarded as being the result of the impact of asteroids during the Late Heavy Bombardment.[5]
Effect of lunar mascons on satellite orbits
Lunar mascons alter the local gravity above and around them sufficiently that low and uncorrected satellite orbits around the Moon are unstable on a timescale of months or years. The small perturbations in the orbits accumulate and eventually distort the orbit enough for the satellite to impact the surface.
Because of its mascons, the Moon has only four "frozen orbit" inclination zones where a lunar satellite can stay in a low orbit indefinitely. Lunar subsatellites were released on two of the last three Apollo crewed lunar landing missions in 1971 and 1972; the subsatellite PFS-2 released from Apollo 16 was expected to stay in orbit for one and a half years, but lasted only 35 days before crashing into the lunar surface since it had to be deployed in a much lower orbit than initially planned. It was only in 2001 that the mascons were mapped and the frozen orbits were discovered.[2]
The Luna 10 orbiter was the first artificial object to orbit the Moon, and it returned tracking data indicating that the lunar gravitational field caused larger than expected perturbations, presumably due to "roughness" of the lunar gravitational field.[6] The Lunar mascons were discovered by Paul M. Muller and William L. Sjogren of the NASA Jet Propulsion Laboratory (JPL) in 1968[7] from a new analytic method applied to the highly precise navigation data from the uncrewed pre-Apollo Lunar Orbiter spacecraft. This discovery observed the consistent 1:1 correlation between very large positive gravity anomalies and depressed circular basins on the Moon. This fact places key limits on models attempting to follow the history of the Moon's geological development and explain the current lunar internal structures.
At that time, one of NASA's highest priority "tiger team" projects was to explain why the Lunar Orbiter spacecraft being used to test the accuracy of Project Apollo navigation were experiencing errors in predicted position of ten times the mission specification (2 kilometers instead of 200 meters). This meant that the predicted landing areas were 100 times as large as those being carefully defined for reasons of safety. Lunar orbital effects principally resulting from the strong gravitational perturbations of the mascons were ultimately revealed as the cause. William Wollenhaupt and Emil Schiesser of the NASA Manned Spacecraft Center in Houston then worked out the "fix"[8][9][10] that was first applied to Apollo 12 and permitted its landing within 163 m (535 ft) of the target, the previously-landed Surveyor 3 spacecraft.[11]
Mapping
In May 2013 a NASA study was published with results from the twin GRAIL probes, that mapped mass concentrations on Earth's Moon.[12]
China's Chang’e 5T1 mission also mapped Moon's mascons. [13]
Earth's mascons
Mascons on Earth are often measured by means of satellite gravimetry, such as the GRACE satellites.[14][15] Mascons are often reported in terms of a derived physical quantity called "equivalent water thickness" or "water equivalent height", obtained dividing the surface mass density redistribution by the density of water.[16][17]
See also
References
Bill [Wilbur R.] Wollenhaupt from JPL joined my group. He and I and Bill [William] Boyce and some others traveled to Langley, and met with the Langley people over the weekend, we spent the whole time reprocessing Langley Lunar Orbiter data day and night.
Somewhere about this time Wilbur R. Wollenhaupt, who went by Bill, joined our group. He had extensive background in ground-based navigation at JPL. He was pretty familiar with the JPL Deep Space Network (DSN) Trackers after which the Apollo trackers were patterned.
If this determination, using the LM data, disagrees substantially with the other data sources, we must consider the possibility that it's due to gravity anomalies. The sort of differences we are willing to tolerate is 0.3° in longitude, which is more or less equivalent to 0.3° pitch misalignment in the platform. True alignment errors in excess of that could present ascent guidance problems. Since 0.3° is equivalent of about five miles, you'd expect the crew's estimate of position could probably be useful in determining the true situation. All they'd have to do is tell us they are short or over-shot the target point a great deal.
- Chao, B. F. (2016-05-07). "Caveats on the equivalent water thickness and surface mascon solutions derived from the GRACE satellite-observed time-variable gravity". Journal of Geodesy. Springer Science and Business Media LLC. 90 (9): 807–813. Bibcode:2016JGeod..90..807C. doi:10.1007/s00190-016-0912-y. ISSN 0949-7714. S2CID 124201548.
Further reading
- Mark Wieczorek & Roger Phillips (1999). "Lunar multiring basins and the cratering process". Icarus. 139 (2): 246–259. Bibcode:1999Icar..139..246W. doi:10.1006/icar.1999.6102.
- A. Konopliv; S. Asmar; E. Carranza; W. Sjogren & D. Yuan (2001). "Recent gravity models as a result of the Lunar Prospector mission". Icarus. 50 (1): 1–18. Bibcode:2001Icar..150....1K. CiteSeerX 10.1.1.18.1930. doi:10.1006/icar.2000.6573.
https://en.wikipedia.org/wiki/Mass_concentration_(astronomy)
Vertical deflection
The vertical deflection (VD) or deflection of the vertical (DoV), also known as deflection of the plumb line and astro-geodetic deflection, is a measure of how far the gravity direction at a given point of interest is rotated by local mass anomalies such as nearby mountains. They are widely used in geodesy, for surveying networks and for geophysical purposes.
The vertical deflection are the angular components between the true zenith–nadir curve (plumb line) tangent line and the normal vector to the surface of the reference ellipsoid (chosen to approximate the Earth's sea-level surface). VDs are caused by mountains and by underground geological irregularities and can amount to angles of 10″ in flat areas or 20–50″ in mountainous terrain).[citation needed]
The deflection of the vertical has a north–south component ξ (xi) and an east–west component η (eta). The value of ξ is the difference between the astronomic latitude and the geodetic latitude (taking north latitudes to be positive and south latitudes to be negative); the latter is usually calculated by geodetic network coordinates. The value of η is the product of cosine of latitude and the difference between the astronomic longitude and the longitude (taking east longitudes to be positive and west longitudes to be negative). When a new mapping datum replaces the old, with new geodetic latitudes and longitudes on a new ellipsoid, the calculated vertical deflections will also change.
Determination
The deflections reflect the undulation of the geoid and gravity anomalies, for they depend on the gravity field and its inhomogeneities.
Vertical deflections are usually determined astronomically. The true zenith is observed astronomically with respect to the stars, and the ellipsoidal zenith (theoretical vertical) by geodetic network computation, which always takes place on a reference ellipsoid. Additionally, the very local variations of the vertical deflection can be computed from gravimetric survey data and by means of digital terrain models (DTM), using a theory originally developed by Vening-Meinesz.
VDs are used in astrogeodetic levelling: as a vertical deflection describes the difference between the geoidal and ellipsoidal normal direction, it represents the horizontal spatial gradient of the geoid undulations of the geoid (i.e., the separation between geoid and reference ellipsoid).
In practice, the deflections are observed at special points with spacings of 20 or 50 kilometers. The densification is done by a combination of DTM models and areal gravimetry. Precise vertical deflection observations have accuracies of ±0.2″ (on high mountains ±0.5″), calculated values of about 1–2″.
The maximal vertical deflection of Central Europe seems to be a point near the Großglockner (3,798 m), the highest peak of the Austrian Alps. The approx. values are ξ = +50″ and η = −30″. In the Himalaya region, very asymmetric peaks may have vertical deflections up to 100″ (0.03°). In the rather flat area between Vienna and Hungary the values are less than 15", but scatter by ±10″ for irregular rock densities in the subsurface.
More recently, a combination of digital camera and tiltmeter have also been used, see zenith camera.[1]
Application
Vertical deflections are principally used in four matters:
- For precise calculation of survey networks. The geodetic theodolites and levelling instruments are oriented with respect to the true vertical, but its deflection exceeds the geodetic measuring accuracy by a factor of 5 to 50. Therefore, the data have to be corrected exactly with respect to the global ellipsoid. Without these reductions, the surveys may be distorted by some centimeters or even decimeters per km.
- For the geoid determination (mean sea level) and for exact transformation of elevations. The global geoidal undulations amount to 50–100 m, and their regional values to 10–50 m. They are adequate to the integrals of VD components ξ,η and therefore can be calculated with cm accuracy over distances of many kilometers.
- For GPS surveys. The satellites measurements refer to a pure geometrical system (usually the WGS84 ellipsoid), whereas the terrestrial heights refer to the geoid. We need accurate geoid data to combine the different types of measurements.
- For geophysics. Because VD data are affected by the physical structure of the Earth's crust and mantle, geodesists are engaged in models to improve our knowledge of the Earth's interior. Additionally and similar to applied geophysics, the VD data can support the future exploration of raw materials, oil, gas or ores.
Historical implications
Vertical deflections were used to measure Earth's density in the Schiehallion experiment.
Vertical deflection is the reason why modern prime meridian passes more than 100 m to the east of the historical astronomic prime meridian in Greenwich.[2]
The meridian arc measurement made by Nicolas-Louis de Lacaille north of Cape Town in 1752 (de Lacaille's arc measurement) was affected by vertical deflection.[3] The resulting discrepancy with Northern Hemisphere measurements was not explained until a visit to the area by George Everest in 1820; Maclear's arc measurement resurvey ultimately confirmed Everest's conjecture.[4]
Errors in the meridian arc of Delambre and Méchain determination, which affected the original definition of the metre,[5] were long known to be mainly caused by an uncertain determination of Barcelona's latitude later explained by vertical deflection.[6][7][8] When these errors where acknowledged in 1866,[9] it became urgent to proceed to a new measurement of the French arc between Dunkirk and Perpignan. The operations concerning the revision of the French arc linked to Spanish triangulation were completed only in 1896. Meanwhile the French geodesists had accomplished in 1879 the junction of Algeria to Spain, with the help of the geodesists of the Madrid Institute headed by the late Carlos Ibañez Ibáñez de Ibero (1825-1891), who had been president of the International Geodetic Association (now called International Association of Geodesy), first president of the International Committee for Weights and Measures and one of the 81 initial members of the International Statistical Institute.[10] Until Hayford ellipsoid was calculated in 1910, vertical deflections were considered as random errors.[11] Plumb line deviations were identified by Jean Le Rond d'Alembert as an important source of error in geodetic surveys as early as 1756, a few years later, in 1828, Carl Friedrich Gauss proposed the concept of geoid.[12][13]
See also
References
see page 811
- US Department of Commerce, National Oceanic and Atmospheric Administration. "What is the geoid?". geodesy.noaa.gov. Retrieved 2022-12-23.
External links
https://en.wikipedia.org/wiki/Vertical_deflection
A plumb bob, plumb bob level, or plummet, is a weight, usually with a pointed tip on the bottom, suspended from a string and used as a vertical reference line, or plumb-line. It is a precursor to the spirit level and used to establish a vertical datum. It is typically made of stone, wood, or lead, but can also be made of other metals. If it is used for decoration, it may be made of bone or ivory.
The instrument has been used since at least the time of ancient Egypt[1] to ensure that constructions are "plumb", or vertical. It is also used in surveying, to establish the nadir with respect to gravity of a point in space. It is used with a variety of instruments (including levels, theodolites, and steel tapes) to set the instrument exactly over a fixed survey marker or to transcribe positions onto the ground for placing a marker.[2]
https://en.wikipedia.org/wiki/Plumb_bob
| Operation Plumbbob | |
|---|---|
 Plumbbob Priscilla | |
| Information | |
| Country | United States |
| Test site |
|
| Period | 1957 |
| Number of tests | 29 |
| Test type | balloon, dry surface, high alt rocket (30–80 km), tower, underground shaft, tunnel |
| Max. yield | 74 kilotonnes of TNT (310 TJ) |
| Test series chronology | |
Operation Plumbbob was a series of nuclear tests that were conducted between May 28 and October 7, 1957, at the Nevada Test Site, following Project 57, and preceding Project 58/58A.[1]
https://en.wikipedia.org/wiki/Operation_Plumbbob
|
|
|
|
|
|
A geodetic datum or geodetic system (also: geodetic reference datum, geodetic reference system, or geodetic reference frame) is a global datum reference or reference frame for precisely representing the position of locations on Earth or other planetary bodies by means of geodetic coordinates.[1] Datums[note 1] are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a location across the Earth's surface, in latitude and longitude or another coordinate system; a vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). Since the rise of the global positioning system (GPS), the ellipsoid and datum WGS 84 it uses has supplanted most others in many applications. The WGS 84 is intended for global use, unlike most earlier datums.
Before GPS, there was no precise way to measure the position of a location that was far from universal reference points, such as from the Prime Meridian at the Greenwich Observatory for longitude, from the Equator for latitude, or from the nearest coast for sea level. Astronomical and chronological methods have limited precision and accuracy, especially over long distances. Even GPS requires a predefined framework on which to base its measurements, so WGS 84 essentially functions as a datum, even though it is different in some particulars from a traditional standard horizontal or vertical datum.
A standard datum specification (whether horizontal or vertical) consists of several parts: a model for Earth's shape and dimensions, such as a reference ellipsoid or a geoid; an origin at which the ellipsoid/geoid is tied to a known (often monumented) location on or inside Earth (not necessarily at 0 latitude 0 longitude); and multiple control points that have been precisely measured from the origin and monumented. Then the coordinates of other places are measured from the nearest control point through surveying. Because the ellipsoid or geoid differs between datums, along with their origins and orientation in space, the relationship between coordinates referred to one datum and coordinates referred to another datum is undefined and can only be approximated. Using local datums, the disparity on the ground between a point having the same horizontal coordinates in two different datums could reach kilometers if the point is far from the origin of one or both datums. This phenomenon is called datum shift.
Because Earth is an imperfect ellipsoid, local datums can give a more accurate representation of some specific area of coverage than WGS 84 can. OSGB36, for example, is a better approximation to the geoid covering the British Isles than the global WGS 84 ellipsoid.[2] However, as the benefits of a global system outweigh the greater accuracy, the global WGS 84 datum has become widely adopted.[3]
History
The spherical nature of Earth was known by the ancient Greeks, who also developed the concepts of latitude and longitude, and the first astronomical methods for measuring them. These methods, preserved and further developed by Muslim and Indian astronomers, were sufficient for the global explorations of the 15th and 16th Centuries.
However, the scientific advances of the Age of Enlightenment brought a recognition of errors in these measurements, and a demand for greater precision. This led to technological innovations such as the 1735 Marine chronometer by John Harrison, but also to a reconsideration of the underlying assumptions about the shape of Earth itself. Isaac Newton postulated that the conservation of momentum should make Earth oblate (wider at the equator), while the early surveys of Jacques Cassini (1720) led him to believe Earth was prolate (wider at the poles). The subsequent French geodesic missions (1735-1739) to Lapland and Peru corroborated Newton, but also discovered variations in gravity that would eventually lead to the geoid model.
A contemporary development was the use of the trigonometric survey to accurately measure distance and location over great distances. Starting with the surveys of Jacques Cassini (1718) and the Anglo-French Survey (1784–1790), by the end of the 18th Century, survey control networks covered France and the United Kingdom. More ambitious undertakings such as the Struve Geodetic Arc across Eastern Europe (1816-1855) and the Great Trigonometrical Survey of India (1802-1871) took much longer, but resulted in more accurate estimations of the shape of the Earth ellipsoid. The first triangulation across the United States was not completed until 1899.
The U.S. survey resulted in the North American Datum (horizontal) of 1927 (NAD27) and the Vertical Datum of 1929 (NAVD29), the first standard datums available for public use. This was followed by the release of national and regional datums over the next several decades. Improving measurements, including the use of early satellites, enabled more accurate datums in the later 20th Century, such as NAD83 in North America, ETRS89 in Europe, and GDA94 in Australia. At this time global datums were also first developed for use in satellite navigation systems, especially the World Geodetic System (WGS 84) used in the U.S. global positioning system (GPS), and the International Terrestrial Reference System and Frame (ITRF) used in the European Galileo system.
Dimensions
Horizontal datum
The horizontal datum is the model used to measure positions on Earth. A specific point can have substantially different coordinates, depending on the datum used to make the measurement. There are hundreds of local horizontal datums around the world, usually referenced to some convenient local reference point. Contemporary datums, based on increasingly accurate measurements of the shape of Earth, are intended to cover larger areas. The WGS 84 datum, which is almost identical to the NAD83 datum used in North America and the ETRS89 datum used in Europe, is a common standard datum.[citation needed]
Vertical datum
A vertical datum is a reference surface for vertical positions, such as the elevations of Earth features including terrain, bathymetry, water level, and man-made structures.
An approximate definition of sea level is the datum WGS 84, an ellipsoid, whereas a more accurate definition is Earth Gravitational Model 2008 (EGM2008), using at least 2,159 spherical harmonics. Other datums are defined for other areas or at other times; ED50 was defined in 1950 over Europe and differs from WGS 84 by a few hundred meters depending on where in Europe you look. Mars has no oceans and so no sea level, but at least two martian datums have been used to locate places there.
Geodetic coordinates
In geodetic coordinates, Earth's surface is approximated by an ellipsoid, and locations near the surface are described in terms of geodetic latitude (), longitude (), and ellipsoidal height ().[note 2]
Earth reference ellipsoid
Defining and derived parameters
The ellipsoid is completely parameterised by the semi-major axis and the flattening .
| Parameter | Symbol |
|---|---|
| Semi-major axis | |
| Reciprocal of flattening |
From and it is possible to derive the semi-minor axis , first eccentricity and second eccentricity of the ellipsoid
| Parameter | Value |
|---|---|
| Semi-minor axis | |
| First eccentricity squared | |
| Second eccentricity squared |
Parameters for some geodetic systems
The two main reference ellipsoids used worldwide are the GRS80[4] and the WGS 84.[5]
A more comprehensive list of geodetic systems can be found here.
Geodetic Reference System 1980 (GRS80)
| Parameter | Notation | Value |
|---|---|---|
| Semi-major axis | 6378137 m | |
| Reciprocal of flattening | 298.257222101 |
World Geodetic System 1984 (WGS 84)
The Global Positioning System (GPS) uses the World Geodetic System 1984 (WGS 84) to determine the location of a point near the surface of Earth.
| Parameter | Notation | Value |
|---|---|---|
| Semi-major axis | 6378137.0 m | |
| Reciprocal of flattening | 298.257223563 |
| Constant | Notation | Value |
|---|---|---|
| Semi-minor axis | 6356752.3142 m | |
| First eccentricity squared | 6.69437999014×10−3 | |
| Second eccentricity squared | 6.73949674228×10−3 |
Datum transformation
The difference in co-ordinates between datums is commonly referred to as datum shift. The datum shift between two particular datums can vary from one place to another within one country or region, and can be anything from zero to hundreds of meters (or several kilometers for some remote islands). The North Pole, South Pole and Equator will be in different positions on different datums, so True North will be slightly different. Different datums use different interpolations for the precise shape and size of Earth (reference ellipsoids). For example, in Sydney there is a 200 metres (700 feet) difference between GPS coordinates configured in GDA (based on global standard WGS 84) and AGD (used for most local maps), which is an unacceptably large error for some applications, such as surveying or site location for scuba diving.[6]
Datum conversion is the process of converting the coordinates of a point from one datum system to another. Because the survey networks upon which datums were traditionally based are irregular, and the error in early surveys is not evenly distributed, datum conversion cannot be performed using a simple parametric function. For example, converting from NAD27 to NAD83 is performed using NADCON (later improved as HARN), a raster grid covering North America, with the value of each cell being the average adjustment distance for that area in latitude and longitude. Datum conversion may frequently be accompanied by a change of map projection.
Discussion and examples
A geodetic reference datum is a known and constant surface which is used to describe the location of unknown points on Earth. Since reference datums can have different radii and different center points, a specific point on Earth can have substantially different coordinates depending on the datum used to make the measurement. There are hundreds of locally developed reference datums around the world, usually referenced to some convenient local reference point. Contemporary datums, based on increasingly accurate measurements of the shape of Earth, are intended to cover larger areas. The most common reference Datums in use in North America are NAD27, NAD83, and WGS 84.
The North American Datum of 1927 (NAD 27) is "the horizontal control datum for the United States that was defined by a location and azimuth on the Clarke spheroid of 1866, with origin at (the survey station) Meades Ranch (Kansas)." ... The geoidal height at Meades Ranch was assumed to be zero, as sufficient gravity data was not available, and this was needed to relate surface measurements to the datum. "Geodetic positions on the North American Datum of 1927 were derived from the (coordinates of and an azimuth at Meades Ranch) through a readjustment of the triangulation of the entire network in which Laplace azimuths were introduced, and the Bowie method was used." (http://www.ngs.noaa.gov/faq.shtml#WhatDatum ) NAD27 is a local referencing system covering North America.
The North American Datum of 1983 (NAD 83) is "The horizontal control datum for the United States, Canada, Mexico, and Central America, based on a geocentric origin and the Geodetic Reference System 1980 (GRS80). "This datum, designated as NAD 83 ...is based on the adjustment of 250,000 points including 600 satellite Doppler stations which constrain the system to a geocentric origin." NAD83 may be considered a local referencing system.
WGS 84 is the World Geodetic System of 1984. It is the reference frame used by the U.S. Department of Defense (DoD) and is defined by the National Geospatial-Intelligence Agency (NGA) (formerly the Defense Mapping Agency, then the National Imagery and Mapping Agency). WGS 84 is used by DoD for all its mapping, charting, surveying, and navigation needs, including its GPS "broadcast" and "precise" orbits. WGS 84 was defined in January 1987 using Doppler satellite surveying techniques. It was used as the reference frame for broadcast GPS Ephemerides (orbits) beginning January 23, 1987. At 0000 GMT January 2, 1994, WGS 84 was upgraded in accuracy using GPS measurements. The formal name then became WGS 84 (G730), since the upgrade date coincided with the start of GPS Week 730. It became the reference frame for broadcast orbits on June 28, 1994. At 0000 GMT September 30, 1996 (the start of GPS Week 873), WGS 84 was redefined again and was more closely aligned with International Earth Rotation Service (IERS) frame ITRF 94. It was then formally called WGS 84 (G873). WGS 84 (G873) was adopted as the reference frame for broadcast orbits on January 29, 1997.[7] Another update brought it to WGS 84 (G1674).
The WGS 84 datum, within two meters of the NAD83 datum used in North America, is the only world referencing system in place today. WGS 84 is the default standard datum for coordinates stored in recreational and commercial GPS units.
Users of GPS are cautioned that they must always check the datum of the maps they are using. To correctly enter, display, and to store map related map coordinates, the datum of the map must be entered into the GPS map datum field.
Examples
Examples of map datums are:
- WGS 84, 72, 66 and 60 of the World Geodetic System
- NAD83, the North American Datum which is very similar to WGS 84
- NAD27, the older North American Datum, of which NAD83 was basically a readjustment [1]
- OSGB36 of the Ordnance Survey of Great Britain
- ETRS89, the European Datum, related to ITRS
- ED50, the older European Datum
- GDA94, the Australian Datum[8]
- JGD2011, the Japanese Datum, adjusted for changes caused by 2011 Tōhoku earthquake and tsunami[9]
- Tokyo97, the older Japanese Datum[10]
- KGD2002, the Korean Datum[11]
- TWD67 and TWD97, different datum currently used in Taiwan.[12]
- BJS54 and XAS80, old geodetic datum used in China[13]
- GCJ-02 and BD-09, Chinese encrypted geodetic datum.
- PZ-90.11, the current geodetic reference used by GLONASS[14]
- GTRF, the geodetic reference used by Galileo; currently defined as ITRF2005[15]
- CGCS2000, or CGS-2000, the geodetic reference used by BeiDou Navigation Satellite System; based on ITRF97[15][16][17]
- International Terrestrial Reference Frames (ITRF88, 89, 90, 91, 92, 93, 94, 96, 97, 2000, 2005, 2008, 2014), different realizations of the ITRS.[18][19]
- Hong Kong Principal Datum, a vertical datum used in Hong Kong.[20][21]
- SAD69 - South American Datum 1969
Plate movement
The Earth's tectonic plates move relative to one another in different directions at speeds on the order of 50 to 100 mm (2.0 to 3.9 in) per year.[22] Therefore, locations on different plates are in motion relative to one another. For example, the longitudinal difference between a point on the equator in Uganda, on the African Plate, and a point on the equator in Ecuador, on the South American Plate, increases by about 0.0014 arcseconds per year.[citation needed] These tectonic movements likewise affect latitude.
If a global reference frame (such as WGS84) is used, the coordinates of a place on the surface generally will change from year to year. Most mapping, such as within a single country, does not span plates. To minimize coordinate changes for that case, a different reference frame can be used, one whose coordinates are fixed to that particular plate. Examples of these reference frames are "NAD83" for North America and "ETRS89" for Europe.
See also
- Axes conventions
- ECEF
- ECI (coordinates)
- Engineering datum
- Figure of the Earth
- Geographic coordinate conversion
- Grid reference
- International Terrestrial Reference System
- Kilometre zero
- Local tangent plane coordinates
- Ordnance Datum
- Milestone
- Planetary coordinate system
- Reference frame
- World Geodetic System
Footnotes
- About the right/left-handed order of the coordinates, i.e., or , see Spherical coordinate system#Conventions.
References
{{cite web}}: |first= missing |last= (help)
- Read HH, Watson Janet (1975). Introduction to Geology. New York: Halsted. pp. 13–15.
Further reading
- List of geodetic parameters for many systems from University of Colorado
- Gaposchkin, E. M. and Kołaczek, Barbara (1981) Reference Coordinate Systems for Earth Dynamics Taylor & Francis ISBN 9789027712608
- Kaplan, Understanding GPS: principles and applications, 1 ed. Norwood, MA 02062, USA: Artech House, Inc, 1996.
- GPS Notes
- P. Misra and P. Enge, Global Positioning System Signals, Measurements, and Performance. Lincoln, Massachusetts: Ganga-Jamuna Press, 2001.
- Peter H. Dana: Geodetic Datum Overview – Large amount of technical information and discussion.
- US National Geodetic Survey
External links
- GeographicLib includes a utility CartConvert which converts between geodetic and geocentric (ECEF) or local Cartesian (ENU) coordinates. This provides accurate results for all inputs including points close to the center of Earth.
- A collection of geodetic functions that solve a variety of problems in geodesy in Matlab.
- NGS FAQ – What is a geodetic datum?
- About the surface of the Earth on kartoweb.itc.nl
https://en.wikipedia.org/wiki/Geodetic_datum
Direction
Gravity acceleration is a vector quantity, with direction in addition to magnitude. In a spherically symmetric Earth, gravity would point directly towards the sphere's centre. As the Earth's figure is slightly flatter, there are consequently significant deviations in the direction of gravity: essentially the difference between geodetic latitude and geocentric latitude. Smaller deviations, called vertical deflection, are caused by local mass anomalies, such as mountains.
https://en.wikipedia.org/wiki/Gravity_of_Earth#Direction
Estimating g from the law of universal gravitation
From the law of universal gravitation, the force on a body acted upon by Earth's gravitational force is given by
where r is the distance between the centre of the Earth and the body (see below), and here we take to be the mass of the Earth and m to be the mass of the body.
Additionally, Newton's second law, F = ma, where m is mass and a is acceleration, here tells us that
Comparing the two formulas it is seen that:
So, to find the acceleration due to gravity at sea level, substitute the values of the gravitational constant, G, the Earth's mass (in kilograms), m1, and the Earth's radius (in metres), r, to obtain the value of g:[21]
This formula only works because of the mathematical fact that the gravity of a uniform spherical body, as measured on or above its surface, is the same as if all its mass were concentrated at a point at its centre. This is what allows us to use the Earth's radius for r.
The value obtained agrees approximately with the measured value of g. The difference may be attributed to several factors, mentioned above under "Variations":
- The Earth is not homogeneous
- The Earth is not a perfect sphere, and an average value must be used for its radius
- This calculated value of g only includes true gravity. It does not include the reduction of constraint force that we perceive as a reduction of gravity due to the rotation of Earth, and some of gravity being counteracted by centrifugal force.
There are significant uncertainties in the values of r and m1 as used in this calculation, and the value of G is also rather difficult to measure precisely.
If G, g and r are known then a reverse calculation will give an estimate of the mass of the Earth. This method was used by Henry Cavendish.
https://en.wikipedia.org/wiki/Gravity_of_Earth#Direction
See also
- Escape velocity – Concept in celestial mechanics
- Atmospheric escape – Loss of planetary atmospheric gases to outer space
- Figure of the Earth – Size and shape used to model the Earth for geodesy
- Geopotential – Energy related to Earth's gravity
- Geopotential model – Theoretical description of Earth's gravimetric shape
- Bouguer anomaly – Type of gravity anomaly
- Gravitation of the Moon
- Gravitational acceleration – Change in speed due only to gravity
- Gravity – Attraction of masses and energy
- Gravity anomaly – Difference between ideal and observed gravitational acceleration at a location
- Gravity of Mars – Gravitational force exerted by the planet Mars
- Newton's law of universal gravitation – Classical mechanics physical law
- Vertical deflection – Measure of the downward gravitational force's shift due to nearby mass
https://en.wikipedia.org/wiki/Gravity_of_Earth#Direction
In geodesy and geophysics, the Bouguer anomaly (named after Pierre Bouguer) is a gravity anomaly, corrected for the height at which it is measured and the attraction of terrain.[1] The height correction alone gives a free-air gravity anomaly.
https://en.wikipedia.org/wiki/Bouguer_anomaly
Free-air gravity anomaly
In geophysics, the free-air gravity anomaly, often simply called the free-air anomaly, is the measured gravity anomaly after a free-air correction is applied to account for the elevation at which a measurement is made. It does so by adjusting these measurements of gravity to what would have been measured at a reference level, which is commonly taken as mean sea level or the geoid.[1][2]
Applications
Studies of the subsurface structure and composition of the earth's crust and mantle employ surveys using gravimeters to measure the departure of observed gravity from a theoretical gravity value to identify anomalies due to geologic features below the measurement locations. The computation of anomalies from observed measurements involves the application of corrections that define the resulting anomaly. The free-air anomaly can be used to test for isostatic equilibrium over broad regions.
Survey methods
The free-air correction adjusts measurements of gravity to what would have been measured at mean sea level, that is, on the geoid. The gravitational attraction of earth below the measurement point and above mean sea level is ignored and it is imagined that the observed gravity is measured in air, hence the name. The theoretical gravity value at a location is computed by representing the earth as an ellipsoid that approximates the more complex shape of the geoid. Gravity is computed on the ellipsoid surface using the International Gravity Formula.
For studies of subsurface structure, the free-air anomaly is further adjusted by a correction for the mass below the measurement point and above the reference of mean sea level or a local datum elevation.[3] This defines the Bouguer anomaly.
Calculation
The free-air gravity anomaly is given by the equation:[1]
Here, is observed gravity, is the free-air correction, and is theoretical gravity.
It can be helpful to think of the free-air anomaly as comparing observed gravity to theoretical gravity adjusted up to the measurement point instead of observed gravity adjusted down to the geoid. This avoids any confusion of assuming that the measurement is made in free air.[4] Either way, however, the earth mass between the observation point and the geoid is neglected. The equation for this approach is simply rearranging terms in the first equation of this section so that reference gravity is adjusted and not the observed gravity:
Correction
Gravitational acceleration decreases as an inverse square law with the distance at which the measurement is made from the mass. The free air correction is calculated from Newton's Law, as a rate of change of gravity with distance:[5]
The free-air correction is the amount that must be added to a measurement at height to correct it to the reference level:
Here we have assumed that measurements are made relatively close to the surface so that R does not vary significantly. The value of the free-air correction is positive when measured above the geoid, and negative when measured below. There is the assumption that no mass exists between the observation point and the reference level. The Bouguer and terrain corrections are used to account for this.
Significance
Over the ocean where gravity is measured from ships near sea level, there is no or little free-air correction. In marine gravity surveys, it was observed that the free-air anomaly is positive but very small over the Mid-Ocean Ridges in spite of the fact that these features rise several kilometers above the surrounding seafloor.[6] The small anomaly is explained by the lower density crust and mantle below the ridges resulting from seafloor spreading. This lower density is an apparent offset to the extra height of the ridge indicating that Mid-Ocean Ridges are in isostatic equilibrium.
See also
References
- Cochran, James R.; Talwani, Manik (1977-09-01). "Free-air gravity anomalies in the world's oceans and their relationship to residual elevation". Geophysical Journal International. 50 (3): 495–552. Bibcode:1977GeoJ...50..495C. doi:10.1111/j.1365-246X.1977.tb01334.x. ISSN 0956-540X.
https://en.wikipedia.org/wiki/Free-air_gravity_anomaly











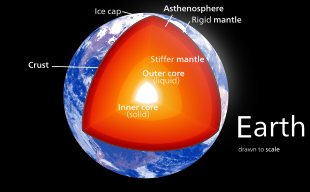




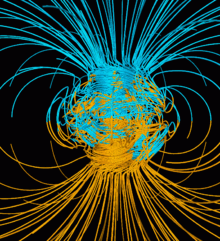















































![{\displaystyle \Phi =\int _{0}^{z}\left[{\frac {Gm}{(a+z)^{2}}}\right]dz}](https://wikimedia.org/api/rest_v1/media/math/render/svg/395d89aabf8c65ec32edfdd9cd8b2a1c1f89b349)
![{\displaystyle \Phi =Gm\left[{\frac {1}{a}}-{\frac {1}{a+z}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3332cef81dc6c8dd82874a30f19a0e5c86f2a080)
















































No comments:
Post a Comment