Sonoluminescence is the emission of light from imploding bubbles in a liquid when excited by sound.
History[edit]
The sonoluminescence effect was first discovered at the University of Cologne in 1934 as a result of work on sonar.[1] Hermann Frenzel and H. Schultes put an ultrasound transducer in a tank of photographic developer fluid. They hoped to speed up the development process. Instead, they noticed tiny dots on the film after developing and realized that the bubbles in the fluid were emitting light with the ultrasound turned on.[2] It was too difficult to analyze the effect in early experiments because of the complex environment of a large number of short-lived bubbles. This phenomenon is now referred to as multi-bubble sonoluminescence (MBSL).
In 1960 Peter Jarman from Imperial College of London proposed the most reliable theory of sonoluminescence phenomenon. He concluded that sonoluminescence is basically thermal in origin and that it might possibly arise from microshocks with the collapsing cavities.[3]
In 1989 an experimental advance was introduced which produced stable single-bubble sonoluminescence (SBSL).[citation needed] In single-bubble sonoluminescence, a single bubble trapped in an acoustic standing wave emits a pulse of light with each compression of the bubble within the standing wave. This technique allowed a more systematic study of the phenomenon, because it isolated the complex effects into one stable, predictable bubble. It was realized that the temperature inside the bubble was hot enough to melt steel, as seen in an experiment done in 2012; the temperature inside the bubble as it collapsed reached about 12,000 kelvins.[4]Interest in sonoluminescence was renewed when an inner temperature of such a bubble well above one million kelvins was postulated.[5] This temperature is thus far not conclusively proven; rather, recent experiments indicate temperatures around 20,000 K (19,700 °C; 35,500 °F).[6]
Properties[edit]
Sonoluminescence can occur when a sound wave of sufficient intensity induces a gaseous cavity within a liquid to collapse quickly. This cavity may take the form of a pre-existing bubble, or may be generated through a process known as cavitation. Sonoluminescence in the laboratory can be made to be stable, so that a single bubble will expand and collapse over and over again in a periodic fashion, emitting a burst of light each time it collapses. For this to occur, a standing acoustic wave is set up within a liquid, and the bubble will sit at a pressure anti-node of the standing wave. The frequencies of resonance depend on the shape and size of the container in which the bubble is contained.
Some facts about sonoluminescence:[citation needed]
- The light that flashes from the bubbles last between 35 and a few hundred picoseconds long, with peak intensities of the order of 1–10 mW.
- The bubbles are very small when they emit the light—about 1 micrometre in diameter—depending on the ambient fluid (e.g., water) and the gas content of the bubble (e.g., atmospheric air).
- Single-bubble sonoluminescence pulses can have very stable periods and positions. In fact, the frequency of light flashes can be more stable than the rated frequency stability of the oscillator making the sound waves driving them. However, the stability analyses of the bubble show that the bubble itself undergoes significant geometric instabilities, due to, for example, the Bjerknes forces and Rayleigh–Taylor instabilities.
- The addition of a small amount of noble gas (such as helium, argon, or xenon) to the gas in the bubble increases the intensity of the emitted light.
Spectral measurements have given bubble temperatures in the range from 2300 K to 5100 K, the exact temperatures depending on experimental conditions including the composition of the liquid and gas.[7] Detection of very high bubble temperatures by spectral methods is limited due to the opacity of liquids to short wavelength light characteristic of very high temperatures.
A study describes a method of determining temperatures based on the formation of plasmas. Using argon bubbles in sulfuric acid, the data shows the presence of ionized molecular oxygen O2+, sulfur monoxide, and atomic argon populating high-energy excited states, which confirms a hypothesis that the bubbles have a hot plasma core.[8] The ionization and excitation energy of dioxygenyl cations, which they observed, is 18 electronvolts. From this they conclude the core temperatures reach at least 20,000 kelvins[6]—hotter than the surface of the sun.
Rayleigh–Plesset equation[edit]
The dynamics of the motion of the bubble is characterized to a first approximation by the Rayleigh–Plesset equation (named after Lord Rayleigh and Milton Plesset):
This is an approximate equation that is derived from the Navier–Stokes equations (written in spherical coordinate system) and describes the motion of the radius of the bubble R as a function of time t. Here, μ is the viscosity, p the pressure, and γ the surface tension. The over-dots represent time derivatives. This equation, though approximate, has been shown to give good estimates on the motion of the bubble under the acoustically driven field except during the final stages of collapse. Both simulation and experimental measurement show that during the critical final stages of collapse, the bubble wall velocity exceeds the speed of sound of the gas inside the bubble.[9] Thus a more detailed analysis of the bubble's motion is needed beyond Rayleigh–Plesset to explore the additional energy focusing that an internally formed shock wave might produce.
Mechanism of phenomenon[edit]
The mechanism of the phenomenon of sonoluminescence is unknown. Hypotheses include: hotspot, bremsstrahlung radiation, collision-induced radiation and corona discharges, nonclassical light, proton tunneling, electrodynamic jets and fractoluminescent jets (now largely discredited due to contrary experimental evidence).[citation needed]
In 2002, M. Brenner, S. Hilgenfeldt, and D. Lohse published a 60-page review that contains a detailed explanation of the mechanism.[10] An important factor is that the bubble contains mainly inert noble gas such as argon or xenon (air contains about 1% argon, and the amount dissolved in water is too great; for sonoluminescence to occur, the concentration must be reduced to 20–40% of its equilibrium value) and varying amounts of water vapor. Chemical reactions cause nitrogen and oxygen to be removed from the bubble after about one hundred expansion-collapse cycles. The bubble will then begin to emit light.[11] The light emission of highly compressed noble gas is exploited technologically in the argon flash devices.
During bubble collapse, the inertia of the surrounding water causes high pressure and high temperature, reaching around 10,000 kelvins in the interior of the bubble, causing the ionization of a small fraction of the noble gas present. The amount ionized is small enough for the bubble to remain transparent, allowing volume emission; surface emission would produce more intense light of longer duration, dependent on wavelength, contradicting experimental results. Electrons from ionized atoms interact mainly with neutral atoms, causing thermal bremsstrahlung radiation. As the wave hits a low energy trough, the pressure drops, allowing electrons to recombine with atoms and light emission to cease due to this lack of free electrons. This makes for a 160-picosecond light pulse for argon (even a small drop in temperature causes a large drop in ionization, due to the large ionization energy relative to photon energy). This description is simplified from the literature above, which details various steps of differing duration from 15 microseconds (expansion) to 100 picoseconds (emission).
Computations based on the theory presented in the review produce radiation parameters (intensity and duration time versus wavelength) that match experimental results[citation needed] with errors no larger than expected due to some simplifications (e.g., assuming a uniform temperature in the entire bubble), so it seems the phenomenon of sonoluminescence is at least roughly explained, although some details of the process remain obscure.
Any discussion of sonoluminescence must include a detailed analysis of metastability. Sonoluminescence in this respect is what is physically termed a bounded phenomenon meaning that the sonoluminescence exists in a bounded region of parameter space for the bubble; a coupled magnetic field being one such parameter. The magnetic aspects of sonoluminescence are very well documented.[12]
Other proposals[edit]
Quantum explanations[edit]
An unusually exotic hypothesis of sonoluminescence, which has received much popular attention, is the Casimir energy hypothesis suggested by noted physicist Julian Schwinger[13] and more thoroughly considered in a paper by Claudia Eberlein[14] of the University of Sussex. Eberlein's paper suggests that the light in sonoluminescence is generated by the vacuum within the bubble in a process similar to Hawking radiation, the radiation generated at the event horizon of black holes. According to this vacuum energy explanation, since quantum theory holds that vacuum contains virtual particles, the rapidly moving interface between water and gas converts virtual photons into real photons. This is related to the Unruh effect or the Casimir effect. The argument has been made that sonoluminescence releases too large an amount of energy and releases the energy on too short a time scale to be consistent with the vacuum energy explanation,[15] although other credible sources argue the vacuum energy explanation might yet prove to be correct.[16]
Nuclear reactions[edit]
Some have argued that the Rayleigh–Plesset equation described above is unreliable for predicting bubble temperatures and that actual temperatures in sonoluminescing systems can be far higher than 20,000 kelvins. Some research claims to have measured temperatures as high as 100,000 kelvins, and speculates temperatures could reach into the millions of kelvins.[17] Temperatures this high could cause thermonuclear fusion. This possibility is sometimes referred to as bubble fusion and is likened to the implosion design used in the fusion component of thermonuclear weapons.
On January 27, 2006, researchers at Rensselaer Polytechnic Institute claimed to have produced fusion in sonoluminescence experiments.[18][19]
Experiments in 2002 and 2005 by R. P. Taleyarkhan using deuterated acetone showed measurements of tritium and neutron output consistent with fusion. However, the papers were considered low quality and there were doubts cast by a report about the author's scientific misconduct. This made the report lose credibility among the scientific community.[20][21][22]
Biological sonoluminescence[edit]
Pistol shrimp (also called snapping shrimp) produce a type of cavitation luminescence from a collapsing bubble caused by quickly snapping its claw. The animal snaps a specialized claw shut to create a cavitation bubble that generates acoustic pressures of up to 80 kPa at a distance of 4 cm from the claw. As it extends out from the claw, the bubble reaches speeds of 60 miles per hour (97 km/h) and releases a sound reaching 218 decibels. The pressure is strong enough to kill small fish. The light produced is of lower intensity than the light produced by typical sonoluminescence and is not visible to the naked eye. The light and heat produced may have no direct significance, as it is the shockwave produced by the rapidly collapsing bubble which these shrimp use to stun or kill prey. However, it is the first known instance of an animal producing light by this effect and was whimsically dubbed "shrimpoluminescence" upon its discovery in 2001.[23] It has subsequently been discovered that another group of crustaceans, the mantis shrimp, contains species whose club-like forelimbs can strike so quickly and with such force as to induce sonoluminescent cavitation bubbles upon impact.[24] A mechanical device with 3D printed snapper claw at five times the actual size was also reported to emit light in a similar fashion,[25] this bioinspired design was based on the snapping shrimp snapper claw molt shed from an Alpheus formosus, the striped snapping shrimp.[26]
See also[edit]
https://en.wikipedia.org/wiki/Sonoluminescence
Cavitation is a phenomenon in which the static pressure of a liquid reduces to below the liquid's vapour pressure, leading to the formation of small vapor-filled cavities in the liquid. When subjected to higher pressure, these cavities, called "bubbles" or "voids", collapse and can generate shock waves that may damage machinery. These shock waves are strong when they are very close to the imploded bubble, but rapidly weaken as they propagate away from the implosion.
Cavitation is a significant cause of wear in some engineering contexts. Collapsing voids that implode near to a metal surface cause cyclic stress through repeated implosion. This results in surface fatigue of the metal causing a type of wear also called "cavitation". The most common examples of this kind of wear are to pump impellers, and bends where a sudden change in the direction of liquid occurs. Cavitation is usually divided into two classes of behavior: inertial (or transient) cavitation and non-inertial cavitation.
The process in which a void or bubble in a liquid rapidly collapses, producing a shock wave, is called inertial cavitation. Inertial cavitation occurs in nature in the strikes of mantis shrimps and pistol shrimps, as well as in the vascular tissues of plants. In man-made objects, it can occur in control valves, pumps, propellers and impellers.
Non-inertial cavitation is the process in which a bubble in a fluid is forced to oscillate in size or shape due to some form of energy input, such as an acoustic field. Such cavitation is often employed in ultrasonic cleaning baths and can also be observed in pumps, propellers, etc.
Since the shock waves formed by collapse of the voids are strong enough to cause significant damage to parts, cavitation is typically an undesirable phenomenon in machinery (although desirable if intentionally used, for example, to sterilize contaminated surgical instruments, break down pollutants in water purification systems, emulsify tissue for cataract surgery or kidney stone lithotripsy, or homogenize fluids). It is very often specifically avoided in the design of machines such as turbines or propellers, and eliminating cavitation is a major field in the study of fluid dynamics. However, it is sometimes useful and does not cause damage when the bubbles collapse away from machinery, such as in supercavitation.
Physics[edit]
Inertial cavitation was first observed in the late 19th century, considering the collapse of a spherical void within a liquid. When a volume of liquid is subjected to a sufficiently low pressure, it may rupture and form a cavity. This phenomenon is coined cavitation inception and may occur behind the blade of a rapidly rotating propeller or on any surface vibrating in the liquid with sufficient amplitude and acceleration. A fast-flowing river can cause cavitation on rock surfaces, particularly when there is a drop-off, such as on a waterfall.
Other ways of generating cavitation voids involve the local deposition of energy, such as an intense focused laser pulse (optic cavitation) or with an electrical discharge through a spark. Vapor gases evaporate into the cavity from the surrounding medium; thus, the cavity is not a vacuum at all, but rather a low-pressure vapor (gas) bubble. Once the conditions which caused the bubble to form are no longer present, such as when the bubble moves downstream, the surrounding liquid begins to implode due its higher pressure, building up inertia as it moves inward. As the bubble finally collapses, the inward inertia of the surrounding liquid causes a sharp increase of pressure and temperature of the vapor within. The bubble eventually collapses to a minute fraction of its original size, at which point the gas within dissipates into the surrounding liquid via a rather violent mechanism which releases a significant amount of energy in the form of an acoustic shock wave and as visible light. At the point of total collapse, the temperature of the vapor within the bubble may be several thousand kelvin, and the pressure several hundred atmospheres.[1]
Inertial cavitation can also occur in the presence of an acoustic field. Microscopic gas bubbles that are generally present in a liquid will be forced to oscillate due to an applied acoustic field. If the acoustic intensity is sufficiently high, the bubbles will first grow in size and then rapidly collapse. Hence, inertial cavitation can occur even if the rarefaction in the liquid is insufficient for a Rayleigh-like void to occur. High-power ultrasonics usually utilize the inertial cavitation of microscopic vacuum bubbles for treatment of surfaces, liquids, and slurries.
The physical process of cavitation inception is similar to boiling. The major difference between the two is the thermodynamic paths that precede the formation of the vapor. Boiling occurs when the local temperature of the liquid reaches the saturation temperature, and further heat is supplied to allow the liquid to sufficiently phase change into a gas. Cavitation inception occurs when the local pressure falls sufficiently far below the saturated vapor pressure, a value given by the tensile strength of the liquid at a certain temperature.[2]
In order for cavitation inception to occur, the cavitation "bubbles" generally need a surface on which they can nucleate. This surface can be provided by the sides of a container, by impurities in the liquid, or by small undissolved microbubbles within the liquid. It is generally accepted that hydrophobic surfaces stabilize small bubbles. These pre-existing bubbles start to grow unbounded when they are exposed to a pressure below the threshold pressure, termed Blake's threshold.
The vapor pressure here differs from the meteorological definition of vapor pressure, which describes the partial pressure of water in the atmosphere at some value less than 100% saturation. Vapor pressure as relating to cavitation refers to the vapor pressure in equilibrium conditions and can therefore be more accurately defined as the equilibrium (or saturated) vapor pressure.
Non-inertial cavitation is the process in which small bubbles in a liquid are forced to oscillate in the presence of an acoustic field, when the intensity of the acoustic field is insufficient to cause total bubble collapse. This form of cavitation causes significantly less erosion than inertial cavitation, and is often used for the cleaning of delicate materials, such as silicon wafers.
Hydrodynamic cavitation[edit]
Hydrodynamic cavitation is the process of vaporisation, bubble generation and bubble implosion which occurs in a flowing liquid as a result of a decrease and subsequent increase in local pressure. Cavitation will only occur if the local pressure declines to some point below the saturated vapor pressure of the liquid and subsequent recovery above the vapor pressure. If the recovery pressure is not above the vapor pressure then flashing is said to have occurred. In pipe systems, cavitation typically occurs either as the result of an increase in the kinetic energy (through an area constriction) or an increase in the pipe elevation.
Hydrodynamic cavitation can be produced by passing a liquid through a constricted channel at a specific flow velocity or by mechanical rotation of an object through a liquid. In the case of the constricted channel and based on the specific (or unique) geometry of the system, the combination of pressure and kinetic energy can create the hydrodynamic cavitation cavern downstream of the local constriction generating high energy cavitation bubbles.
Based on the thermodynamic phase change diagram, an increase in temperature could initiate a known phase change mechanism known as boiling. However, a decrease in static pressure could also help one pass the multi-phase diagram and initiate another phase change mechanism known as cavitation. On the other hand, a local increase in flow velocity could lead to a static pressure drop to the critical point at which cavitation could be initiated (based on Bernoulli's principle). The critical pressure point is vapor saturated pressure. In a closed fluidic system where no flow leakage is detected, a decrease in cross-sectional area would lead to velocity increment and hence static pressure drop. This is the working principle of many hydrodynamic cavitation based reactors for different applications such as water treatment, energy harvesting, heat transfer enhancement, food processing, etc.[3]
There are different flow patterns detected as a cavitation flow progresses: inception, developed flow, supercavitation, and choked flow. Inception is the first moment that the second phase (gas phase) appears in the system. This is the weakest cavitating flow captured in a system corresponding to the highest cavitation number. When the cavities grow and becomes larger in size in the orifice or venturi structures, developed flow is recorded. The most intense cavitating flow is known as supercavitation where theoretically all the nozzle area of an orifice is filled with gas bubbles. This flow regime corresponds to the lowest cavitation number in a system. After supercavitation, the system is not capable of passing more flow. Hence, velocity does not change while the upstream pressure increase. This would lead to an increase in cavitation number which shows that choked flow occurrence.[4]
The process of bubble generation, and the subsequent growth and collapse of the cavitation bubbles, results in very high energy densities and in very high local temperatures and local pressures at the surface of the bubbles for a very short time. The overall liquid medium environment, therefore, remains at ambient conditions. When uncontrolled, cavitation is damaging; by controlling the flow of the cavitation, however, the power can be harnessed and non-destructive. Controlled cavitation can be used to enhance chemical reactions or propagate certain unexpected reactions because free radicals are generated in the process due to disassociation of vapors trapped in the cavitating bubbles.[5]
Orifices and venturi are reported to be widely used for generating cavitation. A venturi has an inherent advantage over an orifice because of its smooth converging and diverging sections, such that it can generate a higher flow velocity at the throat for a given pressure drop across it. On the other hand, an orifice has an advantage that it can accommodate a greater number of holes (larger perimeter of holes) in a given cross sectional area of the pipe.[6]
The cavitation phenomenon can be controlled to enhance the performance of high-speed marine vessels and projectiles, as well as in material processing technologies, in medicine, etc. Controlling the cavitating flows in liquids can be achieved only by advancing the mathematical foundation of the cavitation processes. These processes are manifested in different ways, the most common ones and promising for control being bubble cavitation and supercavitation. The first exact classical solution should perhaps be credited to the well-known solution by Hermann von Helmholtz in 1868.[7] The earliest distinguished studies of academic type on the theory of a cavitating flow with free boundaries and supercavitation were published in the book Jets, wakes and cavities[8] followed by Theory of jets of ideal fluid.[9] Widely used in these books was the well-developed theory of conformal mappings of functions of a complex variable, allowing one to derive a large number of exact solutions of plane problems. Another venue combining the existing exact solutions with approximated and heuristic models was explored in the work Hydrodynamics of Flows with Free Boundaries[10] that refined the applied calculation techniques based on the principle of cavity expansion independence, theory of pulsations and stability of elongated axisymmetric cavities, etc.[11] and in Dimensionality and similarity methods in the problems of the hydromechanics of vessels.[12]
A natural continuation of these studies was recently presented in The Hydrodynamics of Cavitating Flows[13] – an encyclopedic work encompassing all the best advances in this domain for the last three decades, and blending the classical methods of mathematical research with the modern capabilities of computer technologies. These include elaboration of nonlinear numerical methods of solving 3D cavitation problems, refinement of the known plane linear theories, development of asymptotic theories of axisymmetric and nearly axisymmetric flows, etc. As compared to the classical approaches, the new trend is characterized by expansion of the theory into the 3D flows. It also reflects a certain correlation with current works of an applied character on the hydrodynamics of supercavitating bodies.
Hydrodynamic cavitation can also improve some industrial processes. For instance, cavitated corn slurry shows higher yields in ethanol production compared to uncavitated corn slurry in dry milling facilities.[14]
This is also used in the mineralization of bio-refractory compounds which otherwise would need extremely high temperature and pressure conditions since free radicals are generated in the process due to the dissociation of vapors trapped in the cavitating bubbles, which results in either the intensification of the chemical reaction or may even result in the propagation of certain reactions not possible under otherwise ambient conditions.[15]
Applications[edit]
Chemical engineering[edit]
In industry, cavitation is often used to homogenize, or mix and break down, suspended particles in a colloidal liquid compound such as paint mixtures or milk. Many industrial mixing machines are based upon this design principle. It is usually achieved through impeller design or by forcing the mixture through an annular opening that has a narrow entrance orifice with a much larger exit orifice. In the latter case, the drastic decrease in pressure as the liquid accelerates into a larger volume induces cavitation. This method can be controlled with hydraulic devices that control inlet orifice size, allowing for dynamic adjustment during the process, or modification for different substances. The surface of this type of mixing valve, against which surface the cavitation bubbles are driven causing their implosion, undergoes tremendous mechanical and thermal localized stress; they are therefore often constructed of super-hard or tough materials such as stainless steel, Stellite, or even polycrystalline diamond (PCD).
Cavitating water purification devices have also been designed, in which the extreme conditions of cavitation can break down pollutants and organic molecules. Spectral analysis of light emitted in sonochemical reactions reveal chemical and plasma-based mechanisms of energy transfer. The light emitted from cavitation bubbles is termed sonoluminescence.
Use of this technology has been tried successfully in alkali refining of vegetable oils.[16]
Hydrophobic chemicals are attracted underwater by cavitation as the pressure difference between the bubbles and the liquid water forces them to join together. This effect may assist in protein folding.[17]
Biomedical[edit]
Cavitation plays an important role for the destruction of kidney stones in shock wave lithotripsy.[18] Currently, tests are being conducted as to whether cavitation can be used to transfer large molecules into biological cells (sonoporation). Nitrogen cavitation is a method used in research to lyse cell membranes while leaving organelles intact.
Cavitation plays a key role in non-thermal, non-invasive fractionation of tissue for treatment of a variety of diseases[19] and can be used to open the blood-brain barrierto increase uptake of neurological drugs in the brain.[20]
Cavitation also plays a role in HIFU, a thermal non-invasive treatment methodology for cancer.[21]
In wounds caused by high velocity impacts (like for example bullet wounds) there are also effects due to cavitation. The exact wounding mechanisms are not completely understood yet as there is temporary cavitation, and permanent cavitation together with crushing, tearing and stretching. Also the high variance in density within the body makes it hard to determine its effects.[22]
Ultrasound sometimes is used to increase bone formation, for instance in post-surgical applications.[23]
It has been suggested that the sound of "cracking" knuckles derives from the collapse of cavitation in the synovial fluid within the joint.[24]
Cleaning[edit]
In industrial cleaning applications, cavitation has sufficient power to overcome the particle-to-substrate adhesion forces, loosening contaminants. The threshold pressure required to initiate cavitation is a strong function of the pulse width and the power input. This method works by generating acoustic cavitation in the cleaning fluid, picking up and carrying contaminant particles away in the hope that they do not reattach to the material being cleaned (which is a possibility when the object is immersed, for example in an ultrasonic cleaning bath). The same physical forces that remove contaminants also have the potential to damage the target being cleaned.
Food and beverage[edit]
Eggs[edit]
Cavitation has been applied to egg pasteurization. A hole-filled rotor produces cavitation bubbles, heating the liquid from within. Equipment surfaces stay cooler than the passing liquid, so eggs don't harden as they did on the hot surfaces of older equipment. The intensity of cavitation can be adjusted, making it possible to tune the process for minimum protein damage.[25]
Cavitation damage[edit]
Cavitation is, in many cases, an undesirable occurrence. In devices such as propellers and pumps, cavitation causes a great deal of noise, damage to components, vibrations, and a loss of efficiency. Cavitation has also become a concern in the renewable energy sector as it may occur on the blade surface of tidal stream turbines.[26]
When the cavitation bubbles collapse, they force energetic liquid into very small volumes, thereby creating spots of high temperature and emitting shock waves, the latter of which are a source of noise. The noise created by cavitation is a particular problem for military submarines, as it increases the chances of being detected by passive sonar.
Although the collapse of a small cavity is a relatively low-energy event, highly localized collapses can erode metals, such as steel, over time.[27] The pitting caused by the collapse of cavities produces great wear on components and can dramatically shorten a propeller's or pump's lifetime.
After a surface is initially affected by cavitation, it tends to erode at an accelerating pace. The cavitation pits increase the turbulence of the fluid flow and create crevices that act as nucleation sites for additional cavitation bubbles. The pits also increase the components' surface area and leave behind residual stresses. This makes the surface more prone to stress corrosion.[28]
Pumps and propellers[edit]
Major places where cavitation occurs are in pumps, on propellers, or at restrictions in a flowing liquid.
As an impeller's (in a pump) or propeller's (as in the case of a ship or submarine) blades move through a fluid, low-pressure areas are formed as the fluid accelerates around and moves past the blades. The faster the blade moves, the lower the pressure can become around it. As it reaches vapor pressure, the fluid vaporizes and forms small bubbles of gas. This is cavitation. When the bubbles collapse later, they typically cause very strong local shock waves in the fluid, which may be audible and may even damage the blades.
Cavitation in pumps may occur in two different forms:
Suction cavitation[edit]
Suction cavitation occurs when the pump suction is under a low-pressure/high-vacuum condition where the liquid turns into a vapor at the eye of the pump impeller. This vapor is carried over to the discharge side of the pump, where it no longer sees vacuum and is compressed back into a liquid by the discharge pressure. This imploding action occurs violently and attacks the face of the impeller. An impeller that has been operating under a suction cavitation condition can have large chunks of material removed from its face or very small bits of material removed, causing the impeller to look spongelike. Both cases will cause premature failure of the pump, often due to bearing failure. Suction cavitation is often identified by a sound like gravel or marbles in the pump casing.
Common causes of suction cavitation can include clogged filters, pipe blockage on the suction side, poor piping design, pump running too far right on the pump curve, or conditions not meeting NPSH (net positive suction head) requirements.[29]
In automotive applications, a clogged filter in a hydraulic system (power steering, power brakes) can cause suction cavitation making a noise that rises and falls in synch with engine RPM. It is fairly often a high pitched whine, like set of nylon gears not quite meshing correctly.
Discharge cavitation[edit]
Discharge cavitation occurs when the pump discharge pressure is extremely high, normally occurring in a pump that is running at less than 10% of its best efficiency point. The high discharge pressure causes the majority of the fluid to circulate inside the pump instead of being allowed to flow out the discharge. As the liquid flows around the impeller, it must pass through the small clearance between the impeller and the pump housing at extremely high flow velocity. This flow velocity causes a vacuum to develop at the housing wall (similar to what occurs in a venturi), which turns the liquid into a vapor. A pump that has been operating under these conditions shows premature wear of the impeller vane tips and the pump housing. In addition, due to the high pressure conditions, premature failure of the pump's mechanical seal and bearings can be expected. Under extreme conditions, this can break the impeller shaft.
Discharge cavitation in joint fluid is thought to cause the popping sound produced by bone joint cracking, for example by deliberately cracking one's knuckles.
Cavitation solutions[edit]
Since all pumps require well-developed inlet flow to meet their potential, a pump may not perform or be as reliable as expected due to a faulty suction piping layout such as a close-coupled elbow on the inlet flange. When poorly developed flow enters the pump impeller, it strikes the vanes and is unable to follow the impeller passage. The liquid then separates from the vanes causing mechanical problems due to cavitation, vibration and performance problems due to turbulence and poor filling of the impeller. This results in premature seal, bearing and impeller failure, high maintenance costs, high power consumption, and less-than-specified head and/or flow.
To have a well-developed flow pattern, pump manufacturer's manuals recommend about (10 diameters?) of straight pipe run upstream of the pump inlet flange. Unfortunately, piping designers and plant personnel must contend with space and equipment layout constraints and usually cannot comply with this recommendation. Instead, it is common to use an elbow close-coupled to the pump suction which creates a poorly developed flow pattern at the pump suction.[30]
With a double-suction pump tied to a close-coupled elbow, flow distribution to the impeller is poor and causes reliability and performance shortfalls. The elbow divides the flow unevenly with more channeled to the outside of the elbow. Consequently, one side of the double-suction impeller receives more flow at a higher flow velocity and pressure while the starved side receives a highly turbulent and potentially damaging flow. This degrades overall pump performance (delivered head, flow and power consumption) and causes axial imbalance which shortens seal, bearing and impeller life.[31] To overcome cavitation: Increase suction pressure if possible. Decrease liquid temperature if possible. Throttle back on the discharge valve to decrease flow-rate. Vent gases off the pump casing.
Control valves[edit]
Cavitation can occur in control valves.[32] If the actual pressure drop across the valve as defined by the upstream and downstream pressures in the system is greater than the sizing calculations allow, pressure drop flashing or cavitation may occur. The change from a liquid state to a vapor state results from the increase in flow velocity at or just downstream of the greatest flow restriction which is normally the valve port. To maintain a steady flow of liquid through a valve the flow velocity must be greatest at the vena contracta or the point where the cross sectional area is the smallest. This increase in flow velocity is accompanied by a substantial decrease in the fluid pressure which is partially recovered downstream as the area increases and flow velocity decreases. This pressure recovery is never completely to the level of the upstream pressure. If the pressure at the vena contracta drops below the vapor pressure of the fluid bubbles will form in the flow stream. If the pressure recovers after the valve to a pressure that is once again above the vapor pressure, then the vapor bubbles will collapse and cavitation will occur.
Spillways[edit]
When water flows over a dam spillway, the irregularities on the spillway surface will cause small areas of flow separation in a high-speed flow, and, in these regions, the pressure will be lowered. If the flow velocities are high enough the pressure may fall to below the local vapor pressure of the water and vapor bubbles will form. When these are carried downstream into a high pressure region the bubbles collapse giving rise to high pressures and possible cavitation damage.
Experimental investigations show that the damage on concrete chute and tunnel spillways can start at clear water flow velocities of between 12 and 15 m/s (27 and 34 mph), and, up to flow velocities of 20 m/s (45 mph), it may be possible to protect the surface by streamlining the boundaries, improving the surface finishes or using resistant materials.[33]
When some air is present in the water the resulting mixture is compressible and this damps the high pressure caused by the bubble collapses.[34] If the flow velocities near the spillway invert are sufficiently high, aerators (or aeration devices) must be introduced to prevent cavitation. Although these have been installed for some years, the mechanisms of air entrainment at the aerators and the slow movement of the air away from the spillway surface are still challenging.[35][36][37][38]
The spillway aeration device design is based upon a small deflection of the spillway bed (or sidewall) such as a ramp and offset to deflect the high flow velocity flow away from the spillway surface. In the cavity formed below the nappe, a local subpressure beneath the nappe is produced by which air is sucked into the flow. The complete design includes the deflection device (ramp, offset) and the air supply system.
Engines[edit]
Some larger diesel engines suffer from cavitation due to high compression and undersized cylinder walls. Vibrations of the cylinder wall induce alternating low and high pressure in the coolant against the cylinder wall. The result is pitting of the cylinder wall, which will eventually let cooling fluid leak into the cylinder and combustion gases to leak into the coolant.
It is possible to prevent this from happening with the use of chemical additives in the cooling fluid that form a protective layer on the cylinder wall. This layer will be exposed to the same cavitation, but rebuilds itself. Additionally a regulated overpressure in the cooling system (regulated and maintained by the coolant filler cap spring pressure) prevents the forming of cavitation.
From about the 1980s, new designs of smaller gasoline engines also displayed cavitation phenomena. One answer to the need for smaller and lighter engines was a smaller coolant volume and a correspondingly higher coolant flow velocity. This gave rise to rapid changes in flow velocity and therefore rapid changes of static pressure in areas of high heat transfer. Where resulting vapor bubbles collapsed against a surface, they had the effect of first disrupting protective oxide layers (of cast aluminium materials) and then repeatedly damaging the newly formed surface, preventing the action of some types of corrosion inhibitor (such as silicate based inhibitors). A final problem was the effect that increased material temperature had on the relative electrochemical reactivity of the base metal and its alloying constituents. The result was deep pits that could form and penetrate the engine head in a matter of hours when the engine was running at high load and high speed. These effects could largely be avoided by the use of organic corrosion inhibitors or (preferably) by designing the engine head in such a way as to avoid certain cavitation inducing conditions.
In nature[edit]
Geology[edit]
Some hypotheses[by whom?][example needed]relating to diamond formation posit a possible role for cavitation—namely cavitation in the kimberlite pipes providing the extreme pressure needed to change pure carbon into the rare allotrope that is diamond.The loudest three sounds ever recorded, during the 1883 eruption of Krakatoa, are now[when?]understood as the bursts of three huge cavitation bubbles, each larger than the last, formed in the volcano's throat. Rising magma, filled with dissolved gasses and under immense pressure, encountered a different magma that compressed easily, allowing bubbles to grow and combine.[39][40]
Vascular plants[edit]
Cavitation occurs in the xylem of vascular plants when the tension of water within the xylem exceeds atmospheric pressure. The sap vaporizes locally so that either the vessel elements or tracheids are filled with water vapor. Plants are able to repair cavitated xylem in a number of ways. For plants less than 50 cm tall, root pressure can be sufficient to redissolve the vapor. Larger plants direct solutes into the xylem via ray cells, or in tracheids, via osmosis through bordered pits. Solutes attract water, the pressure rises and vapor can redissolve. In some trees, the sound of the cavitation is audible, particularly in summer, when the rate of evapotranspiration is highest. Some deciduous trees have to shed leaves in the autumn partly because cavitation increases as temperatures decrease.[41]
Spore dispersal in plants[edit]
Cavitation plays a role in the spore dispersal mechanisms of certain plants. In ferns, for example, the fern sporangium acts as a catapult that launches spores into the air. The charging phase of the catapult is driven by water evaporation from the annulus cells, which triggers a pressure decrease. When the negative pressure reaches approximately 9 MPa, cavitation occurs. This rapid event triggers spore dispersal due to the elastic energy released by the annulus structure. The initial spore acceleration is extremely large – up to 105 times the gravitational acceleration.[42]
Marine life[edit]
Just as cavitation bubbles form on a fast-spinning boat propeller, they may also form on the tails and fins of aquatic animals. This primarily occurs near the surface of the ocean, where the ambient water pressure is low.
Cavitation may limit the maximum swimming speed of powerful swimming animals like dolphins and tuna.[43] Dolphins may have to restrict their speed because collapsing cavitation bubbles on their tail are painful. Tuna have bony fins without nerve endings and do not feel pain from cavitation. They are slowed down when cavitation bubbles create a vapor film around their fins. Lesions have been found on tuna that are consistent with cavitation damage.[44]
Some sea animals have found ways to use cavitation to their advantage when hunting prey. The pistol shrimp snaps a specialized claw to create cavitation, which can kill small fish. The mantis shrimp (of the smasher variety) uses cavitation as well in order to stun, smash open, or kill the shellfish that it feasts upon.[45]
Thresher sharks use 'tail slaps' to debilitate their small fish prey and cavitation bubbles have been seen rising from the apex of the tail arc.[46][47]
Coastal erosion[edit]
In the last half-decade,[when?] coastal erosion in the form of inertial cavitation has been generally accepted.[48] Bubbles in an incoming wave are forced into cracks in the cliff being eroded. Varying pressure decompresses some vapor pockets which subsequently implode. The resulting pressure peaks can blast apart fractions of the rock.
History[edit]
As early as 1754, the Swiss mathematician Leonhard Euler (1707–1783) speculated about the possibility of cavitation.[49] In 1859, the English mathematician William Henry Besant (1828–1917) published a solution to the problem of the dynamics of the collapse of a spherical cavity in a fluid, which had been presented by the Anglo-Irish mathematician George Stokes (1819–1903) as one of the Cambridge [University] Senate-house problems and riders for the year 1847.[50][51][52] In 1894, Irish fluid dynamicist Osborne Reynolds (1842–1912) studied the formation and collapse of vapor bubbles in boiling liquids and in constricted tubes.[53]
The term cavitation first appeared in 1895 in a paper by John Isaac Thornycroft (1843–1928) and Sydney Walker Barnaby (1855–1925) — son of Sir Nathaniel Barnaby (1829 – 1915), who had been Chief Constructor of the Royal Navy — to whom it had been suggested by the British engineer Robert Edmund Froude (1846–1924), third son of the English hydrodynamicist William Froude (1810–1879).[54][55] Early experimental studies of cavitation were conducted in 1894-5 by Thornycroft and Barnaby and by the Anglo-Irish engineer Charles Algernon Parsons (1854-1931), who constructed a stroboscopic apparatus to study the phenomenon.[56][57][58]Thornycroft and Barnaby were the first researchers to observe cavitation on the back sides of propeller blades.[59]
In 1917, the British physicist Lord Rayleigh (1842–1919) extended Besant's work, publishing a mathematical model of cavitation in an incompressible fluid (ignoring surface tension and viscosity), in which he also determined the pressure in the fluid.[60] The mathematical models of cavitation which were developed by British engineer Stanley Smith Cook (1875–1952) and by Lord Rayleigh revealed that collapsing bubbles of vapor could generate very high pressures, which were capable of causing the damage that had been observed on ships' propellers.[61][62] Experimental evidence of cavitation causing such high pressures was initially collected in 1952 by Mark Harrison (a fluid dynamicist and acoustician at the U.S. Navy's David Taylor Model Basin at Carderock, Maryland, USA) who used acoustic methods and in 1956 by Wernfried Güth (a physicist and acoustician of Göttigen University, Germany) who used optical Schlieren photography.[63][64][65]
In 1944, Soviet scientists Mark Iosifovich Kornfeld (1908–1993) and L. Suvorov of the Leningrad Physico-Technical Institute (now: the Ioffe Physical-Technical Institute of the Russian Academy of Sciences, St. Petersburg, Russia) proposed that during cavitation, bubbles in the vicinity of a solid surface do not collapse symmetrically; instead, a dimple forms on the bubble at a point opposite the solid surface and this dimple evolves into a jet of liquid. This jet of liquid damages the solid surface.[66] This hypothesis was supported in 1951 by theoretical studies by Maurice Rattray, Jr., a doctoral student at the California Institute of Technology.[67] Kornfeld and Suvorov's hypothesis was confirmed experimentally in 1961 by Charles F. Naudé and Albert T. Ellis, fluid dynamicists at the California Institute of Technology.[68]
A series of experimental investigations of the propagation of strong shock wave (SW) in a liquid with gas bubbles, which made it possible to establish the basic laws governing the process, the mechanism for the transformation of the energy of the SW, attenuation of the SW, and the formation of the structure, and experiments on the analysis of the attenuation of waves in bubble screens with different acoustic properties were begun by pioneer works of Soviet scientist prof.V.F. Minin at the Institute of Hydrodynamics (Novosibirsk, Russia) in 1957–1960, who examined also the first convenient model of a screen - a sequence of alternating flat one-dimensional liquid and gas layers.[69] In an experimental investigations of the dynamics of the form of pulsating gaseous cavities and interaction of SW with bubble clouds in 1957–1960 V.F. Minin discovered that under the action of SW a bubble collapses asymmetrically with the formation of a cumulative jet, which forms in the process of collapse and causes fragmentation of the bubble.[69]
See also[edit]
- Cavitation number
- Cavitation modelling
- Erosion corrosion of copper water tubes
- Rayleigh-Plesset equation
- Sonoluminescence
- Supercavitation
- Supercavitating propeller – Marine propeller designed to operate with a full cavitation bubble
- Water hammer – Pressure surge when a fluid is forced to stop or change direction suddenly
- Water tunnel (hydrodynamic)
- Ultrasonic cavitation device
https://en.wikipedia.org/wiki/Cavitation
Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas) and the forces on them.[1]: 3 It has applications in a wide range of disciplines, including mechanical, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology.
It can be divided into fluid statics, the study of fluids at rest; and fluid dynamics, the study of the effect of forces on fluid motion.[1]: 3 It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a macroscopic viewpoint rather than from microscopic. Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems are partly or wholly unsolved and are best addressed by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics (CFD), is devoted to this approach.[2] Particle image velocimetry, an experimental method for visualizing and analyzing fluid flow, also takes advantage of the highly visual nature of fluid flow.
https://en.wikipedia.org/wiki/Fluid_mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century.
https://en.wikipedia.org/wiki/Continuum_mechanics
Hydraulic shock (colloquial: water hammer; fluid hammer) is a pressure surge or wave caused when a fluid in motion, usually a liquid but sometimes also a gas, is forced to stop or change direction suddenly; a momentumchange. This phenomenon commonly occurs when a valve closes suddenly at an end of a pipeline system, and a pressure wave propagates in the pipe.
This pressure wave can cause major problems, from noise and vibration to pipe rupture or collapse. It is possible to reduce the effects of the water hammer pulses with accumulators, expansion tanks, surge tanks, blowoff valves, and other features. The effects can be avoided by ensuring that no valves will close too quickly with significant flow, but there are many situations that can cause the effect.
Rough calculations can be made using the Zhukovsky (Joukowsky) equation,[1] or more accurate ones using the method of characteristics.[2]
https://en.wikipedia.org/wiki/Water_hammer
A water tunnel is an experimental facility used for testing the hydrodynamic behavior of submerged bodies in flowing water. It functions similar to a recirculating wind tunnel, but uses water as the working fluid, and related phenomena are investigated, such as measuring the forces on scale models of submarines or lift and drag on hydrofoils. Water tunnels are sometimes used in place of wind tunnels to perform measurements because techniques like particle image velocimetry (PIV) are easier to implement in water. For many cases as long as the Reynolds number is equivalent, the results are valid, whether a submerged water vehicle model is tested in air or an aerial vehicle is tested in water. For low Reynolds number flows, tunnels can be made to run oil instead of water. The advantage is that the increased viscosity will allow the flow to be a faster speed (and thus easier to maintain in a stable manner) for a lower Reynolds number.
Whereas in wind tunnels the driving force is usually sophisticated multiblade propellers with adjustable blade pitch, in water and oil tunnels the fluid is circulated with pumps, effectively using a net pressure head difference to move the fluid rather than imparting momentum on it directly. Thus the return section of water and oil tunnels does not need any flow management; typically it is just a pipe sized for the pump and desired flow speeds. The upstream section of a water tunnels generally consists of a pipe (outlet from the pump) with several holes along its side and with the end open followed by a series of coarse and fine screens to even the flow before the contraction into the test section. Wind tunnels may also have screens before the contraction, but in water tunnels they may be as fine as the screen used in window openings and screen doors.
Additionally, many water tunnels are sealed and can reduce or increase the internal static pressure, to perform cavitation studies. These are referred to as cavitation tunnels.
https://en.wikipedia.org/wiki/Water_tunnel_(hydrodynamic)
The supercavitating propeller is a variant of a propeller for propulsion in water, where supercavitation is actively employed to gain increased speed by reducing friction. They are being used for military purposes and for high performance racing boats as well as model racing boats.
This article distinguishes a supercavitating propeller from a subcavitating propeller running under supercavitating conditions. In general, subcavitating propellers become less efficient when they are running under supercavitating conditions.
The supercavitating propeller operates submerged with the entire diameter of the blade below the water line. Its blades are wedge-shaped to force cavitation at the leading edge and to avoid water skin friction along the whole forward face. As the cavity collapses well behind the blade, the supercavitating propeller avoids the spalling damage due to cavitation that is a problem with conventional propellers.
An alternative to the supercavitating propeller is the surface piercing, or ventilated propeller. These propellers are designed to intentionally leave the water and entrainatmospheric air to fill the void, which means that the resulting gas layer on the forward face of the propeller blade consists of air instead of water vapour. Less energy is thus used, and the surface-piercing propeller generally enjoys lower drag than the supercavitating principle. The surface-piercing propeller also has wedge-shaped blades, and propellers may be designed that can operate in both supercavitating and surface-piercing mode.
Supercavitating propellers were developed to usefulness for very fast military vessels by Vosper & Company.
The pioneer of this technology and other high speed offshore boating technologies was Albert Hickman (1877–1957), early in the 20th century. His Sea Sled designs used a surface piercing propeller.
See also[edit]
Early developments[edit]
The principle employed in using a screw propeller is derived from sculling. In sculling, a single blade is moved through an arc, from side to side taking care to keep presenting the blade to the water at the effective angle. The innovation introduced with the screw propeller was the extension of that arc through more than 360° by attaching the blade to a rotating shaft. Propellers can have a single blade, but in practice there are nearly always more than one so as to balance the forces involved.
The origin of the screw propeller starts at least as early as Archimedes (c. 287 – c. 212 BC), who used a screw to lift water for irrigation and bailing boats, so famously that it became known as Archimedes' screw. It was probably an application of spiral movement in space (spirals were a special study of Archimedes) to a hollow segmented water-wheel used for irrigation by Egyptians for centuries. A flying toy, the bamboo-copter, was enjoyed in China beginning around 320 AD. Later, Leonardo da Vinci adopted the screw principle to drive his theoretical helicopter, sketches of which involved a large canvas screw overhead.
In 1661, Toogood and Hays proposed using screws for waterjet propulsion, though not as a propeller.[4] Robert Hooke in 1681 designed a horizontal watermill which was remarkably similar to the Kirsten-Boeing vertical axis propeller designed almost two and a half centuries later in 1928; two years later Hooke modified the design to provide motive power for ships through water.[5] In 1693 a Frenchman by the name of Du Quet invented a screw propeller which was tried in 1693 but later abandoned.[6][7] In 1752, the Academie des Sciences in Paris granted Burnelli a prize for a design of a propeller-wheel. At about the same time, the French mathematician Alexis-Jean-Pierre Paucton, suggested a water propulsion system based on the Archimedean screw.[5] In 1771, steam-engine inventor James Watt in a private letter suggested using "spiral oars" to propel boats, although he did not use them with his steam engines, or ever implement the idea.[8]
Physical principle[edit]
Cavitation is the formation of vapour bubbles in liquid caused by flow around an object. Bubbles form when water accelerates around sharp corners and the pressure drops below the vapour pressure. Pressure increases upon deceleration, and the water generally reabsorbs the vapour; however, vapour bubbles can implode and apply small concentrated impulses that may damage surfaces like ship propellers and pump impellers.
The potential for vapour bubbles to form in a liquid is given by the nondimensional cavitation number. It equals local pressure minus vapour pressure, divided by dynamic pressure. At increasing depths (or pressures in piping), the potential for cavitation is lower because the difference between local pressure and vapour pressure is greater.
A supercavitating object is a high-speed submerged object that is designed to initiate a cavitation bubble at its nose. The bubble extends (either naturally or augmented with internally generated gas) past the aft end of the object and prevents contact between the sides of the object and the liquid. This separation substantially reduces the skin friction drag on the supercavitating object.
A key feature of the supercavitating object is the nose, which typically has a sharp edge around its perimeter to form the cavitation bubble.[1] The nose may be articulated and shaped as a flat disk or cone. The shape of the supercavitating object is generally slender so the cavitation bubble encompasses the object. If the bubble is not long enough to encompass the object, especially at slower speeds, the bubble can be enlarged and extended by injecting high-pressure gas near the object's nose.[1]
The very high speed required for supercavitation can be temporarily reached by underwater-fired projectiles and projectiles entering water. For sustained supercaviation, rocket propulsion is used, and the high-pressure rocket gas can be routed to the nose to enhance the cavitation bubble. In principle, supercavitating objects can be maneuvered using various methods, including the following:
- Drag fins that project through the bubble into the surrounding liquid[2] (p. 22)
- A tilted object nose
- Gas injected asymmetrically near the nose to distort the cavity's geometry
- Vectoring rocket thrust through gimbaling for a single nozzle
- Differential thrust from multiple nozzles[1]
Flow and effect on skin friction drag[edit]
Laminar flow over a body occurs when layers of the fluid move smoothly past each other in parallel lines. In nature, this kind of flow is rare. As the fluid flows over an object, it applies frictional forces to the surface of the object which works to impede forward movement of the object; the result is called skin friction drag. Skin friction drag is often the major component of parasitic drag on objects in a flow.
The flow over a body may begin as laminar. As a fluid flows over a surface shear stresses within the fluid slow additional fluid particles causing the boundary layer to grow in thickness. At some point along the flow direction, the flow becomes unstable and becomes turbulent. Turbulent flow has a fluctuating and irregular pattern of flow which is made obvious by the formation of vortices. While the turbulent layer grows, the laminar layer thickness decreases. This results in a thinner laminar boundary layer which, relative to laminar flow, depreciates the magnitude of friction force as fluid flows over the object.
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other.[2] There are several types of friction:
- Dry friction is a force that opposes the relative lateral motion of two solid surfaces in contact. Dry friction is subdivided into static friction ("stiction") between non-moving surfaces, and kinetic friction between moving surfaces. With the exception of atomic or molecular friction, dry friction generally arises from the interaction of surface features, known as asperities (see Figure 1).
- Fluid friction describes the friction between layers of a viscous fluid that are moving relative to each other.[3][4]
- Lubricated friction is a case of fluid friction where a lubricant fluid separates two solid surfaces.[5][6][7]
- Skin friction is a component of drag, the force resisting the motion of a fluid across the surface of a body.
- Internal friction is the force resisting motion between the elements making up a solid material while it undergoes deformation.[4]
When surfaces in contact move relative to each other, the friction between the two surfaces converts kinetic energy into thermal energy (that is, it converts work to heat). This property can have dramatic consequences, as illustrated by the use of friction created by rubbing pieces of wood together to start a fire. Kinetic energy is converted to thermal energy whenever motion with friction occurs, for example when a viscous fluid is stirred. Another important consequence of many types of friction can be wear, which may lead to performance degradation or damage to components. Friction is a component of the science of tribology.
Friction is desirable and important in supplying traction to facilitate motion on land. Most land vehicles rely on friction for acceleration, deceleration and changing direction. Sudden reductions in traction can cause loss of control and accidents.
Friction is not itself a fundamental force. Dry friction arises from a combination of inter-surface adhesion, surface roughness, surface deformation, and surface contamination. The complexity of these interactions makes the calculation of friction from first principles impractical and necessitates the use of empirical methods for analysis and the development of theory.
Friction is a non-conservative force – work done against friction is path dependent. In the presence of friction, some kinetic energy is always transformed to thermal energy, so mechanical energy is not conserved.
https://en.wikipedia.org/wiki/Friction
History
The Greeks, including Aristotle, Vitruvius, and Pliny the Elder, were interested in the cause and mitigation of friction.[8] They were aware of differences between static and kinetic friction with Themistius stating in 350 A.D. that "it is easier to further the motion of a moving body than to move a body at rest".[8][9][10][11]
The classic laws of sliding friction were discovered by Leonardo da Vinci in 1493, a pioneer in tribology, but the laws documented in his notebooks were not published and remained unknown.[12][13][14][15][16][17] These laws were rediscovered by Guillaume Amontons in 1699[18] and became known as Amonton's three laws of dry friction. Amontons presented the nature of friction in terms of surface irregularities and the force required to raise the weight pressing the surfaces together. This view was further elaborated by Bernard Forest de Bélidor[19] and Leonhard Euler (1750), who derived the angle of repose of a weight on an inclined plane and first distinguished between static and kinetic friction.[20] John Theophilus Desaguliers (1734) first recognized the role of adhesion in friction.[21] Microscopic forces cause surfaces to stick together; he proposed that friction was the force necessary to tear the adhering surfaces apart.
Laws of dry friction
The elementary property of sliding (kinetic) friction were discovered by experiment in the 15th to 18th centuries and were expressed as three empirical laws:
- Amontons' First Law: The force of friction is directly proportional to the applied load.
- Amontons' Second Law: The force of friction is independent of the apparent area of contact.
- Coulomb's Law of Friction: Kinetic friction is independent of the sliding velocity.
Radiation friction
As a consequence of light pressure, Einstein[65] in 1909 predicted the existence of "radiation friction" which would oppose the movement of matter. He wrote, “radiation will exert pressure on both sides of the plate. The forces of pressure exerted on the two sides are equal if the plate is at rest. However, if it is in motion, more radiation will be reflected on the surface that is ahead during the motion (front surface) than on the back surface. The backward-acting force of pressure exerted on the front surface is thus larger than the force of pressure acting on the back. Hence, as the resultant of the two forces, there remains a force that counteracts the motion of the plate and that increases with the velocity of the plate. We will call this resultant 'radiation friction' in brief.”
Coefficient of friction
The coefficient of friction (COF), often symbolized by the Greek letter µ, is a dimensionless scalar value which equals the ratio of the force of friction between two bodies and the force pressing them together, either during or at the onset of slipping. The coefficient of friction depends on the materials used; for example, ice on steel has a low coefficient of friction, while rubber on pavement has a high coefficient of friction. Coefficients of friction range from near zero to greater than one. It is an axiom of the nature of friction between metal surfaces that it is greater between two surfaces of similar metals than between two surfaces of different metals— hence, brass will have a higher coefficient of friction when moved against brass, but less if moved against steel or aluminum.[23]
For surfaces at rest relative to each other , where is the coefficient of static friction. This is usually larger than its kinetic counterpart. The coefficient of static friction exhibited by a pair of contacting surfaces depends upon the combined effects of material deformation characteristics and surface roughness, both of which have their origins in the chemical bonding between atoms in each of the bulk materials and between the material surfaces and any adsorbed material. The fractality of surfaces, a parameter describing the scaling behavior of surface asperities, is known to play an important role in determining the magnitude of the static friction.[1]
For surfaces in relative motion , where is the coefficient of kinetic friction. The Coulomb friction is equal to , and the frictional force on each surface is exerted in the direction opposite to its motion relative to the other surface.
Arthur Morin introduced the term and demonstrated the utility of the coefficient of friction.[12] The coefficient of friction is an empirical measurement – it has to be measured experimentally, and cannot be found through calculations.[24] Rougher surfaces tend to have higher effective values. Both static and kinetic coefficients of friction depend on the pair of surfaces in contact; for a given pair of surfaces, the coefficient of static friction is usually larger than that of kinetic friction; in some sets the two coefficients are equal, such as teflon-on-teflon.
Most dry materials in combination have friction coefficient values between 0.3 and 0.6. Values outside this range are rarer, but teflon, for example, can have a coefficient as low as 0.04. A value of zero would mean no friction at all, an elusive property. Rubber in contact with other surfaces can yield friction coefficients from 1 to 2. Occasionally it is maintained that μ is always < 1, but this is not true. While in most relevant applications μ < 1, a value above 1 merely implies that the force required to slide an object along the surface is greater than the normal force of the surface on the object. For example, silicone rubber or acrylic rubber-coated surfaces have a coefficient of friction that can be substantially larger than 1.
While it is often stated that the COF is a "material property," it is better categorized as a "system property." Unlike true material properties (such as conductivity, dielectric constant, yield strength), the COF for any two materials depends on system variables like temperature, velocity, atmosphere and also what are now popularly described as aging and deaging times; as well as on geometric properties of the interface between the materials, namely surface structure.[1] For example, a copper pin sliding against a thick copper plate can have a COF that varies from 0.6 at low speeds (metal sliding against metal) to below 0.2 at high speeds when the copper surface begins to melt due to frictional heating. The latter speed, of course, does not determine the COF uniquely; if the pin diameter is increased so that the frictional heating is removed rapidly, the temperature drops, the pin remains solid and the COF rises to that of a 'low speed' test.[citation needed]
Approximate coefficients of friction
| Materials | Static Friction, | Kinetic/Sliding Friction, | |||
|---|---|---|---|---|---|
| Dry and clean | Lubricated | Dry and clean | Lubricated | ||
| Aluminium | Steel | 0.61[25] | 0.47[25] | ||
| Aluminium | Aluminium | 1.05–1.35[25] | 0.3[25] | 1.4[25]–1.5[26] | |
| Gold | Gold | 2.5[26] | |||
| Platinum | Platinum | 1.2[25] | 0.25[25] | 3.0[26] | |
| Silver | Silver | 1.4[25] | 0.55[25] | 1.5[26] | |
| Alumina ceramic | Silicon nitride ceramic | 0.004 (wet)[27] | |||
| BAM (Ceramic alloy AlMgB14) | Titanium boride (TiB2) | 0.04–0.05[28] | 0.02[29][30] | ||
| Brass | Steel | 0.35–0.51[25] | 0.19[25] | 0.44[25] | |
| Cast iron | Copper | 1.05[25] | 0.29[25] | ||
| Cast iron | Zinc | 0.85[25] | 0.21[25] | ||
| Concrete | Rubber | 1.0 | 0.30 (wet) | 0.6–0.85[25] | 0.45–0.75 (wet)[25] |
| Concrete | Wood | 0.62[25][31] | |||
| Copper | Glass | 0.68[32] | 0.53[32] | ||
| Copper | Steel | 0.53[32] | 0.36[25][32] | 0.18[32] | |
| Glass | Glass | 0.9–1.0[25][32] | 0.005–0.01[32] | 0.4[25][32] | 0.09–0.116[32] |
| Human synovial fluid | Human cartilage | 0.01[33] | 0.003[33] | ||
| Ice | Ice | 0.02–0.09[34] | |||
| Polyethene | Steel | 0.2[25][34] | 0.2[25][34] | ||
| PTFE (Teflon) | PTFE (Teflon) | 0.04[25][34] | 0.04[25][34] | 0.04[25] | |
| Steel | Ice | 0.03[34] | |||
| Steel | PTFE (Teflon) | 0.04[25]−0.2[34] | 0.04[25] | 0.04[25] | |
| Steel | Steel | 0.74[25]−0.80[34] | 0.005–0.23[32][34] | 0.42–0.62[25][32] | 0.029–0.19[32] |
| Wood | Metal | 0.2–0.6[25][31] | 0.2 (wet)[25][31] | 0.49[32] | 0.075[32] |
| Wood | Wood | 0.25–0.62[25][31][32] | 0.2 (wet)[25][31] | 0.32–0.48[32] | 0.067–0.167[32] |
Under certain conditions some materials have very low friction coefficients. An example is (highly ordered pyrolytic) graphite which can have a friction coefficient below 0.01.[35] This ultralow-friction regime is called superlubricity.
Static friction
Static friction is friction between two or more solid objects that are not moving relative to each other. For example, static friction can prevent an object from sliding down a sloped surface. The coefficient of static friction, typically denoted as μs, is usually higher than the coefficient of kinetic friction. Static friction is considered to arise as the result of surface roughness features across multiple length scales at solid surfaces. These features, known as asperities are present down to nano-scale dimensions and result in true solid to solid contact existing only at a limited number of points accounting for only a fraction of the apparent or nominal contact area.[36] The linearity between applied load and true contact area, arising from asperity deformation, gives rise to the linearity between static frictional force and normal force, found for typical Amonton–Coulomb type friction.[37]
The static friction force must be overcome by an applied force before an object can move. The maximum possible friction force between two surfaces before sliding begins is the product of the coefficient of static friction and the normal force: . When there is no sliding occurring, the friction force can have any value from zero up to . Any force smaller than attempting to slide one surface over the other is opposed by a frictional force of equal magnitude and opposite direction. Any force larger than overcomes the force of static friction and causes sliding to occur. The instant sliding occurs, static friction is no longer applicable—the friction between the two surfaces is then called kinetic friction. However, an apparent static friction can be observed even in the case when the true static friction is zero.[38]
An example of static friction is the force that prevents a car wheel from slipping as it rolls on the ground. Even though the wheel is in motion, the patch of the tire in contact with the ground is stationary relative to the ground, so it is static rather than kinetic friction.
The maximum value of static friction, when motion is impending, is sometimes referred to as limiting friction,[39] although this term is not used universally.[3]
Kinetic friction
Kinetic friction, also known as dynamic friction or sliding friction, occurs when two objects are moving relative to each other and rub together (like a sled on the ground). The coefficient of kinetic friction is typically denoted as μk, and is usually less than the coefficient of static friction for the same materials.[40][41] However, Richard Feynman comments that "with dry metals it is very hard to show any difference."[42] The friction force between two surfaces after sliding begins is the product of the coefficient of kinetic friction and the normal force: . This is responsible for the Coulomb damping of an oscillating or vibrating system.
New models are beginning to show how kinetic friction can be greater than static friction.[43] Kinetic friction is now understood, in many cases, to be primarily caused by chemical bonding between the surfaces, rather than interlocking asperities;[44] however, in many other cases roughness effects are dominant, for example in rubber to road friction.[43] Surface roughness and contact area affect kinetic friction for micro- and nano-scale objects where surface area forces dominate inertial forces.[45]
The origin of kinetic friction at nanoscale can be explained by thermodynamics.[46] Upon sliding, new surface forms at the back of a sliding true contact, and existing surface disappears at the front of it. Since all surfaces involve the thermodynamic surface energy, work must be spent in creating the new surface, and energy is released as heat in removing the surface. Thus, a force is required to move the back of the contact, and frictional heat is released at the front.
Angle of friction
For certain applications, it is more useful to define static friction in terms of the maximum angle before which one of the items will begin sliding. This is called the angle of friction or friction angle. It is defined as:
where θ is the angle from horizontal and μs is the static coefficient of friction between the objects.[47] This formula can also be used to calculate μs from empirical measurements of the friction angle.
Friction at the atomic level
Determining the forces required to move atoms past each other is a challenge in designing nanomachines. In 2008 scientists for the first time were able to move a single atom across a surface, and measure the forces required. Using ultrahigh vacuum and nearly zero temperature (5 K), a modified atomic force microscope was used to drag a cobalt atom, and a carbon monoxide molecule, across surfaces of copper and platinum.[48]
Limitations of the Coulomb model
The Coulomb approximation follows from the assumptions that: surfaces are in atomically close contact only over a small fraction of their overall area; that this contact area is proportional to the normal force (until saturation, which takes place when all area is in atomic contact); and that the frictional force is proportional to the applied normal force, independently of the contact area. The Coulomb approximation is fundamentally an empirical construct. It is a rule-of-thumb describing the approximate outcome of an extremely complicated physical interaction. The strength of the approximation is its simplicity and versatility. Though the relationship between normal force and frictional force is not exactly linear (and so the frictional force is not entirely independent of the contact area of the surfaces), the Coulomb approximation is an adequate representation of friction for the analysis of many physical systems.
When the surfaces are conjoined, Coulomb friction becomes a very poor approximation (for example, adhesive tape resists sliding even when there is no normal force, or a negative normal force). In this case, the frictional force may depend strongly on the area of contact. Some drag racing tires are adhesive for this reason. However, despite the complexity of the fundamental physics behind friction, the relationships are accurate enough to be useful in many applications.
"Negative" coefficient of friction
As of 2012, a single study has demonstrated the potential for an effectively negative coefficient of friction in the low-load regime, meaning that a decrease in normal force leads to an increase in friction. This contradicts everyday experience in which an increase in normal force leads to an increase in friction.[49] This was reported in the journal Nature in October 2012 and involved the friction encountered by an atomic force microscope stylus when dragged across a graphene sheet in the presence of graphene-adsorbed oxygen.[49]
Dry friction and instabilities
Dry friction can induce several types of instabilities in mechanical systems which display a stable behaviour in the absence of friction.[56] These instabilities may be caused by the decrease of the friction force with an increasing velocity of sliding, by material expansion due to heat generation during friction (the thermo-elastic instabilities), or by pure dynamic effects of sliding of two elastic materials (the Adams–Martins instabilities). The latter were originally discovered in 1995 by George G. Adams and João Arménio Correia Martins for smooth surfaces[57][58] and were later found in periodic rough surfaces.[59] In particular, friction-related dynamical instabilities are thought to be responsible for brake squeal and the 'song' of a glass harp,[60][61] phenomena which involve stick and slip, modelled as a drop of friction coefficient with velocity.[62]
A practically important case is the self-oscillation of the strings of bowed instruments such as the violin, cello, hurdy-gurdy, erhu, etc.
A connection between dry friction and flutter instability in a simple mechanical system has been discovered,[63] watch the movie for more details.
Frictional instabilities can lead to the formation of new self-organized patterns (or "secondary structures") at the sliding interface, such as in-situ formed tribofilms which are utilized for the reduction of friction and wear in so-called self-lubricating materials.[64]
Fluid friction
Fluid friction occurs between fluid layers that are moving relative to each other. This internal resistance to flow is named viscosity. In everyday terms, the viscosity of a fluid is described as its "thickness". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity. The less viscous the fluid, the greater its ease of deformation or movement.
All real fluids (except superfluids) offer some resistance to shearing and therefore are viscous. For teaching and explanatory purposes it is helpful to use the concept of an inviscid fluid or an ideal fluid which offers no resistance to shearing and so is not viscous.
Lubricated friction
Lubricated friction is a case of fluid friction where a fluid separates two solid surfaces. Lubrication is a technique employed to reduce wear of one or both surfaces in close proximity moving relative to each another by interposing a substance called a lubricant between the surfaces.
In most cases the applied load is carried by pressure generated within the fluid due to the frictional viscous resistance to motion of the lubricating fluid between the surfaces. Adequate lubrication allows smooth continuous operation of equipment, with only mild wear, and without excessive stresses or seizures at bearings. When lubrication breaks down, metal or other components can rub destructively over each other, causing heat and possibly damage or failure.
Skin friction
Skin friction arises from the interaction between the fluid and the skin of the body, and is directly related to the area of the surface of the body that is in contact with the fluid. Skin friction follows the drag equation and rises with the square of the velocity.
Skin friction is caused by viscous drag in the boundary layer around the object. There are two ways to decrease skin friction: the first is to shape the moving body so that smooth flow is possible, like an airfoil. The second method is to decrease the length and cross-section of the moving object as much as is practicable.
Internal friction
Internal friction is the force resisting motion between the elements making up a solid material while it undergoes deformation.
Plastic deformation in solids is an irreversible change in the internal molecular structure of an object. This change may be due to either (or both) an applied force or a change in temperature. The change of an object's shape is called strain. The force causing it is called stress.
Elastic deformation in solids is reversible change in the internal molecular structure of an object. Stress does not necessarily cause permanent change. As deformation occurs, internal forces oppose the applied force. If the applied stress is not too large these opposing forces may completely resist the applied force, allowing the object to assume a new equilibrium state and to return to its original shape when the force is removed. This is known as elastic deformation or elasticity.
Other types of friction
Rolling resistance
Rolling resistance is the force that resists the rolling of a wheel or other circular object along a surface caused by deformations in the object or surface. Generally the force of rolling resistance is less than that associated with kinetic friction.[66] Typical values for the coefficient of rolling resistance are 0.001.[67] One of the most common examples of rolling resistance is the movement of motor vehicle tires on a road, a process which generates heat and sound as by-products.[68]
Braking friction
Any wheel equipped with a brake is capable of generating a large retarding force, usually for the purpose of slowing and stopping a vehicle or piece of rotating machinery. Braking friction differs from rolling friction because the coefficient of friction for rolling friction is small whereas the coefficient of friction for braking friction is designed to be large by choice of materials for brake pads.
Triboelectric effect
Rubbing dissimilar materials against one another can cause a build-up of electrostatic charge, which can be hazardous if flammable gases or vapours are present. When the static build-up discharges, explosions can be caused by ignition of the flammable mixture.
Belt friction
Belt friction is a physical property observed from the forces acting on a belt wrapped around a pulley, when one end is being pulled. The resulting tension, which acts on both ends of the belt, can be modeled by the belt friction equation.
In practice, the theoretical tension acting on the belt or rope calculated by the belt friction equation can be compared to the maximum tension the belt can support. This helps a designer of such a rig to know how many times the belt or rope must be wrapped around the pulley to prevent it from slipping. Mountain climbers and sailing crews demonstrate a standard knowledge of belt friction when accomplishing basic tasks.
Reducing friction
Devices
Devices such as wheels, ball bearings, roller bearings, and air cushion or other types of fluid bearings can change sliding friction into a much smaller type of rolling friction.
Many thermoplastic materials such as nylon, HDPE and PTFE are commonly used in low friction bearings. They are especially useful because the coefficient of friction falls with increasing imposed load.[69] For improved wear resistance, very high molecular weight grades are usually specified for heavy duty or critical bearings.
Lubricants
A common way to reduce friction is by using a lubricant, such as oil, water, or grease, which is placed between the two surfaces, often dramatically lessening the coefficient of friction. The science of friction and lubrication is called tribology. Lubricant technology is when lubricants are mixed with the application of science, especially to industrial or commercial objectives.
Superlubricity, a recently discovered effect, has been observed in graphite: it is the substantial decrease of friction between two sliding objects, approaching zero levels. A very small amount of frictional energy would still be dissipated.
Lubricants to overcome friction need not always be thin, turbulent fluids or powdery solids such as graphite and talc; acoustic lubrication actually uses sound as a lubricant.
Another way to reduce friction between two parts is to superimpose micro-scale vibration to one of the parts. This can be sinusoidal vibration as used in ultrasound-assisted cutting or vibration noise, known as dither.
Energy of friction
According to the law of conservation of energy, no energy is destroyed due to friction, though it may be lost to the system of concern. Energy is transformed from other forms into thermal energy. A sliding hockey puck comes to rest because friction converts its kinetic energy into heat which raises the thermal energy of the puck and the ice surface. Since heat quickly dissipates, many early philosophers, including Aristotle, wrongly concluded that moving objects lose energy without a driving force.
When an object is pushed along a surface along a path C, the energy converted to heat is given by a line integral, in accordance with the definition of work
where
- is the friction force,
- is the vector obtained by multiplying the magnitude of the normal force by a unit vector pointing against the object's motion,
- is the coefficient of kinetic friction, which is inside the integral because it may vary from location to location (e.g. if the material changes along the path),
- is the position of the object.
Energy lost to a system as a result of friction is a classic example of thermodynamic irreversibility.
Work of friction
In the reference frame of the interface between two surfaces, static friction does no work, because there is never displacement between the surfaces. In the same reference frame, kinetic friction is always in the direction opposite the motion, and does negative work.[70] However, friction can do positive work in certain frames of reference. One can see this by placing a heavy box on a rug, then pulling on the rug quickly. In this case, the box slides backwards relative to the rug, but moves forward relative to the frame of reference in which the floor is stationary. Thus, the kinetic friction between the box and rug accelerates the box in the same direction that the box moves, doing positive work.[71]
The work done by friction can translate into deformation, wear, and heat that can affect the contact surface properties (even the coefficient of friction between the surfaces). This can be beneficial as in polishing. The work of friction is used to mix and join materials such as in the process of friction welding. Excessive erosion or wear of mating sliding surfaces occurs when work due to frictional forces rise to unacceptable levels. Harder corrosion particles caught between mating surfaces in relative motion (fretting) exacerbates wear of frictional forces. As surfaces are worn by work due to friction, fit and surface finish of an object may degrade until it no longer functions properly.[72] For example, bearing seizure or failure may result from excessive wear due to work of friction.
Applications
Friction is an important factor in many engineering disciplines.
Transportation
- Automobile brakes inherently rely on friction, slowing a vehicle by converting its kinetic energy into heat. Incidentally, dispersing this large amount of heat safely is one technical challenge in designing brake systems. Disk brakes rely on friction between a disc and brake pads that are squeezed transversely against the rotating disc. In drum brakes, brake shoes or pads are pressed outwards against a rotating cylinder (brake drum) to create friction. Since braking discs can be more efficiently cooled than drums, disc brakes have better stopping performance.[73]
- Rail adhesion refers to the grip wheels of a train have on the rails, see Frictional contact mechanics.
- Road slipperiness is an important design and safety factor for automobiles[74]
- Split friction is a particularly dangerous condition arising due to varying friction on either side of a car.
- Road texture affects the interaction of tires and the driving surface.
Measurement
- A tribometer is an instrument that measures friction on a surface.
- A profilograph is a device used to measure pavement surface roughness.
Household usage
- Friction is used to heat and ignite matchsticks (friction between the head of a matchstick and the rubbing surface of the match box).[75]
- Sticky pads are used to prevent object from slipping off smooth surfaces by effectively increasing the friction coefficient between the surface and the object.
See also
https://en.wikipedia.org/wiki/Friction
Friction torque is the torque caused by the frictional force that occurs when two objects in contact move. Like all torques, it is a rotational force which may be measured in newton metres or pounds-feet.
Engineering[edit]
Friction torque can be disruptive in engineering. There are a variety of measures engineers may choose to take to eliminate these disruptions. Ball bearings are an example of an attempt to minimize the friction torque.
Friction torque can also be an asset in engineering. Bolts and nuts, or screws are often designed to be fastened with a given amount of torque, where the friction is adequate during use or operation for the bolt, nut or screw to remain safely fastened. This is true with such applications as lug nuts retaining wheels to vehicles, or equipment subjected to vibration with sufficiently well attached bolts, nuts or screws to prevent the vibration from shaking them loose.
Examples[edit]
- When a cyclist applies the brake to his/her forward wheel, the bike tips forwards due to the frictional torque between the wheel and the ground.
- When a golf ball hits the ground it begins to spin in part because of the friction torque applied to the golf ball from the friction between the golf ball and the ground.
See also[edit]
Transient friction loading, also known as TFL, is the mechanical stress induced on an object due to transient or vibrational frictional forces.[1]
Examples[edit]
A classic example of TFL is the wooden block sliding over an unlevel, non-planar surface.[2] Due to the transient response of the contact force, the resultant frictional force is noisy. The induced stress is concisely described as TFL.
Another example of TFL is the internal stresses on a hydraulic ram operating in a vibrational environment.[3] Due to the oscillatory nature of the acceleration experienced by the ram, in n-dimensions, the resulting frictional response is described as transient friction loading.
See also[edit]
An adhesion railway relies on adhesion traction to move the train. Adhesion traction is the friction between the drive wheels and the steel rail.[1] The term "adhesion railway" is used only when it is necessary to distinguish adhesion railways from railways moved by other means, such as by a stationary engine pulling on a cable attached to the cars or by railways that are moved by a pinion meshing with a rack.
The friction between the wheels and rails occurs in the wheel-rail interface or contact patch. The traction force, the braking forces and the centering forces, all contribute to stable running. However, running friction increases costs by requiring higher fuel consumption and by increasing the maintenance needed to address fatigue (material) damage, wear on rail heads and on the wheel rims and rail movement from traction and braking forces.
With perfect rolling contact between the wheel and rail, this coning behaviour manifests itself as a swaying of the train from side to side. In practice, the swaying is damped out below a critical speed, but is amplified by the forward motion of the train above the critical speed. This lateral swaying is known as hunting oscillation. The phenomenon of hunting was known by the end of the 19th century, although the cause was not fully understood until the 1920s and measures to eliminate it were not taken until the late 1960s. The limitation on maximum speed was imposed not by raw power but by encountering an instability in the motion.
The kinematic description of the motion of tapered treads on the two rails is insufficient to describe hunting well enough to predict the critical speed. It is necessary to deal with the forces involved. There are two phenomena which must be taken into account. The first is the inertia of the wheelsets and vehicle bodies, giving rise to forces proportional to acceleration; the second is the distortion of the wheel and track at the point of contact, giving rise to elastic forces. The kinematic approximation corresponds to the case which is dominated by contact forces.
An analysis of the kinematics of the coning action yields an estimate of the wavelength of the lateral oscillation:[6]
where d is the wheel gauge, r is the nominal wheel radius and k is the taper of the treads. For a given speed, the longer the wavelength and the lower the inertial forces will be, so the more likely it is that the oscillation will be damped out. Since the wavelength increases with reducing taper, increasing the critical speed requires the taper to be reduced, which implies a large minimum radius of turn.
A more complete analysis, taking account of the actual forces acting, yields the following result for the critical speed of a wheelset:[clarification needed]
where W is the axle load for the wheelset, a is a shape factor related to the amount of wear on the wheel and rail, C is the moment of inertia of the wheelset perpendicular to the axle, m is the wheelset mass.
The result is consistent with the kinematic result in that the critical speed depends inversely on the taper. It also implies that the weight of the rotating mass should be minimised compared with the weight of the vehicle. The wheel gauge appears in both the numerator and denominator, implying that it has only a second-order effect on the critical speed.
The true situation is much more complicated, as the response of the vehicle suspension must be taken into account. Restraining springs, opposing the yaw motion of the wheelset, and similar restraints on bogies, may be used to raise the critical speed further. However, in order to achieve the highest speeds without encountering instability, a significant reduction in wheel taper is necessary. For example, taper on Shinkansen wheel treads was reduced to 1:40 (when the Shinkansen first ran) for both stability at high speeds and performance on curves.[7] That said, from the 1980s onwards, the Shinkansen engineers developed an effective taper of 1:16 by tapering the wheel with multiple arcs, so that the wheel could work effectively both at high speed as well as at sharper curves.[7]
Forces on wheels, creep[edit]
The behaviour of vehicles moving on adhesion railways is determined by the forces arising between two surfaces in contact. This may appear trivially simple from a superficial glance but it becomes extremely complex when studied to the depth necessary to predict useful results.
The first error to address is the assumption that wheels are round. A glance at the tyres of a parked car will immediately show that this is not true: the region in contact with the road is noticeably flattened, so that the wheel and road conform to each other over a region of contact. If this were not the case, the contact stress of a load being transferred through a line contact would be infinite. Rails and railway wheels are much stiffer than pneumatic tyres and tarmac but the same distortion takes place at the region of contact. Typically, the area of contact is elliptical, of the order of 15 mm across.[8]
The distortion in the wheel and rail is small and localised but the forces which arise from it are large. In addition to the distortion due to the weight, both wheel and rail distort when braking and accelerating forces are applied and when the vehicle is subjected to side forces. These tangential forces cause distortion in the region where they first come into contact, followed by a region of slippage. The net result is that, during traction, the wheel does not advance as far as would be expected from rolling contact but, during braking, it advances further. This mix of elastic distortion and local slipping is known as "creep" (not to be confused with the creep of materials under constant load). The definition of creep[9] in this context is:
In analysing the dynamics of wheelsets and complete rail vehicles, the contact forces can be treated as linearly dependent on the creep [10](Joost Jacques Kalker's linear theory, valid for small creepage) or more advanced theories can be used from frictional contact mechanics.
The forces which result in directional stability, propulsion and braking may all be traced to creep. It is present in a single wheelset and will accommodate the slight kinematic incompatibility introduced by coupling wheelsets together, without causing gross slippage, as was once feared.
Provided the radius of turn is sufficiently great (as should be expected for express passenger services), two or three linked wheelsets should not present a problem. However, 10 drive wheels (5 main wheelsets) are usually associated with heavy freight locomotives.
Getting the train moving[edit]
The adhesion railway relies on a combination of friction and weight to start a train. The heaviest trains require the highest friction and the heaviest locomotive. The friction can vary a great deal, but it was known on early railways that sand helped, and it is still used today, even on locomotives with modern traction controls. To start the heaviest trains, the locomotive must be as heavy as can be tolerated by the bridges along the route and the track itself. The weight of the locomotive must be shared equally by the wheels that are driven, with no weight transfer as the starting force builds. The wheels must turn with a steady driving force on the very small contact area of about 1 cm2 between each wheel and the top of the rail. The top of the rail must be dry, with no man-made or weather-related contamination, such as oil or rain. Friction-enhancing sand or an equivalent is needed. The driving wheels must turn faster than the locomotive is moving (known as creep control) to generate the maximum coefficient of friction, and the axles must be driven independently with their own controller because different axles will see different conditions. The maximum available friction occurs when the wheels are slipping/creeping. If contamination is unavoidable the wheels must be driven with more creep because, although friction is lowered with contamination, the maximum obtainable under those conditions occurs at greater values of creep.[11] The controllers must respond to different friction conditions along the track.
Some of the starting requirements were a challenge for steam locomotive designers – "sanding systems that did not work, controls that were inconvenient to operate, lubrication that spewed oil everywhere, drains that wetted the rails, and so on.."[12] Others had to wait for modern electric transmissions on diesel and electric locomotives.
The frictional force on the rails and the amount of wheel slip drops steadily as the train picks up speed.
A driven wheel does not roll freely but turns faster than the corresponding locomotive velocity. The difference between the two is known as the "slip velocity". "Slip" is the "slip velocity" compared to the "vehicle velocity". When a wheel rolls freely along the rail the contact patch is in what is known as a "stick" condition. If the wheel is driven or braked the proportion of the contact patch with the "stick" condition gets smaller and a gradually increasing proportion is in what is known as a "slip condition". This diminishing "stick" area and increasing "slip" area supports a gradual increase in the traction or braking torque that can be sustained as the force at the wheel rim increases until the whole area is "slip".[13] The "slip" area provides the traction. During the transition from the "all-stick" no-torque to the "all-slip" condition the wheel has had a gradual increase in slip, also known as creep and creepage. High adhesion locomotives control wheel creep to give maximum effort when starting and pulling a heavy train slowly.
Slip is the additional speed that the wheel has and creep is the slip level divided by the locomotive speed. These parameters are those that are measured and which go into the creep controller.[14]
Sanding[edit]
On an adhesion railway, most locomotives will have a sand containment vessel. Properly dried sand can be dropped onto the rail to improve traction under slippery conditions. The sand is most often applied using compressed air via tower, crane, silo or train.[15][16] When an engine slips, particularly when starting a heavy train, sand applied at the front of the driving wheels greatly aids in tractive effort causing the train to "lift", or to commence the motion intended by the engine driver.
Sanding however also has some negative effects. It can cause a "sandfilm", which consists of crushed sand, that is compressed to a film on the track where the wheels make contact. Together with some moisture on the track, which acts as a light adhesive and keeps the applied sand on the track, the wheels "bake" the crushed sand into a more solid layer of sand. Because the sand is applied to the first wheels on the locomotive, the following wheels may run, at least partially and for a limited time, on a layer of sand (sandfilm). While traveling this means that electric locomotives may lose contact to the track-ground, causing the locomotive to create electromagnetic interference and currents through the couplers. In standstill, when the locomotive is parked, track circuits may detect an empty track because the locomotive is electrically isolated from the track.[17]
See also[edit]
https://en.wikipedia.org/wiki/Adhesion_railway#Factor_of_adhesion
The stick-slip phenomenon, also known as the slip-stick phenomenon or simply stick-slip, is the spontaneous jerking motion that can occur while two objects are sliding over each other.
https://en.wikipedia.org/wiki/Stick-slip_phenomenon
Chemical force microscopy (CFM) is a variation of atomic force microscopy (AFM) which has become a versatile tool for characterization of materials surfaces. With AFM, structural morphology is probed using simple tapping or contact modes that utilize van der Waals interactions between tip and sample to maintain a constant probe deflection amplitude (constant force mode) or maintain height while measuring tip deflection (constant height mode). CFM, on the other hand, uses chemical interactions between functionalized probe tip and sample. Choice chemistry is typically gold-coated tip and surface with R-SH thiols attached, R being the functional groups of interest. CFM enables the ability to determine the chemical nature of surfaces, irrespective of their specific morphology, and facilitates studies of basic chemical bonding enthalpy and surface energy. Typically, CFM is limited by thermal vibrations within the cantilever holding the probe. This limits force measurement resolution to ~1 pN which is still very suitable considering weak COOH/CH3 interactions are ~20 pN per pair.[1][2]Hydrophobicity is used as the primary example throughout this consideration of CFM, but certainly any type of bonding can be probed with this method.
https://en.wikipedia.org/wiki/Chemical_force_microscopy#Frictional_force_mapping
Wind tunnels are large tubes with air blowing through them which are used to replicate the interaction between air and an object flying through the air or moving along the ground. Researchers use wind tunnels to learn more about how an aircraft will fly. NASA uses wind tunnels to test scale models of aircraft and spacecraft. Some wind tunnels are large enough to contain full-size versions of vehicles. The wind tunnel moves air around an object, making it seem as if the object is flying.
Most of the time, large powerful fans blow air through the tube. The object being tested is held securely inside the tunnel so that it remains stationary. The object can be an aerodynamic test object such as a cylinder or an airfoil, an individual component, a small model of the vehicle, or a full-sized vehicle. The air moving around the stationary object shows what would happen if the object was moving through the air. The motion of the air can be studied in different ways; smoke or dye can be placed in the air and can be seen as it moves around the object. Coloured threads can also be attached to the object to show how the air moves around it. Special instruments can often be used to measure the force of the air exerted against the object.
The earliest wind tunnels were invented towards the end of the 19th century, in the early days of aeronautic research, when many attempted to develop successful heavier-than-air flying machines. The wind tunnel was envisioned as a means of reversing the usual paradigm: instead of the air standing still and an object moving at speed through it, the same effect would be obtained if the object stood still and the air moved at speed past it. In that way a stationary observer could study the flying object in action, and could measure the aerodynamic forces being imposed on it.
The development of wind tunnels accompanied the development of the airplane. Large wind tunnels were built during World War II. Wind tunnel testing was considered of strategic importance during the Cold War development of supersonic aircraft and missiles.
Later, wind tunnel study came into its own: the effects of wind on man-made structures or objects needed to be studied when buildings became tall enough to present large surfaces to the wind, and the resulting forces had to be resisted by the building's internal structure. Determining such forces was required before building codes could specify the required strength of such buildings and such tests continue to be used for large or unusual buildings.
Circa the 1960s,[1] wind tunnel testing was applied to automobiles, not so much to determine aerodynamic forces per se but more to determine ways to reduce the power required to move the vehicle on roadways at a given speed. In these studies, the interaction between the road and the vehicle plays a significant role, and this interaction must be taken into consideration when interpreting the test results. In an actual situation the roadway is moving relative to the vehicle but the air is stationary relative to the roadway, but in the wind tunnel the air is moving relative to the roadway, while the roadway is stationary relative to the test vehicle. Some automotive-test wind tunnels have incorporated moving belts under the test vehicle in an effort to approximate the actual condition, and very similar devices are used in wind tunnel testing of aircraft take-off and landing configurations.
Wind tunnel testing of sporting equipment has also been prevalent over the years, including golf clubs, golf balls, Olympic bobsleds, Olympic cyclists, and race car helmets. Helmet aerodynamics is particularly important in open cockpit race cars (Indycar, Formula One). Excessive lift forces on the helmet can cause considerable neck strain on the driver, and flow separation on the back side of the helmet can cause turbulent buffeting and thus blurred vision for the driver at high speeds.[2]
The advances in computational fluid dynamics (CFD) modelling on high-speed digital computers has reduced the demand for wind tunnel testing.
https://en.wikipedia.org/wiki/Wind_tunnel
A propeller is a device with a rotating hub and radiating blades that are set at a pitch to form a helical spiral, that, when rotated, exerts linear thrust upon a working fluid, such as water or air.[1] Propellers are used to pump fluid through a pipe or duct, or to create thrust to propel a boat through water or an aircraft through air. The blades are specially shaped so that their rotational motion through the fluid causes a pressure difference between the two surfaces of the blade by Bernoulli's principle which exerts force on the fluid.[2] Most marine propellers are screw propellers with helical blades rotating on a propeller shaft with an approximately horizontal axis.[3]
https://en.wikipedia.org/wiki/Propeller#Marine_propeller_cavitation
An axial compressor is a gas compressor that can continuously pressurize gases. It is a rotating, airfoil-based compressor in which the gas or working fluid principally flows parallel to the axis of rotation, or axially. This differs from other rotating compressors such as centrifugal compressor, axi-centrifugal compressors and mixed-flow compressors where the fluid flow will include a "radial component" through the compressor. The energy level of the fluid increases as it flows through the compressor due to the action of the rotor blades which exert a torque on the fluid. The stationary blades slow the fluid, converting the circumferential component of flow into pressure. Compressors are typically driven by an electric motor or a steam or a gas turbine.[1]
https://en.wikipedia.org/wiki/Axial_compressor
In fluid dynamics, stagnation pressure (or pitot pressure) is the static pressure at a stagnation point in a fluid flow.[1] At a stagnation point the fluid velocity is zero. In an incompressible flow, stagnation pressure is equal to the sum of the free-stream static pressure and the free-stream dynamic pressure.[2]
Stagnation pressure is sometimes referred to as pitot pressure because it is measured using a pitot tube.
Compressible flow[edit]
Stagnation pressure is the static pressure a gas retains when brought to rest isentropically from Mach number M.[6]
or, assuming an isentropic process, the stagnation pressure can be calculated from the ratio of stagnation temperature to static temperature:
where:
- is the stagnation pressure
- is the static pressure
- is the stagnation temperature
- is the static temperature
- is the ratio of specific heats
The above derivation holds only for the case when the gas is assumed to be calorically perfect (specific heats and the ratio of the specific heats are assumed to be constant with temperature).
https://en.wikipedia.org/wiki/Stagnation_pressure
In incompressible fluid dynamics dynamic pressure (indicated with , or Q, and sometimes called velocity pressure) is the quantity defined by:[1]
where (using SI units):
dynamic pressure in pascals (i.e., kg/m⋅s2), fluid mass density (e.g. in kg/m3, in SI units), flow speed in m/s.
It can be thought of as the fluid's kinetic energy per unit volume.
For incompressible flow, the dynamic pressure of a fluid is the difference between its total pressure and static pressure. From Bernoulli's law, dynamic pressure is given by
where and are the total and static pressures, respectively.
https://en.wikipedia.org/wiki/Dynamic_pressure






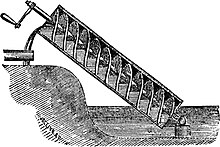
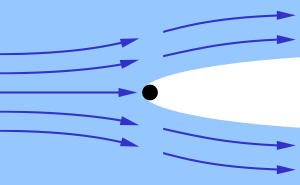






























 , or Q, and sometimes called velocity pressure) is the quantity defined by:
, or Q, and sometimes called velocity pressure) is the quantity defined by:






No comments:
Post a Comment