In physics and geometry, a catenary (US: /ˈkætənɛri/, UK: /kəˈtiːnəri/) is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends.
The catenary curve has a U-like shape, superficially similar in appearance to a parabolic arch, but it is not a parabola.
The curve appears in the design of certain types of arches and as a cross section of the catenoid—the shape assumed by a soap film bounded by two parallel circular rings.
The catenary is also called the alysoid, chainette,[1] or, particularly in the materials sciences, funicular.[2] Rope statics describes catenaries in a classic statics problem involving a hanging rope.[3]
Mathematically, the catenary curve is the graph of the hyperbolic cosine function. The surface of revolution of the catenary curve, the catenoid, is a minimal surface, specifically a minimal surface of revolution. A hanging chain will assume a shape of least potential energy which is a catenary.[4] Galileo Galilei in 1638 discussed the catenary in the book Two New Sciences recognizing that it was different from a parabola. The mathematical properties of the catenary curve were studied by Robert Hooke in the 1670s, and its equation was derived by Leibniz, Huygens and Johann Bernoulli in 1691.
Catenaries and related curves are used in architecture and engineering (e.g., in the design of bridges and arches so that forces do not result in bending moments). In the offshore oil and gas industry, "catenary" refers to a steel catenary riser, a pipeline suspended between a production platform and the seabed that adopts an approximate catenary shape. In the rail industry it refers to the overhead wiring that transfers power to trains. (This often supports a lighter contact wire, in which case it does not follow a true catenary curve.)
In optics and electromagnetics, the hyperbolic cosine and sine functions are basic solutions to Maxwell's equations.[5] The symmetric modes consisting of two evanescent waves would form a catenary shape.[6][7][8]
https://en.wikipedia.org/wiki/Catenary
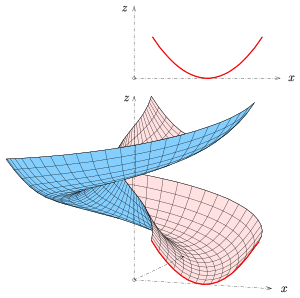
A catenoid is a type of surface, arising by rotating a catenary curve about an axis.[1] It is a minimal surface, meaning that it occupies the least area when bounded by a closed space.[2] It was formally described in 1744 by the mathematician Leonhard Euler.
Soap film attached to twin circular rings will take the shape of a catenoid.[2] Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa.
https://en.wikipedia.org/wiki/Catenoid
In geometry and physics, spinors /spɪnər/ are elements of a complex vector space that can be associated with Euclidean space.[b] Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation.[c] However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms).
https://en.wikipedia.org/wiki/Spinor
The helicoid, after the plane and the catenoid, is the third minimal surface to be known.
https://en.wikipedia.org/wiki/Helicoid
In geometry, a generalized helicoid is a surface in Euclidean space generated by rotating and simultaneously displacing a curve, the profile curve, along a line, its axis. Any point of the given curve is the starting point of a circular helix. If the profile curve is contained in a plane through the axis, it is called the meridian of the generalized helicoid. Simple examples of generalized helicoids are the helicoids. The meridian of a helicoid is a line which intersects the axis orthogonally.
Essential types of generalized helicoids are
- ruled generalized helicoids. Their profile curves are lines and the surfaces are ruled surfaces.
- circular generalized helicoids. Their profile curves are circles.
In mathematics helicoids play an essential role as minimal surfaces. In the technical area generalized helicoids are used for staircases, slides, screws, and pipes.
https://en.wikipedia.org/wiki/Generalized_helicoid
In geometry, Dini's surface is a surface with constant negative curvature that can be created by twisting a pseudosphere.[1] It is named after Ulisse Dini[2] and described by the following parametric equations:[3]
Another description is a helicoid constructed from the tractrix.[4]
https://en.wikipedia.org/wiki/Dini%27s_surface
Wallis's conical edge is a ruled surface given by the parametric equations:
where a, b and c are constants.
Wallis's conical edge is also a kind of right conoid.
Figure 2 shows that the Wallis's conical edge is generated by a moving line.
Wallis's conical edge is named after the English mathematician John Wallis, who was one of the first to use Cartesian methods to study conic sections.[1]
https://en.wikipedia.org/wiki/Wallis%27s_conical_edge
In geometry, a right conoid is a ruled surface generated by a family of straight lines that all intersect perpendicularly to a fixed straight line, called the axis of the right conoid.
Using a Cartesian coordinate system in three-dimensional space, if we take the z-axis to be the axis of a right conoid, then the right conoid can be represented by the parametric equations:
where h(u) is some function for representing the height of the moving line.
https://en.wikipedia.org/wiki/Right_conoid
A tractrix (from the Latin verb trahere "pull, drag"; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a tractor (pulling) point that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1693).[1]
https://en.wikipedia.org/wiki/Tractrix















No comments:
Post a Comment