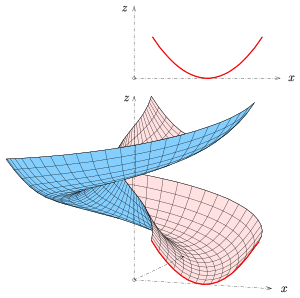
In geometry, a generalized helicoid is a surface in Euclidean space generated by rotating and simultaneously displacing a curve, the profile curve, along a line, its axis. Any point of the given curve is the starting point of a circular helix. If the profile curve is contained in a plane through the axis, it is called the meridian of the generalized helicoid. Simple examples of generalized helicoids are the helicoids. The meridian of a helicoid is a line which intersects the axis orthogonally.
Essential types of generalized helicoids are
- ruled generalized helicoids. Their profile curves are lines and the surfaces are ruled surfaces.
- circular generalized helicoids. Their profile curves are circles.
In mathematics helicoids play an essential role as minimal surfaces. In the technical area generalized helicoids are used for staircases, slides, screws, and pipes.
https://en.wikipedia.org/wiki/Generalized_helicoid
References[edit]
- Elsa Abbena,Simon Salamon,Alfred Gray:Modern Differential Geometry of Curves and Surfaces with Mathematica,3. edition, studies in advanced mathematics, Chapman & Hall, 2006, ISBN 1584884487, p. 470
- E. Kreyszig: Differential Geometry. New York: Dover, p. 88, 1991.
- U. Graf, M. Barner: Darstellende Geometrie. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9, p.218
- K. Strubecker: Vorlesungen über Darstellende Geometrie, Vandenhoek & Ruprecht, Göttingen, 1967, p. 286
No comments:
Post a Comment