In geometry, a Catalan surface, named after the Belgian mathematician Eugène Charles Catalan, is a ruled surface all of whose rulings are parallel to a fixed plane.
A Catalan surface.
https://en.wikipedia.org/wiki/Catalan_surface
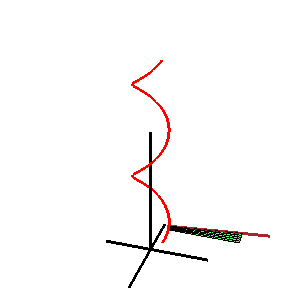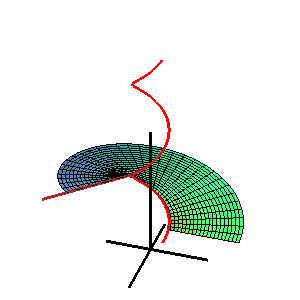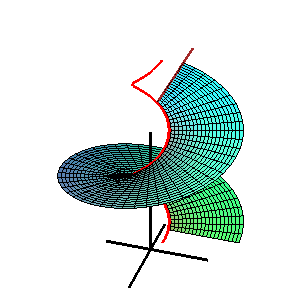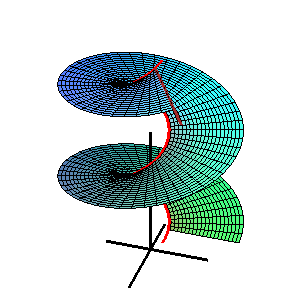
In differential geometry, Catalan's minimal surface is a minimal surface originally studied by Eugène Charles Catalan in 1855.[1]
It has the special property of being the minimal surface that contains a cycloid as a geodesic. It is also swept out by a family of parabolae.[2]
The surface has the mathematical characteristics exemplified by the following parametric equation:[3]
External links[edit]
- Weisstein, Eric W. "Catalan's Surface." From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CatalansSurface.html
- Weiqing Gu, The Library of Surfaces. https://web.archive.org/web/20130317011222/http://www.math.hmc.edu/~gu/curves_and_surfaces/surfaces/catalan.html
Catalan's minimal surface.
https://en.wikipedia.org/wiki/Catalan%27s_minimal_surface


No comments:
Post a Comment